大学物理 机械波习题思考题及答案
大学物理机械波习题附答案
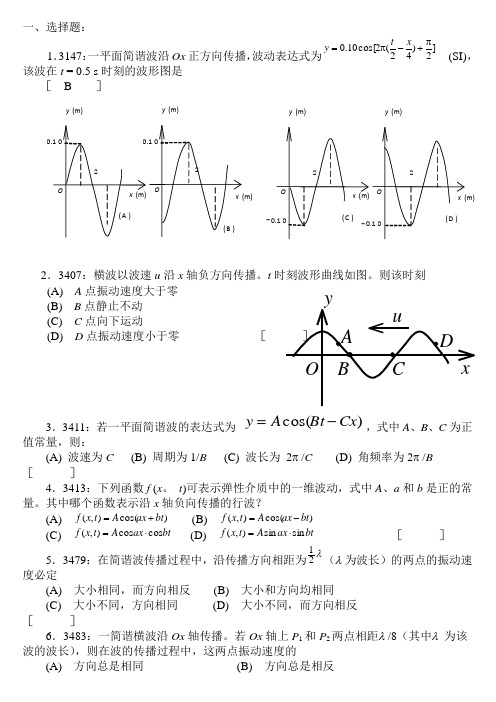
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) btax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C)大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反y (m) y (m) - y (m) y (m)(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长(B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理2,12第十二章思考题

1、机械波的波函数为y = 0.03cos6π(t + 0.01x )上式中的各个物理量均采用国际单位。
该波的振幅、周期和波速分别为多少?该波沿着什么方向传播?【答案:0.03m ;1/3s ;100m/s ,x 轴负方向】详解:该波的振幅、周期和波速分别为m 03.0=Aπ6π2π2==ωT )s (31= (m/s)10001.01==u 由于变量x 前的符号为+,因此该波沿着x 轴负方向传播。
2、已知一列平面简谐波的波函数为y = A cos[ (at -bx ) +α](a 、b 和α均为正常量)则该波的频率、波长、周期和波速分别为多少? 【答案:π2a ;b 2π;a π2;ba 】 详解:将题目所给的平面简谐波的波函数与标准平面简谐波的波函数](cos[ϕω+-=uxt A y比较,即得该平面简谐波的频率、周期和波速分别为π2π2a ==ων a T π21==ν ba bu ==ω该波的波长为buT 2π==λ 3、一列平面简谐波沿x 正方向传播,波函数为]2π)42(π2cos[10.0--=x t y上式中的各个物理量均采用国际单位。
试画出该波在0.5s 时刻的波形图。
【答案:见题解图】详解:在0.5s 时刻的波形方程为]2π)425.0(π2cos[10.0--=x y )2πcos(10.0x -=x 2πcos 10.0= 因此,该时刻的波形图为4、在简谐波传播的过程中,沿传播方向相距为半个波长的两点的振动速度之比等于多少?(设这两点都不在最大位移处) 【答案:-1】详解:根据波长的定义,在简谐波传播的过程中,沿传播方向相距为一个波长的两点振动的相位相同,那么相距为半个波长的两点振动必然相位相同,即它们的速度大小相等、方向相反,如果这两点不处于最大位移处,它们振动速度之比必然等于-1。
5、一列声波在空气中的波长是0.25m ,传播速度是340m/s ,当它进入另一种介质时,波长变成了0.35m ,则它在该介质中的传播速度为多少? 【答案:503m/s 】详解:一列波从一种介质进入另一种介质时,其频率保持不变。
大学物理波动篇机械波复习题及答案课件

种不同的媒质中传播, 在分界面上的 P 点
相遇, 频率n = 200Hz, 振幅A1=A2=2.00 10-
2m, S2 的位相比 S1 落后 /2。在媒质1中
波速 u1= 800 m s-1, 在媒质2中波速 u2=
1000 m s-1 , S1P=r1=4.00m,
静止的点。求两波的波长和两波源间最 小位相差。
o
S1
S2
x
d
29
解: 设S1 和 S2的振动初位相分别为 1 和 2在 x1点两波引起的振动位相差
2 2 d x1/ 1 2 x1 / 2k 1
2 1 2 d 2 x1/ 2k 1 (1)
在x2点两波引起的振动位相差
2 2 d x2/ 1 2 x2 / 2k 3
波分别通过图中的 o1和 o2 点,通过 o1 点 的简谐波在 M1M2 平面反射后,与通过 o2 点的简谐波在 P 点相遇,假定波在M1M2平 面反射时有半波损失,o1 和 o2 两点的振动
方程为,y10=Acos(2t) 和 y20=Acos(2t) , 且 o1m+mp=16,o2P = 6 (为波长) 求:
(A)波速为C/B; (B)周期为 1/B;
(C)波长为C/2 ; (D)圆频率为 B。
[]
5
5.一平面简谐波沿正方相传播, t=0 时刻的
波形如图所示, 则 P 处质点的振动在 t=0 时
刻的旋转矢量图是
y
u
A
x
o
P
( A)
o
x
A
(B)
o
x
A
(C ) A o
x
A
(D)
大学物理机械波习题附问题详解
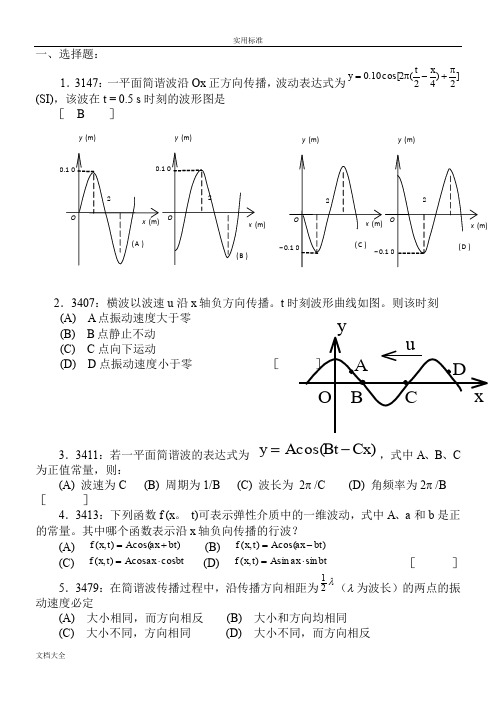
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt axA t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C) 大小不同,方向相同(D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理课后习题答案第五章

大学物理课后习题答案第五章-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第五章 机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示.[解答](1)与标准波动方程2cos()xy A t πωλ=-比较得:2π/λ = 0.6,因此波长为:λ = 10.47(m);圆频率为:ω = 10π,频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv = 52.36(m·s -1). 且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为0.03cos(4)2A y t ππ=-(m).试求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:cos[()]Ax x y A t uωϕ-=-+;即 0.050.03cos[4()]0.22x y t ππ-=--= 0.03cos[4π(t – 5x ) + π/2].(2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2] = 0.03cos(4πt - π/2).5.3 已知平面波波源的振动表达式为20 6.010sin 2y t π-=⨯(m).求距波源5m处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为:26.010sin ()2xy t u π-=⨯- 50.06sin()24t ππ=-,位相差为 Δφ = 5π/4(rad).5.4 有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少?[解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m . 由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π.当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2.原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:0.03cos[50()]2x y t u ππ=-+= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.5.5 一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求:(1)P 点的振动表达式; (2)波动方程; (3)画出O 点的振动曲线. [解答](1)设P 点的振动方程为 y P = A cos(ωt + φ),其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m), 所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程; (2)画出x = λ/2处质点的振动曲线; (3)图中波线上a 和b 两点的位相差φa – φb 为多少?[解答](1)设此波的波动方程为:图5.5cos[2()]t xy A T πϕλ=++,当t = T /4时的波形方程为:cos(2)2x y A ππϕλ=++sin(2)xA πϕλ=-+.在x = 0处y = 0,因此得sin φ = 0, 解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0.因此波动方程为:cos 2()t xy A T πλ=+.(2)在x = λ/2处质点的振动方程为:cos(2)cos 2t t y A A T Tπππ=+=-, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为 cos(2)2a t y A T ππ=+; x b = λ处的质点的振动方程为 cos(22)b t y A Tππ=+. 波线上a 和b 两点的位相差φa – φb = -3π/2.5.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点( 2)画出t = 4.2s 时的波形曲线. [解答]波的波动方程可化为:y = A cos2π(2t – x ), 与标准方程cos[2()]t xy A T πϕλ=-+比较, 可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1.(1)当t = 4.2s 时的波形方程为y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…),各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8 一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示.(1)写出时x = 0处质点的振动方程; (2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1). (1)设x = 0处的质点的振动方程为y = A cos(ωt + φ),其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3). (2)波的表达式为:cos[2()]t xy A T πϕλ=-+ cos[()]23t x ππ=-+. (3)t = 1s 时刻的波形方程为 5cos()26y x ππ=-,波形曲线如图所示.5.9 在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.[解答] 设波动方程为:cos[2()]t xy A T πϕλ=-+,那么A 和B 两点的振动方程分别为:cos[2()]A A xt y A T πϕλ=-+,cos[2()]B B xt y A T πϕλ=-+.两点之间的位相差为:2(2)6B A x x πππλλ---=-,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1).5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程; (2)如以距A 点5m 处的B 点为坐标原点,写出波动方程;(3)写出传播方向上B ,C ,D 点的振动方程.[解答](1)以A 点为坐标原点,波动方程为3cos 4()3cos(4)5x xy t t u πππ=+=+.(2)以B 点为坐标原点,波动方程为3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-.(3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为3cos 4()3cos(4)B B xy t t u πππ=+=-,33cos 4()3cos(4)5C C x y t t u πππ=+=-,93cos 4()3cos(4)5D D x y t t u πππ=+=+.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量. [解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1),波的平均能量密度为:2212w A ρω== 158(J·m -3),平均能流密度为:I wu == 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5.12 一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强此时声强相当于多少分贝已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1),声波的平均能量密度为:2212w A ρω== 6.37×10-6(J·m -3),平均能流密度为:I wu == 2.16×10-3(W·m -2), 标准声强为:I 0 = 1×10-12(W·m -2),图5.10此声强的分贝数为:010lgIL I == 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为BB S Su u u u νν-=-,其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为33060033030B S S u u u νν==--= 660(Hz).火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为33060033030B S S u u u νν==-+= 550(Hz).(2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为3301060033030B B S S u u u u νν-+==--= 680(Hz).当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为3301060033030B B S S u u u u νν--==-+= 533(Hz).[注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m);在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m);在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).(2)反射面接收到的频率为1033165108033130B S u u u u νν++==⨯--= 1421(Hz). 将反射面作为波源,其频率为ν1,反射声音的频率为`11331142133165B u u u νν==⨯--= 1768(Hz).反射声音的波长为`1111331651421B B uu u u λννν--=-===0.1872(m).或者 `1`13311768u λν=== 0.1872(m).[注意]如果用下式计算波长`111650.27871768B u λλν=-=-=0.2330(m),结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15 S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为 1cos[2()]t xy A T πϕλ=++, 那么S 2在S 1左侧产生的波的波动方程为2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为1cos[2()]t xy A T πϕλ=-+,那么S 2在其右侧产生的波的波动方程为2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16 两相干波源S 1与S 2相距5m ,其振幅相等,频率都是100Hz ,位相差为π;波在媒质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为1 2121/2cos[2()]x l y A t u πνϕ+=-+ 5cos(2)24A t x πππνϕ=-+-,那么S 2在其左侧产生的波的波动方程为2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-.两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).5.17 设入射波的表达式为1cos 2()t xy A T πλ=+,在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为2cos 2()t xy A T πλ=-.(2)合成波为y = y 1 + y 2,将三角函数展开得222cos cos y A x t Tππλ=,这是驻波的方程.5.18 两波在一很长的弦线上传播,设其表达式为:1 6.0cos (0.028.0)2y x t π=-,2 6.0cos(0.028.0)2y x t π=+,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:1 6.0cos 2()0.5200t x y π=-,2 6.0cos 2()0.5200t xy π=+,可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).。
大学物理学教程第二(马文蔚)练习册答案6第六章 机械波

解:
6-8 图示为平面简谐波在t=0时刻的波形图,此简谐波 的频率为250Hz,且此图中P点的运动方向向上,求: 第 (1)此波的波动方程;(2)距原点7.5m处质点的运 六 动方程与t=0时该点的振动速度。 y/m 章 解: P点的运动方向向上
习 题 分 析
6-8
波向负方向传播
0.10 0.05 O
6-9
六 章 习 题 分 析
解:
xP 0.2 m
O 0.04
P
0.2 0.4 0.6
x/m
2 0.2 y P 0.04cos[ (t ) ]m 5 0.08 2 2 3 0.04cos[ t ] m 5 2 2 x y 0.04cos[ (t ) ]m 5 0.08 2
第 六 章 习 题 分 析
6-7
y15 A cos 100 t 15 cm 2
y5 A cos 100 t 5 cm 2
解:
15 15.5
5 5.5
2 2 波源振动方程: y0 A cos t cm 2 T 2 x 波动方程:
6-11
6-11 平面简谐波的波动方程为:
第 六 章 习 题 分 析
求:(1)t=2.1s时波源及距波源0.10m两处的相位;(2)离 波源0.80m及0.30m两处的相位差。 解:(1)
y 0.08cos 4 t 2 x (SI 制)
t 2.1s, x 0处, 4 2.1 8.4
x t x y A cos[ (t ) ] A cos[ 2 π ( ) ] u T
) 14-3 已知一波动方程为 y 0.05sin(10 t 2 x)(SI , (1)求波长、频率、波速和周期; (2)说明 x 0 第 六 时方程的意义,并作图表示。
《大学物理》习题册题目及答案第16单元 机械波

第16单元 机械波(一)学号 姓名 专业、班级 课程班序号一 选择题[ C ]1.在下面几种说法中,正确的说法是: (A) 波源不动时,波源的振动周期与波动的周期在数值上是不同的 (B) 波源振动的速度与波速相同 (C) 在波传播方向上的任一质点振动相位总是比波源的相位滞后 (D) 在波传播方向上的任一质点的振动相位总是比波源的相位超前[ A ]2. 一横波沿绳子传播时的波动方程为)104cos(05.0t x y ππ-= (SI),则(A) 其波长为0.5 m (B) 波速为5 m ⋅s -1(C) 波速为25 m ⋅s -1 (D)频率为2 Hz[ C ]3. 一简谐波沿x 轴负方向传播,圆频率为ω,波速为u 。
设t = T /4时刻的波形如图所示,则该波的表达式为: (A) )/(cos u x t A y -=ω (B) ]2/)/([cos πω+-=u x t A y (C) )/(cos u x t A y +=ω (D) ])/([cos πω++=u x t A y[ D ]4. 一平面简谐波沿x 轴正向传播,t = T/4时的波形曲线如图所示。
若振动以余弦函数表示,且此题各点振动的初相取π-到π之间的值,则 (A) 0点的初位相为00=ϕ(B) 1点的初位相为 21πϕ-=(C) 2点的初位相为 πϕ=2(D) 3点的初位相为 23πϕ-=[ D ]5. 一平面简谐波在弹性媒质中传播,在媒质质元从平衡位置运动到最大位移处的过程中: (A) 它的动能转换成势能。
(B) 它的势能转换成动能。
(C) 它从相邻的一段质元获得能量其能量逐渐增大。
(D) 它把自己的能量传给相邻的一段质元,其能量逐渐减小。
二 填空题1.频率为100Hz 的波,其波速为250m/s ,在同一条波线上,相距为0.5m 的两点的相位差为52π. 2. 一简谐波沿x 轴正向传播。
1x 和2x 两点处的振动曲线分别如图(a)和(b)所示。
大学物理 第五章机械波 课后习题 参考答案

对于 O 点:∵ y O 0, vO 0 ,∴ O
对于 A 点:∵ y A A, v A 0 ,∴ A 0 对于 B 点:∵ y B 0, v B 0 ,∴ B
.k
2 3 对于 C 点:∵ y C 0, vC 0 ,∴ C 2 (取负值:表示 A、B、C 点位相,应落后于 O 点的位相) (2)波沿 x 轴负向传播,则在 t 时刻,有 0, vO 0 ,∴ O 对于 O 点:∵ y O
2
2 代入上式,即得 C
( x 2 x1 )
Cd .
2
v max A 10 0.05 0.5 m s 1
a max 2 A (10 ) 2 0.05 5 2 m s 2
.c
x)
B 2 ,波速 u , C C 1 2 波动周期 T . B (2)将 x l 代入波动方程即可得到该点的振动方程
如题 5-11(c)图所示. 5-12 如题5-12图所示,已知 t =0时和 t =0.5s时的波形曲线分别为图中曲线(a)和(b) ,波沿 x 轴正向传播,试根据图中绘出的条件求: (1)波动方程; (2) P 点的振动方程.
hd aw
题 5-11 图(c)
y 0.1cos(5t
5 0.5 3 ) 0.1cos(5t ) m 0.5 2
此介质中任一质元离开平衡位置的位移既是坐标位置 x , 又是时间 t 的函数, 即 y f ( x, t ) . (2)在谐振动方程 y f (t ) 中只有一个独立的变量时间 t ,它描述的是介质中一个质元偏离
平衡位置的位移随时间变化的规律;平面谐波方程 y f ( x, t ) 中有两个独立变量,即坐标
物理-机械波习题库(含答案)
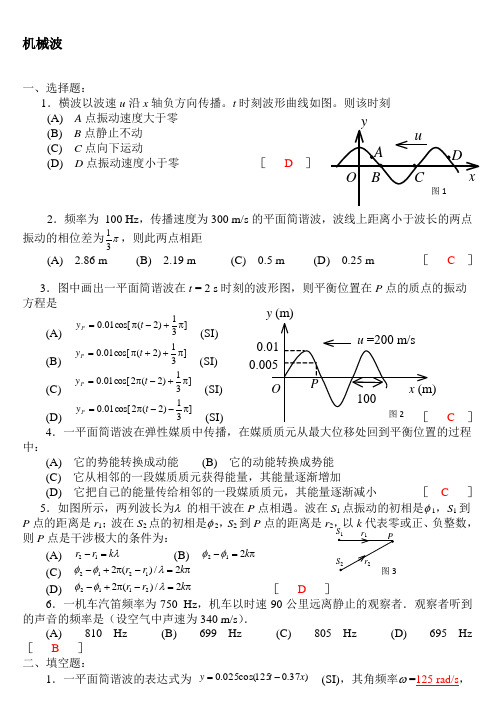
y (m)机械波一、选择题:1.横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动 (D) D 点振动速度小于零 [ D ]2.频率为 100 Hz ,传播速度为300 m/s 的平面简谐波,波线上距离小于波长的两点振动的相位差为π31,则此两点相距(A) 2.86 m (B) 2.19 m (C) 0.5 m (D) 0.25 m [ C ]3.图中画出一平面简谐波在t = 2 s 时刻的波形图,则平衡位置在P 点的质点的振动方程是 (A)]31)2(cos[01.0π+-π=t y P (SI) (B)]31)2(cos[01.0π++π=t y P (SI) (C) ]31)2(2cos[01.0π+-π=t y P(SI) (D)]31)2(2cos[01.0π--π=t y P (SI) C ]4中:(A) 它的势能转换成动能 (B) 它的动能转换成势能(C) 它从相邻的一段媒质质元获得能量,其能量逐渐增加(D) 它把自己的能量传给相邻的一段媒质质元,其能量逐渐减小 [ C ]5.如图所示,两列波长为λ 的相干波在P 点相遇。
波在S 1点振动的初相是φ 1,S 1到P 点的距离是r 1;波在S 2点的初相是φ 2,S 2到P 点的距离是r 2,以k 代表零或正、负整数,则P 点是干涉极大的条件为: (A) λk r r =-12 (B) π=-k 212φφ (C) π=-π+-k r r 2/)(21212λφφ(D) π=-π+-k r r 2/)(22112λφφ [ D ]6.一机车汽笛频率为750 Hz ,机车以时速90公里远离静止的观察者.观察者听到的声音的频率是(设空气中声速为340 m/s ).(A) 810 Hz (B) 699 Hz (C) 805 Hz (D) 695 Hz [ B ]二、填空题:1.一平面简谐波的表达式为 )37.0125cos(025.0x t y -= (SI),其角频率ω =125 rad/s ,波速u = 338m/s ,波长λ = 17.0m 。
大学物理机械波习题附答案
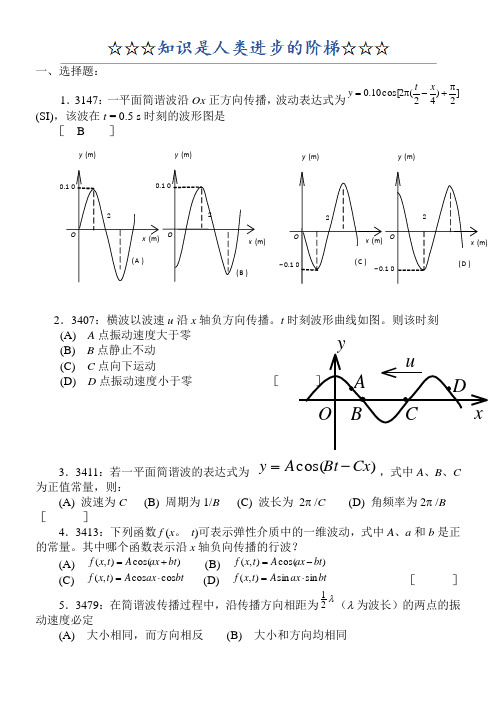
一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = 0.5 s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻 (A) A 点振动速度大于零 (B) B 点静止不动(C) C 点向下运动(D) D 点振动速度小于零 [ ]3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2π /C (D) 角频率为2π /B [ ]4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D) bt ax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(λ 为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同xu A B C D Ox (m) O 2 0.1 0y (m) ( A ) xO 2 0.1 0 y (m) ( B ) x (m) O 2 - 0.1 0 y (m) ( C ) x (m)O 2 y (m) ( D )- 0.1 0(C) 大小不同,方向相同 (D) 大小不同,而方向相反 [ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距λ /8(其中λ 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
大学物理机械波习题附答案

一、选择题:1.3147:一平面简谐波沿Ox 正方向传播,波动表达式为]2)42(2cos[10.0π+-π=x t y (SI),该波在t = s 时刻的波形图是[ B ]2.3407:横波以波速u 沿x 轴负方向传播。
t 时刻波形曲线如图。
则该时刻(A) A 点振动速度大于零 (B) B 点静止不动 (C) C 点向下运动(D) D 点振动速度小于零 [3.3411:若一平面简谐波的表达式为 )cos(Cx Bt A y -=,式中A 、B 、C 为正值常量,则:(A) 波速为C (B) 周期为1/B (C) 波长为 2? /C (D) 角频率为2? /B []4.3413:下列函数f (x 。
t )可表示弹性介质中的一维波动,式中A 、a 和b 是正的常量。
其中哪个函数表示沿x 轴负向传播的行波?(A) )cos(),(bt ax A t x f += (B) )cos(),(bt ax A t x f -=(C) bt ax A t x f cos cos ),(⋅= (D)bt ax A t x f sin sin ),(⋅= [ ]5.3479:在简谐波传播过程中,沿传播方向相距为λ21(??为波长)的两点的振动速度必定(A) 大小相同,而方向相反 (B) 大小和方向均相同(C)大小不同,方向相同 (D) 大小不同,而方向相反y (m) y (m) - y (m) y (m)[ ]6.3483:一简谐横波沿Ox 轴传播。
若Ox 轴上P 1和P 2两点相距? /8(其中? 为该波的波长),则在波的传播过程中,这两点振动速度的(A) 方向总是相同 (B) 方向总是相反(C) 方向有时相同,有时相反 (D) 大小总是不相等 [ ]7.3841:把一根十分长的绳子拉成水平,用手握其一端。
维持拉力恒定,使绳端在垂直于绳子的方向上作简谐振动,则 (A) 振动频率越高,波长越长 (B) 振动频率越低,波长越长(C) 振动频率越高,波速越大 (D) 振动频率越低,波速越大 [ ] 8.3847:图为沿x 轴负方向传播的平面简谐波在t = 0时刻的波形。
大学物理-机械波习题思考题及答案

习题88-1.沿一平面简谐波的波线上,有相距2.0m 的两质点A 与B ,B 点振动相位比A 点落后6π,振动周期为2.0s ,求波长和波速。
解:根据题意,对于A 、B 两点,m x 2612=∆=-=∆,πϕϕϕ, 而m 242=⇒∆=∆λλπϕx ,m/s 12==T u λ 8-2.一平面波沿x 轴正向传播,距坐标原点O 为1x 处P 点的振动式为)cos(ϕω+=t A y ,波速为u ,求:〔1〕平面波的波动式;〔2〕假设波沿x 轴负向传播,波动式又如何"解:〔1〕设平面波的波动式为0cos[]xy A t uωϕ=-+(),则P 点的振动式为: 10cos[]P x y A t uωϕ=-+(),与题设P 点的振动式cos()P y A t ωϕ=+比拟, 有:10x uωϕϕ=+,∴平面波的波动式为:1cos[()]x x y A t u ωϕ-=-+; 〔2〕假设波沿x 轴负向传播,同理,设平面波的波动式为:0cos[]x y A t uωϕ=++(),则P 点的振动式为: 10cos[]P x y A t uωϕ=++(),与题设P 点的振动式cos()P y A t ωϕ=+比拟, 有:10x uωϕϕ=-+,∴平面波的波动式为:1cos[()]x x y A t u ωϕ-=++。
8-3.一平面简谐波在空间传播,如下图,A 点的振动规律为cos(2)y A t πνϕ=+,试写出: 〔1〕该平面简谐波的表达式;〔2〕B 点的振动表达式〔B 点位于A 点右方d 处〕。
解:〔1〕仿照上题的思路,根据题意,设以O 点为原点平面简谐波的表达式为:0cos[2]x y A t uπνϕ=++(),则A 点的振动式:0cos[2]A l y A t uπνϕ-=++() 题设A 点的振动式cos(2)y A t πνϕ=+比拟,有:02l u πνϕϕ=+, ∴该平面简谐波的表达式为:]2cos[ϕπν+++=)(ux u l t A y 〔2〕B 点的振动表达式可直接将坐标x d l =-,代入波动方程:8-4.一沿x 正方向传播的平面余弦波,s 31=t 时的波形如下图,且周期T 为s 2。
大学物理机械波练习习题思考题包括答案.doc

习题 88-1.沿一平面简谐波的波线上,有相距 2.0 m 的两质点A与B,B点振动相位比 A 点落后,已知振动周期为 2.0 s ,求波长和波速。
6解:根据题意,对于A、 B 两点,21 , x 2m ,2 6而x 24m , u 12m/sT8-2 .已知一平面波沿x 轴正向传播,距坐标原点O 为x1处 P 点的振动式为y A cos( t) ,波速为 u ,求:(1)平面波的波动式;(2)若波沿x轴负向传播,波动式又如何解:( 1)设平面波的波动式为y Acos[ (t x)0 ] ,则 P 点的振动式为:x 1 )uy P A cos[ ( t 0 ] ,与题设P点的振动式 y P Acos( t ) 比较,x1 ux x1有:0 ,∴平面波的波动式为:y Acos[ (t ) ] ;u u ( 2)若波沿x轴负向传播,同理,设平面波的波动式为:y A cos[ ( t x0 ] ,则P点的振动式为:)uy P A cos[ ( t x1)0 ] ,与题设P点的振动式 y P Acos( t ) 比较,x1 uxx1 )有:0 ,∴平面波的波动式为:y A cos[ (tu ] 。
u8-3 .一平面简谐波在空间传播,如图所示,已知A点的振动规律为y A cos(2 t ) ,试写出:( 1)该平面简谐波的表达式;( 2)B点的振动表达式( B 点位于 A 点右方 d 处)。
解:( 1)仿照上题的思路,根据题意,设以O 点为原点平面简谐波的表达式为:y A cos[2 (t x )0 ] ,则 A 点的振动式:uy A A cos[2 (tl ) 0]u题设 A 点的振动式 yA cos(2t) 比较,有:2 l 0,lx )u∴ 该平面简谐波的表达式为:yAcos[ 2 ( t ]u u( 2) B 点的振动表达式可直接将坐标x d l ,代入波动方程:l d l ] A cos[2 ( tdy Acos[ 2 ( tu )) ]uu8-4.已知一沿 x 正方向传播的平面余弦波, t1s 时的波形如图所示, 且周期 T3为 2s 。
大学物理课后习题答案第五章

第五章 机械波5.1 已知一波的波动方程为y = 5×10-2sin(10πt – 0.6x ) (m). (1)求波长、频率、波速及传播方向;(2)说明x = 0时波动方程的意义,并作图表示. [解答](1)与标准波动方程比较得:2π/λ = 0.6, 因此波长为:λ = 10.47(m);圆频率为:ω = 10π,频率为:v =ω/2π = 5(Hz);波速为:u = λ/T = λv = 52.36(m·s -1).且传播方向为x 轴正方向.(2)当x = 0时波动方程就成为该处质点的振动方程: y = 5×10-2sin10πt = 5×10-2cos(10πt – π/2), 振动曲线如图.5.2 一平面简谐波在媒质中以速度为u = 0.2m·s -1沿x 轴正向传播,已知波线上A 点(x A = 0.05m )的振动方程为(m).试求:(1)简谐波的波动方程;(2)x = -0.05m 处质点P 处的振动方程.[解答](1)简谐波的波动方程为:; 即 = 0.03cos[4π(t – 5x ) + π/2]. (2)在x = -0.05m 处质点P 点的振动方程为:y = 0.03cos[4πt + π + π/2] = 0.03cos(4πt -π/2).5.3 已知平面波波源的振动表达式为(m).求距波源5m 处质点的振动方程和该质点与波源的位相差.设波速为2m·s -1.[解答]振动方程为: , 位相差为 Δφ = 5π/4(rad).5.4 有一沿x 轴正向传播的平面波,其波速为u = 1m·s -1,波长λ = 0.04m ,振幅A = 0.03m .若以坐标原点恰在平衡位置而向负方向运动时作为开始时刻,试求:(1)此平面波的波动方程;(2)与波源相距x = 0.01m 处质点的振动方程,该点初相是多少? [解答](1)设原点的振动方程为:y 0 = A cos(ωt + φ),其中A = 0.03m .由于u = λ/T ,所以质点振动的周期为:T = λ/u = 0.04(s),圆频率为:ω = 2π/T = 50π. 当t = 0时,y 0 = 0,因此cos φ = 0;由于质点速度小于零,所以φ = π/2. 原点的振动方程为:y 0 = 0.03cos(50πt + π/2), 平面波的波动方程为:= 0.03cos[50π(t – x ) + π/2).(2)与波源相距x = 0.01m 处质点的振动方程为:y = 0.03cos50πt . 该点初相φ = 0.5.5 一列简谐波沿x 轴正向传播,在t 1 = 0s ,t 2 = 0.25s 时刻的波形如图所示.试求:2cos()xy A t πωλ=-0.03cos(4)2A y t ππ=-cos[()]Ax x y A t uωϕ-=-+0.050.03cos[4()]0.22x y t ππ-=--20 6.010sin 2y t π-=⨯26.010sin()2xy t u π-=⨯-50.06sin()24t ππ=-0.03cos[50()]2x y t u ππ=-+(1)P 点的振动表达式; (2)波动方程;(3)画出O 点的振动曲线.[解答](1)设P 点的振动方程为 y P = A cos(ωt + φ), 其中A = 0.2m .在Δt = 0.25s 内,波向右传播了Δx = 0.45/3 = 0.15(m),所以波速为u = Δx/Δt = 0.6(m·s -1).波长为:λ = 4Δx = 0.6(m), 周期为:T = λ/u = 1(s), 圆频率为:ω = 2π/T = 2π.当t = 0时,y P = 0,因此cos φ = 0;由于波沿x 轴正向传播,所以P 点在此时向上运动,速度大于零,所以φ = -π/2.P 点的振动表达式为:y P = 0.2cos(2πt - π/2). (2)P 点的位置是x P = 0.3m ,所以波动方程为. (3)在x = 0处的振动方程为y 0 = 0.2cos(2πt + π/2),曲线如图所示.5.6 如图所示为一列沿x 负向传播的平面谐波在t = T /4时的波形图,振幅A 、波长λ以及周期T 均已知.(1)写出该波的波动方程;(2)画出x = λ/2处质点的振动曲线;(3)图中波线上a 和b 两点的位相差φa – φb 为多少? [解答](1)设此波的波动方程为: ,当t = T /4时的波形方程为:. 在x = 0处y = 0,因此得sin φ = 0,解得φ = 0或π.而在x = λ/2处y = -A ,所以φ = 0. 因此波动方程为:. (2)在x = λ/2处质点的振动方程为:, 曲线如图所示.(3)x a = λ/4处的质点的振动方程为; x b = λ处的质点的振动方程为.波线上a 和b 两点的位相差0.2cos[2()]2P x x y t u ππ-=--100.2cos(2)32t x πππ=-+cos[2()]t xy A T πϕλ=++cos(2)2xy A ππϕλ=++sin(2)xA πϕλ=-+cos 2()t x y A T πλ=+cos(2)cos 2t t y A A T Tπππ=+=-cos(2)2a t y A T ππ=+cos(22)b ty A Tππ=+图5.5φa – φb = -3π/2.5.7 已知波的波动方程为y = A cosπ(4t – 2x )(SI ).(1)写出t = 4.2s 时各波峰位置的坐标表示式,并计算此时离原点最近的波峰的位置,该波峰何时通过原点?(2)画出t = 4.2s 时的波形曲线.[解答]波的波动方程可化为:y = A cos2π(2t – x ),与标准方程比较,可知:周期为T = 0.5s ,波长λ = 1m .波速为u = λ/T = 2m·s -1. (1)当t = 4.2s 时的波形方程为y = A cos(2πx – 16.8π)= A cos(2πx – 0.8π). 令y = A ,则cos(2πx – 0.8π) = 1,因此 2πx – 0.8π = 2k π,(k = 0, ±1, ±2,…), 各波峰的位置为x = k + 0.4,(k = 0, ±1, ±2,…).当k = 0时的波峰离原点最近,最近为:x = 0.4(m).通过原点时经过的时间为:Δt = Δx/u = (0 – x )/u = -0.2(s), 即:该波峰0.2s 之前通过了原点.(2)t = 0时刻的波形曲线如实线所示.经过t = 4s 时,也就是经过8个周期,波形曲线是重合的;再经Δt = 0.2s ,波形向右移动Δx = u Δt = 0.4m ,因此t = 4.2s 时的波形曲线如虚线所示.[注意]各波峰的位置也可以由cos(2πx – 16.8π) = 1解得,结果为x = k + 8.4,(k = 0, ±1, ±2,…),取同一整数k 值,波峰的位置不同.当k = -8时的波峰离原点最近,最近为x = 0.4m .5.8 一简谐波沿x 轴正向传播,波长λ = 4m ,周期T = 4s ,已知x = 0处的质点的振动曲线如图所示. (1)写出时x = 0处质点的振动方程;(2)写出波的表达式;(3)画出t = 1s 时刻的波形曲线.[解答]波速为u = λ/T = 1(m·s -1).(1)设x = 0处的质点的振动方程为y = A cos(ωt + φ), 其中A = 1m ,ω = 2π/T = π/2.当t = 0时,y = 0.5,因此cos φ = 0.5,φ = ±π/3.在0时刻的曲线上作一切线,可知该时刻的速度小于零,因此φ = π/3.振动方程为:y = cos(πt /2 + π/3).(2)波的表达式为:.(3)t = 1s 时刻的波形方程为,波形曲线如图所示.5.9 在波的传播路程上有A 和B 两点,都做简谐振动,B 点的位相比A 点落后π/6,cos[2()]t x y A T πϕλ=-+cos[2()]t xy A T πϕλ=-+cos[()]23t x ππ=-+5cos()26y x ππ=-图5.8已知A 和B 之间的距离为2.0cm ,振动周期为2.0s .求波速u 和波长λ.[解答] 设波动方程为:, 那么A 和B 两点的振动方程分别为:,.两点之间的位相差为:,由于x B – x A = 0.02m ,所以波长为:λ = 0.24(m).波速为:u = λ/T = 0.12(m·s -1).5.10 一平面波在介质中以速度u = 20m·s -1沿x 轴负方向传播.已知在传播路径上的某点A 的振动方程为y = 3cos4πt .(1)如以A 点为坐标原点,写出波动方程;(2)如以距A 点5m 处的B 点为坐标原点,写出波动方程; (3)写出传播方向上B ,C ,D 点的振动方程. [解答](1)以A 点为坐标原点,波动方程为 .(2)以B 点为坐标原点,波动方程为. (3)以A 点为坐标原点,则x B = -5m 、x C = -13m 、x D = 9m ,各点的振动方程为, ,.[注意]以B 点为坐标原点,求出各点坐标,也能求出各点的振动方程.5.11 一弹性波在媒质中传播的速度u = 1×103m·s -1,振幅A = 1.0×10-4m ,频率ν= 103Hz .若该媒质的密度为800kg·m -3,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量. [解答](1)质点的圆频率为:ω = 2πv = 6.283×103(rad·s -1), 波的平均能量密度为:= 158(J·m -3), 平均能流密度为:= 1.58×105(W·m -2).(2)1分钟内垂直通过面积S = 4×10-4m 2的总能量为:E = ItS = 3.79×103(J).5.12 一平面简谐声波在空气中传播,波速u = 340m·s -1,频率为500Hz .到达人耳时,振幅A = 1×10-4cm ,试求人耳接收到声波的平均能量密度和声强?此时声强相当于多少分贝?已知空气密度ρ = 1.29kg·m -3.[解答]质点的圆频率为:ω = 2πv = 3.142×103(rad·s -1),cos[2()]t xy A T πϕλ=-+cos[2()]A A xt y A T πϕλ=-+cos[2()]B B xt y A T πϕλ=-+2(2)6B A x x πππλλ---=-3cos 4()3cos(4)5x x y t t u πππ=+=+3cos 4()Ax x y t u π-=+3cos(4)5x t πππ=+-3cos 4()3cos(4)BB x y t t u πππ=+=-33cos 4()3cos(4)5C C x y t t u πππ=+=-93cos 4()3cos(4)5D D x y t t u πππ=+=+2212w A ρω=I wu =图5.10声波的平均能量密度为:= 6.37×10-6(J·m -3), 平均能流密度为:= 2.16×10-3(W·m -2), 标准声强为:I 0 = 1×10-12(W·m -2), 此声强的分贝数为:= 93.4(dB).5.13 设空气中声速为330m·s -1.一列火车以30m·s -1的速度行驶,机车上汽笛的频率为600Hz .一静止的观察者在机车的正前方和机车驶过其身后所听到的频率分别是多少?如果观察者以速度10m·s -1与这列火车相向运动,在上述两个位置,他听到的声音频率分别是多少?[解答]取声速的方向为正,多谱勒频率公式可统一表示为, 其中v S 表示声源的频率,u 表示声速,u B 表示观察者的速度,u S 表示声源的速度,v B 表示观察者接收的频率.(1)当观察者静止时,u B = 0,火车驶来时其速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 660(Hz). 火车驶去时其速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 550(Hz). (2)当观察者与火车靠近时,观察者的速度方向与声速相反,u B = -10m·s -1;火车速度方向与声速方向相同,u S = 30m·s -1,观察者听到的频率为= 680(Hz). 当观察者与火车远离时,观察者的速度方向与声速相同,u B = 10m·s -1;火车速度方向与声速方向相反,u S = -30m·s -1,观察者听到的频率为= 533(Hz). [注意]这类题目涉及声速、声源的速度和观察者的速度,规定方向之后将公式统一起来,很容易判别速度方向,给计算带来了方便.5.14.一声源的频率为1080Hz ,相对地面以30m·s -1速率向右运动.在其右方有一反射面相对地面以65m·s -1的速率向左运动.设空气中声速为331m·s -1.求:(1)声源在空气中发出的声音的波长; (2)反射回的声音的频率和波长.[解答](1)声音在声源垂直方向的波长为:λ0 = uT 0 = u /ν0 = 331/1080 = 0.306(m); 在声源前方的波长为:λ1 = λ0 - u s T 0 = uT 0 - u s T 0 = (u - u s )/ν0 = (331-30)/1080 = 0.2787(m); 在声源后方的波长为:λ2 = λ0 + u s T 0 = uT 0 + u s T 0 = (u + u s )/ν0= (331+30)/1080 = 0.3343(m).(2)反射面接收到的频率为 = 1421(Hz).将反射面作为波源,其频率为ν1,反射声音的频率为2212w A ρω=I wu =010lgIL I =BB S Su u u u νν-=-33060033030B S S u u u νν==--33060033030B S S u u u νν==-+3301060033030B B S S u u u u νν-+==--3301060033030B B S S u u u u νν--==-+1033165108033130B Su u u u νν++==⨯--= 1768(Hz). 反射声音的波长为=0.1872(m).或者 = 0.1872(m). [注意]如果用下式计算波长=0.2330(m), 结果就是错误的.当反射面不动时,作为波源发出的波长为u /ν1 = 0.2330m ,而不是入射的波长λ1.5.15 S 1与S 2为两相干波源,相距1/4个波长,S 1比S 2的位相超前π/2.问S 1、S 2连线上在S 1外侧各点的合成波的振幅如何?在S 2外侧各点的振幅如何?[解答]如图所示,设S 1在其左侧产生的波的波动方程为,那么S 2在S 1左侧产生的波的波动方程为,由于两波源在任意点x 产生振动反相,所以合振幅为零.S 1在S 2右侧产生的波的波动方程为,那么S 2在其右侧产生的波的波动方程为,由于两波源在任意点x 产生振动同相,所以合振幅为单一振动的两倍.5.16 两相干波源S 1与S 2相距5m ,其振幅相等,频率都是质中的传播速度为400m·s -1,试以S 1S 2连线为坐标轴x ,以S 1S 2连线中点为原点,求S 1S 2间因干涉而静止的各点的坐标.[解答]如图所示,设S 1在其右侧产生的波的波动方程为 ,那么S 2在其左侧产生的波的波动方程为. 两个振动的相差为Δφ = πx + π,当Δφ = (2k + 1)π时,质点由于两波干涉而静止,静止点为x = 2k , k 为整数,但必须使x 的值在-l /2到l /2之间,即-2.5到2.5之间.当k = -1、0和1时,可得静止点的坐标为:x = -2、0和2(m).`11331142133165B u u u νν==⨯--`1111331651421BBu u u u λννν--=-==`1`13311768u λν==`111650.27871768Bu λλν=-=-1cos[2()]t xy A T πϕλ=++2/4cos[2()]2t x y A T λππϕλ-=++-cos[2()]t xA T πϕπλ=++-1cos[2()]t xy A T πϕλ=-+2/4cos[2()]2t x y A T λππϕλ-=-+-cos[2()]t xA T πϕλ=-+1/2cos[2()]x l y A t u πνϕ+=-+5cos(2)24A t x πππνϕ=-+-2/2cos[2()]x l y A t u πνϕπ-=+++cos(2)24A t x πππνϕ=++-S 1 S 2S 125.17 设入射波的表达式为,在x = 0处发生反射,反射点为一自由端,求:(1)反射波的表达式; (2)合成驻波的表达式.[解答](1)由于反射点为自由端,所以没有半波损失,反射波的波动方程为.(2)合成波为y = y 1 + y 2,将三角函数展开得,这是驻波的方程.5.18 两波在一很长的弦线上传播,设其表达式为:,,用厘米、克、秒(cm,g,s )制单位,求:(1)各波的频率,波长、波速;(2)节点的位置;(3)在哪些位置上,振幅最大?[解答](1)两波可表示为:,, 可知它们的周期都为:T = 0.5(s),频率为:v = 1/T = 2(Hz);波长为:λ = 200(cm);波速为:u = λ/T = 400(cm·s -1).(2)位相差Δφ = πx /50,当Δφ = (2k + 1)π时,可得节点的位置x = 50(2k + 1)(cm),(k = 0,1,2,…).(3)当Δφ = 2k π时,可得波腹的位置x = 100k (cm),(k = 0,1,2,…).1cos 2()t xy A T πλ=+2cos 2()t xy A T πλ=-222coscosy A x t Tππλ=1 6.0cos(0.028.0)2y x t π=-2 6.0cos(0.028.0)2y x t π=+1 6.0cos 2()0.5200t x y π=-2 6.0cos 2()0.5200t x y π=+。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题88-1.沿一平面简谐波的波线上,有相距2.0m 的两质点A 与B ,B 点振动相位比A 点落后6π,已知振动周期为2.0s ,求波长和波速。
解:根据题意,对于A 、B 两点,m x 2612=∆=-=∆,πϕϕϕ,而m 242=⇒∆=∆λλπϕx ,m/s 12==Tu λ8-2.已知一平面波沿x 轴正向传播,距坐标原点O 为1x 处P 点的振动式为)cos(ϕω+=t A y ,波速为u ,求:(1)平面波的波动式;(2)若波沿x 轴负向传播,波动式又如何?解:(1)设平面波的波动式为0cos[]xy A t uωϕ=-+(),则P 点的振动式为:10cos[]P x y A t uωϕ=-+(),与题设P 点的振动式cos()P y A t ωϕ=+比较, 有:10x uωϕϕ=+,∴平面波的波动式为:1cos[()]x x y A t u ωϕ-=-+;(2)若波沿x 轴负向传播,同理,设平面波的波动式为:0cos[]xy A t u ωϕ=++(),则P 点的振动式为:10cos[]P xy A t u ωϕ=++(),与题设P 点的振动式cos()P y A t ωϕ=+比较,有:10x uωϕϕ=-+,∴平面波的波动式为:1cos[()]x x y A t u ωϕ-=++。
8-3.一平面简谐波在空间传播,如图所示,已知A 点的振动规律为cos(2)y A t πνϕ=+,试写出: (1)该平面简谐波的表达式;(2)B 点的振动表达式(B 点位于A 点右方d 处)。
解:(1)仿照上题的思路,根据题意,设以O 点为原点平面简谐波的表达式为:0cos[2]x y A t u πνϕ=++(),则A 点的振动式:0cos[2]A l y A t uπνϕ-=++() 题设A 点的振动式cos(2)y A t πνϕ=+比较,有:02luπνϕϕ=+,∴该平面简谐波的表达式为:]2cos[ϕπν+++=)(ux u l t A y (2)B 点的振动表达式可直接将坐标x d l =-,代入波动方程:]2cos[]2cos[ϕπνϕπν++=+-++=)()(ud t A u l d u l t A y8-4.已知一沿x 正方向传播的平面余弦波,s 31=t 时的波形如图所示,且周期T 为s 2。
(1)写出O 点的振动表达式; (2)写出该波的波动表达式; (3)写出A 点的振动表达式; (4)写出A 点离O 点的距离。
解:由图可知:0.1A m =,0.4m λ=,而2T s =,则:/0.2/u T m s λ==,2T πωπ==,25k ππλ==,∴波动方程为:00.1cos(5)y t x ππϕ=-+ O 点的振动方程可写成:00.1cos()O y t πϕ=+由图形可知:s 31=t 时:0.05O y =,有:00.050.1cos()3πϕ=+考虑到此时0O d y d t <,∴03πϕ=,53π(舍去) 那么:(1)O 点的振动表达式:0.1cos()3O y t ππ=+;(2)波动方程为:0.1cos(5)3y t x πππ=-+;(3)设A 点的振动表达式为:0.1cos()A A y t πϕ=+由图形可知:s 31=t 时:0A y =,有:cos()03A πϕ+=考虑到此时0A d y d t >,∴56A πϕ=-(或76A πϕ=) ∴A 点的振动表达式:50.1cos()6A y t ππ=-,或70.1cos()6A y t ππ=+;(4)将A 点的坐标代入波动方程,可得到A 的振动方程为:0.1cos(5)3A A y t x πππ=-+,与(3)求得的A 点的振动表达式比较,有:5563A t t x πππππ-=-+,所以:m x A 233.0307== 。
8-5.一平面简谐波以速度m/s 8.0=u 沿x 轴负方向传播。
已知原点的振动曲线如图所示。
试写出:(1)原点的振动表达式; (2)波动表达式;(3)同一时刻相距m 1的两点之间的位相差。
解:这是一个振动图像!由图可知A =,设原点处的振动方程为:30510cos()O y t ωϕ-=⨯+。
(1)当0t =时,302.510O t y -==⨯,考虑到:0O t d y d t=>,有:03πϕ=-,当1t =时,10Ot y ==,考虑到:10O t d y d t=<,有:32ππω-=,56πω=, ∴原点的振动表达式:35510cos()63O y t ππ-=⨯-; (2)沿x 轴负方向传播,设波动表达式:35510cos()63y t k x ππ-=⨯+- 而512460.825k u ωππ==⨯=,∴3524510cos()6253y t x πππ-=⨯+-;(3)位相差:252 3.2724x k x rad ϕππλ∆∆==∆== 。
8-6.一正弦形式空气波沿直径为cm 14的圆柱形管行进,波的平均强度为39.010-⨯/()J s m ⋅,频率为Hz 300,波速为m/s 300。
问波中的平均能量密度和最大能量密度各是多少?每两个相邻同相面间的波段中含有多少能量? 解:(1)已知波的平均强度为:39.010I -=⨯/()J s m ⋅,由I w u =⋅ 有:3539.010310/300I w J m u --⨯===⨯53max 2610/w w J m -==⨯;(2)由W w V =⋅,∴221144uW w d w d πλπν=⋅=5327310/(0.14)1 4.62104J m m m J π--=⨯⨯⋅⋅=⨯ 。
8-7.一弹性波在媒质中传播的速度310/u m s =,振幅41.010A m -=⨯,频率310Hz ν=。
若该媒质的密度为3800/kg m ,求:(1)该波的平均能流密度;(2)1分钟内垂直通过面积24m 100.4-⨯=S 的总能量。
解:(1)由:2212I u A ρω=,有: 34232110800102102I π-=⨯⨯⨯⨯()()521.5810/W m =⨯; (2)1分钟为60秒,通过面积24m 100.4-⨯=S 的总能量为:W I S t =5431.581041060 3.7910J -=⨯⨯⨯⨯=⨯ 。
8-8.1S 与2S 为左、右两个振幅相等相干平面简谐波源,它们的间距为4/5λ=d ,2S 质点的振动比1S 超前2π,设1S 的振动方程为t TA y π2cos10=,且媒质无吸收,(1)写出1S 与2S 之间的合成波动方程;(2)分别写出1S 与2S 左、右侧的合成波动方程。
解:(1)如图,以1S 为原点,有振动方程:t TA y π2cos10=, 则波源1S 在右侧产生的行波方程为:122cos()y A t x T ππλ=-, 由于2S 质点的振动比1S 超前2π,∴2S 的振动方程为202cos()2y A t T ππ=+,设以1S 为原点,波源2S 在其左侧产生的行波方程为:222cos()y A t x T ππϕλ=++,由于波源2S 的坐标为5/4λ,代入可得振动方程: 20225cos()4y A t T ππλϕλ=+⋅+,与202cos()2y A t T ππ=+比较,有:2ϕπ=-。
∴22222cos(2)cos()y A t x A t x T T πππππλλ=+-=+。
可见,在1S 与2S 之间的任一点x 处,相当于两列沿相反方向传播的波的叠加,••1S x2S合成波为:t Tx A y y y πλπ2cos2cos221=+=,为驻波;(2)∵波源1S 在左侧产生的行波方程为:122'cos()y A t x T ππλ=+, 与222cos()y A t x T ππλ=+叠加,有:1222'2cos y y y A t x T ππλ=+=+左(); (3)设波源2S 在其右侧产生的行波方程为:222'cos(')y A t x T ππϕλ=-+, 代入波源2S 的坐标为5/4λ,可得振动方程:20225'cos(')4y A t T ππλϕλ=-⋅+,与20202'cos()2y y A t T ππ==+比较,有:'3ϕπ=。
∴22222'cos(3)cos()y A t x A t x T T ππππππλλ=-+=-+。
与122cos()y A t x T ππλ=-叠加,有:12'0y y y =+=右。
表明两列波正好是完全反相的状态,所以合成之后为0。
8-9.设1S 与2S 为两个相干波源,相距41波长,1S 比2S 的位相超前2π。
若两波在在1S 、2S 连线方向上的强度相同且不随距离变化,问1S 、2S 连线上在1S 外侧各点的合成波的强度如何?又在2S 外侧各点的强度如何? 解:(1)如图,1S 、2S 连线上在1S 外侧, ∵212122()24r r πππλϕϕϕπλλ∆=---=--⋅=-,∴两波反相,合成波强度为0;(2)如图,1S 、2S 连线上在2S 外侧, ∵212122('')()024r r πππλϕϕϕλλ∆=---=---=, ∴两波同相,合成波的振幅为2A ,合成波的强度为:220(2)44I A A I === 。
8-10.测定气体中声速的孔脱(Kundt )法如下:一细棒的中部夹住,一端有盘DS S ••1S 2S 'r o伸入玻璃管,如图所示。
管中撒有软木屑,管的另一端有活塞P ,使棒纵向振动,移动活塞位置直至软木屑形成波节和波腹图案。
若已知棒中纵波的频率ν,量度相邻波节间的平均距离d ,可求得管内气体中的声速u 。
试证:d u ν2=。
证明:根据驻波的定义,相邻两波节(腹)间距:2x λ∆=,再根据已知条件:量度相邻波节间的平均距离d ,所以:2d λ=,那么:2d λ=,所以波速为:2u d λνν== 。
8-11.图中所示为声音干涉仪,用以演示声波的干涉。
S 为声源,D 为声音探测器,如耳或话筒。
路径SB D 的长度可以变化,但路径SAD 是固定的。
干涉仪内有空气,且知声音强度在B 的第一位置时为极小值100单位,而渐增至B 距第一位置为cm 65.1的第二位置时,有极大值900单位。
求:(1)声源发出的声波频率;(2)抵达探测器的两波的振幅之比。
解:根据驻波的定义,相邻两波节(腹)间距:2x λ∆=,相邻波节与波腹的间距:4x λ∆=,可得:4 6.6x cm λ=∆=。
