第一章 汽轮机级的工作原理-第二节 蒸汽在喷嘴和动叶通道中的流动过程
汽轮机原理 第一章

目前常见的复速级内总的反动度 值约在5%~15%之间。
图1-23 带反动度的复速级的热力过程线
复速级的轮周功:复速级的轮周功等于两列动叶 上产生的机械功之和。
Wu Wu Wu u c1 cos1 c2 cos2 c1cos1 c2cos2
➢ β 的大小与喷嘴的进口状态( 、 p0* v0* )、压力比εn和蒸汽的 绝热指数κ有关。
Gn Gnc
k
2
1
2
k n
k 1
nk
k 1
2 k 1 k 1
1
0.546 n 1
n 0.546
三、蒸汽在喷嘴斜切部分中的膨胀
汽轮机弯曲型渐缩叶栅通道,在喉部后形成斜切出口通道,将此称为 斜切部分。它的存在极大地改变了叶栅通道的流动特性。
极限膨胀压力比 1d
k
1d
p1d p0
2 k1
k 1
sin 1
2k k1
汽流偏转角
sin 1 1
sin
1
ccr c1t
cr 1t
图1-13 蒸汽在喷嘴斜切部分的膨胀
第三节 蒸汽在动叶中的流动
圆周速度: u dmn
60
相对速度:W1、W2
绝对速度:C1、C2
➢ 进口速度三角形 ➢ 出口速度三角形
➢ 叶栅流道:喷嘴叶栅和动叶栅的安
装角s和s、喷嘴叶栅和动叶栅的 叶型进口几何角0g和0g、喷嘴叶 栅和动叶栅的叶型出口几何角1g和 1g、喷嘴出口汽流角1和动叶出口 汽流角2等
喷嘴叶栅和动叶栅的几何参数
喷嘴叶栅结构尺寸:
汽轮机原理第一章课件

1 p1 kk 2k 0 0 p0 v0 [1 ( 0 ) ] k 1 p0 k 1 2k 0 0 p0 v0 (1 n k ) k 1
0 h Δhn
Δhn
1 1t
p1
式中: n
p1 0 p0
喷嘴压比
s
一、蒸汽在喷嘴中的膨胀过程
(一)喷嘴出口汽流速度
(2)喷嘴实际出口速度:
三. 级的类型和特点
带反动度的冲动级(冲动级)
在冲动级中带少量反动度
特点:
m 0.05 ~ 0.30
①蒸汽主要在喷嘴中膨胀,小部分在 动叶中膨胀; ②作用力:主要是冲动力; ③作功能力大,级所承担的滞止理想 焓降较大,效率有所提高; ④喷嘴:渐缩喷嘴;动叶:汽道横截 面沿汽流方向有所收缩; 实际的冲动级汽轮机都是带反动度 的冲动级,应用广泛。
u
ห้องสมุดไป่ตู้
db n
u -动叶平均直径处的圆周速度 60 c -喷嘴出口速度(动叶进口绝对 w1 c12 u 2 2uc1 cos 1 1 速度 )
c1 sin 1 1 arcsin w1
w1 -动叶进口的相对速度
c2-动叶出口的相对速度 2 c2 w2 u 2 2uw2 cos 2 w2-动叶出口绝对速度 w2 sin 2 2 arcsin c2
2、压力级和速度级
(1)压力级:蒸汽的动能转换为转子的机械能的过程 在级内只进行一次的级。 (2)速度级:蒸汽的动能转换为转子的机械能的过程 在级内进行一次以上的级。
3、调节级和非调节级
(1)调节级:通流面积能随负荷改变的级,如喷嘴调 节的第一级。 (2)非调节级:通流面积能不随负荷改变的级,可以 全周进汽,也可以部分进汽。
第一章汽轮机的工作原理

第二节 汽轮机的工作过程
与绝热指 数及喷嘴压力 比有关,其关 系式如右。
k
2
1
2
k n
k 1
n k
k 1
2 k1
k
1
在亚临界条件下: <1,在临界和超临界条 件下:=1
❖ 与n的关系绘成如图 所示的曲线。计算时,先在 图上查 取 值,然后利用下式计算:
G Gcr 0.648An
p0* RT0*
(四)蒸汽在喷嘴斜切部分中的流动
出口截面:
G Anc1t 1t
ln sin1 tnc1t 1t
在实际结构中, lnln´,所以:
sin1
crccr 1t c1t
s in 1
对等熵流动,有以下等式成立:
1
1
1
cr 1t
pcr p1t
k
cr n
k
k
2
1
k
1
1
nk
ccr c1t
k1
k
1
1
k k1 k 1
临界压力比:临界压力与滞止初压之比 即
cr
pcr p0*
对过热蒸汽,k = 1.3,则0.546 对于干饱和蒸汽,k = 1.135则0.577
3.喷嘴出口汽流实际速度: c1=c1t
----喷嘴速度系数 喷嘴的动能损失:
hn 1 2 hn*
1.2蒸汽在喷嘴和动叶通道中的流动过程解析

(二)喷嘴中蒸汽参数、流速与等比熵比焓 降之间的关系 如图1.2.3所示。 当等比熵焓将降达到临界值时,喷嘴通道截 面积最小,此处是临界截面,此处的蒸汽流速 等于当地音速。 由于喷嘴内沿汽流方向的流通各截面处蒸汽 的温度逐渐降低,故音速也逐渐降低。蒸汽的 压力沿喷嘴流道是逐渐降低的,汽流速度是逐 渐增大的。 蒸汽比容是逐渐增大的。
7
0 c1 c1t 2hn
由它可求出实际流动过程中的喷嘴动能损失, 即喷嘴损失:
2 c0 c12t 2 hn (1 2 ) 1 2 hn 2 2 2
c12t
0 2 hn 是喷嘴实际出口动能,因此 2Fra bibliotek也称为
喷嘴效率。
8
蒸汽在喷嘴中的膨胀过 程如左图所示。 在其出口,喷嘴的实际 汽流速度c1比理想速度 c1t要小,所损失的动能 又重新转变为热能,在 等压下被蒸汽吸收,比 熵增加,使喷嘴出口汽 流的比焓值升高。因此, 蒸汽在喷嘴内的实际膨 胀过程不再按等比熵线 进行,而是一条熵增曲 线。
0 2(h0 h1t )
2 0
2 0 2hn c0 2hn
2
若用初始状态参数计算(无H-S图的情况下用此表达式计算)
c p cv R cp cv k
pv k const h c pT k k RT pv k 1 k 1 2 c12t c 0 k h0 h1t ( p 0 v 0 p1v1 ) 2 k 1 k 1 k p k 1 p 0 v 0 1 k 1 p0
4
称为喷嘴压比,即喷嘴后的 压力与喷嘴前的滞止压力之比。 喷嘴出口的实际速度 摩擦阻力使蒸汽出口焓值升高,出口速度比 理想速度降低。 喷嘴速度系数 :喷嘴出口实际速度与喷 嘴出口的理想速度之比。速度系数正是反映喷 嘴内由于各种损失而使汽流速度减小的一个修 正值。 c1
第一章 第二节 汽轮机级的工作原理

pcr 2k * * ccr p0 v0 [1 * p k 1 0
2 pcr p ( ) k 1
* 0 k k 1
k 1 k
喉部
]
Байду номын сангаас
p0 c0
p1 p1c c1c
ccr
2k * * p 0 v0 k+1
ccr只与蒸汽滞止初 参数有关,而与流 动过程中有无损失 及损失的大小无关。 11
2
第二节 蒸汽在级内的流动过程
基本控制方程
1、连续方程 在稳定流动的情况下,每单位时间流过流管任 一截面的蒸汽流量不变,用公式表示为 G=Ac 1 A1c1 2 A2c2 常数
G-单位时间的蒸汽质量流量,kg/s A-汽道内任一横截面面积,m2 c-垂直于截面A的蒸汽速度,m/s ρ-截面A上蒸汽的密度,kg/m3
Gcr 0.647An
cdc
5
第二节 蒸汽在级内的流动过程
能量方程
对于稳定绝热流动,汽流进入系统的能量必须等于离 开系统的能量。若在流动系统中忽略摩擦力做功和势能等 因素,则系统的能量方程式可以写为,
2 c0 c12 h0 q h1 W 2 2
c0 、 式中: h0 、h1-蒸汽进入和流出系统的焓值,J/kg; c1-蒸 汽进入和流出系统时的速度 ,m/s ; q-1kg 蒸汽通过系统时, 对外界所吸收的热量,J/kg;W-1kg蒸汽通过系统时对外界 所作的机械功 ,J/kg。
绝热q=0
蒸汽在流经喷管时不做功w=0
1.喷管出口汽体的理想速度
2 c0 c12t h0 h1t 2 2
2 c0 c12 h0 h1 2 2
热力叶轮机械原理第一章 透平级工作原理 2

k
带入上式得:
c1s
2k k 1
p0
0
1 (
p1 p0
)
k 1 k
c02
2k k 1
RT0
1
(
p1 p0
)
k 1 k
c02
2019/11/1
8
基本方程
4)能量方程
如果忽略摩擦力作功和势能的变化等因素:
系统的能量方程为: i1
v1
v2
出口截面积:
A1
G
1c1
喉部截面积:
Acr
G
crccr
2019/11/1
26
2)喷管中的实际流动过程
特点:
实际蒸汽是粘性流体,蒸汽在喷管中的 流动过程是有阻力的;
蒸汽将消耗一部分能量来克服流动阻力;
因此,喷管中的流动不再是等熵流动,但 还是绝热流动。
2019/11/1
临界压比: cr
pcr p0*
(
2
k
) k 1
k 1
( 空气: cr 0.528 ;过热蒸汽: cr 0.546 )
临界密度:cr
0 (
pcr p0
1
)k
2019/11/1
25
设计与计算过程
③ 计算喷管出口截面积 A1 和喉部(临界) 截面积 Acr
连续方程:
A1c1 A2c2 G const
2019/11/1
13
二、蒸汽在喷管中的流动过程
喷管膨胀效果: → 设计工况
1)收缩喷管出口截面的汽流速度 ≦ 音速; 2)缩放喷管出口截面的汽流速度 > 音速。
汽轮机的工作原理

反动级
三、汽轮机级旳类型
(二)压力级与速度级
压力级—以利用级组中合理分配旳压力降 或焓降为主旳级。(效率高,单列级)
速度级—以利用蒸汽流速为主旳级。(做 功能力大)
双列速度级 多列速度级
三、汽轮机级旳类型
(三)调整级与非调整级
调整级—通流面积能够随负荷变化旳级。 (第一级)
非调整级—通流面积不随负荷变化旳级 (第一级后来旳各级)
(3)蒸汽在叶栅通道旳流动是绝热流动:即蒸汽在叶栅通道中流动时与 外界没有热互换。
2、基本方程
(1)连续性方程 微分形式
(2)运动方程
G cA
dA dc d 0 Ac
dp Rdx cdc
(3)能量方程
h0
c02 2
q
h1
c12 2
w
(4)状态方程
pv RT
pvk const.
第二节 蒸汽在汽轮机级中旳流动
2、级内能量转换过程:
具有一定压力、温度旳蒸汽经过汽轮机旳级时,首 先在静叶栅通道中得到膨胀加速,将蒸汽旳热能转化为 高速汽流旳动能,然后进入动叶通道,在其中变化方向 或者既变化方向同步又膨胀加速,推动叶轮旋转,将高
速汽流旳动能转变为旋转机械能。
3、冲动级:
当汽流经过动叶通道时,因为受到动叶通道形状旳限制 而弯曲被迫变化方向,因而产生离心力,离心力作用于叶 片上,被称为冲动力。这时蒸汽在汽轮机旳级所作旳机械 功等于蒸汽微团流进、流出动叶通道时其动能旳变化量。 而这种级称为冲动级。
一、蒸汽在喷嘴中旳膨胀过程
喷嘴旳作用是让蒸汽在其通道中流动时得到膨胀
加速,将热能转变为动能。喷嘴是固定不动旳,蒸汽
流过时,不对外作功,W = 0;同步与外界无热互换,
第一章汽轮机工作原理

理想能量扣除喷管、动叶和余速损失外,其余的 能量全部转化为轮周功,则有: Wu E0 hn hb (1 1 )hc2 ht* hn hb hc2
u
E0 hn hb (1 1 )hc2 E0 1 n b (1 1 ) c 2
Fu F G(c1 cos 1 c2 cos 2 )
' u
2、轴向力 F
Z
蒸汽在轴向上所受的总力:为流道壁对蒸汽的轴向反作用力 与动叶片前后压差所产生的力 Ab ( p1 p2 )之和。
蒸汽在轴向的动量改变量应等于轴向的作用冲量,即:
[ Fz' Ab ( p1 p2 )] t m(c2 z c1z )
Fz' m (c1 z c2 z ) Ab ( p1 p2 ) t
Fz Fz' G(c1 sin 1 c2 sin 2 ) Ab ( p1 p2 )
F Fz 2 Fu 2
(二).轮周功率 Pu
单位时间内蒸汽推动叶轮旋转所作出的机械功称为轮周功率。
(二)流量计算
通过喷嘴的质量流量决定于流道的出口面积、出口流速和对 应出口点的蒸汽比容。 对出口面积为 An 的喷嘴,其流过的理想质量流量为: An c1t Gnt 1t 考虑流动损失,实际流过的质量流量为: An c1 Gn 1 Gn 令 为流量系数,则有: Gnt A n c1 / 1 1t c1 / 1 A n c1t / 1t c1t / 1t 1
G nc 0.65 An p / v
二、蒸汽在渐缩斜切喷嘴中的膨胀
为了保证喷嘴出口汽流按良好 方向进入动叶通道,喷嘴出口都有 一段斜切部分abc,这种喷嘴称为 斜切喷嘴。
汽轮机原理(第一章)

微分形式程
dA dc d
0
AC -
2.动量方程
dpRdxcdc
式中 R-作用在单位质量汽流上的摩擦阻 力,若流动是无损失的等熵流动,则R=0, 于是
dp cdc
-
3.能量方程 h0c202 qh1c212 w
式中 h0、h1-蒸汽进入和流出系统的比焓值; c0、c1-蒸汽进入和流出系统的速度; q-1kg蒸汽通过系统时从外界吸入的热量; w- 1kg蒸汽通过系统时对外界所做的机 械功。
负荷改变时,级的通流面积不变。
-
四、级的工作过程的研究方法
(一)基本假设 (1)一元流动,也称轴对称流动。 (2)定常流动,也称稳定流动。 (3)绝热流动。
-
(二)基本方程 1.连续方程
G c A1 c 1 A 12 c 2A 2 常数
式中
G-蒸汽质量流量; A-汽道内任一横截面积; c -垂直于截面A的蒸汽流速; ρ-截面A上的蒸汽密度。
Ωm=0的级, Δhb=0, Δh*n= Δh*t, 做功能力较大,但效率较低,如图1-3所示。 2.冲动级(带反动度的冲动级)
ΔhbΩ<mΔ=h0n,.0做5~功0能.2力0的和级效,率介Δ于hb纯>冲0,动但级和 反动级之间。
-
图1-3 纯冲动级中蒸汽压力和速度的变化 示意
图1-4 反动动级中蒸汽压力和速度的变化示意
-
3.反动级 Ωm≈0 .5的级, Δhb=Δhn,动、静叶
型相同,做功能力较小,但效率高,如图1- 4所示。 (二)按能量转换过程分 1.速度级
以利用蒸汽流速为主的级,有双列和多列之 分。双列速度级又称复速级,如图1-5所示。
-
复速级是由一列喷嘴叶栅和 装在同一叶轮上的两列动叶栅以 及第一列动叶栅后的固定不动的 导向叶栅所组成。蒸汽在喷嘴中 膨胀,在第一列动叶栅中作一部 分功,在固定的导向叶栅中改变 蒸汽流动方向,在第二列动叶栅 内继续作功。
汽轮机原理教材1
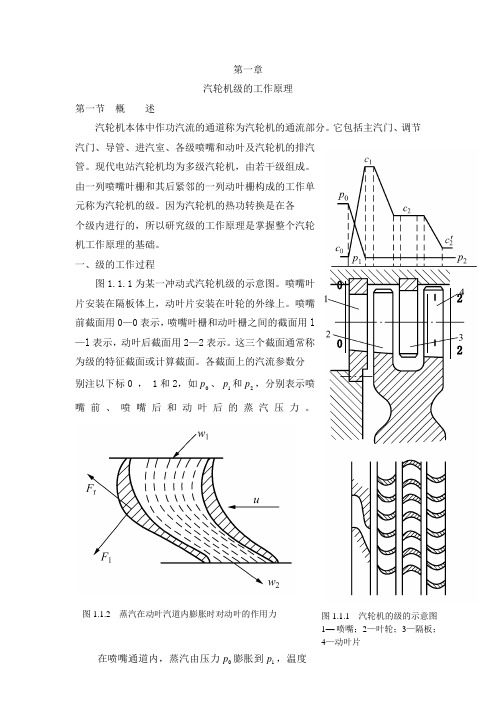
第一章 汽轮机级的工作原理第一节 概 述汽轮机本体中作功汽流的通道称为汽轮机的通流部分。
它包括主汽门、调节汽门、导管、进汽室、各级喷嘴和动叶及汽轮机的排汽管。
现代电站汽轮机均为多级汽轮机,由若干级组成。
由一列喷嘴叶栅和其后紧邻的一列动叶栅构成的工作单元称为汽轮机的级。
因为汽轮机的热功转换是在各 个级内进行的,所以研究级的工作原理是掌握整个汽轮 机工作原理的基础。
一、级的工作过程图1.1.1为某一冲动式汽轮机级的示意图。
喷嘴叶 片安装在隔板体上,动叶片安装在叶轮的外缘上。
喷嘴前截面用0—0表示,喷嘴叶栅和动叶栅之间的截面用l —l 表示,动叶后截面用2—2表示。
这三个截面通常称为级的特征截面或计算截面。
各截面上的汽流参数分 别注以下标0 , 1和2,如0p 、1p 和2p ,分别表示喷嘴前、喷嘴后和动叶后的蒸汽压力。
在喷嘴通道内,蒸汽由压力0p 膨胀到1p ,温度由0t 下降到1t ,汽流速度相应地由0c 升到1c 。
可见,蒸汽从四嘴的进口到出口实现了由热能向动能的转换。
高速流动的蒸汽由喷嘴出口进入动叶时,给予动叶以冲动力i F 。
通常汽流在动叶槽道中继续膨胀,并转变方向,当汽流离开动叶槽道时,它给叶片以反动力r F (见图1.1.2),这两个力的合力,推动动叶带动叶轮和轴旋转,作出机械功。
动叶以转速n 绕汽轮机轴旋转,用u 表示动叶平均直径b d 处(即1/2叶高处,见图(1.1.1)的圆周速度,其大小为(1.1.1)其方向为动叶运动的圆周方向。
由于动叶以圆周速度u 运动,所以,以1c 表示的喷嘴出口汽流的绝对速度,是以相对速度1w 进入动叶的。
1c ,u 与1w 构成动叶进口速度三角形,如 图1.1.3(a )所示,即1w =1c u - (1.1.2) 汽流以相对速度2w 离开动叶,由于动叶以圆周速度u 运动,所以动叶出口汽流的绝对速度是2c 。
2w , u 与2c 构成动叶出口速度三角形,如图1.1.3(a)所示,即2c =2w u - (1.1.3)图中ß表示叶轮旋转平面与相对汽流速度的夹角,ą表示叶轮旋转平面与绝对汽流速度的夹角。
第16课时单元_电厂热力设备及运行_第09章_汽轮机工作原理

质的汽化潜热重新在循环中得到利用,减少工质冷源损失,
漏入空气,回收工质和热量。
汽轮机设备的组成:
供油设备:供给机组调节、保安、轴承润滑和顶轴等处的
工作用油。
旁路设备:机组启动期间,使蒸汽和再热蒸汽参数尽快达
到汽轮机冲转要求;机组正常运行期间,协调机炉之间蒸
汽量;机组甩负荷或运行工况急剧变化时,排出锅炉产生 的过量蒸汽。旁路系统还可用于保护锅炉再热器。 调节保护系统:控制汽轮机转速,使汽轮机发电机能并入 电网;在外界负荷变化时及时地调节汽轮机功率,以满足 用户用电量变化的需要,同时保证汽轮发电机组的工作转 速在正常允许范围内。
喷嘴中的热力过程
2.喷嘴出口汽流的理想速度
1 2 1 2 h0 h1t c1t c0 2 2
2 c1t 2(h0 h1t ) c0
(9 1) (9 2)
h0 喷嘴叶栅进口蒸汽的焓,j / kg。 c0 喷嘴叶栅进口蒸汽的速度,m / s。 h1t 喷嘴叶栅出口蒸汽的理想焓,j / kg。 c1t 喷嘴叶栅出口蒸汽的理想速度,m / s。
四、作业
(1)汽轮机本体由哪些部件组成? (2)汽轮机的辅助设备主要有哪些?
图9-6 冲动级工作原理
二、冲动级 的工作原理
单级汽轮机:由一个 级构成的汽轮机。 多级汽轮机:由多个 级构成的汽轮机。
图9-7 单级冲动级汽轮机结构简图
1-轴;2-叶轮;3-动叶栅;4-喷嘴
三、反动级的工作原理
反动级:当汽流通过动叶
通道时,一方面要改变方
向,同时还要膨胀加速, 改变方向会对叶片产生一 个冲动力,膨胀加速会对 叶片产生一个反作用力,
原动机:拖动发电机旋转发电的机械或设备。 汽轮机:把蒸汽的热能转换为机械能,拖动其它机械 转动的原动机。 汽轮发电机组:汽轮机与发电机的组合体。 汽轮机设备:汽轮机本体及其辅助设备由管道和阀门 连成的一个整体。
汽轮机原理课件第一章

叶轮摩擦损失
– 叶轮两侧及围带表面的粗糙度引起的摩擦损失 – 子午面内的涡流损失引起的损失
部分进汽损失
– 装有喷嘴的弧段长度Z*L(Z为喷嘴片数)于整个圆周长度∏*Dm的比值来表 示部分进汽的程度,称为部分进气度,用e表示。 – 由于部分进汽带来的能量损失称为部分进汽损失,由鼓风损失和斥汽损失组 成。鼓风损失发生再不装喷嘴的弧段内,斥汽损失欲鼓风损失相反。
理想等环流流型
– 等环流流型的气流速度沿叶高的变化规律:C1z=const ,C1u*r=const,C1r=0 – 使轴向间隙中汽流保持径向平衡且C1r=0,喷嘴出口汽流的切向分速C1u必须 随半径的增加而减少。 – 自由涡流流型,正因为没有漩涡产生,所以能量转换较高。 下一页
– 反动度的变化规律
简单流动模型易用一元稳定等比熵流动的基本方程
– 连续方程:G*v=A*c – 能量方程: h0 + c02/2 = h + c12/2 + w – 状态或过程方程:p*v=const
蒸汽在喷嘴和动叶通道中的流动过程
临界参数的概念
– 蒸汽流量不变时,当喷嘴中等比熵焓降达到临界值时,喷嘴通道面积为最小, 此处便是临界截面,其蒸汽流速等于当地音速。临界状态下的参数称为临界参 数。 – 临界速度,临界压力,临界压比,临界流量,实际流量
汽轮机级的工作原理
第 八 节 节 第 七 节 效 率 和 动 率 轮 轴 第 六 节 第 五 节 轮 轴 效 第 四 和 节 率 第 三 动 和 动 节 流 嘴 第 二 节 第 一
概述
汽轮机本体作工气流的通道称为汽轮机的通流部分,他包括主气门,导 管,调节气门,进汽室,各级喷嘴和动叶及汽轮机的排汽管。 汽轮机的级是由一列喷嘴叶栅和其后紧邻的一列动叶栅构成的工作单元。 动叶栅进出口汽流速度三角形 喷嘴及动叶的热力过程及热力过程线,以及蒸汽在此的流动过程 喷嘴损失,动叶损失和余速损失之和称为轮周损失。
第一章 汽轮机级的工作原理

p0
如图所示, AB为渐缩 喷嘴的出口截面,即吼口 截面,ABC 即为斜切部分。 当喷嘴出口压力p1大于临 界压力p1c时,蒸汽在斜切 部分不发生膨胀。
pt αt ct 图1-13 喷管斜切部分
(1) n cr ,当喷管出口截面上的压力比大于或等于临界 压力比时,喷管喉部截面AB上的流速小于或等于声速, 这时蒸汽仅在喷管的收缩部分中膨胀, 而在其斜切部分 中不膨胀,喷管斜切部分只起导向作用,汽流方向与轮 周方向的夹角称为喷管的出汽角 1
h ∆hn
2 h1t 1
p1 h1
图1-7蒸汽在喷嘴中的热力过程
s
2、几何条件
dA dc 2 ( M 1) A c
(1)当喷管内汽流为亚声速流动时(M<1),dA<0,这 种喷管成为渐缩喷管; (2)当喷管内汽流为超声速流动时(M>1),dA>0,这 种喷管成为渐扩喷管; (3)当喷管内汽流速度等于当地声速时(M=1),dA=0, 喷管的截面为最小值,这个截面为临界截面(喉部截 面) (4)欲使汽流在喷管中自亚声速增加至超声速,则截面 应由渐缩变为渐扩,这种喷管成为缩放喷管或拉伐尔 喷管。
p1 ——喷管后压力与喷管前滞止压力之比, n * p0
p ( v
0 0 0
0
2 k n
k 1 k n
)
p p 2 A p A ) G A K( K 1 v p
ntc n 0 0 n 0 0 n 0 0
K 1 K 1
0
式中
n ——喷管的流量系数
v1t 1 n 1t v1
图1-11喷管和动叶的流量系数
第一章§2 蒸汽在喷嘴和动叶通道中的流动过程.

第二节
蒸汽在喷嘴和动叶通道中的流动过程
一、蒸汽在喷嘴中的膨胀过程
2、喷嘴中蒸汽参数、流速与等比熵比焓降的关系
d: A c
c Ma a
航空发动机,哪个是 超音速发动机?
第二节
蒸汽在喷嘴和动叶通道中的流动过程
一、蒸汽在喷嘴中的膨胀过程
2、喷嘴中蒸汽参数、流速与等比熵比焓降的关系
喉部 p0 c0 p1 pcr ccr
pcr 2 kk cr * ( ) 1 p0 k 1
等商过程,临界压比εcr只与蒸汽绝热指数k有关。 对于过热蒸汽:k=1.3, εcr = 0.546 饱和蒸汽:k=1.135, εcr = 0.577 空气:k=1.4, εcr = 0.528
第二节
蒸汽在喷嘴和动叶通道中的流动过程
一、蒸汽在喷嘴中的膨胀过程
2、喷嘴中蒸汽参数、流速与等比熵比焓降的关系
?蒸汽经过喷嘴时为什么能够在较小能量损失的情
况下进行能量转换
答:因为喷嘴几何形状满足空气动力学公式:
dA dc 2 M a 1 A c
dA dc d 0 A c
1.连续方程式
p1
1 1t
实际喷嘴出口速度:
c1 c1t 2h 2hn c
* n
2 0
s
喷嘴损失: 喷嘴损失系数:
2 c12t c12 2 c1t * hn (1 ) (1 2 )hn 2 2 2
c12t c12 hn 2 2 n * 1 2 2 c1t hn 2
蒸汽在喷嘴和动叶通道中的流动过程
一、蒸汽在喷嘴中的膨胀过程
P0* 0* p0
* h Δhn
第一章汽轮机级的工作原理

第一章汽轮机级的工作原理第一章汽轮机级的工作原理第一节概述一、蒸汽的冲动作用原理和反动作用原理在汽轮机中,级是最基本的工作单元,在结构上它是由喷嘴和其后的动叶栅所组成。
蒸汽的热能转变成机械能的能量转变过程就是在级内进行的。
汽轮机从结构上可分为单级汽轮机和多级汽轮机。
只有一个级的汽轮机称单级汽轮机。
有多个级的汽轮机称多级汽轮机。
图1-1是最简单的单级汽轮机主要部分结构图。
动叶按一定的距离和一定的角度安装在叶轮上形成动叶栅,并构成许多相同的蒸汽通道。
动叶栅装在叶轮上,与叶轮以及转轴组成汽轮机的转动部分,称为转子。
静叶按一定的距离和一定的角度排列形成静叶栅,静叶栅固定不动,构成的蒸汽通道称为喷嘴。
具有一定压力和温度的蒸汽先在喷嘴中膨胀,蒸汽压力、温度降低,速度增加,使其热能转换成动能,从喷嘴出来的高速汽流,以一定的方向进入动叶通道,在动叶通道中汽流速度改变,对动叶产生一个作用力,推动转子转动,完成动能到机械能的转换。
图1-1 单级汽轮机结构简图(a)立体图(b)剖面图1-主轴2—叶轮3—动叶4—喷嘴5—汽缸6—排汽口在汽轮机的级中能量的转变是通过冲动作用原理和反动作用原理两种方式实现的。
(一)冲动作用原理由力学可知,当一运动的物体碰到另一个静止的或速度不同的物体时,就会受到阻碍而改变其速度的大小和方向,同时给阻碍它运动的物体一个作用力,这个力称为冲动力。
冲动力的大小取决于运动物体的质量和速度变化,质量越大,冲动力越大;速度变化越大,冲动力越大。
若在冲动力的作用下,阻碍运动的物体速度改变,则运动物体就做出了机械功。
根据能量守恒定律,运动物体动能的变化值就等于其做出的机械功。
利用冲动力做功的原理就是冲动作用原理。
在汽轮机中,从喷嘴中流出的高速汽流冲击在汽轮机的动叶上,受到动叶的阻碍,而改变了其速度的大小和方向,同时汽流给动叶施加了一个冲动力。
图1-2所示为无膨胀的动叶通道,蒸汽以速度w r1进入通道,由于受到动叶的阻碍不断地改变运动方向,最后以速度w r2流出动叶,则蒸汽对动叶施加了一个轮周方向的冲动力i F ,该力对动叶做功使动叶带动转子转动。
第一章 汽轮机级的工作原理-第二节 蒸汽在喷嘴和动叶通道中的流动过程

第二节 蒸汽在喷嘴和动叶通道中的流动过程在第一节中介绍了级的工作过程。
本节主要分析蒸汽流经喷嘴和动叶通道过程中,对级的工作特性有重要影响的通流特性、通流能力和流动效率问题。
一、蒸汽在喷嘴中的膨胀过程(一)喷嘴出口汽流速度蒸汽在喷嘴通道中的理想膨胀过程如图1.1.4中的线段01’所示。
当喷嘴前的蒸汽参数及初速0c 为已知时,则 02000002c c h h h h δ=+=+ (1.2.1) 将式(1.2.1)代入式(1.1.16),因为喷嘴是固定的,不对外做功,w=0,则喷嘴理想出口速度1t c 为1t c ====理想气体在等比熵膨胀过程中的比焓差可表示为 000001010011()()11t t t h h R T T p v p v κκκκ-=-=--- (1.2.3)将式(1.2.3)代入式(1.2.2)得1t c = (1.2.4) 或1t c =式中,010n p p ε=,称为喷嘴压比,即喷嘴后的压力与喷嘴前的滞止压力之比。
式(1.2.2)用于喷嘴的计算,它表示喷嘴汽流理想速度的大小取决于喷嘴的滞止理想比焓降。
式(1.2.5)常用于理论分析.它表明影响喷嘴出口速度的因素。
在给定蒸汽性质和初态的情况下,1t c 仅是压比的单值函数。
在喷嘴的实际流动过程中。
蒸汽粘性所产生的摩擦等损失使蒸汽出口速度由1t c 减小为1c 即11==t c c ϕ式中,ϕ称为喷嘴速度系数。
由它可求出实际流动过程中的喷嘴动能损失,即喷嘴损失,其值为 22222011111222t t n n c c c h h δϕϕ=-=-=-∆()() (1.2.7) 影响喷嘴速度系数ϕ的因素多(如喷嘴高度、叶型、汽道形状、压比及表面粗糙度等)而复杂,很难用理论计算精确求得,一般由试验确定。
ϕ与叶片高度n l 关系密切,故实验数据常绘制为ϕ随n l 的变化曲线,如图1.2.1 所示。
由图可见,当喷嘴高度n l >100mm 时,ϕ值基本上不再随n l 而变化;当n l <12~15mm 时,ϕ值剧烈下降。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二节 蒸汽在喷嘴和动叶通道中的流动过程在第一节中介绍了级的工作过程。
本节主要分析蒸汽流经喷嘴和动叶通道过程中,对级的工作特性有重要影响的通流特性、通流能力和流动效率问题。
一、蒸汽在喷嘴中的膨胀过程(一)喷嘴出口汽流速度蒸汽在喷嘴通道中的理想膨胀过程如图1.1.4中的线段01’所示。
当喷嘴前的蒸汽参数及初速0c 为已知时,则 02000002c c h h h h δ=+=+ (1.2.1) 将式(1.2.1)代入式(1.1.16),因为喷嘴是固定的,不对外做功,w=0,则喷嘴理想出口速度1t c 为1t c ====理想气体在等比熵膨胀过程中的比焓差可表示为 000001010011()()11t t t h h R T T p v p v κκκκ-=-=--- (1.2.3)将式(1.2.3)代入式(1.2.2)得1t c = (1.2.4) 或1t c =式中,010n p p ε=,称为喷嘴压比,即喷嘴后的压力与喷嘴前的滞止压力之比。
式(1.2.2)用于喷嘴的计算,它表示喷嘴汽流理想速度的大小取决于喷嘴的滞止理想比焓降。
式(1.2.5)常用于理论分析.它表明影响喷嘴出口速度的因素。
在给定蒸汽性质和初态的情况下,1t c 仅是压比的单值函数。
在喷嘴的实际流动过程中。
蒸汽粘性所产生的摩擦等损失使蒸汽出口速度由1t c 减小为1c 即11==t c c ϕ式中,ϕ称为喷嘴速度系数。
由它可求出实际流动过程中的喷嘴动能损失,即喷嘴损失,其值为 22222011111222t t n n c c c h h δϕϕ=-=-=-∆()() (1.2.7) 影响喷嘴速度系数ϕ的因素多(如喷嘴高度、叶型、汽道形状、压比及表面粗糙度等)而复杂,很难用理论计算精确求得,一般由试验确定。
ϕ与叶片高度n l 关系密切,故实验数据常绘制为ϕ随n l 的变化曲线,如图1.2.1 所示。
由图可见,当喷嘴高度n l >100mm 时,ϕ值基本上不再随n l 而变化;当n l <12~15mm 时,ϕ值剧烈下降。
因此在设计时,为了减少喷嘴损失,应尽量使n l >15mm 。
图中上面一条是喷嘴宽度n B 为55mm 的曲线,下面一条是月n B 为80mm 的曲线,可见,在强度允许的条件下应采用宽度较小的喷嘴。
式(1.2.7)中,22012nc h ϕ∆=是喷嘴实际出口动能,因此2ϕ也称为喷嘴效率。
喷嘴速度系数ϕ值一般在0.920.98之间。
对于渐缩喷嘴,常把其中与叶片高度有关的损失抽出来另用经验公式计算(详见本章第五节),这时取ϕ=0.97。
由于喷嘴中的实际膨胀过程有损失(如图1.1.4所示),即是沿着有损失的绝热过程线0l 膨胀的,所以实际过程是一个多变过程而不是等比熵过程。
多变过程方程为npv=常数 (1.2.8)式中,多变过程指数n是小于定熵指数κ但大于1的一个数值。
当n=κ时,0l 过程线就与等比熵过程线01’重合;当n=1时,蒸汽在喷嘴中的流动成了等温过程,01线接近水平的等比焓线。
由此可见,n与κ之间的关系必与喷嘴效率2ϕ有关,因2ϕ的大小决定了0l线在h-s图上的实际位置。
对于给定的喷嘴,ϕ可视为定值。
在这样的条件下,由热力学基本关系式可以推导出n与2ϕ和κ的关系为2(1)nκκϕκ=+-(1.2.9)由上式可知,当2ϕ=l时,n=κ;2ϕ<1时,n<κ。
图1.2.2表示n与2ϕ的关系曲线在ϕ的实用范围内,它基本上是直线规律的。
(二)喷嘴中蒸汽参数、流速与等比熵比焓降之间的关系当蒸汽流量G不变时,在图1.1.4的喷嘴等比熵过程线01’上选取若干中间状态点,查得这些点的蒸汽比焓值h、压力p、比容v,按式(1.2.2)算出这些状态点的流速1c,按连续方程A=Gv/1c算出这些状态点的通流面积A然后以等比熵比焓降xh∆=0xh h∆=为横坐标,画出蒸汽参数、流速与等比熵比焓降之间的关系,如图1.2.3所示。
由图可见,当等比熵比焓降xh∆ch∆时,喷嘴通道截面积为最小,此处是临界截面,临界截面积以cA表示,此处的蒸汽流速等于当地音速。
由于喷嘴内沿汽流方向的流通各截面处蒸汽温度逐渐降低,故音速αα所示。
由工程热力学可知当x h ∆<c h ∆时,喷嘴通道截面是渐缩的,当x h ∆>c h ∆时,喷嘴通道截面是渐扩的,喷嘴截面积的变化规律如曲线A 所示。
由图还可看出,蒸汽压力p 沿喷嘴流道是逐渐降低的;汽流速度1c 是逐渐增大的;蒸汽比容v 是逐渐增大的;在亚临界区域,即在喷嘴的渐缩段.1c 约增大较v 的增大快得多,在超音速区域,即渐扩段,1c 较v 增大得慢。
(三)喷嘴中汽流的临界状态汽流速度等于当地音速时的状态称为临界状态。
临界状态下的所有参数称为临界参数。
临界参数的特性对研究级的工作过程有重要意义,其中最主要的是临界速度1c c 、临界压比εnc 、临界截面积c A 和临界流量tc G 。
1.临界速度1c c音速计算式为(1.2.10) 对于任一截面,能量方程h ˚=h+21c /2可写为200100112c p v pv κκκκ=+-- (1.1.11) 或 200100112c p v pv κκκκ=+-- (1.2.12) 对于临界截面,1c =α=1c c ,则可求得临界速度:(1.2.13) 由式(1.2.13)可知,在κ值确定后.1c c 只与蒸汽滞止初参数有关,而与流动过程中有无损失以及损失的大小无关。
图1.2.4的h —s 图中画出了等临界速度线,也是等pv 线,或等比焓线。
由于021/2ncc h c ∆=,不论流动中有无损失或损失大小,只要00p ,00v 不变, 则1c c 不变,故0nc h ∆也就不变,如图所示。
2.临界压力1c p 和临界压比nc ε由式(1.2.10)和式(1.2.13)得1c c ==(1.2.14) 将等比熵过程方程000011()c c p v p v κκ=代入上式,求解得(1.2.15) 则 (1.2.16)由式(1.2.16)可知,等比熵过程中,nc ε只与κ有关。
过热蒸汽κ=1.3,则εnc=0.546;干饱和蒸汽κ=1.135,则nc ε=0.577。
(四)喷嘴的通流能力当喷嘴出口截面积为n A 时,通过喷嘴的理想流量为11n t nt tA c G v = (1.2.17) 将式(1.2.4)和由式(1.1.19)解出的1t v 代入上式,可得nt G = (1.2.18) 或nt G A =(1.2.19) 式(1.2.19)表明喷嘴的通流能力与蒸汽滞止初参数、蒸汽性质、喷嘴出口面积和压比有关。
在蒸汽性质、滞止初参数和出口面积n A 一定的情况下,喷嘴的通流能力只取决于喷嘴压比,即nt G =f(n ε),如图1.2.5中曲线0BC 所示。
通过最大流量时的压比可以通过对函数式(1.2.19)求极值得到,即令0nt n G ε∂=∂解得1n 2()1nc κκεεκ-==+ (1.2.20) 可见,喷嘴通过最大流量时的压比就是临界压比εnc ,因此.最大流量就是临界流量。
将式(1.2.20)代入式(1.2.19).即得喷嘴理想临界流量表达式:ntc G A = (1.2.21) 将κ=1.3及κ=1.135分别带入上式,得过热蒸汽0.6673ntc G A = (1.2.22) 饱和蒸汽0.6356ntc G A =式(1.2.22)和式(1.2.23)中,00p 的单位是Pa ,00v 的单位是3m /kg ,n A 的单位是2m ,G ntc 的单位是kg/s 。
可见,喷嘴出口面积和蒸汽性质确定后,临界流量只与滞止初参数有关。
图1.2.5中的虚线0B 只运用于缩放喷嘴的各种设计工况(见第三章第一节),对于直轴渐缩喷嘴(没有斜切部分)是不适用的.因为试验表明,直轴渐缩喷嘴在n εnc ε≤时,出口流速为临界速度,流量始终保持临界流量不变,如图中BA 线所示。
这是因为n ε=nc ε时,出口汽流已达音速、此后继续降低背压1p 由临界压力c p 到1p 的膨胀是在喷嘴后实现的,不可能改变喷嘴出口截面的临界状态,所以流量仍然保持临界流量不变。
直轴渐缩喷嘴的流量与压比的关系如曲线ABC 所示。
由于蒸汽流动过程有损失,故喷嘴的实际流量为 111111n n t t n nt n nt A c A c v G G G v v v ϕϕμ==== (1.2.24)式中,11t n υμϕυ=等称为喷嘴的流量系数,它是喷嘴的实际流量与理想流量之比。
就非等熵绝热过程来说,由于流动损失加热了蒸汽,故1υ>1t υ即于11t υυ<1,那么应该是n μ<ϕ。
但由于蒸汽过热度、湿度、进口压力、压比、反动度以及速度系数等许多因素都会影响比值11t υυ。
因此此比值可能小于1,等于1或大于1。
正是这种复杂的关系,使n μ很难用理论方法准确计算通常用试验方法求得,如图1.2.6所示。
当喷嘴在过热区工作时,由于喷嘴损失所引起的比容变化较小,故1υ≈1t υ,因而图中所示的流量系数近似等于速度系数,即n μ≈ϕ=0.97。
当喷嘴在湿蒸汽区工作时,由于蒸汽通过喷嘴的时间极短,有一部分应凝结的饱和蒸汽来不及凝结,出现了凝结滞后的过饱和现象,即大部分蒸汽没有获得这一部分蒸汽凝结时应放出的汽化潜热,故整个蒸汽温度较低,使蒸汽的实际比容1υ反而小于理想比容1t υ,即11t υυ>1,于是实际流量大于理想流量,如图1.2.6所示,n μ=1.02。
当蒸汽在喷嘴中流动有过饱和现象时,如图1.2.7所示,喷嘴进口蒸汽虽已处于湿蒸汽区(0χ=0.98),但它还是过饱和蒸汽,按过热蒸汽的膨胀规律进行膨胀。
在蒸汽膨胀到湿度大约为3.5%时,喷嘴内部中段某截面上会发生突跃,突然出现水分凝结,突跃前后有一个明显的压力升高,如图中的a 、b 两点所示。
在突跃后,由b 点到出口,蒸汽是湿蒸汽状态,按湿蒸汽的膨胀规律进行膨胀。
考虑流量系数之后,计算实际临界流量的公式为ncn ntc G G μ=,即 过热蒸汽 (n μ=0.97)0.6473nc G A = (1.2.25) 饱和蒸汽 (n μ=1.02)0.6483nc G A = (1.2.26) 实际上,无论是过热蒸汽还是饱和蒸汽,都可以采用下式计算:0.648nc G A = (1.2.27) 式(1.2.27)中各变量的单位与式(1.2.22)和式(1.2.23)相同。
必须指出,用上述公式计算流量时,不论是渐缩喷嘴还是缩放喷嘴,都必须先判断喷嘴喉部是否在临界状态下工作,然后才能确定选用式(1.2.19)或式(1.2.27)。
为了计算方便,引入流量比,即彭台门系数β:=n nc G G β== 可见β只与n ε和κ有关。
