第八章图论概念和一笔画问题
一笔画问题与图论
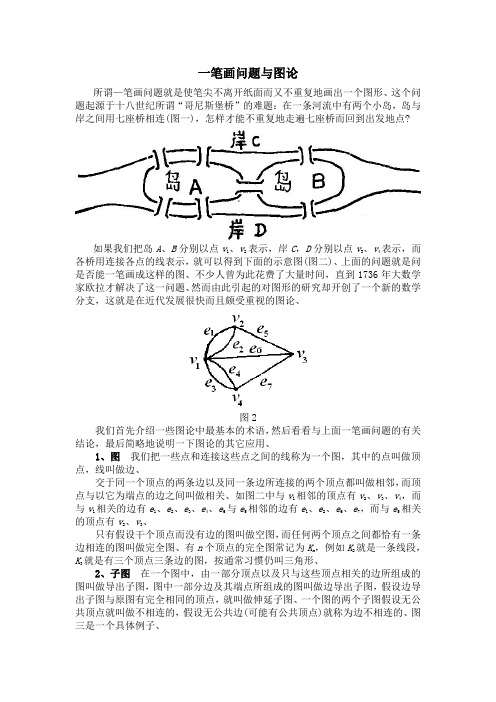
一笔画问题与图论所谓—笔画问题就是使笔尖不离开纸面而又不重复地画出一个图形、这个问题起源于十八世纪所谓“哥尼斯堡桥”的难题:在一条河流中有两个小岛,岛与岸之间用七座桥相连(图一),怎样才能不重复地走遍七座桥而回到出发地点?如果我们把岛A、B分别以点v l、v2表示,岸C,D分别以点v3、v4表示,而各桥用连接各点的线表示,就可以得到下面的示意图(图二)、上面的问题就是问是否能一笔画成这样的图、不少人曾为此花费了大量时间,直到1736年大数学家欧拉才解决了这一问题、然而由此引起的对图形的研究却开创了一个新的数学分支,这就是在近代发展很快而且颇受重视的图论、图2我们首先介绍一些图论中最基本的术语,然后看看与上面一笔画问题的有关结论,最后简略地说明一下图论的其它应用、1、图我们把一些点和连接这些点之间的线称为一个图,其中的点叫做顶点,线叫做边、交于同一个顶点的两条边以及同一条边所连接的两个顶点都叫做相邻,而顶点与以它为端点的边之间叫做相关、如图二中与v l相邻的顶点有v2、v3、v4,而与v l相关的边有e l、e2、e3、e4、e6与e5相邻的边有e l、e2、e6、e7,而与e5相关的顶点有v2、v3、只有假设干个顶点而没有边的图叫做空图,而任何两个顶点之间都恰有一条边相连的图叫做完全图、有n个顶点的完全图常记为K n,例如K2就是一条线段,K就是有三个顶点三条边的图,按通常习惯仍叫三角形、32、子图在一个图中,由一部分顶点以及只与这些顶点相关的边所组成的图叫做导出子图,图中一部分边及其端点所组成的图叫做边导出子图,假设边导出子图与原图有完全相同的顶点,就叫做伸延子图、一个图的两个子图假设无公共顶点就叫做不相连的,假设无公共边(可能有公共顶点)就称为边不相连的、图三是一个具体例子、子图是一个相对的概念,假设H是G的子图,那么G可称为H的上图、通过子图来研究较复杂的图是图论中一个基本方法、3、顶点的度在一个图中与任一顶点v有关的边的数目,叫做这个顶点的度,记作d(v),如图三中的G,d(v l)=2,d(v2)=5,d(v3)=4,d(v4)=2,d(v5)=3、这样一来,我们就看到在计算各个顶点的度时,实际上就是计算了边的数目,但每一条边在它的两个顶点处各计算一次,从而我们可以得到:定理一任一个图中各顶点的度数之总和等于其边数的二倍、由此事实,我们知道图中顶点度数之和为偶数,从而奇数度顶点的个数必为偶数、4、连通性在一个图中,我们从任一顶点v0出发,经过与之相关的一条边el到达另一个顶点v l,再经过与v l相关的一条边e2到达v2,……,如此继续下去,便得到一个顶点和边交替出现的序列v0e l v l e2v2……e k v k、当其中所经过的边彼此皆不相同时,我们就叫做一条迹,这时其中诸顶点有可能相同,假设连顶点也都彼此不同,这种迹就叫做路,起点与终点闭合的路又叫做圈、这些都是一些特殊的边导出子图,如图三中的G,假设取v l av2cv3dv2f v5gv3就是—条迹,而v l av2f v5gv3就是—条路,假设取v l av2f v5gv3bv l就得到一个圈、一条迹可以删去一段而成为路、图3一个图中的任意两点都存在一条连接这两点的路,那么称这个图是连通的、对于一个不连通的图,我们可以把它分成假设干个连通的分支、有了这些概念以后,我们就来看看上面的一笔画问题、为了表达方便起见,我们把包含图中所有的边的迹叫做欧拉迹,首尾闭合的欧拉迹叫做欧拉途、如果一个图含有一个欧拉途就说明从任一顶点山发,可以经过每一条边恰好一次并且回到出发点,换言之,它可以一笔画成、这种含有欧拉途的图就叫做欧拉图、不难证明下面两个定理:定理二 一个连通图是欧拉图的充分必要条件是它不含奇数度顶点、定理三 一个连通图含有欧拉迹的充分必要条件是最多有两个奇数度顶点、 由这两个定理可知,一个图可以一笔画成的充分必要条件是,或者不含奇数度顶,或者恰含有两个奇数度顶点、即使复杂的图,也不消一分钟就可以看出它是否能够一笔画成、在我们上面提到的七桥问题中,相应的图的四个顶点皆是奇数度的,所以无法—笔画成,即使不要求回到原出发点,也无法—笔画成、 一笔画问题只是图论中一个很小的侧面、事实上,我们在画出—个图的时候,可以赋予图中的顶点和边以各种不同的含义,从而也就可以用来研究五花八门的问题、下面举几个简单的例子、例— 在世界各国中,必能找到这样两个国家,它们与同样数目的国家有外交关系、我们用顶点表示国家,两国间有外交关系的就用边相连,这样一来就只须证明在任意—个这种图中必有两个顶点有相同的度数,事实上,设诸顶点以v l ,v 2,……v n 表示,假设各顶点的度数皆不相同,那么它们分别是0,1,2,…,(n -1)这n 个数、但这是不可能的,因为既然有0度的顶点就不可能再有n -1度的顶点,故必有两个顶点具有相同的度数、可见与之相应的两国与同样数目的国家有外交关系、例二 平面上有n 个点,其任意两点之间的距离不小于1,试证至多存在3n 对点,其距离恰是l 、以v l ,v 2,…,v n 表示平面上这n 个点,我们规定某两点v i 与v j 的距离恰是1时才用边相连,在如此所得到的图中,边的数日就是距离恰是1的顶点的对数、与任一顶点v 相邻的顶点必在以v 为圆心,1为半径的圆周上,但题设这些点之间的距离又不小于1,所以至多只能有六个顶点与v 相邻,换言之,对于任意1≤i ≤n 皆d 〔v i 〕≤6,于是,1()6ni i d v n =≤∑由定理一,左边就是图中边数的二倍,所以边数≤3n ,即至多有3n 对点距离恰是1、例三 在随意凑集的六个人中,一定能找列三个人,他们或者彼此认识,或者彼此不认识、这是一个Ramsey 问题,曾经是著名的难解问题之一,现在用图论方法很齐易解决、我们用六个点表示六个人,两个人认识就将扪应的两点用线连起来、于是这个问题就转化成下述形式:在任何一个六个顶点的图中,必有三个顶点存在,它们或者连成—个三角形,或者彼此不相邻、设v 是某一顶点,那么其余五个顶点中与v 相邻的顶点数和与v 不相邻的顶点数中必有一个是超过3的、不妨设u 1,u 2,u 3,是与v 相邻的,假设u l ,u 2,u 3中有某两点是相邻的,那么它们与v 将构成——个三角形,假设u 1,u 2,u 3中任意两点都不相邻,那么它们就是题中所要求的三点、下面我们再来看看图论中所研究的其它—些问题、邮路:利用欧拉途的概念可以解决所谓邮递路线问题、我们知道,邮递员总想从邮局出发以最短的路程走遍每一条街道,最后回到邮局,如果这位邮递员所负责的街道可以画成一个欧拉图,那么只须求出其欧拉途就一定是最理想的邮路了、而对于欧拉图要求出其中的欧拉途是不成问题的、但当街道画出一个非欧拉图时,情形就比较复杂了、这时须引入“重量”的概念而转化成求欧拉途的问题、当合理地规定图中的每一条边的重量以后,我们就得到一个所谓“赋重图”、这里的重量可以表示路程的长短,也可以表示运费的多少,也可以表示造价的高低,如此等等,于是有许多实际问题便可转化成求赋重图中的最轻通路问题、图论中已经建立了一些有效的方法、可靠性:要建立一个交通或通讯系统,就要设法使假设干个点之间皆有通路相连,并且还力求使总的造价是比较少的、这一类问题在图论中已通过对一种特殊的子图——“树”的研究得以解决、另一方面,如果在—种交通或通讯系统中任意两点之间都只有一条路相通,那么这种系统是很不可靠的,一旦有一处发生故障,就可能仗整个系统陷于瘫痪,于是图论中又进一步研究了连通的可靠性问题,这主要是将连通程度数量化、货郎担问题:我们把包含图中每一个顶点的路叫做哈密顿路,假设是闭的就叫做哈密顿圈,相应的图就叫做哈密顿图、与欧拉途不同的是哈密顿圈只要求走遍每一个顶点,并不要走遍每条边,著名的货郎担问题与此有关、这个问题是:寻找一条最短路线,使一个货郎不走回头路而走遍几个村镇,这是一个看起来简单却尚未得到解决的问题,没有一个有效方法可以用来判断一个图是否为哈密顿图、印刷电路:当我们设计一种印刷电路时,必须要求有关的电路图是一个平面图,由于我们在画出一个图的时候,其边的长短以及准确位置是无关紧要的,只是关心某条边是连接哪两个顶点而已、所以—个图是否为一个平面图并不是一眼就能看出来的、某些图乍看起来不是平面的,但可以重新画出使成平面图、这在图论中叫做平面嵌入,并且已经找到一些有效方法可以判断任意给出的图是否为平面图,以及如果是平面图怎样进行平面嵌入、四色问题:我们可以把图的顶点或边涂以各种颜色,并研究任意一个图最少要几种颜色)才能合理地进行上色(即使得相邻的顶点或边颜色不同)、著名的四色问题与此有关,四色问题是一种猜想:任一平面图只须四种颜色即可将顶点染色,使每每两相邻顶点皆有不同颜色、这与地图的染色是密切相关的、在图论中图论是一门比较新的学科,它当然可以尽量采取近代数学的概念及方法,诸如集合、映射、矩阵等等来处理其内容,还可以建立图与图之间的一些运算关系、用它可以解决的问题无法估量、图论的内容是丰富的,方法是新颖的,上面罗列的仅是其【一】二而已、。
第八章 图与网络分析

16
赋权图 网络
赋权图:设图G=(V,E),对G的每一条边(vi,vj)相应赋 予数量指标 wij , wij 称为边 (vi,vj) 的权 , 赋予权的图 G 称 为赋权图。赋权图中的权可以代表距离、费用、通 过能力(容量)等等。 网络:若G=(V,E)为一赋权图,并在其顶点集合V中 指定了起点和终点,其余的点为中间点,这样的赋 权图称为网络图(简称网络)。
v2 9 v1 20
10
v3
15 7 v4 14 6 19 25
v5
v6
子图,支撑子图
图G1={V1、E1}和图G2={V2,E2},如果有
V1 V2和E1 E2 称G1是G2的一个子图。
若有 V1=V2,E1 E2 ,则称G1是G2的一个 支撑子图。 v2
v1 e4 e3 v3 e6 e8 e6 e2
第8章 图与网络优化
8.1 8.2 8.3 8.4 8.5 8.6 图的基本概念 树 最短路问题 网络最大流 最小费用最大流问题 中国邮递员问题
图论起源——哥尼斯堡七桥问题
A C B
问题:一个散步者能否从任一 块陆地出发,走过七座桥,且 每座桥只走过一次,最后回到 出发点?
A
D
C
B 欧拉证明了上述图形一笔画 是不可能的,因为图中每一个 点都只和奇数条线相关联. 他的结论是:图形能一笔画 的充要条件是图形的奇顶点 (连接奇数条线的顶点)的个 数为零
图的基本性质:
定理1 图G=(V,E),顶点次数之和等于所有边数的2 倍。
证明:由于每条边必与两个顶点关联,在计算点的次时,每 条边均被计算了两次,所以顶点次数的总和等于边数的2倍。
定理2 任何图中,次为奇数的顶点必为偶数个。
不重复的路-一笔画问题

在一笔画过程中,如果起点和终点是同一点,则称该路径为欧拉回路。如果一个 图存在一个遍历其所有边且每条边只遍历一次的路径,则称该路径为欧拉路径。
一笔画问题的数学描述
图论
一笔画问题属于图论的范畴,图论是研究图 的结构、性质和应用的数学分支。在一笔画 问题中,主要关注的是图的连通性和遍历性 。
在计算机图形学中的应用
图形渲染
一笔画问题在计算机图形学中常用于绘制复杂的图形,如地 图、电路图等。通过解决一笔画问题,可以确定从一个点到 另一个点的最短路径,从而高效地渲染图形。
游戏开发
在游戏开发中,一笔画问题也具有广泛应用。例如,在角色 移动、地图导航等方面,可以利用一笔画算法找到不重复的 路径,提高游戏的流畅性和用户体验。
人才培养
为了推动一笔画问题的研究和发展,需要加强人才培养。未来可以加强图论学科的建设, 提高教师的学术水平和教学能力,培养更多具有创新能力和实践精神的人才,为解决一笔 画问题提供人才保障。Leabharlann HANKS感谢观看05
结论
一笔画问题的研究意义
理论意义
一笔画问题作为图论中的经典问题,对于推动图论学科的发展具有重要意义。通过对一笔画问题的研 究,可以深入探讨图论中的连通性、遍历性和最优化等核心问题,为图论学科的理论研究提供支持。
应用价值
一笔画问题在现实生活中具有广泛的应用价值。例如,在地图导航中,如何规划一条不重复的路径; 在电路设计中,如何避免线路交叉;在物流配送中,如何规划最优的送货路线等。因此,一笔画问题 的研究成果可以为这些领域提供理论指导和技术支持。
问题背景
起源
一笔画问题起源于文艺复兴时期 的数学游戏,后来被欧拉等人系 统化并深入研究。
离散数学 教案 第八章 图论

西南科技大学
6
计算机科学与技术学院
Discrete Mathematics 为方便起见,在无向图中往往用字母ei表示 边。例如,在上图中,用e1表示边(v2,v2),e2 表示边(v1,v2)等。 对于一个确定的图,我们不关心顶点的位置, 边的长短与形状,因此,所画出的图的图形可 能不唯一。 定义 一个有向图G是一个二元组<V,E>,即 G=<V,E>,其中
西南科技大学
4
计算机科学与技术学院
Discrete Mathematics 定义 一个无向图G是一个二元组<V,E>,即 G=<V,E>,其中
(1). V是一个非空的集合,称为G的顶点集, V中元素称为顶点或结点;
(2). E是无序积 的一个多重子集 (元素可重复 出现的集合为多重集),称E为G的边集,E中元 素称为无向边或简称边。 在一个图G=<V,E>中,为了表示V和E分别 为G的顶点集和边集,常将V记成V(G),而将E 记成E(G)。
由于2m,
为偶数,所以
也为偶数。
可是,vV1时,d(v)为奇数,偶数个奇数之和才能 为偶数,所以|V1|为偶数。结论得证。
西南科技大学
17
计算机科学与技术学院
Discrete Mathematics 对有向图来说,还有下面的定理: 定理 设G=<V,E>为有向图, V={v1,v2,…,vn} , |E|=m,则
(5).设E´ E且E´ ≠Φ ,以E´为边集,以E´中边
关联的顶点的全体为顶点集的G的子图,则称G´是由 边集E´导出的G的子图。
西南科技大学
26
计算机科学与技术学院
Discrete Mathematics 例如,在下图中,(2),(3)均为(1)的子图;(3)是 生成子图;(2)是顶点子集{v1,v2}的导出子图,也
运筹学 第八章 图论 - 全

(a)明显为二部图,(b)也是二部图,但不明显,改画为(c) 时即可看出。
2017/7/13 11
图与网络的基本知识
次,奇点,偶点,孤立点 与某一个点vi相关联的边的数目称为 点vi的次(也叫做度),记作d(vi)。 右图中d(v1)=4,d(v3)=5,d(v5)=1。次 为奇数的点称作奇点,次为偶数的
2017/7/13
18
图与网络的基本知识
有向图 无向图
道路
回路
链
圈
道路(边的方向一致)
2017/7/13 19
图与网络的基本知识
连通图
定义10 一个图中任意两点间至少有一条链相连,则称此图为 连通图。任何一个不连通图总可以分为若干个连通子图,每 一个称为原图的一个分图(连通分支)。
连通图
2017/7/13
边,对余下的图重复这个步骤,直至无圈为止。
2、避圈法:每次增加一条边,且与已有边不构成圈,直至恰 有n-1条边为止。
2017/7/13
24
树
例1、下图是某建筑物的平面图,要求在其内部从每一房间都能走到 别的所有的房间,问至少要在墙上开多少门? 试给出一个开门的方案。
三
七
Байду номын сангаас
三 八 一 四 二 五
七 八 九 六
无向图
2017/7/13
有向图
8
图与网络的基本知识
环, 多重边, 简单图 如果边e的两个端点相重,称该边为 环。如右图中边e1为环。如果两个点 之间边多于一条,称为多重边,如右
v2 e5
多重边
e2
e1 v1
环
e3 v3
e4
图中的e4和e5,对无环、无多重边的
一笔画问题

一笔画问题2014-7-15一笔画问题简单学习总结今天学的还是图论的内容——一笔画问题。
一笔画就是把一个无向图(或有向图)所有的边都遍历一遍且不重复走同样的边。
这个新知识的算法都是建立在几个数学性质上面的,分别如下:1、这个有向图(或无向图)必须是连通的。
这是最基本的条件。
2、每个点之间度的要求:无向图:满足①所有点的度数为偶数或者②有两个点度数为奇数,其他点度数为偶数,且这两个奇数点必须为一笔画中的开端和结尾。
有向图:满足①所有点出入度相等或者②有一个点出度比入度大1,另一个点入度比出度大1,其他点的出入度相等,且出度大的点为一笔画开端,入度大的点为一笔画结尾。
数学简单证明还是比较容易的,如果一个点度数为奇数,那么从该点出发,去到的无非就两种情况:偶点或奇点,偶点我们总可以绕一个圈回到该偶点重新出发。
奇点就到达终点了。
(圈套圈的思路)对于无向边,有一个特殊处理:无向边路过一条边后,要把它的反向边去掉。
这个过程可以用指针实现,用一个指针指向它的反向边。
或者,如果用数组来储存边时,因为反向边是同时申请的,所以它们的下标一定是相邻的,可以用异或操作得到。
下面介绍几种算法:1、圈套圈算法算法思想:每次在某个点随便找一条边,一直走,如果找到环,那么就相应地插入到一笔画的顺序中,环中若有嵌套环,那么同样地找下去。
算法实现:可以用链表实现插入之类的操作,但若用深搜回溯写的话,程序会非常简单。
就是从奇点(或任意点)出发,任意地深度遍历,如果当前点已经不能往下搜,那么就回溯看祖先节点是否有其他可以遍历的点,按回溯的顺序弹出的边,在无向图里面正反顺序都是一笔画正确解法,有向图里需要取反顺序。
算法优化:由于系统栈的空间局限性,在朴素的递归算法里面不能支持较大数据范围的题目,可以改成用stack栈模拟递归的操作,这样就不再会爆栈。
2、弗罗莱算法算法思想:首先在奇点出发,尽量先不走桥(若去掉该边图不连通,则该边为桥),先走环路。
一笔画问题

一笔画问题
数学定理
01 定义
目录
02 例子
03 一笔画的规律
04 相关名词含义
05 欧拉图
06 一笔画定理
传统意义上的几何学是研究图形的形状大小等性质,而存在一些几何问题,它们所研究的对象与图形的形状 和线段的长短没关系,而只和线段的数目和它们之间的连接关系有关,比如一笔画问题就是如此。即平面上由曲 线段构成的一个图形能不能一笔画成,使得在每条线段上都不重复。例如汉字“日”和“中”字都可一笔画,而 “田”和“目”则不能。两两相连区域可一笔画,例如,平面4个区域两两相连区域可一笔划;轮胎状上7个两两 相连区域可一笔画;我们可以构造一个多维空间的无穷个两两相连区域一笔划。
比如附图:(a)为⑴情况,因此可以一笔画成;(b)(c)(d)则没有符合以上两种情况,所以不能一笔 画成。
相关名词含义
◎顶点与指数:设一个平面图形是由有限个点及有限条弧组成的,这些点称为图形的顶点,从任一顶点引出 的该图形的弧的条数,称为这个顶点的指数。
◎奇顶点:指数为奇数的顶点。 ◎偶顶点:指数为偶数的顶点
一笔画的规律
数学家欧拉找到一笔画的规律是:
⒈凡是由偶点组成的连通图,一定可以一笔画成。画时可以把任一偶点为起点,最后一定能以这个点为终点 画完此图。图B的平面图
⒉凡是只有两个奇点的连通图(其余都为偶点),一定可以一笔画成。画时必须把一个奇点为起点,另一个 奇点终点。
小学数学一笔画课件

THANKS FOR WATCHING
感谢您的观看
03
一笔画问题的解题方法
逐步推理法
总结词
通过逐步推理,按照一定的逻辑顺序,确定笔画的路径。
详细描述
逐步推理法是一种常用的解题方法,它通过逐步分析图形的特点和规律,推断出 笔画的路径。这种方法需要有一定的逻辑推理能力,对于一些较为复杂的图形, 需要仔细分析其结构,找出正确的笔画路径。
奇偶点分析法
拉回路是指一条通过图形的每条边且每条边只通过一次的闭合路径。
02
奇点与偶点
在图形中,如果一个节点发出的线条数是奇数,则该节点称为奇点;如
果一个节点发出的线条数是偶数,则该节点称为偶点。
03
哈密顿路径和哈密顿回路
哈密顿路径是指一条通过图形的每条边且每条边只通过一次的路径,但
不一定是闭合路径;哈密顿回路是指一条通过图形的每条边且每条边只
计算机科学
一笔画问题在计算机科学 中也有广泛应用,例如在 计算机图形学、算法设计 等领域。
实际应用
一笔画问题在现实生活中 也有很多应用,如地图的 绘制、电路设计、交通规 划等。
02
一笔画问题的数学原理
欧拉公式
欧拉公式
对于一个连通图,其边数和顶点数的关系可以用公式(V - E + F = 2)来表示,其中(V)表示顶点数,(E)表示边数,(F)表示面 数。这个公式是解决一笔画问题的重要依据。
问题的能力。
创新的一笔画问题
总结词
创意问题,挑战性
VS
详细描述
创新的一笔画问题通常涉及更为复杂和创 意的图形,如不规则多边形、立体图形等 ,这类问题旨在激发学生的创造力和挑战 精神。同时,这类问题也可能涉及到数学 中的其他知识点,如平面几何、立体几何 等。
离散数学第8章 图论

为d(vi,vj)。
8.2
图的矩阵表示
一、图的邻接矩阵 二、图的连接矩阵
三、图的关联矩阵
二、图的连接矩阵 定义 8-9 设图 G= ( V , E ),其中 V={v1 ,
v2 , … , vn } , n 阶方阵 C= ( cij ),称为图 G 的连接 矩阵,其中第i行j列的元素
1 c ij 0
利用邻接矩阵,我们可以 (1)判断G中任意两个结点是否相连接;
方法是:对 l=1,2,…,n–1,依次检查Al的(i,j)
项元素
(l ( ) ij)是否为0,若都为0,那么结点v 与v 不 a ij i j
相连接,否则vi与vj有路相连接。 (2)计算结点vi与vj之间的距离。
(1) ( 2) ( n 1) 中至少有一个不为0, 若 aij , aij , , aij 则可断定vi与vj相连接,使 a (l ) 0 的最小的 l 即
若中有相同的结点,设为ur= uk(r<k),则子路ur+1…uk可以从 中删去而形成一条较短的路= viu1…ur uk+1…uh–1 vj,仍连接vi到 vj 。 若中还有相同的结点,那么重复上述过程又可形成一条 更短的路,…。这样,最后必得到一条真路,它连接vi到vj, 并短于前述任一非真路。因此,只有真路才能是短程。
非真 生成
真 生成
真 非生成
非真 非生成
真 非生成
七、路与回路 定义:图G中l条边的序列{v0,v1}{v1,v2}…{vl–1,vl}称为连
接v0到vl的一条长为 l 的路。它常简单地用结点的序列 v0v1v2…vl–1vl来表示。其中v0和vl分别称为这条路的起点和终点。 开路:若v0vl,则称路v0v1v2…vl–1vl为开路; 回路:若v0=vl,则称路v0v1v2…vl–1vl为回路; 真路:若开路v0v1v2…vl–1vl中,所有结点互不相同(此时所有 边也互不相同),则称该路为真路; 环:在回路v0v1v2…vl–1v0中,若v0,v1,v2,…,vl–1 各不相同 (此时所有边也互不相同),则称该回路为环。
第八章图论

3. 图的结点与边之间的关系 定义 如果边e={vi,vj}是G的边, 则称结点vi 和vj邻接的, 边e和结点vi ,边e和结点vj称为关联的。 没有与边关联的结点称为孤立点。 关联于同一结点的相异边称为邻接的。 不与任何边邻接的边称为孤立边。
例1
在上图中显然e1和e2, e1与e4是邻接的, 结点v1和v2,v2和v4等是邻接的, 没有孤立点和孤立边。
例2.如下图中:
图(a)是伪图。图(b)是有向多重 图。 最右第三个图是简单图有权图。
三、结点的度
1.定义 图G中关联于结点vi的边的总数称为 结点vi的度, 用deg(vi)表示。
2.定理1(握手定理) 图G的所有结点的度的总和为边数 的二倍。即若G为具有n结点的(n,m)图, 则有: n deg(vi ) 2m
例8 如下图
(a)是连通图。 (b)是一个具有三个分图 的非连通图。 结论: (1)一个图的分图必是连通的; (2)一个连通图一定只能有一个分图。
例11 对于图的连通性,常常由于删除了 图中的结点和边而影响了图的连通性。
在连通图(a)中删除边e后, 则变成了不连通 的图(b)。
8.2 图的矩阵表示
2. 有向图的定义 定义 设G=(V,E), V是一个有限非空集合, E是V中不同元素的有序对偶的集合, 则称G是一有向图。在有向图G中 若vi≠vj,则(vi,vj)和(vj,vi)表示两条 不同的边,且用一个从结点vi指向vj 的箭头表示边(vi,vj)。
定义 具有n个结点和m条边的图称为(n,m)图。 (n,0)图称为零图。(1,0)图称为平凡图。
三、边割集、点割集 定义3 设图G=<V,E>是连通图,若有E的子集S, 使得在图G中删去了S的所有边后, 得到的子图G-S变成具有两个分图的不连通图, 删去了S的任一真子集后所得子图仍是连通图, 则称S是G的一个边割集。 注:割边是边割集的一个特例。
关于一笔画问题的经典探讨PPT培训课件

一笔画定理及其证明
一笔画定理
一个连通图形可以一笔画成当且仅当该图形中奇数个顶点的度数之和为2。
证明过程
首先,根据连通性规则,图形必须是连通的。然后,根据奇偶性规则,如果图 形中奇数个顶点的度数之和为2,则该图形可以一笔画成;如果图形中奇数个顶 点的度数之和不为2,则该图形不能一笔画成。
一笔画定理的应用实例
应用
一笔画问题在计算机科学、电子工 程、运筹学等领域都有广泛的应用。
一笔画问题的重要性和应用领域
理论价值
一笔画问题在数学理论中具有重 要的价值,是图论、组合数学等 领域的重要研究课题之一。
应用价值
一笔画问题在计算机图形学、电 路设计、物流规划等领域都有广 泛的应用,可以帮助人们解决一 系列实际问题。
06
一笔画问题的实际应用案例
地图着色问题
算法设计
解决地图着色问题需要设计一种有效的算法,能够判断给定的地图是否可以一笔画成,并找出最少所需的颜色数 量。常用的算法包括贪心算法、回溯算法等。
实例分析
地图着色问题可以通过实例来分析,例如给定一个包含多个国家的地图,如何使用最少的颜色对各个国家进行着 色,使得相邻的国家颜色不同。
判断一笔画图形
通过计算图形中奇数个顶点的度数之 和,可以判断该图形是否可以一笔画 成。
设计一笔画图案
解决实际问题
一笔画定理在计算机科学、电子工程、 机械工程等领域都有广泛的应用,例 如在电路设计和布线、机器人路径规 划等方面。
利用一笔画定理,可以设计出具有特 定形状和结构的一笔画图案。
03
一笔画问题的经典问题解析
THANKS
感谢观看
一个顶点的度数为奇数,意味着该顶点是起点或 终点。
一笔画问题与图论
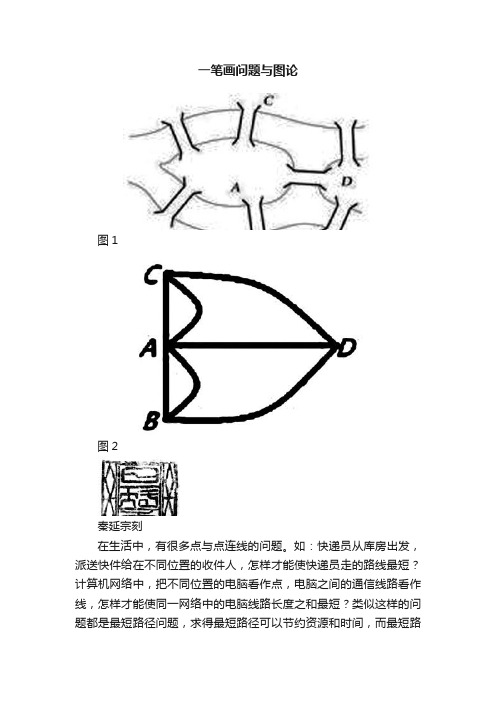
一笔画问题与图论图1图2秦延宗刻在生活中,有很多点与点连线的问题。
如:快递员从库房出发,派送快件给在不同位置的收件人,怎样才能使快递员走的路线最短?计算机网络中,把不同位置的电脑看作点,电脑之间的通信线路看作线,怎样才能使同一网络中的电脑线路长度之和最短?类似这样的问题都是最短路径问题,求得最短路径可以节约资源和时间,而最短路径问题与图论密切相关。
快递员最短路径、计算机网络最短路径,这两个问题有些复杂。
为了理解图论的基本原理,我们先看一个简单的一笔画问题:对一个有若干个点(大于等于2)和若干条线的图形,从一个点开始,能否用一支笔,在不离开纸面的情况下,不遗漏、不重复地沿线画完图形。
你或许求解过很多一笔画问题,但有没有想过这类问题是否有统一的解答方法呢?即:什么样的一笔画问题可求解?可求解的一笔画问题有没有确定的解法?最先给出一笔画问题统一解法的是瑞士数学家欧拉。
欧拉对图论的研究是从哥尼斯堡七桥问题开始的。
18世纪初普鲁士的哥尼斯堡(今俄罗斯加里宁格勒)有一条河穿过,河上有两个小岛(A和D),有七座桥把两个岛与河岸(B和C)连接起来(如图1)。
当地居民有一个休闲活动,就是从一块陆地出发,怎样才能不重复、不遗漏地一次走完七座桥,再回到出发点。
当地的人们试验了无数多次,都没有人做到。
1735年,有几名大学生写信给数学家欧拉,请他帮忙解决这一问题。
欧拉在亲自观察了哥尼斯堡的七座桥后,认真思考走法,也没能成功,于是他怀疑七桥问题是不是原本就无解。
在经过一年的研究之后,欧拉写出了《哥尼斯堡七桥问题》的论文,圆满地解决了这一问题,同时开创了新的数学分支——图论。
欧拉的解法是:将四块陆地看作四个点,分别记作A、B、C、D;将七座桥看作连接陆地的线,将与偶数条线相连的点叫做偶点,与奇数条线相连的点叫作奇点,如图2所示。
在图2中,每一个点都与奇数条线相连,每一个点都是奇点,这样的图不可能不重复地一笔画完,因此哥尼斯堡七桥问题无解。
第8章图论方法

Page 12
【例题·计算题】某城市东到西的交通道路如下图所示,线 上标注的数字为两点间距离(单位:千米)。某公司现需从市 东紧急运送一批货物到市西。假设各条线路的交通状况相同, 请为该公司寻求一条最佳路线。
2 东3
4
3 1
7
2
5
7
3
3
4
4
7 5
6
4 6
7 3
7
西
8
【答案】
1-4-7-西 10 3
9
2
3
5
7
3.5
4
6
10
1
6
4
3
8
2
5
【答案】
2 5
4
6
1
3
5
3 3.5 4
2
Page 8
【解析】按照克鲁斯喀尔的算法很轻松得出答案。
1.(11年7月)已知连接5个城镇的公路交通图如图。为了沿公路架设5个城镇的
光缆线,并要求光缆线架设的总长度为最小,试以最小枝杈树方法求出Pa最ge优9 方 案并计算光缆线的总长度。
8.2 树和树的逐步生成法
Page 4
1、树:连通且不含圈(回路)的图称为树。 2、树的边数=结点数-1。
【选择题】以下叙述中,正确的是( ) A.树的点数为线数加1 B.图的点数小于线数 C.图的点数大于线数 D.树可能含有圈 【答案】A 【解析】树的点数和边数差1,普通图的点数和边数谁多谁少不 确定。 【知识点】图和树的基本概念
Page 22
5.(09年7月)某网络如图,线上标注的数字是单位时间通过两节点的流量。
Page 23
试求单位时间由网络始点到网络终点的最大流量(单位:吨)。
一笔画问题(欧拉图)

2010-10-18 17:32 by EricZhang(T2噬菌体), 3556 visits, 网摘, 收藏, 编辑关于一笔画问题的数学分析(对一道面试题的总结与扩展思考)摘要前几天参加了一个公司的面试,其中被问到了一个题。
面试官在纸上画了一个图形(具体图形见下文),问我能不能一笔画出这个图形,要求每条边必须只走一次,并且画的过程中笔不能离开纸。
当时我没有试着去画,而是凭着自己图论方面的知识在几秒钟之内告诉面试官不可能做到,然后简单说了一下理由。
面试结束后我翻阅了图论相关的资料,发现当时自己虽然给出了正确答案,但理由并不完全正确。
昨天我花了几个小时仔细研究了一下相关的理论,总结了一下这类问题的类型和解法,写成此文,分享给大家。
问题的提出当时面试官给我出的问题是这样的:对于下面这个图形,让我一笔画出,要求每条边必须只走一次,并且画的过程中笔不能离开纸。
面试时我给出的回答是不可能做到,面试结束后我也从数学上证明了这个这个回答。
当然有兴趣的朋友可以试着画画看。
这个问题其实就是我们小时候会玩到的一笔画游戏。
这类问题看似简单直观,但是仔细研究下来却蕴含了很多东西,而且涉及了图论中一个非常重要的研究课题——欧拉迹。
而且这类问题可以扩展出很多东西,例如任意给一个图可不可以完成一笔画且最后回到起始点?再如到底什么样的图可以一笔画出来?什么样的图一笔画不出来?如果一个图可以一笔画出来,那么应该如何画?有没有对一切可一笔画图形的通用解法?下面我们将这个问题抽象成一般问题,然后从图论角度寻找上述疑问的答案。
图论中的一些概念因为在下文论述过程中需要用到一些图论的基本概念,为了照顾在这方面不熟悉的朋友,我先将要用到的定义和概念列出来,如果您对图论的基本内容已经了然于胸,可以跳过这一节。
另外如不做特殊说明,下文所有的“图”都默认指“无向图”,本文的讨论不涉及“有向图”。
简单图——一个简单图可表示为G=(V, E),其中V是顶点集合,其中每个元素是图的一个顶点;E是边集合,其中每一个的元素是一个顶点对(a, b),其中a和b均属于V,这个顶点对表示顶点a和b 间有一条边相连。
离散数学第8章 图论

软件学院
图论原理 两个图同构的必要条件: 1.结点个数相等. 2.边数相等. 3.度数相同的结点数相等. 4.对应的结点的度数相等. 下面是同构的图:
a b c e d 3 5 1 4 2 b c d a f e 2 4 6 1 3 5
软件学院
图论原理
软件学院
图论原理
图的同构 设G=<V,E>和G’=<V’,E’>是图,如果存在双射f:VV’ 且任何 vi,vj∈V,若边(vi,vj)∈E,当且仅当 边(f(vi),f(vj))∈E’, (则称G与G’同构,记作G≌G’. (同构图要保持边的“关联”关系) 例如:右边所示的两个图: a b 1 4 G=<V,E> G’=<V’,E’> c d 3 2 构造映射f:VV’ a 1 b 2 c 3 d 4 a 1 b 2 c 3 d 4
c
d
v2
v4 v6 G2
v3
v5
f g h G1
软件学院
图论原理
欧拉通路的判定方法: 定理:无向连通图G中结点a和b间存在欧拉通路的充分必要 条件是a与b的次数均为奇数而其他结点的次数均为偶数。 如果G有两个奇数度结点:就从一个奇数度结点出发,每当到 达一个偶数度结点,必然可以再经过另一条边离开此结点, 如此重复下去,经过所有边后到达另一个奇数度结点 如果G无奇数度结点,则可以从任何一个结点出发,去构造一 条欧拉路. a b 1 2 c d 4 3
v3
是一个结点,则称此路 是一个回路. 如果一条路中所有边都不同,则称此路为迹或简单通路. 如果一条回路中所有边都不同,则称此回路为闭迹或简 单回路. 如果一条路中所有结点都不同,则称此路为基本通路. 如果一条回路中所有结点都不同,则称此路为基本回路. 一条基本通路一定是简单通路,但是一条简单通路不 一定是基本通路
山东省实验中学高一数学组优秀稿件教案:第八讲图论概念和一笔画问题(竞赛题)

第八讲图论概念和一笔画问题山东省实验中学杨芳(教材:第八章图论概念和一笔画问题)一.图的基本概念二.欧拉环游及弗莱里算法三.中国邮递员问题四.实际问题应用举例一.图的基本概念图现实生活中,我们经常碰到一些现象,如:在一群人中有些人互相认识,有些人互相不认识。
又如:某干航线,某些城市间有直达航班,而另一些城市间没有直达航班等等。
以上现象都有共同内容:一是有二是这些对象之间存在着某种关系:如互相认识,有直达航班等。
为了表示这些对象以及对象之间的关“边”表示“对象之间的关系”,引出了“图”这个概念。
图:由若干个不同的点与连接其中某些顶点的边所组成的图形,称为图。
由此可见,图有二要素:“点”和“边”:“点”表示对象,“边”反映对象之间的关系。
图由顶点集注解:这里点和边并不是通常的欧氏空间内的对象,例如,这里边没有“长度”的概念,边不是由点构表示图时,点的位置、边的长度、曲直都无关紧要,但是点和点是否有边连接是一定的。
网络:对图中的顶点和边赋以具体的含义和权,这样的图称为网络。
边e可以表示为e=(),称和是边e的端点,边e与点和关联。
次:与某一点关联的边的数目称为点的次。
奇点:次为奇数的点。
偶点:次为偶数的点。
对于图G中一个点、边交错的序列链:如果,且互不相同,称这个序列是到的链。
闭链:如与相同,称这条链为闭链。
路:如果链中的各点也不同,称这样的链为路。
圈:如互不相同的闭链称为圈。
连通:若G中两点u和v之间存在路,则称u和v是连通的。
连通关系是一种等价关系,可以把图中的是连通的,不同的部分总是不连通的。
每个部分连同连接它们的边(两个端点都在同一部分的边)称为注解:要说明连通关系是等价关系,只要说明连通关系具有下面三个性质:1、每一个点自己总是和自己连通的;如果u和v连通,则v和u也是连通的;如果u和v连通,v和w连通,则u和w也连通。
)若G只有一个分图,则G是连通的。
在一个网络N=(V,E,W)中,环游:经过N中每一边至少一次的闭链称为N的环游。
离散数学图论
1
2
3
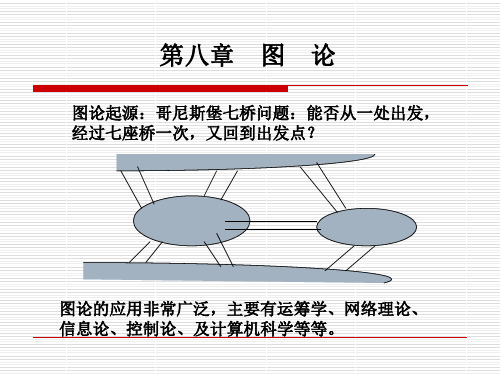
(3)为(1)的生成子图,(2)为(1)的真子图。
补图
定义7 设图G=<V, E> ,若G是n阶无向图,则G的补图为: KnG。即为n阶完全无向图与G的差。若G是n阶有向图, 则G的补图为:n阶有向完全图与G的差。
(这一节介绍了图的一些基本概念,如图的定义,图 中顶点的度,图的所有顶点的度为边的2倍,且一个 图中有偶数个奇顶点,简单图等的定义,图的运算, 子图,补图的一些概念。要掌握这些简单的定义)
e3
d e2
d 1 1 1 0 0
c
e
0
0
0
0
0
有向图的矩阵表示
与无向图相对应,有向图也有类似的矩阵表示。 如右图:
称e关联于顶点a和b;称a和b是邻接的。 若边e对应的是无序偶{a,b},则称e为无向边。同样
称a,b是端点,称e关联于顶点a和b;称a和b是邻接 的。 每一条边都是有向边的图,称为有向图。每条边都 是无向边的图,称为无向图。
图中不与任何顶点邻接的点称为 孤立点。全都是孤 立点的图称为零图。关联于一个顶点的边称为自回路, 也称为自圈。
哥尼斯堡七桥问题
城的四个陆地部分分别表以A,B(大岛),C,D(小岛), 将陆地设想为图的顶点,把桥画成相应的边,
A
B
D
C
则问题等价于在图中从某一顶点出发找一条回径,通过它的每条 边一次且仅一次,并回到原顶点。
(你能否看出,此问题无解,即这样的走法不存在呢?)
主要内容
1.图的基本概念 2.路径与回路 3.图的矩阵表示 4.几种特殊的图 5.无向树, 有向树
定义5 在有向图G中,如果在任两个顶点中,存在从一个顶点到 另一个顶点的路径,则称图G为单向连通的。如果在G中,任 何两个顶点都互相可达,则称G为强连通的。如果它的基础图 (底图)是连通的,则称之为弱连通的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
图论概念和 一笔画问题
第八章 图论概念和一笔画问题
§1 图的基本概念 为了表示对象以及对象之间的关系,我们 可以在 纸上画一些点和线。每一点代表一个对 象,称这些点为顶点,简称点;如果两个对象 之间有所讨论的关系,我们就在相应的两点之 间用线连接,称这些线为边 。这样就构成了 一个几何图形,这种由若干种不同的顶点与连 接其中某些顶点的边所组成的图形,称为图。
u
1
x
6
4 y 15 2
2 2
w
x
11 2
3
z
2 2
11 2 2 2 z 22 6
4 5 y
w
2
v
v
图8.4
(a)
(b )
下面是一种有关引进重复边的算法。将边e的两 个端点再用一条权为w(e)的新边连接时,称为边e的重 复边。 因此,中国邮递员问题可以重新叙述如下:给定 一个具有非负权的网络N, ① 用添重复边的方法求得N的一个欧拉赋权母图N+ , ∑ W ( e ) 尽可能小; 使得
(2)若两扫雪车性能不同,或出发时间不同等造成两 车的差异,可将网络按比例划分。 (3)若首先应该清扫主干道积雪,这就要考虑如何规 定主干道。 (4)若遇到大风,就要考虑顺风与逆风时车速不同等 因素。
2.模型的假设 可作如下的假设: (1)扫雪过程中没有下雪,所有室内道路都有积雪需 要清除。 (2)两辆扫雪车性能相同,都能正常工作。 (3)两辆扫雪车司机驾驶技术相同,扫雪时,车速相 同。 (4)在所有交叉路口,包括室内道路与高速公路的接 口,扫雪车可不减速地转弯。 (5)两辆车出发的时间相同。 (6)每条路面的积雪范围、厚度相同。 3.模型的建立 (1)双行道问题 假设:每条道路有两条相反的行车道。
完全偶图:两顶点集中每一对不同集合的顶点之间都 有一条边 相连的偶图 子图:若图G1的顶点集包含于图G2的顶点集,图 G1的边集包含于图G2的边集,则称图G1是图G2的子 图 生成子图:若图G1、图G2的顶点集相同,图G1 的边集包含于图G2的边集,则称图G1是图G2的生成 子图 V
V1
1
V4
V5
V4
V2
V2
V3
V3
V5
§2 一笔画问题与中国邮递员问题 邮递员从邮局中取出邮件,递送到不同地点, 然后再返回邮局。假设要求他至少一次走过他投递 范围内的每一条街道,我们希望选择一条尽可能短 的路线。这个问题称为中国邮递员问题,因为他是 由我国数学家管梅谷首先研究的。 欧拉链:在一个网络N中,经过它的每条边的链 N的环游:经过N中每条边至少一次的闭链 欧拉环游:经过N中每条边恰好一次的环游 一个图能一笔画就是该图就有欧拉环游 若N有欧拉环游,则它的每一条欧拉环游具有 相同的权,它也必然是最优环游。对有欧拉环游的 网络,我们可以用弗莱里算法求得N的最优环游
度超过该圈总长的一半时,将该圈中的所有重复边去 掉,该圈中的未重复的边重复,所得到的图也是欧拉 赋权母图。 例 设某邮递员负责投递邮件的街道如图8.5(a)所 示,求出该邮递员的最短投递路线。 解 该网络中有8个奇点:v2 , v4 , v5 , v7 , v8 , v9 , v11 , v12 用添重复边的办法得到图8.5(b) 按结论2进行调整,圈 v4 v10 v11v5 总长为12,而重 复边长为11,此时去掉重复边 v4 v10 , v10 v11 , v11v5 添加重复边 v4 v5 。同样在圈 v2 v3v9 v7 v6 v2 中其总 长为21 ,重复边长为12也超过一半。经调整后得新的 网络图8.5(c)。 检查8.5(c)的每一个圈,其重复边的长度均不大于 该圈长的一半,因此用弗拉里算法求得8.5(c)中网络的 欧拉环游即为要求的最优环游。
链:设图G中有一个点边交错的序列,v0e1v1e2 Lvm−1emvm 如果 ei ( vi −1 , vi )(1 ≤ i ≤ m ) ,且 ei (1 ≤ i ≤ m ) 互不相同, v vm v vm 则称这个序列是从 到0 的链。 和0 称为这条链的两个端点。 闭链:如果 v0 和 vm 相同,则称这条链是闭链 路:各顶点互不相同的链 圈:除初始顶点外,各顶点互不相同的闭链 点连通:图G中存在点u到点v的路 分图:图G中连通的顶点连同边构成的图 连通图:只有一个分图的图 完全图:任意两点之间均有边连接的简单图 偶图(二分图):顶点集是两个互不相交的非空集 合,并且同一个集合中任意两顶点均不相邻的简单 图
的总边长已知,在总长较大的子网络中划出一些与 另一子网络相连的边,添加到总长较小的子网络中。 (2)单行道问题 先加对应的网络N分成两个子网络 和 。 N1 N2 要求 N1和 N 2 子网络边总长度相等,再利用中国 邮递员问题的解法,可以分别求得 和 的欧拉环游, 得到近似解。 注解 4.进一步讨论 (1)不管双行道问题还是单行道问题,都须对原网络 进行划分。可测量图中各路径的长度,并将数 据输入计算机,由计算机划分网络。
e∈E N + \ E ( N )
( )
② 求N+ 的欧拉环游。
解 ② 可用弗莱里算法;解 ①可用爱德蒙斯和约翰逊 算法,这里不作介绍。 当点数较少时,可用奇偶点图上作业法。 结论1 网络N有欧拉环游当且仅当N中每一点的次数 为偶数。
结论2 最优环游具有这样的性质:⑴每条边至多重复 重复一次;⑵每一圈上重复边的长度不超过该圈总长 的一半。 当某一圈上重复边的长度超过该圈总长的一半时, 将该圈中所有重复边去掉,该圈中未重复的边重复, 从而的奇偶点作图法如下: ⑴若N每一点的次均为偶数,则用弗莱里算法求得其 欧拉环游,此即为N的最优环游。 ⑵若不然,则用添重复边的办法得到N的欧拉赋权母 图N*。求得N* 的欧拉环游。(用弗拉里算法) ⑶若某一条边在欧拉赋权母图N*中重复多次,只要去 掉该边的偶数次重复边,总可以使得该边至多重复一 次,这样的图仍为欧拉赋权母图。 ⑷然后逐一检查N*的每一圈,当某一圈上重复边的长
图有两个要素:点,边 点表示对象,边反映对象之间的关系 顶点组成的集合称为顶点集,记作V, 边 组成的集合称为边集,记作E。图由(V,E) 组成,记作G= (V,E)。若给出一个图G,G的 顶点集可用V(G),G的边集可用E(G)表示,G 的顶点数可用∣G∣表示。 如果对图G的每条边赋一个相应的数(称 为边的权),G连通边上的权称为赋权图。 如果对图中的顶点和边赋以具体的含义和 权,这样的图称为网络。
弗莱里算法
计算步骤如下:
⑴任意取N的一个顶点 V0 ,置于Z= V0 ⑵假设链 Z = v0e1v1e2 Lei vi 已选定,从 E \ {e1 , e2 ,L , ei } 中按下述方法选取 ei +1: ①
ei +1和 vi 相关联;
② ei +1 尽量不选 Gi(是G中去掉边 e1 , e2 ,L , ei 而得 到的图)的割边(即去掉此边后,图 Gi 变为不连 通),除非没有非割边可选择。
e1
v1
e2
e3
e4
v2
e5
v4
e6
v5
v3
e7
若边e表示为 e = vi , v j ,这时称 vi 和 v j 是边e的 端点,便e与点 vi 或 v j 关联。 两点相邻:如果两个点与同一条边关联。
(
)
两边邻接:如果两条边有一个公共端点。 环:两个端点重合的边。 重边:具有两个公共端点的两条边。 孤立点:不与任何边关联的点。 简单图:一个既没有换也没有重边的图。 空图:没有任何边的图。 平凡图:只有一点的图。 点 vi 的次:与 vi 关联的边的条数,记作 dG ( vi ) 或 d ( vi ) *注意:在计算点的次时,环作两条边计算,孤立 点的次为0 奇点:次为奇数的点;偶点:次为偶数的点。 ∆ ( G ) 和δ ( G ) 分别表示图G的最大次和最小次。
v1
4
1Hale Waihona Puke v4 v5124
5
v2
5
5
v8
7
4
v 2 6 v7
2
4
v10 2 v11 v12
4
v3 v1
v2 v8
图8.5(a)
v9
4
v13
v1 v2 v4 v5 v6 v7
图8.5(c)
v4 v5
v6 v7
图8.5(b)
v10 v11 v12 v13 v3
v10 v11 v12 v13
v8
v3
§3 城镇道路扫学模型 教材第104页上,图8.6(a)中的实线表示美国 马里兰州威克尔米市需要清除积雪的双向行车道路, 虚线是州高速公路。雪后两辆扫雪车分别从地图* 号标出的两点以西约4英里处出发清扫道路上的积 雪。扫雪车可以通过高速公路进入市内道路。假定 扫雪过程中扫雪车不会损坏或停止,并且道路交叉 处不需要另外附加的扫雪程序。试为两车找出有效 的路径。 1.问题的分析 我们的目的是寻求一个有效的办法用两台扫雪 车 清除威克米尔市内道路(不包括州高速公路)的 积雪。
A.可将地图中每个交叉路口看成点,每条市内道路 看成边,道路的长度看成该边对应的权,这样就将 地图变成一个网络N=(V,E,W) B.由假设,每条道路均是双行道,即网络N上的点 均为偶点,由上一节的结论1可知,该网络N是一个 欧拉有向图,可用弗莱里算法求得N的欧拉环游。 C C.若只有一辆扫雪车,该问题转化为中国邮递员问 题。 现在有两辆扫雪车,工作性能完全相等,要使工作 N '和 N '' 时间尽量少,我们可将网络N分成两个子网络 ' N 和 N '' 均连通,且两网络的权尽可能相同。可用如下 方法实现网络的分割:把网络N分成两个连通子网络, 分别算出两个子网络中所有边的总长度。由于N
⑶设 ei +1 另一关联点 vi +1 。若 E \ {e1 ,L , ei } ≠ ∅ ,重复 步骤⑵;否则 v1e1v2 Lei vi +1 即为N的一条欧拉 环游
