2018届重庆中考复习：重庆中考几何题分类汇编(含答案)

合集下载

2018届重庆中考复习_重庆中考几何题分类汇编(含答案解析)

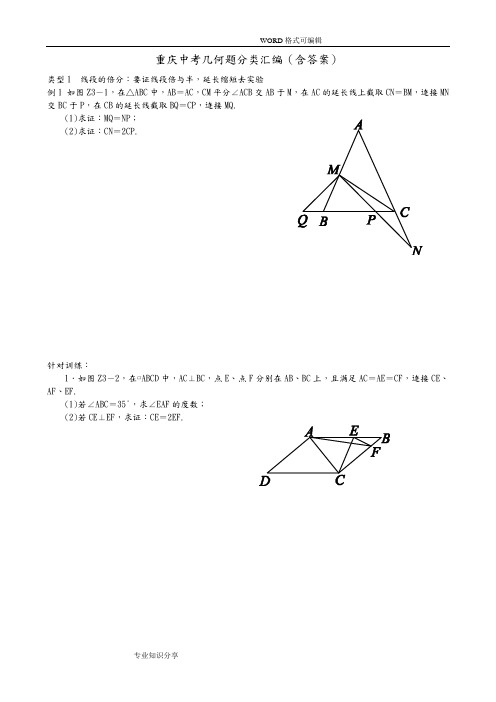
重庆中考几何题分类汇编（含答案）类型1 线段的倍分：要证线段倍与半，延长缩短去实验例1 如图Z3－1，在△ABC中，AB＝AC，CM平分∠ACB交AB于M，在AC的延长线上截取CN＝BM，连接MN 交BC于P，在CB的延长线截取BQ＝CP，连接MQ.(1)求证：MQ＝NP；(2)求证：CN＝2CP.针对训练：1．如图Z3－2，在▱ABCD中，AC⊥BC，点E、点F分别在AB、BC上，且满足AC＝AE＝CF，连接CE、AF、EF.(1)若∠ABC＝35°，求∠EAF的度数；(2)若CE⊥EF，求证：CE＝2EF.2．已知，在△ABC 中，AB ＝AC ，∠BAC ＝90°，E 为边AC 任意一点，连接BE.(1)如图①，若∠ABE＝15°，O 为BE 中点，连接AO ，且AO ＝1，求BC 的长；(2)如图②，F 也为AC 上一点，且满足AE ＝CF ，过A 作AD⊥BE 交BE 于点H ，交BC 于点D ，连接DF 交BE于点G ，连接AG.若AG 平分∠CAD，求证：AH ＝12AC.3．在△ACB 中，AB ＝AC ，∠BAC ＝90°，点D 是AC 上一点，连接BD ，过点A 作AE⊥BD 于E ，交BC 于F.(1)如图①，若AB ＝4，CD ＝1，求AE 的长；(2)如图②，点G 是AE 上一点，连接CG ，若BE ＝AE ＋AG ，求证：CG ＝2AE.4．在等腰直角三角形ABC 中，∠BAC ＝90°，AB ＝AC ，D 是斜边BC 的中点，连接AD.(1)如图①，E 是AC 的中点，连接DE ，将△CDE 沿CD 翻折到△CDE′，连接AE′，当AD ＝6时，求AE′的值．(2)如图②，在AC 上取一点E ，使得CE ＝13AC ，连接DE ，将△CDE 沿CD 翻折到△CDE′，连接AE′交BC 于点F ，求证：DF ＝CF.类型2 线段的和差：要证线段和与差，截长补短去实验例2 如图，在△ABC中，∠BAC＝90°，在BC上截取BD＝BA，连接AD，在AD左侧作∠EAD＝45°交BD于E.(1)若AC＝3，则CE＝________(直接写答案)；(2)如图①，M、N分别为AB和AC上的点，且AM＝AN，连接EM、DN，若∠AME＋∠AND＝180°，求证：DE ＝DN＋ME；(3)如图②，过E作EF⊥AE，交AD的延长线于F，在EC上选取一点H，使得EH＝BE，连接FH，在AC上选取一点G，使得AG＝AB，连接BG、FG，求证：FH＝FG.针对训练：1．如图Z3－7，在▱ABCD中，AE⊥BC于E，AE＝AD，EG⊥AB于G，延长GE、DC交于点F，连接AF.(1)若BE＝2EC，AB＝13，求AD的长；(2)求证：EG＝BG＋FC.2．如图，在正方形ABCD 中，点P 为AD 延长线上一点，连接AC 、CP ，过点C 作CF⊥CP 于点C ，交AB 于点F ，过点B 作BM⊥CF 于点N ，交AC 于点M.(1)若AP ＝78AC ，BC ＝4，求S △ACP ；(2)若CP －BM ＝2FN ，求证：BC ＝MC.3．如图，在△ABC 中，AB ＝BC ，以AB 为一边向外作菱形ABDE ，连接DC ，EB 并延长EB 交AC 于F ，且CB⊥AE 于G.(1)若∠EBG＝20°，求∠AFE；(2)试问线段AE ，AF ，CF 之间的数量关系并证明．类型3 倍长中线：三角形中有中线，延长中线等中线例3 如图Z3－10①，在Rt△ABC中，∠ABC＝90°，D、E分别为斜边AC上两点，且AD＝AB，CE＝CB，连接BD、BE.(1)求∠EBD的度数；(2)如图Z3－10②，过点D作FD⊥BD于点D，交BE的延长线于点F，在AB上选取一点H，使得BH＝BC，连接CH，在AC上选取一点G，使得GD＝CD，连接FH、FG，求证：FH＝FG.针对训练：1．如图，已知在▱ABCD中，G为BC的中点，点E在AD边上，且∠1＝∠2.(1)求证：E是AD中点；(2)若F为CD延长线上一点，连接BF，且满足∠3＝∠2，求证：CD＝BF＋DF.2．如图Z 3－12，在菱形ABCD 中，点E 、F 分别是BC 、CD 上的点，连接AE ，AF ，DE 、EF ，∠DAE ＝∠BAF.(1)求证：CE ＝CF ；(2)若∠ABC＝120°，点G 是线段AF 的中点，连接DG ，EG.求证：DG⊥GE.3．在Rt △ABC 中，∠ACB ＝90°，点D 与点B 在AC 同侧，∠ADC ＞∠BAC，且DA ＝DC ，过点B 作BE∥DA 交DC 于点E ，M 为AB 的中点，连接MD ，ME.(1)如图①，当∠ADC＝90°时，线段MD 与ME 的数量关系是________；(2)如图②，当∠ADC＝60°时，试探究线段MD 与ME 的数量关系，并证明你的结论；(3)如图③，当∠ADC＝α时，求ME MD的值．(3)如图③，把图3－14②中的△CDE绕点C顺时针旋转任意角度，然后连接BE，点P为BE中点，连接AP，PD，AD，问第(2)问中的结论还成立吗？若成立，请证明；若不成立，请说明理由．5．在△ABC中，以AB为斜边，作直角三角形ABD，使点D落在△ABC内，∠ADB＝90°.(1)如图①，若AB＝AC，∠BAD＝30°，AD＝6 3，点P、M分别为BC、AB边的中点，连接PM，求线段PM 的长；(2)如图②，若AB＝AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP＝CP；(3)如图③，若AD＝BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE＝EC，请直接写出线段BF、FC、AD之间的关系(不需要证明)．例4 2017·河南如图①，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图①中，线段PM与PN的数量关系是__________，位置关系是__________；(2)探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．针对训练：1．如图①，在任意的三角形ABC中，分别以AB和AC为一边作等腰三角形ABE和等腰三角形ACD，AB＝AE，AC＝AD，且∠BAE＋∠CAD＝180°，连接DE，延长CA交DE于F.(1)求证：∠CAB＝∠AED＋∠ADE；(2)若∠ACB＝∠BAE＝∠CAD＝90°，如图②，求证：BC＝2AF；(3)若在△ABC中，如图③所示，作等腰三角形ABE和等腰三角形ACD，AB与DE交于点F，F为DE的中点，请问(2)中的结论还成立吗？若成立，请给出证明，若不成立，请说明理由．连接BE、CD，F为BE的中点，连接AF.(1)如图①，当∠BAE＝90°时，求证：CD＝2AF；(2)当∠BAE≠90°时，(1)的结论是否成立？请结合图②说明理由．3．如图①，在等腰三角形ABC中，AB＝AC，在底边BC上取一点D，在边AC上取一点E，使AE＝AD，连接DE，在∠ABD的内部作∠ABF＝2∠EDC，交AD于点F.(1)求证：△ABF是等腰三角形；(2)如图②，BF的延长交AC于点G.若∠DAC＝∠CBG，延长AC至点M，使GM＝AB，连接BM，点N是BG的中点，连接AN，试判断线段AN、BM之间的数量关系，并证明你的结论．图中有角平分线，可向两边作垂线；也可将图对折看，对称以后关系现．角平分线平行线，等腰三角形来添．角平分线加垂线，三线合一试试看．例5．如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP＝FP＝6，EF＝6 3，∠BAD＝60°，且AB＞6 3.(1)求∠EPF的大小；(2)若AP＝10，求AE＋AF的值．针对训练：1．已知：如图①，AD平分∠BAC，∠B＋∠C＝180°，∠B＝90°，易知：DB＝DC.探究：如图②，AD平分∠BAC，∠ABD＋∠ACD＝180°，∠ABD＜90°，求证：DB＝DC.F.(1)如图①，若AB＝4，CD＝1，求AE的长；(2)如图②，点P是AC上一点，连接FP，若AP＝CD，求证：∠ADB＝∠CPF.3．已知，在▱ABCD中，∠BAD＝45°，AB＝BD，E为BC上一点，连接AE交BD于F，过点D作DG⊥AE 于G，延长DG交BC于H.(1)如图①，若点E与点C重合，且AF＝5，求AD的长；(2)如图②，连接FH，求证：∠AFB＝∠HFB.4．如图，将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连接EP.当点M在边AD上移动时，连接BM、BP.(1)求证：BM是∠AMP的平分线；(2)△PDM的周长是否发生变化？证明你的结论．类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6．△ABC 中，∠BAC ＝90°，AB ＝AC ，点D 为直线BC 上一动点(点D 不与B ，C 重合)，以AD 为边在AD 右侧作正方形ADEF ，连接CF.(1)观察猜想：如图①，当点D 在线段BC 上时，①BC 与CF 的位置关系为：________．②BC ，CD ，CF 之间的数量关系为：___________；(将结论直接写在横线上)(2)数学思考：如图Z 3－25②，当点D 在线段CB 的延长线上时，结论①，②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．(3)拓展延伸：如图Z 3－25③，当点D 在线段BC 的延长线上时，延长BA 交CF 于点G ，连接GE.若已知AB＝2 2，CD ＝14BC ，请求出GE 的长．针对训练：1．在四边形ABCD 中，∠B ＋∠D＝180°，对角线AC 平分∠BAD.(1)如图①，若∠DAB＝120°，且∠B＝90°，试探究边AD 、AB 与对角线AC 的数量关系并说明理由．(2)如图②，若将(1)中的条件“∠B＝90°”去掉，(1)中的结论是否成立？请说明理由．(3)如图③，若∠DAB＝90°，探究边AD 、AB 与对角线AC 的数量关系并说明理由．2．如图①，在正方形ABCD中，点E为边BC上一点，将△ABE沿AE翻折得△AHE，延长EH交边CD于F，连接AF.(1)求证：∠EAF＝45°；(2)延长AB，AD，如图②，射线AE、AF分别交正方形两个外角的平分线于M、N，连接MN，若以BM、DN、MN为三边围成三角形，试猜想三角形的形状，并证明你的结论．3．如图①，在正方形ABCD内有一点P，PA＝5，PB＝2，PC＝1，求∠BPC的度数．【分析问题】根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A(如图Z3－28②)，然后连接PP′.(1)请你通过计算求出图Z3－28②中∠BPC的度数；(2)如图③，若在正六边形ABCDEF内有一点P，且PA＝2 13，PB＝4，PC＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1. 证明：(1)∵AB＝AC ，∴∠ABC ＝∠ACB.∵∠MBQ ＋∠ABC＝180°，∠ACB ＋∠PCN＝180°，∴∠MBQ ＝∠PCN.在△QBM 和△PCN 中，⎩⎪⎨⎪⎧QB ＝PC ，∠MBQ ＝∠PCN，BM ＝CN ，∴△QBM ≌△PCN(SAS)．∴MQ＝NP.(2)过M 作MG∥AC 交BC 于G ，∵MG ∥AC ，∴∠MGB ＝∠ACB，∠MGC ＝∠PCN，∵由(1)知，∠ABC ＝∠ACB，∴∠ABC ＝∠MGB，∴MB ＝MG ，∵MB ＝CN ，∴MG ＝CN.在△MGP 和△NCP 中，⎩⎪⎨⎪⎧∠MPG＝∠CPN，∠MGC ＝∠PC N ，MG ＝NC ，∴△MGP ≌△NCP(AAS)．∴PG ＝CP ，∴CG ＝CP ＋PG ，即CG ＝2CP.∵CM 平分∠ACB，∴∠BCM ＝∠MCA，∵MG ∥AC ，∴∠MCA ＝∠GMC，∴∠BCM ＝∠GMC，∴MG ＝CG ，∵MG ＝CN ，∴CN ＝CG ，∴CN ＝2CP.针对训练1. 解：(1)∵AC⊥BC，∴∠ACB ＝90°，又∵AC＝CF ，∴∠AFC ABC＝35°，∴∠EAF ＝10°；(2)证明：方法1：取CF 的中点M ，连接EM 、AM ，∵CE ⊥EF ，∴EM ＝CM ＝FM ＝12CF ，又∵AC＝AE ，∴AM 为EC 的中垂线，∴∠CAM ＋∠ACE＝90°，又∵∠ECF＋∠ACE＝90°，∴∠CAM ＝∠FCE，又∵∠CEF＝∠ACM＝90°，∴△ACM ∽△CEF ，∴AC CM ＝CE EF，又∵CF＝AC ＝2CM ，∴AC CM ＝CE EF ＝21，即CE ＝2EF ；方法2：延长FE 至M ，使EF ＝EM ，连接CM ，∵CE ⊥EF ，∴△CMF 为等腰三角形，又∵AC＝AE ＝CF ，且∠ACE＝∠CFE(易证)，∴△CMF ≌△CEA ，∴FM ＝CE ＝2EF.2. 解：(1)如图①，在AB 上取一点M ，使得BM ＝ME ，连接ME.在Rt △ABE 中，∵OB ＝OE ，∴BE ＝2OA ＝2，∵MB ＝ME ，∴∠MBE ＝∠MEB＝15°，∴∠AME ＝∠MBE＋∠MEB＝30°，设AE ＝x ，则ME ＝BM ＝2x ，AM ＝3x ，∵AB 2＋AE 2＝BE 2，∴(2x ＋3x)2＋x 2＝22，∴x ＝6－22(负根舍弃)，∴AB ＝AC ＝(2＋ 3)·6－22， ∴BC ＝2AB ＝3＋1.(2)证明：如图②，作CP⊥AC，交AD 的延长线于P ，GM ⊥AC 于M.∵BE ⊥AP ，∴∠AHB ＝90°，∴∠ABH ＋∠BAH＝90°，∵∠BAH ＋∠PAC＝90°，∴∠ABE ＝∠PAC，∴△ABE ≌△CAP ，∴AE ＝CP ＝CF ，∠AEB ＝∠P，在△DCF 和△DCP 中，⎩⎪⎨⎪⎧CD ＝CD ，∠DCF ＝∠DCP，CF ＝CP ，∴△DCF ≌△DCP ，∴∠DFC ＝∠P，∴∠GFE ＝∠GEF，∴GE ＝GF ，∵GM ⊥EF ，∴FM ＝ME ，∵AE ＝CF ，∴AF ＝CE ，∴AM ＝CM ，在△GAH 和△GAM 中，⎩⎪⎨⎪⎧∠GAH＝∠GAM，∠AHG ＝∠AMG，AG ＝AG ，∴△AGH ≌△AGM ，∴AH ＝AM ＝CM ＝12AC.3. 解：(1)∵AB＝4，∴AC ＝AB ＝4.∵CD ＝1，∴AD ＝AC －CD ＝3.∵在Rt △ABD 中，∠BAC ＝90°，∴BD ＝AB 2＋AD 2＝5，∵S △ABD ＝12AB·AD＝12AE·BD，∴AE ＝2.4. (2)证明：如图，在线段EB 上截取EH ＝AE ，并连接AH.∵AE ⊥BD ，EH ＝AE ，∴AH ＝2AE.∵BE ＝AE ＋AG ，∴BH ＝BE －HE ＝AG.∵∠BAD ＝∠BEA＝90°，∴∠ABE ＋∠BAE＝∠CAG＋∠BAE＝90°，∴∠ABE ＝∠CA G.∵BA ＝AC ，∴△ABH ≌△CAG ，∴CG ＝AH ＝2AE.4. 解：(1)∵∠BAC＝90°，AB ＝AC ，D 是斜边BC 的中点，∴∠ADC ＝90°，∠ACD ＝45°.在Rt △ADC 中，AC ＝AD÷sin45°＝2 3.∵E 是AC 的中点，∴CE ＝12AC ＝ 3.∵将△CDE 沿CD 翻折到△CDE′，∴CE ′＝CE ＝3，∠ACE ′＝90°.由勾股定理，得AE′＝CE′2＋AC 2＝15.(2)证明：如图，过B 作AE′的垂线交AD 于点G ，交AC 于点H.∵∠ABH ＋∠BAF＝90°，∠CAF ＋∠BAF＝90°，∴∠ABH ＝∠CAF.又∵AB＝AC ，∠BAH ＝∠ACE′＝90°，∴△ABH ≌△CAE ′.∴AH ＝CE′＝CE ，∵CE ＝13AC ，∴AH ＝HE ＝CE. ∵D 是BC 中点，∴DE ∥BH ，∴G 是AD 中点．在△ABG 和△CAF 中：AB ＝AC ，∠BAD ＝∠ACD＝45°，∠ABH ＝∠CAF，∴△ABG ≌△CAF.∴AG ＝CF.∵AG ＝12AD ，∴CF ＝12AD ＝12CD.∴DF＝CF.类型2 线段的和差：要证线段和与差，截长补短去实验例2：解：（1）3（2）证明：延长DN 到K ，使得NK ＝ME ，连接AK ，如图①，因为∠1＋∠3＝180°，∠1＋∠2＝180°，∴∠2＝∠3.⎩⎪⎨⎪⎧AM ＝AN ，∠2＝∠3，ME ＝NK ，∴△AME ≌△ANK (SAS)．∴AE ＝AK ，∠4＝∠5，∴∠4＋∠EAC ＝90°，∴∠5＋∠EAC ＝90°，即∠EAK ＝90°，∵∠EAD ＝45°，∴∠KAD ＝∠EAK －∠EAD ＝90°－45°＝45°.∴∠EAD ＝∠KAD .在△EAD 和△KAD 中，⎩⎪⎨⎪⎧EA ＝KA ，∠EAD ＝∠KAD ，AD ＝AD ，∴△EAD ≌△KAD (SAS)，∴ED ＝KD .∵DK ＝DN ＋KN ，∴ED ＝DN ＋KN ，又NK ＝ME ，∴ED ＝DN ＋ME .(3)证明：延长AE 到J ，使得EJ ＝AE ，连接JH ，JF.如图②，在△ABE 和△JHE 中，⎩⎪⎨⎪⎧AE ＝JE ，∠AEB ＝∠JEH，BE ＝HE ，∴△ABE ≌△JHE(SAS)，∴JH ＝AB ，∠1＝∠2，∵AB ＝AG ，∴JH ＝AG ，∵AE ＝EJ ，EF ⊥AJ ，∴AF ＝JF ，∴∠JAF ＝∠AJF＝45°，即∠2＋∠3＝45°，∵∠BAC ＝90°，∴∠1＋∠EAD＋∠4＝90°，∴∠1＋∠4＝90°－∠EAD，＝90°－45°＝45°，∵∠1＝∠2，∴∠3＝∠4，在△JHF 和△AGF 中，⎩⎪⎨⎪⎧JH ＝AG ，∠3＝∠4，JF ＝AF ，∴△JHF ≌△AGF(SAS)，∴FH ＝FG.针对训练：1. 解：(1)∵四边形ABCD 是平行四边形，∴AD ＝BC.∵BE ＝2EC ，设CE ＝x ，BE ＝2x ，∴BC ＝AD ＝AE ＝3x.又∵EG⊥AB，∴∠AEB ＝90°，∴AB 2＝AE 2＋BE 2，即13＝9x 2＋4x 2，∴x ＝1，∴AD ＝3x ＝3.(2)证明：如图，过C 作CH⊥AB 于H ，则四边形CHGF 为矩形．∴CF ＝HG ，∠CHB ＝90°，GF ＝CH.∵AE ⊥BC ，EG ⊥AB ，∴∠AEB ＝∠CHB＝90°，∠BCH ＋∠B＝90°，∠BAE ＋∠B＝90°，∴∠BCH ＝∠BAE.又∵AE＝BC ，∴△AGE ≌△CHB ，∴GE ＝BH ，AG ＝GF ，∴GE ＝BH ＝BG ＋GH ＝BG ＋CF.2. 解：(1)∵四边形ABCD 是正方形，BC ＝4，∴AB ＝AD ＝CD ＝BC ＝4，∠ADC ＝∠ABC＝90°.∵在Rt △ABC 中，AC ＝AB 2＋BC 2＝4 2，∴AP ＝78AC ＝72 2， ∴S △ACP ＝12AP·CD＝7 2.∵四边形ABCD 是正方形，∴AB ＝BC ＝DC ，∠ABC ＝∠BCD＝∠ADC＝90°.∵∠BCD ＝90°，CF ⊥CP ，∴∠1＋∠DCF＝∠2＋∠DCF＝90°，∴∠1＝∠2，∵在△FBC 和△PDC 中，⎩⎪⎨⎪⎧∠FBC＝∠3，BC ＝DC ，∠1＝∠2，∴△FBC ≌△PDC(ASA)，∴CF ＝CP ，∵CP －2FN ＝BM ，∴CF －FK ＝BM ，即CK ＝BM ，∵∠FBC ＝90°，BM ⊥CF ，∴∠1＋∠NBC＝∠4＋∠NBC＝90°，∴∠1＝∠4，∵在△ABM 和△BCK 中，⎩⎪⎨⎪⎧AB ＝BC ，∠4＝∠1，BM ＝CK ，∴△ABM ≌△BCK(SAS)，∴∠7＝∠6.∵BM ⊥CF ，NK ＝NF ，∴BF ＝BK ，∵BF ＝BK ，BM ⊥CF ，∴∠4＝∠5，∴∠4＋∠7＝∠5＋∠6，∵∠8＝∠4＋∠7，∴∠8＝∠MBC，∴BC ＝解：方法二：如图②，延长BM 交AD 于点G ，过A 作AE⊥BG 于E先证△AEB ≌△BNC(AAS)，∴AE ＝BN ，又证△AEG ≌△BNF(AAS)，∴EG ＝NF ，再证四边形BCPG 为平行四边形，∴BG ＝CP ，∵CP －BM ＝2FN ，∴BG －BM ＝2EG ，∴MG ＝2EG ，∴点E 为MG 中点，∵AE ⊥MG ，EM ＝EG ，∴AM ＝AG ，∴∠3＝∠4，∵∠2＝∠3，∠1＝∠4，∴∠1＝∠2，∴BC ＝MC.3. 解：(1)∵∠EBG＝20°，CB ⊥AE ，∴∠BEG ＝70o ，∠CBF ＝∠EBG＝20°，∵四边形ABDE 是菱形，∴∠ABE ＝∠BEG＝70°，∴∠ABG ＝50°，∵AB ＝BC ，∴∠FCB ＝25°，∴∠AFE ＝∠CBF＋∠FCB＝45°；(2)AE ，AF ，CF 之间的数量关系是AF 2＋CF 2＝2AE 2，证明如下：连接DF ，∵四边形ABDE 是菱形，∴AB ＝DB ，∠DBE ＝∠ABE，∴∠DBF ＝∠ABF，∵BF ＝BF ，∴△DBF ≌△ABF(SAS)，∴DF ＝AF ，∠BDF ＝∠BAF，∵∠BCF ＝∠BAF，∴∠BCF ＝∠BDF，∵CB ⊥AE ，AE ∥DB ，∴DB ⊥CB ，∵CB ＝AB ＝BD ，∴△DBC 是等腰直角三角形，∴DC ＝2BD ＝2AE ，∵∠DPB ＝∠CPF，∴∠CFP ＝∠DBP＝90°，∴DF 2＋CF 2＝DC 2，即有：AF 2＋CF 2＝2AE 2.类型3 倍长中线：三角形中有中线，延长中线等中线例3解：(1)设∠BEC ＝α，∠BDA ＝β，则∠C ＝180°－2α，∠A ＝180°－2β.∵在Rt △ABC 中，∠ABC ＝90°，∴∠A ＋∠C ＝90°，即180°－2α＋180°－2β＝90°，∴α＋β＝135°，∴∠EBD ＝45°.(2)证明：法一：如图①，延长BD 至点B′，使得DB′＝DB ，连接FB′、GB′.在△GDB′和△CDB 中，⎩⎪⎨⎪⎧GD ＝CD ，∠GDB ′＝∠CDB，B ′D ＝BD ，∴△GDB ′≌△CDB.∴GB ′＝BC ＝BH ，∠GB ′D ＝∠CBD.∵FD ⊥BD ，BD ＝DB′，∴FB ＝FB′.∵∠FB ′G ＝45°－∠GB′D，∠HBF ＝90°－45°－∠CBD＝45°－∠CBD，∴∠FB ′G ＝∠HBF.在△FHB 和△FGB′中，⎩⎪⎨⎪⎧HB ＝GB′，∠HBF ＝∠GB′F，BF ＝B′F，∴△FHB ≌△FGB ′，∴HF ＝GF.法二：如图②，延长FD 至点F ′，使得DF ′＝DF ，连接BF ′.先证△DGF ≌△DCF ′，再证△BHF ≌△BCF ′，∴HF ＝GF .针对训练1. 证明：(1)∵四边形ABCD 是平行四边形，∴AB ＝CD ，AD ＝BC ，∠A ＝∠C .又∵∠1＝∠2，∴△ABE ≌△CDG (ASA)，∴AE ＝CG .∵G 为BC 中点，∴CG ＝12BC ， ∴AE ＝CG ＝12BC ＝12AD ，∴E 是AD 中点．(2)如图，延长BE ，CD 交于点H.∵四边形ABCD 是平行四边形，∴AB 綊CD ，∴∠A ＝∠ADH，∠1＝∠4，又∵∠1＝∠2，∠3＝∠2，∴∠1＝∠2＝∠3＝∠4，∴FH ＝FB.由(1)，E 是AD 中点，∴AE ＝DE ，∴△ABE ≌△DHE(AAS)，∴AB ＝DH ，∴CD ＝AB ＝DH ＝DF ＋FH ＝DF ＋BF ，即CD ＝BF ＋DF.2. 证明：(1)在菱形ABCD 中，AB ＝BC ＝CD ＝AD ，∠ADF ＝∠ABE，∵∠DAE ＝∠BAF，∴∠DAE －∠EAF＝∠BAF－∠EAF，即∠DAF＝∠BAE.∴△DAF ≌△BAE ，∴BE ＝DF.又∵BC＝CD ，∴CE ＝CF∵在菱形ABCD 中，AB ∥CD ，∴∠DFA ＝∠GAH.∵G 为AF 中点，∴AG ＝GF.又∵∠DGF＝∠AGH，∴△DGF ≌△HGA.∴DG ＝GH ，AH ＝DF.又∵AB＝CD ，∴BH ＝CF.又∵AB∥CD，∠ABC ＝120°，∴∠C ＝60°.又∵CE ＝CF ，∴△CEF 为等边三角形，∴CF ＝EF ，∠CFE ＝60°，∴EF ＝BH ，∠DFE ＝∠ABC＝120°.又∵BE＝DF ，∴△EFD ≌△HBE ，∴HE ＝ED ，又∵HG＝DG ，∴DG ⊥GE.3. 解：（1）MD=ME2)MD ＝3ME.理由如下：如图①，延长EM 交DA 于点F.∵BE ∥DA ，∴∠FAM ＝∠EBM.又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.∵DA ＝DC ，∠ADC ＝60°，∴∠BED ＝∠ADC＝60°，∠ACD ＝60°.∵∠ACB ＝90°，∴∠ECB ＝30°，∴∠EBC ＝30°，∴CE ＝BE ，∴AF ＝EC ，∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∴∠MDE ＝30°.在Rt △MDE 中，tan ∠MDE ＝ME MD ＝33. ∴MD ＝3ME.(3)如图②，延长EM 交DA 于点F ，∵BE ∥DA ，∴∠FAM ＝∠EBM，又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.延长BE 交AC 于点N ，∴∠BNC ＝∠DAC.∵DA ＝DC ，∴∠DCA ＝∠DAC，∴∠BNC ＝∠DCA，∵∠ACB ＝90°，∴∠ECB ＝∠EBC，∴CE ＝BE ，∴AF ＝CE.∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∵∠ADC ＝α，∴∠MDE ＝α2. ∴在Rt △MDE 中，ME MD ＝tan ∠MDE ＝tan α2.4.解：(1)如图①，作EH ⊥BC 于点H .∵△ABC 是等边三角形，∴∠ACB ＝60°.∵CE 平分∠ACB ，∴∠ECH ＝12∠ACB ＝30°， ∵EC ＝4，∠ECH ＝30°，∴EH ＝2，HC ＝2 3.∵BC ＝6 3，∴BH ＝6 3－2 3＝4 3.在Rt △BHE 中，BE 2＝(4 3)2＋22＝52，∴BE ＝2 13.(2)如图②，延长DP 至M ，使DP ＝PM ，连接BM 、AM .在△PDE 和△PMB 中，⎩⎪⎨⎪⎧PD ＝PM ，∠EPD ＝∠BPM ，PE ＝PB ，∴△PDE ≌△PMB (SAS)．∴BM ＝DE ，∠1＝∠2.∴BM ∥DE .∴∠MBD ＋∠BDE ＝180°.∵CE 平分∠ACB ，DE ＝CD ，∴∠BDE ＝30°＋30°＝60°.∴∠MBD ＝120°.∵△ABC 是等边三角形，∴∠ABC ＝60°，∴∠3＝60°.∵BM ＝DE ，DE ＝CD ，∴BM ＝CD .在△ABM 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，∠3＝∠ACD ，BM ＝CD ，∴△ABM ≌△ACD (SAS)．∴AD ＝AM ，∠4＝∠5.∵PD ＝PM ，∴AP ⊥PD .∵∠4＝∠5，∠BAD ＋∠5＝60°，∴∠4＋∠BAD ＝60°，即∠MAD ＝60°.∴∠PAD ＝12∠MAD ＝30°.∵在Rt △APD 中，tan30°＝PD AP，∴AP ＝3PD .(3)第(2)问中的结论成立，理由如下：如图③，延长DP 至N ，使DP ＝PN ，连接BN 、AN ，取BE 、AC 交于点O.在△PDE 和△PNB 中，⎩⎪⎨⎪⎧PD ＝PN ，∠EPD ＝∠BPN，PE ＝PB ，∴△PDE ≌△PNB(SAS)．∴BN ＝DE ，∠1＝∠2.∵DE ＝CD ，∴BN ＝CD.∵∠AOB ＝∠EOC，∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO ＝60°，∠DEC ＝∠DCE＝30°，∴∠1＋∠3＝∠2＋∠4，∴∠3＝∠4.在△ABN 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，∠3＝∠4，BN ＝CD ，∴△ABN ≌△ACD(SAS)．∴∠5＝∠6，AN ＝AD.∵PD ＝PN ，∴AP ⊥PD.∵∠NAC ＋∠5＝60°，∴∠NAC ＋∠6＝60°，即∠NAD＝60°.∴∠PAD ＝12∠NAD＝30°， ∵在Rt △APD 中，tan ∠PAD ＝PD AP，∴AP ＝3PD.5. 解：(1)∵∠ADB ＝90°，∠BAD ＝30°，AD ＝6 3，∴cos ∠BAD ＝AD AB ，∴32＝6 3AB，∴AB ＝12. 又∵AB ＝AC ，∴AC ＝12，∴PM 为△ABC 的中位线，∴PM ＝12AC ＝6.(2)证明：方法一：如图①，在截取ED 上截取EQ ＝PD ，∵∠ADB ＝90°，∴∠1＋∠2＝90°，又∵AD＝AE ，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4.在△BDP 和△CEQ 中，PD ＝QE ，∠1＝∠4，BD ＝CE ，∴△BDP ≌△CEQ.∴BP ＝CQ ，∠DBP ＝∠QCE，又∵∠5＝∠1＋∠DBP，∠6＝∠4＋∠QCE，∴∠5＝∠6，∴PC ＝CQ ，∴BP ＝CP.方法二：如图②，过点B 作EP 的垂线交EP 的延长线于点M ，过C 点作EP EP 于点N.∵∠ADB ＝90°，∴∠1＋∠2＝90°，又∵AD＝AE ，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4，在△BMD 和△CNE 中，∠1＝∠4，∠BMD ＝∠CNE＝90°，BD ＝CE ，∴△BMD ≌△CNE.∴BM ＝CN.在△BMP 和△CNP 中，∠5＝∠6，∠BMP ＝∠CNP，BM ＝CN ，∴△BMP ≌△CNP，∴BP ＝CP.方法三：如图③，过点B 作BM ∥CE 交EP 的延长线于点M .略证△BMP ≌△CEP ，∴BP ＝CP .(3)BF 2＋FC 2＝2AD 2.类型4 中位线：三角形中两中点，连接则成中位线例4: 解：（1）PM=PN;PM ⊥PN(2)△PMN 为等腰直角三角形，理由如下：由题意知△ABC 和△ADE 均为等腰直角三角形，∴AB ＝AC ，AD ＝AE ，∠BAC ＝∠DAE＝90°，∴∠BAD ＋∠DAC＝∠CAE＋∠DAC，∴∠BAD ＝∠CAE，∴△BAD ≌△CAE ，∴∠ABD ＝∠ACE，BD ＝CE.又∵M、P 、N 分别是DE 、CD 、BC 的中点，∴PM 是△CDE 的中位线，∴PM ∥CE 且PM ＝12CE ，∠MPD ＝∠ECD＝∠ACD＋∠ACE. 同理，PN ∥BD 且PN ＝12BD ，∠DBC ＝∠PNC，又∵BD＝CE ，∠ABD ＝∠ACE，∴PM ＝PN ，∴∠MPN ＝∠MPD＋∠DPN＝∠ECD ＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°，∴PM ⊥PN ，∴△PMN 为等腰直角三角形；(3)△PMN 面积的最大值为492.提示：在旋转的过程中，由(2)中的结论知△PMN 为等腰直角三角形，S △PMN ＝12PN 2＝18BD 2，当S △PMN 有最大值时，则BD 的值最大，由三角形三边关系可推断出当B 、A 、D 三点共线时，BD的值最大，其最大值为14，此时S △PMN ＝12PN 2＝18BD 2＝18×14×14＝492.针对训练：1. 解：(1)证明：延长DA 交BE 于G 点．∵∠BAE ＋∠CAD ＝180°，即∠EAG ＋∠GAB ＋∠CAD ＝180°，∵∠GAB ＋∠BAC ＋∠CAD ＝180°，∴∠EAG ＝∠CAB .∵∠EAG ＝∠AED ＋∠ADE ，∴∠CAB ＝∠AED ＋∠ADE .(2)证明：如图①，过E 点作DA 延长线的垂线，垂足为H .∴∠AHE ＝∠ACB ＝90°，由(1)可知，∠EAH ＝∠BAC ，又∵AE ＝AB ，∴△AHE ≌△ACB ，∴EH ＝BC ，AH ＝AC .∵AC ＝AD ，∴AH ＝AD .∵∠EHA ＝∠FAD ＝90°，∴AF ∥EH .∵A 为DH 中点，∴AF 为△DHE 中位线，∴EH ＝2AF ，∴BC ＝2AF .(3)成立．证明如下：如图②，延长DA 至M 点，使AM ＝DA ，连接EM ，∵∠BAE ＋∠CAD ＝180°，∠CAD ＋∠CAM ＝180°，∴∠BAE ＝∠CAM ，∴∠BAE ＋∠CAC ＝∠CAM ＋∠EAC ，即∠BAC ＝∠CAM .∵AM ＝AD ，AD ＝AC ，∴AM ＝AC .又∵AB ＝AE ，∠BAC ＝∠EAM ，∴△BAC ≌△EAM ，∴BC ＝EM .∵F 、A 分别为DE 、DM 中点，∴AF 为△DEM 中位线，∴EM ＝2AF ，∴BC ＝2AF .2. 解：(1)证明：∵∠BAC＋∠EAD＝180°，∠BAE ＝90°，∴∠DAC ＝90°，在△ABE 与△ACD 中，AE ＝AD ，∠BAE ＝∠CAD＝90°，AB ＝AC ，∴△ABE ≌△ACD(SAS)，∴CD ＝BE ， ∵在Rt △ABE 中，F 为BE 的中点，∴BE ＝2AF ，∴CD ＝2AF.(2)成立，证明：如图，延长EA 交BC 于G ，在AG 上截取AH ＝AD ，∵∠BAC ＋∠EAD＝180°，∴∠EAB ＋∠DAC＝180°，∵∠EAB ＋∠BAH＝180°，∴∠DAC ＝∠BAH，在△ABH 与△ACD 中，AH ＝AD ，∠BAH ＝∠CAD，AB ＝AC ，∴△ABH ≌△ACD(SAS)，∴BH ＝DC ，∵AD ＝AE ，AH ＝AD ，∴AE ＝AH ，∵EF ＝FB ，∴BH ＝2AF ，∴CD ＝2AF.3. 解：(1)证明：∵AB＝AC ，∴∠ABD ＝∠ACD，∵AE ＝AD ，∴∠ADE ＝∠AED，∵∠BAD ＋∠ABD＝∠ADE＋∠EDC，∠EDC ＋∠ACD＝∠AED ，∴∠BAD ＝2∠EDC，∵∠ABF ＝2∠EDC，∴∠BAD ＝∠ABF，∴△ABF 是等腰三角形；(2)方法一：如图①，延长CA 至点H ，使AG ＝AH ，连接BH ，∵点N 是BG 的中点，∴AN ＝12BH ， ∵∠BAD ＝∠ABF，∠DAC ＝∠CBG，∴∠CAB ＝∠CBA，∴△ABC 是等边三角形．∴AB ＝BC ＝AC ，∠BAC ＝∠BCA＝60°，∵GM ＝AB ，AB ＝AC ，∴CM ＝AG ，∴AH ＝CM ，在△BAH 和△BCM 中，⎩⎪⎨⎪⎧AB ＝BC ，∠BAH ＝∠BCM＝120°，AH ＝CM ，∴△BAH ≌△BCM(SAS)，∴BH ＝BM ，∴AN ＝12BM ，方法二：如图②，延长AN 至K ，使NK ＝AN ，连接KB ，同方法一，先证△ABC 是等边三角形，再证△ANG ≌△KNB (SAS)，所以BK ＝AG ＝CM ，然后可以证得∠ABK ＝∠BCN ＝120°，最后证△ABK ≌△BCN (SAS)，所以BM ＝AK ＝2AN .类型5 角的和差倍分例5：解：(1)如图，过点P 作PG⊥EF 于G.∵PE ＝PF ＝6，EF ＝6 3，∴FG ＝EG ＝3 3，∠FPG ＝∠EPG＝12∠EPF. 在Rt △FPG 中，sin ∠FPG ＝FG PF ＝3 36＝32. ∴∠FPG ＝60°，∴∠EPF ＝2∠FPG＝120°.(2)如图，作PM ⊥AB 于M ，PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线，∴∠DAC ＝∠BAC ，AM ＝AN ，PM ＝PN .在Rt △PME 和Rt △PNF 中，PM ＝PN ，PE ＝PF ，∴Rt △PME ≌Rt △PNF ，∴NF ＝ME .又∵AP ＝10，∠PAM ＝12∠DAB ＝30°， ∴AM ＝AN ＝AP cos30°＝10×32＝5 3. ∴AE ＋AF ＝(AM ＋ME )＋(AN －NF )＝AM ＋AN ＝10 3.针对训练：1. 证明：如图，过D 作DE ⊥AB 于E ，过D 作DF ⊥AC 于F ，∵DA 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∵∠B ＋∠ACD ＝180°，∠ACD ＋∠FCD ＝180°，∴∠B ＝∠FCD ，在△DFC 和△DEB 中，⎩⎪⎨⎪⎧∠F ＝∠DEB ，∠FCD ＝∠B ，DF ＝DB ，∴△DFC ≌△DEB ，∴DC ＝DB .2. 解：(1)∵AC＝AB ＝4，且CD ＝1，∴AD ＝AC －CD ＝3.在Rt △ABD 中，∠BAD ＝90°，∴BD ＝AB 2＋AD 2＝5，∵S △ABD ＝12AB·AD＝12AE·BD， ∴AE ＝2.4.(2)证明：如图，取BC 的中点M ，连接AM 交BD 于点N .∵∠BAC ＝90°，AB ＝AC ，点M 为BC 的中点，∴AM ＝BM ＝CM ，AM ⊥BC ，∠NAD ＝∠FCP ＝45°，∴∠AMF ＝∠BMN ＝90°.∵AE ⊥BD ，∴∠MAF ＋∠ANE ＝∠MBN ＋∠BNM ＝90°，又∠ANE ＝∠BNM ，∴∠MAF ＝∠MBN ，∴△AMF ≌△BMN ，∴MF ＝MN ，∴AM －MN ＝CM －MF ，即AN ＝CF .∵AP ＝CD ，∴AC －CD ＝AC －AP ，即AD ＝CP .∴△ADN ≌△CPF ，∴∠ADB ＝∠CPF .3. 解：(1)∵AB ＝BD ，∠BAD ＝45°，∴∠BDA ＝45°，即∠ABD ＝90°.∵四边形ABCD 是平行四边形，∴当E 、C 重合时，BF ＝12BD ＝12AB . ∵在Rt △ABF 中，AB 2＋BF 2＝AF 2，∴(2BF )2＋BF 2＝(5)2，∴BF ＝1，AB ＝2.在Rt △ABD 中，AD ＝AB 2＋BD 2＝2AB 2＝2 2.(2)证明：如图，在AF 上截取AK ＝HD ，连接BK.∵∠AFD ＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°，∴∠2＝∠3.在△ABK 与△DBH 中，⎩⎪⎨⎪⎧AB ＝BD ，∠2＝∠3，AK ＝HD ，∴△ABK ≌△DBH ，∴BK ＝BH ，∠6＝∠5.∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠5＝∠4＝45°，∴∠6＝∠5＝45°，∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK 与△BFH 中，⎩⎪⎨⎪⎧BK ＝BH ，∠7＝∠5，BF ＝BF ，∴△BFK ≌△BFH.∴∠BFK ＝∠BFH，即∠AFB＝∠HFB.4. 解：(1)证明：由折叠知∠EMN＝∠ABC＝90°，BE ＝EM ，∴∠EMB ＝∠EBM，∴∠EMN －∠EMB＝∠ABC－∠EBM，即∠BMP＝∠MBC.∵在正方形ABCD 中，AD ∥BC ，∴∠AMB ＝∠MBC，∴∠AMB ＝∠BMP，∴BM 是∠AMP 的平分线．(2)△PDM 的周长没有发生变化．证明如下：如图，过B 作BQ ⊥MP∵∠A ＝90°，且由(1)知BM 是∠AMP 的平分线，∴BA ＝BQ ，∵∠A ＝∠MQB ＝90°，∠AMB ＝∠BMP ，MB ＝MB ，∴△AMB ≌△QMB (AAS)．∴MA ＝MQ .∵BA ＝BC ，∴BQ ＝BC ，又∵∠BQP ＝90°＝∠C ，BP ＝BP ，∴Rt △BPC ≌Rt △BPQ (HL)．∴PC ＝PQ ，∴△PDM 的周长＝MD ＋MP ＋DP ＝MD ＋MQ ＋QP ＋PD＝MD ＋MA ＋PC ＋PD ＝AD ＋DC ＝2AD .∴△PDM 的周长没有发生变化．类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6：解：(1)①∵四边形ADEF 是正方形，∴AD ＝AF ，AB ＝AC ，∵∠BAC ＝∠DAF＝90°，∴∠BAD ＝∠CAF，∴△DAB ≌△FAC ，∴∠B ＝∠ACF，∴∠ACB ＋∠ACF＝90°，即CF⊥BC；②∵△DAB ≌△FAC ，∴CF ＝BD ，∵BC ＝BD ＋CD ，∴BC ＝CF ＋CD.(2)结论①成立，结论②不成立．∵四边形ADEF 是正方形，∴AD ＝AF ，AB ＝AC.∵∠BAC ＝∠DAF＝90°，∴∠BAD ＝∠CAF，∴△DAB ≌△FAC ，∴∠ABD ＝∠ACF，CF ＝BD ，∴∠BCF ＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°，即CF⊥BC；∵BC＝CD －BD ，∴BC ＝CD －CF.(3)如图，过A 作AH ⊥BC 于H ，过E 作EM ⊥BD 于M ，EN ⊥CF 于∵∠BAC ＝90°，AB ＝AC ，∴BC ＝2AB ＝4，AH ＝CH ＝12BC ＝2，∴CD ＝14BC ＝1，∴DH ＝3，同(2)证得△BAD ≌△CAF ， ∴∠ABD ＝∠ACF ＝45°，∴∠BCF ＝∠ACB ＋∠ACF ＝90°，∴BC ⊥CF ，CF ＝BD ＝5.∵四边形ADEF 是正方形，∴AD ＝DE ，∠ADE ＝90°，∵BC ⊥CF ，EM ⊥BD ，EN ⊥CF ，∴四边形CMEN 是矩形，∴NE ＝CM ，EM ＝CN ，∵∠AHD ＝∠ADE ＝∠EMD ＝90°，∴∠ADH ＋∠EDM ＝∠EDM ＋∠DEM ＝90°，∴∠ADH ＝∠DEM ，∴△ADH ≌△DEM ，∴EM ＝DH ＝3，DM ＝AH ＝2，∴CN ＝EM ＝3，EN ＝CM ＝3，∵∠ABC ＝45°，∴∠BGC ＝45°，∴△BCG 是等腰直角三角形，∴CG ＝BC ＝4，∴GN ＝1，∴EG ＝GN 2＋EN 2＝10.针对训练：1. 解：(1)AC ＝AD ＋AB .证明如下：∵∠B ＋∠D ＝180°，∠B ＝90°，∴∠D ＝90°.∵∠DAB ＝120°，AC 平分∠DAB ，∴∠DAC ＝∠BAC ＝60°，∵∠B ＝90°，∴AB ＝12AC ，同理AD ＝12AC . ∴AC ＝AD ＋AB .(2)(1)中的结论成立，理由如下：如图①，以C 为顶点，AC 为一边作∠ACE＝60°，∠ACE 的另一边交AB 的延长线于点E ，∵∠BAC ＝60°，∴△AEC 为等边三角形，∴AC ＝AE ＝CE ，∠E ＝60°，∵∠ABC ＋∠D＝180°，∠DAB ＝120°，∴∠DCB ＝60°，∴∠DCA ＝∠ECB.在△DAC 和△BEC 中，⎩⎪⎨⎪⎧∠DAC＝∠E，AC ＝CE ，∠DCA ＝∠BCE，∴△DAC ≌△BEC ，∴AD ＝BE ，∴AC ＝AE ＝AD ＋AB.(3)AD ＋AB ＝2AC.理由如下：如图②，过点C 作CE⊥AC 交AB 的延长线于点E∵∠ABC ＋∠D＝180°，∠DAB ＝90°，∴∠DCB ＝90°，∵∠ACE ＝90°，∴∠DCA ＝∠BCE，又∵AC 平分∠DAB，∴∠CAB ＝45°，∴∠E ＝45°，∴AC ＝CE.∴△CDA ≌△CBE ，∴AD ＝BE ，∴AD ＋AB ＝AE.∵在Rt △ACE 中，∠CAB ＝45°，∴AE ＝AC cos45°＝2AC ， ∴AD ＋AB ＝2AC.2. 解：(1)证明：∵四边形ABCD 是正方形，∴∠B ＝∠D＝∠BAD＝90°，AB ＝AD ，∵△ABE 沿AE 翻折得到△AHE，∴△ABE ≌△AHE ，∴AH ＝AB ＝AD ，BE ＝EH ，∠AHE ＝∠AHF＝∠B＝∠D＝90°.在Rt △AHF 和Rt △ADF 中，⎩⎪⎨⎪⎧AF ＝AF ，AH ＝AD ， ∴Rt △AHF ≌Rt △ADF(HL)，∴∠HAF ＝∠DAF，∴∠EAF ＝∠EAH＋∠FAH＝12∠BAH＋12∠HAD＝12∠BAD＝45°，(2)以BM ，DN ，MN 为三边围成的三角形为直角三角形．证明如下：如图，过点A 作AH ⊥AN 并截取AH ＝AN ，连接BH 、HM ，∵∠1＋∠BAN ＝90°，∠3＋∠BAN ＝90°，∴∠1＝∠3，在△ABH 和△ADN 中，⎩⎪⎨⎪⎧AB ＝AD ，∠1＝∠3，AH ＝AN ，∴△ABH ≌△ADN (SAS)，∴BH ＝DN ，∠HBA ＝∠NDA ＝135°，∵∠HAN ＝90°，∠MAN ＝45°，∴∠1＋∠2＝∠HAM ＝∠MAN ＝45°，在△AHM 和△ANM 中，⎩⎪⎨⎪⎧AH ＝AN ，∠HAM ＝∠MAN ，AM ＝AM ，∴△AHM ≌△ANM (SAS)，∴HM ＝NM ，∴∠HBP ＝180°－∠HBA ＝180°－135°＝45°，∴∠HBP ＋∠PBM ＝45°＋45°＝90°，∴△HBM 是直角三角形，∵HB ＝DN ，HM ＝MN ，∴以BM ，DN ，MN 为三边围成的三角形为直角三角形．3. 解：(1)如图①，将△PBC 绕点B 逆时针旋转90°得△P ′BA ，连接PP ′，则△AP ′B ≌△CPB ， ∴P ′B ＝PB ＝2，P ′A ＝PC ＝1，∠1＝∠2，∠AP ′B ＝∠BPC .∵四边形ABCD 是正方形，∴AB ＝BC ，∠ABC ＝90°，∴∠2＋∠3＝90°，∴∠1＋∠3＝90°，即∠P ′BP ＝90°，∴∠BP ′P ＝45°.在Rt △P ′BP 中，由勾股定理，得PP ′2＝4.∵P ′A ＝1，AP ＝5∴P ′A 2＝1，AP 2＝5，∴P ′A 2＋PP ′2＝AP 2，∴△P ′AP 是直角三角形，∴∠AP ′P ＝90°，∴∠AP′B＝45°＋90°＝135°，∴∠BPC＝135°.(2)仿照【分析】中的思路，将△BPC绕点B逆时针旋转120°，得到了△BP′A，连接PP′，如图②.则△PBC≌△P′BA，∴P′B＝PB＝4，P′A＝PC＝2，∠BPC＝∠BP′A，∴△BPP′为等腰三角形，∵∠ABC ＝120°，∴∠PBP′＝120°，∴∠BP′P＝30°，过点B作BG⊥PP′于G，则∠P′GB＝90°，∴PP′＝2P′G.∵P′B＝PB＝4，∠BP′P＝30°，∴BG＝2，∴P′G＝2 3.∴PP′＝4 3，在△APP′中，∵PA＝2 13，P′A＝2，PP′＝4 3，∴P′A2＋P′P2＝PA2，∴△PP′A是直角三角形，∴∠AP′P＝90°，∴∠BPC＝∠BP′A＝∠PP′B＋∠AP′P＝30°＋90°＝120°.。

2018重庆中考几何专题1学生版.docx

25.在AABC中，以AB为斜边，作直角AABD,使点D落在AABC内，ZADB=90°.H A图1 图2 图3(1) 如图1,若AB=AC, ZBAD=30°, AD二6馅，点P、M分别为BC、AB边的中点，连接PM,求线段PM的长；(2) 如图2,若AB=AC,把AABD绕点A逆时针旋转一定角度，得到AACE,连接ED 并延长交BC于点P,求证：BP=CP且ZADE=75°.25.在厶ABC屮，AB=AC,点D,点E在边BC上不同的两点,(1)如图1,若ZBAC=90°, CDf/耳求BC 的 2；(2)如图2,若ZBAC=90°, ZEAD=45°,求证：DCr/^BE；25. (1)如图1,若点D为等腰直角三角形ABC斜边BC的屮点，点E、F分别在AB、AC 边上，且ZEDF二90。

，连接AD、EF,当BO5典，FO2时，求EF的长度；(2)如图2,若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且ZEDF=90°； M 为EF 的中点，连接CM,当DF//AB 时，证明：3ED二2MC；图225.在Z\ABC中，AB二AC,点F是BC延长线上一点，以CF为边，作菱形CDEF,使菱形CDEF 与点A在BC的同侧，连结BE,点G是BE的中点，连结AG、DG.(1)如图①，当ZBAOZDCF二90°时，已知AC二3血，CD二2,求AG的氏度；(2)如图②，当ZBAC二ZDCF二60°时，AG与DG有怎样的位置和数量关系，并证明；25.如图，四边形ABCD为矩形，连接AC, AD=2CD,点E在AD边上.(1)如图1,若ZECD=30° , CE二4,求Z\AEC 的面积；・(2)如图2,延长BA至点F使得AF二2CD,连接FE并延长交CD于点G,过点D作DH丄EGEDGC25.己知四边形ABCD为菱形，连接BD,点E为菱形ABCD外任一点.图1 图2 图3(1)如图(1),若ZA二45° , AB=V6，点E为过点B作AD边的垂线与CD边的延长线的交点，BE, AD交于点F, •求DE的长.(2)如图(2),若2ZAEB=180° - ZBED, ZABE二60°,求证：BOBE+DE已知在LABC中，乙4^0=45°,过:点C作CD丄A5干点D, ZACD=^BDE,过点占作恥丄交加干点E.⑴如图4若眈=3私=，求40的长；2⑵如图2,过点C作少丄干点化点G是巧C中点，求证：ZC^G=45°；己知在中，ZABC=45\过点C作CD丄40于点D, AACD=^BDE t过点尸作庞丄4万交DE千点E.⑴如图1,若BG=3,BE =求人C的长;(2如图2,过点c作铮丄a于点兀点G是召C中点，求证：FC = j2FG+DF;2•如国，P为正方形ABCDi^BC M-点.BG1AP于点&在朋的延£线上取点臥使AG= GE,连^BS, CE.(1)如国1，咅正方形的逍辰为㊇、P"•求0G的£度：(2)如因2・当P点为方C的中点时，求证：CE』BG ：AN(3)如图3, ZCBE的平分线交直E干N点，连接DN,请直接写出河‘的値。

2018年重庆市中考数学试卷(a卷)答案及答案解析-名师推荐

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分，共48分。

) 1.2的相反数是A .2-B .12-C.12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“-”即可求解【点评】本题考查了相反数的定义，属于中考中的简单题2．下列图形中一定是轴对称图形的是A.40°直角三角形B.四边形C.平行四边形D.矩形【答案】D【解析】A40°的直角三角形不是对称图形；B 两个角是直角的四边形不一定是轴对称图形；C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

3.为调查某大型企业员工对企业的满意程度，以下样本最具代表性的是 A.企业男员工 B.企业年满50岁及以上的员工 C.用企业人员名册，随机抽取三分之一的员工 D.企业新进员工【答案】C【解析】A 调查对象只涉及到男性员工；B 调查对象只涉及到即将退休的员工；D 调查对象只涉及到新进员工【点评】此题主要考查考生对抽样调查中科学选取样本的理解，属于中考当中的简单题。

4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为A ．12B ．14C ．16D ．18【答案】C 【解析】∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6; 第3个图案中的三角形个数为:2+2+2+2=2×4=8; ……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;【点评】此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，从而计算出正确结果。

(完整版)2018年重庆市中考数学试卷(A卷)答案及解析(可编辑)

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分，共48分。

)1.2的相反数是 A .2-B .12-C.12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“-”即可求解【点评】本题考查了相反数的定义，属于中考中的简单题2．下列图形中一定是轴对称图形的是A.B.C.D.【答案】D【解析】A40°的直角三角形不是对称图形；B 两个角是直角的四边形不一定是轴对称图形；C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为A ．12B ．14C ．16D ．18 【答案】C 【解析】40°直角三角形四边形平行四边形矩形∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6;第3个图案中的三角形个数为:2+2+2+2=2×4=8;……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;【点评】此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，从而计算出正确结果。

2018年重庆市中考数学试卷(a卷)答案及答案解析

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分，共48分。

) 1.2的相反数是A .2-B .12-C .12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“-”即可求解【点评】本题考查了相反数的定义，属于中考中的简单题2．下列图形中一定是轴对称图形的是A.直角三角形B.四边形C.平行四边形D.矩形【答案】D【解析】A40°的直角三角形不是对称图形；B 两个角是直角的四边形不一定是轴对称图形；C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

3.为调查某大型企业员工对企业的满意程度，以下样本最具代表性的是 A.企业男员工B.企业年满50岁及以上的员工C.用企业人员名册，随机抽取三分之一的员工D.企业新进员工【答案】C【解析】A 调查对象只涉及到男性员工；B 调查对象只涉及到即将退休的员工；D 调查对象只涉及到新进员工【点评】此题主要考查考生对抽样调查中科学选取样本的理解，属于中考当中的简单题。

4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为A．12 B．14 C．16 D．18【答案】C【解析】∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6;第3个图案中的三角形个数为:2+2+2+2=2×4=8;……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;【点评】此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，从而计算出正确结果。

比较简单。

重庆市2018年中考数学试题(含解析)

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分，共48分。

)1.2的相反数是 A .2- B .12-C .12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“-”即可求解【点评】本题考查了相反数的定义，属于中考中的简单题2．下列图形中一定是轴对称图形的是A.B.C.D.【答案】D【解析】A40°的直角三角形不是对称图形；B 两个角是直角的四边形不一定是轴对称图形；C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为A ．12B ．14C ．16D ．18【答案】C 【解析】40°直角三角形四边形平行四边形矩形∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6;第3个图案中的三角形个数为:2+2+2+2=2×4=8;……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;【点评】此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，从而计算出正确结果。

全国中考数学真题分类汇编专题复习(八)函数与几何图形综合探究题(答案不全)(2021年整理)

全国2018年中考数学真题分类汇编专题复习（八）函数与几何图形综合探究题（答案不全）编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（全国2018年中考数学真题分类汇编专题复习（八）函数与几何图形综合探究题（答案不全））的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为全国2018年中考数学真题分类汇编专题复习（八）函数与几何图形综合探究题（答案不全）的全部内容。

（分类)专题复习（八)函数与几何图形综合探究题类型1 探究线段最值问题（2018·烟台）（2018·广西六市）（2018·淮安）（2018·郴州)（2018·咸宁）（2018·山西）(2018·菏泽）24。

（本小题满分9分）(2018·淄博）如图，抛物线2y ax bx =+经过OAB ∆的三个顶点，其中点(3A ，点(3,3B -，O 为坐标原点．（1)求这条抛物线所对应的函数表达式；（2）若()()P m Q t n为该抛物线上的两点,且n m4,,,<，求t的取值范围；(3）若C为线段AB上的一个动点,当点A，点B到直线OC的距离之和最大时，求BOC∠的大小及点C的坐标.（2018·湘潭)(2018·永州）(2018·泸州）25. 如图11，已知二次函数23(2)34y ax a x =--+的图象经过点A （4，0），与y 轴交于点B.在x轴上有一动点C(m ，0) （0〈m<4），过点C 作x 轴的垂线交直线AB 于点E,交该二次函数图象于点D.（1)求a 的值和直线AB 的解析式；(2）过点D 作DF ⊥AB 于点F ，设△ACE ，△DEF 的面积分别为1S ，2S ，若124S S =,求m 的值； (3）点H 是该二次函数图象上位于第一象限的动点，点G 是线段AB 上的动点,当四边形DEGH是平行四边形，且DEGH 周长取最大值时，求点G 的坐标.xyOHGFEDCB A24．（2018·宜宾）(本小题12分）（注意．．：在试题卷上作答无效．．．．．．．．．）在平面直角坐标系xOy 中，已知抛物线的顶点坐标为(2,0），且经过点(4，1），如图，直线y=错误!x 与抛物线交于A 、B 两点，直线l 为y= –1。

2018年重庆市中考数学试卷-答案

2018年重庆市中考数学试卷-答案重庆市2018年初中学业⽔平暨⾼中招⽣考试（A 卷）数学答案解析第Ⅰ卷⼀、选择题 1．【答案】A【解析】根据题意，2(2)0+-=，∴2的相反数是-2，故选A. 【考点】相反数的概念. 2．【答案】D【解析】A 中的直⾓三⾓形不是轴对称图形；B 中的直⾓梯形不是轴对称图形；C 中的平⾏四边形是中⼼对称图形，不是轴对称图形；D 中的矩形是轴对称图形，故选D.【提⽰】判断⼀个图形是不是轴对称图形，要将这个图形沿某条直线对折，对折的两部分能完全重合，则这个图形是轴对称图形，常见的轴对称图形有线段、⾓、等腰三⾓形、菱形、矩形、正⽅形、圆、正多边形等。

【考点】轴对称图形的概念. 3．【答案】C【解析】根据题意，采取随机抽取的⽅法进⾏调查⽐较全⾯，结果也会⽐较真实有效，故选C. 【提⽰】选择抽取样本的恰当的⽅法是解答本题的关键. 【考点】调查中的样本选择. 4．【答案】C【解析】由题可知，每增加⼀个图案则增加2个三⾓形，∴第○n 个图案中有42(1)n +-个三⾓形，∴第⑦个图案中有16个三⾓形，故选C. 【考点】探索规律. 5．【答案】C【解析】根据题意可知两个三⾓形相似，设最长边为x cm ，则592.5x=，解得 4.5x =，即这个三⾓形的最长边为4.5 cm ，故选C .【提⽰】理解相似三⾓形的性质是解答本题的关键. 【考点】相似三⾓形的性质． 6．【答案】D【解析】平⾏四边形的对⾓线互相平分⽽不垂直，∴命题A 不正确；矩形的对⾓线相等且互相平分⽽不垂直，∴命题B 不正确；菱形的对⾓线互相垂直平分⽽不相等，∴命题C 不正确；正⽅形的对⾓线互相垂直平分且相等，∴命题D 正确，故选D.【提⽰】掌握特殊四边形的对⾓线的性质是解答本题的关键. 【考点】命题的判断． 7．【答案】B【解析】24255223==<∴<<，，，即在2和3之间，故选B .【考点】⼆次根式的运算、估算⽆理数. 8．【答案】C【解析】根据题意，当输⼊33x y ==，时，2021512y x y ∴+=≥，≠；当输⼊42x y =-=-，时，20,22012y x y ∴-=＜≠；当输⼊24x y ==，时，20,212y x y ∴+=≥；当输⼊42x y ==，时，20,22012y x y ∴+=≥≠，故选C.【提⽰】根据y 的范围分情况求值是解答本题的关键。

2018重庆中考几何专题-教师版

25．在△A B C中，以A B为斜边，作直角△A B D，使点D落在△A B C内，∠A D B=90°．（1）如图1，若AB=AC，∠BAD=30°，AD=6，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；（2）如图2，若AB=AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC 于点P，求证：BP=CP【分析】（1）在直角三角形中，利用锐角三角函数求出AB，即可；（2）先利用互余判断出，∠BDP=∠PEC，得到△BDP和△CEQ，再用三角形的外角得到∠EPC=∠PQC，即可；【解答】（1）解：∵∠ADB=90°，∠BAD=30°，AD=6，∴cos∠BAD=，∴AB===12，∴AC=AB=12，∵点P、M分别为BC、AB边的中点，∴PM=AC=6，（2）如图2，在ED上截取EQ=PD，∵∠ADB=90°，∴∠BDP+∠ADE=90°，∵AD=AE，∴∠ADE=∠AED，∵把△ABD绕点A逆时针旋转一定角度，得到△ACE，∴∠AEC=∠ADB=90°∵∠AED+∠PEC=90°，∴∠BDP=∠PEC，在△BDP和△CEQ中，，∴△BDP≌△CEQ，∴BP=CQ，∠DBP=∠QCE，∵∠CPE=∠BDP+∠DBP，∠PQC=∠PEC+∠QCE，∴∠EPC=∠PQC，∴PC=CQ，∴BP=CP25．在△ABC中，AB=AC，点D，点E在边BC上不同的两点，且∠ADE=75°．（1）如图1，若∠BAC=90°，CD=，求BC的长；（2）如图2，若∠BAC=90°，∠EAD=45°，求证：DC=BE；【考点】相似形综合题．【分析】（1）作DG⊥AC于G，证明出△ABC是等腰直角三角形，进而求出AG的长，即可求出BC的长；（2）作DH⊥AE于H，设DC=a，利用a表示出BC、DE和CD的长，根据线段之间的关系得到结论；【解答】解：（1）如图1所示，作DG⊥AC于G，∵∠BAC=90°，AB=AC，∴△ABC是等腰直角三角形，∴∠1=∠B=45°，∵∠ADE=75°，∴∠2=60°，∠DAG=30°，∴DG=CG=CD=1，AD=2DG=2，∴AG==，∴AC=AG+CG=+1，∴BC=AG=+；（2）如图2所示，作DH⊥AE于H，设DC=a，则DG=CG=a，∴AD=2DG=a，AG=a，∴AC=AG+CG=a，∴BC=AC=（+1）a，∵∠EAD=45°，∴△ADH是等腰直角三角形，∴AH=DH=AD=a，∵∠4=180°﹣∠ADE﹣∠DAE=60°，∴DE=2EH，∴DE=DH÷=a，∴BE=BC﹣DE﹣CD=a=DC，∴DC=BE；25.（1）如图1，若点D为等腰直角三角形ABC斜边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°，连接AD、EF，当BC=5，FC=2时，求EF的长度；（2）如图2，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；M为EF 的中点，连接CM，当DF∥AB时，证明：3ED=2MC；【考点】三角形综合题；全等三角形的判定与性质；线段垂直平分线的性质；等腰三角形的性质；勾股定理；等腰直角三角形．【分析】（1）根据等腰直角三角形的性质，证得△ADE≌△CDF，根据全等三角形对应边相等，求得AE=CF=2，最后在在Rt△AEF中根据勾股定理求得EF的长；（2）先设等边三角形边长为2，在Rt△BDE中求得DE的长，再根据CM垂直平分DF，在Rt△CDN中求得CN，在Rt△MND中求得MN的长，最后根据CM与DE的长度之比求得3ED=2MC；【解答】解：（1）如图1∵点D为等腰直角三角形ABC斜边BC的中点∴AD⊥BC，AD=BC=CD=，∠DAE=∠C=45°∴AC=CD=5又∵∠EDF=90°，FC=2∴∠ADE=∠CDF，AF=5﹣2=3在△ADE和△CDF中∴△ADE≌△CDF（ASA）∴AE=CF=2∴在Rt△AEF中，EF==（2）设等边三角形边长为2，则BD=CD=1∵等边三角形ABC中，DF∥AB∴∠FDC=∠B=60°∵∠EDF=90°∴∠BDE=30°∴DE⊥BE∴BE=，DE=如图2，连接DM，则Rt△DEF中，DM=EF=FM∵∠FDC=∠FCD=60°∴△CDF是等边三角形∴CD=CF=1∴CM垂直平分DF∴∠DCN=30°∴Rt△CDN中，DN=，CN=，DF=1∴在Rt△DEF中，EF==∵M为EF的中点∴FM=DM=∴Rt△MND中，MN==∴CM=+=∴==∴3ED=2MC25.在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF与点A在BC的同侧，连结BE，点G是BE的中点，连结AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，已知AC=32，CD=2，求AG的长度；（2）如图②，当∠BAC=∠DCF=60°时，AG与DG有怎样的位置和数量关系，并证明；【答案】(1)、5；(2)、AG⊥GD，AG=DG；证明过程见解析；【解析】试题分析：(1)、延长DG与BC交于H，先证△BG△≌EGD，得到BH=DC，=ED，HG=DG，得出BH，再证△ABH≌△ACD，得出∠BAH∠=∠CAD，AH=AD，进而求得∠HAD=90°，即可；(2)、延长DG与BC交于H，先证△BG△≌EGD，得到BH=DC，=ED ，HG=DG ，得出BH ，再证△ABH ≌△ACD ，得出∠BAH ∠=∠CAD ，AH=AD ，得到△H △AD 为等边三角形，即可；(3)、延长DG 与BC 交于H ，先证△BG △≌EGD ，得到BH=DC ，=ED ，HG=DG ，得出BH ，再证△ABH ≌△ACD ，得出∠BAH ∠=∠CAD ，AH=AD ，得到△H △AD 为等腰三角形，即可．试题解析：(1)、如图1，延长DG 与BC 交于H ，连接AH 、AD ，∵四边形D CEF 是正方形， ∴DE=DC ，DE ∥CF ， ∴∠GBH=∠GED ，∠GHB=∠GDE ， ∵G 是BC 的中点， ∴BG=EG ，在△BGH 和△EGD 中， ∵∠GBH=∠GED ，∠GHB=∠GDE ，BG=EG ， ∴△BGH ≌△EGD （AAS ），∴BH=ED ，HG=DG ， ∴BH=DC ， ∵AB=AC ，∠BAC=90°， ∴∠ABC=∠ACB=45°， ∵∠DCF=90°，∴∠DCB=90°， ∴∠ACD=45°， ∴∠ABH=∠ACD=45°，在△ABH 和△ACD 中， ∵AB=AC ，∠ABH=∠ACD ，BH=CD ， ∴△ABH ≌△ACD （SAS ）， ∴∠BAH=∠CAD ，AH=AD ， ∵∠BAH+∠HAC=90°，∴∠CAD+∠HAC=90°，即∠HAD=90°， ∴AG ⊥GD ，AG=GD ；在Rt △ABC 中，AB=AC=2，∴BC=6 在Rt △DCH 中，DC=2，HC=BC ﹣BH=6﹣2=4， ∴DH=22DC HC =25， ∴GD=21DH=5， ∴AG=GD=5．（2）AG ⊥GD ，AG=DG ；如图2，延长DG 与BC 交于H ，连接AH 、AD ，∵四边形DCEF 是正方形， ∴DE=DC ，DE ∥CF ， ∴∠GBH=∠GED ，∠GHB=∠GDE ， ∵G 是BC 的中点， ∴BG=EG ，在△BGH 和△EGD 中， ∵∠GBH=∠GED ，∠GHB=∠GDE ，BG=EG ， ∴△BGH ≌△EGD （AAS ）， ∴BH=ED ，HG=DG ， ∴BH=DC ， ∵AB=AC ，∠BAC=∠DCF=60， ∴∠ABC=60°，∠ACD=60°，∴∠ABC=∠ACD=60°，在△ABH 和△ACD 中， ∵AB=AC ，∠ABH=∠ACD ，BH=CD ， ∴△ABH ≌△ACD （SAS ）， ∴∠BAH=∠CAD ，AH=AD ， ∴∠BAC=∠HAD=60°， ∴AG ⊥HD ，∠HAG=∠DAG=30°，∴tan ∠DAG=tan30°=33， ∴AG=DG ； 25．如图，四边形ABCD 为矩形，连接AC ，AD=2CD ，点E 在AD 边上．（1）如图1，若∠ECD=30°，CE=4，求△AEC 的面积；（2）如图2，延长B A 至点F 使得AF=2CD ，连接FE 并延长交CD 于点G ，过点D 作DH ⊥EG 于点H ，连接AH ，求证：；（【解析】试题分析：（1）根据30°的直角三角形求CD 和ED ，再利用面积公式求△AEC 的面积；（2）作辅助线，构建全等三角形，证明△AFM ≌△ADH ，得AM=AH ，FM=DH ，则△MAH 是等腰直角三角形，有AH ，根据线段的和代入得结论；（3）根据将线段AE 绕点A 旋转一定的角度α（0°＜α＜30°）得到线段AE′，先计算当AE 旋转时DN 的最小值和最大值，当α=0°时，DN 最小；当α=180°时，DN 最大，分别计算，写出结论．试题解析：（1）在Rt △EDC 中，∵∠EDC=30°，∴ED=12EC=12×4=2，cos30°=DC EC，∴DC=EC•cos30°=4×2，∴AE=2DC ﹣2，∴AEC S =12×AE ×DC=12（2）×﹣ （2）过A 作AM ⊥AH ，交FG 于M ，∴∠MAH=∠MAD+∠DAH=90°，又∵∠FAD=∠MAD+∠FAM=90°，∴∠FAM=∠DAH ，∵AF∥CD，∴∠F=∠FGD∵DH⊥EG，∴∠DHE=∠HDG+∠FGD=90°，∠EDG=∠EDH+∠HDG=90°，∴∠FGD=∠EDH，∴∠F=∠EDH，又∵AF=2CD，AD=2CD，∴AF=AD，∴△AFM≌△ADH，∴AM=AH，FM=DH，∴△MAH是等腰直角三角形，∴AH，∵FH=MH+FM，∴AH+DH；25.（12分）已知四边形ABCD为菱形，连接BD，点E为菱形ABCD外任一点．（1）如图（1），若∠A=45°，E为过点B作AD边的垂线与CD边的延长线的交点，BE，AD交于点F，求DE的长．（2）如图（2），若2∠AEB=180°﹣∠BED，∠ABE=60°，求证：BC=BE+DE【答案】（1）2）证明参见解析；【解析】试题分析：（1）首先证明△AFB与△EFD为等腰直角三角形，然后在△ABF中依据勾股定理可求得BF和AF的长，从而得到DF的长，然后在Rt△EDF中，可求得DE的长；（2）延长DE至K，使EK=EB，连结AK．首先证明∠AEB=∠AEK ，然后依据SAS 证明△AEB ≌△AEK ，由全等三角形的性质及等边三角形的判断定理可证明△AKD 为等边三角形，于是得到KD=BC ，通过等量代换可得到问题的答案；（3）记AB 与DE 的交点为O ．首先证明依据菱形的性质可得到∠ABC=2∠ABD ，然后依据平行四边形的性质可证明∠CDE=∠BOE ，最后依据三角形外角的性质可得到问题的答案．试题解析：（1）如图1所示：∵四边形ABCD 为菱形，∴AB ∥CD ．∴∠A=∠ADE=45°．∵AD ⊥BE ，∴∠AFB=DFE=90°．∴△AFB 与△EFD 为等腰直角三角形．∴BF 2+AF 2=AB 2，即：2BF 2=6，∴BF=AF=∵△EFD 为等腰直角三角形，∴EF=DF=AD ﹣．∴）（2）如图2所示：延长DE 至K ，使EK=EB ，联结AK ．∵2∠AEB=180°﹣∠BED ，∴∠BED=180°﹣2∠AEB=180°﹣∠AEB ﹣∠AEK ．∴∠AEB=∠AEK ．在△AEB 和△AEK 中BK KE AEB AEK AE AE ⎧=⎪∠=∠⎨⎪=⎩，∴△AEB ≌△AEK ．∴∠K=∠ABE=60°，Ak=AB ．又∵AB=AD ，∴AK=AD ．∴△AKD 为等边三角形．∴KD=AD ．∴KD=BC ．∵KD=KE+DE ，∴CB=EB+DE ．7.已知两个全等的等腰直角ABC 、△D EF ，其中∠ACB=∠DFE=90，E 为AB 中点，△DE F 可绕顶点E 旋转，线段DE ，EF 分别交线段CA ，CB(或它们所在直线)于M 、N ．(1)如图l ，当线段EF 经过ABC 的顶点C 时，点N 与点C 重合，线段DE 交AC于M,求证：AM=MC ；(2)如图2，当线段EF 与线段BC 边交于N 点，线段DE 与线段AC 交于M 点，连MN,EC,请探究AM ，MN,CN 之间的等量关系，并说明理由；（1）∵AC =BC ，E 为AB 中点∴CE ⊥AB, ∠ACE ＝∠BCE =12ACB=45o∴∠AEC ＝90o∴∠A =∠ACE=45o∴AE =CE∵DF =EF , ∠DFE ＝90o∴∠FED =45o ∴∠FED =12∠AEC又∵AE =CE ∴AM =MC（2）AM =MN +CN ，理由如下:在AM 截取AH ，使得AH =CN ，连接BH由（1）知AE =CE ，∠A =∠BCE =45o在AHE ∆与CNE ∆中：⎪⎩⎪⎨⎧=∠=∠=CE AE NCE A CN AH ∴AHE ∆≌CNE ∆∴HE =NE ，∠AEH ＝∠CEN∴∠HEM =∠AEC －∠AEH －MEC =∠AEC －∠CEN －MEC =∠AEC －∠MEF = 4590-=45o ∴∠HEM =∠NEM =45o在HEM ∆与NEM ∆中：⎪⎩⎪⎨⎧=∠=∠=CE AE NCE A CNAH ∴HEM ∆≌NEM ∆∴HM =MN ∴AM =AH+HM= CN +MN即AM =MN +CN。

[2018年中考真题数学卷]2018重庆市中考数学试题[B]含答案解析[版](word版可编辑修改)

[2018年中考真题数学卷]2018重庆市中考数学试题[B]含答案解析[版](word 版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（[2018年中考真题数学卷]2018重庆市中考数学试题[B]含答案解析[版](word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为[2018年中考真题数学卷]2018重庆市中考数学试题[B]含答案解析[版](word版可编辑修改)的全部内容。

点A 的横坐标为2,将直线沿y 轴向下平移4个单位长度,得到直线 ,直线与y 轴交于点B,1l 3l 3l 与直线交于点C,点C 的纵坐标为-2，直线与y 轴交于点D 。

2l 2l （1）求直线的解析式；2l （2）求△BDC 的面积.23.在美丽乡村建设中，某县政府投入专项资金,用于乡村沼气池和垃圾集中处理点建设，该县政府计划:2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍。

(1)按计划,2018年前5个月至少要修建多少个沼气池?（2）到2018年5月底，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值，据核算，前5个月,修建每个沼气池与垃圾集中处理点的平均费用之比为1:2,为加大美丽乡村建设的力度,政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投人10a ％，全部用于沼气池和垃圾集中处理点建设，经测算：从今年6月起，修建每个沼气池和垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a ％ ,5a%,新建沼气池和垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a% ,8a%。

2018年全国中考数学真题重庆中考数学(解析版-精品文档)

重庆市2018年初中学业水平暨高中招生考试数学试题（B卷）（全卷共五个大题，满分150分，考试时间120分钟）注意事项1．试题的答案书写在答题卡上，不得在试卷上直接作答；2．作答前认真阅读答题卡上的注意事项；3．作图（包括作辅助线）请一律用黑色签字笔完成；4．考试结束，由监考人员将试题和答题卡一并收回．参考公式：抛物线y＝ax2＋bx＋c（a≠0）的顶点坐标为（－2ba，244ac ba），对称轴为x＝－2ba．一、选择题（本大题12个小题，每小题4分，共48分．在每小题所给的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置．．．．．．．上）1．（2018·重庆B卷，1，4）下列四个数中，是正整数的是（）A．－1 B．0 C．12D．1【答案】D．【解析】易知－1是负整数，12是分数，1是正整数，而整数包括正整数、0和负整数，故选D．【知识点】实数的概念整数正整数．2．（2018·重庆B卷，2，4）下列图形中，是轴对称图形的是（）【答案】D．【解析】根据轴对称图形的定义，沿某条直线将图形折叠，直线两旁的部分能够完全重合的图形才是轴对称图形，故只有选项D满足要求，因此选D．【知识点】图形的变换轴对称图形．3．（2018·重庆B卷，3，4）下列图形都是由同样大小的黑色正方形纸片组成，其中第①个图A．B．C．D．形中有3张黑色正方形纸片，第②个图形中有5张黑色正方形纸片，第③个图形中有7张黑色正方形纸片，…，按此规律排列下去，第⑥个图形中黑色正方形纸片的张数为（）①③②A．11 B．13 C．15 D．17【答案】B．【解析】根据第1个图形中小正方形的个数为2×1＋1，第1个图形中小正方形的个数为2×1＋1，第2个图形中小正方形的个数为2×2＋1；第3个图形中小正方形的个数为2×3＋1，……，第n 个图形中小正方形的个数为2n＋1，故第6个图形中小正方形的个数为2×6＋1＝13，故选B．【知识点】规律探究题代数式代数式的值．4．（2018·重庆B卷，4，4）下列调查中，最适合采用全面调查（普查）的是（）A．对我市中学生每周课外阅读时间情况的调查B．对我市市民知晓“礼让行人”交通新规情况的调查C．对我市中学生观看电影《厉害了，我的国》情况的调查D．对我国首艘国产航母002型各零部件质量情况的调查【答案】D．【解析】选项A、B、C中，调查的对象的数量多，分布广，不适合普查；选项D中，由于对我国首艘国产航母002型各零部件质量情况的调查，每一个零部件都不能有任何的疏忽懈怠，必须一个一个检查，要采用普查方式，故选择D．【知识点】普查与抽样调查5．（2018·重庆B卷，5，4）制作一块3m×2m长方形广告牌的成本是120元，在每平方米制作成本相同的情况下，若将此广告牌的四边都扩大到原来的3倍，那么扩大后长方形广告牌的成本是（）A．360元 B．720元 C．1080元 D．2160元【答案】C．【解析】∵将此广告牌的四边都扩大到原来的3倍后面积为原长方形面积的9倍，而120×9＝1080（元），∴扩大后长方形广告牌的成本是1080元．故选C．【知识点】有理数的应用6．（2018·重庆B 卷，6，4）下列命题是真命题的是（） A ．如果一个数的相反数等于这个数的本身，那么这个数一定是0 B ．如果一个数的倒数等于这个数本身，那么这个数一定是1 C ．如果一个数的平方等于这个数的本身，那么这个数一定是0 D ．如果一个数的算术平方根等于这个数的本身，那么这个数一定是0 【答案】A ．【解析】易知A 选项正确，因为倒数等于其本身的数是±1，平方数等于其本身的数有0和1，算术平方根等于其本身的数有0和1，故选A ．【知识点】有理数的概念相反数倒数平方数算术平方根7．（2018·重庆B 卷，7，4）估计的值应在（） A ．5和6之间 B ．6和7之间 C ．7和8之间 D ．8和9之间【答案】C ．【解析】∵＝－＝而7＝8，∴在7和8之间，故选C ．【知识点】二次根式的计算估算8．（2018·重庆B 卷，8，4）根据如图所示的程序计算函数y 的值，若输入的x 的值是4或7时，输出的y 的值相等，则b 等于（） A ．9 B ． 7 C ．－9 D ．－7【答案】C ．【解析】由题意得2×4＋b ＝6－7，解得b ＝－9，故选C ．8题图【知识点】代数式求代数式的值程序求值题函数值分段函数9．（2018·重庆B卷，9，4）如图，AB是一垂直于水平面的建筑物．某同学从建筑物底端B出发，先沿水平方向向右行走20米到达点C，再经过一段坡度（或坡比）为i＝1﹕0.75、坡长为10米的斜坡CD到达点D，然后再沿水平方向向右行走40米到达点E（A，B，C，D，E均在同一平面内）．在E处测得建筑物顶端A的仰角为24°，则建筑物AB的高度约为（参考数据：sin24°≈0.41，cos24°≈0.91，tan24°≈0.45）（）A．21.7米 B．22.4米 C．27.4米 D．28.8米【答案】A．【解析】过点C作CN⊥DE于点N，延长AB交ED的延长线于点M，则BM⊥DE于点M，则MN＝BC＝20米．∵斜坡CD的坡比i＝1﹕0.75，∴令CN＝x，则DN＝0.75x．在Rt△CDN中，由勾股定理，得x2＋(0.75x)2＝102，解得x＝8，从而CN＝8米，DN＝6米．∵DE＝40米，∴ME＝MN＋ND＋DE＝66米，AM＝(AB＋8)米．在Rt△AME中，tan E＝AM EM，即8tan2466AB+=︒，从而0.45＝866AB+，解得AB＝21.7，故选A．【知识点】解直角三角形坡度10．（2018·重庆B卷，10，4）如图，△ABC中，∠A＝30°，点O是边AB上一点，以点O为圆心，以OB为半径作圆，⊙O恰好与AC相切于点D，连接BD．若BD平分∠ABC，AD＝9题图段CD的长是（）A．2 B．32D【答案】B．【解析】如下图，连接OD，则由AD切⊙O于点D，得OD⊥AC．∵在Rt△AOD中，∠A＝30°，AD＝，tan A＝ODAD，∴OD＝AD•，tan A＝tan30°＝3＝2．∴AO＝2OD＝4，AB＝OA＋OB＝6．∵∠AOD＝90°－∠A＝60°，∴∠ABD＝12∠AOD＝30°．∵BD平分∠ABC，∴∠ABC＝2∠ABD＝60°．∴∠C＝90°＝∠ADO．∴OD∥BC．∴AD AODC OB=42=．∴DC【知识点】圆圆的切线相似三角形10题图11．（2018·重庆B卷，11，4）如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y＝kx（k≠0，x＞0）的图象同时经过顶点C，D．若点C的横坐标为5，BE＝3DE，则k的值为（）A．52B．3 C．154D．5【答案】C．【解析】．∵菱形ABCD的边AD⊥y轴，点C的横坐标为5，∴BC＝5，DE＝1．∵BE＝3DE，∴BE＝3．令OB＝m，则OE＝m＋3，C(5，m)，D(1，m＋3)，由C、D两点均在双曲线y＝kx上，得5m＝m＋3，解得m＝34，从而k＝5m＝154，故选C．【知识点】反比例函数菱形反比例函数的图像与性质12．（2018·重庆B卷，12，4）若数a使关于x的不等式组111(1)3223(1)x xx a x⎧-≤-⎪⎨⎪-≤-⎩有且仅有三个整数解，且使关于y的分式方程312122y ay y++=--有整数解，则满足条件的所有a的值之和是（）A．－10 B．－12 C．－16 D．－18 【答案】B．【解析】解不等式组，得－3≤x≤35a+，由该不等式组有且仅有三个整数解，得－1≤35a+＜0，11题图从而－8≤a ＜－3．解方程312122y a y y ++=--，得y ＝2a＋5．又∵y ≠2，即2a＋5≠2， ∴a ≠－6．又∵y 为整数，∴满足条件的整数a 为－8和－4，其和为－12．故选B ．【知识点】一元一次不等式组的解法分式方程的解法二、填空题（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上）．13．（2018·重庆B 卷，13，4）计算：1-＋20＝．【答案】2．【解析】∵原式＝1＋1＝2，∴答案为2．【知识点】实数的运算绝对值零指数14．（2018·重庆B 卷，14，4）如图，在边长为4的正方形ABCD 中，以点B 为圆心，以AB 为半径画弧，交对角线BD 于点E ，则图中阴影部分的面积是（结果保留π）．【答案】8－2π．【解析】∵正方形ABCD 的边长为4，∴∠BAD ＝90°，∠ABD ＝45°，AB ＝AD ＝4．∴S 阴影＝S Rt △ABD －S 扇形BAE ＝12×4×4－2454360π⋅＝8－2π．14题图【知识点】圆的有关计算扇形面积正方形15．（2018·重庆B 卷，15，4）某企业对一工人在五个工作日里生产零件的数量进行调查，并绘制了如图所示的折线统计图，则在这五天里该工人每天生产零件的平均数年是个．【答案】34．【解析】由图可知这组数据是36，34，31，34，35，故x ＝15(36＋34＋31＋34＋35)＝15×170＝34，因此答案为34．【知识点】．统计平均数折线统计图16．（2018·重庆B 卷，16，4）如图，在Rt △ABC 中，∠ACB ＝90°，BC ＝6，CD 是斜边AB 上的中线，将△BCD 沿直线CD 翻折至△ECD 的位置，连接AE ．若DE ∥AC ，计算AE 的长度等于．【答案】．【解析】∵在Rt △ABC 中，∠ACB ＝90°，BC ＝6，CD 是斜边AB 上的中线， ∴CD ＝12AB ＝DA ＝DB ．令∠B ＝x °，则∠DCB ＝∠B ＝x °，15题图期五期四期三期二期一16题图EDCBA由翻折知，DE＝DB，∠ECD＝∠DCB＝x°＝∠CED．∵DE∥AC，∴∠ACE＝∠CED＝x°．∴由∠ACB＝90°，得3x＝90，x＝30，从而∠B＝30°，于是AC＝12 AB．在Rt△ABC中，tan B＝ACBC，得AC＝BC tan B＝6tan30°＝．∴AC∥DE，AC＝DE，从而四边形ACDE是平行四边形．又∵CD＝DE，∴四边形ACDE是菱形．∴AE＝AC＝O E DC BA【知识点】翻折直角三角形菱形三角函数17．（2018·重庆B卷，17，4）一天早晨，小玲从家出发匀速步行到学校．小玲出发一段时间后，她的妈妈发现小玲忘带了一件必需的学习用品，于是立即下楼骑自行车，沿小玲行进的路线，匀速去追小玲．妈妈追上小玲将学习用品交给小玲后，立即沿原路线匀速返回家里，但由于路上行人渐多，妈妈返回时骑车的速度只是原来的一半．小玲继续以原速度步行前往学校．妈妈与小玲之间的距离y（米）与小玲从家出发后步行的时间x（分）之间的函数关系如图所示（小玲和妈妈上、下楼以及妈妈交学习用品给小玲耽搁的时间忽略不计）．当妈妈刚回到家时，小玲离学校的距离为米．【答案】200．【解析】由图可知：玲玲用30分钟从家里步行到距家1200米的学校，因此玲玲的速度为40米/分；妈妈在玲玲步行10分钟后从家时出发，用5分钟追上玲玲，因此妈妈的速度为40×15÷5＝120米/分，返回家的速度为120÷2＝60米/分．设妈妈用x 分钟返回到家里，则60x ＝40×15，解得x ＝10，此时玲玲已行走了25分钟，共步行25×40＝1000米，还离学校1200－1000＝200（米），故答案为200．【知识点】一次函数的实际应用18．（2018·重庆B 卷，18，4）为实现营养套餐的合理搭配，某电商推出两款适合不同人群的甲、乙两种袋装的混合粗粮．甲种袋装粗粮每袋含有3千克A 粗粮，1千克B 粗粮，1千克C 粗粮；乙种袋装粗粮每袋含有1千克A 粗粮，2千克B 粗粮，2千克C 粗粮．甲、乙两种袋装粗粮每袋成本分别等于袋中的A 、B 、C 三种粗粮的成本之和．已知每袋甲粗粮的成本是每千克A 种粗粮成本的7.5倍，每袋乙种粗粮售价比每袋甲种粗粮的售价高20%，乙种袋装粗粮的销售利润率是20%．当销售这两款袋装粗粮的销售利润率为24%时，该电商销售甲、乙两种袋装粗粮的袋数之比是．（商品的销售利润率＝100%-⨯商品的售价商品的成本价商品的成本价）【答案】4﹕7．【解析】设1千克A 粗粮的成本为m 元，则甲袋成本为7.5m 元，且B 、C 两种粗粮各1千克的成本之和为7.5m －3m ＝4.5m 元，从而乙袋粗粮的成本为m ＋2×4.5m ＝10m 元，由乙种袋装粗粮的销售利润率是20%，得乙种袋装粗粮的销售利润为10m ×20%＝2m 元；而由每袋乙种粗粮售价比每袋甲种粗粮的售价高20%，知甲种袋装粗粮的售价为12m ÷(1＋20%)＝10m 元，其利润为2.5m 元，现将以上信息列表如下：17题图分2m2.5m10m 12m 10m 7.5m221113CBA每袋粗粮组成成分（千克）每袋售价（元）每袋成本（元）每袋利润（元）乙袋甲袋设甲袋装粗粮销售x 袋，乙袋装粗粮销售y 袋时，销售这两款袋装粗粮的销售利润率为24%，根据题意，得2.5224%7.510m x m ym x m y⋅+⋅=⋅+⋅，整理，得7x ＝4y ，从而x ﹕y ＝4﹕7，故答案为4﹕7．【知识点】方程组的应用销售问题三、解答题（本大题2个小题，每小题8分，共16分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上．19．（2018·重庆B 卷，19，8）如图，AB ∥CD ，△EFG 的顶点F ，G 分别落在直线AB ，CD 上，GE 交AB 于点H ，GE 平分∠FGD ．若∠EFG ＝90°，∠E ＝35°，求∠EFB 的度数．【思路分析】本题解答分四步走：一是由三角形内角和定理，求出∠EGF ＝55°；二是由角平分线定义，得∠EGD ＝55°；三是由平行线性质，得∠EHB ＝55°；四是由三角形外角性质，求得∠EFB ＝∠EGB －∠E ＝55°－35°＝20°．【解题过程】19．解：∵在△EFG 中，∠EFG ＝90°，∠E ＝35°，∴∠EGF ＝90°－∠E ＝55°． ∵GE 平分∠FGD ， ∴∠EGF ＝∠EGD ＝55°． ∵AB ∥CD ，H GFEDCBA19题图∴∠EHB ＝∠EGD ＝55°．又∵∠EHB ＝∠EFB ＋∠E ，∴∠EFB ＝∠EGB －∠E ＝55°－35°＝20°．【知识点】平行线三角形内角和角平分线20．（2018·重庆B 卷，20，8）某学校开展以素质提升为主题的研学活动，推出了以下四个项目供学生选择：A ．模拟驾驶；B ．军事竞技；C ．家乡导游；D ．植物识别．学校规定：每个学生都必须报名且只能选择其中一个项目．八年级（3）班班主任刘老师对全班学生选择的项目情况进行了统计，并绘制了如下两幅不完整的统计图．请结合统计图中的信息，解决下列问题：（1）八年级（3）班学生总人数是___________，并将条形统计图补充完整；（2）刘老师发现报名参加“植物识别”的学生中恰有两名男生，现准备从这些学生中任意挑选两名担任活动记录员，请用列表或画树状图的方法，求恰好选中1名男生和1名女生担任活动记录员的概率．【思路分析】数．（1）由条形图可知，A 选项有12人；由扇形图可知，A 选项占全班人数的30%，两者相除即可得到全班总人数为40；再用全班人数分别减去A 、B 、D 三个选项的人数可知C 选项的人数为10人，在条形图中补图即可；（2）由条形图知D 选项有4人，且男生有2人，用列表法或画树状图法，可求得恰好选中1名男生和1名女生担任活动记录员的概率为23．【解题过程】20．解：（1）∵12÷30%＝40（人），40－12－14－4＝10（人），∴八年级（3）班学生总人数是40，补图如下：20题图DCBA 30%八年级（3）班研学项目选择情况的扇形统计图八年级（3）班研学项目选择情况的条形统计图八年级（3）班研学项目选择情况的条形统计图（2）由题意可知从4名学生（其中男、女生各2人）任选2人，记男生为a 1，a 2，女生为b 1，b 2，现列表和画树状图分别如下：(b 2,b 1)(b 2,a 2)(b 2,a 1)(b 1,b 2)(b 1,a 1)(a 2,b 2)(a 2,b 1)(a 1,b 2)(b 1,a 2)(a 2,a 1)(a 1,b 1)(a 1,a 2)b 1b 2a 1a 2b 2b 1a 2a 1(b 2,b 1)(b 2,a 2)(b 2,a 1)(b 1,b 2)(b 1,a 2)(b 1,a 1)(a 2,b 2)(a 2,b 1)(a 2,a 1)(a 1,b 2)(a 1,b 1)(a 1,a 2)结果：第2人：第1人：开始b 2a 1a 21a 1a 2b 1b 21a 2b 2a 1a 2b 1b 1b 2由上面表格或树状图可知，共有12种等可能结果，其中“恰好选中1名男生和1名女生担任活动记录员”的共有8种，故P (恰好选中1名男生和1名女生担任活动记录员)＝812＝23．【知识点】统计概率条形统计图扇形统计图列表法或画树状图求概率四、解答题（本大题5个小题，每小题10分，共50分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上． 21．（2018·重庆B 卷，21，10）计算：（1）(x ＋2y )2－(x ＋y )(x －y )；（2）(a －1－411a a -+)÷28161a a a -++．【思路分析】（1）利用乘法公式将式子展开，然后合并同类项即可得到结果；（2）按分式的运算法则和运算顺序进行计算即可，注意结果的化简．【解题过程】21．解：（1）原式＝x 2＋4xy ＋4y 2－(x 2－y 2)＝x 2＋4xy ＋4y 2－x 2＋y 2＝4xy ＋5y 2．（2）原式＝2(1)(1)(41)11(4)a a a a a a -+--+⋅+- ＝2(4)11(4)a a a a a -+⋅+- ＝4aa -．【知识点】整式的乘法乘法公式分式的运算22．（2018·重庆B 卷，22，10）如图，在平面直角坐标系中，直线l 1：y ＝12x 与直线l 2交点A 的横坐标为2，将直线l 1沿y 轴向下平移4个单位长度，得到直线l 3，直线l 3与y 轴交于点B ，与直线l 2交于点C ，点C 的纵坐标为－2，直线l 2与y 轴交于点D ．（1）求直线l 2的解析式；（2）求△BDC 的面积．【思路分析】（1）先求出点A 的坐标，再由平移求出直线l 3的为y ＝12x －4，进而求出点C 的坐标；直线l 2的解析式为y ＝kx ＋b ，将A 、C 两点坐标代入得方程组解答即可锁定直线l 2的解析式；（2）先求出B 、D 两点坐标，进而得到线段BD 的长，C 点的横坐标的绝对值即为△BDC 的边BD 上的高，由三角形的面积公式计算即可．【解题过程】 22．解：（1）在y ＝12x 中，当x ＝2时，y ＝1；易知直线l 3的解析式为y ＝12x －4，当y ＝－2时，x＝4，故A(2，1)，C(4，－2)．设直线l2的解析式为y＝kx＋b，则2142k bk b+=⎧⎨+=-⎩，解得324kb⎧=-⎪⎨⎪=⎩，故直线l2的解析式为y＝－32x＋4．（2）易知D(0，4)，B(0，－4)，从而DB＝8．由C(4，－2)，知C点到y轴的距离为4，故S△BDC＝12BD•Cx＝12×8×4＝16．【知识点】一次函数的应用平移一次函数解析式的求法23．（2018·重庆B卷，23，10）在美丽乡村建设中，某县政府投入专项资金，用于乡村沼气池和垃圾集中处理点建设．该县政府计划：2018年前5个月，新建沼气池和垃圾集中处理点共计50个，且沼气池的个数不低于垃圾集中处理点个数的4倍．（1）按计划，2018年前5个月至少要修建多少个沼气池？（2）到2018年5月底前，该县按原计划刚好完成了任务，共花费资金78万元，且修建的沼气池个数恰好是原计划的最小值．据核算，前5个月，修建每个沼气池与垃圾集中处理点的平均费用之比为1﹕2．为加大美丽乡村建设的力度，政府计划加大投入，今年后7个月，在前5个月花费资金的基础上增加投入10a%，全部用于沼气池和垃圾集中处理点建设．经测算：从今年6月起，修建每个沼气池与垃圾集中处理点的平均费用在2018年前5个月的基础上分别增加a%，5a%，新建沼气池与垃圾集中处理点的个数将会在2018年前5个月的基础上分别增加5a%，8a%．求a的值．【思路分析】（1）根据“沼气池的个数不低于垃圾集中处理点个数的4倍”列不等式，并求不等式的最小整数解即可；（2）先求出到2018年5月底前，该县修建的沼气池40个，修建垃圾集中处理点10个；再求出前5个月修建每个沼气池与垃圾集中处理点的平均费用；最后根据题意，列出关于a的一元二次方程，解方程即可求出a的值．【解题过程】23．解：（1）设2018年前5个月要修建x个沼气池，则修建垃圾集中处理点(50－x)个，根据题意，得x≥4(50－x)，解得x≥40．答：按计划，2018年前5个月至少要修建40个沼气池．（2）由题意可知，到2018年5月底前，该县修建的沼气池40个，修建垃圾集中处理点10个，若令修建的沼气池每个y元，则修建的垃圾集中处理点的每个2y元，从而由题意得40y＋10×2y ＝78，解得y＝1.3，即到2018年5月底前，修建的每个沼气池与垃圾集中处理点的费用分别为1.3万元和2.6万元．根据题意，得40•(1＋5a%)•1.3(1＋a%)＋10•(1＋8a%)•2.6(1＋5a%)＝78•(1＋10a%)．令a %＝t ，则52(1＋5t )(1＋t )＋26(1＋8t )(1＋5t )＝78(1＋10t )，整理，得 10t 2－t ＝0，解得t 1＝0.1，t 2＝0（不合题意，舍去），从而a %＝0.1，a ＝10．答：a 的值为10．【知识点】一元一次不等式的应用一元二次方程的应用24．（2018·重庆B 卷，24，10）如图，在□ABCD 中，∠ACB ＝45°，点E 在对角线AC 上，BE ＝BA ，BF ⊥AC 于点F ，BF 的延长线交AD 于点G ．点H 在BC 的延长线上，且CH ＝AG ，连接EH ．（1）若BC ＝，AB ＝13，求AF 的长；（2）求证：EB ＝EH ．【思路分析】（1）在Rt △FBC 中，由sin ∠FCB ＝BFBC，求出BF ＝×sin45°＝×2＝12；在Rt △ABF 中，由勾股定理，得AF=5．（2）本题有两种证法，一是在BF 上取点M ，使AM ＝AG ，连接ME 、GE ．通过证明四边形AMEG 是正方形，进而得到∠AMB ＝∠HCE ＝45°，BM ＝CE ，AM ＝CH ，于是△AMB ≌△CHE ，从而EH ＝AB ，进而EB ＝EH ．第二种方法是连接EG ，GH ．通过证明△GBE ≌△GHE （SAS ）锁定答案．【解题过程】24．解：（1）∵BF ⊥AC ，∴∠BFC ＝∠AFB ＝90°．在Rt △FBC 中，sin ∠FCB ＝BFBC，而∠ACB ＝45°，BC ＝， ∴sin45． ∴BF ＝×sin45°＝＝12．在Rt △ABF 中，由勾股定理，得AF=5．24题图HG FEDC BA（2）方法一：如下图，在BF 上取点M ，使AM ＝AG ，连接ME 、GE ．MABC DEF G H∵∠BFC ＝90°，∠ACB ＝45°，∴△FBC 是等腰直角三角形． ∴FB ＝FC ．∵在□ABCD 中，AD ∥BC ， ∴∠GAC ＝∠ACB ＝45°． ∴∠AGB ＝45°． ∵AM ＝AG ，AF ⊥MG ，∴∠AMG ＝∠AGM ＝45°，MF ＝GF ． ∴∠AMB ＝∠ECG ＝135°． ∵BA ＝BE ，BF ⊥AE ， ∴AF ＝EF ．∴四边形AMEG 是正方形． ∴FM ＝FE ． ∴BM ＝CE ．又∵CH ＝AG ， ∴CH ＝AM ． ∴△AMB ≌△CHE ． ∴EH ＝AB ． ∴EH ＝EB ．方法二：如下图，连接EG ，GH ．A BDE FG∵BF ⊥AC 于点F ，BA ＝BE ， ∴∠ABF ＝∠EBF ． ∵GB ＝GB ，∴△GBA ≌△GBE （SAS ）． ∴∠AGB ＝∠EGB ．在△FBC 中，∵∠BFC ＝90°，∠ACB ＝45°， ∴∠FBC ＝45°． ∵在□ABCD 中，AD ∥BC ，∴∠GAC ＝∠ACB ＝45°，∠AGB ＝∠FBC ＝45°． ∴∠EGB ＝45°． ∵CH ＝AG ，∴四边形AGHC 是平行四边形． ∴∠BHG ＝∠GAC ＝45°． ∴∠BHG ＝∠GBH ＝45°． ∴GB ＝GH ，∠BGH ＝90°． ∴∠HGE ＝∠BGE ＝45°． ∵GE ＝GE ，∴△GBE ≌△GHE （SAS ）． ∴EH ＝EB ．【知识点】勾股定理等腰三角形的性质全等三角形平行四边形25．（2018·重庆B 卷，25，10）对任意一个四位数n ，如果千位与十位上的数字之和为9，百位与个位上的数字之和也为9，则称n 为“极数”．（1）请任意写出三个“极数”；并猜想任意一个“极数”是否是99的倍数，请说明理由；（2）如果一个正整数a 是另一个正整数b 的平方，则称正整数a 是完全平方数．若四位数m 为“极数”，记D (m )＝33m，求满足D (m )是完全平方数的所有m ．【思路分析】（1）先根据“极数”的定义，较易写出千位与十位上的数字之和为9且百位与个位上的数字之和为9的四位数三个，答案不唯一；再设n 的千位数字为s ，百位数字为t （1≤s ≤9，0≤t ≤9且s 、t 均为整数），用代数式表示出n ，化简后因式分解，即可证明n 是99的倍数；（2）先求出D (m )＝33m ，其中m ＝1000s ＋100t ＋10(9－s )＋9－t ，化简后得D (m )＝33m＝3(10s ＋t ＋1)；再根据D (m )是完全平方数，且10s ＋t ＋1是一个两位数，从而10s ＋t ＋1＝3×22、3×32、3×42、3×52，即10s ＋t ＋1＝12或27或48或75，于是得到方程组112s t =⎧⎨+=⎩或217s t =⎧⎨+=⎩或418s t =⎧⎨+=⎩或715s t =⎧⎨+=⎩，解方程组即可锁定符合条件的所有m ．【解题过程】25．解：（1）答案不唯一，如5346，1782，9405，等．任意一个“极数”都是99的倍数，理由如下：设n 的千位数字为s ，百位数字为t （1≤s ≤9，0≤t ≤9且s 、t 均为整数），则n ＝1000s ＋100t ＋10(9－s )＋9－t ＝990s ＋99t ＋99＝99(10s ＋t ＋1)，而10s ＋t ＋1是整数，故n 是99的倍数．（2）易由（1）设m ＝1000s ＋100t ＋10(9－s )＋9－t ＝990s ＋99t ＋99＝99(10s ＋t ＋1)，其中1≤s ≤9，0≤t ≤9且s 、t 均为整数，从而D (m )＝33m＝3(10s ＋t ＋1)，而D (m )是完全平方数，故3(10s ＋t ＋1)是完全平方数．∵10＜10s ＋t ＋1＜100， ∴30＜3(10s ＋t ＋1)＜300．∴10s ＋t ＋1＝3×22、3×32、3×42、3×52． ∴(s ，t )＝(1，1)，(2，6)，(4，7)，(7，4)． ∴m ＝1188，2673，4752，7425．【知识点】整式的运算完全平方数不等式的解法新定义运算题二元一次方程的特殊解五、解答题（本大题1个小题，共12分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上．26．（2018·重庆B 卷，26，12）抛物线y 2x 与x 轴交于点A ，B （点A 在点B 的左边），与y 轴交于点C ，点D 是该抛物线的顶点．（1）如图1，连接CD ，求线段CD 的长；（2）如图2，点P 是直线AC 上方抛物线上一点，PF ⊥x 轴于点F ，PF 与线段AC 交于点E ；将线段OB 沿x 轴左右平移，线段OB 的对应线段是O 1B 1．当PE ＋12EC 的值最大时，求四边形P O 1B 1C 周长的最小值，并求出对应的点O 1的坐标；（3）如图3，点H是线段AB的中点，连接CH，将△OBC沿直线CH翻折至△O2B2C的位置，再将△O2B2C绕点B2旋转一周，在旋转过程中，点O2，C的对应点分别是O3，C1，直线O3C1分别与直线AC，x轴交于点M，N．那么，在△O2B2C的整个旋转过程中，是否存在恰当的位置，使△OMN是以MN为腰的等腰三角形？若存在，请直接写出所有符合条件的线段O2M的长；若不存在，请说明理由．【思路分析】（1）过点D作DE⊥y轴于点E，由题意易知点C(0)，再根据抛物线的顶点公式求出D点坐标，最后在Rt△CDE中，由勾股定理，易求出CD的长度；（2）①在y＝－6x2－3x中，令y＝0，得到关于x的一元二次方程，求解得A、B两点的坐标；②再设直线AC的解析式为y＝kx，将A点坐标代入即可得到k的值为3；③令P(t，－62－3t)， E(t，＋)，从而PE2，并根据两点间的距离公式求出EC的长；④计算出PE＋12EC＝－t＋2)2，由二次函数的性质易知当t＝－时，PE＋12EC，此时P(－)，且PC∥x轴，易知PC＝O1B1＝OB，要使四边形PO1B1C周长的值最小，就是要求PO1＋B1C的值最小，此时利用平移、轴对称知识，先将点P个单位长度，得点P1)，则PO1＝P1B1．再作P1关于x轴的对称点P2)，则P1B1＝P2B1．连接P2C与x轴的交点即为使PO1＋B1C的值最小的点B1．⑤在Rt△P1P2C中，由勾股定理，得PO1＋B1C＝P2CP O1B1C周长的最小值为，所求的点O1的坐标为(－2，0)．（3）分类讨论如下：如答图3，通过计算可得O2M＝NA＝NM；如答图4，若点C与M点重合时，MA＝MN，此时，O2M＝O2C＝12AC＝6；如答图5，通过计算可得O2M＝226+时，NA＝NM；如答图6，通过计算可得O2M＝63时，MA＝MN，此时C1，H，N重合．综上，符合条件的O2M的长为6或6或22＋6或22－6．【解题过程】26．解：（1）如下图，过点D作DE⊥y轴于点E，由题意易知点C(0，6)．∵2332262()6ba--=-=-⨯-，226234()6()44663464()6ac ba⨯-⨯---==⨯-，∴D(－2，463)，从而CE＝63，DE＝2．∴在Rt△CDE中，由勾股定理，得CD＝22626(2)()3+=．第26题答图3 第26题答图4第26题答图5 第26题答图6（2）在y2－x中，令y＝02x＝0，解得x1＝－，x2，从而A(－，0)，B，0)．令直线AC的解析式为y＝kx，则－k＝0，解得k∴直线AC的解析式为y．令P(t，－62－3t)， E(t，3t)，从而PE＝－62t，EC3t=-．∴PE＋12EC＝－2＝－2tt＋)2．∴当t＝－PE＋12EC，此时P(－)．∴PC＝，O1B1＝OB．要使四边形PO1B1C周长的值最小，就是要求PO1＋B1C的值最小，将点P个单位长度，得点P1)，则PO1＝P1B1．再作P1关于x轴的对称点P2)，则P1B1＝P2B1．连接P2C与x轴的交点即为使PO1＋B1C的值最小的点B1．∴B1（－2，0)，将B1向个单位长度即得点O1．此时，PO1＋B1C＝P2C，从而四边形P O1B1C周长的最小值为，所求的点O1的坐标为(－2，0)．2（3）O2M或或．【知识点】二次函数；一元二次方程的解法；勾股定理；平移；旋转；轴对称；最值问题；等腰三角形；分类思想；数形结合思想；探究性问题；压轴题；。

2018年全国各地中考数学压轴题汇编：几何综合(中南西南)(解析卷)

2018年全国各地中考数学压轴题汇编（中南西南）几何综合参考答案与试题解析一．选择题（共3小题）1．（2018•重庆）如图，已知AB是⊙O的直径，点P在BA的延长线上，PD与⊙O相切于点D，过点B作PD的垂线交PD的延长线于点C，若⊙O的半径为4，BC=6，则PA的长为（）A．4 B．2C．3 D．2.5解：连接DO，∵PD与⊙O相切于点D，∴∠PDO=90°，∵∠C=90°，∴DO∥BC，∴△PDO∽△PCB，∴===，设PA=x，则=，解得：x=4，故PA=4．故选：A．2．（2018•海南）如图1，分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC，EG剪开，拼成如图2所示的▱KLMN，若中间空白部分四边形OPQR恰好是正方形，且▱KLMN 的面积为50，则正方形EFGH的面积为（）A．24 B．25 C．26 D．27解：如图，设PM=PL=NR=KR=a，正方形ORQP的边长为b．由题意：a2+b2+（a+b）（a﹣b）=50，∴a2=25，∴正方形EFGH的面积=a2=25，故选：B．3．（2018•曲靖）如图，在正方形ABCD中，连接AC，以点A为圆心，适当长为半径画弧，交AB、AC于点M，N，分别以M，N为圆心，大于MN长的一半为半径画弧，两弧交于点H，连结AH并延长交BC于点E，再分别以A、E为圆心，以大于AE长的一半为半径画弧，两弧交于点P，Q，作直线PQ，分别交CD，AC，AB于点F，G，L，交CB的延长线于点K，连接GE，下列结论：①∠LKB=22.5°，②GE∥AB，③tan∠CGF=，④S△CGE：S△CAB=1：4．其中正确的是（）A．①②③B．②③④C．①③④D．①②④解：①∵四边形ABCD是正方形，∴∠BAC=∠BAD=45°，由作图可知：AE平分∠BAC，∴∠BAE=∠CAE=22.5°，∵PQ是AE的中垂线，∴AE⊥PQ，∴∠AOL=90°，∵∠AOL=∠LBK=90°，∠ALO=∠KLB，∴∠LKB=∠BAE=22.5°；故①正确；②∵OG是AE的中垂线，∴AG=EG，∴∠AEG=∠EAG=22.5°=∠BAE，∴EG∥AB，故②正确；③∵∠LAO=∠GAO，∠AOL=∠AOG=90°，∴∠ALO=∠AGO，∵∠CGF=∠AGO，∠BLK=∠ALO，∴∠CGF=∠BLK，在Rt△BKL中，tan∠CGF=tan∠BLK=，故③正确；④连接EL，∵AL=AG=EG，EG∥AB，∴四边形ALEG是菱形，∴AL=EL=EG＞BL，∴，∵EG∥AB，∴△CEG∽△CBA，∴=，故④不正确；本题正确的是：①②③，故选：A．二．填空题（共9小题）4．（2018•广东）如图，矩形ABCD中，BC=4，CD=2，以AD为直径的半圆O与BC相切于点E，连接BD，则阴影部分的面积为π．（结果保留π）解：连接OE，如图，∵以AD为直径的半圆O与BC相切于点E，∴OD=2，OE⊥BC，易得四边形OECD为正方形，∴由弧DE、线段EC、CD所围成的面积=S正方形OECD ﹣S扇形EOD=22﹣=4﹣π，∴阴影部分的面积=×2×4﹣（4﹣π）=π．故答案为π．5．（2018•深圳）如图，四边形ACDF是正方形，∠CEA和∠ABF都是直角且点E，A，B 三点共线，AB=4，则阴影部分的面积是8．解：∵四边形ACDF是正方形，∴AC=AF，∠CAF=90°，∴∠EAC+∠FAB=90°，∵∠ABF=90°，∴∠AFB+∠FAB=90°，∴∠EAC=∠AFB，在△CAE和△AFB中，，∴△CAE≌△AFB，∴EC=AB=4，∴阴影部分的面积=×AB×CE=8，故答案为：8．6．（2018•广州）如图，CE是▱ABCD的边AB的垂直平分线，垂足为点O，CE与DA的延长线交于点E．连接AC，BE，DO，DO与AC交于点F，则下列结论：①四边形ACBE是菱形；②∠ACD=∠BAE；③AF：BE=2：3；④S四边形AFOE ：S△COD=2：3．其中正确的结论有①②④．（填写所有正确结论的序号）解：∵四边形ABCD是平行四边形，∴AB∥CD，AB=CD，∵EC垂直平分AB，∴OA=OB=AB=DC，CD⊥CE，∵OA∥DC，∴===，∴AE=AD，OE=OC，∵OA=OB，OE=OC，∴四边形ACBE是平行四边形，∵AB⊥EC，∴四边形ACBE是菱形，故①正确，∵∠DCE=90°，DA=AE，∴AC=AD=AE，∴∠ACD=∠ADC=∠BAE，故②正确，∵OA∥CD，∴==，∴==，故③错误，设△AOF的面积为a，则△OFC的面积为2a，△CDF的面积为4a，△AOC的面积=△AOE 的面积=3a，∴四边形AFOE的面积为4a，△ODC的面积为6a∴S四边形AFOE ：S△COD=2：3．故④正确，故答案为①②④．7．（2018•河南）如图，在△ABC中，∠ACB=90°，AC=BC=2，将△ABC绕AC的中点D 逆时针旋转90°得到△A'B′C'，其中点B的运动路径为，则图中阴影部分的面积为π﹣．解：△ABC绕AC的中点D逆时针旋转90°得到△A'B′C'，此时点A′在斜边AB上，CA′⊥AB，DB′==，A′B′==2，1×2÷2﹣（2﹣）×÷2=π﹣．∴S阴=﹣故答案为π﹣．8．（2018•深圳）在Rt△ABC中，∠C=90°，AD平分∠CAB，BE平分∠ABC，AD、BE相交于点F，且AF=4，EF=，则AC=．解：如图，∵AD，BE是分别是∠BAC和∠ABC的平分线，∴∠1=∠2，∠3=∠4，∵∠ACB=90°，∴2（∠2+∠4）=90°，∴∠2+∠4=45°，∴∠EFG=∠2+∠4=45°，过点E作EG⊥AD于G，在Rt△EFG中，EF=，∴FG=EG=1，∵AF=4，∴AG=AF﹣FG=3，根据勾股定理得，AE==，连接CF，∵AD平分∠CAB，BE平分∠ABC，∴CF是∠ACB的平分线，∴∠ACF=45°=∠AFE，∵∠CAF=∠FAE，∴△AEF∽△AFC，∴，∴AC===，故答案为．9．（2018•河南）如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为4或4．解：当△A′EF为直角三角形时，存在两种情况：①当∠A'EF=90°时，如图1，∵△A′BC与△ABC关于BC所在直线对称，∴A'C=AC=4，∠ACB=∠A'CB，∵点D，E分别为AC，BC的中点，∴D、E是△ABC的中位线，∴DE∥AB，∴∠CDE=∠MAN=90°，∴∠CDE=∠A'EF，∴AC∥A'E，∴∠ACB=∠A'EC，∴∠A'CB=∠A'EC，∴A'C=A'E=4，Rt△A'CB中，∵E是斜边BC的中点，∴BC=2A'E=8，由勾股定理得：AB2=BC2﹣AC2，∴AB==4；②当∠A'FE=90°时，如图2，∵∠ADF=∠A=∠DFB=90°，∴∠ABF=90°，∵△A′BC与△ABC关于BC所在直线对称，∴∠ABC=∠CBA'=45°，∴△ABC是等腰直角三角形，∴AB=AC=4；综上所述，AB的长为4或4；故答案为：4或4；10．（2018•重庆）如图，把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE、FG，得到∠AGE=30°，若AE=EG=2厘米，则△ABC的边BC的长为6+4厘米．解：∵把三角形纸片折叠，使点B、点C都与点A重合，折痕分别为DE，FG，∴BE=AE，AG=GC，∵∠AGE=30°，AE=EG=2厘米，∴AG=6，∴BE=AE=2，GC=AG=6，∴BC=BE+EG+GC=6+4，故答案为：6+4，11．（2018•昆明）如图，正六边形ABCDEF的边长为1，以点A为圆心，AB的长为半径，作扇形ABF，则图中阴影部分的面积为﹣（结果保留根号和π）．解：正六边形的中心为点O，连接OD、OE，作OH⊥DE于H，∠DOE==60°，∴OD=OE=DE=1，∴OH=，∴正六边形ABCDEF的面积=×1××6=，∠A==120°，∴扇形ABF的面积==，∴图中阴影部分的面积=﹣，故答案为：﹣．12．（2018•曲靖）如图：在△ABC中，AB=13，BC=12，点D，E分别是AB，BC的中点，连接DE，CD，如果DE=2.5，那么△ACD的周长是18．解：∵D，E分别是AB，BC的中点，∴AC=2DE=5，AC∥DE，AC2+BC2=52+122=169，AB2=132=169，∴AC2+BC2=AB2，∴∠ACB=90°，∵AC∥DE，∴∠DEB=90°，又∵E是BC的中点，∴直线DE是线段BC的垂直平分线，∴DC=BD，∴△ACD的周长=AC+AD+CD=AC+AD+BD=AC+AB=18，故答案为：18．三．解答题（共16小题）13．（2018•广东）如图，四边形ABCD中，AB=AD=CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E．（1）证明：OD∥BC；（2）若tan∠ABC=2，证明：DA与⊙O相切；（3）在（2）条件下，连接BD交⊙O于点F，连接EF，若BC=1，求EF的长．解：（1）连接OC，在△OAD和△OCD中，∵，∴△OAD≌△OCD（SSS），∴∠ADO=∠CDO，又AD=CD，∴DE⊥AC，∵AB为⊙O的直径，∴∠ACB=90°，∴∠ACB=90°，即BC⊥AC，∴OD∥BC；（2）∵tan∠ABC==2，∴设BC=a、则AC=2a，∴AD=AB==，∵OE∥BC，且AO=BO，∴OE=BC=a，AE=CE=AC=a，在△AED中，DE==2a，在△AOD中，AO2+AD2=（）2+（a）2=a2，OD2=（OE+DE）2=（a+2a）2=a2，∴AO2+AD2=OD2，∴∠OAD=90°，则DA与⊙O相切；（3）连接AF，∵AB是⊙O的直径，∴∠AFD=∠BAD=90°，∵∠ADF=∠BDA，∴△AFD∽△BAD，∴=，即DF•BD=AD2①，又∵∠AED=∠OAD=90°，∠ADE=∠ODA，∴△AED∽△OAD，∴=，即OD•DE=AD2②，由①②可得DF•BD=OD•DE，即=，又∵∠EDF=∠BDO，∴△EDF∽△BDO，∵BC=1，∴AB=AD=、OD=、ED=2、BD=、OB=，∴=，即=，解得：EF=．14．（2018•广州）如图，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD．（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；（2）在（1）的条件下，①证明：AE⊥DE；②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值．解：（1）如图，∠ADC的平分线DE如图所示．（2）①延长DE交AB的延长线于F．∵CD∥AF，∴∠CDE=∠F，∵∠CDE=∠ADE，∴∠ADF=∠F，∴AD=AF，∵AD=AB+CD=AB+BF，∴CD=BF，∵∠DEC=∠BEF，∴△DEC≌△FEB，∴DE=EF，∵AD=AF，∴AE⊥DE．②作点B关于AE的对称点K，连接EK，作KH⊥AB于H，DG⊥AB于G．连接MK．∵AD=AF，DE=EF，∴AE平分∠DAF，则△AEK≌△AEB，∴AK=AB=4，在Rt△ADG中，DG==4，∵KH∥DG，∴=，∴=，∴KH=，∵MB=MK，∴MB+MN=KM+MN，∴当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长，∴BM+MN的最小值为．15．（2018•广东）已知Rt△OAB，∠OAB=90°，∠ABO=30°，斜边OB=4，将Rt△OAB绕点O顺时针旋转60°，如图1，连接BC．（1）填空：∠OBC=60°；（2）如图1，连接AC，作OP⊥AC，垂足为P，求OP的长度；（3）如图2，点M，N同时从点O出发，在△OCB边上运动，M沿O→C→B路径匀速运动，N沿O→B→C路径匀速运动，当两点相遇时运动停止，已知点M的运动速度为1.5单位/秒，点N的运动速度为1单位/秒，设运动时间为x秒，△OMN的面积为y，求当x为何值时y取得最大值？最大值为多少？解：（1）由旋转性质可知：OB=OC，∠BOC=60°，∴△OBC是等边三角形，∴∠OBC=60°．故答案为60．（2）如图1中，∵OB=4，∠ABO=30°，∴OA=OB=2，AB=OA=2，=•OA•AB=×2×2=2，∴S△AOC∵△BOC是等边三角形，∴∠OBC=60°，∠ABC=∠ABO+∠OBC=90°，∴AC==2，∴OP===．（3）①当0＜x≤时，M在OC上运动，N在OB上运动，此时过点N作NE⊥OC且交OC于点E．则NE=ON•sin60°=x，=•OM•NE=×1.5x×x，∴S△OMN∴y=x2．∴x=时，y有最大值，最大值=．②当＜x≤4时，M在BC上运动，N在OB上运动．作MH⊥OB于H．则BM=8﹣1.5x，MH=BM•sin60°=（8﹣1.5x），∴y=×ON×MH=﹣x2+2x．当x=时，y取最大值，y＜，③当4＜x≤4.8时，M、N都在BC上运动，作OG⊥BC于G．MN=12﹣2.5x，OG=AB=2，∴y=•MN•OG=12﹣x，当x=4时，y有最大值，最大值=2，综上所述，y有最大值，最大值为．16．（2018•深圳）已知菱形的一个角与三角形的一个角重合，然后它的对角顶点在这个重合角的对边上，这个菱形称为这个三角形的亲密菱形，如图，在△CFE中，CF=6，CE=12，∠FCE=45°，以点C为圆心，以任意长为半径作AD，再分别以点A和点D为圆心，大于AD 长为半径作弧，交EF于点B，AB∥CD．（1）求证：四边形ACDB为△FEC的亲密菱形；（2）求四边形ACDB的面积．（1）证明：∵由已知得：AC=CD，AB=DB，由已知尺规作图痕迹得：BC是∠FCE的角平分线，∴∠ACB=∠DCB，又∵AB∥CD，∴∠ABC=∠DCB，∴∠ACB=∠ABC，∴AC=AB，又∵AC=CD，AB=DB，∴AC=CD=DB=BA∴四边形ACDB是菱形，∵∠ACD与△FCE中的∠FCE重合，它的对角∠ABD顶点在EF上，∴四边形ACDB为△FEC的亲密菱形；（2）解：设菱形ACDB的边长为x，∵四边形ACDB是菱形，∴AB∥CE，∴∠FAB=∠FCE，∠FBA=∠E，∴△FAB∽△FCE∴，即，解得：x=4，过A点作AH⊥CD于H点，∵在Rt△ACH中，∠ACH=45°，∴，∴四边形ACDB的面积为：．17．（2018•广州）如图，在四边形ABCD中，∠B=60°，∠D=30°，AB=BC．（1）求∠A+∠C的度数；（2）连接BD，探究AD，BD，CD三者之间的数量关系，并说明理由；（3）若AB=1，点E在四边形ABCD内部运动，且满足AE2=BE2+CE2，求点E运动路径的长度．解：（1）如图1中，在四边形ABCD中，∵∠A+∠B+∠C+∠D=360°，∠B=60°，∠C=30°，∴∠A+∠C=360°﹣60°﹣30°=270°．（2）如图2中，结论：DB2=DA2+DC2．理由：连接BD．以BD为边向下作等边三角形△BDQ．∵∠ABC=∠DBQ=60°，∴∠ABD=∠CBQ，∵AB=BC，DB=BQ，∴△ABD≌△CBQ，∴AD=CQ，∠A=∠BCQ，∵∠A+∠BCD=∠BCQ+∠BCD=270°，∴∠DCQ=90°，∴DQ2=DC2+CQ2，∵CQ=DA，DQ=DB，∴DB2=DA2+DC2．（3）如图3中，连接AC，将△ACE绕点A顺时针旋转60°得到△ABR，连接RE．则△AER是等边三角形，∵EA2=EB2+EC2，EA=RE，EC=RB，∴RE2=RB2+EB2，∴∠EBR=90°，∴∠RAE+∠RBE=150°，∴∠ARB+∠AEB=∠AEC+∠AEB=0°，∴∠BEC=150°，∴点E的运动轨迹在O为圆心的圆上，在⊙O上取一点K，连接KB，KC，OB，OC，∵∠K+∠BEC=180°，∴∠K=30°，∠BOC=60°，∵OB=OC，∴△OBC是等边三角形，∴点E的运动路径==．18．（2018•河南）如图，AB是⊙O的直径，DO⊥AB于点O，连接DA交⊙O于点C，过点C作⊙O的切线交DO于点E，连接BC交DO于点F．（1）求证：CE=EF；（2）连接AF并延长，交⊙O于点G．填空：①当∠D的度数为30°时，四边形ECFG为菱形；②当∠D的度数为22.5°时，四边形ECOG为正方形．（1）证明：连接OC，如图，∵CE为切线，∴OC⊥CE，∴∠OCE=90°，即∠1+∠4=90°，∵DO⊥AB，∴∠3+∠B=90°，而∠2=∠3，∴∠2+∠B=90°，而OB=OC，∴∠4=∠B，∴∠1=∠2，∴CE=FE；（2）解：①当∠D=30°时，∠DAO=60°，而AB为直径，∴∠ACB=90°，∴∠B=30°，∴∠3=∠2=60°，而CE=FE，∴△CEF为等边三角形，∴CE=CF=EF，同理可得∠GFE=60°，利用对称得FG=FC，∵FG=EF，∴△FEG为等边三角形，∴EG=FG，∴EF=FG=GE=CE，∴四边形ECFG为菱形；②当∠D=22.5°时，∠DAO=67.5°，而OA=OC，∴∠OCA=∠OAC=67.5°，∴∠AOC=180°﹣67.5°﹣67.5°=45°，∴∠AOC=45°，∴∠COE=45°，利用对称得∠EOG=45°，∴∠COG=90°，易得△OEC≌△OEG，∴∠OEG=∠OCE=90°，∴四边形ECOG为矩形，而OC=OG，∴四边形ECOG为正方形．故答案为30°，22.5°．19．（2018•深圳）如图在⊙O中，BC=2，AB=AC，点D为AE上的动点，且cosB=．（1）求AB的长度；（2）求AD•AE的值；（3）过A点作AH⊥BD，求证：BH=CD+DH．解：（1）作AM⊥BC，∵AB=AC，AM⊥BC，BC=2BM，∴CM=BC=1，∵cosB==，在Rt△AMB中，BM=1，∴AB==；（2）连接DC，∵AB=AC，∴∠ACB=∠ABC，∵四边形ABCD内接于圆O，∴∠ADC+∠ABC=180°，∵∠ACE+∠ACB=180°，∴∠ADC=∠ACE，∵∠CAE公共角，∴△EAC∽△CAD，∴=，∴AD•AE=AC2=10；（3）在BD上取一点N，使得BN=CD，在△ABN和△ACD中，∴△ABN≌△ACD（SAS），∴AN=AD，∵AN=AD，AH⊥BD，∴NH=HD，∵BN=CD，NH=HD，∴BN+NH=CD+HD=BH．20．（2018•海南）已知，如图1，在▱ABCD中，点E是AB中点，连接DE并延长，交CB的延长线于点F．（1）求证：△ADE≌△BFE；（2）如图2，点G是边BC上任意一点（点G不与点B、C重合），连接AG交DF于点H，连接HC，过点A作AK∥HC，交DF于点K．①求证：HC=2AK；②当点G是边BC中点时，恰有HD=n•HK（n为正整数），求n的值．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE=∠BFE，∠A=∠FBE，在△ADE和△BFE中，，∴△ADE≌△BFE；（2）如图2，作BN∥HC交EF于N，∵△ADE≌△BFE，∴BF=AD=BC，∴BN=HC，由（1）的方法可知，△AEK≌△BEN，∴AK=BN，∴HC=2AK；（3）如图3，作GM∥DF交HC于M，∵点G是边BC中点，∴CG=CF，∵GM∥DF，∴△CMG∽△CHF，∴==，∵AD∥FC，∴△AHD∽△GHF，∴===，∴=，∵AK∥HC，GM∥DF，∴△AHK∽△HGM，∴==，∴=，即HD=4HK，∴n=4．．（2018•云南）如图，已知AB是⊙O的直径，C是⊙O上的点，点D在AB的延长线上，∠BCD=∠BAC．（1）求证：CD是⊙O的切线；（2）若∠D=30°，BD=2，求图中阴影部分的面积．解：（1）连接OC，∵OA=OC，∴∠BAC=∠OCA，∵∠BCD=∠BAC，∴∠BCD=∠OCA，∵AB是直径，∴∠ACB=90°，∴∠OCA+OCB=∠BCD+∠OCB=90°∴∠OCD=90°∵OC是半径，∴CD是⊙O的切线（2）设⊙O的半径为r，∴AB=2r，∵∠D=30°，∠OCD=90°，∴OD=2r，∠COB=60°∴r+2=2r，∴r=2，∠AOC=120°∴BC=2，∴由勾股定理可知：AC=2=×2×1=易求S△AOCS扇形OAC==∴阴影部分面积为﹣22．（2018•重庆）如图，在平行四边形ABCD中，点O是对角线AC的中点，点E是BC 上一点，且AB=AE，连接EO并延长交AD于点F．过点B作AE的垂线，垂足为H，交AC于点G．（1）若AH=3，HE=1，求△ABE的面积；（2）若∠ACB=45°，求证：DF=CG．解：（1）∵AH=3，HE=1，∴AB=AE=4，又∵Rt△ABH中，BH==，=AE×BH=×4×=；∴S△ABE（2）如图，过A作AM⊥BC于M，交BG于K，过G作GN⊥BC于N，则∠AMB=∠AME=∠BNG=90°，∵∠ACB=45°，∴∠MAC=∠NGC=45°，∵AB=AE，∴BM=EM=BE，∠BAM=∠EAM，又∵AE⊥BG，∴∠AHK=90°=∠BMK，而∠AKH=∠BKM，∴∠MAE=∠NBG，设∠BAM=∠MAE=∠NBG=α，则∠BAG=∠45°+α，∠BGA=∠GCN+∠GBC=45°+α，∴AB=BG，∴AE=BG，在△AME和△BNG中，，∴△AME≌△BNG（AAS），∴ME=NG，在等腰Rt△CNG中，NG=NC，∴GC=NG=ME=BE，∴BE=GC，∵O是AC的中点，∴OA=OC，∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴∠OAF=∠OCE，∠AFO=∠CEO，∴△AFO≌△CEO（AAS），∴AF=CE，∴AD﹣AF=BC﹣EC，即DF=BE，∴DF=BE=CG．23．（2018•昆明）如图，AB是⊙O的直径，ED切⊙O于点C，AD交⊙O于点F，AC平分∠BAD，连接BF．（1）求证：AD⊥ED；（2）若CD=4，AF=2，求⊙O的半径．（1）证明：连接OC，如图，∵AC平分∠BAD，∴∠1=∠2，∵OA=OC，∴∠1=∠3，∴∠2=∠3，∴OC∥AD，∵ED切⊙O于点C，∴OC⊥DE，∴AD⊥ED；（2）解：OC交BF于H，如图，∵AB为直径，∴∠AFB=90°，易得四边形CDFH为矩形，∴FH=CD=4，∠CHF=90°，∴OH⊥BF，∴BH=FH=4，∴BF=8，在Rt△ABF中，AB===2，∴⊙O的半径为．24．（2018•云南）如图，在平行四边形ABCD中，点E是CD的中点，点F是BC边上的点，AF=AD+FC，平行四边形ABCD的面积为S，由A、E、F三点确定的圆的周长为l．（1）若△ABE的面积为30，直接写出S的值；（2）求证：AE平分∠DAF；（3）若AE=BE，AB=4，AD=5，求l的值．解：（1）如图，作EG⊥AB于点G，=×AB×EG=30，则AB•EG=60，则S△ABE∴平行四边形ABCD的面积为60；（2）延长AE交BC延长线于点H，∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE=∠HCE，∠DAE=∠CHE，∵E为CD的中点，∴CE=ED，∴△ADE≌△HCE，∴AD=HC、AE=HE，∴AD+FC=HC+FC，由AF=AD+FC和FH=HC+FC得AF=FH，∴∠FAE=∠CHE，又∵∠DAE=∠CHE，∴∠DAE=∠FAE，∴AE平分∠DAF；（3）连接EF，∵AE=BE、AE=HE，∴AE=BE=HE，∴∠BAE=∠ABE，∠HBE=∠BHE，∵∠DAE=∠CHE，∴∠BAE+∠DAE=∠ABE+∠HBE，即∠DAB=∠CBA，由四边形ABCD是平行四边形得∠DAB+∠CBA=180°，∴∠CBA=90°，∴AF2=AB2+BF2=16+（5﹣FC）2=（FC+CH）2=（FC+5）2，解得：FC=，∴AF=FC+CH=，∵AE=HE、AF=FH，∴FE⊥AH，∴AF是△AEF的外接圆直径，∴△AEF的外接圆的周长l=π．25．（2018•曲靖）如图：在平行四边形ABCD的边AB，CD上截取AF，CE，使得AF=CE，连接EF，点M，N是线段EF上两点，且EM=FN，连接AN，CM．（1）求证：△AFN≌△CEM；（2）若∠CMF=107°，∠CEM=72°，求∠NAF的度数．（1）证明：∵四边形ABCD是平行四边形，∴CD∥AB，∴∠AFN=∠CEM，∵FN=EM，AF=CE，∴△AFN≌△CEM（SAS）．（2）解：∵△AFN≌△CEM，∴∠NAF=∠ECM，∵∠CMF=∠CEM+∠ECM，∴107°=72°+∠ECM，∴∠ECM=35°，∴∠NAF=35°．26．（2018•昆明）如图1，在矩形ABCD中，P为CD边上一点（DP＜CP），∠APB=90°．将△ADP沿AP翻折得到△AD′P，PD′的延长线交边AB于点M，过点B作BN∥MP交DC于点N．（1）求证：AD2=DP•PC；（2）请判断四边形PMBN的形状，并说明理由；（3）如图2，连接AC，分别交PM，PB于点E，F．若=，求的值．解：（1）过点P作PG⊥AB于点G，∴易知四边形DPGA，四边形PCBG是矩形，∴AD=PG，DP=AG，GB=PC∵∠APB=90°，∴∠APG+∠GPB=∠GPB+∠PBG=90°，∴∠APG=∠PBG，∴△APG∽△PBG，∴，∴PG2=AG•GB，即AD2=DP•PC；（2）∵DP∥AB，∴∠DPA=∠PAM，由题意可知：∠DPA=∠APM，∴∠PAM=∠APM，∵∠APB﹣∠PAM=∠APB﹣∠APM，即∠ABP=∠MPB∴AM=PM，PM=MB，∴PM=MB，又易证四边形PMBN是平行四边形，∴四边形PMBN是菱形；（3）由于=，可设DP=1，AD=2，由（1）可知：AG=DP=1，PG=AD=2，∵PG2=AG•GB，∴4=1•GB，∴GB=PC=4，AB=AG+GB=5，∵CP∥AB，∴△PCF∽△BAF，∴==，∴，又易证：△PCE∽△MAE，AM=AB=∴===∴，∴EF=AF﹣AE=AC﹣=AC，∴==27．（2018•曲靖）如图，AB为⊙O的直径，点C为⊙O上一点，将弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，连接OC，CD，BD，过点C的切线与线段BA 的延长线交于点P，连接AD，在PB的另一侧作∠MPB=∠ADC．（1）判断PM与⊙O的位置关系，并说明理由；（2）若PC=，求四边形OCDB的面积．解：（1）PM与⊙O相切．理由如下：连接DO并延长交PM于E，如图，∵弧BC沿直线BC翻折，使弧BC的中点D恰好与圆心O重合，∴OC=DC，BO=BD，∴OC=DC=BO=BD，∴四边形OBDC为菱形，∴OD⊥BC，∴△OCD和△OBD都是等边三角形，∴∠COD=∠BOD=60°，∴∠COP=∠EOP=60°，∵∠MPB=∠ADC，而∠ADC=∠ABC，∴∠ABC=∠MPB，∴PM∥BC，∴OE⊥PM，∴OE=OP，∵PC为⊙O的切线，∴OC⊥PC，∴OC=OP，∴OE=OC，而OE⊥PC，∴PM是⊙O的切线；（2）在Rt△OPC中，OC=PC=×=1，=2××12=．∴四边形OCDB的面积=2S△OCD28．（2018•河南）（1）问题发现如图1，在△OAB和△OCD中，OA=OB，OC=OD，∠AOB=∠COD=40°，连接AC，BD交于点M．填空：①的值为1；②∠AMB的度数为40°．（2）类比探究如图2，在△OAB和△OCD中，∠AOB=∠COD=90°，∠OAB=∠OCD=30°，连接AC交BD 的延长线于点M．请判断的值及∠AMB的度数，并说明理由；（3）拓展延伸在（2）的条件下，将△OCD绕点O在平面内旋转，AC，BD所在直线交于点M，若OD=1，OB=，请直接写出当点C与点M重合时AC的长．解：（1）问题发现①如图1，∵∠AOB=∠COD=40°，∴∠COA=∠DOB，∵OC=OD，OA=OB，∴△COA≌△DOB（SAS），∴AC=BD，∴=1，②∵△COA≌△DOB，∴∠CAO=∠DBO，∵∠AOB=40°，∴∠OAB+∠ABO=140°，在△AMB中，∠AMB=180°﹣（∠CAO+∠OAB+∠ABD）=180°﹣（∠DBO+∠OAB+∠ABD）=180°﹣140°=40°，故答案为：①1；②40°；（2）类比探究如图2，=，∠AMB=90°，理由是：Rt△COD中，∠DCO=30°，∠DOC=90°，∴，同理得：，∴，∵∠AOB=∠COD=90°，∴∠AOC=∠BOD，∴△AOC∽△BOD，∴=，∠CAO=∠DBO，在△AMB中，∠AMB=180°﹣（∠MAB+∠ABM）=180°﹣（∠OAB+∠ABM+∠DBO）=90°；（3）拓展延伸①点C与点M重合时，如图3，同理得：△AOC∽△BOD，∴∠AMB=90°，，设BD=x，则AC=x，Rt△COD中，∠OCD=30°，OD=1，∴CD=2，BC=x﹣2，Rt△AOB中，∠OAB=30°，OB=，∴AB=2OB=2，在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，，x2﹣x﹣6=0，（x﹣3）（x+2）=0，x1=3，x2=﹣2，∴AC=3；②点C与点M重合时，如图4，同理得：∠AMB=90°，，设BD=x，则AC=x，在Rt△AMB中，由勾股定理得：AC2+BC2=AB2，+（x+2）2=x2+x﹣6=0，（x+3）（x﹣2）=0，x1=﹣3，x2=2，∴AC=2；综上所述，AC的长为3或2．。

2018重庆中考几何专题-教师版

25．在△ABC中，以AB为斜边，作直角△ABD，使点D落在△ABC内，∠ADB=90°．（1）如图1，若AB=AC，∠BAD=30°，AD=6，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；（2）如图2，若AB=AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP=CP【分析】（1）在直角三角形中，利用锐角三角函数求出AB，即可；（2）先利用互余判断出，∠BDP=∠PEC，得到△BDP和△CEQ，再用三角形的外角得到∠EPC=∠PQC，即可；【解答】（1）解：∵∠ADB=90°，∠BAD=30°，AD=6，∴cos∠BAD=，∴AB===12，∴AC=AB=12，∵点P、M分别为BC、AB边的中点，∴PM=AC=6，（2）如图2，在ED上截取EQ=PD，∵∠ADB=90°，∴∠BDP+∠ADE=90°，∵AD=AE，∴∠ADE=∠AED，∵把△ABD绕点A逆时针旋转一定角度，得到△ACE，∴∠AEC=∠ADB=90°∵∠AED+∠PEC=90°，∴∠BDP=∠PEC，在△BDP和△CEQ中，，∴△BDP≌△CEQ，∴BP=CQ，∠DBP=∠QCE，∵∠CPE=∠BDP+∠DBP，∠PQC=∠PEC+∠QCE，∴∠EPC=∠PQC，∴PC=CQ，∴BP=CP25．在△ABC中，AB=AC，点D，点E在边BC上不同的两点，且∠ADE=75°．（1）如图1，若∠BAC=90°，CD=，求BC的长；（2）如图2，若∠BAC=90°，∠EAD=45°，求证：DC=BE；【考点】相似形综合题．【分析】（1）作DG⊥AC于G，证明出△ABC是等腰直角三角形，进而求出AG的长，即可求出BC的长；（2）作DH⊥AE于H，设DC=a，利用a表示出BC、DE和CD的长，根据线段之间的关系得到结论；【解答】解：（1）如图1所示，作DG⊥AC于G，∵∠BAC=90°，AB=AC，∴△ABC是等腰直角三角形，∴∠1=∠B=45°，∵∠ADE=75°，∴∠2=60°，∠DAG=30°，∴DG=CG=CD=1，AD=2DG=2，∴AG==，∴AC=AG+CG=+1，∴BC=AG=+；（2）如图2所示，作DH⊥AE于H，设DC=a，则DG=CG=a，∴AD=2DG=a，AG=a，∴AC=AG+CG=a，∴BC=AC=（+1）a，∵∠EAD=45°，∴△ADH是等腰直角三角形，∴AH=DH=AD=a，∵∠4=180°﹣∠ADE﹣∠DAE=60°，∴DE=2EH，∴DE=DH÷=a，∴BE=BC﹣DE﹣CD=a=DC，∴DC=BE ；25.（1）如图1，若点D为等腰直角三角形ABC斜边BC的中点，点E、F分别在AB、AC 边上，且∠EDF=90°，连接AD、EF，当BC=5，FC=2时，求EF的长度；（2）如图2，若点D为等边三角形ABC边BC的中点，点E、F分别在AB、AC边上，且∠EDF=90°；M为EF的中点，连接CM，当DF∥AB时，证明：3ED=2MC；【考点】三角形综合题；全等三角形的判定与性质；线段垂直平分线的性质；等腰三角形的性质；勾股定理；等腰直角三角形．【分析】（1）根据等腰直角三角形的性质，证得△ADE≌△CDF，根据全等三角形对应边相等，求得AE=CF=2，最后在在Rt△AEF中根据勾股定理求得EF的长；（2）先设等边三角形边长为2，在Rt△BDE中求得DE的长，再根据CM垂直平分DF，在Rt△CDN中求得CN，在Rt△MND中求得MN的长，最后根据CM与DE的长度之比求得3ED=2MC；【解答】解：（1）如图1∵点D为等腰直角三角形ABC斜边BC的中点∴AD⊥BC，AD=BC=CD=，∠DAE=∠C=45°∴AC=CD=5又∵∠EDF=90°，FC=2∴∠ADE=∠CDF，AF=5﹣2=3在△ADE和△CDF中∴△ADE≌△CDF（ASA）∴AE=CF=2∴在Rt△AEF中，EF==（2）设等边三角形边长为2，则BD=CD=1∵等边三角形ABC中，DF∥AB∴∠FDC=∠B=60°∵∠EDF=90°∴∠BDE=30°∴DE⊥BE∴BE=，DE=如图2，连接DM，则Rt△DEF中，DM=EF=FM ∵∠FDC=∠FCD=60°∴△CDF是等边三角形∴CD=CF=1∴CM垂直平分DF∴∠DCN=30°∴Rt△CDN中，DN=，CN=，DF=1∴在Rt△DEF中，EF==∵M为EF的中点∴FM=DM=∴Rt△MND中，MN==∴CM=+=∴==∴3ED=2MC25.在△ABC中，AB=AC，点F是BC延长线上一点，以CF为边，作菱形CDEF，使菱形CDEF 与点A在BC的同侧，连结BE，点G是BE的中点，连结AG、DG．（1）如图①，当∠BAC=∠DCF=90°时，已知AC=32，CD=2，求AG的长度；（2）如图②，当∠BAC=∠DCF=60°时，AG与DG有怎样的位置和数量关系，并证明；【答案】(1)、5；(2)、AG⊥GD，AG=DG；证明过程见解析；【解析】试题分析：(1)、延长DG与BC交于H，先证△BG△≌EGD，得到BH=DC，=ED，HG=DG，得出BH，再证△ABH≌△ACD，得出∠BAH∠=∠CAD，AH=AD，进而求得∠HAD=90°，即可；(2)、延长DG与BC交于H，先证△BG△≌EGD，得到BH=DC，=ED，HG=DG，得出BH，再证△ABH ≌△ACD，得出∠BAH∠=∠CAD，AH=AD，得到△H△AD为等边三角形，即可；(3)、延长DG 与BC交于H，先证△BG△≌EGD，得到BH=DC，=ED，HG=DG，得出BH，再证△ABH≌△ACD，得出∠BAH∠=∠CAD，AH=AD，得到△H△AD为等腰三角形，即可．试题解析：(1)、如图1，延长DG与BC交于H，连接AH、AD，∵四边形D CEF是正方形，∴DE=DC，DE∥CF，∴∠GBH=∠GED，∠GHB=∠GDE，∵G是BC的中点，∴BG=EG，在△BGH和△EGD中，∵∠GBH=∠GED，∠GHB=∠GDE，BG=EG，∴△BGH ≌△EGD（AAS），∴BH=ED，HG=DG，∴BH=DC，∵AB=AC，∠BAC=90°，∴∠ABC=∠ACB=45°，∵∠DCF=90°，∴∠DCB=90°， ∴∠ACD=45°， ∴∠ABH=∠ACD=45°，在△ABH 和△ACD 中， ∵AB=AC ，∠ABH=∠ACD ，BH=CD ， ∴△ABH ≌△ACD （SAS ）， ∴∠BAH=∠CAD ，AH=AD ， ∵∠BAH+∠HAC=90°，∴∠CAD+∠HAC=90°，即∠HAD=90°， ∴AG ⊥GD ，AG=GD ；在Rt △ABC 中，AB=AC=2， ∴BC=6 在Rt △DCH 中，DC=2，HC=BC ﹣BH=6﹣2=4， ∴DH=22DC HC =25， ∴GD=21DH=5， ∴AG=GD=5．（2）AG ⊥GD ，AG=DG ；如图2，延长DG 与BC 交于H ，连接AH 、AD ，∵四边形DCEF 是正方形， ∴DE=DC ，DE ∥CF ， ∴∠GBH=∠GED ，∠GHB=∠GDE ， ∵G 是BC 的中点，∴BG=EG ，在△BGH 和△EGD 中， ∵∠GBH=∠GED ，∠GHB=∠GDE ，BG=EG ， ∴△BGH ≌△EGD （AAS ），∴BH=ED ，HG=DG ， ∴BH=DC ， ∵AB=AC ，∠BAC=∠DCF=60， ∴∠ABC=60°，∠ACD=60°，∴∠ABC=∠ACD=60°，在△ABH 和△ACD 中， ∵AB=AC ，∠ABH=∠ACD ，BH=CD ， ∴△ABH ≌△ACD （SAS ），∴∠BAH=∠CAD ，AH=AD ， ∴∠BAC=∠HAD=60°， ∴AG ⊥HD ，∠HAG=∠DAG=30°，∴tan ∠DAG=tan30°=33， ∴AG=DG ；25．如图，四边形ABCD 为矩形，连接AC ，AD=2CD ，点E 在AD 边上．（1）如图1，若∠ECD=30°，CE=4，求△AEC 的面积；（2）如图2，延长B A 至点F 使得AF=2CD ，连接FE 并延长交CD 于点G ，过点D 作DH ⊥EG 于点H ，连接AH ，求证：FH=2AH+DH ；（【解析】试题分析：（1）根据30°的直角三角形求CD 和ED ，再利用面积公式求△AEC 的面积；（2）作辅助线，构建全等三角形，证明△AFM ≌△ADH ，得AM=AH ，FM=DH ，则△MAH 是等腰直角三角形，有2AH ，根据线段的和代入得结论；（3）根据将线段AE 绕点A 旋转一定的角度α（0°＜α＜30°）得到线段AE′，先计算当AE 旋转时DN 的最小值和最大值，当α=0°时，DN 最小；当α=180°时，DN 最大，分别计算，写出结论．试题解析：（1）在Rt △EDC 中，∵∠EDC=30°， ∴ED=12EC=12×4=2，cos30°=DC EC， ∴DC=EC•cos30°=4×323 ∴AE=2DC ﹣3﹣2，∴AEC S =12×AE ×DC=12（3﹣2）×3=12﹣3 （2）过A 作AM ⊥AH ，交FG 于M ，∴∠MAH=∠MAD+∠DAH=90°，又∵∠FAD=∠MAD+∠FAM=90°，∴∠FAM=∠DAH，∵AF∥CD，∴∠F=∠FGD∵DH⊥EG，∴∠DHE=∠HDG+∠FGD=90°，∠EDG=∠EDH+∠HDG=90°，∴∠FGD=∠EDH，∴∠F=∠EDH，又∵AF=2CD，AD=2CD，∴AF=AD，∴△AFM≌△ADH，∴AM=AH，FM=DH，∴△MAH是等腰直角三角形，∴MH=2AH，∵FH=MH+FM，∴FH=2AH+DH；25.（12分）已知四边形ABCD为菱形，连接BD，点E为菱形ABCD外任一点．（1）如图（1），若∠A=45°，AB=6，点E为过点B作AD边的垂线与CD边的延长线的交点，BE，AD交于点F，求DE的长．（2）如图（2），若2∠AEB=180°﹣∠BED，∠ABE=60°，求证：BC=BE+DE【答案】（1）362）证明参见解析；【解析】试题分析：（1）首先证明△AFB与△EFD为等腰直角三角形，然后在△ABF中依据勾股定理可求得BF和AF的长，从而得到DF的长，然后在Rt△EDF中，可求得DE的长；（2）延长DE至K，使EK=EB，连结AK．首先证明∠AEB=∠AEK，然后依据SAS证明△AEB≌△AEK，由全等三角形的性质及等边三角形的判断定理可证明△AKD为等边三角形，于是得到KD=BC，通过等量代换可得到问题的答案；（3）记AB与DE的交点为O．首先证明依据菱形的性质可得到∠ABC=2∠ABD，然后依据平行四边形的性质可证明∠CDE=∠BOE，最后依据三角形外角的性质可得到问题的答案．试题解析：（1）如图1所示：∵四边形ABCD为菱形，∴AD=AB=6，AB∥CD．∴∠A=∠ADE=45°．∵AD⊥BE，∴∠AFB=DFE=90°．∴△AFB与△EFD为等腰直角三角形．∴BF2+AF2=AB2，即：2BF2=6，∴BF=AF=3．∵△EFD为等腰直角三角形，∴EF=DF=AD﹣AF=6﹣3．∴DE=2EF=2（6﹣3）=23﹣6．（2）如图2所示：延长DE至K，使EK=EB，联结AK．∵2∠AEB=180°﹣∠BED，∴∠BED=180°﹣2∠AEB=180°﹣∠AEB﹣∠AEK．∴∠AEB=∠AEK．在△AEB和△AEK中BK KEAEB AEKAE AE⎧=⎪∠=∠⎨⎪=⎩，∴△AEB≌△AEK．∴∠K=∠ABE=60°，Ak=AB．又∵AB=AD，∴AK=AD．∴△AKD为等边三角形．∴KD=AD．∴KD=BC．∵KD=KE+DE，∴CB=EB+DE．7.已知两个全等的等腰直角ABC 、△D EF ，其中∠ACB=∠DFE=90，E 为AB 中点，△DE F 可绕顶点E 旋转，线段DE ，EF 分别交线段CA ，CB(或它们所在直线)于 M 、N ．(1)如图l ，当线段EF 经过ABC 的顶点C 时，点N 与点C 重合，线段DE 交AC 于M,求证：AM=MC ；(2)如图2，当线段EF 与线段BC 边交于N 点，线段DE 与线段AC 交于M 点，连 MN,EC,请探究AM ，MN,CN 之间的等量关系，并说明理由；（1）∵AC =BC ，E 为AB 中点∴CE ⊥AB, ∠ACE ＝∠BCE =12ACB=45o∴∠AEC ＝90o∴∠A =∠ACE=45o∴AE =CE∵DF =EF , ∠DFE ＝90o ∴∠FED =45o ∴∠FED =12∠AEC又∵AE =CE∴AM =MC（2）AM =MN +CN ，理由如下:在AM 截取AH ，使得AH =CN ，连接BH由（1）知AE =CE ，∠A =∠BCE =45o在AHE ∆与CNE ∆中：⎪⎩⎪⎨⎧=∠=∠=CE AE NCE A CNAH ∴AHE ∆≌CNE ∆∴HE =NE ，∠AEH ＝∠CEN∴∠HEM =∠AEC －∠AEH －MEC =∠AEC －∠CEN －MEC =∠AEC －∠MEF = 4590-=45o∴∠HEM =∠NEM =45o在HEM ∆与NEM ∆中：⎪⎩⎪⎨⎧=∠=∠=CE AE NCE A CNAH ∴HEM ∆≌NEM ∆∴HM =MN ∴AM =AH+HM= CN +MN即AM =MN +CN。

重庆市2018年中考数学试题(A卷,含解析)【精品】.docx

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分，共48分。

) 1.2的相反数是A .2-B .12-C .12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“-”即可求解【点评】本题考查了相反数的定义，属于中考中的简单题2．下列图形中一定是轴对称图形的是A.B.C.D.【答案】D【解析】A40°的直角三角形不是对称图形；B 两个角是直角的四边形不一定是轴对称图形；C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…，按此规律排列下去，则第⑦个图案中三角形的个数为A ．12B ．14C ．16D ．18【答案】C 【解析】∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6; 第3个图案中的三角形个数为:2+2+2+2=2×4=8; ……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;40°直角三角形四边形平行四边形矩形【点评】此题考查图形的变化规律，找出图形之间的联系，得出数字之间的运算规律，从而计算出正确结果。

2018年重庆市中考数学试题(A卷)及答案(word版)

2018年重庆市中考数学试卷（A 卷）答案及解析一、选择题 (本大题12个小题，每小题4分,共48分。

）1.2的相反数是 A .2- B 。

12-C .12D .2【答案】A【解析】根据一个数的相反数就是在这个数的前面添加上“—”即可求解【点评】本题考查了相反数的定义,属于中考中的简单题2．下列图形中一定是轴对称图形的是A。

B。

C。

D。

【答案】D【解析】A40°的直角三角形不是对称图形;B 两个角是直角的四边形不一定是轴对称图形;C 平行四边形是中心对称图形不是轴对称图形；D 矩形是轴对称图形，有两条对称轴【点评】此题主要考查基本几何图形中的轴对称图形和中心对称图形，难度系数不大，考生主要注意看清楚题目要求。

3。

为调查某大型企业员工对企业的满意程度，以下样本最具代表性的是 A 。

企业男员工B 。

企业年满50岁及以上的员工 C.用企业人员名册，随机抽取三分之一的员工D.企业新进员工【答案】C【解析】A 调查对象只涉及到男性员工；B 调查对象只涉及到即将退休的员工；D 调查直角三角形四边形平行四边形矩形对象只涉及到新进员工【点评】此题主要考查考生对抽样调查中科学选取样本的理解，属于中考当中的简单题.4.把三角形按如图所示的规律拼图案，其中第①个图案中有4个三角形，第②个图案中有6个三角形，第③个图案中有8个三角形，…,按此规律排列下去，则第⑦个图案中三角形的个数为A．12 B．14 C．16 D．18【答案】C【解析】∵第1个图案中的三角形个数为:2+2=2×2=4;第2个图案中的三角形个数为:2+2+2=2×3=6;第3个图案中的三角形个数为:2+2+2+2=2×4=8;……∴第7个图案中的三角形个数为:2+2+2+2+2+2+2+2=2×8=16;【点评】此题考查图形的变化规律，找出图形之间的联系,得出数字之间的运算规律，从而计算出正确结果。

比较简单。

相关主题

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

重庆中考几何题分类汇编（含答案）类型1 线段的倍分：要证线段倍与半，延长缩短去实验例1 如图Z3－1，在△ABC中，AB＝AC，CM平分∠ACB交AB于M，在AC的延长线上截取CN＝BM，连接MN交BC于P，在CB的延长线截取BQ＝CP，连接MQ.(1)求证：MQ＝NP；(2)求证：CN＝2CP.针对训练：1．如图Z3－2，在▱ABCD中，AC⊥BC，点E、点F分别在AB、BC上，且满足AC＝AE＝CF，连接CE、AF、EF.(1)若∠ABC＝35°，求∠EAF的度数；(2)若CE⊥EF，求证：CE ＝2EF.2．已知，在△ABC 中，AB ＝AC ，∠BAC ＝90°，E 为边AC 任意一点，连接BE.(1)如图①，若∠ABE＝15°，O 为BE 中点，连接AO ，且AO ＝1，求BC 的长；(2)如图②，F 也为AC 上一点，且满足AE ＝CF ，过A 作AD⊥BE 交BE 于点H ，交BC 于点D ，连接DF 交BE 于点G ，连接AG.若AG 平分∠CAD，求证：AH ＝12AC.3．在△ACB中，AB＝AC，∠BAC＝90°，点D是AC上一点，连接BD，过点A作AE⊥BD于E，交BC于F.(1)如图①，若AB＝4，CD＝1，求AE的长；(2)如图②，点G是AE上一点，连接CG，若BE＝AE＋AG，求证：CG＝2AE.4．在等腰直角三角形ABC中，∠BAC＝90°，AB＝AC，D是斜边BC的中点，连接AD.(1)如图①，E是AC的中点，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′，当AD＝6时，求AE′的值．(2)如图②，在AC上取一点E，使得CE＝13AC，连接DE，将△CDE沿CD翻折到△CDE′，连接AE′交BC于点类型2 线段的和差：要证线段和与差，截长补短去实验例2 如图，在△ABC中，∠BAC＝90°，在BC上截取BD＝BA，连接AD，在AD 左侧作∠EAD＝45°交BD于E.(1)若AC＝3，则CE＝________(直接写答案)；(2)如图①，M、N分别为AB和AC上的点，且AM＝AN，连接EM、DN，若∠AME ＋∠AND＝180°，求证：DE＝DN＋ME；(3)如图②，过E作EF⊥AE，交AD的延长线于F，在EC上选取一点H，使得EH ＝BE，连接FH，在AC上选取一点G，使得AG＝AB，连接BG、FG，求证：FH＝FG.针对训练：1．如图Z 3－7，在▱ABCD 中，AE ⊥BC 于E ，AE ＝AD ，EG ⊥AB 于G ，延长GE 、DC 交于点F ，连接AF.(1)若BE ＝2EC ，AB ＝13，求AD 的长；(2)求证：EG ＝BG ＋FC.2．如图，在正方形ABCD 中，点P 为AD 延长线上一点，连接AC 、CP ，过点C 作CF⊥CP 于点C ，交AB 于点F ，过点B 作BM⊥CF 于点N ，交AC 于点M.(1)若AP ＝78AC ，BC ＝4，求S △ACP ；(2)若CP －BM ＝2FN ，求证：BC ＝MC.3．如图，在△ABC中，AB＝BC，以AB为一边向外作菱形ABDE，连接DC，EB并延长EB交AC于F，且CB⊥AE于G.(1)若∠EBG＝20°，求∠AFE；(2)试问线段AE，AF，CF之间的数量关系并证明．类型3 倍长中线：三角形中有中线，延长中线等中线例3 如图Z3－10①，在Rt△ABC中，∠ABC＝90°，D、E分别为斜边AC上两点，且AD＝AB，CE＝CB，连接BD、BE.(1)求∠EBD的度数；(2)如图Z3－10②，过点D作FD⊥BD于点D，交BE的延长线于点F，在AB上选取一点H，使得BH＝BC，连接CH，在AC上选取一点G，使得GD＝CD，连接FH、FG，求证：FH＝FG.针对训练：1．如图，已知在▱ABCD中，G为BC的中点，点E在AD边上，且∠1＝∠2.(1)求证：E是AD中点；(2)若F为CD延长线上一点，连接BF，且满足∠3＝∠2，求证：CD＝BF＋DF.2．如图Z3－12，在菱形ABCD中，点E、F分别是BC、CD上的点，连接AE，AF，DE、EF，∠DAE＝∠BAF.(1)求证：CE＝CF；(2)若∠ABC＝120°，点G是线段AF的DG，EG.求证：DG⊥GE.3．在Rt △ABC 中，∠ACB ＝90°，点D 与点B 在AC 同侧，∠ADC ＞∠BAC，且DA ＝DC ，过点B 作BE∥DA 交DC 于点E ，M 为AB 的中点，连接MD ，ME.(1)如图①，当∠ADC＝90°时，线段MD 与ME 的数量关系是________；(2)如图②，当∠ADC＝60°时，试探究线段MD 与ME 的数量关系，并证明你的结论；(3)如图③，当∠ADC＝α时，求ME MD的值．4．如图①，等边三角形ABC 中，CE 平分∠ACB，D 为BC 边上一点，且DE ＝CD ，连接BE.(1)若CE ＝4，BC ＝6 3，求线段BE 的长；(2)如图②，取BE中点P，连接AP，PD，AD，求证：AP⊥PD且AP＝3PD；(3)如图③，把图Z3－14②中的△CDE绕点C顺时针旋转任意角度，然后连接BE，点P为BE中点，连接AP，PD，AD，问第(2)问中的结论还成立吗若成立，请证明；若不成立，请说明理由．5．在△ABC中，以AB为斜边，作直角三角形ABD，使点D落在△ABC内，∠ADB ＝90°.(1)如图①，若AB＝AC，∠BAD＝30°，AD＝6 3，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；(2)如图②，若AB＝AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP＝CP；(3)如图③，若AD＝BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE＝EC，请直接写出线段BF、FC、AD之间的关系(不需要证明)．类型4 中位线：三角形中两中点，连接则成中位线例4 2017·河南如图①，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．(1)观察猜想：图①中，线段PM与PN的数量关系是__________，位置关系是__________；(2)探究证明：把△ADE绕点A按逆时针方向旋转到图②的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；(3)拓展延伸：把△ADE绕点自由旋转，若AD＝4，AB＝10写出△PMN面积的最大值．针对训练：1．如图①，在任意的三角形ABC中，分别以AB和AC为一边作等腰三角形ABE 和等腰三角形ACD，AB＝AE，AC＝AD，且∠BAE＋∠CAD＝180°，连接DE，延长CA交DE于F.(1)求证：∠CAB＝∠AED＋∠ADE；(2)若∠ACB＝∠BAE＝∠CAD＝90°，如图②，求证：BC＝2AF；(3)若在△ABC中，如图③所示，作等腰三角形ABE和等腰三角形ACD，AB与DE 交于点F，F为DE的中点，请问(2)中的结论还成立吗若成立，请给出证明，若不成立，请说明理由．2．如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＋∠EAD＝180°，△ABC 不动，△ADE绕点A旋转，连接BE、CD，F为BE的中点，连接AF.(1)如图①，当∠BAE＝90°时，求证：CD＝2AF；(2)当∠BAE≠90°时，(1)的结论是否成立请结合图②说明理由．3．如图①，在等腰三角形ABC中，AB＝AC，在底边BC上取一点D，在边AC上取一点E，使AE＝AD，连接DE，在∠ABD的内部作∠ABF＝2∠EDC，交AD 于点F.(1)求证：△ABF是等腰三角形；(2)如图②，BF的延长交AC于点G.若∠DAC＝∠CBG，延长AC至点M，使GM＝AB，连接BM，点N是BG段AN、BM类型5 角的和差倍分图中有角平分线，可向两边作垂线；也可将图对折看，对称以后关系现．角平分线平行线，等腰三角形来添．角平分线加垂线，三线合一试试看．例5．如图，把△EFP放置在菱形ABCD中，使得顶点E，F，P分别在线段AB，AD，AC上，已知EP＝FP＝6，EF＝6 3，∠BAD＝60°，且AB＞6 3.(1)求∠EP F的大小；(2)若AP＝10，求AE＋AF的值．针对训练：1．已知：如图①，AD平分∠BAC，∠B＋∠C＝180°，∠B＝90°，易知：DB＝DC.探究：如图②，AD平分∠BAC，∠ABD＋∠ACD＝180°，∠ABD＜90°，求证：DB＝DC.2．在△ACB中，AB＝AC，∠BAC＝90°，点D是AC上一点，连接BD，过点A作AE⊥BD于E，交BC于F.(1)如图①，若AB＝4，CD＝1，求AE的长；(2)如图②，点P是AC上一点，连接FP，若AP＝CD，求证：∠ADB＝∠CPF.3．已知，在▱ABCD中，∠BAD＝45°，AB＝BD，E为BC上一点，连接AE 交BD于F，过点D作DG⊥AE于G，延长DG交BC于H.(1)如图①，若点E与点C重合，且AF＝5，求AD的长；(2)如图②，连接FH，求证：∠AFB＝∠HFB.4．如图，将正方形纸片ABCD沿EF折叠(点E、F分别在边AB、CD上)，使点B 落在AD边上的点M处，点C落在点N处，MN与CD交于点P，连接EP.当点M在边AD上移动时，连接BM、BP.(1)求证：BM是∠AMP的平分线；(2)△PDM的周长是否发生变化证明你的结类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6．△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点(点D不与B，C重合)，以AD为边在AD右侧作正方形ADEF，连接CF.(1)观察猜想：如图①，当点D在线段BC上时，①BC与CF的位置关系为：________．②BC，CD，CF之间的数量关系为：___________；(将结论直接写在横线上)否仍然成立若成立，请给予证明；若不成立，请你写出正确结论再给予证明．(3)拓展延伸：如图Z 3－25③，当点D 在线段BC 的延长线上时，延长BA 交CF于点G ，连接GE.若已知AB2，CD ＝14BC ，请求出GE的长．针对训练：1．在四边形ABCD 中，∠B ＋∠D＝180°，对角线AC 平分∠BAD.(1)如图①，若∠DAB＝120°，且∠B＝90°，试探究边AD 、AB 与对角线AC 的数量关系并说明理由．(2)如图②，若将(1)中的条件“∠B＝90°”去掉，(1)中的结论是否成立请说明理由．(3)如图③，若∠DAB＝90°，探究边AD、AB与对角线AC的数量关系并说明理由．2．如图①，在正方形ABCD中，点E为边BC上一点，将△ABE沿AE翻折得△AHE，延长EH交边CD于F，连接AF.(1)求证：∠EAF＝45°；(2)延长AB，AD，如图②，射线AE、AF分别交正方形两个外角的平分线于M、N，连接MN，若以BM、DN、MN为三边围成三角形，试猜想三角形的形状，并证明你的结论．3．如图①，在正方形ABCD内有一点P，PA＝5，PB＝2，PC＝1，求∠BPC的度数．【分析问题】根据已知条件比较分散的特点，我们可以通过旋转变换将分散的已知条件集中在一起，于是将△BPC绕点B逆时针旋转90°，得到了△BP′A(如图Z3－28②)，然后连接PP′.(1)请你通过计算求出图Z3－28②中∠BPC的度数；(2)如图③，若在正六边形ABCDEF内有一点P，且PA＝2 13，PB＝4，PC ＝2.请求出∠BPC的度数．重庆中考几何题分类汇编答案例1. 证明：(1)∵AB＝AC ，∴∠ABC ＝∠ACB.∵∠MBQ ＋∠ABC＝180°， ∠ACB ＋∠PCN＝180°，∴∠MBQ ＝∠PCN.在△QBM 和△PCN 中， ⎩⎪⎨⎪⎧QB ＝PC ，∠MBQ ＝∠PCN，BM ＝CN ，∴△QBM ≌△PCN(SAS)．∴MQ＝NP. (2)过M 作MG∥AC 交BC 于G ，∵MG ∥AC ，∴∠MGB ＝∠ACB，∠MGC ＝∠PCN，∵由(1)知，∠ABC ＝∠ACB，∴∠ABC ＝∠MGB，∴MB ＝MG ，∵MB ＝CN ， ∴MG ＝CN.在△MGP 和△NCP 中，⎩⎪⎨⎪⎧∠MPG＝∠CPN，∠MGC ＝∠PCN，MG ＝NC ，∴△MGP ≌△NCP(AAS)． ∴PG ＝CP ，∴CG ＝CP ＋PG ，即CG ＝2CP.∵CM 平分∠ACB，∴∠BCM ＝∠MCA，∵MG ∥AC ，∴∠MCA ＝∠GMC，∴∠BCM ＝∠GMC， ∴MG ＝CG ，∵MG ＝CN ，∴CN ＝CG ，∴CN ＝2CP. 针对训练1. 解：(1)∵AC⊥BC，∴∠ACB ＝90CF ，∴∠AFC ＝45°，∵∠ABC ＝35°，∴∠EAF 10°；(2)证明：方法1：取CF 的中点M ，连接EM 、AM ， ∵CE ⊥EF ，∴EM ＝CM ＝FM ＝12CF ，又∵AC＝AE ，∴AM 为EC 的中垂线，∴∠CAM ＋∠ACE＝90°，又∵∠CEF＝∠ACM＝90°，∴△ACM ∽△CEF又∵CF＝AC ＝2CM ，∴AC CM ＝CE EF ＝21，即CE ＝2EF 方法2：延长FE 至M ，使EF ＝EM ，连接CM ， ∵CE ⊥EF ，∴△CMF 为等腰三角形，又∵AC＝AE ＝CF ，且∠ACE＝∠CFE(易证)， ∴△CMF ≌△CEA ，∴FM ＝CE ＝2EF.2. 解：(1)如图①，在AB 上取一点M ，使得BM ＝ME ，连接ME.在Rt △ABE 中，∵OB ＝OE ，∴BE ＝2OA∵MB ＝ME ，∴∠MBE ＝∠MEB＝15°， ∴∠AME ＝∠MBE＋∠MEB＝30°，设AE ＝x ，则ME ＝BM ＝2x ，AM ＝3x ，∵AB 2＋AE 2＝BE 2，∴(2x ＋3x)2＋x 2＝22， ∴x ＝6－22(负根舍弃)，∴AB ＝AC ＝(2＋ 3)·6－22，∴BC ＝2AB ＝3＋1.(2)证明：如图②，作CP⊥AC，交AD 的延长线于P ，GM ⊥AC 于M. ∵BE ⊥AP ，∴∠AHB ＝90°，∴∠ABH ＋∠BAH＝90°，又∵AB＝AC，∠BAE＝∠ACP＝90°，∴△ABE≌△CAP，∴AE＝CP＝CF，∠AEB＝∠P，在△DCF和△DCP中，⎩⎪⎨⎪⎧CD＝CD，∠DCF＝∠DCP，CF＝CP，∴△DCF≌△DCP，∴∠DFC＝∠P，∴∠GFE＝∠GEF，∴GE＝GF，∵GM⊥EF，∴FM＝ME，∵AE＝CF，∴AF＝CE，∴AM＝CM，在△GAH和△GAM中，⎩⎪⎨⎪⎧∠GAH＝∠GAM，∠AHG＝∠AMG，AG＝AG，∴△AGH≌△AGM，∴AH＝AM＝CM＝12AC.3. 解：(1)∵AB＝4，∴AC＝AB＝4.∵CD＝1，∴AD＝AC－CD＝3.∵在Rt△ABD中，∠BAC＝90°，∴BD＝AB2＋AD2＝5，∵S△ABD＝12AB·AD＝12AE·BD，∴AE＝.(2)证明：如图，在线段EB上截取EH＝AE，并连接AH.∵AE⊥BD，EH＝AE，∴AH＝2AE.∵BE＝AE＋AG，∴BH＝BE－HE＝AG.∵∠BAD＝∠BEA＝90°，∴∠ABE ＋∠BAE＝∠CAG＋∠BAE＝90°， ∴∠ABE ＝∠CAG.∵BA ＝AC ，∴△ABH ≌△CAG ， ∴CG ＝AH ＝2AE.4. 解：(1)∵∠BAC＝90°，AB ＝AC ，D 是斜边BC 的中点， ∴∠ADC ＝90°，∠ACD ＝45°.在Rt △ADC 中，AC ＝AD÷sin45°＝2 3. ∵E 是AC 的中点，∴CE ＝12AC ＝ 3.∵将△CDE 沿CD 翻折到△CDE′，∴CE ′＝CE ＝3ACE ′＝90°.由勾股定理，得AE′＝CE′2＋AC 2＝15.(2)证明：如图，过B 作AE′的垂线交AD 于点G ，交AC 于点H. ∵∠ABH ＋∠BAF＝90°，∠CAF ＋∠BAF＝90°，∴∠ABH ＝∠CAF. 又∵AB＝AC ，∠BAH ＝∠ACE′＝90°，∴△ABH ≌△CAE ′. ∴AH ＝CE′＝CE ，∵CE ＝13AC ，∴AH ＝HE ＝CE.∵D 是BC 中点，∴DE ∥BH ，∴G 是AD 中点．在△ABG 和△CAF 中：AB ＝AC ，∠BAD ＝∠ACD＝45°，∠ABH ＝∠CAF， ∴△ABG ≌△CAF.∴AG ＝CF.∵AG ＝12AD ，∴CF ＝12AD ＝12CD.∴DF＝CF.类型2 线段的和差：要证线段和与差，截长补短去实验例2：解：（1）3（2）证明：延长DN 到K ，使得NK ＝ME ，连接AK ，如图①，因为∠1＋∠3＝180°，∠1＋∠2＝180°，∴∠2＝∠3. 在△AME 和△ANK 中，⎩⎪⎨⎪⎧AM ＝AN ，∠2＝∠3，ME ＝NK ，∴△AME ≌△ANK (SAS)．∴AE ＝AK ∴∠4＋∠EAC ＝90°，∴∠5＋∠EAC ＝90°，即90°，∵∠EAD ＝45°，∴∠KAD ＝∠EAK －∠EAD ＝90°－45°＝45°.∴∠EAD ＝∠KAD .在△EAD 和△KAD 中，⎩⎪⎨⎪⎧EA ＝KA ，∠EAD ＝∠KAD ，AD ＝AD ，∴△EAD ≌△KAD (SAS)， ∴ED ＝KD .∵DK ＝DN ＋KN ，∴ED ＝DN ＋KN ，又NK ＝ME ，∴ED ＝DN ＋ME .(3)证明：延长AE 到J ，使得EJ ＝AE ，连接JH ，在△ABE 和△JHE 中，⎩⎪⎨⎪⎧AE ＝JE ，∠AEB ＝∠JEH，BE ＝HE ，∴△ABE ≌△JHE(SAS)， ∴JH ＝AB ，∠1＝∠2，∵AB ＝AG ，∴JH ＝AG ，∵AE ＝EJ ，EF ⊥AJ ，∴AF ＝JF ，∴∠JAF ＝∠AJF＝45°，即∠2＋∠3＝45°，∵∠BAC ＝90°，∴∠1＋∠EAD＋∠4＝90°， ∴∠1＋∠4＝90°－∠EAD，＝90°－45°＝45°， ∵∠1＝∠2，∴∠3＝∠4，在△JHF 和△AGF 中，⎩⎪⎨⎪⎧JH ＝AG ，∠3＝∠4，JF ＝AF ，∴△JHF ≌△AGF(SAS)，∴FH ＝FG.针对训练：1. 解：(1)∵四边形ABCD 是平行四边形，∴AD ∵BE ＝2EC ，设CE ＝x ，BE ＝2x ，∴BC ＝AD ＝又∵EG⊥AB，∴∠AEB ＝90°，∴AB 2＝AE 2＋BE 2，即13＝9x 2＋4x 2，∴x ＝1，∴AD ＝3x ＝3.(2)证明：如图，过C 作CH⊥AB 于H ，则四边形CHGF 为矩形． ∴CF ＝HG ，∠CHB ＝90°，GF ＝CH.∵AE ⊥BC ，EG ⊥AB ，∴∠AEB ＝∠CHB＝90°，∠BCH ＋∠B＝90°，∠BAE ＋∠B＝90°，∴∠BCH ＝∠BAE. 又∵AE＝BC ，∴△AGE ≌△CHB ，∴GE ＝BH ，AG ＝GF ， ∴GE ＝BH ＝BG ＋GH ＝BG ＋CF.2. 解：(1)∵四边形ABCD 是正方形，BC ＝4，∴AB ＝AD ＝CD ＝BC ＝4，∠ADC ＝∠ABC＝90°. ∵在Rt △ABC 中，AC ＝AB 2＋BC 2＝4 2， ∴AP ＝78AC ＝72 2，∴S △ACP ＝12AP·CD＝7 2.(2)证明：方法一：如图①，在NC 上截取NK ＝NF ，连接BK. ∵四边形ABCD 是正方形，∴AB ＝BC ＝DC ，∠ABC ＝∠BCD＝∠ADC＝90°. ∵∠BCD ＝90°，CF ⊥CP ，∴∠1＋∠DCF＝∠2＋＝90°，∴∠1＝∠2，∵在△FBC 和△PDC 中，∴△FBC ≌△PDC(ASA)，∴CF ＝CP ，∵CP －2FN ＝BM ，∴CF －FK ＝BM ，即CK ＝BM ，∵∠FBC ＝90°，BM ⊥CF ，∴∠1＋∠NBC＝∠4＋∠NBC＝90°， ∴∠1＝∠4，∵在△ABM 和△BCK 中，⎩⎪⎨⎪⎧AB ＝BC ，∠4＝∠1，BM ＝CK ，∴△ABM ≌△BCK(SAS)，∴∠7＝∠6.∵BM ⊥CF ，NK ＝NF ，∴BF ＝BK ，∵BF ＝BK ，BM ⊥CF ，∠4＝∠5，∴∠4＋∠7＝∠5＋∠6，∵∠8＝∠4＋∠7，∴∠8＝∠MBC，∴BC ＝MC.解：方法二：如图②，延长BM 交AD 于点G ，过A 作AE⊥BG 于E先证△AEB≌△BNC(AAS)，∴AE＝BN，又证△AEG≌△BNF(AAS)，∴EG＝NF，再证四边形BCPG为平行四边形，∴BG＝CP，∵CP－BM＝2FN，∴BG－BM＝2EG，∴MG＝2EG，∴点E为MG中点，∵AE⊥MG，EM＝EG，∴AM＝AG，∴∠3＝∠4，∵∠2＝∠3，∠1＝∠4，∴∠1＝∠2，∴BC＝MC.3. 解：(1)∵∠EBG＝20°，CB⊥AE，∴∠BEG＝70o，∠CBF＝∠EBG＝20°，∵四边形ABDE是菱形，∴∠ABE＝∠BEG＝70°，∴∠ABG＝50°，∵AB＝BC，∴∠FCB＝25°，∴∠AFE＝∠CBF＋∠FCB＝45°；(2)AE，AF，CF之间的数量关系是AF2＋CF2＝2AE2，证明如下：连接DF，∵四边形ABDE是菱形，∴AB＝DB，∠DBE＝∠ABE，∴∠DBF＝∠ABF，∵BF＝BF，∴△DBF≌△ABF(SAS)，∴DF＝AF，∠BDF＝∠BAF，∵∠BCF＝∠BAF，∴∠BCF＝∠BDF，∵CB⊥AE，AE∥DB，∴DB⊥CB，∵CB＝AB＝BD，∴△DBC是等腰直角三角形，∴DC ＝2BD ＝2AE ，∵∠DPB ＝∠CPF，∴∠CFP ＝∠DBP＝90°，∴DF 2＋CF 2＝DC 2，即有：AF 2＋CF 2＝2AE 2.类型3 倍长中线：三角形中有中线，延长中线等中线例3解：(1)设∠BEC ＝α，∠BDA ＝β，则∠C ＝180°－2α，∠A ＝180°－2β.∵在Rt △ABC 中，∠ABC ＝90°， ∴∠A ＋∠C ＝90°，即180°－2α＋180°－2β＝90°，∴α＋β＝135°，∴∠EBD ＝45°.(2)证明：法一：如图①，延长BD 至点B′，使得＝DB ，连接FB′、GB′.在△GDB′和△CDB 中，⎩⎪⎨⎪⎧GD ＝CD ，∠GDB ′＝∠CDB，B ′D ＝BD ，∴△GDB ′≌△CDB.∴GB ′＝BC ＝BH ，∠GB ′D ＝∠CBD.∵FD ⊥BD ，BD ＝DB′，∴FB ＝FB′.∵∠FB ′G ＝45°－∠GB′D，∠HBF ＝90°－45°－∠CBD＝45°－∠CBD，∴∠FB ′G ＝∠HBF.在△FHB 和△FGB′中，⎩⎪⎨⎪⎧HB ＝GB′，∠HBF ＝∠GB′F，BF ＝B′F，∴△FHB ≌△FGB ′，∴HF ＝GF.法二：如图②，延长FD 至点F ′，使得DF ′＝DF ，连接CF ′、BF ′.先证△DGF ≌△DCF ′，再证△BHF ≌△BCF ′，∴HF ＝GF .针对训练1. 证明：(1)∵四边形ABCD 是平行四边形，∴AB ＝CD ，AD ＝BC ，∠A ＝∠C .又∵∠1＝∠2，∴△ABE ≌△CDG (ASA)，∴AE ＝CG .∵G 为BC 中点，∴CG ＝12BC ， ∴AE ＝CG ＝12BC ＝12AD ，∴E 是AD 中点．(2)如图，延长BE ，CD 交于点H.∵四边形ABCD 是平行四边形，∴AB 綊CD ，∴∠A ＝∠ADH，∠1＝∠4，又∵∠1＝∠2，∠3＝∠2，∴∠1＝∠2＝∠3＝∠4，∴FH＝FB.由(1)，E是AD中点，∴AE＝DE，∴△ABE≌△DHE(AAS)，∴AB＝DH，∴CD＝AB＝DH＝DF＋FH＝DF＋BF，即CD＝BF＋DF.2. 证明：(1)在菱形ABCD中，AB＝BC＝CD＝AD，∠ADF＝∠ABE，∵∠DAE＝∠BAF，∴∠DAE－∠EAF＝∠BAF－∠EAF，即∠DAF＝∠BAE.∴△DAF≌△BAE，∴BE＝DF.又∵BC＝CD，∴CE＝CF(2)如图，延长DG交AB于H，连接EH，∵在菱形ABCD中，AB∥CD，∴∠DFA＝∠GAH.∵G为AF中点，∴AG＝GF.又∵∠DGF＝∠AGH，∴△DGF≌△HGA.∴DG＝GH，AH＝DF.又∵AB＝CD，∴BH＝CF.又∵AB∥CD，∠ABC＝120°，∴∠C＝60°.又∵CE＝CF，∴△CEF为等边三角形，∴CF ＝EF ，∠CFE ＝60°，∴EF ＝BH ，∠DFE ＝∠ABC＝120°.又∵BE＝DF ，∴△EFD ≌△HBE ，∴HE ＝ED ，又∵HG＝DG ，∴DG ⊥GE.3. 解：（1）MD=ME2)MD ＝3ME.理由如下：如图①，延长EM 交DA 于点F.∵BE ∥DA ，∴∠FAM ＝∠EBM.又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.∵DA ＝DC ，∠ADC ＝60°，∴∠BED ＝∠ADC＝60°，∠ACD ＝60°.∵∠ACB ＝90°，∴∠ECB ＝30°，∴∠EBC ＝30°，∴CE ＝BE ，∴AF ＝EC ，∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∴∠MDE ＝30°.在Rt △MDE 中，tan ∠MDE ＝ME MD ＝33. ∴MD ＝3ME.(3)如图②，延长EM 交DA 于点F ∵BE ∥DA ，∴∠FAM ＝∠EBM，又∵AM＝BM ，∠AMF ＝∠BME，∴△AMF ≌△BME ，∴AF ＝BE ，MF ＝ME.延长BE 交AC 于点N ，∴∠BNC ＝∠DAC.∵DA ＝DC ，∴∠DCA ＝∠DAC，∴∠BNC ＝∠DCA，∵∠ACB ＝90°，∴∠ECB ＝∠EBC，∴CE ＝BE ，∴AF ＝CE.∴DF ＝DE ，∴DM ⊥EF ，DM 平分∠ADC，∵∠ADC ＝α，∴∠MDE ＝α2. ∴在Rt △MDE 中，ME MD ＝tan ∠MDE ＝tan α2.4.解：(1)如图①，作EH ⊥BC 于点H .∵△ABC 是等边三角形，∴∠ACB ＝60°.∵CE 平分∠ACB ，∴∠ECH ＝12∠ACB ＝30°， ∵EC ＝4，∠ECH ＝30°，∴EH ＝2，HC ＝2 3.∵BC ＝6 3，∴BH ＝6 3－2 3＝4 3.在Rt △BHE 中，BE 2＝(4 3)2＋22＝52，∴BE ＝2 13.(2)如图②，延长DP 至M ，使DP ＝PM ，连接BM 、AM .在△PDE 和△PMB 中，⎩⎪⎨⎪⎧PD ＝PM ，∠EPD ＝∠BPM ，PE ＝PB ，∴△PDE≌△PMB(SAS)．∴BM＝DE，∠1＝∠2.∴BM∥DE.∴∠MBD＋∠BDE＝180°.∵CE平分∠ACB，DE＝CD，∴∠BDE＝30°＋30∴∠MBD＝120°.∵△ABC是等边三角形，∴∠ABC＝60.∵BM＝DE，DE＝CD，∴BM＝CD.在△ABM和△ACD中，⎩⎪⎨⎪⎧AB＝AC，∠3＝∠ACD，BM＝CD，∴△ABM≌△ACD(SAS)．∴AD＝AM，∠4＝∠5.∵PD＝PM，∴AP⊥PD.∵∠4＝∠5，∠BAD＋∠5＝60°，∴∠4＋∠BAD＝60°，即∠MAD＝60°.∴∠PAD＝12∠MAD＝30°.∵在Rt△APD中，tan30°＝PDAP，∴AP＝3PD.(3)第(2)至N，使DP＝PN，连接BN、AN，取BE、AC交于点O.在△PDE和△PNB中，⎩⎪⎨⎪⎧PD＝PN，∠EPD＝∠BPN，PE＝PB，∴△PDE≌△PNB(SAS)．∴BN＝DE，∠1＝∠2.∵DE＝CD，∴BN＝CD.∵∠AOB＝∠EOC，∴∠1＋∠3＋∠BAO＝∠2＋∠4＋∠DEC＋∠DCE.∵∠BAO ＝60°，∠DEC ＝∠DCE＝30°，∴∠1＋∠3＝∠2＋∠4，∴∠3＝∠4.在△ABN 和△ACD 中，⎩⎪⎨⎪⎧AB ＝AC ，∠3＝∠4，BN ＝CD ，∴△ABN ≌△ACD(SAS)．∴∠5＝∠6，AN ＝AD.∵PD ＝PN ，∴AP ⊥PD.∵∠NAC ＋∠5＝60°，∴∠NAC ＋∠6＝60°，即∠NAD＝60°.∴∠PAD ＝12∠NAD＝30°， ∵在Rt △APD 中，tan ∠PAD ＝PD AP，∴AP ＝3PD.5. 解：(1)∵∠ADB ＝90°，∠BAD ＝30°，AD ＝6 3，∴cos ∠BAD ＝AD AB ，∴32＝6 3AB，∴AB ＝12. 又∵AB ＝AC ，∴AC ＝12，∴PM 为△ABC 的中位线，∴PM ＝12AC ＝6.(2)证明：方法一：如图①，在截取ED 上截取∵∠ADB ＝90°，∴∠1＋∠2＝90°，又∵AD＝AE ，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4.在△BDP和△CEQ中，PD＝QE，∠1＝∠4，BD＝CE，∴△BDP≌△CEQ.∴BP＝CQ，∠DBP＝∠QCE，又∵∠5＝∠1＋∠DBP，∠6＝∠4＋∠QCE，∴∠5＝∠6，∴PC＝CQ，∴BP＝CP.方法二：如图②，过点B作EP的垂线交EP的延长线于点M，过C点作EP的垂线交EP于点N.∵∠ADB＝90°，∴∠1＋∠2＝90°，又∵AD＝AE，∴∠2＝∠3，又∵∠3＋∠4＝90°，∴∠1＝∠4，在△BMD和△CNE中，∠1＝∠4，∠BMD＝∠CNE＝90°，BD＝CE，∴△BMD≌△CNE.∴BM＝CN.在△BMP和△CNP中，∠5＝∠6，∠BMP＝∠CNP，BM＝CN，∴△BMP≌△CNP，∴BP＝CP.方法三：如图③，过点B作BM∥CE交EP的延长线于点M.略证△BMP≌△CEP，∴BP＝CP.(3)BF2＋FC2＝2AD2.类型4 中位线：三角形中两中点，连接则成中位线例4: 解：（1）PM=PN;PM⊥PN(2)△PMN为等腰直角三角形，理由如下：由题意知△ABC和△ADE均为等腰直角三角形，∴AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＋∠DAC＝∠CAE＋∠DAC，∴∠BAD＝∠CAE，∴△BAD≌△CAE，∴∠ABD＝∠ACE，BD＝CE.又∵M、P、N分别是DE、CD、BC的中点，∴PM是△CDE的中位线，∴PM∥CE且PM＝12CE，∠MPD＝∠ECD＝∠ACD＋∠ACE.同理，PN∥BD且PN＝12BD，∠DBC＝∠PNC，又∵BD＝CE，∠ABD＝∠ACE，∴PM＝PN，∴∠MPN＝∠MPD＋∠DPN＝∠ECD＋∠DCN＋∠CNP＝∠ACD＋∠ACE＋∠DCN＋∠CBD＝∠ACD＋∠DCN＋∠ABD＋∠CBD＝∠ACB＋∠ABC＝90°，∴PM⊥PN，∴△PMN为等腰直角三角形；(3)△PMN 面积的最大值为492.提示：在旋转的过程中，由(2)中的结论知△PMN 为等腰直角三角形，S △PMN ＝12PN 2＝18BD 2，当S △PMN 有最大值时，则BD 的值最大，由三角形三边关系可推断出当B 、A 、D 三点共线时，BD 的值最大，其最大值为14，此时S △PMN ＝12PN 2＝18BD 2＝18×14×14＝492.针对训练：1. 解：(1)证明：延长DA 交BE 于G 点．∵∠BAE ＋∠CAD ＝180°，即∠EAG ＋∠GAB ＋∠CAD ＝180°，∵∠GAB ＋∠BAC ＋∠CAD ＝180°，∴∠EAG ＝∠CAB .∵∠EAG ＝∠AED ＋∠ADE ，∴∠CAB ＝∠AED ＋∠ADE .(2)证明：如图①，过E 点作DA ∴∠AHE ＝∠ACB ＝90°，由(1)可知，∠EAH ＝∠BAC ，又∵AE ＝AB ，∴△AHE ≌△ACB ，∴EH ＝BC ，AH ＝AC .∵AC＝AD，∴AH＝AD.∵∠EHA＝∠FAD＝90°，∴AF∥EH.∵A为DH中点，∴AF为△DHE中位线，∴EH＝2AF，∴BC＝2AF.(3)成立．证明如下：如图②，延长DA至M点，使AM＝DA，连接EM∵∠BAE＋∠CAD＝180°，∠CAD＋∠CAM＝∴∠BAE＝∠CAM，∴∠BAE＋∠CAC＝∠CAM＋∠EAC，即∠BAC＝∠CAM.∵AM＝AD，AD＝AC，∴AM＝AC.又∵AB＝AE，∠BAC＝∠EAM，∴△BAC≌△EAM，∴BC＝EM.∵F、A分别为DE、DM中点，∴AF为△DEM中位线，∴EM＝2AF，∴BC＝2AF.2. 解：(1)证明：∵∠BAC＋∠EAD＝180°，∠BAE＝90°，∴∠DAC＝90°，在△ABE与△ACD中，AE＝AD，∠BAE＝∠CAD＝90°，AB＝AC，∴△ABE≌△ACD(SAS)，∴CD＝BE，∵在Rt△ABE中，F为BE的中点，∴BE＝2AF，∴CD(2)成立，证明：如图，延长EA交BC于G，在AG上截取AH＝AD，∵∠BAC＋∠EAD＝180°，∴∠EAB＋∠DAC＝180°，∵∠EAB＋∠BAH＝180°，∴∠DAC＝∠BAH，在△ABH与△ACD中，AH＝AD，∠BAH＝∠CAD，AB＝AC，∴△ABH≌△ACD(SAS)，∴BH＝DC，∵AD＝AE，AH＝AD，∴AE＝AH，∵EF＝FB，∴BH＝2AF，∴CD＝2AF.3. 解：(1)证明：∵AB＝AC，∴∠ABD＝∠ACD，∵AE＝AD，∴∠ADE＝∠AED，∵∠BAD＋∠ABD＝∠ADE＋∠EDC，∠EDC∴∠BAD＝2∠EDC，∵∠ABF＝2∠EDC，∴∠BAD＝∠ABF，∴△ABF是等腰三角形；(2)方法一：如图①，延长CA至点H，使AG＝AH，连接BH，∵点N 是BG 的中点，∴AN ＝12BH ， ∵∠BAD ＝∠ABF，∠DAC ＝∠CBG，∴∠CAB ＝∠CBA，∴△ABC 是等边三角形．∴AB ＝BC ＝AC ，∠BAC ＝∠BCA＝60°，∵GM ＝AB ，AB ＝AC ，∴CM ＝AG ，∴AH ＝CM ，在△BAH 和△BCM 中，⎩⎪⎨⎪⎧AB ＝BC ，∠BAH ＝∠BCM＝120°，AH ＝CM ，∴△BAH ≌△BCM(SAS)，∴BH ＝BM ，∴AN ＝12BM ，方法二：如图②，延长AN 至K ，使NK ＝AN ，连接KB ，同方法一，先证△ABC 是等边三角形，再证△ANG ≌△KNB (SAS)，所以BK ＝AG ＝CM ，然后可以证得∠ABK ＝∠BCN ＝120°，最后证△ABK ≌△BCN (SAS)，所以BM ＝AK ＝2AN .类型5 角的和差倍分例5：解：(1)如图，过点P 作PG⊥EF 于G.∵PE ＝PF ＝6，EF ＝6 3，∴FG ＝EG ＝3 3，∠FPG ＝∠EPG＝12∠EPF. 在Rt △FPG 中，sin ∠FPG ＝FG PF ＝3 36＝32. ∴∠FPG ＝60°，∴∠EPF ＝2∠FPG＝120°.(2)如图，作PM ⊥AB 于M ，PN ⊥AD 于N .∵AC 为菱形ABCD 的对角线，∴∠DAC ＝∠BAC ，AM ＝AN ，PM ＝PN .在Rt △PME 和Rt △PNF 中，PM ＝PN ，PE ＝PF ∴Rt △PME ≌Rt △PNF ，∴NF ＝ME .又∵AP ＝10，∠PAM ＝12∠DAB ＝30°， ∴AM ＝AN ＝AP cos30°＝10×32＝5 3. ∴AE ＋AF ＝(AM ＋ME )＋(AN －NF )＝AM ＋AN ＝10 3.针对训练：1. 证明：如图，过D 作DE ⊥AB 于E ，过D 作DF ⊥AC 于F ，∵DA 平分∠BAC ，DE ⊥AB ，DF ⊥AC ，∴DE ＝DF ，∵∠B ＋∠ACD ＝180°，∠ACD ＋∠FCD ＝180°，∴∠B ＝∠FCD ，在△DFC 和△DEB 中，⎩⎪⎨⎪⎧∠F ＝∠DEB ，∠FCD ＝∠B ，DF ＝DB ，∴△DFC ≌△DEB ，∴DC ＝DB .2. 解：(1)∵AC＝AB ＝4，且CD ＝1，∴AD ＝AC －CD ＝3.在Rt △ABD 中，∠BAD ＝90°，∴BD ＝AB 2＋AD 2＝5，∵S △ABD ＝12AB·AD＝12AE·BD， ∴AE ＝.(2)证明：如图，取BC 的中点M ，连接AM 交BD 于点N .∵∠BAC ＝90°，AB ＝AC ，点M 为BC 的中点，∴AM ＝BM ＝CM ，AM ⊥BC ，∠NAD ＝∠FCP ＝45°，∴∠AMF ＝∠BMN ＝90°.∵AE ⊥BD ，∴∠MAF ＋∠ANE ＝∠MBN又∠ANE ＝∠BNM ，∴∠MAF ＝∠MBN ，∴△AMF ≌△BMN ，∴MF ＝MN ，∴AM －MN ＝CM －MF ，即AN ＝CF .∵AP ＝CD ，∴AC －CD ＝AC －AP ，即AD ＝CP .∴△ADN ≌△CPF ，∴∠ADB ＝∠CPF .3. 解：(1)∵AB ＝BD ，∠BAD ＝45°，∴∠BDA ＝45°，即∠ABD ＝90°.∵四边形ABCD 是平行四边形，∴当E 、C 重合时，BF ＝12BD ＝12AB .∵在Rt △ABF 中，AB 2＋BF 2＝AF 2，∴(2BF )2＋BF 2＝(5)2，∴BF ＝1，AB ＝2.在Rt △ABD 中，AD ＝AB 2＋BD 2＝2AB 2＝2 2.(2)证明：如图，在AF 上截取AK ＝HD ，连接BK.∵∠AFD ＝∠ABF＋∠2＝∠FGD＋∠3且∠ABF＝∠FGD＝90°，∴∠2＝∠3.在△ABK 与△DBH 中，错误!∴△ABK ≌△DBH ，∴BK ＝BH ，∠6＝∠5.∵四边形ABCD 是平行四边形，∴AD ∥BC ，∴∠5＝∠4＝45°，∴∠6∴∠7＝∠ABD－∠6＝45°＝∠5.在△BFK 中，⎩⎪⎨⎪⎧BK ＝BH ，∠7＝∠5，BF ＝BF ，∴△BFK ≌△BFH.∴∠BFK ＝∠BFH，即∠AFB＝∠HFB.4. 解：(1)证明：由折叠知∠EMN＝∠ABC＝90°，BE ＝EM ，∴∠EMB ＝∠EBM， ∴∠EMN －∠EMB＝∠ABC－∠EBM，即∠BMP＝∠MBC.∵在正方形ABCD 中，AD ∥BC ，∴∠AMB ＝∠MBC，∴∠AMB ＝∠BMP，∴BM 是∠AMP 的平分线．(2)△PDM 过B 作BQ ⊥MP 于Q .∵∠A ＝90°，且由(1)知BM 是∠AMP 的平分线，∴BA ＝BQ ，∵∠A ＝∠MQB ＝90°，∠AMB ＝∠BMP ，MB ＝MB ，∴△AMB≌△QMB(AAS)．∴MA＝MQ.∵BA＝BC，∴BQ＝BC，又∵∠BQP＝90°＝∠C，BP＝BP，∴Rt△BPC≌Rt△BPQ(HL)．∴PC＝PQ，∴△PDM的周长＝MD＋MP＋DP＝MD＋MQ＋QP＋PD＝MD＋MA＋PC＋PD＝AD＋DC＝2AD.∴△PDM的周长没有发生变化．类型6 旋转型全等问题：图中若有边相等，可用旋转做实验例6：解：(1)①∵四边形ADEF是正方形，∴AD＝AF，AB＝AC，∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，∴△DAB≌△FAC，∴∠B＝∠ACF，∴∠ACB＋∠ACF＝90°，即CF⊥BC；②∵△DAB≌△FAC，∴CF＝BD，∵BC＝BD＋CD，∴BC＝CF＋CD.(2)结论①成立，结论②不成立．∵四边形ADEF是正方形，∴AD＝AF，AB＝AC.∵∠BAC＝∠DAF＝90°，∴∠BAD＝∠CAF，∴△DAB≌△FAC，∴∠ABD＝∠ACF，CF＝BD，∴∠BCF＝∠ACF－∠ACB＝∠ABD－∠ACB＝90°，即CF⊥BC；∵BC＝CD－BD，∴BC＝CD－CF.(3)如图，过A作AH⊥BC于H，过E作EM⊥BD于N ，∵∠BAC ＝90°，AB ＝AC ，∴BC ＝2AB ＝4，AH ＝CH ＝12BC ＝2， ∴CD ＝14BC ＝1，∴DH ＝3，同(2)证得△BAD ≌△CAF ， ∴∠ABD ＝∠ACF ＝45°，∴∠BCF ＝∠ACB ＋∠ACF ＝90°， ∴BC ⊥CF ，CF ＝BD ＝5.∵四边形ADEF 是正方形，∴AD ＝DE ，∠ADE ＝90°，∵BC ⊥CF ，EM ⊥BD ，EN ⊥CF ，∴四边形CMEN 是矩形，∴NE ＝CM ，EM ＝CN ，∵∠AHD ＝∠ADE ＝∠EMD ＝90°，∴∠ADH ＋∠EDM ＝∠EDM ＋∠DEM ＝90°，∴∠ADH ＝∠DEM ，∴△ADH ≌△DEM ，∴EM ＝DH ＝3，DM ＝AH ＝2，∴CN ＝EM ＝3，EN ＝CM ＝3，∵∠ABC ＝45°，∴∠BGC ＝45°，∴△BCG 是等腰直角三角形， ∴CG ＝BC ＝4，∴GN ＝1，∴EG ＝GN 2＋EN 2＝10.针对训练：1. 解：(1)AC ＝AD ＋AB .证明如下：∵∠B ＋∠D ＝180°，∠B ＝90°，∴∠D ＝90°.∵∠DAB ＝120°，AC 平分∠DAB ，∴∠DAC ＝∠BAC ＝60°，∵∠B ＝90°，∴AB ＝12AC ，同理AD ＝12AC . ∴AC ＝AD ＋AB .(2)(1)中的结论成立，理由如下：如图①，以C 为顶点，AC 为一边作∠ACE＝60°， ∠ACE 的另一边交AB 的延长线于点E ，∵∠BAC ＝60°，∴△AEC 为等边三角形， ∴AC ＝AE ＝CE ，∠E ＝60°，∵∠ABC ＋∠D＝180°，∠DAB ＝120°，∴∠DCB ＝60°，∴∠DCA ＝∠ECB.在△DAC 和△BEC 中，⎩⎪⎨⎪⎧∠DAC＝∠E，AC ＝CE ，∠DCA ＝∠BCE，∴△DAC ≌△BEC ，∴AD ＝BE ，∴AC ＝AE ＝AD ＋AB.(3)AD ＋AB ＝2AC.理由如下：如图②，过点C 作CE⊥AC 交AB 的延线于点E ，∵∠ABC ＋∠D＝180°，∠DAB ＝90°，∴∠DCB ＝90°，∵∠ACE ＝90°，∴∠DCA ＝∠BCE，。

2018届重庆中考复习：重庆中考几何题分类汇编(含答案)