直线圆弧插补程序
G02 G03圆弧插补指令编程

圆弧终点坐标
确定圆心位置 进给速度
绝对值 X、Z 增量值 U、W 混合编程 X、W
α≤180° 用+R 360°>α>180° 用-R
车床刀架前后置,圆弧顺逆不相同 刀架后置为标准,前置顺逆方向反
教学重点
圆弧顺、逆的判断和圆心位置R正负的确定。
教学难点
圆弧顺逆的判断。
主目录
能力训练题:
YHCNC实 习 卡 片
N78 G01X21
(切断工件 )
N80 G00X100
(X轴方向退刀)
N82 Z120 M09 (回换刀点,切削液关 )
N84 M30
(程序结束,返回第一条程序段 )
四、典型零件加工演示
(用YHCNC仿真软件)
课堂小结
G02(G03)X(U)——Z(W)—— R—— F——
圆弧顺、逆
刀架后置 刀架前置
N62 T0404
(换切断刀)
N64 G00X82S400M03(点定位到φ82,正转,400r/min )
N66 Z-44
(快速点定位到离端面44处)
N68 G01X75F200 (切槽 )
N70 G00X82
(退刀到φ82 )
N72 W2
(增量移动2mm )
N74 G01X80F200 (进刀到φ80 ) N76 G?03X76W-2R2 (车R2圆弧 )
模块 学习单元
FANUC-0i数控车
G02、G03圆弧插补 指令编程
考核项目 考 核 标 准 配 分 得 分 总 分
编程考核 任错一处扣5分 70
设 YHCNC 学时
软件操作考核 任错一处扣10分 30
备 仿真软件 件数 1 记 事
g代码编程实例

g代码编程实例本文将介绍几个g代码编程实例,包括基础的线性插补程序、圆弧插补程序、螺旋线插补程序以及基于变量的程序设计。
读者可以通过这些实例更深入地了解 g 代码编程的基本原理和应用技巧。
1. 线性插补程序线性插补是 g 代码编程中最基础的插补方式之一,它可以实现简单的直线运动。
下面是一个简单的线性插补程序示例:G01 X10 Y10 F100该程序的意思是,从当前位置开始,以每分钟 100 毫米的速度沿着 X 轴和 Y 轴移动 10 毫米的距离。
在实际应用中,我们可以根据需要调整速度和距离,实现不同的线性运动。
2. 圆弧插补程序圆弧插补是 g 代码编程中常用的一种插补方式,它可以实现圆弧运动。
下面是一个简单的圆弧插补程序示例:G02 X50 Y50 I20 J20 F200该程序的意思是,从当前位置开始,以每分钟 200 毫米的速度沿着圆弧运动,半径为 20 毫米,起点坐标为当前位置,在以 X 轴正方向为基准线向右移动 50 毫米,以 Y 轴正方向为基准线向上移动 50 毫米的位置。
在实际应用中,我们可以根据需要调整半径、起点坐标和运动方向,实现不同的圆弧运动。
3. 螺旋线插补程序螺旋线插补是 g 代码编程中比较复杂的一种插补方式,它可以实现螺旋线运动。
下面是一个简单的螺旋线插补程序示例:G17 G03 X50 Y50 Z0 I5 J5 R10 F100该程序的意思是,以 XY 平面为基准面,从当前位置开始,以每分钟 100 毫米的速度沿着螺旋线运动,半径从 10 毫米开始,每转一圈增加 5 毫米,Z 轴方向不变。
在实际应用中,我们可以根据需要调整起点坐标、半径增量和运动方向,实现不同的螺旋线运动。
4. 基于变量的程序设计除了上述基础的插补程序外, g 代码编程还支持基于变量的程序设计,可以实现更加灵活多样的运动方式。
下面是一个基于变量的程序设计示例:#1=10 #2=20G01 X#1 Y#2 F100该程序的意思是,在程序开始前定义两个变量 #1 和 #2,分别赋值为 10 和 20。
欧姆龙NJ直线插补及圆弧插补
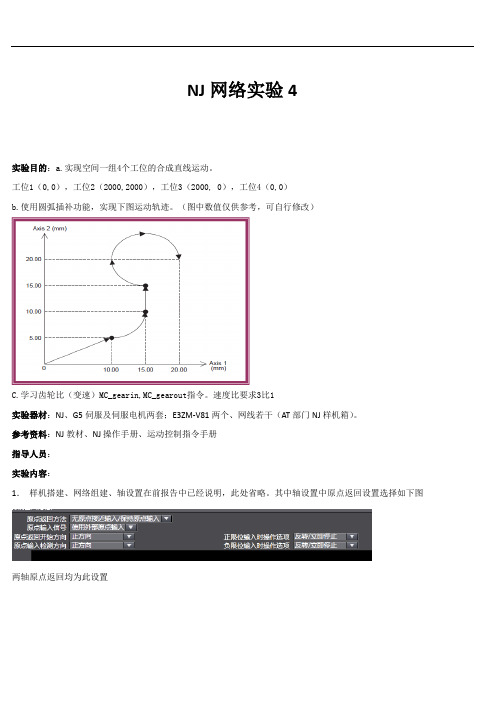
NJ网络实验4实验目的:a.实现空间一组4个工位的合成直线运动。
工位1(0,0),工位2(2000,2000),工位3(2000, 0),工位4(0,0)b.使用圆弧插补功能,实现下图运动轨迹。
(图中数值仅供参考,可自行修改)C.学习齿轮比(变速)MC_gearin,MC_gearout指令。
速度比要求3比1实验器材:NJ、G5伺服及伺服电机两套;E3ZM-V81两个、网线若干(AT部门NJ样机箱)。
参考资料:NJ教材、NJ操作手册、运动控制指令手册指导人员:实验内容:1.样机搭建、网络组建、轴设置在前报告中已经说明,此处省略。
其中轴设置中原点返回设置选择如下图两轴原点返回均为此设置2.建立轴组:轴设置完毕后,在“配置和设置”中右键点击轴组设置,在下拉菜单中左键点击添加轴组设置,如下图添加后,左键双击MC_Group000;在轴组基本设置中“轴组使用”选择“使用轴组”如下图:构成选择“2轴”分别将“轴A0”分配MC_Axis000(0);“轴A1”分配MC_Axis001(1)如下图点击左侧“轴组操作设置”在下图中设置最大插补速度及加速度等,轴设置完毕3.编写程序A、准备程序程序本次程序依然需要MC_POWER及MC_HOME指令由于与上次程序相同这里不多介绍,程序如下图:原点返回指令“MC_GroupEnable”轴组使能指令,以下为手册截图由于直线插补指令属于轴组指令,如想进行直线插补首先要进行轴组使能指令,否则无法使用对应指令。
将上一步设置好的MC_Group000使能,程序如下指令“MC_GroupDisable”使能解除指令与MC_GroupEnable对应指令,被轴组使能后被使能轴只能使用轴组指令,而不能使用轴指令,例如MC_Move等指令,所以程序中需要编写MC_GroupEnable程序程序如下B、实验程序实验a、实现空间一组4个工位的合成直线运动。
工位1(0,0),工位2(2000,2000),工位3(2000, 0),工位4(0,0)需要用到“MC_MoveLinear”进行直线插补,程序编写如下其中P1、P2、P3、P4分别赋值1、(0,0),2、(2000,2000),3、(2000, 0),4、(0,0),v:=500如下图实验a、完成。
数控机床逐点比较法圆弧插补
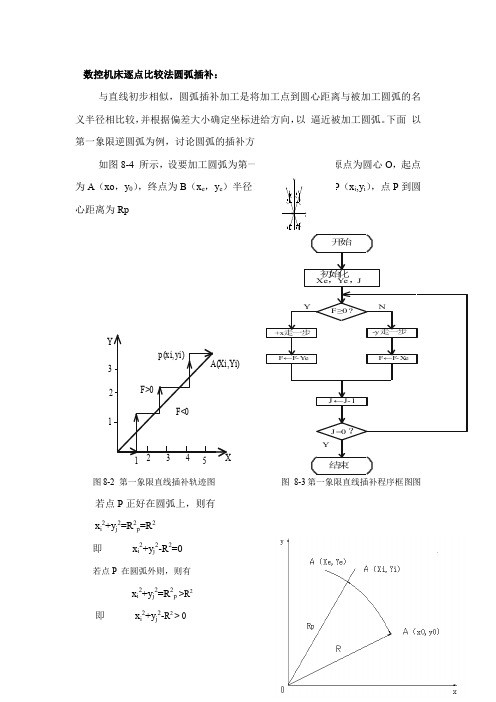
第一象限逆圆弧为例,讨论圆弧的插补方法。
如图8-4 所示,设要加工圆弧为第一象限逆圆弧AB ,原点为圆心O ,起点为A (xo ,y 0),终点为B (x e ,y e )半径R ,瞬时加工点为P (x i ,y i ),点P 到圆心距离为Rp<0+△y>0-△x <0+△x <0+△y>0-△x<0-△y <0-△y>0+△x yx图8-2 第一象限直线插补轨迹图 图 8-3第一象限直线插补程序框图图12345X123YF>0p(xi,yi)A(Xi,Yi)F<0开始初始化Xe ,Y e ,JF≥0?+x 走一步F←F -Y e F←F -X e-y 走一步YNJ ←J-1J =0?Y结束若点P 在圆弧内则,则有x i2+y j2=R2p<R2即x i2+y j2-R2 < 0显然,若令F i,j= x i2+y j2-R2(8-4)图8-4 逆圆弧插补则有:(1)F i,j= F i,j=0, 则点P在圆弧上(2)F i,j >0则点P在圆弧外则(3)F i,j<0则点P在圆弧不则常将8-4称为圆弧插补偏差判别式。
当F i,j≥时,为逼近圆弧,应向-x方向进给一步;当F i,j<0时,应向+y 方向走一步。
这样就可以获得逼近圆弧的折线图。
与直线插补偏差计算相似,圆弧插补的偏差的计算也采用递推的方法以简化计算。
若加工点P(x i,y i)在圆弧外或者圆弧上,则有:F i,j=x i2+y j2-R2≥0 为逼近该圆沿-x方向进给一步,移动到新加工点P(x i=1,y i),此时新加工点的坐标值为x i+1=x i-1,y i=y i新加工点的偏差为:F i+1,j=(x i-1)2+y i2-R2=x i2-2x i+1+ y i2-R2= x i2+ y i2-R2+1即F i+1,j= F i,j-2x i+1 (8-5)若加工P(x i,y i)在圆弧内,则有F i,j=x i2+y j2-R2<0若逼近该圆需沿+y方向进给一步,移到新加工点P(x i,y i),此时新加工点的坐标值图8-5 第一象限圆弧插补程序框图为新加工点的偏为:F i,j+1=x i2+(y i+1)2-R2=x i2+ y i2+1 -R2= x i2+ y i2-R2+1+2y iF i,j+1= F i,j-2y i+1 (8-6)从(8-5)和式(8-6)两式可知,递推偏差计算仅为加法(或者减法)运算,大大降低了计算的复杂程度。
(二)逐点比较法圆弧插补PPT课件

同理,对于第一象限顺圆加工时,即B→A,当Fi≥0时, 应向-Y方向进给一步,当Fi<0时,应向+X方向进给 一步。
Y
B(Xe,Ye)
Pi(Xi,Yi)
A(Xo,Yo)
O
X
6
当Fi≥0时,向-Y方向进给一步,动点由Pi(Xi,Yi) 移动到 Pi+1(Xi,Yi +1),则新动点的坐标为 Yi+1=Yi -1
偏差计算
终点判别
0
F0=0,Xo=5,Yo=0 ∑=10
1 F0=0 -X F1=F0-2Xo+1= -9,X1=4,Y1=0∑=9
2 F1=-9 +Y F2=F1+2Y1+1= -8,X2=4,Y2=∑1=8
3 F2=-8 +Y F3=F2+2Y2+1= -5,X3=4,Y3=∑2=7
4 F3= -5 +Y F4=F3 +2Y3+1 =0, X4=4,Y4=3∑=6
2 F1=-5 +Y F2=F1+2Y1+1= -4,X2=2,Y2=∑1=4
3 F2=-4 +Y 4 F3= -1 +Y 5 F4=4 -X
F3=F2+2Y2+1= -1,X3=2,Y3=∑2=3 F4=F3 +2Y3+1 =4, X4=2,Y4=3∑=2 F5=F4-2X4+1 =1, X5=1,Y5=3∑=1
Y
Fi<0
Fi≥0
Fi≥0 Fi<0
Fi<0
O Fi≥0
X
Fi<0 Fi≥0
17
2、圆弧插补的象限处理
前面的圆弧插补(顺圆、逆圆)只限于第一象限,其他 情况如图所示: Y
数控系统中直线与圆弧插补算法的探讨

数控系统中直线与圆弧插补算法的探讨导言数控系统是一种广泛应用于机械加工领域的自动化控制系统。
其中,直线与圆弧插补算法是数控系统中的核心算法之一。
本文将深入探讨直线与圆弧插补算法的原理、方法以及应用。
直线插补算法直线插补是数控系统中最基本的插补运动方式之一。
它的目标是实现两个给定点之间的直线路径。
在直线插补算法中,我们需要考虑以下几个方面:1.起始点和终点的坐标:为了实现直线插补,我们需要明确起始点和终点的空间坐标。
2.运动速度和加速度:直线插补需要考虑加速度和速度的变化,以实现平滑而又快速的运动。
3.插补精度:直线插补的精度决定了运动轨迹的平滑度和误差控制的能力。
直线插补算法的基本思路是将插补路径划分为多个小段,然后通过控制每个小段的加速度和速度,以达到平滑运动的效果。
常用的直线插补算法包括线性插补算法和B样条插补算法。
线性插补算法线性插补算法是最简单和最基础的直线插补算法之一。
它假设插补路径是一条直线,并根据起始点和终点的坐标以及插补周期,计算出每个插补周期点的位置。
线性插补算法的优点是计算简单,实现容易,但缺点是对于曲线路径的插补效果较差。
B样条插补算法B样条插补算法是一种基于样条曲线的插补算法。
在B样条插补算法中,我们将插补路径表示为一条样条曲线,并通过控制样条曲线的控制点来实现运动轨迹的控制。
B样条插补算法的优点是对曲线路径的插补效果较好,但是计算复杂度较高。
圆弧插补算法除了直线插补,圆弧插补算法也是数控系统中常用的插补方式之一。
圆弧插补用于实现两个给定点之间的圆弧路径。
与直线插补类似,圆弧插补算法也需要考虑起始点和终点的坐标、运动速度和加速度等因素。
圆弧插补算法的基本思路是通过指定起始点、终点和圆心,计算出圆弧路径上每个插补点的位置。
常用的圆弧插补算法包括圆心法和半径法。
圆心法圆心法是一种基于圆心坐标的圆弧插补算法。
在圆心法中,我们通过指定起始点、终点和圆心的坐标,计算出圆弧路径上每个插补点的位置。
直线插补流程图
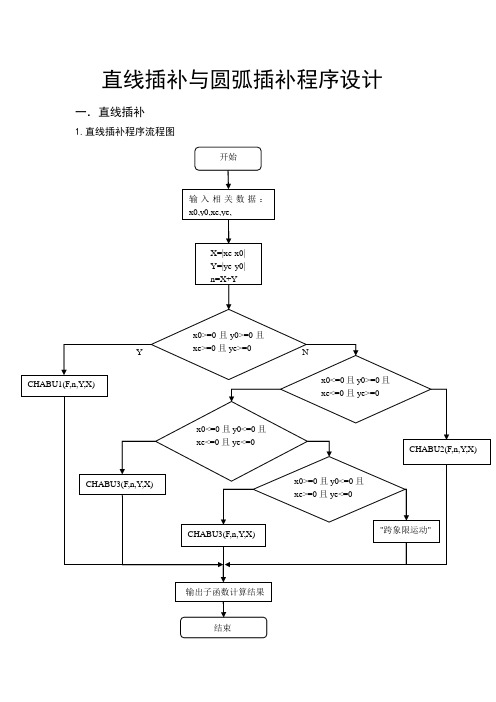
直线插补与圆弧插补程序设计一.直线插补1.直线插补程序流程图直线插补程序设计:#include"stdio.h"#include"math.h"void CHABU1 (int F,int n,int Y,int X) /*第一象限调用函数*/{int nx=0,ny=0;for(;n>0; n--){printf("运算前:F=%d ",F);i f(F>=0){printf("需走步数:n=%d\n",n);printf("------向+xe方向走一步 ");F=F-Y;printf("F=%d",F);printf("+X\n");nx++; /*X方向走的总步数*/}e lse{printf("需走步数:n=%d\n",n);printf("------向+ye方向走一步 ");F=F+X;printf("F=%d",F);printf("+Y\n");ny++; /*y方向走的总步数*/}}printf("nx=%d,ny=%d\n",nx,ny);void CHABU2(int F,int n,int Y,int X) /*第二象限调用函数*/{int nx=0,ny=0;for(;n>0; n--){printf("运算前:F=%d ",F);if(F>=0){printf("需走步数:n=%d\n",n);printf("------向-xe方向走一步 ");F=F-Y;printf("F=%d ",F);printf("-X\n");nx++; /*X方向走的总步数*/}else{printf("需走步数:n=%d\n",n);printf("------向+ye方向走一步 ");F=F+X;printf("F=%d ",F);printf("+Y\n");ny++; /*y方向走的总步数*/}}printf("nx=%d,ny=%d\n",nx,ny);}void CHABU3(int F,int n,int Y,int X) /*第三象限调用函数*/{int nx=0,ny=0;for(;n>0; n--){printf("运算前:F=%d ",F);if(F>=0){printf("需走步数:n=%d\n",n);printf("------向-xe方向走一步 ");F=F-Y;printf("F=%d ",F);printf("-X\n");nx++; /*X方向走的总步数*/}else{printf("需走步数:n=%d\n",n);printf("------向-ye方向走一步 ");F=F+X;printf("F=%d ",F);printf("-Y\n");ny++; /*y方向走的总步数*/}}printf("nx=%d,ny=%d\n",nx,ny);}void CHABU4(int F,int n,int Y,int X) /*第四象限调用函数*/{int nx=0,ny=0;for(;n>0; n--){printf("运算前:F=%d ",F);if(F>=0){printf("需走步数:n=%d\n",n);printf("------向+xe方向走一步 ");F=F-Y;printf("F=%d ",F);printf("+X\n");nx++; /*X方向走的总步数*/}else{printf("需走步数:n=%d\n",n);printf("------向-ye方向走一步 ");F=F+X;printf("F=%d ",F);printf("-Y\n");ny++; /*y方向走的总步数*/}}printf("nx=%d,ny=%d\n",nx,ny);}main(){int F=0,X=0,Y=0,n,xe,ye,x0,y0,ny,nx;void CHABU1 (int,int,int,int);/*函数声明*/void CHABU2(int,int,int,int);void CHABU3(int,int,int,int);void CHABU4(int,int,int,int);/*函数声明*/printf("输入相关数据\n");printf("x0=");scanf("%d",&x0);printf("xe=");scanf("%d",&xe);printf("y0=");scanf("%d",&y0);printf("ye=");scanf("%d",&ye);X=abs(xe-x0); /*取绝对值*/Y=abs(ye-y0); /*取绝对值*//*printf("X=%d\n",X);验证绝对值函数*/n=X+Y;printf("n=%d\n",n); /*总步数*/printf("运动结果如下:\n");if(x0>=0&&y0>=0&&xe>=0&&ye>=0) { printf("第一象限\n");CHABU1(F,n,Y,X);}else if(x0<=0&&y0>=0&&xe<=0&&ye>=0) { printf("第二象限\n");CHABU2(F,n,Y,X);}else if(x0<=0&&y0<=0&&xe<=0&&ye<=0) { printf("第三象限\n");CHABU3(F,n,Y,X);}else if(x0>=0&&y0<=0&&xe>=0&&ye<=0) { printf("第四象限\n");CHABU4(F,n,Y,X);}else printf("跨象限运动");}。
数控车床直线插补G01圆弧插补G02G03技术材料

技术课件
上一页 下一页
16 返回
* 1.用圆心半径R指定圆心位置,其指令格式为:
G02/G03 X(U) Z(W) R F; 2.用圆心坐标(I,K)指定圆心位置,其指令格式为:
G02/G03 X(U) Z(W) I K F;
参数含义:
R——圆弧半径。
I、K——圆心相对于圆弧起点的增量坐标,I为
半径增量(即X方向增量),K为Z方向增量。
技术课件
上一页 下一页
23 返回
参考程序
O....; G00 X80 Z80 ; M03 S1000 T0100;
G00 X20 Z3 ; G01 Z0 F80; X24 Z-2 ; Z-12; G03 X40 W-8 R8; G01 Z-70;
G00 X80 Z80 ; M05 T0202; S500 M03;
技术课件
上一页 下一页
1 返回
1 2 3
技术课件
上一页 下一页
2 返回
指令格式:G01 X(U) Z(W) F;
参数含义:
X、Z—— 绝对编程时的目标点坐标,单位为mm。
U、W——相对编程时的目标点坐标,单位为mm。
F——切削进给速度,单位为mm/min或mm/r。
上一页
下一页
技术课件
3 返回
G01用于刀具直线插补运动。它是通过程序段中的信息,使机床各坐标 轴上产生与其移动距离成比例的速度。其运动轨迹如下:G01指令的运动轨 迹按切削进给速度运行,以一定的的切削进给速度,刀具意使用。
2.本例题采用绝对坐标编程。
技术课件
A
上一页 下一页
8 返回
技术课件
上一页 下一页
9 返回
3.5.2 直线和圆弧DDA法插补原理

JY-1 JY 5
5 5 5 5-1=4 4-1=3 3-1=2 2-1=1
终点判 别 NX NY
+Y +Y +Y -X,+Y 10-8=2 -X,+Y 10-8=2 -X -X 12-8=4 9-8=1
10-8=2 12-8=4 9-8=1 11-8=3 11-8=3
2012-5-30
数字积分法直线插补运算过程(前五步)
累加 次数 X积分器 Y积分器 终点计 数 器 JE 000
JRX+JVX
1 0+101=101
溢出 △X 0 1
0 1 1
JRY+JVY
0+010=010
溢 出 △Y 0 0
0 1 0
2
3 4 5
101+101=010
010+101=111 111+101=100 100+101=001
一 插补的基本概念; 二 插补方法的分类; 三 逐点比较法; 四 数字积分法; 五 数据采样法(时间分割法); 六 插补算法中的速度处理。
2012-5-30
四 数字积分法插补
特点:
易于实现多坐标联动插补 Y 1 数字积分法的工作原理 如右图,函数在[t0 , tn ]的定 积分,即为函数在该区间 的面积: O t0 t1 t2 如果从t=0开始,取自变量 t的一系列等间隔值为△t, 当△t足够小时,可得
2 设圆弧AB为第一象限逆圆弧,起点A (3,0),终点为B(0,3),用DDA法加工圆弧 AB。
2012-5-30
逐点比较法第一象限直线圆弧插补

逐点比较法第一象限直线,圆弧插补编程逐点比较法是以折线来逼近给定的轨迹,就是每走一步控制系统都要将加工点与给定的图形轨迹相比较,以决定下一步进给的方向,使之逼近加工轨迹。
逐点比较法以折线来逼近直线或圆弧,其最大的偏差不超过一个最小设定单位。
只要将脉冲当量取得足够小,就可以达到精度要求。
逐点比较插补法在脉冲当量为0.01mm,系统进给速度小于3000mm/min时,能很好的满足要求。
一、逐点比较法直线插补如下图所示设直线 oA 为第一象限的直线,起点为坐标原点o (0 , 0) ,终点坐标为, A( ) , P() 为加工点。
若 P 点正好处在直线 oA 上,由相似三角形关系则有即点在直线 oA 上方 ( 严格为直线 oA 与 y 轴正向所包围的区域 ) ,则有即若 P 点在直线 oA 下方 ( 严格为直线 oA 与 x 轴正向所包围的区域 ) ,则有图 3 — 1 逐点比较法第一象限直线插补即令则有:①如,则点 P 在直线 oA 上,既可向 +x 方向进给一步,也可向 +y 方向进给一步;②如,则点 P 在直线 oA 上方,应向 +x 方向进给一步,以逼近oA 直线;③如,则点 P 在直线 oA 下方,应向 +y 方向进给一步,以逼近 oA 直线一般将及视为一类情况,即时,都向 +x 方向进给一步。
当两方向所走的步数与终点坐标相等时,停止插补。
这即逐点比较法直线插补的原理。
对第一象限直线 oA 从起点 ( 即坐标原点 ) 出发,当 F 时, +x 向走一步;当 F<0 时,y 向走一步。
特点:每一步都需计算偏差,这样的计算比较麻烦。
递推的方法计算偏差:每走一步后新的加工点的偏差用前一点的加工偏差递推出来。
采用递推方法,必须知道开始加工点的偏差,而开始加工点正是直线的起点,故。
下面推导其递推公式。
设在加工点 P( ) 处,,则应沿 +x 方向进给一步,此时新加工点的坐标值为新加工点的偏差为即若在加工点 P( ) 处,,则应沿 +y 方向进给一步,此时新加工点的坐标值为,新加工点的偏差为即综上所述,逐点比较法直线插补每走一步都要完成四个步骤 ( 节拍 ) ,即:(1) 位置判别根据偏差值大于零、等于零、小于零确定当前加工点的位置。
数控车床 直线插补G01 圆弧插补G02,G03

精车A--J点的轮廓
快速返回刀具起点 主轴停止,换2号切断刀,刀宽为3 mm 主轴正转,转速500r/min
G00 X45 Z-33; G01 X40 F50; G02 X20 W-10 R10; G01 Z-60; X40;
精车K—I的轮廓
上一页
下一页
返回
参考程序 G00 X80 Z80; T0100 M05; M30;
注释 快速返回刀具起点 主轴停止,换回基准刀 程序结束
1. 由于T0100偏刀加工F-H的轮廓时刀具与工件有干涉,所以采用T0202切 槽刀来加工。 2.本程序G02/G03的程序段采用混合坐标编程。 3.刀具精加工时应根据刀具的性能采用不同的转速。 4. 本例切槽刀对刀时以左刀位点为基准,在定位加工时,应考虑刀宽与定 位点的位置。
程序名 快速定位至安全换刀点(刀具起点) 使用1号基准刀,主轴正转,转速600r/min 靠近工件
快速返回刀具起点 主轴停止 程序结束
上一页
下一页
返回
下一页 上一页
返回
如图所示,工件已粗加工完毕,各位置留有余量 0.2mm,要求重新编写精加工程序,不切断。
参考程序
注释
O....; G00 X100 Z100; M03 S800 T0101; G00 X20 Z2; G01 Z0 F60; X26 Z-3 ; Z-48; X60 Z-58 ; X80 W-73 ; G00 X100 Z100; M05 T0100; M30;
程序名 快速定位至安全换刀点(刀具起点) 使用1号基准刀,主轴正转,转速800r/min 靠近工件 快速定位到A点 加工到B点(顺圆弧加工) 加工到C点 加工到D点(逆圆弧加工) 加工到E点(顺圆弧加工) 加工到F点 快速返回刀具起点 主轴停止 程序结束
数控原理直线插补课程设计

太原工业学院课程设计任务书系部:机械工程系专业:机械设计制造及其自动化学生姓名:学号:设计题目:数控插补程序设计–第×象项直线(圆弧)插补起迄日期:设计地点:指导教师:发任务书日期: 年月日一.实验名称:直线插补(第一象限)二.实验要求:1.了解数控插补的原理;掌握第××象项直线(圆弧)插补算法2.设计流程图,并根据流程图编制程序,学会用软件方法实现插补运算。
3.学会调试程序三.实验内容:算法设计:上图为第一象限直线,其终点坐标为(Xe,Ye),现分析其插补规律。
刀尖点位置不外乎3种情况:轮廓线上方(点A),轮廓线上(B点),轮廓线下方(点C)。
显然,在点A处,为使刀尖点向轮廓直线靠拢,应+X向走一步;C点处,应+Y向走一步;至于B点,看来两个方向均可以,但考虑汇编编程时的方便,现规定往+X向走一步。
A(X,Y)点处有:Y/X e XeY-XYe > 0e XeY-XYe = 0C(X,Y)点处有:Y/X< e XeY-XYe < 0F=XeY-XYe为原始的偏差计算公式(X,Y为当前插补点动态坐标),F称为偏差,每走一步到达新位置点,就要计算相应这个F值。
显然,F≥0时,须+X向走一步;F<0时,须+Y向走一步。
为方便汇编编程和提高计算速度,现对偏差F的计算公式加以简化:插补点位于A、B点时,走完下一步(+X):动态坐标变为(X=X+1,Y=Y),新偏差变为F=XeY-(X+1)Ye=XeY-XYe-Ye=F-Ye。
这个公式比F=XeY-XYe计算要方便。
插补点位于C点时,走完下一步(+Y):动态坐标变为(X=X,Y=Y+1),新偏差变为F=Xe(Y+1)-XYe=XeY-XYe+Xe=F+Xe。
因此,走完+X后:偏差计算公式为F=F-Ye;走完+Y后:偏差计算公式为F=F+Xe。
●程序流程图:●源程序设计:#include <stdio.h>#include <math.h>void main(){int x=0,y=0; /*x,y分别为运行过程中各点的横纵坐标值*/int f=0; /*f存偏差判别的值*/int n,i,j,t; /*n为终点横纵坐标绝对值之和,i,j分别为终点横纵坐标*/printf("请输入终点坐标:");scanf("%d,%d",&i,&j);n=abs(i)+abs(j);if(i>=0) /*终点的横坐标大于0,说明在一或四象限中*/{if(j>=0){ /*纵坐标大于0,说明终点在第一象限*/for(t=1;t<=n;t++){if(f>=0){x=x+1;f=f-j;printf("x=%d,y=%d\n",x,y);}else{y=y+1;f=f+i;printf("x=%d,y=%d\n",x,y);}}}}}程序编译与调试:编译环境为TurboC2.0,一次编译通过。
数控车床 圆弧插补指令 G02 G03PPT幻灯片

1、G41、G42、G40指令不能与G02、G03写在一个程序段内,但可与G01、G00指令写 在同一程序段内,即它是通过直线运动来建立或取消刀具补偿的。
2、为了安全,通常采用G01运动方式建立或取消刀补。 3、在G41或G42程序段后加G40程序段,便可取消刀尖半径补偿,其格式为:
G41(或G42)……; …………; G40……; 程序的最后必须以取消偏置状态结束,否则刀具不能在终点定位且为下次程序 中出现G41(G42)时可能带来错误。 4、在G41方式中,不要再指定G42指令,同样在G42方式中,不要再指定G41指令。当 补偿取负值(R为负)时,G41和G42互相转化。 5、在使用G41和G42之后的程序段中,不能出现连续两个或两个以上的不移动指令, 否则G41和G42会失效。 6、G41、G42、G40是模态指令代码。
1、由于图样上给定的几个尺寸公差数值较小,因 此在编程时不必取平均值进行编程,全部取基本尺 寸即可。但是在加工时必须用其它手段来保证尺寸 精度。
2、毛坯选用:φ45×120mm棒料。
二、确定装夹方案
采用三爪自定心 卡盘装夹(一 次装夹完成粗、 精加工)
伸出加工长度80mm
18
三、确定加工顺序及进给路线
五、切削用量的选用
1、背吃刀量的选用:粗车外圆轮廓ap=1mm; 精车外圆轮廓ap=0.5mm。
2、主轴转速的选用:粗车外圆及端面n=800r/min; 精车外圆n=1400r/min; 切断n=350r/min。
3、进给速度的选用:端面F=0.1 mm/r; 粗车外圆F=0.2mm/r; 精车外圆F=0.1mm/r ; 切断F=0.05mm/r 。
21
六、数控加工工艺卡
产品名称
直线、圆弧插补指令编程

说 明
① 用绝对值编程时,圆弧终点坐标为圆弧终点在工件坐标系中的坐标值,用X、Z 表 示。当用增量值编程时,圆弧终点坐标为圆弧终点相对于圆弧起点的增量值,用U、W表示。 ② 圆心坐标(I, K)为圆弧起点到圆弧中心点所作矢量分别在X、Z坐标轴方向上分矢 量(矢量方向指向圆心)。本系统I、K为增量值,并带有“±”号,当矢量的方向与坐标轴 的方向不一致时取“−”号。 ③ R为圆弧半径,不与I、K同时使用。当用半径R指定圆心位置时,由于在同一半径R 的情况下,从圆弧的起点到终点有两个圆弧的可能性,为区别两者,规定圆心角α ≦180° 时,用“+R”表示,α ≧180°时,用“−R”表示。用半径R指定圆心位置时,不能描述整圆。
图5-1 G00定位轨迹图
5-2 绝对、相对、混合编程实例
表5-1 绝对、相对、混合编程方法表 绝对编程(G90) 相对编程 混合编程 G00 G00 G00 G00 X70 U40 U40 X70 Z40
W−60
Z40
W−60
直线插补
G01直线插补 直线插补
G01代码用于刀具直线插补运动。功能:G01指令使刀具以一定的进给速度,从所在点出 发,直线移动到目标点。 指令格式:G01 X(U)_ Z(W)_ F 式中:X、Z:为绝对编程时目标点在工件坐标系中的坐标; U、W:为增量编程时目标点 坐标的增量;F:进给速度。
图5-7 倒角指令示意图
顺/逆时针圆弧插补
圆弧顺、 圆弧顺、逆的判断
圆弧插补的顺、逆可按如图5-9所示的方向判断 (点击箭头进入 )
G02/G03指令编程格式 指令编程格式
① 用I、K指定圆心位置: 指令格式:G02/G03 X(U)Z(W) I K F ② 用圆弧半径R指定圆心位置: 指令格式:G02/G03 X(U)Z(W) R F
3,4---第二章 数控机床的插补原理――直线插补与圆弧插补计算原理
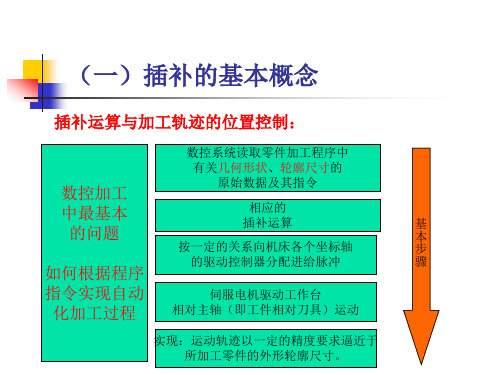
直线上
=
YmXe―XmYe=0
直线上方
>
YmXe―XmYe>0
直线下方
<
YmXe―XmYe<0
{ 偏差判别函数:Fm = ymxe-xmye
= 0 在直线上; >0在直线上方
< 0 在直线下方
(五)逐点比较法直线插补
2. 算法分析(第Ⅰ象限)
坐标进给:
根据判定的进给方向,向该坐标 方向发一进给脉冲
特点:以折线逼近直线、圆弧或各类曲线。
精度高:最大偏差不超过一个脉冲当量。
(四)逐点比较法
插补开始 方向判定
逐点比较法 工作循环过程
坐标进给
偏差计算
终点到?
N
插补结束
Y
(五)逐点比较法直线插补
y A(xe,ye)
o
x
每次插补计算输出一个脉冲,不是进给到X轴 方向,就是进给到Y轴方向,不可能两个坐标轴都进给
数据采样插补:(又称为时间标量插补或数字增量插 补,8ms,10.24ms)数控装置产生的不是单个脉冲,而 是采样周期内,各坐标的位移量
①直线函数法;②扩展数字积分法;③二阶递归扩展数字积分插 补法;④双数字积分插补法;⑤角度逼近圆弧插补法。
(四)逐点比较法
思想:“走一步看一步”:就是每走一步都要和给定 轨迹上的坐标值进行一次比较,视该点在给定轨迹 的上方或下方,或者给定轨迹的里面或者外面,从 而决定下一步的进给方向,使之趋近加工轨迹。
(五)逐点比较法直线插补
1.基本原理:
在刀具按要求轨迹运动加工零件轮廓的过程中, 不断比较刀具与被加工零件轮廓之间的相对位置,并 根据比较结果决定下一步的进给方向,使刀具向减小 误差的方向进给。其算法最大偏差不会超过一个脉冲 当量δ。
直线、圆弧插补

插补是在组成轨迹的直线段或曲线段的起点和终点之间,按一定的算法进行数据点的密化工作,以确定一些中间点。
从而为轨迹控制的每一步提供逼近目标。
逐点比较法是以四个象限区域判别为特征,每走一步都要将加工点的瞬时坐标与相应给定的图形上的点相比较,判别一下偏差,然后决定下一步的走向。
如果加工点走到图形外面去了,那么下一步就要向图形里面走;如果加工点已在图形里面,则下一步就要向图形外面走,以缩小偏差,这样就能得到一个接近给定图形的轨迹,其最大偏差不超过一个脉冲当量(一个进给脉冲驱动下工作台所走过的距离)。
直线插补是用在计算机图形显示,或则数控加工的近似走刀等情况下的.以数控加工为例子一个零件的轮廓往往是多种多样的,有直线,有圆弧,也有可能是任意曲线,样条线等. 数控机床的刀具往往是不能以曲线的实际轮廓去走刀的,而是近似地以若干条很小的直线去走刀,走刀的方向一般是x和y方向.插补方式有:直线插补,圆弧插补,抛物线插补,样条线插补等所谓直线插补就是只能用于实际轮廓是直线的插补方式(如果不是直线,也可以用逼近的方式把曲线用一段段线段去逼近,从而每一段线段就可以用直线插补了).首先假设在实际轮廓起始点处沿x方向走一小段(一个脉冲当量),发现终点在实际轮廓的下方,则下一条线段沿y 方向走一小段,此时如果线段终点还在实际轮廓下方,则继续沿y方向走一小段,直到在实际轮廓上方以后,再向x方向走一小段,依次循环类推.直到到达轮廓终点为止.这样,实际轮廓就由一段段的折线拼接而成,虽然是折线,但是如果我们每一段走刀线段都非常小(在精度允许范围内),那么此段折线和实际轮廓还是可以近似地看成相同的曲线的--------这就是直线插补.联动与插补决定质点空间位置需要三个坐标,决定刚体空间位置需要六个坐标。
一个运动控制系统可以控制的坐标的个数称做该运动控制系统的轴数。
一个运动控制系统可以同时控制运动的坐标的个数称做该运动控制系统可联动的轴数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线插补Private Sub Command1_Click() Command1.Enabled = FalseLine (x(0), y(0))-(xa, ya)f(0) = 0For i = 0 To n - 1If (xa >= 0) And (ya >= 0) ThenIf f(i) >= 0 ThenFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) - yaElseFor j = y(i) To y(i) + 1 Step 0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) + xaEnd IfEnd IfIf (xa > 0) And (ya < 0) ThenIf f(i) >= 0 ThenFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) + yaElseFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) + xaEnd IfEnd IfIf (xa < 0) And (ya > 0) ThenIf f(i) >= 0 ThenFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) - yaElseFor j = y(i) To y(i) + 1 Step 0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) - xaEnd IfEnd IfIf (xa < 0) And (ya < 0) ThenIf f(i) >= 0 ThenFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) + yaElseFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) - xaEnd IfEnd IfNext iEnd SubN圆插补Private Sub Command3_Click() Command3.Enabled = Falser = ((xa ^ 2) + (ya ^ 2)) ^ (1 / 2) Circle (0, 0), rCommand3.Enabled = Falsef(0) = 0For i = 0 To n - 1If (x(0) > 0) And (y(0) >= 0) Then If f(i) >= 0 ThenFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) - 2 * x(i) + 1ElseFor j = y(i) To y(i) + 1 Step 0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) + 2 * y(i) + 1End IfEnd IfIf (x(0) <= 0) And (y(0) > 0) Then If f(i) < 0 ThenFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) - 2 * x(i) + 1ElseFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) - 2 * y(i) + 1End IfEnd IfIf (x(0) < 0) And (y(0) <= 0) Then If f(i) >= 0 ThenFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) + 2 * x(i) + 1ElseFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) - 2 * y(i) + 1End IfEnd IfIf (x(0) >= 0) And (y(0) < 0) Then If f(i) < 0 ThenFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) + 2 * x(i) + 1ElseFor j = y(i) To y(i) + 1 Step 0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) + 2 * y(i) + 1End IfEnd IfNext iEnd SubS圆插补Private Sub Command5_Click() Command5.Enabled = Falser = ((xa ^ 2) + (ya ^ 2)) ^ (1 / 2) Circle (0, 0), rCommand3.Enabled = Falsef(0) = 0For i = 0 To n - 1If (x(0) >= 0) And (y(0) > 0) Then If f(i) >= 0 ThenFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) - 2 * y(i) + 1ElseFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) + 2 * x(i) + 1End IfEnd IfIf (x(0) > 0) And (y(0) <= 0) Then If f(i) < 0 ThenFor j = y(i) To y(i) - 1 Step -0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) - 1x(i + 1) = x(i)f(i + 1) = f(i) - 2 * y(i) + 1ElseFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) - 2 * x(i) + 1End IfEnd IfIf (x(0) <= 0) And (y(0) < 0) Then If f(i) >= 0 ThenFor j = y(i) To y(i) + 1 Step 0.0001 PSet (x(i), j), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) + 2 * y(i) + 1ElseFor j = x(i) To x(i) - 1 Step -0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) - 1y(i + 1) = y(i)f(i + 1) = f(i) - 2 * x(i) + 1End IfEnd IfIf (x(0) < 0) And (y(0) >= 0) Then If f(i) < 0 ThenFor j = y(i) To y(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jy(i + 1) = y(i) + 1x(i + 1) = x(i)f(i + 1) = f(i) + 2 * y(i) + 1ElseFor j = x(i) To x(i) + 1 Step 0.0001 PSet (j, y(i)), 255Next jx(i + 1) = x(i) + 1y(i + 1) = y(i)f(i + 1) = f(i) + 2 * x(i) + 1End IfEnd IfNext iEnd Sub任意象限圆弧插补r = Sqr((X(0) - xa) ^ 2 + (Y(0) - ya) ^ 2)Circle (xa, ya), rf(0) = 0i = 0DoIf (X(i) > xa) And (Y(i) >= ya) ThenIf f(i) >= 0 ThenFor j = X(i) To X(i) - 1 Step -0.0001PSet (j, Y(i)), 255Next jX(i + 1) = X(i) - 1Y(i + 1) = Y(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 ElseFor j = Y(i) To Y(i) + 1 Step 0.0001PSet (X(i), j), 255Y(i + 1) = Y(i) + 1Next jY(i + 1) = Y(i) + 1X(i + 1) = X(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 End Ifi = i + 1If (y1 = Y(i)) And (x1 = X(i)) Then Exit DoEnd IfIf (X(i) <= xa) And (Y(i) > ya) ThenIf f(i) < 0 ThenFor j = X(i) To X(i) - 1 Step -0.0001PSet (j, Y(i)), 255Next jX(i + 1) = X(i) - 1Y(i + 1) = Y(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 ElseFor j = Y(i) To Y(i) - 1 Step -0.0001PSet (X(i), j), 255Next jY(i + 1) = Y(i) - 1X(i + 1) = X(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2End IfIf (y1 = Y(i)) And (x1 = X(i)) Then Exit Doi = i + 1End IfIf (X(i) < xa) And (Y(i) <= ya) ThenIf f(i) >= 0 ThenFor j = X(i) To X(i) + 1 Step 0.0001PSet (j, Y(i)), 255Next jX(i + 1) = X(i) + 1Y(i + 1) = Y(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 ElseFor j = Y(i) To Y(i) - 1 Step -0.0001PSet (X(i), j), 255Next jY(i + 1) = Y(i) - 1X(i + 1) = X(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 End Ifi = i + 1If (y1 = Y(i)) And (x1 = X(i)) Then Exit DoEnd IfIf (X(i) >= xa) And (Y(i) < ya) ThenIf f(i) < 0 ThenFor j = X(i) To X(i) + 1 Step 0.0001PSet (j, Y(i)), 255Next jX(i + 1) = X(i) + 1Y(i + 1) = Y(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 ElseFor j = Y(i) To Y(i) + 1 Step 0.0001PSet (X(i), j), 255Next jY(i + 1) = Y(i) + 1X(i + 1) = X(i)f(i + 1) = (X(i + 1) - xa) ^ 2 + (Y(i + 1) - ya) ^ 2 - r ^ 2 End Ifi = i + 1If (y1 = Y(i)) And (x1 = X(i)) Then Exit DoEnd If第一象限插补直线插补整圆插补。
