统计学 典型相关分析
统计学中常用的数据分析方法10典型相关分析与ROC分析

统计学中常用的数据分析方法
典型相关分析
相关分析一般分析两个变量之间的关系,而典型相关分析是分析两组变量(如3个学术能力指标与5个在校成绩表现指标)之间相关性的一种统计分析方法。
典型相关分析的基本思想和主成分分析的基本思想相似,它将一组变量与另一组变量之间单变量的多重线性相关性研究转化为对少数几对综合变量之间的简单线性相关性的研究,并且这少数几对变量所包含的线性相关性的信息几乎覆盖了原变量组所包含的全部相应信息。
R0C分析
R0C曲线是根据一系列不同的二分类方式(分界值或决定阈).以真阳性率(灵敏度)为纵坐标,假阳性率(1-特异度)为横坐标绘制的曲线
用途:
1、R0C曲线能很容易地査出任意界限值时的对疾病的识别能力用途;
2、选择最佳的诊断界限值。
R0C曲线越靠近左上角,试验的准确性就越高;
3、两种或两种以上不同诊断试验对疾病识别能力的比较,一股用R0C曲线下面积反映诊断系统的准确性。
统计学第9章 相关分析和回归分析

回归模型的类型
回归模型
一元回归
线性回归
10 - 28
多元回归
线性回归 非线性回归
非线性回归
统计学
STATISTICS (第二版)
一元线性回归模型
10 - 29
统计学
STATISTICS (第二版)
一元线性回归
1. 涉及一个自变量的回归 2. 因变量y与自变量x之间为线性关系
被预测或被解释的变量称为因变量 (dependent variable),用y表示 用来预测或用来解释因变量的一个或多个变 量称为自变量 (independent variable) ,用 x 表示
统计学
STATISTICS (第二版)
3.相关分析主要是描述两个变量之间线性关 系的密切程度;回归分析不仅可以揭示 变量 x 对变量 y 的影响大小,还可以由 回归方程进行预测和控制 4.回归系数与相关系数的符号是一样的,但 是回归系数是有单位的,相关系数是没 有单位的。
10 - 27
统计学
STATISTICS (第二版)
10 - 19
统计学
STATISTICS (第二版)
相关系数的经验解释
1. 2. 3. 4.
|r|0.8时,可视为两个变量之间高度相关 0.5|r|<0.8时,可视为中度相关 0.3|r|<0.5时,视为低度相关 |r|<0.3时,说明两个变量之间的相关程度 极弱,可视为不相关
10 - 20
10 - 6
统计学
STATISTICS (第二版)
函数关系
(几个例子)
某种商品的销售额 y 与销售量 x 之间的关系 可表示为 y = px (p 为单价)
统计学专业基础课与专业课之间的典型相关分析

统计学专业基础课与专业课之间的典型相关分析摘要本文基于统计学系0301-0302两个班的66名学生17门课程(包括专业基础课和专业课)的考试成绩,运用典型相关分析法研究了统计学系基础课和专业课的相关程度。
通过运用统计分析软件SAS运行得到变量间的相关系数以及标准化后的典型相关系数,进而求出典型相关变量。
最后结合分析结果和实际情况对教学提了一点小小的建议。
关键词:基础课;专业课;典型相关分析;典型相关系数Canonical Correlation Analysis Between The Major and BasicSubjects of The Statistics MajorAbstractWith the method of canonical correlation analysis,I study about the correlation between the major and basic subjects of the statistics major.The research is based on the examination scores of66students of classes0301and0302who are in the major of statistics,including only17 subjects,the major and basic subjects.The article then gives the standard canonical correlations between the variables from which we can know the canonical correlative variables.In the end,I give some suggestions about education,according to the output of the analysis and the matter of fact.Key word:basic subject,major,canonical correlation,canonical coefficients1引言对于统计学系的学生来说,对数学理论的理解和掌握要求比较高,而且更重要的是要做到融会贯通,举一反三,学会理论联系实际,并利用统计分析的方法来解决日常生产生活中的问题,因而专业基础课程(如数学分析和高等代数等)的学习无疑是相当重要的,因为它直接关系到后续专业课的学习效果。
统计学案例分析

1/6陳例13-1]我国人身保险业的发展情况保险可分为财产保险和人身保险两大类。
人身意外伤害险是人身保险的一部分。
随着我国国民经济的快速发展,我国保险业也呈现出良好的发展态势,由人身意外伤害险的保费收入的变化可见一斑。
案例思考与分析要求:1.利用Excel绘制岀该动态序列的折线图。
2.按本章第四节中所讲的动态数列构成因素的分类和特征,观察折线图并说明我国人身意外伤害险保费收入的变化中受哪几种构成因素的影响?3.对上述月度数据计算同比增长速度和环比增长速度各有什么意义?4.汇总出各年度保费收入总额,并根据年度数据计算2000—2006 年间的:(1)年平均发展水平。
(2)各年的逐期增长量、累计增长量和年平均增长量,验证逐期增长量与累计增长量之间的关系。
(3)各年的增长速度(环比、定基)、平均发展速度和平均增长速度, 并指岀增长速度超过一般水平的是哪几年?(4)年度保费收入总额呈现岀哪种形态的长期趋势?用恰当的数学模拟合效果的好坏,并预测2007年和2008年的发展水平。
5.如果要根据月度数据来测定保费收入序列的长期趋势,适合采用移动平均法还是数学模型拟合法?为什么?若采用移动平均法,平均的项数应为几项?试用Excel的移动平均工具进行计算并输出图表。
[案例1KL]表8—12中是16只公益股票某年的每股账面价值和当年红利:2/6根据表8—12屮的资料:⑴画出这些数据的散点图;⑵根据散点图,表明二变量之间存在什么关系?(3)求出当年红利是如何依赖每股账面价值的估计的回归方程;(4)对估计的回归方程屮的估计回归系数(斜率)的经济意义作出解释;(5)若序号为6的公司的股票每股账面价值增加1元,估计当年红利可能为多少?[案例口・2]股票分析案例背景随着中国经济的发展和经济体制改革的深入,建立一个繁荣有效的金融市场势在必行,证券市场作为它的重要组成部分,正在发挥越来越重要的作用。
在这一进程中,股票投资成为了一个越来越被普遍接受的投资选择。
典型相关分析的应用前提是

典型相关分析的应用前提是典型相关分析是统计学中一种重要的分析方法,用于研究两组变量之间的关系。
在进行典型相关分析之前,有一些前提条件需要满足,以确保结果的有效性和可靠性。
1. 数据的正态性:典型相关分析是基于正态分布假设的。
因此,在进行分析之前,需要确保所使用的变量满足正态分布的要求。
可以通过正态性检验(如Shapiro-Wilk检验)来判断数据是否符合正态分布。
如果数据不符合正态分布,可以尝试进行变换(如对数变换或Box-Cox变换)来使其满足正态分布假设。
2. 相关性:典型相关分析是用于研究两组变量之间的关系的方法。
因此,在进行分析之前,需要确保所选择的变量之间存在相关性。
可以通过计算变量之间的相关系数(如Pearson相关系数或Spearman相关系数)来评估它们之间的相关性。
如果两个变量之间不存在或弱相关,则不适合使用典型相关分析方法。
3. 样本量要求:典型相关分析需要有足够的样本量才能获得可靠的结果。
一般来说,至少需要50个观测样本以进行典型相关分析。
较小的样本量可能会导致结果的不稳定性和不可靠性。
如果样本量较小,可以考虑使用其他方法(如相关分析或线性回归)进行数据分析。
4. 独立性:在进行典型相关分析之前,需要确保所选取的样本是独立的。
独立的样本是指各个观测值之间相互独立,不受其他观测值的影响。
如果样本之间存在依赖关系或相关性,可能会导致结果的偏差和不准确性。
5. 同方差性:典型相关分析假设不同组变量的方差是相等的。
因此,在进行分析之前,需要检验不同组变量的方差是否相等。
可以使用方差齐性检验(如Levene检验)来评估不同组变量的方差是否具有显著差异。
如果不同组变量的方差不相等,可能会对典型相关分析的结果产生影响。
总之,典型相关分析是一种有用的统计分析方法,可以帮助研究人员探索和理解两组变量之间的关系。
然而,在进行典型相关分析之前,需要确保数据满足正态分布、具有相关性、样本量足够、样本独立以及方差相等等前提条件,以保证分析结果的有效性和可靠性。
典型相关分析和协整
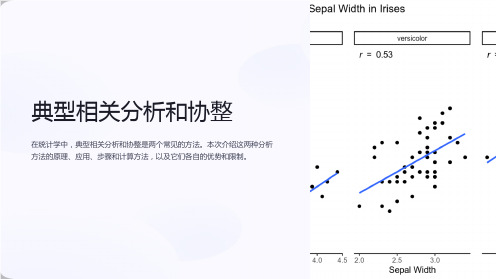
2 应用领域
具体应用领域也是选择方 法的一个因素,例如需要 研究市场平衡时可以使用 协整分析。
3 实际需求
根据实际问题中的需求, 选择合适的分析方法。
总结
典型相关分析和协整是两种不同的统计分析方法,各自有其适用领域和局限 性。使用这些方法可以从不同维度和角度解读变量之间的关系,有助于更好 地理解和分析数据。
原理和应用领域
适用于研究两个或两个以上时间序列之间的长期关 系,可以用于股票市场、汇率、商品价格等领域的 分析。
步骤和计算方法
选择需要分析的时间序列,进行单位根检验以判断
优势和限制
可以排除短期市场波动的影响,更容易发现市场中
典型相关分析与协整的不同之处
基础理论
典型相关分析基于主成分分析, 而协整分析基于时间序列分析。
原理和应用领域
适用于研究多个变量之间的关系,既可以揭示 变量之间的线性关系,也可以检测非线性关系。
优势和限制
可以提高变量之间的关系解释效果,但需要数 据具有一定的正态性和线性性。也会受到样本 数量的限制,在样本量较少时易受到误导。
什么是协整分析
定义
在时间序列分析中,指两个或两个以上的时间序列 彼此关联,但是它们的差分是平稳的。即可以通过 线性组合消除非平稳性。
分析对象
典型相关分析基于多个变量之 间的关系,而协整分析常用于 两个或两个以上时间序列的分 析。
数据要求
典型相关分析对数据正态分布 和线性相关性的要求较高,而 协整分析对数据平稳性的要求 较高。
如何选择方法
1 数据类型
对于数量型变量,可以考 虑使用典型相关分析;对 于时间序列数据,可以使 用协整分析。
典型相关分析ቤተ መጻሕፍቲ ባይዱ协整
统计学-线性相关分析

二、计算公式
样本相关系数 r 的计算公式为:
r ( X X )(Y Y ) l XY ( X X )2 (Y Y )2 l XX lYY
例13-2:
第三节 相关系数的假设检验
目的是推断总体相关系数 是否等于0 ?
检验统计量 t 的计算公式为:
tr
r 0 Sr
r ,v n2 1 r2 n2
零相关(r=0)
相关系数 r 的取值及两变量间相关关系的直观图示:
r=0
零相关(r=0)
相关系数 r 的取值及两变量间相关关系的直观图示:
r=0
零相关(r=0)
相关系数 r 的取值及两变量间相关关系的直观图示:
r=0
零相关(r=0)
第二节 线性相关系数
一、概念
相关系数又称pearson积差相关系数, 符号: 常用 r 表示样本相关系数,用 表示总体相 关系数。相关系数可用来说明具有直线关系 的两变量间相关的方向和密切程度。
第十二章 线性相关分析
第一节 线性相关的概念
一、散点图
例13-1 为研究中年女性体重指数和收缩压 之间的关系,随机测量了16名40岁以上女性 的体重指数和收缩压,见表13-1,试作分析。
编号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
合计
体重指数 X 2.86 3.41 3.62 3.20 2.79 2.96 3.84 4.01 3.75 3.96 3.36 3.62 3.91 4.12 3.33 3.76
4. 不能直接根据样本相关系数r绝对值的大小 来说明两事物间有无相关关系及相关的紧密方 向而需对总体相关系数作假设检验。
第六节 直线回归与直线相关的区别和联系
统计学 第 七 章 相关与回归分析

(一)回归分析与相关分析的关系
回归分析与相关分析是研究现象 之间相互关系的两种基本方法。
区别:
1、相关分析研究两个变量之间相关的 方向和相关的密切程度。但是相关分析不 能指出两变量相互关系的具体形式,也无 法从一个变量的变化来推测另一个变量的 变化关系。
2、按研究变量多少分为单相关和 复相关
单相关即一元相关,亦称简单相 关,是指一个因变量与一个自变量 之间的依存关系。复相关又称多元 相关,是指一个因变量与两个或两 个以上自变量之间的复杂依存关系。
3、按相关形式分为线性相关和非 线性相关
从相关图上观察:观察的样本点的 分布近似表现为直线形式,即观察点近 似地分布于一直线的两边,则称此种相 关为直线相关或线性相关。如果这些样 本点近似地表现为一条曲线,则称这种 相关为曲线相关或非线性相关(curved relationship).
不确定性的统计关系 —相关关系
Y= f(X)+ε (ε为随机变量)
在这种关系中,变量之间的关系值 是随机的,当一个(或几个)变量的值 确定以后,另一变量的值虽然与它(们) 有关,但却不能完全确定。然而,它们
之间又遵循一定的统计规律。
相关关系的例子
▪ 商品的消费量(y)与居民收入(x)
之间的关系
▪ 商品销售额(y)与广告费支出(x)
▲相关系数只反映变量间的线性相关程度,不 能说明非线性相关关系。
▲相关系数不能确定变量的因果关系,也不能 说明相关关系具体接近于哪条直线。
例题1: 经验表明:商场利润额与 其销售额之间存在相关关系。下表为 某市12家百货公司的销售额与利润额 统计表,试计算其相关系数。
学术研究中的典型相关分析方法

学术研究中的典型相关分析方法一、引言典型相关分析是一种广泛应用于社会科学和生物统计学领域的统计方法,主要用于研究两个或多个变量之间的关系。
典型相关分析能够从大量数据中提取出有用的信息,帮助研究者更好地理解研究对象之间的相互作用。
本文将详细介绍典型相关分析的基本原理、步骤和应用,为学术研究提供有益的参考。
二、典型相关分析的基本原理典型相关分析是一种用于探索多个变量之间关系的方法。
它通过寻找一组代表性变量,来反映原始变量之间的相关关系。
这些代表性变量通常被称为主成分或典型变量,它们能够反映原始变量的绝大部分信息。
通过分析典型变量之间的关系,可以推断出原始变量之间的潜在关系。
典型相关分析的基本原理可以概括为以下三个步骤:1.数据的降维:通过主成分分析或类似的方法,将原始数据从多个维度降至少数几个典型变量。
2.寻找代表性变量:根据典型变量的方差贡献和相关性,选择最重要的几个典型变量。
3.解释原始变量之间的关系:通过分析典型变量之间的关系,推断出原始变量之间的潜在关系。
三、典型相关分析的步骤典型相关分析通常包括以下步骤:1.准备数据:收集并整理需要进行分析的数据,确保数据的质量和准确性。
2.降维:使用主成分分析、独立成分分析或其他降维方法,将数据从多个维度降至少数几个典型变量。
3.确定典型变量:根据方差贡献和相关性,选择最重要的几个典型变量。
4.统计分析:使用适当的统计方法,如线性回归、相关系数等,分析典型变量之间的关系,并解释其意义。
5.结果解释:将典型变量之间的关系与原始变量之间的相关性进行比较,推断出原始变量之间的潜在关系。
四、典型相关分析的应用典型相关分析在许多领域都有广泛的应用,包括但不限于社会学、心理学、生物学和医学。
以下是一些典型相关分析的应用实例:1.研究社会现象:在研究社会现象时,典型相关分析可以用于探索人口统计学特征(如年龄、性别、教育水平等)与行为、态度和价值观之间的关系。
通过分析典型变量,可以更深入地了解社会现象的内在机制。
多元统计分析 典型相关分析

第六步:验证与诊断
与其他的多元分析方法一样,典型相关分析的结 果应该验证,以保证结果不是只适合于样本,而是 适合于总体。最直接的方法是构造两个子样本(如 果样本量允许),在每个子样本上分别做分析。这 样结果可以比较典型函数的相似性、典型载荷等。 如果存在显著差别,研究者应深入分析,保证最后 结果是总体的代表而不只是单个样本的反映。
现在的问题是为每一组变量选取一个综合 变量作为代表;而一组变量最简单的综合形 式就是该组变量的线性组合。
由于一组变量可以有无数种线性组合(线 性组合由相应的系数确定),因此必须找到 既有意义又可以确定的线性组合。
典型相关分析的概念
典型相关分析(canonical correlation analysis)就是要找到这两组变量线性组 合的系数使得这两个由线性组合生成的 变量(和其他线性组合相比)之间的相 关系数最大。
2、典型载荷
由于典型权重的缺陷,典型载荷逐步成为 解释典型相关分析结果的基础。典型载荷, 也称典型结构相关系数,是原始变量(自变 量或者因变量)与它的典型变量间的简单线 性相关系数。典型载荷反映原始变量与典型 变量的共同方差,它的解释类似于因子载荷, 就是每个原始变量对典型函数的相对贡献。
3、典型交叉载荷
第五步:解释典型变量.
建立典型相关分析模型后,需要对模型的结果 进行解释,可以用以下三种方法来说明。
三种方法:
1 典型权重(标准化的典型变量系数)
2 典型载荷(解释典型相关分析结果的基础; 反应原始变量与典型变量的共同方差,即每 个原始变量对典型变量的相对贡献)
典型相关分析因子分析

结论和总结
本文介绍了典型相关分析和因子分析的概念、公式、步骤和应用案例。这两 种数据分析方法可以帮助研究者从不同角度分析数据,揭示潜在关系,并为 决策提供依据。
2
定变量之间的关联程度。
利用特征向量和特征值,计算出典型相关变
量,即两组变量之间的最大相关性。
3
解释结果
分析典型相关系数和贡献率,解释典型相关 分析的结果。
因子分析的公式与步骤
1
提取因子
2
根据主成分分析或最大似然估计等方法,提
取潜在因子,解释变量之间的共变异。
3
解释结果
4
Hale Waihona Puke 分析因子载荷和解释方差,解释因子分析的 结果。
金融
典型相关分析可以用于分析金融市场上不同变量之间的关系,为投资决策提供参考。
因子分析的应用案例
心理学
因子分析可以帮助心理学家理解人 的多个特质和行为之间的关系,揭 示心理结构。
教育研究
因子分析可以帮助研究者理解学生 学习成绩和学习动机等变量之间的 关系,指导教育改革。
市场调研
通过因子分析,市场研究人员可以 揭示消费者对产品特性的偏好和认 知结构。
典型相关分析因子分析
典型相关分析与因子分析是统计学中重要的数据分析方法。本文将介绍这两 种分析方法的基本概念、公式与步骤,并提供一些实际应用案例。
典型相关分析介绍
典型相关分析是一种用于探究两组变量之间关系的方法。它能够找到两组变量之间存在的最大相关性,并且给出相 应的统计量。该方法在市场研究、社会科学和金融等领域被广泛应用。
因子分析介绍
因子分析是一种用于揭示观测数据之间潜在关系的方法。通过将观测变量转 化为几个潜在因子,因子分析可以简化数据结构,帮助研究者理解复杂性问 题。该方法在心理学、教育研究和市场调研等领域得到广泛应用。
第四讲-统计学中的相关分析

3.当 r =1 时,即零相关,表示 x和 y 没有线性相关关系。
零相关表示x和y不相关或存在非线性关系。 4.当 0< r < 1时,表示 x和 y存在着一定的线性相关关系。
r < 0.3称为微弱相关; 0.3 ≤ r < 0.5称为低度相关;
0.5 ≤ r < 0.8称为显著相关;
0.8 ≤ r < 1称为高度相关;
如果相关关系表现为因素标志和结果标志的数值在变动方向上保持 一致,则称为正相关。 例如家庭收入增加,银行储蓄也会增加。
如果相关关系表现为因素标志和结果标志的数值在变动方向上相 反,则称为负相关。 例如企业的生产规模越大,产品的单位成本就越低。
现象总体表现出来的正相关或负相关是有一定条件和范围的。某种 现象不会永远以正相关表现,也不会永远以负相关表现。 例如,在一定的范围内,增加施肥量能提高农作物的产量,但如果 施肥过多,反而使庄稼只长叶子,不长果实, 最后可能收获量很少。
0.99
6 9 080 2082 6 27 124 4022
即产品产量与单位成本呈现高度负相关。
2019/11/22
21
例8‐3 试根据下表分组资料计算某地人均收入与人均支出的相关系数。
某地人均收入与人均支出的样本资料
0123456
人均年收入 (千元)
1.0以下 1.0~2.0 2.0~3.0 3.0~4.0 4.0~5.0 5.0以上
2019/11/22
第八章 相关分析
14
协方差的正负号与相关方向的关系图示:
0123456
y
Ⅱ
Ⅰ
xx0 y y 0 (x x)( y y)为负
y
Ⅲ
统计学课后题

统计学课后题第二章均值向量和协方差阵的检验1、试谈willks统计量在多元方差分析中的重要意义。
2、形象分析的基本思路是什么?形象又称轮廓图,是将总体样本的均值绘制到同一坐标轴里所得的折线图,每一个指标都表示为折线图上的一点。
形象分析是将两总体的形象绘制到同一个坐标下,根据形象的形状对总体的均值进行比较分析。
第三章聚类分析1、聚类分析的基本思想和功能是什么?聚类分析的核心思想是根据具体的指标对所研究的个体或者对象进行分类,使得同一类中的对象之间的相似性比其他类的对象的相似性更强。
聚类分析不仅可以用来对样品进行分类,也可以用来对变量进行分类。
对样品的分类常称为Q型聚类分析,对变量的分类常称为R型的聚类分析。
聚类分析的目的或功能就是把相似的研究对象归成类,即使类间对象的同质性最大化和类与类间对象的异质性最大化。
2、试述系统聚类法的原理和具体步骤系统聚类的基本思想是:距离相近的样品先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品总能聚到合适的类中。
系统聚类的具体步骤:假设总共有N个样品第一步:将每个样品独自聚成一类,共有N类;第二步:根据所确定的样品“距离”公式,把距离较近的两个样品聚合为一类,其他的样品仍各自聚为一类,共聚成N-1类;第三步:将“距离”最近的两个类进一步聚成一类,共聚成N-2类;。
,以上步骤一直进行下去,最后将所有的样品全聚成一类。
3、试述K-均值聚类的方法原理这种聚类方法的思想是把每个样品聚集到其最近形心类中。
首先随机从数据集中选取 K个点作为初始聚类中心,然后计算各个样本到聚类中的距离,把样本归到离它最近的那个聚类中心所在的类。
计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心,如果相邻两次的聚类中心没有任何变化,说明样本调整结束,聚类准则函数已经收敛。
4、试述模糊聚类的思想方法模糊聚类分析是根据客观事物间的特征、亲疏程度、相似性,通过建立模糊相似关系对客观事物进行聚类的分析方法。
相关分析与回归分析

家卡尔·皮尔逊设计的统计量,如果散点图的n个点基本在一条直线附近,但又不完全在
一条直线上,此时就可以使用该统计量来表示变量关系的密切程度。它的计算公式:
r
n xy x y
, r被称为随机变量X与Y的Pearson线性相关系数。
n x2 ( x)2 n y2 ( y)2
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:两个变 量之间是线性关系,都是连续数据,可以使用散点图查看;两个变量的总体是正态分布, 或接近正态的单锋分布;两个变量的观测值是成对的,每对观测值之间相互独立。
计算机之间的远程通信。
9.1.2 数字调制技术在数字电视(DTV)上的 应用
DTV 是将活动图像、声音和数据,通过 数字技术进行压缩、编码、传输、存储,实 时发 送、广播,供观众接收、播放的视听系
统。 数字高清晰度电视的图像信息速率接近 1GB/s,要在实际信道中传输,除应采用高效
数字电视信号经信源编码及信道编码后 ,要进行信号传输,传输目的是最大限度地提 高数字电视覆盖率,根据数字电视信道的特 点,要进行地面信道、卫星信道、有线信道 的编 码调制后,才能进行传输。由于数字电 视系统中传送的是数字电视信号,因此必须 采用高 速数字调制技术来提高频谱利用率, 从而进一步提高抗干扰能力,以满足数字高
目前,国际上数字高清晰度电视传输系 统中采用的调制技术主要有:四相移相键控 (QPSK)、多电平正交幅度调制(MQAM)、 多电平残留边带调制(MVSB)和正交频分复
用 调制(OFDM)。
9.2 偏移四相相移键控
恒定包络调制可以采用限幅的方法去除干扰引起的幅度 变化,其具有较高的抗干扰能 力。在数字调相中,若基带信号 为矩形方波,则数字调相信号也具有恒定包络特性,但这时 已 调信号的频谱为无穷宽。而实际的信道总是有限的,为了对 数字调相信号的带宽进行限 制,先将基带信号经过成形滤波 器,然后进行数字调相,再经过带通滤波器送入信道。
统计学原理第七章_相关分析

各类相关关系的表现形态图
三、相关分析与回归分析
• (一)相关分析 • 是用一个指标(相关系数)来表明现象 之间相互依存的密切程度。 • (二)回归分析 • 是根据相关关系的具体形态,选择一个 合适的数学模型,来近似地表达变量之 间的平均变化关系。(高度相关)
• (三)相关分析与回归分析的联系
• 1. 它们有具有共同的研究对象。
n
(x x )(y y ) n
σx
(x x )
n
2
(x x ) n
(y y ) n
1
1
2
σy
(y y )
n
2
2
再代入到原公式中,得:
r σ
2 xy
σx y σ
( x x ) ( y y ) ( x x ) ( y y )
2
·· ·②
销售收入 (百万元)
40 30 20 10 0 0 20 40 60 80 100
广告费(万元)
钢材消费量与国民收入
2500
2000
1500
钢材消费量(万吨)
1000
500
0
(相关图)
0
500
1000
1500
2000
2500
3000
国民收入(亿元)
例子
表1 某企业产量与生产费用的关系
企业编号 1 2 3 4 5 6 7 8
量,哪个是因变量,变量都是随机的。
• 2. 回归分析是对具有相关关系的变量间
的数量联系进行测定,必须事先确定变
量的类型。通常因变量是随机的,自变
量可以是随机的,也可以是非随机的。
第二节 简单线性相关分析
相关分析

相关分析
学
天津财经大学 统计学系
一、变量间的数量关系
众所周知,自然科学和社会科学研究的目的就是揭示客观主
统 计
体的属性以及这些属性的相互联系,通常使用变量表示客观主体 的属性,同时,按照变量取值的确定与否,变量一般被划分为确 定性变量和随机性变量。 例如,星体的质量m、两星体球心之间的距离R是确定性变 量;一国经济的失业率 u 和通货膨胀率 i 是随机性变量。
n X tYt X t Yt
学
0.999697
由于样本相关系数0.999697接近于1,所以,我 国城镇居民人均年消费性支出与人均年可支配收入之 间高度正相关关系。
天津财经大学 统计学系
五、相关分析实例
统 计
【例2】 假设根据38个样本观测数据计算出某公司的“产品
质量”和“用户满意度”变量的样本相关系数r=0.75,试问 是否可以根据5%的显著水平认为该公司的“产品质量”和 “用户满意度”之间存在一定程度的线性相关关系? 解:将样本相关系数代入t 统计量计算式,计算在零假设下,r 的t值
天津财经大学 统计学系
学
二、相关关系及其种类
统 计
• 完全相关:当一个变量变化完全由另一个变量 变化所确定时,称这两个变量间的关系为完全 相关。
– 例如:在价格不变的条件下,某种商品的销售额与其 销售量是成正比例完全相关关系。
学
• 不相关:当两个变量彼此互不影响,其数量变 化各自独立时,称这两变量之间为不相关。
年份 1996 1997 1998 1999 2000 2001 2002 2003 人均可支 人均消费 配收入 支出 X Y 4.839 3.919 5.16 4.186 5.425 4.332 5.854 4.616 6.28 4.998 6.86 5.309 7.703 6.03 8.472 6.511 年份 2004 2005 2006 2007 2008 2009 2010 2011 人均可支 人均消费 配收入 支出 X Y 9.422 7.182 10.493 7.943 11.759 8.697 13.786 9.997 15.781 11.243 17.175 12.265 19.109 13.471 21.81 15.161
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
我们知道如何衡量两个变量之间是否相关的问题; 这是一个简单的公式就可以解决的问题(Pearson相关 系数、 Kendall’s t、 Spearman 秩相关系数)。公 式
如果我们有两组变量,如何能够表明它们之间的关
系呢?
h
2
例子(数据tv.txt)
业内人士和观众对于一些电视节目的观点有什么样的关系 呢?该数据是不同的人群对30个电视节目所作的平均评分 。
观众评分来自低学历(led)、高学历(hed)和网络(net)调查 三种,它们形成第一组变量;
而 业 内 人 士 分 评 分 来 自 包 括 演 员 和 导 演 在 内 的 艺 术 家 (arti)、发行(com)与业内各部门主管(man)三种,形成第 二组变量。人们对这样两组变量之间的关系感到兴趣。
99.427%。它们的典型相关系数也都在0.95之上。
h
11
计算结果
对于众多的计算机输出挑出一些来介绍。下面表格给出的是第一组变量相应于上面三个特征根的三个典型变量V1、V2 和V3的系数,即典型系数(canonical coefficient)。注意,SPSS把第一组变量称为因变量(dependent variables), 而把第二组称为协变量(covariates);显然,这两组变量是完全对称的。这种命名仅仅是为了叙述方便。
h
7
典型相关系数
这里所涉及的主要的数学工具还是矩阵的特征
值和特征向量问题。而所得的特征值与V和W的典
型相关系数有直接联系。 由于特征值问题的特点,实际上找到的是多组
典相关型,变而量V(2V和1,W2W次1)之, 等(V等2,,W2),…,其中V1和W1最
h
8
典型相关系数
不而相且关V1。, 这V2样, 又V3,出…现之了间选及择而多且少W组1,典W型2,变W量3,…(V之,
h
5
14.2 典型相关分析
由于一组变量可以有无数种线性组合(线性组合由 相应的系数确定),因此必须找到既有意义又可以确 定的线性组合。
典 型 相 关 分 析 (canonical correlation analysis) 就是要找到这两组变量线性组合的系数使得这两个由 线性组合生成的变量(和其他线性组合相比)之间的 相关系数最大。
h
6
典型变量
假定两组变量为X1,X2…,Xp和Y1,Y2,…,Yq,那么,问题就在于 要寻找系数a1,a2…,ap和b1,b2,…,bq,和使得新的综合变量( 亦称为典型变量(canonical variable))
Va1X1a2X2 apXp Wb1Y1b2Y2 bqYq
• 之间的相关关系最大。这种相关关系是用典型相关系数 (canonical correlation coefficient)来衡量的。
h
3
h
4
寻找代表
如直接对这六个变量的相关进行两两分析,很难得 到关于这两组变量之间关系的一个清楚的印象。
希望能够把多个变量与多个变量之间的相关化为两 个变量之间的相关。
现在的问题是为每一组变量选取一个综合变量作为 代表;
而 一 组 变 量 最 简 单 的 综 合 形 式 就 是 该 组 变 量 的 线 性 组合。
h
16
SPSS的实现
对例tv.sav,首先打开例14.1的SPSS数据tv.sav, 通过File-New-Syntax打开一个空白文件(默认文件名为Syntax1.sps),再在其中键入下面命令行:
MANOVA led hed net WITH arti com man
/DISCRIM ALL ALPHA(1)
h
13
计算结果
类似地,也可以得到被称为协变量(covariate)的标准化的第 二组变量的相应于头三个特征值得三个典型变量W1、W2和W2的 系数: 。
h
14
h
15
例子结论
从这两个表中可以看出,V1主要和变量hed相关,而V2主要和 led及net相关;W1主要和变量arti及man相关,而W2主要和com 相关;这和它们的典型系数是一致的。
代由表于的V1和艺W术1最家相(a关rt,i)这及说各明部V门1所经代理表(m的an高)观学点历相观关众;和而W1所由主于要V2 和W2也相关,这说明V2所代表的低学历(led)及以年轻人为主 的 网 民 (net) 观 众 和 W2 所 主 要 代 表 的 看 重 经 济 效 益 的 发 行 人 (com)观点相关,但远远不如V1和W1的相关那么显著(根据特 征值的贡献率)。
的F值,两个自由度和p值(均为0.000)。
h
10
计算结果
下面一个表给出了特征根(Eigenvalue),特征根所占的百分比(Pct)和 累 积 百 分 比 (Cum. Pct) 和 典 型 相 关 系 数 (Canon Cor) 及 其 平 方 (Sq.
Cor)。看来,头两对典型变量(V, W)的累积特征根已经占了总量的
这些系数以两种方式给出;一种是没有标准化的原始变量的线性组合的典型系数(raw canonical coefficient),一 种是标准化之后的典型系数(standardized canonical coefficient)。标准化的典型系数直观上对典型变量的构成给 人以更加清楚的印象。
h
12
可以看出,头一个典型变量V1相应于前面第一个(也 是最重要的)特征值,主要代表高学历变量hed;而 相应于前面第二个(次要的)特征值的第二个典型变 量V2主要代表低学历变量led和部分的网民变量net, 但高学历变量在这里起负面作用。
间互
W)的
问题了。实际上,只要选择特征值累积总贡献占主要
部分的那些即可。
软件还会输出一些检验结果;于是只要选择显著的
那些(V, W)。
对实际问题,还要看选取的(V, W)是否有意义,是
否能够说明问题才行。至于得到(V, W)的计算,则很
简单,下面就tv.txt数据进行分析。数学原理?
h
9
计算结果
第一个表为判断这两组变量相关性的若干检验,包括Pillai迹 检验,Hotelling-Lawley迹检验,Wilks l检验和Roy的最大根 检验;它们都是有两个自由度的F检验。该表给出了每个检验
