应力强度因子的计算
计算应力强度因子

基于ANSYS的断裂参数的计算本文介绍了断裂参数的计算理论,并使用ANSYS进展了实例计算。
通过计算说明了ANSYS可以用于计算断裂问题并且可以取得很好的计算结果。
1 引言断裂事故在重型机械中是比拟常见的,我国每年因断裂造成的损失十分巨大。
一方面,由于传统的设计是以完整构件的静强度和疲劳强度为依据,并给以较大的安全系数,但是含裂纹在役设备还是常有断裂事故发生。
另一方面,对于一些关键设备,缺乏对不完整构件剩余强度的估算,让其提前退役,从而造成了不必要的浪费。
因此,有必要对含裂纹构件的断裂参量进展评定,如应力强度因了和J积分。
确定应力强度因了的方法较多,典型的有解析法、边界配位法、有限单元法等。
对于工程上常见的受复杂载荷并包含不规如此裂纹的构件,数值模拟分析是解决这些复杂问题的最有效方法。
本文以某一锻件中取出的一维断裂试样为计算模型,介绍了利用有限元软件ANSYS计算应力强度因子。
2 断裂参量数值模拟的理论根底对于线弹性材料裂纹尖端的应力场和应变场可以表述为:其中K是应力强度因子,r和θ是极坐标参量,可参见图1,(1)式可以应用到三个断裂模型的任意一种。
图1 裂纹尖端的极坐标系应力强度因子和能量释放率的关系:G=K/E" (3)其中:G为能量释放率。
平面应变:E"=E/(1-v2)平面应力:E=E"3 求解断裂力学问题断裂分析包括应力分析和计算断裂力学的参数。
应力分析是标准的ANSYS线弹性或非线性弹性问题分析。
因为在裂纹尖端存在高的应力梯度,所以包含裂纹的有限元模型要特别注意存在裂纹的区域。
如图2所示,图中给出了二维和三维裂纹的术语和表示方法。
图2 二维和三维裂纹的结构示意图3.1 裂纹尖端区域的建模裂纹尖端的应力和变形场通常具有很高的梯度值。
场值得准确度取决于材料,几何和其他因素。
为了捕获到迅速变化的应力和变形场,在裂纹尖端区域需要网格细化。
对于线弹性问题,裂纹尖端附近的位移场与成正比,其中r是到裂纹尖端的距离。
关于管道裂纹应力强度因子的计算

是管道内半径 R i 和外 半径 R 0 比值 ∃= R i / R 0
第1期
&设计与研究& 考应力的作用下 , 其应力强度因子分别为: KB 1r =
B 2r = 0
3
式( 9) 、 ( 10) 中的参数 M iA 和 M iB 可根据两个参考 应力强度因子解和第三个条件确定。对于表面半椭圆 裂纹最深 点的权 函数, 确定参 数 M iA 的第 三个 条件 为
权函数, 则在任何应力条件下 , 应力强度因子均可通过 积分式( 1) 求得。下面分别讨论含轴向裂纹和纵向表 面半椭圆裂纹管道应力强度因子的权函数计算方法。
3
轴向裂纹的应力强度因子
如图 1 所示 , 管壁中有一轴向裂纹 , 类似于平板中
的边缘裂纹。对于这种类似的 边缘裂纹 , Pet roski 和 Achenbach 提出了裂纹张开位移的近似表达式!4∀ : u( a, x ) =
M 2B( x ) + M 3B ( x ) a a !a F = Q 1
dx
1+ M 1B + M 2B + M 3B= 0
选取均布应力和线形减少分布应力作为两个参考 x) = x) =
%
a 0
0( 1
x) a
1 2 1 + M 1B ( x ) 2+ a !x
0 0(
! x x 3 M 2B ( a ) + M 3B ( a ) 2 d x
ext
E∋ 2
!4f ( a / w )
a
a- x ( 3)
+ G ( a/ w )
( a - x ) 3/ 2 ∀ a
2
权函数法
由权函数理论可证明
应力强度因子的计算
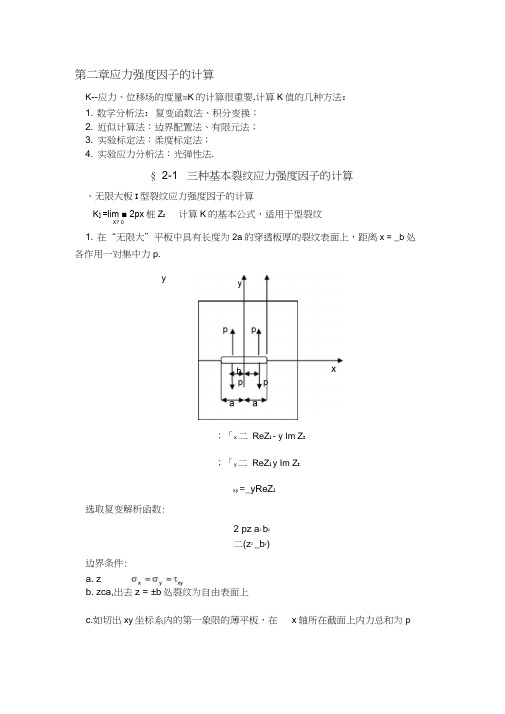
第二章应力强度因子的计算K--应力、位移场的度量=K的计算很重要,计算K值的几种方法:1. 数学分析法:复变函数法、积分变换;2. 近似计算法:边界配置法、有限元法;3. 实验标定法:柔度标定法;4. 实验应力分析法:光弹性法.§ 2-1 三种基本裂纹应力强度因子的计算、无限大板I型裂纹应力强度因子的计算K] =lim ■ 2px桩Z I计算K的基本公式,适用于型裂纹X? 01. 在“无限大”平板中具有长度为2a的穿透板厚的裂纹表面上,距离x = _b处各作用一对集中力p.y;「x 二ReZ i - y Im Z I;「y 二ReZ i y Im Z Ixy =_yReZ l选取复变解析函数:2 pz a2b2二(z2_b2)边界条件:a. zb. zca,出去z = ±b处裂纹为自由表面上c.如切出xy坐标系内的第一象限的薄平板,在x轴所在截面上内力总和为p2 p (匕 +a) Ja 2+孑二[(a)2-b 2] ; (2a)2p 、、 a二(a 2-b 2)2. 在无限大平板中,具有长度为2a 的穿透板厚的裂纹表面上,在距离x= _印的 范围内受均布载荷q 作用.yb.11yqn____ r~Kq 1旺x------ ►J 2 a利用叠加原理:a2q\a i . ---------------- dxo _ / 2 2、二(a -x )令x=acos : a 2-x 2= acosv , dx = acos 二当整个表面受均布载荷时,c -• a. =K i = 2^-s in3. 受二向均布拉力作用的无限大平板,在x 轴上有一系列长度为2a ,间距为2b的裂纹.以新坐标表示:K i微段 > 集中力qdx > dK i2q烏 dx 护(a 2_x 2)-K isin 4(J)广;)竺吗=a cos^二0, -a ::: x ::: a, -a 二2b ::: x ::: a 二2b 在区间内;-y =°,,xy =c.所有裂纹前端;匚y.匚单个裂纹时又Z应为2b的周期函数采用新坐标:=z-an ..-sin ( a) 2b当© t 0时,sin 二© =厶Jcos 厶© =12b 2b 2b迟JL乜JL JL乜= sin——( a) =sin—— cos一a cos一sin — a 2b2b 2b 2b 2b边界条件是周期的:a. z —二二xb.在所有裂纹内部应力为零.y~2 2z - a-sin2b二a、2(Sin" %2b 仙2b)JI u 31ji.二 a 二 sin - 2b 1 -a . -a ——cos ——sin — 2b 2b 2b =;「2b tan a \ 2b—a, 2b tan :aYn a2b2a 1若裂纹间距离比裂纹本身尺寸大很多(兰乞丄)可不考虑相互作用,按单个裂纹2b 5计算•二、无限大平板n>m 型裂纹问题应力强度因子的计算1. u 型裂纹应力强度因子的普遍表达形式(无限大板):心计吋(人尹2. 无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切 力作用.JT JT cos a sin a 2b 2b2bfTTfTTfTTfTTHTfTTfTT.. 2 ■22 2[sin (a)] = ( ) cos a 2 cos a sin a (sin a) 2b2b 2b 2b 2b 2b2b•2::.2[%(a)] -(sin2b a)JI=2 -2bn Jicos asin a2b 2b:二 sin2b—2/ ?.a .二 acos ——sin2b 2b2b 修正系数,大于1,表示其他裂纹存在对K ]的影响.二a 2 药)心=帆 J 2 兀©Z (©) = i V^a J^tan 舒3.川型裂纹应力强度因子的普遍表达形式(无限大板):4.周期性裂纹:sin二z 2b n : …sin ( a) 2bZ()二訓n 2?+a)]2-伽訝H Z 2伽亦)一伽§ 2-2 深埋裂纹的应力强度因子的计算1950年,格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力 和应变,得到椭圆表面上任意点,沿y 方向的张开位移为:2 2 1x z . 2 y =y 0(1 2 2)a c2(1 -」2);「a 其中:yo =(丘丿.-为第二类椭圆积分•有Ji | 2 2=o 2、1-c;asin 2d 「(于仁东书丿匹 a^2 二 2[sin 2「(-)2cos 2] d (王铎书丿 0c1962年,lrwin 利用上述结果计算在这种情况下的应力强度因子xz2 2 2 2 2N 二 Qcos : ,x ,-『sin :2 2 X i 乙-2~~2acacc 2sin 2「a 2cos 2假设:椭圆形裂纹扩展时,其失径「的增值r 与「成正比.边缘上任一点p (x ,z ),有:x j (「r)sin 炉=(1 f^?sin 》=(1 f)x iz = r)cos 即=(1 f )z 1=■ p (x ;z), p (M,Z i )均在 y=0 的平面内.— ,:2 ・2-2 24 2 2・2 ・2=c x a z (i f)ac a c=新的裂纹面仍为椭圆•长轴c =(i • f)c ,短轴a '=(i • f)a .=y 向位移2 2原有裂纹面:二 二,上)2=ia c y o2 2扩展后裂纹面:笃•务•(工)2=i a c y o以x'x i , z'z,代入=原有裂纹面的边缘y 向位移y ,有原裂纹面y o2(i 」2)二 a2(i-」2)ri f)aE=(i f)y oc 2片2a 2zj 二 a 2c 2sin 2「亠 a 2cos2 :2 2 2 2 2 2「-(1-2门笃一(1一2门刍=1一笃一乌2f (笃吕)ac a ca c=2f二 y 2=2fy °2=2f (1 f )2y o 2L 2fy 。
应力强度因子的一般表达式和用途
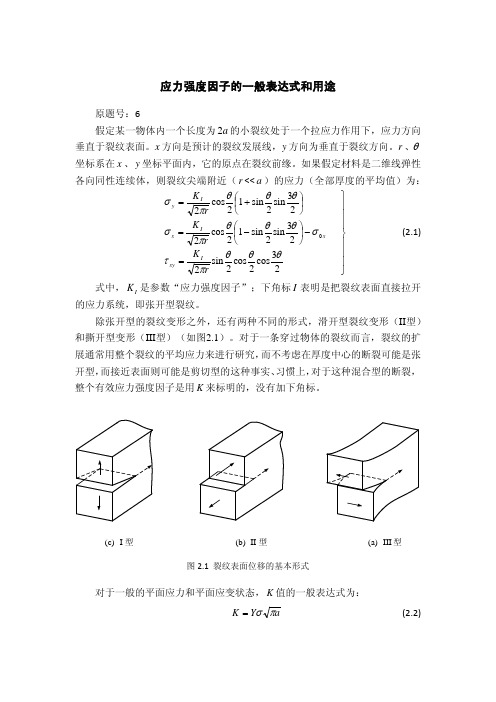
应力强度因子的一般表达式和用途原题号:6假定某一物体内一个长度为a 2的小裂纹处于一个拉应力作用下,应力方向垂直于裂纹表面。
x 方向是预计的裂纹发展线,y 方向为垂直于裂纹方向。
r 、θ坐标系在x 、y 坐标平面内,它的原点在裂纹前缘。
如果假定材料是二维线弹性各向同性连续体,则裂纹尖端附近(r <<a )的应力(全部厚度的平均值)为:=− −= +=23cos 2cos 2sin 223sin 2sin 12cos 223sin 2sin 12cos 20θθθπτσθθθπσθθθπσr K rK rK I xy x I x Iy (2.1) 式中,I K 是参数“应力强度因子”;下角标I 表明是把裂纹表面直接拉开的应力系统,即张开型裂纹。
除张开型的裂纹变形之外,还有两种不同的形式,滑开型裂纹变形(II 型)和撕开型变形(III 型)(如图2.1)。
对于一条穿过物体的裂纹而言,裂纹的扩展通常用整个裂纹的平均应力来进行研究,而不考虑在厚度中心的断裂可能是张开型,而接近表面则可能是剪切型的这种事实、习惯上,对于这种混合型的断裂,整个有效应力强度因子是用K 来标明的,没有加下角标。
图2.1 裂纹表面位移的基本形式 对于一般的平面应力和平面应变状态,K 值的一般表达式为:a Y K πσ= (2.2)(c) I 型 (b) II 型(a) III 型式中σ——应力;a ——裂纹尺寸;Y ——应力强度因子修正系数,为裂纹形状和所考虑的有裂纹物体的函数,参考文献[1]对Y 值的计算公式进行了归纳。
K 是建立在线弹性断裂力学基础上的,它研究的是理想弹性体的低应力脆性断裂问题,其主要对象是高强度低韧性钢,这种材料认为其断裂没有塑性变形。
但实际一般钢结构在裂纹尖端或多或少存在塑性变形区(屈服区),塑性区的形状和尺寸因材料性质、几何形状和应力状态等因素而异。
当屈服区小于裂纹尺寸,称为小范围屈服。
研究表明对裂纹尖端的塑性区进行修正,小范围屈服的裂纹体仍可应用线弹性断裂力学。
abaqus计算应力强度因子

重庆大学课题: Abaqus 计算裂纹应力强度因子学院:专业:学号:姓名:一、计算裂纹应力强度因子问题描绘:以无穷大平板含有一单边裂纹为例,裂纹长度为 a=10mm,平板宽度 h=30,弹性模量 E=210000Pa,泊松比 v=,在远场受双向均布拉应力。
使用 Abaqus 计算该问题:1、进入 part 模块成立平板 part ,平板的尺寸相关于裂纹足够大,本例尺寸为50x30(mm);使用 Partation Face:sketch 工具,将 part 分开成如图 1 形式图 12、进入 property 模块成立弹性资料;截面选择平面问题的solid,homogeneous;给予截面。
3、进入 Assembly 模块实体的种类( instance type)选择 independent 。
4、进入 mesh 模块区分单元格如图 2 所示。
图 25、进入 interaction 模块指定裂纹 special/creak/assign seam;生成裂纹 crack 1,special/crack/create ;special/crack/edit ,对两个裂纹进行应力奇怪的设置。
6、进入 step 模块在 initial 步以后成立 static , general 步;在output/history output requests/create/中创立输出变量。
7、进入 load 模块定义位移和荷载界限,如图 3 所示。
图 38、进入 job 模块,提交计算Mises 应力散布见图4,在 .dat 文件中(图 5)查察应力强度因子。
图 4图 5计算分析解:由公式F=- (a/h)+(a/h) 2- (a/h)3+(a/h)4计算得分析解为k=1001应力强度因子偏差为%二、偏差剖析改变板的长度,其余条件不变1.当长度L=100时偏差为 %2.当板长L=30偏差为 %结论:当板长改变,板长没法表现无穷大的状况,计算结果的偏差会变大。
应力强度因子的计算.doc

第二章 应力强度因子的计算K --应力、位移场的度量⇒K 的计算很重要,计算K 值的几种方法: 1.数学分析法:复变函数法、积分变换; 2.近似计算法:边界配置法、有限元法; 3.实验标定法:柔度标定法; 4.实验应力分析法:光弹性法.§2-1 三种基本裂纹应力强度因子的计算一、无限大板Ⅰ型裂纹应力强度因子的计算K Z ξ→=→ⅠⅠ计算K 的基本公式,适用于Ⅱ、Ⅲ型裂纹.1.在“无限大”平板中具有长度为2a 的穿透板厚的裂纹表面上,距离x b =±处各作用一对集中力p .Re Im x Z y Z σ'=-ⅠⅠRe Im y Z y Z σ'=+ⅠⅠRe xy y Z τ'=-Ⅰ选取复变解析函数:222()Z z b π=- 边界条件:a.,0x y xy z σστ→∞===.b.,z a <出去z b =±处裂纹为自由表面上0,0y xy στ==。
c.如切出xy 坐标系内的第一象限的薄平板,在x 轴所在截面上内力总和为p 。
y '以新坐标表示:Z=⇒lim()K Zξξ→==Ⅰ2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上,在距离1x a=±的范围内受均布载荷q作用.利用叠加原理:微段→集中力qdx→dK=Ⅰ⇒K=⎰Ⅰ令cos cosx a aθθ==,cosdx a dθθ=⇒111sin()1cos22(cosaa aaaK daθθθ--==Ⅰ当整个表面受均布载荷时,1a a→.⇒12()aaK-==Ⅰ3.受二向均布拉力作用的无限大平板,在x轴上有一系列长度为2a,间距为2b 的裂纹.边界条件是周期的: a. ,y x z σσσ→∞==.b.在所有裂纹内部应力为零.0,,22y a x a a b x a b =-<<-±<<±在区间内0,0y xy στ==c.所有裂纹前端y σσ> 单个裂纹时Z =又Z 应为2b 的周期函数⇒sinzZ πσ=采用新坐标:z a ξ=-⇒sin()a Z πσξ+=当0ξ→时,sin,cos1222bbbπππξξξ==⇒sin()sincos cos sin22222a a a bbbbbπππππξξξ+=+σcossin222a a bbbπππξ=+2222[sin()]()cos 2cos sin(sin)2222222a a a a a bbbbbb bπππππππξξξ+=++22[sin()](sin )2cos sin22222a a a a bbbbbπππππξξ⇒+-=sinaZ ξπσ→⇒=sinlim aK ξπσ→⇒===Ⅰ=取w M =修正系数,大于1,表示其他裂纹存在对K Ⅰ的影响. 若裂纹间距离比裂纹本身尺寸大很多(2125a b ≤)可不考虑相互作用,按单个裂纹计算.二、无限大平板Ⅱ、Ⅲ型裂纹问题应力强度因子的计算 1.Ⅱ型裂纹应力强度因子的普遍表达形式(无限大板):lim (K Z ξξ→=Ⅱ2.无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切力作用.τsin()zZ z πτ=sin()()a Z πτξξ+=lim ()K ξξ→⇒==Ⅱ3.Ⅲ型裂纹应力强度因子的普遍表达形式(无限大板):lim ()K ξξ→=Ⅲ4.周期性裂纹:K =§2-2 深埋裂纹的应力强度因子的计算1950年,格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力和应变,得到椭圆表面上任意点,沿y 方向的张开位移为:1222022(1)x z y y a c=--其中:202(1)ay E μσ-=Γ.Γ为第二类椭圆积分.有φϕ= (于仁东书) 1222220[sin ()cos ]a d cπϕϕϕ=+⎰(王铎书)1962年,Irwin 利用上述结果计算在这种情况下的应力强度因子σ原裂纹面11cos ,sin z x ρϕρϕ==又222222221111221x z c x a z a c a c+=⇒+= ⇒ρ=假设:椭圆形裂纹扩展时,其失径ρ的增值r 与ρ成正比.r f ρ= (f 远小于1)r f ρ⇒==边缘上任一点(,)p x z ''',有:1()sin (1)sin (1)x r f f x ρϕρϕ'=+=+=+1()cos (1)z r f z ρϕ'=+=+11(,),(,)p x z p x z '''⇒均在0y =的平面内. 222242222(1)c x a z f a c a c ''''''⇒+=+=⇒新的裂纹面仍为椭圆.长轴(1)c f c '=+,短轴(1)a f a '=+. ⇒y 向位移22002(1)2(1)(1)(1)a f a y f y E E μσμσϕϕ'--+'===+原有裂纹面:222220()1x z ya c y ++=扩展后裂纹面:222220()1x z y a c y '''++='''以1x x '=,1z z '=,代入⇒原有裂纹面的边缘y 向位移y ',有2222211112222222011(1)(1)x z x z y y a c f a f c'=-+=--'''++。
如何使用ABAQUS计算应力强度因子

如何使用ABAQUS计算应力强度因子ABAQUS是一种广泛使用的有限元分析软件,可用于计算应力强度因子。
应力强度因子用于评估材料中的裂纹扩展性能,是断裂力学中的重要参数。
以下是使用ABAQUS计算应力强度因子的一般步骤:1.准备模型:在使用ABAQUS计算应力强度因子之前,需要先准备好模型。
模型应包含有裂纹的几何形状,以及材料的属性。
2.确定边界条件:要使用ABAQUS计算应力强度因子,必须指定适当的边界条件。
这些条件可以是约束的位移或力。
3.定义材料特性:为了计算应力强度因子,需要定义材料的特性,如弹性模量和泊松比。
这些特性通常可以从实验数据中获取。
4.创建网格:在使用ABAQUS计算应力强度因子之前,需要对模型进行离散化处理,将其划分为有限个单元。
这可以通过使用ABAQUS提供的网格生成工具来完成。
5.应用载荷:定义适当的载荷类型和大小,以便在模型上施加负载。
这可以是施加在边界上的力或位移。
6.定义裂纹:使用ABAQUS的初始裂纹命令或裂纹离散化工具来创建裂纹几何。
裂纹可以是直线裂纹,也可以是不规则或曲线裂纹。
7.定义断裂准则:使用ABAQUS的断裂准则定义工具,指定在何种条件下认为破坏发生。
常用的断裂准则包括应力强度因子法和能量释放率法。
8.运行ABAQUS求解器:在定义了模型、边界条件、材料特性、网格和载荷之后,可以运行ABAQUS求解器。
根据模型的复杂程度,可能需要较长的计算时间。
9.后处理结果:一旦ABAQUS求解器完成计算,可以使用ABAQUS提供的后处理工具来分析结果。
这些工具可以用于计算应力强度因子及其分布。
10.计算应力强度因子:通过使用ABAQUS的应力强度因子计算工具,可以计算裂纹尖端处的应力强度因子。
这些结果可以用来预测裂纹的扩展和破坏行为。
应力强度因子的数值计算方法

应力强度因子的数值计算方法应力强度因子是用来描述裂纹尖端应力场的重要参数,它在研究裂纹扩展、断裂行为等问题中具有重要的应用价值。
本文将介绍应力强度因子的数值计算方法,包括解析方法和数值方法。
一、解析方法解析方法是指通过求解弹性力学方程,得到应力场的解析表达式,进而计算应力强度因子。
常见的解析方法有:1. 爱尔兰函数法:该方法适用于轴对称问题,通过引入爱尔兰函数,将弹性力学方程转化为常微分方程,进而得到应力强度因子的解析表达式。
2. 奇异积分法:该方法适用于不规则裂纹形状或复杂载荷情况。
通过奇异积分的性质,将应力场分解为奇异和非奇异两部分,进而得到应力强度因子的解析表达式。
3. 线性弹性断裂力学方法:该方法通过建立合适的应力强度因子与裂纹尺寸之间的关系,利用裂纹尖端应力场的奇异性,通过分析弹性力学方程的边界条件,得到应力强度因子的解析表达式。
二、数值方法数值方法是指通过数值计算的方式,求解弹性力学方程,得到应力场的数值解,从而计算应力强度因子。
常见的数值方法有:1. 有限元法:有限元法是一种广泛应用的数值方法,通过将结构离散为有限个单元,建立节点间的关系,利用数值方法求解离散方程组,得到应力场的数值解,进而计算应力强度因子。
2. 边界元法:边界元法是一种基于边界积分方程的数值方法,通过将边界上的应力场表示为边界积分方程的形式,利用数值方法对积分方程进行离散求解,得到应力场的数值解,进而计算应力强度因子。
3. 区域积分法:区域积分法是一种基于区域积分方程的数值方法,通过将应力场表示为积分方程的形式,利用数值方法对积分方程进行离散求解,得到应力场的数值解,进而计算应力强度因子。
以上介绍了应力强度因子的数值计算方法,包括解析方法和数值方法。
解析方法适用于问题简单、载荷条件规则的情况,可以得到解析表达式并具有较高的精度;数值方法适用于问题复杂、载荷条件不规则的情况,通过数值计算可以得到应力场的数值解,并利用数值解计算应力强度因子。
焊接接头的应力强度因子计算与预测

焊接接头的应力强度因子计算与预测焊接接头是工程中常见的连接方式之一,它能够将两个或多个金属材料牢固地连接在一起。
然而,焊接接头在使用过程中会受到各种力的作用,导致应力集中和应力集中因子的产生。
因此,计算和预测焊接接头的应力强度因子是非常重要的。
焊接接头的应力强度因子是评估焊接接头强度的关键参数之一。
它描述了焊接接头中应力的分布情况,可以帮助工程师判断焊接接头是否能够承受外部力的作用。
应力强度因子的计算和预测需要考虑多种因素,如焊接接头的几何形状、应力分布和材料的力学性能等。
在计算焊接接头的应力强度因子时,通常会采用有限元分析方法。
有限元分析是一种数值计算方法,通过将复杂的结构分割成许多小的有限元素,然后根据力学原理和边界条件来计算每个元素的应力和变形。
通过对整个结构的所有元素进行求和,可以得到焊接接头的应力强度因子。
在进行有限元分析之前,需要先确定焊接接头的几何形状和边界条件。
几何形状包括焊缝的长度、宽度和高度等参数,边界条件包括外部力的大小和方向等。
这些参数的选择需要根据具体的工程要求和实际情况来确定。
在进行有限元分析时,还需要考虑材料的力学性能。
焊接接头通常由不同种类的金属材料组成,其力学性能也会有所差异。
因此,在计算应力强度因子时,需要考虑材料的弹性模量、屈服强度和断裂韧性等参数。
通过有限元分析计算得到的应力强度因子可以用于预测焊接接头的强度。
如果应力强度因子超过了材料的断裂韧性,就意味着焊接接头可能会发生裂纹或破裂。
因此,在设计焊接接头时,需要根据实际情况来选择合适的焊接参数和材料,以确保接头的强度满足工程要求。
除了有限元分析,还有其他方法可以用于计算和预测焊接接头的应力强度因子。
例如,可以使用解析方法来推导出焊接接头的应力分布和应力强度因子的解析表达式。
这种方法通常适用于简单几何形状和边界条件的焊接接头。
总之,焊接接头的应力强度因子计算和预测是工程设计中重要的一部分。
通过合理选择焊接参数、材料和几何形状,以及采用适当的计算方法,可以有效地评估焊接接头的强度,并确保其在使用过程中不会发生破裂或失效。
使用ABAQUS计算应力强度因子

------------------------------------------------------------------------------------------------------- 如何使用ABAQUS计算应力强度因子Simwefanhj(fanhjhj@)2011.9.9------------------------------------------------------------------------------------------------------- 问题描述:以无限大平板含有一贯穿裂纹为例,裂纹长度为10mm(2a),在远场受双向均布拉应力σ=100N/mm2。
按解析解,此I型裂纹计算出的应力=396.23(N.mm-3/2)强度因子πσaK=I以下为使用ABAQUS6.10的计算该问题的过程。
第一步:进入part模块①建立平板part(2D Planar;Deformation;shell),平板的尺寸相对于裂纹足够大,本例的尺寸为100×50(mm)。
②使用Partation Face:sketch工具,将part分隔成如图1形式。
图1第二步:进入property模块①建立弹性材料;②截面选择平面问题的solid,homogeneous;③赋予截面。
第三步:进入Assembly模块不详述。
需注意的是:实体的类型(instance type)选择independent。
第四步:进入mesh模块除小圈内使用CPS6单元外,其它位置使用CPS8单元离散(图2)。
裂纹尖端的奇异在interaction模块中(图4)考虑。
图2第五步:进入interaction模块①指定裂纹special/creak/assign seam,选中示意图3中的黄色线,done!②生成裂纹crack 1,special/crack/create,name:crack 1,type: contour integral.当提示选择裂纹前端时,选则示意图的红圈区域,当提示裂纹尖端区域时选择红圈的圆心,用向量q表示裂纹扩展方向(示意图3绿色箭头)。
应力强度因子的求解方法的综述

应力强度因子的求解方法的综述摘要:应力强度因子是结构断裂分析中的重要物理量,计算应力强度因子的方法主要有数学分析法、有限元法、边界配置法以及光弹性法。
本文分别介绍了上述几种方法求解的原理和过程,并概述了近几年来求解应力强度因子的新方法,广义参数有限元法,利用G*积分理论求解,单元初始应力法,区间分析方法,扩展有限元法,蒙特卡罗方法,样条虚边界元法,无网格—直接位移法,半解析有限元法等。
关键词:断裂力学;应力强度因子;断裂损伤;Solution Methods for Stress Intensity Factor of Fracture MechanicsShuanglin LU(HUANGSHI Power Survey&Design Ltd.)Abstract: The solution methods for stress intensity factor of fracture mechanics was reviewed, which include mathematical analysis method, finite element method, boundary collocation method and photo elastic method. The principles and processes of those methods were introduced, and the characteristics of each method were also simply analyzed in this paper.Key words: fracture mechanics; stress intensity factors0 引言断裂力学的基础理论最初起源于1920年Griffith的研究工作[1]。
Griffith在研究玻璃、陶瓷等脆性材料的断裂现象时,认为裂纹的存在及传播是造成断裂的原因。
应力强度因子

断裂与损伤力学应力强度因子数值计算方法综述2013年6月第一章应力强度因子求解方法概述含有裂纹的工程结构的断裂力学分析一直是一个重要问题,在断裂力学理论中应力强度因子是线弹性断裂力学中最重要的参量。
它是由构件的尺寸、形状和所受的载荷形式而确定。
由于裂尖应力场强度取决于应力强度因子,因此在计算各种构件或试件的应力强度因子是线弹性断裂力学的一项重要任务。
由于应力强度因子在裂纹体分析中的中心地位,它的求解自断裂力学问世以来就受到了高度的重视。
迄今为止,已经产生了众多的理论和致值解法。
70年代中期以前的有关工作在文献中已有相当全面的总结,近20年来,求解的方法又得刭了明显的发展与完善。
下文将穿透裂纹问题(二维)与部分穿透裂纹问题(三维)分开讨论。
第二章 二维裂纹问题2.1 复变函数法由Muskhelishvili 的复变函数法,应力函数为:_])()()([2/1)]()(Re[z z z z z z z z χψψχψ++=+=Φ平面应变情况下的应力与位移为: )]('Re[42222z yx y x ϕφφσσ=∂∂+∂∂=+ )]('')(''[22z z z i xy y x χϕτσσ+=+-)](')('[21)(243x z z z iv u χϕμϕμμ+--=+ 可以证明,在裂纹尖端区域:)]('lim[220z z z iK K K I ϕπ-=-=∏由上式可见。
由于k 仅与)(z φ有关,因此只需确定一个解析函数)(z φ,就能求得k I ,这一方法一般只能用来解无限体裂纹问题。
对于含孔边裂纹的无限大板,通常可利用复变函数的保角映射原理来简化解题过程。
如采用复变(解析)变分方法,则可求解具有复杂几何形状的含裂纹有限大板的应力强度因子。
2.2 积分方程法弹性边值问题可以变为求解下列形式的积分方程:)())(()().,(r f dt t b a t t P t r M -=--⎰ 由积分方程解出沿裂纹的坐标的函数,便能直接求出应力强度因子k 。
微分求积单元法计算应力强度因子

l l
+
一
~
加筋圆柱曲板 的稳定性 问题[ Zog 9 hn 应用类似分单元的概念 , 1 。 提出 了多 域微分求积 法解材 料不连续 的弹性平 面应力 问题_, 雄华等 首次将 】吴 0 1 微分求 积法结合 区域分裂法 形成 了微分求积 区域分裂 法对裂缝问题进 行 了求 解_1 l 也采用分单元 的思想 , I J 研究的是一个数 学意义上不 连续的 问题 。 由于平 面问题仅涉及二 阶偏微分方程 , 边界条件处理不需要采用 多 自由度 , 本文将直接从 弹性力 学平 面问题基本位移控制方 程出发 , 建 立平 面应力板单元 ,首次采用微分 求积单元法来分析线 弹性 断裂力学 问题 , 以拓展微分求积法 的应用范 围。 先计算 出裂尖附近位移场和应力 场, 然后通过裂尖应力强度 因子与位移 的关系直接求解应力强度因子。
的节点划分 。 G G 1 微分求积平面应 力矩形板单元 . 2 考虑 弹性力学平面应力 问题 ,在直 角坐标 系下其 位移法基本微分 方程 ( 体力不计 ) 为旧
G V
N-X) (= ,, Ⅳ) - 1 j l …, 2
G V
() 6
a a 一 一
+
一
一
∑ ( ,…Ⅳ l,,) 2
应力强度因子的计算.

以1x x '=, 1z z '=,代入⇒原有裂纹面的边缘y向位移y ',有
22222
11112222222
011(1 (1 x z x z y y a c f a f c
'=-+=--'''++
222222
1111112222221(12 (12 12( x z x z x z f f f a c a c a c
r f ρ= (f远小于
1
r
f ρ
⇒=
=
边缘上任一点(, p x z ''',有:
1(sin (1 sin (1 x r f f x ρϕρϕ'=+=+=+
1(cos (1 z r f z ρϕ'=+=+
11(, , (, p x z p x z '''⇒均在0y =的平面内. 222242222(1 c x a z f a c a c ''''''⇒+=+=
a. , 0x y xy z σστ→∞===.
b. , z a <出去z b =±处裂纹为自由表面上0, 0y xy στ==。
c.如切出xy坐标系内的第一象限的薄平板,在x轴所在截面上内力总和为p。
y '
以新坐标表示:
Z =
⇒( K Z ξ→==
Ⅰ
2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上,在距离1x a =±的范围内受均布载荷q作用.
⇒新的裂纹面仍为椭圆.长轴(1 c f c '=+,短轴(1 a f a '=+. ⇒y向位移
单位分解有限元方法求解应力强度因子

单位分解有限元方法求解应力强度因子
一、有限元法的基本概念
有限元法(Finite Element Method,FEM)是一种应用于结构力学、流体力学以及固
体力学等众多研究领域的数值计算方法,是建立在离散一阶相对论基础上的数学解析方法。
其基本思路是:将对象划分成若干小的有限域,然后对每个有限域建立起离散的误差限制
条件,把原本的等价边界条件经过离散化处理后作为这些有限域的边界条件,将未知的空
间量化,然后分别针对这些有限元的非线性函数建立数学模型,最后求解出各元素的空间量,从而得到对象的总体函数解析模型。
二、应力强度因子有限元法求解
1、基本原理
应力强度因子(Stress Intensity Factor, SIF)是用于分析结构力学中弯曲、压缩、扭转、拉伸等力学载荷情况下结构的破坏程度,它的基本原理是根据St. Venant-
Kirchhoff理论,建立起材料应力应变关系和对应的力学载荷,并计算在周边某点结构的
分析结果,从而得出该点的SIF值。
2、有限元法求解
有限元法可以很好地用于求解应力强度因子。
若要求解某个结构的应力强度因子,首
先应当将其划分成多个相互交错的有限域,每个有限域内进行逐一求解,并使用对应的离
散构件模型与约束条件,得出不同结点的截断应力和截断应变的变化规律,最终归并各节
点的解析结果,从而计算出相应结构的应力强度因子。
应力强度因子的计算

应力强度因子的计算应力强度因子(Stress Intensity Factor)是应用于裂纹尖端的一个参数,用于描述裂纹尖端应力场的强度和分布情况,是计算裂纹扩展速率和破裂韧性的重要参数。
本文将详细介绍应力强度因子的计算方法。
一、引言在构件中存在裂纹时,应力场的分布将发生变化,通常存在一个应力集中区域,即裂纹尖端。
在裂纹尖端附近,裂纹两侧的应力强度具有很大的梯度,因此需要引入应力强度因子来准确描述和分析裂纹尖端的应力状态。
二、应力强度因子的定义应力强度因子可以描述裂纹尖端应力场的强度和分布情况。
对于模式I或拉应力模式下的裂纹,应力强度因子K是一个标量,具有长度的物理意义。
对于一种给定的应力场,应力强度因子K与应力强度因子K对应的应力场是相似的。
此外,由于应力强度因子K的引入,裂纹尖端附近的应力场能够用一个等效应力来代替,从而使裂纹尖端的破坏准则能够使用等效应力来描述。
三、常用的计算方法1.解析方法解析方法是通过对裂纹尖端附近应力场的数学分析,推导出裂纹尖端的应力强度因子。
常用的方法有:格里菲斯公式、韦尔奇定理、赵万江公式等。
这些方法通常需要对裂纹尖端应力场进行严格的数学推导和分析,适用于简单几何形状的裂纹。
2.应力分析方法应力分析方法是通过有限元分析、边界元分析等数值方法,对裂纹附近的应力场进行数值模拟,进而计算应力强度因子。
通过数值模拟可以得到更为复杂的几何形状下的应力强度因子。
通常需要使用计算机软件进行模拟和计算。
3.基于实验的方法基于实验的方法是通过实验测定裂纹尖端的应力强度因子,从而得到一种实验估算的方法。
常用的实验方法有高约束比压缩试验法、断口法、几何函数法等。
与解析方法和数值方法相比,实验方法具有直接、可靠、全面的优点,但通常对实验设备和技术要求较高。
四、应力强度因子的应用应力强度因子的计算在材料科学、工程结构分析和破坏力学等领域具有广泛的应用价值。
它可用于计算裂纹扩展速率、破断韧性、疲劳寿命等。
应力强度因子的数值计算方法

应力强度因子的数值计算方法引言一、理论计算方法1.弹性理论解法弹性理论解法是应力强度因子计算中最常用的一种方法。
它假设材料是弹性线性的,并忽略了材料的塑性变形。
常用的解法有Westergaard解和Westergaard-Hankel解。
2.能量解法能量解法是一种基于弹性力学的解法,通过计算裂纹尖端处的应力场能量和应变能量来计算应力强度因子。
常用的解法有Line-spring法和Irwin法。
3.有限元法有限元法是一种数值计算方法,通过将复杂的问题离散化为多个小区域,并在每个小区域上建立适当的数学模型进行计算。
通过求解离散化的方程组,可以得到裂纹尖端处的应力强度因子。
有限元法可以处理各种复杂的边界条件和几何形状的问题,并且可以考虑非线性和塑性变形。
这使得它成为计算应力强度因子的一种重要方法。
二、实验计算方法实验计算方法主要是通过设计和进行试验来测量裂纹尖端区域的应力和应变场,然后根据测量数据计算应力强度因子。
常用的方法有:1.发光全场法发光全场法是一种全场应变测量技术,通过在被测结构表面涂覆一层发光材料,然后利用高速摄像机记录结构在加载过程中的应变分布。
通过分析图像数据,可以得到裂纹尖端区域的应力和应变场,进而计算应力强度因子。
2.特征裂纹法特征裂纹法是一种利用疲劳试验得到应力强度因子的方法。
通过在试样上开几何形状确定的裂纹,然后在加载过程中观察裂纹的扩展行为,通过测量裂纹长度和加载荷载的关系,可以计算应力强度因子。
3.数值模拟法数值模拟法是一种将实验和数值计算相结合的方法。
通过建立几何和材料特性相似的数值模型,并在模型中模拟加载过程,可以得到裂纹尖端区域的应力和应变场,进而计算应力强度因子。
三、应力强度因子的应用1.疲劳断裂评估基于应力强度因子的计算结果,可以对工程结构在疲劳载荷下的断裂寿命进行评估和预测。
这对于提高结构的可靠性和安全性具有重要意义。
2.材料断裂韧性评定3.裂纹扩展行为研究通过分析应力强度因子的变化规律,可以研究裂纹在不同加载条件下的扩展行为,揭示断裂的机理和规律。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 应力强度因子的计算K --应力、位移场的度量⇒K 的计算很重要,计算K 值的几种方法: 1.数学分析法:复变函数法、积分变换; 2.近似计算法:边界配置法、有限元法; 3.实验标定法:柔度标定法; 4.实验应力分析法:光弹性法.§2-1 三种基本裂纹应力强度因子的计算一、无限大板Ⅰ型裂纹应力强度因子的计算K Z ξ→=→ⅠⅠ计算K 的基本公式,适用于Ⅱ、Ⅲ型裂纹.1.在“无限大”平板中具有长度为2a 的穿透板厚的裂纹表面上,距离x b =±处各作用一对集中力p .Re Im x Z y Z σ'=-ⅠⅠ!Re Im y Z y Z σ'=+ⅠⅠRe xy y Z τ'=-Ⅰ选取复变解析函数:Z =边界条件:a.,0x y xy z σστ→∞===.b.,z a <出去z b =±处裂纹为自由表面上0,0y xy στ==。
c.如切出xy 坐标系内的第一象限的薄平板,在x 轴所在截面上内力总和为p 。
/y '以新坐标表示:Z=⇒lim()K Zξξ→==Ⅰ\2.在无限大平板中,具有长度为2a的穿透板厚的裂纹表面上,在距离1x a=±的范围内受均布载荷q作用.利用叠加原理:微段→集中力qdx→dK=Ⅰ⇒aK=⎰Ⅰ、令cos cosx a aθθ==,cosdx a dθθ=⇒111sin()1cos22()cosaa aaaK daθθθ--==Ⅰ当整个表面受均布载荷时,1a a→.⇒12(aaK-==Ⅰ3.受二向均布拉力作用的无限大平板,在x轴上有一系列长度为2a,间距为2b的裂纹.边界条件是周期的: a. ,y x z σσσ→∞==.b.在所有裂纹内部应力为零.0,,22y a x a a b x a b =-<<-±<<±在区间内0,0y xy στ==c.所有裂纹前端y σσ> 单个裂纹时Z =#又Z 应为2b 的周期函数⇒sinzZ πσ=采用新坐标:z a ξ=-⇒sin()a Z πσξ+=当0ξ→时,sin,cos1222bbbπππξξξ==σ⇒sin()sincos cossin22222a a a bbbbbπππππξξξ+=+cos sin222a a bbbπππξ=+2222[sin()]()cos 2cos sin(sin)2222222a a a a a bbbbbbbπππππππξξξ+=++22[sin()](sin )2cos sin22222a a a a bbbbbπππππξξ⇒+-=sinaZ ξπσ→⇒=sinlim aK ξπσ→⇒===Ⅰ!=取w M =修正系数,大于1,表示其他裂纹存在对K Ⅰ的影响. 若裂纹间距离比裂纹本身尺寸大很多(2125a b ≤)可不考虑相互作用,按单个裂纹计算.二、无限大平板Ⅱ、Ⅲ型裂纹问题应力强度因子的计算 1.Ⅱ型裂纹应力强度因子的普遍表达形式(无限大板):lim (K Z ξξ→=Ⅱ2.无限大平板中的周期性的裂纹,且在无限远的边界上处于平板面内的纯剪切力作用.sin()zZ z πτ=sin()()a Z πτξξ+=lim ()K ξξ→⇒==Ⅱ3.Ⅲ型裂纹应力强度因子的普遍表达形式(无限大板):;lim ()K ξξ→=Ⅲ4.周期性裂纹:K =、τ*§2-2 深埋裂纹的应力强度因子的计算1950年,格林和斯内登分析了弹性物体的深埋的椭圆形裂纹邻域内的应力和应变,得到椭圆表面上任意点,沿y 方向的张开位移为:1222022(1)x z y y a c=--其中:202(1)ay E μσ-=Γ.Γ为第二类椭圆积分.有φϕ= (于仁东书) |σ1222220[sin ()cos ]a d cπϕϕϕ=+⎰(王铎书)1962年,Irwin 利用上述结果计算在这种情况下的应力强度因子原裂纹面11cos ,sin z x ρϕρϕ==又222222221111221x z c x a z a c a c+=⇒+=⇒ρ=假设:椭圆形裂纹扩展时,其失径ρ的增值r 与ρ成正比.r f ρ= (f 远小于1)r f ρ⇒==边缘上任一点(,)p x z ''',有:<1()sin (1)sin (1)x r f f x ρϕρϕ'=+=+=+1()cos (1)z r f z ρϕ'=+=+11(,),(,)p x z p x z '''⇒均在0y =的平面内.222242222(1)c x a z f a c a c ''''''⇒+=+=⇒新的裂纹面仍为椭圆.长轴(1)c f c '=+,短轴(1)a f a '=+. ⇒y 向位移22002(1)2(1)(1)(1)a f a y f y E E μσμσϕϕ'--+'===+原有裂纹面:222220()1x z ya c y ++=扩展后裂纹面:222220()1x z y a c y '''++='''以1x x '=,1z z '=,代入⇒原有裂纹面的边缘y 向位移y ',有222221111222222211(1)(1)x z x z y y a c f a f c '=-+=--'''++ }2222221111112222221(12)(12)12()x z x z x z f f f a c a c a c----=--++2f =2222200022(1)2y fy f f y fy ''⇒==+又f =⇒2y '=设各边缘的法向平面为平面应变,有:31)sin sin ]22v k θθ=+- 其中34k μ=-当θπ=时24(1)v K E μ-=222216(1)2I r K E μπ-⇒=:22021E ()41I K y acπμ⇒=-又202(1)ay E μσϕ-=14122222()(sin cos )I a K c a cϕϕφ⇒=+在椭圆的短轴方向上,即2πϕ=,有I ImaxK K φ== 危险部位 →椭圆片状深埋裂纹的应力强度因子当a c =时→圆片状裂纹,2πφ=2I K π⇒=#§2-3 半椭圆表面裂纹的应力强度因子计算一、表面浅裂纹的应力强度因子当aB (板厚)→线裂纹⇒可以忽略后自由表面对A 点应力强度的影响—欧文假设:半椭圆片状表面线裂纹I K 与深埋椭圆裂纹的I K 之比等于边裂纹平板与中心裂纹平板的I K 值之比。
I I I I K K K K =表边埋中又有:1220.1sin(1)tanI I AK W A K Wππ=+边中其中:A ----裂纹长度;W---板宽度 当1A W 时22sin A A W W ππ≈,tan A A W Wππ≈1.1I I K K ⇒≈≈边中1.1I I K K ⇒=表埋1.1I I K K ⇒==埋表→椭圆片状表面裂纹A 处的I K 值二、表面深裂纹的应力强度因子:深裂纹:引入前后二个自由表面⇒使裂纹尖端的弹性约束减少⇒裂纹容易扩展⇒I K 增大()I IK Me K ⇒=⋅表面(埋藏) 其中:Me —弹性修正系数,应大于1,由实验确定 一般情况下12Me M M =⋅其中:1M —前自由表面的修正系数2M —后自由表面的修正系数关于Me 表达式两种形式的论述 1. 巴里斯和薛a .0a c →时⇒接近于单边切口试样1 1.12M =b .1a c→时⇒接近于半圆形的表面裂纹11M =利用线性内插法110.12(1)aM c=+-%利用中心穿透裂纹弹性件的厚度校正系数⇒ 1222(tan )2B a M a Bππ=B —板厚a —裂纹深度 c —裂纹长度当aB 时21M ≈⇒浅裂纹不考后自由表面的影响2. 柯巴亚希.沙.莫斯2110.12(1)2a M c=+-1222(tan )2B a M a Bππ=⇒表面裂纹的应力强度因子(应为最深点处):I K =】|§2-4 其他问题应力强度因子的计算一、 Ⅰ.Ⅱ型复合问题应力强度因子的计算 复变数:iy x z +=,iy x z -=取复变解析函数:()x z p iq =+,11()z p iq ψ=+取应力函数:2()()()()z z zx z zx z ϕψψ=+++或Re[()()]z zx z ϕψ=+⇒满足双调和方程分析第一应力不变量:22'224Re[()]x y x z x yϕϕσσ∂∂+=+=∂∂ (推导过程略)对于Ⅰ.Ⅱ型复合裂纹Ⅰ型:'Re Im x I I Z y Z σ=-, 'Re Im y I I Z y Z σ=+⇒ ||0||0|0()2Re 2x y IIZ ξξξσσ→→→+==Ⅱ型:'2Im Re x II II Z y Z σ=+ 'Re y II y Z σ=-—000()|2Im |2|x y Z ξξξσσ→→→⇒+==ⅡⅡ⇒Ⅰ、Ⅱ型复合裂纹在裂纹前端处的不变量.000()|2|2|x y ξξξσσ+→→→+=+ⅠⅡ02)]|K iK ξ→⇒-ⅠⅡ 取复数形式的应力强度因子.K K iK =-ⅠⅡ00()|2|x y ξξσσ+→→⇒+=ⅠⅡ 又()4Re[()]x y x Z σσ'+=lim ()K Z ξ→'⇒=若采用z 坐标:()z aZ a K Z ξ→'=-⇒=选择()x z '满足具体问题的应力边界条件.⇒这种方法利用普遍形式函数求解应力强度因子. '1144()()()()f F Z F Z ZF Z ZF Z =+++ (14(),()F Z F Z 为解析函数)---复变解析函数表达的双调和函数的普遍形式(或复变应力函数为普遍形式). 利用这个方法可以求解很多”无限大”平板中的穿透裂纹问题. 二、有限宽板穿透裂纹应力强度因子的计算实际情况:应看成有限宽计算.→必须考虑的自由边界对裂纹尖端应力场和位移场的影响.→在理论上得不到完全解.→通过近似的简化或数值计算方法→数值解.方法:边界配置法,有限单元法等.针对有限宽板问题:寻找一个满足双调和方程和边界条件的应力函数或复变解析应力函数.边界配置法:将应力函数用无穷级数表达,使其满足双调和方程和边界条件,但不是满足所有的边界条件,而是在有限宽板的边界上,选足够多的点,用以确定应力函数,然后再由这样符合边界条件的应力函数确定K 值.边界配置法:计算平面问题的单边裂纹问题,只限于讨论直边界问题. 以三点弯曲试样为例进行说明.(1)威廉氏(Williams)应力函数和应力公式 。
