等值线专题高考题
2024年高考地理二轮热点题型归纳与变式演练:专题03 “等值线型”选择题答题技巧 (解析版)
等值线图是以相等数值点的连线表示连续分布且逐渐变化的数量特征的一种图形。图中数值相等的点连成曲线即等值线。等值线既是高考命题的重要考点,又是材料背景的重要表达形式。常见的等值线图有等高线图、等压线图、等温线图、等降水量线图、等深线图、等太阳高度线图、等盐度线图等,比文字叙述更严谨、更直观。不仅要关注各类等值线表达的地理事实,更要关注其背后的地理规律。
【例题3】(2023年河北高考真题)海水温度分布状况影响大气环流,对天气系统和长期气候变化有着重要影响。下图为某年赤道附近(5°S-5° N)部分海域海表温度距平时间-经度剖面(单位:℃)。据此完成下面小题。
5.上图反映该年赤道附近中、东太平洋出现()
A.厄尔尼诺现象B.厄尔尼诺现象一拉尼娜现象
C.拉尼娜现象D.拉尼娜现象→厄尔尼诺现象
1.图中“魔鬼地”是()
A.甲B.乙C.丙D.丁
【答案】1.A
【解析】1.依据信息:甲、乙、丙、丁四个营地中,其中一个营地由于空气流通不畅,易引起高原反应,被称为“魔鬼营地”。从图中可以看出,甲、乙、丙、丁四个营地中,丙、丁位于山脊,乙位于鞍部,这三个营地所处的地形部位都有利于空气流动,只有甲位于山谷,地形封闭,空气流通不畅,容易引起高原反应,故A对,BCD错。故选A。
A.冷干B.冷湿C.暖干D.暖湿
4.未来我国受该气旋过境影响最大的地区是()
A.华中地区B.华北地区C.东北地区D.西北地区
【答案】2.B 3.C 4.C
【解析】
2.根据图示信息可知,此时蒙古气旋与周围地区之间等压线密集,水平气压梯度大,且冷锋所处位置等压线比暖锋更密集,说明冷锋活动强于暖锋,B正确,ACD错误。所以选B。
8.1月渤海与黄海海水交换的模式是()
A.南进北出B.北进南出C.中间进南北出D.南北进中间出
等值线专题复习题.doc
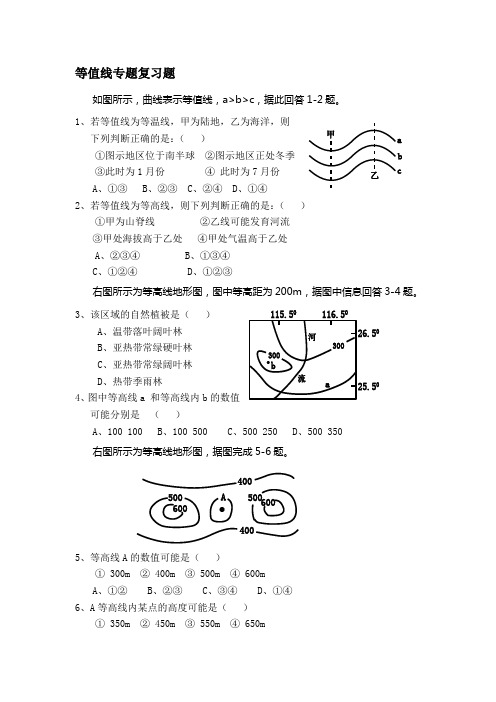
等值线专题复习题如图所示,曲线表示等值线,a>b>c ,据此回答1-2题。
1、若等值线为等温线,甲为陆地,乙为海洋,则 下列判断正确的是:( )①图示地区位于南半球 ②图示地区正处冬季 ③此时为1月份 ④ 此时为7月份 A 、①③ B 、②③ C 、②④ D 、①④2、若等值线为等高线,则下列判断正确的是:( )①甲为山脊线 ②乙线可能发育河流 ③甲处海拔高于乙处 ④甲处气温高于乙处 A 、②③④ B、①③④ C 、①②④ D 、①②③右图所示为等高线地形图,图中等高距为200m ,据图中信息回答3-4题。
3、该区域的自然植被是( )A 、温带落叶阔叶林B 、亚热带常绿硬叶林C 、亚热带常绿阔叶林D 、热带季雨林4、图中等高线a 和等高线内b 的数值 可能分别是 ( )A 、100 100B 、100 500C 、500 250D 、500 350 右图所示为等高线地形图,据图完成5-6题。
5、等高线A 的数值可能是( )① 300m ② 400m ③ 500m ④ 600m A 、①② B 、②③ C 、③④ D 、①④ 6、A 等高线内某点的高度可能是( )① 350m ② 450m ③ 550m ④ 650ma bc甲乙26.5025.5500600400400A 、①③B 、②③C 、②④D 、①④ 右图所示为等温线图,据图完成7-8题。
7、图中B 地的地形应是( )A 、高原B 、平原C 、山地D 、盆地 8、图中 A-B-C 一线气温的变化情况为 ( ) A 、A-B 增 B-C 减 B 、A-B 减 B-C 增C 、A-B-C 一直增D 、A-B 增 B-C 先减后增 右图所示为等值线,据图完成9-11题。
9、若等值线表示高空垂直面等压线,则下列判断正确的是 ( )①数值a>b ②A 处为高压③B 处气流上升 ④A 对应的近地面天气阴雨 A 、①②B 、②③C 、②④D 、③④10、若等值线表示近地垂直面等压线,则下列判断正确的是( )①数值a<b ②A 处为高压 ③B 处气流上升 ④A 处天气阴雨A 、①③④B 、①②④C 、①②③D 、②③④11、若等值线表示水平面等压线,且a>b ,则下列判断正确的是( )①A 虚线为高压脊 ②A 虚线为低压槽 ③B 虚线附近天气阴雨 ④B 虚线附近天气晴朗 A 、①③ B 、①④ C 、②③ D 、②④右图所示为北半球500 hpa 等压面上的等高线图,据图完成12-14题。
高考地理专项练习:等值线图(解析版)

高考地理专项练习:等值线图(解析版)一、选择题1.图为〝中纬度某地某日河流、风向、等压线、等高线、等温线、昏线的组合图〞,据此回答下题。
〔1〕该地域〔〕A. 位于南半球B. 该日昼长夜短C. 图中河段无凌汛现象D. 典型植被为亚热带常绿阔叶林〔2〕此时以下发作的现象中,能够的是〔〕A. 长江河口表层海水盐度到达一年中的最小值B. 青岛的海滨浴场人满为患C. 巴西利亚左近的草原一片翠绿D. 中国长城站出现极昼现象2.以下图是〝地球自转等线速度表示图〞,R、T在同一纬线上。
据此回答下面小题。
〔1〕该区域所在的半球位置和纬度位置是〔〕A. 南半球、低纬度B. 北半球、中纬度C. 南半球、中纬度D. 北半球、高纬度〔2〕R点地形最有能够是〔〕A. 山地B. 丘陵C. 高原D. 盆地3.以下图为我国西北沿海某城市功用分区表示图,图中字母代表的是不同的功用区,一条河流穿过该郊区〔图中没有画出河流,需依据等高线判别大致流向〕。
完成以下各题。
〔1〕假定在该河开发漂流旅游项目,那么漂流的动身地应设在〔〕A. a区B. d区C. e区D. g区〔2〕假定该市包括以下功用区且规划合理,那么g区最有能够是〔〕A. 住宅区B. 文明区C. 工业区D. 中央商务区4.〝雨舌〞是指丰沛降水区域呈〝舌头〞状向某中央向延伸的现象。
读西藏年等降水量线(单位:mm)和〝雨舌〞位置图,完成以下效果。
〔1〕影响〝雨舌〞区域的主要降水要素是〔〕A. 洋流B. 地形C. 植被D. 纬度〔2〕位于〝舌尖〞上的波密县,拥有共同的自然景观是〔〕A. 喀斯特别貌广布B. 冰川与森林相连C. 水网密布,水流湍急D. 土壤深沉,无机质多5.以下图中等值线为房价〔元/平方米〕,A处房价高于周围,其缘由不能够是〔〕A. 左近公路支线交汇,车辆过多B. 接近初等院校,文明气氛浓郁C. 临近景色区,环境优美D. 地势平整,工厂林立,失业方便6.四幅等降水量线图中,画法正确的选项是〔〕A. ①②B. ①③④C. ①④D. ①②③④7.气温、降水量和日照时数过高或过低都会给柑橘的生长发育带来风险,气候风险度越大,柑橘增产的能够性也越大。
高考地理等值线专题练习(含答案)

高考地理等值线专题练习巩固练习部分读某值线图,图中数值a<b<c。
据此回答1-4题。
1.若该图为我国某地等温线分布图,则影响其弯曲的主要原因可能是A.纬度位置B.沿岸暖流C.地形因素D.夏季风影响2.若该图为等高线图,且等高距为l00米,则①坡的朝向为A.西北B.西南C.东北D.东南3.若该图为等高线图,且该地区为我国东南某地区,则A.①处坡度小于②处B.①处山坡降水较多C.②处为山脊D.③处山坡比①处山坡马尾松长得好4.若该图为我国某地等压线图,则:A.①处吹偏南风B.②处易出现锋面C.③处降水较多D.该地区天气晴朗读图“某区域年太阳总辐射量(单位:千卡/平方厘米)分布图”,回答 5-7题。
5.M地的年太阳总辐射量可能为A.90千卡/平方厘米 B.85千卡/平方厘米C.95千卡/平方厘米 D.105千卡/平方厘米6.N处等值线向北弯曲的原因是A.海拔较低,为平原地形B.海拔较高,气压较低C.地处背风地带,降水较少D.与同纬度东部相比,晴天偏少,云雾偏多7.西南部地区等值线密集的原因是A.地形陡峭 B.太阳高度变化大C.气温变化大 D.海洋影响显著读图“世界某区域及附近海域表层海水等盐度线图”,完成8-10题。
8.图中J河是A.拉普拉塔河B.湄公河C.密西西比河D.墨累河9.J河流水位最高季节时,世界各地可能出现的现象是A.墨累达令盆地正收获小麦B.南极臭氧空洞范围达最大C.长江中下游地区干旱少雨D.珠江口附近出现咸潮现象10.通常情况下,图示N、M、P之间的距离为一年中较大的时期,该时期有可能为A.一月B.三月C.八月D.十月当地面或物体表面温度在0℃以下时,空气中的水汽会在其表面凝化成白色结晶,称为霜。
一般把入秋后最早出现的一次霜叫初霜,而入春后最末出现的一次霜叫终霜。
一年中,终霜后至初霜前的这段时间期叫无霜期。
下面是两地无霜期等值线图(单位:日)。
读图回答11-13题。
11.乙地比甲地无霜期长的原因是乙地A.纬度比甲地低B.地势起伏比甲地大C.海拔比甲地低D.气候海洋性比甲地强12.甲图中①、②两地无霜期差值T的范围是A.100<T<150 B.50<T<150 C.150<T<200 D.50<T<10013.关于两地主要粮食作物和作物熟制的叙述,正确的是A.甲地:冬小麦,一年两热B.乙地:春小麦,一年两熟C.甲地:春小麦,一年一熟D.乙地:冬小麦,一年一熟读我国大陆部分地壳等厚度线图,完成14-16题。
等值线专题高考真题

等值线专题高考真题(2012.上海)等高线地形图可以帮助人们正确认识地形地貌。
读下图回答下列1-2小题。
1.右图所示地区地形地势的基本特点是()①以丘陵、平原为主②中部高,西南、东北低③以平原、盆地为主④中部低,西南、东北高A.③④B.②③C.①②D.①④2.图中甲、乙两条虚线所在的地形部位分别是()A.山脊、山谷 B.山脊、山脊C.山谷、山脊 D.山谷、山谷(2016.上海)等高线图可以反映一个地方的地貌特征。
右图为某地区等高线(单位:m)图,回答3-4题。
3.图中主体部分表示的地表景观最可能是()A.新月形沙丘B.山地梯田C.三角洲平原D.滨海沙滩4.图中河流的流向及河流与水渠的关系是()A.河流自南向北流,河流水补给水渠B.河流自北向南流,河流水补给水渠C.河流自北向南流,水渠水汇入河流D.河流自南向北流,水渠水汇入河流(2013.四川)下图示意我国黄土高原某地林木的分布状况,图中相邻等高线之间高差均为 30 米。
读图回答5-6题。
5.林木生长与土壤水分条件相关图中林木密集区位于()A.鞍部B.山谷C.山脊D.山顶6.图示区域内东、西两侧最大高差可能是()A.156 米B.178 米C.220 米D.255 米(2012.I)下图示意某小区域地形。
图中等高距为100米,瀑布的落差为72米。
据此完成7-8题。
7.Q地的海拔可能为()A. 90米B. 230米C. 340米D. 420米8.桥梁附近河岸与山峰的高差最接近()A. 260米B. 310米C. 360米D. 410米(2011.I)读图,回答9-11题:9.图示区域内最大高差可能为( )A.50 mB.55 mC.60 mD.65 m10.图中①②③④附近河水流速最快的是( )A.①B.②C.③D.④11.在图示区域内拟建一座小型水库,设计坝高约13 m。
若仅考虑地形因素,最适宜建坝处的坝顶长度( )A.15 mB.40 mC.65 mD.90 m(2011.四川)右图为我国部分地区地表年蒸发量等值线图。
等值线高考试题
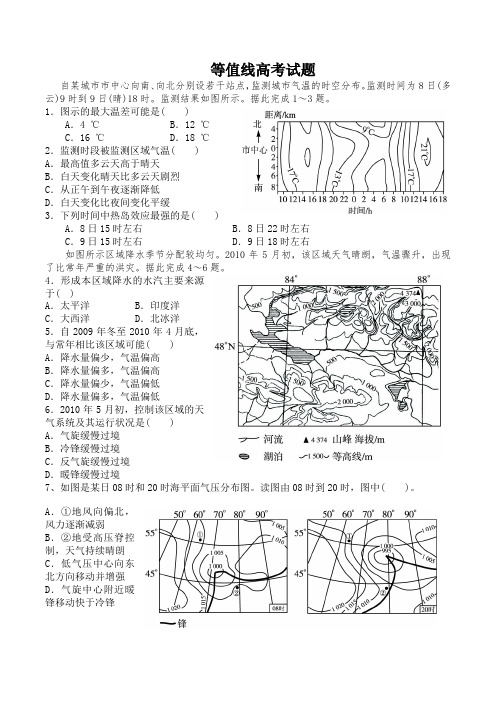
等值线高考试题自某城市市中心向南、向北分别设若干站点,监测城市气温的时空分布。
监测时间为8日(多云)9时到9日(晴)18时。
监测结果如图所示。
据此完成1~3题。
1.图示的最大温差可能是( )A.4 ℃ B.12 ℃C.16 ℃ D.18 ℃2.监测时段被监测区域气温( )A.最高值多云天高于晴天B.白天变化晴天比多云天剧烈C.从正午到午夜逐渐降低D.白天变化比夜间变化平缓3.下列时间中热岛效应最强的是( )A.8日15时左右 B.8日22时左右C.9日15时左右 D.9日18时左右如图所示区域降水季节分配较均匀。
2010年5月初,该区域天气晴朗,气温骤升,出现了比常年严重的洪灾。
据此完成4~6题。
4.形成本区域降水的水汽主要来源于( )A.太平洋 B.印度洋C.大西洋 D.北冰洋5.自2009年冬至2010年4月底,与常年相比该区域可能( )A.降水量偏少,气温偏高B.降水量偏多,气温偏高C.降水量偏少,气温偏低D.降水量偏多,气温偏低6.2010年5月初,控制该区域的天气系统及其运行状况是( )A.气旋缓慢过境B.冷锋缓慢过境C.反气旋缓慢过境D.暖锋缓慢过境7、如图是某日08时和20时海平面气压分布图。
读图由08时到20时,图中( )。
A.①地风向偏北,风力逐渐减弱B.②地受高压脊控制,天气持续晴朗C.低气压中心向东北方向移动并增强D.气旋中心附近暖锋移动快于冷锋水温图(单位:℃)。
读图,回答8~10题。
8.四位同学绘制的图中,正确的是( )A.① B.② C.③ D.④9.当新疆喀什(39°24′N,75°54′E)区时为6月10日8:00时,甲地的景象可能是( )A.旭日东升 B.艳阳当空C.夕阳西下 D.夜阑人静10.乙地所属气候类型分布范围最广的大洲是( )A.亚洲 B.非洲 C.欧洲 D.南美洲11、材料:亚洲冷高压一般形成于9月份,并逐步受其影响,2006年9月3日至5日,四川盆地经历一次暴雨过程。
高考地理高频题型专项训练等值线图的判读(1)作业(通用版)

题型一等值线图的判读(1)——2023届高考地理高频题型专项训练下图为“某地区等高线地形图”(单位:米)。
读图,完成下列问题。
1.图中“P~Q”一线()A.经过两个鞍部B.最低处海拔为30米地处于谷地之中 D.高差最大可达300米2.在a、b、c、d四地观察()地能看到b地地能看到c地地能看到c地地能看到d地海水透明度是表示海水能见程度的一个量度,影响透明度分布和变化的主要因素是海水的光学性质、水中的悬浮物质等,下图为局部海域6月和10月等透明度线分布图(单位:米)。
据此完成下面小题。
3.下列说法正确的是()A.等透明度线与等深线的分布比较接近B.夏季渤海海域透明度低于秋季C.夏季东海近岸与外海透明度差异较大D.近岸海区较外海的能见程度好4.10月份甲地等透明度线形成向外海突出的“水舌”,主要影响因素是()A.洋流B.地表径流C.海底地形D.人类活动下图为某区域年平均气温(单位:℃)等温线图。
据此完成下面小题。
5.图示地区常见的小尺度环流是()A.锋面气旋B.山谷风C.湖陆风D.暖性高压6.①②③④四地中,最易出现大气逆温层的是()A.①B.②C.③D.④下图为南半球某地等压线(单位:百帕)示意图。
完成下面小题。
7.四地中风力最大的是()A.①B.②C.③D.④8.④处的风向为()A.西北风B.东北风C.西南风D.东南风读图,完成下面小题。
9.影响图中①②③三条等温线基本走向及数值递变的主导因素是()A.纬度B.海陆位置C.地形D.洋流10.图中R地的气温数值,最可能是()读下图,完成下面小题。
11.此图若为北半球等温线图,且甲、丙为海洋,乙为陆地,则气温数值()A.d>b>c>aB.c>d>a>bC.c>a>d>bD.d>b>c>a12.若此图为等高线,则()A.沿a、c线能发育河流B.沿b、d线成为河流的分水岭C.该区域的地势起伏不大、c两地的气温差与b、d两地的气温差接近13.下图为该区域等高线(单位:m)地形图,完成下列问题。
高考地理等值线专题训练

高考地理:等值线专题训练一、单选题1.重庆年太阳年辐射总量数值约为:()A.80B.86C.95D.1072.受年太阳辐射总量的影响:()A.重庆市应鼓励居民广泛使用太阳能B.上海、福州可以太阳能取代常规能源C.昆明四季如春,适宜发展花卉园林业D.台北年降水量大,年太阳辐射总量小3.与广州比,兰州的年太阳年辐射总量比广州丰富,主要原因是:()A.纬度高,昼更长B.纬度高,正午太阳高度更大C.降水更少,多晴天D.位于黄土高原,海拔更高图为“非洲大陆局部区域某月份平均气温(°C)分布图”。
读图完成下列各题。
4.控制图中①②③三条等温线基本走向及数值递变的主导因素是A.纬度B.地形C.洋流D.海陆位置5.图中R地的气温数值,可能是A.27B.23C.20D.16干燥度是蒸发量与降水量的比值,通常反映某地某时段水分的收入和支出状况。
下图为海南岛等年日照时数线分布图,读下图完成下列各题6.关于图示甲、乙、丙三地干燥度的叙述,正确的是A.干燥度甲>乙>丙B.甲地太阳辐射强,降低了甲地的干燥度C.乙地比丙地距海近,干燥度更小D.丙地干燥度最低,最适合种植业的发展7.关于图中盐场的叙述,正确的是①处于夏季风的背风坡,降水较少②沿岸暖流增温,利于晒盐③晴天多,太阳辐射强,蒸发旺盛④产盐最多的季节为春季⑤夏秋季节多受台风影响,利于晒盐A.①②④B.②③⑤C.①③④D.①③⑤下图为我国某月某日某时刻气压分布图(单位:百帕),读图完成下列各题。
8.此时,A.台北天气晴朗B.西安西北风强劲C.广州天气晴朗D.渤海不可能有冰情9.该日,我国北方出现大范围雾霾,据图推测此时雾霾最重的城市是A.哈尔滨B.北京C.大连D.青岛读如图,完成下列各题。
10.根据图示信息,推断当地主要地形特征A.地势起伏较小,以平原为主B.东高西低,东部为山地C.周边山脉围绕,应为盆地D.地势起伏大,可能为高原11.区域内沿-10℃等温线,自南向北走A.自然景观由荒漠逐渐变为森林B.自然带由亚寒带森林带逐渐变为温带草原带C.降水中来自北冰洋的水汽含量比例增大D.越往北土壤层越深厚,有机质含量越大12. 读某区域小比例尺等温线分布图,若a>b,阴影部分为陆地,则图中所示为()A.北半球7月等温线分布B.南半球1月等温线分布C.南半球7月等温线分布D.北半球1月等温线分布图1所示区域陆地地势平坦,图2为图1中河流甲、乙两处的年径流量曲线。
高考一轮复习等值线图专题训练

高考一轮复习等值线图专题训练练习1:下图是欧洲西部农业产值分布示意图,回答(1)~(2)题。
(1)影响其产值分布的最主要区位因素是A、科技B.地形C.气候D、市场答案:D 点拨:本图等值线的高值分布在欧洲西部英国、法国、德国等发达国家,所以影响该农业产值分布的最主要因素是市场。
(2)X地农业地域生产类型是A、商品谷物农业B.乳畜业C、混合农业D.种植园农业答案:B 点拨:欧洲西部属于温带海洋性气候,热量不足,主要农业是利用这里牧草和市场发展的乳畜业。
练习2:下图为我国某城市城区地租分布等值线图(数值:a>b>c),读图判断(1)~(3)题。
(1)该市重工业不断向东北部迁移,主要原因可能是①城区地价上涨①为了缓解城区日益严重的环境污染①北部人口众多,有大量剩余劳动力①北部地区矿产资源丰富A.①①B.①①C.①①D.①①答案:A 点拨:重工业占地广,地租在成本中的比重比较大,而且往往污染严重,随着城市区域发展,中心城区污染加重,地价上涨,加重了地租成本和治理污染成本,所以重工业向外迁移。
(2)从重工业生产的特点看,该重工业区的交通运输方式主要是①水运①公路运输①航空运输①铁路运输A.①①B.①①C.①①D.①①答案:D 点拨:重工业原料和产品庞大,运费在成本中的比重较高,主要配合的运输方式为铁路运输和水路运输。
(3)近年来,甲地出现了高级住宅群,主要原因是甲地A.位于城区外缘,环境质量好B.远离中心城区,地价便宜C.地势开阔,便于建立住宅区D.位于河流附近,取水方便答案:A 点拨:高级住宅区要求的主要区位条件是环境质量高和交通便利。
练习3:读下图回答(1)~(2)题。
(1)图中①地的地下径流方向是:A.自东南向西北B.自东向西C.自西南向东北D.从北向南答案:C 点拨:地下径流方向垂直于等值线,从高到低。
(2)在资源利用上,图中显示该地存在的问题是A.不合理利用土地资源,导致土地盐碱化B.过度利用水资源,导致沙漠化C.滥砍乱伐森林,破坏生态平衡D.过度抽取地下水,形成地下水漏斗区答案:D点拨:沿着XY方向,出现了一个地下水低值区,对应地形剖面图中,有一个城市,说明是城市过度抽取地下水,导致地下水漏斗区。
高中地理等值线专题训练(精华版)含答案
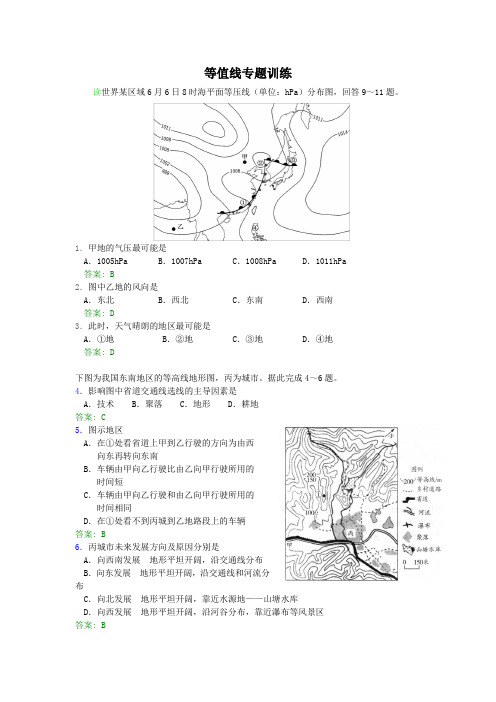
等值线专题训练读世界某区域6月6日8时海平面等压线(单位:hPa)分布图,回答9~11题。
1.甲地的气压最可能是A.1005hPa B.1007hPa C.1008hPa D.1011hPa答案: B2.图中乙地的风向是A.东北 B.西北 C.东南 D.西南答案: D3.此时,天气晴朗的地区最可能是A.①地B.②地C.③地D.④地答案: D下图为我国东南地区的等高线地形图,丙为城市。
据此完成4~6题。
4.影响图中省道交通线选线的主导因素是A.技术 B.聚落 C.地形 D.耕地答案: C5.图示地区A.在①处看省道上甲到乙行驶的方向为由西向东再转向东南B.车辆由甲向乙行驶比由乙向甲行驶所用的时间短C.车辆由甲向乙行驶和由乙向甲行驶所用的时间相同D.在①处看不到丙城到乙地路段上的车辆答案: B6.丙城市未来发展方向及原因分别是A.向西南发展地形平坦开阔,沿交通线分布B.向东发展地形平坦开阔,沿交通线和河流分布C.向北发展地形平坦开阔,靠近水源地——山塘水库D.向西发展地形平坦开阔,沿河谷分布,靠近瀑布等风景区答案: B下图示意某区域1月份0℃气温等温线分布,读图完成9~10题。
7.导致图中0℃等温线弯曲的主要因素是A.太阳辐射B.大气降水C.沿岸洋流D.曲折海岸答案: C8.图示地区A.河流短小湍急,水力资源丰富B.南北温差大,降水量东多西少C.峭耸悬崖多分布在陆地东南岸D.荒漠草原广布,森林面积较小答案: A下图为某山区等高线图(单位:米)。
为了让游客体验悬空、惊险、刺激,该地旅游局将原有登山线路中的某段改造为玻璃栈道(小图所示)。
完成7~8题。
9.图中甲、乙、丙、丁四处人类活动布局合理的是A. 甲—水文站B. 乙—农田C. 丙—瞭望台D. 丁—聚落答案: B10.最适宜改造为玻璃栈道的是A. ①段B. ②段C. ③段D. ④段答案: C下图为2014年12月14日8时(北京时间)世界局部地区海平面等压线(单位:百帕)分布图,完成5~6题。
等值线专题(有答案)

专题一:等值线一、等值线的定义及类型1、定义:在地图上,某些地理现象数值相等的点的连线2、常见的等值线:等温线、等高线、等压线、等降水量线等。
3、等值线的一般规律(1)数值相等组成的线(2)相邻等值线之间的差值相等(3)闭合(有的不闭合,是因图幅所限)(4)多不相交二、等温线图的判读1、影响气温分布的因素(1)纬度因素:在纬度因素影响下,等温线大致与纬度平行,且由低纬向高纬递减。
(2)海陆因素:①海洋性和大陆性气候的温度差异,如下左图(以北半球为例):②海陆之间的温度差异,如上右甲、乙两图:a、甲图为___半球,陆地等温线向___纬凸出,气温___;海洋则相反。
此时为北半球的___季。
b、乙图为___半球,陆地等温线向___纬凸出,气温___;海洋则相反。
此时为北半球的___季。
c、等温线分布规律:“高高低低”。
(3)地形因素:地势高气温低,地势低气温高。
所以对等温线弯曲的影响可根据“高高低低”规律,地势高的地方等温线总是向低纬凸出。
如右图:(4)洋流因素:洋流流经地区等温线的弯曲情况也可根据“高高低低”规律。
如下图:2、等温线图的判读和应用(1)判断某地的气温①最低月0℃等温线是划分暖温带和亚热带的分界线。
②根据某地地形判断气温高低:山地则气温低于周围地区,盆地则气温高于周围地区。
如下左图中甲地为____,乙地为____。
③根据等温线的变化趋势判断气温高低:如上右图判断甲、乙两地的气温。
甲地气温:_____,地形为_____;乙地气温______,地形为_____。
(2)判断南北半球、海陆分布气温从南向北递减为北半球;气温从北向南递减为南半球。
a、A图位于___半球,如该地在海洋,则图中的洋流为___流;b、B图位于___半球,如该地在海洋,则图中的洋流为___流;c、如C、D所示地区为北半球冬季,则C地为____,D地为____(陆地或海洋)。
(3)根据凸向判读季节根据“高高低低”规律。
如甲图陆地气温低,为北半球的冬季,南半球的夏季。
高考地理考前专题强化训练(卷二)等值线图的判读专题(8k版,可直接打印制卷)

学校:____________班级:___________姓名:_____________得分:____________高考地理考前专题强化训练(卷二)等值线图的判读本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分100分,考试用时60分钟。
第Ⅰ卷(选择题)单项选择题右图阴影部分为世界某大洲的局部某月(1月或7月)的等温线分布图,该处为高原地形,a 、b 为两条等温线,据此回答1~2题。
1.下列哪种现象可能出现( )A.圭亚那高原北部正值一年中的湿季B.此时正值华北平原小麦旺盛生长季节C.此时正值墨累-达令盆地小麦的收割季节D.塔里木河正值枯水期. 2.图中a 、b 等温线向北延伸的主要成因( )A.风带、气压带的季节移动B.洋流的影响C.山脉的分布D.厄尔尼诺现象影响; 读某群岛及附近海域部分等深线示意图,回答3~4题。
3.若要完整表示P 点附近的海水深度变化,应再补画几条等深线( ) A.3条 B.4条 C.5条 D.6条.4.P 点附近的海底地形是( )A.海岭B.海沟C.海盆D.大陆架;读“某地区某日平均气温分布和M地全年降水和昼夜情况示意图”。
完成5~6题。
5.图中,可用于判断M地位于北半球或是南半球的主要信息有( )①山地走向②昼夜长短的变化③纬度分布④降水量季节变化A.①②B.②③C.③④D.①④;6.该地区( ) A.分布在中纬度大陆东岸 B.植被以亚热带常绿硬叶林为主 C.农业以水稻种植业为主 D.白昼最长时降水量最多读右图,等值线a <b <c ,据此完成7~8题。
7.如果甲为陆地,乙为海洋,a 、b 、c 为等温线。
则图示区域为( ) A.南半球7月等温线图 B.北半球1月等温线图 C.北半球7月等温线图 D.南半球1月等温线图, 8.如果a 、b 、c 为等压线,则甲地天气最可能是( ) A.阴雨 B.晴朗 C.暴雨 D.偏北风;读某海城等深线和表层年平均等温线分布图回答9~10题。
高考地理必考点专练等值线

高考地理必考点专练-等值线必考点专练-等值线(建议用时:45分钟)一、选择题(2019·浙江杭州)下图为“我国华北某地区图”,图中实线表示等高线,R1为输水管道,R2R3为天然河流。
读图回答1~2题。
1.图中某村与甲处的相对高度可能是( )。
A.42米B.18米C.62米D.20米2.下列关于图示地区的说法正确的是( )。
A.该地自然植被是常绿阔叶林B.R1可自流输水C.R2西流补给R3D.R3可能有凌汛解析读图可知,图示地区为华北地区,植被为落叶阔叶林;图例是用题干中文字告诉我们的,图中实线表示等高线,R1为输水管道,R2、R3为天然河流。
根据图中等高线及河流位置可以判断甲的海拔为250~270m,某村海拔为210~230 m。
两地相对高度为20~60 m,但是不等于20m。
引水路线R1由低处向高处引水,不能自流输水;R2地势东高西低,河流向西流;R3由高纬流向低纬,不会有凌讯。
3.(2019·山东省临沂市)甲为“我国北方某区域等高线地形图”,乙为“沿甲图中某剖面线所作的地形剖面图”。
乙图所示地形剖面是沿甲图中的哪条线段所作A.ab B.cd C.ef D.gh解析乙图中,起点处海拔约为210米左右,故a、g两点不符合。
最高点靠近右端点,故cd线不符合。
答案C(2019·(浙江卷))某校学生于台风过后,前往某山区实习,观测溪谷的变化情况。
下图为学生实习地区的等高线地形图。
读图完成4~5题。
4.学生在实习中可以得知的是( )。
A.溪谷的坡度;溪谷的蒸发量B.溪谷的蒸发量;溪流的水深和流速C.溪谷的台风降雨量;堆积物粒径大小D.溪谷的坡度;堆积物粒径大小5.学生在溪谷的观测点是( )。
A.甲、乙B.甲、丙C.乙、丁D.乙、戊解析第4题,台风过后,学生在实习中不可能得到溪谷的蒸发量和台风的降雨量;但根据等高线地形图,可以求出溪谷的坡度,也可测量出堆积物粒径大小。
第5题,甲、丙两点位于溪谷中。
等值线专题高考题精粹.

等值线专题高考题精粹/平方米.年)图。
据此回答1-3题。
1. ①、②两地太阳年辐射总量的最大差值R可能是A.2900 <R <3000B.3400 <R <3500C.3900 <R <4000D.4400 <R <45002. 导致①、②两地太阳年辐射总量差异的主要因素是A.副热带高压B.纬度位置C.地形地势D.西南季风自某城市市中心向南、向北分别设若干站点,监测城市气温的时空分布。
监测时间为8日(多云)9时到9日(晴)18时。
监测结果如图2所示。
据此完成3~5题。
3.图示的最大温差可能是A.4 ℃B.12 ℃C.16 ℃D.18 ℃4.监测时段被监测区域气温A.最高值多云天高于晴天B.白天变化晴天比多云天剧烈C.从正午到午夜逐渐降低D.白天变化比夜间变化平缓5.下列时间中热岛效应最强的是A.8日15时左右B.8日22时左右C.9日15时左右D.9日18时左右下图所示区域属于湿润的亚热带季风气候。
回答6~8题。
6.R、Q两点的相对高度可能为A.800米B.900米C.1000米D.1100米7.M、N、P、Q四地中,海拔可能相等的两地是A.M、N B.M、PC.M、Q D.P、Q8.若在Q地建一小型度假村,应特别注意防治的自然灾害是A.风沙B.洪涝C.滑坡D.寒冻读图回答9~10题。
9、M处的气压数值可能为A.1 020、1 012.5B.1 017.5、1 020C.1 017.5、1 015D.1 015、1 012.510、N处的盛行风向不可能是A.南风B.西风C.西南风D.东北风11.图示地区4月份因大陆气团与海洋气团交绥而降水较多的地方为A.①B.②C.③D.④右图是世界某地区一月等温线图,其中a是25℃等温线,b是20℃等温线,读图完成12.造成ab两条等温线温度差异及b等温线走向的主要影响因素分别是①太阳辐射②地形③降水④洋流⑤大气环流A.①② B.③④C.①④D.②⑤13.此时图中PQ两点的温差最大不可能超过A.0℃ B.5℃C.10℃ D.15℃①图中①地的7月均温可能为A.18℃ B.16℃ C.14℃ D.10℃某种生物的种密度指单位面积该种生物的个体数量。
2023届新高考数学复习:专项(等高线问题)经典题提分练习(附答案)

2023届新高考数学复习:专项(等高线问题)经典题提分练习一、单选题1.(2023ꞏ全国ꞏ高三专题练习)设函数()22,0ln ,0x x x f x x x ⎧--≤⎪=⎨>⎪⎩①若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x ⋅⋅⋅的取值范围是()0,1②若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x +++的取值范围是()0,∞+③若方程()f x ax =有四个不同的实根,则a 的取值范围是10,e ⎛⎫⎪⎝⎭④方程()()2110f x a f x a ⎛⎫-++= ⎪⎝⎭的不同实根的个数只能是1,2,3,6四个结论中,正确的结论个数为( )A .1B .2C .3D .42.(2023ꞏ全国ꞏ高三专题练习)已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的解1234,,,,x x x x 且1234x x x x <<<,则()3122341x x x x x ⋅++⋅的取值范围是( )A .(]1,1-B .[]1,1-C .[)1,1-D .()1,1-3.(2023秋ꞏ四川泸州ꞏ高一四川省泸县第四中学校考阶段练习)已知函数()32log ,031108,333x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩,若方程()f x m =有四个不同的实根1x ,2x ,3x ,4x ,满足1234x x x x <<<,则()()341233x x x x --的取值范围是( )A .()0,3B .(]0,4C .(]3,4D .()1,34.(2023ꞏ全国ꞏ高三专题练习)已知函数f (x )=11,1211,12xx x x ⎧⎛⎫-⎪ ⎪⎪⎝⎭⎨⎪-+>⎪⎩…,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则123111222x x x⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎭⎝的取值范围是( )A .(95,42)B .(1,4)C .4)D .(4,6)5.(2023ꞏ全国ꞏ高三专题练习)已知定义域为()0,6的函数()y f x =的图象关于3x =对称,当(]0,3x ∈时,()ln f x x =,若方程()f x t =有四个不等实根1x ,2x ,3x ,()41234x x x x x <<<时,都有()223412190k x x x x -++-≥成立,则实数k 的最小值为( )A .724 B .13C .12D .1136.(2023ꞏ全国ꞏ高三专题练习)已知函数()22,0,()2,0xx x f x g x x x e x >⎧==-+⎨≤⎩(其中e 是自然对数的底数),若关于x 的方程(())0g f x m -=恰有三个不等实根123,,x x x ,且123x x x <<,则21322x x x --的最小值为( ) A .ln 33-B .3ln 22-C .ln 23-D .1-7.(2023ꞏ吉林长春ꞏ东北师大附中校考模拟预测)已知函数3e ,0()3,0x x f x x x ⎧≤=⎨>⎩,()22g x x x=-+(其中e 是自然对数的底数),若关于x 的方程()(())F x g f x m =-恰有三个不同的零点123,,x x x ,且123x x x <<,则12333x x x -+的最大值为( )A .31ln 4+B .41ln 3+C .3ln 3-D .3ln 3+8.(2023ꞏ全国ꞏ高三专题练习)已知函数()22322,,log ,,x mx m x m f x x x m ⎧-++≤⎪=⎨>⎪⎩,其中01m <<,若存在实数a ,使得关于x 的方程()f x a =恰有三个互异的实数解,则实数m 的取值范围是( ) A .1,14⎛⎫⎪⎝⎭B .1,19⎛⎫ ⎪⎝⎭C .10,4⎛⎫ ⎪⎝⎭D .10,9⎛⎫ ⎪⎝⎭9.(2023ꞏ全国ꞏ高三专题练习)已知函数lg ,0()lg(),0x x g x x x ⎧>⎪=⎨--<⎪⎩,若关于x 的方程()()5222g x g x -+=有四个不等根1234,,,x x x x ,则()()()()12341234x x x x g x g x g x g x +++++++的值是( )A .0B .2C .4D .810.(2023秋ꞏ宁夏ꞏ高三宁夏大学附属中学校考阶段练习)已知函数22,0(){|log |,0x x f x x x +≤=>,若关于x 的方程()()f x a a R =∈有四个不同实数解1234,,,x x x x ,且1234x x x x <<<,则1234x x x x +++的取值范围为 ( ) A .1(2,4-B .1[2,]4-C .[2,)-+∞D .(2,)-+∞11.(2023秋ꞏ湖北武汉ꞏ高一期末)已知函数()()2242,1,log 1,1,x x x f x x x ⎧++≤⎪=⎨->⎪⎩,若关于x 的方程()f x t =有四个不同的实数解1x ,2x ,3x ,4x ,且1234x x x x <<<,则)1234122x x x x ++的最小值为( ) A .72B .8C .92D .1212.(2023秋ꞏ河南郑州ꞏ高一新密市第一高级中学校考阶段练习)已知函数()()22log 1,131255,322x x f x x x x ⎧+-<≤⎪=⎨-+>⎪⎩,若关于x 的方程()f x m =有四个不同的实数解1234,,,x x x x ,且满足1234x x x x <<<,则下列结论正确的是( )A .121x x =-B .[]3421,25x x ∈C .3422x x +=D .12111x x +=- 13.(2023秋ꞏ江西上饶ꞏ高一统考期末)已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的实数解1x ,2x ,3x ,4x 且1234x x x x <<<,则()3122342x x x x x -+的取值范围是( ) A .()4,5 B .(]4,5C .()4,+∞D .[)4,+∞14.(2023春ꞏ全国ꞏ高三校联考专题练习)已知函数11()||||f x x a x b xa x=++-+--有五个不同的零点,且所有零点之和为52,则实数b 的值为( )A .1B .3C .5D .7二、多选题15.(2023秋ꞏ云南昆明ꞏ高一统考期末)已知函数ln(2),(2,0]()(2),(0,2]x x f x f x x ⎧+∈-=⎨-∈⎩,函数()y f x m =-有四个不同的零点,且从小到大依次为1x ,2x ,3x ,4x ,则下列结论正确的是( )A .121=x xB .1201≤<x xC .341x x =D .2410-<≤x x16.(2023ꞏ全国ꞏ高三专题练习)已知函数()e ,0,lg ,010,11,10,x x x f x x x x x ⎧⋅≤⎪=<<⎨⎪-+≥⎩,若22()3()()2g x f x mf x m =--有6个不同的零点分别为123456,,,,,x x x x x x ,且()()()123456345,x x x x x x f x f x f x <<<<<==,则下列说法正确的是( )A .当0x ≤时,()10ef x -≤≤B .34x x +的取值范围为1012,10⎛⎫⎪⎝⎭C .当0m <时,()()()()1234563f x f x f x x x f x +++的取值范围为1,0e ⎛⎫- ⎪⎝⎭D .当0m >时,()()()()1234563f x f x f x x x f x +++的取值范围为20,3e ⎛⎫⎪⎝⎭17.(2023ꞏ全国ꞏ高三专题练习)设函数22,0()ln ,0x x x f x x x ⎧--⎪=⎨>⎪⎩…,则下列命题中正确的是( )A .若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x ⋅⋅⋅的取值范围是(0,1)B .若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x +++的取值范围是(0,)+∞C .若方程()f x ax =有四个不同的实根,则a 的取值范围是10,e ⎛⎫⎪⎝⎭D .方程21()()()10f x a f x a-++=的不同实根的个数只能是1,2,3,618.(2023秋ꞏ辽宁大连ꞏ高一育明高中校考期末)已知函数()()22log 2,241617,42x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩,若方程()f x m =有四个不同的实根1234,,,x x x x ,满足1234x x x x <<<,则下列说法正确的是( )A .()121242x x x x +=+B .3412x x +=C .()3432,34x x ∈D .函数()()()()21g x f x m f x m =+--的零点为12346,,,,x x x x19.(2023秋ꞏ山西太原ꞏ高一古交市第一中学校校考阶段练习)已知函数22log ,02()813,2x x f x x x x ⎧<<=⎨-+≥⎩,若f (x )=a 有四个不同的实数解x 1,x 2,x 3,x 4,且满足x 1<x 2<x 3<x 4,则下列命题正确的是( ) A .0<a <1B.12922x x ⎡⎫+∈⎪⎢⎣⎭C .12342110,2x x x x ⎛⎫+++∈ ⎪⎝⎭D.)122x x ⎡+∈⎣20.(2023秋ꞏ重庆铜梁ꞏ高一校考期中)已知奇函数()f x 的定义域为R ,()3f x +为偶函数,且()f x 在[]0,3上单调递减.若关于x 的方程()f x a =在区间[]12,12-上有4个不同的根1234,,,x x x x ,则( ) A .()()6f x f x =+B .()f x 的图象关于直线3x =对称C .1234x x x x +++的值可能为12-D .1234x x x x +++的值可能为1221.(2023ꞏ全国ꞏ高三专题练习)设函数()2101,0lg ,0x x x f x x x ⎧++≤⎪=⎨>⎪⎩,若关于x 的方程()()f x a a R =∈有四个实数解1234,,,x x x x ,且1234x x x x <<<,则()()1234x x x x +-的值可能是( ) A .0B .1C .99D .100三、填空题22.(2023秋ꞏ石河子一中校考阶段练习)已知函数()2e ,0ln ,>0x x x f x x x ⎧-≤⎪=⎨⎪⎩,若函数()y f x b=-有四个不同的零点1x 、2x 、3x 、4x ,且1234x x x x <<<,则以下结论正确的是_____.①22342x x +>;②20eb <<; ③122x x +=-; ④()13422x x x x +<-.23.(2023ꞏ贵州贵阳ꞏ校联考模拟预测)已知函数()()22log 1,13,1910,3,22x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩若方程()f x m =有四个不同的实根1234,,,x x x x ,满足1234x x x x <<<,则()()()()34121111x x x x ----的取值范围是______.24.(2023秋ꞏ河南郑州ꞏ高一郑州市第七中学校考期末)已知函数()()2121xx f x f x x ⎧≤⎪=⎨->⎪⎩,,,若方程()f x a =有四个不相等的实数根1x ,2x ,3x ,4x ,则22222341x x x x +++的取值范围为__________.25.(2023春ꞏ广东揭阳ꞏ高一校考阶段练习)已知函数()()ln ,036,36x x f x f x x ⎧<≤⎪=⎨-<<⎪⎩,若当方程()f x m =有四个不等实根()12341234,,,x x x x x x x x <<<时,不等式22341230kx x x x k ++≤+恒成立,则实数k 的最大值为____________.26.(2023秋ꞏ江西宜春ꞏ高一江西省丰城中学校考阶段练习)设()()ln ,024,24x x f x f x x ⎧<≤⎪=⎨-<<⎪⎩若方程()f x m =有四个不相等的实根()1,2,3,4i x i =,且1234x x x x <<<,则()2221234x x x x +++的取值范围为___________.27.(2023秋ꞏ湖北ꞏ高一赤壁一中校联考阶段练习)()22log ,0269,2x x f x x x x ⎧<<=⎨-+≥⎩,若关于x 的方程()()()()222100f x t f x t t t -+++=≤有且仅有四个不相等的实数根1x 、2x 、3x 、()41234x x x x x <<<,则1234x x x x t +++的取值范围为__________.28.(2023ꞏ江苏ꞏ高一期末)已知函数22122,0()2log ,0x x x f x x x ⎧++≤⎪=⎨⎪>⎩,若关于x 的方程 f (x ) =a 有四个不同的解1234,,,x x x x ,且1234x x x x <<<,则212344x x x x x ++的取值范围是 _________ 29.(2023秋ꞏ河南濮阳ꞏ高三濮阳南乐一高校考阶段练习)已知函数()()()333322f x x a x b x a x =++-+--有五个不同的零点,且所有零点之和为52,则实数b 的值为______.30.(2023秋ꞏ福建福州ꞏ高一福州四中校考期末)已知函数22sin (10)()44(01)log (1)x x f x x x x x x π-<⎧⎪=-<⎨⎪-⎩………,若()()h x f x a =-有5个零点,则这五个零点之和的取值范围是____________. 四、双空题31.(2023秋ꞏ江西抚州ꞏ高二校联考阶段练习)已知函数ln ,02()(4),24x x f x f x x ⎧<≤=⎨-<<⎩,若当方程()f x m =有四个不等实根1x 、2x 、3x 、4x ,(1x <2x <3x <4x ) 时,不等式22341211kx x x x k ⋅++≥+恒成立,则x 1ꞏx 2=________,实数k 的最小值为___________.32.(2023秋ꞏ天津和平ꞏ高三耀华中学校考阶段练习)设()()ln ,024,24x x f x f x x ⎧<≤⎪=⎨-<<⎪⎩,若方程() f x m =恰有三个不相等的实根,则这三个根之和为________;若方程() f x m =有四个不相等的实根()1,2,3,4i x i =,则()2221234x x x x +++的取值范围为______. 33.(2023ꞏ全国ꞏ高三专题练习)已知函数()12,011,04x e x f x x x x -⎧>⎪=⎨--+≤⎪⎩ ,若函数3()()2g x f x =-有4个零点1x ,2x ,3x ,4x ,则1234x x x x +++=____________;若关于x 的方程25()()02f x f x a -+= ()a R ∈有8个不相等的实数根,则a 的取值范围是____________. 34.(2023秋ꞏ广东汕头ꞏ高一统考期末)设函数()22122,02log ,0x x x f x x x ⎧++≤⎪=⎨⎪>⎩,若关于x 的方程()f x m =有四个不同的解,1x ,2x ,3x ,4x ,且1234x x x x <<<,则m 的取值范围是_____,1234244x x x x x ++的取值范围是__________.参考答案一、单选题1.(2023·全国·高三专题练习)设函数()22,0ln ,0x x x f x x x ⎧--≤⎪=⎨>⎪⎩①若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x ⋅⋅⋅的取值范围是()0,1②若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x +++的取值范围是()0,∞+ ③若方程()f x ax =有四个不同的实根,则a 的取值范围是10,e ⎛⎫⎪⎝⎭④方程()()2110f x a f x a ⎛⎫-++= ⎪⎝⎭的不同实根的个数只能是1,2,3,6四个结论中,正确的结论个数为( ) A .1 B .2C .3D .4【答案】B【过程解析】对于①:作出()f x 的图像如下:若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则01a <<,不妨设1234x x x x <<<, 则1x ,2x 是方程220x x a ---=的两个不等的实数根,3x ,4x 是方程|ln |x a =的两个不等的实数根,所以12x x a =,34ln ln x x -=,所以43ln ln 0x x +=,所以341x x =, 所以1234(0,1)x x x x a =∈,故①正确;对于②:由上可知,122x x +=-,34ln ln x x a -==,且01a <<, 所以341x x =,所以31,1ex ⎛⎫∈ ⎪⎝⎭,4e (1,)x ∈,所以344411(2,e ex x x x +=+∈+, 所以12341(0,e e2)x x x x +++∈+-,故②错误;对于③:方程()f x ax =的实数根的个数,即为函数()y f x =与y ax =的交点个数,因为y ax =恒过坐标原点,当0a =时,有3个交点,当a<0时最多2个交点,所以0a >, 当y ax =与ln (1)y x x =>相切时,设切点为()00,ln x x , 即1y x '=,所以0000ln 1|x x x y x x ='==,解得0e x =,所以0e 1|x x y ='=,所以1ea =,所以当y ax =与ln (1)y x x =>相切时, 即1ea =时,此时有4个交点,若()f x ax =有4个实数根,即有4个交点,当1e>a 时由图可知只有3个交点,当10e a <<时,令()ln g x x ax =-,()1,x ∈+∞,则()11ax g x a x x-'=-=,则当11x a <<时()0g x '>,即()g x 单调递增,当1x a>时()0g x '<,即()g x 单调递减, 所以当1x a =时,函数取得极大值即最大值,()max 1ln 10g x g a a ⎛⎫==--> ⎪⎝⎭, 又()10g a =-<及对数函数与一次函数的增长趋势可知,当x 无限大时()0g x <,即()g x 在11,a ⎛⎫ ⎪⎝⎭和1,a ⎛⎫+∞ ⎪⎝⎭内各有一个零点,即()f x ax =有5个实数根,故③错误; 对于④:21()(()10f x a f x a -++=,所以1[()][()]0f x a f x a--=, 所以()f x a =或1()f x a =, 由图可知,当1m >时,()f x m =的交点个数为2, 当1m =,0时,()f x m =的交点个数为3, 当01m <<时,()f x m =的交点个数为4, 当0m <时,()f x m =的交点个数为1,所以若1a >时,则1(0,1)a∈,交点的个数为246+=个, 若1a =时,则11a=,交点的个数为3个,若01a <<,则11a>,交点有426+=个, 若a<0且1a ≠-时,则10a<且1a a ≠,交点有112+=个,若11a a=-=,交点有1个,综上所述,交点可能有1,2,3,6个,即方程不同实数根1,2,3,6,故④正确; 故选:B .2.(2023·全国·高三专题练习)已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a =有四个不同的解1234,,,,x x x x 且1234x x x x <<<,则()3122341x x x x x ⋅++⋅的取值范围是( ) A .(]1,1- B .[]1,1-C .[)1,1-D .()1,1-【答案】A【过程解析】21log 12x x =-⇒=. 先作()f x 图象,由图象可得12343121,1.2x x x x x ⎡⎫+=-=∈⎪⎢⎣⎭,,因此()31232343112x x x x x x x ⋅++=-+⋅为1,12⎡⎫⎪⎢⎣⎭单调递减函数, 11121,2111212-⨯+=-⨯+=-, 从而()(]31223411,1x x x x x ⋅++∈-⋅. 故选:A3.(2023秋·四川泸州·高一四川省泸县第四中学校考阶段练习)已知函数()32log ,031108,333x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩,若方程()f x m =有四个不同的实根1x ,2x ,3x ,4x ,满足1234x x x x <<<,则()()341233x x x x --的取值范围是( )A .()0,3B .(]0,4C .(]3,4D .()1,3【答案】A【过程解析】作出函数()32log ,031108,333x x f x x x x ⎧<≤⎪=⎨-+>⎪⎩的图象,如图所示:方程()f x m =有四个不同的实根1x ,2x ,3x ,4x ,满足1234x x x x <<<, 则01m <<,()33,4x ∈3log x m =即:3231log ,log x m x m ==-,所以3231log log 0x x +=, 321log 0x x =,所以211x x =,根据二次函数的对称性可得:3410x x +=,()()()()341212343423333391*********x x x x x x xx x x x x x x --==-+--=-+-+,()33,4x ∈考虑函数()21021,3,4y x x x =-+-∈单调递增,3,0x y ==,4,3x y ==所以()33,4x ∈时2331021x x -+-的取值范围为()0,3.故选:A4.(2023·全国·高三专题练习)已知函数f (x )=11,1211,12xx x x ⎧⎛⎫-⎪ ⎪⎪⎝⎭⎨⎪-+>⎪⎩…,若互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3),则123111222x x x⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎭⎝的取值范围是( )A .(95,42)B .(1,4)C .4)D .(4,6)【答案】A【过程解析】画出分段函数f (x )=11,1211,12xx x x ⎧⎛⎫-⎪ ⎪⎪⎝⎭⎨⎪-+>⎪⎩…的图像如图:令互不相等的实数x 1,x 2,x 3满足f (x 1)=f (x 2)=f (x 3)=t ,t ∈(0,12), 则x 1∈22(log ,0)3,x 2∈(0,1),x 3∈(1,2), 则123111222xxx⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎭⎝=1+t +1﹣t +22t ﹣2=2+22t ﹣2, 又t ∈(0,12),∴123111222x x x⎛⎫⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭+⎭⎝∈(95,42).故选:A .5.(2023·全国·高三专题练习)已知定义域为()0,6的函数()y f x =的图象关于3x =对称,当(]0,3x ∈时,()ln f x x =,若方程()f x t =有四个不等实根1x ,2x ,3x ,()41234x x x x x <<<时,都有()223412190k x x x x -++-≥成立,则实数k 的最小值为( )A .724 B .13C .12D .113【答案】A【过程解析】作出函数()f x 的图象,如图,作直线y t =,它与()f x 图象的四个交点的横坐标依次为1x ,2x ,3x ,()41234x x x x x <<<,因为函数()y f x =的图象关于3x =对称,所以32416,6x x x x =-=-,12ln ln x x -=,即121=x x ,且213x <<,显然341x x >,不等式()223412190k x x x x -++-≥变形为2212349()1x x k x x -+≥-,3421121212(6)(6)366()376()x x x x x x x x x x =--=-++=-+,222212121212()2()2x x x x x x x x +=+-=+-,所以222121234129()11()1366()x x x x x x x x -+-+=--+,由勾形函数性质知12221x x x x +=+在2(1,3)x ∈时是增函数,所以12221102,3x x x x ⎛⎫+=+∈ ⎪⎝⎭, 令12t x x =+,则102,3t ⎛⎫∈ ⎪⎝⎭,211()6(6)t g t t -=-2116(6)t t -=-,22(6)25()6(6)t g t t --'=-,当102,3t ⎛⎫∈ ⎪⎝⎭时,()0g t '<,()g t 单调递减,所以7()(2)24g t g <=,所以724k ≥,即k 的最小值是724. 故选:A .6.(2023·全国·高三专题练习)已知函数()22,0,()2,0xx x f x g x x x e x >⎧==-+⎨≤⎩(其中e 是自然对数的底数),若关于x 的方程(())0g f x m -=恰有三个不等实根123,,x x x ,且123x x x <<,则21322x x x --的最小值为( )A .ln 33-B .3ln 22-C .ln 23-D .1-【答案】A【过程解析】由题意设()f x t =,根据方程(())0g f x m -=恰有三个不等实根, 即2()20g t t t m =-+-=必有两个不相等的实根12,t t ,不妨设12t t <122t t ∴+=,则212t t =-,作出()f x 的图象,函数y t =与()f x 三个不等实根123,,x x x ,且123x x x <<,那么1221xx e t ==,可得312x t =-,101t <≤,所以21311223ln 4x x x t t --=--,构造新函数1()3ln 4(01),()3h t t t t h t t'=--<≤=-当()0h t '<时,10,,()3t h t ⎛⎫∈∴ ⎪⎝⎭在10,3⎛⎫⎪⎝⎭单调递减;当()0h t '>时,1,1,()3t h t ⎛⎫∈∴ ⎪⎝⎭在1,13⎛⎫ ⎪⎝⎭单调递增;∴当13t =时,(t)h 取得最小值为ln 33-,即21322x x x --的最小值为ln 33-; 故选:A7.(2023·吉林长春·东北师大附中校考模拟预测)已知函数3e ,0()3,0x x f x x x ⎧≤=⎨>⎩,()22g x x x =-+(其中e 是自然对数的底数),若关于x 的方程()(())F x g f x m =-恰有三个不同的零点123,,x x x ,且123x x x <<,则12333x x x -+的最大值为( )A .31ln 4+B .41ln 3+C .3ln 3-D .3ln 3+【答案】A【过程解析】由()f x 过程解析式,在(,0]-∞上()f x 单调递增且值域为(0,1],在(0,)+∞上()f x 单调递增且值域为(0,)+∞, 函数()f x 图象如下:所以,()f x 的值域在(0,1]上任意函数值都有两个x 值与之对应,值域在(1,)+∞上任意函数值都有一个x 值与之对应,要使()(())F x g f x m =-恰有三个不同的零点123,,x x x ,则()g x 与y m =的交点横坐标一个在(0,1]上,另一个在(1,)+∞上,由2()2g x x x =-+开口向下且对称轴为1x =,由上图知:01m <<,此时12()()g t g t m ==且12012t t <<<<,122t t +=,结合()f x 图象及123x x x <<有1321e 3xx t ==,323x t =,则112123ln ,,333t t tx x x ===, 所以11123121433ln ln 233t tx x x t t t -+=-+=-+,且101t <<, 令4()ln 23h x x x =-+且01x <<,则1434()33xh x x x -=='-,当3(0,4x ∈时()0h x '>,()h x 递增;当3(,1)4x ∈时()0h x '<,()h x 递减;所以max 33()()ln 144h x h ==+,故12333x x x -+最大值为3ln 14+.故选:A8.(2023·全国·高三专题练习)已知函数()22322,,log ,,x mx m x m f x x x m ⎧-++≤⎪=⎨>⎪⎩,其中01m <<,若存在实数a ,使得关于x 的方程()f x a =恰有三个互异的实数解,则实数m 的取值范围是( ) A .1,14⎛⎫⎪⎝⎭B .1,19⎛⎫ ⎪⎝⎭C .10,4⎛⎫ ⎪⎝⎭D .10,9⎛⎫ ⎪⎝⎭【答案】D【过程解析】因为01m <<, 所以()f x 的大致图象,如图所示:当x m ≤时,()()222f x x m =-+≥,因为存在实数a ,使得关于x 的方程()f x a =恰有三个互异的实数解, 所以3log 2m >,又01m <<, 解得109m <<, 故选:D9.(2023·全国·高三专题练习)已知函数lg ,0()lg(),0x x g x x x ⎧>⎪=⎨--<⎪⎩,若关于x 的方程()()5222g x g x -+=有四个不等根1234,,,x x x x ,则()()()()12341234x x x x g x g x g x g x +++++++的值是( )A .0B .2C .4D .8【答案】A【过程解析】由方程()()5222g x g x -+=可得()1g x =±, 因为函数lg ,0()lg(),0x x g x x x ⎧>⎪=⎨--<⎪⎩, 设0x >,则0x -<,则()()|lg |(|lg ()|)|lg ||lg |0g x g x x x x x +-=+---=-=, 所以()g x 为奇函数且1x ,2x ,3x ,4x 是()1g x =±的根, 所以12340x x x x +++=,不妨有12()()1g x g x ==-,34()()1g x g x ==, 所以1234()()()()0g x g x g x g x +++=.故12341234()()()()x x x x g x g x g x g x +++++++的值是0. 故选:A .10.(2023秋·宁夏·高三宁夏大学附属中学校考阶段练习)已知函数22,0(){|log |,0x x f x x x +≤=>,若关于x 的方程()()f x a a R =∈有四个不同实数解1234,,,x x x x ,且1234x x x x <<<,则1234x x x x +++的取值范围为 ( ) A .1(2,4-B .1[2,]4-C .[2,)-+∞D .(2,)-+∞【答案】A【过程解析】作出函数()f x 的图象,如图,作直线y a =,当02a <≤时,直线y a =与函数()f x 图象有四个交点,由图象知124x x +=-,2324log log x x -=,即341x x =,(0)2f =, 2log 2x -=,14x =,所以3114x ≤<, 所以12343314x x x x x x +++=-++,由对勾函数性质知函数3314y x x =-++在31,14x ⎡⎫∈⎪⎢⎣⎭上是减函数,所以31,14x ⎡⎫∈⎪⎢⎣⎭时,331142,4y x x ⎛⎤=-++∈- ⎥⎝⎦.故选:A .11.(2023秋·湖北武汉·高一期末)已知函数()()2242,1,log 1,1,x x x f x x x ⎧++≤⎪=⎨->⎪⎩,若关于x 的方程()f x t =有四个不同的实数解1x ,2x ,3x ,4x ,且1234x x x x <<<,则)1234122x x x x ++的最小值为( ) A .72B .8C .92D .12【答案】D【过程解析】函数图像如图所示,()17f =,(]0,7t ∈,1234212x x x x <-<≤<<<,124x x +=-,由()()()()()()333433434log 1log 1log 110111x x x x x x --=-⇒--=⇒--=,∴()()34342112122251x x x x =-+++-5922≥=, 当且仅当343,32x x ==时,等号成立,此时1t =;)()2212121212422x x x x x x x x ⎛⎫+⎛⎫-=-≥-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭,当且仅当1222x x =-=-+1t =.所以)1234122x x x x ++的最小值为91422-=. 故选:D12.(2023秋·河南郑州·高一新密市第一高级中学校考阶段练习)已知函数()()22log 1,131255,322x x f x x x x ⎧+-<≤⎪=⎨-+>⎪⎩,若关于x 的方程()f x m =有四个不同的实数解1234,,,x x x x ,且满足1234x x x x <<<,则下列结论正确的是( )A .121x x =-B .[]3421,25x x ∈C .3422x x +=D .12111x x +=- 【答案】D【过程解析】作函数()y f x =和y m =的图象,如图所示:当1m =时,()()2122log 1log 1x x +=+,即()()2122log 11,log 11x x +=-+=,解得121,12x x =-=,此时1212x x =-,故A 错误;结合图象知,02m <<,当3x >时,可知34,x x 是方程()2125522f x x x m =-+=,即2102520x x m -+-=的二根,故3410x x +=,()3425221,25x x m =-∈,端点取不到,故BC错误;当13x -<≤时,()()2122log 1log 1x x +=+,即()()2122log 1log 1x x -+=+, 故()2221log log 111x x =++,即21111x x =++,所以()()21111x x ++=, 故1212x x x x +=-,即12121x x x x +=-,所以12111x x +=-,故D 正确. 故选:D.13.(2023秋·江西上饶·高一统考期末)已知函数()()221,0log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩,若方程()f x a=有四个不同的实数解1x ,2x ,3x ,4x 且1234x x x x <<<,则()3122342x x x x x -+的取值范围是( )A .()4,5B .(]4,5C .()4,+∞D .[)4,+∞【答案】B【过程解析】作出函数()221,0()log ,0x x f x x x ⎧+≤⎪=⎨>⎪⎩的图象如下:因为方程()f x a =有四个不同的解1x ,2x ,3x ,4x ,且1234x x x x <<<, 所以有122x x +=-,341x x =, 故3123234322()2x x x x x x x -+=+, 再由2log 1x =可得2x =或12x =,即3112x <≤, 令2()2g x x x =+,(112x ≤<), 任取12112x x ≤<<,则120x x -<,12110x x ->, 所以()12121212122211()()2222g x g x x x x x x x x x ⎛⎫⎛⎫⎛⎫-=+-+=-+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭()12121210x x x x ⎛⎫=--< ⎪⎝⎭,即12()()<g x g x , 所以函数2()2g x x x =+在1,12⎡⎫⎪⎢⎣⎭上单调递减, 又152g ⎛⎫= ⎪⎝⎭,4(1)g =,所以()(4,5]g x ∈.即3122342()x x x x x -+的取值范围是(4,5]. 故选:B.14.(2023春·全国·高三校联考专题练习)已知函数11()||||f x x a x b x a x=++-+--有五个不同的零点,且所有零点之和为52,则实数b 的值为( ) A .1 B .3 C .5 D .7【答案】C【过程解析】因为11()||||f x x a x b x a x =++-+--,11()||||()f a x a x x b f x a x x-=-+++-=-,所以函数()f x 的图象关于直线2ax =对称, 设五个零点分别为12345,,,,x x x x x ,且12345x x x x x <<<<, 则15243,,2a x x a x x a x +=+==, 所以1234555222a a x x x x x a a ++++=++==,所以1a =, 则312x =,由3333311()|||1|01f x x x b x x =++-+-=-,可得11|2||12|22b ++-+=,则5b =.故选:C. 二、多选题15.(2023秋·云南昆明·高一统考期末)已知函数ln(2),(2,0]()(2),(0,2]x x f x f x x ⎧+∈-=⎨-∈⎩,函数()y f x m =-有四个不同的零点,且从小到大依次为1x ,2x ,3x ,4x ,则下列结论正确的是( )A .121=x xB .1201≤<x xC .341x x =D .2410-<≤x x【答案】BCD【过程解析】因为ln(2),(2,0]()(2),(0,2]x x f x f x x ⎧+∈-=⎨-∈⎩,所以当(2,0]x ∈-时,()ln(2)f x x =+, 当2(]0,x ∈时,()(2)f x f x =-,所以2(2,0]x -∈-时,(2)ln(22)ln f x x x -=-+=, 所以ln(2),(2,0]()ln ,(0,2]x x f x x x ⎧+∈-⎪=⎨∈⎪⎩, 作出()f x 的图象如图所示,若()f x m =有4个解,则()y f x =与y m =的图象有4个交点,如图(0,ln 2]m ∈,所以1113,1,()ln(2)2x f x x ⎡⎫∈--=-+⎪⎢⎣⎭,(]2221,0,()ln(2)x f x x ∈-=+,由12()()f x f x =,得12ln(2)ln(2)x x -+=+, 即12ln(2)ln(2)0x x +++=,所以12ln[(2)(2)]0x x ++=,所以12(2)(2)1x x ++=, 所以12122()30x x x x +++=,当20x =时,120x x =; 当20x <时,由基本不等式可得12x x +<-所以1230x x ->,解得01<<3>(舍); 所以12[0,1)x x ∈, 所以A 错误,B 正确,对于C ,3331,1,()ln 2x f x x ⎡⎫∈=-⎪⎢⎣⎭,(]4441,2,()ln x f x x ∈=,因为34()()f x f x =,所以34ln ln x x -=,所以34ln ln 0x x +=,即()34ln 0x x =, 所以341x x =,所以C 正确,对于D ,因为2424(1,0],(1,2],2x x x x ∈-∈+=,所以()()224222211(1,0]x x x x x =+=+-∈-,所以D 正确. 故选:BCD16.(2023·全国·高三专题练习)已知函数()e ,0,lg ,010,11,10,x x x f x x x x x ⎧⋅≤⎪=<<⎨⎪-+≥⎩,若22()3()()2g x f x mf x m =--有6个不同的零点分别为123456,,,,,x x x x x x ,且()()()123456345,x x x x x x f x f x f x <<<<<==,则下列说法正确的是( )A .当0x ≤时,()10ef x -≤≤B .34x x +的取值范围为1012,10⎛⎫⎪⎝⎭C .当0m <时,()()()()1234563f x f x f x x x f x +++的取值范围为1,0e ⎛⎫- ⎪⎝⎭D .当0m >时,()()()()1234563f x f x f x x x f x +++的取值范围为20,3e ⎛⎫⎪⎝⎭【答案】AC【过程解析】当0x ≤时,()e x f x x =⋅,此时()(1)e x f x x '=+⋅,令()0f x '>,解得10-<≤x ,令()0f x '<,解得1x <-,可得()f x 在(,1)-∞-上单调递减,在(1,0)-上单调递增,且1(1),(0)0ef f -=-=,∴当0x ≤时,1()0ef x -≤≤,故A 正确; 作出如图所示图像:由22()3()()2g x f x mf x m =--有6个不同的零点, 等价于223()()20f x mf x m --=有6个不同的实数根, 解得()f x m =或2()3m f x =-, ∵341x x ⋅=,∴若343311012,10x x x x ⎛⎫+=+∈ ⎪⎝⎭,可得31110x <<,而当0m >时,120e 3m -<-<,可得302e m <<,而3112e 10f ⎛⎫<= ⎪⎝⎭;当0m <时,10e m -<<,可得22033e m <-<而2113e 10f ⎛⎫<= ⎪⎝⎭, 故3x 的范围为1,110⎛⎫ ⎪⎝⎭的子集,34x x +的取值范围不可能为1012,10⎛⎫⎪⎝⎭,故B 选项错误;该方程有6个根,且()()()345f x f x f x ==,知341x x ⋅=且()()()126f x f x f x ==,当0m <时,()()()1261,0e f x f x f x m ⎛⎫===∈- ⎪⎝⎭,()()()3452(0,1)3m f x f x f x ===-∈,联立解得1,0e m ⎛⎫∈- ⎪⎝⎭, ()()()()()()12345615133332,0e f x f x f x x x f x f x f x m m m ⎛⎫+++=+=-=∈- ⎪⎝⎭,故C 正确;当0m >时,()()()12621,03e m f x f x f x ⎛⎫===-∈- ⎪⎝⎭, ()()()345(0,1)f x f x f x m ===∈,联立解得30,2e m ⎛⎫∈ ⎪⎝⎭,()()()()()()123456153333230,2e f x f x f x x x f x f x f x m m m ⎛⎫+++=+=-+=∈ ⎪⎝⎭.故D 错误.故选:AC.17.(2023·全国·高三专题练习)设函数22,0()ln ,0x x x f x x x ⎧--⎪=⎨>⎪⎩…,则下列命题中正确的是( )A .若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x ⋅⋅⋅的取值范围是(0,1)B .若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则1234x x x x +++的取值范围是(0,)+∞C .若方程()f x ax =有四个不同的实根,则a 的取值范围是10,e ⎛⎫⎪⎝⎭D .方程21()()()10f x a f x a -++=的不同实根的个数只能是1,2,3,6【答案】AD【过程解析】对于A :作出()f x 的图像如下:若方程()f x a =有四个不同的实根1x ,2x ,3x ,4x ,则01a <<,不妨设1234x x x x <<<, 则1x ,2x 是方程220x x a ---=的两个不等的实数根,3x ,4x 是方程|ln |x a =的两个不等的实数根,所以12x x a =,34ln ln x x -=,所以43ln ln 0x x +=,所以341x x =, 所以1234(0,1)x x x x a =∈,故A 正确;对于B :由上可知,122x x +=-,34ln ln x x a -==,且01a <<, 所以341x x =,所以31,1ex ⎛⎫∈ ⎪⎝⎭,4e (1,)x ∈,所以344411(2,1)e x x x x +=+∈+,所以12341(0,1)ex x x x +++∈+,故B 错误;对于C :方程()f x ax =的实数根的个数,即可函数()y f x =与y ax =的交点个数,因为y ax =恒过坐标原点,当0a =时,有3个交点,当a<0时最多2个交点,所以0a >, 当y ax =与ln (1)y x x =>相切时,设切点为()00,ln x x , 即1y x '=,所以0000ln 1|x x x y x x ='==,解得0e x =,所以0e 1|x x y ='=,所以1ea =,所以当y ax =与ln (1)y x x =>相切时, 即1ea =时,此时有4个交点,若()f x ax =有4个实数根,即有4个交点,当1e>a 时由图可知只有3个交点,当10e a <<时,令()ln g x x ax =-,()1,x ∈+∞,则()11ax g x a x x-'=-=,则当11x a <<时()0g x '>,即()g x 单调递增,当1x a >时()0g x '<,即()g x 单调递减,所以当1x a =时,函数取得极大值即最大值,()max 1ln 10g x g a a ⎛⎫==--> ⎪⎝⎭,又()10g a =-<及对数函数与一次函数的增长趋势可知,当x 无限大时()0g x <,即()g x 在11,a ⎛⎫ ⎪⎝⎭和1,a ⎛⎫+∞ ⎪⎝⎭内各有一个零点,即()f x ax =有5个实数根,故C 错误; 对于D :21()()()10f x a f x a -++=,所以1[()][()]0f x a f x a--=,所以()f x a =或1()f x a=, 由图可知,当1m >时,()f x m =的交点个数为2, 当1m =,0时,()f x m =的交点个数为3, 当01m <<时,()f x m =的交点个数为4, 当0m <时,()f x m =的交点个数为1,所以若1a >时,则1(0,1)a∈,交点的个数为246+=个, 若1a =时,则11a=,交点的个数为3个, 若01a <<,则11a>,交点有426+=个, 若a<0且1a ≠-时,则10a<且1a a ≠,交点有112+=个,若11a a=-=,交点有1个,综上所述,交点可能由1,2,3,6个,即方程不同实数根1,2,3,6,故D 正确; 故选:AD .18.(2023秋·辽宁大连·高一育明高中校考期末)已知函数()()22log 2,241617,42x x f x x x x ⎧-<≤⎪=⎨-+>⎪⎩,若方程()f x m =有四个不同的实根1234,,,x x x x ,满足1234x x x x <<<,则下列说法正确的是( )A .()121242x x x x +=+B .3412x x +=C .()3432,34x x ∈D .函数()()()()21g x f x m f x m =+--的零点为12346,,,,x x x x【答案】BCD【过程解析】由过程解析式可得()f x 图象如下图所示:若()f x m =有四个不同的实数根,则()f x 与y m =有四个不同的交点, 由图象可知:123423468x x x x <<<<<<<<,01m <<; 对于A ,()()12f x f x = ,即()()2122log 2log 2x x -=-,()()2122log 2log 2x x ∴--=-,()22211log log 22x x ∴=--,()()12221x x ∴--=, 整理可得:()1212412x x x x +=++,A 错误;对于B ,()()34f x f x = ,3x ∴与4x 关于直线6x =对称,3412x x ∴+=,B 正确; 对于C ,3x 与4x 是方程()2161702x m f m x x -+-==-的两根, ()34217342x x m m ∴=-=-,又01m <<,()3432,34x x ∴∈,C 正确;对于D ,()()()()()()211g x f x m f x m f x m f x =+--=-+⎡⎤⎡⎤⎣⎦⎣⎦,由()0g x =得:()f x m =或()1f x =-,()f x m =的根为1234,,,x x x x ;()1f x =-的根为6,()g x ∴的零点为12346,,,,x x x x ,D 正确.故选:BCD.19.(2023秋·山西太原·高一古交市第一中学校校考阶段练习)已知函数22log ,02()813,2x x f x x x x ⎧<<=⎨-+≥⎩,若f (x )=a 有四个不同的实数解x 1,x 2,x 3,x 4,且满足x 1<x 2<x 3<x 4,则下列命题正确的是( )A .0<a <1B.12922x x ⎡⎫+∈⎪⎢⎣⎭C .12342110,2x x x x ⎛⎫+++∈ ⎪⎝⎭D.)122x x ⎡+∈⎣【答案】ACD 【过程解析】函数()f x 的图象如上所示,方程()f x a =的解可以转化为函数()f x 与y a =图象交点的横坐标,由图可知01a <<,故A 正确;由题意可知2122log log x x -=,即212log 0x x =,解得121=x x ,由图可知212x <<,所以1222122x x x x +=+,令2212=+y x x ,则函数2212=+y x x 在()1,2上单调递增,当21x =时,3y =,22x =时,92y =,所以122xx +的范围为93,2⎛⎫⎪⎝⎭,故B 错;函数2813y x x =-+的对称轴为4x =,所以348x x +=,又121=x x ,所以12342218x x x x x x +++=++,函数()22218g x x x =++在()1,2上单调递增,()110g =,()2122g =,所以12342110,2x x x x ⎛⎫+++∈ ⎪⎝⎭,故C 正确;122222x x x x +=+,函数()2222h x x x =+在(上单调递减,)2上单调递增,h=,()13h =,()23h =,所以)122x x ⎡+∈⎣,故D 正确.故选:ACD.20.(2023秋·重庆铜梁·高一校考期中)已知奇函数()f x 的定义域为R ,()3f x +为偶函数,且()f x 在[]0,3上单调递减.若关于x 的方程()f x a =在区间[]12,12-上有4个不同的根1234,,,x x x x ,则( )A .()()6f x f x =+B .()f x 的图象关于直线3x =对称C .1234x x x x +++的值可能为12-D .1234x x x x +++的值可能为12【答案】BCD【过程解析】()()()()()12939366f x f x f x f x f x +=++=--+=--=-+()()()()3333f x f x f x f x =-++=---+=--=.所以()()12f x f x =+,A 错误.因为()()33f x f x +=-+,所以()f x 的图象关于直线3x =对称,B 正确. 画出()f x 的一种可能图象,如图所示,不妨假设1234x x x x <<<.根据对称性有: 当()03a f <<-时,126x x +=-,3418x x +=,123412x x x x +++=,C 正确. 当()30f a <<时,1218x x +=-,346x x +=,123412x x x x +++=-,D 正确. 故选:BCD21.(2023·全国·高三专题练习)设函数()2101,0lg ,0x x x f x x x ⎧++≤⎪=⎨>⎪⎩,若关于x 的方程()()f x a a R =∈有四个实数解1234,,,x x x x ,且1234x x x x <<<,则()()1234x x x x +-的值可能是( )A .0B .1C .99D .100【答案】BC【过程解析】如图所示:因为关于x 的方程()()f x a a R =∈有四个实数解1234,,,x x x x ,且1234x x x x <<<,所以01a <≤.2101y x x =++的对称轴为5x =-,所以1210x x +=-. 因为34lg lg x x =,所以34lg lg 0x x +=,即341x x =,431x x =. 因为3lg 1x ≤,所以31110x ≤<. 所以()()123433110x x x x x x ⎛⎫+-=-- ⎪⎝⎭, 因为110y x x ⎛⎫=-- ⎪⎝⎭,1110x ≤<为减函数,所以()()(]1234330110,99x x x x x x ⎛⎫∈ ⎪⎭-⎝+-=-.故选:BC 三、填空题22.(2023秋·石河子一中校考阶段练习)已知函数()2e ,0ln ,>0xx x f x x x ⎧-≤⎪=⎨⎪⎩,若函数()y f x b=-有四个不同的零点1x 、2x 、3x 、4x ,且1234x x x x <<<,则以下结论正确的是_____.①22342x x +>;②20eb <<; ③122x x +=-; ④()13422x x x x +<-. 【答案】①②④【过程解析】设()2e xg x x =-,其中x ∈R ,则()()21e xg x x '=-+,当1x <-时,()0g x ¢>,此时函数()g x 单调递增, 当1x >-时,()0g x ¢<,此时函数()g x 单调递减, 所以,函数()g x 的极大值为()21eg -=,且当0x <时,()0g x >, 作出函数()f x 、y b =的图象如下图所示:。
高考地理必考专题等值线图专题(文档版)

高考地理必考专题等值线图专题(文档版)4.交通线路选择:应用有利的地形地势,既要思索距离长短,又要思索路途颠簸〔间距、坡度等〕,普通是在两条等高线间绕行,沿等高线走向〔延伸方向〕散布,以增加坡度,只要必要时才可穿过一、两条等高线;尽能够少地经过河流,少建桥梁等,以增加施工难度和投资;防止经过断崖、沼泽地、沙漠等地段。
5.水库树立:要思索库址、坝址及修建水库后能否需求移民等。
①.选在河流较窄处或盆地、洼地的出口(即〝口袋形〞的地域,〝口小〞利于建坝,〝袋大〞库容量大。
由于工程量小,工程造价低);②.选在地质条件较好的中央,尽量避开断层、喀斯特别貌等,防止诱发水库地震;③.思索占地搬迁状况,尽量少淹良田和村镇。
④还要留意修建水库时,水源要较充足。
6.河流流向:由海拔高处向低处流,发育于河谷〔等高线凸向高值〕,河流流向与等高线凸出方向相反。
7.水系特征:山地构成放射状水系,盆地构成向心状水系,山脊成为水系分水岭。
8.水文特征:等高线密集的河谷,河流流速大,水能丰厚;河流流量除与气候特别是降水量有关外,还与流域面积大小有关。
9.农业规划:依据等高线地形图反映出来的地形类型、地势坎坷、坡度缓急、结合气候和水源条件,量体裁衣地提出农林牧渔业合理规划的方案;如平原地域开展耕作业,山地、丘陵地域开展林业、畜牧业。
10.城市规划形状与地形:平原适宜集中紧凑式;山区适宜分散疏松式。
11.地形特征的描画:地形类型〔平原、高原、山地、丘陵、盆地〕;地势及坎坷状况;主要地形区散布;重要地形剖面图特征。
12.地形相关剖析:①地构成因剖析:运用地质作用〔内力作用——地壳运动、岩浆活动、蜕变作用、地震;、外力作用——流水、风、海浪、冰川的腐蚀、搬运、堆积作用等〕与板块运动〔板块外部地壳比拟动摇,板块接壤处,地壳比拟生动及板块的碰撞或张裂〕来解释判读剖析与地形有关的天文知识②剖析某地气候特点,应结合该地天文纬度,地势上下坎坷,山脉走向,阴、阳坡,距离陆地远近等停止综合剖析。
高考地理专题《等值线图的判读》真题练习含答案

高考地理专题《等值线图的判读》真题练习含答案选择题[2024·湖南长沙高三期中]城市土地租金受距市中心远近和交通通达度影响最大,下图示意四川某山区县城中心城区地租等值线图。
据此完成1~3题。
1.四地中地租最高的是()A.甲B.乙C.丙D.丁答案:D解析:城市土地租金受距市中心远近和交通通达度影响最大,地租由市中心向外递减,根据等值线变化规律可以判断,等地租线由内向外递减,故丁地地租最高。
其次是甲地、丙地、乙地,D正确,A、B、C错误。
故选D。
2.该城市地势变化特点最可能是()A.南部地势起伏和缓B.北部地势相对和缓C.东南地势相对最低D.地势东部高西部低答案:B解析:根据材料信息可以判断,该图示意四川某山区城市中心城区地租等值线,地形对交通影响大。
地形平坦的地区交通相对便利,地租高;地形起伏大的地方交通条件较差,地租低。
整体而言,与南部、东南、东部相比,该地北部地区等地租线稀疏,说明地租相对较高,反映其交通比南部便利,地势起伏和缓。
B正确,A、C、D错误。
故选B。
3.甲地附近等值线向西北弯曲,反映该地()A.交通相对便利B.距市中心最远C.有地铁线通过D.靠近重工业区答案:A解析:城市土地租金受距市中心远近和交通通达度影响最大,甲地等地租线向西北(低地租处)弯曲,反映西北方向地租相对较高,反映其交通比两侧地区便利,A正确。
距市中心远近与等值线弯曲没有关系,B错误。
依据材料信息无法判断是否有地铁线通过和靠近重工业区,且需靠近地铁站,地租才会升高,靠近重工业区,污染较大,地租会降低,C、D 错误。
故选A。
[2024·成都摸底]如图为世界某大洲局部地区某月等温线(单位:℃)分布示意图。
据此完成4~5题。
4.M地气温最有可能是()A.18 ℃B.22 ℃C.28 ℃D.32 ℃答案:A解析:根据等温线的“大于大值,小于小值”规律,因为M地外围等值线未标数值,故M地外部等温线数值可能是20 ℃,也可能是25 ℃,M所处地点应位于安第斯山区,其气温应低于周边地区,故M地外部等温线数值应为20 ℃,M地气温为15 ℃~20 ℃,故A 项正确。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
地理高考专题训练之
等值线专题
一、等值线分布特征描述
1.读我国油菜开花日期等值线示意图,回答下列问题。
油菜生长需要一定的温度和水分条件。
我国北起黑龙江,南至海南,西起新疆,东至沿海各省,不论是青藏高原,还是长江中下游平原,总可以看到一片片金灿灿的油菜花。
(1)根据图示信息,归纳我国东南地区油菜开花日期等值线分布的基本特征,并解释其原因。
(4)新疆塔里木盆地周边地区,油菜开花日期等值线的分布特点是什么?为什么?
【答案】(1)油菜开花日期等值线大致呈纬向分布(或油菜花由南向北依次开放)。
我国东南部气温从低纬向高纬递减(或太阳直射点位置由南向北推进,气温也随之由南向北逐渐上升)。
(4)油菜开花日期等值线呈半环状分布,随海拔上升而推迟。
地势成为这里主要的制约因素,地势低处气温高,开花日期早;高处气温低,开花日期晚。
二、等值线数值判读
[2015·龙岩质检]霜冻是指地表温度骤降到0 ℃以下,使农作物受到损害,甚至死亡的现象。
春季最后一次霜冻出现的日期称为终霜冻日。
下图示意我国某省等高线和终霜冻日分布,读图完成2~3题。
2.等终霜冻日线a、b表示的数值分别为( )
A.100、90 B.100、100 C.90、100 D.110、100
答案 B
解析分析等高线图,据等高线“凸低为高”、“凸高为低”的特征,可知a地位于山谷,地势低,气温高,在终霜冻日线图中为低值区,所以a的数值为100;b地地势稍高,所以气温较低,在终霜冻日线图中为高值区,故b的数值为100。
3.下列因素中对该省终霜冻日影响最小的是( )
A.纬度位置 B.地形地势 C.大气环流 D.海陆位置
答案 D
解析从图中可以看出,该省为山西省,不是沿
海城市,所以海陆位置对终霜冻日影响最小。
(2016·四川绵阳二诊)下图为辽宁省年平均风速
等值线图。
读图回答4~5题。
4.甲地的风速数值可能为 ( )
A.2.0 B.2.3 C.2.6 D.3.1
5.影响辽宁省风速等值线走向的主要因素是 ( )
A.地形地势 B.海陆位置
C.海陆轮廓 D.纬度位置
(2016·安徽安庆期末)下图为黄土高原局部黄土分布等值线图,实线是黄土表面等高线,虚线是黄土底面(基岩表面)等高线(单位:米)。
读图回答6~7题。
6.甲处黄土层的厚度可能是( )
A.10米 B.20米 C.30米 D.40米
7.从适宜人们居住的环境考虑,最适合开凿窑洞的地点是( )
A.甲B.乙 C.丙D.丁
(2016·河北保定期末)读“世界部分区域年平均气温分布图”,完成8~9题。
8.图中a的值可能是( )
A.-10 ℃ B.0 ℃ C.10 ℃ D.20 ℃
9.造成图中0 ℃等温线陆地上向南凸出的主要影响因素是( )
A.太阳辐射 B.地形 C.海陆热力性质差异 D.洋流
三、等值线疏密
[2015·龙岩质检]下图为我国东南某地区等坡度线(地表坡度值相等的点连成的线)图,图中数字代表坡度(坡面与水平面的夹角)。
读图完成10~11题。
10.图中河流,流速最快的河段是( )
A.甲 B.乙 C.丙 D.丁
答案 A
解析四河段甲河段坡度最大,介于25°~30°,乙河段介于15°~25°,丙河段小于10°,但大于丁河段(略高于5°)。
坡度越大,地势起伏越大,地表径流流速越大。
故A 为正确选项。
11.图示区域( )
A.P地坡度最陡 B.河流从东北流向西南
C.适宜发展果林业 D.Q地位于背风坡,土壤水分条件差
答案 C
解析图示区域P地坡度小于甲区域,坡度大小不能反映海拔高低,不能确定河流流向。
该区域地势起伏较大,位于我国东南地区,水热充沛,适宜发展果林业。
Q地位于北坡,背风地带,但坡度较小,地下水储藏条件较好,土壤水分条件好。
四、等值线弯曲及原因分析
[2015·忻州联考]读“某区域小流域图”,
回答12~13题。
12.关于该区域的叙述,正确的是( )
A.该地区的自然植被是亚热带常绿硬叶林
B.该河东部地区的降水转变为地下水更充
分
C.图示时期河流水补给地下水
D.图示时期河流处于枯水期
答案 C
解析该区域位于长江下游地区,海拔较
低。
自然植被是亚热带常绿阔叶林,该河东部地
区等高线密集,坡度较大,坡面径流流速快,降
水不易转变为地下水。
据地下水等值线可判断,图示时期河流处于丰水期,河水补给地下水。
13.A处潜水自由水面离地表面可能是( )
A.8米 B.32米 C.24米D.16米
答案 B
解析分析等值线可知,A处潜水自由水面高程为(70,80),地面高程为110,则潜水自由水面离地表面高度为(30,40)。
A处潜水自由水面离地表面可能是32 m。
[2015·江淮模拟]交通通达性是指一个地方能够从另一地方到达的容易程度,它可以用空间距离、旅行时间、旅途距离或运输费用等来衡量。
高铁建设将普遍改善我国城市间的通达性。
读2020年我国部分地区高铁通达性等值线图(图中数值为预测值,数值大小与交通通达性呈负相关),回答14~15题。
14.影响甲城的旅行时间等值线向北弯曲的主要影响因素是( )
A.高铁线的分布与走向B.所在地区的降水多
C.农业发达运输量大D.东北平原地形平坦
答案 A
解析等值线向北弯曲表明该处交通通达性好,其弯曲与高铁线的分布与走向有关。
15.2020~2025年随着东北交通通达性的进一步提高,下列说法正确的是( ) A.甲处的等值线的数值将变大 B.10小时等值线范围将变大
C.单位时间出行距离将会减少 D.对民航客运没有影响
答案 B
解析2020~2025年随着东北交通通达性的进一步提高,甲处的等值线的数值将变小;甲以北地区交通更加便利,10小时等值线范围将变大;列车速度提高,单位时间出行距离将会增大;铁路提速,乘火车出行的人增多,对民航客运有一定冲击。
故B为正确选项。
16.读我国油菜开花日期等值线示意图,回答下列问题。
(2)4月1日的油菜开花日期等值线在黄淮流域有明显向北凸出之势,为什么?
(3)我国东部6月1日和7月1日油菜开花日期等值线向什么方向延伸?为什么?
【答案】(2)该地区春天升温比东部沿海地区和西部山地更快。
(3)向东北—西南方向延伸。
此时,全国普遍高温,水分条件成为主要制约因素,距海洋越近,水分越足,开花日期相对越早。
