实验二香农编码的计算与分析1
实验四_香农编码
实验名称:实验四香农编码一、实验目的:加深对香农公式的理解及其具体的实现过程。
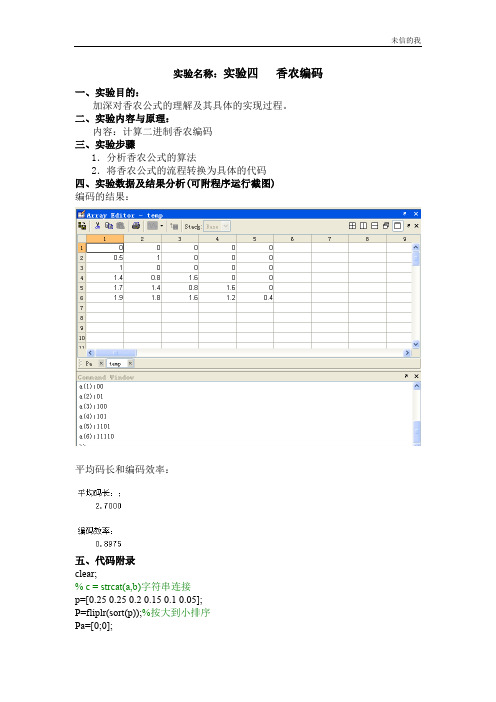
二、实验内容与原理:内容:计算二进制香农编码三、实验步骤1.分析香农公式的算法2.将香农公式的流程转换为具体的代码四、实验数据及结果分析(可附程序运行截图)编码的结果:平均码长和编码效率:五、代码附录clear;% c = strcat(a,b)字符串连接p=[0.25 0.25 0.2 0.15 0.1 0.05];P=fliplr(sort(p));%按大到小排序Pa=[0;0];%累加和的定义----第一行为累加和,第二行为Ki %求累加和for x=1for y=1:1:5%Pa(x,y)=1;Pa(x,y+1)=P(x,y)+ Pa(x,y);endend%ceil 是取向离它最近的大整数圆整for i=2for j=1:1:6Pa(i,j)=ceil( -log2(P(1,j)) );endend%信源熵H=0;L=0;for i=1:1:6H=H-P(i)*log2(P(i));L=L+P(i)*Pa(2,i);endu=H/L;disp('平均码长:;');disp(L);disp('编码效率:');disp(u);%求各符号的编码temp=[];%临时的编码值:1:6for m=1:1:6fprintf('a(%d):',m);for n=1:1:abs(Pa(2,m))temp(m,n)=Pa(1,m)*2;if temp(m,n)>=1O(m,n)=1;Pa(1,m)=temp(m,n)-1;elseO(m,n)=0;Pa(1,m)=temp(m,n);endfprintf('%d',O(m,n));endfprintf('\n');end六、其他:实验总结、心得体会及对本实验方法、手段及过程的改进建议等。
实验起初是想把累加和及Ki和编码放在一个二维矩阵中,但具体的实现较为复杂,所以最后改为逐行存放并成功完成了实验。
编码度量算法实验报告(3篇)

第1篇一、实验目的1. 理解编码度量算法的基本原理和重要性。
2. 掌握常见编码度量算法(如香农熵、信息增益、增益率等)的应用。
3. 通过实验验证不同编码度量算法在数据压缩中的应用效果。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.73. 数据集:使用某自然语言处理数据集,包含1000条文本数据。
三、实验原理编码度量算法用于评估编码的效率,其主要目的是在保证信息完整性的前提下,尽量减少编码长度。
以下介绍几种常见的编码度量算法:1. 香农熵:香农熵是衡量信息熵的指标,用于衡量数据的不确定性。
香农熵越大,表示数据越复杂,编码长度越长。
2. 信息增益:信息增益是衡量特征重要性的指标,用于评估特征对分类结果的贡献。
信息增益越大,表示该特征对分类结果的贡献越大。
3. 增益率:增益率是信息增益与特征熵的比值,用于衡量特征在降低数据不确定性方面的效果。
增益率越大,表示该特征对编码的优化效果越好。
四、实验步骤1. 数据预处理:将数据集划分为训练集和测试集,分别用于训练模型和评估模型性能。
2. 编码度量算法实现:根据实验原理,实现香农熵、信息增益、增益率等编码度量算法。
3. 模型训练:使用支持向量机(SVM)作为分类模型,对训练集进行训练。
4. 编码度量评估:对测试集进行编码度量评估,计算香农熵、信息增益、增益率等指标。
5. 结果分析:比较不同编码度量算法对编码性能的影响,分析其优缺点。
五、实验结果与分析1. 香农熵:通过计算测试集的香农熵,发现数据集的复杂度较高,编码长度较长。
2. 信息增益:通过计算测试集的特征信息增益,发现特征A、B、C的信息增益较高,说明这三个特征对分类结果的贡献较大。
3. 增益率:通过计算测试集的特征增益率,发现特征A的增益率最高,说明特征A在降低数据不确定性方面效果最好。
4. 结果分析:根据实验结果,香农熵反映了数据集的复杂度,信息增益和增益率反映了特征对分类结果的贡献。
香农编码--信息论大作业

信息论与编码课程大作业题目:香农编码学生姓名:******学号:&**********专业班级:*******************2013 年 5 月10 日香农编码1.香农编码的原理/步骤香农第一定理指出了平均码长与信源之间的关系,同时也指出了可以通过编码使平均码长达到极限值,这是一个很重要的极限定理。
如何构造这种码?香农第一定理指出,选择每个码字的长度K i将满足式I(x i)≤K i<I p(x i)+1就可以得到这种码。
这种编码方法就是香农编码。
香农编码步骤如下:(1)将信源消息符按从大到小的顺序排列。
(2)计算p[i]累加概率;(3)确定满足自身要求的整数码长;(4)将累加概率变为二进制数;(5)取P[i]二进制数的小数点后Ki位即为该消息符号的二进制码字。
2. 用C语言实现#include <stdio.h>#include <math.h>#include <stdlib.h>#define max_CL 10 /*maxsize of length of code*/#define max_PN 6 /*输入序列的个数*/typedef float datatype;typedef struct SHNODE {datatype pb; /*第i个消息符号出现的概率*/datatype p_sum; /*第i个消息符号累加概率*/int kl; /*第i个消息符号对应的码长*/int code[max_CL]; /*第i个消息符号的码字*/struct SHNODE *next;}shnolist;datatype sym_arry[max_PN]; /*序列的概率*/void pb_scan(); /*得到序列概率*/void pb_sort(); /*序列概率排序*/void valuelist(shnolist *L); /*计算累加概率,码长,码字*/void codedisp(shnolist *L);void pb_scan(){int i;datatype sum=0;printf("input %d possible!\n",max_PN);for(i=0;i<max_PN;i++){ printf(">>");scanf("%f",&sym_arry[i]);sum=sum+sym_arry[i];}/*判断序列的概率之和是否等于1,在实现这块模块时,scanf()对float数的缺陷,故只要满足0.99<sum<1.0001出现的误差是允许的*/if(sum>1.0001||sum<0.99){ printf("sum=%f,sum must (<0.999<sum<1.0001)",sum);pb_scan();}}/*选择法排序*/void pb_sort(){int i,j,pos;datatype max;for(i=0;i<max_PN-1;i++){max=sym_arry[i];pos=i;for(j=i+1;j<max_PN;j++)if(sym_arry[j]>max){max=sym_arry[j];pos=j;}sym_arry[pos]=sym_arry[i];sym_arry[i]=max;}}void codedisp(shnolist *L){int i,j;shnolist *p;datatype hx=0,KL=0; /*hx存放序列的熵的结果,KL存放序列编码后的平均码字的结果*/p=L->next;printf("num\tgailv\tsum\t-lb(p(ai))\tlenth\tcode\n");printf("\n");for(i=0;i<max_PN;i++){printf("a%d\t%1.3f\t%1.3f\t%f\t%d\t",i,p->pb,p->p_sum,-3.332*log10(p->pb),p ->kl);j=0;for(j=0;j<p->kl;j++)printf("%d",p->code[j]);printf("\n");hx=hx-p->pb*3.332*log10(p->pb); /*计算消息序列的熵*/KL=KL+p->kl*p->pb; /*计算平均码字*/p=p->next;}printf("H(x)=%f\tKL=%f\nR=%fbit/code",hx,KL,hx/KL); /*计算编码效率*/ }shnolist *setnull(){ shnolist *head;head=(shnolist *)malloc(sizeof(shnolist));head->next=NULL;return(head);}shnolist *my_creat(datatype a[],int n){shnolist *head,*p,*r;int i;head=setnull();r=head;for(i=0;i<n;i++){ p=(shnolist *)malloc(sizeof(shnolist));p->pb=a[i];p->next=NULL;r->next=p;r=p;}return(head);}void valuelist(shnolist *L){shnolist *head,*p;int j=0;int i;datatype temp,s;head=L;p=head->next;temp=0;while(j<max_PN){p->p_sum=temp;temp=temp+p->pb;p->kl=-3.322*log10(p->pb)+1;/*编码,*/{s=p->p_sum;for(i=0;i<p->kl;i++)p->code[i]=0;for(i=0;i<p->kl;i++){p->code[i]=2*s;if(2*s>=1)s=2*s-1;else if(2*s==0)break;else s=2*s;}}j++;p=p->next;}}int main(void){shnolist *head;pb_scan();pb_sort();head=my_creat(sym_arry,max_PN); valuelist(head);codedisp(head);}3.运行结果及分析(本程序先定义了码字长度的最大值和信源概率的个数,然后有设定了概率的和的范围。
信息论与编码实验报告

信息论与编码实验报告一、实验目的本实验主要目的是通过实验验证信息论与编码理论的基本原理,了解信息的产生、传输和编码的基本过程,深入理解信源、信道和编码的关系,以及各种编码技术的应用。
二、实验设备及原理实验设备:计算机、编码器、解码器、信道模拟器、信噪比计算器等。
实验原理:信息论是由香农提出的一种研究信息传输与数据压缩问题的数学理论。
信源产生的消息通常是具有统计规律的,信道是传送消息的媒体,编码是将消息转换成信号的过程。
根据信息论的基本原理,信息的度量单位是比特(bit),一个比特可以表示两个平等可能的事件。
信源的熵(Entropy)是用来衡量信源产生的信息量大小的物理量,熵越大,信息量就越多。
信道容量是用来衡量信道传输信息的极限容量,即信道的最高传输速率,单位是比特/秒。
编码是为了提高信道的利用率,减少传输时间,提高传输质量等目的而进行的一种信号转换过程。
常见的编码技术有霍夫曼编码、香农-费诺编码、区块编码等。
三、实验步骤1.运行编码器和解码器软件,设置信源信息,编码器将信源信息进行编码,生成信道输入信号。
2.设置信道模拟器的信道参数,模拟信道传输过程。
3.将信道输出信号输入到解码器,解码器将信道输出信号进行解码,恢复信源信息。
4.计算信道容量和实际传输速率,比较两者的差异。
5.改变信道参数和编码方式,观察对实际传输速率的影响。
四、实验结果与分析通过实验,我们可以得到不同信道及编码方式下的信息传输速率,根据信道参数和编码方式的不同,传输速率有时会接近信道容量,有时会低于信道容量。
这是因为在真实的传输过程中,存在信噪比、传输距离等因素导致的误码率,从而降低了实际传输速率。
在实验中,我们还可以观察到不同编码方式对传输速率的影响。
例如,霍夫曼编码适用于信源概率分布不均匀的情况,可以实现数据压缩,提高传输效率。
而区块编码适用于数据容量较大的情况,可以分块传输,降低传输错误率。
此外,通过实验我们还可以了解到信息论中的一些重要概念,如信源熵、信道容量等。
实验四-香农编码

海南大学信息科学技术学院信息安全专业《信息论与编码》实验报告一、 实验目的:了解掌握香农编码二、 实验环境:CodeBlocks三、 实验要求编程,对某一离散无记忆信源实现香农编码,输出消息符号及其对应的码字。
设离散无记忆信源⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛01.010.015.017.018.019.020.0)(7654321a a a a a a a X p X ,∑==ni ia p 11)(。
二进制香农编码过程如下: 1、将信源发出的N 个消息符号按其概率的递减次序依次排列。
2、按下式计算第i 个消息的二进制代码组的码长,并取整。
3、为了编成唯一可译码,首先计算第i 个消息的累加概率4、将累加概率Pi (为小数)变成二进制数5、除去小数点,并根据码长li ,取小数点后li 位数作为第i 个消息的码字。
四、 实验过程:代码:#include<stdio.h>#include<math.h>void main(){int i,n, j,k;float sum=0;float p[100]={0}; //无记忆信源X 的概率分布float m;float Pa[100]={0}; //累加概率的数组int l[100];char c[100][100];printf("请输入信源X的个数:");scanf("%d",&n);printf("请输入p[X]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<=n;i++) //判断概率和为1sum=sum+p[i];while(sum!=1){printf("错误输入,请重输\n");printf("请输入x的个数\n");scanf("%d",&n);printf("\n");printf("请输入p[i]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<n;i++)sum=sum+p[i];}for(j=0;j<n-1;j++) //将概率按从大到小排序 for(i=0;i<n-1-j;i++)if(p[i]<p[i+1]){m=p[i];p[i]=p[i+1];p[i+1]=m;}printf("p[i]由大到小的顺序为\n:");for(i=0;i<n;i++)printf("%5.2f",p[i]);printf("\n");Pa[0]=0;for(j=1;j<n+1;j++) //计算累加概率{Pa[j]=Pa[j-1]+p[j-1];}printf("累加和Pi为:");for(j=0;j<n;j++)printf("%5.2f",Pa[j]);printf("\n");printf("码长:");for(i=0;i<n;i++) //计算码长{m=log(1/p[i])/log(2);if(m==(int)m)l[i]=(int)m;elsel[i]=(int)(m+1);}for(i=0;i<n;i++)printf(" %d ",l[i]);printf("\n");for(i=0;i<n;i++) //将累加概率转换成二进制数{for(k=0;k<l[i];k++){Pa[i]=Pa[i]*2;if(Pa[i]>=1){Pa[i]=Pa[i]-1;c[i][k]='1';}else{c[i][k]='0';}}}for(i=0;i<n;i++){for(k=0;k<l[i];k++)printf("%c",c[i][k]);printf("\n");}}五、实验结果:。
香农编码实验报告

中南大学《信息论与编码》实验报告目录一、香农编码 (3)实验目的 (3)实验要求 (3)编码算法 (3)调试过程 (3)参考代码 (4)调试验证 (7)实验总结 (7)二、哈夫曼编码 (8)实验目的 (8)实验原理 (8)数据记录 (9)实验心得 (10)一、香农编码1、实验目的(1)进一步熟悉Shannon 编码算法;(2)掌握C 语言程序设计和调试过程中数值的进制转换、数值与字符串之间的转换等技术。
2、实验要求(1)输入:信源符号个数q 、信源的概率分布p ;(2)输出:每个信源符号对应的Shannon 编码的码字。
3、Shannon 编码算法 1:procedure SHANNON(q,{Pi })2: 降序排列{Pi } 3: for i=1 q do 4: F(i s ) 5:i l 2[]log 1/()i p s 6:将累加概率F(i s )(十进制小数)变换成二进制小数。
7:取小数点后i l 个二进制数字作为第i 个消息的码字。
8:end for9:end procedure------------------------------------------------------------------------------------------------------------------4、调试过程1、fatal error C1083: Cannot open include file: 'unistd.h': No such file or directoryfatal error C1083: Cannot open include file: 'values.h': No such file or directory原因:unistd.h 和values.h 是Unix 操作系统下所使用的头文件纠错:删去即可2、error C2144: syntax error : missing ')' before type 'int'error C2064: term does not evaluate to a function原因:l_i(int *)calloc(n,sizeof(int)); l_i 后缺少赋值符号使之不能通过编译纠错:添加上赋值符号11()i k k p s -=∑3、error C2018: unknown character '0xa1'原因:有不能被识别的符号纠错:在错误处将不能识别的符号改为符合C语言规范的符号4、error C2021: expected exponent value, not ' '原因:if(fabs(sum-1.0)>DELTA); 这一行中DELTA宏定义不正确纠错:# define DELTA 0.0000015、error C2143: syntax error : missing ';' before '}'原因:少写了“;”号纠错:在对应位置添加上“;”号5、参考代码# include<stdio.h># include<math.h># include<stdlib.h># include<string.h># define DELTA 0.000001/*精度*/void sort(float*,int);/*排序*/int main(void){register int i,j;int n; /*符号个数*/int temp;/*中间变量*/float *p_i; /*符号的概率*/float *P_i; /*累加概率*/int *l_i; /*码长*/char * *C; /*码集合*//*用sum来检验数据,用p来缓存了中间数据*/float sum,p;/*输入符号数*/fscanf(stdin,"%d",&n);/*分配内存地址 */p_i=(float *)calloc(n,sizeof(float));P_i=(float *)calloc(n,sizeof(float));l_i=(int *)calloc(n,sizeof(int));/* 存储信道传输的概率*/for(i=0;i<n;i++)fscanf(stdin,"%f",&p_i[i]);/*确认输入的数据*/sum=0.0;for(i=0;i<n;i++)sum+=p_i[i];if(fabs(sum-(1.0))>DELTA)fprintf(stderr,"Invalid input data \n");fprintf(stdout,"Starting…\n\n");/*以降序排列概率*/sort (p_i,n);/*计算每个符号的码长*/for(i=0;i<n;i++){p=(float)(-(log(p_i[i])))/log(2.0);l_i[i]=(int)ceil(p);}/*为码字分配内存地址*/C=(char **)calloc(n,sizeof(char *));for(i=0;i<n;i++){C[i]=(char *)calloc(l_i[i]+1,sizeof(char));C[i][0]='\0';}/*计算概率累加和*/P_i[0]=0.0;for(i=1;i<n;i++)P_i[i]=P_i[i-1]+p_i[i-1];/*将概率和转变为二进制编码*/for(i=0;i<n;i++){for(j=0;j<l_i[i];j++){/*乘2后的整数部分即为这一位的二进制码元*/ P_i[i]=P_i[i]*2;temp=(int)(P_i[i]);P_i[i]=P_i[i]-temp;/*整数部分大于0为1,等于0为0*/if(temp==0)C[i]=strcat(C[i],"0");elseC[i]=strcat(C[i],"1");}}/*显示编码结果*/fprintf(stdout,"The output coding is :\n"); for(i=0;i<n;i++)fprintf(stdout,"%s",C[i]);fprintf(stdout,"\n\n");/*释放内存空间*/for(i=n-1;i>=0;i--)free(C[i]);free(C);free(p_i);free(P_i);free(l_i);exit(0);}/*冒泡排序法*/void sort(float *k,int m){int i=1;/*外层循环变量*/int j=1;/*内层循环变量*/int finish=0;/*结束标志*/float temp;/*中间变量*/while(i<m&&!finish){finish=1;for(j=0;j<m-i;j++){/*将小的数后移*/if(k[j]<k[j+1]){temp=k[j];k[j]=k[j+1];k[j+1]=k[j];finish=0;}i++;}}}6、调试验证:程序结果:7、实验总结1949年香农在《有噪声时的通信》一文中提出了信道容量的概念和信道编码定理,为信道编码奠定了理论基础。
验证香农定理实验报告

验证香农定理实验报告引言香农定理是信息论的基石,它描述了在理想条件下,通过无噪声信道传输的信息的极限速率。
然而,在实际应用中,我们需要验证香农定理是否适用于当前的通信系统。
本实验旨在通过实际操作和数据分析,验证香农定理的正确性。
实验目的1. 通过测量信道带宽和信噪比,定量评估系统的传输速率。
2. 对比理论计算得到的最大传输速率与实际测得的传输速率,验证香农定理的正确性。
实验设备与方法设备:1. 一台计算机2. 一个无线局域网路由器3. 一根网线方法:1. 将计算机通过网线连接到无线局域网路由器。
2. 使用网络分析工具测量信道带宽。
3. 制造不同信噪比的环境,并通过计算机传输信息。
4. 测量传输速率。
实验步骤1. 将计算机通过网线连接到无线局域网路由器,并确保连接正常。
2. 使用网络分析工具测量信道带宽,并记录测得的数值。
结果:测得的信道带宽为20Mbps。
3. 制造不同信噪比的环境。
通过在实验室内调整无线信号的接收强度和背景噪声水平,实现不同信噪比。
记录每个信噪比下的相关参数。
结果:信噪比为10dB,背景噪声水平为-80dBm。
4. 在计算机上选择一个文件,并将其复制到另一台计算机上。
记录文件传输所需的时间,并计算传输速率。
结果:传输文件所需时间为10秒。
数据分析与结果根据香农定理,系统的最大传输速率(C)为信道带宽(B)乘以以2为底的信噪比(S)的乘方,即C=Blog(1+S)。
根据步骤2的结果,信道带宽B=20Mbps。
根据步骤3的结果,信噪比S=10dB,转换为线性单位为10^(S/10)=10^(10/10)=10。
根据步骤4的结果,传输时间T=10秒。
根据以上数据,可计算出实际传输速率R=文件大小/T。
通过将实际传输速率R与理论计算得到的最大传输速率C进行比较,即可验证香农定理的正确性。
根据计算:C=20Mbps * log(1+10) ≈47.7Mbps实际传输速率R=文件大小/10 ≈X1Mbps比较R和C的数值,若R接近C,则验证香农定理的正确性。
香农公式计算例题

香农公式计算例题
香农公式是用来计算信息论中的信息量的公式。
它由克劳德·香农在1948年提出,被广泛应用于通信和数据压缩领域。
香农公式可以表示为:
H = -Σ(p * log2(p))
其中,H代表信息的熵(entropy),p代表事件发生的概率。
下面是一个计算信息量的例题:
假设有一个事件,该事件有4种可能的结果,每种结果发生的概率分别是0.2、0.3、0.4和0.1。
我们需要计算这个事件的信息量。
首先,我们可以计算每种结果的贡献信息量:
- 第一种结果:0.2 * log2(0.2) ≈-0.4644
- 第二种结果:0.3 * log2(0.3) ≈-0.5211
- 第三种结果:0.4 * log2(0.4) ≈-0.5283
- 第四种结果:0.1 * log2(0.1) ≈-0.3322
然后,将每种结果的贡献信息量相加:
- 总信息量= -0.4644 + (-0.5211) + (-0.5283) + (-0.3322) ≈-1.8459
因此,这个事件的信息量约为1.8459个比特。
希望这个例题能够帮助你理解香农公式的计算方式。
如果还有其他问题,请随时提问。
香农编码上机报告

西华大学计算机系上机实践报告课程名称:信息论与编码年级:2009级上机实践成绩:指导教师:王晓明姓名:唐梁尧上机实践名称:香农编码学号:35 上机实践日期:上机实践编号:实验一组号:上机实践时间:一、目的1、熟悉C/C++编程环境,提高自己的实践动手能力。
2、利用已学的程序语言知识,编写相应的程序实现对信源的香农编码。
二、内容与设计思想1、使用结构体数组来存储各信源的相应信息,对于编码过程中的每一个过程书写一函数,然后再主函数中调用这些函数实现程序功能。
2、其中对信源按概率大小排序时采用冒泡排序算法,在对pa转换为二进制时采用乘二取整法实现。
三、使用环境Windowns 7,VC++四、核心代码及调试过程排序算法:void sort(aaa *&temp) /*对各符号按照概率从大到小排序*/{aaa t;int i,j;for(i=0;i<n-1;i++)for(j=0;j<n-i-1;j++){if(temp[j].p<temp[j+1].p){t=temp[j];temp[j]=temp[j+1];temp[j+1]=t;}}}Pa的转换算法:void exchange(aaa *&temp) /*讲pa转换为二进制*/ {int i,j;float s;for(i=0;i<n;i++){s=temp[i].pa;for(j=0;j<temp[i].k;j++){if(2*s>=1){temp[i].code[j]='1';s=2*s-1;}else{temp[i].code[j]='0';s=2*s;}}temp[i].code[j]='\0';}}调试过程:五、总结通过本次上机,我对香农编码有了进一步的了解,掌握了其具体的过程的实现方法,也对信源编码这一概念有了更加深刻的理解,在编码的过程中,使我对C以及C++语言的基础知识掌握更加牢固,特别是巩固了对输出流格式控制的相关知识,总而言之,这次上机实践让我受益匪浅。
香农编码的MATLAB实现

• (2)令 p(a0) = 0,用 pa (aj)(j = i+1)表示第 i 个码字的累加概率,则:
j 1
pa (a j ) p(ai ) i0
j 1,2,..., n
二、实验原理
1. 香农编码步骤
• (3)令 ki 为第 i 个码字的码长,按照下式计算 出各概率对应的码字长度 ki :
三、实验内容
• (5)十进制小数转换成二进制小数
➢ k_max = max(k);
➢ bin = zeros(n,k_max);
% 对二进制小数矩阵初始化
➢ for i = 1:n
➢ for j = 1:k_max
➢
bin(i,j)=floor(pa(i)*2); % 将累加概率转换成二进制
➢
pa(i)=pa(i)*2-floor(pa(i)*2);
三、实验内容
• (7)计算平均码长、信息率和编码效率
➢ K = sum(p.* k); % 平均码长
➢ R = K;
% 信息率
➢ eff = H/R; % 编码效率
三、实验内容
• (8)输出结果
➢ disp(['信源分布 P(X) = [',num2str(p),']']); ➢ disp('编码结果:'); ➢ for i = 1:n ➢ disp([num2str(p(i)),' -> ' ,num2str(codeword(i,:))]); ➢ end ➢ disp(['信源熵 H(X) = ' ,num2str(H),' (bit/sign)']); ➢ disp(['平均码长 K = ' ,num2str(K),' (bit/sign)']); ➢ disp(['信息率 R = ' ,num2str(R),' (bit/sign)']); ➢ disp(['编码效率 η = ' ,num2str(eff)]);
香农编码例题

香农编码例题香农编码是一种将符号转化为二进制代码的编码方式,它是由美国数学家克劳德·香农在1948年提出的。
这种编码方式最初被应用于通信领域,但现在已经广泛应用于数据压缩、图像处理和音频处理等领域。
香农编码的基本思想是根据符号出现的概率来确定其对应的二进制代码。
出现概率较高的符号使用较短的二进制代码表示,而出现概率较低的符号使用较长的二进制代码表示。
这样可以有效地减少使用的二进制位数,从而达到数据压缩的目的。
下面我们来看一个例题:假设有5个符号A、B、C、D、E,它们出现的概率分别为0.4、0.2、0.15、0.15和0.1,请使用香农编码将它们转化为二进制代码。
首先需要按照概率大小对这些符号进行排序,从大到小依次为A、B、C、D和E。
接下来需要计算每个符号对应的编码长度。
根据香农编码原理可知,每个符号对应的编码长度等于其出现概率取对数后向上取整得到的值。
因此,A的编码长度为ceil(log2(1/0.4))=ceil(1.3219)=2,B的编码长度为ceil(log2(1/0.2))=ceil(2.3219)=3,C和D的编码长度均为4,E的编码长度为5。
然后可以根据每个符号对应的编码长度来确定它们对应的二进制代码。
具体地,A对应的二进制代码为00,B对应的二进制代码为010,C和D均对应的二进制代码为0110,E对应的二进制代码为01110。
最后将这些二进制代码按照符号出现概率大小从小到大排列起来就可以得到它们对应的香农编码:E=01110、D=0110、C=0110、B=010、A=00。
通过这个例题我们可以看出,在使用香农编码进行数据压缩时,出现概率较高的符号所对应的二进制代码较短,而出现概率较低的符号所对应的二进制代码较长。
这样可以有效地减少使用的二进制位数,并且在解压缩时也能够快速地还原原始数据。
因此,在实际应用中香农编码是一种非常有效和常用的数据压缩方式。
信息论与编码实验报告

信息论与编码实验报告一、实验目的本实验旨在通过实践,使学生们对信息论与编码理论有一个更深入的理解,掌握信息论与编码的基本原理和应用方法。
二、实验环境本次实验使用MATLAB软件来实现相关编码算法。
三、实验内容1.信息熵的计算信息熵是信息理论中的一个重要概念,用来度量一些信息源的不确定性。
在实验中,我们将计算给定的一组消息的信息熵。
首先,我们将给定的消息编码为二进制序列。
然后,我们根据信息熵的定义,使用公式计算信息熵:H(X) = -Σ(p(x) * log2(p(x)))其中,H(X)表示信息熵,p(x)表示消息x发生的概率。
2.香农编码的实现香农编码是一种无失真的编码方法,用于将离散的符号序列编码为二进制码字。
在实验中,我们将实现香农编码算法。
首先,我们需要计算给定符号序列中各个符号的概率。
然后,根据概率大小,将概率最高的符号分配最短的二进制码字,将概率较低的符号分配较长的二进制码字。
实现香农编码算法后,我们将计算编码后的码字的平均码长,并与信息熵进行比较,了解香农编码的效率。
3.赫夫曼编码的实现赫夫曼编码是一种常用的无失真编码方法,也被广泛应用于数据压缩中。
在实验中,我们将实现赫夫曼编码算法。
首先,我们需要计算给定符号序列中各个符号的概率。
然后,根据概率大小,使用最小堆数据结构构建赫夫曼树。
最后,根据赫夫曼树的性质,将每个符号的编码确定下来。
实现赫夫曼编码算法后,我们将计算编码后的码字的平均码长,并与信息熵进行比较,了解赫夫曼编码的效率。
四、实验结果与分析1.实验一结果我们选取了一个包含1000个等概率的二进制消息的序列进行实验。
通过计算,我们得到了该消息序列的信息熵为12.实验二结果我们选取了一个包含1000个符号的序列进行实验。
通过计算,我们得到了编码后的平均码长为2.8、与信息熵的比较发现,香农编码的效率很高。
3.实验三结果我们选取了一个包含1000个符号的序列进行实验。
通过计算,我们得到了编码后的平均码长为2.6、与信息熵的比较发现,赫夫曼编码的效率也很高。
香农编码定理

香农编码定理香农编码定理是一种信息论中的定理,它描述了在给定一系列符号和它们出现的概率的情况下,如何设计一个最优的编码方案。
这个定理由克劳德·香农在1948年提出,并被认为是信息论的基石之一。
在现代通信中,信息的传输、存储和处理是非常重要的。
编码是其中的一个关键环节,而编码的目的是将信息转化为二进制(或其他进制)形式的数据。
例如,将人类语言转化为可以被计算机理解的形式,或者将数字音乐文件压缩为更小的文件格式。
香农编码定理的核心思想是用更少的比特数来代表一个出现频率较高的符号,用更多的比特数来代表一个出现较低的符号。
这样做能够达到节省存储和传输空间的目的。
这个编码方案是通过构建一颗二叉树来实现的。
在这个二叉树中,每一个叶子节点代表一个符号,而从根节点到叶子节点路径上的编码实际就是用0和1来表示符号出现的频率。
假设有n个符号,每一种符号的出现概率分别为p1、p2、p3......pn。
通过香农编码定理,可以得到一个最优的编码方案,使得整个编码的长度最短。
这个最优的编码方案可以表示为H(S)≤L(S)≤H(S)+1,其中H(S)是符号熵,L(S)是这个编码的平均长度。
符号熵(也称为信息熵)指的是每一个符号所能够传递的信息的平均值,它可以用公式E=-Σi=1 to np(i) log2p(i)来计算,其中p(i)代表第i种符号的概率。
符号熵是香农编码定理的核心概念,它表示了一个平均的信息量,即需要多少比特来表示一个符号的信息。
通过香农编码定理,我们可以得出一个最优的编码方案,即每一个符号的编码长度都是整数位的比特数。
这个编码方案可以用于压缩数据,使得数据传输的速度更快,同时也可以节省存储空间。
总之,香农编码定理在现代通信和计算机科学中具有非常重要的作用,它为我们提供了一种最优的编码方案,使得数据能够被更加高效地传输和处理。
最新《信息论基础》实验报告-实验1

最新《信息论基础》实验报告-实验1实验目的:1. 理解信息论的基本概念,包括信息熵、互信息和编码理论。
2. 通过实验掌握香农信息熵的计算方法。
3. 学习并实践简单的数据压缩技术。
实验内容:1. 数据集准备:选择一段英文文本作为实验数据集,统计各字符出现频率。
2. 信息熵计算:根据字符频率计算整个数据集的香农信息熵。
3. 编码设计:设计一种基于频率的霍夫曼编码方案,为数据集中的每个字符分配一个唯一的二进制编码。
4. 压缩与解压缩:使用设计的霍夫曼编码对原始文本进行压缩,并验证解压缩后能否恢复原始文本。
5. 性能评估:比较压缩前后的数据大小,计算压缩率,并分析压缩效果。
实验步骤:1. 从文本文件中读取数据,统计每个字符的出现次数。
2. 利用统计数据计算字符的相对频率,并转换为概率分布。
3. 应用香农公式计算整个数据集的熵值。
4. 根据字符频率构建霍夫曼树,并为每个字符生成编码。
5. 将原始文本转换为编码序列,并记录压缩后的数据大小。
6. 实现解压缩算法,将编码序列还原为原始文本。
7. 分析压缩前后的数据大小差异,并计算压缩率。
实验结果:1. 原始文本大小:[原始文本大小]2. 压缩后大小:[压缩后大小]3. 压缩率:[压缩率计算结果]4. 霍夫曼编码表:[字符与编码的对应表]实验讨论:- 分析影响压缩效果的因素,如字符集大小、字符频率分布等。
- 讨论在实际应用中,如何优化编码方案以提高压缩效率。
- 探讨信息论在数据压缩之外的其他应用领域。
实验结论:通过本次实验,我们成功地应用了信息论的基本原理,通过霍夫曼编码技术对文本数据进行了有效压缩。
实验结果表明,基于字符频率的霍夫曼编码能够显著减少数据的存储空间,验证了信息论在数据压缩领域的有效性和实用性。
信息论与编码实验报告

本科生实验报告实验课程信息理论与编码学院名称信息科学与技术学院专业名称学生姓名学生学号指导教师实验地点实验成绩二〇一六年九月----二〇一六年十一月填写说明1、适用于本科生所有的实验报告(印制实验报告册除外);2、专业填写为专业全称,有专业方向的用小括号标明;3、格式要求:①用A4纸双面打印(封面双面打印)或在A4大小纸上用蓝黑色水笔书写。
②打印排版:正文用宋体小四号,1.5倍行距,页边距采取默认形式(上下2.54cm,左右2.54cm,页眉1.5cm,页脚1.75cm)。
字符间距为默认值(缩放100%,间距:标准);页码用小五号字底端居中。
③具体要求:题目(二号黑体居中);摘要(“摘要”二字用小二号黑体居中,隔行书写摘要的文字部分,小4号宋体);关键词(隔行顶格书写“关键词”三字,提炼3-5个关键词,用分号隔开,小4号黑体);正文部分采用三级标题;第1章××(小二号黑体居中,段前0.5行)1.1 ×××××小三号黑体×××××(段前、段后0.5行)1.1.1小四号黑体(段前、段后0.5行)参考文献(黑体小二号居中,段前0.5行),参考文献用五号宋体,参照《参考文献著录规则(GB/T 7714-2005)》。
实验一:香农(Shannon )编码一、实验目的掌握通过计算机实现香农编码的方法。
二、实验要求对于给定的信源的概率分布,按照香农编码的方法进行计算机实现。
三、实验基本原理给定某个信源符号的概率分布,通过以下的步骤进行香农编码 1.将信源消息符号按其出现的概率大小排列)()()(21n x p x p x p ≥≥≥ 2.确定满足下列不等式的整数码长K i ;1)(log )(log 22+-<≤-i i i x p K x p3.为了编成唯一可译码,计算第i 个消息的累加概率∑-==11)(i k k i x p p4.将累加概率P i 变换成二进制数。
实验二香农编码的计算与分析

实验二香农编码的计算与分析The final edition was revised on December 14th, 2020.实验二香农编码的计算与分析一、[实验冃的]1、理解香农第一定理指出平均码长与信源之间的关系。
2、加深理解香农编码具有的重要理论意义。
3、掌握Shannon编码的原理。
4、掌握Shannon编码的方法和步骤。
3、熟悉shannnon编码的各种效率二、[实验环境]windows XP, MATLAB 7三、[实验原理]香农第一定理:设离散无记忆信源为I SI I 5\s2 ■….sq[_ ^p(s2) .... p(sq)嫡为H(S),其N次扩展信源为种编鲁盟駕擁驚爲缢席每籍黑霧需為證器到-竺+丄厶空logr N N logr当\ts时lim H = H Q)」\jxN瓦是平均码长四、[实验内容]人是匕对应的码字长度r-l1、根据实验原理,设计shannon编码方法,在给定C •SP 二L J<厂si s2 s3 s4 s5 s6 s7丿条件下,实现香农编码并算出编码效率。
2、请自己构造两个信源空间,根据求Shannon编码结果说明其物理意义。
五、[实验过程]每个实验项目包括:1)设计思路2)实验中岀现的问题及解决方法;要求:1)有标准的实验报告(10分)2)程序设计和基本算法合理(30分)3)实验仿真具备合理性(30分)4)实验分析合理(20分)5)能清晰的对实验中出现的问题进行分析并提出解决方案(10分)附录:程序设计与算法描述参考⑴)按降序排列概率的函数%[p,x]二arnxy(P)为按降序排序的函数%%P为信源的概率矢量,x为概率元素的下标矢量%%p为排序后返回的信源的概率矢量%%乂为排序后返回的概率元素的下标矢量%function[p,x]=array(P) n=length(P);X=l:n;P=[P; XI;for i=l:nmax 二P(lj); maxN=i; MAX=P(:,i);for j=i:n if(max<P(l j)) MAX=P(: j); max 二P(l,j); maxN=j;endendif (maxN>l)if (i<n)for k=(maxN-l):-l:iP(:,k+l)=P(:,k);endendendP(:,i)=MAX;endP=P(1,:);x 二P(2,:);(2) Shannon编码算法% shannon编码生成器%%函数说明:%% [W.L.q]=shannon(p)为Shannon 编码函数 %% P为信源的概率矢量,W为编码返回的码字%%L%编码返回的平均码字长度,q为编码概率%| ir \■/11 * ^T> ^T> ^T> 【管function [W,L,q] =shannon(p)%提示错误信息%if (length(伽d(pv=0))〜=0)error('Not a component*); %判断是否符合概率分布条件%1)排序if (abs(sum(p)-l)> 1 Oe-10)error(r Not a do not add up to 1') %判断是否符合概率和为1 end [p,x]=array(p); % 2)计算代码组长度1 l=ceil(-log2(p));% 3)计算累加概率PP(l)=0;n=len gtli(p);for i=2:nP(i)=P(M)+p(M);end% 4)求得二进制代码组W%町将十进制数转为二进制数for i=I:nforj=l:l(i) temp(i,j)=floor(P(i)*2); P(i)=P(i)*2-temp(i,j);endend%3给\¥赋ASCII码值,用于显示二进制代码组W for i=l:n forj=l:l(i)if (temp(ij)==0)W(i,j)=4 &elseW(i,j)=49;endendendL=sum(p.*I); %计算平均码字长度H=entropyl(p,2); % 计算信源嫡q=H/L; %计算编码效率for i=l:nB{i)=x(i);end% [n,m]=size(W);% TEMP=32*ones(n,6);% W=[W,TEMP];% W=W ;% [n,m]=size(W);% W=reshape(W, 1 ,n*m);% W=sprintfC%s,,W);[m,n]=size(W);TEMP=blanks(m);W=[W,TEMP\TEM P、TEMP];[m,n]=size(W);W=reshape(W\ 1,m*n);sO・很好!输入正确,编码结果如下:s^'Shannon编码所得码字W : s2=*Shannon编码平均码字长度L : s3=Shannon编码的编码效率q : disp(sO); disp(sl),disp(B),disp(W); disp(s2),disp(L);disp(s3),disp(q);。
信息论与编码实验一解析

实验一香农编码和Huffman编码 香农编码:clear;clc;N=input('the number of input N=');fprintf('input the probability distribution of X\n')for i=1:Ninput_p(i)=input('the probability is:');if input_p(i)<0error('Don''t accord with the distribution') endends=0;for i=1:Ns=s+input_p(i);endif(s<=0.999999||s>=1.000001)error('Don''t accord with the distribution')endp=input_p;for i=1:Nfor j=1:Nif p(i)>p(j)t=p(i);p(i)=p(j);p(j)=t;elsep(i)=p(i);endendendpa(1)=0;for j=2:Npa(j)=0;for i=1:j-1pa(j)=pa(j)+p(i);endendfor i=1:Nk(i)=ceil(-log2(p(i))); %ceil()向正无穷大取整endfor i=1:Nz=pa(i)*2;for j=1:10if z>=1d(i,j)=1;z=z-1;z=z*2;elsed(i,j)=0;z=z*2;endendendfprintf('the probability distribution of X is:\n');disp(input_p);fprintf('the output from the largest to the least is:\n');disp(p);fprintf('the output of shannon coding is:\n');for i=1:Nfor j=1:k(i)output(j)=d(i,j);enddisp(output);endHuffman编码:clcclear all%取得信源概率矩阵,并进行合法性判断clear;P=input('请输入信源概率向量P=');N=length(P);for component=1:1:Nif(P(component)<0)error('信源概率不能小于0');endendif((sum(P)-1)>0.0001)error('信源概率之和必须为1');end%建立各概率符号的位置索引矩阵Index,利于编码后从树根进行回溯,从而得出对应的编码Q=PIndex=zeros(N-1,N); %初始化Indexfor i=1:N-1[Q,L]=sort(Q); %将P中的元素按升序排序后,元素放到Q中,对应的索引值存到L中Index(i,:)=[L(1:N-i+1),zeros(1,i-1)]G(i,:)=Q%缩减信源得到的最终矩阵%Index为N-1行、N列矩阵,用来记录每行最小两概率叠加后概率排列次序,元素不足的地方补0%参考doc sort%************************************************************** **********%************************************************************** **********% Q=[Q(1)+Q(2),Q(3:N),1]; ******原来的语句 %将Q中概率最小的两个元素合并,元素不足的地方补1Q=[Q(3:N),Q(1)+Q(2),1];%************************************************************* **********%************************************************************* **********end%根据以上建立的Index矩阵,进行回溯,获取信源编码for i=1:N-1Char(i,:)=blanks(N*N);%初始化一个由空格符组成的字符矩阵N*N,用于存放编码end%从码树的树根向树叶回溯,即从G矩阵的最后一行按与Index中的索引位置的对应关系向其第一行进行编码Char(N-1,N)='1';%G中的N-1行即最后一行第一个元素赋为1,存到Char 中N-1行的N列位置Char(N-1,2*N)='0';%G中的N-1行即最后一行第二个元素赋为0,存到Char 中N-1行的2*N列位置%以下从G的倒数第二行开始向前编码for i=2:N-1%*************************************************************** **********%*************************************************************** **********% Char(N-i,1:N-1)=Char(N-i+1,N*(find(Index(N-i+1,:)==1)) -(N-2):N*(find(Index(N-i+1,:)==1)));% 上面是原来的语句Char(N-i,1:N-1)=Char(N-i+1,N*(find(Index(N-i+1,:)==N-1))-(N-2):N*(find(Index(N-i+1,:)==N-1)));%************************************************************ **********%************************************************************ **********%将Index后一行中索引为1的编码码字填入到当前行的第一个编码位置 Char(N-i,N)='1'; %然后在当前行的第一个编码位置末尾填入'1' Char(N-i,N+1:2*N-1)=Char(N-i,1:N-1); %将G后一行中索引为1的编码码字填入到当前行的第二个编码位置Char(N-i,2*N)='0'; %然后在当前行的第二个编码位置末尾填入'0' for j=1:i-1%内循环作用:将Index后一行中索引不为1处的编码按照左右顺序填入当前行的%第3个位置开始的地方,最后计算到Ind5ex的首行为止%*************************************************************** **********%*************************************************************** **********%Char(N-i,(j+1)*N+1:(j+2)*N)=Char(N-i+1,N*(find(Index(N-i+1,:)== j+1)-1)+1:N*find(Index(N-i+1,:)==j+1))% 上面是原来的语句Char(N-i,(j+1)*N+1:(j+2)*N)=Char(N-i+1,N*(find(Index(N-i+1,:)==j)-1)+ 1:N*find(Index(N-i+1,:)==j));%********************************************************** **********%********************************************************** **********endend%Char中第一行的编码结果就是所需的Huffman 编码输出,通过Index中第一行索引将编码对应到相应概率的信源符号上。
信息论与编码技术实验指导书

2、写出程序代码, 3、写出在调试过程中出现的问题 , 4、对实验的结果进行分析。
实验六 模p信道编码实验 一 实验目的:掌握通过计算机实现模p信道编码 二实验要求: 对于给定的消息序列,按照模p信道编码的方法进行 计算机实现. 三实验原理 在实际生活中,有时侯“1”和“I”很相似。 p=37(符号的个数) 数字“0”-“9”和字母“A”-“Z”和空格 共37种符号。 “0” 0 “1” 1 ¨ “A” 10 “B” 11 设有某消息的符号序列为X=X1X2X3X4, 用下表的方式来求它们的和及累加和,然后加上 适当的监督元,使累加和是模37的倍数。 消息符号
型如下图:
在给定信源概率分布条件下, 各种熵的求解方法如下: 1) 信源熵 2) 条件熵
3) 联合熵
4) 交互熵 5) 信道容量 ◼一般离散信道容量对计算步骤总结如下:
4、 实验设备:计算机 c++ 五、实验报告要求 1、 画出程序设计的流程图, 2、 写出程序代码, 3、 写出在调试过程中出现的问题 , 4、 对实验的结果进行分析。
和 累加和 X1 X1 X1 X2 X1+X2 2*X1+X2 X3 X1+X2+X3 3*X1+2*X2+X3 X4 X1+X2+X3+X4 4*X1+3*X2+2*X3+X4
ψ X1+X2+X3+X4+ψ 5*X1+4*X2+3*X3+2*X4+ψ 四实验设备 计算机 c++ 五实验报告 1、画出程序设计的流程图, 2、写出程序代码, 3、写出在调试过程中出现的问题 , 实验目的:通过该实验,掌握通过计算机实验信息量 和信道容量的计算方法 2、 实验要求:对一个离散的无记忆信源,给定信源的输 入概率分布,给定一个信道特性,计算各种信息量和 熵,并计算信道容量。 3、 实验原理:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 香农编码的计算与分析
一、[实验目的]
1、
理解香农第一定理指出平均码长与信源之间的关系。
2、
加深理解香农编码具有的重要理论意义。
3、
掌握Shannon 编码的原理。
4、
掌握Shannon 编码的方法和步骤。
5、
熟悉shannnon 编码的各种效率
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
香农第一定理:
设离散无记忆信源为 12 (1)
(2)....()S s s sq
P p s p s p sq ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 熵为H(S),其N 次扩展信源为 12 (1)
(2)....()N q S p p p q P αααααα⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ 熵为H(S N )。
码符号集X=(x1,x2,…,xr )。
先对信源N S 进行编码,总可以找到一种编码方法,构成惟一可以码,使S 中每个信源符号所需的平均码长满足: 1N L H S H S N N +>≥()()logr logr
当N →∞时 lim ()N r N L H S N
→∞= N L 是平均码长 1
()N
q N i i i L p αλ==∑ i λ是i α对应的码字长度
四、[实验内容]
1、根据实验原理,设计shannon 编码方法,在给定
条件下,实现香农编码并算出编码效率。
2、请自己构造两个信源空间,根据求Shannon 编码结果说明其物理意义。
五、[实验过程]
每个实验项目包括:1)设计思路2)实验中出现的问题及解决方法;
要求:
1)有标准的实验报告 (10分)
2)程序设计和基本算法合理(30分)
3)实验仿真具备合理性(30分)
4)实验分析合理(20分)
5)能清晰的对实验中出现的问题进行分析并提出解决方案(10分)
S P s1 s2 s3 s4 s5 s6
s7 =
附录:程序设计与算法描述参考
(1))按降序排列概率的函数
%[p,x]=array(P)为按降序排序的函数 %
%P为信源的概率矢量,x为概率元素的下标矢量%
%P为排序后返回的信源的概率矢量 %
%x为排序后返回的概率元素的下标矢量 %
%******************************%
function[p,x]=array(P)
n=length(P);
X=1:n;
P=[P;X];
for i=1:n
max=P(1,i);
maxN=i;
MAX=P(:,i);
for j=i:n
if(max<P(1,j))
MAX=P(:,j);
max=P(1,j);
maxN=j;
end
end
if (maxN>1)
if (i<n)
for k=(maxN-1):-1:i
P(:,k+1)=P(:,k);
end
end
end
P(:,i)=MAX;
end
p=P(1,:);
x=P(2,:);
(2)Shannon编码算法
% shannon编码生成器 %
% 函数说明: %
% [W,L,q]=shannon(p) 为 Shannon编码函数 %
% p 为信源的概率矢量,W为编码返回的码字 %
% L 为编码返回的平均码字长度,q 为编码概率 %
% ******************************************************* %
function [W,L,q] =shannon(p)
% 提示错误信息 %
if (length(find(p<=0)) ~=0)
error('Not a component'); % 判断是否符合概率分布条件
end
% 1) 排序
if (abs(sum(p)-1)>10e-10)
error('Not a do not add up to 1') %判断是否符合概率和为 1 end
[p,x]=array(p);
% 2) 计算代码组长度l
l=ceil(-log2(p));
% 3) 计算累加概率P
P(1)=0;
n=length(p);
for i=2:n
P(i)=P(i-1)+p(i-1);
end
% 4) 求得二进制代码组W
% a) 将十进制数转为二进制数
for i=1:n
for j=1:l(i)
temp(i,j)=floor(P(i)*2);
P(i)=P(i)*2-temp(i,j);
end
end
% b) 给W赋ASCII码值,用于显示二进制代码组W
for i=1:n
for j=1:l(i)
if (temp(i,j)==0)
W(i,j)=48;
else
W(i,j)=49;
end
end
end
L=sum(p.*l); % 计算平均码字长度
H=entropy1(p,2); % 计算信源熵
q=H/L; % 计算编码效率
for i=1:n
B{i}=x(i);
end
% [n,m]=size(W);
% TEMP=32*ones(n,6);
% W=[W,TEMP];
% W=W';
% [n,m]=size(W);
% W=reshape(W,1,n*m);
% W=sprintf('%s',W);
[m,n]=size(W);
TEMP=blanks(m);
W=[W,TEMP',TEMP',TEMP'];
[m,n]=size(W);
W=reshape(W',1,m*n);
s0='很好!输入正确,编码结果如下:'; s1='Shannon编码所得码字W:';
s2='Shannon编码平均码字长度L:';
s3='Shannon编码的编码效率q:';
disp(s0);
disp(s1),disp(B),disp(W);
disp(s2),disp(L);
disp(s3),disp(q);。
