实验二 香农编码的计算与分析1
实验四_香农编码
实验名称:实验四香农编码一、实验目的:加深对香农公式的理解及其具体的实现过程。
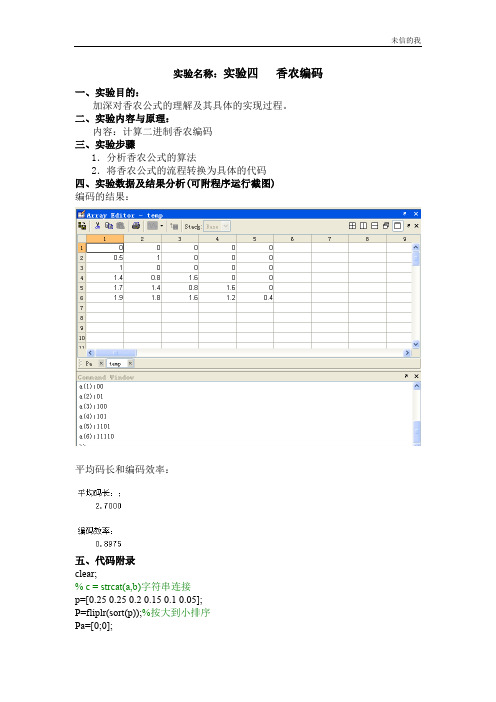
二、实验内容与原理:内容:计算二进制香农编码三、实验步骤1.分析香农公式的算法2.将香农公式的流程转换为具体的代码四、实验数据及结果分析(可附程序运行截图)编码的结果:平均码长和编码效率:五、代码附录clear;% c = strcat(a,b)字符串连接p=[0.25 0.25 0.2 0.15 0.1 0.05];P=fliplr(sort(p));%按大到小排序Pa=[0;0];%累加和的定义----第一行为累加和,第二行为Ki %求累加和for x=1for y=1:1:5%Pa(x,y)=1;Pa(x,y+1)=P(x,y)+ Pa(x,y);endend%ceil 是取向离它最近的大整数圆整for i=2for j=1:1:6Pa(i,j)=ceil( -log2(P(1,j)) );endend%信源熵H=0;L=0;for i=1:1:6H=H-P(i)*log2(P(i));L=L+P(i)*Pa(2,i);endu=H/L;disp('平均码长:;');disp(L);disp('编码效率:');disp(u);%求各符号的编码temp=[];%临时的编码值:1:6for m=1:1:6fprintf('a(%d):',m);for n=1:1:abs(Pa(2,m))temp(m,n)=Pa(1,m)*2;if temp(m,n)>=1O(m,n)=1;Pa(1,m)=temp(m,n)-1;elseO(m,n)=0;Pa(1,m)=temp(m,n);endfprintf('%d',O(m,n));endfprintf('\n');end六、其他:实验总结、心得体会及对本实验方法、手段及过程的改进建议等。
实验起初是想把累加和及Ki和编码放在一个二维矩阵中,但具体的实现较为复杂,所以最后改为逐行存放并成功完成了实验。
编码度量算法实验报告(3篇)

第1篇一、实验目的1. 理解编码度量算法的基本原理和重要性。
2. 掌握常见编码度量算法(如香农熵、信息增益、增益率等)的应用。
3. 通过实验验证不同编码度量算法在数据压缩中的应用效果。
二、实验环境1. 操作系统:Windows 102. 编程语言:Python3.73. 数据集:使用某自然语言处理数据集,包含1000条文本数据。
三、实验原理编码度量算法用于评估编码的效率,其主要目的是在保证信息完整性的前提下,尽量减少编码长度。
以下介绍几种常见的编码度量算法:1. 香农熵:香农熵是衡量信息熵的指标,用于衡量数据的不确定性。
香农熵越大,表示数据越复杂,编码长度越长。
2. 信息增益:信息增益是衡量特征重要性的指标,用于评估特征对分类结果的贡献。
信息增益越大,表示该特征对分类结果的贡献越大。
3. 增益率:增益率是信息增益与特征熵的比值,用于衡量特征在降低数据不确定性方面的效果。
增益率越大,表示该特征对编码的优化效果越好。
四、实验步骤1. 数据预处理:将数据集划分为训练集和测试集,分别用于训练模型和评估模型性能。
2. 编码度量算法实现:根据实验原理,实现香农熵、信息增益、增益率等编码度量算法。
3. 模型训练:使用支持向量机(SVM)作为分类模型,对训练集进行训练。
4. 编码度量评估:对测试集进行编码度量评估,计算香农熵、信息增益、增益率等指标。
5. 结果分析:比较不同编码度量算法对编码性能的影响,分析其优缺点。
五、实验结果与分析1. 香农熵:通过计算测试集的香农熵,发现数据集的复杂度较高,编码长度较长。
2. 信息增益:通过计算测试集的特征信息增益,发现特征A、B、C的信息增益较高,说明这三个特征对分类结果的贡献较大。
3. 增益率:通过计算测试集的特征增益率,发现特征A的增益率最高,说明特征A在降低数据不确定性方面效果最好。
4. 结果分析:根据实验结果,香农熵反映了数据集的复杂度,信息增益和增益率反映了特征对分类结果的贡献。
对香农三大定理的分析与探讨

对香农三大定理的分析与探讨摘要本文针对香农三大定理的内容,进行理论分析,探讨了无失真信源编码、有噪信道编码和保真度准则下的信源编码定理。
通过对离散信源熵的分析,延伸到了对扩展信源的理解,同时结合著名的香农公式和信息论与编码的发展史,指出了香农三大定理的意义。
一、香农第一定理香农第一定理主要研究信息的测度,对应的是无失真信源编码定理。
采用无失真最佳信源编码,可以使得用于每个信源符号的编码位数尽可能地小,但它的极限是原始信源的熵值,超过了这一极限就不可能实现无失真的译码。
1.1 离散信源熵1.1.1 信源的概念信源发出消息,消息载荷信息,而消息又具有不确定性,故而可以用随机变量或随机矢量来描述信源输出的消息。
从随机变量出发来研究信息,这正是香农信息论的基本假说。
而离散信源指的是这类信源输出的消息常以一个符号、一个符号的形式出现,这些符号的取值是有限的或者是可数的。
单符号离散信源只涉及一个随机事件,多符号离散信源则涉及多个随机事件。
1.1.2 信源熵的概念及其性质在度量信息的各种方法中,香农提出了解决信息度量问题的方法——熵,这是香农信息论最基本的,也是最重要的概念[1]。
信源熵,即信源的信息熵,又称香农熵、无条件熵,简称熵。
信源各个离散消息的自信息量的数学期望是信源的平均信息量,实质上是无记忆信源平均不确定度的度量。
信源熵表示在信源输出消息前,信源的平均不确定度,也表示在信源输出消息后,平均每个离散消息所提供的信息量,能够反映变量的随机性。
当消息出现的概率相同时,猜测每一个消息发生错误的概率均相同,说明等概率信源的不确定性最大,具有最大熵[2]。
1.2 无失真离散信源编码1.2.1 信源编码的概念信源编码处于通信系统的前端,直接对信源发出的信号进行变换处理。
通过压缩每个信源符号的平均比特数或信源的码率,以较少的码率来传送同样多的信息,增加单位时间内传送的平均信息量,来压缩信源的冗余度,从而提高通信的有效性。
信息论与编码实验报告-Shannon编码

实验报告课程名称:信息论与编码姓名:系:专业:年级:学号:指导教师:职称:年月日实验三 Shannon 编码一、实验目的1、熟悉离散信源的特点;2、学习仿真离散信源的方法3、学习离散信源平均信息量的计算方法4、熟悉 Matlab 编程二、实验原理给定某个信源符号的概率分布,通过以下的步骤进行香农编码 1、信源符号按概率从大到小排列;12.......n p p p ≥≥≥2、确定满足下列不等式的整数码长i K 为()()1i i i lb p K lb p -≤<-+3、为了编成唯一可译码,计算第i 个消息的累加概率:4、将累加概率i P 变换成二进制数;5、取i P 二进制数的小数点后i K 位即为该消息符号的二进制码字。
三、实验内容1、写出计算自信息量的Matlab 程序2、写出计算离散信源平均信息量的Matlab 程序。
3、将程序在计算机上仿真实现,验证程序的正确性并完成习题。
四、实验环境Microsoft Windows 7 Matlab 6.5五、编码程序计算如下信源进行香农编码,并计算编码效率:⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡01.01.015.017.018.019.02.06543210a a a a a a a P X MATLAB 程序:(1) a=[0.2 0.18 0.19 0.15 0.17 0.1 0.01]; k=length(a);y=0; for i=1:k-111()i i k k P p a -==∑for n=i+1:kif (a(i)<a(n))t=a(i);a(i)=a(n);a(n)=t;endendends=zeros(k,1);b=zeros(k,1);for m=1:ks(m)=y;y=y+a(m);b(m)=ceil(-log2(a(m)));z=zeros(b(m),1);x=s(m);p=b2d10(x);for r=1:b(m)z(r)=p(r);enddisp('Êä³ö½á¹ûΪ£º')disp('³öʸÅÂÊ'),disp(a(m))disp('ÇóºÍ½á¹û'),disp(s(m))disp('±àÂëλÊý'),disp(b(m))disp('×îÖÕ±àÂë'),disp(z')end(2) function y=b2d10(x)for i=1:8temp=x.*2;if(temp<1)y(i)=0;x=temp;elsex=temp-1;y(i)=1;endend(3) p=[0.2 0.19 0.18 0.17 0.15 0.1 0.01]; sum=0;sum1=0;for i=1:7a(i)=-log2(p(i));K(i)=ceil(a(i));R(i)=p(i)*K(i);sum=sum+R(i);c(i)=a(i)*p(i);sum1=sum1+c(i);endK1=sum;H=sum1;Y=H/K1;disp('ƽ¾ùÐÅÏ¢Á¿'),disp(H)disp('ƽ¾ùÂ볤'),disp(K1)disp('±àÂëЧÂÊ'),disp(Y)六、实验结果输出结果为:出事概率0.2000,求和结果0,编码位数3,最终编码000出事概率0.1900,求和结果0.2000,编码位数3,最终编码001出事概率0.1800,求和结果0.3900,编码位数3,最终编码011出事概率0.1700,求和结果0.5700,编码位数3,最终编码100出事概率0.1500,求和结果0.7400,编码位数3,最终编码101出事概率0.1000,求和结果0.8900,编码位数4,最终编码1110出事概率0.0100,求和结果0.9900,编码位数7,最终编码1111110编码效率:平均信息量2.6087平均码长3.1400编码效率0.8308七、实验总结通过本次的实验,掌握了Shannon编码的实验原理以及编码过程。
香农编码实验报告

中南大学《信息论与编码》实验报告目录一、香农编码 (3)实验目的 (3)实验要求 (3)编码算法 (3)调试过程 (3)参考代码 (4)调试验证 (7)实验总结 (7)二、哈夫曼编码 (8)实验目的 (8)实验原理 (8)数据记录 (9)实验心得 (10)一、香农编码1、实验目的(1)进一步熟悉Shannon 编码算法;(2)掌握C 语言程序设计和调试过程中数值的进制转换、数值与字符串之间的转换等技术。
2、实验要求(1)输入:信源符号个数q 、信源的概率分布p ;(2)输出:每个信源符号对应的Shannon 编码的码字。
3、Shannon 编码算法 1:procedure SHANNON(q,{Pi })2: 降序排列{Pi } 3: for i=1 q do 4: F(i s ) 5:i l 2[]log 1/()i p s 6:将累加概率F(i s )(十进制小数)变换成二进制小数。
7:取小数点后i l 个二进制数字作为第i 个消息的码字。
8:end for9:end procedure------------------------------------------------------------------------------------------------------------------4、调试过程1、fatal error C1083: Cannot open include file: 'unistd.h': No such file or directoryfatal error C1083: Cannot open include file: 'values.h': No such file or directory原因:unistd.h 和values.h 是Unix 操作系统下所使用的头文件纠错:删去即可2、error C2144: syntax error : missing ')' before type 'int'error C2064: term does not evaluate to a function原因:l_i(int *)calloc(n,sizeof(int)); l_i 后缺少赋值符号使之不能通过编译纠错:添加上赋值符号11()i k k p s -=∑3、error C2018: unknown character '0xa1'原因:有不能被识别的符号纠错:在错误处将不能识别的符号改为符合C语言规范的符号4、error C2021: expected exponent value, not ' '原因:if(fabs(sum-1.0)>DELTA); 这一行中DELTA宏定义不正确纠错:# define DELTA 0.0000015、error C2143: syntax error : missing ';' before '}'原因:少写了“;”号纠错:在对应位置添加上“;”号5、参考代码# include<stdio.h># include<math.h># include<stdlib.h># include<string.h># define DELTA 0.000001/*精度*/void sort(float*,int);/*排序*/int main(void){register int i,j;int n; /*符号个数*/int temp;/*中间变量*/float *p_i; /*符号的概率*/float *P_i; /*累加概率*/int *l_i; /*码长*/char * *C; /*码集合*//*用sum来检验数据,用p来缓存了中间数据*/float sum,p;/*输入符号数*/fscanf(stdin,"%d",&n);/*分配内存地址 */p_i=(float *)calloc(n,sizeof(float));P_i=(float *)calloc(n,sizeof(float));l_i=(int *)calloc(n,sizeof(int));/* 存储信道传输的概率*/for(i=0;i<n;i++)fscanf(stdin,"%f",&p_i[i]);/*确认输入的数据*/sum=0.0;for(i=0;i<n;i++)sum+=p_i[i];if(fabs(sum-(1.0))>DELTA)fprintf(stderr,"Invalid input data \n");fprintf(stdout,"Starting…\n\n");/*以降序排列概率*/sort (p_i,n);/*计算每个符号的码长*/for(i=0;i<n;i++){p=(float)(-(log(p_i[i])))/log(2.0);l_i[i]=(int)ceil(p);}/*为码字分配内存地址*/C=(char **)calloc(n,sizeof(char *));for(i=0;i<n;i++){C[i]=(char *)calloc(l_i[i]+1,sizeof(char));C[i][0]='\0';}/*计算概率累加和*/P_i[0]=0.0;for(i=1;i<n;i++)P_i[i]=P_i[i-1]+p_i[i-1];/*将概率和转变为二进制编码*/for(i=0;i<n;i++){for(j=0;j<l_i[i];j++){/*乘2后的整数部分即为这一位的二进制码元*/ P_i[i]=P_i[i]*2;temp=(int)(P_i[i]);P_i[i]=P_i[i]-temp;/*整数部分大于0为1,等于0为0*/if(temp==0)C[i]=strcat(C[i],"0");elseC[i]=strcat(C[i],"1");}}/*显示编码结果*/fprintf(stdout,"The output coding is :\n"); for(i=0;i<n;i++)fprintf(stdout,"%s",C[i]);fprintf(stdout,"\n\n");/*释放内存空间*/for(i=n-1;i>=0;i--)free(C[i]);free(C);free(p_i);free(P_i);free(l_i);exit(0);}/*冒泡排序法*/void sort(float *k,int m){int i=1;/*外层循环变量*/int j=1;/*内层循环变量*/int finish=0;/*结束标志*/float temp;/*中间变量*/while(i<m&&!finish){finish=1;for(j=0;j<m-i;j++){/*将小的数后移*/if(k[j]<k[j+1]){temp=k[j];k[j]=k[j+1];k[j+1]=k[j];finish=0;}i++;}}}6、调试验证:程序结果:7、实验总结1949年香农在《有噪声时的通信》一文中提出了信道容量的概念和信道编码定理,为信道编码奠定了理论基础。
香农编码上机报告

西华大学计算机系上机实践报告课程名称:信息论与编码年级:2009级上机实践成绩:指导教师:王晓明姓名:唐梁尧上机实践名称:香农编码学号:35 上机实践日期:上机实践编号:实验一组号:上机实践时间:一、目的1、熟悉C/C++编程环境,提高自己的实践动手能力。
2、利用已学的程序语言知识,编写相应的程序实现对信源的香农编码。
二、内容与设计思想1、使用结构体数组来存储各信源的相应信息,对于编码过程中的每一个过程书写一函数,然后再主函数中调用这些函数实现程序功能。
2、其中对信源按概率大小排序时采用冒泡排序算法,在对pa转换为二进制时采用乘二取整法实现。
三、使用环境Windowns 7,VC++四、核心代码及调试过程排序算法:void sort(aaa *&temp) /*对各符号按照概率从大到小排序*/{aaa t;int i,j;for(i=0;i<n-1;i++)for(j=0;j<n-i-1;j++){if(temp[j].p<temp[j+1].p){t=temp[j];temp[j]=temp[j+1];temp[j+1]=t;}}}Pa的转换算法:void exchange(aaa *&temp) /*讲pa转换为二进制*/ {int i,j;float s;for(i=0;i<n;i++){s=temp[i].pa;for(j=0;j<temp[i].k;j++){if(2*s>=1){temp[i].code[j]='1';s=2*s-1;}else{temp[i].code[j]='0';s=2*s;}}temp[i].code[j]='\0';}}调试过程:五、总结通过本次上机,我对香农编码有了进一步的了解,掌握了其具体的过程的实现方法,也对信源编码这一概念有了更加深刻的理解,在编码的过程中,使我对C以及C++语言的基础知识掌握更加牢固,特别是巩固了对输出流格式控制的相关知识,总而言之,这次上机实践让我受益匪浅。
Huffman编码实验报告

Huffman编码实验报告1 二进制哈夫曼编码的原理及步骤(1)信源编码的计算设有N 个码元组成的离散、无记忆符号集,其中每个符号由一个二进制码字表示,信源符号个数n 、信源的概率分布P={p(s i )},i=1,…..,n 。
且各符号xi 的以li 个码元编码,在变长字编码时每个符号的平均码长为∑==ni li xi p L 1)( ;信源熵为:)(log )()(1xi p xi p X H ni ∑=-= ;唯一可译码的充要条件:11≤∑=-ni Ki m ;其中m 为码符号个数,n 为信源符号个数,Ki 为各码字长度。
构造哈夫曼数示例如下图所示。
(2)二元霍夫曼编码规则(1)将信源符号依出现概率递减顺序排序。
(2)给两个概率最小的信源符号各分配一个码位“0”和“1”,将两个信源符号合并成一个新符号,并用这两个最小的概率之和作为新符号的概率,结果得到一个只包含(n-1)个信源符号的新信源。
称为信源的第一次缩减信源,用s1 表示。
(3)将缩减信源 s1 的符号仍按概率从大到小顺序排列,重复步骤(2),得到只含(n-2)个符号的缩减信源s2。
0.0.0.0.1.000.0.0.00.0.0.0.(4)重复上述步骤,直至缩减信源只剩两个符号为止,此时所剩两个符号 的概率之和必为 1,然后从最后一级缩减信源开始,依编码路径向前返回,就得到各信源符号所对应的码字。
2 功能介绍输入一段字符序列,通过本程序可得出该字符序列中各个字符出现的次数,以及每个字符出现的概率,并能计算出信源符号熵,每个字符的哈弗曼编码,和相应的平均码长,编码效率,码方差。
3 算法基本步骤描述4 C 语言源代码#include<stdio.h>#include<string.h>#include<math.h>#define MAX 100//定义全局变量h 存放信息熵double h=0; 得到信得出信源得出信源计算信输输输输输信源符号的码编码平均输//定义结构体用于存放信源符号,数目及概率typedef struct{//不同的字符char SOURCECODE;//不同字符出现的次数int NUM;//不同字符出现的概率double PROBABILITY;//哈夫曼编码符号int Code[MAX];int start;//哈夫曼树的父结点int parent;//哈夫曼树的左右子结点int lchild;int rchild;//哈夫曼编码的长度int lengthofhuffmancode;}Hcode;Hcode INFORMATION[MAX];//该函数用来求信源所包含的符号,以及不同符号出现的次数和概率int Pofeachsource(char informationsource[MAX],int a){int i,j=1,m,flag=0;char temp;//预先存入第一个字符,便于与后面的字符进行比较//统计不同的字符存入结构体数组中//利用flag标签来标记每个字符是否出现过,若出现过标记为1,否则置为零INFORMATION[0].SOURCECODE=informationsource[0];for(i=1;i<a;i++){ for(m=0;m<i;m++){flag=0;if(informationsource[m]==informationsource[i]){flag=1;break;}}if(flag==1)continue;elseINFORMATION[j++].SOURCECODE=informationsource[i];}INFORMATION[j].SOURCECODE='\0';printf("信源符号数为:%d\n",j);//统计相同的字符出现的次数//每做一个字符出现次数的统计都将结构体数组里的NUM置为零for(i=0;i<j;i++){ INFORMATION[i].NUM=0;for(m=0;m<a;m++)if(informationsource[m]==INFORMATION[i].SOURCECODE)INFORMATION[i].NUM++;}//统计每个字符出现的概率for(i=0;i<j;i++) INFORMATION[i].PROBABILITY=(float)INFORMATION[i].NUM/a;//将每个不同字符出现的次数概率都显示出来for(i=0;i<j;i++)printf("The NUM and PROBABILITY of Code'%c'is %dand %.3f\n",INFORMATION[i].SOURCECODE,INFORMATION[i].NUM,INFORMATION [i].PROBABILITY);return j;}//求信源符号的熵void H(int a){int i;for(i=0;i<a;i++){h+=((-1)*(INFORMATION[i].PROBABILITY)*(log(INFORMATION[i].PROBABI LITY)/log(2)));}}//哈夫曼编码函数void Huffman(int a){Hcode cd;int i,j,m=0,lm=0,p,c;double min,lmin;//顺序初始化每个信源父子结点为-1for(i=0;i<a;i++){INFORMATION[i].parent=-1;INFORMATION[i].lchild=-1;INFORMATION[i].lchild=-1;}cd.start--; /* 求编码的低一位 */c=p;p=INFORMATION[c].parent; /* 设置下一循环条件 */}//保存求出的每个叶结点的哈夫曼编码和编码的起始位for(j=cd.start+1;j<m;j++){ INFORMATION[i].Code[j]=cd.Code[j];}INFORMATION[i].start=cd.start;}}void main(){//定义存放信源符号的数组char informationsource[MAX];int i,j,m;double averageofhuffmancode=0.0,Eita,cV=0.0;printf("please input the source of information:");for(i=0;;i++){scanf("%c",&informationsource[i]);if(informationsource[i]=='\n')break;}informationsource[i]='\0';printf("信源序列为:");//显示已输入的一串信源符号puts(informationsource);//返回不同信源符号的数目m=Pofeachsource(informationsource,i);//求信源的符号熵H(m);printf("信源的符号熵:H(X)=%.3f(比特/符号)\n",h);Huffman(m);//输出已保存好的所有存在编码的哈夫曼编码for(i=0;i<m;i++){printf("%c's Huffman code is: ",INFORMATION[i].SOURCECODE); for(j=INFORMATION[i].start+1;j<m;j++)printf("%d",INFORMATION[i].Code[j]);INFORMATION[i].lengthofhuffmancode=m-INFORMATION[i].start-1; printf("\n");}//求哈夫曼编码的平均码长和编码效率for(i=0;i<m;i++)averageofhuffmancode+=INFORMATION[i].PROBABILITY*INFORMATION[i].l engthofhuffmancode;printf("哈夫曼编码的平均码长为:%lf(码元/信源符号)\n",averageofhuffmancode);Eita=h/averageofhuffmancode;printf("哈夫曼编码的编码效率为:%lf\n",Eita);//求哈弗曼编码的码方差for(i=0;i<m;i++)cV+=INFORMATION[i].PROBABILITY*INFORMATION[i].lengthofhuffmancode *INFORMATION[i].lengthofhuffmancode;cV-=averageofhuffmancode*averageofhuffmancode;printf("哈弗曼编码的码方差为:%lf\n",cV);}5 运行结果截图:6 实验分析(1)在哈弗曼编码的过程中,对缩减信源符号按概率有大到小的顺序重新排列,应使合并后的新符号尽可能排在靠前的位置,这样可使合并后的新符号重复编码次数减少,使短码得到充分利用。
信息论与编码课程实验报告

福建农林大学计算机与信息学院信息工程类信息论与编码课程实验报告实验项目列表实验名称1:信源建模一、实验目的和要求(1)进一步熟悉信源建模;(2)掌握MATLAB程序设计和调试过程中数值的进制转换、数值与字符串之间的转换等技术。
二、实验内容(1)假设在一个通信过程中主要传递的对象以数字文本的方式呈现。
(2)我们用统计的方式,发现这八个消息分别是由N1,N2,…,N8个符号组成的。
在这些消息是中出现了以下符号(符号1,符号2,…,符号M)每个符号总共现了(次数1,次数2,…,次数M)我们认为,传递对象的信源模型可表示为:X为随机变量(即每次一个字符);取值空间为:(符号1,符号2,…,符号M);其概率分布列为:(次数1/(N1+…+N8),…,次数M/( N1+…+N8))三、实验环境硬件:计算机软件:MATLAB四、实验原理图像和语声是最常用的两类主要信源。
要充分描述一幅活动的立体彩色图像,须用一个四元的随机矢量场X(x,y,z,t),其中x,y,z为空间坐标;t 为时间坐标;而X是六维矢量,即表示左、右眼的亮度、色度和饱和度。
然而通常的黑白电视信号是对平面图像经过线性扫描而形成。
这样,上述四元随机矢量场可简化为一个随机过程X(t)。
图像信源的最主要客观统计特性是信源的幅度概率分布、自相关函数或功率谱。
关于图像信源的幅度概率分布,虽然人们已经作了大量的统计和分析,但尚未得出比较一致的结论。
至于图像的自相关函数,实验证明它大体上遵从负指数型分布。
其指数的衰减速度完全取决于图像类型与图像的细节结构。
实际上,由于信源的信号处理往往是在频域上进行,这时可以通过傅里叶变换将信源的自相关函数转换为功率谱密度。
功率谱密度也可以直接测试。
语声信号一般也可以用一个随机过程X(t)来表示。
语声信源的统计特性主要有语声的幅度概率分布、自相关函数、语声平均功率谱以及语声共振峰频率分布等。
实验结果表明语声的幅度概率分布可用伽玛(γ)分布或拉普拉斯分布来近似。
香农编码的MATLAB实现

• (2)令 p(a0) = 0,用 pa (aj)(j = i+1)表示第 i 个码字的累加概率,则:
j 1
pa (a j ) p(ai ) i0
j 1,2,..., n
二、实验原理
1. 香农编码步骤
• (3)令 ki 为第 i 个码字的码长,按照下式计算 出各概率对应的码字长度 ki :
三、实验内容
• (5)十进制小数转换成二进制小数
➢ k_max = max(k);
➢ bin = zeros(n,k_max);
% 对二进制小数矩阵初始化
➢ for i = 1:n
➢ for j = 1:k_max
➢
bin(i,j)=floor(pa(i)*2); % 将累加概率转换成二进制
➢
pa(i)=pa(i)*2-floor(pa(i)*2);
三、实验内容
• (7)计算平均码长、信息率和编码效率
➢ K = sum(p.* k); % 平均码长
➢ R = K;
% 信息率
➢ eff = H/R; % 编码效率
三、实验内容
• (8)输出结果
➢ disp(['信源分布 P(X) = [',num2str(p),']']); ➢ disp('编码结果:'); ➢ for i = 1:n ➢ disp([num2str(p(i)),' -> ' ,num2str(codeword(i,:))]); ➢ end ➢ disp(['信源熵 H(X) = ' ,num2str(H),' (bit/sign)']); ➢ disp(['平均码长 K = ' ,num2str(K),' (bit/sign)']); ➢ disp(['信息率 R = ' ,num2str(R),' (bit/sign)']); ➢ disp(['编码效率 η = ' ,num2str(eff)]);
香农编码例题

香农编码例题香农编码是一种将符号转化为二进制代码的编码方式,它是由美国数学家克劳德·香农在1948年提出的。
这种编码方式最初被应用于通信领域,但现在已经广泛应用于数据压缩、图像处理和音频处理等领域。
香农编码的基本思想是根据符号出现的概率来确定其对应的二进制代码。
出现概率较高的符号使用较短的二进制代码表示,而出现概率较低的符号使用较长的二进制代码表示。
这样可以有效地减少使用的二进制位数,从而达到数据压缩的目的。
下面我们来看一个例题:假设有5个符号A、B、C、D、E,它们出现的概率分别为0.4、0.2、0.15、0.15和0.1,请使用香农编码将它们转化为二进制代码。
首先需要按照概率大小对这些符号进行排序,从大到小依次为A、B、C、D和E。
接下来需要计算每个符号对应的编码长度。
根据香农编码原理可知,每个符号对应的编码长度等于其出现概率取对数后向上取整得到的值。
因此,A的编码长度为ceil(log2(1/0.4))=ceil(1.3219)=2,B的编码长度为ceil(log2(1/0.2))=ceil(2.3219)=3,C和D的编码长度均为4,E的编码长度为5。
然后可以根据每个符号对应的编码长度来确定它们对应的二进制代码。
具体地,A对应的二进制代码为00,B对应的二进制代码为010,C和D均对应的二进制代码为0110,E对应的二进制代码为01110。
最后将这些二进制代码按照符号出现概率大小从小到大排列起来就可以得到它们对应的香农编码:E=01110、D=0110、C=0110、B=010、A=00。
通过这个例题我们可以看出,在使用香农编码进行数据压缩时,出现概率较高的符号所对应的二进制代码较短,而出现概率较低的符号所对应的二进制代码较长。
这样可以有效地减少使用的二进制位数,并且在解压缩时也能够快速地还原原始数据。
因此,在实际应用中香农编码是一种非常有效和常用的数据压缩方式。
信息论与编码实验指导书

没实验一 绘制二进熵函数曲线(2个学时)一、实验目的:1. 掌握Excel 的数据填充、公式运算和图表制作2. 掌握Matlab 绘图函数3. 掌握、理解熵函数表达式及其性质 二、实验要求:1. 提前预习实验,认真阅读实验原理以及相应的参考书。
2. 在实验报告中给出二进制熵函数曲线图 三、实验原理:1. Excel 的图表功能2. 信源熵的概念及性质()()[]()[]())(1)(1 .log )( .)( 1log 1log )(log )()(10 , 110)(21Q H P H Q P H b nX H a p H p p p p x p x p X H p p p x x X P X ii i λλλλ-+≥-+≤=--+-=-=≤≤⎩⎨⎧⎭⎬⎫-===⎥⎦⎤⎢⎣⎡∑四、实验内容:用Excel 或Matlab 软件制作二进熵函数曲线。
具体步骤如下:1、启动Excel 应用程序。
2、准备一组数据p 。
在Excel 的一个工作表的A 列(或其它列)输入一组p ,取步长为0.01,从0至100产生101个p (利用Excel 填充功能)。
3、取定对数底c ,在B 列计算H(x) ,注意对p=0与p=1两处,在B 列对应位置直接输入0。
Excel 中提供了三种对数函数LN(x),LOG10(x)和LOG(x,c),其中LN(x)是求自然对数,LOG10(x)是求以10为底的对数,LOG(x,c)表示求对数。
选用c=2,则应用函数LOG(x,2)。
在单元格B2中输入公式:=-A2*LOG(A2,2)-(1-A2)*LOG(1-A2,2) 双击B2的填充柄,即可完成H(p)的计算。
4、使用Excel 的图表向导,图表类型选“XY 散点图”,子图表类型选“无数据点平滑散点图”,数据区域用计算出的H(p)数据所在列范围,即$B$1:$B$101。
在“系列”中输入X值(即p值)范围,即$A$1:$A$101。
信息论与编码实验报告

本科生实验报告实验课程信息理论与编码学院名称信息科学与技术学院专业名称学生姓名学生学号指导教师实验地点实验成绩二〇一六年九月----二〇一六年十一月填写说明1、适用于本科生所有的实验报告(印制实验报告册除外);2、专业填写为专业全称,有专业方向的用小括号标明;3、格式要求:①用A4纸双面打印(封面双面打印)或在A4大小纸上用蓝黑色水笔书写。
②打印排版:正文用宋体小四号,1.5倍行距,页边距采取默认形式(上下2.54cm,左右2.54cm,页眉1.5cm,页脚1.75cm)。
字符间距为默认值(缩放100%,间距:标准);页码用小五号字底端居中。
③具体要求:题目(二号黑体居中);摘要(“摘要”二字用小二号黑体居中,隔行书写摘要的文字部分,小4号宋体);关键词(隔行顶格书写“关键词”三字,提炼3-5个关键词,用分号隔开,小4号黑体);正文部分采用三级标题;第1章××(小二号黑体居中,段前0.5行)1.1 ×××××小三号黑体×××××(段前、段后0.5行)1.1.1小四号黑体(段前、段后0.5行)参考文献(黑体小二号居中,段前0.5行),参考文献用五号宋体,参照《参考文献著录规则(GB/T 7714-2005)》。
实验一:香农(Shannon )编码一、实验目的掌握通过计算机实现香农编码的方法。
二、实验要求对于给定的信源的概率分布,按照香农编码的方法进行计算机实现。
三、实验基本原理给定某个信源符号的概率分布,通过以下的步骤进行香农编码 1.将信源消息符号按其出现的概率大小排列)()()(21n x p x p x p ≥≥≥ 2.确定满足下列不等式的整数码长K i ;1)(log )(log 22+-<≤-i i i x p K x p3.为了编成唯一可译码,计算第i 个消息的累加概率∑-==11)(i k k i x p p4.将累加概率P i 变换成二进制数。
《信息论与编码技术》实验教案

《信息论与编码技术》实验教案一、实验目的1. 理解信息论基本概念,如信息量、信道容量等。
2. 掌握编码技术的基本原理,如Hamming 编码、卷积编码等。
3. 学会使用仿真工具进行信息论与编码技术的实验。
二、实验原理1. 信息论基本概念:信息量、信道容量、误码率等。
2. 编码技术原理:Hamming 编码、卷积编码、解码算法等。
3. 仿真工具的使用:调用相关函数,设置参数,观察实验结果。
三、实验内容1. 实验一:信息量计算与信道容量分析利用仿真工具随机比特序列,计算信息量。
改变信道参数,分析信道容量变化。
2. 实验二:Hamming 编码与解码编写Hamming 编码器和解码器,进行编码和解码操作。
分析误码率与编码位数的关系。
3. 实验三:卷积编码与解码编写卷积编码器和解码器,进行编码和解码操作。
分析误码率与卷积编码器参数的关系。
4. 实验四:不同编码方案性能比较分别使用Hamming 编码和卷积编码对相同长度比特序列进行编码。
比较两种编码方案的误码率和信息传输效率。
5. 实验五:信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用。
了解信息论与编码技术在无线通信、图像传输等领域的应用。
四、实验步骤1. 实验一:信息量计算与信道容量分析随机比特序列,计算信息量。
设置信道参数,观察信道容量变化。
2. 实验二:Hamming 编码与解码编写Hamming 编码器和解码器,进行编码和解码操作。
改变编码位数,分析误码率变化。
3. 实验三:卷积编码与解码编写卷积编码器和解码器,进行编码和解码操作。
改变卷积编码器参数,分析误码率变化。
4. 实验四:不同编码方案性能比较使用Hamming 编码和卷积编码对相同长度比特序列进行编码。
比较两种编码方案的误码率和信息传输效率。
5. 实验五:信息论与编码技术在实际应用中的案例分析分析数字通信系统中信息论与编码技术的应用案例。
了解信息论与编码技术在无线通信、图像传输等领域的应用。
信源编码实验

实验2 信源编码实验一、实验目的● 掌握香农、霍夫曼编码的方法和手段。
● 通过信源编译码,理解香农第一定理。
二、实验原理 设离散无记忆信源12112,,,,,,()1(),(),,(),,()()=⎧⎫⎡⎤==⎨⎬⎢⎥⎣⎦⎩⎭∑ni n ii i n x x x x X p x p x p x p x p x P X二进制香农码的编码步骤如下:⏹ 将信源符号按概率从大到小的顺序排列,为方便起见,令 p (x 1)≥ p (x 2)≥…≥ p (x n )⏹ 令p (x 0)=0,用p a (x j ),j =i +1表示第i 个码字的累加概率,则:10()(),1,2,,-===∑j a j i i p x p x j n⏹ 确定满足下列不等式的整数k i ,并令k i 为第i 个码字的长度 -log 2 p (x n )≤k i <- log 2 p (x n )+1⏹ 将p a (x j ) 用二进制表示,并取小数点后k i 位作为符号x i 的编码。
霍夫曼编码步骤如下:⏹ 将信源符号按概率从大到小的顺序排列,令p (x 1)≥ p (x 2)≥…≥ p (x n )⏹ 给两个概率最小的信源符号p (x n -1)和p (x n )各分配一个码位“0”和“1”,将这两个信源符号合并成一个新符号,并用这两个最小的概率之和作为新符号的概率,结果得到一个只包含(n -1)个信源符号的新信源。
称为信源的第一次缩减信源,用S 1表示。
⏹ 将缩减信源S 1的符号仍按概率从大到小顺序排列,重复步骤2,得到只含(n -2)个符号的缩减信源S 2。
⏹ 重复上述步骤,直至缩减信源只剩两个符号为止,此时所剩两个符号的概率之和必为1。
然后从最后一级缩减信源开始,依编码路径向前返回,就得到各信源符号所对应的码字。
三、实验内容1、有一单符号离散无记忆信源123456,,,,,()0.250.250.200.150.100.05⎡⎤⎧⎫=⎨⎬⎢⎥⎣⎦⎩⎭X x x x x x x P X对该信源编二进制香农码。
信息论实验报告2信源编码

function [W,L,q]=shannon(p)
if (length(find(p<=0)) ~=0)
error('Not a prob.vector,negative component'); end
if (abs(sum(p)-1)>10e-10)
error('Not a prob.vector,component do not add up to 1'); end
n=length(P); %计算输入元素个数
p=P; mark=zeros(n-1,n);
% mark为n-1行、n列矩阵,用来记录每行最小两概率叠加后概率排列次序
% 1)确定概率大小值的排列,得到mark矩阵。
for i=1:n-1
[p,num]=sort(p); mark(i,:)=[num(1:n-i+1),zeros(1,i-1)];
s2='Shannon编码平均码字长度L:'; s3='Shannon编码的编码效率q:';
disp(s0);disp(s1),disp(B),disp(W);disp(s2),disp(L);disp(s3),disp(q);
function H=entropy(P,r)
if (length(find(P<=0))~=0) %判断是否符合概率分布条件
[c,k]=min(temp);
if (current_index<=k)
next_index=current_index; code_num=48;
next_P=current_P(1:k);
else
信道编码第二次试验实验报告

信道编码第二次试验实验报告一、实验目的1、实现F2(x)多项式的加法、乘法以及除法运算;求多项式的周期;2、编写同余类域的生成、加法计算、乘法运算、除法运算、幂运算、元素求阶以及求解极小多项式的程序;二、实验原理1、多项式运算:加、乘多项式相加:同次项系数按照二元域中的加法相加;多项式相乘:按普通多项式的乘法相乘,计算系数按二元域上的加法和乘法运算。
2、多项式的除法:给定任意两个多项式f(x)、g(x),一定存在唯一的多项式q(x)和r(x),使:f(x)=q(x)g(x)+r(x) ə(r(x))≤ə(g(x))r(x)称为f(x)模g(x)的余式3、多项式的周期:定义:设f(x)为二元域上次数不为0的多项式,且f(0)≠0,则f(x)|(xn+1)的最小正整数n称为多项式f(x)的周期,(n>=ə(f(x)))实现方法:方法一:长除法求多项式周期用多项式f(x)按升幂排列去除1,当所得余式是单项xn时,f(x)的周期即为n。
方法二:利用欧拉-费尔马定理4、GF(2)的扩域GF(2^n)扩域GF(2^n):设p(x)为GF(2)上的n次既约多项式,模p(x)的所有2^n个余式在模p(x)加法和乘法下构成2^n元域,称为GF(2)的扩域(也称为模p(x)的剩余类域),记为GF(2^n)。
5、幂运算:元素累乘6、元素求阶:具有性质a^n=e的最小正整数n称为a的阶7、求解元素的极小多项式:最小多项式:以扩域GF(2m)上的非零元素β为根的最低次多项式称为β的最小多项式,记为M (x)求解方法:待定系数法三、实验结果我在我的函数中规定:代表多项式的向量,从左到右为多项式高次到低次1、多项式的加、乘运算:在进行多项式的加法、乘法运算的编程时,思路来自于老蒋蒋凌云。
加法:二元域上的多项式加法遵从模2加的运算规则。
在编程时,输入的两个向量必须维度一致,MATLAB才能对其进行处理和运算。
因此,先将输入的两个多项式向量维度设定一致,再运用mod函数求出最终结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验二 香农编码得计算与分析
一、[实验目得]
1、理解香农第一定理指出平均码长与信源之间得关系。
2、加深理解香农编码具有得重要理论意义。
3、掌握Shannon 编码得原理。
4、掌握Shannon 编码得方法与步骤。
5、熟悉shannnon 编码得各种效率
二、[实验环境]
windows XP,MATLAB 7
三、[实验原理]
香农第一定理:
设离散无记忆信源为
熵为H(S),其N 次扩展信源为
熵为H(S N
)。
码符号集X=(x1,x2,…,xr)。
先对信源进行编码,总可以找到一种编码方法,构成惟一可以码,使S 中每个信源符号所需得平均码长满足:
当N 时
就是平均码长 就是对应得码字长度
四、[实验内容]
1、根据实验原理,设计shannon 编码方法,在给定
条件下,实现香农编码并算出编码效率。
2、请自己构造两个信源空间,根据求Shannon 编码结果说明其物理意义。
五、[实验过程]
每个实验项目包括:1)设计思路2)实验中出现得问题及解决方法;
要求:
1)有标准得实验报告 (10分)
S P s1 s2 s3 s4 s5 s6 s7 0、01 0、17 0、19 0、10 0、15 0、=
2)程序设计与基本算法合理(30分)
3)实验仿真具备合理性(30分)
4)实验分析合理(20分)
5)能清晰得对实验中出现得问题进行分析并提出解决方案(10分) 附录: 程序设计与算法描述参考
(1))按降序排列概率得函数
%[p,x]=array(P)为按降序排序得函数%
%P为信源得概率矢量,x为概率元素得下标矢量%
%P为排序后返回得信源得概率矢量%
%x为排序后返回得概率元素得下标矢量%
%******************************%
function[p,x]=array(P)
n=length(P);
X=1:n;
P=[P;X];
for i=1:n
max=P(1,i);
maxN=i;
MAX=P(:,i);
for j=i:n
if(max<P(1,j))
MAX=P(:,j);
max=P(1,j);
maxN=j;
end
end
if (maxN>1)
if (i<n)
for k=(maxN-1):-1:i
P(:,k+1)=P(:,k);
end
end
end
P(:,i)=MAX;
end
p=P(1,:);
x=P(2,:);
(2)Shannon编码算法
% shannon编码生成器%
% 函数说明: %
% [W,L,q]=shannon(p) 为Shannon编码函数%
% p 为信源得概率矢量,W为编码返回得码字%
% L 为编码返回得平均码字长度,q 为编码概率%
% ******************************************************* %
function [W,L,q] =shannon(p)
% 提示错误信息%
if (length(find(p<=0)) ~=0)
error('Not a prob、vector、negative ponent'); % 判断就是否符合概率分布条件end
% 1) 排序
if (abs(sum(p)-1)>10e-10)
error('Not a prob、vetor、ponent do not add up to 1') %判断就是否符合概率与为1
end
[p,x]=array(p);
% 2) 计算代码组长度l
l=ceil(-log2(p));
% 3) 计算累加概率P
P(1)=0;
n=length(p);
for i=2:n
P(i)=P(i-1)+p(i-1);
end
% 4) 求得二进制代码组W
% a) 将十进制数转为二进制数
for i=1:n
for j=1:l(i)
temp(i,j)=floor(P(i)*2);
P(i)=P(i)*2-temp(i,j);
end
end
% b) 给W赋ASCII码值,用于显示二进制代码组W for i=1:n
for j=1:l(i)
if (temp(i,j)==0)
W(i,j)=48;
else
W(i,j)=49;
end
end
end
L=sum(p、*l); % 计算平均码字长度
H=entropy1(p,2); % 计算信源熵
q=H/L; % 计算编码效率
for i=1:n
B{i}=x(i);
end
% [n,m]=size(W);
% TEMP=32*ones(n,6);
% W=[W,TEMP];
% W=W';
% [n,m]=size(W);
% W=reshape(W,1,n*m);
% W=sprintf('%s',W);
[m,n]=size(W);
TEMP=blanks(m);
W=[W,TEMP',TEMP',TEMP'];
[m,n]=size(W);
W=reshape(W',1,m*n);
s0='很好!输入正确,编码结果如下:';
s1='Shannon编码所得码字W:';
s2='Shannon编码平均码字长度L:'; s3='Shannon编码得编码效率q:'; disp(s0);
disp(s1),disp(B),disp(W);
disp(s2),disp(L);
disp(s3),disp(q);。
