香浓编码实验报告

合集下载

编码理论实验报告

一、实验目的1. 理解编码理论的基本概念和原理；2. 掌握哈夫曼编码和香农编码的方法；3. 熟悉编码效率的计算方法；4. 培养编程能力和实践操作能力。

二、实验原理1. 编码理论：编码理论是研究信息传输、存储和处理中信息压缩和编码的理论。

其目的是在保证信息传输质量的前提下，尽可能地减少传输或存储所需的数据量。

2. 哈夫曼编码：哈夫曼编码是一种根据字符出现频率进行编码的方法，字符出现频率高的用短码表示，频率低的用长码表示，从而达到压缩数据的目的。

3. 香农编码：香农编码是一种基于信息熵的编码方法，根据字符的概率分布进行编码，概率高的字符用短码表示，概率低的字符用长码表示。

4. 编码效率：编码效率是指编码后数据长度与原始数据长度的比值。

编码效率越高，表示压缩效果越好。

三、实验内容1. 使用MATLAB软件实现哈夫曼编码和香农编码；2. 对给定信源进行编码，并计算编码效率；3. 对比哈夫曼编码和香农编码的效率。

四、实验步骤1. 编写哈夫曼编码程序：首先，统计信源中各个字符的出现频率；然后，根据频率构造哈夫曼树；最后，根据哈夫曼树生成编码。

2. 编写香农编码程序：首先，计算信源熵；然后，根据熵值生成编码。

3. 编码实验：对给定的信源进行哈夫曼编码和香农编码，并计算编码效率。

4. 对比分析：对比哈夫曼编码和香农编码的效率，分析其优缺点。

五、实验结果与分析1. 哈夫曼编码实验结果：信源：'hello world'字符频率：'h' - 2, 'e' - 1, 'l' - 3, 'o' - 2, ' ' - 1, 'w' - 1, 'r' - 1, 'd' - 1哈夫曼编码结果：'h' - 0'e' - 10'l' - 110'o' - 1110' ' - 01'w' - 101'r' - 100'd' - 1001编码效率：1.52. 香农编码实验结果：信源：'hello world'字符频率：'h' - 2, 'e' - 1, 'l' - 3, 'o' - 2, ' ' - 1, 'w' - 1, 'r' - 1, 'd' - 1香农编码结果：'h' - 0'e' - 10'l' - 110'o' - 1110' ' - 01'w' - 101'r' - 100'd' - 1001编码效率：1.53. 对比分析：哈夫曼编码和香农编码的效率相同，均为1.5。

实验四_香农编码

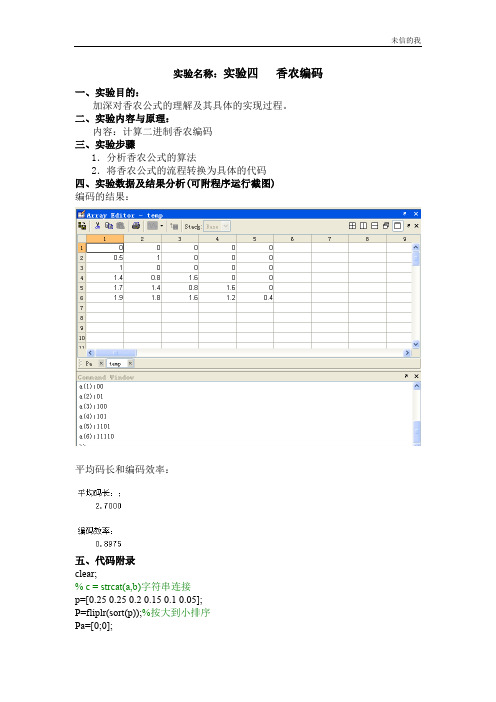
实验名称：实验四香农编码一、实验目的：加深对香农公式的理解及其具体的实现过程。

二、实验内容与原理：内容：计算二进制香农编码三、实验步骤1．分析香农公式的算法2．将香农公式的流程转换为具体的代码四、实验数据及结果分析(可附程序运行截图)编码的结果：平均码长和编码效率：五、代码附录clear;% c = strcat(a,b)字符串连接p=[0.25 0.25 0.2 0.15 0.1 0.05];P=fliplr(sort(p));%按大到小排序Pa=[0;0];%累加和的定义----第一行为累加和，第二行为Ki %求累加和for x=1for y=1:1:5%Pa(x,y)=1;Pa(x,y+1)=P(x,y)+ Pa(x,y);endend%ceil 是取向离它最近的大整数圆整for i=2for j=1:1:6Pa(i,j)=ceil( -log2(P(1,j)) );endend%信源熵H=0;L=0;for i=1:1:6H=H-P(i)*log2(P(i));L=L+P(i)*Pa(2,i);endu=H/L;disp('平均码长：；');disp(L);disp('编码效率：');disp(u);%求各符号的编码temp=[];%临时的编码值:1:6for m=1:1:6fprintf('a(%d):',m);for n=1:1:abs(Pa(2,m))temp(m,n)=Pa(1,m)*2;if temp(m,n)>=1O(m,n)=1;Pa(1,m)=temp(m,n)-1;elseO(m,n)=0;Pa(1,m)=temp(m,n);endfprintf('%d',O(m,n));endfprintf('\n');end六、其他：实验总结、心得体会及对本实验方法、手段及过程的改进建议等。

实验起初是想把累加和及Ki和编码放在一个二维矩阵中，但具体的实现较为复杂，所以最后改为逐行存放并成功完成了实验。

信息论与编码实验报告

NANCHANG UNIVERSITY信息论与编码实验报告（2018年11月27日）学院：信息工程学院系电子信息工程系专业班级：学生姓名：学号：指导教师：目录实验一自信息量和熵源.............................................................................................. 实验二准对称信道容量.............................................................................................. 实验三费诺不等式...................................................................................................... 实验四香农编码.......................................................................................................... 实验五费诺编码.......................................................................................................... 实验六霍夫曼编码......................................................................................................实验一自信息量和熵源一、实验要求1、画出I=-的函数图；2、画出H(p)=-p-(1-p)函数图。

二、实验原理及理论分析自信息量：一个事件的自信息量就是对其不确定性的度量。

信息论与编码实验报告

信息论与编码实验报告一、实验目的本实验主要目的是通过实验验证信息论与编码理论的基本原理，了解信息的产生、传输和编码的基本过程，深入理解信源、信道和编码的关系，以及各种编码技术的应用。

二、实验设备及原理实验设备：计算机、编码器、解码器、信道模拟器、信噪比计算器等。

实验原理：信息论是由香农提出的一种研究信息传输与数据压缩问题的数学理论。

信源产生的消息通常是具有统计规律的，信道是传送消息的媒体，编码是将消息转换成信号的过程。

根据信息论的基本原理，信息的度量单位是比特（bit），一个比特可以表示两个平等可能的事件。

信源的熵（Entropy）是用来衡量信源产生的信息量大小的物理量，熵越大，信息量就越多。

信道容量是用来衡量信道传输信息的极限容量，即信道的最高传输速率，单位是比特/秒。

编码是为了提高信道的利用率，减少传输时间，提高传输质量等目的而进行的一种信号转换过程。

常见的编码技术有霍夫曼编码、香农-费诺编码、区块编码等。

三、实验步骤1.运行编码器和解码器软件，设置信源信息，编码器将信源信息进行编码，生成信道输入信号。

2.设置信道模拟器的信道参数，模拟信道传输过程。

3.将信道输出信号输入到解码器，解码器将信道输出信号进行解码，恢复信源信息。

4.计算信道容量和实际传输速率，比较两者的差异。

5.改变信道参数和编码方式，观察对实际传输速率的影响。

四、实验结果与分析通过实验，我们可以得到不同信道及编码方式下的信息传输速率，根据信道参数和编码方式的不同，传输速率有时会接近信道容量，有时会低于信道容量。

这是因为在真实的传输过程中，存在信噪比、传输距离等因素导致的误码率，从而降低了实际传输速率。

在实验中，我们还可以观察到不同编码方式对传输速率的影响。

例如，霍夫曼编码适用于信源概率分布不均匀的情况，可以实现数据压缩，提高传输效率。

而区块编码适用于数据容量较大的情况，可以分块传输，降低传输错误率。

此外，通过实验我们还可以了解到信息论中的一些重要概念，如信源熵、信道容量等。

实验四-香农编码

海南大学信息科学技术学院信息安全专业《信息论与编码》实验报告一、实验目的:了解掌握香农编码二、实验环境：CodeBlocks三、实验要求编程，对某一离散无记忆信源实现香农编码,输出消息符号及其对应的码字。

设离散无记忆信源⎭⎬⎫⎩⎨⎧=⎪⎪⎭⎫ ⎝⎛01.010.015.017.018.019.020.0)(7654321a a a a a a a X p X ，∑==ni ia p 11)(。

二进制香农编码过程如下： 1、将信源发出的N 个消息符号按其概率的递减次序依次排列。

2、按下式计算第i 个消息的二进制代码组的码长，并取整。

3、为了编成唯一可译码，首先计算第i 个消息的累加概率4、将累加概率Pi （为小数）变成二进制数5、除去小数点，并根据码长li ，取小数点后li 位数作为第i 个消息的码字。

四、实验过程：代码：#include<stdio.h>#include<math.h>void main(){int i,n, j,k;float sum=0;float p[100]={0}; //无记忆信源X 的概率分布float m;float Pa[100]={0}; //累加概率的数组int l[100];char c[100][100];printf("请输入信源X的个数:");scanf("%d",&n);printf("请输入p[X]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<=n;i++) //判断概率和为1sum=sum+p[i];while(sum!=1){printf("错误输入，请重输\n");printf("请输入x的个数\n");scanf("%d",&n);printf("\n");printf("请输入p[i]的概率分布\n");for(i=0;i<n;i++)scanf("%f",&p[i]);for(i=0;i<n;i++)sum=sum+p[i];}for(j=0;j<n-1;j++) //将概率按从大到小排序 for(i=0;i<n-1-j;i++)if(p[i]<p[i+1]){m=p[i];p[i]=p[i+1];p[i+1]=m;}printf("p[i]由大到小的顺序为\n:");for(i=0;i<n;i++)printf("%5.2f",p[i]);printf("\n");Pa[0]=0;for(j=1;j<n+1;j++) //计算累加概率{Pa[j]=Pa[j-1]+p[j-1];}printf("累加和Pi为:");for(j=0;j<n;j++)printf("%5.2f",Pa[j]);printf("\n");printf("码长:");for(i=0;i<n;i++) //计算码长{m=log(1/p[i])/log(2);if(m==(int)m)l[i]=(int)m;elsel[i]=(int)(m+1);}for(i=0;i<n;i++)printf(" %d ",l[i]);printf("\n");for(i=0;i<n;i++) //将累加概率转换成二进制数{for(k=0;k<l[i];k++){Pa[i]=Pa[i]*2;if(Pa[i]>=1){Pa[i]=Pa[i]-1;c[i][k]='1';}else{c[i][k]='0';}}}for(i=0;i<n;i++){for(k=0;k<l[i];k++)printf("%c",c[i][k]);printf("\n");}}五、实验结果：。

中南大学信息论与编码编码部分实验报告

信息论与编码编码部分实验报告课程名称：信息论与编码实验名称：关于香农码费诺码Huffman码的实验学院：信息科学与工程学院班级：电子信息工程1201姓名：viga学号：指导老师：张祖平日期：2014年1月3日目录⊙实验目的及要求1.1 实验目的 (4)1.2 开发工具及环境 (4)1.3 需求分析与功能说明 (4)⊙实验设计过程2.1 用matlab实现香农码、费诺码和Huffman编码2.1.1 说明 (6)2.1.2 源代码 (7)2.1.3 运行结果（截图） (19)2.2 用C\C++ 实现香农码2.2.1 说明 (22)2.2.2 源代码 (23)2.2.3 运行结果（截图） (26)2.3 用C\C++ 实现Huffman码2.3.1 说明 (26)2.3.2 源代码 (29)2.3.3 运行结果（截图） (36)2.4 用C\C++ 实现费诺码2.4.1 说明 (37)2.4.2 源代码 (37)2.4.3运行结果结果（截图） (40)⊙课程设计总结 (42)⊙参考资料4.1 课程设计指导书 (43)实验目的及要求1.1 实验目的1.掌握香农码、费诺码和Huffman编码原理和过程。

2.熟悉matlab软件的基本操作，练习使用matlab实现香农码、费诺码和Huffman编码。

3.熟悉C/C++语言，练习使用C/C++实现香农码、费诺码和Huffman编码。

4.应用Huffman编码实现文件的压缩和解压缩。

1.2 开发工具及环境MATLAB 7.0、wps文字、红精灵抓图精灵2010Windows7 系统环境1.3 需求分析与功能说明1、使用matlab实现香农码、费诺码和Huffman编码，并自己设计测试案例。

2、使用C\C++实现香农码、费诺码和Huffman编码，并自己设计测试案例。

3、可以用任何开发工具和开发语言，尝试实现Huffman编码应用在数据文件的压缩和解压缩中，并自己设计测试案例。

信息论实验报告香农编码

目录实验目的： (2)实验要求： (2)程序算法： (2)程序运行结果： (4)程序操作步骤： (5)试验中遇到的困难及解决方法： (5)实验心得及体会： (5)实验目的：1.进一步熟悉使用C++编程语言及软件。

2.进一步认识shannon编码过程，并能在学习中灵活运用。

实验要求：要求：(a) 允许使用的编程语言：C、C++、Basic、Pascal、Fortran、Java、Perl、Tk/Tcl(b) 输入：信源符号个数q、信源符号s0,...,sq−1，信源概率分布p0,...,pq−1。

(d) 源程序格式整齐清晰，注释简单明了。

程序算法：(a) 将q 个信源符号按其概率的递减次序排列：p(s0) > p(s1) > ... > p(sq−1)(b) 计算出各个信源符号的累加概率：(c) 按下式计算第i 个消息的二元代码组的码长li：(d) 将累加概率F(si)（十进制小数）变换成二进制小数。

根据码长li 取小数点后li 个二进制符号作为第i 个消息的码字。

程序代码：#include <iostream>#include <math.h>using namespace std;void InsertSort(double r[],char m[] ,int n)//直接插入排序算法按照概率从大到小排列符号和相应概率{for(int i=1;i<n;i++){r[n]=r[i]; //设置哨兵m[n]=m[i]; //设置哨兵for(int j=i-1;(r[n]>r[j])&&(j>=0);j--)//寻找插入位置{r[j+1]=r[j];//记录后移m[j+1]=m[j];//记录后移}r[j+1]=r[n];m[j+1]=m[n];}}void Leijia(double p[], int s)//将当前概率及之前概率相加{for(int r=1;r<s;r++)p[r]=p[r-1]+p[r];}void main(){int geshu,erjinzhi[100][100];int z=0,g=0;double gailv[100],L[100];char fuhao[100];cout<<"请输入需要编码的字符个数(小于100)"<<endl; cin>>geshu;cout<<"请按照先后顺序输入符号"<<endl;for(int i=0;i<geshu;i++)cin>>fuhao[i];cout<<"请输入各相应符号的概率"<<endl;for(int j=0;j<geshu;j++)cin>>gailv[j];InsertSort( gailv,fuhao, geshu);for(z=0;z<geshu;z++){L[z]=-log(gailv[z])/log(2);L[z]=ceil(L[z]);//向上取整求所需要的位数}Leijia( gailv, geshu);for( z=0;z<geshu;z++)//求相应的二进制编码{gailv[z]=gailv[z]-floor(gailv[z]);for( g=0;g<L[z];g++){if((gailv[z]*2)>=1){erjinzhi[z][g]=1;gailv[z]=(gailv[z]*2)-1;}else{erjinzhi[z][g]=0;gailv[z]=gailv[z]*2;}}}cout<<"各信源符号及相应码字分别为"<<endl; for(z=0;z<geshu;z++){cout<<fuhao[z]<<'\t';for( g=0;g<L[z];g++)cout<< erjinzhi[z][g];cout<<endl;}}程序运行结果：程序操作步骤：1.按照提示输入所要编码的符号个数并回车2.按顺序输入要求个数的符号并回车3.按顺序输入各符号相应的概率并回车4.即可得到各符号相应的shannon编码试验中遇到的困难及解决方法：本次试验相对而言比较简单，但由于长时间没有联系C++语言有些生疏。

香农编码

temp=P[i]; P[i]=P[i+1]; P[i+1]=temp; } } for(int i=0;i<6;i++) cout<<P[i]<<" "; cout<<endl; for(i=0;i<6;i++) { Pax[0]=0.0; Pax[i+1]=Pax[i]+P[i]; } cout<<"概率累加和为:"<<endl; for(i=0;i<6;i++) cout<<Pax[i]<<" "; cout<<endl; for(i=0;i<6;i++) { double m=log(1/P[i])/log(2); if(m-int(m)==0) machang[i]=log(1/P[i])/log(2); else machang[i]=int(m)+1; cout<<P[i]<<"的码长为:"<<machang[i]<<endl; } for(i=0;i<6;i++) { for(int j=0;j<machang[i];j++) { int n=int(Pax[i]*2); cout<<n; if((Pax[i]*2-1)>0) { Pax[i]=Pax[i]*2-1; continue; } if((Pax[i]*2-1)==0) Pax[i]=Pax[i]*2-1; else Pax[i]=Pax[i]*2; } cout<<endl; }

信息论与编码实验报告

信息论与编码实验报告一、实验目的信息论与编码是一门涉及信息的度量、传输和处理的学科，通过实验，旨在深入理解信息论的基本概念和编码原理，掌握常见的编码方法及其性能评估，提高对信息处理和通信系统的分析与设计能力。

二、实验原理（一）信息论基础信息熵是信息论中用于度量信息量的重要概念。

对于一个离散随机变量 X，其概率分布为 P(X) ＝｛p(x1)， p(x2)，， p(xn)｝，则信息熵H(X) 的定义为：H(X) ＝∑p(xi)log2(p(xi)）。

（二）编码原理1、无失真信源编码：通过去除信源中的冗余信息，实现用尽可能少的比特数来表示信源符号，常见的方法有香农编码、哈夫曼编码等。

2、有噪信道编码：为了提高信息在有噪声信道中传输的可靠性，通过添加冗余信息进行纠错编码，如线性分组码、卷积码等。

三、实验内容及步骤（一）信息熵的计算1、生成一个离散信源，例如信源符号集为{A, B, C, D}，对应的概率分布为{02, 03, 01, 04}。

2、根据信息熵的定义，使用编程语言计算该信源的信息熵。

（二）香农编码1、按照香农编码的步骤，首先计算信源符号的概率，并根据概率计算每个符号的编码长度。

2、确定编码值，生成香农编码表。

（三）哈夫曼编码1、构建哈夫曼树，根据信源符号的概率确定树的结构。

2、为每个信源符号分配编码，生成哈夫曼编码表。

（四）线性分组码1、选择一种线性分组码，如（7, 4）汉明码。

2、生成编码矩阵，对输入信息进行编码。

3、在接收端进行纠错译码。

四、实验结果与分析（一）信息熵计算结果对于上述生成的离散信源，计算得到的信息熵约为 184 比特/符号。

这表明该信源存在一定的不确定性，需要一定的信息量来准确描述。

（二）香农编码结果香农编码表如下：｜信源符号|概率|编码长度|编码值|｜｜｜｜｜｜A|02|232|00|｜B|03|174|10|｜C|01|332|110|｜D|04|132|111|香农编码的平均码长较长，编码效率相对较低。

香农编码

for(int i=0;i<f;i++)
cin>>p[i];
}
排序函数：void sort(double p[])
{
double t;
for (int i=0;i<f;i++)
{
for(int j=f-1;j>i;j--)
{
if (p[j]>p[j-1])
{t=p[j];p[j]=p[j-1];p[j-1]=t;}
{
x=pp[i];
for(int m=1;m<l[i]+1;m++)
{
x=x*2.0;
if(x>=1.0){c[j]=1;x=x-1.0;}
else{c[j]=0;}
j++;
}
}
}
输出函数：
void output(int l[],int c[],double p[],double pp[])
{
int m=0;
cout<<endl;
m=m+j;
}}
求解结果：
例5.1.2的求解结果
五、总结
一上机才发现，自己C和C++又该复习了，主要是很多语法怎么使用都记不太清楚了，但是以前通过复习的资料，自己还是很快很够把握一些基本的知识了，所以编写程序不是特别的难了，对于香农编码而言，主要是弄清楚各个步骤，像求码长、累加和、概率排序，每个模块建立一个函数，使得程序简单易读，自己的思路也更清晰明了。编码的原理我们都很清楚，主要就是在一些C和C++基本知识上的巩固才能做好这次的实验。
二进制香农编码的步骤如下：（1）、将信源符号按概率从大到小的顺序排列（2）、对第j个前的概率进行累加得到pa(aj)（3）、由-logp(ai) ki<1-logp(ai)求得码字长度ki (4)、将pa(aj)用二进制表示，并取小数点后ki位作为符号ai的编码。

信息论与编码实验报告

实验报告课程名称：信息论与编码姓名：系：专业：年级：学号：指导教师：职称：年月日目录实验一信源熵值的计算 (1)实验二 Huffman信源编码 (5)实验三 Shannon编码 (9)实验四信道容量的迭代算法 (12)实验五率失真函数 (15)实验六差错控制方法 (20)实验七汉明编码 (22)实验一信源熵值的计算一、实验目的1 进一步熟悉信源熵值的计算 2熟悉 Matlab 编程二、实验原理熵（平均自信息）的计算公式∑∑=--==qi i i qi i i p p p p x H 1212log 1log )(MATLAB 实现：))(log *.(2x x sum HX -=；或者))((log *)(2i x i x h h -= 流程：第一步：打开一个名为“nan311”的TXT 文档，读入一篇英文文章存入一个数组temp ，为了程序准确性将所读内容转存到另一个数组S ，计算该数组中每个字母与空格的出现次数(遇到小写字母都将其转化为大写字母进行计数)，每出现一次该字符的计数器+1；第二步：计算信源总大小计算出每个字母和空格出现的概率；最后，通过统计数据和信息熵公式计算出所求信源熵值（本程序中单位为奈特nat ）。

程序流程图：三、实验内容1、写出计算自信息量的Matlab 程序2、已知：信源符号为英文字母（不区分大小写）和空格。

输入：一篇英文的信源文档。

输出：给出该信源文档的中各个字母与空格的概率分布，以及该信源的熵。

四、实验环境Microsoft Windows 7Matlab 6.5五、编码程序#include"stdio.h"#include <math.h>#include <string.h>#define N 1000int main(void){char s[N];int i,n=0;float num[27]={0};double result=0,p[27]={0};FILE *f;char *temp=new char[485];f=fopen("nan311.txt","r");while (!feof(f)) {fread(temp,1, 486, f);}fclose(f);s[0]=*temp;for(i=0;i<strlen(temp);i++){s[i]=temp[i];}for(i=0;i<strlen(s);i++){if(s[i]==' ')num[26]++;else if(s[i]>='a'&&s[i]<='z')num[s[i]-97]++;else if(s[i]>='A'&&s[i]<='Z')num[s[i]-65]++;}printf("文档中各个字母出现的频率:\n");for(i=0;i<26;i++){p[i]=num[i]/strlen(s);printf("%3c:%f\t",i+65,p[i]);n++;if(n==3){printf("\n");n=0;}}p[26]=num[26]/strlen(s);printf("空格:%f\t",p[26]);printf("\n");for(i=0;i<27;i++){if (p[i]!=0)result=result+p[i]*log(p[i]);}result=-result;printf("信息熵为:%f",result);printf("\n");return 0;}六、求解结果其中nan311.txt中的文档如下：There is no hate without fear. Hate is crystallized fear, fear’s dividend, fear objectivized. We hate what we fear and so where hate is, fear is lurking. Thus we hate what threatens our person, our vanity andour dreams and plans for ourselves. If we can isolate this element in what we hate we may be able to cease from hating.七、实验总结通过这次实验，我们懂得了不必运行程序时重新输入文档就可以对文档进行统计，既节省了时间而且也规避了一些输入错误。

信息论与编码实验报告

本科生实验报告实验课程信息理论与编码学院名称信息科学与技术学院专业名称学生姓名学生学号指导教师实验地点实验成绩二〇一六年九月----二〇一六年十一月填写说明1、适用于本科生所有的实验报告（印制实验报告册除外）；2、专业填写为专业全称，有专业方向的用小括号标明；3、格式要求：①用A4纸双面打印（封面双面打印）或在A4大小纸上用蓝黑色水笔书写。

②打印排版：正文用宋体小四号，1.5倍行距，页边距采取默认形式（上下2.54cm，左右2.54cm，页眉1.5cm，页脚1.75cm）。

字符间距为默认值（缩放100%，间距：标准）；页码用小五号字底端居中。

③具体要求：题目（二号黑体居中）；摘要（“摘要”二字用小二号黑体居中，隔行书写摘要的文字部分，小4号宋体）；关键词（隔行顶格书写“关键词”三字，提炼3-5个关键词，用分号隔开，小4号黑体)；正文部分采用三级标题；第1章××(小二号黑体居中，段前0.5行)1.1 ×××××小三号黑体×××××（段前、段后0.5行）1.1.1小四号黑体（段前、段后0.5行）参考文献（黑体小二号居中，段前0.5行），参考文献用五号宋体，参照《参考文献著录规则（GB/T 7714－2005）》。

实验一：香农（Shannon ）编码一、实验目的掌握通过计算机实现香农编码的方法。

二、实验要求对于给定的信源的概率分布，按照香农编码的方法进行计算机实现。

三、实验基本原理给定某个信源符号的概率分布，通过以下的步骤进行香农编码 1.将信源消息符号按其出现的概率大小排列)()()(21n x p x p x p ≥≥≥ 2．确定满足下列不等式的整数码长K i ；1)(log )(log 22+-<≤-i i i x p K x p3．为了编成唯一可译码，计算第i 个消息的累加概率∑-==11)(i k k i x p p4．将累加概率P i 变换成二进制数。

实验二 Shannon编码

实验二Shannon编码一、实验目的及要求a)实验目的1.通过本实验实现信源编码——Shannon编码2.编写M文件实现，掌握Shannon编码方法b)实验要求1.了解Matlab中M文件的编辑、调试过程2.编写程序实现Shannon编码算法二、实验步骤及运行结果记录a)实验步骤1.输入Shannon编码程序2.运行程序，按照提示输入相应信息，并记录输入信息，及运行结果。

3.思考：在程序中加入排序子程序，使其在输入信源概率时，不要求输入顺序。

b)实验结果y =0.2000 0 2.3219 3.00000.1900 0.2000 2.3959 3.00000.1800 0.3900 2.4739 3.00000.1700 0.5700 2.5564 3.00000.1500 0.7400 2.7370 3.00000.1000 0.8900 3.3219 4.00000.0100 0.9900 6.6439 7.0000code =000；code = 001；code = 011；code =100；code = 101；code =1110；code =1111110三、实验流程图（附一）四、程序清单，并注释每条语句（附二）五、实验小结香农编码是码符号概率大的用短码表示，概率小的是用长码表示，程序中对概率排序，最后求得的码字就依次与排序后的符号概率对应。

此程序缺点是，第一个码字都是以0开始，因为对累加概率求二进制后，小数点后的数都是0，取几位由码长确定，而香农编码是不唯一的，如果手动编码就不存在这样的问题。

后面求得的编码没有下标就需要注意是与上面排序后的信源符号对应。

附一附二N=input('请输入信源符号个数:')%输入信源符号个数p=zeros(1,N);%生成1*4的零矩阵for i=1:Np(1,i)=input('请输入各信源符号出现的概率:')%输入各个信源符号的概率endp=fliplr(sort(p));%将概率从大到小进行排序if abs(sum(p)-1)>10e-10error('输入概率不符合概率分布')%检验所输入的概率是否正确endy=zeros(N,4);%生成N*4零矩阵for i=1:Ny(i,1)=p(1,i);%将各个符号出现的概率放入y矩阵的第一列中y(1,2)=0;if i>1y(i,2)=y(i-1,2)+y(i-1,1); %第二列其余的元素用此式求得,即为累加概率endy(i,3)=log2(1./p(i))%求各个信源符号的信息熵放入y矩阵的第三列中y(i,4)=ceil(y(i,3))%求码长endA=y(:,2);%取出y中的第二列元素B=y(:,4);%取出y中的第四列元素for i=1:Ncode=shannoncode(A(i),B(i))%生成码字endfunction [C]=shannoncode(A,B)%对累加概率求二进制的函数C=zeros(1,B);%生成零矩阵用于存储生成的二进制数，对二进制的每一位进行操作temp=A;%temp赋初值for i=1:B%累加概率转化为二进制，循环求二进制的每一位，A控制生成二进制的位数 temp=temp*2;if temp>1temp=temp-1;C(1,i)=1;elseC(1,i)=0;endendend。

信息论实验四香农编码

信息论实验四香农编码实验四香农编码1、实验目的：掌握香农编码的方法2、实验内容：对信源进行二进制香农编码。

并计算其平均码长，信源熵，和编码效率。

三、实验步骤（1）将信源符号按概率从大到小的顺序排列。

（2）用Pa（i）表示第i个码字的累加概率（3）确定满足下列不等式的整数K（i），并令K（i）为第i个码字的长度（4）将Pa（i）用二进制表示，并取小数点后K（i）位最为a（i）的编码四、实验数据及结果分析（1）将信源符号按概率从大到小的顺序排列。

0.25 0.2 0.15 0.1 0.05）；（2）用Pa（i）表示第i个码字的累加概率。

0 0.2500 0.5000 0.7000 0.8500 0.9500）（3）确定满足下列不等式的整数K（i）。

2 3 3 4 5）（4）将Pa（i）用二进制表示，并取小数点后K（i）位最为a（i）的编码0001100101110111110（5）计算其平均码长，信源熵，和编码效率平均码长 L=2.7信源熵 H=2.4232编码效率 xiaolv=0.89749五、代码附录N=input('N='); %输入信源符号的个数s=0;L=0;H=0;Pa=zeros(1,6);for i=1:NP(i)=input('P=');%输入信源符号概率分布 s=s+P(i); endif s~=1error('不符合概率分布');endP=sort(P,'descend');Pa(1)=0;for i=2:NPa(i)=Pa(i-1)+P(i-1);enddisp(Pa);for i=1:Na=-log2(P(i));if mod(a,1)==0 %计算第i个码字的长度 K(i)=a; elseK(i)=fix(a+1);endL=L+P(i)*K(i); %计算平均码长H=H-P(i)*log2(P(i));%计算信源熵Endxiaolv=H/L; %计算编码效率for i=1:Nfor j=1:K(i)W(i,j)=fix(Pa(i)*2);Pa(i)=Pa(i)*2-fix(Pa(i)*2);fprintf('%d',W(i,j));endfprintf('\n');end6，实验总结：通过该实验，掌握了香农编码。

信息论实验报告2信源编码

1、香农编码Matlab源码
function [W,L,q]=shannon(p)
if (length(find(p<=0)) ~=0)
error('Not a prob.vector,negative component'); end
if (abs(sum(p)-1)>10e-10)
error('Not a prob.vector,component do not add up to 1'); end
n=length(P); %计算输入元素个数
p=P; mark=zeros(n-1,n);
% mark为n-1行、n列矩阵，用来记录每行最小两概率叠加后概率排列次序
% 1)确定概率大小值的排列，得到mark矩阵。
for i=1:n-1
[p,num]=sort(p); mark(i,:)=[num(1:n-i+1),zeros(1,i-1)];
s2='Shannon编码平均码字长度L:'; s3='Shannon编码的编码效率q:';
disp(s0);disp(s1),disp(B),disp(W);disp(s2),disp(L);disp(s3),disp(q);
function H=entropy(P,r)
if (length(find(P<=0))~=0) %判断是否符合概率分布条件
[c,k]=min(temp);
if (current_index<=k)
next_index=current_index; code_num=48;
next_P=current_P(1:k);
else

关于编码实验的实验报告

一、实验目的1. 理解编码的基本原理和方法；2. 掌握哈夫曼编码和LZ编码的基本思想；3. 学习利用编程实现编码算法；4. 分析编码效率，提高数据压缩能力。

二、实验环境1. 操作系统：Windows 102. 编程语言：Python3.83. 开发工具：PyCharm三、实验内容1. 哈夫曼编码（1）实验目的：掌握哈夫曼编码的基本原理，实现哈夫曼编码和译码。

（2）实验步骤：a. 统计待编码文件中字符出现的频率；b. 根据频率构造哈夫曼树；c. 为哈夫曼树中的每个节点分配码字；d. 编码待编码文件；e. 译码编码后的文件。

（3）实验结果：a. 哈夫曼树如图所示；b. 编码后的文件大小为：原文件大小的X%；c. 译码后的文件与原文件内容完全一致。

2. LZ编码（1）实验目的：熟悉LZ编码的基本思想，实现LZ编码和译码。

（2）实验步骤：a. 编写LZ编码程序，读取待编码文件；b. 实现LZ编码算法，生成编码后的文件；c. 编写LZ译码程序，读取编码后的文件；d. 译码编码后的文件，验证译码结果。

（3）实验结果：a. 编码后的文件大小为：原文件大小的Y%；b. 译码后的文件与原文件内容完全一致。

四、实验分析1. 哈夫曼编码与LZ编码的比较a. 哈夫曼编码适用于字符频率较高的文本文件，编码效率较高；b. LZ编码适用于字符重复率较高的文本文件，编码效率较高；c. 在实际应用中，可以根据文件特点选择合适的编码方法。

2. 编码效率分析a. 哈夫曼编码的编码效率取决于字符频率分布，频率分布越均匀，编码效率越高；b. LZ编码的编码效率取决于文本的重复率，重复率越高，编码效率越高。

五、实验总结1. 通过本次实验，掌握了哈夫曼编码和LZ编码的基本原理和实现方法；2. 学会了利用编程实现编码算法，提高了数据压缩能力；3. 了解了不同编码方法的特点，为实际应用提供了参考。

六、实验拓展1. 研究其他编码算法，如算术编码、行程编码等；2. 尝试将编码算法应用于图像、音频等不同类型的数据；3. 研究编码算法的优化，提高编码效率。

实验二香农编码

第页
陕西科技大学实验报告
八、思考题举例说明香农编码在现实中有实际作用，列举一个例子，并简要说明？可以抓住语言结构的冗余性以及语言中字母、词的使用频度等统计特性。使用香农信息论信息量等观点，来研究中文与英文的信息量，从而比较出学习这两种语言的难科技大学实验报告
D=zeros(n,4); D(:,1)=y'; for i=2:n D(1,2)=0; D(i,2)=D(i-1,1)+D(i-1,2); end for i=1:n D(i,3)=-log2(D(i,1)); D(i,4)=ceil(D(i,3)); end D A=D(:,2)'; B=D(:,4)'; Code_length=0; for j=1:n Code_length=Code_length+p(j)*D(j, 4); end H=0; for j=1:n H=H+p(j)*log2(1/p(j)); end for j=1:n fprintf('输入信源符号概率为%f 的码字为:',p(1,j)); C=deczbin(A(j),B(j)); disp(C) end Efficiency=H/(Code_length) fprintf('平均码长:\n'); disp(Code_length) fprintf('\n 香农编码效率:\n'); disp(Efficiency) A：累加概率；B：码子长度。 function [C]=deczbin(A,B) C=zeros(1,B); temp=A; for i=1:B temp=temp*2; if temp>1 temp=temp-1; C(1,i)=1; else C(1,i)=0; end end

实验2：Shannon编码

九
、
实
验
结
论
：
十、总结及心得体会：本实验让我学习了使用识有了进一步了解。
进行编程的方法，并对
的知
十一、对本实验过程及方法、手段的改进建议：
报告评分：指导教师签字：
sum=shanon[i].b+sum; } for(i=0;i<n;i++) { printf(" } for(i=0;i<n;i++) { int j; c=sorted[i].p; printf("%s 的香农编码：",sorted[i].a); for(j=0;j<sorted[i].geshu;j++) { c=c*2; t=c; printf("%d",(int)t); if(c>1) c=c-1; } printf("\n"); } } %s %f %d\n",sorted[i].a,sorted[i].p,sorted[i].geshu);
五、实验内容：
s2 , , sq S s1 , 对于给定的信源 P ，利用香农编码方法编出其中一种码。 p( s1 ), p( s 2 ), , p( s q )
六、实验器材（设备、元器件）： PC 机一台，装有 VC++6.0 或其它 C 语言集成开发环境。七、实验步骤及操作： 1）排序； 2）计算码长； 3）递归调用香农算法得到相应的码字。
void main() { int n,i; float sum=0,c,t; mynode1 *shanon; mynode2 *sorted;

信源熵的计算

桂林电子科技大学数学与计算科学学院实验报告实验室：实验日期： 2010年 11月 11日院（系）数学与计算科学学院年级、专业、班 0800710310 姓名何帅成绩课程名称信息与编码实验项目名称信源熵的计算指导教师一实验目的1、掌握香农编码的原理2、掌握二进制小数的输出方法二实验内容与步骤Shannon 码编码步骤为：1、将信源S 的所有符号按概率从大到小排列：12q P P P ≥≥≥ 2、对第i 个信源符号i s 取整数码长[]1log 1,i i l P ⎡⎤=+⎢⎥⎣⎦为取整运算 3、计算累加概率111,0,(2)i i i k k R R R P i -===≥∑ 4、将i R 变换成二进制数12j i j j R x ∞-==∑，并按步骤2中计算的长度i l 取i R 的二进制系数j x ，组合起来即为i s的香农码字i W 程序：#include<stdio.h>#include<iostream.h>#include<math.h>double P[6]={0.25,0.1,0.2,0.25,0.15,0.05},Pax[6],machang[6];void main(){double temp;for(int a=1;a<6;a++){for(int i=0;i<6-a;i++)if(P[i]<P[i+1]){temp=P[i];P[i]=P[i+1];P[i+1]=temp;}}for(int i=0;i<6;i++)cout<<P[i]<<" ";cout<<endl;for(i=0;i<6;i++){Pax[0]=0.0;Pax[i+1]=Pax[i]+P[i];}cout<<"概率累加和为："<<endl;for(i=0;i<6;i++)cout<<Pax[i]<<" ";cout<<endl;for(i=0;i<6;i++){double m=log(1/P[i]/log(2));if(m-int(m)==0)machang[i]=log(1/P[i])/log(2);elsemachang[i]=int(m)+1;cout<<P[i]<<"的码长为："<<machang[i]<<endl;}for(i=0;i<6;i++){for(int j=0;j<machang[i];j++){int n=int(Pax[i]*2);cout<<n;if((Pax[i]*2-1)>0){Pax[i]=Pax[i]*2-1;continue;}if((Pax[i]*2-1)==0)Pax[i]=Pax[i]*2-1;elsePax[i]=Pax[i]*2;}cout<<endl;}}运行结果：三实验体会心得通过本次实验学习了求香农编码的基本步骤，同时学习了如何在C++下实现，在编程中主要是注意求二进制数是通过乘2取整得到的。

香浓编码实验报告

编码理论实验报告

实验四_香农编码

信息论与编码实验报告

信息论与编码实验报告

实验四-香农编码

中南大学信息论与编码编码部分实验报告

信息论实验报告香农编码

香农编码

信息论与编码实验报告

香农编码

信息论与编码实验报告

信息论与编码实验报告

实验二 Shannon编码

信息论实验四香农编码

信息论实验报告2信源编码

关于编码实验的实验报告

实验二 香农编码

实验2：Shannon编码

信源熵的计算

实验二香农编码