卷积码实验报告

合集下载

无线通信技术实验一卷积码

实验二：卷积码一、实验仪器:PC两台、USRP两台二、实验目的：1、了解grc仿真中的信号处理模块、流程图以及使用方法2、了解卷积码的基本原理3、了解GunRadio实现信道编码的方法4、了解不同SNR对于误码率的影响5、了解卷积码对误码率的影响6、了解不同的卷积码对于误码率的影响三、实验要求：1.了解Grc的基本操作方法，要求仿真的流程中信道编码部分使用卷积编码2.通过单机实验和GnuRadio+USRP的实验两种实验方式进行仿真3.搭建有信道编码与无信道编码的Grc仿真模型4.比较上述两种情况下的误码率，并且分析结果5.比较不同的卷积码对于误码率的影响，并且分析结果。

四、实验原理：卷积码将k个信息比特编码成n个比特，但k和n通常很小，特别适合以串行形式进行传输，时延小。

与分组码不同，卷积码编码后的n个码元不仅与当前段的k个信息有关，还与前面的N-1段信息有关，编码过程中互相关联的码元个数为nN。

卷积码的纠错性能随N的增加而增大，而差错率随N的增加而指数下降。

卷积码的纠错能力不仅与约束长度有关，还与采用的译码方式有关。

GRC提供译码方式是维特比译码，它是卷积码译码方式中非常经典的以及广泛使用的一种译码方式。

该实验可以考察编码前后数据有什么变化，译码后能不能恢复原来数据，通过Number Sink考察加噪声后误比特率怎么样，对性能有什么提高，并且划出BER图形。

下面为卷积码的一般流程：五、实验步骤及分析：1、单机实验：单机实验分成（2,1,3）码、无信道编码、（2,1,8）码三个部分进行。

（一）实验流程图：首先，我们利用（2,1,3）卷积码进行信道编码，用DPSK进行调制，来进行单机实验，最终设计的流程图和参数如下图所示：先是Vector Source，即信源，设置的数据是1,0,0,1,1。

然后是Throttle限流模块。

接下来是Packed to Unpacked模块，将pack成byte或short型的数据以unpacked型的数据输出。

卷积实验报告

新乡学院实验报告实验内容及步骤1、按1.3节用设置“信号A组”的输出为指数衰减信号（模式二，信号A组的信号输出指示灯为000000），并经放大器缓冲输出；1、按1.3节用按键2使使对应的“信号B组”产生270Hz信号（模式二，信号B组的信号输出指示灯为000101），并经放大器缓冲输出。

2、卷积输出：用短路线将A缓冲信号连接到乘法器的一端S，将信号源1KHz接到乘法器1的输入端X，示波器同时观察这两个信号（会观察到这两个信号在发生相对移动）；并将乘法器1的输出端接低通滤波器（300～3400Hz）输入端，最后并观察滤波器的输出y。

3、验证卷积器的交换率：)(*)()(*)(1221tftftftf=。

在上例中，交换乘法器的两个输入，观察滤波器的输出y，并与上一步进行比较。

4、验证卷积器的分配率：)(*)()(*)()]()([*)(3121321tftftftftftftf+=+(1)用短路线将信号A、B组两信号通过加法器相加，并将加法器的输出与乘法器1的S端相连将，将标准信号源1KHz信号连接到乘法器1的输入端X；并将乘法器1的输出端接低通滤波器（300～3400Hz）输入端，最后并观察滤波器的输出y。

(2)用短路线将信号A、B组两信号分别与乘法器1、2的Ｓ端相连，将标准信号源1KHz信号分别连接到乘法器1、2的输入端X，同时将两乘法器的结果经加法器相加，观察加法器的输出。

(3)比较上两步测量结果。

注意事项1.要注意示波器的表笔要接地。

2.函数信号发生器为模式2。

3.正确连接实验电路。

实验数据︵现象︶记录及结果处理(不够可附页)。

【报告】卷积码实验报告

【报告】卷积码实验报告一、实验目的本次卷积码实验的主要目的是深入理解卷积码的编码与译码原理，掌握其在数字通信系统中的应用，并通过实际实验操作和结果分析，评估卷积码的纠错性能和对通信质量的改善效果。

二、实验原理（一）卷积码的基本概念卷积码是一种有记忆的非分组码，它将输入的信息序列经过特定的编码器生成输出的码序列。

卷积码的编码过程不仅取决于当前输入的信息位，还与之前的若干个信息位有关。

（二）编码原理卷积码的编码器通常由若干个移位寄存器和模 2 加法器组成。

输入的信息位在时钟的控制下依次进入移位寄存器，同时与寄存器中的内容进行模 2 加法运算，生成输出的编码位。

（三）译码原理卷积码的译码方法有多种，常见的有维特比译码算法。

维特比译码算法基于最大似然准则，通过在码的网格图上寻找最有可能的路径来实现译码。

三、实验环境与设备本次实验在计算机上进行，使用了以下软件和工具：1、 MATLAB 编程环境，用于实现卷积码的编码、传输和译码过程，并进行性能分析。

2、通信系统仿真工具，用于构建通信系统模型，模拟信号的传输和接收。

四、实验步骤（一）编码实现1、在 MATLAB 中定义卷积码的编码器结构，包括移位寄存器的数量和连接方式，以及模 2 加法器的位置。

2、编写编码函数，输入信息序列，按照编码器的工作原理生成编码后的序列。

（二）信道传输1、模拟加性高斯白噪声信道，设置不同的信噪比条件。

2、将编码后的序列通过信道传输，引入噪声干扰。

（三）译码实现1、使用维特比译码算法对接收序列进行译码。

2、编写译码函数，输入接收序列和信道参数，输出译码后的信息序列。

（四）性能评估1、计算误码率，即错误译码的比特数与总传输比特数的比值。

2、绘制误码率曲线，分析卷积码在不同信噪比条件下的纠错性能。

五、实验结果与分析（一）不同卷积码参数对性能的影响1、改变卷积码的约束长度，观察其对纠错性能的影响。

结果表明，约束长度越长，卷积码的纠错能力越强，但编码效率会有所降低。

缩短卷积码MATLAB仿真实训实习报告

缩短卷积码MATLAB仿真实训实习报告缩短卷积码MATLAB仿真实训实习报告（一）摘要现代通信系统的信道编码中几乎毫无例外的采用了先进的编码方式：卷积编码,如：码分多址通信系统CDMA，数字蜂窝通信系统GSM，数字集群通信系统TETRA等等,在差错控制中，卷积码表现出了优秀的纠错能力。

但是优秀的纠错能力是以降低频道利用率为代价。

在功能完备的通信系统中有许多使命不同的逻辑信道.不同的逻辑信道因为任务不同，对应的差错控制能力与频道利用率的要求是不一样的，有两种实现的方法：构建不同的卷积码或者应用同一个卷积码但是运用不同的缩短方案以适应不同的传输数码率，自然也有着相应的纠错能力和频带利用率。

在先进的数字集群系统中就是用的第二种方案，实践证明，删除型缩短卷积码的性能与最好的卷积码可以做到相当接近。

关键词：信道编码、缩短卷积码、纠错能力（二）缩短卷积码基本原理本实训目的是要构建一个具有卷积、解卷积和打孔、插零功能以及相应的传输环境的仿真系统来对各类卷积码进行缩短卷积码的仿真研究，得到相同频带利用率下不同打孔图形的差错控制能力定量结果。

用相同的生成多项式构建的维特比译码器和不同的压缩图形卷积码都可以在原打孔图形位置上嵌入填充的码元后进行译码。

仿真采用具有缩短卷积码和调制功能的仿真系统，用BernoulliRandomBinary产生每帧2码元的随机二进制码，进入卷积编码器后变成每帧6码元的二进制码流，再经过Puncture（打孔）模块后，变为删去选择码元后剩下的码元数，在调制和解调过程中，数据帧的大小不变，通过InsertZero（插零）模块在原来删去码元的位置插入码元0，解卷积，恢复每帧2码元。

Puncture模块中的打孔矢量应与输入信号具有相同的帧长度，而且要与InsertZero模块中的插零矢量相同，矢量（vector）中的0就是打掉马远的位置，也是在解卷积之前插入0的位置，1是保留码元的位置，而矢量的长度与0的数目以及卷积码的结构共同决定了编码效率。

通信原理实验19卷积码的编解码实验

通信原理实验19卷积码的编解码实验实验十九卷积码的编解码实验实验内容1. 熟悉卷积码编码实验2．熟悉卷积码译码实验一、实验目的1．了解卷积码的基本概念和原理2．加深对卷积码的编解码过程的理解3. 学习通过CPLD编程实现卷积码编译码实验二、实验电路工作原理卷积码又称连环码，是1955年提出来的一种纠错码，它和分组码有明显的区别，但在编码器复杂度相同的情况下, 卷积码的性能优于分组码,因此卷积码几乎被应用在所有无线通信的标准之中, 如GSM, IS95和CDMA 2000 的标准中。

1．卷积码编码方法：卷积码通常记作( n0 , k0 , m) ,它将k0 个信息比特编为n0 个比特, 其编码效率为k0/ n0 , m为约束长度。

( n0 , k0 , m )卷积码可用k0 个输入、n0 个输出、输入存储为m的线性有限状态移位寄存器及模2 加法计数器来实现。

实验中所选(2 ,1 ,6) 卷积编码器上图所示,其子生成元为: g(1 ,1) ( D) = 1 , g(1 ,2) ( D) = 1 + D2 + D5 +D6 , 生成矩阵G( D) = (1 ,1 + D2 + D5 + D6) 。

设输入信息序列M = (1111) ,即M( D) = 1 + D + D2 + D3 ,则编码器的输出C( D) =M( D) ·G( D) ,即:C( D) = (1+D+D2+D3)·(1,1+D2+D5+D6)=(1+D+D2+D3 ,1+D+D2+D3+D2+D3+D4+D5+D5+D6+D7+D8 +D6+D7+D8+D9)= (1+D+D2+D3 ,1+D+D4+D9)=(11)+(11)D+(10)D2+(10)D3+(01)D4+(00)D5+(00)D6+(00)D7+(0 0)D8+(01)D9+?因此,编码器输出序列为11111010010000000001。

2．卷积码编码算法process(clk,clr)beginif(clr='1')thenif(clk'event and clk='1')thentemp(0)<=datain;temp(1)<=temp(0);temp(2)<=temp(1);temp(3)<=temp(2);temp(4)<=temp(3);end if;else temp<="00000";end if;end process;y2j<= (datain xor temp(2) xor temp(3) xor temp(4));y1j<=datain;3．大数逻辑解码器大数逻辑解码器是卷积码代数解码最主要的解码方法, 既可用于纠随机错误, 又可用于纠突发错误,但要求卷积码是自正交码或可正交码。

卷积码实验报告

卷积码实验报告篇一：卷积码实验报告实验五信道编解码（）本章目标掌握数字频带传输系统调制解调的仿真过程掌握数字频带传输系统误码率仿真分析方法 5.1实验目的1. 使用MATLAB进行卷积码编/译码器的仿真。

2. 熟练掌握MATLAB软件、语句。

3. 了解卷积码编/译码器的原理、知识。

5.2实验要求1. 编写源程序、准备测试数据。

2. 在 MATLAB环境下完成程序的编辑、编译、运行，获得程序结果。

如果结果有误，应找出原因，并设法更正之。

5.3 实验原理（一）卷积码编码器 1. 连接表示卷积码由3个整数n，k，N描述。

k/n也表示编码效率（每编码比特所含的信N称为约束长度，息量）；但n与线性分组码中的含义不同，不再表示分组或码子长度；表示在编码移位寄存器中k元组的级数。

卷积码不同于分组码的一个重要特征就是编码器的记忆性，即卷积码编码过程中产生的n元组，不仅是当前输入k元组的函数，而且还是前面N?1个输入k元组的函数。

实际情况下，n和k经常取较小的值，而通过N的变化来控制编码的能力和复杂性。

下面以图1中的卷积码编码器为例介绍卷积码编码器。

该图表示一个约束长度K?3的（2，1）卷积译码器，模2加法器的数目为n?2，因此，编码效率k/n?1/2。

在每个输入比特时间上，1位信息比特移入寄存器最左端的一级，同时将寄存器中原有比特均右移一级，接着便交替采样两个模2加法器，得到的码元就是与该输入比特相对应的分支字。

对每一个输入信号比特都重复上述采样过程。

图1卷积码编码器（编码效率1/2，K?3）用于描述反馈移位寄存器实现循环码时所使用的生成多项式也可用户描述卷积码编码器的连接。

应用n个生成多项式描述编码的移位寄存器与模2加法器的连接方式，n个生成多项式分别对应n个模2加法器，每个生成多项式不超过K?1阶。

仍以图1中的编码器为例，用生成多项式g1(X)代表上方连接，g2(X)代表下方连接，则有：g1(X)?1?X?X2g2(X)?1?X2多项式中的最低阶项对应于寄存器的输入级。

卷积算法实验报告程序

一、实验目的通过本次实验，加深对卷积算法的理解，掌握离散时间系统中的卷积运算方法，并学会使用MATLAB进行卷积运算的仿真。

二、实验原理卷积是一种线性时不变（LTI）系统的数学运算，用于描述系统输入信号与系统冲激响应的卷积结果。

在离散时间系统中，卷积运算可以表示为：\[ y[n] = \sum_{k=-\infty}^{\infty} x[k]h[n-k] \]其中，\( y[n] \) 是系统的输出信号，\( x[k] \) 是系统的输入信号，\( h[n] \) 是系统的冲激响应，\( n \) 是时间变量。

MATLAB提供了`conv`函数来进行卷积运算，其语法为：\[ y = conv(x, h) \]其中，\( x \) 和 \( h \) 分别是输入信号和冲激响应的向量。

三、实验内容1. 创建输入信号和冲激响应使用MATLAB创建一个简单的输入信号 \( x[n] \) 和一个冲激响应 \( h[n] \)。

```matlab% 创建输入信号 x[n] = cos(2pi0.5n)n = 0:100;x = cos(2pi0.5n);% 创建冲激响应 h[n] = u[n] - u[n-10]h = [ones(1,10), zeros(1,90)];```2. 进行卷积运算使用`conv`函数进行卷积运算，并绘制输入信号、冲激响应和输出信号的图形。

```matlab% 进行卷积运算y = conv(x, h);% 绘制图形figure;subplot(3,1,1);stem(n, x);title('输入信号 x[n]');subplot(3,1,2);stem(n, h);title('冲激响应 h[n]');subplot(3,1,3);stem(n, y);title('输出信号 y[n]');```3. 分析卷积结果分析卷积结果，观察输出信号的特性，并与理论预期进行对比。

卷积码实验报告

2. 熟练掌握MATLAB软件、语句。

3. 了解卷积码编/译码器的原理、知识。

5.2实验要求1. 编写源程序、准备测试数据。

2. 在 MATLAB环境下完成程序的编辑、编译、运行，获得程序结果。

如果结果有误，应找出原因，并设法更正之。

5.3 实验原理（一）卷积码编码器 1. 连接表示卷积码由3个整数n，k，N描述。

实际情况下，n和k经常取较小的值，而通过N的变化来控制编码的能力和复杂性。

下面以图1中的卷积码编码器为例介绍卷积码编码器。

该图表示一个约束长度K?3的（2，1）卷积译码器，模2加法器的数目为n?2，因此，编码效率k/n?1/2。

对每一个输入信号比特都重复上述采样过程。

图1卷积码编码器（编码效率1/2，K?3）用于描述反馈移位寄存器实现循环码时所使用的生成多项式也可用户描述卷积码编码器的连接。

应用n个生成多项式描述编码的移位寄存器与模2加法器的连接方式，n个生成多项式分别对应n个模2加法器，每个生成多项式不超过K?1阶。

仍以图1中的编码器为例，用生成多项式g1(X)代表上方连接，g2(X)代表下方连接，则有：g1(X)?1?X?X2g2(X)?1?X2多项式中的最低阶项对应于寄存器的输入级。

卷积编码实验报告

实验名称：___ 卷积编码_______1、使用MATLAB进行卷积编码的代码编写、运行、仿真等操作；2、熟练掌握MATLAB软件语句；3、理解并掌握卷积编码的原理知识。

二、实验原理卷积码是由Elias于1955 年提出的，是一种非分组码，通常它更适用于前向纠错法，因为其性能对于许多实际情况常优于分组码，而且设备较简单。

卷积码的结构与分组码的结构有很大的不同。

具体地说，卷积码并不是将信息序列分成不同的分组后进行编码，而是将连续的信息比特序列映射为连续的编码器输出符号。

卷积码在编码过程中，将一个码组中r 个监督码与信息码元的相关性从本码组扩展到以前若干段时刻的码组，在译码时不仅从此时刻收到的码组中提取译码信息，而且还可从与监督码相关的各码组中提取有用的译码信息。

这种映射是高度结构化的，使得卷积码的译码方法与分组译码所采用的方法完全不同。

可以验证的是在同样复杂度情况下，卷积码的编码增益要大于分组码的编码增益。

对于某个特定的应用，采用分组码还是卷积码哪一种更好则取决于这一应用的具体情况和进行比较时可用的技术。

（一）卷积编码的图形表示卷积码的编码器是由一个有k 个输人位，n 个输出位，且有m 个移位寄存器构成的有限状态的有记忆系统，其原理如图1所示。

图1 卷积码编码器的原理图描述这类时序网络的方法很多，它大致可分为两大类型：解析表示法与图形表示法。

在解析法中又可分为离散卷积法、生成矩阵法、码多项式法等；在图形表示法中也可分为状态图法、树图法和网络图法等。

图2给出的是一个生成编码速率为1／2 卷积码的移位寄存器电路。

输人比特在时钟触发下从左边移人到电路中，每输入一位，分别去两个模2加法器的输出值并复用就得到编码器的输出。

对这一编码，每输入一比特就产生两个输出符号，故编码效率为1／2。

可以看出，每个特定的输入比特不仅影响本时间间隔内的编码器输出，同时还影响紧接着的下两个输入比特时间间隔的编码器输出。

卷积编码由移位寄存器的阶数、输出的数量（即模2加法器的个数）和移位寄存器与模2 加法器间的连接所决定。

实验九 (2,1,5)卷积码编码译码技术

实验九 (2,1,5）卷积码编码译码技术一、实验目的1、掌握(2,1,5）卷积码编码译码技术2、了解纠错编码原理。

二、实验内容1、(2,1,5）卷积码编码。

2、(2,1,5）卷积码译码。

三、预备知识1、纠错编码原理。

2、(2,1,5）卷积码的工作原理。

四、实验原理卷积码是将发送的信息序列通过一个线性的，有限状态的移位寄存器而产生的编码。

通常卷积码的编码器由K级（每级K比特）的移位寄存器和n个线性代数函数发生器（这里是模2加法器）组成。

若以（n,k,m）来描述卷积码，其中k为每次输入到卷积编码器的bit数，n 为每个k元组码字对应的卷积码输出n元组码字，m为编码存储度，也就是卷积编码器的k元组的级数，称m+1= K为编码约束度m称为约束长度。

卷积码将k 元组输入码元编成n元组输出码元，但k和n通常很小，特别适合以串行形式进行传输，时延小。

与分组码不同，卷积码编码生成的n元组元不仅与当前输入的k元组有关，还与前面m-1个输入的k元组有关，编码过程中互相关联的码元个数为n*m。

卷积码的纠错性能随m的增加而增大，而差错率随N的增加而指数下降。

在编码器复杂性相同的情况下，卷积码的性能优于分组码。

编码器随着信息序列不断输入，编码器就不断从一个状态转移到另一个状态并同时输出相应的码序列，所以图3所示状态图可以简单直观的描述编码器的编码过程。

因此通过状态图很容易给出输入信息序列的编码结果，假定输入序列为110100，首先从零状态开始即图示a状态，由于输入信息为“1”，所以下一状态为b并输出“11”，继续输入信息“1”，由图知下一状态为d、输出“01”……其它输入信息依次类推，按照状态转移路径a->b->d->c->b->c->a输出其对应的编码结果“110101001011”。

译码方法⒈代数代数译码是将卷积码的一个编码约束长度的码段看作是[n0(m+1），k0(m+1)]线性分组码，每次根据（m+1）分支长接收数字，对相应的最早的那个分支上的信息数字进行估计，然后向前推进一个分支。

卷积编码设计与仿真实验报告

卷积编码设计与仿真实验报告一、实验目的了解卷积码对信号的纠错性能，掌握维特比译码算法，分析卷积码不同码率下纠错能力的强弱，深刻理解CCSDS标准、信道编译码等相关概念和算法。

二、实验内容1、自己编码实现（2,1,3）卷积码的编译码，对比不同信噪比条件下，是否采用编码对于误码率性能的影响；2、基于MATLAB自带的vitdec函数实现对（2,1,7）卷积码以及2/3、3/4码率删除码的编译码，并对于不同码率抗噪声能力的强弱；3、构造BPSK调制、加性高斯白噪声的传输环境。

三、实验原理卷积码一般表示为(n,k,N)的形式，即将k个信息比特编码为n个比特的码组，N为编码约束长度，说明编码过程中相互约束的码段个数。

卷积码编码后的n个码元不仅与当前组的k个信息比特有关，还与前N-1个输入组的信息比特有关。

编码过程中相互关联的码元有N*n个。

R=k/n是编码效率。

编码效率和约束长度是衡量卷积码的两个重要参数。

典型的卷积码一般选n,k较小，但N值可取较大(>10)，以获得简单而高性能的卷积码。

1、卷积码的编码原理卷积码的编码器一般比较简单，为一个具有k个输入端，n个输出端，m 级移位寄存器的有限状态有记忆系统。

下图所示为(2,1,7)卷积码的编码器。

图1 （2,1,7）卷积码编码器若输入序列为u=(u0u1u2u3……),则对应两个码字序列 C1=(ca0ca1ca2ca3……)和C2=(cb0cb1cb2cb3……)，相应的编码方程可写为 P1=u*C1，P2=u*C2，P=(P1,P2)。

“*”符号表示卷积运算，P1，P2表示编码器的两个冲激响应，即编码器的输出可以由输入序列和编码器的两个冲击响应卷积而得到，故称为卷积码。

这里的冲激响应指：当输入为[1 0 0 0 0 … … ]序列时，所观察到的两个输出序列值。

由于上图N 值为7，故冲激响应至多可持续到第7位，可写为P1=[1 1 1 1 0 0 1]，P2=[1 0 1 1 0 1 1]然后将两个输出端的码字序列合并为一个码字序列为C=(ca0cb0ca1cb1ca2cb2……)。

实验二--卷积码编码及译码实验

实验二--卷积码编码及译码实验实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。

二、实验内容1、观察NRZ基带信号及其卷积编码信号。

2、观察帧同步信号的生成及巴克码的特性。

3、观察卷积编码信号打孔及码速率匹配方法。

4、观察接收端帧同步过程及帧同步信号。

5、观察译码结果并深入理解维特比译码的过程。

6、观察随机差错及突发差错对卷积译码的影响。

三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。

卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k 段，共Nk 个寄存器；一组n 个模2和相加器；一个由n 级组成的输出移位寄存器,对应于每段k 个比特的输入序列,输出n 个比特。

12…k 12…k …12…k12…n 卷积码输出序列信息比特一次移入k 个Nk 级移位寄存器…图17-1 卷积编码器的一般形式由图17-1可以看到，n 个输出比特不仅与当前的k 个输入信息有关,还与前（N -1）k 个信息有关。

通常将N 称为约束长度（有的书中也把约束长度定为nN 或N -1）。

常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。

编码效率定义为：/c R k n (17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。

一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。

（1）图解表示法（2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。

（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。

序列卷积运算实验报告

一、实验目的1. 理解序列卷积的概念和原理。

2. 掌握序列卷积的运算方法，包括连续时间信号卷积和离散时间信号卷积。

3. 通过实验验证序列卷积运算的结果，加深对卷积概念的理解。

4. 学习利用计算机软件进行序列卷积运算的原理和方法。

二、实验原理序列卷积是指两个序列相乘后的和，即一个序列中的每个元素与另一个序列中对应位置的元素相乘后求和。

序列卷积分为连续时间信号卷积和离散时间信号卷积。

1. 连续时间信号卷积：设连续时间信号f(t)和g(t)的卷积为F(t)，则有：F(t) = ∫f(τ)g(t - τ)dτ2. 离散时间信号卷积：设离散时间信号f[n]和g[n]的卷积为F[n]，则有：F[n] = ∑f[k]g[n - k]三、实验环境1. 实验软件：MATLAB R2019b2. 实验设备：计算机四、实验步骤1. 创建连续时间信号和离散时间信号（1）在MATLAB中创建连续时间信号f(t)和g(t)，例如：t = 0:0.01:5; % 时间向量，步长为0.01，范围为0到5f = sin(2pit); % 正弦信号g = cos(2pit); % 余弦信号（2）在MATLAB中创建离散时间信号f[n]和g[n]，例如：n = 0:10; % 取n的范围为0到10f = sin(2pin/10); % 正弦信号g = cos(2pin/10); % 余弦信号2. 计算连续时间信号卷积（1）使用MATLAB的conv函数计算连续时间信号f(t)和g(t)的卷积：F = conv(f, g);（2）绘制卷积结果F(t)的图形：plot(t, F);xlabel('t');ylabel('F(t)');title('连续时间信号卷积');3. 计算离散时间信号卷积（1）使用MATLAB的conv函数计算离散时间信号f[n]和g[n]的卷积：F = conv(f, g);（2）绘制卷积结果F[n]的图形：stem(n, F);xlabel('n');ylabel('F[n]');title('离散时间信号卷积');五、实验结果与分析1. 连续时间信号卷积结果分析：通过绘制连续时间信号卷积结果F(t)的图形，可以看出卷积结果呈现周期性变化，且在t=0处取得最大值。

2019年卷积码实验报告-word范文模板 (18页)

本文部分内容来自网络整理，本司不为其真实性负责，如有异议或侵权请及时联系，本司将立即删除！== 本文为word格式，下载后可方便编辑和修改！ ==卷积码实验报告篇一：卷积码实验报告 (C++)计算机科学与工程系一、实验名称：卷积码二、实验环境软件环境：Windows 201X，Microsoft Visual C++6.0硬件环境：P4，2.4GHz，256内存，IBM-PC及兼容机三、实验目的了解卷积码的编码原理，给定基本监督矩阵，导出一致监督矩阵、基本生成矩阵、一致生成矩阵，能够通过监督矩阵或生成矩阵编出截断码或非截断码。

四、实验过程与实验结果源程序：#include<iostream>#include<string>using namespace std;class JuanjiCode{private:int i,j,t;int n0,k0,r0,m;int **h,**H,**g,**G;//实现编码所需变量int code;string Info_str,Code_str;int total_num,extra_num;public:void Initializing();void Trans_h_to_H();void Trans_h_to_g();void Print_g();void Trans_g_to_G();void Print_G();//编码void Before_Encoding();//编码前的准备int Check(string);void Encoding();};/**********************初始化模块**********************/ void JuanjiCode::Initializing(){cout<<"请输入码字长n0=";cin>>n0;cout<<"请输入信息元个数k0=";cin>>k0;cout<<"请输入关联长度m=";cin>>m;//监督元个数r0=n0-k0;//动态分配存储单元h=new int*[r0];for(i=0;i<r0;i++)h[i]=new int[m*n0];cout<<"请输入（"<<n0<<","<<k0<<","<<m<<"）卷积码的基本监督矩阵h["<<r0<<"]["<<m*n0<<"]："<<endl;for(i=0;i<r0;i++)for(j=0;j<m*n0;j++)cin>>h[i][j];//检测，输出hcout<<"您输入的基本监督矩阵h["<<r0<<"]["<<m*n0<<"]如下：\n"<<endl; for(i=0;i<r0;i++){for(j=0;j<m*n0;j++){cout<<h[i][j];if((j+1)%n0==0)cout<<" ";}cout<<endl;}cout<<endl;//动态分配存储单元H=new int*[m*r0];for(i=0;i<m*r0;i++)H[i]=new int[m*n0];g=new int*[m*k0];for(i=0;i<m*k0;i++)g[i]=new int[n0];G=new int*[m*k0];for(i=0;i<m*k0;i++)G[i]=new int[m*n0];}//由基本监督矩阵h导出一致监督矩阵H并打印输出void JuanjiCode::Trans_h_to_H(){cout<<"该卷积码对应的一致监督矩阵H["<<m*r0<<"]["<<m*n0<<"]如下（未输出部分全为0）：\n"<<endl;for(t=0;t<m;t++){for(i=0;i<r0;i++){for(j=0;j<(t+1)*n0;j++){H[t*r0+i][j]=h[i][(m-t-1)*n0+j];cout<<H[t*r0+i][j];。

卷积码编译码实验报告

厦门理工学院实验报告书课程名称：信息论与编码实验实验名称：卷积码编译码m•个有效的寄存器单元，而输出移位寄存器仅中输入移位寄存器最多只有k起一个并串转换作用。

因此称参量m为卷积吗的记忆长度（段）2、维比特译码原理它的基本思想是把接收到的矢量，和网格图上诸种可能的路径比较，删去距离大的路径，保留距离小的路径，以距离最小路径作为发码的估值五、实验内容在MATLAB环境下卷积码编/解码器的实现。

1、主函数main.mclear;clc;msg = randint(1,20,[0,1])word = encode_conv213(msg)word(1) =~word(1); %信道中存在污染，人为的模拟传输过word(10) =~word(10); %程中的出错码字word(15) =~word(15);word1=wordmsg_1 = decode_conv213(word1)msg-msg_12 、状态积state_machine.mfunction [output,nextState] = state_machine(input,current_state)output(1) = mod(current_state(1)+current_state(3),2);output(2) = mod(input+current_state(2)+current_state(1),2);nextState(1) = current_state(2);nextState(2) = current_state(3);nextState(3) = input;3、汉明距离hamming_distance.mfunction distance = hamming_distance(a,b)temp = a+b;temp = mod(temp,2);distance = sum(temp);4 、213编码程序encode_conv213.mfunction word = encode_conv213(msg)word = zeros(1,length(msg)*2);current = [0 0 0];for i = 1:length(msg)[out,next] = state_machine(msg(i),current);current = next;word(2*i-1) = out(1);word(2*i) = out(2);End5、213维比特译码decode_conv213.mfunction msg = decode_conv213(word)chip = 10; %初始状态选十个信息for i = 1:2^chipM(i,:) = de2bi(i-1,chip); %把所有可能性按二进制输出W(i,:) = encode_conv213(M(i,:));%得到相应的二进制编译后的码字D(i) = hamming_distance(W(i,:),word(1:chip*2));%与出错码字对比得到汉明距end[val,index] = sort(D);%val中存汉明距从小到大排列，index中存对应val数据所在位置ret_msg = zeros(1,length(word)/2); %开辟译出码字的存放空间for i = 1:6%1024种选择6种最小距离，并输出在ret_msg中，最小汉明距存于ret_dis ret_msg(i,1:chip) = M(index(i),:);ret_dis(i) = D(index(i));enditer = (length(word)-chip*2)/2; %剩余要译出的码字个数for i=1:iter %迭代过程for j=1:6msg_temp1 = [ret_msg(j,1:chip+i-1) 0]; %下一状态出“0”msg_temp2 = [ret_msg(j,1:chip+i-1) 1]; %下一状态出“1”word_temp1 = encode_conv213(msg_temp1);%下一状态为“0”时的编码word_temp2 = encode_conv213(msg_temp2);%下一状态为“1”时的编码dis_temp1 = hamming_distance(word_temp1,word(1:chip*2+2*i));dis_temp2 = hamming_distance(word_temp2,word(1:chip*2+2*i)); %算两种汉明距if (dis_temp1<dis_temp2)ret_msg(j,1:chip+i) = msg_temp1;ret_dis(j) = dis_temp1;elseret_msg(j,1:chip+i) = msg_temp2;ret_dis(j) = dis_temp2;%选择较小汉明距的状态储存并输出在ret_msg中，最小汉明距存于ret_disendendend[val,index] = sort(ret_dis); %把最终选择的6种最小汉明距按从小到大排列msg =ret_msg(index(1),:); %选出维特比译码最小的距离所译出的信息六、实验数据记录及分析（包括源程序清单及运行结果）：。

卷积码实验报告

现代编码理论基于MATLAB的卷积码编码及译码仿真姓姓名名：闫嘉川学学号号：1433170所在院系：电子与信息工程学院实验名称：基于MAATLAB的卷积码编码及译码仿真实验目的：卷积码是一种性能优越的信道编码。

它的编码器和译码器都比较容易实现，同时它具有较强的纠错能力。

随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。

本实验简明地介绍了卷积码的编码原理和Viterbi译码原理。

并在SIMULINK模块设计中，完成了对卷积码的编码和译码以及误比特统计整个过程的模块仿真。

最后，通过在仿真过程中分别改变卷积码的重要参数来加深理解卷积码的这些参数对卷积码的误码性能的影响。

经过仿真和实测，并对测试结果作了分析。

实验原理：1、卷积码编码原理卷积码是一种性能优越的信道编码，它的编码器和解码器都比较易于实现，同时还具有较强的纠错能力，这使得它的使用越来越广泛。

卷积码一般表示为(n,k,K)的形式，即将 k个信息比特编码为 n 个比特的码组，K 为编码约束长度，说明编码过程中相互约束的码段个数。

卷积码编码后的 n 各码元不经与当前组的 k 个信息比特有关，还与前 K-1 个输入组的信息比特有关。

编码过程中相互关联的码元有 K*n 个。

R=k/n 是编码效率。

编码效率和约束长度是衡量卷积码的两个重要参数。

典型的卷积码一般选 n,k 较小，K 值可取较大(>10)，但以获得简单而高性能的卷积码。

卷积码的编码描述方式有很多种：冲激响应描述法、生成矩阵描述法、多项式乘积描述法、状态图描述，树图描述，网格图描述等。

2、卷积码Viterbi译码原理卷积码概率译码的基本思路是:以接收码流为基础，逐个计算它与其他所有可能出现的、连续的网格图路径的距离，选出其中可能性最大的一条作为译码估值输出。

概率最大在大多数场合可解释为距离最小，这种最小距离译码体现的正是最大似然的准则。

卷积码的最大似然译码与分组码的最大似然译码在原理上是一样的，但实现方法上略有不同。

卷积计算的实验报告

1. 理解卷积的基本概念和原理；2. 掌握卷积的计算方法；3. 通过MATLAB软件实现卷积运算；4. 分析卷积运算在信号处理中的应用。

二、实验原理卷积是一种线性运算，它描述了两个信号之间的相互作用。

对于两个离散信号x[n]和h[n]，它们的卷积y[n]定义为：y[n] = Σx[k]h[n-k]其中，n和k为离散时间变量，Σ表示求和。

卷积运算具有以下性质：1. 交换律：x[n] h[n] = h[n] x[n]2. 结合律：(x[n] h[n]) g[n] = x[n] (h[n] g[n])3. 分配律：x[n] (h[n] + g[n]) = x[n] h[n] + x[n] g[n]卷积运算在信号处理中具有重要的应用，如信号滤波、系统分析、图像处理等。

三、实验内容1. 熟悉MATLAB软件环境；2. 编写MATLAB程序实现卷积运算；3. 分析卷积运算的结果，验证卷积性质；4. 应用卷积运算解决实际问题。

四、实验器材1. 计算机；2. MATLAB软件；3. 离散信号数据。

1. 创建离散信号数据：在MATLAB中创建两个离散信号x[n]和h[n]，分别代表输入信号和系统响应。

2. 编写卷积程序：使用MATLAB内置函数conv实现卷积运算，计算y[n] = x[n] h[n]。

3. 分析卷积结果：观察卷积运算的结果，验证卷积性质，如交换律、结合律、分配律等。

4. 应用卷积运算解决实际问题：选择一个实际问题，如信号滤波，使用卷积运算进行求解。

六、实验结果与分析1. 卷积运算结果：运行卷积程序，得到卷积运算结果y[n]。

观察y[n]的波形，分析卷积运算对信号的影响。

2. 验证卷积性质：通过比较x[n] h[n]和h[n] x[n]的卷积结果，验证交换律；通过比较(x[n] h[n]) g[n]和x[n] (h[n] g[n])的卷积结果，验证结合律；通过比较x[n] (h[n] + g[n])和x[n] h[n] + x[n] g[n]的卷积结果，验证分配律。

卷积码编译实验报告

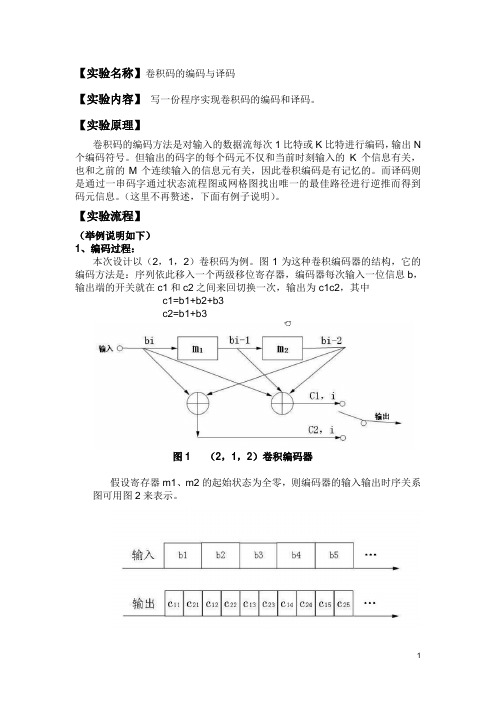
【实验名称】卷积码的编码与译码【实验内容】写一份程序实现卷积码的编码和译码。

【实验原理】卷积码的编码方法是对输入的数据流每次1比特或K比特进行编码，输出N 个编码符号。

但输出的码字的每个码元不仅和当前时刻输入的K个信息有关，也和之前的M个连续输入的信息元有关，因此卷积编码是有记忆的。

而译码则是通过一串码字通过状态流程图或网格图找出唯一的最佳路径进行逆推而得到码元信息。

（这里不再赘述，下面有例子说明）。

【实验流程】（举例说明如下）1、编码过程：本次设计以（2，1，2）卷积码为例。

图1为这种卷积编码器的结构，它的编码方法是：序列依此移入一个两级移位寄存器，编码器每次输入一位信息b，输出端的开关就在c1和c2之间来回切换一次，输出为c1c2，其中c1=b1+b2+b3c2=b1+b3图1（2，1，2）卷积编码器假设寄存器m1、m2的起始状态为全零，则编码器的输入输出时序关系图可用图2来表示。

图2 （2，1，2）卷积编码器输入输出时序如果输入的数据流是101011，则根据上面编码器我们可以得到输出的编码数据流为11 10 00 10 00 01。

.2、解码过程解码是编码的逆过程，了解了编码过程后，理解解码过程的操作就相对容易了。

首先我们根据卷积码的特点，我们采用了两种图解对卷积码进行研究，一种是状态转移图，另一种是网格图。

其状态转移图如图3所示，椭圆里面的数据代表当前状态，箭头方向代表转移的方向，0/11代表输入的码元为0，输出11。

.图3 （2，1，2）卷积编码器状态转移图另一种更为常用的是网格图，横坐标表示时间轴，每一次状态转移利用连接相邻的时间点上的两个状态的有向线段来表示。

图4便是对应的网格图。

图4 （2，1，2）卷积编码器网格图我们解码的思路是由于信息序列和编码序列有着一一对应的关系，而这种关系又唯一对应网格图的一条路径，因此译码就是根据接收序列在网格图上的路径逆推出源码码元信息序列。

但是这样的最大似然译码在现实编码难以实现，因为找出最佳路径用的是逐步比较，把接收序列的第j个分支码字和网格图上相应的两个时刻t1和t2之间进行比较，计算和记录他们的汉明距离等，这样比较分支较多不易实现。

移动通信实验报告卷积编码

西安邮电学院移动通信实验报告实验名称：卷积编码专业：通信工程系班级：通工0713班姓名：***学号：********实验日期：一、实验目的1、对卷积码要掌握2、根据原理框图计算其输出3、掌握气生成矩阵4、熟悉软件实现的算法二、卷积编码原理（2,1,3）卷积编码方框图：（2，1，3）码，n=2 模2加法器个数，k=1 输入维数，m=2 移位寄存器个数，一个转换开关使输出成串行。

对于信息序列()012,,,u u u u =，编码器的两个输出为： (1)(1)(1)(1)012(2)(2)(2)(2)012(,,,)(,,,)c c c c cc c c ==三、编码器输出可以由下式来确定： 01m 01m 01m 01m ∞⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦G G G G G G G G G G G G G 输入U ＝（10111）要求:1）根据图求出G111011111011111011G ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦(1)(2)(1)(2)(1)(2)001122(,,,,,,)c c c c c c c =c =uG2)在给定u的时候计算输出码字C（手工）输出码字为：11 10 00 01 1011101100000011101111101111101111 10 00 01 10 01 113)在给定u的时候计算输出码字C四、 C语言代码如下：#include"stdio.h"#include"iostream.h"void main(){int i;int j;int n;int k;int m;int l;int flag;int num;int b[100];int G[3][6]={{1,1,1,1,1,0},{1,0,1,1,1,1},{1,1,1,0,1,1}};int c[500];cout<<"卷积码(2,1,3)编码方案"<<endl;cout<<"矩阵G:"<<endl;for(i=0;i<=2;i++){for(j=0;j<=5;j++)cout <<G[i][j]<<" ";cout<<endl;}cout <<"input the number of the sequence (<=100):"<<endl;cin >>num;for(i=0;i<num;i++){cin >>b[i];}cout<<"-------------------"<<endl;c[0]=b[0];c[1]=b[0];c[2]=b[0]+b[1];c[3]=b[1];n=3;m=-1;flag=0;i=0;j=0;do{for(k=0;k<=5;k++){m++;for(l=0;l<=1;l++){n++;c[n]=(b[m]*G[i][j]+b[m+1]*G[(i+1)%3][j]+b[m+2]*G[(i+2)%3][j])%2;cout <<"c[n]="<<c[n]<<endl;j=(j+1)%6;if(num<m+2){flag=1;break;}}if(flag==1)break;i=(i+1)%3;}}while(flag==0);for(i=0;i<2*num;i++)cout <<c[i]<<endl;}五、实验分析及心得体会卷积码的应用很广泛。