卷积码(2,1,3)编译码课程设计

合集下载

卷积码（2,1,3）编译码课程设计

卷积码（2,1,3）编译码课程设计电信系08信息工程《信息论与编码课程设计》——卷积码（2,1,3）杨耀武任刚张明航王飞唐军指导老师：梁维海刘晓丽2010.6.25目录目录........................................................................................................ - 2 - （2,1,3）卷积码 .................................................................... - 3 -1 摘要： ............................................................................... - 3 -2 信道编码发展简史： ............................................................... -3 -3 卷积码编码： ........................................................................... - 5 -3.1 编码原理 ........................................................................ - 5 -3.2 编码器的一般结构 ........................................................ - 6 -3.3 编码原理框图 ................................................................ - 7 -3.4 卷积码（2,1,3）状态转移方程 .................................... - 7 -3.5 卷积码（2,1,3）状态转移表 ........................................ - 8 -3.6 卷积码（2,1,3）状态转移图 ........................................ - 9 -4 维特比译码.............................................................................. - 10 -4.1 维比特译码原理 .......................................................... - 11 -4.2 维特比译码器原理图 .................................................. - 13 -5 编程思路.................................................................................. - 13 -6 卷积码编译码程序 ................................................................. - 14 -6.1 主函数main.m ............................................................. - 14 -6.2 状态积state_machine.m .............................................. - 14 -6.3 汉明距离hamming_distance.m ................................... - 15 -6.4 213编码程序encode_conv213.m ................................ - 15 -6.5 213维比特译码decode_conv213.m ............................ - 15 -7 实验结果及分析 ..................................................................... - 17 -8 心得体会.................................................................................. - 17 -9 参考文献.................................................................................. - 18 -（2,1,3）卷积码1 摘要：本文一开始给出了信道编码的发展历史及研究状况，然后详细讨论了（2，1，3）卷积码的编码过程和译码过程，通过状态转移方程和输出方程得出状态转移表和状态转移图，继而得到了编码程序；然后通过维特比译码器研究，总结出了维特比译码算法，最后编译出了译码程序，而且此编码程序和译码程序都在MATLAB中调试，验证了其正确性。

卷积码的设计与实现

湖南文理学院课程设计报告课程名称：通信系统课程设计院部：电气与信息工程学院专业班级：学生姓名：指导教师：完成时间： 2011 年 12 月 29日报告成绩：目录目录 (2)摘要 (3)Abstract (4)一、引言 (5)1.1设计任务及基本要求 (5)1.2设计目的 (6)1.3 设计所用仪器设备.................................................................................. 错误！未定义书签。

二、基本概念 (6)2.1 卷积码的编码原理 (6)2.2 卷积码编码描述 (6)2.3 卷积码译码描述 (6)三、卷积码的编译码原理 (6)3.1卷积码的图形描述 (6)3.1.1 树状图 (8)3.1.2 网格图 (8)3.1.3 状态图 (9)3.2 卷积积码的编码算法 (9)3.3卷积码的Viterbi译码 (10)四、卷积码的仿真及性能分析 (12)4.1 SIMULINK仿真模块 (12)4.2 卷积码的参数对误码率的影响 (13)4.2.1 码率对误码性能的影响 (13)4.2.2 约束长度对误码性能的影响 (15)4.2.3 回溯长度对卷积码性能的影响 (16)4.3 仿真分析 (17)总结 (18)参考文献： (19)摘要卷积码是深度空间通信系统和无线通信系统中常用的一种差错控制编码。

在编码过程中,卷积码充分利用了各码字间的相关性。

在与分组码同样的码率和设备复杂性的条件下,无论从理论上还是从实践上都证明,卷积码的性能都比分组码具有优势。

而且卷积码在实现最佳译码方面也较分组码容易。

因此卷积码广泛应用于卫星通信，CDMA数字移动通信等通信系统，是很有前途的一种编码方式。

对其进行研究有很大的现实意义。

为了解决传统的维特比译码器结构复杂、译码速度慢、消耗资源大的问题，提出一种新型的适用于FPGA 特点，路径存储于译码输出并行工作，同步存储路径矢量和状态矢量的译码器设计方案。

(完整word版)利用VHDL实现(2,1,2)卷积码编码

专业课程设计报告题目：利用VHDL 实现（2,1,2）卷积码编码南昌航空大学信息工程学院20 17 年 6 月 27 日姓名：专业：通信工程班级学号：同组人：指导教师：专业课程设计任务书2016－2017学年第2 学期第17 周－19 周题目利用VHDL实现（2,1,2）卷积码编码内容及要求1.设计一个（2，1，2）卷积码编码器。

2.在FPGA上用VHDL硬件描述语言实现上述编码器和译码器。

3. 通在试验箱上过拨码开关输入信息序列，观察编码输出（即指示灯的亮灭）进度安排第17周：查阅资料，确定方案，完成原理图设计及仿真；第18周：领取元器件、仪器设备，制作、焊接电路，调试电路，完成系统的设计；第19周：检查设计结果、撰写课设报告。

学生姓名：指导时间：第17～19周指导地点：E楼610室任务下达2017年6 月12 日任务完成2017年6月30日考核方式 1.评阅□√ 2.答辩□ 3.实际操作□√ 4.其它□指导教师夏思满系（部）主任徐新河摘要在现代数字通信中，为降低数据传输的误码率，提高通信质量及其可靠性，常在通信中采用纠错编码技术。

其中卷积码就是一种具有较强纠错能力的纠错码。

由于Vitebrbi译码算法比较容易实现，卷积码得到了广泛应用。

本课题简明地介绍了用EDA技术实现卷积码编码器的实现。

卷积码纠错性能常常优于分组码，是一种性能优越的信道编码。

由于码字之间的相关性，其编码器要利用移位寄存器来存储状态。

随着纠错编码理论研究的不断深入，卷积码的实际应用越来越广泛。

卷积码作为通信系统中重要的编码方式，以其良好的编码性能，合理的译码方式，被广泛应用。

本文在阐述卷积码编码器基本工作原理的基础上，给出了（2,1,2）卷积编码器的VHDL设计，在QuartusⅡ环境下进行了波形功能仿真，并下载到EP1C6T144C8N芯片上进行验证，最终实现输入四位序列，编码输出八位通过指示灯显示。

关键词：卷积码QuartusⅡEP1C6T144C8N目录：摘要 (3)目录： (4)第一章系统设计要求 (5)1.1系统设计要求 (5)第二章系统组成与工作原理 (5)2.1系统组成 (5)2.2编码器设计原理 (5)2.2.1结构图法描述编码器 (6)2.2.2（2,1,2）卷积码的状态转移图 (7)第三章编码器设计方案与对比选择 (8)第四章VHDL语言实现及仿真调试 (9)4.1编码器电路设计 (9)4.2VHDL描述编码器 (10)4.2调试 (12)第五章FPGA编程下载 (15)第六章实验心得 (17)参考文献 (18)第一章系统设计要求1.1系统设计要求1.设计一个（2，1，2）卷积码编码器。

MATLAB实现卷积码编译码

本科生毕业论文（设计）题目：MATLAB实现卷积码编译码专业代码：作者姓名：学号：单位：指导教师：年月日目录前言----------------------------------------------------- 1 1. 纠错码基本理论---------------------------------------- 21.1纠错码基本理论 ----------------------------------------------- 21.1.1纠错码概念 ------------------------------------------------- 21.1.2基本原理和性能参数 ----------------------------------------- 21.2几种常用的纠错码 --------------------------------------------- 62. 卷积码的基本理论-------------------------------------- 82.1卷积码介绍 --------------------------------------------------- 82.1.1卷积码的差错控制原理----------------------------------- 82.2卷积码编码原理 ---------------------------------------------- 102.2.1卷积码解析表示法-------------------------------------- 102.2.2卷积码图形表示法-------------------------------------- 112.3卷积码译码原理---------------------------------------------- 152.3.1卷积码三种译码方式------------------------------------ 152.3.2V ITERBI译码原理---------------------------------------- 163. 卷积码编译码及MATLAB仿真---------------------------- 183.1M ATLAB概述-------------------------------------------------- 183.1.1M ATLAB的特点------------------------------------------ 193.1.2M ATLAB工具箱和内容------------------------------------ 193.2卷积码编码及仿真 -------------------------------------------- 203.2.1编码程序 ---------------------------------------------- 203.3信道传输过程仿真-------------------------------------------- 213.4维特比译码程序及仿真 ---------------------------------------- 223.4.1维特比译码算法解析------------------------------------ 233.4.2V ITERBI译码程序--------------------------------------- 253.4.3 VITERBI译码MATLAB仿真----------------------------------- 283.4.4信噪比对卷积码译码性能的影响 -------------------------- 283.4.5码率对卷积码译码性能的影响 ---------------------------- 303.4.6约束长度对卷积码误码性能的影响------------------------ 313.4.7回溯长度对卷积码误码性能的影响 ------------------------ 323.4.8判决方式对卷积码误码性能的影响------------------------ 324. 结论及展望------------------------------------------ 344.1结论-------------------------------------------------------- 344.2展望 -------------------------------------------------------- 355. 结束语----------------------------------------------- 36参考文献------------------------------------------------ 37致谢---------------------------------------------------- 38附录---------------------------------------------------- 39摘要在数字通信系统中，通常采用差错控制编码来提高系统的可靠性。

213卷积码编码和译码

No.15 (2,1,3)卷积码的编码及译码摘要：本报告对于（2,1,3）卷积码原理部分的论述主要参照啜刚教材和课件，编程仿真部分绝对原创，所有的程序都是在Codeblocks 8.02环境下用C语言编写的，编译运行都正常。

完成了卷积码的编码程序，译码程序，因为对于短于3组的卷积码，即2 bit或4 bit纠错是没有意义的，所以对正确的短序列直接译码，对长序列纠错后译码，都能得到正确的译码结果。

含仿真结果和程序源代码。

如果您不使用Codeblocks运行程序，则可能不支持中文输出显示，但是所有的数码输出都是正确的。

一、卷积码编码原理卷积码编码器对输入的数据流每次1bit 或k bit 进行编码，输出n bit 编码符号。

但是输出的分支码字的每个码元不仅于此时可输入的k 个嘻嘻有关，业余前m 个连续式可输入的信息有关，因此编码器应包含m 级寄存器以记录这些信息。

通常卷积码表示为 (n,k,m). 编码率 k r n=当k=1时，卷积码编码器的结构包括一个由m 个串接的寄存器构成的移位寄存器（成为m 级移位寄存器、n 个连接到指定寄存器的模二加法器以及把模二加法器的输出转化为穿行的转换开关。

本报告所讲的（2,1,3）卷积码是最简单的卷积码。

就是2n =，1k =，3m =的卷积码。

每次输入1 bit 输入信息，经过3级移位寄存器，2个连接到指定寄存器的模二加法器，并把加法器输出转化为串行输出。

编码器如题所示。

二、卷积码编码器程序仿真 C 语言编写的仿真程序。

为了简单起见，这里仅仅提供数组长度30 bit 的仿真程序，当然如果需要可以修改数组大小。

为了更精练的实现算法，程序输入模块没有提供非法字符处理过程，如果需要也可以增加相应的功能。

进入程序后，先提示输入数据的长度，请用户输入int （整型数）程序默认用户输入的数据小于30，然后提示输入01数码，读入数码存储与input 数组中，然后运算输出卷积码。

实验二卷积码编码及译码实验

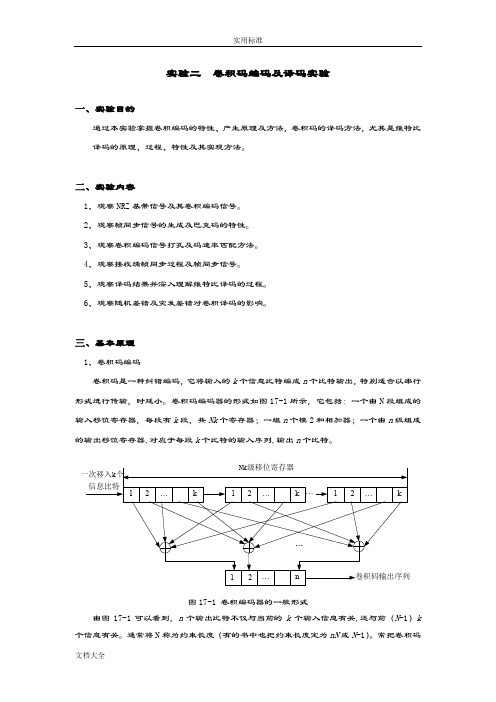
实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。

二、实验内容1、观察NRZ基带信号及其卷积编码信号。

2、观察帧同步信号的生成及巴克码的特性。

3、观察卷积编码信号打孔及码速率匹配方法。

4、观察接收端帧同步过程及帧同步信号。

5、观察译码结果并深入理解维特比译码的过程。

6、观察随机差错及突发差错对卷积译码的影响。

三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。

卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k段，共Nk个寄存器；一组n个模2和相加器；一个由n级组成的输出移位寄存器,对应于每段k个比特的输入序列,输出n个比特。

图17-1 卷积编码器的一般形式由图17-1可以看到，n个输出比特不仅与当前的k个输入信息有关,还与前（N-1）k 个信息有关。

通常将N称为约束长度（有的书中也把约束长度定为nN或N-1）。

常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。

编码效率定义为：/c R k n =(17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。

一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。

（1）图解表示法（2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。

（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。

jj图17-2 （2,1,3）卷积编码器这里我们主要介绍码多项式法。

我们可以用多项式来表示输入序列、输出序列、编码器中移位寄存器与模2和的连接关系。

14卷积码编解码

实验四卷积码的编解码一、实验目的1、掌握卷积码的编解码原理。

2、掌握卷积码的软件仿真方法。

3、掌握卷积码的硬件仿真方法。

4、掌握卷积码的硬件设计方法。

二、预习要求1、掌握卷积码的编解码原理和方法。

2、熟悉matlab 的应用和仿真方法。

3、熟悉Quatus 的应用和FPGA 的开发方法。

三、实验原理1、卷积码编码原理在编码器复杂度相同的情况下，卷积码的性能优于分组码，因此卷积码几乎被应用在所有无线通信的标准之中，如GSM ， IS95和CDMA 2000 的标准中。

卷积码通常记作( n0 ， k0 ， m) ，它将k 0 个信息比特编为n 0 个比特，其编码效率为k0/ n0 ， m 为约束长度。

( n0 ， k0 ， m ) 卷积码可用k0 个输入、n0 个输出、输入存储为m 的线性有限状态移位寄存器及模2 加法计数器来实现。

本实验以（2，1，3）卷积码为例加以说明。

图1就是卷积码编码器的结构。

图1 （2，1，3）卷积码编码器其生成多项式为：21()1G D D D =++； 22()1G D D =+；如图1 所示的(2，1，3)卷积码编码器中，输入移位寄存器用转换开关代替，每输入一个信息比特经编码产生二个输出比特。

假设移位寄存器的初始状态为全0，当第一个输入比特为0时，输出比特为00；若输入比特为１，则输出比特为11。

随着第二个比特输入，第一个比特右移一位，此时输出比特同时受到当前输入比特和前一个输入比特的影响。

第三个比特输入时，第一、二个比特分别右移一位，同时输出二个由这三位移位寄存器存储内容所共同决定的比特。

依次下去就完成了编码过程。

下面是卷积码的网格图表示。

他是比较清楚而又紧凑的描述卷积码的一种方式，它是最常用的描述方式之一。

图2(2，1，3)卷积码的网格图表示2、Viterbi译码原理2k N-种状态，每个节点（即每个状态）有2k条支路引入也有2k条如图2所示，卷积码网格图中共有(1)支路引出。

卷积编译码

实验四：卷积编/译码一．实验目的1．学习卷积编码的方法与码字测量。

2．学习维特比译码方法及译码的测量。

3．观察卷积码的纠错能力。

二．实验仪器1．RZ8621D实验箱一台2．20MHZ双踪示波器一台三．实验电路连接及测量点说明图7-1 用单片机AT89C2051进行卷积编码电路图图7-2 用单片机AT89C2051进行维特比译码电路图差错控制编码的方法很多，卷积码是一种既能纠随机错，又能纠实发错的编码，在同样的传输速率和设备复杂的条件下，性能较优良的一种编码。

卷积码常采用维特比软判决译码，具有较好的纠错功能。

本实验为卷积码的编译码，它是由一片AT80C2051芯片用软件编程方法实现。

其编译码电路框图如下：图中各主要测量点说明如下：TP401—源码序列TP402—卷积码序列TP403—加错或不加错卷积码序列(模拟信道的传输)TP405—卷积码译码输出序列四．实验步骤及内容（一）卷积码编码1．拨线开关介绍。

用拨动开关SW401设置输入信息。

开关拨动至上面为1，下面为0。

拨动开关共9位，左起1-8位为信息位，第九位为状态位。

第九位为“1”表示无错误，第九位为“0”表示有错误。

2．信息码设置。

如上所述，信息码设置共8位，由SW401开关位置决定，例如设置信息为DCH则八位码为1101 1100。

3．信息码观察。

为了示波器上能看到周期性的信息码和编出的卷积码，本机规定在信息位第一位前加一个“1”，在末位加两个“0”。

因此信息码序列变成1 1101 110000，我们称它们为源码序列。

将示波器1通道探头接于TP401（DTAT3），便可看到该序列波形。

4．卷积编码序列手工编码。

根据源码序列和（2.1.3）卷积码编码规秩，写出卷积码编码序列。

上述源码序列的卷积码为1101 1001 0001 1001 110000。

5．无错卷积码编码序列观察。

将拨动开关第九位（状态位）置于“1”表示无错码。

示波器1通道探头接至TP402（DATA1），2通道探头接至TP403（DATA2），观察示波器上显示的波形，看看它是否与上述卷积编码的码型一致。

信道编码课程设计

课程设计三信道编解码（）本章目标掌握数字频带传输系统调制解调的仿真过程掌握数字频带传输系统误码率仿真分析方法5.1实验目的1.使用MATLAB进行卷积码编/译码器的仿真。

2.熟练掌握MATLAB软件、语句。

3.了解卷积码编/译码器的原理、知识。

5.2实验要求1.编写源程序、准备测试数据。

2.在 MATLAB环境下完成程序的编辑、编译、运行，获得程序结果。

如果结果有误，应找出原因，并设法更正之。

5.3 实验原理（一）卷积码编码器1.连接表示卷积码由3个整数n，k，N描述。

/k n也表示编码效率（每编码比特所含的信息量）；但n与线性分组码中的含义不同，不再表示分组或码子长度；N称为约束长度，表示在编码移位寄存器中k元组的级数。

卷积码不同于分组码的一个重要特征就是编码器的记忆性，即卷积码编码过程中产生的n元组，不仅是当前输入k元组的函数，而且N-个输入k元组的函数。

实际情况下，n和k经常取较小的值，而通过N 还是前面1的变化来控制编码的能力和复杂性。

下面以图1中的卷积码编码器为例介绍卷积码编码器。

该图表示一个约束长度3n=，因此，编码效率/1/2k n=。

K=的（2，1）卷积译码器，模2加法器的数目为2在每个输入比特时间上，1位信息比特移入寄存器最左端的一级，同时将寄存器中原有比特均右移一级，接着便交替采样两个模2加法器，得到的码元就是与该输入比特相对应的分支字。

对每一个输入信号比特都重复上述采样过程。

图1卷积码编码器（编码效率1/2，3K =）用于描述反馈移位寄存器实现循环码时所使用的生成多项式也可用户描述卷积码编码器的连接。

应用n 个生成多项式描述编码的移位寄存器与模2加法器的连接方式，n 个生成多项式分别对应n 个模2加法器，每个生成多项式不超过1K -阶。

仍以图1中的编码器为例，用生成多项式1()X g 代表上方连接，2()X g 代表下方连接，则有：2122()1()1X X X X X=++=+g g多项式中的最低阶项对应于寄存器的输入级。

实验二--卷积码编码及译码实验

实验二--卷积码编码及译码实验实验二卷积码编码及译码实验一、实验目的通过本实验掌握卷积编码的特性、产生原理及方法，卷积码的译码方法，尤其是维特比译码的原理、过程、特性及其实现方法。

二、实验内容1、观察NRZ基带信号及其卷积编码信号。

2、观察帧同步信号的生成及巴克码的特性。

3、观察卷积编码信号打孔及码速率匹配方法。

4、观察接收端帧同步过程及帧同步信号。

5、观察译码结果并深入理解维特比译码的过程。

6、观察随机差错及突发差错对卷积译码的影响。

三、基本原理1、卷积码编码卷积码是一种纠错编码，它将输入的k个信息比特编成n个比特输出，特别适合以串行形式进行传输，时延小。

卷积码编码器的形式如图17-1所示，它包括：一个由N段组成的输入移位寄存器，每段有k 段，共Nk 个寄存器；一组n 个模2和相加器；一个由n 级组成的输出移位寄存器,对应于每段k 个比特的输入序列,输出n 个比特。

12…k 12…k …12…k12…n 卷积码输出序列信息比特一次移入k 个Nk 级移位寄存器…图17-1 卷积编码器的一般形式由图17-1可以看到，n 个输出比特不仅与当前的k 个输入信息有关,还与前（N -1）k 个信息有关。

通常将N 称为约束长度（有的书中也把约束长度定为nN 或N -1）。

常把卷积码记为：（n 、k 、N ），当k =1时，N -1就是寄存器的个数。

编码效率定义为：/c R k n (17-1)卷积码的表示方法有图解表示法和解析表示法两种：解析法，它可以用数学公式直接表达，包括离散卷积法、生成矩阵法、码生成多项式法；图解表示法，包括树状图、网络图和状态图（最的图形表达形式）三种。

一般情况下，解析表示法比较适合于描述编码过程，而图形法比较适合于描述译码。

（1）图解表示法（2）解析法下面以（2，1，3）卷积编码器为例详细讲述卷积码的产生原理和表示方法。

（2，1，3）卷积码的约束长度为3，编码速率为1/2，编码器的结构如图17-2所示。

开题报告-卷积码的编码译码的设计与实现

一、选题的依据及意义：（一）选题依据现代通讯技术正以其前所未有的速度发展着，信息传输对于信道的要求越来越高。

为了提高通信的可靠性，就需要对于信道状况进行控制。

增加发送信号功率的做法在实际中经常要受到条件的限制，而采用编程的方法则可以有效的对信道的差错进行控制，因而，在实际中编程控制差错的途径有着广泛的应用。

近年来，随着大规模集成电路的发展，电路实现技术水平获得较大程度的提高，卷积码在众多通信系统和计算机系统中得到了越来越广泛的应用。

对于卷积码的研究，编码器比较简单，模式也很统一。

主要是研究提高卷积码的译码速度和可靠性。

为实现通信的可靠性，基本有两种途径：一是增加输出信号的功率，增加接受端的信噪比；第二种是利用编码的方式对信道干扰误码进行控制。

前一种方法容易受到实际条件的限制，不是任何情况都能使用。

而这个问题可以利用编码来解决，使得实用性增加，成本下降。

译码算法中最重要的Viterbi算法问世以来，软件仿真和实现都得到了迅速的发展。

由于Viterbi 译码算法简单，易于实现，并且能够得到较大的编码增益，因此基于Viterbi 译码算法的卷积码得到了广泛应用。

事实上，Viterbi算法的过程可以看做是在状态机模型基础内逐渐减少概率路径的过程。

因为解码是编码的一个逆序过程，接受信息和初始信息是我们已知的信息，我们无法找到一个逆序的算法来计算所输入的信息。

Viterbi算法是利用重新编码的思想，计算每一条路径可能的概率的大小，用几率最大的那一条路径来模拟编码的过程。

从而译出输入信息比特。

而状态机模型的使用大幅度提升了解码过程中寻找正确路径的速度。

因此viterbi译码算法具有非常实用的意义。

（二）选题意义近年来，信息技术和通信技术的突出成就和急剧发展。

集中表现在个人通信，多媒体信息业务，互联网络应用三个方面。

把信息送给个人，使移动通信走向个人通信，在任何地方和任何状态都可打通电话的移动通信给人们带来了极大的方便。

（2,1,3）卷积码C语言

（2,1,3）卷积码C语言(2,1,3)卷积码C语言#include#include "Conio.h"#define N 7#include "math.h"#include#include#define randomize() srand((unsigned)time(NULL))encode(unsigned int *symbols, /*编码输出*/unsigned int *data, /*编码输入*/unsigned int nbytes, /*nbytes=n/16,n为实际输入码字的数目*/ unsigned int startstate /*定义初始化状态*/){int j;unsigned int input,a1=0,a2=0;for(j=0;j<nbytes;j++)< p="">{ input=*data;data++;*symbols = input^a1^a2;symbols++;*symbols = input^a2;symbols++;a2=a1;a1=input;}return 0;}int trandistance(int m, /*符号m与从state1到state2时输出符号的汉明距离,如果state1无法到state2则输出度量值为100*/ int state1,int state2){int c;int sym,sym1,sym2;sym1=((state2>>1)&1)^(state2&1)^(state1&1);sym2=((state2>>1)&1)^(state1&1);sym=(sym1<<1) | sym2;if ( ((state1&2)>>1)==(state2&1))c=((m&1)^(sym&1))+(((m>> 1)&1)^((sym >> 1)&1));elsec=10000;return(c);}int traninput(int a,int b) /*状态从a到b时输入卷积码的符号*/ {int c;c=((b&2)>>1);return(c);}int tranoutput(int a,int b) /*状态从a到b时卷积码输出的符号*/{int c,s1,s2;s1=(a&1)^((a&2)>>1)^((b&2)>>1);s2=(a&1)^((b&2)>>1);c=(s1<<1)|s2;return(c);}void viterbi(int initialstate, /*定义解码器初始状态*/int *viterbiinput, /*解码器输入码字序列*/int *viterbioutput /*解码器输出码字序列*/){struct sta /*定义网格图中每一点为一个结构体,其元素包括*/ {int met; /*转移到此状态累计的度量值*/int value; /*输入符号 */struct sta *last; /*及指向前一个状态的指针*/struct sta state[4][N];struct sta *g,*head;int i,j,p,q,t,r,u,l;for(i=0;i<4;i++) /* 初始化每个状态的度量值*/for(j=0;j<n;j++)< p="">state[i][j].met=0;for(l=0;l<4;l++){state[l][0].met=trandistance(*viterbiinput,initialstate,l);state[l][0].value=traninput(initialstate,l);state[l][0].last=NULL;}viterbiinput++; /*扩展第一步幸存路径*/for(t=1;t<n;t++)< p="">{for(p=0;p<4;p++){state[p][t].met=state[0][t-1].met+trandistance(*viterbiinput,0,p);state[p][t].value=traninput(0,p);state[p][t].last=&state[0][t-1];for(q=0;q<4;q++){if(state[q][t-1].met+trandistance(*viterbiinput,q,p)state[p][t].last=&state[q][t-1];}}}viterbiinput++;} /*计算出剩余的幸存路径*/r=state[0][N-1].met; /*找出n步后度量值最小的状态，准备回溯路由*/g=&state[0][N-1];for(u=N;u>0;u--) /*向前递归的找出最大似然路径 */{*(viterbioutput+(u-1))=g->value;g=g->last;}/* for(u=0;u<8;u++)*(viterbioutput+u)=state[u][2].met; */ /*此行程序可用于检测第n列的度量值*/}void decode(unsigned int *input, int *output,int n){int viterbiinput[100];int j;for(j=0;j<n+2;j++)< p="">{viterbiinput[j]=(input[j*2]<<1)|input[j*2+1];//printf("%3d",viterbiinput[j]);}viterbi(0,viterbiinput,output);}void main(){unsigned int encodeinput[100],wrong[10]={0,0,0,0,0,0,0,0,0,0},encodeoutput[ 100]; int n=5,i,m,j=0,decodeinput[100],decodeoutput[100];randomize();for(i=0; i<="" p="">encodeinput[i]=rand()%2;encodeinput[n]= encodeinput[n+1]=0;encode(encodeoutput,encodeinput,n+2,0);printf("the input of encoder is :\n");for(i=0;i<="" p="">printf("%2d",encodeinput[i]);printf("\n");printf("the output of encoder is :\n");for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");printf("please input the number of the wrong bit\n"); scanf("%d",&m);printf("please input the positions of the wrong bit(0-9)\n"); for(i=0;i<m;i++)< p="">{ scanf("%d",&wrong[m]);if(encodeoutput[wrong[m]]==0)encodeoutput[wrong[m]]=1;elseencodeoutput[wrong[m]]=0;}printf("the input of decoder is :\n");for(i=0;i<(n+2)*2;i++){printf("%2d",encodeoutput[i]);if(i%20==19)printf("\n");}printf("\n");decode(encodeoutput,decodeoutput,n+2); printf("the output of decoder is :\n");for(i=0;i<n;i++)< p="">printf("%2d",decodeoutput[i]);printf("\n");for(i=0;i<n;i++)< p="">{ if(encodeinput[i]!=decodeoutput[i])j++;}printf("the number of incorrect bit is:%d\n",j); }</n;i++)<></n;i++)<></m;i++)<></n+2;j++)<></n;t++)<></n;j++)<></nbytes;j++)<>。

卷积码译码器设计

卷积码译码器设计1 完成（2，1，4）卷积码编码器设计2 完成相应的维特比译码器设计卷积码编译码基本原理(n,k,m)卷积码中编码后的n个码元不仅与当前段的k个信息有关，而且也与前面段的信息有关，编码过程中相互关联的码元为n(m+1)个。

因此，这N时间内的码元数目n(m+1)通常被称为这种码的约束长度。

卷积码的纠错能力随着m的增加而增大。

因为任何一个发送序列对应于编码器网格图中的一条路径。

似然函数可以用接收序列与编码器网格图中的路径对应输出序列之间的距离来度量，译码的过程即是在网格图中寻找一条与接收序列距离最小的路径。

2个状态，若输入的信息序列的长度是(L+m)K 一般情况下，(n，k，m)卷积码编码器共有km(后mk个码元全为0)，则进入和离开每一状态各有k2条分支在网格图上共有kl2条不同的路径，相应于编码器输出的kl2个码序列。

具体理论见各种书籍介绍。

(2,1,4)卷积器结构及其性质本实验中所涉及的（2，1，4）卷积码编码器结构如图1所示：图1其对应的编码规则为:C[1]=input+D2+D3;C[0]=input+D0+D2+D3;该编码器的viterbi译码的篱笆图如图2所示：0 1 2 3 4 5……图2注：a) 0走实线，1走虚线；b) 在16个状态全部达到之后，状态图中间状态开始循环出现；viterbi卷积器的verilog实现一．设计和测试的总结构设计如图3所示：…图3Test_decode //to test the basic function of this project…….encode //to encode the original 01 code, and output the convoluted codes …….decode //input the codes which are generated by encoder and interfered by //random noise//to compute the length of the two paths linked to node x andx)//generated when a new code comes in (}15'1,0{,...,……..acs0……..acs1……..acs23……..acs_4_7……..acs_8_15……..mod2 //to computer the distance between this inputted code and 00//01 10 or 11, and the result is inputted into acs0,acs1 and//the like.//get the result of acs0, acs1 and the like, compare the//distance of the two paths linked to a single nod and choose//the shorter paths as the path value as the basic value of//the nod when a new code comes in……..path01……..path23……..path_4_7……..path_8_15Notation:1. 因为初始截断树的存在，各结点有着不同的特点，故分成acs0,acs1,acs23,acs_4_7,acs_8_15 5个不同的模块，其实他们功用相同;同样，path01,path23,path_4_7,path_8_15也由此原因得出；二．编码器设计利用上述(2，1,4)卷积编码器的结构生成相应的编码，见encode.v文件用R[3:0]寄存器寄存已输入的码，最多寄存之前输入的4位，所以为4位。

卷积码的编译码原理和仿真论文

卷积码的编译原理及仿真摘要本课程设计主要解决对一个卷积码序列进行维特比(Viterbi)译码输出,并通过Matlab 软件进行设计与仿真，并进行误码率分析。

实验原理QPSK ：QPSK 是英文QuadraturePhaseShiftKeying 的缩略语简称，意为正交相移键控，是一种数字调制方式。

四相相移键控信号简称“QPSK ”。

它分为绝对相移和相对相移两种。

卷积码：又称连环码，是由伊莱亚斯(P.elias)于1955年提出来的一种非分组码。

积码将k 个信息比特编成n 个比特，但k 和n 通常很小，特别适合以串行形式进行传输，时延小。

卷积码是在一个滑动的数据比特序列上进行模2和操作，从而生成一个比特码流。

卷积码和分组码的根本区别在于，它不是把信息序列分组后再进行单独编码，而是由连续输入的信息序列得到连续输出的已编码序列。

卷积码具有误码纠错的能力，首先被引入卫星和太空的通信中。

NASA 标准（2，1，6）卷积码生成多项式为：346134562()1()1g D D D D Dg D D D D D=++++=++++ 其卷积编码器为：输入序列++输出c1输出c2图1.1 K=7，码率为1/2的卷积码编码器维特比译码：采用概率译码的基本思想是：把已接收序列与所有可能的发送序列做比较，选择其中码距最小的一个序列作为发送序列。

如果接收到L 组信息比特，每个符号包括v 个比特。

接收到的Lv 比特序列与2L 条路径进行比较，汉明距离最近的那一条路径被选择为最有可能被传输的路劲。

当L 较大时，使得译码器难以实现。

维特比算法则对上述概率译码做了简化，以至成为了一种实用化的概率算法。

它并不是在网格图上一次比较所有可能的2kL 条路径(序列)，而是接收一段，计算和比较一段，选择一段最大似然可能的码段，从而达到整个码序列是一个最大似然值得序列。

下面以图2.1的(2，1，3)卷积码编码器所编出的码为例，来说明维特比解码的方法和运作过程。

卷积码编译实验报告

【实验名称】卷积码的编码与译码【实验内容】写一份程序实现卷积码的编码和译码。

【实验原理】卷积码的编码方法是对输入的数据流每次1比特或K比特进行编码，输出N 个编码符号。

但输出的码字的每个码元不仅和当前时刻输入的K个信息有关，也和之前的M个连续输入的信息元有关，因此卷积编码是有记忆的。

而译码则是通过一串码字通过状态流程图或网格图找出唯一的最佳路径进行逆推而得到码元信息。

（这里不再赘述，下面有例子说明）。

【实验流程】（举例说明如下）1、编码过程：本次设计以（2，1，2）卷积码为例。

图1为这种卷积编码器的结构，它的编码方法是：序列依此移入一个两级移位寄存器，编码器每次输入一位信息b，输出端的开关就在c1和c2之间来回切换一次，输出为c1c2，其中c1=b1+b2+b3c2=b1+b3图1（2，1，2）卷积编码器假设寄存器m1、m2的起始状态为全零，则编码器的输入输出时序关系图可用图2来表示。

图2 （2，1，2）卷积编码器输入输出时序如果输入的数据流是101011，则根据上面编码器我们可以得到输出的编码数据流为11 10 00 10 00 01。

.2、解码过程解码是编码的逆过程，了解了编码过程后，理解解码过程的操作就相对容易了。

首先我们根据卷积码的特点，我们采用了两种图解对卷积码进行研究，一种是状态转移图，另一种是网格图。

其状态转移图如图3所示，椭圆里面的数据代表当前状态，箭头方向代表转移的方向，0/11代表输入的码元为0，输出11。

.图3 （2，1，2）卷积编码器状态转移图另一种更为常用的是网格图，横坐标表示时间轴，每一次状态转移利用连接相邻的时间点上的两个状态的有向线段来表示。

图4便是对应的网格图。

图4 （2，1，2）卷积编码器网格图我们解码的思路是由于信息序列和编码序列有着一一对应的关系，而这种关系又唯一对应网格图的一条路径，因此译码就是根据接收序列在网格图上的路径逆推出源码码元信息序列。

但是这样的最大似然译码在现实编码难以实现，因为找出最佳路径用的是逐步比较，把接收序列的第j个分支码字和网格图上相应的两个时刻t1和t2之间进行比较，计算和记录他们的汉明距离等，这样比较分支较多不易实现。

(2,1,2)卷积码的译码设计(0)

前言卷积码是由伊莱亚斯(Elias)于1954 年首先提出来的。

它充分利用了各组之间的相关性，本组的信息元不但决定本组的监督元，而且也参与决定以后若干组的监督元。

同时在译码过程中，不但从该时刻所收到的码组中提取译码信息，而且还利用以后若干时刻内所收到的码组来提取有关信息。

无论从理论上还是实际上均已证明其性能优于线性分组码。

近年来众多有关卷积码研究结果表明，卷积码最有希望实现香农信道编码定理。

但卷积码在译码理论及实际应用较为复杂，这些缺点限制了其进一步发展和应用。

维特比译码算法由维特比（Viterbi）1964年提出，算法实质是最大似然译码，但它利用了编码网格图的特殊结构，在网格图中选择一条路径，使相应的译码序列与接收到的序列之间的汉明距(即量度)最小的一种最大似然译码方法，从而大大降低了计算的复杂性。

目前，第三代移动通信系统(3G) 在我国已经开始紧锣密鼓地实施，它带来的高速度、高品质的无线通信服务，将使我们领略到信息技术的无穷魅力。

信道纠错编码技术作为保证信息可靠传输的技术，在3G各系统中广泛采用，并且我们现在所使用的第二代移动通信系统，如GSM、 CDMA 通信系统，还有卫星与空间通信系统广泛采用了卷积码信道编、译码技术。

本次设计将以（2，1，2）卷积码为例，通过单片机，实现卷积码的译码，借助RS232完成单片机与单片机、单片机与计算机的串口通信，借助7279完成键盘扫描和数码管显示。

第一章系统组成及工作原理本次设计的（2，1，2）卷积码的译码由89C52单片机为工具，接收来自另一单片机或计算机的编码信息，通过7279的键盘扫描和数码管显示功能可以方便地观察到单片机接收的信息和译码结果。

其系统框图如下图1－1所示。

MAX232芯片能实现EIA-RS-232C的正负电压与TTL的高低电平之间的转换，通过它能够方便实现单片机与单片机、单片机与计算机间的串口通信。

HD7279是一片具有串行接口的, 可同时驱动8位共阴极数码管的智能显示驱动芯片, 该芯片同时还可连接多达64键的键盘矩阵, 单片即可独立完成显示、键盘接口的全部功能。

卷积码(2,1,3)编译码课程设计