CRC编码实验实验报告
CRC检验码实验报告
CRC 检验码实验报告一 实验题目(1) 实现CRC 的校验过程,生成多项式为CRC12,要求设计简单的图形界面。
(2) 完成内容包括:输入发送数据序列,根据生成多项式完成余数计算,输出带有校验码的发送数据序列。
模拟正确发送、出现离散的一位错、离散的两位错以及长度小于12的突发错,给出相应的输出。
二 实验工具及环境实验语言:JAVA 实验工具:eclipese 三 实验思路 (1) 实验原理CRC 校验码的编码方法是用待发送的二进制数据t(x)移位生成多项式位数,其结果r(x)除以生成 多项式g(x),将最后的余数与上r(x)作为CRC 校验码。
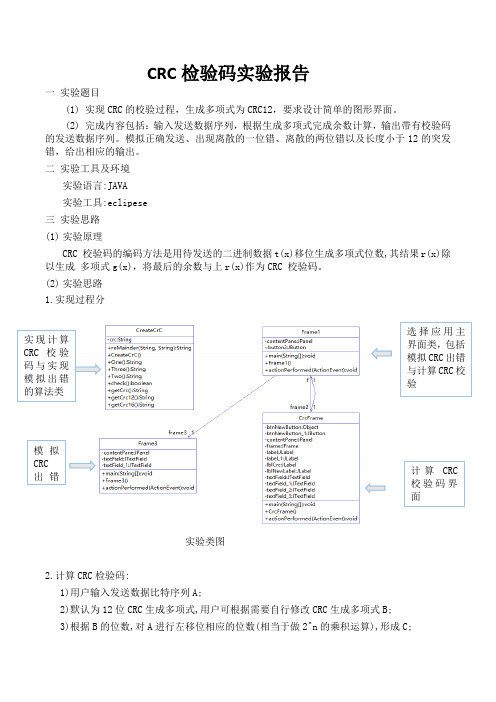
(2) 实验思路 1.实现过程分实验类图2.计算CRC 检验码:1)用户输入发送数据比特序列A;2)默认为12位CRC 生成多项式,用户可根据需要自行修改CRC 生成多项式B; 3)根据B 的位数,对A 进行左移位相应的位数(相当于做2^n 的乘积运算),形成C;实现计算CRC 校验码与实现模拟出错的算法类选择应用主界面类,包括模拟CRC 出错与计算CRC 校验计算CRC 校验码界面模拟CRC 出错4)对生成多项式和发送数据流进行异或运算,计算余数D;5)余数D+C就形成了带有CRC检验码的数据比特序列。
3. CRC检验码出错模拟:用户输入原CRC检验码的数据比特序列A,选择待模拟的错误类型;程序给出相应模拟出错结果。
四实验结论1.优点1)实现了多种生成多项式CRC检验码的生成与检验2)检验与计算分开,功能明确3)可对用户输入数据进行检查,动态交互2.缺点1)在检验CRC校验码时,只能有用户手动输入数据,不能粘贴复制,比较麻烦2)页面布局与外观有待提高。
ADIJ链路层实验——基于CRC编码的检错程序的实现实验报告

实验九、基于CRC编码的检错程序的实现实验报告序号:姓名:学号:成绩指导老师:一、实验目的1、通过实验,掌握CRC编码和解码的原理。
2、掌握基于CRC编码的差错检测技术。
二、实验指导现在计算机网络广泛采用的差错检测技术是基于CRC(cyclic redundancy check)循环冗余检测编码,CRC也称为多项式编码(polynomial code),CRC算法非常容易用硬件实现。
CRC编码操作如下:对给定的数据D,发送者选择r个附加位,追加到D的末尾,形成d+r位的新位型,该位型正好能被G模2除尽。
其中,G称为生成器。
CRC编码算法实现:1、选择生成多项式G,其最高次方为r,即r+1位的二进制位串2、计算D·2r, 即在数据D后面补r个0,构成d+r位的位串3、按模2除法求(D·2r/G)的余数R,即:4、从D·2r中模2减去R,得到新的数据T,即加了CRC的帧三、实验要求1、设置一个d位的数据D,r+1位的多项式G,生成CRC码,并把此CRC码作为数据帧进行传送。
2、编写两个子程序,分别实现CRC编码和CRC解码,在主函数中对子程序进行调用。
解码子程序应能根据解码情况判断出接收到的数据帧是否出错,并给出提示。
3、要求分别以正确和错误的数据来检验此检错程序。
4、将编写程序的源代码加必要注释和程序运行结果一起填入实验报告中。
提示:1、编写程序时数据直接用二进制数,可能用到位操作符^(异或)和<<(左移)。
2、在设置错误的编码时,错误位数最好不要超过r+1位。
四、程序代码:#include <stdio.h>int crc(int D[],int G[], int x,int n) //该函数用于进行异或运算{int i,j,k,result;printf("以下输出异或运算的全过程,最后一行为余数\n");for (k=0;k<=x-1;k++) //x=d+rprintf(" %d",D[k]); //输出补后的数for (i=0;i<=x-n+1;i++) //输出异或运算的全过程{if (D[i]==1) //当首位为1时进行异或{for (j=0;j<=n-1;j++) //n=g{if (D[i+j]==G[j]) //G[]的第j+1个数和D[]的第i+j+1个数相同时D[i+j]=0; //异或运算,相同为,不同为else D[i+j]=1;}printf("\n"); //输出每次异或后的结果for (k=0;k<=x-1;k++)printf(" %d",D[k]); //输出最后余数}}for (k=0;k<=x-1;k++)result=D[k];return result;}void main (){int d,g,n,m,result;g;int D[100],M[100],G[100],i,j; //D[]余数,M[]被除数printf("请输入生成器长度=");scanf("%d",&g);printf("\n请输入生成器为(空格输入):\n");for (j=0;j<=g-1;j++) //将输入的除数按位存储在数组G[j]scanf("%d",&G[j]);printf("请选择你要进行的操作:1,CRC编码2,CRC解码:\n");scanf("%d",&n);if(n==1){printf("请输入原始数据长度=");scanf("%d",&d);printf("\n请输入原始数据为(空格输入):\n");for (i=0;i<=d-1;i++) //将输入的数据按位存储进数组M[i]scanf("%d",&M[i]);for (i=0;i<=d-1;i++)D[i]=M[i]; //将数组M[i]中的数据赋值给D[i]for (i=d;i<=d+g-2;i++) //将数据左移r位,后面补r+1个零D[i]=0;crc(D,G,d+g-1,g); //调用函数,进行异或运算for (i=0;i<=d-1;i++)D[i]=D[i]+M[i]; //将g-1位的余数加到数据后面,即为发送方发送的完整数据printf ("\n发送方发送的数据为:");for (i=0;i<=d+g-2;i++)printf ("%d",D[i]);printf ("\n");}if(n==2){printf("请输入你要进行校验的数据长度=");scanf("%d",&m);printf("请输入要进行校验的数据为(空格输入):\n");for (i=0;i<=m-1;i++)scanf("%d",&M[i]);result=crc(M,G,m,g); //调用函数,进行异或运算,并返回结果if(result==0)printf("\n数据完全正确\n");if(result!=0)printf("\n数据有错误\n");}}五、运行结果:测试数据:生成器:110原始数据:10101生成的发送数据为:1010101当要校验数据为1010101时数据正确。
CRC实验报告

沈阳工程学院学生实验报告实验室名称:信息工程系软件实验室实验课程名称:计算机网络实验项目名称:CRC校验编程实现班级:软本094姓名:王诗娟陈志银刘云峰学号:02、10、14实验日期:2012年03月26日实验台编号:15 指导教师:郑秀颖批阅教师(签字):成绩:一.实验目的掌握并理解CRC校验算法,编程实现CRC。
二.实验内容1.设计CRC校验算法。
.2.编程实现CRC校验。
三.实验前的准备1.复习、熟悉CRC校验算法。
2.编写好程序,上机调试。
四.实验要求及实验软硬件环境【基本要求】1.掌握并理解CRC校验算法。
2.编程实现CRC。
3.完成实验报告。
【实验组织方式】小组实验。
【实验条件】配置有java运行环境的微机一台,MyEclipse。
五.实验步骤1.掌握并理解CRC校验算法。
2.设计发送界面。
3.编程实现CRC校验。
4.设计接收界面。
5.调试并实现程序。
6.参加答辩,并撰写实验报告。
六.主要程序部分(Java语言实现)1.发送端主界面MainFrame.java 的主要代码如下所示。
jb.addActionListener(new ActionListener(){public void actionPerformed(ActionEvent e) {String input1 = new String(jtf1.getText());String input2 = new String(jtf2.getText());if("".equals(input1) || "".equals(input2) || input1 == null || input2 == null){JOptionPane.showMessageDialog(jf, "请输入。
", "错误", JOptionPane.ERROR_MESSAGE);}else{ if(dealer.legal_binary(input1)){if(dealer.legal_g_p(input2)){String checkSum = dealer.get_cheksum(input1, input2);String endResult = new String(input1+checkSum);jtf3.setText(checkSum);jtf4.setText(endResult);try {String tem =endResult + "." +input2;fo.inputFile(tem);} catch (Exception e1) {e1.printStackTrace();}}else{JOptionPane.showMessageDialog(jf, "输入的生成多项式不正确", "错误", JOptionPane.ERROR_MESSAGE);}}else{JOptionPane.showMessageDialog(jf, "输入不正确", "错误", JOptionPane.ERROR_MESSAGE);} }}});jb2.addActionListener(new ActionListener(){public void actionPerformed(ActionEvent arg0) {jp1.setVisible(false);GetMessage gm = new GetMessage();String str="";try {str = fo.outputFile();} catch (Exception e) {e.printStackTrace();}String L="";String R="";int k= str.length();for (int i = 0; i < str.length(); i++){if (str.substring(i, i + 1).equals(".")){L=str.substring(0,i).trim();R=str.substring(i+1,k).trim();}}gm.jtf1.setText(L);gm.jtf2.setText(R);String res = dealer. get_cheksum (str, R);gm.jtf3.setText(res);gm.setVisible(true);jf.add(gm);}});2.对发送和接收的处理类Dealer.java的主要代码如下所示。
循环冗余校验编解码电路设计实验报告

循环冗余校验编解码电路设计实验报告一、引言循环冗余校验(CRC)是一种常用于检测和校正数据传输错误的技术。
在通信领域,CRC编解码电路是一种重要的硬件设计,用于验证数据传输的准确性。
本实验旨在通过设计循环冗余校验编解码电路,探索其工作原理和实际应用。
二、背景知识1.循环冗余校验原理循环冗余校验利用多项式除法的性质来实现数据校验。
发送端将数据和校验值进行运算得到余数,并将余数附加到数据后一起发送。
接收端通过对接收到的数据进行除法运算,得到的余数判断数据是否正确。
2.CRC编码过程–发送端:将数据进行扩展,加上用于校验的位数,并使用预定的生成多项式进行除法运算得到余数,将余数附加在数据后面发送出去。
–接收端:接收到数据后,再次进行除法运算,得到的余数为0则说明数据传输正确,否则说明存在错误。
3.CRC解码过程–发送端:发送数据和余数。
–接收端:接收数据和余数,使用与发送端一样的生成多项式进行除法运算,得到的余数判断数据是否正确。
三、实验设计与实现1. 实验目的了解循环冗余校验的原理,并通过设计和实现循环冗余校验编解码电路加深对其理解。
2. 实验器材与材料•FPGA开发板:用于搭建实验电路•Vivado软件:用于设计和验证电路•扁平电缆:用于连接FPGA开发板和外部设备3. 实验步骤1.了解所用的生成多项式,确定校验位数和除法运算方式。
2.使用Vivado软件创建工程,选择适合的FPGA开发板型号。
3.设计循环冗余校验编码模块,并使用Verilog语言进行描述。
4.设计循环冗余校验解码模块,并使用Verilog语言进行描述。
5.设计测试模块,用于生成测试数据和验证结果。
6.进行RTL级仿真,验证电路设计的正确性。
7.将设计文件综合、实现和下载到FPGA开发板。
8.在FPGA开发板上测试编解码电路的功能和性能。
9.分析实验结果,总结经验和教训。
四、实验结果与分析1. RTL级仿真结果在RTL级仿真中,我们生成了不同的输入数据,并通过编解码电路计算得到校验值和余数。
实验九基于CRC编码的检错程序的实现

软件学院实验报告课程:计算机网络原理实验任课教师:姓名:学号:专业:成绩:实验九、链路层实验——基于CRC编码的检错程序的实现实验报告一、实验目的1、通过实验,掌握CRC编码和解码的原理。
2、掌握基于CRC编码的差错检测技术。
二、实验指导现在计算机网络广泛采用的差错检测技术是基于CRC(cyclic redundancy check)循环冗余检测编码,CRC也称为多项式编码(polynomial code),CRC算法非常容易用硬件实现。
CRC编码操作如下:对给定的数据D,发送者选择r个附加位,追加到D的末尾,形成d+r位的新位型,该位型正好能被G模2除尽。
其中,G称为生成器。
CRC编码算法实现:1、选择生成多项式G,其最高次方为r,即r+1位的二进制位串2、计算D·2r, 即在数据D后面补r个0,构成d+r位的位串3、按模2除法求(D·2r/G)的余数R,即:4、从D·2r中模2减去R,得到新的数据T,即加了CRC的帧三、实验要求1、设置一个d位的数据D,r+1位的多项式G,生成CRC码,并把此CRC码作为数据帧进行传送。
2、编写两个子程序,分别实现CRC编码和CRC解码,在主函数中对子程序进行调用。
解码子程序应能根据解码情况判断出接收到的数据帧是否出错,并给出提示。
3、要求分别以正确和错误的数据来检验此检错程序。
4、将编写程序的源代码加必要注释和程序运行结果一起填入实验报告中。
提示:1、编写程序时数据直接用二进制数,可能用到位操作符^(异或)和<<(左移)。
2、在设置错误的编码时,错误位数最好不要超过r+1位。
源代码:#include<stdio.h>void crc(int A[],int G[], int x,int n)//编码程序{int i,j,k;printf("\n\t\t");for (k=0;k<=x-1;k++)printf(" %d",A[k]); //输出补后的数for (i=0;i<=x-n+1;i++){if (A[i]==1) //当首位为时进行异或{for (j=0;j<=n-1;j++){if (A[i+j]==G[j])A[i+j]=0; //异或运算,相同为,不同为else A[i+j]=1;}printf("\n\t\t"); //输出每次异或后的结果for (k=0;k<=x-1;k++)printf(" %d",A[k]); //输出余数}}}#include<stdio.h>void cr(int M[],int A[],int m,int n)//检验解码程序{int k=0,i;for(i=0;i<=m-1;i++){if(M[i]!=A[i]){printf("第%d位出现错误\n",i+1);k++;}}if(k==0){printf("数据完全正确\n");}}int main (){int m,n;int A[20],M[20],G[20],i,j;printf("请输入M[x]的长度m=");scanf("%d",&m);printf("请输入G[x]的长度n=");scanf("%d",&n);printf("\n请输入M[x]=\n");for (i=0;i<=m-1;i++)scanf("%d",&M[i]);printf("\n请输入G[n]=\n");for (j=0;j<=n-1;j++)scanf("%d",&G[j]);for (i=0;i<=m-1;i++)A[i]=M[i];for (i=m;i<=m+n-2;i++)A[i]=0; //对被除数进行补crc(A,G,m+n-1,n); //调用异或函数for (i=0;i<=m-1;i++)A[i]=A[i]+M[i];printf ("\n\n结果为:");for (i=0;i<=m+n-2;i++)printf ("%d",A[i]);printf ("\n");printf("\n请输入你想要进行解码的数据:\n");for (i=0;i<=m-1;i++)scanf("%d",&M[i]);cr(M,A,m,n);}编码:解码:数据出错:。
CRC实验报告 2011-06-16

数电实验报告题目 CRC校验原理仿真实验班级 29001040班姓名刘奎学号 2903003015 时间 2011年5月25日地点英才实验学院创新实验室指导教师李尚泽摘要本实验利用循环校验码(CRC)校验原理通过对通信系统发射端的原始数据生成CRC校验位,并按照RS-232的传输协议组帧,在传输过程中加入随机的噪声,在接收端对RS-232传输帧格式进行解析,并完成CRC校验。
整个过程在Modelsim上仿真实现。
关键词CRC校验仿真目录第一章实验原理与任务 (2)第二章设计思路、方法及方案 (3)第三章 FPGA模块程序设计与仿真 (3)第四章结束语 (4)附录 (4)第一章 实验任务与原理1、任务指标利用VHDL 完成16比特CRC 校验程序的设计,并能利用modelsim 仿真得到电路的时序波形。
2、实验要求在了解CRC 校验原理的前提下,在发送端对原始数据生成CRC 校验位,并按照RS-232的传输协议组帧,在接收端对RS-232传输帧格式进行解析,并完成CRC 校验。
整个过程在Modelsim 上仿真实现。
3、原理阐述循环校验码(CRC )是数据通信领域中常用的一种差错校验码,其特点是信息字段和校验字段的长度可以任意选定。
生成CRC 校验码的基本原理:任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’或‘1’的多项式一一对应,例如‘1010111’对应的多项式为6421x x x x ++++。
CRC 码集选择的原则:若设码字长度为N ,信息字段长度为K ,校验字段长度为R ,则N=K+R ;对于CRC 码集中的任一码字,存在且仅存在一个R 次多项式g(x)使得:()()()()()RV x A x g x x m x r x ==+其中m(x)为K 次信息多项式,r(x)为R-1次校验多项式,g(x)称为生成多项式。
V(x)为发送的信息加码字多项式。
2012()...RR g x g g x g x g x=++++发送方通过指定的g(x)产生CRC 码字,接收方则通过g(x)来验证CRC 码字,若传输码字多项式V(x)能除尽g(x),则传输正确。
计算机网络实验 CRC校验

XXXXXXXX大学(计算机网络)实验报告实验名称 CRC校验实验时间年月日专业姓名学号预习操作座位号教师签名总评一、实验目的:掌握CRC冗余码校验的基本原理,编程实现CRC冗余码校验。
二、实验原理:1、循环校验码(CRC码):是数据通信领域中最常用的一种差错校验码,其特征是信息字段和校验字段的长度可以任意选定。
2、生成CRC码的基本原理:任意一个由二进制位串组成的代码都可以和一个系数仅为‘0’和‘1’取值的多项式一一对应。
例如:代码1010111对应的多项式为x6+x4+x2+x+1,而多项式为x5+x3+x2+x+1对应的代码101111。
3、CRC码集选择的原则:若设码字长度为N,信息字段为K位,校验字段为R位(N=K+R),则对于CRC码集中的任一码字,存在且仅存在一个R次多项式g(x),使得V(x)=A(x)g(x)=x R m(x)+r(x);其中:m(x)为K次信息多项式,r(x)为R-1次校验多项式,g(x)称为生成多项式:g(x)=g0+g1x+g2x2+...+g(R-1)x(R-1)+g R x R发送方通过指定的g(x)产生CRC码字,接收方则通过该g(x)来验证收到的CRC码字。
4、CRC校验码软件生成方法:借助于多项式除法,其余数为校验字段。
发送方:发出的传输字段为: 1 0 1 1 0 0 1 1 0 10信息字段校验字段接收方:使用相同的生成码进行校验:接收到的字段/生成码(二进制除法)如果能够除尽,则正确,三、实验内容:1.设置CRC寄存器,并给其赋值FFFF(hex)。
2.将数据的第一个8-bit字符与16位CRC寄存器的低8位进行异或,并把结果存入CRC寄存器。
3.CRC寄存器向右移一位,MSB(最高位)补零,移出并检查LSB(最低位)。
4.如果LSB为0,重复第三步;若LSB为1,CRC寄存器与多项式码相异或。
5.重复第3与第4步直到8次移位全部完成。
此时一个8-bit数据处理完毕。
CRC校验码编码实验

实验四CRC校验码编码实验班级:电子C073 姓名:赵宣学号:075584一、实验目的1、复习C++语言基本编写方法,熟悉面向对象编程方法。
2、学习CRC编码基本流程, 学会调试循环冗余校验码编码程序。
3、根据给出资料,掌握CRC校验码的编码原理,重点掌握按字节(Byte)编码方法二、实验内容与原理(一)实验原理:1. CRC 校验码介绍CRC 校验的基本思想是利用线性编码理论,在发送端根据要传送的k 位二进制码序列,以一定的规则产生一个校验用的监督码(CRC 码)r 位,并附在信息后边,构成一个新的二进制码序列数共 (k+r) 位,最后发送出去。
在接收端,则根据信息码和CRC 码之间所遵循的规则进行检验,以确定传送中是否出错。
16 位的CRC 码产生的规则是先将要发送的二进制序列数左移16 位(乘以216)后,再除以一个多项式,最后所得到的余数既是CRC 码。
求CRC 码所采用模2 加减运算法则,既是不带进位和借位的按位加减,这种加减运算实际上就是逻辑上的异或运算,加法和减法等价,乘法和除法运算与普通代数式的乘除法运算是一样,符合同样的规律。
接收方将接收到的二进制序列数(包括信息码和CRC 码)除以多项式,如果余数为0,则说明传输中无错误发生,否则说明传输有误。
2.按位计算CRC一个二进制序列数可以表示为求此二进制序列数的CRC 码时,先乘以216后(左移16位),再除以多项式G(X) ,所得的余数就是所要求的CRC 码。
可以设:其中Q n (X) 为整数, R n (X) 为16位二进制余数,将上式代入前式得:再设:其中Qn-1(X) 为整数, Rn-1(X) 为16位二进制余数,继续代入前式,多次迭代得到:根据CRC 的定义,很显然,十六位二进制数R0(X) 即是要求的CRC 码。
3.按字节计算CRC对于一个二进制序列数可以按字节表示为下式,其中Bn(X) 为一个字节(共8位):求此二进制序列数的CRC码时,先乘以216后(左移16位),再除以多项式G(X),所得的余数即是所要求的CRC 码。
循环冗余校验编解码电路设计实验报告

循环冗余校验编解码电路设计实验报告在数字通信中,循环冗余校验(CRC)是一种常用的错误检测和纠正技术,它通过在数据包中添加校验位来检测数据传输过程中的错误。
为了更好地理解和应用CRC技术,我们进行了循环冗余校验编解码电路设计的实验。
我们需要了解CRC的基本原理。
CRC是通过对数据进行除法运算,得到余数然后将余数添加到数据包中作为校验位。
接收端在接收到数据包后,再次进行除法运算,如果余数为0,则说明数据传输正确,否则说明数据传输过程中出现了错误。
在实验中,我们首先设计了CRC编码电路。
编码电路的主要功能是对输入的数据进行除法运算,然后将余数作为校验位添加到数据包中。
我们使用了Verilog HDL语言来实现CRC编码电路,在编码过程中需要考虑多项式的选取、除法运算的实现等问题。
接下来,我们设计了CRC解码电路。
解码电路的主要功能是对接收到的数据包进行除法运算,然后判断余数是否为0,从而确定数据传输是否正确。
同样,我们使用Verilog HDL语言来实现CRC解码电路,需要考虑多项式的选取、除法运算的实现等方面。
在实验中,我们还需要对设计的CRC编解码电路进行仿真和验证。
通过仿真可以检查电路的功能是否符合设计要求,验证其在不同情况下的正确性和稳定性。
我们可以使用仿真工具如ModelSim等来进行仿真,观察电路的输入输出情况,验证其正确性。
我们需要在实际硬件平台上实现设计的CRC编解码电路,并进行性能测试。
通过性能测试可以评估电路在实际应用中的性能表现,包括速度、准确性等方面。
我们可以使用FPGA等硬件平台来实现CRC编解码电路,并进行性能测试,验证其在实际应用中的可靠性。
总的来说,通过本次实验,我们深入了解了循环冗余校验的原理和实现方法,掌握了CRC编解码电路的设计与实现技术。
这将有助于我们在数字通信领域中更好地应用CRC技术,提高数据传输的可靠性和安全性。
希望通过不懈的努力和实践,我们能够进一步完善和优化CRC编解码电路,为数字通信技术的发展做出贡献。
循环冗余校验编解码电路设计实验报告

循环冗余校验编解码电路设计实验报告在数字通信领域中,循环冗余校验(CRC)是一种常用的错误检测和纠正技术。
通过在数据中添加冗余校验位,接收方可以根据这些校验位检测出数据传输过程中是否发生了错误,并且还可以纠正部分错误。
本实验旨在设计一个循环冗余校验编解码电路,以验证CRC技术的可靠性和有效性。
一、实验背景循环冗余校验是一种基于多项式运算的错误检测和纠正技术,广泛应用于数据传输和存储系统中。
其原理是将数据视为多项式,并通过除法运算生成校验位,接收方根据收到的数据和校验位再次进行除法运算,以验证数据的完整性。
CRC技术具有高效性和低成本的优点,因此在现代通信系统中得到了广泛应用。
二、实验设计设计一个基于CRC技术的编解码电路,包括数据发送端和数据接收端两部分。
在发送端,将数据和校验位进行拼接,并通过CRC生成多项式进行运算,得到最终的发送数据。
在接收端,接收到数据后,同样进行CRC多项式运算,以验证数据的准确性,并在有错误时进行纠正。
通过实验验证CRC技术在数据传输中的可靠性和有效性。
三、实验步骤1. 确定CRC生成多项式和初始寄存器值。
2. 在发送端,将数据和校验位进行拼接,并进行CRC多项式运算。
3. 发送带有校验位的数据。
4. 在接收端,接收数据后,进行CRC多项式运算,验证数据的准确性。
5. 如果有错误发生,进行纠正操作。
6. 测试不同数据长度和错误位情况下的CRC编解码性能。
四、实验结果经过多次实验,我们验证了设计的CRC编解码电路的可靠性和有效性。
在大多数情况下,CRC技术能够有效检测和纠正数据传输中的错误,提高了数据传输的可靠性和稳定性。
同时,我们也发现CRC 技术在处理大量数据时,能够快速进行校验,减少了传输延迟。
五、结论通过本次实验,我们深入了解了循环冗余校验技术的原理和应用,设计并验证了一个CRC编解码电路,证明了CRC技术在数据传输中的重要性和有效性。
CRC技术不仅可以检测和纠正数据传输中的错误,还可以提高数据传输的稳定性和可靠性,为数字通信系统的发展提供了重要支持。
网络实验报告 crc

【实验组织方式】
个人实验
【实验条件】
微机与编程软件。
五.实验步骤
1.基础理论知识
CRC检错方法的工作原理是:将要发送的数据比特序列当做一个多项式f(x)的系数,在发送端用收发双方预先约定的生成多项式G(x)去除,求得一个余数多项式。将余数多项式加到数据多项式后发送到接收端。在接收端,用同样的生成多项式G(x)去除接收数据多项式f’(x),得到计算余数多项式。如果计算余数多项式与接收余数多项式相同,表示传输无差错;否则,表示传输有差错,由发送方重发数据,直至正确为止。
}
UpdateData(FALSE);
}
七.结果分析
图1
图2
教
师
评
语
教师签名:
年月日
⑵f(x)=1100001101, G(x)=x^16+x^15+x^2+1
CRC校验码的生成过程:
①发送数据比特序列为1100001101。
②生成多项式比特序列为11000000000000101。
③将发送数据比特序列乘以216,那么产应为生的乘积11000011010000000000000000。
④将乘积用生成多项式比特序列去除,求得余数比特序列为110010111000。
⑤将余数比特序列加到乘积中,得10001101000000110010111000。
⑥如果在数据传输过程中没有发生错误,接收端收到的带有CRC校验码的数据比特序列一定能被相同的生成多项式整除,即余数等于0。说明数据传输正确。
调试的步骤:
保存为c或c++文件。
根据断点调试找到错误处。
采用F10或F11单步调试找到精确的错误处。其中f10是跳过函数调用,F11是进入函数体调试。一般是先用F10,确定函数输入输出是否正确(与自己想的一样),如不一样,则用F11进入函数体一步一步调试。
单片机crc校验实验报告

单片机课程总实验——实现CRC校验一、实验目的⒈通过学习CRC原理,验证,检错,掌握其工作原理;⒉编写CRC编码程序;⒊总结实验过程,编写提交实验报告:方案、编程、调试、结果、分析、结论。
二、实验要求用单片机实现CRC校验码(10比特数据或任意数据长度、生成多项式用G (x)= x5 + x4 + x2 + 1 ),校验码显示在单片机实验系统数码管上。
二、实验器材1、装有Keil C51开发工具的PC机一台2、TD-PIT/TD-PIT-B实验装置一套三、实验原理1.设置CRC寄存器,并给其赋初始值。
2.将数据的第一个8-bit 字符与16 位CRC 寄存器的低8 位进行异或,并把结果存入CRC寄存器。
3.CRC 寄存器向右移一位,最高位补零,移出并检查最低位。
4.如果LSB 为0,重复第三步;若LSB 为1,CRC 寄存器与多项式码相异或。
5.重复第 3 与第4 步直到8 次移位全部完成。
此时一个8-bit 数据处理完毕。
6.重复第 2 至第5 步直到所有数据全部处理完成。
7.最终CRC 寄存器的内容即为CRC 值。
常用的CRC循环冗余校验标准多项式如下:CRC (12 位) =X12+X11+X3+X2+X+1 CRC (16 位) = X16+X15+X2+1CRC (CCITT) = X16+X12 +X5+1 CRC (32 位) = X32+X26+X23+X16+X12+X11+X10+ X8+X7+ X5+X4+X2+X+1 以CRC (16 位)多项式为例,其对应校验二进制位列为1 1000 0000 0000 0101本次实验以10比特为例。
显示到六位数码管中。
其实验连接图如下图所示。
四、实验步骤1.打开Keil C51开发工具,新建开发工具,并保存至相应路径。
2.新建文件,编写代码。
3.按照实验连线图在实验箱上连线。
4.编译运行代码勿误后,打开实验箱,点击调试,运行。
五、实验结果经过调试程序,在实验箱数码管上显示二进制数001110.六、实验源代码#include "Absacc.h"#define C8255_A XBYTE[0x7F00] //8255端口地址定义#define C8255_B XBYTE[0x7F01]#define C8255_C XBYTE[0x7F02]#define C8255_CON XBYTE[0x7F03]//数码管显示编号unsigned char a[] = {0x3f, 0x06, 0x5b, 0x4f, 0x66, 0x6d, 0x7d, 0x07, 0x7f,0x6f, 0x77, 0x7c, 0x39, 0x5e, 0x79, 0x71};unsigned char b[] = {0x00, 0x00, 0x00, 0x00, 0x00, 0x00};long MD;long GD;void delay(unsigned int time){unsigned int i;for(i=0; i<time; i++);}void display() //显示函数{unsigned char i, j = 0xDF;for(i=0; i<6; i++){C8255_A = 0xFF;C8255_B = a[b[i]]; //查表输出显示C8255_A = j;delay(0x100);j = (j>>1)|(j<<7);}}void clear() //清屏{C8255_B = 0x00;}void CRC_check(long MD1,long GD1){ long MD = MD1 ; // 需要校验的数据long GD = GD1;long tmp; //临时变量保存多个移位,或恢复原值信息int count_MD; //校验数据的位数int count_GD; //多项式的位数int count; //两者位数差long tst0 = 1; //判断余数最高位是否为0int i;tmp = MD; //数MD 有多少位tmp用于暂存MDfor(count_MD = 0 ; MD != 0 ; count_MD++)MD >>= 1;MD = tmp;tmp = GD; //数GD有多少位tmp用于暂存GDfor(count_GD = 0 ; GD != 0 ; count_GD++)GD >>= 1;GD = tmp ;//构造CRC码序列for(tmp = 1 ; tmp < count_GD ; tmp ++) //左移count_GD-1位MD <<= 1;count = count_MD - 1;//将GD 与MD 构造等长,低位用0填充tmp = count; //长度均为count_GD+count_MD-1while(count--){GD <<= 1 ;}count = tmp;//tst0 和MD 求与运算,确定MD最高位是否为1,确定是否应该求模tmp = count_GD + count_MD -1 ;while(--tmp) //循环tmp-1次,位数为1+tmp-1tst0 <<= 1;//模二除法的实现for( ; count >= 0 ; count--){ if(tst0 == (tst0&MD)) //MD与最高位为1 当除不尽时最高位为0,//余数比除数少一位{MD ^= GD ; // 异或除法,被除数应该异或之后少一位}tst0 >>= 1; //位数减一,最高位降低一位GD >>= 1; //除数保持和被除数最高位对齐,相当于竖式除法左对齐}i=0;while(1) //转化为2进制输出,16进制数模2取余,移位 {b[i] = MD % 2;i++;MD /= 2;if(MD == 0 || i > 6)break;}}void main(){C8255_CON = 0x81; //8255初始化CRC_check(0x28D,0x35); //16进制while(1) //显示{display();delay(0x80);clear();}}七、实验心得实验指导书上写的还是很好懂,只是最初接触的时候确实感觉代码好多陌生,因为这个调用机制,变量基本上都是公有变量,直接在函数里面使用,赋值,在另一个函数里面接着用。
通信原理实验17 CRC码的编解码实验

实验十七CRC码的编解码实验实验内容1. 熟悉CRC码编码实验。
2.熟悉CRC码译码实验。
一、实验目的1.加深对CRC码的理解2.掌握CRC码的编解码过程3. 学习通过CPLD编程实现CRC码编译码实验二、实验电路工作原理在实际的基带传输系统中,并不是所有码字都能在信道中传输。
例如,含有直流和低频成分的基带信号就不适宜在信道中传输,因为它有可能造成信号严重畸变。
同时,一般基带传输系统都从接收到的基带信号流中提取收定时信号,而收定时信号却又依赖于传输的码型,如果码型出现长时间的连“0”或连“1”符号,则基带信号可能会长时间的出现0电位。
从而使收定时恢复系统难以保证收定时信号的准确性。
实际的基带传输系统还可能提出其它要求,因而对基带信号也存在各种可能的要求。
归纳起来,对传输用的基带信号的主要要求有两点:①对各种代码的要求,期望将原始信息的符号编制成适合于传输用的码型,②对所传码型的电波波形要求,期望电波波形适宜于在信道中传输。
前一问题称为传输码型选择,后一问题称为基带脉冲的选择。
这是两个既有独立性又有联系的问题,也是基带传输原理中十分重要的两个问题。
传输码(又称线路码)的结构将取决于实际信道特性和系统工作的条件。
在较为复杂的基带传输系统中,传输码的结构应具有下列主要特性:①能从其相应的基带信号中获取定时信息;②相应的基带信号无直流成分和只有很小的低频成分;③不受信息源统计特性的影响,即能适应于信息源的变化;④尽可能地提高传输码型的传输效率;⑤具有内在的检错能力,等等。
1.CRC简介91CRC 又称循环冗余校验码,属于循环码的一种,在计算机通信和移动通信中广为应用。
它能够检测出如下错误:(1) 突发长度≤n-k 的突发错误;(2) 大部分突发长度=n-k+1的错误,其中不可检测的这类错误只占(1)2n k ---;(3) 大部分突发长度〉n-k+1的错误,不可检测的这类错误只占()2n k --;(4) 所有与许用码组码距≤min d -1的错误;(5) 所有基数个随机错误。
实验报告-CRC编程及以太网协议分析

int k=06; //输入信息码,这里的信息选为7位
int g=0x13; //生成多项式系数(这里的生成多项式是4次的,所以系数有5个,为10011,用十六进制表示)
k<<=4; //信息左移4位,相当于信息码后面加上(g-1)个0.
g=g<<6; //多项式系数左移到开始位异或的位置
实
验
目
的
或
要
求
1、使用WireShark捕获Ethernet帧和高层协议数据包并对Ethernet帧和高层协议数据包进行分析。
2、学习CRC编程实现的基本方法。
实
验
过
程
及
步
骤
1、安装WireShark软件、启动WireShark、设置捕获接口和选项、捕获数据包
2、CRC编码实现(主函数)
#include <stdio.h>
计算机网络课程实实验报告书第第2次实验塔里木大学信息工程学院计算机网络课程第第2实验报告班别机计算机175班学号实验室号逸夫楼309组号计算机号48日期2015年年12月月7日姓名成绩评定实验名称crc编程及以太网协议分析老师签名所用设备及及软件在windowsxp2000环境下安装wiresharkcrc需要vc60
printf("%d\n",sizeof(int));
for (int i=0;i<7;)
{
if (k<0x400) //表示首位为0,所以要继续往左移动
{k<<=1;
i++;
}
else
k^=g;
}
k>>=7; //现在的t是余数
CRC校验码编码实验

实验四CRC校验码编码实验班级:电子C073 姓名:赵宣学号:075584一、实验目的1、复习C++语言基本编写方法,熟悉面向对象编程方法。
2、学习CRC编码基本流程, 学会调试循环冗余校验码编码程序。
3、根据给出资料,掌握CRC校验码的编码原理,重点掌握按字节(Byte)编码方法二、实验内容与原理(一)实验原理:1. CRC 校验码介绍CRC 校验的基本思想是利用线性编码理论,在发送端根据要传送的k 位二进制码序列,以一定的规则产生一个校验用的监督码(CRC 码)r 位,并附在信息后边,构成一个新的二进制码序列数共 (k+r) 位,最后发送出去。
在接收端,则根据信息码和CRC 码之间所遵循的规则进行检验,以确定传送中是否出错。
16 位的CRC 码产生的规则是先将要发送的二进制序列数左移16 位(乘以216)后,再除以一个多项式,最后所得到的余数既是CRC 码。
求CRC 码所采用模2 加减运算法则,既是不带进位和借位的按位加减,这种加减运算实际上就是逻辑上的异或运算,加法和减法等价,乘法和除法运算与普通代数式的乘除法运算是一样,符合同样的规律。
接收方将接收到的二进制序列数(包括信息码和CRC 码)除以多项式,如果余数为0,则说明传输中无错误发生,否则说明传输有误。
2.按位计算CRC一个二进制序列数可以表示为求此二进制序列数的CRC 码时,先乘以216后(左移16位),再除以多项式G(X) ,所得的余数就是所要求的CRC 码。
可以设:其中Q n (X) 为整数, R n (X) 为16位二进制余数,将上式代入前式得:再设:其中Qn-1(X) 为整数, Rn-1(X) 为16位二进制余数,继续代入前式,多次迭代得到:根据CRC 的定义,很显然,十六位二进制数R0(X) 即是要求的CRC 码。
3.按字节计算CRC对于一个二进制序列数可以按字节表示为下式,其中Bn(X) 为一个字节(共8位):求此二进制序列数的CRC码时,先乘以216后(左移16位),再除以多项式G(X),所得的余数即是所要求的CRC 码。
CRC编码模块设计实验报告

湖南科技大学《数字系统设计》综合实验报告实验题目:CRC编码模块设计班级:学号:姓名:日期:一:题目功能分析;设计一个在数字传输中常用的校验、纠错模块,CRC循环冗余校验模块设计简介:循环冗余校验(CRC)是一种根据网络数据封包或电脑档案等数据产生简短固定位数校验码的一种散列函数,主要用来检测或校验数据传输或者保存后可能出现的错误。
生成的数字在传输或者储存之前计算出来并且附加到数据后面,然后接收方进行检验确定数据是否发生变化。
而且CRC码是目前通信系统中最常用的一种差错控制编码,利用其进行检错的过程可简单描述为:在发送端根据要传送的二进制码序列,以一定的规则产生一个校验用的监督码,附在原始信息后边,构成一个新的二进制码序列数,然后发送出去。
在接收端根据信息码和CRC 码之间所遵循的规则进行检验,一旦传输过程中发生差错,则信息码元与监督码元之间的关系遭到破坏,从而可以发现错误,乃至纠正错误。
CRC实验原理: CRC检验原理实际上就是在一个p位二位进制数据序列之后附加一个r位二进制检验码(序列),从而构成一个总长为n=p+r位的二进制序列;附加在数据序列之后的这个检验码与数据序列的内容之间存在着某种特定的关系。
如果因干扰等原因使数据序列中的某一位或某些位发生错误,这种特定关系就会被破坏。
因此,通过检查这一关系,就可以实现对数据正确性的检验。
本设计需要完成16位信息和5位CRC校验码发送、接收,其功能实现为:采用平台上的A、B两组开关输入16位二进制数,输出为X、Y、Z三组发光二极管,同时要求6个数码管显示其相对应的16进制编码结果。
二:总模块划分;由两个模块构成:CRC校验生成模块(发送)和CRC校验检错模块(接收),采用输入、输出否为并行的CRC校验生成方式。
(结构图)三:代码实现;VHDL代码:library ieee;use ieee.std_logic_1164.all;use ieee.std_logic_arith.all;use ieee.std_logic_unsigned.all;entity crc isport(clk :in std_logic;sdata:in std_logic_vector(15 downto 0);smg:out std_logic_vector(7 downto 0);led:out std_logic_vector(7 downto 0);error,hsend:out std_logic);end crc;architecture comm of crc isconstant multi_coef:std_logic_vector(5 downto 0):="110101";--signal sdata:std_logic_vector(15 downto 0):="1010001000100011";signal datacrco:std_logic_vector(23 downto 0);signal cnt:std_logic_vector(4 downto 0);signal dtemp:std_logic_vector(15 downto 0);signal sdatam:std_logic_vector(15 downto 0);signal rdtemp:std_logic_vector(15 downto 0);signal rdatacrc:std_logic_vector(20 downto 0);signal rcnt:std_logic_vector(4 downto 0);signal st:std_logic;signal rt:std_logic;signal cn:std_logic;signal state:integer range 0 to 8;signaltdata1,tdata2,tdata3,tdata4,tdata5,tdata6,data:std_logic_vector(3 downto 0);beginp1:process(clk)variable crcvar:std_logic_vector(5 downto 0);beginif clk'event and clk='1' thenif (st='0') thendtemp<=sdata;sdatam<=sdata;cnt<=(others=>'0');hsend<='0';st<='1';elsif(st='1'and cnt<11)thencnt<=cnt+1;if(dtemp(15)='1')thencrcvar:=dtemp(15 downto 10)xor multi_coef;dtemp<=crcvar(4 downto 0) & dtemp(5 downto 0) & '0'& '0'& '0'& '0'& '0';else dtemp<=dtemp(14 downto 0)&'0';end if;elsif(st='1'and cnt=11)thendatacrco<='0'& '0'& '0'&sdata&dtemp(15 downto 11);hsend<='1';cnt<=cnt+1;elsif(st='1' and cnt=11)thenhsend<='0';st<='0';end if;end if;end process p1;tdata1<=datacrco(23 downto 20);tdata2<=datacrco(19 downto 16);tdata3<=datacrco(15 downto 12);tdata4<=datacrco(11 downto 8);tdata5<=datacrco(7 downto 4);tdata6<=datacrco(3 downto 0);cn<='1';process(clk)beginif (clk'event and clk='1'and cn='1') then state<=state+1;end if;end process;process(data,state)begincase data iswhen "0000"=>smg<="10111111"; when "0001"=>smg<="10000110"; when "0010"=>smg<="11011011";when "0011"=>smg<="11001111";when "0100"=>smg<="11100110";when "0101"=>smg<="11101101";when "0110"=>smg<="11111101";when "0111"=>smg<="10000111";when "1000"=>smg<="11111111";when "1001"=>smg<="11101111";when "1010"=>smg<="11110111";when "1011"=>smg<="11011110";when "1100"=>smg<="10111001";when "1101"=>smg<="11111100";when "1110"=>smg<="11111001";when "1111"=>smg<="11110001";when others=>smg<="00000000";end case;end process;process(tdata1,tdata2,tdata3,tdata4,tdata5,tdata6,state) begincase state iswhen 1=>led<="11111110";data<=tdata1;when 2=>led<="11111101";data<=tdata2;when 3=>led<="11111011";data<=tdata3; when 4=>led<="11110111";data<=tdata4; when 5=>led<="11101111";data<=tdata5; when 6=>led<="11011111";data<=tdata6; when others=>led<="11111111";data<="1111"; end case;end process;end comm;四:仿真与实验结果;首先在工程下VHDL file编写上述代码,编写完成,点击电脑上的complication图标,然后再点击assignments,选择pins选项,按照所编程程序的要求,完成对输入输出引脚的绑定,在点击仿真模拟的图标,将程序仿真模拟,在实验平台上显示结果如上图。
CRC校验实验报告

实验三CRC校验一、CRC校验码的基本原理编码过程:CRC校验码的编码方法是用待发送的二进制数据t(x)除以生成多项式g(x),将最后的余数作为CRC校验码。
其实现步骤如下:1 设待发送的数据块是m位的二进制多项式t(x),生成多项式为r阶的g(x)。
在数据块的末尾添加r个0,数据块的长度增加到m+r位。
2 用生成多项式g(x)去除,求得余数为阶数为r-1的二进制多项式y(x)。
此二进制多项式y(x)就是t(x)经过生成多项式g(x)编码的CRC校验码。
3 将y(x)的尾部加上校验码,得到二进制多项式。
就是包含了CRC校验码的待发送字符串。
解码过程:从CRC的编码规则可以看出,CRC编码实际上是将代发送的m位二进制多项式t(x)转换成了可以被g(x)除尽的m+r位二进制多项式所以解码时可以用接收到的数据去除g(x),如果余数位零,则表示传输过程没有错误;如果余数不为零,则在传输过程中肯定存在错误。
许多CRC的硬件解码电路就是按这种方式进行检错的。
同时,可以看做是由t(x)和CRC校验码的组合,所以解码时将接收到的二进制数据去掉尾部的r位数据,得到的就是原始数据。
解码过程示例:运行结果:附录(实现代码):using System;using System.Collections.Generic;using System.Text;namespace CRC{public abstract class Change{/// <summary>/// 字节数组转进制/// </summary>/// <param name="bytes">字节数组</param>/// <param name="b1">字节数组长度</param>public static string ByteToHex(byte[] bytes, int b1){string returnStr = "";if (bytes != null){for (int i = 0; i < b1; i++){returnStr += bytes[i].ToString("x2").ToUpper();} }return returnStr;}/// <summary>/// 16进制转字节数组/// </summary>/// <param name="hexStr">16进制数</param>public static byte[] HexToByte(string hexStr){hexStr = hexStr.Replace(" ", "");if ((hexStr.Length % 2) != 0)hexStr += " ";//空格byte[] bytes = new byte[hexStr.Length / 2];for (int i = 0; i < bytes.Length; i++){bytes[i] = Convert.ToByte(hexStr.Substring(i * 2, 2), 16);} return bytes;}/// <summary>/// 字符串转进制/// </summary>/// <param name="str">字符串</param>/// <returns></returns>public static string StrToHex(string str){if (str == "") return "";byte[] bTemp = System.Text.Encoding.Default.GetBytes(str);return ByteToHex(bTemp, bTemp.Length);}/// <summary>/// 16进制转字符串/// </summary>/// <param name="str">16进制</param>/// <returns></returns>public static string HexToStr(string str){byte[] bytes = new byte[str.Length];bytes = HexToByte(str);return Encoding.Default.GetString(bytes);}}}namespace CRC{//哈夫曼树150// 结点类Node的定义如下:public class Node{private int weight; //结点权值private int lChild; //左孩子结点private int rChild; //右孩子结点private int parent; //父结点//结点权值属性public int Weight{get{return weight;}set{weight = value;}}//左孩子结点属性public int LChild{get{return lChild;}set{lChild = value;}}//右孩子结点属性public int RChild{get{ return rChild;}set { rChild = value; } } //父结点属性public int Parent{ get{ return parent; }set {parent = value; } } //构造器public Node(){weight = 0;lChild = -1;rChild = -1; parent = -1; }//构造器public Node(int w, int lc, int rc, int p){weight = w;lChild = lc;rChild = rc;parent = p;}}public class HuffmanTree{private List<Node> data = new List<Node>(); //结点数组private int leafNum; //叶子结点数目//索引器public Node this[int index]{get{return data[index];}set{data[index] = value;}}//叶子结点数目属性public int LeafNumpublic int LeafNum{get{ return leafNum;set{ leafNum = value; } }//构造器public HuffmanTree(){ }public HuffmanTree(List<NumKindchar> m_NumKind){leafNum = m_NumKind.Count;for (int j = 0; j < 2 * m_NumKind.Count - 1; j++)//n中字符共需要2n-1个节点{Node databuff = new Node();if (j < this.leafNum){databuff.Weight = m_NumKind[j].num; }data.Add(databuff);//每创建一个节点将节点加入节点数组data当中} }public List<Node> Create(){int max1, max2, tmp1, tmp2;//处理n个叶子结点,建立哈夫曼树for (int i = 0; i < this.leafNum - 1; ++i){ max1 = max2 = Int32.MaxValue;tmp1 = tmp2 = 0;//在全部结点中找权值最小的两个结点for (int j = 0; j < this.leafNum + i; ++j){ if ((data[j].Weight < max1) && (data[j].Parent == -1)){ max2 = max1;tmp2 = tmp1;tmp1 = j;max1 = data[j].Weight; }else if ((data[j].Weight < max2) && (data[j].Parent == -1)){ max2 = data[j].Weight;tmp2 = j;} }data[tmp1].Parent = this.leafNum + i;data[tmp2].Parent = this.leafNum + i;data[this.leafNum + i].Weight = data[tmp1].Weight + data[tmp2].Weight;data[this.leafNum + i].LChild = tmp1;data[this.leafNum + i].RChild = tmp2;}return data; }}public class NumKindchar{ public char letter { get; set; }//字符public int num { get; set; }//字符出现的次数public List<bool> huffmancode { get; set; }//字符对应的huffman编码}public class codeChar{public char numChar { get; set; }public string codeCharater { get; set; }}}。
12CRC编解码实验

实验二 CRC (循环冗余校验码)编解码实验一、实验目的1、掌握CRC 码的编解码原理。
2、掌握CRC 码的软件仿真方法。
3、掌握CRC 码的硬件仿真方法。
4、掌握CRC 码的硬件设计方法。
二、预习要求1、掌握CRC 码的编解码原理和方法。
2、熟悉matlab 的应用和仿真方法。
3、熟悉Quatus 的应用和FPGA 的开发方法。
三、实验原理CRC 码是一种循环码,有着极强的检错能力,在计算机通信和移动通信种广为应用。
定义变量m(x)为信息码元;T(x)为编码码组;g(x)为生成多项式。
CRC 码的编码步骤如下:(1) 用n k x - 乘m(x)。
这一运算实际上就是把信息码后附加上(n-k)个“0”。
例如,信息码为110,它相当m(x)=2x x +。
当n-k=7-3=4时,4265()()n k x m x x x x x x -=+=+,相当于1100000。
(2) 用g(x)除()n k x m x -,得到商Q(x)和余式r(x),即()()()()()n kxm x r x Q x g x g x -=+例如,若选定42()1g x x x x =+++,则65224242()1(1)()11n kxm x x xx xx g x xx x xxx -++==+++++++++相当于11000001011111011110111=+(3)编码码组T(x)为:()()()n kT x x m x r x -=+在上例中,T(x)=1100000+101=1100101。
上述几个步骤用硬件实现时,可以由除法电路来实现。
除法电路的主体由一些移位寄存器和模2加法器组成。
例如,上述(7,3)循环码的编码器组成如下图所示。
图 1 (7,3)循环码编码器图1中有四级移存器,分别用a,b,c,d 表示。
另外有一单刀双掷开关S 。
当信息位输入时,开关S 倒向下,输入信息码一方面送入除法器进行运算,另一方面直接输出。
CRC校验实验

实验一、CRC校验实验一、实验目的1.熟悉西门子S7-200编程软件SETP7-Micro/WIN SP6的编程和调试方法。
2.掌握CRC校验的原理和在S7-200 PLC中的实现方法。
二、实验设备计算机、西门子S7-200 PLC、RS485编程下载线。
三、实验原理(一)CRC校验基本原理校验码的具体生成过程为:假设被传输的数据流为BYTE[n]BYTE[n-1].... BYTE[1]BYTE[0],将此数据流看成系数为0或1的多项式M(x)。
收发双方约定一个生成多项式G(x)。
本实验中,多项式设为G(x)= X8+X7+X2+1。
在发送端将M(x)所对应的位串左移8位后按模2除法除以G(x)所对应的位串,余数为8位,称为CRC校验码,将CRC校验码附加在被传输的数据流后边,则被传输的带校验码的数据流为BYTE[n]BYTE[n-1]....BYTE[1]BYTE[0]CRC。
在接收端,也进行同样的除法过程,如果接收端的除法结果不为0,则表明数据传输产生了差错,数据接收端自动请求重发,实现纠错。
(二)CRC校验码生成方法和步骤1. 将被传输的数据流左移8位(共n+2个字节),高8位BYTE[n])放入一个长度为8的寄存器。
2. 将寄存器左移1位(寄存器的最低位从下一个字节获得),如果移出位为1,将寄存器中的值与生成多项式G(x)的简记式进行异或运算,运算结果存回寄存器中。
G(x)对应的位串共9位,其最高位总是1,G(x)的简记式为其后8位,为10000101。
如果移出位为0,则仅将寄存器左移1位(寄存器的最低位从下一个字节获得)。
3. 重复第2步,直到扩展后的数据流(n+2个字节)全部移入寄存器。
4. 寄存器中的值则为CRC校验码。
四、实验内容1.根据CRC校验码生成原理编写一段程序,调试并要求能够实现正确计算出任意长度数据串的CRC校验码。
七、实验源程序Network 1LD SM0.0MOVW VW301,VW400 //被传输数据高16位送入16位寄存器MOVW 16#8005,VW100 //VW100中存入生成多项式MOVD &VB303,AC1 //被传输数据下一个字节的地址存入AC1MOVB *AC1,VB20 //VB303中的被传输数据第3个字节存入VB20MOVB VB300,VB10//VB300输数据流的字节数送入VB10Network 2LD SM0.0FOR VW2,1,VW9 //外循环次数为被传输数据的字节数VB10Network 3LD SM0.0FOR VW0,1,8 //内循环次数为8位Network 4LD SM0.0SHRB V20.7,V401.0,16 //将V303.7移入V401.0LD SM1.1XORW VW100,VW400Network 5LD SM0.0SLB VB20.1 //将VB20左移一位Network 6NEXTNetwork 7LD SM0.0INCB AC1MOVB *AC1,VB20 Network 8NEXT。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11001———————除数
————
11110
1001
————
11111
11001
————
000100——————余数
2)
input=[1 0 1 1 0 0 1 1];crc_no=4;
k = size(input,2);
generator = zeros(1,crc_no+1);
output = zeros(1,k+crc_no);
end
output = [input output(1:crc_no)];
n = size(input,2);
output = input(1:n-crc_no);
forii = 1:n-crc_no
if(input(1) == 1)
input(1:crc_no+1) = mod((input(1:crc_no+1)+generator),2);
而发送信息位 1111,可转换为数据多项式为C(x)=x^3+x^2+x+1。
2)、生成多项式
是接受方和发送方的一个约定,也就是一个二进制数,在整个传输过程中,这个数始终保持不变。
在发送方,利用生成多项式对信息多项式做模2除生成校验码。在接受方利用生成多项式对收到的编码多项式做模2除检测和确定错误位置。
3.完成练习题。
4.实验结果分析
练习题:
1.选择CRC的生成多项式为G(X)=X4+X3+1. 求二进制序列10110011的CRC校验码。
要求:
1)将计算过程写在实验报告中
2)用程序验证结果正确性
解:
1)
11010100——————商
————————————
101100110000————————被除数
程序运行结果:
output =
0 1 1 1 1 0 1 1 0 1 0 0
output_after_check =
0 1 1 1 1 0 1 1
indicate =
1
5.心得体会
1.本次试验我学会了基本的CRC编码流程
2.了解了模二除的计算方法是异或运算,即相同为0不同为1。
3.同时在·实验中又暴露出我对编码的生疏,遇到了一些问题,通过网上查阅和请教同学解决了问题。在以后实验中应该多发现问题,锻炼动手实践的能力,也有助于更好的理解信息论的原理,还能运用在以后通信工程中。
实验三CRC编码实验实验报告
班级:通信162班
姓名:李浩坤学号:163977
实验名称:CRC编码实验实验日期:6.7
1.实验目的
1、复习matlab的基本编写方法。
2、学习CRC编码基本流程, 学会调试循环冗余校验码编码程序。
3、根据给出的资料,掌握CRC校验码的编码原理。
2.实验原理及内容
原理:
1.CRC码简介:
应满足以下条件:
a、生成多项式的最高位和最低位必须为1。
b、当被传送信息(CRC码)任何一位发生错误时,被生成多项式做模2除后应该使余数不为0。
c、不同位发生错误时,应该使余数不同。
d、对余数继续做模2除,应使余数循环。
3)、模2除(按位除)
模2除做法与算术除法类似,但每一位除(减)的结果不影响其它位,即不向上一位借位。所以实际上就是异或。然后再移位移位做下一位的模2减。步骤如下:
1)、多项式与二进制数码
多项式和二进制数有直接对应关系:x的最高幂次对应二进制数的最高位,以下各位对应多项式的各幂次,有此幂次项对应1,无此幂次项对应0。可以看出:x的最高幂次为R,转换成对应的二进制数有R+1位。
多项式包括生成多项式G(x)和信息多项式C(x)。
如生成多项式为G(x)=x^4+x^3+x+1, 可转换为二进制数码11011。
generator = [1 1 0 0 1];%D^4+D^3+1
output(1:k)=input;
forii = 1:k
if(output(1) == 1)
output(1:crc_no+1) = mod((output(1:crc_no+1)+generator),2);
end
output = [output(2:end) output(1)];
a、用除数对被除数最高几位做模2减,没有借位。
b、除数右移一位,若余数最高位为1,商为1,并对余数做模2减。若余数最高位为0,商为0,除数继续右移一位。
c、一.实验步骤
1.了解crc编码原理,分析理解检验crc程序的含义。
2.运行mycrc编码程序,观察结果,计算验证程序是否正确。
2.循环冗余校验码(CRC)的基本原理:
在K位信息码后再拼接R位的校验码,整个编码长度为N位,因此,这种编码又叫(N,K)码。对于一个给定的(N,K)码,可以证明存在一个最高次幂为N-K=R的多项式G(x)。根据G(x)可以生成K位信息的校验码,而G(x)叫做这个CRC码的生成多项式。
几个需要提前了解的基本概念:
endinput = [input(2:end) input(1)];
end
ifsum(input) == 0
indicate = 0;
else
indicate = 1;
end
end
output = crc_add(input, crc_no)
[output_after_check, indicate] =crc_check(output,crc_no)
