汉明码编码实验报告
汉明码编码实验报告详细解释

汉明码的实现详细实验报告一、实验目的1、掌握线性分组码的编码原理2、掌握汉明码编码方法3、了解编码对误码性能的改善二、实验内容1、自行设置汉明码的参数,生成矩阵,计算所设计出的汉明码;写出产生(3,1)汉明码的生成矩阵,给出生成码的源程序,并给出运行结果。
2、利用encode库函数实现汉明编码;3、搭建一个通信仿真模块,并给出运行结果,分析汉明码对通信性能的影响;4、整理好所有的程序清单或设计模块,并作注释。
三、实验原理(一)、汉明码的介绍汉明码是1951年由汉明(R.W.Hamming)提出的能纠正单个错误的线性分组码。
它性能良好,既具有较高的可靠性,又具有较高的传输效率,而且编译码电路较为简单,易于工程实现,因此汉明码在发现后不久,就得到了广泛的应用。
我们的目的是要寻找一个能纠正单个错误,且信息传输率(即码率r=k/n )最大的线性分组码。
我们已经知道,具有纠正单个错误能力的线性分组码的最小距离应为 3,即要求其H 矩阵中至少任意两列 线性无关。
要做到这一点,只要H 矩阵满足“两无”一一无相同的列, 无全零列就可以了。
(n,k )线性分组码的H 矩阵是一个⑴-"n 訂n 阶矩阵,这里 r =n —k 是校验元的数目。
显然,r 个校验元能组成2r 列互不相同的r 重 矢量,其中非全零矢量有2r -1个。
如果用这2r -1个非全零矢量作为H 矩阵的全部列,即令H 矩阵的列数n =2「一1,则此H 矩阵的各列均不 相同,且无全零列,由此可构造一个纠正单个错误的(n ,k )线性分 组码同时,2r -1是n 所能取的最大值,因为如果n 2r -1,那么H 矩 阵的n 列中必会出现相同的两列,这样就不能满足对 H 矩阵的要求。
而由于n =2 -1是门所能取的最大值,也就意味着码率 R 取得了最大 值,即这样设计出来的码是符合我们的要求的,这样的码就是汉明码 定义 若H 矩阵的列是由非全零且互不相同的所有二进制r 重矢量组成,则由此得到的线性分组码,称为 GF (2)上的(2r -1, 2r -1-r )汉 明码。
hamming实验报告

hamming实验报告Hamming实验报告引言:Hamming实验是一项重要的计算机科学实验,旨在研究和验证Hamming码的纠错能力。
Hamming码是一种用于纠正单一比特错误的错误检测和纠正编码方式,被广泛应用于数据传输和存储中。
本实验将通过模拟数据传输过程,并使用Hamming码进行纠错,来验证其在实际应用中的有效性。
实验目的:本实验的目的是通过模拟数据传输过程,验证Hamming码的纠错能力。
具体而言,我们将通过引入人为制造的错误,检测和纠正这些错误,以验证Hamming码的可靠性和有效性。
实验步骤:1. 设计Hamming码生成矩阵和校验矩阵。
2. 生成待发送的数据,并使用Hamming码进行编码。
3. 引入人为制造的错误,模拟数据传输过程中的错误。
4. 使用Hamming码进行错误检测和纠正。
5. 比较纠错前后的数据,验证Hamming码的纠错能力。
实验结果:在本次实验中,我们成功设计并实现了Hamming码的纠错过程。
通过引入人为制造的错误,我们模拟了数据传输过程中的错误情况。
使用Hamming码进行错误检测和纠正后,我们成功恢复了原始数据,并验证了Hamming码的纠错能力。
讨论:Hamming码作为一种常用的纠错编码方式,具有较高的纠错能力和可靠性。
通过本次实验,我们进一步验证了Hamming码的有效性。
然而,Hamming码并不能纠正所有错误,它只能纠正单一比特错误。
对于多比特错误或连续错误,Hamming码的纠错能力将受到限制。
因此,在实际应用中,我们需要综合考虑数据传输的可靠性需求,并选择适当的纠错编码方式。
结论:通过本次实验,我们验证了Hamming码的纠错能力。
Hamming码作为一种常用的纠错编码方式,在数据传输和存储中具有重要的应用价值。
然而,我们也需要认识到Hamming码的局限性,它只能纠正单一比特错误。
在实际应用中,我们需要根据具体需求选择适当的纠错编码方式,以确保数据的可靠性和完整性。
11汉明码编解码实验

010 011 100 101 110 111 3、信道选择(选择加错位置) SW103-6,SW103-5,SW103-4,SW103-3 0000 0001 0010 0011 …… 1111 4、加错数目选择 SW103-2,SW103-1 00 01 10 11
BCH 码编码 卷积码编码 Turbo 码编码 扩展用 扩展用 汉明码交织编码
加错位置 从 0 位置加错 从 1 位置加错 从 2 位置加错 从 3 位置加错 ……. 从 15 位置加错
加错位置 加 0 位错 加 1 位错 加 2 位错 加 3 位错
从 SW103-6,SW103-5,SW103-4,SW103-3 指示的位置开始,每帧加错的位数有 SW103-2,SW103-1 的状 态决定。 5、编码输出设置 D116,D115,D114,D113,D112,D111,D110,D109,D108,D107,D106,D105,D104,D103, D102,D101 为 16 位编码输出位。TP102 和 TP103 分别可以测量编码输出的帧和对应该帧的时钟信号。 6、解码方式选择 SW201-3,SW201-2,SW201-1 000 001 010 解码方式 汉明码解码 CRC 解码 BCH 码解码
AWGN Channel的参数SNR设置为SNR; Bernoulli Binary Generator的参数Sample Time设置为SampleTime。 2、仿真程序 clear all; SampleTime=1; SNR=1; sim('hammingsim'); figure(1); subplot(2,2,1); stem(hammingin); title('编码输入序列'); subplot(2,2,2); stem(hammingen); title('编码输出序列'); subplot(2,2,3); stem(hammingene); title('解码输出序列'); subplot(2,2,4); stem(hammingde); title('解码输出序列'); clear all; SampleTime=1/1000; for i=1:8 SNR=i-3; sim('hammingsim'); biterr(i)=0; for j=1:length(err) biterr(i)=biterr(i)+err(j,1); end; biterr(i)=biterr(i)/length(err); end; figure(2);
实验三 汉明码编码与译码
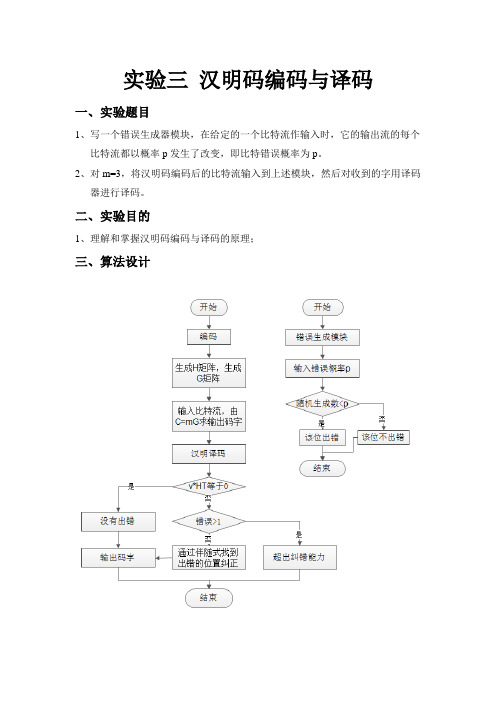
实验三汉明码编码与译码一、实验题目1、写一个错误生成器模块,在给定的一个比特流作输入时,它的输出流的每个比特流都以概率p发生了改变,即比特错误概率为p。
2、对m=3,将汉明码编码后的比特流输入到上述模块,然后对收到的字用译码器进行译码。
二、实验目的1、理解和掌握汉明码编码与译码的原理;三、算法设计四、程序分析1、错误生成模块:任一给以p,系统任意生成一数,若比p小则让其出错,否则不出错。
2、编码:首先随机生成H矩阵,由H矩阵生成G矩阵,利用C=mG编码。
3、解码:若v*H’=0,则没有出错,直接输出v中前k位;若v*H’!=0,列出所有的e和e*H’得到伴随阵s,若能在s中找到s=v*H则c0=v-e,输出c0中前k位;若找不到s,则输出“错误位数大于纠错能力,无法解码”。
五、程序代码#include <iostream>#include <string> // 字符串处理头文件#include <iomanip> // 输入输出控制头文件#include <math.h>#include <stdlib.h>#include <time.h>using namespace std;void Err_Pro();void Hamming_Decode();intm,n,k,t,err,r,R[100],N[100],COUNT[100],num[100][100],Th[100][100],PT_S[100][100],PT_D[1 00][100];intH[100][100],HT[100][100],Ig[100][100],P[100][100],G[100][100],Ibit[100],Cbit[100],Err_Cbit[1 00],V[100];/**************************************************************************//*函数名:void Binary_Conversion(int i) *//*功能:十-二进制转换*//*说明:该函数输出二进制数为低位在前,高位在后*//**************************************************************************/ void Binary_Conversion(int i){int j=0,temp=0;do // 生成完整n个二进制{temp = i % 2; // 判断相应最低位为0或1(若为2的倍数则为0,否则为1)i = i / 2; // 为考虑前一位为0或1做准备if(j < m) // m确定二进制的位数{N[j] = temp;j++;}}while(i != 0); // 等待i等于0(即等待十进制数为0时不进行二进制转换)}/**************************************************************************/ /*函数名:void Random_Array() */ /*功能:将数组的列随机排放*/ /**************************************************************************/ void Random_Array(){srand(unsigned(time(NULL))); // 随机生成条件(抵消rand函数伪随机效果)cout << endl << "产生随机数为:" << endl;for(int j=0;j<n;j++){loop:r= rand() % n; // 随机生成范围为0~n-1的正整数for(int i=0;i<j;i++){if(R[i] == r) // 如果随机产生的数与已产生的数相等,则重新随机产生数{goto loop;}}R[j] = r; // 产生不重复的随机数cout << setw(4) << r + 1;for(int i=0;i<m;i++){PT_D[i][j] = PT_S[i][r]; // 顺序转置系数矩阵->随机转置系数矩阵}}}/**************************************************************************/ /*函数名:void Creat_H() */ /*功能:创建系统型奇偶校验矩阵H */ /*说明:系统型奇偶校验矩阵H由转置负系数矩阵和单位矩阵组成*/ /**************************************************************************/ void Creat_H(){int i,j,count0=0,count1=0,count2=0,count3=0;/*************生成单位矩阵Ih************/ //教材P101for(i=0;i<m;i++) //i表示行j表示列{for(j=0;j<n;j++){if((j >= k) && (i+k == j))Ih[i][j] = 1;elseIh[i][j] = 0;}}/*********生成转置负系数矩阵PT**********/for(i=0;i<m;i++) // 转置二进制转换数组到PT_S{for(j=0;j<n;j++){PT_S[i][j] = num[j][i]; // 生成顺序转置系数矩阵}}Random_Array();//将数组的列随机排放for(j=0;j<n;j++){for(i=0;i<m;i++){if(PT_D[i][j] == 0)count0 ++;}count1 = count0; // count1记录每一列1的个数count0 = 0;if(count1 == (m-1)) // 将只有一位为1其余位为0的列的所有位置0{for(i=0;i<m;i++){PT_D[i][j] = 0;}}else// COUNT数组记录只有一位为1其余位为0的列为0,其余位的值为PT_D列的位置值+1 COUNT[count2] = j + 1;count2 ++;}for(int q=0;q<n;q++) // 将PT_D的至少有两个1的列赋给PT{if(COUNT[q] > 0){for(i=0;i<m;i++)PT[i][count3] = PT_D[i][q];count3 ++;}}cout << endl;/********生成系统型奇偶校验矩阵H********/for(i=0;i<m;i++){for(j=0;j<n;j++){H[i][j] = PT[i][j] + Ih[i][j];}}cout << endl << "系统型奇偶校验矩阵H为:" << endl;for(i=0;i<m;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << H[i][j] << setw(2);}cout << endl;}}/**************************************************************************/ /*函数名:void Creat_G() *//*功能:创建系统型生成矩阵G */ /*说明:系统型生成矩阵G由单位矩阵和系数矩阵组成*/ /**************************************************************************/ void Creat_G(){int i,j;/*************生成单位矩阵Ig************/for(i=0;i<k;i++){for(j=0;j<n;j++){if(i == j)Ig[i][j] = 1;elseIg[i][j] = 0;}}/*************生成系数矩阵P*************/for(j=0;j<n;j++){for(i=0;i<k;i++){if(j>k-1)P[i][j] = PT[j-k][i];}}/**********生成系统型生成矩阵G**********/for(i=0;i<k;i++){for(j=0;j<n;j++){G[i][j] = P[i][j] + Ig[i][j];}}cout << endl << "系统型生成矩阵G为:" << endl;for(i=0;i<k;i++) // 显示系统型奇偶校验矩阵H{for(j=0;j<n;j++){cout << setw(2) << G[i][j] << setw(2);}cout << endl;}}/*******************************主函数*************************************/ int main(){int i,j;cout << setw(30) << "汉明码" << endl;cout << "请输入校验元位数m = ";cin >> m;n = pow(2,m) - 1; //码长k = pow(2,m) - 1 -m; //信息源位数cout << "提示:" << setw(10) << "您输入的为(" <<n<< "," <<k<< ")汉明码,可纠正" << t << "个错误" << endl;cout << endl;for(i=0;i<n;i++) // 将n个转换二进制数组存入二维数组{Binary_Conversion(i+1);for(j=0;j<m;j++){num[i][j] = N[j];//num[i][m-j-1] = N[j]; // m-j-1意义在于将二进制高位在前,低位在后}}cout << "n个二进制转换表为:" << endl;for(i=0;i<n;i++) // 输出二进制转换对应表低位在前高位在后{for(j=0;j<m;j++){cout << num[i][j] << setw(2);}cout << setw(4);}cout << endl;Creat_H();Creat_G();cout << endl << "请输入" << k << "位信息比特流:" << endl;for(i=0;i<k;i++)cin >> Ibit[i];for(i=0;i<n;i++){for(j=0;j<k;j++){Cbit[i] += (Ibit[j] * G[j][i]); // 十进制加法Cbit[i] = Cbit[i] % 2; // 将十进制转换二进制}}cout << endl << "输出" << n << "位码字比特流:" << endl;for(i=0;i<n;i++) //输出编码后的码字cout << setw(3) << Cbit[i];cout << endl;Err_Pro(); //错误概率函数Hamming_Decode(); //汉明译码return 0;}/**************************************************************************/ /*函数名:void Err_Pro() */ /*功能:产生错误概率函数*/ /**************************************************************************/ void Err_Pro(){float p;cout << endl << "请输入错误概率p = ";cin >> p;for(int x=0;x<n;x++){if((float)((rand() % 1001) * 0.001) < p) // 如果小于概率,则原码0与1互换{err ++;Err_Cbit[x] = (Cbit[x] + 1) % 2;}elseErr_Cbit[x] = Cbit[x]; // 如果大于错误概率,则赋值原码}cout << endl << "输出" << n << "位码字比特流(每位等概出错):" << endl;for(int y=0;y<n;y++)cout << setw(3) << Err_Cbit[y];cout << endl;}/**************************************************************************/ /*函数名:void Hamming_Decode() */ /*功能:汉明译码函数*//**************************************************************************/ void Hamming_Decode(){int i,j,flag=0,d;for(i=0;i<n;i++) // 得到H的转置矩阵HT{for(j=0;j<m;j++){HT[i][j] = H[j][i];}cout << endl << "输出转置奇偶校验矩阵HT为:" << endl;for(i=0;i<n;i++){for(j=0;j<m;j++){cout << setw(3) << HT[i][j] << setw(3);}cout << endl;}for(i=0;i<m;i++) // 计算伴随矩阵{for(j=0;j<n;j++){V[i] += Err_Cbit[j] * HT[j][i];}if(V[i] % 2 == 0) // 将十进制转换二进制V[i] = 0;elseV[i] = 1;}cout << endl << "输出伴随矩阵为:" << endl;for(i=0;i<m;i++)cout << V[i] << setw(2);cout << endl;for(i=0;i<m;i++){if(V[i] == 0) // 如果伴随矩阵为零矩阵,则直接输出原码流{if(i == m-1){cout << endl << "<译码正确!>输出码流为:" << endl;for(j=0;j<n;j++)cout << Err_Cbit[j] << setw(3);cout << endl;}}else{flag ++; // 如果伴随矩阵为非零矩阵,则标志位自加1break;}if(flag != 0){if(err == 1) // 伴随矩阵为非零矩阵时执行{for(i=0;i<n;i++){for(j=0;j<m;j++){if(V[j] == HT[i][j]){if(j == (m-1)) d = i;//d记录行}elsebreak;}}cout << endl << "<译码正确!>输出码流为:"<< endl;Err_Cbit[d] = (Err_Cbit[d] + 1) % 2;for(i=0;i<n;i++)cout << setw(3) << Err_Cbit[i] << setw(3);cout << endl;}elsecout << endl << "由于本次编码有" << err << "个错误位,大于纠错能力" << t << ",故<译码错误!>" << endl;}}六、程序运行结果。
Hamming码实验报告(孙鹏跃)

信息论与编码基础实验报告学院:电子科学与工程学院队别:四院二队专业: 2006级通信工程专业姓名:孙鹏跃学号: 200604015002国防科学技术大学电子科学与工程学院实验三 汉明码编译码一、【设计思想】1948年,Bell 实验室的C.E.Shannon 发表的《通信的数学理论》,是关于现代信息理论的奠基性论文,它的发表标志着信息与编码理论这一学科的创立。
Shannon 在该文中指出,任何一个通信信道都有确定的信道容量C,如果通信系统所要求的传输速率R 小于C,则存在一种编码方法,当码长n 充分大并应用最大似然译码(MLD ,MaximumLikelihoodDecdoding)时,信息的错误概率可以达到任意小。
从Shannon 信道编码定理可知,随着分组码的码长n 或卷积码的约束长度N 的增加,系统可以取得更好的性能(即更大的保护能力或编码增益),而译码的最优算法是MLD,MLD 算法的复杂性随n 或N 的增加呈指数增加,因此当n 或N 较大时,MLD 在物理上是不可实现的。
因此,构造物理可实现编码方案及寻找有效译码算法一直是,信道编码理论与技术研究的中心任务。
信息传输的可靠性是所有通信系统努力追求的首要目标。
要实现高可靠性的传输,可采用诸如增大发射功率、增加信道带宽、提高天线增益等传统方法,但这些方法往往难度比较大,有些场合甚至无法实现。
而香农信息论指出:对信息序列进行适当的编码后可以提高信道传输的可靠性,这种编码即是信道编码。
信道编码是在著名的信道编码定理指导下发展起来的,几十年来已取得了丰硕的成果。
现将信道编码定理简述如下:每一个信道都具有确定的信道容量C,对于任何小于C 的信息传输速率R,总存在一个码长为n,码率等于R 的分组码,若采用最大似然译码,则其译码错误概率Pe 满足: )(R nE E Ae P −≤其中A 为常数,E(R )为误差函数。
香农编码定理仅仅是一个存在性定理,他只是告诉我们确实存在这样的好码,但并没有说明如何构造这样的码,但定理却为寻找这种码指明了方向。
实验五 汉明码的编译码

《数据通信原理》实验报告实验题目:汉明码的编译码专业班级:信息工程2班姓名学号:赵星敏201342351 李明阳201342300指导教师:刘钰实验五 汉明码的编译码一、实验目的1、理解汉明码的编码原理2、掌握利用simulink 进行汉明码编译码仿真的方法3、掌握利用matlab 指令进行汉明码编译码的方法 二、实验原理在数字通信系统中,为了实现信息的可靠传输,需要采用差错控制来发现并纠正错误。
进行差错控制的方法就是对信息进行差错控制编码,差错控制编码种类较多,其中线性分组码是常用的一类编码,具有编码效率高,实现较简单以及检纠错能力较强等特点。
一般数字通信系统模型由信源信宿、加解密、编解码、调制解调等模块组成,其中有些通信模块是组成整个通信系统所必不可少的,有些模块是可以不需要的。
差错控制编解码属于编解码器通信模块,为了方便分析差错控制编码性能,通过将通信系统简化为如图5-1所示的信息传输系统来搭建仿真实验平台进行分析研究。
图5-1编码,有时也称为纠错编码。
不同的编码方法,有不同的检错或纠错能力,有的编码只能检错,不能纠错。
一般说来,付出的代价越大,检纠错的能力就越强。
在选择差错控制编码时需要考虑到编码效率、检纠错的能力等方面因素的影响。
按照是否将信息码元进行分组可以将差错控制编码分为分组码和非分组码,线性码是指信息位和监督位满足一组线性方程的码,任一(n,k)线性分组码的编码效率为k/n 。
Simulink 通信模块中提供了二进制线性分组码编解码器:Binary Linear Encoder 和Binary Linear Decoder 。
汉明码是汉明(Hamming)于1950年提出的能纠正一位错码且编码效率较高的线性分组码,它可以用一种简洁有效的方法进行解码。
汉明码不是仅指某一种码,而是指一类码。
二进制汉明码应满足条件:2n-k =1+n,令m=n-k,汉明码n 和k 服从关系式:码长n=2m -1;信息位k=2m -1-m ;最小距离dmin=3(指汉明距离)。
Hamming码实验.

云南大学数学与统计学实验教学中心实验报告课程名称:计算机网络实验学期:2012-2013学年第二学期成绩:指导教师:陆正福学生姓名:卢富毓学生学号:20101910072实验名称:Hamming码实验实验要求:必做实验学时:4学时实验编号: No.9 实验日期:2013/5/28完成日期:2013/6/3学院:数学与统计学院专业:信息与计算科学年级: 2010级一、实验目的:通过实验掌握Hamming码编码实验的构造算法,以及其重要思想。
二、实验内容:Hamming码编码实验1.熟悉Hamming码的设计原理;2.编程实现(15,11,3)Hamming的编码和译码算法;3.验证Hamming码的检错能力和纠错能力三、实验环境Win7、Eclipse四、实验过程(请学生认真填写):实验过程、结果以及相应的解释:1. 预备知识A、与其他的错误校验码类似,汉明码也利用了奇偶校验位的概念,通过在数据位后面增加一些比特,可以验证数据的有效性。
利用一个以上的校验位,汉明码不仅可以验证数据是否有效,还能在数据出错的情况下指明错误位置。
B、Hamming码中主要的是生成矩阵以及校验矩阵。
通过得到这二者,我们就可以对需要的字符串进行编码、检错、纠错、译码的工作了。
C、具体如下:2. 实验过程A、原理分析:这里主要对如何纠错进行简要分析:编码所对应的码字为C = 0110011。
若接收到R = 0110001 。
有H*x=0可以判断其存在错误。
Erro={1 1 0}。
用Erro中的元素与校验矩阵中的每一列表,与其中一列全部相同。
则带便这一列有错。
找到第六位有错。
异或运算后得到R = 0110011。
当然这里需要注意的是Hamming 码只能纠正一位错误。
当出现两位错误时,将无法纠错后得到正确结果。
好了,废话不多说了。
先把代码贴上来。
B、具体代码如下:/* HammingCode的实验**1.熟悉Hamming码的设计原理;*2.编程实现(15,11,3)Hamming的编码和译码算法;*3.验证Hamming码的检错能力和纠错能力。
汉明码编译码及纠错能力验证实验

课程名称通信原理实验序号实验8实验名称汉明码编译码及纠错能力验证实验实验地点B702实验学时 2 实验类型验证性指导教师实验员专业_电子信息工程__ 班级14电信一班学号姓名2016年12 月15 日五、测试/调试及实验结果分析图片说明:CH1(黄色)帧同步信号CH2(浅蓝色)编码后信号CH3(粉红色)编码前信号CH4(深蓝色)译码后信号保护位无加错的时候设置的原始信号是:1100,编码后的信号是:1100001,译码后的信号为:1100。
对照图片的波形图,无误输出,汉明码正确。
有延时的现象。
1位加错的时候:设置的原始信号是:1100,编码后的信号是:1101001译码后的信号是:1100 通过计算S1、S2、S3可知错误位为:a3 对照译码后的波形与编码前的波形,可知已经纠错成功。
汉明码的一位纠错功能实现。
有延时的现象。
2位加错的时候:设置的原始信号是:1100,编码后的信号是:1111001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4 对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的2位纠错功能无法实现。
3位加错的时候:设置的原始信号是:1100,编码后的信号是:1011001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 ,对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的3位纠错功能无法实现。
4位加错的时候:设置的原始信号是:1100,编码后的信号是:0011001码后的信号是:0111 对照无错的编码后序列,可知错误位为:a3、a4、a5 、a6 ,对照译码后的波形与编码前的波形,可知译码后的波形与编码前的波形对不上。
(7,4)汉明码的4位纠错功能无法实现。
六、实验结论与体会1.课堂上对汉明码的理解不够深入,经过本次实验明显加深了我对汉明码的理论的认识和理解,实际动手才是关键2.经过编码后的编码序列,在加错码的时候,对a0、a1、a2位没有影响,也就是说这三位不会在无错的时候编码是什么,加错后这三位的编码还是一样3.一位加错时,(7,4)汉明码有检错以及纠错的功能,两位加错的时候,只有检错的功能,却没有纠错的功能,三位或三位以上加错时,既没有检错的功能,也没有纠错的功能;4.(7,4)汉明码作为一种信道编码的方式,具有一定的纠错检错能力。
实验报告书汉明码设计与实现
实验报告书------汉明码设计与实现汉明码编译码器系统班级: 姓名: 学号:一.实验原理描述1.1汉明码编码原理一般来说,若汉明码长为n ,信息位数为k ,则监督位数r=n-k 。
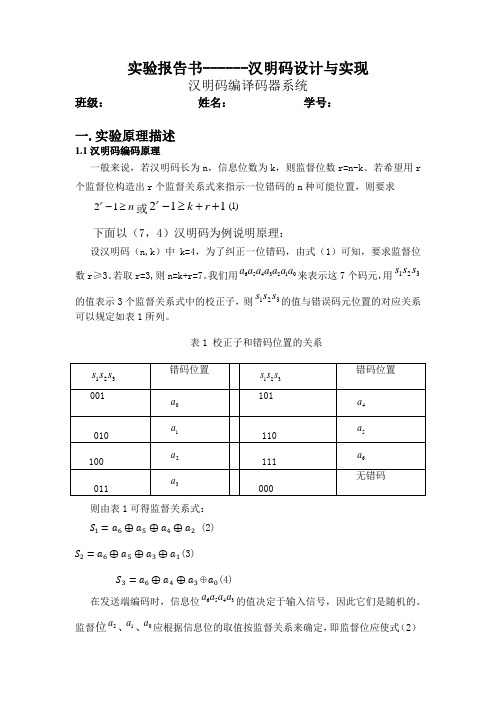
若希望用r 个监督位构造出r 个监督关系式来指示一位错码的n 种可能位置,则要求21r n -≥或211rk r -≥++(1)下面以(7,4)汉明码为例说明原理:设汉明码(n,k )中k=4,为了纠正一位错码,由式(1)可知,要求监督位数r ≥3。
若取r=3,则n=k+r=7。
我们用6543210a a a a a a a 来表示这7个码元,用123s s s 的值表示3个监督关系式中的校正子,则123s s s 的值与错误码元位置的对应关系可以规定如表1所列。
表1 校正子和错码位置的关系则由表1可得监督关系式: S 1=a 6⊕a 5⊕a 4⊕a 2 (2)S 2=a 6⊕a 5⊕a 3⊕a 1(3)S 3=a 6⊕a 4⊕a 3⊕a 0(4) 在发送端编码时,信息位6543a a a a 的值决定于输入信号,因此它们是随机的。
监督位2a 、1a 、0a 应根据信息位的取值按监督关系来确定,即监督位应使式(2)~式(4)中1s 、2s 、3s的值为0(表示编成的码组中应无错码){a 6⊕a 5⊕a 4⊕a 2=0a 6⊕a 5⊕a 3⊕a 1=0a 6⊕a 4⊕a 3⊕a 0=0(5)式(5)经过移项运算,接触监督位{a 2=a 6⊕a 5⊕a 4a 1=a 6⊕a 5⊕a 3a 0=a 6⊕a 4⊕a 3(6)式(5)其等价形式为: [1 1 1 0 1 0 01 1 0 1 0 1 01 0 1 1 0 0 1][ a 6a 5a 4a 3a 2a 1a 0]=[000](7)式(6)还可以简记为H ∙A T =0T 或A ∙H T =0 (8)其中H =[1 1 1 0 1 0 01 1 0 1 0 1 01 0 1 1 0 0 1]A =[a 6a 5a 4a 3a 2a 1a 0]P =[1 1 1 01 1 0 11 0 1 1]I r =[1 0 00 1 00 0 1]0=[0 0 0]所以有H =[PI r ](9)式(6)等价于[a 2a 1a a ]=[a 6 a 5 a 4 a 3][1 1 11 1 01 0 10 1 1]=[a 6 a 5 a 4a 3]Q (10)其中Q 为P 的转置,即T Q P (11)式(10)表示,信息位给定后,用信息位的行矩阵乘矩阵Q 就产生出监督位。
汉明码编码实验报告

汉明码实验报告一、实验目的实现汉明码纠错编码算法二、实验步骤1、判断是否执行程序2、输入要查错的码字3、分析输入的码字并输出码字4、继续判断三、源代码#include<iostream>using namespace std;void input(int *a){cout<<"请输入7位要查错的码字(输入一个数(0或1)就空格):"<<endl;for(int i=0;i<7;i++)cin>>a[i];}void analyze(int *a,int ht[7][3]){ //二维数组ht[7][3]调用之前一定要明确定义int p[3]={0};int q=0; //数据要初始化int h[3][7];int out[7];for(int k=0;k<3;k++){for(int i=0, j=0;j<7;i++,j++){p[k]=p[k]+a[i]*ht[j][k];p[k]=p[k]%2; //使数值小于2}if(p[k]==1){q++;}}cout<<"伴随式为:"<<p[0]<<p[1]<<p[2]<<endl;if(q==2||q==3){cout<<"一共有"<<q<<"位错误,超越了纠错范围"<<endl; }if(q==0){cout<<"码字没有错误!!"<<endl;cout<<"输出的码字为:";for(int i=0;i<7;i++){out[i]=a[i];cout<<out[i];}cout<<endl;}if(q==1){for(int i=0;i<3;i++){for(int j=0;j<7;j++){if((h[i][j]==p[0])&&(h[i+1][j]==p[1])&&(h[i+2][j]==p[2])){cout<<"要查错的码字的第"<<j+1<<"位出错"<<endl;a[j]=(a[j]+1)%2;cout<<"输出的码字应为";for(i=0;i<7;i++){out[i]=a[i];cout<<a[i];}cout<<endl;}}}}}void main(){int H[4][7]={{1,0,0,0,0,1,1}, //生成矩阵{0,1,0,0,1,0,1},{0,0,1,0,1,1,0},{0,0,0,1,1,1,1}};int h[3][7]={{0,0,0,1,1,1,1}, // 校验矩阵{0,1,1,0,0,1,1},{1,0,1,0,1,0,1}};int ht[7][3]={{0,0,1}, //ht (h的转置矩阵) {0,1,0},{0,1,1},{1,0,0},{1,0,1},{1,1,0},{1,1,1}};int in[7];int c;while(c){cout<<"是否需要查错(是请输入1不是输入0): ";cin>>c;switch(c){case 1: input(in);analyze(in,ht);break;case 0: break; }}}四、运行结果。
北交大通原实验5_实验十五汉明编码和译码实验

实验十五 汉明编码和译码实验一、 实验前的准备(1) 预习本实验的相关内容。
(2) 熟悉实验指导书附录B 和附录C 中实验箱面板分布及测试孔位置相关模块的跳线状态。
(3) 实验前重点熟悉的内容:汉明码的编码规则、汉明码的纠错能力。
二、 实验目的(1) 掌握汉明码编译码原理。
(2) 掌握汉明码纠错检错原理。
(3) 通过纠错编解码实验,加深对纠错编解码理论的理解。
三、 实验仪器(1) ZH5001A 通信原理综合实验系统(2) 20MHz 双踪示波器四、 基本原理差错控制编码的基本原理是:由发送端的信道编码器在信息码元序列中增加一些监督码元。
这冗余的码元与信息之间以某种确定的规则建立校验关系,使接收端可以利用这种关系由信道译码器来发现或纠正可能存在的错码。
不同的编码方法有不同的检错或纠错能力。
为了纠正位错码,在分组码中最少要加入多少监督位才可行呢?编码效率能否提高呢?从这种思想出发进行研究,便导致了汉明码的诞生。
汉明码是一种能够纠正一位错码且编码效率较高的线性分组码。
下面介绍汉明码的编码原理。
一般来说,若码长为n ,信息位数为k ,记作(,)n k 码,则监督位数r n k =-,如果希望用r 个监督位构造出r 个监督关系式来指示一位错码的n 种可能位置,则要求2121r n r k r -≥≥++或 通信原理综合实验系统中的纠错码系统采用(7,4)汉明码。
用650a a a … 表示这7个码元,用123S S S 、、表小3个监督关系式中的校正子,则123S S S 的值与码元间构成偶数监督关系:165422443136530S a a a a S a a a a S a a a a =⊕⊕⊕=⊕⊕⊕=⊕⊕⊕在发送端编码时,信息位654a a a 、、和3a 的值决定于输入信号,因此它们是随机的。
监督位21a a 、和0a 应根据信息位的取值按监督关系来确定,即监督位应使以上=式中123S S S 、、的值为零(表示变成的码组中应无错码),即 654254316530000a a a a a a a a a a a a ⊕⊕⊕=⎫⎪⊕⊕⊕=⎬⎪⊕⊕⊕=⎭上式经移项运算,解出监督位265415430653a a a a a a a a a a a a =⊕⊕⎫⎪=⊕⊕⎬⎪=⊕⊕⎭给定信息位后,可直接按上式算出监督位,其结果如下表接收端收到每个码组后,先计算出123S S S 、、,再按上表判断错码情况。
汉明码编译码实验报告

汉明码编译码实验报告引言:汉明码是一种检错纠错编码方法,常用于数字通信和计算机存储中。
它通过在数据中插入冗余位,以检测和纠正错误,提高数据传输的可靠性。
本实验旨在通过编写汉明码的编码和解码程序,对汉明码的编译码原理进行实际验证,并分析其性能。
一、实验目的:1. 了解汉明码的编码和解码原理;2. 掌握汉明码编码和解码的具体实现方法;3. 验证汉明码在检测和纠正错误方面的有效性;4. 分析汉明码的性能及其应用范围。
二、实验原理:1. 汉明码编码原理:汉明码的编码过程主要包括以下几个步骤:(1)确定数据位数和冗余位数:根据要传输的数据确定数据位数n,并计算冗余位数m。
(2)确定冗余位的位置:将数据位和冗余位按照特定规则排列,确定冗余位的位置。
(3)计算冗余位的值:根据冗余位的位置和数据位的值,计算每个冗余位的值。
(4)生成汉明码:将数据位和冗余位按照一定顺序排列,得到最终的汉明码。
2. 汉明码解码原理:汉明码的解码过程主要包括以下几个步骤:(1)接收数据:接收到经过传输的汉明码数据。
(2)计算冗余位的值:根据接收到的数据,计算每个冗余位的值。
(3)检测错误位置:根据冗余位的值,检测是否存在错误,并确定错误位的位置。
(4)纠正错误:根据错误位的位置,纠正错误的数据位。
(5)输出正确数据:输出经过纠正后的正确数据。
三、实验过程:1. 编码程序设计:根据汉明码编码原理,编写编码程序,实现将输入的数据进行编码的功能。
2. 解码程序设计:根据汉明码解码原理,编写解码程序,实现将输入的汉明码进行解码的功能。
3. 实验数据准备:准备一组数据,包括数据位和冗余位,用于进行编码和解码的实验。
4. 编码实验:将准备好的数据输入编码程序,得到编码后的汉明码。
5. 传输和接收实验:将编码后的汉明码进行传输,模拟数据传输过程,并接收传输后的数据。
6. 解码实验:将接收到的数据输入解码程序,进行解码,检测和纠正错误。
7. 实验结果分析:分析编码和解码的正确性,检测和纠正错误的能力,并对汉明码的性能进行评估。
通信报告 汉明编译码

汉明编译码实验一、实验目的1、通过实验,进一步了解差错控制的概念;2、通过纠错编解码实验,加深对纠错编解码理论的理解;3、加深对hanming码的产生、加错、纠错、译码的过程。
二、实验仪器1、JH5001通信原理综合实验系统一台2、20MHz双踪示波器一台3、JH9001型误码测试仪(或GZ9001型)一台三、实验原理差错控制编码的基本作法是:在发送端被传输的信息序列上附加一些监督码元,这些多余的码元与信息之间以某种确定的规则建立校验关系。
接收端按照既定的规则检验信息码元与监督码元之间的关系,一旦传输过程中发生差错,则信息码元与监督码元之间的校验关系将受到破坏,从而可以发现错误,乃至纠正错误。
通信原理综合实验系统中的纠错码系统采用汉明码(7,4)。
所谓汉明码是能纠正单个错误的线性分组码。
它有以下特点:码长n=2m-1 最小码距d=3信息码位k=2n-m-1 纠错能力t=1监督码位r=n-k这里m位≥2的正整数,给定m后,既可构造出具体的汉明码(n,k)。
用a6、a5、a4、a3代表4个信息元,a2、a1、a0三个监督码元可表示为:a2=a6+a5+a4a1=a6+a5+a3a0=a6+a4+a3汉明译码的方法,可以采用计算校正子,然后确定错误图样并加以纠正的方法。
校正子可表示为:s1=a6+a5+a4+a2;s2=a6+a5+a3+a1s3=a6+a4+a3+a0图9.1和图9.2给出汉明编码器和译码器电原理图。
a6a5a4a3a2a1a0a6a5a4a3图9.1汉明编码器电原理图a6a5a4a3a3a3a3图9.2汉明译码器电原理图表9.1 (7,4)汉明编码输入数据与监督码元生成表a6bit,其次是a5、a4……,最后输出a0位。
四、程序设计1、设计分析首先根据实验要求绘制出框图。
如下:图1 时钟产生框图实验的输入时钟为14.336MHz,编码输入的码元速率为32kbps,生成的4位m序列码元信息,再经编码器后变成7位汉明码发送,码元速率为32*7/4=56kbps。
Hamming码实验

云南大学数学与统计学实验教学中心实验报告一、实验目的:通过实验掌握Hamming码编码实验的构造算法,以及其重要思想。
二、实验内容:Hamming码编码实验1.熟悉Hamming码的设计原理;2.编程实现(15,11,3)Hamming的编码和译码算法;3.验证Hamming码的检错能力和纠错能力三、实验环境Win7、Eclipse四、实验过程(请学生认真填写):实验过程、结果以及相应的解释:1. 预备知识A、与其他的错误校验码类似,汉明码也利用了奇偶校验位的概念,通过在数据位后面增加一些比特,可以验证数据的有效性。
利用一个以上的校验位,汉明码不仅可以验证数据是否有效,还能在数据出错的情况下指明错误位置。
B、Hamming码中主要的是生成矩阵以及校验矩阵。
通过得到这二者,我们就可以对需要的字符串进行编码、检错、纠错、译码的工作了。
C、具体如下:2. 实验过程A、原理分析:这里主要对如何纠错进行简要分析:编码所对应的码字为C = 0110011。
若接收到R = 0110001 。
有H*x=0可以判断其存在错误。
Erro={1 1 0}。
用Erro中的元素与校验矩阵中的每一列表,与其中一列全部相同。
则带便这一列有错。
找到第六位有错。
异或运算后得到R = 0110011。
当然这里需要注意的是Hamming 码只能纠正一位错误。
当出现两位错误时,将无法纠错后得到正确结果。
好了,废话不多说了。
先把代码贴上来。
B、具体代码如下:/* HammingCode的实验**1.熟悉Hamming码的设计原理;*2.编程实现(15,11,3)Hamming的编码和译码算法;*3.验证Hamming码的检错能力和纠错能力。
*/package HammingCode;import java.util.Scanner;/*** @author卢富毓* @see实现HammingCode的生成、检错、纠错**/public class HammingCode {int[][] H;int[][] G;/*** @param start* () Hamming码的具体实现* @param HMC* 类的实例*/public void start(HammingCode HMC) {int send[] = new int[11];int receive[] = new int[15];// step1 15,11Hamming 码的校验矩阵生成H = HMC.CreateCheckArray();// step1 15,11Hamming 码的生成矩阵生成G = HMC.GenerateArray();// 输入四个字符进行编码System.out.print("请输入需编码的字符(0、1)11个:");Scanner sc = new Scanner(System.in);for (int i = 0; i < 11; i++) {send[i] = sc.nextInt();}sc.reset();HMC.encode(G, send); // 编码System.out.println("\n----------------------------------------------------------");// 输入四个字符检测编码System.out.print("请输入需译码字符(0、1)15个:");for (int i = 0; i < 15; i++) {receive[i] = sc.nextInt();}HMC.checkAndDecode(H, receive);// 检错以及译码// sc.close();}/*** @param ToBinary* 校验矩阵十进制数转为二进制矩阵* @return返回校验矩阵*/public int[][] CreateCheckArray() { // 二进制校验矩阵int m = 1;int l = 1;int[][] b = new int[4][16];for (int i = 0; i < b.length; i++) {for (int j = 1; j < b[i].length; j++) {b[i][j] = 0;}}for (int i = 1; i < 16; i++) { // 二进制m = i;if (i != 1 && i != 2 && i != 4 && i != 8) {for (int j = 3; j >= 0; j--) {b[j][l] = m % 2;m = m / 2;if (m < 0) {break;}}l++;}}for (int j = 0; j < 4; j++) { // 二进制for (int i = 12; i < 16; i++) {if (i - 12 == j) {b[j][i] = 1;}}}System.out.println("(15,11)HammingCode校验矩阵生成:");System.out.println("----------------------------------------------------------");for (int i = 0; i < 4; i++) {for (int j = 1; j < 16; j++) {System.out.print(b[i][j] + " ");}System.out.println();}System.out.println("----------------------------------------------------------");return b;}/*** @param Generate* 生成矩阵十进制数转为二进制矩阵* @return*/public int[][] GenerateArray() {// 生成矩阵增加还没有做int g[][] = new int[4][12];int l = 1;int m = 1;for (int i = 1; i < 16; i++) { // 二进制m = i;if (i != 1 && i != 2 && i != 4 && i != 8) {for (int j = 3; j >= 0; j--) {g[j][l] = m % 2;m = m / 2;if (m < 0) {break;}}l++;}}// G 生成int[][] G = new int[11][15];for (int i = 0; i < G.length; i++) {for (int j = 0; j < G[i].length; j++) {if (j == i) {G[i][j] = 1;} else {G[i][j] = 0;}}}for (int j = 11; j < 15; j++) {for (int i = 0; i < G.length; i++) {G[i][j] = g[j - 11][i + 1];}}System.out.println("(15,11)HammingCode生成矩阵:");System.out.println("----------------------------------------------------------");for (int i = 0; i < 11; i++) {for (int j = 0; j < 15; j++) {System.out.print(G[i][j] + " ");}System.out.println();}System.out.println("----------------------------------------------------------");return G;}/*** @param encode* 用生成矩阵编码* @param G* 代表生成矩阵* @param send* 输入的字符诸位 1、0 等* @return*/public int[] encode(int[][] G, int[] send) { // 利用生成矩阵编码int[] newArray = new int[G[1].length]; // 得到X*G的一个矩阵for (int i = 0; i < newArray.length; i++) {newArray[i] = 0;for (int j = 0; j < G.length; j++)newArray[i] += send[j] * G[j][i];if ((newArray[i] & 1) == 1) {newArray[i] = 1;} else {newArray[i] = 0;}}System.out.print("(15,11)HammingCode的编码:");for (int i = 0; i < newArray.length; i++) {System.out.print(newArray[i] + " ");}return newArray;}/**** @param H* 校验矩阵错误* @param receive* 收到的信息* @return返回海明码的译码*/public int[] checkAndDecode(int[][] H, int[] receive) { // 检测错误以及纠正错误int[] e = new int[H.length]; // H*x得到int flag = 0;for (int i = 0; i < e.length; i++) { // 得到Hx的一个矩阵e[i] = 0;for (int j = 0; j < receive.length; j++) {e[i] = e[i] ^ (receive[j] & H[i][j + 1]);}}// 检测编码是否有错 H*x=0System.out.print("H*x为:");for (int i = 0; i < e.length; i++) {System.out.print(e[i] + " ");}System.out.println();for (int i = 0; i < e.length; i++) {if (e[i] != 0) {flag = -1;break;}}if (flag == -1) { // 代表有错 flag 得到位错的下标flag = 0;int k = 0;for (int i = e.length - 1; i >= 0; i--) {flag += Math.pow(2, i) * e[k];k++;}System.out.print("接收的数据第" + flag + "位有错:");for (int i = 0; i < receive.length; i++) {System.out.print(receive[i]);}System.out.println();// 进行纠错flag = flag - 1;receive[flag] = receive[flag] ^ 1;System.out.print("接收的数据纠错后:");for (int i = 0; i < receive.length; i++) {System.out.print(receive[i]);}} else {// System.out.println();System.out.print("接收正确,数据为:");for (int i = 0; i < receive.length; i++) {System.out.print(receive[i]);}}System.out.println();System.out.print("(15,11)HammingCode译码为:");for (int i = 0; i < 11; i++) {System.out.print(receive[i] + " ");}System.out.println();return e;}public static void main(String[] args) {HammingCode HMC = new HammingCode();HMC.start(HMC);}}结果如下:校验矩阵和生成矩阵结果如图:当输入正确与接收相同时结果如图:当收到结果有错的时候(其中错误为非校验位)结果如图:当收到结果有错的时候(其中错误为校验位)结果如图://进过三种不同的形式的检验,得到编写的15,11,3海明码的算法正确。
汉明码编码

HUNAN UNIVERSITY信息论与编码实验报告题目:汉明编码****:***学生学号: ***********专业班级:通信工程5班课程老师:肖竹一、实验名称:汉明码二、实验环境软件环境:Windows 2000,Microsoft Visual C++6.0硬件环境:P4,2.4GHz,256内存,IBM-PC及兼容机三、实验目的了解汉明码的编码原理,纠错原理,译码原理;给定汉明码的监督矩阵,能够写出生成矩阵,能够通过监督矩阵或生成矩阵进行编码,能够通过监督矩阵进行校码与译码,会计算汉明码的错误概率以及导出增余汉明码等相关知识。
四、实验内容在Microsoft Visual c++ 6.0软件环境下,编写一个程序,使之实现汉明码以及增余汉明码的编码、检码、译码过程。
1、通过对书本的学习,以及对课堂知识的掌握,了解汉明码的纠错原理,编写出汉明码的纠错程序。
2、基于汉明码的编写,进一步完成对检码译码及增余汉明码的实现。
3、实验验证程序的合理性,结果的正确性,和结构的完善性。
五、实验过程与实验结果源程序:#include<iostream>#include<string>using namespace std;#define Pe 0.0001class HMCoding{private:int n,k,r;//汉明码参数int i,j;//用于指示循环次数int **H,*X,**G,**check_code;string *H_Column,*H_Column_Z,code_str;int code_num,code_num_z;public:void Initializing(int,int);void Show_H(int,int);void Get_G();void Show_G(int,int);void HM_Efficiency_Analysing();/*对汉明码进行编码效率分析*/int Binary_Str_Check(string);void Encoding();//汉明码编码void Encoding_Z();//增余汉明码编码void Decoding();//汉明码译码void Decoding_Z();//增余汉明码译码void Get_H_Column();//获取汉明码监督矩阵的每一列void Get_H_Column_Z();//获取增余汉明码监督矩阵的每一列void Get_Judge_Result();//获取汉明码校码结果void Get_Judge_Result_Z();//获取增余汉明码校码结果void Checking();//汉明码校码void Checking_Z();//增余汉明码校码void GOTO_HMCding_Z();};HMCoding hmcoding;//全局变量/*********************************初始化模块*********************************/void HMCoding::Initializing(int _n,int _k){n=_n;k=_k;r=_n-_k;cout<<"请给定("<<n<<","<<k<<")汉明码的监督矩阵H["<<r<<"]["<<n<<"]:"<<endl;H=new int *[r+1];//初始化(n,k)汉明码监督矩阵for(i=0;i<r+1;i++)H[i]=new int[n+1];for(i=0;i<r;i++)for(j=0;j<n;j++)cin>>H[i][j];//初始化增余项for(j=0;j<n+1;j++)H[r][j]=1;for(i=0;i<r;i++)H[i][n]=0;//为X分配存储单元X=new int[n+1];for(j=0;j<n+1;j++)X[j]=0;Get_H_Column();//获取监督矩阵的每一列Get_H_Column_Z();//进一步获取增余监督矩阵的每一列}//获取监督矩阵的每一列,用于汉明码校码void HMCoding::Get_H_Column(){string temp;H_Column=new string[n+1];for(i=0;i<n;i++){temp="";for(j=0;j<r;j++){if(!H[j][i])temp+='0';elsetemp+='1';}H_Column[i]=temp;}H_Column[n]="000";}//获取增余监督矩阵的每一列,用于增余汉明码校码void HMCoding::Get_H_Column_Z(){H_Column_Z=new string[n+2];for(i=0;i<n+1;i++)H_Column_Z[i]=H_Column[i]+'1';H_Column_Z[n+1]="0000";}void HMCoding::Show_H(int x,int y){for(i=0;i<x;i++){for(j=0;j<y;j++)cout<<H[i][j]<<" ";cout<<endl;}}void HMCoding::Get_G(){G=new int *[k];for(i=0;i<k;i++)G[i]=new int[n];for(i=0;i<k;i++)for(j=0;j<k;j++){if(i==j)G[i][j]=1;elseG[i][j]=0;}for(i=0;i<r;i++)for(j=0;j<k;j++)G[j][i+k]=H[i][j];}void HMCoding::Show_G(int x,int y){Get_G();for(i=0;i<x;i++){for(j=0;j<y;j++)cout<<G[i][j]<<" ";cout<<endl;}}void HMCoding::HM_Efficiency_Analysing(){cout<<"对("<<n<<","<<k<<")汉明码的评价如下:"<<endl;cout<<"("<<n<<","<<k<<")汉明码的效率E=k/n*100%="<<k*1.0/n*100<<"%"<<endl;cout<<"("<<n<<","<<k<<")汉明码的错误概率P=n*(n-1)*Pe*Pe="<<n*(n-1)*Pe*Pe<<endl;}/*********************************编码模块*********************************///二进制序列合理性检测int HMCoding::Binary_Str_Check(string temp){int flag=1;//先假设输入的消息串不含除0、1外的字符for(int i=0;temp[i]!='\0';i++){if(!(temp[i]=='0'||temp[i]=='1')){flag=0;break;}}return flag;}//汉明码编码void HMCoding::Encoding(){A: string binary_str;int flag;int binary_num=0;cout<<"请输入待编码的二进制序列:"<<endl;cin>>binary_str;flag=Binary_Str_Check(binary_str);while(binary_str[binary_num]!='\0')binary_num++;/*统计输入的二进制序列所含码元个数*/if(binary_num%k!=0&&flag)/*序列所含码元个数不是k的整数倍,无法全部编码*/{cout<<"您输入的二进制序列存在冗余,请重新输入!\n";goto A;}if(binary_num%k!=0&&!flag){cout<<"您输入的二进制序列存在冗余且含除0、1外的字符,请重新输入!\n";goto A;}if(binary_num%k==0&&!flag){cout<<"您输入的二进制序列含除0、1外的字符,请重新输入!\n";goto A;}code_str="";for(i=0;i<binary_num;i=i+k){for(j=0;j<k;j++)/*获取k位信息元*/{if(binary_str[i+j]=='0')X[j]=0;elseX[j]=1;}int temp;string partial_str="";for(int t=0;t<n;t++){/*用k位信息元组成的向量与生成矩阵作矩阵乘法,得到对应n元码组*/temp=0;for(j=0;j<k;j++)temp+=X[j]*G[j][t];if(temp%2==0)partial_str+='0';elsepartial_str+='1';}code_str+=partial_str;}cout<<"进行("<<n<<","<<k<<")汉明码编码后的二进制序列为:\n"<<code_str<<endl;}//增余汉明码编码void HMCoding::Encoding_Z(){code_str="";A_Z:string binary_str;int flag;int binary_num=0;cout<<"请输入待编码的二进制序列:"<<endl;cin>>binary_str;flag=Binary_Str_Check(binary_str);while(binary_str[binary_num]!='\0')binary_num++;/*统计输入的二进制序列所含码元个数*/if(binary_num%k!=0&&flag)/*序列所含码元个数不是k的整数倍,无法全部编码*/{cout<<"您输入的二进制序列存在冗余,请重新输入!\n";goto A_Z;}if(binary_num%k!=0&&!flag){cout<<"您输入的二进制序列存在冗余且含除0、1外的字符,请重新输入!\n";goto A_Z;}if(binary_num%k==0&&!flag){cout<<"您输入的二进制序列含除0、1外的字符,请重新输入!\n";goto A_Z;}for(i=0;i<binary_num;i=i+k){for(j=0;j<k;j++)/*获取k位信息元*/{if(binary_str[i+j]=='0')X[j]=0;elseX[j]=1;}int temp;string partial_str="";for(int t=0;t<n;t++){/*用k位信息元组成的向量与生成矩阵作矩阵乘法,得到对应n元码组*/temp=0;for(j=0;j<k;j++)temp+=X[j]*G[j][t];if(temp%2==0){partial_str+='0';X[j+k]=0;}else{partial_str+='1';X[j+k]=1;}}//生成增余汉明码最后一位//监督规则:对原汉明码所有n个码元取模2和int sum=0;for(j=0;j<n;j++)sum+=X[j];if(sum%2==0)partial_str+='0';elsepartial_str+='1';code_str+=partial_str;}cout<<"进行("<<n+1<<","<<k<<")增余汉明码编码后的二进制序列为:\n"<<code_str<<endl;}/*********************************校码模块*********************************///利用汉明码校码void HMCoding::Checking(){B: string binary_str;int flag;int binary_num=0;cout<<"请输入待译的二进制序列:"<<endl;cin>>binary_str;flag=Binary_Str_Check(binary_str);while(binary_str[binary_num]!='\0')binary_num++;/*统计输入的二进制序列所含码元个数*/if(binary_num%n!=0&&flag)/*序列所含码元个数不是n的整数倍,无法全部译码*/{cout<<"您输入的二进制序列存在冗余,请重新输入!\n";goto B;}if(binary_num%n!=0&&!flag){cout<<"您输入的二进制序列存在冗余且含除0、1外的字符,请重新输入!\n";goto B;}if(binary_num%n==0&&!flag){cout<<"您输入的二进制序列含除0、1外的字符,请重新输入!\n";goto B;}code_num=binary_num/n;//统计n元码组的个数check_code=new int*[code_num];for(i=0;i<code_num;i++)check_code[i]=new int[n];for(i=0;i<code_num;i++){/*每次取n个码元进行校正*/for(j=0;j<n;j++){check_code[i][j]=binary_str[i*n+j]-'0';}}Get_Judge_Result();}//利用增余汉明码校码void HMCoding::Checking_Z(){B_Z:string binary_str;int flag;int binary_num=0;cout<<"请输入待译的二进制序列:"<<endl;cin>>binary_str;flag=Binary_Str_Check(binary_str);while(binary_str[binary_num]!='\0')binary_num++;/*统计输入的二进制序列所含码元个数*/if(binary_num%(n+1)!=0&&flag)/*序列所含码元个数不是n+1的整数倍,无法全部译码*/{cout<<"您输入的二进制序列存在冗余,请重新输入!\n";goto B_Z;}if(binary_num%(n+1)!=0&&!flag){cout<<"您输入的二进制序列存在冗余且含除0、1外的字符,请重新输入!\n";goto B_Z;}if(binary_num%(n+1)==0&&!flag){cout<<"您输入的二进制序列含除0、1外的字符,请重新输入!\n";goto B_Z;}code_num_z=binary_num/(n+1);//统计n+1元码组的个数check_code=new int*[code_num_z];for(i=0;i<code_num_z;i++)check_code[i]=new int[n+2];for(i=0;i<code_num_z;i++){/*每次取n+1个码元进行校正*/for(j=0;j<n+1;j++){check_code[i][j]=binary_str[i*(n+1)+j]-'0';}}Get_Judge_Result_Z();}//获取汉明码校码结果void HMCoding::Get_Judge_Result(){int temp;int flag;string partial_str;cout<<"("<<n<<","<<k<<")汉明码校码结果如下:"<<endl;cout<<"码组状态校正后"<<endl;for(int t=0;t<code_num;t++){flag=0;partial_str="";for(i=0;i<r;i++){temp=0;for(j=0;j<n;j++)temp+=H[i][j]*check_code[t][j];if(temp%2==0)partial_str+='0';elsepartial_str+='1';}//对partial_str进行判断for(i=0;i<n+1;i++){if(H_Column[i]==partial_str){flag=1;break;}}if(flag&&i<n)//表示第i个码元出错,将其改正{for(j=0;j<n;j++)cout<<check_code[t][j];cout<<" 第"<<i+1<<"位错,可纠正";check_code[t][i]=(check_code[t][i]+1)%2;//1变0,0变1for(j=0;j<n;j++)cout<<check_code[t][j];}if(flag&&i==n)//表示全对{for(j=0;j<n;j++)cout<<check_code[t][j];cout<<" 全对";for(j=0;j<n;j++)cout<<check_code[t][j];}cout<<endl;}}//获取增余汉明码校码结果void HMCoding::Get_Judge_Result_Z(){int temp;int flag;string partial_str;cout<<"("<<n+1<<","<<k<<")增余汉明码校码结果如下(注:* 表示无法识别的码元):"<<endl;cout<<"码组状态校正后"<<endl;for(int t=0;t<code_num_z;t++){flag=0;partial_str="";for(i=0;i<r+1;i++){temp=0;for(j=0;j<n+1;j++)temp+=H[i][j]*check_code[t][j];if(temp%2==0)partial_str+='0';elsepartial_str+='1';}//对partial_str进行判断for(i=0;i<n+2;i++){if(H_Column_Z[i]==partial_str){flag=1;break;}}if(flag&&i<n+1)//表示第i个码元出错,将其改正{check_code[t][n+1]=1;//表示正确接收for(j=0;j<n+1;j++)cout<<check_code[t][j];cout<<" 第"<<i+1<<"位错,可纠正";check_code[t][i]=(check_code[t][i]+1)%2;//1变0,0变1for(j=0;j<n+1;j++)cout<<check_code[t][j];}if(flag&&i==n+1)//表示全对{check_code[t][n+1]=1;//表示正确接收for(j=0;j<n+1;j++)cout<<check_code[t][j];cout<<" 全对";for(j=0;j<n+1;j++)cout<<check_code[t][j];}if(!flag){check_code[t][n+1]=0;//表示两位出错并无法纠正for(j=0;j<n+1;j++)cout<<check_code[t][j];cout<<" 某两位出错,无法纠正";for(j=0;j<n+1;j++)cout<<'*';//* 表示无法正确识别的码元}cout<<endl;}}/*********************************译码模块*********************************///利用汉明码译码void HMCoding::Decoding(){cout<<"("<<n<<","<<k<<")汉明码译码结果为:"<<endl;for(i=0;i<code_num;i++){for(j=0;j<k;j++)cout<<check_code[i][j];}cout<<endl;}//利用增余汉明码译码void HMCoding::Decoding_Z(){cout<<"("<<n+1<<","<<k<<")增余汉明码译码结果为(注:* 表示无法识别的码元):"<<endl;for(i=0;i<code_num_z;i++){if(check_code[i][n+1]==1){for(j=0;j<k;j++)cout<<check_code[i][j];}else{for(j=0;j<k;j++)cout<<'*';}}cout<<endl;}/*********************************主函数*********************************/void HMCoding::GOTO_HMCding_Z(){char choice1=' ';cout<<"\n ***************欢迎进入("<<n+1<<","<<k<<")增余汉明码编码/校码/译码系统****************\n";cout<<"由汉明监督矩阵导出的增余监督矩阵H["<<r+1<<"]["<<n+1<<"]为:"<<endl;hmcoding.Show_H(r+1,n+1);码编码/校码/译码系统<<<<<<<<<<<<<<<<<<<<\n";cout<<" "<<"E.增余汉明码编码"<<" "<<"D.增余汉明码校码/译码"<<" "<<"R.返回"<<" "<<"Q.退出"<<endl;cout<<"请输入您要操作的步骤:";cin>>choice1;if(choice1=='E'||choice1=='e')//进行编码{hmcoding.Encoding_Z();goto Z;}else if(choice1=='D'||choice1=='d'){hmcoding.Checking_Z();hmcoding.Decoding_Z();goto Z;}else if(choice1=='R'||choice1=='r')return;else if(choice1=='Q'||choice1=='q')//退出{exit(0);}else//如果选了选项之外的就让用户重新选择{cout<<"您没有输入正确的步骤,请重新输入!"<<endl;goto Z;}cout<<endl;}void main(){char choice=' ';//用于记录初始化情况int flag=0;int n,k;cout<<"\n *************************汉明码编码/校码/译码系统*************************\n";cout<<"请输入汉明码的码长n=";cin>>n;cout<<"请输入汉明码的信息元个数k=";cin>>k;while(choice!='Q'&&choice!='q')//当choice的值不为q且不为Q时循环{码编码/校码/译码系统<<<<<<<<<<<<<<<<<<<<\n";cout<<" "<<"I.输入建立"<<" "<<"E.汉明码编码"<<" "<<"D.汉明码校码/译码\n";cout<<" "<<"Z.进入相应的增余汉明码系统"<<" "<<"Q.退出\n";cout<<"请输入您要操作的步骤:";cin>>choice;if(choice=='I'||choice=='i')//初始化{if(!flag){//初次执行初始化操作flag=1;}hmcoding.Initializing(n,k);cout<<"您输入的监督矩阵H["<<n-k<<"]["<<n<<"]为:"<<endl;hmcoding.Show_H(n-k,n);cout<<"该监督矩阵对应的生成矩阵G["<<k<<"]["<<n<<"]为:"<<endl;hmcoding.Show_G(k,n);hmcoding.HM_Efficiency_Analysing();}else if(choice=='E'||choice=='e')//进行编码{if(!flag){cout<<"操作错误!请执行输入建立操作后再进行本操作!"<<endl;goto C;}hmcoding.Encoding();}else if(choice=='D'||choice=='d')//校码、译码{if(!flag){cout<<"操作错误!请执行输入建立操作后再进行本操作!"<<endl;goto C;}hmcoding.Checking();hmcoding.Decoding();}else if(choice=='Z'||choice=='z'){if(!flag){cout<<"操作错误!请执行输入建立操作后再进行本操作!"<<endl;goto C;}//进入增余汉明码系统hmcoding.GOTO_HMCding_Z();}else if(choice=='Q'||choice=='q')//退出{exit(0);}else//如果选了选项之外的就让用户重新选择{cout<<"您没有输入正确的步骤,请重新输入!"<<endl;goto C;}cout<<endl;}}运行结果:1、首先需输入建立(n,k)汉明码2、给定监督矩阵,导出相应的生成矩阵,显示出错误概率及编码效率3、汉明码编码注:输入的信息序列应为k的整数倍,否则会报错。
实验三 汉明码编译码实验

实验三汉明码编译码实验
汉明码编译码实验
一、实验目的
1、了解信道编码在通信系统中的重要性。
2、掌握汉明码编译码的原理。
3、掌握汉明码检错纠错原理。
4、理解编码码距的意义。
二、实验原理
1、实验原理框图汉明码编译码实验框图汉明码编码过程:数字终端的信号经过串并变换后,进行分组,分组后的数据再经过汉明码编码,数据由4bit变为7bit。
三、实验器材
1、主控&信号源、6号、2号模块各一块
2、双踪示波器一台
3、连接线若干
四、实验步骤汉明码编码规则验证连线汉明码1、2号模块的拨码开关S12#拨为 S22#、S32#、S42#均拨为;2、6号模块的拨码开关S16#拨为0001, S36#拨为0000按下6号模块S2系统复位键。
3、此时2号模块提供32K编码输入数据,6号模块进行汉明编译码,无差错插入模式。
4、用示波器观测6号模块TH5处编码输出波形。
汉明码检纠错性能检验1、6号模块S3拨成0001
按下6号模块S2系统复位。
2、对比观测译码结果与输入信号,验证汉明码的纠错能力。
3、对比观测插错指示与误码指示,验证汉明码的检错能力。
4、、6号模块S3按照插错控制表中的拨码方式,逐一插入不同错误,按下6号模块S2系统复位。
重复步骤2,验证汉明码的检纠错能力。
5、将示波器触发源通道接TP2帧同步信号,示波器另外一个通道接TP1插错指示,可以观测插错的位置。
五、实验数据错2位码时错码检测指示输出波形汉明译码纠错性能检验六、实验分析开头数字序号1。
实验七 汉明码

实验七汉明码一、实验目的1、掌握线性分组码的编码原理2、掌握汉明码编码方法3、了解编码对误码性能的改善二、实验原理3、实验分析1、汉明码的编码输出编码输出(CH1通道)和延时输出(CH2通道)分析:延时输出作为输出编码波形的对比观测点是因为编码过程存在延时,而延时输出的延时与编码输出一致,这样就可以根据直接根据输入波形和编码输出的对应得出编码数据。
编码输出(CH1通道)延时输出和(CH2通道)从后往前读上图为延时输出(直接认为编码输入)为:1010编码输出为:信息位(a6 a5 a4 a3)监督位(a2 a1 a0)信息位(a6 a5 a4 a3)监督位(a2 a1a0)000000010001110001011100110000101011010010001111010110 010100110110000101011011101010011001111101000111000111111 1分析:读数据时从后往前读,读出7位编码输出,然后得出监督位。
进而可以得出监督位的表达式。
2、汉明码的纠错能力译码输入(CH1通道)和译码输出(CH2通道)分析:插入一位误码后仍能恢复出原始信号,故汉明码能纠正一个误码。
编码输入时钟(CH1通道)与编码输出时钟(CH2通道)分析:编码输入时钟为32KHZ,编码输出时钟为56KHZ。
32*(7/4)=56KHZ插错指示(CH1通道)和误码指示( CH2通道)分析:能准确的指出误码的位置。
帧同步信号与插错指示总结:汉明码是一种能纠错一个错误的效率较高的线性编码分组。
3、 QPSK的调制及解调DIN1(CH1通道)与DOUT (CH2通道)分析:能解调出调制信号,波形一致,存在一定延时。
原始时钟信号与解调恢复时钟信号四、实验思考题1、汉明码编码效率?纠检错与码距的关系。
实验中信源传输速率、信道编码以后的速率各是多少?答:汉明码的编码效率为当r很大时,编码效率趋近于1,所以汉明码是一种高效率编码;检错纠错其中最小码距为3,故能检测2个错码,纠正一个错码;信源传输速率为,信道编码以后的速率为。
汉明码编码译码实验报告(信息论与编码)及源程序

}
printf("经过译码后变为: \n");
for(i=0;i<N/4;i++)
{for(j=0;j<3;j++)
{f[j]=0;
for(k=A;k<A+7;k++)
f[j]+=w[k]*H[k-A][j];/////计算伴随式
}
for(m=0;m<7;m++)
{for(j=0;j<3;j++)
printf("%d",ww[A+m]);//没有出错的地方
}
}
A=A+7;//向后移动7位
L=8;//复位
M=0;///清零,复位
printf("\n");
}
}
4
5
这次的实验是实现汉明码的编码与译码,达到纠错功能。通过信息论的课程,我基本了解了汉明码编译的原理和方法,但在编程的过程中遇到了不小的困难。首先还是理解汉明码概念的问题,因为还存在纠错的功能,所以汉明码的编码方式和以前学的哈夫曼编码或Fano编码比起来要复杂不少,开始的时候理解起来有些困难。不过通过仔细看PPT,很快就弄懂了汉明码的原理。但是最开始编出来的程序运行的结果总是不正确,和书上的码字不一样,后来发现是在校验矩阵上出了问题,自己对矩阵方面的知识一直把握得不是很好。经过调试,程序很快就能够正确运行了。
if((f[j]%2)==H[m][j])M=M+1;
if(M==3)L=m ;
M=0;//清零
} ///根据伴随式找到出错的位置
for(m=0;m<7;m{ww[A+m]=(w[A+m]+1)%2;//将出错的地方更正
汉明编码和译码实验

通信原理实验——汉明编码和译码实验学生:XX学号:******XX指导教师:**同组成员:00日期: 2014年12月上课时间:星期三第四大节14:00—16:00目录一、实验目的 (1)二、实验仪器 (1)三、实验原理 (1)1、汉明码的编码规则和纠错能力 (1)四、汉明编译码实验电路的构成 (3)汉明编码模块实验电路工作原理描述如下: (4)1、输入数据 (4)2、m序列发生器 (4)3、编码使能开关 (4)4、错码产生 (4)汉明译码模块实验电路工作原理描述如下: (5)1、输入信号选择开关 (5)2、汉明译码器 (5)3、汉明译码使能开关 (5)五、实验内容 (6)(一)准备工作 (6)(二)编码规则验证 (6)(三)译码数据输出测试 (8)(五)发端加错信号和汉明译码检错能力观测 (10)(六)汉明译码纠错性能测量 (12)六、思考题 (14)1、汉明编码器模块的使能开关、译码器模块的使能开关(H_EN断路器)起什么作用? (14)2、根据实验数据分析汉明码的纠错功能。
(14)3、本实验中汉明编码器的输入数据速率为32kbps,输出数据速率为多少?为什么? (14)参考文献 (14)姓名:XX 学号:122110XX 班级:通信120X第十五周星期三第四大节得分实验名称:汉明编码和译码实验一、实验目的1、掌握汉明码编译码原理。
2、掌握汉明码纠错检错原理。
3、通过纠错编解码实验,加深对纠错编解码理论的理解。
二、实验仪器1、ZH5001A通信原理综合实验系统一台2、20MHz双踪示波器一台三、实验原理1、汉明码的编码规则和纠错能力一般来说,若码长为n,信息位数为k,记作(n,k)码,则监督位数r=n-k。
如果希望用r 个监督位构造出r个监督关系式来指示一位错码的n种可能位置,则要求通信原理综合实验系统中的纠错码系统采用(7,4)汉明码。
用表示这7个码元,用表示3个监督关系式中的校正子,则的值与码元间构成偶数监督关系:在发送端编码时,信息位的值决定于输入信号,因此它们是随机的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
重庆工程学院
电子信息学院
实验报告
课程名称:_ 数据通信原理开课学期:__ 2015-2016/02_ 院(部): 电子信息学院开课实验室:实训楼512
学生姓名: 舒清清梁小凤专业班级: 1491003
学号: ********* *********
重庆工程学院学生实验报告
输入1000,编码1000111 输入1001,编码1001100 输入1010,编码1010010
输入1011,编码1011001 输入1100,编码1100001 输入1101,编码1101010
输入1110,编码1110100 输入1111,编码1111111
六、实验结果及分析
输入和输出会有一个时延,当计算机存储或移动数据时,可能会产生数据位错误,这时可以利用汉明码来检测并纠错,利用了奇偶校验位概念。
七、实验心得、体会及意见
通过实验我对汉明码有了进一步的认识,对生成矩阵有了一定得了解,重要的是我能够用我所学到的理论知识来解决我现所遇到的问题。
