人教版九年级上册数学:圆复习课件示范
合集下载
第二十四章圆 复习课课件(共35张PPT)人教版九年级数学上册

学习目标
知识梳理
典型例题
当堂检测
课堂总结
4.会画三角形的外接圆和内切圆,知道三角形内心和外心的性质,知 道圆内接多边形并会相关计算. 5.知道弧长和扇形面积的计算公式,并能用这些公式进行相关计算.
学习目标
知识梳理
典型例题
当堂检测
课堂总结
1 圆的有关概念及性质 1.定义:平面上到定点的距离等于定长的所有点组成的图形叫做圆. 2.有关概念:
(1)弦、直径(圆中最长的弦)
O.
(2)弧、优弧、劣弧、等弧
(3)弦心距
3.不在同一条直线上的三个点确定一个圆.
学习目标
知识梳理
典型例题
当堂检测
课堂总结
2 圆的对称性 1.圆是轴对称图形,经过圆心的每一条直线都是它的对称轴.圆有无数 条对称轴. 2.圆是中心对称图形,并且绕圆心旋转任何一个角度都能与自身重合, 即圆具有旋转不变性.
解:设直径BC与弦AD交于点E
A
∵∠D=36°,∴∠ABC=36°
∵AD⊥BC,
B
∴在直角三角形ABE中,∠BAD=90°-36°=54°
C E D
学习目标
知识梳理
典型例题
当堂检测
课堂总结
例2.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. (1)若∠CBD=39°,求∠BAD的度数;(2)求证明:∠1=∠2.
典型例题
当堂检测
课堂总结
例3.工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直 径是10mm,测得钢珠顶端离零件表面的距离为8mm,如图所示,则这 个小圆孔的宽口AB的长度为 8 mm.
解析:设圆心为O,连接AO,作出过点O的 弓形高CD,垂足为D,可AO=5mm,OD=3mm 利用勾股定理进行计算,AD=4mm, 所以AB=8mm.
全国优质课一等奖人教版九年级数学上册《圆(复习课件)》公开课课件

符号语言:
04
基础巩固(圆心角与圆周角)
圆心角的定义:顶点在圆心的角叫做圆心角。
圆心角的判断方法:观察顶点是否在圆心。
圆周角的定义:顶点在圆上,两边都和圆相交的角叫做圆周角。
圆周角的特征: ①顶点在圆上;②两边都和圆相交。
05
基础巩固(弧、弦、圆心角之间的关系)
在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相
基础回顾
02
热考题型
03
直击中考
CONTENTS
基础回顾
01
基础巩固(圆的概念)
如图,在一个平面内,线段OA绕它固定的一个端点O旋转一周,
另一个端点A所形成的图形叫做圆。
其中,固定的端点O叫做圆心。
线段OA叫做半径。
以点O为圆心的圆,记作“⊙O”,读作“圆O”。
02
基础巩固(圆的特征)
【特征一】圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点组成的图形。
( n 2) 180
正n边形的一个内角的度数是____________;
n
360
中心角是___________;
n
相等
正多边形的中心角与外角的大小关系是________.
正n边形的周长为 P=na (P为正n边形的周长,α为边长)
正n边形的周长为 S
A
B
1
Pr (S为正多边形的面积,P为正多边形的周长,
①三角形内切圆半径公式: r
C
其中S为三角形的面积;C为三角形的周长.
ab
a +b- c
.
或r =
②特殊的直角三角形内切圆半径公式:r =
a+b+c
人教版九年级上册教材数学:圆复习课件演示
圆的定义(集合观点)
• 圆是到定点的距离等于定长的点的集合。 – 圆上各点到定点(圆心)的距离都等于定长 (半径); – 到定点的距离等于定长的点都在圆上。
• 一个圆把平面内的所有点 分成了多少类?
• 你能模仿圆的集合定义思 想,说说什么是圆的内部 和圆的外部吗?
人教版九年级上册教材数学:圆复习 课件演 示
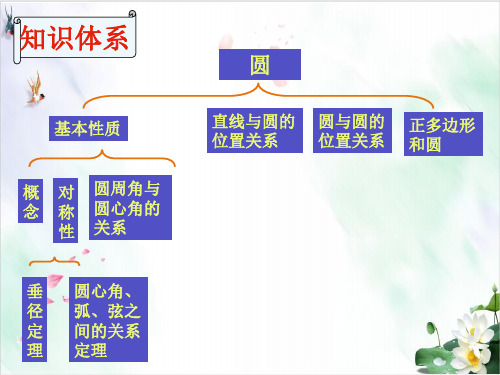
知识体系
基本性质
概 对 圆周角与 念 称 圆心角的
性 关系
垂 圆心角、 径 弧、弦之 定 间的关系 理 定理
圆
直线与圆的 圆与圆的 正多边形 位置关系 位置关系 和圆
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
B
人教版九年级上册教材数学:圆复习 课件演 示
A
人教版九年级上册教材数学:圆复习 课件演 示
C
O
C O
B
A B
B A
A
C
O
圆周角:顶点在圆上,并且两边都和圆相 交的角。 圆心角: 顶点在圆心的角.
人教版九年级上册教材数学:圆复习 课件演 示
人教版九年级上册教材数学:圆复习 课件演 示
画图:同一条弧所对的圆周角和圆心角 之间可能出现哪几种不同的位置关系?
人教版九年级上册教材数学:圆复习 课件演 示
A
AO=BO=CO=DO,
侧想半一弧=圆想弧A会D:B有=D将。什弧一么B个C关,圆系弧沿?A着C任一C 条直径O 对折D ,两
性A质O:=B圆O是=C轴O对=D称O图,形,任何B 一条直A 径所在
第24章 圆的复习-九年级数学上册教学课件(人教版)

原 所示,则这个小圆孔的宽口AB的长度为 8 mm.
理
C
精
炼
O
8mm
A
B
提
D
升
与圆有关的概念
典 1.圆:平面内到定点的距离等于定长的所有点组成的图形.
例 2.弦:连结圆上任意两点的线段.
3.直径:经过圆心的弦是圆的直径,直径是最长的弦.
原 4.劣弧:小于半圆周的圆弧.
理 5.优弧:大于半圆周的圆弧.
炼 【注意】(1)三角形的外心是三角形三边的垂直平分线的交点.
(2)一个三角形的外接圆是唯一的.
提
(3)三角形的内心是三角形三条角平分线的交点.
升
(4)一个三角形的内切圆是唯一的.
点与圆的位置关系
典 1.在△ABC中,∠C=90º,AC=1,BC=2,M是AB的中点,以点C为圆 例 心,1为半径作⊙C,则( C )
原 2.垂径定理的推论:平分弦(不是直径)的直径垂直于这条弦, 理 并且平分这条弦所对的两条弧;
精 3.垂径定理的推论:平分弧的直径垂直平分这条弧所对的弦. 炼
提 升
圆的基本性质
典 1.圆的对称性: 例 圆是轴对称图形,任意一条直径所在的直线都是它的对称轴.
原 2.有关圆心角、弧、弦的性质:
理
在同圆或等圆中,如果两个圆心角、
° 精 炼
提 升
典 6.如图,已知A、B、C、D是⊙O上的四点,延长DC,AB相交于点 例 E.若BC=BE.求证:△ADE是等腰三角形.
原 理
精 炼
提 升
典 7.如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 例 (1)若∠CBD=39º,求∠BAD的度数; 原 (2)求证:∠1=∠2. 理
【公开课】人教版九年级数学上册圆复习课课件PPT

2
在Rt△ABC中,由勾股定理得:
AC AB2 BC 2 22 12 3
由(1)知,∠PAC= ∠PCA = ∠P= 60 °
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
PA=AC
3
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
3. 切线长定理
∵PA、PB是⊙O的两条切线
∴PA=PB,∠APO=∠BPO
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
A
O
P
B
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
例2、如图,已知AB为⊙O的直径,PA、PC为⊙O的切线,
A、C为切点, ∠BAC=30°. (1)求∠P的大小 (2)若AB=2,求PA的长(结果保留根号)
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
1. 切线的判定定理
2. 切线的性质定理
∵OC是半径,且AB⊥OC
∴AB与⊙O相切于点C
O
∵ AB与⊙O相切于点C,
OC是半径
.┐
A C B ∴ AB⊥OC
第二十四章 圆复习课 (1)
主要知识 圆的基本性质 与圆有关的位置关系 正多边形和圆 有关圆的计算
垂径定理
垂直于弦的直径平分弦, 并且平分弦所的两条弧.
C
A M└ ●O
B
若 ① CD是直径 ② 弦AB⊥CD
可推得
③AM=BM,
④A⌒C=B⌒C,
⑤A⌒D=⌒BD.
在Rt△ABC中,由勾股定理得:
AC AB2 BC 2 22 12 3
由(1)知,∠PAC= ∠PCA = ∠P= 60 °
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
PA=AC
3
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
3. 切线长定理
∵PA、PB是⊙O的两条切线
∴PA=PB,∠APO=∠BPO
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
A
O
P
B
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
例2、如图,已知AB为⊙O的直径,PA、PC为⊙O的切线,
A、C为切点, ∠BAC=30°. (1)求∠P的大小 (2)若AB=2,求PA的长(结果保留根号)
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
【公开课】人教版九年级数学上册 第24章 圆复习课(课件)(共14张PPT)
1. 切线的判定定理
2. 切线的性质定理
∵OC是半径,且AB⊥OC
∴AB与⊙O相切于点C
O
∵ AB与⊙O相切于点C,
OC是半径
.┐
A C B ∴ AB⊥OC
第二十四章 圆复习课 (1)
主要知识 圆的基本性质 与圆有关的位置关系 正多边形和圆 有关圆的计算
垂径定理
垂直于弦的直径平分弦, 并且平分弦所的两条弧.
C
A M└ ●O
B
若 ① CD是直径 ② 弦AB⊥CD
可推得
③AM=BM,
④A⌒C=B⌒C,
⑤A⌒D=⌒BD.
人教部初三九年级数学上册 圆的复习 名师教学PPT课件

试一试,作辅助线,并讲一讲
注意:
。
●归纳2.
圆在中考常考的题型
1.选择题、填空题、解答题都有。 在填空题、选择题里常考的是单
独的一个知识点如:圆周角、圆心角关系、扇形面积、弧长、圆锥
侧面积的计算等等;
2.解答题常常是几个知识点综合起来考。常考的有:切线的性质与
判定,垂径定理或圆周角定理结合勾股定理或相似三角形来考。
半径与弦长计算,弦心距来中间站。 圆上若有一切线,切点圆心半径连。 切线长度的计算,勾股定理最方便。 要想证明是切线,半径垂线仔细辨。 有直径时径连弦,所对半圆出直角。 弧有中点圆心连,垂径定理要记全。 要想作个外接圆,各边作出中垂线。 还要作个内接圆,内角平分线梦圆。
心,OB为半径的圆交BC于点D,过D作DE⊥AC,垂足为E(如图
①).
证明:DE是☉O 的切线.
三.展示反馈
●归纳1.圆中常用辅助线的添加方法
1.连圆心,造半径; 2.作垂直(弦心距),用垂径和勾股定理; 3.有直径,出直角; 4.证明切线分两类,有交点时作半径,证垂直。
无交点时作垂直证半径; 5.有切线,作过切点的半径。
33. 如图,已知△ABC内接于☉O,AB为直径,∠CBA的平分线交 AC于点F,交☉O于点D,DE⊥AB于点E,且交AC于点P,连接AD.
(1)求证:∠DAC=∠DBA; (2)求证:P是线段AF的中点; (3)连接CD,若CD=3,BD=4,求☉O的半径和DE的长. 的半径和DE的长.
圆常作辅助线的口诀
方法1.(有交点时)连半径→证垂直→推切线 方法2.(没交点时)作垂直→证半径→推切线 切线长定理
二.问题探究
●通过典型例题的探究,归纳圆的常 用辅助线的添加方法. ●通过典型例题的探究,归纳圆的内 容在中考常考的题型.
九年级数学上册(人教版)第二十四章《圆》课件

(1)在同圆或等圆中,如果圆心角相等,那么它所 对的弧相等,所对的弦相等. (2)在圆中,如果弧相等,那么它所对的圆心角相 等,所对的弦相等. (3)在一个圆中,如果弦相等,那么它所对的弧相 等,所对的圆心角相等.
O A 2023/1/4
︵ ︵ D ∵ ∠COD =∠AOB ∴ AB = CD C ∴AB=CD
.r
O
S = nπr2
360
2023/1/4
或
S
=
1
2
lr
4.圆柱的展开图:
A
D
h Br C
S侧 =2πr h S全=2πr h+2 π r2
2023/1/4
5.圆锥的展开图:
a h
r S侧 =πr a S全=πr a+ π r2
2023/1/4
a 侧面
底面
常见的基本图形及结论:
AC
A
2023/1/4
构成等腰解疑难; 灵活应用才方便。
2023/1/4
典型例题:
1.如图, ⊙O的直径AB=12,以OA为直径的 ⊙O1交大圆的弦AC于D,过D点作小圆的 切线交OC于点E,交AB于F.
C
DE A O1 O F B
(1)说明D是AC的中点.
(2)猜想DF与OC的位 置关系,并说明理由. (3)若DF=4,求OF的长.
. (3)弦心距
O
2023/1/4
二. 圆的基本性质 1.圆的对称性: (1)圆是轴对称图形,经过圆心的每一条直 线都是它的对称轴.圆有无数条对称轴. (2)圆是中心对称图形,并且绕圆心旋转 任何一个角度都能与自身重合,即圆具 有旋转不变性.
.
2023/1/4
2.同圆或等圆中圆心角、弧、弦之间的关系:
O A 2023/1/4
︵ ︵ D ∵ ∠COD =∠AOB ∴ AB = CD C ∴AB=CD
.r
O
S = nπr2
360
2023/1/4
或
S
=
1
2
lr
4.圆柱的展开图:
A
D
h Br C
S侧 =2πr h S全=2πr h+2 π r2
2023/1/4
5.圆锥的展开图:
a h
r S侧 =πr a S全=πr a+ π r2
2023/1/4
a 侧面
底面
常见的基本图形及结论:
AC
A
2023/1/4
构成等腰解疑难; 灵活应用才方便。
2023/1/4
典型例题:
1.如图, ⊙O的直径AB=12,以OA为直径的 ⊙O1交大圆的弦AC于D,过D点作小圆的 切线交OC于点E,交AB于F.
C
DE A O1 O F B
(1)说明D是AC的中点.
(2)猜想DF与OC的位 置关系,并说明理由. (3)若DF=4,求OF的长.
. (3)弦心距
O
2023/1/4
二. 圆的基本性质 1.圆的对称性: (1)圆是轴对称图形,经过圆心的每一条直 线都是它的对称轴.圆有无数条对称轴. (2)圆是中心对称图形,并且绕圆心旋转 任何一个角度都能与自身重合,即圆具 有旋转不变性.
.
2023/1/4
2.同圆或等圆中圆心角、弧、弦之间的关系:
最新人教版初中九年级上册数学【圆全章复习】教学课件

请补全解答过程.
E
C
6
4
4D
H4
A
O
BF
10
综合运用
小结:
E
E
C
C
D
D
3
3
1 A2
O
BF
A
12
O
BF
综合运用
小结:
E
E
C D
C D
G
H
A
O
BF
A
O
BF
知识梳理
圆的对称性
圆的有关性质 弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
圆 点、直线和圆的位置关系
点和圆的位置关系 直线和圆的位置关系
综合运用
例 如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为 ________cm.
C
O
A
B
综合运用
方法1:作OD⊥AB于D,连接OA,OB.
∵∠C=60°,
∴∠AOB=2∠C=120°.
∵OA=OB,OD⊥AB于D, AB=6 cm,
∴△AOD中,∠ADO=90°,
知识梳理
圆的有关性质
圆的对称性 垂径定理 弧、弦、圆心角之间的关系 定理 同弧上的圆周角和圆心角的关系
圆周角定理
初中数学
重点回顾
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A2 A1
A3
O
B
C
重点回顾
圆周角定理的推论 推论1:同弧或等弧所对的圆周角相等. 推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 推论3:圆内接四边形的对角互补.
切线的判定定理:经过半径的外端并且垂直于这 条半径的直线是圆的切线.
E
C
6
4
4D
H4
A
O
BF
10
综合运用
小结:
E
E
C
C
D
D
3
3
1 A2
O
BF
A
12
O
BF
综合运用
小结:
E
E
C D
C D
G
H
A
O
BF
A
O
BF
知识梳理
圆的对称性
圆的有关性质 弧、弦、圆心角之间的关系
同弧上的圆周角和圆心角的关系
圆 点、直线和圆的位置关系
点和圆的位置关系 直线和圆的位置关系
综合运用
例 如图,⊙O是△ABC的外接圆,若AB=6cm,∠C=60°,则⊙O的半径为 ________cm.
C
O
A
B
综合运用
方法1:作OD⊥AB于D,连接OA,OB.
∵∠C=60°,
∴∠AOB=2∠C=120°.
∵OA=OB,OD⊥AB于D, AB=6 cm,
∴△AOD中,∠ADO=90°,
知识梳理
圆的有关性质
圆的对称性 垂径定理 弧、弦、圆心角之间的关系 定理 同弧上的圆周角和圆心角的关系
圆周角定理
初中数学
重点回顾
圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半.
A2 A1
A3
O
B
C
重点回顾
圆周角定理的推论 推论1:同弧或等弧所对的圆周角相等. 推论2:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径. 推论3:圆内接四边形的对角互补.
切线的判定定理:经过半径的外端并且垂直于这 条半径的直线是圆的切线.
24.1.1 圆. 教学 课件(共21张PPT) 人教版九年级数学上册

固定一点,拉直卷尺,旋转. 追问3:你能否用数学的几何元素来刻画这些关键的操作字眼吗?同时在 纸上画一画圆.
项目活动 探索定义 追问3:你能否用数学的几何元素来刻画这些关键的操作字眼吗?同时在纸上
画一画圆.
圆的旋转定义(描述性定义): 如图,在平面内,线段 OA 绕它固定的一个端点 O 旋转一周,则另一个端点 A 所形成的封闭曲线叫做圆. 其固定的端点 O 叫做圆心; 线段 OA 叫做半径,一般用 r 表示;
察两个圆是否能够重合.
等圆:能够完全重合的两个圆. 等弧:在同圆或等圆中,能够互相重合的弧.
深入思考 探究概念
思考4:长度︵相等的弧︵是等弧吗?
如图,如果 AB 和 CD 的拉直长度都是 10 cm,移动 并调整小圆的位置,是否能使这两条弧完全重合?
不可能完全重合
B D 这两条弧弯曲程度不同
“等弧”≠“长度相等的弧”
弦:连接圆上任意两点的__线__段__.
B 例如:AB、AC.
A
O
C 直径:经过__圆__心___的__弦____. 例如:AB.
直径是_最__长__的弦.
深入思考 探究概念 思考2:用弦将圆分成两部分,请动手画画有几种情况. A
C
O
A
B
O
弦将圆分成两个_不__相__等_的圆弧. 直径将圆分成两个相__等__的圆弧.
道树木的年龄.把树干的横截面看成是圆形的,如果一棵20 年树龄的树的树干直径是23cm,这棵树的半径平均每年增 加多少?
解:这棵树的直径平均每年增加:23÷20=1.15cm; 则其半径平均每年增加:1.15÷2=0.575cm.
课堂小结 收获反思 定义
旋转定义 集合定义
弦(直径)
人教版九年级上册数学《弧、弦、圆心角》圆教学说课复习课件

练习
1.如图,AB,CD 是圆O 的两条弦.
(1)如果AB =CD,那么_____________,____________;
(2)如果
, 那么_____________,____________;
(3)如果∠AOB =∠COD,那么_________,__________;
(4)如果AB=CD,OE⊥AB,OF⊥CD,垂足分别
BOC COD DOE=35 ,
A
· O
B
75 .
巩固练习
判断正误.
× (1)等弦所对的弧相等. ( ) × (2)等弧所对的弦相等. ( ) × (3)圆心角相等,所对的弦相等. ( )
探究新知
素养考点 2 利用弧、弦、圆心角的关系证明相等
例2 如图,在⊙O中, A⌒B=A⌒C ,∠ACB=60°.
B. A⌒B>C⌒D D. 不能确定
课堂检测
能力提升题
如图,已知AB、CD为⊙O的两条弦,A⌒D=B⌒C
求证:AB=CD.
C
证明:连接AO,BO,CO,DO.
∵ A⌒D=B⌒C
B
O.
AOD BOC.
D
AOD+BOD=BOC+BOD. A
即AOB COD,
AB=CD.
课堂检测
拓广探索题 如图,在⊙O中,2∠AOB=∠COD,那么C⌒D=2A⌒B成立
为E,F,OE与OF 相等吗?为什么?
练习
2.如图,AB 是圆O 的直径, ∠AOE 的度数.
,∠COD=35°. 求
练习——易错点
下面的说法正确吗?为什么? 如图,因为∠AOB =∠A’OB ’, 所以
不正确,在同圆或等圆中,才有相等的圆心角所对弧相等.
第二十四章 圆复习【复习课件】九年级数学上册单元复习(人教版)

【注意】(1)三角形的外心是三角形三条边的垂直平分线 的交点.(2)一个三角形的外接圆是唯一的.
知识梳理 考点2 与圆有关的概念 11.三角形的内切圆 内心:三角形的内切圆的圆心叫做这个这个三角形的内心. 【 注 意 】(1) 三 角 形 的 内 心 是 三 角 形 三 条 角 平 分 线 的 交 点.(2)一个三角形的内切圆是唯一的.
知识梳理 考点8 与切线相关的定理 (1)判定定理:经过圆的半径的外端且垂直于这条半径 的直线是圆的切线. (2)性质定理:圆的切线垂直于经过切点的半径. (3)切线长定理:经过圆外一点所画的圆的两条 切线,它们的切线长相等.这一点和圆心的连线 平分这两条切线的夹角.
课堂检测
1.如图,AB 是⊙O 的直径,点 C 在⊙O 上,过点 C 的直线
4.圆锥的侧面积 (1)圆锥的侧面展开图是一个 扇形 . (2)如果圆锥母线长为l,底面圆的半径为r,那么这
个扇形的半径为 l ,扇形的弧长为 2 r . (3)圆锥的侧面积为 lr .
(4)圆锥的全面积为 lr r2 .
知识梳理
考点9 与圆有关的计算
5.圆内接正多边形的计算
360
(1)正n边形的中心角为 n
半径决定大小;(2) 不在同一条直线上的
·
三个点确定一个圆.
知识梳理 考点2 与圆有关的概念 9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接 各等分点所得到的多边形叫作这个圆的内接正多边形,这个 圆是这个正多边形的外接圆. 10.三角形的外接圆 外心:三角形的外接圆的圆心叫做这个这个三角形的外心.
知识梳理
考点9 与圆有关的计算
1.弧长公式 n R
半径为R的圆中,n°圆心角所对的弧长l=__1_8_0__. 2.扇形面积公式
知识梳理 考点2 与圆有关的概念 11.三角形的内切圆 内心:三角形的内切圆的圆心叫做这个这个三角形的内心. 【 注 意 】(1) 三 角 形 的 内 心 是 三 角 形 三 条 角 平 分 线 的 交 点.(2)一个三角形的内切圆是唯一的.
知识梳理 考点8 与切线相关的定理 (1)判定定理:经过圆的半径的外端且垂直于这条半径 的直线是圆的切线. (2)性质定理:圆的切线垂直于经过切点的半径. (3)切线长定理:经过圆外一点所画的圆的两条 切线,它们的切线长相等.这一点和圆心的连线 平分这两条切线的夹角.
课堂检测
1.如图,AB 是⊙O 的直径,点 C 在⊙O 上,过点 C 的直线
4.圆锥的侧面积 (1)圆锥的侧面展开图是一个 扇形 . (2)如果圆锥母线长为l,底面圆的半径为r,那么这
个扇形的半径为 l ,扇形的弧长为 2 r . (3)圆锥的侧面积为 lr .
(4)圆锥的全面积为 lr r2 .
知识梳理
考点9 与圆有关的计算
5.圆内接正多边形的计算
360
(1)正n边形的中心角为 n
半径决定大小;(2) 不在同一条直线上的
·
三个点确定一个圆.
知识梳理 考点2 与圆有关的概念 9.外接圆、内接正多边形:将一个圆n(n≥3)等分,依次连接 各等分点所得到的多边形叫作这个圆的内接正多边形,这个 圆是这个正多边形的外接圆. 10.三角形的外接圆 外心:三角形的外接圆的圆心叫做这个这个三角形的外心.
知识梳理
考点9 与圆有关的计算
1.弧长公式 n R
半径为R的圆中,n°圆心角所对的弧长l=__1_8_0__. 2.扇形面积公式
九年级数学上册第二十四章圆的教学课件人教版

垂直于弦的直径(1)
探究
一、用纸剪一个圆,沿着圆的任意一 条直径对折,重复做几次,你发现了 什么?
圆是轴对称图形,任
何一条直径所在的直
O
线都是它的对称轴。
探究
二、如图,AB是⊙O的一条弦,作直
径CD,使CD⊥AB,垂足为E。
(1)这个图形是轴对称
C
图形吗?如果是,对
称轴是什么?
O
A
B
D
探究
二、如图,AB是⊙O的一条弦,作直
正方形。
C
若AB与AC不相等,
则ADOE是什么四
边形?
A
D
O B
范例
例2、如图,在以O为圆心的两个同心
圆中,大圆的弦AB交小圆与C、D两
点。
求证:AC=BD。
重要辅助线
O
CD
A
B
垂直于弦的直径
巩固
7、如图,已知AC是⊙O的直径,AB 是弦,OM⊥AB。 求证:BC=2OM。
C O
A
B
巩固
8、已知⊙O的半径为5cm,⊙O的两 条平行弦AB=8cm,CD=6cm,求弦 AB与CD之间的距离。
AC=BC,AD=BD?
C
O AE
D
O
BA D
C A
B
C B
E O
D
范例
例1、如图,在⊙O中,弦AB长8cm, 圆心O到AB的距离为3cm,求的⊙O 半径。
转化思想
A
B
圆的线段问题转化
O
为直角三角形问题
巩固
2、已知:在⊙O中,弦AB长8cm,
⊙O半径为5cm,求圆心O到AB的
距离。
A
B
探究
一、用纸剪一个圆,沿着圆的任意一 条直径对折,重复做几次,你发现了 什么?
圆是轴对称图形,任
何一条直径所在的直
O
线都是它的对称轴。
探究
二、如图,AB是⊙O的一条弦,作直
径CD,使CD⊥AB,垂足为E。
(1)这个图形是轴对称
C
图形吗?如果是,对
称轴是什么?
O
A
B
D
探究
二、如图,AB是⊙O的一条弦,作直
正方形。
C
若AB与AC不相等,
则ADOE是什么四
边形?
A
D
O B
范例
例2、如图,在以O为圆心的两个同心
圆中,大圆的弦AB交小圆与C、D两
点。
求证:AC=BD。
重要辅助线
O
CD
A
B
垂直于弦的直径
巩固
7、如图,已知AC是⊙O的直径,AB 是弦,OM⊥AB。 求证:BC=2OM。
C O
A
B
巩固
8、已知⊙O的半径为5cm,⊙O的两 条平行弦AB=8cm,CD=6cm,求弦 AB与CD之间的距离。
AC=BC,AD=BD?
C
O AE
D
O
BA D
C A
B
C B
E O
D
范例
例1、如图,在⊙O中,弦AB长8cm, 圆心O到AB的距离为3cm,求的⊙O 半径。
转化思想
A
B
圆的线段问题转化
O
为直角三角形问题
巩固
2、已知:在⊙O中,弦AB长8cm,
⊙O半径为5cm,求圆心O到AB的
距离。
A
B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆的定义(集合观点)
• 圆是到定点的距离等于定长的点的集合。 – 圆上各点到定点(圆心)的距离都等于定长 (半径); – 到定点的距离等于定长的点都在圆上。
• 一个圆把平面内的所有点 分成了多少类?
• 你能模仿圆的集合定义思 想,说说什么是圆的内部 和圆的外部吗?
圆的定义辨析
• 篮球是圆吗?
– 圆必须在一个平面内
外接圆的圆心叫做三角形的外心,
C CC
三角形叫做圆的内接三角形。
B
A AA
O OO C
B B
问题1:如何作三角形的外接圆?
如何找三角形的外心?
问在题三角2:形三内角吗形?的外心一定▲▲AABAB∠CCC是是=钝锐9角0角°三三O角角形形
B
A
AO=BO=CO=DO,
侧想半一弧=圆想弧A会D:B有=D将。什弧一么B个C关,圆系弧沿?A着C任一C 条直径O 对折D ,两
思考: 1、“同圆或等圆”的条件能否去掉? 2、判断正误:在同圆或等圆中,如果两个 圆心角、两条弧、两条弦、两条弦心距、两个 圆周角中有一组量相等,那么它们所对应的 其余各组量也相等。
B
C
E
A
O
D
O
A
B
F
C
D
推论2 半圆(或直径)所对的圆周角是90°; 90°的圆周角所对的弦是直径。
推论3 如果三角形一边上的中线等于这条边 的一半,那么这个三角形是直角三角形。
B
立吗?
A
变式3:EA=_F_B__, EC=__F_D__。
C
E
O
F
D
B
AC
DB
O
变式4:_O_A_=_O_B_
AC=BD.
变式5:_O_C_=_O_D_
AC=BD.
• 如图,P为⊙O的弦BA延长线上一点, PA=AB=2,PO=5,求⊙O的半径。
B
M
A
P
关于弦的问题,常常需
O
要过圆心作弦的垂线段,
•
4.根据结构来梳理。按照情节的开端 、发展 、高潮 和结局 来划分 文章层 次,进而 梳理情 节。
•
5.根据场景来梳理。一般一个场景可 以梳理 为一个 情节。 小说中 的场景 就是不 同时间 人物活 动的场 所。
•
6.根据线索来梳理。抓住线索是把握 小说故 事发展 的关键 。线索 有单线 和双线 两种。 双线一 般分明 线和暗 线。高 考考查 的小说 往往较 简单,线 索也一 般是单 线式。
C
C
C
O
化
归
B
A
化
O
归
A
O A
分类讨论 B
完全归纳法 B
圆周角定理
C
O
B
C O
D A
1、已知∠AOB=75°,求: ∠ACB
O
2、已知∠AOB=120°,
A 求: ∠ACB
B
3、已知∠ACD=30°,求: ∠AOB
4、已知∠AOB=110°,求:
B ∠ACB
O
A
C A
B C
• 定理:一条弧所对的圆周角等于它所对 的圆心角的一半。
• 以3cm为半径画圆,能画多少个? • 以点O为圆心画圆,能画多少个? • 由此,你发现半径和圆心分别有什么作用?
– 半径确定圆的大小;圆心确定圆的位置
• 圆是“圆周”还是“圆面”?
– 圆是一条封闭曲线
• 圆周上的点与圆心有什么关系?
点与圆的位置关系
• 点与圆的位置关系是由什么来决定的 呢? 点到圆心的距离
B
A B
B A
A
C
O
圆周角:顶点在圆上,并且两边都和圆相 交的角。
圆心角: 顶点在圆心的角.
画图:同一条弧所对的圆周角和圆心角 之间可能出现哪几种不同的位置关系?
C
C
C
O
O
A
B
A
O A
B
B
回顾:圆周角等于它所对的弧的度数的一半。
猜想:圆周角和圆心角都是与圆有关的角, 它们之间有什么关系?
一条弧所对的圆周角等于它所对 的圆心角的一半
n°弧
C
一般地,n°的圆心角
对着n°的弧。
D
n°圆心角
圆心角的度数
O
A
1°圆心角 B
1°弧 和它所对的弧 的度数相等。
圆周角
角的顶点 在圆心
F
D C
O
圆心角:如∠BOA 圆内角:如∠BCA
圆外角:如∠BFA
圆周角:如∠BDA
•角的顶点在圆周上 •是否顶点在圆周上 的角就是圆周角呢?
B
A
C
C
O
O
知识体系
基本性质
概 对 圆周角与 念 称 圆心角的
性 关系
垂 圆心角、 径 弧、弦之 定 间的关系 理 定理
圆
直线与圆的 圆与圆的 正多边形 位置关系 位置关系 和圆
圆的定义(运动观点)
在一个平面内,线段OA绕它固 定的一个端点O旋转一周,另一 个端点A随之旋转所形成的图形 叫做圆。
固定的端点O叫做圆心,线段 OA叫做半径,以点O为圆心的圆, 记作☉O,读作“圆O”
(如:∠AOB)
A 弦心距:从圆心到弦的距离。
(如:OC)
O
C
B
如图,∠AOB=∠A`OB`,OC⊥AB, OC`⊥A`B`。
猜想:弧AB与弧A`B`,AB与A`B`, OC与OC`之间的关系,
A
定理 在同圆或等圆中, 相等的圆心角所对的弧相等, 所对的弦相等,所对的弦的 弦心距相等。
C O
B A' C'
性A质O:=B圆O是=C轴O对=D称O图,形,任何B 一条直A 径所在
的直弧线A都D=是弧它B的C=对弧称A轴C 。
=弧BD。
C
D
O
观察右图,有什么等量关系?
AO=BO=CO=DO,弧 AD=弧BD,弧AC= C 弧BC, AE=BE 。
垂直于B 弦的直A
径
O
ED
B
垂径定理 垂直于弦的直径平分这 条弦,并且平分弦所对的两条弧。
– 怎样的两个圆叫同心圆?
– 怎样的两个圆叫等圆?
– 同圆和等圆有什么性质?
– 什么叫等弧?
思考:确定一条直线的条件是什么?
类比联想:是否也存在由几个点确定一个圆呢? 讨论:经过一个点,能作出多少个圆?
经过两个点,如何作圆,能作多少个? 经过三个点,如何作圆,能作多少个?
经过三角形的三个顶点的圆叫做三角形的外接圆,
•
2.它由一系列展示人物性格,反映人物 与人物 、人物 与环境 之间相 互关系 的具体 事件构 成。
•
3.把握好故事情节,是欣赏小说的基础,也是整 体感知 小说的 起点。 命题者 在为小 说命题 时,也必 定以情 节为出 发点,从整体 上设置 理解小 说内容 的试题 。通常 从情节 梳理、 情节作 用两方 面设题 考查。
C E
D O
A
B
A O
B C
F 如等图弧,如所果对弧的A圆B=周弧角C相D,等那;么
∠E在和同∠F圆是中什,么关相系等?的反圆过周来角呢?
D
所对的弧也相等
E
如 如图 果,弧⊙ABO等=1和圆弧⊙C也DO成,2是立那等么圆,
O1
A O2
F
∠E和∠F是什么关系?反过
D
来呢?
C
B
推论1 同弧或等弧所对的圆周角相等; 同圆或等圆中,相等的圆周角所对的弧相等。
C
E • 什么时候圆周角是直角?
D
反过来呢?
O
• 直角三角形斜边中线有什
A
B 么性质?反过来呢?
已知:点O是ΔABC的外心, ∠BOC=130°,求∠A的度数。
C
C
A
O
A
B
B O
•
1.情节是叙事性文学作品内容构成的 要素之 一,是叙 事作品 中表现 人物之 间相互 关系的 一系列 生活事 件的发 展过程 。
如果圆的半径为r, 点到圆心的距离为d,则:
点在圆上 d=r 点在圆内 d<r 点在圆外 d>r
• 弦和直径
与圆有关的概念
– 什么是弦?什么是直径?
– 直径是弦吗?弦是直径吗?
• 弧与半圆
– 什么是圆弧(弧)?怎样表示?
– 弧分成哪几类?
– 半圆是弧吗?弧是半圆吗?
• 弓形是什么?
• 同心圆、同圆、等圆和等弧
①④④ ⑤
② ③ ⑤① ② ③
② ④
①① ④② ⑤④
①
C
③
⑤
A
E
O
D
B
(1)平分弦(不是直径)的直径垂直 于弦,并且平分弦所对的两条弧;
(2)弦的垂直平分线经过圆心,并 且平分弦所对的两条弧;
(3)平分弦所对的一条弧的直径, 垂直平分弦并且平分弦所对的另一条弧。
A
E
C
O
D
B
圆的两条平行弦所夹的弧相等。
• 也可以理解为:一条弧所对的圆心角是 它所对的圆周角的二倍;圆周角的度数 等于它所对的弧的度数的一半。
推论
• 弧相等,圆周角是否相等?反过来呢?
• 什么时候圆周角是直角?反过来呢?
• 直角三角形斜边中线有什么性质?反过 来呢?
如图,比较同∠A弧C所B、对∠的AD圆B、 ∠AEB的大小 周角相等
E
B'
题设
结论
在
同
()
前 提
圆 或 等
圆
中
( 条 件 )
圆 心 角 相 等
圆心角所对的弧相等, 圆 心角所对的弦相等, 圆心 角所对弦的弦心距相等。
