实验八高斯白噪声及低通滤波
加噪信号通过滤波器-实验报告

电子科技大学通信与信息工程学院标准实验报告实验名称:加噪信号通过滤波器电子科技大学教务处制表电子科技大学实验报告学生姓名:王务鹏学号:2901312005吴子文学号:2902111011指导教师:周宁实验室名称:通信系统实验室实验项目名称:加噪信号通过滤波器实验学时:6(课外)【实验目的】自定义信号,利用matlab仿真实现信号+白噪声通过低通系统和带通系统的情形。
通过本实验进一步理解随机白噪声的含义和系统对信号的处理。
【实验原理】白噪声白噪声或白杂讯,是一种功率频谱密度为常数的随机信号或随机过程。
换句话说,此信号在各个频段上的功率是一样的,由于白光是由各种频率(颜色)的单色光混合而成,因而此信号的这种具有平坦功率谱的性质被称作是“白色的”,此信号也因此被称作白噪声。
相对的,其他不具有这一性质的噪声信号被称为有色噪声。
理想的白噪声具有无限带宽,因而其能量是无限大,这在现实世界是不可能存在的。
实际上,我们常常将有限带宽的平整讯号视为白噪音,因为这让我们在数学分析上更加方便。
然而,白噪声在数学处理上比较方便,因此它是系统分析的有力工具。
一般,只要一个噪声过程所具有的频谱宽度远远大于它所作用系统的带宽,并且在该带宽中其频谱密度基本上可以作为常数来考虑,就可以把它作为白噪声来处理。
高斯白噪声高斯白噪声:如果一个噪声,它的幅度分布服从高斯分布,而它的功率谱密度又是均匀分布的,则称它为高斯白噪声。
所谓高斯白噪声中的高斯是指概率分布是正态函数,而白噪声是指它的二阶矩不相关,一阶矩为常数,是指先后信号在时间上的相关性。
这是考查一个信号的两个不同方面的问题。
其信号中包含从负无穷到正无穷之间的所有频率分量,且各频率分量在信号中的权值相同。
白光包含各个频率成分的光,白噪声这个名称是由此由此而来的。
它在任意时刻的幅度是随机的,但在整体上满足高斯分布函数。
【实验记录】实验代码如下:N = 1000;Ts = 0.001;B = 0.5*1/Ts;x = 0:Ts:Ts*(N-1);f = 0:1:B;A =0.5;f0 = 20;y1 = A*sin(2*pi*f0*x); %原正弦信号,频率为20a=0;b=0.1; %均值为a,标准差为bw = normrnd(a,b,[1,N]); %高斯白噪声y=y1+w; %加入噪声之后的信号figure(1)subplot(3,1,1);plot(x,y1,'b');title('原信号 y1=A*sin(20pi*x)');ylabel('y');xlabel('x/20pi');grid;subplot(3,1,2);plot(x,w,'b');title('高斯白噪');ylabel('y');xlabel('x/20pi');subplot(3,1,3);plot(x,y,'b');title('叠加了高斯白噪声的信号');ylabel('y');xlabel('x/20pi');grid;%信号通过低通滤波器M1 = [ones(1,50),zeros(1,B+1-50)]; %50Hz低通滤波器系统的幅度增益F1 = 2*f*Ts;[b1,a1]=yulewalk(19,F1,M1);%计算滤波器(19阶)m=filter(b1,a1,y); %加噪后的信号通过低通滤波器figure(2)subplot(1,2,1);plot(x,m,'b');title('叠加了高斯白噪声的信号通过低通滤波器');subplot(1,2,2);periodogram(m,[],N,1/Ts);%绘制功率谱title('功率谱');%带通滤波器M2 = [zeros(1,9),ones(1,40-9),zeros(1,B+1-40)]; %带通滤波器的幅度增益,通带为10——30HzF2 = 2*f*Ts;[b2,a2]=yulewalk(19,F2,M2);%计算滤波器(19阶)n=filter(b2,a2,y); %加噪后的信号通过带通滤波器figure(3)subplot(1,2,1);plot(x,n,'b');title('叠加了高斯白噪声的信号通过带通滤波器');subplot(1,2,2);periodogram(n,[],N,1/Ts);%绘制功率谱title('功率谱');【实验分析】运行实验代码,得到结果如图所示:由图中结果可以看出,不论是低通滤波器,还是带通滤波器,本实验设计的滤波器均能对噪声信号有一个很好的抑制作用,并且对于自定义的信号来说,低通滤波器有更好的性能。
高斯白噪声(whiteGaussiannoise,WGN)

⾼斯⽩噪声(whiteGaussiannoise,WGN)本⽂科普⼀下⾼斯⽩噪声(white Gaussian noise,WGN)。
百度百科上解释为“⾼斯⽩噪声,幅度分布服从⾼斯分布,功率谱密度服从均匀分布”,听起来有些晦涩难懂,下⾯结合例⼦通俗⽽详细地介绍⼀下。
⽩噪声,如同⽩光⼀样,是所有颜⾊的光叠加⽽成,不同颜⾊的光本质区别是的它们的频率各不相同(如红⾊光波长长⽽频率低,相应的,紫⾊光波长短⽽频率⾼)。
⽩噪声在功率谱上(若以频率为横轴,信号幅度的平⽅为功率)趋近为常值,即噪声频率丰富,在整个频谱上都有成分,即从低频到⾼频,低频指的是信号不变或缓慢变化,⾼频指的是信号突变。
由傅⾥叶变换性质可知,时域有限,频域⽆限;频域有限,时域⽆限。
那么频域⽆限的信号变换到时域上,对应于冲击函数的整数倍(由公式也可推得:)。
即说明在时间轴的某点上,噪声孤⽴,与其它点的噪声⽆关,也就是说,该点噪声幅值可以任意,不受前后点噪声幅值影响。
简⽽⾔之,任意时刻出现的噪声幅值都是随机的(这句话实际上说的就是功率谱密度服从均与分布的意思,不同的是,前者从时域⾓度描述,⽽后者是从频域⾓度描述)。
这⾥要指出功率谱密度(Power Spectral Density,PSD)的概念,它从频域⾓度出发,定义了信号的功率是如何随频率分布的,即以频率为横轴,功率为纵轴。
既然⽩噪声信号是“随机”的,那么反过来,什么叫做“相关”呢?顾名思义,相关就是某⼀时刻的噪声点不孤⽴,和其它时刻的噪声幅值有关。
其实相关的情况有很多种,⽐如此时刻的噪声幅值⽐上⼀时刻的⼤,⽽下⼀时刻的噪声幅值⽐此时刻的还⼤,即信号的幅值在时间轴上按从⼩到⼤的顺序排列。
除此之外,幅值从⼤到⼩,或幅值⼀⼤⼀⼩等都叫做“相关”,⽽⾮“随机”的。
解释完了“⽩噪声”,再来谈谈“⾼斯分布”。
⾼斯分布,⼜名正态分布(normal distribution)。
概率密度函数曲线的形状⼜两个参数决定:平均值和⽅差。
实验1 高斯白噪声及低通滤波

本科学生实验报告学号114090389 姓名简安文学院物电学院专业、班级11电子实验课程名称现代通信原理实验教师及职称金争开课学期2013 至2014学年下学期填报时间2014 年05 月10 日云南师范大学教务处编印本函数。
可以求出输出的自相关函数是()()()()yy xx h h d d R R ταβταβαβ∞∞-∞-∞=+-⎰⎰ (4) 由于我们知道自相关函数和功率谱密度函数是一对傅里叶变换对,所以可以得到输出过程的功率密度谱,即为相关函数的傅里叶变换:()()()()22j f yy yy xx f d f H f e R πτττ∞--∞==ΦΦ⎰ (5)由此可以看出,输出信号的功率谱密度就是输入信号的功率谱密度乘以系统的频率响应的模的平方。
当输入随机过程是白噪声时,输出随机过程的自相关特性和功率密度谱将完全由系统的频率响应所决定。
4.3 实验方案设计本实验采用一个高斯白噪声发生器模块来产生高斯白噪声信号,使其通过三个带宽不同的低通滤波器系统,对输出信号的时域波形进行观察和比较。
本实验的仿真模型文件名是gaussian_noise.mdl ,打开该文件可以看到如图1所示的仿真模型的结构图,该模型实现了白噪声(本实验中白噪声均指高斯加性白噪声)信号通过不同带宽的滤波器。
图中最左端是一个高斯噪声发生器发出白噪声,该白噪声信号分别通过三个滤波器(三个滤波器的名字分别是Digital Filter Design1,Digital Filter Design 2,Digital Filter Design 3),这三个滤波器的带宽各不相同,最后用一个可以同时显示四路波形的示波器来观察时域信号。
图1 设计一个高斯白噪声及三个低通滤波器五. 实验步骤5.1 打开matlab应用软件,如图2所示。
5.2 在图2中右边的命令窗(Command Window)的光标处输入:simulink,回车,打开Simulink Library Browser界面,如图3所示,。
第三章高斯白噪声与匹配滤波器

白噪声的功率谱密度 微分后的功率谱密度 低通滤波后的功率谱密度
高斯白噪声与确定信号的内积
Z是零均值高斯随机变量。
图中是内积操作,此图一般称为相关器
高斯白噪声与两个确定信号的内积
高斯白噪声在归一化正交函数上的 投影
24
4.高斯白噪声通过带通滤波器
高斯白噪声通过带通滤波器的输出是一个带通型的随机过程,一般称为窄带高 斯噪声。
解析信号 复包络
同相分量 正交分量 包络 相位
窄带噪声的 3种表示方法
27
28
29
30
31
32
33
34
35
36
37
38
39
例
41
nL nc j ns Aej
42
43
p nc, ns
1
e nc2ns2
f A, A p nc, ns A
f
理想限带高斯白噪声
自相关函数为
13
高斯白噪声
高斯白噪声是理想限带高斯白噪声的极限:
14
高斯白噪声通过滤波器
高斯白噪声通过滤波器后的 输出是零均值平稳高斯过程
15
方差等于功率,为 另一方面,该滤波器的冲激响应的能量为
16
白噪声的功率谱密度 理想低通滤波器的传递函数 滤波器输出的功率谱密度
例:高斯白噪声通过微分器及理想低通滤波器
《通信原理》第3章
3.3 高斯过程
1. 一维高斯分布 2. 联合高斯 3. 高斯过程
1. 一维高斯(正态)分布
2
Q函数
3
erfc函数
4
联合高斯
推论
7
高斯过程
高斯过程与确定信号的乘积
高斯噪声和白噪声

时逼近横轴 <2> x
<3> <4>
x
处有拐点
域内的概率为99.7% m 3 x m 3
m 2 x m 2 域内的概率为95.4%
m x m 域内的概率为68.3%
(2)高斯噪声特性: <1> 高斯噪声的线性组合仍是高斯噪声
•
单(多)脉冲噪声:瞬态分析法
一、高斯噪声(依噪声幅度分布特性判定)
1、定义:幅度起伏遵从高斯分布的噪声
2、中心极限定理(李雅普诺夫定理):大量N个统计独立的、 具有有限的数学期望和方差的随机变量之和 律在
N 的极限情况下趋于高斯分布律。
Z xi
i 1
N
的分布
3、高斯分布律:
(1)一维概率密度函数:
是由均值 m和均方差
2
唯一确定的函数
<1> 概率密度:
p (x ) 1 2
(x m )2
e
2 2
(1.2.63)
<2> 分布函数:
F ( x ) P ( X x )
2
1
2 ( x m ) x 2 2 e dx
(1.2.64)
<3> 当 m0 时,
N sin B 0 R ( ) P P ( ) rect ( ) (1.2.76) n n n B 2 2 B
式中:
P n
N 0B N 0f 2
为噪声平均功率
<2> 高频限带白噪声:
sin( B 2 ) R ( ) P cos n n 0 B 2
实验八-数字频带系统—2FSK系统

西安邮电大学《通信原理》软件仿真实验报告实验名称:实验八数字频带系统——2FSK系统院系:通信与信息工程学院专业班级:通工学生姓名:学号:(班内序号)指导教师:报告日期:2013年5月15日实验八数字频带系统——2FSK系统●实验目的:1、掌握2FSK信号的波形和产生方法;2、掌握2FSK信号的频谱特点;3、掌握2FSK信号的解调方法;4*、掌握2FSK系统的抗噪声性能。
●仿真设计电路及系统参数设置:数字频带系统——2FSK系统仿真设计电路图1 数字频带系统——2FSK系统仿真设计电路时间参数:No. of Samples =8192;Sample Rate =10000Hz单极性不归零码Rate = 100Hz,Amp =1V,Offset = 1V;载波1Amp = 1V,Freq = 1000Hz;载波2Amp = 1V,Freq= 500Hz;功率谱密度选择(dBm/Hz 1 ohm);带通滤波器8、22参数为850Hz-1150Hz,带通滤波器9、23参数为350Hz-650Hz;低通滤波器14、15、26、27参数为0-250Hz;采样器采样频率为100Hz;比较器,Compare=“>=”,True output=2v,False output=0v;仿真波形及实验分析:1、采用键控法,记录2FSK信号的波形和功率谱密度;2、调整载频,观察并记录2FSK信号功率谱密度的变化;载波1Amp = 1V,Frep = 1000Hz;载波2Amp = 1V,Frep =900Hz;带通滤波器8、22参数改为850Hz-1150Hz,带通滤波器9、23参数为750Hz-1050Hz;图2-1 2FSK信号的功率谱密度分析:由上看出2FSK信号功率谱由连续谱和离散谱两部分构成,离散谱出现在f1和f2位置,连续谱由两个中心位于f1和 f2处的双边谱叠加而成。
连续谱的形状随着两个载频之差|f1-f2|的大小而变化,若|f1-f2|≤fs则出现单峰;若|f1-f2|>fs,出现双峰。
随机实验理想白噪声和带限白噪声的产生与分析-5页word资料

实验八理想白噪声和带限白噪声的产生与分析1.实验目的了解理想白噪声和带限白噪声的基本概念并能够区分它们,掌握用matlab或c/c++软件仿真和分析理想白噪声和带限白噪声的方法。
⒉实验原理所谓白噪声是指它的概率统计特性服从某种分布而它的功率谱密度又是均匀的。
确切的说,白噪声只是一种理想化的模型,因为实际的噪声功率谱密度不可能具有无限宽的带宽,否则它的平均功率将是无限大,是物理上不可实现的。
然而白噪声在数学处理上比较方便,所以它在通信系统的分析中有十分重要的作用。
一般地说,只要噪声的功率谱密度的宽度远大于它所作用的系统的带宽,并且在系统的带内,它的功率谱密度基本上是常数,就可以作为白噪声处理了。
白噪声的功率谱密度为:其中为单边功率谱密度。
2 ) ( 0 N f S n 0 N白噪声的自相关函数位:白噪声的自相关函数是位于τ =0 处,强度为的冲击函数。
这表明白噪声在任何两个不同的瞬间的取值是不相关的。
同时也意味着白噪声能随时间无限快的变化,因为它含一切频率分量而无限宽的带宽。
) ( 20 N R )( 20 N若一个具有零均值的平稳随机过程,其功率谱密度在某一个有限频率范围内均匀分布,而在此范围外为零,则称这个过程为带限白噪声。
带限白噪声分为低通型和带通型。
⒊实验任务与要求⑴用matlab 或c/c++语言编写和仿真程序。
系统框图如图19、图20 所示:特性测试绘制图形低通滤波特性测试绘制图形白噪声图1 低通滤波器系统框图特性测试绘制图形带通滤波特性测试绘制图形白噪声图2 带通滤波器系统框图⑵输入信号为:高斯白噪声信号和均匀白噪声信号,图为高斯白噪声。
⑶设计一个低通滤波器和一个带通滤波器。
要求低通滤波器的通带为0KHz-2KHz、通带衰减小于1db、阻带衰减大于35db。
带通滤波器的通带为10KHz-20KHz、通带衰减小于1db、阻带衰减大于35db。
⑷首先计算白噪声的均值、均方值、方差、概率密度、频谱及功率谱密度、自相关函数。
低通滤波器-实验报告
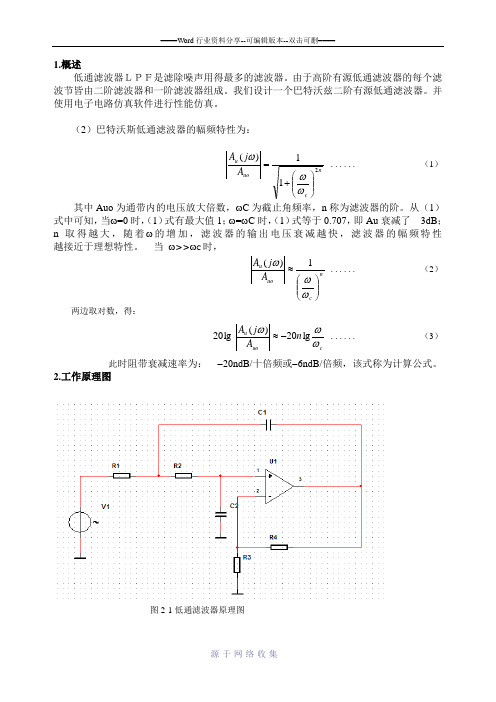
1.概述低通滤波器LPF是滤除噪声用得最多的滤波器。
由于高阶有源低通滤波器的每个滤波节皆由二阶滤波器和一阶滤波器组成。
我们设计一个巴特沃兹二阶有源低通滤波器。
并使用电子电路仿真软件进行性能仿真。
(2)巴特沃斯低通滤波器的幅频特性为:n c uo u A j A 211)(⎪⎪⎭⎫ ⎝⎛+=ωωω . . . . . . (1)其中Auo 为通带内的电压放大倍数,ωC 为截止角频率,n 称为滤波器的阶。
从(1)式中可知,当ω=0时,(1)式有最大值1;ω=ωC 时,(1)式等于0.707,即Au 衰减了 3dB ;n 取得越大,随着ω的增加,滤波器的输出电压衰减越快,滤波器的幅频特性 越接近于理想特性。
当 ω>>ωC 时, n c uo u A j A ⎪⎪⎭⎫ ⎝⎛≈ωωω1)( . . . . . . (2) 两边取对数,得:lg 20cuo u n A j A ωωωlg 20)(-≈ . . . . . . (3) 此时阻带衰减速率为: -20ndB/十倍频或-6ndB/倍频,该式称为计算公式。
2.工作原理图图2-1低通滤波器原理图2-2低通滤波器原理图工作原理:(1)滤波器是具有频率选择作用的电路或运算处理系统。
滤波处理可以利用模拟电路实现,也可以利用数字运算处理系统实现。
滤波器的工作原理是当信号与噪声分布在不同频带中时,可以在频率与域中实现信号分离。
在实际测量系统中,噪声与信号的频率往往有一定的重叠,如果重叠不严重,仍可利用滤波器有效地抑制噪声功率,提高测量精度。
任何复杂地滤波网络,可由若干简单地、相互隔离地一阶与二阶滤波电路级联等效构成。
一阶滤波电路只能构成低通和高通滤波器,而不能构成带通和带阻。
可先设计一个一阶滤波电路来熟悉电路设计思路以及器件使用要求和软件地进一步学习。
有源滤波器地设计,主要包括确定传递函数,选择电路结构,选择有源器件与计算无源元件参数四个过程。
巴特沃斯滤波器的特点是通频带内的频率响应曲线最大限度平坦,没有起伏,而在阻频带则逐渐下降为零。
实验八-高斯白噪声及低通滤波

本科学生综合性实验报告
姓名_石艳红_学院物理与电子信息学院专业电子信息科学与技术班级15级电子班实验课程名称_现代通信原理实验与仿真
指导教师及职称_何文学_副教授__
开课时间2016 至_2017 学年_下学期
云南师范大学教务处编印
一、实验设计方案
图3 SLB界面
5. 用相同的方法创建滤波Digital Filter Design和显示仪器Scope,观察每个设备的连接点,用鼠标左键把设备连接起来,如图4所示。
6. 用鼠标左键选中Gaussian Noise ,再点击右键进行高斯噪声产生器参数设置,如
图 4 一个Gaussian Noise与三个低通滤波器的simulimk设计
图7 Digital Filter Design2参数
图9 设计仿真
9.6.实验结果
该模型仿真后在Scope中看到的波形如图10所示。
图中从上到下的三个波形分别是高斯白噪声通过系统频宽最窄、系统频宽适中、系统频宽最宽的滤波器后的时域波形。
而最后
图11 使用Autoscale功能显示完整的仿真曲线
综述你所了解的Digital Filter Design和Scope模块的功能。
中心极限定理和高斯噪声的产生、白噪声的分析、色噪声的产生。

高斯噪声的自相关函数 10000
0.45 0.4
高斯噪声的概率密度
8000
0.35
6000
0.3 0.25
4000
0.2
2000
0.15 0.1
0
0.05
-2000
0
0.2
0.4
0.6
0.8
1 t
1.2
1.4
1.6
1.8 x 10
2
4
0 -5
-4
-3
-2
-1
0
1
2
3
4
5
实 验 分 析 : 用 matlab 计 算 得 此 高 斯 信 号 的 均 值 为 5.95076876663825e-14 ,约等于 0 。自相关函数近似为一冲击, 功率谱在某一值附近波动,在整个频率轴上均匀分布。这些数学 特征表明该高斯随机信号满足白噪声的相关特性。
d
d d
四、实验总结
1.通过本次实验,我们了解了如何利用同余法中 心极限定理产生白噪声,分析了白噪声的一些数 字特征。 2.对白噪声进行低通滤波后的信号进行功率谱密 度和相关时间的分析,发现此信号较好地符合限 带型高斯白噪声的特性,从而很好地验证了白噪 声理论。
输出信号的功率谱密度函数 0 -5 -10 -15 -20 -25 -30 -35 -40 -45 -50
Power/frequency (dB/rad/sample)
0
0.1
0.2
0.3 0.4 0.5 0.6 0.7 0.8 Normalized Frequency ( rad/sample)
高斯噪声 4 3 2 1 0 -1 -2 -3 -4
0
1000
低通滤波器实验报告

一、实验目的1. 了解低通滤波器的基本原理和设计方法;2. 掌握低通滤波器的性能指标,如截止频率、通带增益、阻带衰减等;3. 学会使用实验仪器对低通滤波器进行测试和调整;4. 培养实验操作能力和数据分析能力。
二、实验原理低通滤波器是一种允许低频信号通过而抑制高频信号的电子滤波器。
根据滤波器的设计方法,低通滤波器可分为有源低通滤波器和无源低通滤波器。
1. 有源低通滤波器:由运算放大器、电阻和电容等元件组成,具有电路简单、易于调整等优点。
其基本原理是利用电容的充放电特性来实现信号的低通功能。
2. 无源低通滤波器:由电阻和电容等元件组成,无源滤波器不具备放大作用,但其电路结构简单,成本较低。
其基本原理是利用电容和电阻的阻抗特性来实现信号的低通功能。
三、实验仪器与设备1. 信号发生器:提供不同频率和幅值的正弦波信号;2. 示波器:观察和分析滤波器输出信号的波形和幅度;3. 函数信号发生器:提供正弦波、方波、三角波等信号;4. 电阻、电容等元件:组成低通滤波器电路;5. 万用表:测量电路中的电压和电流。
四、实验内容与步骤1. 设计有源低通滤波器电路,确定滤波器参数(截止频率、通带增益等);2. 组装电路,连接信号发生器和示波器;3. 输入不同频率的正弦波信号,观察滤波器输出信号的波形和幅度;4. 调整电路参数,使滤波器满足设计要求;5. 测量滤波器的性能指标,如截止频率、通带增益、阻带衰减等;6. 对实验结果进行分析和总结。
五、实验结果与分析1. 有源低通滤波器电路如图1所示,其中R1、R2、C1、C2为电路元件。
图1 有源低通滤波器电路2. 输入频率为1kHz的正弦波信号,观察滤波器输出信号的波形和幅度。
如图2所示。
图2 输入频率为1kHz的滤波器输出信号3. 输入频率为10kHz的正弦波信号,观察滤波器输出信号的波形和幅度。
如图3所示。
图3 输入频率为10kHz的滤波器输出信号4. 调整电路参数,使滤波器满足设计要求。
高斯白噪声滤波

西安电子科技大学课程论文数字图像处理高斯白噪声滤波班级:070821作者:董文凯学号:07082001时间:2018-06-30高斯白噪声滤波实验要求对实际Lena图像分别加入噪声标准差=15,20,25的高斯白噪声,用理想低通滤波器、高斯低通滤波器、算术均值滤波器和中值滤波器对实际Lena图像进行去噪,比较其去噪效果。
b5E2RGbCAP实验内容1.对Lena图像加高斯白噪声1.1原始图例:采用经典Lena图像作为实验样例进行本实验的操作,原始Lena图像见图1.图1 原始Lena图1.2加噪结果:图2 的噪声图图3 的噪声图图4的噪声图结论:经过对以上三图的分析知越大图像越不清晰。
1.3源程序:X=imread('Lena.jpg'>。
J1=imnoise(X,'gaussian',0,0.15^2>。
imshow(J1>;J2=imnoise(X,'gaussian',0,0.20^2>。
imshow(J2>;J2=imnoise(X,'gaussian',0,0.25^2>。
imshow(J2>2对高斯白噪声进行滤波 2.1理想低通滤波器: 2.1.1滤波原理理想低通滤波器:其传递函数为:理想低通滤波器的冲激响应为:2.1.2滤波结果图5 不同值下对图2的滤波结果图6 不同值下对图3的滤波结果图7 不同值下对图4的滤波结果2.1.3源代码X=imread('Lena(25>.jpg'>。
%读取图像 I=rgb2gray(X>。
%将图像变为灰度图 figure 。
%创建图形图像对象 imshow(I>。
%显示灰度图像 title('原始图像'>。
%加标题%将灰度图像的二维不连续Fourier 变换的零频率成分引导频谱的中心s=fftshift(fft2(I>>。
去除高斯白噪声的方法

去除高斯白噪声的方法嘿,咱今儿就来说说去除高斯白噪声这档子事儿啊!你说这高斯白噪声啊,就跟那调皮捣蛋的小鬼似的,老在咱的数据里捣乱。
那咱可得想法子把它给赶跑呀!你想想看,就好比你正听着一首好听的歌呢,结果里面时不时传来一阵滋滋啦啦的声音,多烦人呐!这高斯白噪声就差不多是这么个讨人厌的玩意儿。
那怎么去除它呢?咱可以试试滤波这一招呀!就好像给数据洗个澡,把那些噪声给过滤掉。
比如说中值滤波,就像是个细心的清洁工,把那些突出的噪声给捡走。
还有均值滤波,能让数据变得更平滑,把噪声给抚平咯。
还有啊,咱还能利用一些算法呢!就像武林高手有自己的独门秘籍一样。
比如说小波变换,这可是个厉害的家伙,能把噪声和有用信号给分得清清楚楚,然后把噪声给干掉。
再比如说,咱可以从源头抓起呀!在数据采集的时候就做好防范措施,就跟预防疾病似的,让噪声根本没机会进来。
这就好比你出门的时候带把伞,免得被雨淋了,对吧?还有一种方法呢,就像是给数据穿上一件保护衣。
咱可以对数据进行一些预处理,让它变得更坚强,不那么容易被噪声影响。
你说这去除高斯白噪声是不是挺有意思的呀?咱得跟它斗智斗勇,找到最合适的办法把它给解决掉。
不然它老在那捣乱,咱的工作还怎么进行呀?就好像你家里来了个捣乱的家伙,你不得赶紧把他赶出去呀!所以呀,学会这些去除高斯白噪声的方法,那可真是太重要啦!咱可不能让这小小的噪声影响了咱的大事儿,对吧?总之呢,去除高斯白噪声就像是一场战斗,咱得有策略、有方法,才能把这个小捣蛋鬼给打败。
咱可不能被它给吓住了,得勇敢地去面对它,用咱们的智慧和技巧把它给解决掉。
这样,咱们才能得到干净、准确的数据,才能让我们的工作和研究更顺利地进行下去呀!你说是不是这个理儿呢?。
实验8 图像旋转和去高斯噪声

图像旋转与高斯白噪声姓名:夏夏 班级:2010级信息与计算科学一班 学号:060210055 实验目的1. 掌握图像旋转、图像大小改变的原理。
2. 利用“几何操作”剪切图像、改变图像大小、旋转图像。
3. 了解改变图像大小的方法,包括不同的插值方式。
4. 掌握两种方式下图像的旋转效果。
5. 用3×3的模板处理加了高斯与椒盐噪声之后的图像,比较处理效果。
实验原理:1. 将一幅图像视为一个二维矩阵,用MATLAB 进行图像处理。
2. 利用MATLAB 图像处理工具箱中的函数imread (读)、imshow (显示)、imresize (改变大小)、imrotate (旋转)对图像进行几何操作。
3. 改变图像大小方法:以最近邻插值方法、双线性插值法、双三次插值法。
分析不同的插值法对图像大小的影响。
4. 图像旋转过程:为了观察图像旋转过程的效果,采用不同的方式旋转图像。
5. 对图像旋转自己编程xuanzhuan()进行实现。
6. 高斯白噪声与椒盐噪声处理图像比较。
实验步骤:1. 自己编程xuanzhuan()函数实现图像旋转所说的图像旋转是保持目标区域大小不变化,则整幅图像变大;其实就是用旋转之后的图形覆盖目标区域的面积来确定旋转之后的图,但是由于旋转之后的图有时会有些像素不能被填充,所以会出现很多空点出没数据填充。
旋转之中所用的公式:(,)cos sin a x y x y θθ=-(,)sin cos b x y x y θθ=+(,)cos sin 0(,)sin cos 010011a x y x b x y y θθθθ-⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦或 [][]cos sin 0(,)(,)11sin cos 0001a x y b x y x y θθθθ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦几何运算一般定义为: (,)(',')[(,),(,)]g x y f x y f a x y b x y ==一个几何运算需要两个独立的算法。
产生白噪声的实验报告

一、实验背景白噪声是一种具有平坦频谱特性的噪声,其功率谱密度在所有频率范围内均相等。
白噪声在信号处理、通信、噪声控制等领域具有广泛的应用。
本实验旨在通过搭建实验装置,产生白噪声,并对其进行测量和分析。
二、实验目的1. 了解白噪声的产生原理;2. 掌握白噪声的产生方法;3. 学习白噪声的测量方法;4. 分析白噪声的特性。
三、实验原理白噪声的产生原理是通过随机信号源产生具有平坦频谱特性的噪声。
在实验中,我们可以通过以下方法产生白噪声:1. 采用随机噪声发生器,将随机信号经过滤波器处理后,得到具有平坦频谱特性的白噪声;2. 利用数字信号处理技术,通过随机信号生成算法产生白噪声。
四、实验仪器与设备1. 随机噪声发生器;2. 滤波器;3. 信号分析仪;4. 示波器;5. 数据采集卡;6. 计算机。
五、实验步骤1. 连接实验装置,将随机噪声发生器的输出信号输入滤波器;2. 调整滤波器参数,使滤波器输出信号具有平坦频谱特性;3. 将滤波器输出信号输入信号分析仪,进行频谱分析;4. 使用示波器观察白噪声的波形;5. 使用数据采集卡采集白噪声信号,进行进一步分析。
六、实验结果与分析1. 频谱分析通过信号分析仪对白噪声进行频谱分析,得到白噪声的功率谱密度。
从分析结果可以看出,白噪声的功率谱密度在所有频率范围内均相等,符合白噪声的特性。
2. 波形观察使用示波器观察白噪声的波形,可以看到白噪声的波形具有随机性,无明显规律。
3. 数据分析使用数据采集卡采集白噪声信号,进行进一步分析。
通过分析白噪声的时域特性、频域特性等,可以进一步了解白噪声的特性。
七、实验结论1. 成功搭建了白噪声产生实验装置,并产生了具有平坦频谱特性的白噪声;2. 掌握了白噪声的产生方法、测量方法和特性分析;3. 为后续白噪声在信号处理、通信、噪声控制等领域的应用奠定了基础。
八、实验总结本实验通过对白噪声的产生、测量和分析,使我们了解了白噪声的特性及其应用。
滤波去噪实验报告(3篇)

第1篇一、实验目的本次实验旨在通过计算机辅助技术,对图像进行处理,以实现图像去噪的目的。
通过对比不同滤波算法的效果,分析其优缺点,并了解滤波去噪在图像处理中的应用。
二、实验原理数字图像处理(DIP)是利用计算机对图像信号进行处理的技术。
在图像采集、获取、编码和传输过程中,往往会出现不同程度的噪声污染,影响图像质量。
去噪技术旨在减少或消除图像中的噪声,提高图像质量。
常见的去噪方法包括空域滤波、频域滤波和小波变换滤波等。
本实验主要研究以下几种滤波方法:1. 空域滤波:利用图像像素值的空间相关性,通过局部邻域内的像素值来估计当前像素值,从而达到去噪的目的。
2. 频域滤波:将图像从空间域转换到频域,对频域内的噪声进行处理,再转换回空间域得到去噪后的图像。
3. 小波变换滤波:将图像分解为不同尺度和位置的细节和小波系数,对噪声进行处理,再重构图像。
三、实验设备与软件1. 实验设备:计算机、显示器、鼠标、键盘等。
2. 实验软件:MATLAB。
四、实验步骤1. 加载含噪声的图像。
2. 对图像进行空域滤波,包括均值滤波、中值滤波和高斯滤波等。
3. 对图像进行频域滤波,包括低通滤波和高通滤波等。
4. 对图像进行小波变换滤波,包括小波分解和小波重构等。
5. 对比不同滤波方法的效果,分析其优缺点。
6. 撰写实验报告。
五、实验结果与分析1. 空域滤波效果对比:(1)均值滤波:去除噪声效果较好,但会模糊图像细节。
(2)中值滤波:去除噪声效果较好,且能较好地保留图像细节。
(3)高斯滤波:去除噪声效果较好,但会对图像边缘产生模糊。
2. 频域滤波效果对比:(1)低通滤波:去除高频噪声,保留低频信号,但可能对图像边缘产生模糊。
(2)高通滤波:去除低频噪声,突出高频信号,但可能对图像细节产生模糊。
3. 小波变换滤波效果:(1)小波分解:将图像分解为不同尺度和位置的细节和小波系数,便于噪声处理。
(2)小波重构:将处理后的细节和小波系数进行重构,得到去噪后的图像。
实验1 高斯白噪声及低通滤波-推荐下载

个设备的连接点,用鼠标左键把设备连接起来,如图 4 所示。
对全部高中资料试卷电气设备,在安装过程中以及安装结束后进行高中资料试卷调整试验;通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术通关,1系电过,力管根保线据护敷生高设产中技工资术艺料0不高试仅中卷可资配以料置解试技决卷术吊要是顶求指层,机配对组置电在不气进规设行范备继高进电中行保资空护料载高试与中卷带资问负料题荷试2下卷2,高总而中体且资配可料置保试时障卷,各调需类控要管试在路验最习;大题对限到设度位备内。进来在行确管调保路整机敷使组设其高过在中程正资1常料中工试,况卷要下安加与全强过,看度并22工且22作尽22下可22都能22可地护以缩1关正小于常故管工障路作高高;中中对资资于料料继试试电卷卷保破连护坏接进范管行围口整,处核或理对者高定对中值某资,些料审异试核常卷与高弯校中扁对资度图料固纸试定,卷盒编工位写况置复进.杂行保设自护备动层与处防装理腐置,跨高尤接中其地资要线料避弯试免曲卷错半调误径试高标方中高案资等,料,编试要5写、卷求重电保技要气护术设设装交备备置底4高调、动。中试电作管资高气,线料中课并敷3试资件且、设卷料中拒管技试试调绝路术验卷试动敷中方技作设包案术,技含以来术线及避槽系免、统不管启必架动要等方高多案中项;资方对料式整试,套卷为启突解动然决过停高程机中中。语高因文中此电资,气料电课试力件卷高中电中管气资壁设料薄备试、进卷接行保口调护不试装严工置等作调问并试题且技,进术合行,理过要利关求用运电管行力线高保敷中护设资装技料置术试做。卷到线技准缆术确敷指灵设导活原。。则对对:于于在调差分试动线过保盒程护处中装,高置当中高不资中同料资电试料压卷试回技卷路术调交问试叉题技时,术,作是应为指采调发用试电金人机属员一隔,变板需压进要器行在组隔事在开前发处掌生理握内;图部同纸故一资障线料时槽、,内设需,备要强制进电造行回厂外路家部须出电同具源时高高切中中断资资习料料题试试电卷卷源试切,验除线报从缆告而敷与采设相用完关高毕技中,术资要资料进料试行,卷检并主查且要和了保检解护测现装处场置理设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况,然后根据规范与规程规定,制定设备调试高中资料试卷方案。
图像噪声、均值滤波、高斯滤波、中值滤波

一、图像噪声由于图像采集、处理、传输等过程不可避免的会受到噪声的污染,妨碍人们对图像理解及分析处理。
常见的图像噪声有高斯噪声、椒盐噪声等。
1、椒盐噪声2、高斯噪声高斯噪声是指噪声的密度服从高斯分布的一类噪声,由于高斯噪声在空间和频域中数学上的易处理性,这种噪声(也称为正态噪声)模型经常被用于实践中。
高斯噪声随机变量z的概率密度函数由下式给出:加入高斯噪声后的效果:二、图像平滑图像平滑从信号处理的角度看就是去除其中的高频信息,保留低频信息。
因此我们可以对图像实施低通滤波。
低通滤波可以去除图像中的噪声,对图像进行平滑。
根据滤波器的不同可以分为:均值滤波、高斯滤波、中值滤波、双边滤波我们认为高频信息就是噪声,低频信息就是有用的内容。
1、均值滤波(1)api介绍(2)实例分析import cv2 as cvimport numpy as npimport matplotlib.pyplot as pltfrom matplotlib import font_manager#字体设置my_font = font_manager.fontproperties(fname="c:/windows/fonts/sthupo.ttf")#1、读取图像img = cv.imread("./images/girl.jpg")#2、均值滤波blur = cv.blur(img, (5,5))#3、图像显示plt.figure(figsize=(10,8), dpi=100)# subplot中的121代表[1,2,1],表示在本区域里显示1行2列个图像,最后的1表示本图像显示在第一个位置。
plt.subplot(121)plt.imshow(img[:,:,::-1])plt.title("原图", fontproperties=my_font)plt.xticks([]), plt.yticks([])plt.subplot(122)plt.imshow(blur[:,:,::-1])plt.title("均值滤波后的结果", fontproperties=my_font)plt.xticks([]), plt.yticks([])plt.show()2、高斯滤波图像是二维的,所以使用二维高斯分布。
《高斯噪声和白噪声》课件

# 高斯噪声和白噪声
概述
定义和性质
了解噪声的概念、特性以及对信号处理的影响。
种类
研究不同类型的噪声,如高斯噪声、白噪声等。
应用领域
了解噪声在通信、图像处理等领域中的应用。
高斯噪声
高斯分布的概念
介绍高斯分布及其在噪声中的应用。
性质
探讨高斯噪声的特性,如均值、方差等。
应用场景
了解在不同的应用领域中,高斯噪声和白噪声 的应用。
噪声的处理和降噪
1
噪声的去除方法
介绍降低噪声对信号质量的影响的方法。
2
噪声的抑制方法
探讨噪声抑制技术,如滤波器设计和信号增强。
3
噪声的评估方法了解如何Fra bibliotek估噪声的强度和对信号的影响。
应用案例
语音信号中的噪声抑制
讨论在语音信号处理中抑制噪 声的方法和技术。
统计特性
分析高斯噪声的概率密度函数和累积分布函数。
白噪声
定义和特性
了解白噪声的定义及其在信号处理中的重要性。
白噪声模型及产生机理
介绍白噪声的模型以及产生机理,如随机过程等。
功率谱密度函数
探讨白噪声的频谱特性和谱密度函数。
高斯噪声和白噪声的区别和联系
统计特性上的差异
对比高斯噪声和白噪声在统计特性上的差异。
图像信号中的噪声去除
介绍图像信号处理中的噪声去 除技术。
视频信号中的噪声降噪
了解如何降低视频信号中的噪 声。
结论
1 噪声对信号处理的影响
2 实际应用中的噪声处理策略
总结噪声对信号处理的重要性和影响。
探讨在实际应用中噪声处理的实用策略。
3 未来噪声处理技术的发展方向
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
本科学生综合性实验报告
姓名_石艳红_学院物理与电子信息学院专业电子信息科学与技术班级15级电子班实验课程名称_现代通信原理实验与仿真
指导教师及职称_何文学_副教授__
开课时间2016 至_2017 学年_下学期
云南师范大学教务处编印
一、实验设计方案 实验目的要求 1. 认识Matlab/Simulink 的基本功能。
2. 了解Simulink 的基本图符库,并能做出简单的高斯白噪声仿真。
实验仪器,用具
1. 安装MATLAB 的电脑一台 实验原理:
1. 白噪声
白噪声,是指功率谱密度在整个频域内均匀分布的噪声,即其功率谱密度为
()02n p N ω= (1) 式中,0N 为常数,∞<<∞-ω。
由于1和)(t δ为一对傅里叶变换对,所以白噪声的自
相关函数为
()()02n N R τδτ= (2)
由式(1)、式(2)可知,白噪声的自相关函数仅在0τ=时才不为零,而对于其他任意的τ,白噪声的自相关函数都为零,即在任意两个不同时刻上的随机变量都是不相关的。
2. 随机信号通过线性时不变系统的响应
对于一个线性时不变系统(如滤波器),该系统是由它的冲激响应()h t 或等效地由它的频率响应()H f 表征,这里的()h t 和()H f 是一对傅里叶变换对。
如果令()x t 为系统的输人信号,()y t 是输出信号。
系统的输出可以表示成如下形式:
()()()y t h x t d τττ∞
-∞=-⎰ (3) 如果)(t x 是平稳随机过程)(t X 的样本函数,那么)(t y 就是随机过程)(t Y 的样本函数。
可以求出输出的自相关函数是
()()()()yy xx h h d d R R ταβταβαβ∞∞-∞-∞=+-⎰⎰ (4)
由于我们知道自相关函数和功率谱密度函数是一对傅里叶变换对,所以可以得到输出过程的功率密度谱,即为相关函数的傅里叶变换:
()()()()22j f yy yy xx f d f H f e R πτττ∞--∞==ΦΦ⎰ (5)
由此可以看出,输出信号的功率谱密度就是输入信号的功率谱密度乘以系统的频率响应的模的平方。
当输入随机过程是白噪声时,输出随机过程的自相关特性和功率密度谱将完全
由系统的频率响应所决定。
3. 实验方案设计
本实验采用一个高斯白噪声发生器模块来产生高斯白噪声信号,使其通过三个带宽不同的低通滤波器系统,对输出信号的时域波形进行观察和比较。
本实验的仿真模型文件名是gaussian_noise.mdl,打开该文件可以看到如图1所示的仿真模型的结构图,该模型实现了白噪声(本实验中白噪声均指高斯加性白噪声)信号通过不同带宽的滤波器。
图中最左端是一个高斯噪声发生器发出白噪声,该白噪声信号分别通过三个滤波器(三个滤波器的名字分别是Digital Filter Design1,Digital Filter Design 2,Digital Filter Design 3),这三个滤波器的带宽各不相同,最后用一个可以同时显示四路波形的示波器来观察时域信号。
图1 设计一个高斯白噪声及三个低通滤波器
1. 打开matlab应用软件,如图2所示。
2.在图2中右边的命令窗(Command Window)的光标处输入:simulink,回车,打开Simulink Library Browser界面,如图3所示,。
图2 Matlab界面
3. 在图2中,选择:File>New>Model新建文件,保存在matlab工作目录下,并取名为gaussian_noise.mdl。
4. 在图3 的Find命令行处输入:Gaussian Noise Generator,就在窗口的右边找到了该仿真模块图标。
用鼠标右键选择该模块,将其添加到创建的gaussian_noise窗口中。
模块操作:Ctrl+z逆时针转90度,Ctrl+r顺时针转90度,Ctrl+i转180度。
图3 SLB界面
5. 用相同的方法创建滤波Digital Filter Design和显示仪器Scope,观察每个设备的连接点,用鼠标左键把设备连接起来,如图4所示。
6. 用鼠标左键选中Gaussian Noise ,再点击右键进行高斯噪声产生器参数设置,如
图5所示。
图 4 一个Gaussian Noise与三个低通滤波器的simulimk设计
图5 gaussian noise generator参数设置
7. 同样的方法设置滤波器Digital Filter Design1的参数,如图6所示。
如此法,按需求分别设置其它模块的参数如图7和图8所示。
图6 Digital Filter Design1参数
图7 Digital Filter Design2参数
图8 Digital Filter Design3参数
8.用鼠标点击如图9中的“运行仿真模型按钮”可以运行gaussian_noise. mdl,运行结束后,双击示波器模块(Scope)可以打开仿真结果波形。
图9 设计仿真
9.6.实验结果
该模型仿真后在Scope中看到的波形如图10所示。
图中从上到下的三个波形分别是高斯白噪声通过系统频宽最窄、系统频宽适中、系统频宽最宽的滤波器后的时域波形。
而最后一个则是原始的高斯白噪声信号的时域波形。
可以看到原始的白噪声信号中相邻采样点之间也相互独立,没有相关性,经过低通滤波器之后,相邻样点之间存在明显的相关性,而且滤波器带宽越窄,相关性越强,符合实验原理。
图10 Scope显示的波形
如果Scope的初始坐标设置不方便观察模型,可以用鼠标右键点击曲线,并选择Autoscale功能显示完整的仿真'曲线,然后再用Zoom按钮调节曲线的显示,如图11所示。
图11 使用Autoscale功能显示完整的仿真曲线
讨
论
综述你所了解的Digital Filter Design和Scope模块的功能。
答:此题有多种解答,只需相关表述正确即可。
如Digital Filter Design 模块为数字滤波器模块,current filter information选项区域显示的信息为
当前滤波器的过滤信息,response type选项区域可以选择滤波器的功能类型等。
重新设置滤波器的参数,观察在不同带宽的滤波器下,高斯白噪声通过滤波器后相邻样点的相关性。
答:经过低通滤波器之后,相邻样点之间存在明显的相关性,而且滤波器带宽越窄,相关性越强。
签名:年月日。
