2013年云南省中考数学试题及答案
2013年云南省昆明市中考数学试卷及答案(word整理版)

2013年云南省昆明市中考数学试卷一、选择题(每小题3分,满分24分) 1.﹣6的绝对值是( ) A .﹣6B . 6C . ±6D .2.下面几何体的左视图是( )A .B .C .D .3.下列运算正确的是( ) A .x 6+x 2=x 3 B .C .(x+2y )2=x 2+2xy+4y 2D .4.如图,在△ABC 中,点D ,E 分别是AB ,AC 的中点,∠A=50°,∠ADE=60°,则∠C 的度数为( )A .50°B . 60°C . 70°D . 80°5.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取了1000名学生的数学成绩.下列说法正确的是( ) A . 2013年昆明市九年级学生是总体 B .每一名九年级学生是个体 C . 1000名九年级学生是总体的一个样本 D .样本容量是1000 6.一元二次方程2x 2﹣5x+1=0的根的情况是( )A .有两个不相等的实数根B .有两个相等的实数根C .没有实数根D .无法确定7.如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?设道路的宽为x 米,则可列方程为( ) A .100×80﹣100x ﹣80x=7644 B . (100﹣x )(80﹣x )+x 2=7644 C .(100﹣x )(80﹣x )=7644 D . 100x+80x=356 8.如图,在正方形ABCD 中,点P 是AB 上一动点(不与A ,B 重合),对角线AC ,BD 相交于点O ,过点P 分别作AC ,BD 的垂线,分别交AC ,BD 于点E ,F ,交AD ,BC 于点M ,N .下列结论: ①△APE ≌△AME ;②PM+PN=AC ;③PE 2+PF 2=PO 2;④△POF ∽△BNF ;⑤当△PMN ∽△AMP 时,点P 是AB 的中点. 其中正确的结论有( ) A .5个 B . 4个 C . 3个 D . 2个 二、填空题(每小题3分,满分18分)9.据报道,2013年一季度昆明市共接待游客约为12340000人,将12340000人用科学记数法表示为 人.10.已知正比例函数y=kx 的图象经过点A (﹣1,2),则正比例函数的解析式为 . 11.求9的平方根的值为 . 12.化简:=.13.如图,从直径为4cm 的圆形纸片中,剪出一个圆心角为90°的扇形OAB ,且点O 、A 、B 在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是 cm .14.在平面直角坐标系xOy 中,已知点A (2,3),在坐标轴上找一点P ,使得△AOP 是等腰三角形,则这样的点P 共有 个. 三、解答题(共9题,满分58分)15.(5分)计算:﹣2sin30°.16.(5分)已知:如图,AD ,BC 相交于点O ,OA=OD ,AB ∥CD .求证:AB=CD .17.(5分)在平面直角坐标系中,四边形ABCD的位置如图所示,解答下列问题:(1)将四边形ABCD先向左平移4个单位,再向下平移6个单位,得到四边形A1B1C1D1,画出平移后的四边形A1B1C1D1;(2)将四边形A1B1C1D1绕点A1逆时针旋转90°,得到四边形A1B2C2D2,画出旋转后的四边形A1B2C2D2,并写出点C2的坐标.18.(5分)2013年6月6日第一届南亚博览会在昆明举行.某校对七年级学生开展了“南博会知多少?”的调查活动,采取随机抽样的方法进行问卷调查,问卷调查的结果分为“不太了解”、“基本了解”、“比较了解”、“非常了解”四个等级,对调查结果进行统计后,绘制了如下不完整的条形统计图:根据以上统计图提供的信息,回答下列问题:(1)若“基本了解”的人数占抽样调查人数的25%,此次调查抽取了学生;(2)补全条形统计图;(3)若该校七年级有600名学生,请估计“比较了解”和“非常了解”的学生共有多少人?19.(6分)有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y=上的概率.20.(7分)如图,为了缓解交通拥堵,方便行人,在某街道计划修建一座横断面为梯形ABCD的过街天桥,若天桥斜坡AB的坡角∠BAD为35°,斜坡CD的坡度为i=1:1.2(垂直高度CE与水平宽度DE的比),上底BC=10m,天桥高度CE=5m,求天桥下底AD的长度?(结果精确到0.1m,参考数据:sin35°≈0.57,cos35°≈0.82,tan35°≈0.70)21.(8分)某校七年级准备购买一批笔记本奖励优秀学生,在购买时发现,每本笔记本可以打九折,用360元钱购买的笔记本,打折后购买的数量比打折前多10本.(1)求打折前每本笔记本的售价是多少元?(2)由于考虑学生的需求不同,学校决定购买笔记本和笔袋共90件,笔袋每个原售价为6元,两种物品都打九折,若购买总金额不低于360元,且不超过365元,问有哪几种购买方案?22.(8分)已知:如图,AC⊙O是的直径,BC是⊙O的弦,点P是⊙O外一点,∠PBA=∠C.(1)求证:PB是⊙O的切线;(2)若OP∥BC,且OP=8,BC=2.求⊙O的半径.23.(9分)如图,矩形OABC在平面直角坐标系xOy中,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=4,OC=3,若抛物线的顶点在BC边上,且抛物线经过O,A两点,直线AC交抛物线于点D.(1)求抛物线的解析式;(2)求点D的坐标;(3)若点M在抛物线上,点N在x轴上,是否存在以A,D,M,N为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.2013年云南省昆明市中考数学试卷答案1.B 2.A 3.D 4.C 5.D 6.A 7.C 8.B9. 1.234×107.10.y=﹣2x.11.±3.12.x+2.13..14.8.15.解:原式=1﹣1+3﹣2×=2.16.证明:∵AB∥CD,∴∠B=∠C,∠A=∠D,∵在△AOB和△DOC中,,∴△AOB≌△DOC(SSA),∴AB=CD.17.解:(1)四边形A1B1C1D1如图所示;(2)四边形A1B2C2D2如图所示,C2(1,﹣2).18.解:(1)根据题意得:10÷25%=40(名),则此次调查的学生为40名;(2)根据题意得:“比较了解”的学生为40﹣(4+10+11)=15(名),补全统计图,如图所示;(3)根据题意估计“比较了解”和“非常了解”的学生共有600×=390(名).19.解:(1)根据题意画出树状图如下:;(2)当x=﹣1时,y==﹣2,当x=1时,y==2,当x=2时,y==1,一共有9种等可能的情况,点(x,y)落在双曲线上y=上的有2种情况,所以,P=.20.解:过B作BF⊥AD于F,则四边形BCEF为矩形,则BF=CE=5m,BC=EF=10m,在Rt△ABF中,=tan35°,则AF=≈7.1m,在Rt△CDE中,∵CD的坡度为i=1:1.2,∴=1:1.2,则ED=6m,∴AD=AF+EF+ED=7.1+10+6=23.1(m).答:天桥下底AD的长度为23.1m.21.解:(1)设打折前售价为x,则打折后售价为0.9x,由题意得,+10=,解得:x=4,经检验得:x=4是原方程的根,答:打折前每本笔记本的售价为4元.(2)设购买笔记本y件,则购买笔袋(90﹣y)件,由题意得,360≤4×0.9×y+6×0.9×(90﹣y)≤365,解得:67≤y≤70,∵x为正整数,∴x可取68,69,70,故有三种购买方案:方案一:购买笔记本68本,购买笔袋22个;方案二:购买笔记本69本,购买笔袋21个;方案三:购买笔记本70本,购买笔袋20个;22.(1)证明:连接OB,∵AC是⊙O直径,∴∠ABC=90°,∵OC=OB,∴∠OBC=∠ACB,∵∠PBA=∠ACB,∴∠PBA=∠OBC,即∠PBA+∠OBA=∠OBC+∠ABO=∠ABC=90°,∴OB⊥PB,∵OB为半径,∴PB是⊙O的切线;(2)解:设⊙O的半径为r,则AC=2r,OB=R,∵OP∥BC,∠OBC=∠OCB,∴∠POB=∠OBC=∠OCB,∵∠PBO=∠ABC=90°,∴△PBO∽△ABC,∴=,∴=,r=2,即⊙O的半径为2.23.解:(1)设抛物线顶点为E,根据题意OA=4,OC=3,得:E(2,3),设抛物线解析式为y=a(x﹣2)2+3,将A(4,0)坐标代入得:0=4a+3,即a=﹣,则抛物线解析式为y=﹣(x﹣2)2+3=﹣x2+3x;(2)设直线AC解析式为y=kx+b(k≠0),将A(4,0)与C(0,3)代入得:,解得:,故直线AC解析式为y=﹣x+3,与抛物线解析式联立得:,解得:或,则点D坐标为(1,);(3)存在,分两种情况考虑:①当点M在x轴上方时,如答图1所示:四边形ADMN为平行四边形,DM∥AN,DM=AN,由对称性得到M(3,),即DM=2,故AN=2,∴N1(2,0),N2(6,0);②当点M在x轴下方时,如答图2所示:过点D作DQ⊥x轴于点Q,过点M作MP⊥x轴于点P,可得△ADQ≌△NMP,∴MP=DQ=,NP=AQ=3,将y M=﹣代入抛物线解析式得:﹣=﹣x2+3x,解得:x M=2﹣或x M=2+,∴x N=x M﹣3=﹣﹣1或﹣1,∴N3(﹣﹣1,0),N4(﹣1,0).综上所述,满足条件的点N有四个:N1(2,0),N2(6,0),N3(﹣﹣1,0),N4(﹣1,0).。
云南省中考数学真题试卷

2013云南省中考数学真题试卷和答案一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)1.(3分)﹣6的绝对值是()A.﹣6 B.6C.±6 D.2.(3分)下列运算,结果正确的是()A.m6÷m3=m2B.3mn2•m2n=3m3n3C.(m+n)2=m2+n2D.2mn+3mn=5m2n2 3.(3分)图为某个几何体的三视图,则该几何体是()A.B.C.D.4.(3分)2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,150.5亿元用科学记数法表示为()A.1.505×109元B.1.505×1010元C.0.1505×1011元D.15.05×109元5.(3分)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()A.S▱ABCD=4S△AOB B.A C=BDC.A C⊥BD D.▱ABCD是轴对称图形6.(3分)已知⊙O1的半径是3cm,⊙2的半径是2cm,O1O2=cm,则两圆的位置关系是()A.相离B.外切C.相交D.内切7.(3分)要使分式的值为0,你认为x可取得数是()A.9B.±3 C.﹣3 D.38.(3分)若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是()A.B.C.D.二、填空题(本大题共6个小题,每小题3分,满分18分)9.(3分)25的算术平方根是.10.(3分)分解因式:x3﹣4x=.11.(3分)在函数中,自变量x的取值范围是.12.(3分)已知扇形的面积为2π,半径为3,则该扇形的弧长为(结果保留π).13.(3分)如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD=.14.(3分)下面是按一定规律排列的一列数:,,,,…那么第n个数是.三、解答题(本大题共9个小题,满分58分)15.(4分)计算:sin30°+(﹣1)0+()﹣2﹣.16.(5分)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).(1)你添加的条件是.(2)添加条件后,请说明△ABC≌△ADE的理由.17.(6分)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.(1)把“鱼”向右平移5个单位长度,并画出平移后的图形.(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标.18.(7分)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.组别 A B C D E时间t(分钟)t<40 40≤t<60 60≤t<80 80≤t<100 t≥100人数12 30 a 24 12(1)求出本次被调查的学生数;(2)请求出统计表中a的值;(3)求各组人数的众数及B组圆心角度数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.19.(7分)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.20.(6分)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?21.(7分)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE 是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.22.(7分)某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.(1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.23.(9分)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).(1)求A、D两点的坐标;(2)求经过A、D、C三点的抛物线的函数关系式;(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.答案一、选择题1-4 BBDB 5-8 ACDA二、填空题9、510、x(x+2)(x﹣2)11、x≥﹣1且x≠012、13、44°14、三、解答题15、解:原式=+1+4﹣=5.解答:解:(1)∵AB=AD,∠A=∠A,∴若利用“AAS”,可以添加∠C=∠E,若利用“ASA”,可以添加∠ABC=∠ADE,或∠EBC=∠CDE,若利用“SAS”,可以添加AC=AE,或BE=DC,综上所述,可以添加的条件为∠C=∠E(或∠ABC=∠ADE或∠EBC=∠CDE或AC=AE 或BE=DC);故答案为:∠C=∠E;(2)选∠C=∠E为条件.理由如下:在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).17、解答:解:(1)如图所示:.(2)结合坐标系可得:A'(5,2),B'(0,6),C'(1,0).18、解答:解:(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;(3)众数是12人;(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人).19、解答:解:(1)列表如下:1 2 31 (1,1)(2,1)(3,1)2 (1,2)(2,2)(3,2)3 (1,3)(2,3)(3,3)(2)所有等可能的情况数为9种,其中是x2﹣3x+2=0的解的为(1,2),(2,1)共2种,则P是方程解=.解答:解:过点A作AD⊥BC于D,根据题意得∠ABC=30°,∠ACD=60°,∴∠BAC=∠ACD﹣∠ABC=30°,∴CA=CB.∵CB=50×2=100(海里),∴CA=100(海里),在直角△ADC中,∠ACD=60°,∴CD=AC=×100=50(海里).故船继续航行50海里与钓鱼岛A的距离最近.21、解答:解:(1)∵AB=AC,AD是BC的边上的中线,∴AD⊥BC,∴∠ADB=90°,∵四边形ADBE是平行四边形.∴平行四边形ADBE是矩形;(2)∵AB=AC=5,BC=6,AD是BC的中线,∴BD=DC=6×=3,在直角△ACD中,AD===4,∴S矩形ADBE=BD•AD=3×4=12.22、解答:解:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,根据题意得,,解得,答:榕树和香樟树的单价分别是60元/棵,80元/棵;(2)设购买榕树a棵,则购买香樟树为(150﹣a)棵,根据题意得,,解不等式①得,a≥58,解不等式②得,a≤60,所以,不等式组的解集是58≤a≤60,∵a只能取正整数,∴a=58、59、60,因此有3种购买方案:方案一:购买榕树58棵,香樟树92棵,方案二:购买榕树59棵,香樟树91棵,方案三:购买榕树60棵,香樟树90棵.解答:解:(1)设直线EC的解读式为y=kx+b,根据题意得:,解得,∴y=x+1,当y=0时,x=﹣1,∴点A的坐标为(﹣1,0).∵四边形ABCD是等腰梯形,C(2,3),∴点D的坐标为(0,3).(2)设过A(﹣1,0)、D(0,3)、C(2,3)三点的抛物线的解读式为y=ax2+bx+c,则有:,解得,∴抛物线的关系式为:y=x2﹣2x+3.(3)存在.①作线段AC的垂直平分线,交y轴于点P1,交AC于点F.∵OA=OE,∴△OAE为等腰直角三角形,∠AEO=45°,∴∠FEP1=∠AEO=45°,∴△FEP1为等腰直角三角形.∵A(﹣1,0),C(2,3),点F为AC中点,∴F(,),∴等腰直角三角形△FEP1斜边上的高为,∴EP1=1,∴P1(0,2);②以点A为圆心,线段AC长为半径画弧,交y轴于点P2,P3.可求得圆的半径长AP2=AC=3.连接AP2,则在R t△AOP2中,OP2===,∴P2(0,).∵点P3与点P2关于x轴对称,∴P3(0,﹣);③以点C为圆心,线段CA长为半径画弧,交y轴于点P4,P5,则圆的半径长CP4=CA=3,在Rt△CDP4中,CP4=3,CD=2,∴DP4===,∴O P4=OD+DP4=3+,∴P4(0,3+);同理,可求得:P5(0,3﹣).综上所述,满足条件的点P有5个,分别为:P1(0,2),P2(0,),P3(0,﹣),P4(0,3+),P5(0,3﹣).。
2013年昆明中考数学试卷及答案
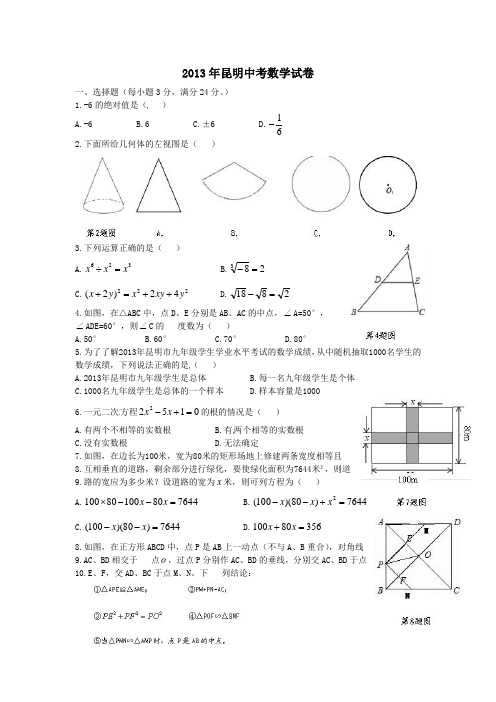
2013年昆明中考数学试卷一、选择题(每小题3分,满分24分。
) 1.-6的绝对值是( )A.-6B.6C.±6D.61- 2.下面所给几何体的左视图是( )3.下列运算正确的是( )A.326x x x =÷ B.283=-C.22242)2(y xy x y x ++=+ D.2818=-4.如图,在△ABC 中,点D 、E 分别是AB 、AC 的中点,∠A=50°, ∠ADE=60°,则∠C 的 度数为( )A.50°B.60°C.70°D.80° 5.为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机抽取1000名学生的 数学成绩,下列说法正确的是( )A.2013年昆明市九年级学生是总体B.每一名九年级学生是个体C.1000名九年级学生是总体的一个样本D.样本容量是1000 6.一元二次方程01522=+-x x 的根的情况是( )A.有两个不相等的实数根B.有两个相等的实数根C.没有实数根D.无法确定7.如图,在边长为100米,宽为80米的矩形场地上修建两条宽度相等且 8.互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米²,则道 9.路的宽应为多少米?设道路的宽为x 米,则可列方程为( )A.76448010080100=--⨯x xB.7644)80)(100(2=+--x x xC.7644)80)(100(=--x xD.35680100=+x x8.如图,在正方形ABCD 中,点P 是AB 上一动点(不与A 、B 重合),对角线 9.AC 、BD 相交于 点o ,过点P 分别作AC 、BD 的垂线,分别交AC 、BD 于点 10.E 、F ,交AD 、BC 于点M 、N 。
下 列结论:其中正确的结论有( )A.5个B.4个C.3个D.2个 二、填空题(每小题3分,满分18分。
2013年大理等八地市中考数学试题(Word版含答案)
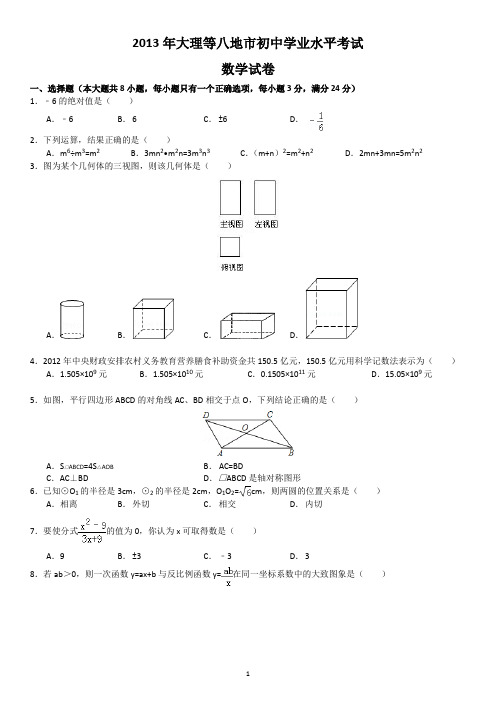
2013年大理等八地市初中学业水平考试数学试卷一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)1.﹣6的绝对值是()A.﹣6 B. 6 C. ±6 D.2.下列运算,结果正确的是()A.m6÷m3=m2B.3mn2•m2n=3m3n3C.(m+n)2=m2+n2D.2mn+3mn=5m2n23.图为某个几何体的三视图,则该几何体是()A.B.C.D.4.2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,150.5亿元用科学记数法表示为()A.1.505×109元B.1.505×1010元C.0.1505×1011元D.15.05×109元5.如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()A.S□ABCD=4S△AOB B. AC=BDC.AC⊥BD D.□ABCD是轴对称图形6.已知⊙O1的半径是3cm,⊙2的半径是2cm,O1O2=cm,则两圆的位置关系是()A.相离B.外切C.相交D.内切7.要使分式的值为0,你认为x可取得数是()A.9 B. ±3 C.﹣3 D. 38.若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是()A.B.C.D.二、填空题(本大题共6个小题,每小题3分,满分18分)9.25的算术平方根是.10.分解因式:x3﹣4x=.11.在函数中,自变量x的取值范围是.12.已知扇形的面积为2π,半径为3,则该扇形的弧长为(结果保留π).13.如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD=.14.下面是按一定规律排列的一列数:,,,,…那么第n个数是.三、解答题(本大题共9个小题,满分58分)15.(4分)计算:sin30°+(﹣1)0+()﹣2﹣.16.(5分)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).(1)你添加的条件是.(2)添加条件后,请说明△ABC≌△ADE的理由.17.(6分)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.(1)把“鱼”向右平移5个单位长度,并画出平移后的图形.(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标.18.(7分)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.组别 A B C D E时间t(分钟)t<40 40≤t<60 60≤t<80 80≤t<100 t≥100人数12 30 a 24 12(1)求出本次被调查的学生数;(2)请求出统计表中a的值;(3)求各组人数的众数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.19.(7分)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.20.(6分)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?21.(7分)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.22.(7分)某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.(1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.23.(9分)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).(1)求A、D两点的坐标;(2)求经过A、D、C三点的抛物线的函数关系式;(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.参考答案1-8.B B D B A C D A9.5 10.x(x+2)(x﹣2)11.x≥﹣1且x≠012.13.44°14.15.解:原式=+1+4﹣=5.16.解:(1)∵AB=AD,∠A=∠A,∴若利用“AAS”,可以添加∠C=∠E,若利用“ASA”,可以添加∠ABC=∠ADE,或∠EBC=∠CDE,若利用“SAS”,可以添加AC=AE,或BE=DC,综上所述,可以添加的条件为∠C=∠E(或∠ABC=∠ADE或∠EBC=∠CDE或AC=AE或BE=DC);故答案为:∠C=∠E;(2)选∠C=∠E为条件.理由如下:在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).17.解:(1)如图所示:.(2)结合坐标系可得:A'(5,2),B'(0,6),C'(1,0).18.解:(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;(3)众数是12人;(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人).19.解:(1)列表如下:1 2 31 (1,1)(2,1)(3,1)2 (1,2)(2,2)(3,2)3 (1,3)(2,3)(3,3)(2)所有等可能的情况数为9种,其中是x2﹣3x+2=0的解的为(1,2),(2,1)共2种,则P是方程解=.20.解:过点A作AD⊥BC于D,根据题意得∠ABC=30°,∠ACD=60°,∴∠BAC=∠ACD﹣∠ABC=30°,∴CA=CB.∵CB=50×2=100(海里),∴CA=100(海里),在直角△ADC中,∠ACD=60°,∴CD=AC=×100=50(海里).故船继续航行50海里与钓鱼岛A的距离最近.21.解:(1)∵AB=AC,AD是BC的边上的中线,∴AD⊥BC,∴∠ADB=90°,∵四边形ADBE是平行四边形.∴平行四边形ADBE是矩形;(2)∵AB=AC=5,BC=6,AD是BC的中线,∴BD=DC=6×=3,在直角△ACD中,AD===4,∴S矩形ADBE=BD•AD=3×4=12.22.解:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,根据题意得,,解得,答:榕树和香樟树的单价分别是60元/棵,80元/棵;(2)设购买榕树a棵,则购买香樟树为(150﹣a)棵,根据题意得,,解不等式①得,a≥58,解不等式②得,a≤60,所以,不等式组的解集是58≤a≤60,∵a只能取正整数,∴a=58、59、60,因此有3种购买方案:方案一:购买榕树58棵,香樟树92棵,方案二:购买榕树59棵,香樟树91棵,方案三:购买榕树60棵,香樟树90棵.23.解:(1)设直线EC的解析式为y=kx+b,根据题意得:,解得,∴y=x+1,当y=0时,x=﹣1,∴点A的坐标为(﹣1,0).∵四边形ABCD是等腰梯形,C(2,3),∴点D的坐标为(0,3).(2)设过A(﹣1,0)、D(0,3)、C(2,3)三点的抛物线的解析式为y=ax2+bx+c,则有:,解得,∴抛物线的关系式为:y=x2﹣2x+3.(3)存在.①作线段AC的垂直平分线,交y轴于点P1,交AC于点F.∵OA=OE,∴△OAE为等腰直角三角形,∠AEO=45°,∴∠FEP1=∠AEO=45°,∴△FEP1为等腰直角三角形.∵A(﹣1,0),C(2,3),点F为AC中点,∴F(,),∴等腰直角三角形△FEP1斜边上的高为,∴EP1=1,∴P1(0,2);②以点A为圆心,线段AC长为半径画弧,交y轴于点P2,P3.可求得圆的半径长AP2=AC=3.连接AP2,则在Rt△AOP2中,OP2===,∴P2(0,).∵点P3与点P2关于x轴对称,∴P3(0,﹣);③以点C为圆心,线段CA长为半径画弧,交y轴于点P4,P5,则圆的半径长CP4=CA=3,在Rt△CDP4中,CP4=3,CD=2,∴DP4===,∴OP4=OD+DP4=3+,∴P4(0,3+);同理,可求得:P5(0,3﹣).综上所述,满足条件的点P有5个,分别为:P1(0,2),P2(0,),P3(0,﹣),P4(0,3+),P5(0,3﹣).。
云南省昆明市年中考数学试卷(解析版)

云南省昆明市2013年中考数学试卷一、选择题(每小题3分,满分24分,在每小题给出的四个选项中,只有一项是正确的。
).2.(3分)(2013•昆明)下面几何体的左视图是()..﹣=3,本选项正确.4.(3分)(2013•昆明)如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()5.(3分)(2013•昆明)为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从中随机27.(3分)(2013•昆明)如图,在长为100M,宽为80M的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644M2,则道路的宽应为多少M?设道路的宽为xM,则可列方程为()8.(3分)(2013•昆明)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有()PE=EM=PM同理,FP=FN=NP.PM FP=FN=NP AC二、填空题(每小题3分,满分18分)9.(3分)(2013•昆明)据报道,2013年一季度昆明市共接待游客约为12340000人,将12340000人用科学记数法表示为 1.234×107人.10.(3分)(2013•昆明)已知正比例函数y=kx的图象经过点A(﹣1,2),则正比例函数的解读式为y=﹣2x.11.(3分)(2013•昆明)求9的平方根的值为±3.12.(3分)(2013•昆明)化简:=x+2.分析:先转化为同分母(x﹣2)的分式相加减,然后约分即可得解.+=﹣13.(3分)(2013•昆明)如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是cm.AB=2AB=2ππr=故答案为14.(3分)(2013•昆明)在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有8个.三、解答题(共9题,满分58分。
2013年云南省曲靖市中考试卷答案

解得:b=﹣3,c=4,
∴抛物线的解析式为:y=﹣x2﹣3x+4.
(2)设点C坐标为(m,0)(m<0),则OC=﹣m,AC=4+m.
∵OA=OB=4,∴∠BAC=45°,
∴△ACD为等腰直角三角形,∴CD=AC=4+m,
∴CE=CD+DE=4+m+4=8+m,
∴点E坐标为(m,8+m).
∵点E在抛物线y=﹣x2﹣3x+4上,
∴8+m=﹣m2﹣3m+4,解得m=﹣2.
∴C(﹣2,0),AC=OC=2,CE=6,
S四边形CAEB=S△ACE+S梯形OCEB﹣S△BCO= ×2×6+ (6+4)×2﹣ ×2×4=12.
(3)设点C坐标为(m,0)(m<0),则OC=﹣m,CD=AC=4+m,BD= OC=﹣ m,则D(m,4+m).
1
2
4
乙
1
0
2
1
1
0
2
(2)∵S甲2= ,S乙2= ,
∴S甲2>S乙2,
∴乙出现次品的波动小.
(3)∵乙的平均数是1,
∴30天出现次品是1×30=30(件).
21.
解:(1)设红球有x个,
根据题意 得, ,
解得x=1;
(2)根据题意画出树状图如下:
一共有9种情况,两次摸到的球颜色不同的有6种情况,
所以,P(两次摸到的球颜色不同)= .
去分母得:x+1=﹣x+1,
解得:x=0,
代入原式检验,分母为0,不合题意,
则原式的值不可能为﹣1.
19.
解:设安排x人生产A部件,安排y人生产B部件,由题意,得
2013年云南中考数学试卷及答案

绝密★2013年云南德宏州中考试题数 学(全卷三个答题,共23个小题,共6页:满分100分,考试用时120分钟) 注意事项:一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分) 1.(2013德宏州,1,3分)-2的绝对值是( )A. 21- B. 21 C. -2 D. 2【答案】D 2.(2013德宏州,2,3分)如图,下列图形中,是中心对称图形的是( )A. B. C. D. 【答案】A3.(2013德宏州,3,3分)-b a 24的次数是( )A. 3B. 2C. 4D.-4 【答案】A 4.(2013德宏州,4,3分)如果a <0,则下列式子错误的是( ) A. a a +>+35 B. a a ->-35C. a a 35>D.35aa >【答案】A5.(2013德宏州,5,3分)如图,三条直线相交于点O.若CO ⊥AB ,∠1= 56, 则∠2等于( ) A . 30 B . 34 C .45D .56【答案】BAB6. (2013德宏州,6,3分)某品牌鞋店在一个月内销售某款女鞋,各种尺码鞋A.平均数B. 众数C. 中位数D.方差 【答案】B7.(2013德宏州,7,3分)在Rt Δ ABC 中,∠C= 90,AB =10. 若以点C 为圆心,CB 为半径的圆恰好经过AB 的中点D ,则AC =( ) A. 5 B. 25 C. 35 D. 6【答案】C 8.(2013德宏州,8,3分)设b a 、是直角三角形的两条直角边,若该三角形的周长为6,斜边长为2.5,则ab 的值是( )A. 1.5B. 2C. 2.5D.3 【答案】D二、填空题(本大题共6个小题,每小题3分,满分18分) 9.(2013德宏州,9,3分) 4的算术平方根是 . 【答案】210.(2013德宏州,10,3分)分解因式:222a -= . 【答案】()()211a a -+-11.(2013德宏州,11,3分)函数的主要表示方法有 、 、 ________三种。
云南省玉溪市2013年中考数学试题及答案

玉溪市2013年初中学业水平考试数学试题卷(全卷三个大题,含23个小题,共8页,满分100分,考试时间120分钟)第一部分(选择题 共30分)一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分,在每小题给出的四个选项中,只。
)1.(2013云南玉溪,1,3分)下列四个实数中,负数是( )A .-2013B .0C .0.8D .22.(2013云南玉溪,2,3分)如图是每个面上都有一个汉字的正方体的一种平面展开图,那么在原正方体中和“国”字相对的面是( )A .中B . 钓C .鱼D .岛3.(2013云南玉溪,3,3分)下列运算正确的是( )A .x +y=xyB . 2x 2-x 2=1C .2x ·3x =6xD .x 2 ÷x =x4.(2013云南玉溪,4,3分)在下列图形中,既是轴对称图形又是中心对称图形的是( )5.(2013云南玉溪,5,3分)一次函数y=x-2的图像不经过( )A .第一象限B .第二象限C .第三象限D .第四象限6.(2013云南玉溪,6,3分)若等腰三角形的两边长分别为4和8,则它的周长为( )A .12B .16C .20D .16或207.(2013云南玉溪,7,3分)如图,点A 、B 、C 、D 都在方格纸的格点上,若△AOB 绕点 O 按逆时针方向旋转到△COD 的位置,则旋转的角度为( )A .300B .450C .900D .13508.(2013云南玉溪,8,3分)如图,在一块菱形菜地ABCD 中,对角线AC 与BD 相交于点O ,若在菱形菜地内均匀地撒上种子,则种子落在阴影部分的概率是( )OBACD 中国的钓鱼岛A .1B .21 C .31D .41二、填空题(本大题共6小题,每小题3分,满分18分.)9.(2013云南玉溪,9,3分)据统计,今年我市参加初中数学学业水平考试的学生人数约为27000人,把27000用科学计数法表示为 .10.(2013云南玉溪,10,3分)若数2,3,x ,5,6五个数的平均数为4,则x 的值为 . 11.(2013云南玉溪,11,3分)如图,AB ∥CD ,∠BAF =115°,则∠ECF 的度数为 .12.(2013云南玉溪,12,3分)分解因式:ax 2-ay 2= .13.(2013云南玉溪,13,3分)若规定“*”的运算法则为:a*b=ab-1,则2*3= .14.(2013云南玉溪,14,3分)反比例函数y =xk(x >0)的图像如图,点B 在图像上,连接OB 并延长到点A ,使AB =2OB ,过点A 作AC ∥y 轴,交y =xk(x >0)的图像于点C ,连接OC ,S △AOC =5,则k = .三、解答题(本大题共9小题,满分58分)15.(2013云南玉溪,15,5分)计算:(-1)2-|-7|+4×(2013-π)0+(31)-1BACDO FEDCAB第11题图yxOABC第14题图16.(2013云南玉溪,16,5分)解不等式组⎩⎨⎧<-<+②①.3)1(2,52x x x17.(2013云南玉溪,17,6分)如图,在□ABCD 中,点E ,F 分别是边AD ,BC 的中点,求证:AF=CE .18.(2013云南玉溪 6分)端午节吃粽子是中华民族的传统习俗,据了解,甲厂家生产了A ,B ,C 三个品种的盒装粽子,乙厂家生产D ,E 两个品种的盒装粽子,端午节前,某商场在甲乙两个厂家中各选购一个品种的盒装粽子销售. (1)试用树状图或列表法写出所有选购方案;(2)如果(1)中各种选购方案被选中的可能性相同,那么甲厂家的B 品种粽子被选中的概率是多少?19.(2013云南玉溪,19,6分)为了解我市家庭月均用电量情况,有关部门随机抽查了我市1000户家庭的月均用电量,并将调查数据整理如下:月均用电量a/度 频数/户 频率 0≤a <50 120 0.12 50≤a <100 240 n 100≤a <150 300 0.30 150≤a <200 m 0.16 200≤a <250 120 0.12 250≤a <300 60 0.06 合 计10001(1)频数分布表中的m= ,n= ; (2)补全频数分布直方图;(3)被调查的1000户家庭月均用电量的众数落在哪一个范围? (4)求月均用电量小于150度的家庭数占被调查家庭总数的百分比.ABCDEF250 150 频数/户 300240120 60 0 50 100 200 300月均用电量/度18020.(2013云南玉溪,20,7分)在一个阳光明媚,微风习习的周末,小明和小强一起到聂耳文化广场放风筝,放了一会儿,两个人争吵起来: 小明说:“我的风筝飞得比你的高”.小强说:“我的风筝引线比你的长,我的风筝飞得更高”.谁的风筝飞得更高呢?于是他们将两个风筝引线的一段都固定在地面上的C 处(如图),现已知小明的风筝引线(线段AC )长30米,小强的风筝引线(线段BC )长36米,在C 处测得风筝A 的仰角为600,风筝B 的仰角为450,请通过计算说明谁的风筝飞得更高?(结果精确到0.1米,参考数据:2≈1.41,3≈1.73)21.(2013云南玉溪,21,7分)某学校为鼓励学生积极参加体育锻炼,派王老师和李老师去购买一些篮球和排球.回校后,王老师和李老师编写了一道题:同学们,请求出篮球和排球的单价各是多少元?22.(2013云南玉溪,22,7分)如图,AB 是⊙O 的直径,弦CD 交AB 于点E ,OF ⊥AC 于点F , (1)请探索OF 和BC 的关系并说明理由; (2)若∠D =30°,BC =1时,求圆中阴影部分的面积.(结果保留π)C A BO DF E23.(2013云南玉溪,23,9分)如图,顶点为A 的抛物线y =a (x +2)2-4交x 轴于点B (1,0),连接AB ,过原点O 作射线OM ∥AB ,过点A 作AD ∥x 轴交OM 于点D ,点C 为抛物线与x 轴的另一个交点,连接CD .(1)求抛物线的解析式(关系式);(2)求点A ,B 所在的直线的解析式(关系式);(3)若动点P 从点O 出发,以每秒1个单位长度的速度沿着射线OM 运动,设点P 运动的时间为t 秒,问:当t 为何值时,四边形ABOP 分别为平行四边形?等腰梯形?(4)若动点P 从点O 出发,以每秒1个单位长度的速度沿线段OD 向点D 运动,同时动点Q 从点C 出发,以每秒2个单位长度的速度沿线段CO 向点O 运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动时间为t 秒,连接PQ .问:当t 为何值时,四边形CDPQ 的面积最小?并求此时PQ 的长.yxOQ PBCAD M。
2013年云南省中考数学试卷及答案

数学试卷 第1页(共16页) 数学试卷 第2页(共16页)绝密★启用前云南省2013年初中学业水平考试数学 .................................................................................. 1 云南省2013年初中学业水平考试数学答案解析 (4)云南省2013年初中学业水平考试数学本试卷满分100分,考试时间120分钟.注意事项:1.本卷为试题卷。
考生解题答题必须在答题卷(答题卡)上,答案书写在答题卷(答题卡)相应的位置上,在试题卷、草稿纸上作答无效。
2.考试结束时,请将试题卷、答题卷(答题卡)一并交回。
一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分) 1.6-的绝对值是( ) A .6-B .6±C .6D .16-2.下列运算,结果正确的是( )A .632m m m ÷=B .223333mn m n m n =C .222()m n m n +=+D .22235mn mn m n +=3.下图是某个几何体的三视图,则该几何体是( )4.2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,150.5亿元用科学记数法表示为( )A .91.50510⨯元B .101.50510⨯元C .110.150510⨯元D .915.0510⨯元5.如图,平行四边形ABCD 的对角线AC BD 、相交于点O ,下列结论正确的是 ( )A .4ABCDAOB SS =△B .AC BD =C .AC BD ⊥D .□ABCD 是轴对称图形6.已知1O 的半径是3cm ,2O 的半径是2cm ,126cm O O =,则两圆的位置关系是( )A .相离B .外切C .相交D .内切 7.要使分式2939x x -+的值为0,你认为x 可取的数是( )A .9B .3±C .3-D .3 8.若0ab >,则一次函数y ax b =+与反比例函数aby x =在同一坐标系中的大致图像可能是( )ABCD二、填空题(本大题共6小题,每小题3分,满分18分) 9.25的算术平方根是 .10.分解因式:34x x -= .11.在函数1x y x+=中,自变量x 的取值范围是 .12.已知扇形的面积为2π,半径为3,则该扇形的弧长为 (结果保留π).13.如图,已知,,68AB CD AB AC ABC ==∥∠,则ACD =∠ .ABCD毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共16页) 数学试卷 第4页(共16页)14.下面是按一定规律排列的一列数:14,37,512,719,……那么第n 个数是 .三、解答题(本大题共9小题,满分58分)15.(本小题4分)计算:0211(2)sin3()0122-+-+.16.(本小题5分)如图,点B 在AE 上,点D 在AC 上,AB AD =.请你添加一个适当的条件,使ABC ADE △≌△(只能添加一个).(1)你添加的条件是 ; (2)添加条件后,请说明ABC ADE △≌△的理由.17.(本小题6分)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.(1)把“鱼”向右平移5个单位长度,并画出平移后的图形; (2)写出A 、B 、C 三点平移后的对应点A '、B '、C '的坐标.18.(本小题7分)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不得少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计(1)求出本次被调查的学生数; (2)请求出统计表中a 的值; (3)求各组人数的众数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.数学试卷 第5页(共16页) 数学试卷 第6页(共16页)19.(本小题7分)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1,2,3三个数字.小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转). (1)请你用画树状图或列表的方法表示出每次游戏可能出现的所有结果; (2)求每次游戏结束得到的一组数恰好是方程2320x x +=-的解的概率.20.(本小题6分)如图,我国的一艘海监船在钓鱼岛A 附近沿正东方向航行,船在B 点时测得钓鱼岛A 在船的北偏东60方向,船以50海里/时的速度继续航行2小时后到达C 点,此时钓鱼岛A 在船的北偏东30方向.请问船继续航行多少海里与钓鱼岛A 的距离最近?21.(本小题7分)已知在ABC △中,5,6,AB AC BC AD ===是BC 边上的中线,四边形ADBE 是平行四边形. (1)求证:四边形ADBE 是矩形; (2)求矩形ADBE 的面积.22.(本小题7分)某中学为了绿化校园,计划购买一批榕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元. (1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵数不少于榕树的1.5倍.请你算一算,该校本次购买榕树和香樟树共有哪几种方案.23.(本小题9分)如图,四边形ABCD 是等腰梯形,下底AB 在x 轴上,点D 在y 轴上,直线AC 与y 轴交于点()0,1E ,点C 的坐标为(2,3). (1)求A 、D 两点的坐标;(2)求经过A 、D 、C 三点的抛物线的函数关系式;(3)在y 轴上是否存在点P ,使ACP △是等腰三角形?若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------。
2013年云南昭通市中考数学试卷及答案(word解析版)

第 1 页 共 15 页2013年昭通市中考试题数 学(主试题共25个题,满分100分;附加题,共4个小题,满分50分。
考试用时150分钟)主试题(三个大题,共25个小题,满分100分)一、选择题(本大题共10个小题,每小题只有一个正确选项,每小题3分,满分30分) 1.(2013昭通市,1,3分)-4的绝对值是( )A .14B .14- C .4 D .-4 【答案】C2. (2013昭通市,2,3分)下列各式计算正确的是( )A .222()a b a b +=+B .235a a a +=C .824a a a ÷=D .23a a a ⋅= 【答案】D3.(2013昭通市,3,3分)如图1,AB ∥CD ,DB ⊥BC ,∠2 =50°,则∠1的度数是( )图1 A .40° B .50° C .60° D .140° 【答案】A4.(2013昭通市,4,3分)已知一组数据:12,5,9,5,14,下列说法不正确...的是( ) A .平均数是9 B .中位数是9 C .众数是5 D .极差是5 【答案】D 5.(2013昭通市,5,3分)如图2,已知AB 、CD 是⊙O 的两条直径,∠ABC =28°,那么∠BAD =( )图2第 2 页 共 15 页图2A .28°B .42°C .56°D .84° 【答案】A6.(2013昭通市,6,3分)图3是一个正方体的表面展开图,则原正方体中与“建”字所 在的面相对的面上标的字是( )A .美B .丽C .云D .南 【答案】D7.(2013昭通市,7,3分)如图4,A 、B 、C 三点在正方形网格线的交点处,若将△ACB 绕着点A 逆时针旋转得到△AC ′B ′,则tan B ′的值为( )图4图4A .12 B .13C .14 D【答案】B8.(2013昭通市,8,3分)已知点P (2a -1,1-a )在第一象限,则a 的取值范围在数轴上表示正确的是( )A. B. C. D. 【答案】C9.(2013昭通市,9,3分)已知二次函数y = ax 2+bx +c (a ≠ 0)的图象如图5所示,则下列结论中正确的是( ) x =1xyO-1第 3 页 共 15 页图5A .a >0B .3是方程ax 2+bx +c =0的一个根C .a +b +c =0D .当x <1时,y 随x 的增大而减小 【答案】B10.(2013昭通市,10,3分)图6所示是某公园为迎接“中国——南亚博览会”设置的一休闲区.∠AOB =90°,弧AB 的半径OA 长是6米,C 是OA 的中点,点D 在弧AB 上,CD ∥OB ,则图中休闲区(阴影部分)的面积是( )图6D B C 小路小 路草 坪休 闲区 A图6 A.(10π米2 B.(π米2C.(6π米2 D.(6π-米2【答案】C二、填空题(本大题共7个小题,每小题3分,满分21分)11.(2013昭通市,11,3分)根据云南省统计局发布我省生产总值的主要数据显示:去年生产总值突破万亿大关,2013年第一季度生产总值为226 040 000 000元人民币,增速居全国第一. 这个数据用科学记数法可表示为 元. 【答案】2.2604×101112.(2013昭通市,12,3分)实数227,8-3π中的无理数是.、3π13.(2013昭通市,13,3分)因式分解:2218x -= . 【答案】2(x +3)(x -3)14.(2013昭通市,14,3分)如图7,AF = DC ,BC ∥EF ,只需补充一个 条件 ,就得△ABC ≌△DEF .第 4 页 共 15 页图7AFB CDE图7【答案】BC = EF (或∠A =∠D ,或∠B =∠E ,或AB ∥DE 等) 15.(2013昭通市,15,3分)使代数式321x -有意义的x 的取值范围是 . 【答案】12x ≠16.(2013昭通市,16,3分)如图8,AB 是⊙O 的直径,弦BC =4cm ,F 是弦BC 的中点,∠ABC =60°.若动点E 以1cm/s 的速度从A 点出发在AB 上沿着A →B →A 运动,设运动时间为t (s) (0≤t <16),连接EF ,当△BEF 是直角三角形时,t (s)的值为 .(填出一个正确的即可)图8B图8【答案】4(或7或9或12)(只需填一个答案即可得分)17.(2013昭通市,17,3分)如图9所示,图中每一个小方格的面积为1,则可根据面积计算得到如下算式:()127531-+⋅⋅⋅++++n = . (用n 表示,n 是正整数)2n -15 12 347 1 1 2 43 3 n图9 【答案】n 2三、解答题(本大题共8个小题,满分49分)第 5 页 共 15 页18. (2013昭通市,18,6分)计算:02013214(3)10sin30(1)()3π----︒--+.【答案】解:02013214(3)10sin 30(1)()3π----︒--+ 21519=--++ 6=19. (2013昭通市,19,5分)小明有2件上衣,分别为红色和蓝色,有3条裤子,其中2条为蓝色、1 条为棕色. 在准备校艺术节的演出服装时突遇停电,小明任意拿出1件上衣和1条裤子穿上.请用画树状图或列表的方法列出所有可能出现的结果,并求小明穿的上衣和裤子恰好都是蓝色的概率.【答案】解:列表如下:裤子 上衣 蓝色蓝色棕色红色 (红色,蓝色) (红色,蓝色) (红色,棕色) 蓝色(蓝色,蓝色)(蓝色,蓝色)(蓝色,棕色)蓝色占2种,所以小明穿的上衣和裤子恰好都是蓝色的概率是13. 20. (2013昭通市,20,5分)为了推动课堂教学改革,打造高效课堂,配合地区“两型课堂”的课题研究,羊街中学对八年级部分学生就一学期以来“分组合作学习”方式的支持程度进行调查,统计情况如图10. 请根据图中提供的信息,回答下列问题.图10 图11(1)求本次被调查的八年级学生的人数,并补全条形统计图11; (2)若该校八年级学生共有540人,请你计算该校八年级有多少名学生支持“分组合作学习”方式(含“非常喜欢”和“喜欢”两种情况的学生)? 【答案】解:(1)设本次被调查的八年级学生有x 人,观察图10和图11,“喜欢”的学生18名,占本次被调查的八年级学生的人数的比为360120,即31,列方程:x 18=31,得第 6 页 共 15 页x =54. 经检验x =54是原方程的解. 由54非常喜欢的人数=360200,得:非常喜欢的人数为30.(2)列方程:120200==540540360+支持人数喜欢的人数+非常喜欢的人数. 由此解得支持的学生有480名.21. (2013昭通市,21,5分)小亮一家在一湖泊中游玩,湖泊中有一孤岛,妈妈在孤岛P 处观看小亮与爸爸在湖中划船(如图12所示). 小船从P 处出发,沿北偏东60°方向划行200米到A 处,接着向正南方向划行一段时间到B 处. 在B 处小亮观测到妈妈所在的P 处在北偏西37°的方向上,这时小亮与妈妈相距多少米(精确到1米)? (参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)图12AB 37°60°P图12【答案】解:过P 作PC ⊥AB 于C ,AB37°60°PC在Rt △APC 中,AP = 200m ,∠ACP = 90°,∠PAC = 60°. ∴ PC= 200×sin60°=200 ×23=1003(m ). ∵ 在Rt △PBC 中,sin37°=PBPC, ∴ 100 1.73288()sin 370.6PC PB m ⨯==≈︒ 答:小亮与妈妈相距约288米.第 7 页 共 15 页22. (2013昭通市,22,6分)如图13,直线y =k 1x +b (k 1≠0)与双曲线y =2k x(k 2≠0)相交于A (1,m )、B (-2,-1)两点. (1)求直线和双曲线的解析式. (2)若A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3)为双曲线上的三点,且x 1<x 2<0<x 3,请直接写出y 1,y 2,y 3的大小关系式.图13【答案】解:(1)∵ 双曲线y = 2k x经过点B (-2,-1), ∴ k 2 = 2. ∴ 双曲线的解析式为:y =2x. ∵ 点A (1,m )在双曲线y = 2x上, ∴ m = 2,则A (1,2). 由点A (1,2),B (-2,-1)在直线y =k 1x +b 上,得 112,2 1.k b k b +=⎧⎨-+=-⎩解得11,1.k b =⎧⎨=⎩ ∴ 直线的解析式为:y = x +1. (2)y 2<y 1<y 3.23. (2013昭通市,23,7分)如图14,已知AB 是⊙O 的直径,点C 、D 在⊙O 上, 点E 在⊙O 外,∠EAC =∠B = 60°.(1)求∠ADC 的度数; (2)求证:AE 是⊙O 的切线.图14第 8 页 共 15 页图14 【答案】解:(1)∵ ∠ABC 与∠ADC 都是弧AC 所对的圆周角, ∴ ∠ADC =∠B =60°. (2)∵ AB 是⊙O 的直径, ∴ ∠ACB =90°, ∴ ∠BAC =30°.∴ ∠BAE =∠BAC +∠EAC =30°+60°=90°, 即 BA ⊥AE .∴ AE 是⊙O 的切线.24. (2013昭通市,24,7分)如图15,在菱形ABCD 中,AB = 2,60DAB ∠=,点E 是AD 边的中点,点M 是AB 边上的一个动点(不与点A 重合),延长ME 交CD 的延长线于点N ,连接MD ,AN .(1)求证:四边形AMDN 是平行四边形.(2)当AM 的值为何值时,四边形AMDN 是矩形?请说明理由. AMBNDCE图15 【答案】(1)证明:∵ 四边形ABCD 是菱形,∴ ND ∥AM . ∴ ∠NDE =∠MAE ,∠DNE =∠AME . ∵ 点E 是AD 中点,∴ DE = AE . ∴ △NDE ≌△MAE ,∴ ND = MA . ∴ 四边形AMDN 是平行四边形. (2)① 1; 理由如下:∵ 四边形ABCD 是菱形, ∴ AD = AB = 2.若平行四边形AMDN 是矩形, 则DM ⊥AB , 即 ∠DMA =90°. ∵ ∠A =60°, ∴ ∠ADM =30°. ∴ AM =12AD =1. 25. (2013昭通市,25,8分)如图16,已知A (3,0)、B (4,4)、原点O (0,0)在抛物线y = ax 2+bx +c (a ≠0)上.第 9 页 共 15 页(1)求抛物线的解析式.(2)将直线OB 向下平移m 个单位长度后,得到的直线与抛物线只有一个交点D ,求m 的值及点D 的坐标.(3)如图17,若点N 在抛物线上,且∠NBO =∠A BO ,则在(2)的条件下,求出所有满足△POD ∽△NOB 的点P 的坐标(点P 、O 、D 分别与点N 、O 、B 对应)OyxABDOyxABDN图16 【答案】(1)∵ A (3,0)、B (4,4)、O (0,0)在抛物线y =ax 2+bx +c (a ≠0)上.∴ 930,1644,0,a b c a b c c ++=⎧⎪++=⎨⎪=⎩ 解得1,3,0.a b c =⎧⎪=-⎨⎪=⎩∴ 抛物线的解析式为:y =x 2-3x …………………2分 (2)设直线OB 的解析式为y = k 1 x ( k 1≠0),由点B (4,4)得 4=4 k 1,解得k 1=1.∴ 直线OB 的解析式为y = x ,∠AOB = 45°. ∵ B (4,4),∴ 点B 向下平移m 个单位长度的点B ′的坐标为(4,0), 故m = 4.∴ 平移m 个单位长度的直线为y = x - 4.解方程组 23,4.y x x y x ⎧=-⎨=-⎩得2,2.x y =⎧⎨=-⎩∴ 点D 的坐标为(2,-2) . …………………………5分(3)∵ 直线OB 的解析式y =x ,且A (3,0). ∵ 点A 关于直线OB 的对称点A ′的坐标为(0,3) .设直线A ′B 的解析式为y =k 2x +3,此直线过点B (4,4) . ∴ 4k 2+3=4, 解得 k 2=14.第 10 页 共 15 页∴ 直线A ′B 的解析式为y =14x +3. ∵ ∠NBO =∠A BO ,∴ 点N 在直线A ′B 上, 设点N (n ,14n +3),又点N 在抛物线y =x 2-3x 上, ∴14n +3=n 2-3n . 解得 n 1=34-,n 2=4(不合题意,舍去)∴ 点N 的坐标为(34-,4516).如图,将△NOB 沿x 轴翻折,得到△N 1OB 1,yxA ′ N BO A P 2DBN 1P 1则 N 1 (34-,4516-),B 1(4,-4). ∴ O 、D 、B 1都在直线y =-x 上.∵ △P 1OD ∽△NOB ,∴ △P 1OD ∽△N 1OB 1, ∴ P 1为O N 1的中点.∴ 1112OP OD ON OB ==,∴ 点P 1的坐标为(38-,4532-). 将△P 1OD 沿直线y =-x 翻折,可得另一个满足条件的点(4532,38). 综上所述,点P 的坐标为(38-,4532-)和(4532,38).第 11 页 共 15 页附加题(共4个小题,满分50分)1.(2013昭通市,附加题1,12分)已知一个口袋中装有7个只有颜色不同、其它都相同的球,其中3个白球、4个黑球.(1)求从中随机取出一个黑球的概率.(2)若往口袋中再放入x 个黑球,且从口袋中随机取出一个白球的概率是14,求代数式223(1)1x x x x x -÷+---的值. 【答案】解:(1)P (取出一个黑球)44347==+ (2)设往口袋中再放入x 个黑球, 从口袋中随机取出一个白球的概率是14即 P (取出一个白球)3174x ==+.由此解得x =5. 经检验x =5是原方程的解.∵ 原式2213(1)1x x x x x ---=÷--21(1)(2)(2)x x x x x x --=⋅--+1(2)x x =+∴ 当x =5时,原式=135. 2.(2013昭通市,附加题2,12分)云南连续四年大旱,学校为节约用水,提醒人们关注漏水的水龙头.因此,两名同学分别做了水龙头漏水实验,他们用于接水的量筒最大容量为100毫升. 实验一:小王同学在做水龙头漏水实验时,每隔10秒观察量筒中水的体积,记录的数据如下表(漏(1)在图1的坐标系中描出上表中数据对应的点.第 12 页 共 15 页(2)如果小王同学继续实验,请求出多少秒后量筒中的水会满而溢出(精确到1秒). (3)按此漏水速度,1小时会漏水_______千克(精确到0.1千克).图1 图2 实验二:小李同学根据自己的实验数据画出的图象如图2所示,为什么图象中会出现与横轴“平行”的部分?【答案】解:实验一: (1)如图所示:V /(2)设V 与t 的函数关系式为V = kt + b ,根据表中数据知:当t = 10时,V = 2;当t = 20时,V = 5;∴ 210,520,k b k b =+=+⎧⎨⎩ 解得:3,101.k b ⎧=⎪⎨⎪=-⎩∴ V 与t 的函数关系式为 3110V t =-. 由题意得:3110010t -≥,解得,1010233633t =≥. ∴ 约337秒后,量筒中的水会满而开始溢出.(3)1.1千克实验二:因为小李同学接水的量筒装满后水开始溢出V /V /第 13 页 共 15 页3. (2013昭通市,附加题3,12分)如图3,在⊙C 的内接△AOB 中,AB = AO = 4,tan ∠AOB= 34,抛物线y = a (x -2)2+m (a ≠0)经过点A (4,0)与点(-2,6). (1)求抛物线的解析式;(2)直线m 与⊙C 相切于点A ,交y 轴于点D ,动点P 在线段OB 上,从点O 出发向点B 运动,同时动点Q 在线段DA 上,从点D 出发向点A 运动,点P 的速度为每秒1个单位长,点Q 的速度为每秒2个单位长. 当PQ ⊥AD 时,求运动时间t 的值.图3 【答案】解:(1)将点A (4,0)和点(-2,6)的坐标代入y = a (x -2)2+m 中,得方程组,40,16 6.a m a m +=⎧⎨+=⎩解之,得1,22.a m ⎧=⎪⎨⎪=-⎩ ∴ 抛物线的解析式为2122y x x =-(2)如图,连接AC 交OB 于E.∵ 直线m 切⊙C 于点A , ∴ AC ⊥m .∵ 弦 AB = AO , ∴ AB AO =. ∴ AC ⊥OB ,∴ m ∥OB . ∴ ∠ OAD =∠AOB .∵ OA =4,tan ∠AOB =43,∴ OD = OA ·tan ∠OAD =4×43= 3. 作OF ⊥AD 于F ,则OF = OA ·sin ∠OAD = 4×53= 2.4 .t 秒时,OP =t ,DQ=2t ,若PQ ⊥AD , 则 FQ =OP = t. DF =DQ -FQ = t. ∴ △ODF 中,t = DF ==1.8秒第 14 页 共 15 页AxP FQD C Bym O E4.(2013昭通市,附加题4,14分)已知△ABC 为等边三角形,点D 为直线BC 上的一个动点(点D 不与B C 、重合),以AD 为边作菱形ADEF (A D E F 、、、按逆时针排列),使60DAF ∠=︒,连接CF .(1)如图4,当点D 在边BC 上时,求证:①BD = CF , ②AC = CF + CD .(2)如图5,当点D 在边BC 的延长线上且其他条件不变时,结论AC = CF + CD 是否成立?若不成立,请写出AC 、CF 、CD 之间存在的数量关系,并说明理由.(3)如图6,当点D 在边CB 的延长线上且其他条件不变时,请补全图形,并直接写出AC 、C F 、CD 之间存在的数量关系ABDCEF ABC DEFA图4 图5 图6 【答案】(1)【证明】:①∵60BAD DAC DAC CAF ∠+∠=∠+∠=︒, ∴ BAD CAF ∠=∠.又∵ ,AB AC AD AF ==. ∴ △ABD ≌ △AFC , ∴ BD CF =. ② 由△ABD ≌ △AFC 知BD CF =, ∴ CF CD BD CD BC +=+=. 又在等边△ABC 中AC BC =, ∴ AC CF CD =+(2)解:AC CF CD =+不成立,应该是CF =AC +CD ,理由为: 如图,延长AC 到H ,使CH CD =,连结BH , 则 在△ACD 与△BCH 中,,,,AC BC ACD BCH CD CH =∠=∠= ∴ △ACD ≌ △BCH .∴ ,.BH AD HBC DAC =∠=∠ ∴ ,.ABH FAC BH AF ∠=∠=第 15 页 共 15 页∴ △ABH 与△CAF 中,,,.AB AC ABH FAC BH AF =∠=∠=∴ △ABH ≌△CAF , ∴AH CF =, ∴CF AC CD =+(3)解:当点D 在边CB 的延长线上且其他条件不变时,补全图形如下图6所示,此时 AC 、CF 、CD 之间存在的数量关系为CD AC CF =+.(备注:连结CF ,容易证明△ABD ≌△AHC ,∴BD HC =,又=,HC CF AC BC =)ABCD EFHADCH BF E。
2013云南省中考数学真题试卷和答案

2013云南省中考数学真题试卷和答案一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)1.(3分)﹣6的绝对值是()A.﹣6 B.6C.±6 D.2.(3分)下列运算,结果正确的是()A.m6÷m3=m2B.3mn2•m2n=3m3n3C.(m+n)2=m2+n2D.2mn+3mn=5m2n2 3.(3分)图为某个几何体的三视图,则该几何体是()A.B.C.D.4.(3分)2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,150.5亿元用科学记数法表示为()A.1.505×109元B.1.505×1010元C.0。
1505×1011元D.15.05×109元5.(3分)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()A.S▱ABCD=4S△AOB B.A C=BDC.A C⊥BD D.▱ABCD是轴对称图形6.(3分)已知⊙O1的半径是3cm,⊙2的半径是2cm,O1O2=cm,则两圆的位置关系是()A.相离B.外切C.相交D.内切7.(3分)要使分式的值为0,你认为x可取得数是()A.9B.±3 C.﹣3 D.38.(3分)若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象是()A.B.C.D.二、填空题(本大题共6个小题,每小题3分,满分18分)9.(3分)25的算术平方根是.10.(3分)分解因式:x3﹣4x=.11.(3分)在函数中,自变量x的取值范围是.12.(3分)已知扇形的面积为2π,半径为3,则该扇形的弧长为(结果保留π).13.(3分)如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD=.14.(3分)下面是按一定规律排列的一列数:,,,,…那么第n个数是.三、解答题(本大题共9个小题,满分58分)15.(4分)计算:sin30°+(﹣1)0+()﹣2﹣.16.(5分)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).(1)你添加的条件是.(2)添加条件后,请说明△ABC≌△ADE的理由.17.(6分)如图,下列网格中,每个小正方形的边长都是1,图中“鱼"的各个顶点都在格点上.(1)把“鱼"向右平移5个单位长度,并画出平移后的图形.(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标.18.(7分)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时"的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.组别 A B C D E时间t(分钟)t<40 40≤t<60 60≤t<80 80≤t<100 t≥100人数12 30 a 24 12(1)求出本次被调查的学生数;(2)请求出统计表中a的值;(3)求各组人数的众数及B组圆心角度数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.19.(7分)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.20.(6分)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?21.(7分)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.22.(7分)某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.(1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.23.(9分)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC 与y轴交于点E(0,1),点C的坐标为(2,3).(1)求A、D两点的坐标;(2)求经过A、D、C三点的抛物线的函数关系式;(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.答案一、选择题1-4 BBDB 5-8 ACDA二、填空题9、510、x(x+2)(x﹣2)11、x≥﹣1且x≠012、13、44°14、三、解答题15、解:原式=+1+4﹣=5.解答:解:(1)∵AB=AD,∠A=∠A,∴若利用“AAS”,可以添加∠C=∠E,若利用“ASA",可以添加∠ABC=∠ADE,或∠EBC=∠CDE,若利用“SAS”,可以添加AC=AE,或BE=DC,综上所述,可以添加的条件为∠C=∠E(或∠ABC=∠ADE或∠EBC=∠CDE或AC=AE 或BE=DC);故答案为:∠C=∠E;(2)选∠C=∠E为条件.理由如下:在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).17、解答:解:(1)如图所示:.(2)结合坐标系可得:A’(5,2),B’(0,6),C’(1,0).18、解答:解:(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;(3)众数是12人;(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人).19、解答:解:(1)列表如下:1 2 31 (1,1)(2,1)(3,1)2 (1,2)(2,2)(3,2)3 (1,3)(2,3)(3,3)(2)所有等可能的情况数为9种,其中是x2﹣3x+2=0的解的为(1,2),(2,1)共2种,则P是方程解=.20、解答:解:过点A作AD⊥BC于D,根据题意得∠ABC=30°,∠ACD=60°,∴∠BAC=∠ACD﹣∠ABC=30°,∴CA=CB.∵CB=50×2=100(海里),∴CA=100(海里),在直角△ADC中,∠ACD=60°,∴CD=AC=×100=50(海里).故船继续航行50海里与钓鱼岛A的距离最近.21、解答:解:(1)∵AB=AC,AD是BC的边上的中线,∴AD⊥BC,∴∠ADB=90°,∵四边形ADBE是平行四边形.∴平行四边形ADBE是矩形;(2)∵AB=AC=5,BC=6,AD是BC的中线,∴BD=DC=6×=3,在直角△ACD中,AD===4,∴S矩形ADBE=BD•AD=3×4=12.22、解答:解:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,根据题意得,,解得,答:榕树和香樟树的单价分别是60元/棵,80元/棵;(2)设购买榕树a棵,则购买香樟树为(150﹣a)棵,根据题意得,,解不等式①得,a≥58,解不等式②得,a≤60,所以,不等式组的解集是58≤a≤60,∵a只能取正整数,∴a=58、59、60,因此有3种购买方案:方案一:购买榕树58棵,香樟树92棵,方案二:购买榕树59棵,香樟树91棵,方案三:购买榕树60棵,香樟树90棵.23、解答:解:(1)设直线EC的解析式为y=kx+b,根据题意得:,解得,∴y=x+1,当y=0时,x=﹣1,∴点A的坐标为(﹣1,0).∵四边形ABCD是等腰梯形,C(2,3),∴点D的坐标为(0,3).(2)设过A(﹣1,0)、D(0,3)、C(2,3)三点的抛物线的解析式为y=ax2+bx+c,则有:,解得,∴抛物线的关系式为:y=x2﹣2x+3.(3)存在.①作线段AC的垂直平分线,交y轴于点P1,交AC于点F.∵OA=OE,∴△OAE为等腰直角三角形,∠AEO=45°,∴∠FEP1=∠AEO=45°,∴△FEP1为等腰直角三角形.∵A(﹣1,0),C(2,3),点F为AC中点,∴F(,),∴等腰直角三角形△FEP1斜边上的高为,∴EP1=1,∴P1(0,2);②以点A为圆心,线段AC长为半径画弧,交y轴于点P2,P3.可求得圆的半径长AP2=AC=3.连接AP2,则在Rt△AOP2中,OP2===,∴P2(0,).∵点P3与点P2关于x轴对称,∴P3(0,﹣);③以点C为圆心,线段CA长为半径画弧,交y轴于点P4,P5,则圆的半径长CP4=CA=3,在Rt△CDP4中,CP4=3,CD=2,∴DP4===,∴OP4=OD+DP4=3+,∴P4(0,3+);同理,可求得:P5(0,3﹣).综上所述,满足条件的点P有5个,分别为:P1(0,2),P2(0,),P3(0,﹣),P4(0,3+),P5(0,3﹣).。
2013云南八地中考数学
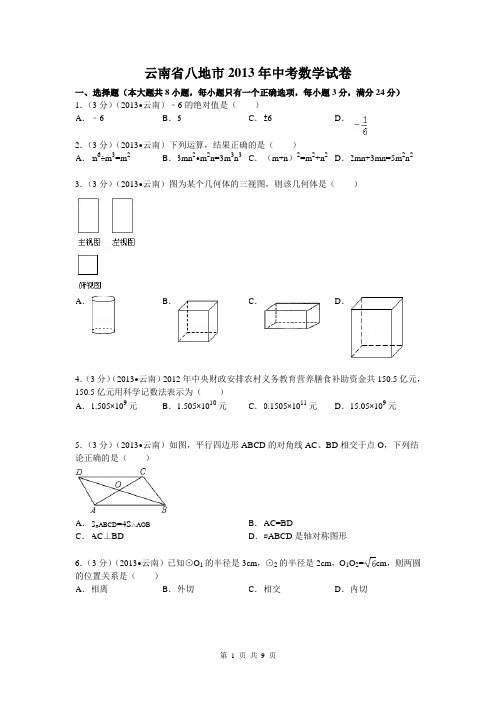
云南省八地市2013年中考数学试卷一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)3.(3分)(2013•云南)图为某个几何体的三视图,则该几何体是()B4.(3分)(2013•云南)2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,5.(3分)(2013•云南)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()6.(3分)(2013•云南)已知⊙O1的半径是3cm,⊙2的半径是2cm,O1O2=cm,则两圆7.(3分)(2013•云南)要使分式的值为0,你认为x 可取得数是( )8.(3分)(2013•云南)若ab >0,则一次函数y=ax+b 与反比例函数y=在同一坐标系数BC二、填空题(本大题共6个小题,每小题3分,满分18分) 9.(3分)(2013•云南)25的算术平方根是 5 .10.(3分)(2013•云南)分解因式:x 3﹣4x= x (x+2)(x ﹣2) .11.(3分)(2013•云南)在函数中,自变量x 的取值范围是 x ≥﹣1且x ≠0 .12.(3分)(2013•云南)已知扇形的面积为2π,半径为3,则该扇形的弧长为(结果保留π). 13.(3分)(2013•云南)如图,已知AB ∥CD ,AB=AC ,∠ABC=68°,则∠ACD= 44° .14.(3分)(2013•云南)下面是按一定规律排列的一列数:,,,,…那么第n个数是 .三、解答题(本大题共9个小题,满分58分)15.(4分)(2013•云南)计算:sin30°+(﹣1)0+()﹣2﹣.16.(5分)(2013•云南)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).(1)你添加的条件是∠C=∠E.(2)添加条件后,请说明△ABC≌△ADE的理由.17.(6分)(2013•云南)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.(1)把“鱼”向右平移5个单位长度,并画出平移后的图形.(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标.18.(7分)(2013•云南)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学(2)请求出统计表中a的值;(3)求各组人数的众数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.19.(7分)(2013•云南)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.=20.(6分)(2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?AC=50 CD=×21.(7分)(2013•云南)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.×==422.(7分)(2013•云南)某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.(1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.,,,23.(9分)(2013•云南)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y 轴上,直线AC与y轴交于点E(0,1),点C的坐标为(2,3).(1)求A、D两点的坐标;(2)求经过A、D、C三点的抛物线的函数关系式;(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P 的坐标;若不存在,请说明理由.,解得,,解得,斜边上的高为.=,),﹣,=3=,=3+),),P4(0,3+),P5(0,3﹣).。
云南省昭通市年中考数学试卷(解析版)

云南省昭通市2013年中考数学试卷一、选择题(本大题共10个小题,每小题只有一个正确选项,每小题3分,满分30分) . .3.(3分)(2013•昭通)如图,AB ∥CD ,DB ⊥BC ,∠2=50°,则∠1的度数是( )4.(3分)(2013•昭通)已知一组数据:12,5,9,5,14,下列说法不正确的5.(3分)(2013•昭通)如图,已知AB 、CD 是⊙O 的两条直径,∠ABC=28°,那么∠BAD=( )∵弧AC对的圆周角是∠BAD 和∠OCB ,∴∠BAD=∠OCB=28°,故选A .点评: 本题考查了等腰三角形性质和圆周角定理的应用,关键是求出∠OCB 的度数和得出∠BAD=∠OCB .6.(3分)(2013•昭通)如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )A . 美B . 丽C . 云D . 南考点:专题:正方体相对两个面上的文字分析: 根据正方体的特点得出其中上面的和下面的是相对的2个面,即可得出正方体中与“建”字所在的面相对的面上标的字是“南”.解答: 解:由正方体的展开图特点可得:“建”和“南”相对;“设”和“丽”相对;“美”和“云”相对;故选D .点评: 此题考查了正方体相对两个面上的文字的知识;掌握常见类型展开图相对面上的两个字的特点是解决本题的关键.7.(3分)(2013•昭通)如图,A 、B 、C 三点在正方形网格线的交点处,若将△ABC 绕着点A 逆时针旋转得到△AC ′B ′,则tanB ′的值为( ) A . B . C . D .考点:锐角三角函数的定义;旋转的性质分析: 过C 点作CD ⊥AB ,垂足为D ,根据旋转性质可知,∠B ′=∠B ,把求tanB ′的问题,转化为在Rt △BCD 中求tanB .解答: 解:过C 点作CD ⊥AB ,垂足为D .根据旋转性质可知,∠B ′=∠B .在Rt △BCD 中,tanB==,∴tanB ′=tanB=.故选B .8.(3分)(2013•昭通)已知点P(2a﹣1,1﹣a)在第一象限,则a的取值范....解:根据题意得:,9.(3分)(2013•昭通)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是()得,y>0,故此选项错误;D、当x<1时,y随x的增大而增大,故此选项错误;故选:B.点评:此题主要考查了二次函数图象与系数的关系,关键是从抛物线中的得到正确信息.①二次项系数a决定抛物线的开口方向和大小.当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;IaI还可以决定开口大小,IaI越大开口就越小.②一次项系数b和二次项系数a共同决定对称轴的位置.当a与b同号时(即ab>0),对称轴在y轴左;当a与b异号时(即ab <0),对称轴在y轴右.(简称:左同右异)③常数项c决定抛物线与y轴交点.抛物线与y轴交于(0,c).④抛物线与x轴交点个数.△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.10.(3分)(2013•昭通)如图所示是某公园为迎接“中国﹣﹣南亚博览会”设置的一休闲区.∠AOB=90°,弧AB的半径OA长是6M,C是OA的中点,点D在弧AB上,CD ∥OB,则图中休闲区(阴影部分)的面积是()A.(10π)M2B.()M2C.(6π)M2D.(6)M2考点:扇形面积的计算.分析:先根据半径OA长是6M,C是OA的中点可知OC=OA=3M,再在Rt△OCD中,利用勾股定理求出CD的长,根据锐角三角函数的定义求出∠DOC的度数,由S阴影=S扇形AOD﹣S△DOC即可得出结论.解答:解:连接OD,∵弧AB的半径OA长是6M,C是OA的中点,∴OC=OA=3M,∵∠AOB=90°,CD∥OB,∴CD⊥OA,在Rt△OCD中,∵OD=6,OC=3,∴CD==3M,DOC==,DOC=﹣×3×3=6二、填空题(本大题共7个小题,每小题3分,满分21分)11.(3分)(2013•昭通)根据云南省统计局发布我省生产总值的主要数据显示:去年生产总值突破万亿大关,2013年第一季度生产总值为226 040 000 000元人民币,增速居全国第一.这个数据用科学记数法可表示为 2.2604×1011元.12.(3分)(2013•昭通)实数中的无理数是.数,而无限不循环小数是无理数.由此即可判定选择项.解:、﹣8、=6,它们都是有理数.是无理数.故答案是;.点评:此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.13.(3分)(2013•昭通)因式分解:2x2﹣18= 2(x+3)(x﹣3).考点:提公因式法与公式法的综合运用分析:提公因式2,再运用平方差公式因式分解.解答:解:2x2﹣18=2(x2﹣9)=2(x+3)(x﹣3),故答案为:2(x+3)(x﹣3).点评:本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.14.(3分)(2013•昭通)如图,AF=DC,BC∥EF,只需补充一个条件BC=EF ,就得△ABC≌△DEF.考点:全等三角形的判定.专题:开放型.分析:补充条件BC=EF,首先根据AF=DC可得AC=DF,再根据BC∥EF可得∠EFC=∠BCF,然后再加上条件CB=EF可利用SAS定理证明△ABC≌△DEF.解答:解:补充条件BC=EF,∵AF=DC,∴AF+FC=CD+FC,即AC=DF,∵BC∥EF,∴∠EFC=∠BCF,∵在△ABC和△DEF中,,∴△ABC≌△DEF(SAS).故答案为:BC=EF.点评:此题主要考查了全等三角形的判定,关键是掌握判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.15.(3分)(2013•昭通)使代数式有意义的x的取值范围是x≠.≠,故答案为:x≠.16.(3分)(2013•昭通)如图,AB是⊙O的直径,弦BC=4cm,F是弦BC的中点,∠ABC=60°.若动点E以1cm/s的速度从A点出发在AB上沿着A→B→A运动,设运动时间为t(s)(0≤t<16),连接EF,当△BEF是直角三角形时,t (s)的值为4s .(填出一个正确的即可)。
2013年云南省曲靖市中考数学试卷详解

2013年云南省曲靖市中考数学试卷参考答案与试题解析一、选择题(共8个小题,每小题3分,共24分)1.(3分)(2013•曲靖)某地某天的最高气温是8℃,最低气温是﹣2℃,则该地这一天的温差是()A.﹣10℃B.﹣6℃C.6℃D.10℃【考点】M114 有理数【难度】容易题【分析】用最高温度减去最低温度,然后根据有理数的减法运算法则,减去一个数等于加上这个数的相反数进行计算即8﹣(﹣2)=8+2=10(℃).故选D.【解答】D.【点评】本题考查了有理数的减法运算法则,熟记减去一个数等于加上这个数的相反数是解题的关键.2.(3分)(2013•曲靖)下列等式成立的是()A.a2•a5=a10 B.C.(﹣a3)6=a18D.【考点】M11D 二次根式及其相关概念M11H 整式M11M 指数幂M11N 乘方【难度】容易题【分析】利用同底数的幂的乘法法则以及幂的乘方、算术平方根定义即可作出判断.J具体为:A、a2•a5=a7,故选项错误;B、当a=b=1时,≠+,故选项错误;C、正确;D、当a<0时,=﹣a,故选项错误.故选C.【解答】C.【点评】本题考查了同底数的幂的乘法法则以及幂的乘方、算术平方根定义,理解算术平方根的定义是关键.注意:同底数幂的相除,底数不变指数相减;合并同类项,系数相加字母和字母的指数不变;同底数幂的乘法,底数不变指数相加;幂的乘方,底数不变指数相乘。
3.(3分)(2013•曲靖)如图是某几何体的三视图,则该几何体的侧面展开图是()A.B.C.D.【考点】M415 视图与投影M419 几何体的展开图【难度】中等题【分析】根据几何体的三视图可以得到该几何体是圆柱,圆柱的侧面展开图是矩形,且高度=主视图的高,宽度=俯视图的周长.故选A.【解答】A.【点评】本题考查了由三视图判断几何体及几何体的侧面展开图的知识,重点考查由三视图还原实物图的能力,及几何体的空间感知能力,是立体几何题中的基础题.4.(3分)(2013•曲靖)某地资源总量Q一定,该地人均资源享有量与人口数n的函数关系图象是()A.B. C.D.【考点】M152 反比例函数的图象、性质【难度】容易题【分析】根据题意有:=;故y与x之间的函数图象是双曲线,且根据,n的实际意义,n应大于0;其图象在第一象限.故选B.【解答】B.【点评】此题考查了反比例函数在实际生活中的应用,现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.5.(3分)(2013•曲靖)在平面直角坐标系中,将点P(﹣2,1)向右平移3个单位长度,再向上平移4个单位长度得到点P′的坐标是()A.(2,4)B.(1,5)C.(1,﹣3)D.(﹣5,5)【考点】M411 图形的平移M418 坐标与图形【难度】容易题【分析】点P(﹣2,1)向右平移3个单位长度,根据向右平移,横坐标加,则点P′的横坐标为﹣2+3=1,向上平移纵坐标加,则点P′的纵坐标为1+4=5,则点P′的坐标为(1,5).故选B.【解答】B.【点评】本题考查了坐标与图形变化﹣平移,熟记平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减是解题的关键.6.(3分)(2013•曲靖)实数a、b在数轴上的位置如图所示,下列各式成立的是()A.B.a﹣b>0 C.ab>0 D.a÷b>0【考点】M117 实数与数轴的关系【难度】容易题【分析】由图可知,﹣2<a<﹣1,0<b<1,A、<0,正确,故本选项正确;B、a﹣b<0,故本选项错误;C、ab<0,故本选项错误;D、a÷b<0,故本选项错误.故选A.【解答】A.【点评】本题考查了实数与数轴,有理数的乘除运算以及有理数的减法运算,根据数轴判断出a、b的取值范围,再根据有理数的乘除法,减法运算对各选项分析判断后利用排除法求解是关键。
2013年云南省昆明市中考数学试卷及答案(Word解析版)

云南省昆明市2013年中考数学试卷一、选择题(每小题3分,满分24分,在每小题给出的四个选项中,只有一项是正确的。
)2.(3分)(2013•昆明)下面几何体的左视图是()B、、﹣=3=,本选项正确.4.(3分)(2013•昆明)如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C的度数为()5.(3分)(2013•昆明)为了了解2013年昆明市九年级学生学业水平考试的数学成绩,从27.(3分)(2013•昆明)如图,在长为100米,宽为80米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为7644米2,则道路的宽应为多少米?设道路的宽为x米,则可列方程为()8.(3分)(2013•昆明)如图,在正方形ABCD中,点P是AB上一动点(不与A,B重合),对角线AC,BD相交于点O,过点P分别作AC,BD的垂线,分别交AC,BD于点E,F,交AD,BC于点M,N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;⑤当△PMN∽△AMP时,点P是AB的中点.其中正确的结论有()PE=EM=PMFP=FN=NPPE=EM=NP OA=二、填空题(每小题3分,满分18分)9.(3分)(2013•昆明)据报道,2013年一季度昆明市共接待游客约为12340000人,将12340000人用科学记数法表示为 1.234×107人.10.(3分)(2013•昆明)已知正比例函数y=kx的图象经过点A(﹣1,2),则正比例函数的解析式为y=﹣2x.11.(3分)(2013•昆明)求9的平方根的值为±3.12.(3分)(2013•昆明)化简:=x+2.+﹣13.(3分)(2013•昆明)如图,从直径为4cm的圆形纸片中,剪出一个圆心角为90°的扇形OAB,且点O、A、B在圆周上,把它围成一个圆锥,则圆锥的底面圆的半径是cm.AB=2cmOB=cmπr=r=(故答案为.14.(3分)(2013•昆明)在平面直角坐标系xOy中,已知点A(2,3),在坐标轴上找一点P,使得△AOP是等腰三角形,则这样的点P共有8个.三、解答题(共9题,满分58分。
【2013中考真题】云南普洱中考数学试卷及答案(有答案)

2013年云南省普洱市初中毕业水平考试数学试题卷(全卷三个大题,共23个小题,共8页,满分100分,考试时间120分钟)注意事项:1.本卷为试题卷,考生解题作答必须在答题卷(答题卡)上,答案书写在答题卷(答题卡)相应位置上,在试题卷、草稿纸上作答无效;2.考试结束后,请将试题卷和答题卷(答题卡)一并交回.一、选择题(本大题共8个小题,每小题只有一个正确选项,每小题3分,满分24分) 1. ( 2013云南普洱,1,3分)-2的绝对值是( ) A.2 B.±2 C.12-D.12【答案】A2. ( 2013云南普洱,2,3分)如左下图所示几何体的主视图是( )【答案】D3. ( 2013云南普洱,3,3分)下列运算正确的是( )A.223x x x =+ B.623x x x =÷ C.235(x x =) D.0(3)1π= 【答案】D4. ( 2013云南普洱,4,3分)方程220x x -=的解为( )A.1x =1,2x =2B. 1x =0,2x =1C. 1x =0,2x =2D. 1x =12,2x =2 【答案】C5. ( 2013云南普洱,5,3分)某县一周的最高气温如下表:星期 星期一 星期二 星期三 星期四 星期五 星期六 星期天最高气温(℃)32 32 34 30 34 32 29 A.32,32 B.32,34 C.34,34 D.30,32 【答案】A6. ( 2013云南普洱,6,3分)矩形ABCD 的对角线AC 、BD 相交于点O ,∠AOD=120°,AC=8,则△ABO 的周长为( )A.16B.12C.24D.20 【答案】B7. ( 2013云南普洱,7,3分)如图,⊙O 是△ABC 的外接圆,∠OCB=40°,则∠A 的度数是( ) A.40° B. 50° C. 60° D.100° 【答案】B8. ( 2013云南普洱,8,3分)若ab <0,则正比例函数y=ax 和反比例函数y=bx在同一坐标系中的大致图象可能是( )【答案】B二、填空题(本大题共6个小题,每小题3分,满分18分)9. ( 2013云南普洱,9,3分)太阳的半径约为696000千米,这个数据用科学记数法表示为 千米. 【答案】6.96×10510. ( 2013云南普洱,10,3分)计算:11()2-= . 【答案】011. ( 2013云南普洱,11,3分)函数y=12x -的自变量x 的取值范围是 . 【答案】x ≠212. ( 2013云南普洱,12,3分)如图,AB ⊥CD ,垂足为点B ,EF 平分∠ABD ,则∠CBF 的度数为 .【答案】45°13. ( 2013云南普洱,13,3分)用一个圆心角为150°,半径为2cm 的扇形作一个圆锥的侧面,则这个圆锥的底面圆的半径为 cm . 【答案】5614. ( 2013云南普洱,14,3分)观察下列一组数:14,39,516,725,936,…,它们是按一定规律排列的,那么这一组数的第n 个数是 . 【答案】221(1)n n -+三、解答题(本大题共9个小题,满分58分)15. ( 2013云南普洱,15,5分)先化简,再求值:2222211a a a aa a a +++÷-+,其中a=2013. 【答案】解:2222211a a a a a a a +++÷-+=222(1)(1)1a a aa a a +⋅-++=211a a a a -++ =21a a a -+=1a a + 当a=2013,原式=201320131+=20132014.16. ( 2013云南普洱,16,5分)解方程:33122x x x-+=-- 【答案】解:两边同时乘以(x-2),得x-3+x-2= -3, 解得x=1.检验:当x=1时,x-2=1-2= -1≠0,∴原方程的解为x =1.17. ( 2013云南普洱,17,6分)如图,方格纸中的每个小方格都是边长为1个单位的小正方形,每个小正方形的顶点称为格点.△ABC 的顶点都在格点上,建立平面直角坐标系后,点A 、B 、C 的坐标分别为(1,1),(4,2),(2,3).(提示:一定要用2B 铅笔作图)(1)画出△ABC 向左平移4个单位,再向上平移1个单位后得到的△A 1B 1C 1; (2)画出△ABC 向关于原点O 对称的△A 2B 2C 2;(3)以点A 、A 1、A 2为顶点的三角形的面积为 .【答案】(1)、(2)答案如图所示:(3)如图所示,以点A 、A 1、A 2为顶点的三角形的面积为: 11134232214222⨯-⨯⨯-⨯⨯-⨯⨯=12-3-2-2=5. 18. ( 2013云南普洱,18,6分)如图,已知点B 、E 、C 、F 在同一条直线上,BE=CF ,AB ∥DE ,∠A=∠D .求证:AB=DE.【答案】证明:∵BE=CF ,∴BC=EF . ∵AB ∥DE ,∴∠B=∠DEF . 在△ABC 与△DEF 中,A DB DEF BC EF ∠=∠⎧⎪∠=∠⎨⎪=⎩, ∴△ABC ≌△DEF (AAS ), ∴AB=DE .19. ( 2013云南普洱,19,7分)我市某中学为了了解本校学生对普洱茶知识的了解程度,在全校范围内随机抽查了部分学生,将收集的数据绘制成如下两幅不完整的统计图.请根据图中提供的信息,解答下列问题:(1)在本次抽样调查中,共抽取了 名学生. (2)在扇形统计图中,“不了解”部分所对应的圆心角的度数为 . (3)补全条形统计图. (提示:一定要用2B 铅笔作图)(4)若该校有1860名学生,根据调查结果,请估算出对普洱茶知识“了解一点”的学生人数. 【答案】解:(1)80; (2)36°;(3)补全条形图如下:(4)80168186080--⨯=1302.答:对普洱茶知识“了解一点”的学生人数为1302.20. ( 2013云南普洱,20,6分)如图,有A 、B 两个可以自由转动的转盘,指针固定不动,转盘各被等分成三个扇形,并分别标上-1,2,3和-4,-6,8这6个数字.同时转动两个转盘各一次(指针落在等分线上时重转),转盘自由停止后,A 转盘中指针指向的数字记为x ,B 转盘中指针指向的数字记为y ,点Q 的坐标记为Q (x ,y ).(1)用列表法或树状图表示(x ,y )所有可能出现的结果; (2)求出点Q (x ,y )落在第四象限的概率.【答案】(1)列表如下:画树状图如下:(2)由(1)中的表格或树状图可知:点Q 出现的所有可能结果有9种,位于第四象限的结果有2种, ∴点Q (x ,y )落在第四象限的概率为29. 21. ( 2013云南普洱,21,6分)据调查,超速行驶是引发交通事故的主要原因之一.上周末,小明和三位同学用所学过的知识在一条笔直的道路上检测车速.如图,观测点C 到公路的距离CD 为100米,检测路段的起点A 位于点C 的南偏西60°方向上,终点B 位于点C 的南偏西45°方向上.某时段,一辆轿车由西向东匀速行驶,测得此车由A 处行驶到B 处的时间为4秒.问此车是否超过了该路段16米/秒的限制速度?(参1.4 1.7)【答案】解:由题意得 在Rt △BCD 中, ∵∠BDC=90°,∠BCD=45°,CD=100米,∴BD=CD=100米. 在Rt △ACD 中,∵∠ADC=90°,∠ACD=60°,CD=100米,∴AD=CD ·tan ∠ACD=米).∴AB=AD-BD=≈70(米). ∴此车的速度为7017.54(米/秒). ∵17.5>16,∴此车超过了该路段16米/秒的限制速度.22. ( 2013云南普洱,22,7分)在茶节期间,某茶商订购了甲种茶叶90吨,乙种茶叶80吨,准备用A 、B 两种型号的货车共20辆运往外地.已知A 型货车每辆运费为0.4万元,B 型货车每辆运费为0.6万元. (1)设A 型货车安排x 辆,总运费为y 万元,写出y 与x 的函数关系式;(2)若一辆A 型货车可装甲种茶叶6吨,乙种茶叶2吨;一辆B 型货车可装甲种茶叶3吨,乙种茶叶7吨.按此要求安排A 、B 两种型号货车一次性运完这批茶叶,共有哪几种运输方案? (3)说明哪种方案运费最少?最少运费是多少万元? 【答案】解:(1)y =0.4x+0.6(20-x )= -0.2x+12 (2)由题意得63(20)9027(20)80x x x x +-≥⎧⎨+-≥⎩, 解得10≤x ≤12. 又∵x 为正整数, ∴x=10,11,12, ∴10-x=10,9,8 .∴有以下三种运输方案:①A 型货车10辆,B 型货车10辆; ②A 型货车11辆,B 型货车9辆; ③A 型货车12辆,B 型货车8辆. (3)∵方案①运费:10×0.4+10×0.6=10(万元); 方案②运费:11×0.4+9×0.6=9.8(万元); 方案③运费:12×0.4+8×0.6=9.6(万元). ∴方案③运费最少,最少运费为9.6万元.23. ( 2013云南普洱,23,10分)如图,在平面直角坐标系中,抛物线212y x bx c =-++经过A (-2,0),C (4,0)两点,和y 轴相交于点B ,连接AB 、BC . (1)求抛物线的解析式(关系式).(2)在第一象限外,是否存在点E ,使得以BC 为直角边的△BCE 和Rt △AOB 相似?若存在,请简要说明如何找到符合条件的点E ,然后直接写出点E 的坐标,并判断是否有满足条件的点E 在抛物线上;若不存在,请说明理由.(3)在直线BC 上方的抛物线上,找一点D ,使S △BCD :S △ABC =1:4,并求出此时点D 的坐标.【答案】解:(1)∵抛物线212y x bx c =-++经过A (-2,0),C (4,0)两点, ∴221(2)(2)0214402b c b c ⎧-⨯-+⨯-+=⎪⎪⎨⎪-⨯+⨯+=⎪⎩,解得14b c =⎧⎨=⎩.∴抛物线的解析式为2142y x x =-++.(2)在第一象限外存在点E ,使得以BC 为直角边的△BCE 和Rt △AOB 相似. ①当BC 为斜边时,△BOC 即为所找的△BCE 是直角三角形,但是它与Rt △AOB 不相似; ②当BC 为直角边时,若点B 为直角顶点,则点E 的坐标为(-8,-4),此时点E 不在抛物线上; 若点B 为直角顶点,则点E 的坐标为(-4,-8),此时点E 在抛物线上.(3)∵S △ABC =164122⨯⨯=,S △BCD :S △ABC =1:4, ∴S △BCD =14S △ABC =11234⨯=.如图所示,设在直线BC 上方的抛物线上,找一点D 的坐标为(x ,2142x x -++),作DE ⊥x 轴于点E ,则S △BCD =S 梯形BOED +S △DCE -S △BOC =2211111(44)(4)(4)44322222x x x x x x ⨯-+++⨯+⨯-⨯-++-⨯⨯=. 即2430x x -+=, 解得1x =1,2x =3.∴点D 的坐标为(1,92)或(3,52).。
2013年云南省昆明市中考数学试卷-答案

,点
【解析】2(5)-∆=
【提示】求出根的判别式【解析】四边形在,正方形又PE AC ⊥F 是矩形,又P E E M =PM PN AC +=四边形是矩形,PE ∴BNF △是等腰直角三角形,而
AMP △是等腰直角三角形,当AMP △和故选B .
【提示】依据正方形的性质以及勾股定理、都是等腰直角三角形,四边形【解析】正比例函数【解析】2(3)9±=故答案为3±.
【提示】根据平方根的定义解答.
AOB=︒,∴
如图,扇形90
90π22
=
180 2
故答案为8.
∥
【答案】AB CD
在
90的对应点
(2)根据题意得:“比较了解”的学生为40(41011)15
-++=(名),补全统计图,如图所示;
1511
+
19.【答案】(1)根据题意画出树状图如下:
222
中,CD的坡度为答:天桥下底AD的长度约为23.1m.
,y为正整数,
,AC 是O 直径,OC OB =PBA ∠=PBA ∴∠=OB PB ∴⊥OB 为半径,是O 的切线;(2)设O 的半径为OP BC ∥,OBC ∠POB OBC =∠PBO ABC ∠=∠PBO ∴△∽△OP OB AC BC
∴=822
r r ,即O 的半径为
①当点M在x轴上方时,如图1所示:
9
⎛⎫。
2013年云南省中考数学试卷-答案

云南省2013年初中学业水平考试数学答案解析 一、选择题1.【答案】B【解析】根据绝对值的性质,|66|-=.故选B .【提示】根据绝对值的性质,当a 是负有理数时,a 的绝对值是它的相反数a -,解答即可.【考点】绝对值2.【答案】B【解析】A .633m m m ÷=,选项错误;B .正确;C .222()2m n m mn n +=++,选项错误;D .235mn mn mn +=,选项错误.故选B .【提示】依据同底数的幂的除法、单项式的乘法以及完全平方公式,合并同类项法则即可判断.【考点】单项式乘单项式,合并同类项,同底数幂的除法,完全平方公式3.【答案】D【解析】由主视图和左视图为矩形判断出是柱体,由俯视图是正方形可判断出这个几何体应该是长方体. 故选D .【提示】由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.【考点】由三视图判断几何体4.【答案】B【解析】将150.5亿元用科学记数法表示101.50510⨯元.故选B .【提示】科学记数法的表示形式为10n a ⨯的形式,其中1||10a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同,当原数绝对值大于1时,n 是正数;当原数的绝对值小于1时,n 是负数.【考点】科学记数法—表示较大的数5.【答案】A【解析】A .行四边形ABCD 的对角线AC ,BD 相交于点O ,AO CO ∴=,DO BO =,ABCD S =,故此选项错误;.ABCD 是中心对称图形,故此选项错误.【提示】根据平行四边形的性质分别判断得出答案即可.【考点】平行四边形的性质【解析】1O 与2O 的半径分别为又325+=>两圆的位置关系是相交..由1O 与2O 的半径分别为R ,r 的数量关系间的联系即可得出两圆位置关系.【考点】圆与圆的位置关系,估算无理数的大小D【解析】2525=,【提示】根据算术平方根的定义即可求出结果.【考点】算术平方根【解析】AB AC =,AB CD ∥【提示】根据等腰三角形两底角相等求出,再根据两直线平行,内错角相等解答.【考点】等腰三角形的性质,平行线的性质【解析】分子分别为,431-==3n +=)AB AD∠=∠可以添加的条件为C∠.E17.【答案】(1)如图所示:50CB =⨯12CD ∴=故船继续航行50海里与钓鱼岛A的距离最近.=)AB AC,是平行四边形,=)AB AC△中,在直角ACDBD AD=⨯34)利用勾股定理求得BD,a只能取正整数,香樟树91棵;方案三:四边形OA OE =1FEP ∴∠=(1,0)A -,,22F ∴ ⎝点【提示】(1)利用待定系数法求出直线EC的解析式,确定点A的坐标;然后利用等腰梯形的性质,确定点D的坐标;(2)利用待定系数法求出抛物线的解析式;(3)满足条件的点P存在,且有多个,需要分类讨论:①作线段AC的垂直平分线,与y轴的交点,即为所求;②以点A为圆心,线段AC长为半径画弧,与y轴的两个交点,即为所求;②以点C为圆心,线段CA长为半径画弧,与y轴的两个交点,即为所求.【考点】二次函数综合题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
云南省2013年中考数学试卷一、选择题(本大题共8小题,每小题只有一个正确选项,每小题3分,满分24分)1.(3分)(2013•云南)﹣6的绝对值是(B)A.﹣6 B.6C.±6 D.2.(3分)(2013•云南)下列运算,结果正确的是()A.m6÷m3=m2B.3mn2•m2n=3m3n3C.(m+n)2=m2+n2D.2mn+3mn=5m2n2点评:本题主要考查了合并同类项的法则,幂的乘方的性质,单项式的乘法法则,熟练掌握运算法则是解题的关键.3.(3分)(2013•云南)图为某个几何体的三视图,则该几何体是()A.B.C.D.考点:由三视图判断几何体.分析:由主视图和左视图确定是柱体,锥体还是球体,再由俯视图确定具体形状.解答:解:由主视图和左视图为矩形判断出是柱体,由俯视图是正方形可判断出这个几何体应该是长方体.故选D.点评:考查学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形.4.(3分)(2013•云南)2012年中央财政安排农村义务教育营养膳食补助资金共150.5亿元,150.5亿元用A.1.505×109元B.1.505×1010元C.0.1505×1011元D.15.05×109元考点:科学记数法—表示较大的数.分析:科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.解答:解:将150.5亿元用科学记数法表示1.505×1010元.故选B.点评:此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.5.(3分)(2013•云南)如图,平行四边形ABCD的对角线AC、BD相交于点O,下列结论正确的是()B.A C=BDA.S▱ABCD=4S△AOBC.A C⊥BD D.▱ABCD是轴对称图形考点:平行四边形的性质.分析:根据平行四边形的性质分别判断得出答案即可.解答:解:A、∵平行四边形ABCD的对角线AC、BD相交于点O,∴AO=CO,DO=BO,∴S△AOD=S△DOC=S△BOC=S△AOB,∴S▱ABCD=4S△AOB,故此选项正确;B、无法得到AC=BD,故此选项错误;C、无法得到AC⊥BD,故此选项错误;D、▱ABCD是中心对称图形,故此选项错误.故选:A.点评:此题主要考查了平行四边形的性质,正确把握平行四边形的性质是解题关键.6.(3分)(2013•云南)已知⊙O1的半径是3cm,⊙2的半径是2cm,O1O2=cm,则两圆的位置关系是()A.相离B.外切C.相交D.内切考点:圆与圆的位置关系;估算无理数的大小分析:由⊙O1与⊙O2的半径分别为3cm、2cm,且圆心距O1O2=cm,根据两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系即可得出两圆位置关系.解答:解:∵⊙O1与⊙O2的半径分别为3cm、2cm,且圆心距O1O2=cm,又∵3+2=5>,3﹣2=1,∴两圆的位置关系是相交.故选C.点评:此题考查了圆与圆的位置关系.解题的关键是掌握两圆位置关系与圆心距d,两圆半径R,r的数量关系间的联系.7.(3分)(2013•云南)要使分式的值为0,你认为x可取得数是()A.9B.±3 C.﹣3 D.3考点:分式的值为零的条件.分析:根据分式的值为零的条件可以求出x的值.解答:解:由分式的值为零的条件得x2﹣9=0,3x+9≠0,由x2﹣9=0,得x=±3,由3x+9≠0,得x≠﹣3,综上,得x=3.故选D.点评:本题考查了分式的值为零的条件,若分式的值为零,需同时具备两个条件:(1)分子为0;(2)分母不为0.这两个条件缺一不可.8.(3分)(2013•云南)若ab>0,则一次函数y=ax+b与反比例函数y=在同一坐标系数中的大致图象A.B.C.D.考点:反比例函数的图象;一次函数的图象.分析:根据ab>0,可得a、b同号,结合一次函数及反比例函数的特点进行判断即可.解答:解:A、根据一次函数可判断a>0,b>0,根据反比例函数可判断ab>0,故符合题意,本选项正确;B、根据一次函数可判断a<0,b<0,根据反比例函数可判断ab<0,故不符合题意,本选项错误;C、根据一次函数可判断a<0,b>0,根据反比例函数可判断ab>0,故不符合题意,本选项错误;D、根据一次函数可判断a>0,b>0,根据反比例函数可判断ab<0,故不符合题意,本选项错误;故选A.点评:本题考查了反比例函数的图象性质和一次函数函数的图象性质,要掌握它们的性质才能灵活解题.二、填空题(本大题共6个小题,每小题3分,满分18分)9.(3分)(2013•云南)25的算术平方根是5.考点:算术平方根.分析:根据算术平方根的定义即可求出结果.解答:解:∵52=25,∴25的算术平方根是5.故填5.点评:易错点:算术平方根的概念易与平方根的概念混淆而导致错误.规律总结:弄清概念是解决本题的关键.10.(3分)(2013•云南)分解因式:x3﹣4x=x(x+2)(x﹣2).考点:提公因式法与公式法的综合运用.分析:应先提取公因式x,再对余下的多项式利用平方差公式继续分解.解答:解:x3﹣4x,=x(x2﹣4),=x(x+2)(x﹣2).点评:本题考查了提公因式法,公式法分解因式,提取公因式后利用平方差公式进行二次因式分解,分解因式一定要彻底,直到不能再分解为止.11.(3分)(2013•云南)在函数中,自变量x的取值范围是x≥﹣1且x≠0.考点:函数自变量的取值范围;分式有意义的条件;二次根式有意义的条件.分析:本题主要考查自变量的取值范围,函数关系中主要有二次根式和分式两部分.根据二次根式的意义,被开方数x+1≥0,根据分式有意义的条件,x≠0.就可以求出自变量x的取值范围.解答:解:根据题意得:x+1≥0且x≠0解得:x≥﹣1且x≠0.故答案为:x≥﹣1且x≠0点评:函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数为非负数.12.(3分)(2013•云南)已知扇形的面积为2π,半径为3,则该扇形的弧长为(结果保留π).考点:扇形面积的计算;弧长的计算分析:利用扇形的面积公式S扇形=lR(其中l为扇形的弧长,R为扇形所在圆的半径)求解即可.解答:解:设扇形的弧长为l,由题意,得l×3=2π,解得l=.故答案为π.点评:本题主要考查了扇形的面积公式,计算扇形的面积有2个公式:S扇形=或S扇形=lR(其中n 为圆心角的度数,R为扇形所在圆的半径,l为扇形的弧长),需根据条件灵活选择公式.13.(3分)(2013•云南)如图,已知AB∥CD,AB=AC,∠ABC=68°,则∠ACD=44°.考点:等腰三角形的性质;平行线的性质.分析:根据等腰三角形两底角相等求出∠BAC,再根据两直线平行,内错角相等解答.解答:解:∵AB=AC,∠ABC=68°,∴∠BAC=180°﹣2×68°=44°,∵AB∥CD,∴∠ACD=∠BAC=44°.故答案为:44°.点评:本题考查了等腰三角形两底角相等的性质,平行线的性质,是基础题,熟记各性质是解题的关键.14.(3分)(2013•云南)下面是按一定规律排列的一列数:,,,,…那么第n个数是.考点:规律型:数字的变化类.专题:规律型.分析:观察不难发现,分子是连续的奇数,分母减去3都是平方数,根据此规律写出第n个数的表达式即可.解答:解:∵分子分别为1、3、5、7,…,∴第n个数的分子是2n﹣1,∵4﹣3=1=12,7﹣3=4=22,12﹣3=9=32,19﹣3=16=42,…,∴第n个数的分母为n2+3,∴第n个数是.故答案为:.点评:本题是对数字变化规律的考查,从分子与分母两个方面考虑求解是解题的关键.三、解答题(本大题共9个小题,满分58分)15.(4分)(2013•云南)计算:sin30°+(﹣1)0+()﹣2﹣.考点:实数的运算;零指数幂;负整数指数幂;特殊角的三角函数值.分析:分别进行零指数幂、负整数指数幂的运算,然后代入特殊角的三角函数值即可.解答:解:原式=+1+4﹣=5.点评:本题考查了实数的运算,解答本题的关键是掌握零指数幂、负整数指数幂的运算法则,熟记特殊角的三角函数值.16.(5分)(2013•云南)如图,点B在AE上,点D在AC上,AB=AD.请你添加一个适当的条件,使△ABC≌△ADE(只能添加一个).(1)你添加的条件是∠C=∠E.(2)添加条件后,请说明△ABC≌△ADE的理由.考点:全等三角形的判定.专题:开放型.分析:(1)可以根据全等三角形的不同的判定方法选择添加不同的条件;(2)根据全等三角形的判定方法证明即可.解答:解:(1)∵AB=AD,∠A=∠A,∴若利用“AAS”,可以添加∠C=∠E,若利用“ASA”,可以添加∠ABC=∠ADE,或∠EBC=∠CDE,若利用“SAS”,可以添加AC=AE,或BE=DC,综上所述,可以添加的条件为∠C=∠E(或∠ABC=∠ADE或∠EBC=∠CDE或AC=AE或BE=DC);故答案为:∠C=∠E;(2)选∠C=∠E为条件.理由如下:在△ABC和△ADE中,,∴△ABC≌△ADE(AAS).点评:本题主要考查了全等三角形的判定,开放型题目,根据不同的三角形全等的判定方法可以选择添加的条件也不相同.17.(6分)(2013•云南)如图,下列网格中,每个小正方形的边长都是1,图中“鱼”的各个顶点都在格点上.(1)把“鱼”向右平移5个单位长度,并画出平移后的图形.(2)写出A、B、C三点平移后的对应点A′、B′、C′的坐标.考点:利用平移设计图案专题:作图题.分析:(1)将各能代表图形形状的点向右平移5个单位,顺次连接即可;(2)结合坐标系,可得出A′、B′、C′的坐标.解答:解:(1)如图所示:.(2)结合坐标系可得:A'(5,2),B'(0,6),C'(1,0).点评:本题考查了平移作图的知识,解答本题的关键是掌握平移的性质,注意按要求规范作图.18.(7分)(2013•云南)近年来,中学生的身体素质普遍下降,某校为了提高本校学生的身体素质,落实教育部门“在校学生每天体育锻炼时间不少于1小时”的文件精神,对部分学生的每天体育锻炼时间进行了调查统计.以下是本次调查结果的统计表和统计图.组别 A B C D E时间t(分钟)t<40 40≤t<60 60≤t<80 80≤t<100 t≥100人数12 30 a 24 12(1)求出本次被调查的学生数;(2)请求出统计表中a的值;(3)求各组人数的众数;(4)根据调查结果,请你估计该校2400名学生中每天体育锻炼时间不少于1小时的学生人数.考点:扇形统计图;用样本估计总体;统计表;众数.分析:(1)根据A组有12人,占被调查总数的10%,据此即可求得总人数;(2)总人数减去其它各组的人数即可求得;(3)根据众数的定义即可求解;(4)利用2400乘以对应的比例即可求解.解答:解:(1)12÷10%=120(人);(2)a=120﹣12﹣30﹣24﹣12=42;(3)众数是12人;(4)每天体育锻炼时间不少于1小时的学生人数是:2400×=1560(人).点评:本题考查的是扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.扇形统计图直接反映部分占总体的百分比大小.19.(7分)(2013•云南)如图,有一个可以自由转动的转盘被平均分成3个扇形,分别标有1、2、3三个数字,小王和小李各转动一次转盘为一次游戏,当每次转盘停止后,指针所指扇形内的数为各自所得的数,一次游戏结束得到一组数(若指针指在分界线时重转).(1)请你用树状图或列表的方法表示出每次游戏可能出现的所有结果;(2)求每次游戏结束得到的一组数恰好是方程x2﹣3x+2=0的解的概率.考点:列表法与树状图法;一元二次方程的解.专题:计算题.分析:(1)列表得出所有等可能的情况数即可;(2)找出恰好是方程x2﹣3x+2=0的解的情况数,求出所求的概率即可.解答:解:(1)列表如下:1 2 31 (1,1)(2,1)(3,1)2 (1,2)(2,2)(3,2)3 (1,3)(2,3)(3,3)(2)所有等可能的情况数为9种,其中是x2﹣3x+2=0的解的为(1,2),(2,1)共2种,则P是方程解=.点评:此题考查了列表法与树状图法,以及一元二次方程的解,用到的知识点为:概率=所求情况数与总情况数之比.20.(6分)(2013•云南)如图,我国的一艘海监船在钓鱼岛A附近沿正东方向航行,船在B点时测得钓鱼岛A在船的北偏东60°方向,船以50海里/时的速度继续航行2小时后到达C点,此时钓鱼岛A在船的北偏东30°方向.请问船继续航行多少海里与钓鱼岛A的距离最近?考点:解直角三角形的应用-方向角问题.分析:过点A作AD⊥BC于D,则垂线段AD的长度为与钓鱼岛A最近的距离,线段CD的长度即为所求.先由方位角的定义得出∠ABC=30°,∠ACD=60°,由三角形外角的性质得出∠BAC=30°,则CA=CB=100海里,然后解直角△ADC,得出CD=AC=50海里.解答:解:过点A作AD⊥BC于D,根据题意得∠ABC=30°,∠ACD=60°,∴∠BAC=∠ACD﹣∠ABC=30°,∴CA=CB.∵CB=50×2=100(海里),∴CA=100(海里),在直角△ADC中,∠ACD=60°,∴CD=AC=×100=50(海里).故船继续航行50海里与钓鱼岛A的距离最近.点评:本题考查了解直角三角形的应用﹣方向角问题,难度适中.解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.21.(7分)(2013•云南)已知在△ABC中,AB=AC=5,BC=6,AD是BC边上的中线,四边形ADBE是平行四边形.(1)求证:四边形ADBE是矩形;(2)求矩形ADBE的面积.考点:矩形的判定与性质;勾股定理;平行四边形的性质.分析:(1)利用三线合一定理可以证得∠ADB=90°,根据矩形的定义即可证得;(2)利用勾股定理求得BD的长,然后利用矩形的面积公式即可求解.解答:解:(1)∵AB=AC,AD是BC的边上的中线,∴AD⊥BC,∴∠ADB=90°,∵四边形ADBE是平行四边形.∴平行四边形ADBE是矩形;(2)∵AB=AC=5,BC=6,AD是BC的中线,∴BD=DC=6×=3,在直角△ACD中,AD===4,∴S矩形ADBE=BD•AD=3×4=12.点评:本题考查了三线合一定理以及矩形的判定,理解三线合一定理是关键.22.(7分)(2013•云南)某中学为了绿化校园,计划购买一批棕树和香樟树,经市场调查榕树的单价比香樟树少20元,购买3棵榕树和2棵香樟树共需340元.(1)请问榕树和香樟树的单价各多少?(2)根据学校实际情况,需购买两种树苗共150棵,总费用不超过10840元,且购买香樟树的棵树不少于榕树的1.5倍,请你算算,该校本次购买榕树和香樟树共有哪几种方案.考点:一元一次不等式组的应用;二元一次方程组的应用.分析:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,然后根据单价之间的关系和340元两个等量关系列出二元一次方程组,求解即可;(2)设购买榕树a棵,表示出香樟树为(150﹣a)棵,然后根据总费用和两种树的棵数关系列出不等式组,求出a的取值范围,在根据a是正整数确定出购买方案.解答:解:(1)设榕树的单价为x元/棵,香樟树的单价是y元/棵,根据题意得,,解得,答:榕树和香樟树的单价分别是60元/棵,80元/棵;(2)设购买榕树a棵,则购买香樟树为(150﹣a)棵,根据题意得,,解不等式①得,a≥58,解不等式②得,a≤60,所以,不等式组的解集是58≤a≤60,∵a只能取正整数,∴a=58、59、60,因此有3种购买方案:方案一:购买榕树58棵,香樟树92棵,方案二:购买榕树59棵,香樟树91棵,方案三:购买榕树60棵,香樟树90棵.点评:本题考查了二元一次方程组的应用,一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.23.(9分)(2013•云南)如图,四边形ABCD是等腰梯形,下底AB在x轴上,点D在y轴上,直线AC 与y轴交于点E(0,1),点C的坐标为(2,3).(1)求A、D两点的坐标;(2)求经过A、D、C三点的抛物线的函数关系式;(3)在y轴上是否在点P,使△ACP是等腰三角形?若存在,请求出满足条件的所有点P的坐标;若不存在,请说明理由.考点:二次函数综合题分析:(1)利用待定系数法求出直线EC的解析式,确定点A的坐标;然后利用等腰梯形的性质,确定点D的坐标;(2)利用待定系数法求出抛物线的解析式;(3)满足条件的点P存在,且有多个,需要分类讨论:①作线段AC的垂直平分线,与y轴的交点,即为所求;②以点A为圆心,线段AC长为半径画弧,与y轴的两个交点,即为所求;②以点C为圆心,线段CA长为半径画弧,与y轴的两个交点,即为所求.解答:解:(1)设直线EC的解析式为y=kx+b,根据题意得:,解得,∴y=x+1,当y=0时,x=﹣1,∴点A的坐标为(﹣1,0).∵四边形ABCD是等腰梯形,C(2,3),∴点D的坐标为(0,3).(2)设过A(﹣1,0)、D(0,3)、C(2,3)三点的抛物线的解析式为y=ax2+bx+c,则有:,解得,∴抛物线的关系式为:y=x2﹣2x+3.(3)存在.①作线段AC的垂直平分线,交y轴于点P1,交AC于点F.∵OA=OE,∴△OAE为等腰直角三角形,∠AEO=45°,∴∠FEP1=∠AEO=45°,∴△FEP1为等腰直角三角形.∵A(﹣1,0),C(2,3),点F为AC中点,∴F(,),∴等腰直角三角形△FEP1斜边上的高为,∴EP1=1,∴P1(0,2);②以点A为圆心,线段AC长为半径画弧,交y轴于点P2,P3.可求得圆的半径长AP2=AC=3.连接AP2,则在Rt△AOP2中,OP2===,∴P2(0,).∵点P3与点P2关于x轴对称,∴P3(0,﹣);③以点C为圆心,线段CA长为半径画弧,交y轴于点P4,P5,则圆的半径长CP4=CA=3,在Rt△CDP4中,CP4=3,CD=2,∴DP4===,∴OP4=OD+DP4=3+,∴P4(0,3+);同理,可求得:P5(0,3﹣).综上所述,满足条件的点P有5个,分别为:P1(0,2),P2(0,),P3(0,﹣),P4(0,3+),P5(0,3﹣).点评:本题是二次函数综合题,考查了二次函数的图象与性质、待定系数法、等腰三角形的判定、勾股定理等知识点.难点在于第(3)问,符合条件的点P有多个,需要分类讨论,避免漏解;其次注意解答中确定等腰三角形的方法,即作垂直平分线、作圆来确定等腰三角形.。
