第8 讲：自组织神经网络(2)
合集下载
自组织竞争神经网络
第23页
3.搜索阶段：
由Reset信号置获胜阶段无效开始，网络进入搜索 阶段。此时R为全0，G1=1 ，在C层输出端又得到了此 次输入模式X。所以，网络又进入识别及比较阶段，得 到新获胜节点（以前获胜节点不参加竞争）。这么重 复直至搜索到某一个获胜节点K，它与输入向量X充分 匹配到达满足要求为止。模式X编制到R层K节点所连 模式类别中，即按一定方法修改K节点自下而上和自上 而下权向量，使网络以后再碰到X或与X相近模式时， R层K节点能很快取得竞争胜利。若搜索了全部R层输 出节点而没有发觉有与X充分靠近模式，则增设一个R 层节点以表示X或与X相近模式。
⑥ 警戒线检测。设向量X中不为0个数用||X||表示，可
有 n || X || xi
n
||C'|| w' j *iXi i1
(5.3.1)
i 1
n
||C'|| w' j *iXi
(5.3.2)
i1
若||C||/||X||>成立，则接收j*为获胜节点，转⑦。
不然发Reset信号，置j*为0（不允许其再参加竞争），
信号1：输入X第i个分量Xi。 信号2：R层第j个单元自上而下返回信号Rj。 信号3：G1控制信号。 设C层第i个单元输出为Ci。 Ci依据“2/3规则”产 生，即Ci含有三个信号中多数相同值。 网络开始运行时， G1 =1，R层反馈信号为0。
自组织竞争神经网络
第18页
2.R 层结构：
R层功效结构相当于一个前向竞争网络，假设输出 层有m个节点，m类输入模式。输出层节点能动态增加， 以满足设置新模式类需要。设由C层自下而上连接到R 层第j个节点权向量用Wj={w1j,w2j,..,wnj} 表示。C层输出向量C沿Wj向前馈送，经过竞争在R层 输出端产生获胜节点，指示此次输入向量类别。
人工智能控制技术课件：神经网络控制
进行的，这种排列往往反映所感受的外部刺激的某些物理特征。
例如，在听觉系统中，神经细胞和纤维是按照其最敏感的频率分
布而排列的。为此，柯赫仑（Kohonen）认为，神经网络在接受外
界输入时，将会分成不同的区域，不同的区域对不同的模式具有
不同的响应特征，即不同的神经元以最佳方式响应不同性质的信
号激励，从而形成一种拓扑意义上的有序图。这种有序图也称之
,
,
⋯
,
)
若 输 入 向 量 X= ( 1
， 权 值 向 量
2
W=(1 , 2 , ⋯ , ) ，定义网络神经元期望输出 与
实际输出 的偏差E为：
E= −
PERCEPTRON学习规则
感知器采用符号函数作为转移函数，当实际输出符合期
望时，不对权值进行调整，否则按照下式对其权值进行
单神经元网络
对生物神经元的结构和功能进行抽象和
模拟，从数学角度抽象模拟得到单神经
元模型，其中 是神经元的输入信号，
表示一个神经元同时接收多个外部刺激；
是每个输入所对应的权重，它对应
于每个输入特征，表示其重要程度；
是神经元的内部状态； 是外部输入信
号； 是一个阈值（Threshold）或称为
第三代神经网络：
2006年，辛顿（Geofrey Hinton）提出了一种深层网络模型——深度
置信网络（Deep Belief Networks，DBN），令神经网络进入了深度
学习大发展的时期。深度学习是机器学习研究中的新领域，采用无
监督训练方法达到模仿人脑的机制来处理文本、图像等数据的目的。
控制方式，通过神经元及其相互连接的权值，逼近系统
例如，在听觉系统中，神经细胞和纤维是按照其最敏感的频率分
布而排列的。为此，柯赫仑（Kohonen）认为，神经网络在接受外
界输入时，将会分成不同的区域，不同的区域对不同的模式具有
不同的响应特征，即不同的神经元以最佳方式响应不同性质的信
号激励，从而形成一种拓扑意义上的有序图。这种有序图也称之
,
,
⋯
,
)
若 输 入 向 量 X= ( 1
， 权 值 向 量
2
W=(1 , 2 , ⋯ , ) ，定义网络神经元期望输出 与
实际输出 的偏差E为：
E= −
PERCEPTRON学习规则
感知器采用符号函数作为转移函数，当实际输出符合期
望时，不对权值进行调整，否则按照下式对其权值进行
单神经元网络
对生物神经元的结构和功能进行抽象和
模拟，从数学角度抽象模拟得到单神经
元模型，其中 是神经元的输入信号，
表示一个神经元同时接收多个外部刺激；
是每个输入所对应的权重，它对应
于每个输入特征，表示其重要程度；
是神经元的内部状态； 是外部输入信
号； 是一个阈值（Threshold）或称为
第三代神经网络：
2006年，辛顿（Geofrey Hinton）提出了一种深层网络模型——深度
置信网络（Deep Belief Networks，DBN），令神经网络进入了深度
学习大发展的时期。深度学习是机器学习研究中的新领域，采用无
监督训练方法达到模仿人脑的机制来处理文本、图像等数据的目的。
控制方式，通过神经元及其相互连接的权值，逼近系统
自组织竞争神经网络
dj =
n
∑ (x
i =1
i
− wi j ) 2
∆wi j = η h( j , j*)( xi − wi j )
j − j*2 h ( j , j *) = exp − σ2
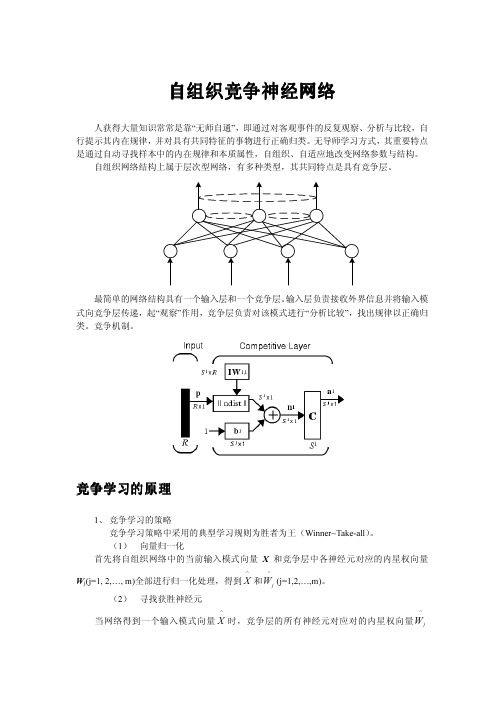
自组织竞争神经网络算法能够进行有效的自适应分类，但它仍存在一些问题： 学习速度的选择使其不得不在学习速度和最终权值向量的稳定性之间进行折中。 有时有一个神经元的初始权值向量离输入向量太远以至于它从未在竞争中获胜， 因 此也从未得到学习，这将形成毫无用处的“死”神经元。
网络结构
%1.ÎÊÌâÌá³ö X=[0 1;0 1]; clusters=8; points=10; std_dev=0.05; P=nngenc(X,clusters,points,std_dev); plot(P(1,:),P(2,:),'+r'); title('ÊäÈëÏòÁ¿'); xlabel('P(1)'); ylabel('P(2)'); %2.ÍøÂçÉè¼Æ net=newc([0 1;0 1],8,.1) w=net.IW{1}; plot(P(1,:),P(2,:),'+r'); hold on; circle=plot(w(:,1),w(:,2),'ob') %3.ÍøÂçѵÁ· net.trainParam.epochs=7; net=train(net,P) w=net.IW{1}; delete(circle); plot(w(:,1),w(:,2),'ob'); %4.ÍøÂç²âÊÔ p=[0.5;0.2]; a=sim(net,p)
BP神经网络RBF神经网络自组织竞争型神经网络
（3）如果在已被占用的输出端中找到一个优胜者，它的由顶向下矢量Z（k）与S（k）的相似度足够高，或者开辟了一个未被占用的新输出端，则对于该端相应的由底向上和由顶向下权重系数进行调整。设此端的编号为L，那么被调整的系数是 和 。下面给出系数调整的计算公式:
概括而言，按照ART（也就是以竞争学习和自稳机制为原则所建立的理论）构成的ANN有如下特点: （1）它能对任何输入观察矢量（包括非平衡输入）进行“实时学习”，这就是说，学习和工作是分不开的。这种学习保证能够达到稳定、可靠的结果，直至记忆容量全部用完为止。任何情况下都不会造成新记忆破坏老记忆的灾难性后果。 （2）学习是自治和自组织的，学习过程无需教师指导，因此是一种无监督（unsupervised）学习。
F2层（STM） 此层的作用是由矢量T计算输出矢量Y，其计算公式为 若 （5-3） 可以看出，在输出层F2进行的是一种竞争抉择运算: 在t0～tM-1之间，有一个最大的分量，其对应输出即定为1，而所有其它分量所对应的输出皆定为0。
下面讨论此系统用于分类时的学习策略 在学习开始以前，首先需要对LTM层中的各个权值系数置以随机初值wij（0），然后依次送入观察矢量X（k），随时按照下列公式将各个权重系数调整成一组新的数值: j=0~(N-1),i=0~(M-1) （5-4）
(5-8) 其中α是步幅, 其值取为一个小正实数。
可以看到, 按照上面给出的算法, 只有当新的输入矢量与已存入记忆中的某个矢量足够相似时, 两者才能互相融合, 即对有关的权重系数进行调整, 从而使长期记忆得以改变。这造成一种自适应谐振（adaptive resonance）状态, 这就是ART这个名称的来源。需要指出, 上面给出的（1）和（2）两项运算, 其运算速度相对而言是快的, 在运算时只有F1和F2这两个STM层的输出发生变化, 而LTM层中的系数不产生改变。当进入自适应谐振状态时（即进入第（3）项运算时）LTM层中的有关系数才发生变化。这类似于人的记忆过程, 当输入一个观察矢量时, 大脑必须在已有的记忆内容中搜索与之相似的矢量, 如果得到了印证, 那么对其记忆就会加强。另一方面, 如果输入的是一个完全新奇的矢量, 这也会造成深刻的印象并被植入长期记忆库之中。
自组织神经网络
❖
PR
- Rx2 矩阵确定输入范围
❖
Di
- 第i层神经元个数,缺省为5× 8
❖ TFCN
- 拓扑函数,缺省为 'hextop'.
❖ DFCN
- 距离函数,缺省为 'linkdist'.
❖
OLR
- 排序阶段学习率,缺省为0.9.
❖ OSTEPS - 排序阶段最大学习步骤,缺省为1000.
❖
TLR
- 调整阶段学习率,缺省为0.02;
例：LVQ网络的设计
❖ 设定输入样本和期望输出 ❖ 构建并设置网络参数 ❖ 根据训练样本对网络进行训练 ❖ 用训练样本测试网络 ❖ 用新样本测试网络 ❖ 讨论比例的影响
小结
❖ 何谓自组织：没有答案的学习
❖ 自组织竞争神经网络的基本概念
神经元：输入与权值的负距离加上阈值 网络结构：竞争网络 学习方法：Kohonen和阈值学习规则 用途：聚类
❖
TND
- 调整阶段最大学习步骤,缺省为1
例八：SOFM网络的构建和训练
❖ 构建网络 ❖ 设置训练样本 待聚类样本 ❖ 观察训练前网络的状态 ❖ 根据样本进行训练
排序阶段 粗调 调整阶段 细调
❖ 观察训练后网络的状态
例九：一维SOFM网络设计
❖ 输入为二维向量,神经元分布为一维 ❖ 将二维空间的特征映射到一维拓扑结构 ❖ 步骤
* IW 1 ,1 ( q 1 )
若分类不正确：
修正第 i个神经元的权值更远离
该样本
i i － ( p ( q ) i ) * IW 1,1 ( q )
* IW 1 ,1 ( q 1 )
* IW 1 ,1 ( q 1 )
神经网络方法-PPT课件精选全文完整版
信号和导师信号构成，分别对应网络的输入层和输出层。输
入层信号 INPi (i 1,根2,3据) 多传感器对标准试验火和各种环境条件
下的测试信号经预处理整合后确定，导师信号
Tk (k 1,2)
即上述已知条件下定义的明火和阴燃火判决结果，由此我们
确定了54个训练模式对，判决表1为其中的示例。
15
基于神经网络的融合算法
11
局部决策
局部决策采用单传感器探测的分析算法，如速率持续 法，即通过检测信号的变化速率是否持续超过一定数值来 判别火情。 设采样信号原始序列为
X(n) x1 (n), x2 (n), x3 (n)
式中，xi (n) (i 1,2,3) 分别为温度、烟雾和温度采样信号。
12
局部决策
定义一累加函数 ai (m为) 多次累加相邻采样值 的xi (差n) 值之和
样板和对应的应识别的结果输入人工神经网络，网络就会通过
自学习功能，慢慢学会识别类似的图像。
第二，具有联想存储功能。人的大脑是具有联想功能的。用人
工神经网络的反馈网络就可以实现这种联想。
第三，具有容错性。神经网络可以从不完善的数据图形进行学
习和作出决定。由于知识存在于整个系统而不是一个存储单元
中，一些结点不参与运算，对整个系统性能不会产生重大影响。
18
仿真结果
19
仿真结果
20
2
7.2 人工神经元模型—神经组织的基本特征
3
7.2 人工神经元模型—MP模型
从全局看，多个神经元构成一个网络，因此神经元模型的定义 要考虑整体，包含如下要素： （1）对单个人工神经元给出某种形式定义； （2）决定网络中神经元的数量及彼此间的联结方式； （3）元与元之间的联结强度（加权值）。
神经网络
人工神经网络
Artificial Neural Networks
小组成员徐渊\孙鹏\张倩\ 武首航：
目录
第一节：神经网络简介 第二节：神经网络基本模型 第三节：传播算法（BP） 第四节：遗传算法 第五节：模糊神经网络（FNN） 第六节：Hopfield网络模型 第七节：随机型神经网络 第八节：自组织神经网络
网络的理论模型。其中包括概念模型、知识模型、物理化学 模型、数学模型等。
（3）网络模型与算法研究。在理论模型研究的基础上构作具体
的神经网络模型，以实现计算机模拟或准备制作硬件，包括 网络学习算法的研究。这方面的工作也称为技术模型研究。
（4）人工神经网络应用系统。在网络模型与算法研究的基础上，利用人工神 经网络组成实际的应用系统，例如，完成某种信号处理或模式识别的功 能、构作专家系统、制成机器人等等。
1, vi = 0, ui > 0 ui ≤ 0
如果把阈值θi看作为一个特殊的权值，则可改写为:
v
i
=
f (
∑
n
w
其中，w0i＝-θi，v0＝1 为用连续型的函数表达神经元的非线性变换 能力，常采用s型函数: 1
j = 0
ji
v
j
)
f (u
i
) =
学习该网络一般选用HUBB学习规则。归结为神经元连接权的变化，表示 为： Δwij＝αuivj若第i和第j个神经元同时处于兴奋状态，则它们之 间的连接应当加强
DALIAN UNIVERSITY
系统辨识
技术讲座
4
wij ——代表神经元i与神经元j之间的连接强度(模拟生物神经元之间突触连接 强度)，称之为连接权； ui——代表神经元i的活跃值，即神经元状态； vj——代表神经元j的输出，即是神经元i的一个输入； θi——代表神经元i的阈值。 函数f表达了神经元的输入输出特性。在MP模型中，f定义为阶跃函数：
Artificial Neural Networks
小组成员徐渊\孙鹏\张倩\ 武首航：
目录
第一节：神经网络简介 第二节：神经网络基本模型 第三节：传播算法（BP） 第四节：遗传算法 第五节：模糊神经网络（FNN） 第六节：Hopfield网络模型 第七节：随机型神经网络 第八节：自组织神经网络
网络的理论模型。其中包括概念模型、知识模型、物理化学 模型、数学模型等。
（3）网络模型与算法研究。在理论模型研究的基础上构作具体
的神经网络模型，以实现计算机模拟或准备制作硬件，包括 网络学习算法的研究。这方面的工作也称为技术模型研究。
（4）人工神经网络应用系统。在网络模型与算法研究的基础上，利用人工神 经网络组成实际的应用系统，例如，完成某种信号处理或模式识别的功 能、构作专家系统、制成机器人等等。
1, vi = 0, ui > 0 ui ≤ 0
如果把阈值θi看作为一个特殊的权值，则可改写为:
v
i
=
f (
∑
n
w
其中，w0i＝-θi，v0＝1 为用连续型的函数表达神经元的非线性变换 能力，常采用s型函数: 1
j = 0
ji
v
j
)
f (u
i
) =
学习该网络一般选用HUBB学习规则。归结为神经元连接权的变化，表示 为： Δwij＝αuivj若第i和第j个神经元同时处于兴奋状态，则它们之 间的连接应当加强
DALIAN UNIVERSITY
系统辨识
技术讲座
4
wij ——代表神经元i与神经元j之间的连接强度(模拟生物神经元之间突触连接 强度)，称之为连接权； ui——代表神经元i的活跃值，即神经元状态； vj——代表神经元j的输出，即是神经元i的一个输入； θi——代表神经元i的阈值。 函数f表达了神经元的输入输出特性。在MP模型中，f定义为阶跃函数：
竞争型神经网络与自组织神经网络
竞争型神经网络是基于无监督学习的神经网络的一种重要类型，作为基本的网络形式，构成了其他一些具有组织能力的网络，如学习向量量化网络、自组织映射网络、自适应共振理论网络等。
与其它类型的神经网络和学习规则相比，竞争型神经网络具有结构简单、学习算法简便、运算速度快等特点。
竞争型神经网络模拟生物神经网络系统依靠神经元之间的兴奋、协调与抑制、竞争的方式进行信息处理。
一个竞争神经网络可以解释为：在这个神经网络中，当一个神经元兴奋后，会通过它的分支对其他神经元产生抑制，从而使神经元之间出现竞争。
当多个神经元受到抑制，兴奋最强的神经细胞“战胜”了其它神经元的抑制作用脱颖而出，成为竞争的胜利者，这时兴奋最强的神经元的净输入被设定为 1，所有其他的神经元的净输入被设定为 0，也就是所谓的“成者为王，败者为寇”。
一般说来，竞争神经网络包含两类状态变量：短期记忆变元（STM）和长期记忆变元（LTM）。
STM 描述了快速变化的神经元动力学行为，而 LTM 描述了无监督的神经细胞突触的缓慢行为。
因为人类的记忆有长期记忆（LTM）和短期记忆（STM）之分，因此包含长时和短时记忆的竞争神经网络在理论研究和工程应用中受到广泛关注。
竞争性神经网络模型图自组织特征映射神经网络（简称SOM），是由输入层和输出层组成的单层神经网络，主要用于对输入向量进行区域分类。
SOM是一种无导师聚类，能将一维输入模式在输出层映射成二维离散图形，此图形分布在网格中，网格大小由m*n 表示，并保持其拓扑结构不变，从而使有相似特征的神经元彼此靠近，不同特征的神经元彼此远离，最终实现区分识别样品的目的。
SOM 通过学习输入向量的分布情况和拓扑结构，靠多个神经元的协同作用来完成模式分类。
当神经网络接受外界输入模式时，神经网络就会将其分布在不同的对应区域，并且记忆各区域对输入模式的不同响应特征，使各神经元形成有序的空间分布。
当输入不同的样品光谱时，网络中的神经元便随机兴奋，经过SOM 训练后神经元在输出层有序排列，作用相近的神经元相互靠近，作用不同的神经元相互远离。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
X1
-0.5 -0.5 0.5 -0.5 0.5 0.5 0.5
H2 H3
Y1
X2
Ym 0.5 -0.5 -0.5
H4
Randomly set up the weights of Wih & Whj
0.5
The example of CPN
Sol: Phase I (1) 代入X=[-1,-1] T=[0,1] net1 =[-1-(-0.5)]2 + [-1-(-0.5)]2 = (-0.52) + (-0.52) = 0.5 net2 =[-1-(-0.5)]2 + [ -1-(0.5)]2 = (-0.52) + ( -1.52) = 2.5 net3 = 2.5 net4 = 4.5 ∴ net 1 has minimum distance and the winner is h* = 1 (2) Update weights of Wih* △W11 = (0.5) [-1-(-0.5)] = -0.25 △W21 = (0.5) [-1-(-0.5)] = -0.25 ∴ W11 = △W11 + W11 = -0.75, W21 = △W21 + W21 = -0.75
自组织特征映射网络的学习算法
o1 W1○
„
ok
„
ol
o1 W1○
„
ok
„
ol
Wk○
Wl
○
yj*
„
Wk○
Wl
○
„
y1○ V1
y2○
„
○ym
Vm
y1○ V1
y2○
„
y j*
○ym
Vm
○
x1
„
○
xi
„
○
xn
○
x1
„
○
xi
„
○
xn
(a)竞争产生获胜节点
(b)获胜节点外星向量决定输出
SOM学习过程的图形表示
n
dj
(x w )
i 1 i ij
2
自组织特征映射网络的学习算法
自组织特征映射学习算法步骤
– (1) 网络初始化
用随机数设定输入层和映射层之间权值的初始值.
– (2) 输入向量
把输入向量输入给输入层.
– (3) 计算映射层的权值向量和输入向量的距离
映射层的神经元和输入向量的距离，按下式给出:
因为输入矢量的模已被单位化为1，所以内星的加权输入 和等于输入矢量p1和p2之间夹角的余弦.
根据不同的情况，内星的加权输入和可分为如下几种情况： 1) p2等于p1，即有θ12＝0，此时，内星加权输入和为1； 2) p2不等于p1，内星加权输入和为0； 3) 当p2＝-p1，即θ12＝180°时，内星加权输入和达到最 小值-1。
Introduction
Input layer : X=[X1, X2, …….Xn] Hidden layer: also called Cluster layer, H=[H1, H2, …….Hn] Output layer: Y=[Y1, Y2, ……Ym] Weights : From InputHidden: Wih , From HiddenOutput : Whj Transfer function: uses linear type
自组织特征映射网络的学习算法
设输入层、Kohonen 层及 Grossberg 层分别为 2、2 及 1 个节点的 CPN 网络架构，如下图所示，其中，W、C 代表 2 个输入（体重、 血糖浓度），O 代表输出（胰岛素补充量）；假设当体重为 45 且血 糖浓度为 180，则补充量为 3，另外当体重为 90 且血糖浓度为 240， 则补充量为 6.
(3)Adjust the weights that connected to the winner node in hidden layer with △Wih* ＝ η1(Xi - Wih* ) Phase II: (Grossberg supervised learning） • Some as (1)& (2)of phase I • Let the link connected to the winner node to output node is set as 1 and the other are set to 0. • Adjust the weights using △Wij ＝ η2‧δ‧Hh
与内星不同，外星联接强度的变化Δw是与输入矢量P成正 比的.这意味着当输入矢量被保持高值，比如接近1时，每 个权值wij将趋于输出ai值，若pj＝1，则外星使权值产生输 出矢量. 当输入矢量pj为0时，网络权值得不到任何学习与修正.
科荷伦学习规则 科荷伦现在来考虑当不同的输入矢量p1和p2分别出现在同一内星 时的情况. 首先，为了训练的需要，必须将每一输入矢量都进行单 位归一化处理.
当第一个矢量p1输入给内星后，网络经过训练，最终达到 W ＝ (p1)T. 此后，给内星输入另一个输入矢量 p2 ，此时内 星的加权输入和为新矢量p2与已学习过矢量p1的点积，即：
(1) W = 45, C = 180，则选择 R1 (输出为1)，输出值 O = 3 (2) W = 90, C = 240，则选择 R2 (输出为1) ，输出值 O = 6.
The example of CPN
• Ex：Use CPN to solve XOR problem
H1
-0.5
X1 X2 T1 T2 -1 -1 1 1 -1 1 -1 1 0 1 1 0 1 0 0 1
内星学习规则 实现内星输入／输出转换的激活函数是硬限制函数. 可以通过内星及其学习规则来训练某一神经元节点只 响应特定的输入矢量P，它是借助于调节网络权矢量W 近似于输入矢量P来实现的.
单内星中对权值修正的格劳斯贝格内星学习规则为： (1) 由(1)式可见，内星神经元联接强度的变化Δw1j是与输出 成正比的。如果内星输出 a 被某一外部方式而维护高值 时，那么通过不断反复地学习，权值将能够逐渐趋近于 输入矢量pj的值，并趋使Δw1j 逐渐减少，直至最终达到 w1j ＝ pj ，从而使内星权矢量学习了输入矢量 P，达到了 用内星来识别一个矢量的目的 . 另一方面，如果内星输 出保持为低值时，网络权矢量被学习的可能性较小，甚 至不能被学习.
dj
(x w )
i 1 i ij
n
2
自组织特征映射网络的学习算法
– (4) 选择与权值向量的距离最小的神经元 计算并选择使输入向量和权值向量的距离最小的神经元，把 其称为胜出神经元并记为 j ，并给出其邻接神经元集合. – (5)调整权值 胜出神经元和位于其邻接神经元的权值，按下式更新：
自组织特征映射神经网络结构
竞争层 输入层
SOM神经网络立体示意图
自组织特征映射网络的学习算法
自组织特征映射学习算法原理
– Kohonen自组织特征映射算法，能够自动找出输入数据 之间的类似度，将相似的输入在网络上就近配置. 因此 是一种可以构成对输入数据有选择地给予响应的网络.
类似度准则
– 欧氏距离:
科荷伦学习规则实际上是内星学习规则的一个特例，但 它比采用内星规则进行网络设计要节省更多的学习，因 而常常用来替代内星学习规则.
CPN 思想
Counter Propagation Network(CPN)
－ Robert Hecht-Nielson 在1987年提出了对传网. CPN为异构网： – Kohonen, 1981年提出的Self-organization map • SOM——Kohonen层 – Grossberg, 1969年提出的Outstar——Grossberg层 让网络的隐藏层执行无导师学习，是解决多级网络训练的另一个思路.
由此可见，对于一个已训练过的内星网络，当输入端再次 出现该学习过的输入矢量时，内星产生1的加权输入和； 而与学习过的矢量不相同的输入出现时，所产生的加权输 入和总是小于1. 当多个相似输入矢量输入内星，最终的训练结果是使网 络的权矢量趋向于相似输入矢量的平均值.
外星学习规则 外星网络的激活函数是线性函数，它被用来学习回忆一 个矢量，其网络输入P也可以是另一个神经元模型的输出. 外星被训练来在一层s个线性神经元的输出端产生一个特 别的矢量A. 对于一个外星，其学习规则为：
内星可以被训练来识别矢量； 外星可以被训练来产生矢量.
CPN算法基础
图1 格劳斯贝格内星模型图
内星是通过联接权矢量W接受一组输入信号P
CPN算法基础
图2 格劳斯贝格外星模型图
外星则是通过联接权矢量向外输出一组信号A. 它们之所以被称为内星和外星，主要是因为其网络的 结构像星形，且内星的信号流向星的内部；而外星的 信号流向星的外部.
由芬兰学者Teuvo Kohonen于1981年提出
I’m Teuvo Kohonen
基本上为输入层和映射层的双层结构 , 映射层的神 经元互相连接，每个输出神经元连接至所有输入神 经元 .
自组织特征映射神经网络结构 竞争层
输入层
SOM神经网络结构
自组织特征映射神经网络结构
输入层
竞争层
SOM神经网络平面示意图
2
2
)
– 由邻域函数可以看到，以获胜神经元为中心设定了一 个邻域半径，称为胜出邻域 . 学习初期，胜出神经元 和其附近的神经元全部接近当时的输入向量，形成粗 略的映射. 2 随着学习的进行而减小，胜出邻域变窄， 胜出神经元附近的神经元数变少.因此，学习方法是一 种从粗调整向微调整变化，最终达到预定目标的过程.
监督式学习
• 依分类的结果建立输入-输出映射表（look-up table） • 依Grossberg 学习法调整隐层优胜神经元的连接向量， 使之能正确的投射到配对（input-output pair）的输出向 量 Y 上.