土的渗透性和渗流问题
土渗透性及渗流

变水头试验法 井孔抽水试验 井孔注水试验
渗透系数的室内测定 渗透系数的现场测定
(1) 常水头渗透试验
是指在整个试验过程中保持土样 两端水头不变的渗流实验。
Q vAt kAth / L
QL kT At h
h
A
土样
L Q V
对于黏性土,由于其渗透系数较小故渗水量较小, 用常水头渗透试验不易准确测定。因此,对于 渗透系数小的土可用变水头试验。
w
B
hB
L
zB
水头梯度(坡降) hydraulic gradient
i
hA hB h L L
水流损失与渗流路径长 度之比
二、地下水的运动方式和判别
地下水是指地下水位以下的重力水
按地下水的流线形态分类 1、层流 2、湍流 按水流特征随时间的变化状况分类 1、稳定流运动 2、非稳定流运动 按水流在空间上的分布状况分类 1、一维流动 2、二维流动 3、三维流动
(紊流)
地下水的渗流速度与 水力梯度成非线性关系
两种特例:
(1)粗粒土: ①砾石类土中的渗流常不符合达西定律 ②砂土中渗透速度 vcr=0.3-0.5cm/s v
v vcr
o
v ki m (m 1)
i
(2)粘性土: 致密的粘土 i > i0 修正:v = k(i - i0 )
o i0
i
五、 渗透系数的测定及其影响因素
渗流问题 土的渗透性 及渗透规律
三、达西定律
四、达西定律的适用范围 五、渗透系数的测定及其影响
因素
1. 水在土中渗流会使土的强度发生变化,引起土体变形,甚至影响建筑地基的 稳定。 2. 在层流渗透情况下,砂土中水的渗流服从达西定律,即水的渗流速度与水力 梯度呈正比。 3. 渗透系数是土的基本力学性能指标之一,用来表征土体被水透过的性能,渗 透系数可通过室内试验或现场试验测定。
土的渗流性和渗流问题习题与答案

⼟的渗流性和渗流问题习题与答案第四章⼟的渗流性和渗流问题⼀、填空题1.当渗流⽅向向上,且⽔头梯度⼤于临界⽔头梯度时,会发⽣流砂现象。
2.渗透系数的数值等于⽔⼒梯度为1时,地下⽔的渗透速度越⼩,颗粒越粗的⼟,渗透系数数值越⼤。
3.⼟体具有被液体透过的性质称为⼟的渗透性或透⽔性。
4.⼀般来讲,室内渗透试验有两种,即常⽔头法和变⽔头法。
5.渗流破坏主要有流砂和管涌两种基本形式。
6.达西定律只适⽤于层流的情况,⽽反映⼟的透⽔性的⽐例系数,称之为⼟的渗透系数。
7.出现流砂的⽔头梯度称临界⽔头梯度。
8.渗透⼒是⼀种体积⼒。
它的⼤⼩和⽔⼒坡度成正⽐,作⽤⽅向与渗流⽅向相⼀致。
⼆、名词解释1.渗流⼒:⽔在⼟中流动时,单位体积⼟颗粒受到的渗流作⽤⼒。
2.流砂:⼟体在向上动⽔⼒作⽤下,有效应⼒为零时,颗粒发⽣悬浮、移动的现象。
3.⽔⼒梯度:⼟中两点的⽔头差与⽔流过的距离之⽐。
为单位长度上的⽔头损失。
4.临界⽔⼒梯度:使⼟开始发⽣流砂现象的⽔⼒梯度。
三、选择题1.流砂产⽣的条件为:(D )(A)渗流由上⽽下,动⽔⼒⼩于⼟的有效重度(B)渗流由上⽽下,动⽔⼒⼤于⼟的有效重度(C)渗流由下⽽上,动⽔⼒⼩于⼟的有效重度(D)渗流由下⽽上,动⽔⼒⼤于⼟的有效重度2.饱和重度为20kN/m3的砂⼟,在临界⽔头梯度I Cr时,动⽔⼒G D⼤⼩为:( C )(A)1 kN/m3(B)2 kN/m3 (C)10 kN/m3 (D)20 kN/m33.反应⼟透⽔性质的指标是(D )。
(A)不均匀系数(B)相对密实度(C)压缩系数(D)渗透系数4.下列有关流⼟与管涌的概念,正确的说法是(C )。
(A)发⽣流⼟时,⽔流向上渗流;发⽣管涌时,⽔流向下渗流(B)流⼟多发⽣在黏性⼟中,⽽管涌多发⽣在⽆黏性⼟中(C)流⼟属突发性破坏,管涌属渐进式破坏(D)流⼟属渗流破坏,管涌不属渗流破坏5.⼟透⽔性的强弱可⽤⼟的哪⼀项指标来反映(D )(A)压缩系数(B)固结系数(C)压缩模量(D)渗透系数6.发⽣在地基中的下列现象,哪⼀种不属于渗透变形(A )(A)坑底隆起(B)流⼟(C)砂沸(D)流砂7.下属关于渗流⼒的描述不正确的是(D )。
2 土力学 第二章 土的渗透性及水的渗流
二、临界水力梯度及渗透破坏 当土中水向上渗流时,渗透力垂直向上而与土样重力方向相反,若渗透力 等于土样浮度,即
j = iγ w = γ , 得临界水力梯度: i cr =
γ' γw
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
因此,若土中水向上渗流: ⑴若i>icr,会发生流土破坏,即“管涌”; ⑵若i=icr,流土处于临界状态,即“悬浮”; ⑶若i<icr,不会发生流土破坏。
h = z + hW + hV
由于水在土中渗流的速度一般很小,hv≈0,因此
h = z + hW = z +
u
γw
式中 u为该点的静水压力
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
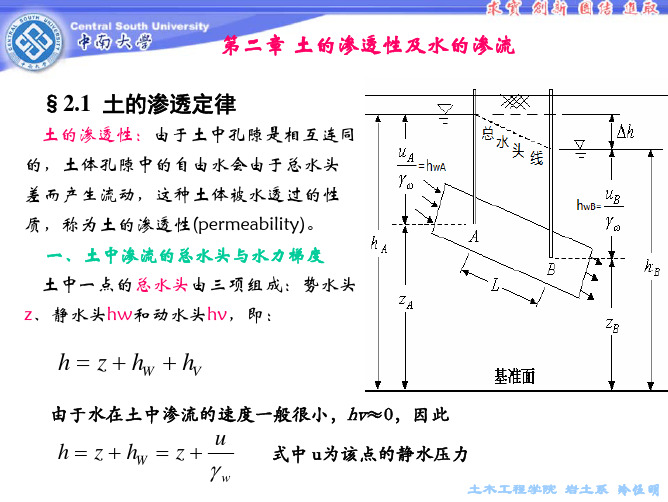
A、B两点的总水头可分别表示为:
hA = z A +
γω
uA
; hB = z B +
γω
uB
A、B两点间的总水头差:
作业题:P54: 2-7,2-9 补题1:什么是渗透力、临界水力梯度?
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流 §2.1 土的渗透定律
土的渗透性:由于土中孔隙是相互连同 的,土体孔隙中的自由水会由于总水头 差而产生流动,这种土体被水透过的性 质,称为土的渗透性(permeability)。 一、土中渗流的总水头与水力梯度 土中一点的总水头由三项组成:势水头 z、静水头hw和动水头hv,即:
土木工程学院 岩土系 冷伍明
第二章 土的渗透性及水的渗流
二、成层土的平均渗透系数 成层土渗透系数的计算方法见P43 三、渗透系数的室内测定方法 渗透系数k不能用理论方法求得,只能通过试验确定。 测定k值室内方法:定水头法、变水头法。 (1)定水头法 保持总水头差Δh不变,在t时间内,量得透过土样的水量为Q,求k: 根据达西定律
土的渗透性及水的渗流

m
kjH j
j 1
三、渗透系数的室内测定
渗透系数不能用理论方法求得,只能通过试验确定。
测定k值室内方法:定水头法、变水头法。
(1)定水头法
保持总水头差Δh不变,在t时间内,量得透过土样的
水量为Q,求k:
注水
根据达西定律
v Q ki k h
t.A
L
k QL A t h
L
h
适用于粗颗粒土,如中砂、粗砂
uA
i h L
△h代表单位重量液体从A点向B点流动时, 为克服阻力而损失的能量。
水力梯度:
水力坡降i 的物理意义为单位渗流长度上的 水力损失。
L为A、B两点间的渗流途径。
2024/11/15
例2-1 如图,求
一.a-a、b-b、c-c静水头 和总水头。
二.a-a至c-c,a-a至b-b,bb至c-c的水头损失;
例题:某基坑在细砂层中开挖,经施工抽水,待水位稳定后, 实测水位情况如图所示。据场地勘察报告提供;细砂层有关 物理力学性质指标如下:
sat 18.7kn / m3
k 4.5102 m m/ s
试求渗透水流的平均速度和 动水力(渗透力),并判断是 否会产生流砂现象?
5.5m
细砂层
分析:1 v ki
v—断面平均渗透速度, 单位m/s或m/d; k—土的渗透系数 单位同v.
流速与水力梯度的 关系-砂土 砂土的水力梯度与 渗透速度呈线性关 系,符合达西渗透 定律。
适用范围:适用于层流范围,如砂土和一般的粘性土, 很粗的土或粘性很强的致密粘土不适合。
单位时间流过土截面A的水量q
流速与水力梯度的关系-粘土
则渗透系数k:
2.3 q lg( r2 )
土的渗透性及渗流

x
§2 土旳渗透性和渗流问题 §2.3 平面渗流与流网
一. 平面渗流旳基本方程及求解 1. 基本方程
▪ 连续性条件
dqe vxdz vzdx
dqo
(vx
v x x
dx)dz
(vz
v z z
dz)dx
dqe dqo
vx vz 0 x z
z
vz
vz z
dz
vx
v
x
vx x
dx
vz
x
▪ 达西定律
§2 土旳渗透性和渗流问题 §2.3 平面渗流与流网
二.流网旳绘制及应用
▪ 流 网——渗流场中旳两族相互正交曲线——等势线和流线所形成旳 网络状曲线簇。 ▪ 流 线——水质点运动旳轨迹线。 ▪ 等势线——测管水头相同旳点之连线 。 ▪ 流网法——经过绘制流线与势线旳网络状曲线簇来求解渗流问题。
△h
第二章 土旳渗透性和渗流问题
§2 土旳渗透性和渗流问题
2.1 概述
碎散性
多孔介质
三相体系
孔隙流体流动
能量差
水、气等在土体孔隙中流动旳现象
渗流
土具有被水、气等液体透过旳性质
渗透性
渗透特征 强度特征 变形特征
非饱和土旳渗透性 饱和土旳渗透性
§2 土旳渗透性和渗流问题 2.1 概述 土石坝坝基坝身渗流
防渗斜墙及铺盖 不透水层
土石坝
浸润线
透水层
渗流量 渗透变形
§2 土旳渗透性和渗流问题 2.1概述 板桩围护下旳基坑渗流
板桩墙
基坑
透水层 不透水层
渗水压力 渗流量 渗透变形 扬压力
§2 土旳渗透性和渗流问题 2.1 概述 水井渗流
土木建筑工程:土的渗透性及渗流测试题(题库版)

土木建筑工程:土的渗透性及渗流测试题(题库版)1、单选美国TIA防治指南建议糖尿病人的空腹血糖控制在()A.<5.0mmol/LB.<6.0mmol/LC.<7.0mmol/LD.<8.0mmol/LE.<(江南博哥)9.0mmol/L正确答案:C2、问答?图3-4为一板桩打入透土层后形成的流网。
已知透水土层深18.0m,渗透系数k=3×10-10mm/s板桩打入土层表面以下,板桩前后水深如图3-4所示。
试求:(1)图中所示a、b、c、d、e各点的孔隙水压力;(2)地基的单位透水量。
(计算题)正确答案:3、判断题达西定律中的渗透速度不是孔隙水的实际流速。
正确答案:对4、判断题绘制流网时必须满足的基本条件之一是流线和等势线必须正交。
正确答案:对5、判断题土的孔隙比愈大,其渗透系数也愈大。
正确答案:错参考解析:对黏性土不成正比。
6、单选下列哪一种土样更容易发生流砂?()A.砂砾或粗砂B.细砂或粉砂C.粉质黏土D.黏土正确答案:B7、单选四个坝基土样的孔隙率和细粒含量(以质量百分率计)如下,试按《水利水电工程地质勘察规范》(GB50287-99)计算判别下列()选项的土的渗透变形的破坏形式属于管涌。
A.B.C.D.正确答案:D参考解析:按规范当时发生管涌。
8、问答?如图3-1所示,在恒定的总水头差之下水自下而上透过两个土样,从土样1顶面溢出。
(计算题)(1)已土样2底面c-c为基准面,求该面的总水头和静水头;(2)已知水流经土样2的水头损失为总水头差的30%,求b-b面的总水头和静水头;(3)已知土样2的渗透系数为0.05cm/s,求单位时间内土样横截面单位面积的流量;(4)求土样1的渗透系数。
正确答案:如图3-1,本题为定水头实验,水自下而上流过两个土样,相关几何参数列于图中。
(1)以c-c为基准面,则有:zc=0,hwc=90cm,hc=90cm(2)已知hbc=30%hac,而hac由图2-16知,为30cm,所以hbc=30%hac=0.330=9cm ∴hb=hc-hbc=90-9=81cm 又∵zb=30cm,故hwb=hb-zb=81-30=51cm(3)已知k2=0.05cm/s,q/A=k2i2=k2hbc/L2=0.059/30=0.015cm3/s/cm2=0.015cm/s(4)∵i1=hab/L1=(hac-hbc)/L1=(30-9)/30=0.7,而且由连续性条件,q/A=k1i1=k2i2 ∴k1=k2i2/i1=0.015/0.7=0.021cm/s9、问答?如图3-2所示,在5.0m厚的黏土层下有一砂土层厚6.0m,其下为基岩(不透水)。
土的渗透性及渗流

3.3.2 不同土渗透3.3系土的渗透系数 数的范围
1、P37,表3-2. 2、卡萨哥兰德三界限值
K=1.0cm/s为土中渗流的层流与紊流的界限; K=10-4cm/s为排水良好与排水不良的界限,也是 对应于发生管涌的敏感范围; K=10-4cm/s大体上为土的渗透系数的下限。
3、在孔隙比相同的情况下,粘性土的渗透系 数一般远小于非性土。
水井渗流
Q
天然水面
不透水层
透水层 渗流量
渠道渗流
原地下水位
渗流量
渗流时地下水位
渗流滑坡
渗流滑坡
板桩围护下的基坑渗流 板桩墙
基坑
透水层 不透水层
渗水压力 渗流量 渗透变形 扬压力
土石坝坝基坝身渗流 防渗斜墙及铺盖
不透水层
土石坝
浸润线
渗流量
透水层 渗透变形
本章研究内 容
土的渗流 土的变形 土的强度
讨论 ❖ 砂土、粘性土:小水流为层流,渗透规律符合
达西定律,-i 为线性关系
❖ 粗粒土: i 小、 大水流为层流,渗透规律符合 达西定律,-i 为线性关系 i 大、 大水流为紊流,渗透规律不符合 达西定律,-i 为非线性关系
3.3.1 渗透系数的3.3 土的渗透系数
影响因素1
1、孔隙比
v
nvs
e 1 e
素2
3、土的饱和度
土的饱和度愈低,渗透系数愈小。因为低饱和土 的孔隙中存在较多气泡会减小过水面积,甚至赌 塞细小孔道。
4、温度
渗透系数k实际上反映流体经由土的孔隙通道时 与土k颗20 粒k间T 摩T 擦20力或粘滞滞T系、性数2。,0分可别而查为流表T℃体和2的0℃粘时水滞的性动力与粘 其温度有关。试验测得的渗透系数kT需经温度修 正(P36,表3-1)
(完整版)第二章土的渗透性和渗流问题要点

第二章 土的渗透性和渗流问题第一节 概 述土是多孔介质,其孔隙在空间互相连通。
当饱和土体中两点之间存在能量差时,水就通过土体的孔隙从能量高的位置向能量低的位置流动。
水在土体孔隙中流动的现象称为渗流;土具有被水等液体透过的性质称为土的渗透性。
土的渗透性是土的重要力学性质之一。
在水利工程中,许多问题都与土的渗透性有关。
渗透问题的研究主要包括以下几个方面:1.渗流量问题。
例如对土坝坝身、坝基及渠道的渗漏水量的估算(图2-la 、b ),基坑开挖时的渗水量及排水量计算(图2-1C ),以及水井的供水量估算(图2-1d )等。
渗流量的大小将直接关系到这些工程的经济效益。
2.渗透变形(或称渗透破坏)问题。
流经土体的水流会对土颗粒和土体施加作用力,这一作用力称为渗透力。
当渗透力过大时就会引起土颗粒或土体的移动,从而造成土工建筑物及地基产生渗透变形。
渗透变形问题直接关系到建筑物的安全,它是水工建筑物和地基发生破坏的重要原因之一。
由于渗透破坏而导致土石坝失事的数量占总失事工程数量的25%~30%。
3.渗流控制问题。
当渗流量和渗透变形不满足设计要求时,要采用工程措施加以控制,这一工作称为渗流控制。
渗流会造成水量损失而降低工程效益;会引起土体渗透变形,从而直接影响土工建筑物和地基的稳定与安全。
因此,研究土的渗透规律、对渗流进行有效的控制和利用,是水利工程及土木工程有关领域中的一个非常重要的课题。
第二节 土的渗透性一、土的渗透定律—达西定律(一)渗流中的总水头与水力坡降液体流动除了要满足连续原理外,还必须要满足液流的能量方程,即伯努里方程。
在饱和土体渗透水流的研究中,常采用水头的概念来定义水体流动中的位能和动能。
水头是指单位重量水体所具有的能量。
按照伯努里方程,液流中一点的总水头h ,可用位置水头Z 、压力水头w uγ和流速水头g v 22之和表示,即 1)-(2 22g v uz h w ++=γ 式(2—1)中各项的物理意义均代表单位重量液体所具有的各种机械能,其量纲为长度。
土的渗透性和渗流问题

第二篇 土力学第四章 土的渗透性和渗流问题第一节 概述土是由固体相的颗粒、孔隙中的液体和气体三相组成的,而土中的孔隙具有连续的性质,当土作为水土建筑物的地基或直接把它用作水土建筑物的材料时,水就会在水头差作用下从水位较高的一侧透过土体的孔隙流向水位较低的一侧。
渗透:在水头差作用下,水透过土体孔隙的现象渗透性:土允许水透过的性能称为土的渗透性。
水在土体中渗透,一方面会造成水量损失,影响工程效益;另一方面将引起土体内部应力状态的变化,从而改变水土建筑物或地基的稳定条件,甚者还会酿成破坏事故。
此外,土的渗透性的强弱,对土体的固结、强度以及工程施工都有非常重要的影响。
本章将主要讨论水在土体中的渗透性及渗透规律,以及渗透力渗透变形等问题。
第二节 土的渗透性一、土的渗透规律——达西定律(一)渗流中的总水头与水力坡降液体流动的连续性原理:(方程式)dw v dw v w w ⎰⎰=2211 2211v w v w =1221w w v v = 表明:通过稳定总流任意过水断面的流量是相等的;或者说是稳定总流的过水断面的 平均流速与过水断面的面积成反比。
前提:流体是连续介质流体是不可压缩的;流体是稳定流,且流体不能通过流面流进或流出该元流。
理想重力的能量方程式(伯努利方程式1738年瑞士数学家应用动能定理推导出来的。
)c gv r p Z =++22饱和土体空隙中的渗透水流,也遵从伯努利方程,并用水头的概念来研究水体流动中 的位能和动能。
水头:实际上就是单位重量水体所具有的能量。
按照伯努利方程,液流中一点的总水头h ,可以用位置水头Z ,压力水头U/r w 和流速水 头V 2/2g 之和表示,即gv r u Z h w 22++= 4-1 此方程式中各项的物理意义均代表单位重量液体所具有的各种机械能,而其量纲都是 长度。
教材P37图22表示渗流在水中流经A ,B 两点时,各种水头的相互关系。
按照公式(4-1),A,B 两点的总水头可分别表示为:gv r u Z h A w A A A 22++= gv r u Z h B w B B B 22++= h h h B A ∆+=式中:Z A ,Z B :为A ,B ,两点相对于任意选定的基准面的高度,代表单位重量液体 所具有的位能(位置高度)故称Z 为位置水头。
第三章土的渗透性及渗流ppt课件

2024年8月1日星期四2时44分59秒
34
3.渗透破坏与控制
J = rwi
(1)流砂 当向上的渗流力与土的浮重
度相等时,粒间有效应力σ'为零, 颗粒群同时发生悬浮、移动的现象 称为流砂现象(流土现象)。
J= r' rwicr= r'
r' icr= rw
i ≥ icr 流砂
2024年8月1日星期四2时44分59秒
水在土中渗透有规律可以遵循吗?
如何定性和定量化评价水在土中的渗透性的大小?如何来描述?
2024年8月1日星期四2时44分58秒
12
一、渗流模型
实际土体中的渗流仅是流 经土粒间的孔隙,由于土体 孔隙的形状、大小及分布极 为复杂,导致渗流水质点的 运动轨迹很不规则。
简化
(1)不考虑渗流路径的迂
回曲折,只分析它的主—“截弯取直” 要流向 ;
9;
由这些特征可进一步知道,流网中等势
线越密的部位,水力梯度越大,流线越
密的部位流速越大。
板桩墙围堰的流网图
2024年8月1日星期四2时44分59秒
28
流网的绘制
(1) 按一定比例绘出结构物和土层的剖面图;
(2) 判定边界条件:透水面(aa' ,bb' )等势线 ; abc 和不透水面 为流线;
27
3.流网的特征与绘制
流网的特征
对于各向同性渗流介质,流网具有下列特征:
(1) 流线与等势线互相正交;
(2) 流线与等势线构成的各个网格的长宽比为常数,当长宽比为
1 时,网格为曲线正方形,这也是最常见的一种流网;
(3) 相邻等势线之间的水头损失相等;Δh= ΔH
(4) 各个流槽的渗流量相等。 q=Nf Δq
土的渗透性和渗流

一、平面渗流的连续性分析
对于一个稳定的渗流来说,渗流场中各点的测管水头h 及流速v等仅是位置的函数而与时间无关,即: h = f (x, z),v = g(x, z)。
z
vz+
v z z
dz
dz vx
图2-9 二维稳定 渗流场中
vz
的某微元
dx
vx+
vx x
dx
x
单位时间流入微元的水量为:
(b) 等效图
图2-8 层状土的垂直渗流情况
其特点有:
(1)通过各层土的流量与等效土层的流量均相 同,即:
qz = q1z = q2z = q3z = ∙∙∙∙∙,v = v1 = v2 = v3 = ∙∙∙∙∙∙ (2)流经等效土层的水头损失等于各土层的水
头损失之和,即:
Δh = Δh1 + Δh2 + Δh3 + ∙∙∙∙∙ = Σhi
分布规律,结合一定的边界条件后,求解该方
程即可得到此条件下的渗流场。
以上就是教材P50-51三个式子的由来。
求解拉普拉斯方程有以下四种方法:
(1)解析法 — 边界条件复杂时,难以求解;
(2)数值解法 — 差分法和有限元方法已应用越 来越广;
(3)实验法 — 用一定比尺的模型实验来模拟渗 流场,应用较广的是电比拟法等;
有
vx
kx
h x
,vz
kz
h z
,将这两式代入连续
方程(2-12)可得:
kx
2h x 2
kz
2h z 2
0
(2-13)
对于各向同性的均质土kx = kz,(2-13)还可变为:
土的渗透性与土中渗流

第4章土的渗透性与土中渗流4.1概述我们在现场挖上时常常看到,只要上坑低于地下水位,水要源源不断渗出,给施工带来不便,为此常要抽水机抽水来保证施工,水能从上体中渗出原因在于,上是具有连续孔隙的介质,水能在水头差作用下,从水位较高的一侧透过上体的孔隙流向水位较低的一侧。
在水头差作用下,水透过土体孔隙的流动现象称为渗透,而上体允许水透过的性能则称为土的渗透性。
研究土的渗透性,是土力学中极英重要的课题,这是由于:①.上是具有连续孔隙的多孔介质,与其它所有材料的物理性质常数的变化范囤相比,上的渗透性的变化范用要大得多。
实际上,干净砾石的渗透系数k值可达30cm/s,纯粘上的k值可以小于相差可达10山倍以上。
其他物理性质参数变化没有这么大。
②.上的三个主要力学性质即强度、变形和渗透性之间,有着密切的相互关系。
在上力学理论中,用有效应力原理将三者有机地联系在一起,形成一个理论体系。
因此渗透性的研究已不限于渗流问题自身的范畴。
例如,控制上在荷重下变形的时间过程的渗透固结阶段,英变形速率就取决于上的渗透性:用有效应力原理研究上的强度和稳定性时,上的孔隙压力消散和有效应力的增长控制着上体强度随时间而增长的过程,而孔隙压力消散速度又主要取决于上的渗透性、压缩性和排水条件。
在无粘性上的动力稳圧性和振动液化的试验研究中,也发现其它条件相同时,渗透性小的土比渗透性大的土更易于液化。
③.土木工程各个领域内许多课题都与土的渗透性有密切关系。
水在丄体中渗透,一方而会造成水虽:损失(如水库),影响工程效益,另一方面会引起上体内部应力状态的变化,如基坑开挖可能会造成基坑坑壁失稳、管涌、流砂等现象,使原有建筑物破坏或施工不便。
承压水补绐区lilHH图4-】地下水类型渗透一般是地下水造成的,存在于地面以下上和岩石的孔隙、裂隙或溶洞中的水,称为地下水:反之,分布在江河、湖泊、海洋内的液态水,或在陆地上的冰、雪,称为地表水。
地下水按英埋藏条件,可分上层滞水、潜水和承压水三种。
(完整版)第二章土的渗透性和渗流问题要点

第二章 土的渗透性和渗流问题第一节 概 述土是多孔介质,其孔隙在空间互相连通。
当饱和土体中两点之间存在能量差时,水就通过土体的孔隙从能量高的位置向能量低的位置流动。
水在土体孔隙中流动的现象称为渗流;土具有被水等液体透过的性质称为土的渗透性。
土的渗透性是土的重要力学性质之一。
在水利工程中,许多问题都与土的渗透性有关。
渗透问题的研究主要包括以下几个方面:1.渗流量问题。
例如对土坝坝身、坝基及渠道的渗漏水量的估算(图2-la 、b ),基坑开挖时的渗水量及排水量计算(图2-1C ),以及水井的供水量估算(图2-1d )等。
渗流量的大小将直接关系到这些工程的经济效益。
2.渗透变形(或称渗透破坏)问题。
流经土体的水流会对土颗粒和土体施加作用力,这一作用力称为渗透力。
当渗透力过大时就会引起土颗粒或土体的移动,从而造成土工建筑物及地基产生渗透变形。
渗透变形问题直接关系到建筑物的安全,它是水工建筑物和地基发生破坏的重要原因之一。
由于渗透破坏而导致土石坝失事的数量占总失事工程数量的25%~30%。
3.渗流控制问题。
当渗流量和渗透变形不满足设计要求时,要采用工程措施加以控制,这一工作称为渗流控制。
渗流会造成水量损失而降低工程效益;会引起土体渗透变形,从而直接影响土工建筑物和地基的稳定与安全。
因此,研究土的渗透规律、对渗流进行有效的控制和利用,是水利工程及土木工程有关领域中的一个非常重要的课题。
第二节 土的渗透性一、土的渗透定律—达西定律(一)渗流中的总水头与水力坡降液体流动除了要满足连续原理外,还必须要满足液流的能量方程,即伯努里方程。
在饱和土体渗透水流的研究中,常采用水头的概念来定义水体流动中的位能和动能。
水头是指单位重量水体所具有的能量。
按照伯努里方程,液流中一点的总水头h ,可用位置水头Z 、压力水头w uγ和流速水头g v 22之和表示,即 1)-(2 22g v uz h w ++=γ 式(2—1)中各项的物理意义均代表单位重量液体所具有的各种机械能,其量纲为长度。
土力学-土的渗透性及渗流

• 防止发生流土破坏的设计要求
所需入土深度
水力梯度 i h h 2h
临界水力梯度 i c r
w
所需入土深度 h Fs w h 2
地下连续墙
h
坑底
渗
透
h
力
向
上
地表
渗 透 力 向 下
• 管涌 piping 在渗流作用下,土中的细粒在粗粒形成的孔隙中移动以至流失→孔
z
(1)连续方程的建立
流入微单元的水量(厚度为1)
dqxvxdz1vxdz dqz vzdx dqxdqzvxdzvzdx
vx
dz
流出微单元的水量
(vz v zzdz)dx(vx v xxdx)dz
vz
vz z
dz
vx
vx x
dx
vz
dx
x
对稳定流,流入量=流出量(忽略土体的变形) z
v x d z v z d x ( v z v z zd z )d x ( v x v x xd x )d z dz vx vx vz 0 x z
(2)水力梯度 水头 hydraulic head:单位重量的水所具有的能量。(故量纲为长度)
测压管水头
总水头 hzhwhv zu/wv2/2g hzu/w
势静 动
孔
渗
水水 水
隙
流
土中渗流速度通常较小,可忽略
头头 头
水
速
头位头压 头速
压
度
置力 度
水水 水
• 水力梯度
uA w
hA zA
测压管 piezometer tube
隙增大,渗流速度增加→粗粒流走→贯通的水流通道→土体塌陷。
管涌
土力学土的渗透性与渗透问题

设饱和土体内某一研究平面的 总面积为A,其中粒间接触面积之 和为As ,则该平面内由孔隙水所占 面积为 Aw =A-As.若由外荷(和/或 自重)在该研究平面上所引起的法 向总应力为,如图所示,那么,它 必将由该面上的孔隙水和粒间接触 面共同来分担,即该面上的总法向 力等于孔隙水所承担的力和粒间所 承担的力之和,于是可以写成:
式中,右端第一项Psv/A为全部竖向 粒间作用力之和除以横断面积A,它 代表全面积A上的平均竖直向粒间应力,并定义为有效应力,习惯上用 ‘ 表示。有端第二项中的As/A,试验研究表明,粒间接触面积As不超过 0.03A,故 As/A可忽略不计。于是上式可简化为:
=‘ 十 u 即为著名的有效应力原理
第18页/共26页
(1)几何条件 土中粗颗粒所构成的孔隙直径必须大于细颗粒的直径,才可能让细 颗粒在其中移动,这是管涌产生的必要条件。 (2)水力条件 渗透力能够带动细颗粒在孔隙间滚动或移动是发生管涌的水力条件, 可用管涌的水力坡降表示。 流土现象发生在土体表面渗流渗出处,不发生在土体内部。而管涌 现象可以发生在渗流逸出处,也可以发生于土体的内部。
渗流量之和,即 将达西定律代入上式可得沿水平方向的等效渗透系数kx:
(二)竖直向渗流 竖直渗流的特点: (1)根据水流连续原理,流经各土层的流速与流经等效土层的流速
相同,即 (2)流经等效土层H的总水头损失h等于各层上的水头损失之和,即 将达西定律代入上式可得沿竖直方向的等效渗透系数kz:
第9页/共26页
测管水头:位置水头与压力水头之和 h= z+ u/w
测管水头代表的是单位重量液体所具有的总势能
伯努里方程用于土中渗流时有两点需要指出: (1)饱和土体中两点间是否出现渗流,完全是由总水头差决定。只有当 两点间的总水头差时,才会发生水从总水头高的点向总水头低的点 流动。 (2)由于土中渗流阻力大,故流速 v 在一般情况下都很小,因而形成的 流速水头也很小,为简便起见可以忽略。渗流中任一点的总水头就可 用测管水头来代替。 水力坡降
3第三章-土的渗透性及渗流

粗颗粒土一般在完全干燥和洒水饱和状态下最容易密 实。主要因为在潮湿状态下,土中的水为毛细水,毛 细水压增加了粒间阻力。
பைடு நூலகம்
土的击实试验
在试验室内通过击实试验研究土的压实性。击实试验有 轻型和重型两种。
护筒
导筒 击实筒
轻型击实试验适用于粒径小于 击锤 5mm的土,击实筒容积为947cm3, 击锤质量为2.5kg。把制备成一定 含水量的土料分三层装入击实筒, 每层土料用击锤均匀锤击25下, 击锤落高为30.5cm
渗透力
J T wi
负号:渗透力方向与土骨架对水流阻力方向相反
三 土的渗透性——渗透力
根据力的平衡条件
wh1 A w LA cos wh2 A TLA 0
cos ( z1 z2 ) / L h1 H1 z1; h 2 H2 z 2
三 土的渗透性——渗透力 渗流过程
若水自上而下渗流:渗透力方向与土粒所受重力方向相同 ——将增加土粒之间的压力 若水自下而上渗流:渗透力方向与土粒所受重力方向相反 ——将减小土粒之间的压力 此时,若渗透力大小等于土的浮重度时,则土粒之间压力为零,理论上 土粒处于悬浮状态,将随水流一起流动,形成流砂现象
三 土的渗透性
三 土的渗透性——基本概念
1 基本概念
土:具有连续孔隙介质,水在重力作用下可以穿过土中孔隙而流动 渗透或渗流——在水头差作用下,水透过土孔隙流动的现象
渗透性——土体可被水透过的性能
土坝、水闸等挡水后,上游水将通过坝体或地基渗到下游——发生渗透
三 土的渗透性——基本概念
渗透引起两个方面问题:
i>icr:土粒处于流砂状态
i= icr:土粒处于临界状态
土力学第二章土的渗透性和渗透问题

§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
A
B
L
h1
h2
zA
zB
Δh
0
0
基准面
水力坡降线
总水头-单位质量水体所具有的能量
流速水头≈0
A点总水头:
B点总水头:
总水头:
水力坡降:
一.渗流中的水头与水力坡降
§2.1 土的渗透性与渗透规律 Permeability and seepage law of soil
概述
Ch2 土的渗透性和渗流问题 Permeability and seepage problem of soil
概述
Teton坝
渗流量
渗透变形
渗水压力
渗流滑坡
土的渗透性及渗透规律
二维渗流及流网
渗透力与渗透变形
扬压力
土坡稳定分析
挡水建筑物 集水建筑物 引水结构物 基坑等地下施工 边坡渗流
§2.3 渗透力与渗透变形 Seepage force and seepage deformaton
学习目标
学习基本要求
参考学习进度
学习指导
学习目标
掌握土的渗透定律与渗透力计算方法,具备对地基渗透变形进行正确分析的能力。
掌握土的渗透定律
01
掌握二维渗流及流网绘制
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章 土的渗透性和渗流问题第一节 概述土是由固体相的颗粒、孔隙中的液体和气体三相组成的,而土中的孔隙具有连续的性质,当土作为水土建筑物的地基或直接把它用作水土建筑物的材料时,水就会在水头差作用下从水位较高的一侧透过土体的孔隙流向水位较低的一侧。
渗透:在水头差作用下,水透过土体孔隙的现象渗透性:土允许水透过的性能称为土的渗透性。
水在土体中渗透,一方面会造成水量损失,影响工程效益;另一方面将引起土体内部应力状态的变化,从而改变水土建筑物或地基的稳定条件,甚者还会酿成破坏事故。
此外,土的渗透性的强弱,对土体的固结、强度以及工程施工都有非常重要的影响。
本章将主要讨论水在土体中的渗透性及渗透规律,以及渗透力渗透变形等问题。
第二节 土的渗透性一、土的渗透规律——达西定律(一)渗流中的总水头与水力坡降液体流动的连续性原理:(方程式)dw v dw v w w ⎰⎰=2211 2211v w v w =1221w w v v = 表明:通过稳定总流任意过水断面的流量是相等的;或者说是稳定总流的过水断面的 平均流速与过水断面的面积成反比。
前提:流体是连续介质流体是不可压缩的;流体是稳定流,且流体不能通过流面流进或流出该元流。
理想重力的能量方程式(伯努利方程式1738年瑞士数学家应用动能定理推导出来的。
)c gv r p Z =++22饱和土体空隙中的渗透水流,也遵从伯努利方程,并用水头的概念来研究水体流动中 的位能和动能。
水头:实际上就是单位重量水体所具有的能量。
按照伯努利方程,液流中一点的总水头h ,可以用位置水头Z ,压力水头U/r w 和流速水头V 2/2g 之和表示,即gv r u Z h w 22++= 4-1 此方程式中各项的物理意义均代表单位重量液体所具有的各种机械能,而其量纲都是 长度。
教材P37图22表示渗流在水中流经A ,B 两点时,各种水头的相互关系。
按照公式(4-1),A,B 两点的总水头可分别表示为:gv r u Z h A w A A A 22++= gv r u Z h B w B B B 22++= h h h B A ∆+=式中:Z A ,Z B :为A ,B ,两点相对于任意选定的基准面的高度,代表单位重量液体 所具有的位能(位置高度)故称Z 为位置水头。
U A ,U B :为A ,B 两点的水压力(空隙水压力)。
代表单位重量液体所具有的压力势 能。
而U A /r w ,U B /r w 则代表A ,B 两点空隙水压力的水柱高度。
故称U/r w 为压力水头。
V A ,V B :为A ,B 两点的渗流速度。
g 为重力加速度。
V 2/2g 即代表单位重量液体所具有的动能,故称V 2/2g 为流速水头。
H A ,h B :为A ,B 两点的单位重量液体所具有的机械能,故称之为总水头。
∆h : 为A ,B 两点之间的总水头差,代表单位重量液体从A 点向B 点流动时,为克服 阻力而损失的能量。
此外,wr u z +称为测管水头,代表单位重量液体所具有的总势能。
当土中渗流阻力大时,V 一般都很小,形成的流速水头V 2/2g 更小,可不计,这时,总 水头h,可用测管水头来代替,即wr u Z h += A,B 两点间的水头损失,可用无量纲的形式来表示,即lh i ∆= i :水力坡降L :为A ,B 两点间的渗流途径水头损失h1的渗流长度。
(二) 渗透试验与达西定律土体中空隙的形状和大小是极不规则的,因而水在土体空隙中的渗透是一种十分复杂的现象,由于土体中的空隙一般非常微小,水在土体中流动时的粘滞阻力很大,流速缓慢,因此,其流动状态大多属于层流。
1956年,达西利用图2-5(教材P40)所示试验装置,对砂土的渗流性进行了研究,发现水在土中的渗流速度与试样两端面间的水头差成正比,而与渗流长度成反比,于是他把渗流速度表示为:Ki lh K v =∆= 或KiA vA Q == 这就是著名的达西定律,式中V :表示断面平均渗透速度,单位:mm/sK :渗透系数,(mm/s )其物理意义是当水力坡降i=1时的渗透速度。
达西定律说明:(1)在层流状态的渗流中,渗流速度V 与水力坡降的一次方成正比,并与土的性质有关。
或:砂土的渗透速度与水力坡降呈线性关系。
(2)但对于密实的粘土,由于吸着水具有较大的粘滞阻力,因此只有当水力坡降达到某一数值,克服了吸着水的粘滞阻力以后,才能发生渗透。
我们将这一开始渗透时的水力坡降称为粘性土的起始水力坡降i.试验资料表明,密实的粘土不但存在起始水力坡降,而且当水力坡降超过起始坡降后,渗透速度与水力坡降的规律还偏离达西定律而呈线性关系。
)(0i i K v -=式中:0i 指密实粘土的起始水力坡降。
此外,试验也表明,在粗颗粒土中(如砾石,卵石),只见在小的水力坡降下,渗透速度与水力坡降才能呈线性关系,而在较大的水力坡降下,水在土中的流动即进入紊流状态,渗透速度与水力坡降呈非线性关系,此时达西定律不能适用。
二.渗透系数的测定和影响因素(一) 渗透系数的测定方法主要分现场试验和室内试验两大类,一般说,现场试验比室内试验所得到的成果要准确可靠。
1.实验室测定法:常水头试验法,透水性大的砂性土变水头试验法,透水性小的无粘性土2.现场测定法:实测流速法:色素法、电解质法、食盐法注水法抽水法:降低水位法:平衡法,不平衡法水位恢复法(二) 影响渗透系数的因素渗透系数是一个代表土的渗透性强弱的定量指标,也是渗透计算时必须用到的一个基本参数。
影响渗透系数的主要有:1.土的粒度成分和矿物成分的影响:土的颗粒大小,形状及级配,影响土中空隙大小及形状,因而影响渗透性。
土粒越粗,越浑圆,越均匀时,渗透性就大。
砂土中含有较多粉土,或粘土颗粒时,其渗透系数就大大降低。
土中含有亲水性较大的粘土矿物或有机质时,也大大降低土的渗透性。
2.孔隙比对渗透系数的影响由e=Vv/Vs 可知,孔隙比e 越大,Vv 越大,渗透系数越大,而孔隙比的影响,主要决定于土体中的孔隙体积,而孔隙体积又决定于孔隙的直径大小,决定于土粒的颗粒大小和级配。
3.土的结构构造的影响天然土层通常不是各向同性的,在渗透性方面往往也是如此。
如黄土特别是具湿陷性黄土,具有竖直方向的渗透系数要比水平方向大得多。
层状粘土常夹有薄的粉砂层,它在水平方向的渗透系数要比竖直方向大得多。
4.结合水膜厚度的影响粘性土中若土粒的结合水膜较厚时,会阻塞土的孔隙,降低土的渗透性。
5.土中气体的影响当土孔隙中存在密闭气泡时,会阻塞水的渗流,从而降低了的渗透性。
这种密闭气泡有时是由溶解于水中的气体分离而形成的,故水的含水量也影响土的渗透系数。
影响因素:水温,试验表明,K 与渗透液体的容重r w 及粘滞系数有关;水温不同,r w 相差不大,但粘滞系数变化较大,水温升高,粘滞系数降低,K 增大.此外,渗透水的性质对K 值的影响。
三.层状地基的等效渗透系数天然沉积土往往是由渗透性不同的土层所组成。
对于与土层层面平行和垂直的简单渗流情况,当各土层的渗透系数和厚度为已知时,我们可求出整个土层与层面平行和垂直的平均渗透系数,作为渗流计算的依据。
(一) 水平渗流情况如图(见教材P47):已知地基内各层土的渗透系数分别为K 1,K 2,K 3,……K n ,厚度分别为H 1,H 2,……H n ,总厚度为H 。
任取两水流断面1-1,2-2;两断面距离为L ,水头损失为h ∆,这种平行于各层面的水平渗流的特点是:1.各土层的水力坡降I(=h 1/L)与等效土层的平均水力坡降之相同。
2.若通过各土层的渗流量为q 1x ,q 2x , ……q nx ,则通过整个土层的总渗流量q x 应为各土层渗流量之总和。
即:∑==+++=ni ix nx x x q q q q qx 121将达西定律代入上式,可得∑∑===⨯=ni n i KiHi i iHi Ki KxiH 11 (kx 等效渗透系数)消去之后,即可得出沿水平方向的等效渗透系数Kx∑==ni KiHi H Kx 11(二)竖直渗流情况对于与层面垂直的渗流的情况如图2-13b(教材P47)所示,我们可用类似的方法来求解。
∑==n i KiHi H Ky 1)( 注意:在实际工程中,选用等效渗透系数时,一定要注意水流的方向,选择正确的等效渗透系数。
第三节 二维渗流与流网上述渗流属简单边界条件下的单向渗流,只要渗透介质的渗透系数和厚度以及两端的水头或水头差为已知,介质内的流动特征均可根据达西定律确定。
然而,在工程上遇到的渗流问题,边界条件要复杂得多,水流形态往往是二向或三向的,如图2-14(见教材P49),这时,介质内的流动特性常逐点不同,并且只能以微分方程的形式表示,然后根据边界条件进行求解。
一.稳定渗流场中的拉普拉斯方程设从稳定渗流场中任取一微分单元土体,其面积为dxdy ,如图若单位时间内在x 方向流入单元体的水量为q x ,流出的水量为q x + dx xq x ∂∂,在y 方向流入的水量为q y ,流出的水量为dy y q q yy ∂∂+。
假定在渗流作用下单元的体积保持不变,水又是不可压缩的,则单位时间内流入单元体的总水量必等于流出的总水量,即 qx+qy=(qx+ dx x q x ∂∂ )+( dy yq q y y ∂∂+ ) 即dx x q x ∂∂+dy yq y ∂∂=0 根据达西定律,qx=K x i x dy , qy=K x i y dx ;其中x 和y 方向的水力坡降分别为i x =x H ∂∂ i y =yH ∂∂ ,将上列关系式代入上式中并经简化后可得: Kx 22y H ∂∂ + Ky 22yH ∂∂ =0 这就是各向异性土在稳定渗流时的连续方程。
式中:K x ,K y 分别为x 和y 方向的渗透系数H 总水头或测压管水头。
如果土是各向同性的,即k x =k y ,则上式可改写成22x H ∂∂+22yH ∂∂=0 这就是著名的拉普拉斯方程,它是描述稳定渗流的基本方程式。
二.流网的特征及应用众所周知,满足拉普拉斯方程的将是两组彼此正交的曲线。
就渗流而言,一组曲线称为等式线,在任一条等势线上各点的势能是相等的,或者说,在同一条等式线上的侧压水位都是同高的,另一组曲线称为流线,它们代表渗流的方向。
但必须指出,只有满足边界条件的那一种流线和等势线的组合形式才是方程式22x H ∂∂+22yH ∂∂=0的正确解答。
流网即为一族流线和等势线交织而成的网格,根据水力学,具有下列特征:(1)流线和等势线彼此正交;(2)每个网格的长宽比值为常数,这时的网格就成为正方形或曲线正方形;(3)相邻等势线的水头损失相等;(4)各流糟的渗流量相等。
为了求得满足边界条件的解答,常用的方法主要有(1)解析法,(2)数值法(3)实验法(4)图解法;在工程上广泛应用的多为图解法。
