天津大学—应用统计学离线作业及答案
天大2017年12月考试《应用统计学》离线作业考核试题

应用统计学要求:一、独立完成,下面五组题目中,请任选其中一组题目作答,满分100分;二、答题步骤:1.使用A4纸打印学院指定答题纸(答题纸请详见附件);2.在答题纸上使用黑色水笔..作答;答题纸上全部信息要求手....按题目要求手写写,包括中心、学号、姓名、科目、答题组数等基本信息和答题内容,请写明题型、题号;三、提交方式:请将作答完成后的整页答题纸以图片形式依次粘贴在一个.......Word....文档中...上传(只粘贴部分内容的图片不给分),图片请保持正向、清晰;1.上传文件命名为“中心-学号-姓名-科目.doc”2.文件容量大小:不得超过20MB。
提示:未按要求作答题目....0.分记..!...及雷同作业........的作业.....,成绩以题目如下:第一组:一、计算题(每小题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
解:设X b b Y 10+=nX Xn Y X Y X b i i i ii i i i i i2616126161611)())((∑∑∑∑∑=====--==62.192.1918.626189002.1960910⨯-⨯-=581.08 X b Y b 10-==18900/6-581.08*19.2/6=1290.54 于是X Y 08.58154.1290+=2、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
答:96.12=αμ二、简答题(每小题25分,共50分) 1. 区间估计与点估计的结果有何不同?答:点估计是使用估计量的单一值作为总体参数的估计值;区间估计是指定估计量的一个取值范围都为总体参数的估计。
天大2017年12月考试《应用统计学》离线作业考核试题

应用统计学要求:一、独立完成,下面五组题目中,请任选其中一组题目作答,满分100分;二、答题步骤:1.使用A4纸打印学院指定答题纸(答题纸请详见附件);2.在答题纸上使用黑色水笔..作答;答题纸上全部信息要求手....按题目要求手写写,包括中心、学号、姓名、科目、答题组数等基本信息和答题内容,请写明题型、题号;三、提交方式:请将作答完成后的整页答题纸以图片形式依次粘贴在一个.......Word....文档中...上传(只粘贴部分内容的图片不给分),图片请保持正向、清晰;1.上传文件命名为“中心-学号-姓名-科目.doc”2.文件容量大小:不得超过20MB。
提示:未按要求作答题目....0.分记..!...及雷同作业........的作业.....,成绩以题目如下:第一组:一、计算题(每小题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
2、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
二、简答题(每小题25分,共50分) 1. 区间估计与点估计的结果有何不同? 2. 解释抽样推断的含义。
第二组:一、 计算题(每小题25分,共50分) 1、设总体X 的概率密度函数为其中为未知参数,是来自X 的样本。
(1)试求的极大似然估计量; (2)试验证 是的无偏估计量。
2、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要? 二、 简答题(每小题25分,共50分) 1、统计调查的方法有那几种?2、时期数列与时点数列有哪些不同的特点?96.12=αμ2(ln )2,0(,)0,0x x f x x μμ--⎧>=≤⎩μn X X X ,...,,2113)(+=μμg )(g ˆμ)(g ˆμ)(μg第三组:一、计算题(每小题25分,共50分)1、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。
天津大学《应用统计学》在线作业一-02

《应用统计学》在线作业一
组间误差是衡量某一水平下样本数据之间的误差,它()。
A:只包括随机误差
B:只包括系统误差
C:既包括随机误差也包括系统误差
D:有时包括随机误差,有时包括系统误差
参考选项:A
当所有观察值y都落在回归直线y^=a+bx上,则x与y之间的相关系数()。
A:r=1
B:-1r0
C:r=1或r=-1
D:0r1
参考选项:C
统计的四个要素是()。
A:总体、样本、标志和指标
B:总体、样本、推断和推断的可靠性
C:总体、总体单位、标志和指标
D:标志、指标、变量和变异
参考选项:B
直方图一般可用来表示()。
A:累积次数的分布
B:次数分布的特征
C:变量之间的函数关系
D:数据之间的相关性
参考选项:B
在数据集中趋势的测度中,不受极端值影响的测度是()。
A:众数
B:几何平均数
C:调和平均数
D:算术平均数
参考选项:A
就人工研磨工序来说,影响该过程质量的主导因素是()。
A:环境
B:工具
C:测量
D:操作人员
参考选项:D
1。
天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案卷4

天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案(图片大小可自由调整)第1卷一.综合考核(共10题)1.若方差分析中,所提出的原假设是H0:μ1=μ2=...=μk,备择假设是()。
A.H1:μ1≠μ2≠...≠μkB.H1:μ1>μ2>...>μkC.H1:μ1D.H1:μ1,μ2,...,μk不全相等2.方差分析所研究的是()。
A.分类型自变量对分类型因变量的影响B.分类型自变量对数值型自变量的影响C.分类型因变量对数值型自变量的影响D.分类型自变量对数值型因变量的影响3.设总体均值为100,总体方差为25,在大样本情况下,无论总体的分布形式如何,样本平均数的分布都服从或近似服从趋近于()。
A.N(100,25)B.N(100,50/n)C.N(100/n,25)D.N(100,25/n)4.价格上涨后,同样多的人民币报告期所购买商品的数量比基期少5%,因此价格上涨了()。
A.95%B.5.26%C.5%D.105.26%5.当所有观察值y都落在回归直线y=a+bx上,则x与y之间的相关系数() 。
A.r=1B.-1C.r=1或r=-1D.0<r<1 6.设X是参数为n=4和p=0.5的二项随机变量,则P(XA.0.6826B.0.3174C.0.3125D.0.02287.无偏估计是指()。
A.样本量扩大到河总体单元相等时与总体参数一致B.样本估计值围绕待估参数使其误差最小C.本统计量的值恰好等于待估的总体参数D.所有可能样本估计值的数学期望等于待估总体参数8.按数字尺度测量的观察值称为()。
A.顺序尺度B.数值型尺度C.数值型变量D.分类尺度9.贝叶斯决策需要调查取得信息来修正先验概率,这个调查是在()中进行的。
A.预后验分析B.最后决策C.后验分析D.先验分析10.一组数据排序后处于25%和75%位置上的值称为()。
A.众数B.中位数C.四分位数D.均值第1卷参考答案一.综合考核1.参考答案:D2.参考答案:D3.参考答案:D4.参考答案:B5.参考答案:C6.参考答案:A7.参考答案:D8.参考答案:B9.参考答案:C10.参考答案:C。
天津大学[应用统计学]附答案
![天津大学[应用统计学]附答案](https://img.taocdn.com/s3/m/92905e0554270722192e453610661ed9ad5155f6.png)
天津⼤学[应⽤统计学]附答案应⽤统计学请在以下五组题⽬中任选⼀组作答,满分100分。
第⼀组:⼀、计算题(每⼩题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学⼠学位的学⽣,毕业后的⽉薪(⽤y 表⽰)和他在校学习时的总评分(⽤x 表⽰)的回归⽅程。
2、设总体X 的概率密度函数为2(ln )2,0(,)0,0x x f x x µµ-->=≤其中µ为未知参数,nX X X ,...,,21是来⾃X 的样本。
(1)试求13)(+=µµg 的极⼤似然估计量)(g ?µ;(2)试验证)(g ?µ 是)(µg 的⽆偏估计量。
⼆、简答题(每⼩题25分,共50分)1. 在统计假设检验中,如果轻易拒绝了原假设会造成严重后果时,应取显著性⽔平较⼤还是较⼩,为什么?2. 加权算术平均数受哪⼏个因素的影响?若报告期与基期相⽐各组平均数没变,则总平均数的变动情况可能会怎样?请说明原因。
第⼆组:⼀、计算题(每⼩题25分,共50分)1、某⼀汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上⼀道装配操作线的影响,⼜影响到下⼀道装配操作线的⽣产,所以保持2.2分钟的标准是很重要的。
⼀个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性⽔平下检验操作线是否达到了2.2分钟的标准。
96.12=αµ2、某商店为解决居民对某种商品的需要,调查了100户住户,得出每⽉每户平均需要量为10千克,样本⽅差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满⾜需要?⼆、简答题(每⼩题25分,共50分)1.解释相关关系的含义,说明相关关系的特点。
2.为什么对总体均值进⾏估计时,样本容量越⼤,估计越精确?第三组:⼀、计算题(每⼩题25分,共50分)1、根据下表中Y与X两个变量的样本数据,建⽴Y与X的⼀元线性回归⽅程。
应用统计学 20年天大离线答案 -第二组

应用统计学要求:一、独立完成,下面已将五组题目列出,请按照学院平台指定..的做题组数作答,每人只答一组题目....,满分100分;........,多答无效平台查看做题组数操作:学生登录学院平台→系统登录→学生登录→课程考试→离线考核→离线考核课程查看→做题组数,显示的数字为此次离线考核所应做哪一组题的标识;例如:“做题组数”标为1,代表学生应作答“第一组”试题;二、答题步骤:1.使用A4纸打印学院指定答题纸(答题纸请详见附件);2.在答题纸上使用黑色水笔..作答;答题纸上全部信息要求手....按题目要求手写写,包括学号、姓名等基本信息和答题内容,请写明题型、题号;三、提交方式:请将作答完成后的整页答题纸以图片形式依次粘贴在一个...........Word文档中...上传(只粘贴部分内容的图片不给分),图片请保持正向、清晰;题目如下:一、计算题(每小题25分,共50分)1、某地区社会商品零售额资料如下:要求:1)用最小平方法配合直线趋势方程:2)预测2005年社会商品零售额。
(a,b及零售额均保留三位小数,2、某商业企业商品销售额1月、2月、3月分别为216,156,180.4万元,月初职工人数1月、2月、3月、4月分别为80,80,76,88人,试计算该企业1月、2月、3月各月平均每人商品销售额和第一季度平均每月人均销售额。
(写出计算过程,结果精确到0.0001万元\人)二、简答题(每小题25分,共50分)1、表示数据分散程度的特征数有那几种?2、回归分析与相关分析的区别是什么?第二组答案:一、计算题(每小题25分,共50分)1、某地区社会商品零售额资料如下:要求:1)用最小平方法配合直线趋势方程:2)预测2005年社会商品零售额。
(a,b及零售额均保留三位小数,答:非简捷法:(1)Σy=138 ,Σt=21 ,Σt2=91 ,Σty=495b=(nΣty-ΣtΣy)/[nΣt2-(Σt)2]=(6×495-21×138)/[6×91-(21)2]=72/105=0.686a=Σy/n-bΣt/n=138/6-0.686×21/6=23-0.686×3.5=20.599yˆ=a+bt=20.599+0.686t(2)2005年t=8y。
天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案1

天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案(图片大小可自由调整)第1卷一.综合考核(共15题)1.第一个X2分布的方差为20,第二个X2分布的方差为30,则它们的和仍然服从X2分布,自由度为()。
A.50B.30C.25D.202.无偏估计是指()。
A.本统计量的值恰好等于待估的总体参数B.所有可能样本估计值的数学期望等于待估总体参数C.样本估计值围绕待估参数使其误差最小D.样本量扩大到河总体单元相等时与总体参数一致3.统计指数划分为个体指数和总指数的依据是()。
A.采用的基期不同B.编制指数的方法不同C.指标性质不同D.反映的对象范围不同4.某工业企业生产的产品单位成本从2005年到2007年的平均发展速度为98%,说明该产品单位成本()。
A.平均每年降低2%B.平均每年降低1%C.2007年比2005年降低98%D.2007年是2005年的98%5.以下关于指数作用的说法中不正确的是()。
A.综合反映现象的变动方向和程度B.反映不同现象之间的联系C.综合反映现象发展的相对规模和水平D.可通过指数体系进行因素分析6.若对一元线性回归方程作F检验,则()。
A.“当F<Fα(1,n-2)时,表示总体回归系数显著的大”B.“当F<Fα(1,n-2)时,表示总体回归系数显著的0”C.“当F>=Fα(1,n-2)时,表示总体回归系数显著的小”D.“当F>=Fα(1,n-2)时,表示总体回归系数显著为0”7.在下面的假定中,哪一个不属于方差分析的假定?()A.每个总体都服从正态分布B.各总体的方差相等C.观测值是独立的D.各总体的方差等于08.用决策树进行分析时,采用的方式是()。
A.顺推B.反推C.逻辑推理D.视情况而定9.若方差分析中,所提出的原假设是H0:μ1=μ2=...=μk,备择假设是()。
A.H1:μ1,μ2,...,μk不全相等B.H1:μ1≠μ2≠...≠μkC.H1:μ1>μ2>...>μkD.H1:μ1<μ2<...<μk10.下列指标属于时点指标的是()。
天津大学—应用统计学离线作业及答案资料
应用统计学要求:1.独立完成,作答时要写明所选题型、题号2.题目要用A4大小纸张,手写作答后将每页纸张拍照或扫描为图片形式3.提交方式:请以图片形式打包压缩上传,请确保上传的图片正向显示4.上传文件命名为“中心-学号-姓名-科目.rar”5.文件容量大小:不得超过10MB。
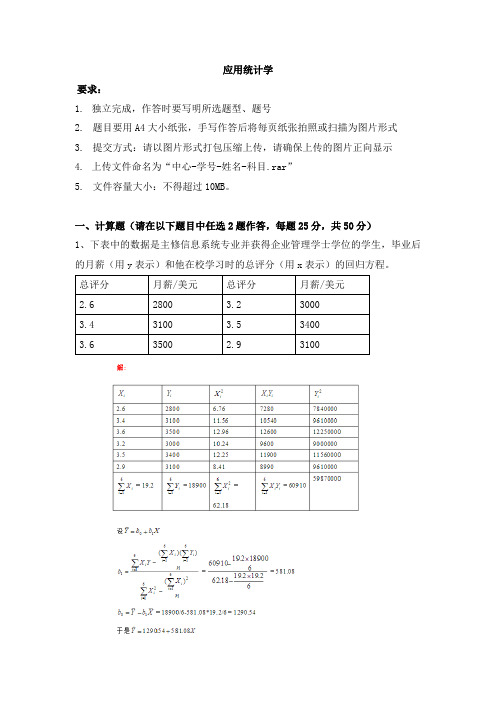
一、计算题(请在以下题目中任选2题作答,每题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
总评分月薪/美元总评分月薪/美元2.6 28003.2 30003.4 3100 3.5 34003.6 3500 2.9 31002、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
96.12=αμ3、设总体X 的概率密度函数为2(ln )2,0(,)2x0,0x x f x x μμπ--⎧>=≤⎩其中μ为未知参数,nX X X ,...,,21是来自X 的样本。
(1)试求13)(+=μμg 的极大似然估计量)(g ˆμ; (2)试验证)(gˆμ 是)(μg 的无偏估计量。
4、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?5、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。
Y ijf X 5 10 15 20yf120 0 0 8 10 18 140 3 4 3 0 10f3 4 11 10 28x6、假定某化工原料在处理前和处理后取样得到的含脂率如下表:处理前0.140 0.138 0.143 0.142 0.144 0.137处理后0.135 0.140 0.142 0.136 0.138 0.140假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。
天津大学《应用统计学》在线作业一

《应用统计学》在线作业一-00001第1题. 按变量的性质和数据的多少划分,变量数列可分为()。
选项A:等距数列与异距数列选项B:开口组数列与闭口组数列选项C:单项数列与组距数列选项D:等差数列与等比数列参考答案:C第2题. 设折中系数为0.7,这表明()。
选项A:未来各种状态具有相同的概率选项B:最不理想的状态不可能出现选项C:最理想的状态出现的可能性较大选项D:最不理想的状态出现的可能性较大参考答案:C第3题. 当时间序列的长期趋势近似于水平趋势时,测定季节变动时()。
选项A:要考虑长期趋势的影响选项B:可不考虑长期趋势的影响选项C:不能直接用原始资料平均法选项D:剔除长期趋势的影响参考答案:B第4题. 绘制产品质量控制图的关键是()。
选项A:数据的选取和分组选项B:计算控制上下限和中心线选项C:计算各个样本数据选项D:确定使用哪种控制图参考答案:B第5题. 如果所有标志值的次数都增加一倍,而标志值不变,则算术平均数()。
选项A:增加选项B:减少选项C:不变选项D:无法确定参考答案:C第6题. 样本均值与总体均值之间的差被称为()。
选项A:抽样误差选项B:点估计选项C:均值的标准误差选项D:区间估计参考答案:A第7题. 实践中常用、理论上最重要的统计指数种类是()。
选项A:动态对比指数选项B:空间对比指数选项C:计划完成情况指数选项D:静态对比指数参考答案:A第8题. 从编制原理的角度看,总指数的两种基本形式为()。
选项A:综合指数和平均指数选项B:简单指数和平均指数选项C:算术平均数和调节平均数选项D:可变构成指数和不变构成指数参考答案:A第9题. 某工业企业产品年生产量为20万件,期末库存5.3万件,它们()。
选项A:是时期指标选项B:是时点指标选项C:前者是时期指标,后者是时点指标选项D:前者是时点指标,后者是时期指标参考答案:C第10题. 环比发展速度与定基发展速度之间的关系是()。
天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案1

天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案(图片大小可自由调整)第1卷一.综合考核(共15题)1.与概率抽样相比,非概率抽样的缺点是()。
A.样本统计量的分布是确定的B.无法使用样本的结果对总体相应的参数进行推断C.调查的成本比较高D.不适合于探索性的研究2.如果所有标志值的次数都增加一倍,而标志值不变,则算术平均数()。
A.无法确定B.增加C.减少D.不变3.在其他条件不变的情况下,要使置信区间的宽度缩小一半,样本量应增加()。
A.四倍B.三倍C.一半D.一倍4.在比较两组数据的离散程度时,不能直接比较两者的方差,因为这两组数据的()。
A.标准差不同B.方差不同C.数据个数不同D.计量单位不同5.从一个正态总体中随机抽取一个容量为n的样本,其均值和标准差分别为50和8。
当n=25时,构造总体均值μ的95%置信区间为()。
A.50±4.97B.50±3.16C.50±1.96D.50±1.656.从均值为200,标准差为50的总体中抽取容量为100的简单随机样本,样本均值的期望值是()A.150B.200C.100D.2507.均值为0,方差为1的标准正态分布的平方服从()。
A.F分布B.正态分布C.X2分布D.无法确定8.均值为0,方差为1的标准正态分布的平方服从()。
A.正态分布B.无法确定C.X2分布D.F分布9.“小中取大”决策准则是()。
A.在各方案的最小收益值中选择最大,对应方案为最优B.在各方案的最小损失值中选择最大,对应方案为最优C.在各方案的最大收益值中选择最小,对应方案为最优D.在各方案的最大损失值中选择最大,对应方案为最优10.当样本统计量的观测值未落入原假设的拒绝域时表示没有充足的理由否定原假设。
()A.正确B.错误11.在某高校中,管理学专业的学生占10%,如果从该高校中随机抽取200名学生进行调查,样本中管理学专业学生所占比例的期望值为()。
天津大学—应用统计学离线作业及答案课件

应用统计学要求:1.独立完成,作答时要写明所选题型、题号2.题目要用A4大小纸张,手写作答后将每页纸张拍照或扫描为图片形式3.提交方式:请以图片形式打包压缩上传,请确保上传的图片正向显示4.上传文件命名为“中心-学号-姓名-科目.rar”5.文件容量大小:不得超过10MB。
一、计算题(请在以下题目中任选2题作答,每题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
总评分月薪/美元总评分月薪/美元2.6 28003.2 30003.4 3100 3.5 34003.6 3500 2.9 31002、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
96.12=αμ3、设总体X 的概率密度函数为2(ln )2,0(,)2x0,0x x f x x μμπ--⎧>=≤⎩其中μ为未知参数,nX X X ,...,,21是来自X 的样本。
(1)试求13)(+=μμg 的极大似然估计量)(g ˆμ; (2)试验证)(gˆμ 是)(μg 的无偏估计量。
4、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?5、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。
Y ijf X 5 10 15 20yf120 0 0 8 10 18 140 3 4 3 0 10f3 4 11 10 28x6、假定某化工原料在处理前和处理后取样得到的含脂率如下表:处理前0.140 0.138 0.143 0.142 0.144 0.137处理后0.135 0.140 0.142 0.136 0.138 0.140假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。
天津大学《应用统计学》在线作业二-01

《应用统计学》在线作业二
"从服从正态分布的无限总体中分别抽取容量为4,16,,3的样本,当样本容量增大时样本均值的标准差()"
A:保持不变
B:增加
C:减小
D:无法确定
参考选项:C
双因素方差涉及()
A:两个分类型自变量
B:两个数值型自变量
C:两个分类型因变量
D:两个数值型因变量
参考选项:A
假设总体比例为0.55,从此总体中抽取容量为100的样本,则样本比列的标准差为()
A:0.01
B:0.05
C:0.06
D:0.55
参考选项:B
设Z服从标准正态分布,则P(Z>1.33)=
A:0.3849
B:0.4319
C:0.0918
D:0.4147
参考选项:C
下面的哪种调查方式样本不是随机选取的()
A:分层抽样
B:系统抽样
C:整群抽样
D:判断抽样
参考选项:D
方差分析所研究的是()。
A:分类型自变量对分类型因变量的影响
B:分类型自变量对数值型自变量的影响
C:分类型因变量对数值型自变量的影响
1。
天津大学[应用统计学]附答案
![天津大学[应用统计学]附答案](https://img.taocdn.com/s3/m/f7528a7d011ca300a6c39073.png)
应用统计学请在以下五组题目中任选一组作答,满分100分。
第一组:一、 计算题(每小题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y 表示)和他在校学习时的总评分(用x 表示)的回归方程。
2、设总体X 的概率密度函数为2(ln )2,0(,)0,0x x f x x μμ--⎧>=≤⎩其中μ为未知参数,nX X X ,...,,21是来自X 的样本。
(1)试求13)(+=μμg 的极大似然估计量)(g ˆμ; (2)试验证)(g ˆμ 是)(μg 的无偏估计量。
二、简答题(每小题25分,共50分)1. 在统计假设检验中,如果轻易拒绝了原假设会造成严重后果时,应取显著性水平较大还是较小,为什么?2. 加权算术平均数受哪几个因素的影响?若报告期与基期相比各组平均数没变,则总平均数的变动情况可能会怎样?请说明原因。
第二组:一、 计算题(每小题25分,共50分)1、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
96.12=αμ2、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?二、简答题(每小题25分,共50分)1.解释相关关系的含义,说明相关关系的特点。
2.为什么对总体均值进行估计时,样本容量越大,估计越精确?第三组:一、计算题(每小题25分,共50分)1、根据下表中Y与X两个变量的样本数据,建立Y与X的一元线性回归方程。
Y ijf X 5 10 15 20yf120 0 0 8 10 18140 3 4 3 0 10fx3 4 11 10 282、某茶叶制造商声称其生产的一种包装茶叶平均每包重量不低于150克,已知茶叶包装重量服从正态分布,现从一批包装茶叶中随机抽取100包,检验结果如下:每包重量(克) 包数(包)f x xfx-(x-)2f148—149 10 148.5 1485 -1.8 32.4 149—150 20 149.5 2990 -0.8 12.8150—151 50 150.5 7525 0.2 2.0151—152 20 151.5 3030 1.2 28.8合计100 -- 15030 -- 76.0要求:(1)计算该样本每包重量的均值和标准差;(2)以99%的概率估计该批茶叶平均每包重量的置信区间(t0.005(99)≈2.626);(3)在ɑ=0.01的显著性水平上检验该制造商的说法是否可信(t0.01(99)≈2.364)(4)以95%的概率对这批包装茶叶达到包重150克的比例作出区间估计(Z0.025=1.96);(写出公式、计算过程,标准差及置信上、下保留3位小数)二、简答题(每小题25分,共50分)1.区间估计与点估计的结果有何不同?2.统计调查的方法有那几种?第四组:一、计算题(每小题25分,共50分)1、假定某化工原料在处理前和处理后取样得到的含脂率如下表:假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。
天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案4

天津大学智慧树知到“物流工程”《应用统计学》网课测试题答案(图片大小可自由调整)第1卷一.综合考核(共15题)1.在假设检验中,如果所计算出的P值越小,说明检验的结果()。
A.越显著B.越不显著C.越真实D.越不真实2.在现实经济生活中,拉氏价格指数一般()帕氏价格指数。
A.大于B.小于C.等于D.不能确定3.三个或三个以上变量之间的相关关系称为()。
A.直线相关B.曲线相关C.复相关D.单相关4.与假设检验相比,方差分析方法可以使犯第1类错误的概率提高。
()A.正确B.错误5.无偏估计是指()。
A.样本量扩大到河总体单元相等时与总体参数一致B.样本估计值围绕待估参数使其误差最小C.本统计量的值恰好等于待估的总体参数D.所有可能样本估计值的数学期望等于待估总体参数6.一组数据排序后处于25%和75%位置上的值称为()。
A.众数B.中位数C.四分位数D.均值7.如果总体单位数较小,则与重复抽样相比,不重复抽样中样本均值的标准差()。
A.较小B.较大C.相等D.无法比较8.一家研究机构从IT从业者中随机抽取500人作为样本进行调查,其中60%回答他们的月收入在5000元以上,50%回答他们的消费支付方式是使用信用卡。
这里的“月收入”是()。
A.顺序变量B.离散型变量C.数值型变量D.分类变量9.当一个现象的数量由小变大,而另一个现象的数量由大变小时,这种相关关系称为()。
A.线性相关B.非线性相关C.正相关D.负相关10.若方差分析中,所提出的原假设是H0:μ1=μ2=...=μk,备择假设是()。
A.H1:μ1≠μ2≠...≠μkB.H1:μ1>μ2>...>μkC.H1:μ1D.H1:μ1,μ2,...,μk不全相等11.若对一元线性回归方程作F检验,则()。
A.“当F<Fα(1,n-2)时,表示总体回归系数显著的大”B.“当F<Fα(1,n-2)时,表示总体回归系数显著的0”C.“当F>=Fα(1,n-2)时,表示总体回归系数显著的小”D.“当F>=Fα(1,n-2)时,表示总体回归系数显著为0”12.指出下面关于N重贝努里试验的陈述中哪一个是错误的()。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
应用统计学要求:1.独立完成,作答时要写明所选题型、题号2.题目要用A4大小纸张,手写作答后将每页纸张拍照或扫描为图片形式3.提交方式:请以图片形式打包压缩上传,请确保上传的图片正向显示4.上传文件命名为“中心-学号-姓名-科目.rar”5.文件容量大小:不得超过10MB。
一、计算题(请在以下题目中任选2题作答,每题25分,共50分)1、下表中的数据是主修信息系统专业并获得企业管理学士学位的学生,毕业后的月薪(用y表示)和他在校学习时的总评分(用x表示)的回归方程。
2、某一汽车装配操作线完成时间的计划均值为2.2分钟。
由于完成时间既受上一道装配操作线的影响,又影响到下一道装配操作线的生产,所以保持2.2分钟的标准是很重要的。
一个随机样本由45项组成,其完成时间的样本均值为2.39分钟,样本标准差为0.20分钟。
在0.05的显著性水平下检验操作线是否达到了2.2分钟的标准。
96.12=αμ3、设总体X的概率密度函数为2(ln )21,0(,)2x0,0x e x f x x μμπ--⎧⎪>=⎨⎪≤⎩其中μ为未知参数,nX X X ,...,,21是来自X 的样本。
(1)试求13)(+=μμg 的极大似然估计量)(g ˆμ; (2)试验证)(gˆμ 是)(μg 的无偏估计量。
4、某商店为解决居民对某种商品的需要,调查了100户住户,得出每月每户平均需要量为10千克,样本方差为9。
若这个商店供应10000户,求最少需要准备多少这种商品,才能以95%的概率满足需要?5、根据下表中Y 与X 两个变量的样本数据,建立Y 与X 的一元线性回归方程。
Yijf X 5 10 15 20yf120 0 0 8 10 18 140 3 4 3 0 10 f x341110286、假定某化工原料在处理前和处理后取样得到的含脂率如下表: 处理前0.140.1380.1430.1420.1440.137处理后0.135 0.140.1420.1360.1380.140假定处理前后含脂率都服从正态分布,问处理后与处理前含脂率均值有无显著差异。
7、某茶叶制造商声称其生产的一种包装茶叶平均每包重量不低于150克,已知茶叶包装重量服从正态分布,现从一批包装茶叶中随机抽取100包,检验结果如下:每包重量(克)包数(包)fx xfx-(x-)2f148—14910 148.5 1485 -1.8 32.4149—15020 149.5 2990 -0.8 12.8150—15150 150.5 7525 0.2 2.0151—20 151.5 3030 1.2 28.8152合计100 -- 15030 -- 76.0 要求:(1)计算该样本每包重量的均值和标准差;(99)≈(2)以99%的概率估计该批茶叶平均每包重量的置信区间(t0.0052.626);(99)(3)在ɑ=0.01的显著性水平上检验该制造商的说法是否可信(t0.01≈2.364)(4)以95%的概率对这批包装茶叶达到包重150克的比例作出区间估=1.96);计(Z0.025(写出公式、计算过程,标准差及置信上、下保留3位小数)8、一种新型减肥方法自称其参加者在第一个星期平均能减去至少8磅体重.由40名使用了该种方法的个人组成一个随机样本,其减去的体重的样本均值为7磅,样本标准差为 3.2磅.你对该减肥方法的结论是什么?(α=0.05,μα/2=1.96,μα=1.647)9、某地区社会商品零售额资料如下:年份零售额(亿元)yt t2 ty t t2 ty19 98 21.5 1 1 21.5-5 25 -107.5199922.0 2 4 44 -3 9 -6620 00 22.5 3 9 67.5-1 1 -22.5200123.0 4 16 92 1 1 2320 02 24.0 5 25 123 9 7220 03 25.0 6 36 155 25 125合计138.0 2191 4950 70 24要求:1)用最小平方法配合直线趋势方程:2)预测2005年社会商品零售额。
(a,b及零售额均保留三位小数,10、某商业企业商品销售额1月、2月、3月分别为216,156,180.4万元,月初职工人数1月、2月、3月、4月分别为80,80,76,88人,试计算该企业1月、2月、3月各月平均每人商品销售额和第一季度平均每月人均销售额。
(写出计算过程,结果精确到0.0001万元\人)二、简答题(请在以下题目中任选2题作答,每题25分,共50分)1.区间估计与点估计的结果有何不同?答:点估计是使用估计量的单一值作为总体参数的估计值;区间估计是指定估计量的一个取值范围都为总体参数的估计。
2.解释抽样推断的含义。
答:简单说,就是用样本中的信息来推断总体的信息。
总体的信息通常无法获得或者没有必要获得,这时我们就通过抽取总体中的一部分单位进行调查,利用调查的结果来推断总体的数量特征。
3.统计调查的方法有那几种?答:三种主要调查方式:普查,抽样调查,统计报表。
实际中有时也用到重点调查和典型调查。
4.时期数列与时点数列有哪些不同的特点?5.为什么要计算离散系数?答:离散系数是指一组数据的标准差与其相应得均值之比,也称为变异系数。
对于平均水平不同或计量单位不同的不同组别的变量值,是不能用方差和标准差比较离散程度的。
为消除变量值水平高低和计量单位不同对离散程度测度值的影响,需要计算离散系数。
离散系数的作用主要是用于比较不同总体或样本数据的离散程度。
离散系数大的说明数据的离散程度也就大,离散系数小的说明数据的离散程度也就小。
6.简述普查和抽样调查的特点。
答:普查是指为某一特定目的而专门组织的全面调查,它具有以下几个特点:(1)普查通常具有周期性。
(2)普查一般需要规定统一的标准调查时间,以避免调查数据的重复或遗漏,保证普查结果的准确性。
(3)普查的数据一般比较准确,规划程度也较高。
(4)普查的使用范围比较窄。
抽样调查指从调查对象的总体中随机抽取一部分单位作为样本进行调查,并根据样本调查结果来推断总体数量特征的一种数据收集方法。
它具有以下几个特点:(1)经济性。
这是抽样调查最显著的一个特点。
(2)时效性强。
抽样调查可以迅速、及时地获得所需要的信息。
(3)适应面广。
它适用于对各个领域、各种问题的调查。
(4)准确性高。
7.简述算术平均数、几何平均数、调和平均数的适用范围。
答:几何平均数主要适用于比率的平均。
一般地说,如果待平均的变量x与另外两个变量f和m 有fx=m 的关系时,若取f为权数,应当采用算术平均方法;若取m 为权数,应当采用调和平均方法。
8.假设检验的基本依据是什么?根据所获得的样本,运用统计分析方法对总体的某种假设作出拒绝或接受的判断。
大数定理和实际推断原理:小概率事件在一次抽样中是不可能发生的。
9.表示数据分散程度的特征数有那几种?答:全距(又称极差),方差和标准差,交替标志的平均数和标准差,变异系数,标准分数。
10.回归分析与相关分析的区别是什么?答:1、在回归分析中,y被称为因变量,处在被解释的特殊地位,而在相关分析中,x与y处于平等的地位,即研究x与y的密切程度和研究y与x的密切程度是一致的;2、相关分析中,x与y都是随机变量,而在回归分析中,y是随机变量,x可以是随机变量,也可以是非随机的,通常在回归模型中,总是假定x是非随机的;3、相关分析的研究主要是两个变量之间的密切程度,而回归分析不仅可以揭示x对y 的影响大小,还可以由回归方程进行数量上的预测和控制。
11.在统计假设检验中,如果轻易拒绝了原假设会造成严重后果时,应取显著性水平较大还是较小,为什么?答:取显著性水平较小,因为如果轻易拒绝了原假设会造成严重后果,那就说明在统计假设检验中,拒绝原假设的概率要小,而假设检验中拒绝原假设的概率正是事先选定的显著性水平α12.加权算术平均数受哪几个因素的影响?若报告期与基期相比各组平均数没变,则总平均数的变动情况可能会怎样?请说明原因。
13.解释相关关系的含义,说明相关关系的特点。
答:变量之间存在的不确定的数量关系为相关关系。
相关关系的特点:一个变量的取值不能由另一个变量唯一确定,当变量x取某个值时,变量y的取值可能有几个;变量之间的相关关系不能用函数关系进行描述,但也不是无任何规律可循。
通常对大量数据的观察与研究,可以发现变量之间存在一定的客观规律。
14.为什么对总体均值进行估计时,样本容量越大,估计越精确?答:因为总体是所要认识的研究对象的全体,它是具有某种共同性质或特征的许多单位的集合体.总体的单位数通常用N来表示,N总是很大的数.样本是总体的一部分,它是从总体中随机抽取出来、代表总体的那部分单位的集合体.样天津大唐国际盘山发电有限责任公司本的单位数称为样本容量,通常用n表示。
样本容量n越大,就越接近总体单位数N,样本均值就越接近总体均值,对总体均值进行估计时,估计越精确。
页脚内容11。
