基于遗传算法的最短路径规划
遗传算法求最短路径

遗传算法求最短路径实例描述配送中⼼数为1,客户数k为8,车辆总数m为2;车辆载重皆为8吨;各客户点需求为g(i = 1, 2, ... , 8)(单位为吨),已知客户点与配送中⼼的距离如表1 (其中0表⽰中⼼仓库),要求合理安排车辆的运输路线,使总运输⾥程最⼩。
客户点与配送中⼼的距离表cij01234567800467.592010168140 6.541057.5111026 6.507.510107.57.57.537.547.501059915491010100107.57.5105205105100797.56107.57.597.570710716117.567.59701088107.515107.510100各客户点需求g1g2g3g4g5g6g7g812121422运⾏结果【Attention】下图并⾮最优结果,只是为了测试程序的正确性。
可以尝试加⼤次数改良结果。
遗传算法分析顾名思义,遗传算法是根据遗传规律写的⼀个算法,但是相⽐于医学中的遗传来讲,这⾥讲的遗传算法原理相对简单很多。
遗传算法的核⼼有三个部分:交叉、变异、轮盘赌。
解决问题的关键和难点就是理解遗传算法的作⽤:通过改变交叉和变异改变基因特性,导致个体发⽣改变,从⽽影响到适应度,最后利⽤轮盘赌的⽅式淘汰掉⼀些个体。
看⼀下整个程序的运⾏流程:4 5 2 7 3 6 1 8 \\ 2 8 1 5 7 6 3 4 \\ 4 6 7 2 5 1 3 8 \\ 4 2 6 5 1 7 8 3 \\ 1 7 3 2 4 8 5 6 \\ 3 2 8 6 4 7 1 5上⾯的数据⼀⽤有6⾏8列,我们可以说有6个个体,每个个体的基因长度是8。
其中6可以说是种群⼤⼩,8可以说是每个个体的特征数⽬。
到⽬前为⽌,我们可以定义⼀种运算规则了:通过每个个体的特征计算出该个体的样⼦(X),然后根据个体的样⼦,求出该个体的适应度(Y)。
整个流程是:个体特征 --->> 个体 --->> 适应度交叉过程:[]假设个体1和个体2发⽣了交叉,交叉点在第7列,那么交叉之前,两个个体为:4 5 2 7 3 6 1 8 \\ 2 8 1 5 7 6 3 4交叉之后,两个个体为:4 5 2 7 3 6 3 4 \\ 2 8 1 5 7 6 1 8可以发现,交叉就是把交叉点后的所有列数据都进⾏交换(包括交叉点所在的列)。
11基于遗传算法的机器人路径规划MATLAB源代码

基于遗传算法的机器人路径规划MATLAB源代码基本思路是:取各障碍物顶点连线的中点为路径点,相互连接各路径点,将机器人移动的起点和终点限制在各路径点上,利用最短路径算法来求网络图的最短路径,找到从起点P1到终点Pn的最短路径。
上述算法使用了连接线中点的条件,因此不是整个规划空间的最优路径,然后利用遗传算法对找到的最短路径各个路径点Pi (i=1,2,…n)调整,让各路径点在相应障碍物端点连线上滑动,利用Pi= Pi1+ti×(Pi2-Pi1)(ti∈[0,1] i=1,2,…n)即可确定相应的Pi,即为新的路径点,连接此路径点为最优路径。
function [L1,XY1,L2,XY2]=JQRLJGH(XX,YY)%% 基于Dijkstra和遗传算法的机器人路径规划% GreenSim团队——专业级算法设计&代写程序% 欢迎访问GreenSim团队主页→/greensim%输入参数在函数体内部定义%输出参数为% L1 由Dijkstra算法得出的最短路径长度% XY1 由Dijkstra算法得出的最短路径经过节点的坐标% L2 由遗传算法得出的最短路径长度% XY2 由遗传算法得出的最短路径经过节点的坐标%程序输出的图片有% Fig1 环境地图(包括:边界、障碍物、障碍物顶点之间的连线、Dijkstra的网络图结构)% Fig2 由Dijkstra算法得到的最短路径% Fig3 由遗传算法得到的最短路径% Fig4 遗传算法的收敛曲线(迄今为止找到的最优解、种群平均适应值)%% 画Fig1figure(1);PlotGraph;title('地形图及网络拓扑结构')PD=inf*ones(26,26);for i=1:26for j=1:26if D(i,j)==1x1=XY(i,5);y1=XY(i,6);x2=XY(j,5);y2=XY(j,6);dist=((x1-x2)^2+(y1-y2)^2)^0.5;PD(i,j)=dist;endendend%% 调用最短路算法求最短路s=1;%出发点t=26;%目标点[L,R]=ZuiDuanLu(PD,s,t);L1=L(end);XY1=XY(R,5:6);%% 绘制由最短路算法得到的最短路径figure(2);PlotGraph;hold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('由Dijkstra算法得到的初始路径')%% 使用遗传算法进一步寻找最短路%第一步:变量初始化M=50;%进化代数设置N=20;%种群规模设置Pm=0.3;%变异概率设置LC1=zeros(1,M);LC2=zeros(1,M);Yp=L1;%第二步:随机产生初始种群X1=XY(R,1);Y1=XY(R,2);X2=XY(R,3);Y2=XY(R,4);for i=1:Nfarm{i}=rand(1,aaa);end% 以下是进化迭代过程counter=0;%设置迭代计数器while counter<M%停止条件为达到最大迭代次数%% 第三步:交叉%交叉采用双亲双子单点交叉newfarm=cell(1,2*N);%用于存储子代的细胞结构Ser=randperm(N);%两两随机配对的配对表A=farm{Ser(1)};%取出父代AB=farm{Ser(2)};%取出父代BP0=unidrnd(aaa-1);%随机选择交叉点a=[A(:,1:P0),B(:,(P0+1):end)];%产生子代ab=[B(:,1:P0),A(:,(P0+1):end)];%产生子代bnewfarm{2*N-1}=a;%加入子代种群newfarm{2*N}=b;for i=1:(N-1)A=farm{Ser(i)};B=farm{Ser(i+1)};newfarm{2*i}=b;endFARM=[farm,newfarm];%新旧种群合并%% 第四步:选择复制SER=randperm(2*N);FITNESS=zeros(1,2*N);fitness=zeros(1,N);for i=1:(2*N)PP=FARM{i};FITNESS(i)=MinFun(PP,X1,X2,Y1,Y2);%调用目标函数endfor i=1:Nf1=FITNESS(SER(2*i-1));f2=FITNESS(SER(2*i));if f1<=f2elsefarm{i}=FARM{SER(2*i)};fitness(i)=FITNESS(SER(2*i));endend%记录最佳个体和收敛曲线minfitness=min(fitness);meanfitness=mean(fitness);if minfitness<Yppos=find(fitness==minfitness);Xp=farm{pos(1)};Yp=minfitness;endif counter==10PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];figure(3)PlotGraph;hold onfor i=1:(length(R)-1)x1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法第10代')hold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendendif counter==20PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];figure(4)PlotGraph;hold onfor i=1:(length(R)-1)x1=XY2(i,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法第20代')hold onx1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendendif counter==30PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];figure(5)PlotGraph;hold onfor i=1:(length(R)-1)x1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法第30代')hold onfor i=1:(length(R)-1)x1=XY1(i,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendendif counter==40PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];figure(6)PlotGraph;hold onx1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法第40代')hold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendendif counter==50PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];figure(7)PlotGraph;hold onfor i=1:(length(R)-1)x1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法第50代')hold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendendLC2(counter+1)=Yp;LC1(counter+1)=meanfitness;%% 第五步:变异for i=1:Nif Pm>rand&&pos(1)~=iAA=farm{i};AA(POS)=rand;farm{i}=AA;endendcounter=counter+1;disp(counter);end%% 输出遗传算法的优化结果PPP=[0.5,Xp,0.5]';PPPP=1-PPP;X=PPP.*X1+PPPP.*X2;Y=PPP.*Y1+PPPP.*Y2;XY2=[X,Y];L2=Yp;%% 绘制Fig3figure(8)PlotGraph;hold onhold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendfor i=1:(length(R)-1)x1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k');hold onendtitle('遗传算法最终结果')figure(9)PlotGraph;hold onfor i=1:(length(R)-1)x1=XY1(i,1);y1=XY1(i,2);x2=XY1(i+1,1);y2=XY1(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',1);hold onendhold onfor i=1:(length(R)-1)x1=XY2(i,1);y1=XY2(i,2);x2=XY2(i+1,1);y2=XY2(i+1,2);plot([x1,x2],[y1,y2],'k','LineWidth',2);hold onendtitle('遗传算法优化前后结果比较')%% 绘制Fig4figure(10);plot(LC1);hold onplot(LC2);xlabel('迭代次数');title('收敛曲线');源代码运行结果展示。
基于遗传算法的最短路径探索

基于遗传算法的最短路径探索摘要:最短路径问题是图论中的典型问题,它在生产和生活中具有广泛的实例。
本文对遗传算法求解最短路径问题作了有益的尝试,详细分析了求解最佳路径的遗传算法的构成要素,着重探讨遗传算法求解最短路径问题的可行性。
关键词:遗传算法;最短路径;适应函数;选择;交叉;变异;可行性研究exploring the shortest path Based on geneticalgorithmsAbstract:As the development of human society, people are for the request on problem solving does not merely stop at the point of feasibility, but turns to concision, efficiency and speediness. It not only meets people’s needs for the general study and life, but also requires using the least resources, suc h as time and space, to achieve the best result. This article tries to work out the shortest path of genetic algorithm, and particularly analyses the constituent elements of the best path of genetic algorithm, and mainly discusses the feasibility of the shortest path of genetic algorithm.Key Words:genetic algorithm; shortest path;feasibility1 引言遗传算法(genetic algorithm,下面简称GA)是基于生物进化原理的一种全局性优化算法,是借鉴生物的自然选择和遗传进化机制而开发出的一种全局优化自适应概率搜索算法,是生物遗传技术和计算机技术结合的产物。
基于改进遗传算法的最短路径路由优化算法的设计与实现的开题报告

基于改进遗传算法的最短路径路由优化算法的设计与实现的开题报告一、题目基于改进遗传算法的最短路径路由优化算法的设计与实现二、研究背景和意义路由优化在计算机网络中具有重要的意义。
在网络传输数据时,由于存在大量的节点和路径,因而将路由优化问题转化为求解最短路径问题是一个比较普遍的做法。
传统的最短路径算法(如Dijkstra算法、Bellman-Ford算法)在小规模网络中表现良好,但随着网络规模的增大,算法的时间复杂度也随之增加。
因此,如何在保证计算时间复杂度不增加的前提下,寻找更优的最短路径成为一个热门的课题。
遗传算法作为一种优化算法,具有全局搜索的特点,能够在个体序列空间上进行搜索,从而解决复杂的优化问题。
因此,将遗传算法应用于路由优化问题,可以有效地解决网络规模越来越大所带来的计算复杂度问题,并得到更优的最短路径方案。
但是,遗传算法自身也存在缺陷,例如容易陷入局部最优解中。
因此,需要进行改进,结合具体的路由优化问题,设计更高效且准确的遗传算法,从而得到更优的最短路径方案。
因此,本研究旨在基于改进遗传算法,设计更优的最短路径路由优化算法,解决网络规模增大所带来的计算复杂度问题,并得到更优的最短路径方案,具有一定的实际应用价值。
三、研究内容1.遗传算法的原理与基本流程学习。
2.调研现有的路由优化算法,分析其优劣,并结合具体的路由优化问题,设计改进遗传算法。
3.设计并实现最短路径路由优化算法,包括种群初始化、选择操作、交叉操作、变异操作等。
4.编写并运行相应的算法程序,测试算法的性能和效果。
5.根据测试结果,分析算法的优劣之处,进一步改进算法。
四、预期成果1.理解遗传算法的基本原理和流程。
2.掌握现有路由优化算法的优缺点并设计改进遗传算法。
3.设计并实现最短路径路由优化算法,并进行实验测试。
4.分析算法的优劣之处,并进一步改进算法。
五、研究计划第一阶段:文献调研和算法学习(3周)•阅读相关文献,了解路由优化算法和遗传算法的相关知识。
python遗传算法多辆车最短路径问题

Python遗传算法多辆车最短路径问题1. 引言遗传算法是一种启发式优化算法,通过模拟生物进化过程中的自然选择、交叉和变异等基本操作,能够搜索问题的解空间并逐步优化。
多辆车最短路径问题是一个经典的组合优化问题,目标是找到多辆车经过一系列点的最短路径。
本文将探讨如何使用Python编写遗传算法来解决多辆车最短路径问题。
2. 问题描述多辆车最短路径问题可以用以下方式来描述:•假设有n个点,编号为0到n-1,其中点0为起始点,点n-1为终点。
•每辆车从起始点出发,经过一系列中间点,最后到达终点。
•每个中间点都有一个对应的非负权重,表示经过该点的路径长度。
•每辆车有一个最大容量,表示该车能够承载的最大路径长度。
•某些点之间可能存在限制条件,即只有满足该条件才能够经过。
问题的目标是找到一种分配方案,使得所有车辆的路径长度之和最短。
3. 算法思路为了解决多辆车最短路径问题,可以使用遗传算法来进行优化搜索。
遗传算法的基本思路如下:1.初始化一组随机的染色体,每个染色体表示一种解决方案,即车辆路径的分配方案。
2.根据染色体计算路径长度,并进行适应度评估,将路径长度作为适应度值。
3.通过选择、交叉和变异等遗传操作,对染色体进行进化。
4.重复步骤2和步骤3,直到达到终止条件(例如达到最大迭代次数或找到满足目标值的解)。
下面将具体介绍遗传算法多辆车最短路径问题的解决过程。
4. 解决方案4.1. 表示方法为了表示车辆路径的分配方案,可以使用一个二维数组来表示染色体。
数组的行数表示车辆的数量,列数表示路径经过的点的数量。
数组元素的值表示经过对应点的顺序。
例如,假设有3辆车,路径经过4个点,其中第一辆车的路径为 [0, 2, 3, 1],第二辆车的路径为 [0, 1, 3, 2],第三辆车的路径为 [0, 3, 1, 2],那么可以表示为以下形式的二维数组:[[0, 2, 3, 1],[0, 1, 3, 2],[0, 3, 1, 2]]4.2. 初始化种群在遗传算法中,种群是染色体的集合。
基于遗传算法的最短路径问题及其MATLAB实现
TRANSPOWORLD 2009 No.12(Jun)104前言在现实生活中,我们经常遇到最短路问题,例如寻找两点之间总长度最短或者费用最低的路径。
在运输、物流、设施选址以及人员调度问题中,最短路径是很常见的问题。
解决最短路问题的方法有很多,例如迪杰斯特拉算法、福特算法。
在这里我们介绍基于遗传算法的最短路径问题的解决方案。
模型遗传算法基本模型遗传算法是模仿生物进化过程,针对复杂问题开发出来的非常有效的方基于遗传算法的最短路径问题及其MATLAB 实现文/张书源 郭 聪法。
根据生物进化过程中的选择机制,在问题的解空间中进行选择,实现“物竞天择,适者生存”。
在遗传算法中,一条染色体代表问题的一个可行解,该染色体的适应值即为对应于该可行解的函数值。
一般来说,遗传算法包括以下几个主要组成部分。
编码即将问题的解表示成一个编码串(染色体),每一染色体对应问题的一个解。
遗传过程对染色体进行操作,以产生新的染色体,通常有不同染色体之间的交叉操作以及一条染色体的变异操作。
评价与选择对每条染色体计算其适应值,用以评价染色体的优劣,从而从父代和子代中选择较优的染色体,进入下一代的繁殖。
初试种群的创建方法其作为问题可行解的集合。
初始种群中染色体个数称为种群规模。
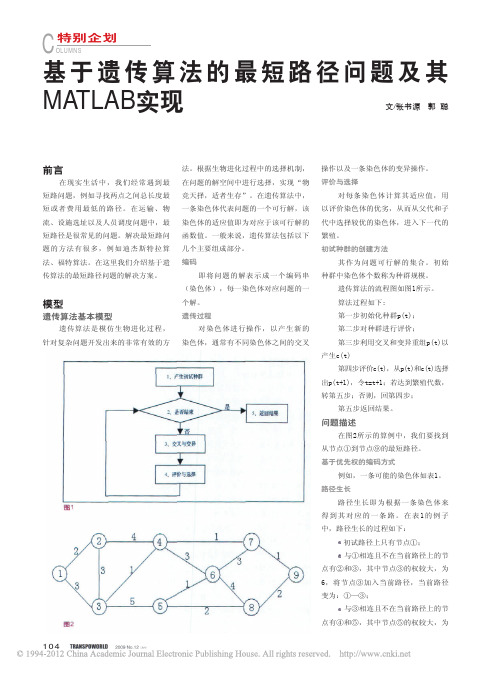
遗传算法的流程图如图1所示。
算法过程如下:第一步初始化种群p(t);第二步对种群进行评价;第三步利用交叉和变异重组p(t)以产生c(t)第四步评价c(t),从p(t)和c(t)选择出p(t+1),令t=t+1;若达到繁殖代数,转第五步;否则,回第四步;第五步返回结果。
问题描述在图2所示的算例中,我们要找到从节点①到节点⑨的最短路径。
基于优先权的编码方式例如,一条可能的染色体如表1。
路径生长路径生长即为根据一条染色体来得到其对应的一条路。
在表1的例子中,路径生长的过程如下:初试路径上只有节点①; 与①相连且不在当前路径上的节点有②和③,其中节点③的权较大,为6,将节点③加入当前路径,当前路径变为:①—③;与③相连且不在当前路径上的节点有④和⑤,其中节点⑤的权较大,为图2COLUMNS特别企划1052009年第12期 《交通世界》(6月下)5,将节点⑤加入到当前路径中,当前路径变为①—③—⑤;与⑤相连且不在当前路径上的节点有⑥和⑧,其中节点⑧的权较大,为9,将节点⑧加入到当前路径中,当前路径变为①—③—⑤—⑧;与⑧相连且不在当前路径上的节点有⑥和⑨,其中节点⑨的权较大,为8,将节点⑨加入到当前路径中,当前路径变为①—③—⑤—⑧—⑨。
基于遗传算法的最短路径问题求解

222008,44(23)cD7印Ⅱ地r E,画册e^昭帆d A即k m抽船计算机工程与应用基于遗传算法的最短路径问题求解康晓军,王茂才KA N G Xiao—j un,W AN G Mao—cai中国地质大学计算机学院,武汉430074D e p a n m e n t of C om put er,Ch ina UI liVe rsi ty of Geos c ie nc e s,Wu h an 430074,Chi naE—mail:xj.-kang@126.comK A N G Xiao.jun,WANG Mao—明i.Shortest path algo r i th m i m p l e m e n ts b鼬屺d o n ge n et i c a lg or it l吼.C om pu te r Engi neering a n d AppHcatio ns,2008,44(23):22—23.Abstmct:nis pap er锄a lyze s th e fa ctor of s o lv e sh on es t pa tIl pro ble m ba sed genetic a190rithm,舀Ves n e w k i nd of crossing and m u t at i o n a190rit hm.111e alg ori mm wh ich ha s b een u sed in simulatiVe network,is p m V e d t o be r e as o n ab l e an d emcient.Furthe卜more tlIe authors A na l yz e t h e ma in ly pedb瑚ance par蛐eter of genetic alg ori thm.1沁y wo rd s:ge ne tic algorithm;sh矾est p at h algori出m;parameter s d ec t io n摘要:详细分析了求解最短路径的遗传算法的构成要素,提出一种新的交叉变异算法,通过仿真实验论证了求解过程是合理而有效的,同时给出了算法的主要性能参数,并对其进行了分析。
遗传算法求最短路径

遗传算法求最短路径
遗传算法可以用来求解最短路径问题。
以下是一种可能的实现方式:
1.初始化种群:随机生成一些包含起点和终点的路径作为初始种群。
2.评估适应度:计算每条路径的总距离作为适应度。
3.选择操作:根据适应度选择一些较优的个体作为父母。
4.交叉操作:将父母中的路径随机交叉生成新的个体。
5.变异操作:对新个体进行随机变异以增加种群的多样性。
6.评估适应度:计算每个新个体的适应度。
7.选择操作:根据适应度选择较优的个体作为下一代种群。
8.重复以上步骤直到达到一个终止条件,例如达到一定的迭代次数或
者找到最优解。
需要注意的是,交叉和变异的具体实现方式可能因问题而异。
在最短
路径问题中,一种可能的方式是在相邻的两段路径中随机选择一个交叉点,然后交换两个个体中对应的路径片段。
变异可以是对个体中的某个路径点
进行随机扰动。
此外,还可以采用其他的启发式算法,如遗传算法和局部
搜索的结合,进一步提高求解效率。
遗传算法求解最短路径问题

遗传算法求解最短路径问题3.3.1最短路径问题的图论描述在G =(V,E,宇)中,与V中的有序偶(Vi, Vj)对应的边e,称为图的有向边,同时与V中的顶点的无序偶Vi*Vj相对应的边e,称为图的无向边,并且如果在G=(V,E,?)中,与V中的顶点的无序偶Vi*Vj相对应的边e,全部都是无向边的话,这个图就叫做无向图,与V中的有序偶(Vi,Vj)对应的边e,都是有向边的话,这个图就叫做有向图。
为了方便实验,与进行仿真分析,本文所有实验的算法都选用的是无向图。
3.3.2染色体编码具体在进行染色体编码的时候,我么对于各顶点号是进行按自然编排的,然后按照编排的顺序将每个待选的顶点作为一个染色体的基因,基因编排的顺序也就是一条路径之中出现的先后顺序,所以可以看出来,具体的染色体的总长度应该和顶点的个数保持持平。
3.3.3适应函数对于前面假设的性能函数在此处可以进行一些稍微的改进,因为是求距离,所以此处我们将前面误差的平方和,看成是各个顶点之间距离的平方和,具体如下面公式(3-6)以及公式(3-7)所示:I 2 Tf (x)=:E v (x) =v )x (V x (3-6)i=1V(X )= d(V j,V i+1)(3-7)具体就是对于求出来多个xi,计算出对应的fi,求出其中最小的f X min对应的X min就是最优解。
3.3.4选择操作从上一次迭代过程之中的染色体,选择二个染色体作为双亲,而这里具体的染色体选择的是交叉的节点,这个是根据前面的适应函数选取的,原理就是选择操作更容易选择距离较短的二个顶点。
3.3.5交叉与变异操作1、交叉操作:将被选中要进行操作的染色体在进行交叉操作的具体步骤是,先在染色体上产生一个随机数,然后弄清楚这个随机基因的具体位置,从而确定与这个随机基因交叉点的位置,一般来说是同一个位置,然后将与这个随机基因在交叉点交叉的基因进行互换。
具体交叉操作的示意图如图3-1所示:1100101010101110111000110110011100110001图3-1交叉操作2、变异操作将被选中要进行操作的染色体在进行变异操作的具体步骤是,先在染色体上产生一个随机数,然后弄清楚这个随机基因的具体位置,然后将这个位置之上的基因从0变成1,或者从1变成0。
基于遗传算法的最短路径研究与编程实践

基于遗传算法的最短路径研究与编程实践作者:刘雪龙来源:《科学与财富》2010年第05期[摘要]最短路径问题的存储结构通常是采用针对图论中的带权图的邻接矩阵。
根据权的性质,这个问题的解可以是任何意义的最佳,如经济最省、时间最快、路程短、或者是其它意义上的“最优”。
本文在最小成本计算、最佳地址选择等问题的基础上,同时进行了编程实践。
[关键词] 最短路径遗传算法编程算法描述一、遗传算法求解最短路径思路遗传算法的基本思想是基于达尔文进化论和孟德尔的遗传变异理论的。
遗传算法把问题的解表示成基因串,每一个基因串都是一个假设解。
然后,把假设解置于问题空间(群体)中,以适应度函数(或日标函数)为依据,通过对个体施加遗传操作实现群体内个体结构重组的迭代处理过程,最后收敛到最适应环境的个体上,它就是问题的最优解。
遗传算法主要考虑六个要素:一是染色体编码,由于遗传算法不能直接处理解空间的数据,因此必须通过编码将它们表示成遗传空间的基因型串结构数据。
基本遗传算法使用固定长度的二进制符号串来表示群体中的个体,其等位基因是由二值符号集{0,1}组成;二是初始种群的生成,由于遗传算法的群体操作需要,所以进化开始前必须准备一个由若干初始解组成的初始群体;三是适应度评价,遗传算法在进化过程中一般不需要其它外部信息,仅用评价函数值来评估个体或解的优劣,并作为遗传操作的依据;四是遗传算子这个要素,基本遗传算法使用三种遗传算子:①选择运算: 比例选择。
选择运算的目的是为了从当前群体中选出优良的个体,使它们有机会作为父代繁殖后代子孙。
判断个体优劣的准则是个体的适应度值。
选择运算模拟了达尔文适者生存、优胜劣汰原则,个体适应度越高,被选择的机会也就越多;②交叉运算:单点交叉。
交叉运算相当于生物进化过程中的有性繁殖的基因重组过程;③变异运算:基本位变异。
变异运算模拟了生物进化过程中的基因突变方法,将某个基因座上的基因变异为其等位基因;选择运算不产生新的个体,交叉运算和变异运算都产生新的个体,因此,选择运算完成的是复制操作,而交叉运算和变异运算则完成繁殖操作。
基于遗传算法的动态网络中最短路径问题算法

收稿日期:2004-09-01 基金项目:广东省自然科学基金资助项目(E5320271)作者简介:邹亮(1979-),男,黑龙江依兰人,博士研究生,主要研究方向:非线性系统控制、智能控制、动态路径诱导、智能交通系统和交通管理; 徐建闽(1960-),男,福建福州人,教授,博士生导师,主要研究方向:自适应控制、鲁棒控制、智能控制、现代交通工程、C M S 、机器人控制.文章编号:1001-9081(2005)04-0742-03基于遗传算法的动态网络中最短路径问题算法邹 亮,徐建闽(华南理工大学交通学院,广东广州540640)(m uscle1979@sina .co m )摘 要:提出了一种以随机D ijkstra 最短路径算法为基础,运用遗传算法来求解动态路径诱导系统中最短路径问题(Shortest Pat h proble m on Dyna m ic Route Guidance Syste m,SPDRGS)的算法。
通过运用该随机D ij k stra 算法解决了将遗传算法应用与最短路径问题中初始种群的产生问题。
考虑到目前动态路径诱导系统(Dyna m ic Route Gui d ance Syste m ,DRGS)对路径诱导算法的时间复杂度和网络约束条件的要求,此算法不仅能够较快地求出较优的路径而且对网络没有任何的约束条件,同时对离散和连续的动态网络模型有效,因此符合DRGS 的要求。
关键词:随机D ijkstra 算法;动态路径诱导系统;最短路径;遗传算法中图分类号:TP18 文献标识码:AM ethod of shortest paths proble m on dyna m ic net work based on genetic algorith mZOU L i a ng ,XU Jian m i n(Co llege of T raff ic and C o mmunications,South Chi na Uni ver sit y of T ec hno l ogy,Guangzhou Guangdong 510640,China)Abstract :A n algo rith m based on rando m D ij kstra a l gor i th m and applying genetic a l gor it h m to so l ve SPDRG S(Sho rtest P ath prob le m on Dyna m ic R oute G ui dance System)w as proposed .By app l y i ng random D ij kstra al go rith m ,t he a l gor it h m cleared outthe b i ggest obstructi on bet ween the genetic a l gor it h m and SPDRG S ,wh ich is ho w to get the i nitial genera ti on of GA (G enetic algorith m ).A ccord i ng t o DRG S s (Dyna m ic R oute G ui dance System )de mand for ti m e complex ity and net w ork constra i nt cond iti on o f route gu i dance a l gor i th m s ,th i s a l gor it h m can qu i ckly find t he excell ent path and does not need any net work constra i nt condition ,which also can so lve t he proble m s on conti nuously and d i screte dyna m ic net w orks .So the a l gor ith m proposed can satisfy t he de m and o f DRG S .K ey words :rando m D ij kstra a l gor ith m ;DRGS ;shortest pa t h ;genetic algorith m0 引言遗传算法是模拟生物进化过程的计算模型,遗传算法作为一种新的全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理以及应用范围广等显著特点,奠定了它作为21世纪关键智能计算算法之一的地位。
基于遗传算法解决TSP问题

基于遗传算法解决TSP问题摘要题目要求给出环游全国全部省会的最短路径方案,是传统的TSP问题,本文将图表数据数字化后,将其转变成为线性规划问题,进而采取遗传算法用Matlab 求解出理论上的最短路径与路线图。
通过第一问求出的路线顺序结合实际情况求解出实际情况下的最短路径与最短时间。
针对第一问,首先建立基本TSP模型,求出其线性规划方程组,用Matlab 对地图做出基本处理,求出其像素坐标的矩阵。
将省会城市初始化为种群数据,用遗传算法求解出模型最优解,即最短路径大小与旅游城市顺序。
针对第二问,由于遗传算法求出的是近似最优解,以及实际道路情况不可能是直线距离,所以理论数据与实际有一定差别。
将旅行顺序求解出后,需要根据实际道路情况重新求解出最短路径大小,并根据题目所给条件求解出最短时间。
根据实际情况,求得最后的最短路径长度为20402.9公里,时间为45天。
题目中给出城市转化为图集,一共有33个顶点,数据较大,用Dijkstra算法和Floyd算法虽然答案可能更精确,但数据处理量大,时间复杂度高。
采用遗传算法可以得到近似最优解,并且精简了时间复杂度。
关键词:最短路径TSP冋题线性规划遗传算法一、问题重述如果从杭州出发,要想开车走遍全国所有的省会城市,而且在到了每个省会城市以后都必须住一晚,第二天早上才能出发,安全起见每天开车时间最多在8小时左右,车速视实际路况而定,一般高速公路可以取平均车速100公里/小时左右,不是高速公路平均车速取60公里/小时左右,从杭州出发要走遍所有省会城市以后回到杭州,开车里程最少需要多少公里?最少需要多少时间?(暂不考虑台湾省)二、问题分析题目要求求出最短路径与时间是典型的TSP问题,即要用最短的总路径走遍所有城市,此处需要设立一个二元组(V(G), E(G)),并且求出一个点的邻接矩阵。
根据经典的TSP模型,得出一般的线性规划方程组。
解TSP模型的一般算法有Dijkstra 算法和Floyd算法,由于TSP问题是典型的NP难题,其可能路径数目与城市总数目n是呈指数型增长,并不适合用以上两种算法。
遗传算法求最短路径

遗传算法求最短路径遗传算法是一种优化问题求解方法,适用于复杂问题的求解。
最短路径问题是一类经典的优化问题,可以通过遗传算法来求解。
最短路径问题是指在一个图中找到一条从起点到终点的最短路径。
图可以用节点和边的集合来表示,每条边都有一个非负的权重表示两个节点之间的距离。
遗传算法是一种模拟生物进化过程的优化算法。
它基于进化生物学中的遗传和进化理论,通过模拟生物个体的基因演化过程,生成新的解决方案,并通过适应度函数来评估每个个体的优劣。
优秀的个体将更有可能被选择为父代,进一步交叉和变异生成下一代。
这个过程将逐步优化解决方案,直到达到一定的停止条件。
对于最短路径问题,可以通过遗传算法来图中的解空间。
首先,需要定义染色体的表示方式。
一种常见的表示方式是使用一个序列来表示路径,例如[1,3,4,2,5]表示从节点1到节点5的路径,经过节点3,4,2、然后,需要定义适应度函数,用于评估每个个体的优劣程度。
在最短路径问题中,可以使用路径的总权重作为适应度函数,即路径上边权重的总和。
接下来,可以使用选择、交叉和变异等遗传算子来生成下一代个体,并通过适应度函数进行评估和选择。
具体的遗传算法求解最短路径问题的步骤如下:1.初始化种群:随机生成一定数量的个体作为初始种群,每个个体表示一个路径。
2.评估适应度:计算每个个体的适应度,即路径的总权重。
3.选择操作:根据适应度函数选择一些优秀的个体作为父代。
4.交叉操作:对选择的父代个体进行交叉操作,生成新的个体。
5.变异操作:对交叉得到的新个体进行变异操作,引入一定的随机性。
6.评估适应度:计算每个新个体的适应度。
7.替换操作:根据适应度函数替换当前种群中的一些个体。
8.重复步骤3-7,直到达到停止条件。
9.输出结果:选择适应度最优的个体作为最短路径。
遗传算法求解最短路径问题的优点是能够在大规模问题中找到较优解,并且不依赖于问题的具体结构。
但是,遗传算法也存在一定的局限性,例如对于复杂的问题,算法收敛速度较慢。
基于遗传算法的机器人路径规划

基于遗传算法的机器人路径规划机器人已经成为现代工业和生活的重要组成部分,广泛应用于自动化生产和服务领域。
机器人路径规划是机器人实现自主移动的重要技术之一,它可以帮助机器人避开障碍物,找到最短路径,提高机器人的运动效率和安全性。
而基于遗传算法的机器人路径规划是一种有效的解决方法,本文将对这一技术进行介绍和分析。
一、遗传算法概述遗传算法是一种启发式搜索算法,常用于求解复杂的优化问题。
遗传算法的基本思想是模拟生物遗传和进化过程中的基本原理,通过模拟交叉、变异、选择等遗传操作,不断地对种群中的个体进行进化,最终得到最优解。
遗传算法一般由以下步骤组成:1. 初始化种群:随机生成一组初始个体并形成初始种群;2. 适应度函数:根据问题的特定需求和目标,设计适应度函数评价每个个体的优劣程度;3. 选择操作:根据适应度函数的评价结果,选择优秀的个体参与下一代进化;4. 遗传操作:包括交叉和变异两种操作,交叉操作模拟生物交配和染色体交换,变异操作模拟基因突变。
5. 收敛判断:通过设定迭代次数或适应度函数的收敛精度,判断算法是否终止。
二、机器人路径规划中的遗传算法机器人路径规划一般可分为静态路径规划和动态路径规划两种,其中动态路径规划又可分为全局路径规划和局部路径规划。
全局路径规划是指在未知环境中,机器人需要从起点到终点找到一条最近、最短、最安全的路径。
全局路径规划一般采用比较复杂的路徑规劃算法解决,例如A*算法、Dijstra算法、基于遗传算法的路径规划算法等。
局部路径规划是指机器人在已知环境中,需要在运动中避开障碍物和遵守运动规则,实现安全有效的路径规划。
局部路径规划一般采用比较简单的算法解决,例如最近邻居算法、虚拟势场法、动态窗口算法等。
基于遗传算法的机器人路径规划一般应用于全局路径规划中,它可以不断优化机器人的行进路径,找到最优解。
具体过程如下:1. 环境建模:将机器人运动环境转化为网络图,确定起点和终点,将网格分为障碍物和可行走区域。
基于遗传算法的最短路径问题及其MATLAB实现(1)
·与@相连且不在当前路径上的节 点有⑥和⑨,其中节点⑨的权较大,为 8.将节点⑨加入到当前路径中,当前 路径变为①一③一⑤一@一⑨。
至此.我们根据染色体找到了一 条路径①一③一⑤一⑥一⑨.这条路径 的长度为12。但是.需要注意的是,并 不是根据优先权编码的染色体都对应一 条路.例如表2染色体。
即将问题的解表示成一个编码串 (染色体).每一染色体对应问题的一 个解。 遗传过程
对染色体进行操作,以产生新的 染色体,通常有不同染色体之间的交叉
操作以及一条染色体的变异操作。 评价与选择
对每条染色体计算其适应值.用 以评价染色体的优劣,从而从父代和子 过程如下: ·初试路径上只有节点①; ·与①相连且不在当前路径上的节 点有②和③.其中节点②的权较大,为 6,将节点②加入当前路径.当前路径 变为:①一②; 重复此过程.我们会找到路径 ①一②一④一@一⑤一③.已经没有与 ③相连且不在当前路径的节点,从而找 不到从①到⑨的一条路。当出现这种情 况时.我们抛弃这条染色体.用一条合 法染色体去取代它。 染色体的适应值 染色体的适应值是我们选择较优 染色体的依据。这里染色体的适应值即 为我们得到的路径长度。由于我们得到 的路径为①一③一⑤一⑨一⑨,因此该 染色体的适应值即为此路径的长度:
104
万方数据
节点号
1
2
3
4
5
6
7
8
9
·变异算子:采用交换变异操作. 随机选择染色体上两个位置,将他们的 优先权进行交换,如图4所示。
·选择:根据每条染色体的适应 值,从父代和子代中选择路径最短的 n条染色体.作为父代,进入下一代繁 殖,其中n为种群规模。
基于遗传算法优化车辆路径规划问题

基于遗传算法优化车辆路径规划问题车辆路径规划问题是指在多个目标地点之间,如何使车辆行驶的路线最优,使得总路程最短或总时间最短等。
这是一个典型的NP问题,在传统计算机算法难以快速得到最优解时,遗传算法成为一种有效的解决方法。
遗传算法是基于自然选择和遗传现象的演化经验,通过不断地进化,筛选出适应度更高的解来解决问题。
在车辆路径规划问题中,我们可以把路线看成一条染色体,将每个目标地点看成基因,通过遗传算法来寻找最佳路径。
遗传算法的核心是一组基因编码方案,通过对其进行演化操作,逐步优化染色体直到找到最优解。
在车辆路径规划问题中,我们可以采用二进制编码方案,将每个目标地点表示为一个二进制数,并将每个二进制数按照一定的顺序排列在染色体上,形成一种基于顺序的编码方案。
由此,我们可以通过遗传算法进行染色体进化和路径规划。
在遗传算法中,主要包含三个重要的操作:选择、交叉和变异。
选择是按照适应度排序,选择优秀的个体进行繁殖;交叉是将两个个体的染色体进行交换,形成新的染色体;变异是在某些极端情况下,改变染色体中的基因,以增加种群的多样性和避免陷入局部最优解。
对于车辆路径规划问题,我们可以使用遗传算法来进行优化搜索,具体流程包括:1. 确定问题的目标函数,例如总路程或者总时间。
2. 通过二进制编码方案将每个目标地点表示为一个二进制数,并将每个二进制数按照一定的顺序排列在染色体上。
3. 初始化种群,即将多个随机生成的染色体加入到染色体群体中。
4. 通过选择、交叉和变异等操作,对种群中的染色体进行进化,得到新的染色体群体。
5. 重复进行进化操作,直到得到满足目标函数条件的染色体,即车辆行驶的最优路线。
值得注意的是,遗传算法虽然能够有效地解决车辆路径规划问题,但其速度较慢,随着问题规模的增大,计算时间也会逐渐增加。
因此,对于大规模问题,我们需要采用一些特殊的优化技巧,如分布式遗传算法、混合遗传算法等。
此外,在车辆路径规划中,还存在一些特殊的约束条件,如限制车辆的行驶距离、车辆的最大速度、道路的限速等。
python遗传算法多辆车最短路径问题

python遗传算法多辆车最短路径问题遗传算法是一种优化算法,它模拟自然界中生物进化的过程,通过基因重组、变异等操作寻找最优解。
在多辆车最短路径问题中,遗传算法可以用来寻找最短路径的解决方案。
下面,我们将介绍如何使用遗传算法来解决多辆车最短路径问题。
问题描述多辆车最短路径问题是一个复杂的问题,它要求在给定的地图上,从起点出发,经过所有的节点(城市),最终回到起点,使得路径最短,并且每辆车的行驶距离不能超过一定的限制。
这个问题可以用图论来描述,其中每个节点表示一个城市,边表示城市间的道路,道路长度表示城市间的距离。
解决方法1.问题建模首先,我们需要将问题转化为数学模型。
假设有m辆车,每辆车最多行驶l的距离,n个城市,$d_{ij}$表示从城市i到城市j之间的距离。
定义一个1到n的排列p表示城市的访问顺序。
我们的目标是找到最优的排列p,使得每辆车的行驶距离不超过l,并且总行驶距离最短。
2.编码方法在遗传算法中,我们需要将问题的解表示为染色体(chromosome),也就是一串基因(gene)序列。
在多辆车最短路径问题中,我们可以将每个城市看作一个基因,那么染色体就是一个n个基因的排列。
3.初始化种群为了使用遗传算法求解最优的排列p,我们需要初始化一个种群(population)来表示可能的解决方案。
我们可以随机生成一组初始染色体来作为初始种群。
4.选择运算在每一代遗传算法中,我们需要对种群进行选择运算(selection),通过选择优秀的染色体来保留种群中的优秀基因。
选择运算可以通过轮盘赌选择、锦标赛选择等方式来实现。
5.交叉运算为了增加种群的变异性,我们可以进行交叉操作(crossover)。
交叉操作是通过随机选择两个父种群,交换部分基因序列来产生新的后代。
在多辆车最短路径问题中,我们可以通过部分匹配交叉(PMX)来实现,也可以采用顺序交叉(OX)等方式。
6.变异运算为了保持种群的多样性,我们可以对某些染色体进行变异操作(mutation)。
基于遗传算法的最短路径问题求解实现

3 . 4 ,变异操作 变异操作就是针对特定的一个染色体,对 其中某个基因位进行变异。在求解最短路问题 时,不光要保证变异成功,而且要保证变异后的 染色体为可行解。具体变异操作实现的相关伪 代码如下。
4,结论
4.1,双锥结构中总体一次薄膜应力不 再是破坏的主要因素,设计时取大锥大端 计算所得的名义厚度为统一壁厚即可。 4.2,这种结构用于中、低压压力容器 时,连接处可不另设加强结构,其壁厚足以 起到加强的作用。 4 . 3 ,这种结构用于高压压力容器时, 连接处应按上述方法进行应力校核,需加 强时应采用整体加强,即增加壁厚;若此方 法行不通,则可采用其它加强结构。 4.4,对于情况一,即小锥体的顶角小 于大锥体的顶角时,在结构允许的情况下 连接缝应尽量靠下,也就是说小锥体越小, 其受力情况越好,结构越安全; 对于情况二,即小锥体的顶角大于大 锥体的顶角时,在结构允许的情况下连接 缝应尽量靠上,也就是说小锥体越大,其受 力情况越好,结构越安全。 如在设计、制造过程中遇到这样的双 锥结构,本文的分析和总结可作为参考,当 然,对于具体问题还要具体分析才能使结 构更合理、更可靠。 参考文献 1 余国琮 化工容器及设备 天津 化学工 业出版社
4,结束语
通过用遗传算法解题,可知遗传算法明显 的优点: 1 ) 算法是使用参数的编码集参数的选 ( 择十分方便; (2)遗传算法是在点群中寻优; (3) 它仅使用问题本身所具有的目标数据进行工 作,而不需其它任何先决条件或辅助信息; 4 ) ( 它使用的是随机规则。本文是遗传算法一个应 用。在用该算法解题时,增加了变异率和交叉率 的自适应性,因而克服了简单遗传算法存在的 收敛速度慢的缺点,改善了算法的收敛性。目 前,对 G A 的理论研究还在深入,应用领域也 在不断地开拓,相信用遗传算法解决的问题将 越来越多。
基于遗传算法的路径规划优化策略

基于遗传算法的路径规划优化策略在现实世界中,路径规划是一个非常重要的问题。
无论是交通运输、物流还是机器人导航,都需要找到最优的路径。
而遗传算法作为一种优化算法,被广泛应用于解决路径规划问题。
本文将介绍基于遗传算法的路径规划优化策略,并通过实例分析说明其效果。
1. 引言路径规划是指在给定地图和起始点与目标点的情况下,找到最佳路径的过程。
最佳路径可以是最短距离、最短时间、最少消耗等,具体取决于实际需求。
传统的路径规划算法,如Dijkstra算法和A*算法,虽然能够找到较优的路径,但是对于复杂的场景或多目标优化问题来说,其求解效果有限。
而基于遗传算法的路径规划优化策略能够通过模拟生物进化的方式,不断优化路径以适应复杂环境和多目标需求。
2. 遗传算法概述遗传算法是一种基于生物进化思想的启发式优化算法。
它模拟了生物进化中的遗传、变异和适应度选择等过程,通过群体的不断演化来搜索问题的解空间。
遗传算法的基本流程包括初始化种群、选择、交叉、变异和适应度评估等步骤。
3. 基于遗传算法的路径规划优化策略在基于遗传算法的路径规划优化中,首先需要将路径规划问题转化为遗传算法的解空间。
一种常见的方法是将地图网格化,每个网格作为遗传算法的一个基因,通过基因组合来表示路径。
接下来,需要定义适应度函数,用于评估每个个体(路径)的好坏程度。
适应度函数可以根据实际需求来设计,如路径长度、时间或消耗等。
然后,通过遗传算法的选择、交叉和变异操作对种群进行迭代,直到满足终止条件。
4. 实例分析以机器人导航为例,假设我们需要将机器人从起始点A导航到目标点B。
我们可以将地图网格化,并将每个网格看作遗传算法的一个基因。
接下来,我们定义适应度函数为路径的长度。
然后,通过选择、交叉和变异操作对种群进行迭代,直到找到最优路径。
通过这样的基于遗传算法的路径规划优化策略,我们可以在复杂环境中找到最短路径,从而实现机器人的导航。
5. 结论基于遗传算法的路径规划优化策略能够有效解决复杂场景和多目标优化问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
置 和 方 向就构 成 了种 群 。而初 始种 群 则是在 算法 开 始运 作之 前 ,通 过随 机数 产生 的 一些 运行 方 向和位 置 。该种 群 需要 包 含足够 多 的随 机因子 ( 即有 许 多不 同 的运行 方 向和位 置 ) ,因此 必须 让它 足够 大 并且 能够 适应 遗传 算法 的 应用 要求 。将2 . 0 中所 设计 的编 码组i n 随机 的产 生0 个 ,并进 行 逐 一记 录 ( 即有 0 个 个体 )。本 文 产 生2 0 0 个i n 编 码 作为 初始 种群 。这 些 个体 的数 值是 由 随机 数构成 的 ,数 量也 足 够 多 。因此 ,可 以对 它们 进 行遗传 算法 操作 。 2 . 3 遗传 算法 的参 数设 定 初始 种群 中的每个个 体均都有 自己的特 征,而每 个特征 的定义都 是未知 的。通过一定 的约束 条件将它们 的特征数据化 ,并通过数据 比对 来进 行保 留或舍 弃,而保 留的个体 又会经历 各种不 同的变化 ( 选择: 保持不变 、变 异:发 生定位变化 、交叉 :发生互相改变等 ),这就是遗 传算 法的基 本思想 。而在此 之上 ,将 约束条件 也进行 一定规律 的数据 化 ,使它们 能够通过 函数 的改变来约束 、引导算法达到预期 的要求 : 将 每一 步 的终 点数据 应 用在 两个 函数 中进行 比对 。 ① 与最 终 目标点 的距 离 函数d 当前这 一步 要运 行到 的位 置 点 , y ) 到 终 点 , ) 的距 离d 为:
( i n f o r ma t i o n S c i e n c e a n d T e c h n o l o g y A c a d e my , N a n j i n g U n i v e r s i t y J i n l i n g C o l l e g e , N a n j i n g 2 l 0 0 8 9 , C h i n a )
E L E C T R oNI C S W 0R L D・ 苁 j 2
基 于遗传 算法 的最短路径规 划
南京大学金陵学院信 息科学与工程学院 林煦涵 刘耀轩 孙海洋
【 摘要 】传统遗传算法在路径规划中对路径长短、终点选择 以及路径安全度等参数进行 多目标选择算法时,很难找到兼顾 多个问题的合适路 径 。 本 文提 出 了一种 改进 遗传 算 法的 思路 ,在 遗传 算 法的选择 、 交叉 、变异 的基 础上 ,增 加 了定代 和 引导收 敛 的方 式 ,并 加入 了适 应度 函数 的选取 和判 定 方法 。将 多 个 问题 的 解决 集成 到 一个 目标 函数 内 ,解 决 了高 效性 和安 全性 无 法兼顾 的 问题 。 最后利 用Ma t l a b 进行 仿真 ,证 明 了
该 改进 算 法 的可行 性 及正 确性 。
【 关键词 o r t es t pa t h pl a nni ng bas e d o n i m pr o ve d ge ne t i c al gor i t hm Li n XuHa n, Li u Ya o X ua n,Su n Ha i ya n g
引言
机 器 人路 径规 划 问题 是 人工 智能 学 术里 必不 可少 的一个 研 究方 向。通 常 我们 关 注两 个方 面 :机 器人 如 何获 取最 短 的运 行路 径 ( 高 效 性 ) ,机 器 人 如 何避 开 已知 或 未 知 的障 碍 物 ( 安 全性 )…。因 此 ,如 何设 计 既兼 顾 高效 性 又兼 顾安 全性 的 路径 规划 算法 就 成 了研 究 的难 点和 重 点 。
1 思路 建模以及参数设置
1 。 1 建模 将 路径 的起 点与 终点 规划 成 一个 直角 坐 标系 。其 中,起 点为 原 点 ( 0 , 0 ) ,并 以起 点和 终 点 作 为矩 形 的 两 个 顶点 ,画 出 一个 矩 形 框 作 为我 们 的路 径 地 图 。在 矩形 内设置 若 干个 大 小 、位 置 随机 的 圆 形作 为障碍 物 。如 图l 所示 。
