第1章 非平衡态热力学3
合集下载
热力学统计物理第一章热力学的基本规律
p p1
p1
p2
§1.5 热力学第一定律
能量守恒定律：自然界一切物质都具有能量，能量有各种不 同的形式，可以从一种形式转化为另一种形式，从一个物体 传递到另一个物体，在传递与转化中能量的数量不变。
另一种表述：第一类永动机是不可能造成的。
热力学U系 BUA 统 W： Q W：以外界对系统所功作为的正 Q：以吸热为正
WW 'QRln V V 1 2(T1T2)
热机效率定义： W Q1
卡 诺 热 W T 1 机 T 21 ： T 21
Q 1 T 1
T 1
§1.10 热力学第二定律 克劳修斯（克氏）表述： 不可能把热量从低温物体传到高温物体而不引起其他变化 卡尔文（开氏）表述： 不可能从单一热源吸热使之完全变成有用的功而不引起 其他变化
AT B T
A BdTQ A BdTQ r SBSA
SB SA
BdQ AT
dS dQ T
第二定律的数学表述
绝热过 :d程 Q0
SBSA0 ——熵增加原理的数学表述
熵增加原理：经绝热过程后，系统的熵永不减少，经可逆 绝热过程后熵不变，经不可逆绝热过程后熵增加，在绝热 条件下熵减少的过程是不可能实现的。
第一章 热力学的基本规律 §1.1 热力学系统的平衡状态及其描述
1.系统
孤立系 （极限概念） 闭系 开系
热力学系统的状态
平衡态 非平衡态
热力学平衡态：
（1）定义： 一个孤立系统，不论其初态如何复杂，经过 足够长的时间后，将会到达这样的状态，系 统的各种宏观性质在长时间内不发生任何变 化，这样的状态称为热力学平衡态。
n称 为 多 方 指 数： 。理 试想 证气 明体 多的 方热 过容 程
热学第1章_导论
粒子流有两种，一种是宏观上能察觉到成群粒子定向移动的粒子流。
3.化学平衡（chemical equilibrium）条件：在无外场作用下 系统各部分的化学组成也应是处处相同的。
例：扩散现象（diffusion） 第二种粒子流，它不存在由于成群粒 子定向运动所导致的粒子宏观迁移. 氧气 氮气 氧氮混合气
普遍性。
2.热力学是具有最大普遍性的一门科学---不提出任何一个特 殊模型，但又可应用于任何的宏观的物质系统.
热力学的局限性：
（1） 它只适用于粒子数很多的宏观系统；
（2）它主要研究物质在平衡态下的性质. 它不能解答系统如何 从非平衡态进入平衡态的过程； （3） 它把物质看为连续体，不考虑物质的微观结构。
孤立系统 系统与外界之间，既无物质交换，又无能量交换。
二、热力学与力学的区别
热物理学研究方法不同于其它学科（例如力学）的宏观 描述方法。 热力学与力学的区别： 1. 热力学的注意力指向系统内部。
热力学的参量：与系统内部状态有关的宏观物理量 （诸如压强、体积、温度等）。 2. 热物理学中一般不考虑系统作为一个整体的宏观的机械运动. 若系统在作整体运动，则常把坐标系建立在运动的物体上。 例：运动卡车上的氧气瓶，其坐标系取在氧气瓶内
例: 1mol物质中就有6.02×1023 个分子。因而有6×6×1023 个方 程。 显然，人类不可能造出一部能计算1023个粒子的运动
方程的计算机。
热物理学研究对象的这一特点决定了它有宏观的与微观 的两种不同的描述方法。
宏观理论 微观理论
热力学
统计物理学
§1.1.2
宏观描述方法与微观描述方法
例：一容器储有氧气0. 1kg，压强为10atm，温度为47℃。因 容器漏气，过一段时间后，压强减到原来的5/8，温度降 到27℃，若把氧气近似看做理想气体，
3.化学平衡（chemical equilibrium）条件：在无外场作用下 系统各部分的化学组成也应是处处相同的。
例：扩散现象（diffusion） 第二种粒子流，它不存在由于成群粒 子定向运动所导致的粒子宏观迁移. 氧气 氮气 氧氮混合气
普遍性。
2.热力学是具有最大普遍性的一门科学---不提出任何一个特 殊模型，但又可应用于任何的宏观的物质系统.
热力学的局限性：
（1） 它只适用于粒子数很多的宏观系统；
（2）它主要研究物质在平衡态下的性质. 它不能解答系统如何 从非平衡态进入平衡态的过程； （3） 它把物质看为连续体，不考虑物质的微观结构。
孤立系统 系统与外界之间，既无物质交换，又无能量交换。
二、热力学与力学的区别
热物理学研究方法不同于其它学科（例如力学）的宏观 描述方法。 热力学与力学的区别： 1. 热力学的注意力指向系统内部。
热力学的参量：与系统内部状态有关的宏观物理量 （诸如压强、体积、温度等）。 2. 热物理学中一般不考虑系统作为一个整体的宏观的机械运动. 若系统在作整体运动，则常把坐标系建立在运动的物体上。 例：运动卡车上的氧气瓶，其坐标系取在氧气瓶内
例: 1mol物质中就有6.02×1023 个分子。因而有6×6×1023 个方 程。 显然，人类不可能造出一部能计算1023个粒子的运动
方程的计算机。
热物理学研究对象的这一特点决定了它有宏观的与微观 的两种不同的描述方法。
宏观理论 微观理论
热力学
统计物理学
§1.1.2
宏观描述方法与微观描述方法
例：一容器储有氧气0. 1kg，压强为10atm，温度为47℃。因 容器漏气，过一段时间后，压强减到原来的5/8，温度降 到27℃，若把氧气近似看做理想气体，
热力学三定律
• S(NO，残余熵)=5.76 J/K.mol
• 由热力学第三定律所求得的物质的熵 称为:
规定熵
• 以前曾将规定熵称为绝对熵, 考虑到 人们对自然的认识是有限的, 随着科 学的发展, 人类可能对熵有更深刻地 认识, 故改称为规定熵.
• 规定熵可用热化学方法测定得到, 也 可由统计热力学理论直接计算得到.
• 2. 热胀系数趋于零:
• ∵ (V/T)p=－(S/p)T
• ∴ limT→0K(V/T)p
•
=－limT→0K(S/p)T
•
=0
• 故热胀系数: 1/V(V/T)p • 在0K时也趋于零.
• 3. 等压热容与等容热容将相同: • Cp－CV=T(V/T)p(p/T)V • ∵ (V/T)p→0 (T→0K) • ∴ Cp－CV →0 (T→0K)
• 一. 标准状态:
• U,H,S,F,G等, 我们都无法获得绝对值. • 为了获得可比且有价值的结果, 人们选择了物
质的某些状态作为参考态, 并规定了物质在这 些参考态所具有的热力学函数值, 以此便可求 出其它任意状态的热力学函数值. • 所有这些函数值仅仅只具有相对性, 它们的绝 对值目前尚无法求得.
• 化学反应的标准吉布斯自由能可以由物质的 规定吉布斯自由能求得:
rGm0(T) =(∑iGT,,i0)产物－(∑iGT,i0)反应物 (7)
• GT,i：i物质在T温度下的摩尔规定吉布斯 自由能.
谢谢
纯物质的标准状态规定如下: 气体: 理想气体 T p=100,000 Pa 液体: 纯液体 T p=100,000 Pa 固体: 纯固体 T p=100,000 Pa
• 二. 热力学函数规定值:
• 1.规定焓:
• 由热力学第三定律所求得的物质的熵 称为:
规定熵
• 以前曾将规定熵称为绝对熵, 考虑到 人们对自然的认识是有限的, 随着科 学的发展, 人类可能对熵有更深刻地 认识, 故改称为规定熵.
• 规定熵可用热化学方法测定得到, 也 可由统计热力学理论直接计算得到.
• 2. 热胀系数趋于零:
• ∵ (V/T)p=－(S/p)T
• ∴ limT→0K(V/T)p
•
=－limT→0K(S/p)T
•
=0
• 故热胀系数: 1/V(V/T)p • 在0K时也趋于零.
• 3. 等压热容与等容热容将相同: • Cp－CV=T(V/T)p(p/T)V • ∵ (V/T)p→0 (T→0K) • ∴ Cp－CV →0 (T→0K)
• 一. 标准状态:
• U,H,S,F,G等, 我们都无法获得绝对值. • 为了获得可比且有价值的结果, 人们选择了物
质的某些状态作为参考态, 并规定了物质在这 些参考态所具有的热力学函数值, 以此便可求 出其它任意状态的热力学函数值. • 所有这些函数值仅仅只具有相对性, 它们的绝 对值目前尚无法求得.
• 化学反应的标准吉布斯自由能可以由物质的 规定吉布斯自由能求得:
rGm0(T) =(∑iGT,,i0)产物－(∑iGT,i0)反应物 (7)
• GT,i：i物质在T温度下的摩尔规定吉布斯 自由能.
谢谢
纯物质的标准状态规定如下: 气体: 理想气体 T p=100,000 Pa 液体: 纯液体 T p=100,000 Pa 固体: 纯固体 T p=100,000 Pa
• 二. 热力学函数规定值:
• 1.规定焓:
第三章热力学第一定律内能
如果是等温膨胀,则
A M RT ln V2 1 8.31 300 ln 10 1.44 103(J )
V1 4
25
P
P1
P2
a
T1
b
T2
V1
V2
V
26
例2. 两个绝热的体积分别为V1和V2的容器, 用一个 带有活塞的管子连起来，打开活塞前，第一个容器
盛有氮气，温度为T1，第二个容器盛有氢气，温度
(Q )V
M
CV dT
从热力学第一定律
用于热力学第一定律则有:
M
dU CV dT
已知理想气体内能
可得
U M i RT
2
从分子运动论
定容摩尔热容 与自由度有关
气体的定压摩尔热容
定压过程:P=常量, d P =0 过程方程: V/T=常量
Q P=恒量
根据
PV M RT
P
Ⅰ
II
P
得 dA PdV M RdT
氧 28.9
21.0
7.9 1.40
三原子 水蒸气 36.2
27.8
8.4 1.31
乙 醇 87.5
79.2
8.2
1.11
例题 一气缸中有氮气,质量为1.25kg,在标准大气
压下缓慢加热,使温度升高1K.试求气体膨胀时所做
的功A、气体内能的增量U及所吸收的热量Q.(活
塞的质量及它与汽缸壁的摩擦均可忽略.)
第一类永动机
§2 热力学第一定律对理想气体等值过程的应用
2.1 理想气体的热容量 气体的定容摩尔热容
定容过程: V=常量, d V =0 过程方程:
Q
P
V=恒量
P2
热学 第一章 导论
我国殷商时期
五行学说：金、木、水、 火、土是构成世界万物的五种基本元素， 称为五行。中国古代提出的元气说，就认 为热（火） 是物质元气聚散变化的表现。
3
从钻木取火到商周的青铜器
伽利略温度计 16世纪 (明)
4
清 初
瓦特早期蒸汽机
5
6
1807年
嘉庆12年
7
1823年
道光3年
8
1892年
33
三、热力学温标 1. 热力学温标是建立在第二定律基 础上，不 依赖于任何物质的特性 的温标。 2. 热力学温度国际单位为“开尔 文”，简称开.记为K 3. 可证明在理想气体温标有效范围 内，热力学温标与理想气体温标 完全一致。 不依赖于测温物质和测温属性的温标
34
开尔文
四、摄氏温标、华氏温标与兰氏温标
V＝V0 1 p t
m，p一定
m,V 一定
22
p p0 1 V t
二、理想气体物态方程
p1V1 p2V2 常量 T1 T2
令1mol气体的常量为R
pVm RT R＝8.31 Jmol 1K 1
若气体的物质的量为
普适气体 常量
与热力学温度 的关系
T=T
通用 情况 国际 通用
热力学温度 K
摄氏温标 华氏温标
C F
t
tF - 459.67 0
32.00 32.02
t T 273 .15 100.00 0 C K t 9 T 459 .67 英美 212.00 0 F 5 K 等国
兰氏温标 R TR
491.67 491.69 67初步知识 • 液体、固体、相变等物性学
热力学 第一章
（3）状态参量：描述热力学系统平 衡状态的宏观性质的物理量。
描述系统状态的宏观参量一般可以 直接测量。
广延量和强度量
3、均匀系与非均匀系
（1）均匀系：一个系统各部分的性质完全
一致，称为一个均匀系。（也称为一个相 —单相系） （2）非均匀系：复相系
§1.2 热平衡定律和温度
一、热平衡定律（热力学第零定律） 实验
2 3 3 6 1
如果保持温度不变，将1mol的水从1 1000 pn ，求：外界所做的功。
pn
加压到
§1.5 热力学第一定律
一、热量：系统与外界仅由于温度差，通过边界 所传递的能量。（通过分子间的碰撞来实现）
Q 过程量 热量是能量传递的另一种方式 Q 0 系统从外界吸收热量
Q 0 系统向外界放出热量
3 6 2 3
1
§1.6 热容量和焓
一、热容量
1、引入：桶的装水量（水容量）
M 水容： C h
Q 电容： C U
2、热容量：一个系统在某一过程中温度升 高1K所吸收的热量。
Q C lim T T dQ C dT
单位：焦耳/开尔文 J / K
3、系统的质量对热容量的影响：
an2 ( p 2 )(V nb) nRT V
1mol : a ( p 2 )( v b) RT v
3、简单固体和液体：
V (T , p) V0 (T0 ,0)1 (T T0 ) KT p
例1、一个简单可压缩系统，已知
nR 1 a ; KT pV p V
作业：1、1mol理想气体，在27℃的恒温下 发生膨胀，其压强由 20Pn 准静态地降到 1Pn ，求：气体所做的功和所吸取的热量。 2、在27℃，压强在0至 1000pn 之间，测得 水的体积为V (18.066 0.71510 p 0.04610 p )cm mol 如果保持温度不变，将1mol的水从1 pn 加压至 1000pn ，求：外界所做的功。
热力学第三定律
热力学第三定律
The Third Law of thermodynamics
热力学第三定律 The Third Law of thermodynamics
热力学第三定律是独立于热力学第一、二定律 之外的一个热力学定律，是研究低温现象而得 到的。它的主要内容是奈斯特热定理，或绝对 零度不能达到原理。
热力学第二定律只定义了过程的熵变,而没有定义熵 本身. 熵的确定，有赖于热力学第三定律的建立.
1902年美国科学家雷查德(T.W.Richard)在研究低温 电池反应时发现：电池反应的G和H随着温度的降 低而逐渐趋于相等,而且两者对温度的斜率随温度同 趋于一个定值:
零
由热力学函数的定义式, G(吉布斯自由能)和H(焓)当温 度趋于绝对零度时,两者必会趋于相等：
当系统发生变化时，G也随之变化。其改变值△G，称为体系的 吉布斯自由能变，只取决于变化的始态与终态，而与变化的途 径无关：△G=G终一G始 按照吉布斯自由能的定义，可以推出 当体系从状态1变化到状态2时，体系的吉布斯自由能变为： △G=G2一Gl=△H一△(TS) 对于等温条件下的反应而言，有 T2=T1=T 则 △G=△H一T △S 上式称为吉布斯一赫姆霍兹公 式（亦称吉布斯等温方程）。由此可以看出，△G包含了△H和 △S的因素，若用△G作为自发反应方向的判据时，实质包含了 △H和△S两方面的影响，即同时考虑到推动化学反应的两个主 要因素。因而用△G作判据更为全面可靠。而且只要是在等温、 等压条件下发生的反应，都可用△G作为反应方向性的判据， 而大部分化学反应都可归人到这一范畴中，因而用△G作为判 别化学反应方向性的判据是很方便可行的。
lim
T 0
C
p
0
（3）物质的Cp和CV随热力学温度同趋于零
The Third Law of thermodynamics
热力学第三定律 The Third Law of thermodynamics
热力学第三定律是独立于热力学第一、二定律 之外的一个热力学定律，是研究低温现象而得 到的。它的主要内容是奈斯特热定理，或绝对 零度不能达到原理。
热力学第二定律只定义了过程的熵变,而没有定义熵 本身. 熵的确定，有赖于热力学第三定律的建立.
1902年美国科学家雷查德(T.W.Richard)在研究低温 电池反应时发现：电池反应的G和H随着温度的降 低而逐渐趋于相等,而且两者对温度的斜率随温度同 趋于一个定值:
零
由热力学函数的定义式, G(吉布斯自由能)和H(焓)当温 度趋于绝对零度时,两者必会趋于相等：
当系统发生变化时，G也随之变化。其改变值△G，称为体系的 吉布斯自由能变，只取决于变化的始态与终态，而与变化的途 径无关：△G=G终一G始 按照吉布斯自由能的定义，可以推出 当体系从状态1变化到状态2时，体系的吉布斯自由能变为： △G=G2一Gl=△H一△(TS) 对于等温条件下的反应而言，有 T2=T1=T 则 △G=△H一T △S 上式称为吉布斯一赫姆霍兹公 式（亦称吉布斯等温方程）。由此可以看出，△G包含了△H和 △S的因素，若用△G作为自发反应方向的判据时，实质包含了 △H和△S两方面的影响，即同时考虑到推动化学反应的两个主 要因素。因而用△G作判据更为全面可靠。而且只要是在等温、 等压条件下发生的反应，都可用△G作为反应方向性的判据， 而大部分化学反应都可归人到这一范畴中，因而用△G作为判 别化学反应方向性的判据是很方便可行的。
lim
T 0
C
p
0
（3）物质的Cp和CV随热力学温度同趋于零
线性非平衡态热力学
线性非平衡态热力学应用
在物质转移和化学反应存在耦合时, 计算结果表明, 耦合系数 L12 =/=0 因此有可能出现下列情况： Je Xe <0 只要
仍满足 说明定态时, 组分可以逆着浓度梯度减小的方向流动，这种现 象称活性扩散。生物体中, 某些元素的浓度远远高于在外界环 境中的浓度， 但生物体仍能继续不断地从外界环境中吸收这 些元素，这种现象在生物过程中起着重要作用。
线性非平衡态热力学特征
图1：线性区总熵产生随时间的变化
时 图1表明，在非平衡态的线性区，系统随着时间的发展总是 朝着总熵产生速率减少的方向进行，直至达到定态。在定态熵 产生速率不再随时间变化。
线性非平衡态热力学特征
由最小熵产生原理得出结论： 线性区非平衡定态是稳定的如图2 X 代表某状态变量，设体系已处 于定态1，由于涨落(扰动) 体系可 偏离定态达到某个与时间有关的 非定态2。 根据最小熵产生原理，体系的 熵产生会随时间减小，最后返回到 图2：最小嫡产生原理及稳定性示意图 与最小熵产生相对应的定态1。这种 现象与力学中的“ 惯性” 原理相似，因而又称“ 惯性”原理或 “ 回归” 原理。
线性非平衡态热力学应用
非平衡态热力学目前主要应用在化学化工、电磁、冶金、 流体力学、固体力学以及生物工程等领域，甚至在社会科学领 域和宇宙领域都有积极地应用成果。 （1）冶金领域 冶金工程领域广泛存在着非平衡态过程问题。例如：物质在 两相间的迁移过程，铁矿球团的焙烧过程，炼钢过程中的脱硫 反应过程【2】等，这些过程都是非平衡态的，需要应用非平衡 态热力学理论和方法来研究。 如东北大学翟玉春【3】等将线性非平衡态过程热力学扩展到 远离平衡的体系，建立了有界面存在的远离平衡的化学反应体 系的非平衡态热力学方法并将其应用于渣-金间的氧化锰反应， 得到氧化锰还原的非平衡态热力学方程与实验数据能很好地吻 合。
《传热学》第1章-绪论
™概念会分析——有思路，给出公式会计算——有 技能；
三、传热学应用实例
● 自然界与生产过程到处存在温差—传热很普遍
日常生活中的例子：
● 人体为恒温体。若房间里气体的温度在夏天和 冬天都保持 20度，那么在冬天与夏天、人在房间里所穿的衣服能否一样？ 为什么？
● 夏天人在同样温度（如：25度）的空气和水中的感觉不一 样。为什么？
v 1904年他在哥廷根大学（Göttingen University）担任流体力学研究所的所 长，同年他发表了其具有历史意义的关于 边界层的著名论文，奠定了现代流体力学 和空气动力学以及对流换热分析的基础。 在风洞实验技术；机翼理论；湍流理论均 有杰出贡献；
v T. von 卡门是他的学生；
传热学名人-4
v 发展对流换热理论的杰出先 驱：对流换热的无量纲准则， 用实验方法求解对流换热问 题；
v 凝结换热理论解 ； v 层流入口段换热机理研究 ；
传热学名人-5
v 施密特（1892－1975）,出生 于1892年2月11日，是德国的 科学家，工程热物理学，尤其 是传热传质学研究领域的先 驱；
v 他是第一个测量自然对流边界 层的速度场和温度场以及膜态 凝结的当量传热系数的人。
™ 偏微分方程（导热）和偏微分方程组（对流） ™ 数值模拟----差分方程
v 实用性也强；
™ 由实验得出的对流换热的经验公式
对学习方法的建议
v 以方法论学习为主
™课堂上要注意学习建立方程的方法; ™不要去记复杂的公式; ™要记住最基本的公式;
v 对学习效果的要求程度
™合上书忘了——不要紧，但是翻开书就能看懂,能 想起来——基本可以;
q1
=
λ1
tw1
− tw2 δ
三、传热学应用实例
● 自然界与生产过程到处存在温差—传热很普遍
日常生活中的例子：
● 人体为恒温体。若房间里气体的温度在夏天和 冬天都保持 20度，那么在冬天与夏天、人在房间里所穿的衣服能否一样？ 为什么？
● 夏天人在同样温度（如：25度）的空气和水中的感觉不一 样。为什么？
v 1904年他在哥廷根大学（Göttingen University）担任流体力学研究所的所 长，同年他发表了其具有历史意义的关于 边界层的著名论文，奠定了现代流体力学 和空气动力学以及对流换热分析的基础。 在风洞实验技术；机翼理论；湍流理论均 有杰出贡献；
v T. von 卡门是他的学生；
传热学名人-4
v 发展对流换热理论的杰出先 驱：对流换热的无量纲准则， 用实验方法求解对流换热问 题；
v 凝结换热理论解 ； v 层流入口段换热机理研究 ；
传热学名人-5
v 施密特（1892－1975）,出生 于1892年2月11日，是德国的 科学家，工程热物理学，尤其 是传热传质学研究领域的先 驱；
v 他是第一个测量自然对流边界 层的速度场和温度场以及膜态 凝结的当量传热系数的人。
™ 偏微分方程（导热）和偏微分方程组（对流） ™ 数值模拟----差分方程
v 实用性也强；
™ 由实验得出的对流换热的经验公式
对学习方法的建议
v 以方法论学习为主
™课堂上要注意学习建立方程的方法; ™不要去记复杂的公式; ™要记住最基本的公式;
v 对学习效果的要求程度
™合上书忘了——不要紧，但是翻开书就能看懂,能 想起来——基本可以;
q1
=
λ1
tw1
− tw2 δ
《热力学第三定律》
整理ppt
热力学第二定律只定义了过程的熵变,而没有定义熵本 身. 熵的确定，有赖于热力学第三定律的建立.
1902年美国科学家雷查德(T.W.Richard)在研究低温 电池反应时发现：电池反应的G和H随着温度的降 低而逐渐趋于相等,而且两者对温度的斜率随温度同 趋于一个定值:
零
整理ppt
由热力学函数的定义式, G(吉布斯自由能)和H(焓)当温 度趋于绝对零度时,两者必会趋于相等：
G= H－TS
limG= H－limTS = H (T→0K) 虽然两者的数值趋于相同，但趋于相同的方式可以有
所不同. 雷查德的实验证明对于所有的低温电池反应, G均只会
以一种方式趋近于H.
整理ppt
吉布斯函数介绍：
1875 年 ， 美 国 耶 鲁 大 学 数 学 物 理 学 教 授 吉 布 斯 （ Josiah Willard Gibbs）发表了 “论多相物质之平衡”的论文。他在 熵函数的基础上，引出了平衡的判据；提出热力学势的重要概 念，用以处理多组分的多相平衡问题；导出相律，得到一般条 件下多相平衡的规律。吉布斯的工作，奠定了热力学的重要基 础。
任何凝聚系在等温过程中的G和H随温度的降低 是以渐近的方式趋于相等，并在0K时两者不但相互会 合，而且共切于同一水平线，即
lim G lim H (7.1)
T 0
T 0
lT i m 0 ( T G )p lT i m 0 ( T H )p 0( 7 .2 )
整理ppt
( T G )p S 和 ( T H )p C p
值。原因是，全部粒子都处于能量可能有的最低的状
态，也就是全部粒子都处于基态。
实上一切实际气体在温度接近-273.15℃时，将表现出
热力学第二定律只定义了过程的熵变,而没有定义熵本 身. 熵的确定，有赖于热力学第三定律的建立.
1902年美国科学家雷查德(T.W.Richard)在研究低温 电池反应时发现：电池反应的G和H随着温度的降 低而逐渐趋于相等,而且两者对温度的斜率随温度同 趋于一个定值:
零
整理ppt
由热力学函数的定义式, G(吉布斯自由能)和H(焓)当温 度趋于绝对零度时,两者必会趋于相等：
G= H－TS
limG= H－limTS = H (T→0K) 虽然两者的数值趋于相同，但趋于相同的方式可以有
所不同. 雷查德的实验证明对于所有的低温电池反应, G均只会
以一种方式趋近于H.
整理ppt
吉布斯函数介绍：
1875 年 ， 美 国 耶 鲁 大 学 数 学 物 理 学 教 授 吉 布 斯 （ Josiah Willard Gibbs）发表了 “论多相物质之平衡”的论文。他在 熵函数的基础上，引出了平衡的判据；提出热力学势的重要概 念，用以处理多组分的多相平衡问题；导出相律，得到一般条 件下多相平衡的规律。吉布斯的工作，奠定了热力学的重要基 础。
任何凝聚系在等温过程中的G和H随温度的降低 是以渐近的方式趋于相等，并在0K时两者不但相互会 合，而且共切于同一水平线，即
lim G lim H (7.1)
T 0
T 0
lT i m 0 ( T G )p lT i m 0 ( T H )p 0( 7 .2 )
整理ppt
( T G )p S 和 ( T H )p C p
值。原因是，全部粒子都处于能量可能有的最低的状
态，也就是全部粒子都处于基态。
实上一切实际气体在温度接近-273.15℃时，将表现出
热力学第一定律
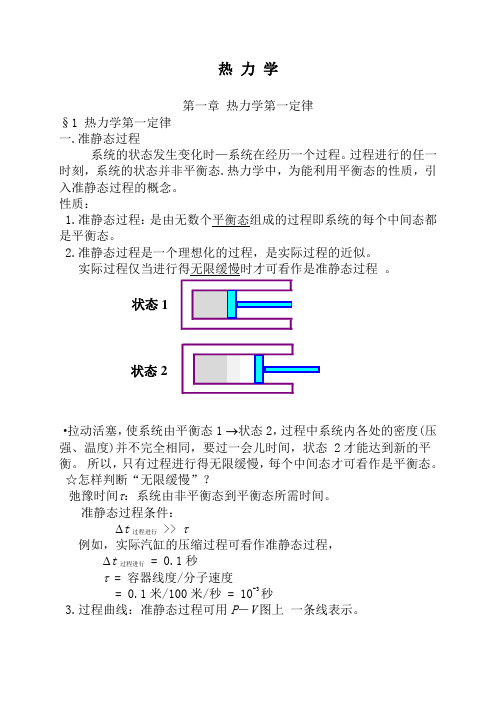
热 力 学第一章 热力学第一定律§1 热力学第一定律 一.准静态过程系统的状态发生变化时—系统在经历一个过程。
过程进行的任一时刻，系统的状态并非平衡态.热力学中，为能利用平衡态的性质，引入准静态过程的概念。
性质：1.准静态过程：是由无数个平衡态组成的过程即系统的每个中间态都是平衡态。
2.准静态过程是一个理想化的过程，是实际过程的近似。
实际过程仅当进行得无限缓慢时才可看作是准静态过程 。
·拉动活塞，使系统由平衡态1 →状态2，过程中系统内各处的密度(压强、温度)并不完全相同，要过一会儿时间，状态 2才能达到新的平衡。
所以，只有过程进行得无限缓慢，每个中间态才可看作是平衡态。
☆怎样判断“无限缓慢”？弛豫时间τ：系统由非平衡态到平衡态所需时间。
准静态过程条件： ∆t 过程进行 >> τ例如，实际汽缸的压缩过程可看作准静态过程， ∆t 过程进行 = 0.1秒τ = 容器线度/分子速度= 0.1米/100米/秒 = 10-3秒3.过程曲线：准静态过程可用P －V 图上 一条线表示。
状态1状态2二.功、内能、热量1.功 ·通过作功可以改变系统的状态。
·机械功(摩擦功、体积功)2.内能·内能包含系统内：(1)分子热运动的能量；(2)分子间势能和分子内的势能；(3)分子内部、原子内部运动的能量； (4)电场能、磁场能等。
·内能是状态的函数*对于一定质量的某种气体，内能一般是T 、V 或P 的函数； *对于理想气体，内能只是温度的函数 E = E (T )*对于刚性理想气体分子, i ：自由度； ν ：摩尔数 ·通过作功改变系统内能的实质是：分子的有规则运动能量和分子的无规则运动能量的转化和传递。
3.热量·传热也可改变系统的状态，其条件是系统和外界的温度不同。
·传热的微观本质：是分子的无规则运动能量从高温物体向低温物体传递。
无机化学——第1章习题解答③
第1章习题解答③一、是非题(1)由于反应N2O5(g)→2NO2(g)+12O2(g)在298K、1kPa时为吸热反应，所以该反应不能自发进行。
（）解：错(2)热力学温度为0K时，任何完整晶体纯物质的熵都是零。
（）解：对(3)在298K下，S(H2,g)=0J·mol-1·K。
（）解：错(4)在298K，标准状态下，稳定的纯态单质的标准熵不为零。
（）解：对(5)反应：3H2(g)+N2(g)→2NH3(g)的△r S值与反应32H2(g)+12N2(g)→NH3(g)的△r S值相同。
.（）解：错(6)已知反应P4(s)+6Cl2(g)→4PCl3(g)的标准摩尔反应熵变为△r S(1)，1 4P4(s)+32Cl2(g)→PCl3(g)的标准摩尔反应熵变为△r S(2)，则△r S(2)=14△r S(1)。
（）解：对(7)按热力学规定：在标准状态下，（参考温度为298K），H+(aq)的△f G，△f H，S(实际上是相对值）均为零。
.（）解：对(8)物质的量增加的反应不一定是熵增加的反应。
.（）解：对(9)某一系统中，反应能自发进行，其熵值一定是增加的。
.（）解：错(10)恒温恒压下，熵增大的反应都能自发进行。
.（）解：错(11)△r S为负值的反应均不能自发进行。
（）解：错S(NH3,g)。
（）(12)在298K时，反应3H2(g)+N2(g)→2NH3(g)的△r S=12解：错(13)在298K时，反应C(s)+O2(g)→CO2(g)的△r S=S(CO2,g)。
.（）解：错(14)298K时，C(石墨)+O2(g)→CO2(g)的△r S<S(CO2,g)。
.（）解：对(15)从物质的热力学性质表中，查出某些水合离子的S可以小于0J·mol-1·K-1。
.（）解：对(16)从物质的热力学性质表中查出的所有水合离子的S>0J·mol-1·K-1。
大学物理第三章热力学第一定律第四章热力学第二定律
A1 A绝热 Q1 0 A2 A绝热 Q2 0
放热 吸热
（B）对
38
补充作业（4692）如图所示，C是固定的绝热壁， D是可动活塞，C、D将容器分成A、B两部分。 开始时A、B两室中各装入同种类的理想气体， 它们的温度T、体积V、压强P均相同，并与大 气压强相平衡。现对A、B两部分气体缓慢地 加热，当对A和B给予相等的热量Q以后，A室 中气体的温度升高度数与B室中气体的温度升 高度数之比为7:5。求:
内能：态函数,系统每个状态都对应着一定内能的数值。 功、热量：只有在状态变化过程中才有意义，状态不
变，无功、热可言。
8
五、热力学第一定律
1. 数学表式
★ 积分形式 Q E A
★ 微分形式 dQ dE dA
9
2. 热力学第一定律的物理意义
（1）外界对系统所传递的热量 Q , 一部分用于 系统对外作功，一部分使系统内能增加。
（4）内能增量： dE 2i（R适dT用于任C何V d过T程!!）
E E2 E1 CV (T2 T1 )
等容过程
Q等容 E E2 E1 CV (T2 T1 )
A等容 0
CV
iR 2
14
2. 等压过程
（1）特征： P=恒量 ，dP=0， P
参量关系: V T 恒量 （2）热一律表式：
E EA EB
E A
3
2
RTA
3 2
RTA
5 EB 2 RTB
C是导热板，因此A、B两部分气体的温度
始终相同。即：TA TB T
T A 4R
5
5
EB 2 RT 8 A
36
例4（4313）一定量的理想气体，从P-V图 上初态a经历（1）或（2）过程到达末 态b，已知a、b两态处于同一条绝热线 上（图中虚线是绝热线），问两过程中 气体吸热还是放热？ （A）（1）过程吸热 （2）过程放热 （B）（1）过程放热 （2）过程吸热
第三章-非稳态导热
工程上认为= 4τc时导热
体已达到热平衡状态
如果导热体的热容量（ Vc ）小、换
cV 热条件好（hA大），那么单位时间所
hA
传递的热量大、导热体的温度变化快， 时间常数小。
时间常数反映了物体对周围环境温度变化响 应的快慢，时间常数小的响应快，时间常数 大的响应慢，其主要影响因素为物体的热容 量和物体表面的对流换热条件。
非稳态导热的不同时刻物体的温度分布
2.两个阶段
非正规状况阶段(初始状况阶段)
在=3时刻之前的阶段，物体内的温度
分布受初始温度分布的影响较大。
正规状况阶段
在 = 3时刻之后，初始温度分布的影
响已经消失，物体内的温度分布主要 受边界条件的影响.
3.热量变化
与稳态导热的另一区别：由于有温 度变化要积聚或消耗热量，同一时刻 流过不同界面的热流量是不同的。
( x, ) e a 2 [ A cos( x ) B sin( x )]
( x, ) e a 2 [ A cos( x) B sin( x)] （a）
常数A、B和β可由边界条件确定。
0, t0-t 0
(1)
x 0, x 0
(2)
x , - x h
(3)
BiV FoV
0
BiV 越小表明内部导热热阻越小或外部热阻越
大，从而内部温度就越均匀，集总参数法
的误差就越小。 对热电偶测温情况，一
般使BiV=0.001量级或最小。
BiV 0.1M
为判定系统是否为集总参数系 统 ，M为形状修正系数。
厚度为2的大平板 V A＝ M 1 直径为2r的长圆柱体 V A＝ r 2 M 0.5
当几何形状及边界条件都比较简单时可获得分 析解。
热力学中的热力学平衡与非平衡态问题
热力学中的热力学平衡与非平衡态问题热力学平衡与非平衡态问题是热力学中一个非常基础的问题，也是极其重要的问题之一。
热力学平衡态是指，物质在一个非常长的时间内，其宏观性质不发生变化，而非平衡态则是指物质的宏观性质随时间的变化而变化。
在自然界和工业生产中，我们常常遇到与平衡态和非平衡态相关的问题，如温度、压力、物质传递等。
本文将对热力学平衡与非平衡态进行详细讨论。
一、热力学平衡态热力学平衡态指的是一种状态，物体在这种状态下，其宏观性质不随时间的变化而改变。
在热力学中，热力学平衡态通常有四种：力学平衡态、热平衡态、化学平衡态和物理平衡态。
1. 力学平衡态力学平衡态指物体中各点受到的所有力都保持平衡，物体的宏观形状保持不变。
比如，把一个木块放在平滑的水平面上，它就处于力学平衡态。
2. 热平衡态热平衡态指物体处于一定温度下，物质内部的热量分布维持不变。
比如，一个恒温水槽中的水就处于热平衡态。
3. 化学平衡态化学平衡态指在某种反应体系中，反应物在一定时间内的摩尔分数维持不变。
比如，在一定条件下，氢气和氧气会发生反应，产生水。
当氢气的摩尔分数和氧气的摩尔分数维持一定比例时，反应体系就处于化学平衡态。
4. 物理平衡态物理平衡态通常是指物质处于状态方程维持不变的状态，比如一个容器中的理想气体在一定温度和压力下，通过状态方程PV=nRT 维持不变的状态就是物理平衡态。
二、热力学非平衡态热力学非平衡态指物体的宏观性质随时间的变化而变化。
热力学非平衡态通常描绘了物质的动态行为，是热力学里面相对较复杂的概念之一。
在非平衡态下，一个系统的各种性质如粘度、流动性等会随着时间的变化而发生改变，而这些变化都受到外部条件的影响。
热力学非平衡态的一个重要问题是系统如何从非平衡态转向平衡态。
在这个过程中，可能会出现许多不同的形态和状态，其中涌现了许多新奇和重要的物理现象和热力学问题。
这些问题涵盖了一些非常广泛的领域，如流变学，热传导，化学反应和生物物理学等。
第一章 热力学定律
§2.4 焓
2.4.2 △H与Qp Qp : 恒压，非体积功为零(dp=0, dW‘=0)的过程中， 系统与环境交换的热。 恒压过程: dp=0，p环=p；W' = 0时 W = -∫p环dV = -p环(V2-V1)= -(p2V2-p1V1) 据热力学第一定律： Qp = △U - W = (U2-U1) + (p2V2 - p1V1) = ( U2 + p2V2 ) - ( U1 + p1V1 ) = △ H
W>0 对系统作功 22
W<0 对环境作功
§2.3 准静态过程与可逆过程
2.3.1 准静态过程与可逆过程 （1） 准静态过程（guasi-static process）
在过程进行的每一瞬间，系统都接近于平衡状态，以致在任意选取 的短时间 dt 内，状态参量在整个系统的各部分都有确定的值，整个过 程可以看成是由一系列极接近平衡的状态所构成，这种过程称为准静态 过程。 准静态过程是一种理想过程，实际上是办不到的。 一个过程的发生必定引起状态的改变而状态改变一定破坏平衡。 但当一个过程进行得非常慢，速度趋于零时，这个过程就趋于准静态 过程。
（3）相平衡（phase equilibrium）多相共存时，各相的组成和数量 不随时间而改变 （4）化学平衡（chemical equilibrium ）反应系统中各物的数量不 再随时间而改变
8
§2.1 热力学基本概念
2.1.2 状态和状态函数 状态：系统的物理，化学性质的综合表现; 状态性质：系统处于某一状态时的性质，是系统本身 所属的宏观物理量。 如：T，p, ，V，m， U，H，S…
特殊形式，说明热力学能、热和功之间可以相互转化，但总的能量不 变。 也可以表述为：第一类永动机是不可能制成的 热力学第一定律是人类经验的总结，事实证明违背该定律的实 验都将以失败告终，这足以证明该定律的正确性。
工程热力学-1第一章 基本概念
例1－2 P23 可逆过程功的计算关键：找到p和v之间的关系
三、过程热量
系统与外界之间依靠温差传递的能量称为热量。 符号：Q ；单位：J 或kJ。
单位质量工质所传递的热量用q 表示，单位为 J/kg 或 kJ/kg。
热量正负的规定： 系统吸热：q > 0 系统放热：q < 0
热量和功量都是系统与外界在相互作用的过程 中所传递的能量，都是过程量而不是状态量
热量如何表达？
热量是否可以用类似于功的
？ 式子表示？
Entropy
引入“熵”
清华大学刘仙洲教授 命名为“熵”
在可逆过程中，系统与外界交换的热量与功量
的计算公式具有相的形式。
功量：
热量：
w pdv
qqTTds?
2
w 1 pdv
2
q 1 Tds
条件 准静态或可逆
可逆
s 称为比熵。比熵同比体积 v 一样是工质的状态 参数。
比熵的定义式：ds q
T
（可逆过程）
比熵的单位为J/ (kg·K) 或 kJ/ (kg·K)
对于质量为m的工质，
Q TdS
2
Q 1 TdS
S为质量为 m 的工质的熵，单位是 J/K。
示热图
2
w 1 pdv
2
q 1 Tds
在可逆过程中单位 质量工质与外界交换 的 热 量 可 以 用 T-s 图 （温熵图）上过程曲 线下的面积来表示。
消除一种 不平衡势差
达到某一 方面平衡
消除一种能量 传递方式
状态公理 对于组成一定的物质系统，该系统平衡态的
独立状态参数有 n +1
n－表示系统与外界进行准静功交换的数目
第一章热力学基础1-2
状态函数共同性质 (1)体系的状态一定，状态函数有确定 (1)体系的状态一定，状态函数有确定值。 体系的状态一定 函数有确 (2)状态函数的改变量只取决于体系的起始状态， (2)状态函数的改变量只取决于体系的起始状态，而与变 状态函数的改变量只取决于体系的起始状态 化过程无关。 代表体系的状态函数，体系由A 化过程无关。若Z代表体系的状态函数，体系由A态，改变 到B态。则△Z = Zb –Za Z (3)对于循环过程， (3)对于循环过程，状态函数的改变量为零 对于循环过程 (4)状态函数之间互为函数关系 (4)状态函数之间互为函数关系 状态函数的特性可描述为：异途同归， 状态函数的特性可描述为：异途同归， 值变相等；周而复始，数值还原。 值变相等；周而复始，数值还原。 状态函数在数学上具有全微分的性质。 状态函数在数学上具有全微分的性质。 全微分的性质
可逆过程(reversible process)
系统经过某一过程从状态（1）变到状态（2）之 后，如果能使体系和环境都恢复 体系和环境都恢复到原来的状态而 体系和环境都恢复 未留下任何永久性的变化，则该过程称为热力学 未留下任何永久性的变化 可逆过程。否则为不可逆过程。 可逆过程
开放系统 有物质和能量交换
隔离系统 封闭系统 只有能量交换 无物质和能量交换
系统＋环境＝孤立系统 系统＋环境＝
2. 相
系统还有一种分类法：单相系统，多相系统 系统还有一种分类法：单相系统， 系统中任何物理和化学性质完全相同的、 系统中任何物理和化学性质完全相同的、均匀部分 称为相。根据相的概念，系统可分为： 称为相。根据相的概念，系统可分为：
系统中相数、组分的确定 系统中相数、组分的确定 相数
气 相
H 2O( g ) ＋ air
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例1 金红石加碳的氯化反应
钛白粉学名为二氧化钛 （ Titanium Dioxide）
由气固相反应的动力学方程可以得到
经计算可知 在1073K以及1273K温度下，进行TiO2和C的氯化，其中TiO2 和C的质量比为1：1。体系的压力为P总＝102.1kPa，PCl2＝35.0kPa， PAr＝67.1kPa，总流速为537ml/min。
3.1 多个子体系中各自进行多个化学反应的体系
不考虑体积黏滞性，不考虑扩散，在各子体系中都同时进行 着多个化学反应，体系的总熵增率为
其中 类似于均相体系，同样有
及
（3.1） （3.2）
（3.3）
式中 ， ， ，…分别为一级、二级、三级、…泰勒展开 系数。在近平衡区，只需取一级近似，则
且有昂萨格关系 该体系的质量守恒方程为
现代物化 非平衡态热力学
PAGE7
2020/9/18
现代物化 非平衡态热力学
PAGE8
2020/9/18
现代物化 非平衡态热力学
PAGE9
2020/9/18
现代物化 非平衡态热力学
PAGE10
2020/9/18
用变分法可以更一般地证明最小熵增原理：
Jk X k Lk,l Xl X k
现代物化 非平衡态热力学
PAGE15
2020/9/18
• 平衡态是定态的特例.
• 体系达平衡态时一般具有空间均匀性, 如理想气 体达平衡态后, 体系的温度, 压力等强度性质都处 处相等.
• 但当体系受到某种外场作用时, 体系达平衡态时 也会具有某种空间不均匀性.
例如: 处于 重力场作用 下的平衡体 系, 其密度 的分布将随 高度而变化, 此变化遵守 玻尔兹曼分 布律.
经典热力学研究的对象是平衡态，面对许多自然现象和社会 现象的非平衡态，它显得有些不足，所以对非平衡态热力学的研 究就尤为重要。
定态时, X 热 常数, L热扩 L扩热 ,
( X 扩 ) X热 2L扩 X 扩 2L热扩 X 热
2J扩 定态时,J 扩 0 （因为定态时熵保持不变）
( X 扩 ) X热 0
( 2
X
2 扩
)
X
热
2L扩
0
现代物化 非平衡态热力学
PAGE6
2020/9/18
小结:
✓一个两组分体系，在体系的两端维持一恒定的温差。热扩散现象也会引起 浓度差，故体系中同时存在力 X热与X扩，以及相应的流 J热和J扩。 ✓恒定温差(X热不变)，存在与之对应的流J热，而X扩和J扩是可以变化的。 ✓随着时间的推移，体系总会达到不随时间而变化的定态。此时，X热与J热还 存在，但是扩散流J扩等于零。 ✓此种非平衡定态仍具有熵增值，但最小熵增原理认为：非平衡定态的熵增 具有极小值。
对于带有电容的电路或含有记忆特性介质的体系, 即 使力和流之间满足线性关系, 熵产生对时间的导数也 不一定是负的, 即最小熵增原理并不一定成立.
在线性非平衡态区间, 最小熵增原理不是普适的.
现代物化 非平衡态热力学
PAGE17
2020/9/18
工业上有许多以热传导为主的传热过程, 如: 1.橡胶制品的加热硫化 2.钢锻件的热处理。 3.在窑炉、传热设备和热绝缘的设计计算及催化剂颗粒的温度分布分 析; 4.在高温高压设备（如氨合成塔及大型乙烯装置中的废热锅炉等）的 设计中，也需用热传导规律来计算设备各传热间壁内的温度分布，以 便进行热应力分析。
线性区总熵产生随时间的变化
现代物化 非平衡态热力学
PAGE12
2020/9/18
单位体积的熵产生率为σ ，整个系统的熵产生率P 则为
P dV V
由于 P 应为系统中的浓度或化学势分布、温度分布和流速分布的函 数，因而是一个泛函。熵产生率具有最小值,说明 P 的一次变分(或简称变 分)为零，二次变分大于零：
第1章 非平衡态热力学
Non-equilibrium Thermodynamics
第三讲 线性热力学及其应用
现代物化 非平衡态热力学
PAGE1
2020/9/18
§1.5 最小熵产生原理
1945 年普利高津确立了最小熵产生原理。它的主要 内容是：对于线性系统，当不可逆过程达到定态或恒稳态， 熵产生率具有最小值。
般是成立的，因此在讨论一个体系内同时进行两个化学反应的情况
时，下式成立：
diS dt
(v1
A1 T
v2
A2 ) T
0
T
T
diS dt
A1v1
A2v2
0
对整体而言，熵增率为正值，如果其中某个（设为反应1），则其Av
值不一定要求为正值：A1v1 0, A2v2 0
A2v2 A1v1
只要满足总的Av值大于零，则两个反应相互耦合，其中A2v2的反应为
什么叫定态？
如图所示，设有一容器充入A、B两种气体形成均匀混合的气体系统。实验 时，把一温度梯度加到容器左右两器壁间，一为热壁、一为冷壁。实验观 测到，一种气体在热壁上富集，而另一种气体则在冷壁上富集。这是由于 热扩散带来的结果。此外，我们还会发现，温度梯度的存在不仅引起热扩 散，同时还导致一个浓度梯度的产生，即自热壁至冷壁会存在A、B两种气 体的浓度梯度。结果，熵一般地总是低于开始时气体均匀混合的熵值。
J热X热 J扩X扩
J热 L热 X 热 L扩热 X 扩
J扩
L扩 X 扩
L 热扩
X热
L热
X
2 热
L扩
X
2 扩
(L热扩
L扩热 ) X 热 X 扩
现代物化 非平衡态热力学
PAGE5
2020/9/18
热 热 热 扩热 扩
J扩
L扩
X扩
L 热扩
X热
L热
X
2 热
L扩
X
2 扩
(L热扩
L扩热) X热 X 扩
定态：当ds/dt=0，即单位时间内的负熵流恰好抵消熵 产生。 定态可以是平衡态，也可以是非平衡态。
现代物化 非平衡态热力学
PAGE3
2020/9/18
举例说明最小熵增原理 设一个两组分的体系，让体系两端维持稳定的温度差 扩散示意图
现代物化 非平衡态热力学
PAGE4
2020/9/18
分析：
（1）温度差会引起一浓度差，于是体系中同时有一个引起 热流J热的力X热和一个引起扩散流J扩的力X扩。
又如在外电 场作用下的 体系, 即令 达到热力学 平衡态, 体 系内部的电 荷分布也不 是空间均匀 的.
现代物化 非平衡态热力学
PAGE16
2020/9/18
• 最小熵增原理对体系所要求的条件比唯象关系 所要求的条件更严格.最小熵增原理需要体系 满足Onsager倒易关系, 而且要求唯象系数是 常数.
变化, 故有:
X k 0 t
k = 1,2,3,
dP 0 故熵增P取极值, 即为最小熵增原理
现代物化d非t 平衡态热力学
PAGE11
2020/9/18
最小熵产生原理表明，在非平衡态的线性区，系统随着时间的 发展总是朝着总熵产生速率减少的方向进行，直至达到定态。 在定态熵产生速率不再随时间变化。如图所示。
取一级近似，则 有昂萨格关系
质量守恒方程为
（2.17） （2.18） （2.19）
将式（2.16）代入式（2.19）得
（2.20） 由（2.20）可见，第i个组元的反应速率不仅与第i个组元所参予的那 个化学反应有关，还与该体系中所有的独立化学反应有关。也就是 说每个化学反应的速率都与同一体系中所有的化学反应的亲和力有 关，这些化学反应是相互耦合的。
唯象方程为
（2.33） （2.34）
（2.35）
三 非均相体系化学反应耦合的动力学
冶金、化工和材料制备等过程，在多相体系中往往有多个 化学反应同时进行，多相体系可以看作由各子体系组成的，每个 相可以看作一个子体系。在多相体系中同时进行的多个化学反应 有两种：一是在每个子体系中同时进行的多个化学反应的反应物 和产物都属于同一子体系；二是同时进行的多个化学反应的反应 物和产物分属于不同的子体系。下面分别加以讨论。
式中 为第j个化学反应的速率。 Aj为第j个化学反应的亲和势。
（2.1） （2.2）
独立的化学反应 对于每个反应的反应物，有
对于每个反应的产物，有
（2.4） （2.5） （2.6）
基于通量和热力学力间存在函数关系的假设，有
（2.7）
将式（2.7）对热力学平衡态作泰勒展开，得
J j
r k 1
下面以同时存在两个化学反应的多元系为例，讨论化学反应的 耦合。化学反应方程式为
（2-1） （2-2）
（2.29）
（2.30）
（2.31）
（2.32） 可见，同一体系的两个化学反应相互耦合。每个化学反应的速 率都与自身的以及另一个化学反应的亲和力有关。
二、 均相且有多个化学反应又有扩散的体系
与上述体系相同考虑，该体系的熵增率为
熵产生P
现代物化 非平衡态热力学
平衡态
PAGE14
定态
状态
2020/9/18
③ 在非平衡态的线性区，自发过程 不会形成多稳态的时空有序结构。 涨落随时可以使体系偏离定态1 而到达某个与时间有关的非定态 如2。最后返回到与最小熵产生 相对应的定态1。与平衡态很接 近的非平衡定态通常有与平衡态 相似的定性行为，例如保持空间 均匀性、时间不变性和对各种扰 动的稳定性。因此在非平衡态热 力学的线性区或者说在平衡态附 近，不会自发形成时空有序的结 构。
现代物化 非平衡态热力学
PAGE18
2020/9/18
例
橡过 胶程 制热 品传 的导 加分 热析 硫及 化等
效 硫 化 时 间 确 定