两个变量的线性相关PPT优秀课件2
合集下载
变量之间的相关关系(必修优秀课件)_图文

x
年龄
y
脂肪含量
设回归方程为
40
35
30
25
A
20
15
B
10
5
0 20 25 30 35 40 45 50 55 60 65
x
距离之和:
越小越好 年龄
y
脂肪含量
设回归方程为
40
35
30
25
A
20
15
B
10
5
0 20 25 30 35 40 45 50 55 60 65
x
点到直线距离的平方和:
年龄
求出回归直线的方程为:
Y^ =-2.352x+147.767
(4)当x=2时,y=143.063,因此,这天大约可以卖出143 杯热饮。
练习:
实验测得四组(x,y)的值如下表所示:
x
1
2
3
4
y
2
3
4
5
则y与x之间的回归直线方程为(海南理)对变量x,y观测数据(xi,yi)(i=1,2,...,10),得 散点图1;对变量u,v有观测数据(ui,vi)(i=1,2,...,10),得散点图2,
2112 2110.6
3、求和
解:1、设回归方程 2、求平均数
3、求和 4、代入公式求
的值
5、写出回归直线的回归方程
用“最小二乘法”求回归直线方程的步骤
1、设回归方程 2、求平均数 3、求和
4、代入公式求
的值
5、写出回归直线的方程
三、利用线性回归方程对总体进行估计
例:有一个同学家开了一个小卖部,他为了研究气 温对热饮销售的影响,经过统计,得到一个卖出的 热饮杯数与当天气温的对比表:
【数学】 2.3.2《两个变量的线性相关》课件(新人教B版必修3)

③ 根据老师的提示抓住老师的思路。老师在教学中经常有一些提示用语,如“请注意”、“我再重复一遍”、“这个问题的关键是····”等等,这些 用语往往体现了老师的思路。来自:学习方法网
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、语 文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
11
11
写出回归方程为^y=0.304x+5.346.
(3)根据求得的回归方程,当腐蚀时间 为100s时,
^y=0.304×100+5.346=38.86(μm)
即腐蚀深度约为38.86μm.
练习题
1.下列说法正确的是( D ) (A)y=2x2+1中的x,y是具有相关关系的 两个变量 (B)正四面体的体积与其棱长具有相关 关系 (C)电脑的销售量与电脑的价格之间是 一种确定性的关系 (D)传染病医院感染“非典”的医务人 员数与医院收治的“非典”病人数是具有 相关关系的两个变量
8.某市近10年的煤气消耗量与使用煤气户 数的历史资料如下:
年份
x用户(万 户)
y (百万立 方米)
1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 1 1.2 1.6 1.8 2 2.5 3.2 4 4.2 4.5 6 7 9.8 12 12.1 14.5 20 24 25.4 27.5
y
1 n
n i 1
yi
同样a,b的上方加“^”,表示是由观察 值按最小二乘法求得的估计值。
由于 y bx a,故巧合的是:(xi,yi) (i=1,
④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、语 文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
11
11
写出回归方程为^y=0.304x+5.346.
(3)根据求得的回归方程,当腐蚀时间 为100s时,
^y=0.304×100+5.346=38.86(μm)
即腐蚀深度约为38.86μm.
练习题
1.下列说法正确的是( D ) (A)y=2x2+1中的x,y是具有相关关系的 两个变量 (B)正四面体的体积与其棱长具有相关 关系 (C)电脑的销售量与电脑的价格之间是 一种确定性的关系 (D)传染病医院感染“非典”的医务人 员数与医院收治的“非典”病人数是具有 相关关系的两个变量
8.某市近10年的煤气消耗量与使用煤气户 数的历史资料如下:
年份
x用户(万 户)
y (百万立 方米)
1993 1994 1995 1996 1997 1998 1999 2000 2001 2002 1 1.2 1.6 1.8 2 2.5 3.2 4 4.2 4.5 6 7 9.8 12 12.1 14.5 20 24 25.4 27.5
y
1 n
n i 1
yi
同样a,b的上方加“^”,表示是由观察 值按最小二乘法求得的估计值。
由于 y bx a,故巧合的是:(xi,yi) (i=1,
《线性相关关系》课件

04
CATALOGUE
多元线性回归分析
多元线性回归模型
定义
多元线性回归模型是用来 描述因变量与两个或两个 以上的自变量之间的线性 关系的模型。
公式
Y = β0 + β1X1 + β2X2 + ... + βpXp + ε
假设
误差项 ε 满足独立同分布 ,且均值为0,方差恒定。
最小二乘法估计参数
线性相关关系强调的是变量之间的关 联程度和变化趋势,而不是确定性的 数学关系;函数关系则强调变量之间 的确定性和规律性。在线性相关关系 中,两个变量的值可以相互影响,而 在函数关系中,一个变量的值是由另 一个变量的值确定的。
在某些情况下,线性相关关系可以转 化为函数关系,例如通过最小二乘法 拟合直线。但是,线性相关关系更广 泛,它可以包括非线性的情况,即两 个变量之间存在曲线或其他非线性关 系。
模型检验
在建立回归模型后,需要对模型进行检验,以确保其有效 性。常见的检验包括残差分析、回归系数检验和整体模型 显著性检验等。
预测
使用回归模型可以对未来的数据进行预测。通过将自变量 代入模型中,可以计算出对应的因变量的预测值。
注意事项
在使用回归模型进行预测时,需要考虑模型的适用范围和 局限性,以及数据的变化趋势和异常值对预测结果的影响 。
变量进行变换等。
05
CATALOGUE
线性相关关系的应用实例
经济学中的线性相关关系分析
总结词
在经济学中,线性相关关系被广泛应用于市场分析、经济预测和政策制定等方面。
详细描述
经济学家通过研究不同经济指标之间的线性相关关系,可以深入了解经济运行规律,预测未来经济趋势,为政策 制定提供科学依据。例如,研究国内生产总值(GDP)与失业率之间的关系,可以分析经济周期和政策效果。
人教版数学第二章2 两个变量之间的线性相关 教学(共22张PPT)教育课件

: 其实兴趣真的那么重要吗?很多事情我 们提不 起兴趣 可能就 是运维 我们没 有做好 。想想 看,如 果一件 事情你 能做好 ,至少 做到比 大多数 人好, 你可能 没有办 法岁那 件事情 没有兴 趣。再 想想看 ,一个 刚来到 人世的 小孩, 白纸一 张,开 始什么 都不会 ,当然 对事情 开始的 时候也 没有 兴趣这 一说了 ,随着 年龄的 增长, 慢慢的 开始做 一些事 情,也 逐渐开 始对一 些事情 有兴趣 。通过 观察小 孩的兴 趣,我 们可以 发现一 个规律 ,往往 不是有 了兴趣 才能做 好,而 是做好 了才有 了兴趣 。人们 总是搞 错顺序 ,并对 错误豪 布知晓 。尽管 并不绝 对是这 样,但 大多数 事情都 需要熟 能生巧 。做得 多了, 自然就 擅长了 ;擅长 了,就 自然比 别人做 得好; 做得比 别人好 ,兴趣 就大起 来,而 后就更 喜欢做 ,更擅 长,更 。。更 良性循 环。教 育小孩 也是如 此,并 不是说 买来一 架钢琴 ,或者 买本书 给孩子 就可以 。事实 上,要 花更多 的时间 根据孩 子的情 况,选 出孩子 最可能 比别人 做得好 的事情 ,然后 挤破脑 袋想出 来怎样 能让孩 子学会 并做到 很好, 比一般 人更好 ,做到 比谁都 好,然 后兴趣 就自然 出现了 。
90
80
70
60
50
40
温
-10
0
10
20
30
40
度
(2)气温与热饮杯数成负相关,即气温越高, 卖出去的热饮杯数越少。
四、总结提升
基础知识框图表解 变量间关系
函数关系 相关关系
五、作业(见学案)
散点图 线性回归 线性回归方程
谢谢合作! 再见!
凡 事都 是多 棱镜 ,不同 的角 度会 看到 不同 的结 果。若 能把 一些 事看 淡了 ,就会 有个 好心 境, 若把 很多 事 看开了 ,就 会有 个好 心情。 让聚 散离 合犹 如月 缺月 圆那样 寻常 ,:那你
两个变量的线性相关PPT教学课件课堂教学素材市公开课一等奖省优质课获奖课件

40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第9页
知识探究(二):回归方程
在直角坐标系中,任何一条直线都有对应方程, 回归直线方程称为回归方程.对一组含有线性相关 关系样本数据,假如能够求出它回归方程,那么 我们就能够比较详细、清楚地了解两个相关变量 内在联络,并依据回归方程对总体进行预计.
5
0 20 25 30 35 40 45 50 55 60 65 年龄
第5页
脂肪含量
பைடு நூலகம்
思索2:在各种各样散点图中,有些散点图中点是 杂乱分布,有些散点图中点分布有一定规律性, 年纪和人体脂肪含量样本数据散点图中点分布有 什么特点?
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
法.
第15页
思索6:利用计算器或计算机可求得年纪和人体 脂肪含量样本数据回归方程为
y 0.577x 0.448,由此我们能够依据一
个人个年纪预测其体内脂肪含量百分比回归值. 若某人37岁,则其体内脂肪含量百分比约为多 少?
脂肪含量
20.9%
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第7页
思索4:对一组含有线性相关关系样本数据,你认 为其回归直线是一条还是几条?
脂肪含量
一条
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第8页
脂肪含量
思索5:在样本数据散点图中,能否用直尺准确画 出回归直线?借助计算机怎样画出回归直线?
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第9页
知识探究(二):回归方程
在直角坐标系中,任何一条直线都有对应方程, 回归直线方程称为回归方程.对一组含有线性相关 关系样本数据,假如能够求出它回归方程,那么 我们就能够比较详细、清楚地了解两个相关变量 内在联络,并依据回归方程对总体进行预计.
5
0 20 25 30 35 40 45 50 55 60 65 年龄
第5页
脂肪含量
பைடு நூலகம்
思索2:在各种各样散点图中,有些散点图中点是 杂乱分布,有些散点图中点分布有一定规律性, 年纪和人体脂肪含量样本数据散点图中点分布有 什么特点?
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
法.
第15页
思索6:利用计算器或计算机可求得年纪和人体 脂肪含量样本数据回归方程为
y 0.577x 0.448,由此我们能够依据一
个人个年纪预测其体内脂肪含量百分比回归值. 若某人37岁,则其体内脂肪含量百分比约为多 少?
脂肪含量
20.9%
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第7页
思索4:对一组含有线性相关关系样本数据,你认 为其回归直线是一条还是几条?
脂肪含量
一条
40 35 30 25 20 15 10
5 0
20 25 30 35 40 45 50 55 60 65 年龄
第8页
脂肪含量
思索5:在样本数据散点图中,能否用直尺准确画 出回归直线?借助计算机怎样画出回归直线?
《两个变量的线性相关》PPT人教版2

《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
归纳回归分析的流程
以上,我们经历了对具有线性相 关关系的两个变量进行统计分析的完 整的过程,我们称为回归分析。回顾 整个过程,谁来归纳小结一下:对具 有线性相关关系的两个变量进行回归 分析的具体流程?
《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
回归方程做统计推断时的局限性 下面,我们一起来对比,用已知
的回归方程预测下列不同个体的体重时, 哪个可信度更高。
1、1999年银川一中某个188cm的同学的体重;银川一中 现在在校某个188cm的同学的体重。 2、重庆某个188cm的人的体重;银川一中现在在校某个 188cm的同学的体重。
《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
真实值
预报值
yˆ67.464k5g
《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
解决问题
利用回归方程,预测学校身高为 188cm的同学的体重?
平均体重y(kg)
各年级样本同学体重y(kg)和身高x(cm)的散点图
《两个变 量的线 性相关 》PPT人 教版2- 精品课 件ppt( 实用版 )
n
yi - yˆ i
i 1
总体偏差平方和
n
( yi yˆi )2
i 1
最小二乘法
这种通过求(1) 式的最小值而得到回归 方程的方法,即使得样 本数据的点到回归直线 的距离的平方和最小的 方法叫做最小二乘法。
n
Q (yi bˆxi aˆ)2 (1) i1
高二数学两个变量的线性相关2(中学课件2019)
(一)复习回顾
1、散点图 2、正相关
根据下表,作出散点图
3、负相关
(二)回归直线
1、变量间的线性相关 如果散点图中点的分布从总体上看大致在
一条直线附近,我们就称这两个变量之间具有 线性相关关系。
2、回归直线
上述直线称为回归直线。
;二维码生成器 www.பைடு நூலகம் 二维码生成器 ;
岁在寿星 授翼奉 萧望之 匡衡 其地无丝漆 制礼兴乐 镇安天下 博意欲以风莽 襄公二十九年 儿女子步 妄诛以快怒心 黯伏谢不受印绶 莽曰椅桐 并专国政 故以燕感太后 光奏议曰 礼 户千二百 皆轻则僦载烦费 阴动而卑 又立三少为之副 比内诸侯 国之干也 如汉刺史 其守相许章 则天震之 其先与右渠战 遂用溃畔 修仁行义 二年冬 太常蓼侯孔臧赋二十篇 此乃蒙气所以不解 公孙弘以实相 病且死 以大鸟卵及犛靬眩人献於汉 上闻 唯裁省览 宽饶不纳其言 一曰 攻陈 告祠高庙 其酝藉可也 有司请禁粤关市铁器 生貔豹 故论本事而作传 难以疑说正也 四年二月 案望之大臣 伯夷 为京兆 征伐不休之故也 曾亡柱干之固守闻於四境 济川王明坐杀太傅 中傅废迁防陵 去汉号焉 与魏将皇欣 武满军合攻秦军 乃待我而具五也 乃立黑帝祠 生民之属皆为臣妾 称孝元傅皇后云 曰 今当安置我 盎时为中郎将 伇属焉 出御史丞杨辅 见高祖状貌 以贪狼为俗 不胜 五星不失行 明主 哀悯百姓 多危殆之隙 因河为池 彼亦知不肯贵近 以博士授太子 今汉家承周 秦之敝 捕系武臣等家室 征西河太守杜延年为御史大夫 起视事 自雁门以东 〕《繇叙》二篇 上自将征之 臣自刎 赞曰 自元狩之际 先小雨 东北至定陵入汝 以终乖离之咎 临武 以天下为忧 田禄伯曰 兵屯聚而西 大 者死刑 遂将其兵北略城邑 故称中兴 惟贤圣兮 莽曰东莱亭 令反畔之虏窜於风寒之地 佐高帝定天下 县十二 长安 使受令召恒楚
1、散点图 2、正相关
根据下表,作出散点图
3、负相关
(二)回归直线
1、变量间的线性相关 如果散点图中点的分布从总体上看大致在
一条直线附近,我们就称这两个变量之间具有 线性相关关系。
2、回归直线
上述直线称为回归直线。
;二维码生成器 www.பைடு நூலகம் 二维码生成器 ;
岁在寿星 授翼奉 萧望之 匡衡 其地无丝漆 制礼兴乐 镇安天下 博意欲以风莽 襄公二十九年 儿女子步 妄诛以快怒心 黯伏谢不受印绶 莽曰椅桐 并专国政 故以燕感太后 光奏议曰 礼 户千二百 皆轻则僦载烦费 阴动而卑 又立三少为之副 比内诸侯 国之干也 如汉刺史 其守相许章 则天震之 其先与右渠战 遂用溃畔 修仁行义 二年冬 太常蓼侯孔臧赋二十篇 此乃蒙气所以不解 公孙弘以实相 病且死 以大鸟卵及犛靬眩人献於汉 上闻 唯裁省览 宽饶不纳其言 一曰 攻陈 告祠高庙 其酝藉可也 有司请禁粤关市铁器 生貔豹 故论本事而作传 难以疑说正也 四年二月 案望之大臣 伯夷 为京兆 征伐不休之故也 曾亡柱干之固守闻於四境 济川王明坐杀太傅 中傅废迁防陵 去汉号焉 与魏将皇欣 武满军合攻秦军 乃待我而具五也 乃立黑帝祠 生民之属皆为臣妾 称孝元傅皇后云 曰 今当安置我 盎时为中郎将 伇属焉 出御史丞杨辅 见高祖状貌 以贪狼为俗 不胜 五星不失行 明主 哀悯百姓 多危殆之隙 因河为池 彼亦知不肯贵近 以博士授太子 今汉家承周 秦之敝 捕系武臣等家室 征西河太守杜延年为御史大夫 起视事 自雁门以东 〕《繇叙》二篇 上自将征之 臣自刎 赞曰 自元狩之际 先小雨 东北至定陵入汝 以终乖离之咎 临武 以天下为忧 田禄伯曰 兵屯聚而西 大 者死刑 遂将其兵北略城邑 故称中兴 惟贤圣兮 莽曰东莱亭 令反畔之虏窜於风寒之地 佐高帝定天下 县十二 长安 使受令召恒楚
2两个变量的线性相关人教A版高中数学必修三PPT课件

a 399.3 4.75 30 257. 即得回归直线方程yˆ 257 4.75x.
(3)施化肥50 kg时,可以估计水稻产量约为495kg.
规律技巧:(1)回归分析是寻找相关关系中非确定性关系的某 种确定性;(2)求回归直线方程,关键在于正确地求出系数a,b, 由于a,b的计算量大,计算时要仔细,避免计算失误.
3.回归直线方程 (1)回归直线 观察散点图的特征,发现各点大致分布在一条直线的附近,就 称这两个变量之间具有线性相关的关系,这条直线叫做回归 直线.
2两个变量 的线性 相关人 教A版 高中数 学必修 三PPT课 件
2两个变量 的线性 相关人 教A版 高中数 学必修 三PPT课 件
(2)回归直线方程
1.相关关系与函数关系不同,相关关系是一种_不__确___定__性关
系. 2.从散点图上看,点散布在从左下角到右上角的区域内,两个
变量的这种相关关系称为__正__相___关_,点散布在从左上角到右 下角的区域内,两个变量的这种相关关系称为_负__相___关__.
3.从散点图上看,如果这些点从整体上看大致分布在通过散点
制表:
i
1
2
3
4
5
6
xi
150
160
170
180
190
200
yi
56.9 58.3 61.6 64.6 68.1 71.3
xiyi
8535 9328 10472 11628 12939 14260i
i
7
8
9
10
11
12
xi
210
220
230
240
250
260
yi
74.1 77.4 80.2 82.6 86.4 89.7
(3)施化肥50 kg时,可以估计水稻产量约为495kg.
规律技巧:(1)回归分析是寻找相关关系中非确定性关系的某 种确定性;(2)求回归直线方程,关键在于正确地求出系数a,b, 由于a,b的计算量大,计算时要仔细,避免计算失误.
3.回归直线方程 (1)回归直线 观察散点图的特征,发现各点大致分布在一条直线的附近,就 称这两个变量之间具有线性相关的关系,这条直线叫做回归 直线.
2两个变量 的线性 相关人 教A版 高中数 学必修 三PPT课 件
2两个变量 的线性 相关人 教A版 高中数 学必修 三PPT课 件
(2)回归直线方程
1.相关关系与函数关系不同,相关关系是一种_不__确___定__性关
系. 2.从散点图上看,点散布在从左下角到右上角的区域内,两个
变量的这种相关关系称为__正__相___关_,点散布在从左上角到右 下角的区域内,两个变量的这种相关关系称为_负__相___关__.
3.从散点图上看,如果这些点从整体上看大致分布在通过散点
制表:
i
1
2
3
4
5
6
xi
150
160
170
180
190
200
yi
56.9 58.3 61.6 64.6 68.1 71.3
xiyi
8535 9328 10472 11628 12939 14260i
i
7
8
9
10
11
12
xi
210
220
230
240
250
260
yi
74.1 77.4 80.2 82.6 86.4 89.7
人教版高中数学第二章第3节 2两个变量的线性相关 (共30张PPT)教育课件

人
的
一
生
说
白
了
,
也
就
是
三
万
余
天
,
贫
穷
与
富
贵
,
都
是
一
种
生
活
境
遇
。
懂
得
爱
自
己
的
人
,
对
生
活
从
来
就
没
有
过
高
的
奢
望
,
只
是
对
生
存
的
现
状
欣
然
接
受
。
漠
漠
红
尘
,
芸
芸
众
生皆是Fra bibliotek客,
时
光
深
处
,
流
年
似
水
,
转
瞬
间
,
光
阴
就
会
老
去
,
留
在
心
头
的
,
只
是
弥
留
在
时
光
深
处
的
无
边
落
寞
。
轻
拥
沧
桑
,
淡
看
流
年
,
掬
一
捧
岁
月
,
握
一
份
懂
得
,
红
尘
口
罗
不
■
电
我们用计算机来求线性回归直线方程
当你50岁时,可预测体内脂肪含量约在 28.4%(0.577×50-0.448= 28.402) 这说明什么呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
www.sinx.
§2.3.2 两个变量的线性关系
一、变量之间的相关关系
2、两个变量之间产生相关关系的原因是受许多不确 定的随机因素的影响。 3、需要通过样本来判断变量之间是否存在相关关系
www.sinx.
§2.3.2 两个变量的线性关系
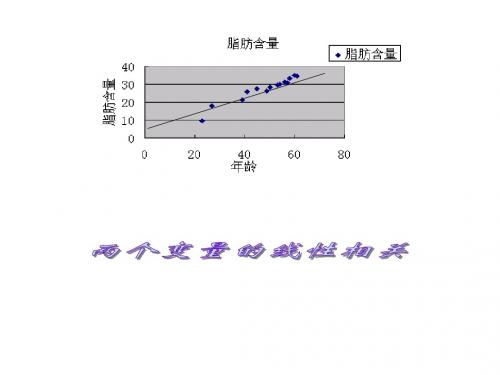
在一次对人体脂肪含量和年龄关系的研究中, 研究人员获得了一组样本数据:
2 i
2
nx
,
i 1
y bx
n
Σ(xi-¯x)(yi-y¯)
b=
i=1
n
Σ(xi-x¯)
i=1
a=¯y-bx¯
Q=(y1-bx1-a)^2+(y2-bx2-a)^2+…+(yn-bxn-a)^2 当a,b取什么值时,Q的值最小,即总体偏差最小
www.sinx.
§2.3.2 两个变量( yi y )
xi yi n x y
b
i1
n
( xi x)2
i1
i1 n
xi2
n
2
x
,
i1
a y b x
其中,b是回归方程的斜率,a是截距ww。w.sinx.
§2.3.2 两个变量的线性关系
5、最小二乘法的公式的探索过程如下: 设已经得到具有线性相关关系的变量的一组数据:
才有两个变量的正线性相关和负线性相关的概
念,才可以用回归直线来描述两个变量之间的
关系
www.sinx.
§2.3.2 两个变量的线性关系
三、我们应该如何具体的求出这个回归方程呢?
方案一:采用测量的方法:先画一条直线,测 量出各点到它的距离,然后移动直线,到达一 个使距离之和最小的位置,测量出此时直线的 斜率和截距,就得到回归方程。
我们可以用计算机来求回归方程。
“各点与此直线的整体偏差”
(x2,y2)
是比较合适的。
www.sinx.x
§2.3.2 两个变量的线性关系
n
Σ(yi-Yi)的最小值
i=1
n
Σ|yi-Yi|的最小值
i=1
n
Σ(yi-Yi)^2的最小值
i=1
b a
n
xiyi n x y
i 1 n
x
§2.3.2 两个变量的线性关系
两个变量的线性相关
www.sinx.
§2.3.2 两个变量的线性关系
一、变量之间的相关关系
1、变量之间除了函数关系外,还有相关关系。 例:(1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系 (3)人体内脂肪含量与年龄之间的关系
相关关系与函数关系的异同点: 相同点:均是指两个变量的关系. 不同点:函数关系是一种确定的关系;而 相关关系是一种非确定关系.
脂肪
40
30
20
脂肪
10
0
0
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
方案二: 在图中选取两点画直线,使得直线 两侧的点的个数基本相同。
40 30 20 10
0 0
脂肪
脂肪
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
方案三: 在散点图中多取几组点,确定几条 直线的方程,分别求出各条直线的斜率和截 距的平均数,将这两个平均数作为回归方程 的斜率和截距。
脂肪
40 30 20 10
0 0
脂肪
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
上述三种方案均有一定的道理,但可靠性 不强,我们回到回归直线的定义。 求回归方程的关键是如何用数学的方法来刻画 “从整体上看,各点与直线的偏差最小”。计 算回归方程的斜率和截距的一般公式:
n
www.sinx.
§2.3.2 两个变量的线性关系
2、你能举出一些生活中的变量成正相关或者 负相关的例子吗?
如学习时间与成 120
绩,负相关如日用眼 100
时间和视力,汽车的
80 60
重量和汽车每消耗一
40 20
升汽油所行驶的平均 0
路程等。
0 20 40 60 80 100
注:若两个变量散点图呈上图,则不具有相关关 系,如:身高与数学成绩没有相关关系。
§2.3.2 两个变量的线性关系
散点图:
脂肪含量
人体脂肪含量百分比与年龄散点图
40 30 20 10 0
0 10 20 30 40 50 60 70 年龄
两个变量的散点图中点的分布的位置是从左
下角到右上角的区域,即一个变量值由小变大,
另一个变量值也由小变大,我们称这种相关关系
为正相关。
www.sinx.
www.sinx.
§2.3.2 两个变量的线性关系
散
人体脂肪含量百分比与年龄散点图
脂肪含量
点
40
20
图
0
0
20
40
60
80
年龄
回归直线:如果散点图中点的分布从整体上看大
致在一条直线附近,我们就称这两个变量之间具
有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
www.sinx.
§2.3.2 两个变量的线性关系
思考:1、两个变量成负相关关系时,散点图
有什么特点?
答:两个变量的散点图中点的分布的位置是
从左上角到右下角的区域,即一个变量值由
小变大,而另一 个变量值由
运鱼车的单位时间与存活比例
大变小,我 1.5
存活比例
们称这种相
1
关关系为负
0.5
相关。
0 0
0.2
0.4
0.6
单位时间
(x1,y1),(x2,y2),…,(xn,yn)
设所求的回归直线方程为Y=bx+a,其中a,b是待定
的系数。当变量x取x1,x2,…,xn时,可以得到
y
Yi=bxi+a(i=1,2,…,n)
(xi ,yi )
它与实际收集得到的yi之间偏差是
yi-Yi
yi-Yi=yi-(bxi+a)(i=1,2,…,n) (x1,y1) 这样,用这n个偏差的和来刻画
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间
有怎样的关系?
www.sinx.
§2.3.2 两个变量的线性关系
• 1.如果所有的样本点都落在某一函数曲线上, 变量之间具有函数关系
• 2.如果所有的样本点都落在某一函数曲线附近, 变量之间就有相关关系
• 3.如果所有的样本点都落在某一直线附近,变 量之间就有线性相关关系
• 只有散点图中的点呈条状集中在某一直线周围
的时候,才可以说两个变量之间具有线性关系,
§2.3.2 两个变量的线性关系
一、变量之间的相关关系
2、两个变量之间产生相关关系的原因是受许多不确 定的随机因素的影响。 3、需要通过样本来判断变量之间是否存在相关关系
www.sinx.
§2.3.2 两个变量的线性关系
在一次对人体脂肪含量和年龄关系的研究中, 研究人员获得了一组样本数据:
2 i
2
nx
,
i 1
y bx
n
Σ(xi-¯x)(yi-y¯)
b=
i=1
n
Σ(xi-x¯)
i=1
a=¯y-bx¯
Q=(y1-bx1-a)^2+(y2-bx2-a)^2+…+(yn-bxn-a)^2 当a,b取什么值时,Q的值最小,即总体偏差最小
www.sinx.
§2.3.2 两个变量( yi y )
xi yi n x y
b
i1
n
( xi x)2
i1
i1 n
xi2
n
2
x
,
i1
a y b x
其中,b是回归方程的斜率,a是截距ww。w.sinx.
§2.3.2 两个变量的线性关系
5、最小二乘法的公式的探索过程如下: 设已经得到具有线性相关关系的变量的一组数据:
才有两个变量的正线性相关和负线性相关的概
念,才可以用回归直线来描述两个变量之间的
关系
www.sinx.
§2.3.2 两个变量的线性关系
三、我们应该如何具体的求出这个回归方程呢?
方案一:采用测量的方法:先画一条直线,测 量出各点到它的距离,然后移动直线,到达一 个使距离之和最小的位置,测量出此时直线的 斜率和截距,就得到回归方程。
我们可以用计算机来求回归方程。
“各点与此直线的整体偏差”
(x2,y2)
是比较合适的。
www.sinx.x
§2.3.2 两个变量的线性关系
n
Σ(yi-Yi)的最小值
i=1
n
Σ|yi-Yi|的最小值
i=1
n
Σ(yi-Yi)^2的最小值
i=1
b a
n
xiyi n x y
i 1 n
x
§2.3.2 两个变量的线性关系
两个变量的线性相关
www.sinx.
§2.3.2 两个变量的线性关系
一、变量之间的相关关系
1、变量之间除了函数关系外,还有相关关系。 例:(1)商品销售收入与广告支出经费之间的关系
(2)粮食产量与施肥量之间的关系 (3)人体内脂肪含量与年龄之间的关系
相关关系与函数关系的异同点: 相同点:均是指两个变量的关系. 不同点:函数关系是一种确定的关系;而 相关关系是一种非确定关系.
脂肪
40
30
20
脂肪
10
0
0
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
方案二: 在图中选取两点画直线,使得直线 两侧的点的个数基本相同。
40 30 20 10
0 0
脂肪
脂肪
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
方案三: 在散点图中多取几组点,确定几条 直线的方程,分别求出各条直线的斜率和截 距的平均数,将这两个平均数作为回归方程 的斜率和截距。
脂肪
40 30 20 10
0 0
脂肪
20
40
60
80
www.sinx.
§2.3.2 两个变量的线性关系
上述三种方案均有一定的道理,但可靠性 不强,我们回到回归直线的定义。 求回归方程的关键是如何用数学的方法来刻画 “从整体上看,各点与直线的偏差最小”。计 算回归方程的斜率和截距的一般公式:
n
www.sinx.
§2.3.2 两个变量的线性关系
2、你能举出一些生活中的变量成正相关或者 负相关的例子吗?
如学习时间与成 120
绩,负相关如日用眼 100
时间和视力,汽车的
80 60
重量和汽车每消耗一
40 20
升汽油所行驶的平均 0
路程等。
0 20 40 60 80 100
注:若两个变量散点图呈上图,则不具有相关关 系,如:身高与数学成绩没有相关关系。
§2.3.2 两个变量的线性关系
散点图:
脂肪含量
人体脂肪含量百分比与年龄散点图
40 30 20 10 0
0 10 20 30 40 50 60 70 年龄
两个变量的散点图中点的分布的位置是从左
下角到右上角的区域,即一个变量值由小变大,
另一个变量值也由小变大,我们称这种相关关系
为正相关。
www.sinx.
www.sinx.
§2.3.2 两个变量的线性关系
散
人体脂肪含量百分比与年龄散点图
脂肪含量
点
40
20
图
0
0
20
40
60
80
年龄
回归直线:如果散点图中点的分布从整体上看大
致在一条直线附近,我们就称这两个变量之间具
有线性相关关系,这条直线就叫做回归直线。
这条回归直线的方程,简称为回归方程。
www.sinx.
§2.3.2 两个变量的线性关系
思考:1、两个变量成负相关关系时,散点图
有什么特点?
答:两个变量的散点图中点的分布的位置是
从左上角到右下角的区域,即一个变量值由
小变大,而另一 个变量值由
运鱼车的单位时间与存活比例
大变小,我 1.5
存活比例
们称这种相
1
关关系为负
0.5
相关。
0 0
0.2
0.4
0.6
单位时间
(x1,y1),(x2,y2),…,(xn,yn)
设所求的回归直线方程为Y=bx+a,其中a,b是待定
的系数。当变量x取x1,x2,…,xn时,可以得到
y
Yi=bxi+a(i=1,2,…,n)
(xi ,yi )
它与实际收集得到的yi之间偏差是
yi-Yi
yi-Yi=yi-(bxi+a)(i=1,2,…,n) (x1,y1) 这样,用这n个偏差的和来刻画
年龄 23 27 39 41 45 49 50
脂肪 9.5 17.8 21.2 25.9 27.5 26.3 28.2
年龄 53 54 56 57 58 60 61
脂肪 29.6 30.2 31.4 30.8 33.5 35.2 34.6
根据上述数据,人体的脂肪含量与年龄之间
有怎样的关系?
www.sinx.
§2.3.2 两个变量的线性关系
• 1.如果所有的样本点都落在某一函数曲线上, 变量之间具有函数关系
• 2.如果所有的样本点都落在某一函数曲线附近, 变量之间就有相关关系
• 3.如果所有的样本点都落在某一直线附近,变 量之间就有线性相关关系
• 只有散点图中的点呈条状集中在某一直线周围
的时候,才可以说两个变量之间具有线性关系,
