基于改进的Goodman曲线的车轮疲劳强度评估方法研究
高速动车组钢制焊接结构疲劳强度的研究方法对比分析

高速动车组钢制焊接结构疲劳强度的研究方法对比分析摘要:伴随我国经济的快速增长,推动了铁路运输的发展步伐,列车承载结构使用日益趋于多样化。
在物质生活提高的当今社会,人们对于铁路交通运输安全性要求越来越高,虽然动车组的出现在很大程度上满足了人们需求,但是对于动力转向架焊接架构载荷提出了较高的要求。
基于此本文重点针对高速动车组钢制焊接结构疲劳强度中的名义应力法、热点应力法、缺口应力法、等效结构应力法进行了对比分析,主要从原理、优劣点进行了阐述,希望为工程设计人员合理评估高速动车组钢制焊接结构疲劳强度提供依据。
关键词:高速动车组;钢制焊接结构;疲劳强度;研究方法引言目前我国机车车辆各关键承载部件的疲劳强度的评估主要是参照European Rail Research Institute B12/RPl7报告给出的方法和Goodman曲线进行评定。
在高速动车组钢制焊接结构的强度评估中,被参考较多的是日本的JIS E 4207标准,但是该标准中的疲劳容许应力的测试条件不够明确,其数值的适用性也有待检验,导致工程技术人员在进行钢制焊接结构的强度评估时无法很好的把握。
鉴于此,该文针对高速动车组钢制焊接结构疲劳强度评估中的疲劳容许应力展开分析验证,以期为减少焊缝的打磨工作量,需要得到准确的实际接头的疲劳性能,对比打磨与非打磨焊缝的差异,为降本增效提供数据支撑。
1高速动车组钢制焊接结构疲劳强度名义应力法原理及优缺点1.1原理名义应力法是根据应力和应力集中系数,以结构的名义应力为实验和寿命估算的基础,结合材料的S-N曲线,按线性累积损伤理论估算结构疲劳寿命。
名义应力是忽略焊接接头的局部应力增长效应,而在所研究的截面中计算出来的应力由于复杂的几何效应,焊接接头无明确定义名义应力,且结构的不连续性与分类构件细节没有可比性。
这种计算方法适用于焊趾的评估。
名义应力的计算:材料力学的梁理论计算公式:式中: -广义名义应力; -因为宏观几何不连续进而导致的应力集中因数; -因为焊接接头错位导致的应力集中因数,此因数由轴向的错位和角度偏差共同决定,分别记为和,按公式(1)计算,即可得到。
基于轮胎六分力的某商用车车架疲劳分析

基于轮胎六分力的某商用车车架疲劳分析刘俊; 张海剑; 王威; 刘亚军; 周福庚【期刊名称】《《中国机械工程》》【年(卷),期】2019(030)021【总页数】7页(P2583-2589)【关键词】车架; 刚柔耦合多体模型; 六分力; 载荷谱; 疲劳分析【作者】刘俊; 张海剑; 王威; 刘亚军; 周福庚【作者单位】合肥工业大学汽车与交通工程学院合肥 230009; 安徽江淮汽车股份有限公司合肥 230601【正文语种】中文【中图分类】U461.71; U467.110 引言随着使用时间的延长,汽车的疲劳断裂问题也越来越容易发生,疲劳可靠性成为了评价汽车重要的指标。
传统的疲劳分析[1-3]基本上是通过台架疲劳试验或者道路测试的方法来完成的,然而这些方法不仅费时费力,而且不能及时得到疲劳分析结果。
随着CAE技术的发展,通过CAE软件进行疲劳仿真分析,能够实现短时间、少投入即可完成疲劳分析的目的,CAE方法也逐渐成为目前进行疲劳分析的主流方法。
陈书聪[4]利用虚拟道路谱对汽车转向节进行疲劳分析,得到了转向节的疲劳寿命。
张少辉[5]运用虚拟迭代的方法对某商用车驾驶室进行疲劳分析,预测结果准确。
黄元毅等[6]通过在某MPV车型上安装轮心六分力仪[7-8]得到实测载荷谱[9],对前副车架进行疲劳分析,预测结果精准。
周炜等[10]对局部应力应变法进行了详细的探索,并在实验中验证了该方法在应力应变疲劳分析中的优势。
本文以某重型商用车车架为研究对象,在车辆的3个轴,即6个车轮上安装共6个六分力仪,在定远试验场进行多种路况的试验,获得六分力信号。
在ADAMS中建立刚柔耦合[11-12]多体动力学模型,将六分力导入模型中,通过仿真获得车架与钢板弹簧、减振器接附处的载荷谱。
在HyperMesh中进行车架的有限元建模,并通过惯性释放方法进行单位力作用下的静力分析。
最后,在nCode中运用线性疲劳累计损伤理论和雨流计数法,并结合材料的应变(ε)-疲劳寿命(N)曲线进行车架的应变疲劳寿命分析。
基于DVS1612标准的轨道车辆转向架构架疲劳强度评估

基于DVS1612标准的轨道车辆转向架构架疲劳强度评估李云召;李欧阳【摘要】采用DVS1612标准对轨道车辆转向架构架的焊缝疲劳强度进行评估,评估结果显示该焊缝的疲劳强度安全余量较大.同时,也说明该焊缝的原结构设计较保守,构架的结构轻量化设计仍有较大的空间.【期刊名称】《技术与市场》【年(卷),期】2017(024)011【总页数】2页(P37-38)【关键词】疲劳强度;转向架构架;焊缝类型【作者】李云召;李欧阳【作者单位】湖南铁道职业技术学院,湖南株洲412001;湖南铁道职业技术学院,湖南株洲412001【正文语种】中文轨道车辆的转向架构架是车辆驱动、制动、轮对等关键部件的安装基础,并承载和传递实际运行过程中的垂向、纵向和横向的各种交变载荷,疲劳破坏是其主要的失效形式。
因此,开展对轨道车辆走行部转向架构架焊接结构的焊缝疲劳评估具有重要意义[1]。
1.1 评估方法根据相关标准如《UIC615-4 动力转向架构架强度试验》[2]的规定,对转向架构架在多种工况载荷下强度计算,计算出主要运营工况中应力较大的点的平均应力σm和应力幅值σa,并将各节点平均应力和应力幅描入到Goodman图中。
依据Goodman疲劳极限图,母材上的节点要落在母材疲劳极限图内,对接焊缝上的节点要落在对接焊缝疲劳极限图内,其他焊缝上的节点要落在其他焊缝疲劳极限图内。
1.2 存在的问题B12/RP17报告给出的Goodman疲劳极限图对转向架构架的焊接结构仅定义了3类评估曲线,母材、对接焊缝和其他焊缝。
评估较保守,不能满足转向架构架结构轻量化的需要。
2.1 标准介绍德国焊接学会的DVS1612《铁路车辆钢结构焊接接头设计与疲劳强度评估》标准认为沿焊缝方向的正应力、垂直于焊缝方向的正应力及沿焊缝方向的剪应力对焊缝的疲劳破坏起决定作用[3]。
DVS1612标准评估曲线最多有11种,母材正应力的疲劳特性为2级,焊缝正应力的疲劳特性分为9个等级。
CRH3型动车组车轮的疲劳寿命分析

CRH3型动车组车轮的疲劳寿命分析李树林;石启龙;杨建伟;张骄【摘要】为了真实计算动车组车轮疲劳寿命,在分析国内外车轮相关标准的基础上,提出了利用车轮静强度分析和有限元名义应力方法的高速动车组车轮强度的分析方法.基于UIC510-5标准,确定了车轮强度分析的计算载荷工况,利用有限元静强度分析方法对CRH3型动车组车轮进行疲劳强度评价,结果表明机械载荷工况下车轮强度满足要求;最后基于线性损伤累积法则,利用有限元名义应力方法和ANSYS/WORKBENCH得出车轮的疲劳寿命预测图及安全系数图,计算结果满足疲劳寿命要求,为动车组的安全性维护提供了理论依据,对动车组的安全运行有极强的实际应用价值.%In order to calculate fatigue life of motor train unit wheels, a method for analyzing wheel strength of high speed motor train unit is put forward based on analyzing domestic and international standards in wheel,by utilizing the wheel static strength analysis and finite element nominal stress method Then the assumed load for wheel strength analysis is determined based UIC510-5 standard,and the evaluation for fatigue strength of the wheel of CRH3 motor train unit is carried out with the help of finite element static strength analysis,which results show that the wheel strength satisfy the requirements under mechanical load conditions; Finally based on the linear cumulative damage law,charts for predicting fatigue life of the wheel and figure safety factor are obtained by adopting nominal stress finite element method and ANSYS/ WORKBENCH, which results calculated meet the requirements of fatigue life and provide a theoreticalbasis for security maintenance of motor train uniuThus it is valuable in practical safe operation of the train.【期刊名称】《机械设计与制造》【年(卷),期】2011(000)012【总页数】3页(P228-230)【关键词】动车组;车轮;有限元;疲劳寿命【作者】李树林;石启龙;杨建伟;张骄【作者单位】太原重工股份有限公司轮轴分公司,太原030024;太原科技大学机械电子工程学院,太原030024;北京建筑工程学院机电与汽车工程学院,北京100044;太原科技大学机械电子工程学院,太原030024【正文语种】中文【中图分类】TH16;U270.21 前言我国铁路全面展开了第6 次大提速后,高速动车组的开行使我国跻身世界高速铁路行列[1],车轮是保证高速动车组安全运行的关键走行部部件。
钢制车体疲劳强度校核方法_李幸人

采用疲劳极限法评定疲劳强度的方法。该方法根据载 荷、试验和 UIC 规 程 使 用 的 评 定 标 准,利 用 ERRI报 告提供的钢材焊接接 头 疲 劳 数 据,对 钢 制 货 车 车 体 焊 接结构进行疲劳强 度 校 核。 国 内 外 的 应 用 证 明,该 方 法也适用于大部分钢制车体焊接结构的疲劳检验。然 而该方法在国内应用时由于受技术资料的限制仍有一
2σA lim =Rp×0.46 当材料的抗拉强度处于表2提供的3种抗拉强度 之 间 时 ,也 可 利 用 表2中 的 值 进 行 线 性 插 值 得 到 焊 缝
钢 制 车 体 疲 劳 强 度 校 核 方 法 李 幸 人 ,邹 涛 ,张 江 田 ,杨 俊 杰
类型 A 的疲劳许用应力极限值。以动荷系数 K=0.3
收 稿 日 期 :2011-07-08;修 订 日 期 :2012-01-10 作 者 简 介 :李 幸 人 (1968-),男 ,高 级 工 程 师 。
焊 接 对 母 材 造 成 的 影 响 ,是 对 静 态 应 力 极 限 值 较 为 适当的取值。
檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨檨
(2)统计能量法对车内噪声的预测可有效 支 持设
计达到车内噪声的目标要求;
(3)声学包仿真技术可应用在没有准确噪 声 数据
的前期开发过程中,指 导 声 学 处 理 措 施 以 达 到 偏 安 全
的 结 果 ,便 于 后 期 根 据 实 际 测 试 结 果 调 整 声 学 包 方 案 。
参考文献:
设 计பைடு நூலகம்制 造
铁 道 车 辆 第 50 卷 第 4 期 2012 年 4 月
文 章 编 号 :1002-7602(2012)04-0021-04
疲劳分析方法

疲劳寿命分析方法摘要:本文简单介绍了在结构件疲劳寿命分析方法方面国内外的发展状况,重点讲解了结构件寿命疲劳分析方法中的名义应力法、局部应力应变法、应力应变场强度法四大方法的估算原理。
疲劳是一个既古老又年轻的研究分支,自Wohler将疲劳纳入科学研究的范畴至今,疲劳研究仍有方兴未艾之势,材料疲劳的真正机理与对其的科学描述尚未得到很好的解决。
疲劳寿命分析方法是疲分研究的主要内容之一,从疲劳研究史可以看到疲劳寿命分析方法的研究伴随着整个历史。
金属疲劳的最初研究是一位德国矿业工程帅风W.A.J.A1bert在1829年前后完成的。
他对用铁制作的矿山升降机链条进行了反复加载试验,以校验其可靠性。
1843年,英国铁路工程师W.J.M.Rankine对疲劳断裂的不同特征有了认识,并注意到机器部件存在应力集中的危险性。
1852年-1869年期间,Wohler对疲劳破坏进行了系统的研究。
他发现由钢制作的车轴在循环载荷作用下,其强度人大低于它们的静载强度,提出利用S-N 曲线来描述疲劳行为的方法,并是提出了疲劳“耐久极限”这个概念。
1874年,德国工程师H.Gerber开始研究疲劳设计方法,提出了考虑平均应力影响的疲劳寿命计算方法。
Goodman讨论了类似的问题。
1910年,O.H.Basquin提出了描述金属S-N曲线的经验规律,指出:应力对疲劳循环数的双对数图在很大的应力范围内表现为线性关系。
Bairstow通过多级循环试验和测量滞后回线,给出了有关形变滞后的研究结果,并指出形变滞后与疲劳破坏的关系。
1929年B.P.Haigh研究缺口敏感性。
1937年H.Neuber指出缺口根部区域内的平均应力比峰值应力更能代表受载的严重程度。
1945年M.A.Miner 在J.V.Palmgren工作的基础上提出疲劳线性累积损伤理论。
L.F.Coffin和S.S.Manson各自独立提出了塑性应变幅和疲劳寿命之间的经验关系,即Coffin—Manson公式,随后形成了局部应力应变法。
电动汽车电池包随机振动疲劳及优化分析
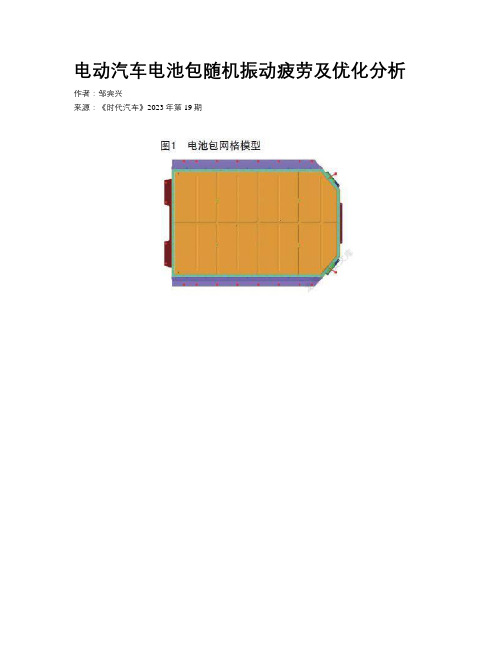
电动汽车电池包随机振动疲劳及优化分析作者:***来源:《时代汽车》2023年第19期摘要:电池包作为电动汽车重要的组成部件,路面传递的随机激励是电池包失效的重要原因。
本文根据有限元建模,单位载荷的应力响应求解及疲劳损伤的计算。
对电池包存在疲劳损伤值过大的情况,研究了通过提升电电池包模态频率以改善随机振动疲劳特性的优化思路。
最后再通过进行台架实验,验证了所分析思路和优化效果的有效性。
关键词:电池包随机振动疲劳功率谱密度近年来,汽车行业面临巨大变革,产业生产模式、竞争格局都在发生深刻变化,全球电动汽车销量再创新高,电动汽车将成为制造业核心竞争力提升中的重要一项。
由此可见,在市场及政策引导下电动车将替代燃油车成为主要的交通运输工具,其相关技术的开发也成为车企重点摸索的方向。
电池包系统作为不可缺少的核心部件,是车辆运行提供动力的心脏,其结构安全至关重要。
在车辆行驶过程过程中,受路面传递而来的外部振动载荷复杂,且随机性大。
因此,研究电池包在随机外部振动载荷下的结构特性,具有重要的工程意义[1]。
戴江梁等[2]基于随机振动理论与频域疲劳分析法,研究了电池包结构的失效机理。
王文伟等[3]基于三区间法计算了测试标准下电池包结构的振动疲劳特性。
孙小卯等[4]基于电池包动态特性,研究了电池包在振动过程中产生的疲劳问题。
本文将主要从电池包结构的随机振动疲劳方面进行分析研究。
1 电池包模型建立本文研究的电池包结构主要包括了电池包箱盖,电池模组,箱体及电池包底板等,为提升计算效率,建模之前,将电池包中包含的线缆、接口、继电器等对电池包结构性能影响不大模块省略。
本文采用Hypermesh软件进行建模,建模过程中将尺寸较小的结构如圆角、翻边进行适当简化[5]。
电池包整个箱体材料为AL6061,电池包箱盖和底板材料为Al5083,电池包整体重量545kg。
电池包本体结构通过抽中面及壳单元对电池包进行网格划分,单元平均尺寸取8mm。
现代机车车辆二系高圆簧的疲劳寿命分析及试验

( kN/
mm2)
(3)
弹簧的横向刚度计算 ,有式 (4) ~ (6)〔1〕,通过
建立横向刚度与垂向刚度间的相互关系 ,从而确定
弹簧的横向刚度 。
王海亮 、范佩鑫 、席德陵 , 上海铁道大学 , 200331 上海市 收稿日期 : 1998209201
kV = kL
0. 295
h D
2
+ 0. 384 λ
下的疲劳极限曲线 ,它和屈服极限曲线 (虚线) 相交
于点 E。
若要求某一 R 下的疲劳极限 ,只要据 R 由下
式求得φ,作射线 OR ,其斜率为
tgφ
=
τmax τmin
=
1 (τmin/ τmax)
=
1 R
(13)
射线 OR 和疲劳极限曲线 AC 交点的纵坐标就
是该循环特征值 R 下的疲劳极限值τe 。
规定 ,限于篇幅 ,此处不一一赘述 。
由于高圆簧三向承载 ,受力状态复杂 ,以上公
式计算结果与实测结果出入较大 ,因此 ,近年来 ,学
术界致力于寻求新的精确计算方法 。
参考文献〔5〕利用几何形状为轴对称的等截面 弹性直杆作为等效计算模型 ,建立弹簧两端作用力 和位移关系的矩阵方程式 ,从而得出弹簧的垂向刚 度 、横向刚度及应力的解析式 ,见式 (7) ~ (10)〔5〕。
119299 年 9 月 内燃机车 第 9 期(总第 307 期)
现代机车车辆二系高圆簧 的疲劳寿命分析及试验
王海亮 范佩鑫 席德陵
摘要 : 在回顾高圆簧设计计算方法的基础上 ,推荐经试验验证计算精度较高的高圆簧垂向横 向刚度 、应力计算公式 ,进而讨论高圆簧的疲劳寿命计算 。结合国内准高速机车高圆簧的寿命分 析和疲劳试验 ,对我国高速机车车辆二系高圆簧的设计和试验提出若干建议 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第14卷第4期 铁道科学与工程学报 Volume 14 Num b e r4 2017 年 4 月Journal of Railway Science and Engineering April 2017基于改进的Goodman曲线的车轮疲劳强度评估方法研究王悦东,张佳宇(大连交通大学交通运输工程学院,辽宁大连116028)摘要:传统的Haigh型式的G o o d m a n曲线计算方法比较简单,疫劳评估结果往往不能完整反应车轮的疫劳状况。
为了弥 补Haigh型式的G o o d m a n曲线法在计算车轮疲劳强度过程中的不足和提高车轮疲劳强度安全系数计算的准确性,在Haigh 型式的G o o d m a n曲线法的基础上进行改进,完善车轮疫劳的计算工况及计算方法,将安全系数作为疫劳评估的关键参数。
以多个不同类型的车轮为对象,进行有限元仿真分析,并分别运用Haigh形式的G o o d m a n曲线法、Crossland准则和改进的 G o o d m a n曲线法对车轮的幅板和福板孔等关键位置进行疲劳强度计算与评估。
对比计算结果表明:3种方法的计算结果趋势 基本一致,在车轮的一些评估位置改进的G o o d m a n曲线法计算的安全系数欠要小于Haigh型式的G o o d m a n曲线方法的计算结 果,说明改进的G o o d m a n曲线计算方法更加安全有效。
但是,对于非轴对称车轮的福板孔等位置,仍必须使用Crossland 准则评估疲劳强度,以保证车轮的运行安全。
关键词:车轮;疲劳强度;G o o d m a n曲线法;疲劳强度评估准则中图分类号:U270.33 文献标志码:A文章编号:1672-7029(2017)04-0827-06Assessment method for fatigue strength of wheel based on improved Goodman curveW A N G Y uedong,Z H A N G Jiayu(Department of Traffic and Transportation Engineering, Dalian Jiaotong University, Dalian 116028, China)A b s tr a c t:D u e to the simplicity of traditional Haigh-Goodman method,the fatigue assessment usually cannot reflect the fatigue condition of wheels.To m a k e up the shortage of Haigh-Goodman method in calculating process of the wheel fatigue strength and improve the accuracy of the calculation of the wheel fatigue strength safety factor,the Haigh-Goodman method was improved,which included putting the safety factor as the key of fatigue assessment and improving the main method of calculation.Taking different types of wheels as objects,the finite element models were carried out.The fatigue strength of the key positions of the wheel was evaluated by the ways of the Haigh-Goodman method,improved G o o d m a n method and Crossland pared with the results, the three methods are basically identical.In m a n y positions of the wheel,the safety factor of the improved G o o d m a n method compared with Haigh-Goodman method are smaller,but for the plate holes of the non-axisymmetrical wheels,Crossland criterion s t i l l be used to evaluate the fatigue strength of wheels,to ensure the safe operation of wheels.K e y w o r d s:wheel;fatigue strength;G o o d m a n curve method;the evaluate criterion of fatigue strength收稿日期:2016-05-14基金项目:国家自然科学基金资助项目(51208072);铁路总公司科学计划项目(2012G002-11);辽宁省教育厅优秀人才资助项目(LGQ2013052) 通信作者:王悦东(1977-),男,黑龙江桦南人,副教授,博士,从事车辆工程结构疲劳可靠性研宄;E-mail: wydstar@828铁道科学与工程学报2017年4月车轮作为转向架关键部件之一,保证了列车运行的安全性。
随着高速铁路的发展,列车运行速度 不断提升,动车组车轮的疲劳问题日益凸显。
由于车轮的承载工况较为复杂,工作环境恶劣,很容易 发生疲劳破坏,车轮的疲劳强度评估显得尤为重 要。
目前,车轮常用的疲劳评估方法大致可分为单 轴疲劳准则和多轴疲劳准则,其中单轴准则主要参 考 U I C510-5 标准[1]和B S E N13979-1-2003 标准[1],多轴准则主要有Sines疲劳准则[1],Crossland准则[1]和Dan g V a n准则[1]等。
对于轴对称车轮,单轴疲劳 准则就可以满足其评估要求,对于更为复杂的非轴 对称车轮,应先使用单轴疲劳准则评估,再使用多 轴疲劳准则对疲劳薄弱处进行二次疲劳评估。
基于 以上标准及准则,多位学者对车轮疲劳强度的评估 做了相关的研究以及应用。
吴正习等[1]以C R H2型动车组车轮为研究对象,考虑了轮对柔性的车轮其 疲劳寿命研究,何莹等[7]提出了高速动车组车轮强 度的分析方法,并对C R H5动车组新轮和磨耗到限 车轮进行了全面的疲劳强度评估。
肖乾等[1]介绍了G o o d m a n曲线的具体计算方法,并对动车组测力轮 进行了疲劳强度评定。
刘旭等[1]分别用G o o d m a n曲线法和Da n g V a n准则对某动车组车轮进行疲劳评 估,对比了单轴疲劳准则和多轴疲劳准则的适用范 围。
张懲湃等[1]提出了主应力法和修正的Crossland 疲劳准则,并与最大剪应变准则和B r o w n-Miller准则进行了对比,通过这2种疲劳评估方法,可以比 较准确地评估车轮疲劳强度。
李定远等[1]根据车轮 疲劳强度计算的方法,对A N S Y S软件进行二次开 发,实现了车轮疲劳强度自动计算。
以上所提的标 准及研究方法多以5个应力方向的安全系数来评估 车轮整体的疲劳强度,而实际运行的车轮疲劳情况 可能更加复杂一些[12-13]。
为了能够相对准确地预测 与评估车轮的疲劳强度,本文在H a i g h型式的 G o o d m a n曲线方法的基础上进行改进,包括完善相 关的计算工况以及计算方法,提高车轮疲劳强度评 估结果的准确性。
分别对轴对称车轮和非轴对称车 轮进行有限元仿真计算,根据H a i g h型式的 G o o d m a n曲线方法、Crossland准则和改进的 G o o d m a n曲线方法的基本算法编制程序,对车轮关 键位置进行疲劳强度评估,并对比疲劳强度评估 结果。
1改进的Goodman曲线方法1.1H a i g h型式的G o o d m a n曲线方法车轮在运行过程中,主要承受垂向和横向的载 荷,其主应力的主要方向是径向和周向。
传统的 H a i g h型式的G o o d m a n曲线方法根据各个工况的最 大主应力分别计算5个方向的安全系数,以此来判 断车轮疲劳强度。
其中5个方向分别是第1主应力 最大时的第1和第2主应力方向,第2主应力最大 时的第一和第2主应力方向,以及第3主应力方向。
H a i g h型式G o o d m a n曲线方法需要通过有限元 仿真来得到评估点的应力张量,找到工况主应力 ^000C T20中最大主应力〇max和最大主应力对00ct3应的方向余弦《;,和《3,其中。
,巧和巧分别 是该工况下的第1,第2和第3主应力,根据公式(1)计算出其他工况对应方向的应力巧,并找出其中 的最小应力〇m m,其中表示工况序号。
O j =[«! n2 n3]•Oj xc Oj xz n1n2Oj xz Oj yz Oj zz_3_C/= l,2,3 …)⑴通过最大和最小应力,根据公式(2)和公式(3)就可以算出平均应力和应力幅值,从而根据公式(4)得到安全系数。
式中:〜为平强度;《为安全系数。
O’max+ O min(2)O m -2O^"max O min(3)O a2a_Oa(4)应力;为应力幅值;C M f为疲劳H a i g h型式的G o o d m a n曲线方法在评价车轮的 疲劳强度时,需要评估第1主应力最大时的第1,第2主应力和^2以及第2主应力最大时的第1,第2主应力和巧2几种情况下的平均应力和应力 幅值。
第4期王悦东,等:基于改进的Goodman曲线的车轮疲劳强度评估方法研宄8291.2改进的G o o d m a n曲线方法考虑到一些车轮的结构相对复杂,尤其是非轴对称车轮,仅以这5个方向的安全系数来评估车轮整体的疲劳强度并不全面,必须増加疲劳计算时选取的方向的数量,以求提高计算的准确性。
改进的G o o d m a n曲线法选取各个工况的主应力和与之对应的方向,并计算出该方向的最大以及最小应力,从而求出安全系数,最后在同一评估位置的多个安全系数中选出最小值。
这种方法可以计算3*«(«表示工况个数)个方向上的安全系数,大大増加了所选取方向的数量。
