干扰对齐优化方案

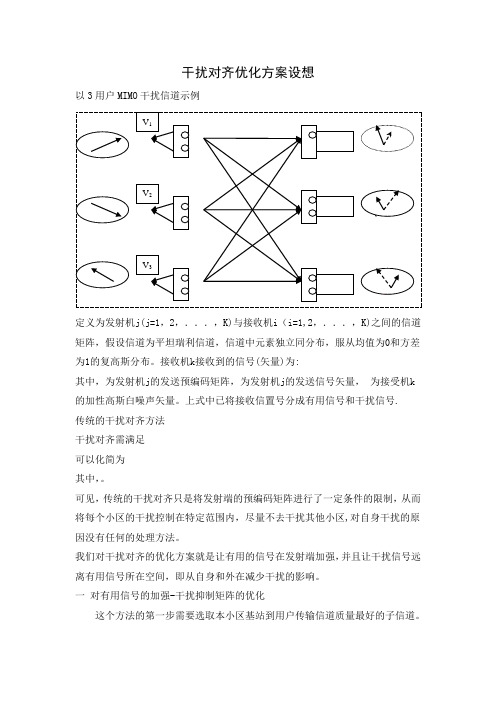
干扰对齐优化方案设想以3用户MIMO干扰信道示例定义()()()()1123231113232111112[][]123()1112323111323211123,,arg max (),,arg min ,kijijijij ij ij M m ij m k k ij ij H m m jm F eig E j m F H H F F H H F H j j H j j kk k kG H U U v v F F F v f F H H F F H H F G G I F F I jG G G H F G λλλ--====--⎛⎫ ⎪⎡⎤⎡⎤=⎪⎣⎦⎣⎦⎪⎝⎭⎧⎫=⎨⎬⎩⎭=====∑∑231231123131/2max arg min (),,()()arg max ()()kkk M Hkk k k k kk kG k FH FkHHHkk k k k kk k kk k k k kk k k H H k kk k k kk k k G M H H k kk k k kk H F G G H F Atr A A G G G tr H F G G H F H F G G H F tr G H F F H G G v H F F H =====-=⎡⎤=--⎣⎦⎡⎤=⎢⎥⎣⎦=∑∑∑∑为发射机j(j=1，2，．．．，K)与接收机i(i=1，2，．．．，K)之间的信道矩阵，假设信道为平坦瑞利信道，信道中元素独立同分布，服从均值为0和方差为1的复高斯分布。

接收机k 接收到的信号(矢量)为：11,kkk kj j j k kk k k kj j j k j j j ky H F s n H F s H F s n ==≠=+=++∑∑其中，j F 为发射机j 的发送预编码矩阵，j s 为发射机j 的发送信号矢量， kn 为接受机k 的加性高斯白噪声矢量。

上式中已将接收信置号分成有用信号kk k k H F s 和干扰信号1,kkj j j j j kH F s =≠∑.传统的干扰对齐方法 干扰对齐需满足()()1212133211233311322span H F span H F H F H F H F H F ===可以化简为()()()()1112323111323211span F span EF F H H F F H H F --===其中，()()()111313212132321E H H H H H H ---=。

可见，传统的干扰对齐只是将发射端的预编码矩阵进行了一定条件的限制，从而将每个小区的干扰控制在特定范围内，尽量不去干扰其他小区，对自身干扰的原因没有任何的处理方法。

我们对干扰对齐的优化方案就是让有用的信号在发射端加强，并且让干扰信号远离有用信号所在空间，即从自身和外在减少干扰的影响。

一 对有用信号的加强—干扰抑制矩阵的优化这个方法的第一步需要选取本小区基站到用户传输信道质量最好的/2M 子信道。

然后对本小区基站到用户的信道矩阵kk H ()1,2,3k =做奇异值分解（SVD ），其原理如下：H kk H U V =∧[]11k k kM mn a U U a ⎛⎫⎪=•••⎪ ⎪⎝⎭ 1Hk H kMV V ⎛⎫ ⎪⎪ ⎪⎝⎭公式中，∧为奇异值从大到小组合而成的对角矩阵，而且其相对应的奇异值为()1,2,3;1,...km a k m M ==；U 和V 分别为奇异值相对应的左右奇异矢量而组成的信道矩阵，并且它相对应的左右奇异矢量分别可以是()1,2,3;1,...km u k m M ==和()1,2,3;1,...km v k m M == ；k 为小区的数目，m 为奇异值从大到小依次排列的数目。

()1,2,3;1,.../2km v k m M ==为小区中信道中，质量最好的所需要的特征子信道。

这样做的目的就是将有用信号聚集到干扰信号的补空间，从而提高有用信号的强度。

二降低干扰信号的干扰作用-预编码矩阵的优化对信道矩阵H做奇异值分解，奇异值越大，说明信道质量越好，所以我们ij要选取奇异值大的信道。

然后再将预编码矩阵F进行优化，得到三个信道分别对应的优化的预编码矩阵的值。

这样便可以算出可以使干扰对齐到同一信号子空间的干扰对齐预编码矩阵，从而减少其他干扰信号的影响。

三总结步骤一和步骤二任何一步都可以将传统的干扰对齐方案进行优化，使其发挥更好的作用，如果同时进行，那么，就可以使在发送端最大化减少干扰，在接收端进一步提高有用信号强度，从而优化了整个通信系统。

仿真部分代码程序：信道容量：close all;clear all;clc;N_loop=100;EbN0=0:5:25;N0=1;Eb=10.^(EbN0/10)*N0;normalized=sqrt(1/2);C_norm=zeros(1,length(EbN0));D=zeros(1,N_loop);n=[1,2,4,8];W=3*10^4;for i=1:4for ee=1:length(EbN0)for s=1:N_loopH=randn(n(i),n(i))+j*randn(n(i),n(i));Q=H'*H;m=n(i);I=eye(m,m); SNR=Eb(ee)/N0;C=W*log2(det(I+SNR/n(i)*Q)); /*2log (1/)C B S N =+*/ D(s)=C; endC_avg=sum(D)/N_loop; C_normal=C_avg/W; C_norm(ee)=C_normal;disp(['When SNR is ',num2str(EbN0(ee)),'dB: C_avg',int2str(i),' = ',num2str(C_avg),'; C_normal ',int2str(i),' = ',num2str(C_normal)]);endP=plot(EbN0,C_norm,'r-d'); set(P,'linewidth',[2]); axis([0 30 0 100]); AX=gca;set(AX,'fontsize',14);title('\fontsize{12}\bfMIMO ÐŵÀÈÝÁ¿'); X=xlabel('Eb/N_0 [dB]£¨ÐÅÔë±È£©'); set(X,'fontsize',12);Y=ylabel('Capacity bit/s/Hz£¨ÐŵÀÈÝÁ¿£©'); set(Y,'fontsize',12); hold on ; grid on ; endlegend('n1=1','n2=2','n3=4','n4=8');对信道矩阵ij H 进行奇异值分解ij H =111ij ijij ij ij M m ij m U U v v λλ⎛⎫ ⎪⎡⎤⎡⎤⎪⎣⎦⎣⎦ ⎪⎝⎭奇异值越大，信道质量越好，需要选择矩阵E 的M ／2个最大的奇异值对应 的奇异矢量作为1F 的预编码矢量集合。

我们引入新的发射机1的发送预编码矩阵E 的计算和优化方法：12[][]1()11arg max ()k k ij ij Hm m jm F eig E j m F v f λ==⎧⎫=⎨⎬⎩⎭∑∑其中jm f 为1F 对应地第m 列在多发射端协作的环境下，我们在选取预编码矩阵时，不仅仅只依靠发射端1来计算预编码矩阵，要同时考虑到三个发射端最优的条件，只有这样才能达到整体最优的效果。

于是我们给出下列等式()()1123231113232112[][]123()11,,arg max ()k k ij ij H m m jm F eig E j m F H H F F H H F F F F v f λ--====⎧⎫=⎨⎬⎩⎭∑∑干扰抑制矩阵的优化算法设j G 为干扰抑制矩阵，不失一般性，我们假设，H j j G G I =,H j j F F I =,j =1,2,3由于已经计算出干扰对齐预编码矩阵j F ，每一个接收端选择他的期望信号子空间j G ，来减少与总的期望信号空间的平方距离。

于是有目标方程：231231,,arg min ,kkk k kG k MG G G H F G ==∑231arg minkHkkk k k kk kG k FHF G G H F ==-∑根据公式()H FAtr A A =，得1231,,()()kH H Hkk k k k kk k kk k k k kk k k G G G tr H F G G H F H F G G H F =⎡⎤=--⎣⎦∑31arg max ()kH Hk kk k k kk k k G tr G H F F H G =⎡⎤=⎢⎥⎣⎦∑()H H k kk k k kk k tr G H F F H G 是有用信号的功率，所以，有用信号功率越大，干扰的抑制效果最好，所以，我们要让有用信号的功率获得最大值，所以我们取/2max ()M H H k kk k k kk G v H F F H =，从而获得了最优的干扰抑制矩阵。