PAT计算机能力考试乙级110题答案
2021年四川省遂宁市全国计算机等级考试网络技术测试卷(含答案)

2021年四川省遂宁市全国计算机等级考试网络技术测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(10题)1.第58题在进行长交易数据的保密传递时,一般是使用自己的私钥加密一个对称加密的密钥,然后用对称加密算法对长报文进行加密,而不是直接使用对方的公钥进行加密,主要原因是()A.对称加密的计算代价很小B.公开密钥加密体系的加密强度不够大C.获得加密方的对称加密的密钥十分困难D.获得一个实体的私钥要比一次一密的对称密码来得简单2.若要打开Windows系统的注册表,可在开始菜单点击“运行”,然后在运行窗口输入()。
A.regedit.exeB.register.exeC.注册表D.register.msc3.一台交换机具有48个100Mbps全双工端口,它的端口总带宽应为()。
A.19.2GbpsB.9.6GbpsC.4.8GbpsD.2.4Gbps4. 在数据通信中使用曼彻斯特编码的主要原因是_______。
A.实现对通信过程中传输错误的恢复B.实现对通信过程中收发双方的数据同步C.提高对数据的有效传输速率D.提高传输信号的抗干扰能力5.IE浏览器将因特网世界划分为因特网区域、本地Intranet区域、可信站点区域和受限站点区域的主要目的是()A.保护自己的计算机B.验证Web站点C.避免他人假冒自己的身份D.避免第三方偷看传输的信息6.下列哪种服务不能在互联网上实现()。
A.网上图书馆B.网上美容C.网上购物D.网上医院7.甲要发给乙一封信,他希望信的内容不会被第三方了解和篡改,他应该()。
A.加密信件B.先加密信件,再对加密之后的信件生成消息认证码,将消息认证码和密文一起传输C.对明文生成消息认证码,加密附有消息认证码的明文,将得到的密文传输D.对明文生成消息认证码,将明文和消息认证码一起传输8.不同AS之间使用的路由协议是()。
信息技术试题库及答案

信息技术试题库及答案一、单选题(共100题,每题1分,共100分)1.在一个具有n个顶点和e条边的无向图的邻接表中,边结点的个数为()。
A、2eB、eC、nD、ne正确答案:A2.在Dreamweaver中,“页面属性”对话框中“页面字体”下拉列表框一旦被修改,则()A、整个页面的文本将以该字体显示B、只有当前页面的文本将以该字体显示C、所有未保存页面的文本将以该字体显示D、当前页面中被选择的文字将以该字体显示正确答案:D3.Hacker是指那些私闯非公开的机构网络进行破坏的人,它的中文俗称是()。
A、朋克B、网虫C、黑客D、海客正确答案:C4.在word中,选择“文件”菜单下的“另存为”命令,可以将当前打开的文档另存为的文档类型是()。
A、.xlsB、.batC、.txtD、.ppt正确答案:C5.PowerPoint在以下( )中,不能进行文字编辑与格式化。
A、幻灯片浏览视图B、大纲视图C、幻灯片视图D、普通视图正确答案:A6.计算机网络通信的一个显著特点是()。
A、间歇性、突发性B、安全性C、易用性D、稳定性正确答案:A7.按软件生命周期方法设计软件的过程中,画数据流图属于下面哪个阶段的工作()A、软件维护B、需求分析C、详细设计D、程序设计正确答案:C8.如果事务T获得了数据对象R上的排它锁,那么( )A、T对R只能读不能写B、T对R只能写不能读C、其它事务对过R只能读不能写D、其它事务对R既不能读也不能写正确答案:D9.利用()可以使文本快速进行格式复制。
A、格式刷B、编辑命令C、段落命令D、格式菜单正确答案:A10.如果在单元格输入数据“2002-3-15”,Excel将把它识别为( )数据。
A、日期时间型B、文本型C、公式D、数值型正确答案:A11.Excel的工作表中,若要对一个区域中的各行数据求和,应使用( )函数,或选用工具栏的Σ按钮进行运算。
A、sumB、sunC、sinD、average正确答案:A12.在WORD编辑状态下,格式刷可以复制()。
PAT计算机能力考试乙级1-10题答案

1001害死人不偿命的(3n+1)猜想(15 分对任何一个正整数n,如果它是偶数,那么把它砍掉一半;如果它是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1。
卡拉兹在 1950 年的世界数学家大会上公布了这个猜想,传说当时耶鲁大学师生齐动员,拼命想证明这个貌似很傻很天真的命题,结果闹得学生们无心学业,一心只证(3n+1),以至于有人说这是一个阴谋,卡拉兹是在蓄意延缓美国数学界教学与科研的进展……我们今天的题目不是证明卡拉兹猜想,而是对给定的任一不超过 1000 的正整数n,简单地数一下,需要多少步(砍几下)才能得到n=1?分析:输入一个正整数n进行循环,n=1循环截止,判断n,如果它是偶数,那么把它砍掉一半;如果它是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1,并计算经过的次数m。
#include"stdlib.h"#include"stdio.h"int main(){int n,m;m=0;scanf_s("%d",&n);while(n!=1){if(n%2==0){n=n/2;}else{n=(3*n+1)/2;}m++;}printf_s("%d\n",m);system("pause");}1002写出这个数(20 分)读入一个正整数n,计算其各位数字之和,用汉语拼音写出和的每一位数字。
分析:输入一个正整数n, while循环求出n的各位数字之和sum;如果sum等于0,那么就输出它的拼音”ling”;如果不等于0,输入数组b存放各位数字之和,在switch对这个数组进行判断数组b各个数的数值为多少,0对应"ling";1对应"yi";2:对应<"er";3对应"san";4对应"si";5对应"wu";6对应"liu";7对应"qi";8对应"ba";9对应"jiu";#include<iostream>using namespace std;int main(){char a[101];cin>>a;int sum=0,i=0;while(a[i]!='\0'){sum+=a[i]-'0';++i;}if(sum==0){cout<<"ling"<<endl;}int b[11],j=0;while(sum!=0){b[j]=sum%10;sum=sum/10;++j;}for(int i=j-1;i>=0;--i){switch(b[i]){case 0:cout<<"ling";break;case 1:cout<<"yi";break;case 2:cout<<"er";break;case 3:cout<<"san";break;case 4:cout<<"si";break;case 5:cout<<"wu";break;case 6:cout<<"liu";break;case 7:cout<<"qi";break;case 8:cout<<"ba";break;case 9:cout<<"jiu";break;}if(i!=0)cout<<" ";}system("pause");return 0;}1003我要通过!(20 分)“答案正确”是自动判题系统给出的最令人欢喜的回复。
PAAT样卷高级组考题+答案

PAAT 全国青少年编程能力等级考试试卷(一)图形化编程(高级)(考试时间 90 分钟,满分 100 分)一、单项选择题(共 18 题,每题 3 分,共 54 分)1. 下列应用不能体现人工智能技术的是( )。
A.使用指纹锁功能打开手机 B.使用 OCR 软件从图像中识别汉字C.某软件支持在线中英文互译 D.某主题餐馆使用机器人代替人工送餐解析:A、使用指纹锁功能打开手机:这是一种人工智能技术,因为每个人的指纹都有特殊的含义,可以通过识别这些特征来实现对某个物体的控制。
B、使用OCR软件从图像中识别汉字:这也是一种人工智能技术,OCR软件可以将图像中的文字转换成文本,并根据文本内容进行处理和分析。
C、某软件支持在线中英文互译:这不属于人工智能技术,它只是一款普通的翻译软件,可以把一种语言的文章或歌词翻译成另外一种语言。
D、某主题餐馆使用机器人代替人工送餐:这也是一种人工智能技术,机器人可以根据顾客的要求提供相应的服务,比如点菜、送餐等。
综上所述,正确答案为C,某软件支持在线中英文互译。
2. 下列有关信息安全、知识产权和虚拟社区的叙述中,不正确的是( )。
A.对数据进行加密可以确保数据得到保护B.版权保护有助于作者维护自己的合法权益C.在朋友圈转发信息前需确定其是否来自正规渠道D.数据加密就是将明文按某种算法处理,使其不可读解析:数据加密是一种技术手段,它可以保证数据的安全性,但不能完全阻止非法用户获取数据。
因此,数据加密并不是将明文按某种算法处理,使其不可读。
答案:D3. 需求分析主要解决的问题是()。
A.“为什么做” B.“做什么” C.“怎么做” D.“谁来做”解析:需求分析主要解决的问题是“怎么做”,即把用户的需求转换成产品设计人员能够识别和理解的形式。
因此,答案为C。
4. 执行如图所示的程序框图,则输出 i 的值为()。
A.8 B.7 C.6 D.5解析:当a=3,i=1→a是奇数,a=3a+1=3*3+1=10,i=2;当a=10,i=2→a是偶数,a=a/2=5,i=3;当a=5,i=3→a是奇数,a=3a+1=3*5+1=16,i=4;当a=16,i=4→a是偶数,a=a/2=8,i=5;当a=8,i=5→a是偶数,a=a/2=4,i=6;当a=4,i=6→ a是偶数,a=a/2=2,i=7;当a=2,i=7→ a是偶数,a=a/2=1,i=8;此时a=1,输出i为8,故选A5. 制作如图 1 所示的钟表,其秒针的脚本如图 2 所示,则秒针的中心点大致位于( )。
2022年广东省珠海市全国计算机等级考试数据库技术真题(含答案)

2022年广东省珠海市全国计算机等级考试数据库技术真题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1.数据管理技术发展阶段中,人工管理阶段与文件系统阶段的主要区别是文件系统()。
A.数据共享性强B.数据可长期保存C.采用一定的数据结构D.数据独立性好2. 下列关于Dephi的叙述中,________是不正确的A.Dephi属于第四代语言,B.Dephi基于面向对象编程方法,是一种可视化开发工具C.Dephi提供了数据迁移工具(DataPump),可以实现数据从一个数据库到另一个数据库的迁移D.Dephi可以方便地支持数据仓库的创建3. 查询全体主管的姓名(m name)、出生年份(birth)和所在部门(dept),要求用小写字母表示所有部门名,数据表名为manager实现该功能的语句为______。
A.select"m name",出生年份:,birth,islower(dept) from managerB.select m_name,"出生年份:",birth,islower(dept)from managerC.selectm_name,"出生年份:",birth,dept from managerD.selectm_name,"出生年份:",birth,upper(dept)from manager4. 用单链表表示的链式队列的队头在链表的哪个位置?A.链头B.链尾C.链中D.任意位置5. 在关系模型中,“关系中不允许出现相同的元组”的约束是通过______实现的。
A.候选键B.主键C.外键D.一般键6. 设栈S和队列Q的初始状态为空,元素e1、e2、e3、e4、e5和e6依次通过栈S,一个元素出栈后即进入队列Q,若6个元素出栈的顺序是e2、e4、e3、e6、e5、e1,则栈D的容量至少应该是______。
【2023年】江西省宜春市全国计算机等级考试数据库技术真题(含答案)
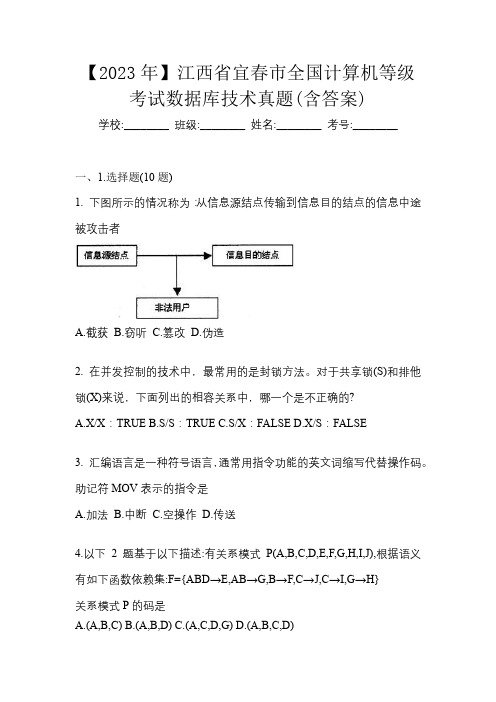
【2023年】江西省宜春市全国计算机等级考试数据库技术真题(含答案)学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1. 下图所示的情况称为:从信息源结点传输到信息目的结点的信息中途被攻击者A.截获B.窃听C.篡改D.伪造2. 在并发控制的技术中,最常用的是封锁方法。
对于共享锁(S)和排他锁(X)来说,下面列出的相容关系中,哪一个是不正确的?A.X/X:TRUEB.S/S:TRUEC.S/X:FALSED.X/S:FALSE3. 汇编语言是一种符号语言,通常用指令功能的英文词缩写代替操作码。
助记符MOV表示的指令是A.加法B.中断C.空操作D.传送4.以下2题基于以下描述:有关系模式P(A,B,C,D,E,F,G,H,I,J),根据语义有如下函数依赖集:F={ABD→E,AB→G,B→F,C→J,C→I,G→H}关系模式P的码是A.(A,B,C)B.(A,B,D)C.(A,C,D,G)D.(A,B,C,D)5. 下列属于人工管理阶段的特点的是A.数据能够保存B.数据无专门软件进行管理C.数据能共享D.数据具有独立性6. 在包括1000个元素的线性表中实现如下各运算,哪一个所需要的执行时间最长?( )A.线性表按顺序方式存储,性表的第10个结点后面插入一个新结点B.线性表按链接方式存储,性表的第10个结点后面插入一个新结点C.线性表按顺序方式存储,删除线性表的第990个结点D.线性表按链接方式存储,删除指针P所指向的结点7. 设有两个事务T1和T2,其并发操作序列如下表所示。
下列说法中正确的是( )。
T1 T2读A=100A=A*2写回读A=200ROLLBACKA.该操作序列不存在问题B.该操作序列丢失修改C.该操作序列不能重复读D.该操作序列读出脏数据8. 在虚拟页式存储管理中,由于所需页面不在内存,则发缺页中断,缺页中断属于______。
【2022年】江西省吉安市全国计算机等级考试数据库技术测试卷(含答案)

【2022年】江西省吉安市全国计算机等级考试数据库技术测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1. 如果二叉树中任何一个节点的值都大于它的左子树上所有节点的值而小于右子树上所有节点的值,要得到各节点值的递增序列,应按下列哪种次序排列节点?A.先根B.中根C.后根D.层次2. 下述哪一个数据库系统属于第一代数据库系统?A.SybaseB.IngressC.IMSD.Object Store3.计算机病毒是指能够侵入计算机系统并在计算机系统中潜伏、传播、破坏系统正常工作的一种具有繁殖能力的( )。
A.指令B.文件C.信号D.程序4. 若采用邻接矩阵法存储一个n个顶点的无向图,则该邻接矩阵是一个( )。
A.上三解矩阵B.稀疏矩阵C.对角矩阵D.对称矩阵5. ( )可能引起磁头臂频繁大幅度移动。
A.先来先服务算法B.最短寻道时间优先算法C.扫描算法D.旋转调度算法6. 区分不同实体的依据是( )。
A.名称B.属性C.对象D.联系7. 计算机软件分为系统软件和应用软件,属于系统软件的是A.数据库管理系统B.操作系统C.财务管理系统D.程序语言系统8. 关系模型中,一个关键字A.可由多个任意属性组成B.至多由一个属性组成C.可由一个或多个其值能惟一标识该关系模式或任何元组的属性组成D.以上都不是9. 在关系数据库设计中,设计关系模式是( )阶段的任务。
A.需求分析B.概念设计C.逻辑设计D.物理设计10. ______能够实现对内外存进行统一管理,为用户提供一种宏观上似乎比实际内存容量大得多的存储器。
A.覆盖技术B.交换技术C.物理扩充D.虚拟存储技术二、填空题(10题)11.运行IP协议的Intemet可以为其高层用户提供___________的、面向无连接的、尽最大努力的数据报投递服务。
12.不可逆加密机制包括Hash算法和消息认证码,用于数字签名和___________。
PAT《C语言程序设计》题目集参考答案(上)

PAT《C语言程序设计》题目集参考答案(上) PAT《C语言程序设计》题目集参考答案(上)参考答案1. 1011 A+B和C (15分)```c#include <stdio.h>int main() {int T, i;long long A, B, C;scanf("%d", &T);for (i = 1; i <= T; i++) {scanf("%lld %lld %lld", &A, &B, &C);if (A + B > C) {printf("Case #%d: true\n", i);} else {printf("Case #%d: false\n", i);}}return 0;}```2. 1024 科学计数法 (20分)```c#include <stdio.h>#include <string.h>int main() {char str[10010];scanf("%s", str);int len = strlen(str);if (str[0] == '-') {printf("-");}int pos = 0; // 记录E的位置 while (str[pos] != 'E') {pos++;}// 输出整数部分if (str[i] == '.') {continue;}printf("%c", str[i]);}int exp = 0; // 指数for (int i = pos + 2; i < len; i++) {exp = exp * 10 + (str[i] - '0');}if (exp == 0) { // 指数为0,直接输出return 0;}if (str[pos + 1] == '-') { // 指数为负数,补零 printf("0.");for (int i = 0; i < exp - 1; i++) {printf("0");}printf("%c", str[1]);printf("%c", str[i]);}} else { // 指数为正数for (int i = 1; i < pos; i++) {if (str[i] == '.') {continue;}printf("%c", str[i]);if (i == exp + 2 && pos - 3 != exp) { printf(".");}}for (int i = 0; i < exp - (pos - 3); i++) { printf("0");}}return 0;}3. 1046 划拳 (15分)```c#include <stdio.h>int main() {int n, aFail = 0, bFail = 0;scanf("%d", &n);for (int i = 0; i < n; i++) {int a, aHan, b, bHan;scanf("%d %d %d %d", &a, &aHan, &b, &bHan); if (a + bHan == aHan && a + bHan != b) {bFail++;} else if (a + bHan == b && a + bHan != aHan) { aFail++;}}printf("%d %d", aFail, bFail);return 0;}4. 1071 小赌怡情 (15分)```c#include <stdio.h>int main() {int T, K;scanf("%d %d", &T, &K);for (int i = 0; i < K; i++) {int n1, b, t, n2;scanf("%d %d %d %d", &n1, &b, &t, &n2);if (T < t) {printf("Not enough tokens. Total = %d.\n", T); continue;}if ((n1 < n2 && b == 1) || (n1 > n2 && b == 0)) { T += t;printf("Win %d! Total = %d.\n", t, T);} else {T -= t;printf("Lose %d. Total = %d.\n", t, T); if (T == 0) {printf("Game Over.\n");break;}}}return 0;}```5. 1076 Wifi密码 (15分)```c#include <stdio.h>int main() {int n;scanf("%d", &n);char ssid[4], password[10010];for (int i = 0; i < n; i++) {scanf("%s %s", ssid, password);if (password[0] == '0') {printf("%c", password[2]); } else if (password[0] == '1') { printf("%c", password[4]); } else if (password[0] == '2') { printf("%c", password[6]); } else if (password[0] == '3') { printf("%c", password[8]); }}return 0;}```6. 1084 外观数列 (20分)```c#include <stdio.h>#include <string.h>int main() {int D, N, count;scanf("%d %d", &D, &N);char str[10010];sprintf(str, "%d", D);for (int i = 1; i < N; i++) {char next[20010] = "\0";int len = strlen(str);int j = 0;while (j < len) {int count = 1;while (j + 1 < len && str[j] == str[j + 1]) { count++;j++;}char temp[10];sprintf(temp, "%d%c", count, str[j]);strcat(next, temp);j++;}strcpy(str, next);}printf("%s", str);return 0;}```7. 1088 三人行 (20分)```c#include <stdio.h>int gcd(int a, int b) {return b == 0 ? a : gcd(b, a % b);}void simplify(int numerator, int denominator) { int flag = 0; // 标记是否输出符号if (numerator < 0) {numerator = -numerator;flag = !flag;}if (denominator < 0) {denominator = -denominator;flag = !flag;}if (flag) {printf("(-");}if (numerator == 0) {printf("0");} else if (numerator >= denominator) {printf("%d", numerator / denominator);if (numerator % denominator != 0) {printf(" ");printf("%d/%d", numerator % denominator, denominator); }} else {printf("%d/%d", numerator, denominator);}if (flag) {printf(")");}}void printResult(int a, int b, int numerator, int denominator) { simplify(a, b);printf(" + ");simplify(numerator, denominator);printf(" = ");simplify(a * denominator + b * numerator, b * denominator); printf("\n");}int main() {int a, b, c, d;scanf("%d/%d %d/%d", &a, &b, &c, &d);int numerator1, denominator1, numerator2, denominator2; // 加法numerator1 = a * d + b * c;denominator1 = b * d;printResult(a, b, c, d);// 减法numerator2 = a * d - b * c;denominator2 = b * d;printResult(a, b, -c, d);// 乘法int numerator3 = a * c;int denominator3 = b * d;simplify(a, b);printf(" * ");simplify(c, d);printf(" = ");simplify(numerator3, denominator3); printf("\n");// 除法int numerator4 = a * d;int denominator4 = b * c;simplify(a, b);printf(" / ");simplify(c, d);printf(" = ");if (c == 0) {printf("Inf");} else {simplify(numerator4, denominator4); }return 0;}```8. 1092 最好吃的月饼 (20分)```c#include <stdio.h>int main() {int N, M;scanf("%d %d", &N, &M);int count[10010] = {0};for (int i = 0; i < M; i++) {int num;scanf("%d", &num);count[num]++;}// 找出最大销量int maxCount = 0;for (int i = 1; i <= N; i++) { if (count[i] > maxCount) { maxCount = count[i];}}// 输出销量最大的月饼int flag = 0;for (int i = 1; i <= N; i++) { if (count[i] == maxCount) { if (flag) {printf(" ");}printf("%d", i);flag = 1;}}return 0;}```9. 1099 build A Binary Search Tree (30分) ```c#include <stdio.h>#include <stdlib.h>#include <algorithm>#include <queue>using namespace std;struct Node {int data;int left;int right;} nodes[110];int values[110], index = 0;void inOrder(int root) {if (root == -1)return;inOrder(nodes[root].left);nodes[root].data = values[index++]; inOrder(nodes[root].right);}void bfs(int root) {queue<int> q;q.push(root);int flag = 0;while (!q.empty()) {int front = q.front();q.pop();if (flag)printf(" ");printf("%d", nodes[front].data); flag = 1;if (nodes[front].left != -1)q.push(nodes[front].left);if (nodes[front].right != -1)q.push(nodes[front].right);}}int main() {int N;scanf("%d", &N);for (int i = 0; i < N; i++) {scanf("%d %d", &nodes[i].left, &nodes[i].right); }for (int i = 0; i < N; i++) {scanf("%d", &values[i]);}sort(values, values + N);inOrder(0);bfs(0);return 0;}```10. 1101 Quick Sort (25分)```c#include <stdio.h>#include <algorithm>#include <stack>using namespace std;int a[100010], b[100010]; // b数组记录在该元素左边的所有元素中最大的元素int result[100010];stack<int> s;int main() {int n;scanf("%d", &n);for (int i = 0; i < n; i++) {scanf("%d", &a[i]);if (i == 0) {b[i] = -1;} else {b[i] = max(b[i - 1], a[i - 1]);}}int minVal = 0x7FFFFFFF; // 最小值,默认为无穷大for (int i = n - 1; i >= 0; i--) {if (i == n - 1) {if (a[i] < minVal) {result[i] = a[i];minVal = a[i];}} else {if (a[i] < minVal && a[i] >= b[i]) { result[i] = a[i];minVal = a[i];}}}int count = 0;for (int i = 0; i < n; i++) {if (result[i] != 0) {count++;s.push(result[i]);}}printf("%d\n", count);while (!s.empty()) {printf("%d", s.top());s.pop();if (!s.empty()) {printf(" ");}}return 0;}```11. 1104 Sum of Number Segments (20分) ```c#include <stdio.h>int main() {int n;scanf("%d", &n);double num, sum = 0;scanf("%lf", &num);sum += num * i * (n - i + 1);}printf("%.2f", sum);return 0;}```12. 1112 Stucked Keyboard (20分)```c#include <stdio.h>#include <string.h>int main() {int k;char s[10010];scanf("%d %s", &k, s);int len = strlen(s);int count[128] = {0}; // 记录字符出现的次数int isPrint[128] = {0}; // 记录字符是否已经输出过count[s[i]]++;}char prev = '\0';for (int i = 0; i < len; i++) {if (count[s[i]] % k != 0) { // 出现次数不是k的倍数,输出该字符 printf("%c", s[i]);isPrint[s[i]] = 1;} else { // 出现次数是k的倍数,如果之前没有输出过,输出一次if (!isPrint[s[i]]) {printf("%c", s[i]);isPrint[s[i]] = 1;}}if (s[i] != s[i + 1]) { // 上一个字符和当前字符不同,说明之前已经输出过isPrint[s[i]] = 0;}}return 0;}```13. 1113 Integer Set Partition (25分) ```c#include <stdio.h>#include <stdlib.h>#include <algorithm>using namespace std;int main() {int n;scanf("%d", &n);int a[100010], sumL = 0, sumR = 0; for (int i = 0; i < n; i++) {scanf("%d", &a[i]);}sort(a, a + n);for (int i = 0; i < n / 2; i++) {sumL += a[i];}for (int i = n / 2; i < n; i++) {sumR += a[i];}printf("%d %d", n % 2, sumR - sumL); return 0;}```14. 1114 Family Property (25分)```c#include <stdio.h>#include <algorithm>using namespace std;struct Person {int id;int fid, mid;int k;int cid[6];int flag;} person[1005];struct Family {int id;int people;double area;double perArea;int flag;} family[10000];int father[10000];bool cmp(Family a, Family b) { if (a.perArea != b.perArea) {return a.perArea > b.perArea; } else {return a.id < b.id;}}int find(int x) {while (x != father[x]) { x = father[x];}while (a != father[a]) { int z = a;a = father[a];father[z] = x;}return x;}void Union(int a, int b) { int faA = find(a);int faB = find(b);if (faA > faB) {father[faA] = faB; } else if (faA < faB) { father[faB] = faA; }}int main() { int n;scanf("%。
pat乙级参考答案

pat乙级参考答案PAT乙级参考答案近年来,随着大学生就业压力的增大,越来越多的学生开始重视并参加计算机等级考试,其中PAT乙级是备受关注的一项考试。
而对于考生来说,了解PAT乙级参考答案对于备考有着重要的指导作用。
本文将从不同科目的角度,为大家提供一些PAT乙级参考答案。
首先,我们来看看PAT乙级的英语科目。
英语是PAT考试中的必考科目,对于很多考生来说,英语可能是相对较难的一门科目。
在英语科目中,阅读理解是一个重要的考点。
在阅读理解中,考生需要通过阅读一段英文文章,回答相关问题。
对于这类题目,考生需要注重理解文章的主旨和细节,并进行准确的答题。
此外,听力也是英语科目中的一项重要内容。
考生需要通过听力材料,听取问题并选择正确的答案。
因此,对于英语科目的备考,考生可以通过大量的阅读和听力练习来提高自己的英语水平,同时也可以参考一些历年的PAT乙级英语参考答案,了解题目的解题思路和答题技巧。
接下来,我们来看看PAT乙级的数学科目。
数学是PAT考试中的另一门必考科目,对于很多考生来说,数学可能是相对较难的一门科目。
在数学科目中,考生需要掌握基本的数学运算和解题方法。
对于选择题,考生需要熟悉各类题型的解题思路,并灵活运用相关的数学知识进行解题。
对于填空题和解答题,考生需要理解题目的要求,并进行逻辑推理和计算。
因此,对于数学科目的备考,考生可以通过大量的练习题来提高自己的数学水平,同时也可以参考一些历年的PAT乙级数学参考答案,了解题目的解题思路和答题技巧。
最后,我们来看看PAT乙级的编程科目。
编程是PAT考试中的一项重要内容,对于很多考生来说,编程可能是相对较难的一项科目。
在编程科目中,考生需要熟悉编程语言的基本语法和常用函数,并能够灵活运用这些知识进行编程。
对于编程题,考生需要理解题目的要求,并设计合适的算法和程序进行解题。
因此,对于编程科目的备考,考生可以通过大量的编程练习来提高自己的编程水平,同时也可以参考一些历年的PAT乙级编程参考答案,了解题目的解题思路和编程技巧。
PAT计算机能力考试乙级1-10题答案教学文稿

1001害死人不偿命的(3n+1)猜想(15 分对任何一个正整数n,如果它是偶数,那么把它砍掉一半;如果它是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1。
卡拉兹在 1950 年的世界数学家大会上公布了这个猜想,传说当时耶鲁大学师生齐动员,拼命想证明这个貌似很傻很天真的命题,结果闹得学生们无心学业,一心只证(3n+1),以至于有人说这是一个阴谋,卡拉兹是在蓄意延缓美国数学界教学与科研的进展……我们今天的题目不是证明卡拉兹猜想,而是对给定的任一不超过 1000 的正整数n,简单地数一下,需要多少步(砍几下)才能得到n=1?分析:输入一个正整数n进行循环,n=1循环截止,判断n,如果它是偶数,那么把它砍掉一半;如果它是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1,并计算经过的次数m。
#include"stdlib.h"#include"stdio.h"int main(){int n,m;m=0;scanf_s("%d",&n);while(n!=1){if(n%2==0){n=n/2;}else{n=(3*n+1)/2;}m++;}printf_s("%d\n",m);system("pause");}1002写出这个数(20 分)读入一个正整数n,计算其各位数字之和,用汉语拼音写出和的每一位数字。
分析:输入一个正整数n, while循环求出n的各位数字之和sum;如果sum等于0,那么就输出它的拼音”ling”;如果不等于0,输入数组b存放各位数字之和,在switch对这个数组进行判断数组b各个数的数值为多少,0对应"ling";1对应"yi";2:对应<"er";3对应"san";4对应"si";5对应"wu";6对应"liu";7对应"qi";8对应"ba";9对应"jiu";#include<iostream>using namespace std;int main(){char a[101];cin>>a;int sum=0,i=0;while(a[i]!='\0'){sum+=a[i]-'0';++i;}if(sum==0){cout<<"ling"<<endl;}int b[11],j=0;while(sum!=0){b[j]=sum%10;sum=sum/10;++j;}for(int i=j-1;i>=0;--i){switch(b[i]){case 0:cout<<"ling";break;case 1:cout<<"yi";break;case 2:cout<<"er";break;case 3:cout<<"san";break;case 4:cout<<"si";break;case 5:cout<<"wu";break;case 6:cout<<"liu";break;case 7:cout<<"qi";break;case 8:cout<<"ba";break;case 9:cout<<"jiu";break;}if(i!=0)cout<<" ";}system("pause");return 0;}1003我要通过!(20 分)“答案正确”是自动判题系统给出的最令人欢喜的回复。
计算机类考试题与答案

计算机类考试题与答案一、单选题(共69题,每题1分,共69分)1.以下选项对总线型拓扑结构描述有错的是()。
A、受故障影响的设备范围大B、维护比较困难,不容易隔离故障节点C、受中心节点的影响大D、形式简单,节点易于扩充正确答案:C2.下列叙述中,正确的是()。
A、中文Windows没有提供汉字输入接口B、中文Windows不能使用五笔字型输入法C、中文Windows已经内置了五笔字型输入法D、中文Windows提供汉字输入法接口,可以挂入五笔字型输入法正确答案:D3.下列关于分层原则说法错误的是()。
A、每层功能明确且相互独立B、结构清晰,易于设计,层数应适中C、层间接口清晰,跨越接口的信息量应尽可能的少D、每一层都使用上层的服务,并为下层提供服务正确答案:D4.若想把设为主页,应该如何操作()A、在cdivtc网站中申请B、在IE属性主页地址栏中键入:C、将cdivtc添加到收藏夹D、在IE窗口中单击主页按钮正确答案:B5.人和计算机下棋,该应用属于()。
A、人工智能B、科学计算C、数据处理D、过程控制正确答案:A6.计算机病毒主要是造成对()的破坏。
A、程序和数据B、光盘驱动器C、主机D、磁盘正确答案:A7.十进制数215用二进制数表示是()。
A、11001B、11010111C、1100001D、1101001正确答案:B8.下列各组设备中,完全属于外部设备的一组是()。
A、CPU、显示器和键盘B、硬盘、软盘驱动器、键盘C、内存储器、磁盘和打印机D、CPU、软盘驱动器和RAM正确答案:B9.在WINDOWS中,对话框是一种特殊的窗口,但一般的窗口可以移动和改变大小,而对话框()。
A、仅可以改变大小,不能移动B、既能移动,也能改变大小C、既不能移动,也不能改变大小D、仅可以移动,不能改变大小正确答案:D10.在同一张磁盘上()。
A、不允许同一文件夹中的两个文件同名,但允许不同文件夹中的两个文件同名B、允许同一文件夹中的两个文件同名,但不允许不同文件夹中的两个文件同名C、不允许同一文件夹中的两个文件同名,也不允许不同文件夹中的两个文件同名D、允许同一文件夹中的两个文件同名,也允许不同文件夹中的两个文件同名正确答案:A11.按快捷键<Ctrl>+<S>的功能是()。
pat乙级 23秋题解

pat乙级 23秋题解一、PAT乙级考试介绍本章节主要介绍PAT乙级的考试目标、内容、形式以及考试的重要性。
PAT 乙级是计算机行业中的一种认证考试,旨在测试考生对计算机基础知识和实际应用能力的掌握程度。
通过本章节的学习,考生可以更好地了解PAT乙级的考试要求和考核重点,做好充分的准备。
二、基础知识回顾本章节涵盖计算机组成、操作系统、网络基础、数据库基础、编程语言等基础知识,并对每个知识点进行回顾和总结。
通过本章节的学习,考生可以巩固和加深对基础知识的理解和掌握,为后续的考试做好准备。
三、PAT乙级考试题目解析本章节是本题解文档的核心部分。
我们将针对PAT乙级23秋的考试题目进行逐一解析。
每个题目都会给出详细的解题步骤和答案,同时还会对相关知识点进行深入的解释和分析,帮助考生更好地理解和掌握相关内容。
1. 题目1:……(解题步骤和答案)相关知识点:计算机组成2. 题目2:……(解题步骤)相关知识点:操作系统基础3. 题目3:……(解题步骤和答案;相关知识点:数据库基础)四、模拟试题及解答本章节提供PAT乙级23秋的模拟试题,并提供相应的解题步骤和答案。
通过模拟试题的练习,考生可以检验自己的学习成果,发现自己的不足之处,并针对性地进行复习和提高。
模拟试题解析如下:1. 模拟试题1:(解题步骤和答案)相关知识点:网络基础2. 模拟试题2:(解题步骤)相关知识点:编程语言基础3. 模拟试题3:(解题步骤和答案;相关知识点:计算机组成)五、常见问题解答在本章节中,我们将回答考生在复习过程中可能遇到的一些常见问题,提供解决问题的方法和技巧。
考生在复习过程中可能会遇到以下问题:……(列举常见问题)针对这些问题,我们将给出详细的解答。
六、附录本附录包含以下内容:1. 考试大纲:提供PAT乙级23秋的考试大纲,帮助考生了解考试内容和考核重点。
2. 参考答案:提供本题解文档中所有模拟试题的参考答案。
请注意,这些参考答案仅供参考,实际考试可能会有所不同。
【2022年】吉林省长春市全国计算机等级考试数据库技术测试卷(含答案)

【2022年】吉林省长春市全国计算机等级考试数据库技术测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、1.选择题(10题)1. 关于数据库系统三级模式的说法,下列论述中正确的是______。
A.外模式、模式、内模式都只有一个B.外模式有多个,模式、内模式只有一个C.模式只有一个,模式和内模式有多个D.3个模式中,只有模式才是真正存在的2. 事务的ACID特性中的C的含义是( )。
A.并发性(Concurrency)B.临近性(Contiguity)C.连续性(Continuity)D.一致性(Consistency)3. 我们平常所说的裸机是指A.无显示器的计算机系统B.无软件系统的计算机系统C.无输入/输出系统的计算机系统D.无硬件系统的计算机系统4. 数据库物理设计完成之后,进入数据库实施阶段,下述工作中,一般不属于实施阶段的工作的是A.建立库结构B.扩充功能C.加载功能D.系统调试5. 关系数据库,实现表与表之间的联系是通过A.实体完整性规则B.参照完整性规则C.用户定义的完整性D.值域6. 系统故障恢复步骤不包括A.正向扫描日志文件B.对撤销队列中的各个事务进行撤销(UNDO)处理C.对该事务的所有更新操作执行逆操作D.对重做队列中的各个事务进行重做(REDO)处理7.8. 设数组data[0…m)作为循环队列sq的存储空间,front为队头指针,rear为队尾指针,则执行出队操作的语句为A.sq↑.front:=sq↑.front+1;B.sq↑.front:=(sq↑.front+1)%maxsize;C.sq↑.rear:=(sq↑.rear+1)%maxsize;D.sq↑.front:=(sq↑.front+1)%(maxsize+1);9. 计算机网络按所涉及的范围大小和计算机之间互联距离的不同,可分为______。
攀括pat乙级java题目

攀括pat乙级java题目
攀括PAT乙级Java题目是用于测试和评估Java开发人员技能水平的题目。
以下是一些常见的攀括PAT乙级Java题目:
1. 计算斐波那契数列的第n项
2. 将一个字符串转换为整数
3. 将一个整数转换为字符串
4. 实现一个简单的栈数据结构
5. 实现一个简单的队列数据结构
6. 实现一个二叉搜索树
7. 实现一个二叉堆
8. 实现一个散列表
9. 实现一个链表数据结构
10. 实现一个递归函数来计算阶乘
这些题目涵盖了Java语言的基础语法、数据结构和算法等方面的知识。
完
成这些题目需要Java开发人员熟练掌握Java编程语言,并具备相关的算法和数据结构知识。
【2021年】陕西省榆林市全国计算机等级考试网络技术测试卷(含答案)

【2021年】陕西省榆林市全国计算机等级考试网络技术测试卷(含答案) 学校:________ 班级:________ 姓名:________ 考号:________一、单选题(10题)1.对计算机安全事故的原因的认定或确定由()作出。
A.人民法院B.公安机关C.发案单位D.以上都可以2.差异备份、增量备份、完全备份三种备份策略一次备份时空间使用由少到多依次为()。
A.增量备份、差异备份、完全备份B.差异备份、增量备份、完全备份C.完全备份、差异备份、增量备份D.完全备份、增量备份、差异备份3.在Cisco路由器上配置RIP vl路由协议,参与RIP路由的网络地址有193.22.56.0/26、193.22.56.64/26、193.22.56.128/26和193.22.56.192/26,正确的配置命令是()。
A.Router(config)#network 193.22.56.0 0.0.0.255B.Router(config—router)#network 193.22.56.0 255.255.255.0C.Router(config)#network 193.22.56.0D.Router(eonfig—router)#network 193.22.56.04.第46题关于以太网交换机错误的描述是()A.允许多个端口之间的并行数据传输B.构成星型网络拓扑C.当交换机从一个端口收到一个帧,但是该帧的目标MAC地址在“MAC 地址端口映射表”没有时,向交换机的所有端口转发D.仍然会出现冲突5.6.当服务器组中一台主机出现故障,该主机上运行的程序将立即转移到组内其他主机。
下列技术中能够实现上述需求的是()A.RAIDB.ClusterC.RISCD.CISC7.在集中式网络管理模式中,网络管理结点与被管结点之间的关系是( )。
A.对等B.主/从C.管理者/代理D.服务器/代理8.在虚拟局域网中.同一逻辑工作组的成员之间希望进行通信,那么它们( )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1001害死人不偿命的(3n+1)猜想(15 分对任何一个正整数n,如果它就是偶数,那么把它砍掉一半;如果它就是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1。
卡拉兹在 1950 年的世界数学家大会上公布了这个猜想,传说当时耶鲁大学师生齐动员,拼命想证明这个貌似很傻很天真的命题,结果闹得学生们无心学业,一心只证(3n+1),以至于有人说这就是一个阴谋,卡拉兹就是在蓄意延缓美国数学界教学与科研的进展……我们今天的题目不就是证明卡拉兹猜想,而就是对给定的任一不超过 1000 的正整数n,简单地数一下,需要多少步(砍几下)才能得到n=1?分析:输入一个正整数n进行循环,n=1循环截止,判断n,如果它就是偶数,那么把它砍掉一半;如果它就是奇数,那么把(3n+1)砍掉一半。
这样一直反复砍下去,最后一定在某一步得到n=1,并计算经过的次数m。
#include"stdlib、h"#include"stdio、h"int main(){int n,m;m=0;scanf_s("%d",&n);while(n!=1){if(n%2==0){n=n/2;}else{n=(3*n+1)/2;}m++;}printf_s("%d\n",m);system("pause");}1002写出这个数(20 分)读入一个正整数n,计算其各位数字之与,用汉语拼音写出与的每一位数字。
分析:输入一个正整数n, while循环求出n的各位数字之与sum;如果sum等于0,那么就输出它的拼音”ling”;如果不等于0,输入数组b存放各位数字之与,在switch对这个数组进行判断数组b各个数的数值为多少,0对应"ling";1对应"yi";2:对应<"er";3对应"san";4对应"si";5对应"wu";6对应"liu";7对应"qi";8对应"ba";9对应"jiu";#include<iostream>using namespace std;int main(){char a[101];cin>>a;int sum=0,i=0;while(a[i]!='\0'){sum+=a[i]-'0';++i;}if(sum==0){cout<<"ling"<<endl;}int b[11],j=0;while(sum!=0){b[j]=sum%10;sum=sum/10;++j;}for(int i=j-1;i>=0;--i){switch(b[i]){case 0:cout<<"ling";break;case 1:cout<<"yi";break;case 2:cout<<"er";break;case 3:cout<<"san";break;case 4:cout<<"si";break;case 5:cout<<"wu";break;case 6:cout<<"liu";break;case 7:cout<<"qi";break;case 8:cout<<"ba";break;case 9:cout<<"jiu";break;}if(i!=0)cout<<" ";}system("pause");return 0;}1003我要通过!(20 分)“答案正确”就是自动判题系统给出的最令人欢喜的回复。
本题属于 PAT 的“答案正确”大派送——只要读入的字符串满足下列条件,系统就输出“答案正确”,否则输出“答案错误”。
得到“答案正确”的条件就是:1.字符串中必须仅有P、A、T这三种字符,不可以包含其它字符;2.任意形如xPATx的字符串都可以获得“答案正确”,其中x或者就是空字符串,或者就是仅由字母A组成的字符串;3.如果aPbTc就是正确的,那么aPbATca也就是正确的,其中a、b、c均或者就是空字符串,或者就是仅由字母A组成的字符串。
现在就请您为 PAT 写一个自动裁判程序,判定哪些字符串就是可以获得“答案正确”的。
分析:首先判断输入的字符串必须仅有P、A、T这三种字符;然后进行这样的判断:PAT p前面有0个A,pt之间有1个A,T 后面有0个A, 0*1=0 正确PAAT p前面有0个A,pt之间有2个A,T 后面有0个A, 0*2=0 正确AAPATAA p前面有2个A,pt之间有1个A,T 后面有2个A, 2*1=2 正确AAPAATAAAA p前面有2个A,pt之间有2个A,T 后面有2个A, 2*2=4 正确#include<stdio、h>#include<iostream>#include<string、h>int main(){char c[100];int i,j,n;int count_P,count_A,count_T,pos_P,pos_T;scanf("%d\n",&n);for(i=0;i<n;i++){gets(c);count_P = 0;count_A = 0;count_T = 0;pos_P = 0;pos_T = 0;for(j=0;j<strlen(c);j++){if(c[j]=='P'){count_P++;pos_P = j;}if(c[j]=='A')count_A++;if(c[j]=='T'){count_T++;pos_T = j;}}if(count_P+count_A+count_T != strlen(c) || pos_T-pos_P<=1 || count_P>1 || count_T>1 || pos_P*(pos_T-pos_P-1)!=strlen(c)-pos_T-1)printf("NO\n");elseprintf("YES\n");}return 0;}1004成绩排名(20 分)读入n(>0)名学生的姓名、学号、成绩,分别输出成绩最高与成绩最低学生的姓名与学号。
分析:首先我们需要输入学生的姓名、学号、成绩。
把她们所有的成绩作为一个整型数组,每个数与学生相对应,然后比较她们的成绩,得到最高与最低成绩。
第i的成绩最大或者最小,对应第i个学生的信息。
#include<stdio、h>#include<iostream>int main(){int i, max=0,min=0, n, score[100];char name[100][8], id[100][8];scanf("%d",&n);for(i=0;i<n;i++){scanf("%s%s%d",name[i], id[i], &score[i]);}for(i=0;i<n;i++)if(score[i]>score[max]) max=i;printf("%s %s\n",name[max],id[max]);for(i=0;i<n;i++)if(score[i]<score[min]) min=i;printf("%s %s\n",name[min],id[min]);system("pause");return 0;}1005继续(3n+1)猜想(25 分)卡拉兹(Callatz)猜想已经在1001中给出了描述。
在这个题目里,情况稍微有些复杂。
当我们验证卡拉兹猜想的时候,为了避免重复计算,可以记录下递推过程中遇到的每一个数。
例如对n=3进行验证的时候,我们需要计算 3、5、8、4、2、1,则当我们对n=5、8、4、2 进行验证的时候,就可以直接判定卡拉兹猜想的真伪,而不需要重复计算,因为这 4 个数已经在验证3的时候遇到过了,我们称 5、8、4、2 就是被3“覆盖”的数。
我们称一个数列中的某个数n为“关键数”,如果n不能被数列中的其她数字所覆盖。
现在给定一系列待验证的数字,我们只需要验证其中的几个关键数,就可以不必再重复验证余下的数字。
您的任务就就是找出这些关键数字,并按从大到小的顺序输出它们。
分析:输入n个数,用数组a存放。
首先把如果碰到数组中有0的项,则跳过。
判断t,如果它就是偶数,那么把它砍掉一半;如果它就是奇数,那么把(3n+1)砍掉一半。
然后进行数组中所有数与运算中出现的数比较,如果数组中有与运算过程中相同的数,就把数组中的该数改为0。
因为输入的数组就是互不相同的数,所以不会存在有多个匹配的情况,为了节省内存减少运行时间,找到有一个匹配就可跳出。
接着进行排序,然后输出。
#include<stdio、h>#include<iostream>int main(){int a[105];int n,i,t,j;scanf("%d",&n);for(i=0;i<n;i++){scanf("%d",&a[i]);}for(i=0;i<n;i++){t=a[i];if(t==0)continue;while(t!=1){if(t%2==0)t/=2;else t=(3*t+1)/2;for(j=0;j<n;j++){if(a[j]==t){a[j]=0;break;}}}}int temp;for(i=0;i<n;i++)for(j=i+1;j<n;j++){if(a[i]<a[j]){temp=a[i];a[i]=a[j];a[j]=temp;}}for(i=0;a[i]>0;i++){printf("%d%s",a[i],a[i+1]>0?" ":"");}system("pause");}1006换个格式输出整数(15 分)让我们用字母B来表示“百”、字母S表示“十”,用12、、、n来表示不为零的个位数字n(<10),换个格式来输出任一个不超过 3 位的正整数。
