第8章贪心算法-分数背包问题
贪心算法之背包问题

贪⼼算法之背包问题问题描述:给定n种物品,1个背包,背包容量为c,每个物品i的价值为vi,重量为wi,如何选择装⼊物品能使背包的总价值最⼤?注意:与0-1背包问题不同,在选择物品i装⼊背包时,可以选择物品i的⼀部分,⽽不⼀定要全部装⼊背包,1<=i<=n形式化描述:给定c >0, wi >0, vi >0 , 1≤i≤n.要求找⼀n元向量A=(x1,x2,…,xn), 0<=xi<=1【0~1表⽰取物品的某⼀部分】,1<=i<=n,使得 ∑wixi≤c【物品的重量和⼩于背包总容量】⽽且∑ vixi达到最⼤。
算法思路:将物品按照单位重量价值进⾏排序(从⼤到⼩),将尽可能多的单位重量价值最⾼的物品装⼊背包,若将这种物品全部装⼊背包后,背包还有多余容量,则选择单位重量价值次⾼的并尽可能多地装⼊背包。
如果最后⼀件物品⽆法全部装⼊,则计算可以装⼊的⽐例,然后按⽐例装⼊。
代码实现:数据结构:结构体1 #include <iostream>2 #include <algorithm>3using namespace std;4struct item{5int weight;//物品的重量6int value;//物品的价值7float bi;//物品单位重量的价值8float rate;//使⽤率:1代表物品完整放⼊,⼩于1代表被分割后放⼊9 }items[100];10bool cmp(const item &a,const item &b){11return a.bi>b.bi;12 }13int main(){14int n;//n件物品15float c;//背包容量为c16 cout<<"输⼊物品件数和背包容量:"<<endl;17 cin>>n>>c;18 cout<<"依次输⼊每件物品的价值和重量:"<<endl;19float v[n],w[n];//v[n]:n件物品的价值,w[n]:n件商品的重量20for(int i=0;i<n;i++){21 cin>>items[i].value>>items[i].weight;22 items[i].bi=items[i].value/items[i].weight;//计算单位重量价值23 items[i].rate=0;//初始化每件物品的使⽤率24 }25 sort(items,items+n,cmp);//按照单位重量的价值排序26int sum=0,j=0;27for(j=0;j<n;j++){28if(items[j].weight<=c){//选择单位价值重量最⼤的并且不超过背包容量的29 items[j].rate=1;30 sum+=items[j].weight;31 c-=items[j].weight;32 cout<<"重:"<<items[j].weight<<"、价值:"<<items[j].value<<"的物品被放⼊了背包"<<endl<<"放⼊⽐例:"<<items[j].rate<<endl;33 }34else break;35 }36if(j<n){//物品未装完37 items[j].rate=c/items[j].weight;//背包容量还剩c,计算出未装⼊的物品能装多少的⽐例38 sum+=items[j].rate*items[j].weight;//加上装⼊部分⽐例物品的重量39 cout<<"重:"<<items[j].weight<<"、价值:"<<items[j].value<<"被放⼊了背包"<<endl<<"放⼊⽐例:"<<items[j].rate<<endl;40 }41return0;424344 }。
贪心算法实验(求解背包问题)

算法分析与设计实验报告第四次实验
}
}
输入较小的结果:
测试结
果
输入较大的结果:
附录:
完整代码(贪心法)
;
cout<<endl;
cout<<"待装物品的价值为:"<<endl;
for (i=0;i<n;i++)
cin>>item[i].v;
cout<<endl;
erval=item[i].v/item[i].w;
clock_t start,end,over; ;
实验心
得
首先这个实验,需要注意的点是背包问题与0-1背包不同,物品可以部分的放入背包中,所以思路也不一样,首先就是将物品按照单位质量价值排序,只这一点就有一点难度。
难度在于要是排序后物品的编号就会发生改变,输出的就不是之前的编号的物品,导致错误,后来发现如果为每一个物品保存一个副本,然后将它们的编号进行对比,就可以进行正确的输出了。
其中这个实验
让我学到了两点:一是结构体的使用,之前一直没有怎么用过,现在才发现自己其实不会用;二十对于库函数sort 函数的使用。
感觉每一次实验都有学到东西,很开心。
实验得
分 助教签名
sort(item,item+n,comparison); >c)
break;
tem[i]=1;
c-=item[i].w;
}
if(i<n) ;
for(i=0;i<n;i++) ==tmp[j])
x[j]=tem[i];
}
}
}。
贪心法解决背包问题

算法分析实验报告贪心法解决背包问题学生姓名:专业:班级:学号:指导教师:2017年6月12日目录一、实验题目 (2)二、实验目的 (2)三、实验要求 (2)四、实现过程 (3)1、实验设计: (3)2、调试分析 (5)3、运行结果: (6)4、实验总结: (6)五、参考文献 (6)一、实验题目贪心法解决背包问题二、实验目的1)以背包问题为例,掌握贪心法的基本设计策略。
2)熟练掌握各种贪心策略情况下的背包问题的算法并实现;其中:量度标准分别取:效益增量v、物品重量w、v/ w比值;3) 分析实验结果来验证理解贪心法中目标函数设计的重要性。
三、实验要求1.[问题描述]:给定n种物品和一个背包。
物品i的重量是Wi,其价值为Vi,背包的容量为C。
应如何选择装入背包的物品,使得装入背包中物品的总价值最大? 与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,但不可以重复装入。
2.[算法]:贪心法的基本思路:从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。
当达到某算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:1)不能保证求得的最后解是最佳的;2)不能用来求最大或最小解问题;3)只能求满足某些约束条件的可行解的范围。
四、实现过程1、实验设计:1.用贪心法求解背包问题的关键是如何选定贪心策略,使得按照一定的顺序选择每个物品,并尽可能的装入背包,直至背包装满。
至少有三种看似合理的贪心策略:1)按物品价值v降序装包,因为这可以尽可能快的增加背包的总价值。
但是,虽然每一步选择获得了背包价值的极大增长,但背包容量却可能消耗太快,使得装入背包得物品个数减少,从而不能保证目标函数达到最大。
2)按物品重量w升序装包,因为这可以装入尽可能多的物品,从而增加背包总价值。
但是,虽然每一步选择使背包得容量消耗得慢了,但背包价值却没能保证迅速增长,从而不能保证目标函数达到最大。
C语言版贪心算法背包问题

C语言版贪心算法背包问题#include#define N 100typedef struct bao{int num;float w;float v;};typedef struct avg{int num;float val;float w;float v;};struct bao b[N];struct avg d[N];int n;float c;void Sort(){int i,j,k;struct avg temp[N];for(i=0;i<n-1;i++)< p="">{k = i;for(j=i+1;j<n;j++)< p="">if(d[k].valif(k != i){temp[i]=d[i];d[i]=d[k];d[k]=temp[i];}}}float knapsack(){int i;float x[N],sum = 0;for(i=0;ifor(i=0;i<n;i++){< p="">if(d[i].w>c) break;x[d[i].num] = 1;sum += d[i].v;c -= d[i].w;}if(i<n){< p="">x[d[i].num] = c/d[i].w;sum += x[d[i].num] * d[i].v;}return sum;}int main(){int i,j,k;float sum;printf("请输入物品总数:");scanf("%d",&n);printf("\n请输入背包容量:");scanf("%f",&c);printf("\n请输入各物品重量及价值(格式:xx,xx):");for(i=0;i<n;i++){< p=""> scanf("%f,%f",&b[i].w,&b[i].v); }for(i=0;i<="" p="">for(i=0;i<n;i++){< p="">d[i].val = b[i].v/b[i].w;d[i].v = b[i].v;d[i].w = b[i].w;}Sort();sum = knapsack();printf("%.2f\n",sum);}</n;i++){<></n;i++){<></n){<></n;i++){<></n;j++)<></n-1;i++)<>。
使用JAVA实现算法——贪心算法解决背包问题

使⽤JAVA实现算法——贪⼼算法解决背包问题解释等全部在代码中,⾃⼰跑了下,是没问题的package BasePart;import java.io.BufferedReader;import java.io.FileInputStream;import java.io.IOException;import java.io.InputStreamReader;/*** 使⽤贪⼼算法解决背包问题* 背包问题:* 旅⾏者有背包容量m公⽄* 现在有重量W1,W2,W3,W4....Wn* 对应的价值V1,V2,V3,V4....Vn* 运⾏重复携带,欲求得最⼤价值* 贪⼼算法:求得最好的选择,但是贪⼼算法不是对于所有的问题都得到整体最优解* 贪⼼算法基本思路:* 1.建⽴数学模型来描述问题* 2.把求解问题分成若⼲个⼦问题* 3.对于每⼀个⾃问题求得局部最优解* 4.把⼦问题的解局部最优解合成原来解问题的⼀个解* 贪⼼算法的实现过程:* 从⼀个初始解出发* while-do朝总⽬标前进* 求出可⾏解的⼀个解元素* 由所有解元素组成合成问题的⼀个可⾏解*/public class Greedy {/*解决背包问题*需要背包容量*背包价值*背包剩余容量*解向量集合*/private double total_weight;private double total_value;private double rest_weight;//储存排序数组private Good[] arrayValue;private Good[] arrayWeight;private Good[] arrayC_P;private int goodsNum;private Good[] goods;private double real_weight;public Greedy() {}public Greedy(int goodsNum,double total_weight) {this.goodsNum=goodsNum;this.total_weight=total_weight;}public void init(String filename) throws IOException {/** 1.初始化程序* 2.从TXT⽂件中得到商品重量和其价值数组* 3.初始化序列数组arrayValue/Weight/C_P*/goods=new Good[goodsNum];BufferedReader data=new BufferedReader(new InputStreamReader(new FileInputStream(filename)));String buff;String[] strs;//循环赋值for(int i=0;i<4;i++){buff=data.readLine();strs=buff.split(" ");//根据位次goods[i]=new Good();//对象数组不仅仅需要初始化数组,对于数组内的每⼀个对象也需要初始化goods[i].setName(strs[0]);goods[i].setValue(Double.parseDouble(strs[1]));goods[i].setWeight(Double.parseDouble(strs[2]));goods[i].figureC_P();}//关闭输⼊流//成员变量初始化arrayValue=new Good[goodsNum];arrayWeight=new Good[goodsNum];arrayC_P=new Good[goodsNum];//初始化数组/** 价值由⼤到⼩数组*/arrayValue=arrayCopy(goods, arrayValue);//按照价值对arrayValue数组进⾏重新排列,使⽤冒泡排序法for(int i=0;i<goodsNum-1;i++){//从⼤到⼩排列for(int j=i+1;j<goodsNum;j++){if(arrayValue[i].getValue()<arrayValue[j].getValue()){Good temp=arrayValue[i];arrayValue[i]=arrayValue[j];arrayValue[j]=temp;}}}/**质量由⼩到⼤数组*/arrayWeight=arrayCopy(goods, arrayWeight);//按照价值对arrayWeight数组进⾏重新排列,使⽤冒泡排序法for(int i=0;i<goodsNum-1;i++){//从⼩到⼤排列for(int j=i+1;j<goodsNum;j++){if(arrayWeight[i].getWeight()>arrayWeight[j].getWeight()){Good temp=arrayWeight[i];arrayWeight[i]=arrayWeight[j];arrayWeight[j]=temp;}}}/** 性价⽐由⼤到⼩排列*/arrayC_P=arrayCopy(goods, arrayC_P);//按照价值对arrayC_P数组进⾏重新排列,使⽤冒泡排序法for(int i=0;i<goodsNum-1;i++){//从⼤到⼩排列for(int j=i+1;j<goodsNum;j++){if(arrayC_P[i].getC_P()<arrayC_P[j].getC_P()){Good temp=arrayC_P[i];arrayC_P[i]=arrayC_P[j];arrayC_P[j]=temp;}}}}//⽤于数组拷贝public Good[] arrayCopy(Good[] goods,Good[] arr2){arr2=goods.clone();return arr2;}private void show(Good[] goodsarr) {for(Good good:goodsarr){System.out.println(good.getName()+"\t"+good.getValue()+"\t"+good.getWeight()+"\t"+good.getC_P()+"\t"+good.getNum()); }}/*三种策略:度量准则* 依次选取价值最⼤填充* 依次选取重量最轻填充* 依次选取⽐价最⼤填充** ⽅法设计:* 按照度量准则* 传递⼀个按照选择优先级排列的对象数组* 迭代计算剩余容量* 返回设计⽅案*/public void strategy(Good[] goodsArray){rest_weight=total_weight;for(Good good:goodsArray){int selectNum=(int)Math.floor(rest_weight/good.getWeight());rest_weight=rest_weight-selectNum*good.getWeight();good.setNum(selectNum);if(rest_weight<arrayWeight[0].getWeight()){continue;}}}public void calculate(Good[] goodsArray,String target){total_value=0;real_weight=0;//处理结果System.out.println("在以"+target+"为准则的情况下");for(Good good:goodsArray){System.out.println(good.getName()+"\t\t数量:"+good.getNum());total_value+=good.getValue()*good.getNum();real_weight+=good.getWeight()*good.getNum();}System.out.println("总价值是:\t"+total_value+"\t总重量是:\t"+real_weight); }public void solve() {/** 业务逻辑* 将优先级数组*/strategy(arrayValue);calculate(arrayValue,"价值");strategy(arrayWeight);calculate(arrayWeight,"重量");strategy(arrayC_P);calculate(arrayC_P,"⽐值");}public static void main(String[] args) throws IOException {Greedy greedy=new Greedy(4,50);greedy.init("goods.txt");greedy.solve();}}Txt⽂本为:ad钙奶 12 5ab胶带 6 1电脑 4000 30⾳响 500 15说明:第⼀列:名称第⼆列:价格第三列:重量程序运⾏结果为:待改善。
贪心算法-分数背包问题(Python实现)
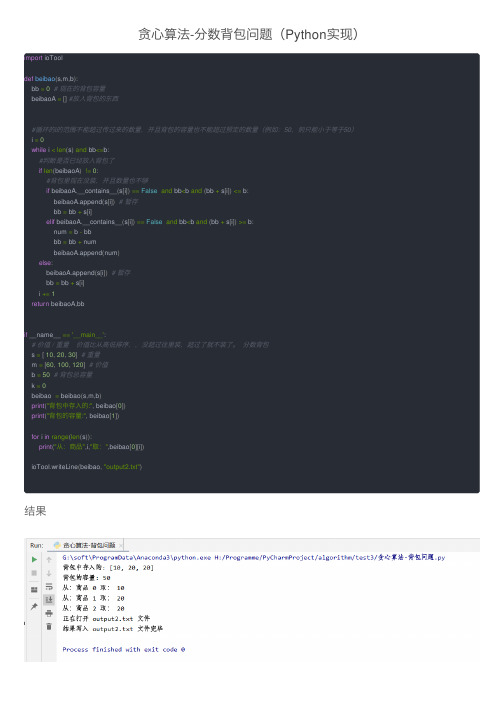
贪⼼算法-分数背包问题(Python实现)import ioTooldef beibao(s,m,b):bb =0# 现在的背包容量beibaoA =[]#放⼊背包的东西#循环的i的范围不能超过传过来的数量,并且背包的容量也不能超过预定的数量(例如:50,则只能⼩于等于50) i =0while i <len(s)and bb<=b:#判断是否已经放⼊背包了if len(beibaoA)!=0:#背包⾥现在没装,并且数量也不够if beibaoA.__contains__(s[i])==False and bb<b and(bb + s[i])<= b:beibaoA.append(s[i])# 暂存bb = bb + s[i]elif beibaoA.__contains__(s[i])==False and bb<b and(bb + s[i])>= b:num = b - bbbb = bb + numbeibaoA.append(num)else:beibaoA.append(s[i])# 暂存bb = bb + s[i]i +=1return beibaoA,bbif __name__ =='__main__':# 价值 / 重量价值⽐从⾼低排序,,没超过往⾥装,超过了就不装了。
分数背包s =[10,20,30]# 重量m =[60,100,120]# 价值b =50# 背包总容量k =0beibao = beibao(s,m,b)print("背包中存⼊的:", beibao[0])print("背包的容量:", beibao[1])for i in range(len(s)):print("从:商品",i,"取:",beibao[0][i])ioTool.writeLine(beibao,"output2.txt")结果。
背包问题的贪心算法

Wi Xi
16.5 20 20 20
Vi X i
24.25 28.2 31 31.5
先检验这四个为可行解*,即满足约束条件(4.2.2),(4.2.3).再比 较目标函数值,∑vixi .知④组解效益值最大.该组解是背包问题的最 优解。(见定理4.2)
6
例4.4 n=3,c=20, (V1,V2,V3) (25, 24,15) (W1,W2,W3) (18,15,10)
7
,且物品2的24/15 = v2/w2 较物品3的15/10= v3/w3效益值高。按 此选择策略,得②即(1, 2/15, 0),∑vixi=28.2 .此解是一个次优解。 显然,按物品效益值的非增次序装包不能得最优解。
原因:背包可用容量消耗过快。
(2)以容量作为量度。即按物品重量的非降次序将物
—选取最优的量度标准实为用贪心方法求解问题的核心.
16
4.3 贪心算法的基本要素
1.贪心选择性质
所谓贪心选择性质是指所求问题的整体最优解可以 通过一系列局部最优的选择,即贪心选择来达到。这 是贪心算法可行的第一个基本要素,也是贪心算法与 动态规划算法的主要区别。
动态规划算法通常以自底向上的方式解各子问 题,而贪心算法则通常以自顶向下的方式进行,以迭 代的方式作出相继的贪心选择,每作一次贪心选择就 将所求问题简化为规模更小的子问题。
品装包。如例4.4中的解③(让背包尽可能慢被消耗)
排序 : (w3,w2,w1)= (10,15,18)
(V3,V2,V1) (15, 24, 25)
V3=15,x3=1,w3=10,背包剩余C-10=10;物品2有次大重量(w2=15), 但包装不下。使用x2=2/3,刚好装满背包且物品2装入2/3与物品1 装入5/9的容量均为10个单位。但前者的效益值24×2/3=16 >后者
python实现贪婪算法解决01背包问题

python实现贪婪算法解决01背包问题⼀、背包问题01背包是在M件物品取出若⼲件放在空间为W的背包⾥,每件物品的体积为W1,W2⾄Wn,与之相对应的价值为P1,P2⾄Pn。
01背包是中最简单的问题。
01背包的约束条件是给定⼏种物品,每种物品有且只有⼀个,并且有权值和体积两个属性。
在01背包问题中,因为每种物品只有⼀个,对于每个物品只需要考虑选与不选两种情况。
如果不选择将其放⼊背包中,则不需要处理。
如果选择将其放⼊背包中,由于不清楚之前放⼊的物品占据了多⼤的空间,需要枚举将这个物品放⼊背包后可能占据背包空间的所有情况。
⼆、求解思路 当遇到这样的问题,我们可以换⼀种⾓度去思考,假设在⼀个100m3的房⼦⾥⾯,现在要将房⼦装满,同时要保证放⼊的物品个数最多以及装⼊的东西最重,现在⾝边有铁球和棉花,请问⼤家是放铁球进去好呢还是放棉花进去好呢?显⽽易见,放⼊铁球进去是最优选择。
但是原因是什么呢?很简单,就是因为铁球的密度较⼤,相同体积的铁球和棉花相⽐,铁球更重。
不过前提是放⼊第⼀个铁球时,铁球的体积V1⼩于等于100m3 ;放⼊第⼆个铁球时,铁球的体积V2 ⼩于等于(100-V1)m3;……;放⼊第n个铁球时,铁球的体积⼩于等于(100-∑n1Vn-1)m3 ,要是第n个铁球的体积⼤于(100- ∑n1Vn-1)m3 ,还真是不如放点单位体积更轻的棉花进去,说的极端点就是所有铁球的体积都⼤于100m3 ,还真不如随便放⼊点棉花进去合算。
所以总是放铁球进去,不考虑是否放⼊棉花,容易产⽣闲置空间,最终会得不到最优选择,可能只是最优选择的近似选择。
现在再次回到背包问题上,要使得背包中可以获得最⼤总价值的物品,参照铁球的例⼦我们可以知道选择单位重量下价值最⾼的物品放⼊为最优选择。
但是由于物品不可分割,⽆法保证能将背包刚好装满,最后闲置的容量⽆法将单位重量价值更⾼的物品放⼊,此时要是可以将单位重量价值相对低的物品放⼊,反⽽会让背包的总价值和单位重量的价值更⾼。
贪心算法背包问题c语言

贪心算法背包问题c语言朋友们!今天咱们要来聊一聊一个超级有趣的话题——贪心算法背包问题,而且还是用C语言来实现哦!想象一下,你现在要出去旅行,有一个容量有限的背包,而面前摆着各种各样的宝贝,每个宝贝都有它自己的价值和重量。
你得想办法在有限的背包容量里,尽可能多地装下价值高的宝贝,这可就像是一场和空间与价值的较量游戏啦!贪心算法呢,就像是一个超级聪明的小助手,它有自己独特的策略来帮你解决这个难题。
它的核心思想就是在每一步选择中,都做出当前看起来最优的决策,不考虑整体的最优解,就有点像那种“走一步看一步,但每一步都尽量往好处走”的感觉。
咱们先来看看用C语言实现贪心算法解决背包问题的基本思路哈。
我们得定义一些结构体来表示物品,结构体里包含物品的重量、价值,还有通过价值除以重量算出来的单位价值。
这个单位价值就像是一个小指标,告诉我们哪个物品相对来说更“值钱”。
接下来,就是排序的环节啦。
我们要按照物品的单位价值从大到小对这些物品进行排序。
这就好比你在挑选宝贝的时候,先把那些性价比最高的挑出来放在前面,准备优先往背包里塞。
然后呢,就是装背包的过程咯。
我们从单位价值最高的物品开始,一个一个地尝试往背包里装。
如果背包还能装得下这个物品,那就毫不犹豫地把它装进去,同时更新一下背包剩余的容量和已经装进去的物品的总价值。
要是背包已经装不下这个物品了,那咱也不气馁,就把这个物品按照比例拆分,装一部分进去,直到把背包填满为止。
下面是一段简单的C语言代码示例来实现这个过程:#include <stdio.h>.#include <stdlib.h>.// 定义物品结构体。
typedef struct {int weight;int value;float unitValue;} Item;// 比较函数,用于qsort排序。
int compare(const void *a, const void *b) {Item *itemA = (Item *)a;Item *itemB = (Item *)b;if (itemB->unitValue > itemA->unitValue).return 1;else if (itemB->unitValue < itemA->unitValue). return -1;else.return 0;}.// 贪心算法解决背包问题。
背包问题的贪心算法

背包问题的贪心算法(总8页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除贪心方法:总是对当前的问题作最好的选择,也就是局部寻优。
最后得到整体最优。
应用:1:该问题可以通过“局部寻优”逐步过渡到“整体最优”。
贪心选择性质与“动态规划”的主要差别。
2:最优子结构性质:某个问题的整体最优解包含了“子”问题的最优解。
代码如下:#include <>struct goodinfo{float p; >goods[i].p) { goods[i+1]=goods[i]; i--; } goods [i+1]=goods[0]; }}=0;cu=M; >cu)=1;cu=cu-goods[i].w;=cu/goods[i].w;lag<goods[i].flag){goods[i+1]=goods[i];i--;}goods[i+1]=goods[0];}<<endl; }}void main(){cout<<"|--------运用贪心法解背包问题---------|"<<endl;cout<<"|---power by zhanjiantao(0)---|"<<endl;cout<<"|-------------------------------------|"<<endl;int j;int n;float M;goodinfo *goods;lag=i; cout<<"请输入第"<<i<<"件物品的重量:"; cin>>g oods[i].w; cout<<"请输入第"<<i<<"件物品的效益:"; cin>>goods[i].p; goods[i].p=goods[i].p/goods[i].w;//得出物品的效益,重量比cout<<en dl; }Insertionsort(goods,n); bag(goods,M,n); cout<<"press <1> to run agian"<<end l; cout<<"press <0> to exit"<<endl; cin>>j; }}#include<>#include<>#define Max 100/*定义栈结构*/typedef struct list{ int data[Max]; int top;}Seqstack; /*定义一个用来存储结果的链表*/typedef struct List{ Seqstack result; struct List * Next;}Seqlist,*Pointer;void Inicial_List(Pointer p){ p=(Pointer)malloc(sizeof(Seqlist));p->Next=NULL;}Seqstack Push_Stack(int n,Seqstack s){ ++;[]=n;return s;}int Add_Stack(Seqstack s){Int total=0,i;if>=0){ for(i=0;i<=;i++)total+=[i];}else{ total=0; }return total;}Seqstack Pop_Stack(Seqstack s){printf("%d",[]);if>=0);return s;}/*执行回溯操作的函数*//*参数说明:n->数的总的个数,a[]用来存放数的数组,k查找的总体积*/Pointer Query_Result(int n,int b[],int k){ int i,j;Seqstack mystack;Seqlist *newnode;Pointer r,p=NULL;Inicial_List(p);r=p; for(i=0;i<n;i++){ =-1;j=i;while(j<n){if(Add_Stack(mystack)+b[j]<k){ mystack=Push_Stack(b[j],mystack);j++; }else if(Add_Stack(mystack)+b[j]==k){ mystack=Push_Stack(b[j],mystack);newnode=(Pointer)malloc(sizeof(Seqlist));newnode->result=mystack;newnode->Next=NULL;r->Next=newnode;r=newnode;mystack=Pop_Stack(mystack);j++;}else if(Add_Stack(mystack)+b[j]>k){}}}return p;}void Print_List(Pointer p){int i,j=0;p=p->Next;printf("welcome the outer\n");if(p==NULL)printf("there no results\n");while(p!=NULL){j++;printf("the %d result is: ",j);for(i=0;i<=p->;i++){ printf(" %d",p->[i]);}p=p->Next;printf("\n"); }printf("\n");}void Sort_Array(int b[],int n){int i,j,temp;for(i=0;i<n;i++){ for(j=0;j<n-i;j++){ if(b[j]<b[j+1]){ temp=b[j];b[j]=b[j+1];b[j+1]=temp;}}}}void main(){int i,n,k,select,a[Max];Pointer head;printf("******************************************\n"); printf ("1 start\n2 exit\n");scanf("%d",&select);while(select==1)printf("please input the total products\n");scanf("%d",&n);printf("please input the volumn of n products\n");for(i=0;i<n;i++){printf("please input the %d integers",i+1);scanf("%d",&a[i]);}printf("\n");printf("please input the volunm to put\n");scanf("%d",&k);Sort_Array(a,n);head=Query_Result(n,a,k);Print_List(head);printf("******************************************\n");printf("1 start\n2 exit\n"); scanf("%d",&select);}}#include<>#include<>#define Max 100/*定义栈结构*/typedef struct list{ int data[Max]; int top;}Seqstack; /*定义一个用来存储结果的链表*/typedef struct List{Seqstack result;struct List * Next;}Seqlist,*Pointer;void Inicial_List(Pointer p){p=(Pointer)malloc(sizeof(Seqlist));p->Next=NULL;}Seqstack Push_Stack(int n,Seqstack s){ ++;[]=n;return s;}int Add_Stack(Seqstack s){ int total=0,i;if>=0){for(i=0;i<=;i++)total+=[i];}else{total=0;}return total;}Seqstack Pop_Stack(Seqstack s){printf("%d",[]);if>=0); return s;}/*执行回溯操作的函数*//*参数说明:n->数的总的个数,a[]用来存放数的数组,k查找的总体积*/Pointer Query_Result(int n,int b[],int k){int i,j;Seqstack mystack;Seqlist *newnode;Pointer r,p=NULL;Inicial_List(p);r=p;for(i=0;i<n;i++){=-1;j=i;while(j<n){if(Add_Stack(mystack)+b[j]<k){mystack=Push_Stack(b[j],mystack);j++;}else if(Add_Stack(mystack)+b[j]==k){mystack=Push_Stack(b[j],mystack);newnode=(Pointer)malloc(sizeof(Seqlist)); newnode->result=mystack;newnode->Next=NULL;r->Next=newnode;r=newnode;mystack=Pop_Stack(mystack);j++;}else if(Add_Stack(mystack)+b[j]>k){j++;}}}return p;}void Print_List(Pointer p){int i,j=0;p=p->Next;printf("welcome the outer\n");if(p==NULL)printf("there no results\n");while(p!=NULL){j++;printf("the %d result is: ",j);for(i=0;i<=p->;i++){printf(" %d",p->[i]);}p=p->Next;printf("\n");}printf("\n");}void Sort_Array(int b[],int n){int i,j,temp;for(i=0;i<n;i++) { for(j=0;j<n-i;j++){if(b[j]<b[j+1]){temp=b[j];b[j]=b[j+1];b[j+1]=temp;}}}}void main(){int i,n,k,select,a[Max]; Pointer head;printf("******************************************\n"); printf("1 start\n2 exit\n"); scanf("%d",&select);while(select==1){printf("please input the total products\n");scanf("%d",&n);printf("please input the volumn of n products\n");for(i=0;i<n;i++){printf("please input the %d integers",i+1);scanf("%d",&a[i]); } printf("\n");printf("please input the volunm to put\n");scanf("%d",&k); Sort_Array(a,n);head=Query_Result(n,a,k);Print_List(head);printf("******************************************\n"); printf("1 start\n2 exit\n");scanf("%d",&select);}}。
贪心算法之背包问题

贪⼼算法之背包问题贪⼼算法(⼜称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪⼼算法不是对所有问题都能得到整体最优解,关键是贪⼼策略的选择,选择的贪⼼策略必须具备⽆后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
完全背包问题:给定n个物品和⼀个容量为C的背包,物品i的重量是Wi,其价值为Vi,背包问题是如何选择⼊背包的物品,使得装⼊背包的物品的总价值最⼤,与0-1背包的区别是,在完全背包问题中,可以将物品的⼀部分装⼊背包,但不能重复装⼊。
设计算法的思路很简单,计算物品的单位价值,然后尽可能多的将单位重量价值⾼的物品放⼊背包中。
python实现代码如下:1# coding=gbk2# 完全背包问题,贪⼼算法3import time4__author__ = 'ice'567class goods:8def__init__(self, goods_id, weight=0, value=0):9 self.id = goods_id10 self.weight = weight11 self.value = value121314# 不适⽤于0-1背包15def knapsack(capacity=0, goods_set=[]):16# 按单位价值量排序17 goods_set.sort(key=lambda obj: obj.value / obj.weight, reverse=True)18 result = []19for a_goods in goods_set:20if capacity < a_goods.weight:21break22 result.append(a_goods)23 capacity -= a_goods.weight24if len(result) < len(goods_set) and capacity != 0:25 result.append(goods(a_goods.id, capacity, a_goods.value * capacity / a_goods.weight))26return result272829 some_goods = [goods(0, 2, 4), goods(1, 8, 6), goods(2, 5, 3), goods(3, 2, 8), goods(4, 1, 2)]3031 start_time = time.clock()32 res = knapsack(6, some_goods)33 end_time = time.clock()34print('花费时间:' + str(end_time - start_time))3536for obj in res:37print('物品编号:' + str(obj.id) + ' ,放⼊重量:' + str(obj.weight) + ',放⼊的价值:' + str(obj.value), end=',')38print('单位价值量为:' + str(obj.value / obj.weight))394041# 花费时间:2.2807240614677942e-0542# 物品编号:3 ,放⼊重量:2,放⼊的价值:8,单位价值量为:4.043# 物品编号:0 ,放⼊重量:2,放⼊的价值:4,单位价值量为:2.044# 物品编号:4 ,放⼊重量:1,放⼊的价值:2,单位价值量为:2.045# 物品编号:1 ,放⼊重量:1,放⼊的价值:0.75,单位价值量为:0.75。
第8章贪心算法-分数背包问题

贪心算法:
算法GREEDY_KANPSACK
输入:表示背包容量的实数C,物品数n,表示n个物品的体积和价值的实数数组s[1..n]和v[1..n]。
输出:装入背包物品的最大总价值maxv和相应的最优解x[1..n]。
for i=1 to n
y[i]=v[i]/s[i]//求n个物品的单位体积价值y[1..n]。
end for
//对y[1..n]按降序地址排序,排序结果返回到数组d[1..n]//中,使得
y[d[1]]>=y[d[2]]>=…>=y[d[n]]。
d=sort(y, n)
for i=1 to nx[i]=0//对x[1..n]初始化。
i=1;maxv=0;rc=C//以下rc表示当前背包的剩余容量。
while rc>0 and i<=n
j=d[i]// u
j为当前考虑选择的物品
if s[j]<=rc then
x[j]=1;rc=rc-s[j]//物品u
j全部装入背包。
else
x[j]=rc/s[j]//选择物品u
j的一部分将背包填满。
rc=0
end if
maxv=maxv+v[j]*x[j]
i=i+1
end while
return maxv, x[1..n]
end GREEDY_KNAPSACK
●算法的时间复杂性:Θ(nlogn)
间)
思考:0/1背包问题可否用贪心法解?(主要为排序的时。
贪心法求解背包问题

问题描述
•
已知有n种物品和一个可容纳M重量的背包,每种物品i的重 量为。假定将物品i的一部分放入背包就会得到的效益,这里,, 。显 然,由于背包容量是M,因此,要求所有选中要装入背包的物品总重 量不得超过M.。如果这n件物品的总重量不超过M,则把所有物品装 入背包自然获得最大效益。现需解决的问题是,在这些物品重量的和 大于M的情况下,该如何装包,使得得到更大的效益值。由以上叙述, 可将这个问题形式表述如下: p i xi • 极 大 化目标函数 1i n • 约束条件 wi xi M • 1i n
0 xi 1, pi 0, wi 0,1 i n
算法分析
•
首先需确定最优的量度标准。这里考虑三种策略: • 策略1:按物品价值p降序装包, • 策略2:按物品重w升序装包 • 策略3:按物品价值与重量比值p/w的降序装包 分别以上面三种策略分别求以下情况背包问题的解: • n=7,M=15, 7 • ( p1 ,, p) =(10,5,15,7,6,18,3) • ( w1 ,, w7)=(2,3,5,7,1,4,1)
结果
The end,thank you!
请提问!
与其他算法比较
• 1.贪心法:处理问题的速度快,思想简单。使用该方法的 必要条件是寻找好的贪心法则。不足之处在于很多时候它 只能求的似优解,却不能求的最优解 • 2.动态规划法:可以求解最优解,重点在于徐兆最优决策 序列但是速度较慢。 • 3.分支限界法:可以求解最优解,重点在于寻找限界值。 易求最优解,但是空间花费较高,效率不是很高。 • பைடு நூலகம்择哪一种算法,不仅要根据问题本身还需要考虑到其他 因素,例如时间复杂度,空间复杂度,易求解等等因素。
贪心算法 背包问题

17 if (temp < tempArray[j])
18 {
19 temp = tempArray[j];
20 index = j;
22 {
23 temp = tempArray[j];
24 index = j;
25 }
26 }
27
28 if (sortResult[index] == 0)
17 index = i;
18
19 for (j = i; j < n; j++)
20 {
21 if ((temp < tempArray[j]) && (sortResult[j] == 0))
temp = sortResult[i];//得到取物体的顺序
if (w[temp] > cu)
{
break;
}
x[temp] = 1;//若合适则取出
cu -= w[temp];//将容量相应的改变
}
if (i <= n)//使背包充满
1 -107374176.000000 1 1.600000 2 1.600000
after arithmetic data: x[i]
0.000000 0.333333 0.000000
可以看到其效益为x[3] = {1.4, 1.6, 1.5},于是在M = 20的情况下,其预想中的输出结果是0,1,0.5。然而事实上是不是就这样呢?
问题就在这里了!排序后的w[i] = {1.6, 1.6, 1.5},因此对w[i]排序后就既改变了w[i]的原有顺序,还改变了w[i]的原来值!
算法分析与设计-贪心算法求解背包问题

算法分析与设计-贪心算法求解背包问题用贪心算法求解背包问题D软件101 薛思雨511020825一、贪心算法介绍顾名思义,贪心算法总是作出在当前看来最好的选择。
也就是说贪心算法并不从整体最优考虑,它所作出的选择只是在某种意义上的局部最优选择。
当然,希望贪心算法得到的最终结果也是整体最优的。
虽然贪心算法不能对所有问题都得到整体最优解,但对许多问题它能产生整体最优解。
如单源最短路经问题,最小生成树问题等。
在一些情况下,即使贪心算法不能得到整体最优解,其最终结果却是最优解的很好近似。
贪心算法求解的问题一般具有两个重要性质:贪心选择性质和最优子结构性质。
所谓贪心选择性质是指所求问题的整体最优解可以通过一系列局部最优解的选择,即贪心选择来达到。
这是贪心算法可行的第一个基本要素,也是贪心算法与动态规划算法的主要区别。
当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
问题的最优子结构性质是该问题可用动态规划算法或贪心算法求解的关键特征。
二、贪心法的基本思路从问题的某一个初始解出发逐步逼近给定的目标,以尽可能快的地求得更好的解。
当达到某算法中的某一步不能再继续前进时,算法停止。
该算法存在问题:1. 不能保证求得的最后解是最佳的;2. 不能用来求最大或最小解问题;3. 只能求满足某些约束条件的可行解的范围。
三、关于贪心算法在背包问题中的应用的探讨①问题描述:0-1背包问题:给定n种物品和一个背包。
物品i的重量是Wi,其价值为Vi,背包的容量为C。
应如何选择装入背包的物品,使得装入背包中物品的总价值最大? 在选择装入背包的物品时,对每种物品i 只有2种选择,即装入背包(1)或不装入背包(0)。
不能将物品i装入背包多次,也不能只装入部分的物品i。
背包问题:与0-1背包问题类似,所不同的是在选择物品i装入背包时,可以选择物品i的一部分,而不一定要全部装入背包,1≤i≤n。
②贪心算法解决背包问题有几种策略:(i) 一种贪婪准则为:从剩余的物品中,选出可以装入背包的价值最大的物品,利用这种规则,价值最大的物品首先被装入(假设有足够容量),然后是下一个价值最大的物品,如此继续下去。
贪心算法求解背包问题C语言描述

贪心算法求解背包问题:#include<stdio.h>#define maxnumber 20typedef struct node{float w;float v;int i;}Object;float find(Object wp[],int n,float M) {float x[maxnumber];int i;float maxprice=0;for(i=1;i<=n;i++)//初始化x[n];{x[i]=0.0;}i=0;while(wp[i].w < M){x[wp[i].i]=1;M=M-wp[i].w;i++;}x[wp[i].i]=M/wp[i].w;//输出解向量printf("解向量是:\n");for(i=1;i<=n;i++){printf("x[%d]=%f",i,x[i]);}printf("\n");//计算最大价值for(i=0;i<n;i++){maxprice=maxprice+wp[i].v*x[wp[i].i];}return maxprice;}void main(){Object wp[maxnumber];int i,j,n;float C;//背包的重量int flag;float maxprice,temp;printf("请输入物品的种数:");scanf("%d",&n);printf("请输入背包的重量:");scanf("%f",&C);printf("\n请输入物品的序号、重量和价值:");for(i=0;i<n;i++){scanf("%d",&wp[i].i);scanf("%f",&wp[i].w);scanf("%f",&wp[i].v);}printf("\n输入的物品是:\n");//输出物品for(i=0;i<n;i++){printf(" %d",wp[i].i);printf(" %f",wp[i].w);printf(" %f",wp[i].v);printf("\n");}//用冒泡排序对物品按照单位价值进行降序排序for(i=1;i<n;i++){flag=0;for(j=n-1;j>=i;j--){if(wp[j-1].v/wp[j-1].w < wp[j].v/wp[j].w){temp=wp[j-1].i;wp[j-1].i=wp[j].i;wp[j].i=temp;temp=wp[j-1].w;wp[j-1].w=wp[j].w;wp[j].w=temp;temp=wp[j-1].v;wp[j-1].v=wp[j].v;wp[j].v=temp;flag=1;}if(flag==0)break;}}printf("\n排序后的物品是:\n");//输出物品for(i=0;i<n;i++){printf(" %d",wp[i].i);printf(" %f",wp[i].w);printf(" %f",wp[i].v);printf("\n");}maxprice=find(wp,n,C);printf("\n物品的重价值为:%f",maxprice);}。
贪心算法实现背包问题算法设计与分析实验报告

算法设计与分析实验报告实验名称 贪心算法实现背包问题 评分 实验日期 年 月 日 指导教师 姓名 专业班级 学号一.实验要求1. 优化问题有n个输入,而它的解就由这n个输入满足某些事先给定的约束条件的某个子集组 成,而把满足约束条件的子集称为该问题的可行解。
可行解一般来说是不唯一的。
那些使目标函数取极值(极大或极小)的可行解,称为最优解。
2.贪心法求优化问题算法思想:在贪心算法中采用逐步构造最优解的方法。
在每个阶段,都作出一个看上去最优的决策(在一定的标准下)。
决策一旦作出,就不可再更改。
作出贪心决策的依据称为贪心准则(greedy criterion)。
3.一般方法1)根据题意,选取一种量度标准。
2)按这种量度标准对这n个输入排序3)依次选择输入量加入部分解中。
如果当前这个输入量的加入,不满足约束条件,则不把此输入加到这部分解中。
procedure GREEDY(A,n) /*贪心法一般控制流程*///A(1:n)包含n个输入//solutions←φ //将解向量solution初始化为空/for i←1 to n dox←SELECT(A)if FEASIBLE(solution,x)then solutions←UNION(solution,x)endifrepeatreturn(solution)end GREEDY4. 实现典型的贪心算法的编程与上机实验,验证算法的时间复杂性函数。
二.实验内容1. 编程实现背包问题贪心算法。
通过具体算法理解如何通过局部最优实现全局最优,并验证算法的时间复杂性。
2.输入5个的图的邻接矩阵,程序加入统计prim算法访问图的节点数和边数的语句。
3.将统计数与复杂性函数所计算比较次数比较,用表格列出比较结果,给出文字分析。
三.程序算法1. 背包问题的贪心算法procedure KNAPSACK(P,W,M,X,n)//P(1:n)和W(1;n)分别含有按P(i)/W(i)≥P(i+1)/W(i+1)排序的n件物品的效益值和重量。
背包问题的贪心算法

方法一
1、 贪心选择方法:我们根据输入的序列构造一个新的序列:P1/W1, P2/W2, …, Pn/Wn;这序 列表示的含义是每件物品单位重量的价值;我们对这个序列进行从大到小排序,按照这 个排序进行选择物品装入包中, 直到包装满为止, 对于最后一件物品可能不能完全装入, 只能装入一部分。 2、 贪心选择性证明:假设序列 P1/W1, P2/W2, …, Pn/Wn 从大到小排序后的第一个值的下标为 k, 表示物品 k 的单位重量的价值最大, 那么我们要证明的是存在一个最优解 A 包含 Xk, 并且若 M≥Wk,则 Xk=1;否则 Xk=M/Wk。 证明:假设 B 是问题的一个最优解,如果 B 包含 Xk,且满足“若 M≥Wk,则 Xk=1;否 则 Xk=M/Wk” ,那么令 A=B,B 就是我们所要寻找的最优解,问题得证。否则,如果 B 中 不包含 Xk 或者是如果 B 包含 Xk 但是不满足“若 M≥Wk,则 Xk=1;否则 Xk=M/Wk” ,可 能是当 M≥Wk 时 Xk<1;或者当 M<Wk 时 Xk< M/Wk。无论何种情况,我们用 H 表示满足 条件“若 M≥Wk,则 Xk=1;否则 Xk=M/Wk”时的 Xk 的取值。用 V(A),V(B)分别表示问题 解为 A 和 B 时的包中物品的价值总和。我们这样来通过 B 构造 A:从 B 的解的包中,任 意取出重为 H*Wk 的物品(这些物品可能是一种,也可能是多种),假设其价值为 V’,包 中剩下的物品价值为 V’’(即 V(B)=V’+V’’),我们再把百分比为 H 的物品 k 装入背包中,这 样构成解 A,下面我们证明 A 是最优解。V(A)=V’’+H*Pk,V(B)=V’+V’’,因为(Pk/Wk)是所 有物品中的最大值,所以在重量均为 H*Wk 的情况下,(Pk/Wk)*( H*Wk)= H*Pk≥V’,所以 V(A)≥V(B);又因为 B 是最优解,所以 V(B)≥V(A)。综上,有 V(A)=V(B),所以 A 也是最 优解,既而得证。 3、 最优子结构的证明: 原问题的解的形式为 Xi1, Xi2, Xi3, …, Xin; 子问题为从物品 S={i2, i3, …, in} 中选择物品,使得
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
贪心算法:
算法GREEDY_KANPSACK
输入:表示背包容量的实数C,物品数n,表示n个物品的体积和价值的实数数组s[1..n]和v[1..n]。
输出:装入背包物品的最大总价值maxv和相应的最优解x[1..n]。
for i=1 to n
y[i]=v[i]/s[i]//求n个物品的单位体积价值y[1..n]。
end for
//对y[1..n]按降序地址排序,排序结果返回到数组d[1..n]//中,使得
y[d[1]]>=y[d[2]]>=…>=y[d[n]]。
d=sort(y, n)
for i=1 to nx[i]=0//对x[1..n]初始化。
i=1;maxv=0;rc=C//以下rc表示当前背包的剩余容量。
while rc>0 and i<=n
j=d[i]// u
j为当前考虑选择的物品
if s[j]<=rc then
x[j]=1;rc=rc-s[j]//物品u
j全部装入背包。
else
x[j]=rc/s[j]//选择物品u
j的一部分将背包填满。
rc=0
end if
maxv=maxv+v[j]*x[j]
i=i+1
end while
return maxv, x[1..n]
end GREEDY_KNAPSACK
●算法的时间复杂性:Θ(nlogn)
间)
思考:0/1背包问题可否用贪心法解?(主要为排序的时。
