数学建模飞机运输问题要点
数学建模之运输问题

数学建模之运输问题1. 引言运输问题是指在给定产地到销售地之间有若干个供应点和需求点的情况下,如何安排运输使得总运输成本最低。
这是一个经济管理中的经典问题,也是数学建模中常见的一个研究方向。
2. 问题描述假设有n个供应点和m个需求点,其中每个供应点的供应量和每个需求点的需求量已知,并且每个供应点到每个需求点的运输成本也已知。
我们的目标是确定供应点到需求点的运输量,使得总运输成本最小。
3. 模型建立为了建立数学模型,我们可以引入一个矩阵来表示供应点和需求点之间的运输成本。
设C为一个n行m列的矩阵,其中Cij表示供应点i到需求点j的运输成本。
我们需要引入决策变量X,其中Xij表示从供应点i到需求点j的运输量。
那么,目标函数可以定义为最小化总运输成本,即$$\min \sum_{i=1}^{n} \sum_{j=1}^{m} C_{ij} X_{ij}$$同时,我们需要保证供应点和需求点的供需平衡,即满足每个供应点的供应量和每个需求点的需求量。
这可以表示为以下约束条件:1. 对于每个供应点i,有 $\sum_{j=1}^{m} X_{ij} = s_i$,其中$s_i$ 表示供应点i的供应量。
2. 对于每个需求点j,有 $\sum_{i=1}^{n} X_{ij} = d_j$,其中$d_j$ 表示需求点j的需求量。
进一步地,我们需要确保运输量的非负性,即$X_{ij} \geq 0$。
4. 求解方法对于较小规模的问题,我们可以使用线性规划方法求解运输问题。
线性规划是一种数学优化方法,可以在满足一定约束条件的前提下,使得目标函数达到最小值。
对于大规模的问题,我们可以使用近似算法或启发式算法进行求解。
这些算法可以快速找到较好的解,但不能保证找到最优解。
常用的算法包括模拟退火算法、遗传算法等。
5. 应用领域运输问题在许多实际应用中都有广泛的应用。
例如,在物流管理中,优化运输方案可以减少运输成本、提高运输效率;在生产计划中,合理安排运输可以确保供应链的稳定性和高效性。
数学建模 飞机运输问题

设4个月飞行员中教练为u1, u2, u3, u4人,新 飞行员数量分别为w1, w2, w3, w4人。其它 符号不变。飞行员的数量限制约束为 第1个月:300+u1+v1=330 第2个月:450+u2+v2= u1+v1+w1, w1<=20u1 第3个月:450+u3+v3= u2+v2+240+w2, w2<=20u2 第4个月:600+u4+v4= u3+v3+360+w3, w3<=20u3
优化目标是:
Min
200x1+195x2+190x3+185x4+10u1+9.9 u2+9.8u3+9.7u4+7v1+6.9v2+6.8v3+6.7 v4
新购买的飞机数量:x1, x2, x3, x4 飞行员中教练和新飞行员数量:u1, u2, u3, u4 闲置的的熟练飞行员数量:v1, v2, v3, v4
约束条件
1)飞机数量限制:4个月中执行飞行任务的飞 机分别为100, 150, 150, 200架,但只有80, 120, 120, 160架能够返回供下个月使用。 第1个月:100+ y1=110 第2个月:150+ y2=80+ y1+ x1 第3个月:150+ y3=120+ y2+ x2 第4个月:200+ y4=120+ y3+ x3 闲置的飞机数量:y1, y2, y3, y4 新购买的飞机数量:x1, x2, x3, x4
用LINDO求解得到: VARIABLE VALUE X1 60.000000 X2 30.000000 X3 80.000000 X4 0.000000 U1 460.000000 U2 220.000000 U3 240.000000 U4 0.000000 V1 7.000000 V2 6.000000 V3 4.000000 V4 4.000000 Y1 10.000000 Y2 0.000000 Y3 0.000000 Y4 0.000000
数学建模-(货机装运Lingo)

约束条件
在货机装运问题中,通常需要考虑 多个约束条件,如货机的载重限制、 货物的体积限制、货物的装卸顺序 等。
优化目标
优化目标可以是最大化货机的装载 量、最小化装载成本、最大化利润 等。
数据分析与预处理
数据收集
数据清洗
收集与货机装运问题相关的数据,包括货 物的重量、体积、价值等信息,以及货机 的载重、容积等限制条件。
数据输入输出
介绍如何使用Lingo进行数据输入和 结果输出,包括数据文件的读写、图 形化界面的使用等。
Lingo在货机装运问题中的应用
问题描述
阐述货机装运问题的背景和实际意义,明确问题的目标和约束条件。
建模过程
详细讲解如何使用Lingo对货机装运问题进行数学建模,包括定义变 量、建立目标函数和约束条件等步骤。
货机装运是物流领域的重要问题,涉 及到如何有效利用货机容量,将不同 规格、重量的货物进行合理搭配,以 达到最优的装载方案。
提高运输效率
通过数学建模对货机装运问题进行优 化,可以提高货物的运输效率,减少 运输成本,为企业带来经济效益。
建模的重要性和应用
重要性
数学建模是一种将实际问题抽象化、形式化的方法,通过建立数学模型,可以对问题进行深入分析,找出问题的 本质和规律,为解决问题提供科学依据。
应用
数学建模在物流、交通、金融、工程等领域有着广泛的应用。在货机装运问题中,数学建模可以帮助企业制定最 优的装载方案,提高运输效率,降低成本。同时,数学建模也可以应用于其他类似的问题,如车辆路径问题、背 包问题等。
02 问题描述与数据分析
02 问题描述与数据分析
货机装运问题描述
货机装运问题
货机装运问题是一个经典的优化 问题,涉及到如何有效地将货物 装入货机以最大化利润或最小化
数学建模,线性规划,运输为问题

X31 30.00000 0.000000
X32 20.00000 0.000000
X33 0.000000 3.000000
X34 0.000000 11.00000
X35 0.000000 23.00000
X36 0.000000 8.000000
X41 0.000000 7.000000
Objective value: 1620.000
Infeasibilities: 0.000000
Total solver iterations: 9
Variable Value Reduced Cost
X11 0.000000 14.00000
X12 0.000000 6.000000
X13 0.000000 4.000000
X55 0.000000 8.000000
X56 0.000000 32.00000
X64 30.00000 0.000000
X65 0.000000 3.000000
X66 0.000000 7.000000
Row Slack or Surplus Dual Price
1 1620.000 -1.000000
X42 0.000000 0.000000
X43 40.00000 0.000000
X44 0.000000 26.00000
X45 0.000000 16.00000
X46 0.000000 13.00000
X52 30.00000 0.000000
X53 0.000000 0.000000
X54 0.000000 21.00000
供应限制:x11+x12+x13+x14+x15+x16=20
第9章 航空运输问题

第九章
Matlab数学建模案例分析
Variable
Value X1 X2 X3
的利润的变化。
第九章
Matlab数学建模案例分析
在问题三中,针对改造飞机是否将带来公司的利润增加的问 题。在此,只需在满足公司的每天货运能力即约束条件,将改
造飞机后公司的收益和改造前公司的收益进行对比,如果收益
增加便值得改造。得到要改造1.25架飞机使的收益最大;最终 计算可得改造一架旧飞机、改造二架旧飞机、改造三架旧飞机 、改造四架旧飞机均使公司利润提升;而改造五架旧飞机时平 每天均收益为24200美元,和不改造飞机的24218.75美元收益作 对比,可以得到改造五架飞机公司将在原来基础上亏损。故在 假设基础上,可以改装四架旧飞机,公司将盈利。但实际中很
第九章 9.5.2 模型的建立与求解
Matlab数学建模案例分析
max Q1 250x1 250x 2 250x3 s.t x1 x 2 x3 100 550x1 800x 2 400x3 50000 0 x1 30 0 x 2 40 0 x3 50
这是一个实际问题,主要针对一个航空运输公司的营业模型的分析及优化 处理,在此运用数学建模的相关理论知识可求解得到优化的市场营业模型, 以此制定最优化营业方式。 此题中,成本是未知量,我们可以不考虑成本的影响,只求出营业额的最 大值即可,由于净利润=营业额-成本,故净利润也相应的较高,也就是营业 方式的最优化。 对于问题一,主要针对求该运输公司的最大利润,我们只需将三种货物在 运输公司要求的体积和质量等的多重约束下,按照某个比例搭配得到最优化 解,得到利润的最大值,利用线性规划模型便易得到一个数学模型,并利用 LINDO 软件求解此模型。在此模型中,求得当运输货物一为 30 吨,货物二 16.875吨,货物三50吨时取得最大收益24218.75美元。
数学建模

货机装运模型问题重述:一架货机有三个货舱:前舱、中舱和后舱。
三个货舱所能装载的货物的最大重量和体积有限制如下表所示。
并且为了飞机的平衡,三个货舱共装载的货物重量必须与其最大的容许量成比例。
应如何安排装运,使得货机本次飞行获利最大?模型假设:(1)每种货物可以无限细分;(2)每种货物可以分布在一个或者多个货舱内;(3)不同的货物可以放在同一个货舱内,并且可以保证不留空隙。
模型建立:决策变量:每种货物放在每个货舱内的重量。
用xij表示第i种货物放在第j 个货舱内的重量,i =1,2,3,4 分别表示货物1,货物2,货物3 和货物4。
j =1,2,3 分别表示前舱、中舱和后舱。
决策目标:总利润的最大化,目标函数为3100( x11 + x12+ x13) +3800( x21+ x22+ x23) +3500( x31+ x32+ x33) + 2850( x41+ x42+ x43)⎪ 约束条件:(1) 供装载的四种货物的总重量约束,⎧ x 11 + x 12 + x 13 ≤ 18 ⎪x 21 + x 22 + x 23 ≤ 15 ⎨⎪x 31 + x 32 + x 33 ≤ 23 x 41 + x 42 + x 43 ≤ 12(2) 三个货舱的空间限制⎪⎪⎧480x 11 + 650x 21 + 580x 31 + 390x 41 ≤ 6800 ⎪⎨480x 12 + 650x 22 + 580x 32 + 390x 42 ≤ 8700 ⎩480x 13 + 650x 23 + 580x 33 + 390x 43 ≤ 5300(3) 三个货舱的重量限制⎧x 11 + x 21 + x 31 + x 41 ≤ 10 ⎪⎨x 12 + x 22 + x 32 + x 42 ≤ 16 ⎩x 13 + x 23 + x 33 + x 43 ≤ 8(4) 三个货舱装入重量的平衡约束x 11 + x 21 + x 31 + x 41= x 12 + x 22 + x 32 + x 42 = x 13 + x 23 + x 33 + x 4310 16 8模型求解:使用计算软件求解(在 M ATLAB 中,可以使用 l inprog 命令求解) 求解结果为:( x 1 ; x 2 ; x 3 ; x 4 ) = (0,0,0;10,0,5;0,12.947,3, ;0,3.053,0)MATLAB 实现线性规划的运算为了避免这种形式多样性带来的不便,Matlab 中规定线性规划的标准形式为minc Txsuch thatAx ≤ b Aeq ⋅ x = beqlb ≤ x ≤ ub其中 c 和 x 为 n 维列向量, A 、 A eq 为适当维数的矩阵, b 、 b eq 为适当维数的列向量。
数学建模-(货机装运Lingo)
如何装运, 使本次飞行 获利最大?
货机装运
模型假设
每种货物可以分割到任意小; 每种货物可以在一个或多个货舱中任意分布; 多种货物可以混装,并保证不留空隙;
模型建立
决策 变量 xij--第i 种货物装入第j 个货舱的重量(吨)
i=1,2,3,4, j=1,2,3 (分别代表前、中、后仓)
货机装运
模型建立
• • • • • • • •
model: sets: hw/1..4/: w,v,c; hc/1..3/: m,v1; links(hw,hc): x; endsets !目标函数; max=@sum(hw(I):c(I)*@s um(hc(J):x(I,J)));
• !货舱重量约束; • @for(hc(J):@sum(hw(I): x(I,J))<=m(J)); • !货舱容积约束; • @for(hc(J):@sum(hw(I): v(I)*x(I,J))<=v1(J)); • !平衡约束; • @for(hc(J)|J#lt#3:@sum(hw (I): x(I,J))/m(J)=@sum(hw(I): x(I,J+1))/m(J+1)); • !货物供应约束; • @for(hw(I): • @sum(hc(J): x(I,J))<=w(I));
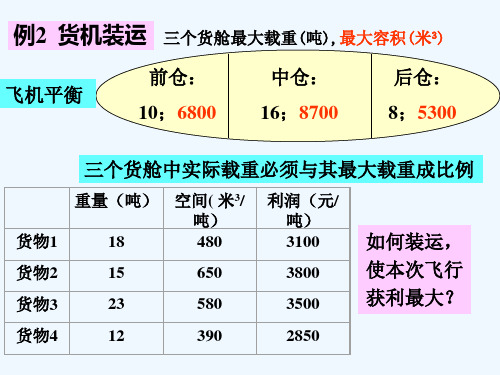
例2 货机装运
飞机平衡
三个货舱最大载重(吨),最大容积(米3)
前仓: 10;6800
中仓: 16;8700
后仓: 8;5300
三个货舱中实际载重必须与其最大载重成比例
重量(吨) 空间( 米3/ 吨) 18 480 货物1 货物2 货物3 货物4 15 23 12 650 580 390 利润(元/ 吨) 3100 3800 3500 2850
数学建模-(货机装运lingo)

数学建模-(货机装运lingo)货机装运是指将货物从一个起点运输到一个终点,在这个过程中需要考虑到货物的重量、体积、运输方式等多种因素。
在货机装运过程中,一个关键问题是如何最大化运载效率,即在保证运输安全和合法的前提下,尽可能地提高货机的装载量,从而降低单位运输成本。
在数学建模中,可以使用lingo等工具进行货机装运的优化。
具体来说,可以将该问题抽象为一个数学模型,以最大化货机的装载量为目标函数,同时考虑到运输安全、货物重量、体积等约束条件。
下面以一个具体例子来说明如何使用lingo进行货机装运的优化:假设有一架货机,其载重量为10000公斤,可以装载两种货物A和B,每种货物的重量和体积如下:货物类型重量(公斤)体积(立方米)A 600 1.5B 400 0.8同时,从起点到终点的运输费用如下:货物类型运输费用(元/公斤)A 10B 15要求在保证运输安全和合法的前提下,最大化货机的装载量,即:subject to:A +B <= 10000(装载量不超过10000公斤)其中,A和B表示货机装载的货物A和B的数量,V是货机的装载体积,运输费用是由货物类型和运输距离等因素决定的,这里简化为一个固定值。
使用lingo进行求解的过程如下:1.首先,在lingo中创建一个新的模型文件,并定义目标函数和约束条件:2.对模型进行求解,并设置模型参数:model:solve;parameters:V = 15;end;在上述代码中,V表示货机的装载体积,这里假设为15立方米。
solve表示对模型进行求解,通过设置end来结束参数定义。
3.对求解结果进行分析和优化,例如考虑不同装载体积下的最优解:for V := 15 to 20 dobeginwriteln('Optimal value for V=',V,': ',model.obj);在以上代码中,for循环遍历不同的装载体积值(15到20),分别求解模型并输出优化结果。
数学在航空运输中的优化

数学在航空运输中的优化航空运输作为现代城市之间最常见的交通方式之一,具有速度快、安全性高等特点,得到了广大乘客的青睐。
然而,在航空运输领域中,有很多复杂的问题需要解决,例如航班调度优化、飞机燃油消耗减少等。
而数学作为一门重要的科学,其在航空运输中的应用也变得日益重要。
本文将重点探讨数学在航空运输中的优化应用。
一、航班调度优化航班调度是航空公司管理的重要方面之一,合理的航班调度可以使得航空公司的运营效率得到最大化。
数学在航班调度中的优化应用主要体现在对于飞机起降顺序、航线规划等方面。
首先,对于飞机起降顺序的优化,可以使用数学模型来帮助确定最佳的起降顺序。
通过基于数学模型的计算,可以分析不同的起降顺序对整体航班流畅度的影响,从而选择出最优的起降顺序。
此外,数学模型还可以考虑到因素如航班延误、航班之间的间隔等,进一步提高航班调度的效率。
其次,航线规划也是航空公司在航班调度中需要考虑的要素之一。
通过数学建模和优化算法,可以确定最佳的航线规划方案。
数学模型可以考虑到不同的航线间的飞行距离、飞行时间、风向等因素,从而优化航线规划,减少燃油消耗和飞行时间。
二、飞机燃油消耗减少在航空运输中,飞机燃油的消耗一直是航空公司非常关注的问题。
数学在减少飞机燃油消耗方面也发挥了重要作用。
首先,通过数学模型和算法,可以对飞机的速度、高度等进行优化,从而降低飞机的燃油消耗。
数学模型可以根据不同的飞行条件和航程,计算出最佳速度和高度的组合,以达到燃油消耗最低的效果。
此外,数学还可以用于优化飞机的轨迹规划。
通过数学建模和优化算法,可以选择飞机最佳的航迹,避免不必要的能量消耗。
例如,可以通过数学模型来计算出最佳的飞行角度和航迹,以减少阻力和燃油消耗。
三、物流运输优化除了航班调度和飞机燃油消耗的优化,数学在航空运输中的优化应用还包括物流运输方面的优化。
航空货运作为现代物流运输中重要的一环,也面临着一系列的复杂问题。
首先,数学可以用于优化货物的装载和卸载方案。
数学建模---第四章-运输问题

p , p , , p i1 j1 i2 j2
ir jr
是线性相关的.
推论 1 若变量组对应的列向量组线性无关,则该变 量组一定不包含闭回路.
Go on
性质 1 的证明
Proof : 由直接计算可知
p p p p i1 j1
i1 j2
i2 j2
从理论上讲,运输问题也可用单纯形法来求解, 但是由于运输问题数学模型具有特殊的结构,存在一 种比单纯形法更简便的计算方法 —— 表上作业法, 用表上作业法来求解运输问题比用单纯形法可节约计 算时间与计算费用.但表上作业法的实质仍是单纯形法
§1 运输问题及其数学模型
§1 运输问题及其数学模型
一、运输问题的数学模型
A3 55
6
3
10 4
10
bj 5500 25 10 15
§2 运输问题的表上作业法 2、最小元素法 规则:优先安排单位运价最小的产地与销地之间的运输
任务. Note : 在某行(或列)填入最后一个数时,如果行和 列同时饱和,规定只划去该行(或列)
z 10 40 5 25 3 5 110
设某种物资共有 m 个产地 A1,A2,…,Am,各 产地的产量分别是a1,a2 ,…,am;有n 个销地 B1, B2,…,Bn ,各销地的销量分别为b1,b2,…,bn .
假定从产地Ai(i =1,2,…,m)向销地Bj(j =1, 2,…,n)运输单位物资的运价是cij,问怎样调运才能 使总运费最小?
j 1
i 1, 2, , m
m
xij bj
i 1
j 1, 2, , n
xij 0 i 1, 2, , m; j 1, 2, , n xij 0 i 1, 2, , m; j 1, 2, , n
飞机运输问题

电子科技大学中山学院数学建模思维竞赛C题姓名:梁创学学号:2012010301036 专业:电子信息工程姓名:李俊龙学号:2012010301029 专业:电子信息工程姓名:黄俊凯学号:2012010301019 专业:电子信息工程摘要本文针对第二次世界大战中甲方部队在被乙方部队包围的情况下如何安排一个飞行方案的问题,建立了数学规划模型,并给出了确定具体费用和如何安排飞行人员的解决方案。
并且结合实际情况运用经济学原理对模型进行了评价。
对于问题我们设置了四个变量(开始时甲方新购买的飞机数量、闲置的飞机数量、飞行员中教练和新飞行员数量、闲置的熟练飞行员数量)通过分析各个变量与计划实施费用总和(优化目标)之间的关系,合理地给出各个变量与优化目标之间的函数表达式。
运用Lingo软件求得问题的最优解,根据最优解作出相关的安排方案。
最后我们结合具体数据分析得出四个变量的结果如下表从表中可以发现甲方部队在第4个月时新购买的飞机数量、闲置的飞机数量、飞行员中教练与新飞行员数量都为0,这可以使得第4个月时的费用达到最低;同时闲置的飞机数量从第2个月开始就为0,有利于提高飞机的使用率,避免了资源的浪费;而且闲置的熟练飞行员数量控制在较低水平,这对于资源的利用也是十分重要的。
本文对在各种客观条件下甲方部队如何购买新飞机的数量、购买时间(精确到月)、招募飞行员的数量进行了系统的分析,并给出了使得甲方运输4个月供给的飞行计划的实施费用最少的具体方案。
即第一个月新购买的飞机数量为60架,第二个月为30架,第三个月为80架,第四个月为0架。
第一个月招募飞行员的数量为10人,第二个月为0人,第三个月0人,第四个月为0人。
由此模型得到的飞行计划的最低费用为4232.40(单位略去)。
关键词:数学规划模型、Lingo软件、经济学原理、最低费用一、问题的重述这个问题是以第二次世界大战中的一个实际问题为背景,经过简化而提出来的。
在甲、已双方的一场战争中,一部分甲方部队被乙方部队包围长达4个月。
数学建模 战争物资飞机运送的安排问题

数学建模——战争物资飞机运送的安排问题一,问题在甲乙双方的一场战争中,一部分甲方部队被乙方部队包围长达4个月.由于乙方封锁了所有水陆交通通道,被包围的甲方部队只能依靠空中交通维持供给.运送4个月的供给分别需要2次,3次,3次,4次飞行,每次飞行编队由50架飞机组成(每架飞机需要3名飞行员),可以运送10万吨货物.每架飞机每个月只能飞行一次,每名飞行员每个月也只能飞行一次.在执行完运输任务后的返回途中有20%的飞机会被乙方部队击落,相应的飞行员也因此牺牲或失踪.在第1个月开始时,甲方拥有110架飞机和330名熟练的飞行员.在每个月开始时,甲方可以招聘新飞行员和购买新飞机.新飞机必须经过一个月的检查后才可以投入使用,新飞行员必须在熟练飞行员的指导下经过一个月的训练才能投入飞行.每名熟练飞行员可以作为教练每个月指导20名飞行员(包括他自己在内)进行训练.每名飞行员在完成一个月的飞行任务后,必须有一个月的带薪假期,假期结束后才能再投入飞行.已知各项费用(单位略去)如下表所示,请你为甲方安排一个飞行计划.如果每名熟练飞行员可以作为教练每个月指导不超过20名飞行员(包括他自己在内)进行训练,模型和结果有哪些改变?二,问题分析由上述问题描述可知,这是一个线性规划问题。
即在满足问题中的各种条件下,求最最低的总费用。
总费用=购买新飞机的费用+闲置的熟练飞行员报酬+教练和新飞行员报酬(包括培训费用)+执行飞行任务的熟练飞行员报酬+休假期间的熟练飞行员报酬。
而约束条件有以下几个:1.在上月有20%损失的前提下,4个月中必须保证分别有100,150,150,200架飞机运送货物。
2.在上月有20%损失的前提下,4个月中必须保证分别有300,450,450,600飞行员参加飞行。
3.在保证上个月返回的飞行员休假一个月的前提下,使闲置飞机和飞行员尽量少。
三.设变量符号1.甲方1-4月购买的飞机数量分别为x1,x2,x3,x4。
数学建模运输问题

数学建模运输问题1. 引言运输问题是数学建模中的经典问题之一,其目的是优化物流调度和资源利用,以降低运输成本和提高运输效率。
在这篇文档中,我们将介绍运输问题的定义、常见的建模方法以及求解运输问题的优化算法。
2. 运输问题的定义运输问题的一般形式是在给定的供应地和需求地之间,通过运输网络将一种货物从供应地运送到需求地,以满足一定的需求量。
运输问题的主要目标是确定如何分配供应地的货物到需求地,并最小化总的运输成本。
运输问题通常基于以下几个假设进行建模:•每个供应地和需求地之间的运输成本是已知的。
•每个供应地和需求地的供应量和需求量是已知的。
•货物在运输过程中没有损耗或浪费。
•每个供应地的供应量等于通过该供应地输出的货物总量。
•每个需求地的需求量等于通过该需求地输入的货物总量。
基于以上假设,我们可以将运输问题抽象为一个线性规划问题,通过求解线性规划问题的最优解,得到最佳的货物分配方案。
3. 运输问题的建模方法运输问题的建模方法可以分为两种:3.1 列生成法列生成法是一种迭代求解运输问题的方法,它从一个初始解开始,逐步地添加新的变量(列)来改善当前解,并最终得到最优解。
具体步骤如下:1.初始化一个基本可行解,即满足供应量和需求量约束的初始解。
2.利用这个基本可行解计算每个可能的新变量的代价,即将某个供应地与某个需求地之间的货物分配量作为新的变量。
3.找到一个具有最小代价的新变量,并将它添加到当前解中。
如果不存在新的变量可以添加,那么当前解就是最优解,算法终止。
4.更新当前解,重新计算供应量和需求量,并返回第2步。
列生成法通过逐步添加新的变量来改善当前解,从而降低运输成本,并且由于每次只添加一个变量,可以减少计算的时间复杂度。
3.2 转运算法转运算法是一种常用的直接求解运输问题的方法,它将运输问题转化为一个线性规划问题,并通过求解线性规划问题的最优解得到最佳的货物分配方案。
具体步骤如下:1.定义决策变量,即每个供应地与需求地之间的货物分配量。
数学建模运输规划问题

T3
4 --- 2 3 1
21 8 2 4
T4
32321 2
1 --- 2 6
B1
31724 1 1
142
B2
11 9 4 8 5 8 --- 1
21
B3
3 2 10 4 2 2 2 4 2
3
B4
10 8 5 6 7 4 6 2 1 3
2021/10/10
2868
解:把此转运问题转化为一般运输问题: 1、把所有产地、销地、转运站都同时看作产地和 销地;
0
100
5’
M M M M 14.0 14.3
0
40
6
M M M M M 13.5.5
0
销2量021/10/10104 75 115 160 103 150
36
80 40
------------------------3
例3 仪器公司在大连和广州有两个分厂生产同一种仪器,大连分厂 每月生产450台,广州分厂每月生产600台。公司在上海和天津有两 个销售公司负责对南京、济南、南昌、青岛四个城市的仪器供应。 因为大连距离青岛较近,公司同意大连分厂向青岛直接供货,运输 费用如下图。应该如何调运仪器,可使总运输费用最低?
0
50
2’
M 15 15.3 15.5 15.7 15.9
0
10
3
M M 13.5 13.8 14.0 14.2
0
90
3’
M M 14.5 14.8 15.0 15.2
0
20
4
M M M 13.0 13.3 13.5
0
100
4’
M M M 14.0 14.3 14.5
数学建模模版之运输问题资料

ui
vj
cij , (i,
j
)
J
,并将其填于格
N
子(i,j)的左下角(基变量格子不填)
最优判别: 如表中各非基格子(i,j)左下角全小于等于零, 则当前解为最优。
例. 由最小元素法求得的可行调运方案为:
B1 B2 B3 B4 B5 ui
A1
7 -8
A2
5 0
10 8 6 4 0
-7 -7
20 20
2.(TP)的特征
k
记 ek (0,,0,1, 0,,0)T Enm , (TP)的系数矩阵:
A (Pij ) E(nm)nm
① Pij=ei+em+j,rank(A)=m+n-1,从而A不是行满秩的,且A的任 何m+n-1行线性无关,故(TP)的基解中有n+m-1个基变量;
② (TP)恒有可行解和最优解
作业:2.14 ①用最小元素法产生初始调运方案
②用伏格尔法产生初始调运方案
2.6.3 产销不平衡TP问题的平衡转换
m
n
1. 供过于求: ai bj
i 1
j 1
①原始数学模型:
mn
min z
cij xij
i1 j 1
n
s.t. xij ai ,i 1,2,, m j 1
m
xij bj , j 1,2,, n
6
6
4
(2) 用伏格尔法产生初始调运方案
|
|
B1 B2 B3 产量 行差额
|
A1
5★ 1★ 8 2 10
12 2 4 4√ 5√
A2
2★ 4 3
0★
14 11
直升机运输公司问题

直升机运输公司问题摘要当今社会,交通运输五彩缤纷,其中以公路、铁路、水运、航空、管道运输为主要运输方式。
而航空运输为最直接也是最快捷的方式。
在以后有很大的发展空间,备受广大人的喜爱。
所以,航空运输问题是最有研究意义的。
关键词数学线性规划模型、经济学原理、最低费用1. 问题重述一家运输公司正考虑用直升飞机从某城市的一摩天大楼运送人员。
你被聘为顾问,现在要确定需要多少架飞机。
1、按照数学建模的全过程对本问题建立模型,并选用合理的数据进行计算(模型求解);2、本问题是否可以抽象为优化模型;除了考虑建立优化模型之外,是否可以采用更简单的方法来建立模型。
注意考虑假设条件。
甚至基于不同的假设建立多个模型。
2. 数据假设1、假设此直升机为直5 载客型直升机,其主要技术数据如下:1)、尺寸数据:旋翼直径21 米;尾桨直径3.6 米;机长25.015 米;机身长16.79 米;机高4.4 米;机身最大宽度2 米;前起落架横向轮距1.53 米;主起落架横向轮3.82米、前主轮距3.79 米;座舱容积16 米;2)、重量数据:空重5121 干克;最大起飞重量7600 千克;正常起飞重量7250 千克;最大有效载重1000 千克;3)、性能数据:最大平飞速度210公里/小时;最大爬升率4.3米/秒;动升限6000米;悬停高度(有地效)2000米;最大航程520公里;续航时间3小时40分;2、假设两地距离为2公里。
3、假设摩天大楼上共有100人。
其中有大人70人,重60千克;有小孩30人, 重20千克。
大人需要容积0.5米,小孩需要0.3米。
4、每千克航空煤油7.1元。
而直升飞机每次装油1110千克。
飞行220分钟。
2.1基本假设为了简化问题,可以考虑如下基本假设:假设运载的直升飞机为统一型号;假设每架飞机每次载人数相同;假设飞机运送人员时互不影响;假定人员上了飞机就是完全,因此最后一次运输时,只考虑上飞机所花时间2.2符号说明3. 问题分析近年来,随着科学技术的逐步发展,我国的交通事业也在蒸蒸日上,有以前的陆路交通逐步变化成为空中交通,使得人们的出行更加方便。
数学建模飞机运输问题

数学建模飞机运输问题 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】多变量有约束最优化问题摘要本文以一家运输航空公司的一架飞机运载能力100吨和运载货物的容量50000立方英尺有限的情况下,有三种货物(即x1、x2、x3)需要运输,公司规定每吨货物收取一定的费用,而要运输的每种货物的吨数都有规定的上限(最多不超过30吨、40吨、50吨),并且公司规定由于飞机需要保养与维护,飞机须停飞115天,因此每年只有250天的工作时间。
在此情况下每天怎样安排运输三种货物使公司每年获得最大利润w。
对于此问题只用线性规划的一般方法建立相应的数学模型,在用数学软件求出在给定限行区域内的最优解(w、x1、x2、x3),在对这些最优解进行分析与讨论,确定其为有效最优解。
并以此作为公司对三种货物运输安排方式。
对于问题一,求使得运输航空公司获得最大利润w的x1、x2、x3三种货物的吨数,建立相应的数学模型。
再根据运输能力最多100吨和运载货物容积的最大50000立方英尺,还有每天公司规定的每种货物的运输上限即x1种货物最多运输30吨,x2种货物最多运输40吨,x3种货物最多50吨,建立约束条件。
并用数学软件mathematica进行求解,即为所求的最优解(也就是w=21875,x1=30,x2=,x3=50)。
对于问题二中,要求计算每个约束的影子价格。
我们将利用问题一中建立的目标函数和约束条件,将其编写成源程序输入到Lindo软件中进行求解。
再将得到的界进行讨论与和模型的稳健性分析并且通过其在题意的理解,解释其含义。
问题三中,对于公司将耗资改装飞机以扩大运货区来增加运输能力,且旧飞机使用寿命为5年,每架飞机的改造要花费200000美元,可以增加2000立方英尺的容积。
重量限制仍保持不变。
假设飞机每年飞行250天,这些旧飞机剩余的使用寿命约为5年。
根据此问题我们将建立数学规划模型,利用Lindo软件计算其影子价格和利润并且与前面进行比较,进行分析。
数学建模培训题航空货运问题(改编自美赛倒煤台问题)点评解析

点评:航空货运问题一、基本参数1、货机:假设均匀分布每天三架货机。
2、工作时间5:00—20:00设置为 t :[0,15]?每天货机到达时间:5:00—20:00;一工作组装满装卸场:6小时;一货机装满:3小时; 装卸台的容量:1.5货机;3、费用系数:停机费(等待装货):15000元/小时架一工作组:每小时9000元;二工作组:每小时12000元 4、服务原则:假设先来先服务二、模型建立:概率计算模型 (一)概率分布1、三架货机到达的时刻3,2,1,=i t i 服从[0,15]上的均匀分布,则:密度函数:()1,01515f t t =≤≤ 分布函数:(),01515tF t t =≤≤ 2、设τ,δ,ε分别是首架货机到达时刻、第一架与第二架间隔、第二架与第三架间隔, (1)τ的分布函数331321321321321321))(1(1))(1(1)()()(1),,(1)()()},,(min{)()(1t F t t P t t P t t P t t P t t t t t t P t t t t t t P t t t t t t P t t t t P t P t F t --=≤--=>>>-=>>>-=≤⋃≤⋃≤-Ω=≤⋃≤⋃≤=≤=≤=τττ的密度函数:()()()112515151)151(3]1[3)(')(22211-=-=-==t t t f t F t F t f t t ττ ]15,0[∈t (2)其余两货机到达与第一个到达的货机的间隔21,t t ∆∆在0到15-τ之间是均匀分布的于是:τ-=∆151)(t f i t , τ-≤≤150t ;τ-=∆15)(t t F i t , τ-≤≤150t ,i =1,2 δ 的密度函数/121212()()()1()1()()F t P t P t t t t P t t t t P t t P t t δτδ=≤=∆≤∆≤=-∆>∆>=-∆>∆>221)](1[1)](1[11t F t t P t ∆--=≤∆--=()()2//15152)()](1[2)(')(11---=-==∆∆τττδτδt t f t F t F t f t t(3)第三架货机到达与第二个到达的货机的间隔ε在0和15-δ-τ之间是均匀分布的, 于是:ε 的密度函数τδτδε--=151),/(f3、联合概率分布条件概率(A|B )公式 ()()b f b a f f b b a ,/=()τδε,,联合概率分布:()()()11252112515*1515*2*151**151**,,22//),/(=------=--==τττδτδτδτδεττδττδτδεf f f f f pdf4、另:顺序统计量前k 个(1)k n ≤≤次序统计量的联合密度为:12112![1()]() ()!(,,,) 0 kn kk i n i n n F x f x a x x x b n k f x x x -=⎧-<<<<<⎪-=⎨⎪⎩∏其他特别地,当3k n ==时有 ……(二)优化模型模型: →只要是优化必须给个优化模型!——如何调用、调用第二班、三班② 目标——费用③——货机到达——随机——概率分布①——费用期望值③ 约束——时间关系(1)决策变量:调用工作组(一、二个) →与到达时间有关 (2)目标:费用费用=工作组装装卸台+第一架停机费+第二架停机费+第三架停机费其中:第一架停机费受前一天工作状态影响,情形比较复杂,我们不直接讨论,而是用迟滞概率讨论代替。
数学建模飞机运输问题要点

多变量有约束最优化问题摘要本文以一家运输航空公司的一架飞机运载能力100吨和运载货物的容量50000立方英尺有限的情况下,有三种货物(即x1、x2、x3)需要运输,公司规定每吨货物收取一定的费用,而要运输的每种货物的吨数都有规定的上限(最多不超过30吨、40吨、50吨),并且公司规定由于飞机需要保养与维护,飞机须停飞115天,因此每年只有250天的工作时间。
在此情况下每天怎样安排运输三种货物使公司每年获得最大利润w。
对于此问题只用线性规划的一般方法建立相应的数学模型,在用数学软件求出在给定限行区域内的最优解(w、x1、x2、x3),在对这些最优解进行分析与讨论,确定其为有效最优解。
并以此作为公司对三种货物运输安排方式。
对于问题一,求使得运输航空公司获得最大利润w的x1、x2、x3三种货物的吨数,建立相应的数学模型。
再根据运输能力最多100吨和运载货物容积的最大50000立方英尺,还有每天公司规定的每种货物的运输上限即x1种货物最多运输30吨,x2种货物最多运输40吨,x3种货物最多50吨,建立约束条件。
并用数学软件mathematica进行求解,即为所求的最优解(也就是w=21875,x1=30,x2=7.5,x3=50)。
对于问题二中,要求计算每个约束的影子价格。
我们将利用问题一中建立的目标函数和约束条件,将其编写成源程序输入到Lindo软件中进行求解。
再将得到的界进行讨论与和模型的稳健性分析并且通过其在题意的理解,解释其含义。
问题三中,对于公司将耗资改装飞机以扩大运货区来增加运输能力,且旧飞机使用寿命为5年,每架飞机的改造要花费200000美元,可以增加2000立方英尺的容积。
重量限制仍保持不变。
假设飞机每年飞行250天,这些旧飞机剩余的使用寿命约为5年。
根据此问题我们将建立数学规划模型,利用Lindo软件计算其影子价格和利润并且与前面进行比较,进行分析。
关键词:线性规划、mathematica软件的应用、Lindo的软件应用。
数学建模中优化模型之运输问题

A B C
d
e f 需量
70 40 80 × 40 × × 0 60 30 90 90 30 -20 -15 -65 25 0 50 20 100 60 50 × -50 × 60 50 0 20 20 70 20 × × -15 30 20 20 0 15 × 60 30 × × 90 100 20 15 0 × 90 × × × 90 90 120 120 120 运费——5550
14
4
5
2
5
7
7 9
6
8
9
13
10
6 6
u2=-2
-11
v1=10 v2=6
13
v4=0
u3=6
v3=4
单位费用变化:5-(10+6)=-11
对偶变量法(13)
1 6 1 8 2 5 3 7 2 5 3 3 4 u1=-4
14
4
5
2
5
7
7 9
6
8
9
13
10
6 6
v3=4
u2=-2
-11
v1=10
-3
14 8
9
13
10
6
6
u2=-2
6
v3=4
13
v4=0
u3=6
u2+v3=c23
u2=-2
对偶变量法(5)
1 6 1 8 2 5 3 v1 v2=6 7 2 5 3 3 u1 4 2 7 4
14 8
9
13
10
6
6
u2=-2
6
v3=4
13
v4=0
u3=6
u2+v2=c22
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
多变量有约束最优化问题
摘要
本文以一家运输航空公司的一架飞机运载能力100吨和运载货物的容量50000立方英尺有限的情况下,有三种货物(即x1、x2、x3)需要运输,公司规定每吨货物收取一定的费用,而要运输的每种货物的吨数都有规定的上限(最多不超过30吨、40吨、50吨),并且公司规定由于飞机需要保养与维护,飞机须停飞115天,因此每年只有250天的工作时间。
在此情况下每天怎样安排运输三种货物使公司每年获得最大利润w。
对于此问题只用线性规划的一般方法建立相应的数学模型,在用数学软件求出在给定限行区域内的最优解(w、x1、x2、x3),在对这些最优解进行分析与讨论,确定其为有效最优解。
并以此作为公司对三种货物运输安排方式。
对于问题一,求使得运输航空公司获得最大利润w的x1、x2、x3三种货物的吨数,建立相应的数学模型。
再根据运输能力最多100吨和运载货物容积的最大50000立方英尺,还有每天公司规定的每种货物的运输上限即x1种货物最多运输30吨,x2种货物最多运输40吨,x3种货物最多50吨,建立约束条件。
并用数学软件mathematica进行求解,即为所求的最优解(也就是w=21875,x1=30,x2=7.5,x3=50)。
对于问题二中,要求计算每个约束的影子价格。
我们将利用问题一中建立的目标函数和约束条件,将其编写成源程序输入到Lindo软件中进行求解。
再将得到的界进行讨论与和模型的稳健性分析并且通过其在题意的理解,解释其含义。
问题三中,对于公司将耗资改装飞机以扩大运货区来增加运输能力,且旧飞机使用寿命为5年,每架飞机的改造要花费200000美元,可以增加2000立方英尺的容积。
重量限制仍保持不变。
假设飞机每年飞行250天,这些旧飞机剩余的使用寿命约为5年。
根据此问题我们将建立数学规划模型,利用Lindo软件计算其影子价格和利润并且与前面进行比较,进行分析。
关键词:线性规划、mathematica软件的应用、Lindo的软件应用。
一、提出问题
一个运输公司每天有100吨的航空运输能力。
公司每吨收空运费250美元。
除了重量的限制外,由于飞机货场容积有限,公司每天只能运50000立方英尺的货物。
每天要运送的货物数量如下:
(1)求使得利润最大的每天航空运输的各种货物的吨数。
(2)计算每个约束的影子价格,解释它们的含义。
(3)公司有能力对它的一些旧的飞机进行改装来增大货运区域的空间。
每架飞机的改造要花费200000美元,可以增加2000立方
英尺的容积。
重量限制仍保持不变。
假设飞机每年飞行250天,这些旧飞机剩余的使用寿命约为5年。
在这种情况下,是否值
得改装?有多少架飞机时才值得改装?
二、提出假设
假设1:飞机每天最多只能运输50000立方英尺的货物。
假设2:飞机每天最多只能运:100吨货物。
假设3:货物1每天都有30吨要运。
假设4:货物2每天都有40吨要运。
假设5:货物3每天都有50吨要运。
四、符号说明
五、模型的建立与求解
第一部分
5.1问题一的模型的建立。
5.1.1问题一的分析。
结合题意,计算航空公司获得的利润,必须将运输航空公司里的飞机的燃料费用及修理维护费用忽略不计,还有每吨货物的运费始终保持不变。
在这种情况下,3种货物总运输吨数不超过100吨,容积不超过50000立方英尺,且3种货物有各自运输上限,建立目标函数和约束条件。
5.1.2问题一模型的建立。
通过对原问题的分析,我们可以建立如下的数学线性规划模型:Max W=250x1+250x2+250x3
550x1+1800x2+400x3<=50000
x1+x2+x3<=100
x1<=30
x2<=40
x3<=50
5.1.3模型的求解
将编写的程序输入到mathematica软件中得到结果
5.1.4结果的分析
由结果可以得到当运输航空公司每天运输x1货物30吨、x2货物7.5吨、
x3货物50,每年得到的利润最大w=21875美元。
即当x1为30吨、x2为8吨、x3为50吨的时候,货物体积超出了飞机的运载体积50000立方英尺。
所以公司应按照以上的x1为30吨,x2为7.5吨,x3为50吨的运输安排运输货物。
第二部分
5.2问题二的模型的建立
5.2.1问题二的分析与建立
Max W=250x1+250x2+250x3
550x1+1800x2+400x3<=50000
x1+x2+x3<=100
x1<=30
x2<=40
x3<=50求解见附录二。
5.2.2 模型的求解
将应用程序输入到Lindo软件中,得到的部分结果为:
最优解下资源增加1“单位”时“效益”的增量:
飞机运载空间每增加1立方英尺时,利润增加0.138889美元,飞机运载能力的增加对利润不影响,
X1种货物每增运1吨时,利润增加173.611115美元,
X2种货物的增运对利润不影响,
X3种货物每增运1吨时,利润增加194.444443美元。
5.2.3结果的分析
部分输出结果(灵敏度分析)(输入程序见附录2)
最优解不变时目标函数系数允许的变化范围(约束条件不变):x1的系数变化范围(173.61,250)
x2的系数变化范围(0,818.2)
x3的系数变化范围(55.6,250)
飞机的运输货物体积最多增加222500立方英尺,
x1货物最多每增运18吨
x3货物最多每增运16吨
第三部分
5.3问题三的模型建立与分析
5.3.1问题的分析
由2问知道每增加1立方英尺,利润就增加0.138889;当增加2000立方英尺时每天增加利润=277.778美元;每架飞机增加的利润=347225美元
因为一架飞机改装后所能获得的利润大于改装费,且能赚147225美元;所以有一架飞机就可以改装了。
5.3.2模型的建立
通过对问题的分析,我们建的数学模型为:
5.3.3模型的求解
输出部分结果为(输入的程序见附录3):
所以由于对结果的检验航空运输公司应该值得改装,应该改装1架飞
机。
六、模型的评价与推广
6.1模型评价
在运输货物领域中,人们常会遇到这样的问题,例如:如何从一切可能的方案中选择最好的、最优的方案。
在我们数学上把这类问题称为最优化问题,如何解决这类问题,在当今商品经济的环境下,是关系到企业生存以及国计民生的问题。
在解决上述如何空运货物能使公司利润最高的问题上,我们采用的是线性规划的方法。
线性规划的理论和方法都比较成熟,并且是一个有广泛应用价值的统筹学分支,如果一个问题的限制条件可以写出某些决策变量的线性方程组或线性不等式组,那我们就可以应用lingo软件将该线性规划方程解出来得到最优解。
应用数学知识中的线性规划在解决这类最优化问题上既简单又精确,在最优解的求解过程中是个很好的选择。
对于我们提出的5个假设,我们都做了灵敏性分析,数据的改变对于最优的结果没有太大的影响。
但是我们的模型还是存在一些缺点,比如我们认定运输每种货物的难易程度是一样的,不会增加其成本。
6.2模型推广
以上建立的模型,在解决最优化问题上方便简单快捷,不仅适用于货物的运输问题上,也适用于钢管的下料问题,接力队的选拔问题,奶产品的生产与销售等一系列问题等。
编程运用LINDO软件,节约计算时间。
七、参考文献
八、附录
附录1:求解问题一的Mathematica程序附录2:求解问题二的LINDO程序
附录3:求解问题三的LINDO程序解法一:
Max 250x1+250x2+250x3
st
550x1+1800x2+400x3<=52000
x1+x2+x3<=100
x1<=30 x2<=40 x3<=50 end。
