七年级数学几何证明题(典型)讲解学习
七年级下册数学几何证明题讲解

七年级下册数学几何证明题讲解
当涉及数学几何证明题时,通常需要遵循一定的逻辑和推理过程来证明一个结论。
在七年级下册数学几何中,常见的证明题可能涉及到角的性质、三角形的性质、平行线性质等。
这里简单介绍一下如何进行几何证明:
1.观察题目:首先仔细阅读题目,并认真理解题目所给的条件和要证明的结
论。
2.列出已知条件:将题目中已知的条件列出来,包括给定的角度、线段长度、
图形性质等。
3.确定证明思路:根据题目中的要求,考虑使用何种方法进行证明,可以根
据条件来尝试使用等腰三角形、相似三角形、平行线性质等。
4.逻辑推理:根据已知条件,运用几何性质和定理展开逻辑推理,逐步推导
出待证结论。
5.结论归纳:最终得出结论,并确保证明过程清晰且连贯,每一步之间都有
明确的推理关系。
在七年级下册的数学几何证明题中,可能包括角的平分线、垂直角的性质、三角形的全等条件等内容。
初一数学几何证明题的常见解题方法

初一数学几何证明题的常见解题方法初一数学几何证明题的常见解题方法初一是刚接触几何的知识,关于几何的证明题是很多的,这些该怎么解答呢?下面就是给大家的初一几何证明题内容,希望大家喜欢。
1)D是三角形ABC的BC边上的点且CD=AB,角ADB=角BAD,AE 是三角形ABD的中线,求证AC=2AE。
(2)在直角三角形ABC中,角C=90度,BD是角B的平分线,交AC于D,CE垂直AB于E,交BD于O,过O作FG平行AB,交BC 于F,交AC于G。
求证CD=GA。
延长AE至F,使AE=EF。
BE=ED,对顶角。
证明ABE全等于DEF。
=》AB=DF,角B=角EDF角ADB=角BAD=》AB=BD,CD=AB=》CD=DF。
角ADE=BAD+B=ADB+EDF。
AD=AD=》三角形ADF全等于ADC=》AC=AF=2AE。
题干中可能有笔误地方:第一题右边的E点应为C点,第二题求证的CD不可能等于GA,是否是求证CD=FA或CD=CO。
如上猜测准确,证法如下:第一题证明:设F是AB边上中点,连接EF角ADB=角BAD,则三角形ABD为等腰三角形,AB=BD;∵ AE是三角形ABD的中线,F是AB边上中点。
∴ EF为三角形ABD对应DA边的中位线,EF∥DA,则∠FED=∠ADC,且EF=1/2DA。
∵∠FED=∠ADC,且EF=1/2DA,AF=1/2AB=1/2CD∴△AFE∽△CDA∴ AE:CA=FE:DA=AF:CD=1:2AC=2AE得证第二题:证明:过D点作DH⊥AB交AB于H,连接OH,则∠DHB=90°;∵∠ACB=90°=∠DHB,且BD是角B的平分线,则∠DBC=∠DBH,直角△DBC与直角△DBH有公共边DB;∴△DBC≌△DBH,得∠CDB=∠HDB,CD=HD;∵ DH⊥AB,CE⊥AB;∴ DH∥CE,得∠HDB=∠COD=∠CDB,△CDO 为等腰三角形,CD=CO=DH;四边形CDHO中CO与DH两边平行且相等,则四边形CDHO为平行四边形,HO∥CD且HO=CD∵ GF∥AB,四边形AHOF中,AH∥OF,HO∥AF,则四边形AHOF为平行四边形,HO=FA∴CD=FA得证有很多题1.已知在三角形ABC中,BE,CF分别是角平分线,D是EF中点,若D到三角形三边BC,AB,AC的距离分别为x,y,z,求证:x=y+z 证明;过E点分别作AB,BC上的高交AB,BC于M,N点.过F点分别作AC,BC上的高交于P,Q点.根据角平分线上的点到角的2边距离相等可以知道FQ=FP,EM=EN.过D点做BC上的高交BC于O点.过D点作AB上的高交AB于H点,过D点作AB上的高交AC于J 点.则X=DO,Y=HY,Z=DJ.因为D 是中点,角ANE=角AHD=90度.所以HD平行ME,ME=2HD 同理可证FP=2DJ。
初中数学几何证明经典试题(含答案)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线APCDB AFGCEBODD 2C 2B 2A 2D 1C 1B1CBDAA 1交MN 于E 、F . 求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 求证:AP =AQ .(初二)F4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边BC 上的任一点,PF ⊥AP ,CF 平分∠DCE .求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEF 为圆的割线,AE 、AF 与直线PO 相交于B 、D .求证:AB =DC ,BC =AD .(初三)经典题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA=∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD中,设E、F分别是BC、AB上的一点,AE与CF相交于P,且AE=CF.求证:∠DPA=∠DPC.(初二)经典难题(五)1、设P是边长为1的正△ABC内任一点,L=PA+PB+PC,求证:≤L<2.2、已知:P是边长为1的正方形ABCD内的一点,求PA+PB+PC的最小值.3、P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
2021七年级几何求证模型归纳总结及解题方法

【考点】 K 7 :三角形内角和定理 【解答】解:(1)A B AOB 180 , C D COD 180 , 又AOB COD , A B C D , 故答案为: A B C D .
(2)①图中,有 6 个“8 字形”. 故答案为 6.
② AP 平分 BAD , 1 2 , PC 平分 BCD , 3 4 , 1 B 3 P ①, 2 P 4 D ②, ① ②得, 2P B D 50 , P 25 .
【考点】 JA :平行线的性质 【解答】解: AB / /CD , C 55 , EFB C 55 , AEC 18 , A EFB AEC 37 , 故答案为:37.
2.(2020 春•太湖县期末)如图(1), AB / /CD ,试求 BPD 与 B 、 D 的数量关系,说 明理由.
2如图2延长ba与cp交于点qcq与am交于点h?an平分?pab??ban??pan??qap?180??2?ban??p?30???cqa??p??qap?30??180??2?ban?210?2?ban?mhc??nhp??nap??p??ban?30??abcd??ecq??cqa?210??2?ban?cm平分?pce11??mch??ecp??210??2?ban?105???ban22??amc?180???mhc??mch??amc?180???ban?30??105???ban?105?
数量关系. (3)如图③,延长线段 BP 、 QC 交于点 E , BQE 中,存在一个内角等于另一个内角的 3
倍,请直接写出 A 的度数.
【解答】(1)解:A 80 .
ABC ACB 100 ,
点 P 是 ABC 和 ACB 的平分线的交点,
P 180 1 (ABC ACB) 180 1 100 130 ,
七年级数学典型几何证明50题

七年级数学典型几何证明50题初一典型几何证明题1、已知:AB=4,AC=2,D 是BC 中点,AD 是整数,求AD 解:延长AD 到E,使AD=DE ∵D 是BC 中点∴BD=DC在△ACD 和△BDE 中AD=DE ∠BDE=∠ADC BD=DC∴△ACD ≌△BDE ∴AC=BE=2 ∵在△ABE 中 AB-BE <AE <AB+BE ∵AB=4即4-2<2AD <4+2 1<AD <3 ∴AD=22、已知:BC=DE ,∠B=∠E ,∠C=∠D ,F 是CD 中点,求证:∠1=∠2证明:连接BF 和EF ∵ BC=ED,CF=DF,∠BCF=∠EDF ∴△BCF ≌△EDF (S.A.S)A BC DEF 21 ADBC∴ BF=EF,∠CBF=∠DEF 连接BE在△BEF 中,BF=EF ∴ ∠EBF=∠BEF 。
∵ ∠ABC=∠AED 。
∴ ∠ABE=∠AEB 。
∴ AB=AE 。
在△ABF 和△AEF 中 AB=AE,BF=EF, ∠ABF=∠ABE+∠EBF=∠AEB+∠BEF=∠AEF ∴△ABF ≌△AEF 。
∴ ∠BAF=∠EAF (∠1=∠2)。
3、已知:∠1=∠2,CD=DE ,EF//AB ,求证:EF=AC过C 作CG∥EF 交AD 的延长线于点G CG∥EF,可得,∠EFD=CGD DE =DC∠FDE=∠GDC(对顶角)∴△EFD≌△CGD EF =CG ∠CGD=∠EFD又,EF∥AB ∴,∠EFD=∠1 ∠1=∠2 ∴∠CGD=∠2∴△AGC 为等腰三角形, AC =CG 又 EF =CG ∴EF =AC4、已知:AD 平分∠BAC ,AC=AB+BD ,求证:∠B=2∠CBA CDF2 1 EA证明:延长AB取点E,使AE=AC,连接DE∵AD平分∠BAC∴∠EAD=∠CAD∵AE=AC,AD=AD∴△AED≌△ACD (SAS)∴∠E=∠C∵AC=AB+BD∴AE=AB+BD∵AE=AB+BE∴BD=BE∴∠BDE=∠E∵∠ABC=∠E+∠BDE∴∠ABC=2∠E∴∠ABC=2∠C5、已知:AC平分∠BAD,CE⊥AB,∠B+∠D=180°,求证:AE=AD+BE证明:在AE上取F,使EF=EB,连接CF∵CE⊥AB∴∠CEB=∠CEF=90°∵EB=EF,CE=CE,∴△CEB ≌△CEF ∴∠B =∠CFE∵∠B +∠D =180°,∠CFE +∠CFA =180° ∴∠D =∠CFA ∵AC 平分∠BAD ∴∠DAC =∠FAC ∵AC =AC∴△ADC ≌△AFC (SAS )∴AD =AF∴AE =AF +FE =AD +BE6、如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD ,且点E 在AD 上。
七年级下册数学期末考试几何大题证明必考题
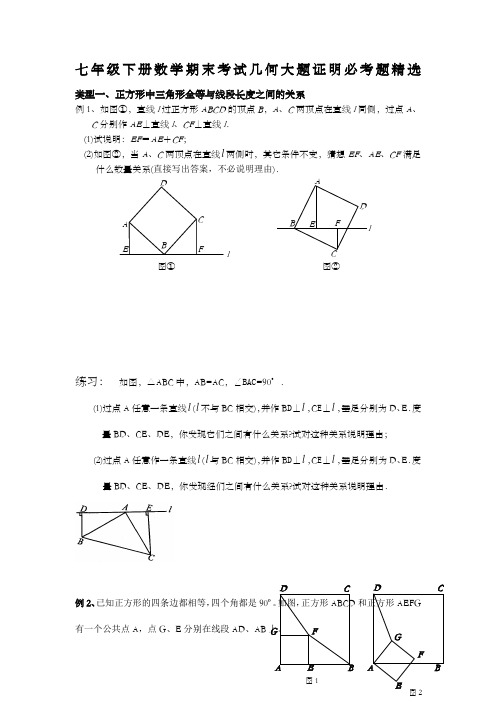
图①DA EC BFl图②ABE F ClD七年级下册数学期末考试几何大题证明必考题精选类型一、正方形中三角形全等与线段长度之间的关系例1、如图①,直线l 过正方形ABCD 的顶点B ,A 、C 两顶点在直线l 同侧,过点A 、C 分别作AE ⊥直线l 、CF ⊥直线l . (1)试说明:EF =AE +CF ;(2)如图②,当A 、C 两顶点在直线l 两侧时,其它条件不变,猜想EF 、AE 、CF 满足什么数量关系(直接写出答案,不必说明理由).练习: 如图,△ABC 中,AB=AC ,∠BAC =90°.(1)过点A 任意一条直线l (l 不与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现它们之间有什么关系?试对这种关系说明理由; (2)过点A 任意作一条直线l (l 与BC 相交),并作B D ⊥l ,C E ⊥l ,垂足分别为D 、E .度量BD 、CE 、DE ,你发现经们之间有什么关系?试对这种关系说明理由.例2、已知正方形的四条边都相等,四个角都是90º。
如图,正方形ABCD 和正方形AEFG 有一个公共点A ,点G 、E 分别在线段AD 、AB 上。
A E B 图1D CG FA BD CG FE图2(1)如图1, 连结DF 、BF ,说明:DF =BF ; (2)若将正方形AEFG 绕点A 按顺时针方向旋转,连结DG ,在旋转的过程中,你能否找到一条长度与线段DG 的长始终相等的线段?并以图2为例说明理由。
练习:如图,正方形ABCD 的边CD 在正方形ECGF 的边CE 上,B 、C 、G 三点在一条直线上,且边长分别为2和3,在BG 上截取GP =2,连结AP 、PF. (1)观察猜想AP 与PF 之间的大小关系,并说明理由.(2)图中是否存在通过旋转、平移、反射等变换能够互相重合的两个三角形?若存在,请说明变换过程;若不存在,请说明理由.(3)若把这个图形沿着PA 、PF 剪成三块,请你把它们拼成一个大正方形,在原图上画出示意图,并请求出这个大正方形的面积.附加:如图,△ABC 与△ADE 都是等边三角形,连结BD 、CE(1)BD 与CE 相等吗?请说明理由.A BCFDE GP32B(2)你能求出BD与CE的夹角∠BFC的度数吗?(3)若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连结BE、DG交点记为点M(如图).请直接写出线段BE和DGF例3、正方形四边条边都相等,四个角都是90o.如图,已知正方形ABCD在直线MN 的上方,BC在直线MN上,点E是直线MN上一点,以AE为边在直线MN的上方作正方形AEFG.(1)如图1,当点E在线段BC上(不与点B、C重合)时:①判断△ADG与△ABE是否全等,并说明理由;②过点F作FH⊥MN,垂足为点H,观察并猜测线段BE与线段CH的数量关系,并说明理由;(2)如图2,当点E在射线CN上(不与点C重合)时:①判断△ADG与△ABE是否全等,不需说明理由;②过点F 作FH ⊥MN ,垂足为点H ,已知GD =4,求△CFH 的面积.练习:如图1,四边形ABCD 是正方形,G 是CD 边上的一个点(点G 与C 、D 不重合),以CG 为一边作正方形CEFG ,连结BG ,DE .(1)如图1,说明BG= DE 的理由(2)将图1中的正方形CEFG 绕着点C 按顺时针方向旋转任意角度 ,得到如图2.请你猜想①BG= DE 是否仍然成立?②BG 与DE 位置关系?并选取图2验证你的猜想.图 2FG DA图 1FDA类型二、探究题例1、如图,已知等边△A B C 和点P ,设点P 到△A B C 三边A B 、A C 、B C (或其延长线)的距离分别为h 1、h 2、h 3,△A B C 的高为h .在图(1)中,点P 是边B C 的中点,此时h 3=0,可得结论:h h h h =++321. 在图(2)--(5)中,点P 分别在线段M C 上、M C 延长线上、△A B C 内、△A B C 外.(1)请探究:图(2)--(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)(2)证明图(2)所得结论; (3)证明图(4)所得结论.(4)(附加题2分)在图(6)中,若四边形R B C S 是等腰梯形,∠B =∠C =60o ,R S =n ,B C =m ,点P 在梯形内,且点P 到四边B R 、R S 、S C 、C B 的距离分别是h 1、h 2、h 3、h 4,桥形的高为h ,则h 1、h 2、h 3、h 4、h 之间的关系为: ;图(4)与图(6)中的等式有何关系?ABC DEPM(3)ABCDE (2)ABCD EM (P )(1)练习:1、如图,在△ABC 中,AB=AC ,P 为底边上任意一点,PE ⊥AB ,PF ⊥AC ,BD ⊥AC.(1)求证:PE+PF=BD ;(2)若点P 是底边BC 的延长线上一点,其余条件不变,(1)中的结论还成立吗?如果成立,请说明理由;如果不成立,请画出图形,并探究它们的关系.CBAPDE2、如图,已知△ABC 三边长相等,和点P ,设点P 到△ABC 三边AB 、AC 、BC (或其延长线)的距离分别为h 1、h 2、h 3,△ABC 的高为h .在图(1)中, 点P 是边BC 的中点,由S △ABP+S △ACP=S △ABC 得,h BC h AC h AB ⋅=⋅+⋅21212121可得h h h =+21又因为h 3=0,所以:h h h h =++321.图(2)~(5)中,点P 分别在线段MC 上、MC 延长线上、△ABC 内、△ABC 外.(1)请探究:图(2)~(5)中, h 1、h 2、h 3、h 之间的关系;(直接写出结论)⑵ ⑶ ⑷ ⑸ (2)说明图(2)所得结论为什么是正确的; (3)说明图(5)所得结论为什么是正确的.ABC DEP ABCDEPM(3)ABCDE P M (2)ABCDEM (P )(1)ABCDEP M(5)FC B E 例2、已知△ABC 是等边三角形,将一块含30o 角的直角三角板DEF 如图1放置,当点E 与点B 重合时,点A 恰好落在三角板的斜边DF 上. (1)AC=CF 吗? 为什么?(2)让三角板在BC 上向右平行移动,在三角板平行移动的过程中,(如图2)是否存在与线段EB 始终相等的线段(设AB ,AC 与三角板斜边的交点分别为G ,H )?如果存练习:1、如图1,一等腰直角三角尺GEF (∠EGF=90°,∠GEF=∠GFE=45°,GE=GF )的两条直角边与正方形ABCD 的两条边分别重合在一起.现正方形ABCD 保持不动,将三角尺GEF 绕斜边EF 的中点O (点O 也是BD 中点)按顺时针方向旋转.(1)如图2,当EF 与AB 相交于点M ,GF 与BD 相交于点N 时,通过观察或测量BM ,FN 的长度,猜想BM ,FN 相等吗?并说明理由;(2)若三角尺GEF 旋转到如图3所示的位置时,线段FE 的延长线与AB 的延长线相交于点M ,线段BD 的延长线与GF 的延长线相交于点N ,此时,(1)中的猜想还成立C图1吗?请说明理由.2、已知:△ABC 为等边三角形,M 是BC 延长线上一点,直角三角尺的一条直角边经过点A ,且60º角的顶点E 在BC 上滑动,(点E 不与点B 、C 重合),斜边∠ACM 的平分线CF 交于点F(1)如图(1)当点B 在BC 边得中点位置时(6分) ○1猜想AE 与BF 满足的数量关系是 。
初中经典几何证明练习题(含问题详解)

初中几何证明题经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQOP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形 ∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初中数学复习几何模型专题讲解4---等腰直角三角形构造三垂直模型

初中数学复习几何模型专题讲解专题04 等腰直角三角形构造三垂直模型一、解答题1.如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).(1)求k值与一次函数y=k1x+b的解析式;(2)在x轴上有一动点P,求当PB+PC最小时P点坐标.(3)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;【答案】(1)k= 43,y=23x+2;(2)P(1,0);(3)(﹣5,3)或(﹣2,5)【分析】(1)根据待定系数法求解即可;(2)作点B关于x轴对称的点B',连接B'C,交x轴于点P,此时PB+PC最小,求出直线B'C的解析式,求出直线B'C与x轴的交点坐标即可;(3)分两种情况讨论:①当∠DAB=90°时;②当∠D'BA=90°时,添加辅助线构造全等三角形进行求解即可.【详解】解:(1)由题意,将点C(3,4)代入y=kx 中,得:4=3k ,解得:k= 43, 再将点C(3,4)、点A (﹣3,0)代入y =k 1x +b 中,得:113034k b k b -+=⎧⎨+=⎩, 解得:1232k b ⎧=⎪⎨⎪=⎩, ∴函数y =k 1x +b 的解析式为:y=23x+2; (2)如图,作点B 关于x 轴对称的点B ',连接B 'C ,交x 轴于点P ,此时PB+PC 最小,在y=23x+2中,令x=0,则y=2, ∴B(0,2),则B '(0,﹣2),设直线B 'C 的解析式为y =k 2x ﹣2,将C (3,4)代入得:4=3k 2﹣2,解得:k 2=2,∴直线B 'C 的解析式为y =2x ﹣2,令y=0,由0=2x ﹣2得:x=1,∴点P 坐标为(1,0);(3)根据题意,OA=3,OB=2,分两种情况:①当∠DAB=90°时,DA=AB ,过点D作DM⊥x轴于E,∵∠DAM+∠BAO=90°,∠BAO+∠ABO=90°,∴∠DAM=∠ABO,∵∠DMA=∠AOB=90°,DA=AB,∴△DAM≌△ABO(AAS),∴DM=OA=3,MA=OB=2,∴D(﹣5,3);②当∠D'BA=90°时,D'B=AB,过D'作D'N⊥y轴于N,同理可证△D'BN≌△BAO(AAS),∴BN=OA=3,D'N=OB=2,∴D'(﹣2,5),故点D的坐标为(﹣5,3)或(﹣2,5).【点睛】本题是一次函数的综合题,主要考查待定系数法求一次函数的解析式、同角的余角相等、全等三角形的判定与性质、一次函数与几何图形及最短路径相关问题、解二元一次方程组等知识,熟练掌握一次函数的相关知识,添加辅助线构造全等三角形和利用分类讨论的数学思想是解答的关键.2.在ABC中,∠ACB=90°,AC=BC,直线,MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.(1)当直线MN绕点C旋转到如图1的位置时,求证:DE=AD+BE;(2)当直线MN绕点C旋转到如图2的位置时,求证:DE=AD﹣BE;(3)当直线MN绕点C旋转到如图3的位置时,线段DE、AD、BE之间又有什么样的数量关系?请你直接写出这个数量关系,不要证明.【答案】(1)见解析;(2)见解析;(3)DE=BE﹣AD【分析】(1)由题意易得∠DAC+∠ACD=90°,则∠DAC=∠BCE,进而可证△ADC≌△CEB,然后根据全等三角形的性质可求解;(2)由题意易得∠CEB=∠ADC=90°,则可求∠CAD=∠BCE,进而可证△CAD≌△BCE,然后根据全等三角形的性质可求解;(3)根据题意可证△CAD≌△BCE,然后根据全等三角形的性质可求解.【详解】(1)证明:∵AD⊥MN,BE⊥MN,∴∠ADC=∠CEB=90°,∴∠DAC+∠ACD=90°,∵∠ACB =90°,∴∠BCE+∠ACD =90°,∴∠DAC =∠BCE ,在△ADC 和△CEB ,ADC CEBDAC ECB AC CB∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△ADC ≌△CEB (AAS ),∴CD =BE ,AD =CE ,∴DE =CE+CD =AD+BE ;(2)证明:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,∴∠DAC+∠ACD =90°,∵∠ACB =90°,∴∠BCE+∠ACD =90°,∴∠DAC =∠BCE ,∵AC=BC ,∴△ADC ≌△CEB ,∴CD =BE ,AD =CE ,∴DE =CE ﹣CD =AD ﹣BE ;(3)解:DE =BE ﹣AD ,理由如下:∵AD ⊥MN ,BE ⊥MN ,∴∠ADC =∠CEB =90°,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠BCE,∵AC=BC,∴△ADC≌△CEB,∴CD=BE,AD=CE,∴DE=BE﹣AD.【点睛】本题主要考查全等三角形的性质与判定及直角三角形的两个锐角互余,熟练掌握全等三角形的性质与判定及直角三角形的两个锐角互余是解题的关键.3.课间,小明拿着老师的等腰三角板玩,不小心掉在两墙之间,如图所示:(1)求证:△ADC≌△CEB;(2)已知DE=35cm,请你帮小明求出砌墙砖块的厚度a的大小(每块砖的厚度相同)【答案】(1)见详解;(2)砌墙砖块的厚度a为5cm.【分析】(1)根据题意可得AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,进而得到∠ADC=∠CEB=90°,再根据等角的余角相等可得∠BCE=∠DAC,再证明△ADC≌△CEB即可.(2)利用(1)中全等三角形的性质进行解答.【详解】(1)证明:由题意得:AC=BC,∠ACB=90°,AD⊥DE,BE⊥DE,∴∠ADC=∠CEB=90°,∴∠ACD+∠BCE=90°,∠ACD+∠DAC=90°,∴∠BCE=∠DAC,在△ADC和△CEB中ADC CEBDAC BCE AC BC∠∠∠∠⎧⎪⎨⎪⎩===,∴△ADC≌△CEB(AAS);(2)解:由题意得:∵一块墙砖的厚度为a,∴AD=4a,BE=3a,由(1)得:△ADC≌△CEB,∴DC=BE=3a,AD=CE=4a,∴DC+CE=BE+AD=7a=35,∴a=5,答:砌墙砖块的厚度a为5cm.【点睛】此题主要考查了全等三角形的应用,关键是正确找出证明三角形全等的条件.4.已知,A(-1,0).(1)如图1,B(0,2),以B点为直角顶点在第二象限作等腰直角△ABC.①求C点的坐标;②在坐标平面内是否存在一点P (不与点C 重合),使△PAB 与△ABC 全等? 若存在,直接写出P 点坐标; 若不存在,请说明理由;(2)如图2,点E 为y 轴正半轴上一动点,以E 为直角顶点作等腰直角△AEM ,设M (a ,b ),求a-b 的值.【答案】(1)①()2,3C -;②存在,()2,1P 或()1,1-或()3,1-;(2)1.【分析】(1)作CD ⊥y 轴于D ,证△CEB ≌△BOA ,推出CE=OB=2,BE=AO=1,即可得出答案;(2)分为三种情况,画出符合条件的图形,构造直角三角形,证三角形全等,即可得出答案;(3)作MF ⊥y 轴于F ,证△EFM ≌△AOE ,求出EF ,即可得出答案.【详解】(1)①作CE ⊥y 轴于E ,如图1,∵A (-1,0),B (0,2),∴OA=1,OB=2,∵∠CBA=90°,∴∠CEB=∠AOB=∠CBA=90°,∴∠ECB+∠EBC=90°,∠CBE+∠ABO=90°, ∴∠ECB=∠ABO ,在△CBE 和△BAO 中ECB ABO CEB AOB BC AB ∠∠⎧⎪∠∠⎨⎪⎩=== ∴△CBE ≌△BAO ,∴CE=BO=2,BE=AO=1,即OE=1+2=3,∴C (-2,3).②存在一点P ,使PAB △与ABC 全等,分为三种情况:①如图2,过P 作PE x ⊥轴于E ,则90PAB AOB PEA ∠=∠=∠=,90EPA PAE ∴∠+∠=,90PAE BAO ∠+∠=,EPA BAO ∴∠=∠,在PEA 和AOB 中EPA BAO PEA AOB PA AB ∠=∠⎧⎪∠=∠⎨⎪=⎩,PEA ∴≌AOB ,1PE AO ∴==,2EA BO ==,123OE ∴=+=,即P 的坐标是()3,1-;②如图3,过C 作CM x ⊥轴于M ,过P 作PE x ⊥轴于E ,则90CMA PEA ∠=∠=, CBA ≌PBA ,45PAB CAB ∴∠=∠=,AC AP =,90CAP ∴∠=,90MCA CAM ∴∠+∠=,90CAM PAE ∠+∠=, MCA PAE ∴∠=∠,在CMA 和AEP △中,CMA PEA AC AP ⎪∠=∠⎨⎪=⎩,CMA ∴≌AEP △,PE AM ∴=,CM AE =,()2,3C -,()1,0A -,211PE ∴=-=,0312OE AE A =-=-=,即P 的坐标是()2,1;③如图4,过P 作PE x ⊥轴于E ,CBA ≌PAB △,AB AP =∴,90CBA BAP ∠=∠=,则90AEP AOB ∠=∠=,90BAO PAE ∴∠+∠=,90PAE APE ∠+∠=,BAO APE ∴∠=∠,在AOB 和PEA 中,AOB PEA AB AP ⎪∠=∠⎨⎪=⎩,AOB ∴≌PEA ,1PE AO ∴==,2AE OB ==,0211E AE AO ∴=-=-=,即P 的坐标是()1,1-,综合上述:符合条件的P 的坐标是()3,1-或()1,1-或()2,1.(2)过M 作MF y ⊥轴于F ,得到下图5∵(),M a b∴,MF a FO b ==,由上图得:90AEM EFM AOE ∠=∠=∠=,90AEO MEF ∠+∠=,90MEF EMF ∠+∠=,AEO EMF ∴∠=∠,在AOE △和EMF △中AOE EFM AEO EMF AE EM ∠=∠⎧⎪∠=∠⎨⎪=⎩,AEO ∴≌()EMF AAS ,1EF AO ∴==,MF OE =,MN x ⊥轴,MF y ⊥轴,90MFO FON MNO ∴∠=∠=∠=,∴四边形FONM 是矩形,MN OF ∴=,1a b MF OF EO OF EF OA -=-=-===.【点睛】本题考查全等三角形的性质和判定,三角形内角和定理,等腰三角形性质的应用,主要考查学生综合运用性质进行推理的能力,用了分类讨论思想.5.公路上,A ,B 两站相距25千米,C 、D 为两所学校,DA AB ⊥于点A ,CB AB ⊥于点B ,如图,已知15DA =千米,现在要在公路AB 上建一报亭H ,使得C 、D 两所学校到H 的距离相等,且90DHC ∠=︒,问:H 应建在距离A 站多远处?学校C 到公路的距离是多少千米?【答案】H 应建在距离A 站10千米处,学校C 到公路的距离是10千米.【分析】先根据垂直的定义可得90A B ∠=∠=︒,再根据直角三角形的两锐角互余、角的和差可得D BHC ∠=∠,然后根据三角形全等的判定定理与性质可得,15AH BC DA HB ===千米,最后根据线段的和差可得.【详解】由题意得:DH HC =,25AB =千米,,DA AB CB AB ⊥⊥,90A B ∴∠=∠=︒,90D AHD ∠∴∠+=︒,90DHC ∠=︒,18090BH D HD C C H A ∴∠+∠=︒-∠=︒,D BHC ∴∠=∠,在ADH 和BHC △中,A B D BHC DH HC ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ADH BHC AAS ∴≅,,AH BC DA HB ∴==,15DA =千米,25AB =千米,15HB ∴=千米,10BC AH AB HB ∴==-=千米,答:H 应建在距离A 站10千米处,学校C 到公路的距离是10千米.【点睛】本题考查了垂直的定义、直角三角形的两锐角互余、三角形全等的判定定理与性质等知识点,熟练掌握三角形全等的判定方法是解题关键.6.如图所示,在ABC ∆和DBC ∆中,∠ACB=∠DBC=90°,点E 是BC 的中点,EF ⊥AB ,垂足为F ,且AB=DE .(1)求证:BC=BD;(2)若BD=10厘米,求AC的长.【答案】(1)证明见解析;(2)5厘米【分析】(1)由DE⊥AB,可得∠BFE=90°,由直角三角形两锐角互余,可得∠ABC+∠DEB=90°,由∠ACB=90°,由直角三角形两锐角互余,可得∠ABC+∠A=90°,根据同角的余角相等,可得∠A=∠DEB,然后根据AAS判断△ABC≌△EDB,根据全等三角形的对应边相等即可得到BD=BC;(2)由(1)可知△ABC≌△EDB,根据全等三角形的对应边相等,得到AC=BE,由E是BC的中点,得到BE=12BC=12BD=5厘米.【详解】解:(1)∵DE⊥AB,可得∠BFE=90°,∴∠ABC+∠DEB=90°,∵∠ACB=90°,∴∠ABC+∠A=90°,∴∠A=∠DEB,在△ABC和△EDB中,ACB DBC A DEBAB DE ∠∠⎧⎪∠∠⎨⎪⎩===, ∴△ABC ≌△EDB (AAS ),∴BD=BC ;(2)∵△ABC ≌△EDB ,∴AC=BE ,∵E 是BC 的中点,BD=10厘米,∴BE=12BC =12BD =5厘米. 【点睛】此题考查了全等三角形的判定与性质,普通两个三角形全等共有四个定理,即AAS 、ASA 、SAS 、SSS ,直角三角形可用HL 定理,但AAA 、SSA ,无法证明三角形全等,本题是一道较为简单的题目,找准全等的三角形是解决本题的关键.7.综合与实践特例研究:将矩形ABCD 和Rt CEF 按如图1放置,已知90,,,FCE AD CD CE CF CF CD ∠=︒==>,连接',BF DE .()1如图1,当点D 在CF 上时,线段BF 与DE 之间的数量关系是__ ;直线BF 与直线DE 之间的位置关系是_ ;拓广探索:()2图2是由图1中的矩形ABCD 绕点C 顺时针旋转一定角度得到的,请探索线段BF 与DE 之间的数量关系和直线BF 与直线DE 之间的位置关系,并说明理由.【答案】(1),BF DE BF DE =⊥;(2),BF DE BF DE =⊥,理由见解析【分析】()1,BF DE BF DE =⊥,延长ED 交B F 于点G 先证△FBC ≌△EDC (SAS ),可知,BF DE CED CFB =∠=∠,由∠DCE=90º,可得∠DEC+∠CDE=90º,可推出∠FDG+∠GFD=90º即可,()2先下结论,,BF DE BF DE =⊥,再证明,证法与(1)类似,延长ED 交CF 于点,M 交FB 于点N .由四边形ABCD 为矩形且AD=CD 可得CD CB =,()DCE BCF SAS ≅可推出,BF DE CED CFB =∠=∠.由90,FCE ∠=︒知90CME CED ∠+∠=︒.由,CME FMN ∠=∠可用等量代换得90,FMN CFB ∠+∠=︒由三角形内角和得90,FNE ∠=︒即可.【详解】解:()1,BF DE BF DE =⊥,延长ED交B F于点G,∵四边形ABCD为矩形,且AD=DC,∴BC=CD,∴∠=∠=90º,BC CEF D由旋转的FC=EC,∴△FBC≌△EDC(SAS),BF DE CED CFB=∠=∠,,∵∠DCE=90º,∴∠DEC+∠CDE=90º,∴∠FDG+∠GFD=90º∠FGD=90º,()2,=⊥,BF DE BF DE理由如下:M交FB于点N.如答图,延长ED交CF于点,,90FCE ∠=︒,四边形ABCD 为矩形,BCD FCE ∴∠=∠,FCB FCD ECD FCD ∠+∠=∠+∠,FCB ECD ∴∠=∠,AD CD =,∴矩形ABCD 为正方形.CD CB ∴=,在DCE 和BCF △中,,,CD CB ECD FCB CE CF =⎧⎪∠=∠⎨⎪=⎩,()DCE BCF SAS ∴≅.,BF DE CED CFB ∴=∠=∠.90,FCE ∠=︒90CME CED ∴∠+∠=︒.,CME FMN ∠=∠90,FMN CFB ∴∠+∠=︒90,FNE ∴∠=︒BF DE ∴⊥.【点睛】本题考查旋转中两线段的数量与位置关系问题,关键是把两线段置于两个三角形中利用全等解决问题,会利用旋转找全等条件,会计算角的和差,和证垂直的方法. 8.已知:在ABC 中,∠BAC =90°,AB =CA ,直线m 经过点A ,BD ⊥直线m 于点D ,CE ⊥直线m 于点E .求证:BDA AEC ≅△△;【答案】证明见解析.【分析】先根据垂直的定义可得90ADB CEA ∠=∠=︒,再根据直角三角形的两锐角互余、角的和差可得BAD ACE =∠∠,然后根据三角形全等的判定定理即可得证.【详解】,BD m CE m ⊥⊥,90ADB CEA ∴∠=∠=︒,90ACE CAE ∴∠+∠=︒,90BAC ∠=︒,18090BAD CAE BAC ∴∠+∠=︒-∠=︒,BAD ACE ∴∠=∠,在BDA 和AEC 中,ADB CEA BAD ACE AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()BDA AEC AAS ∴≅.【点睛】本题考查了垂直的定义、直角三角形的性质、三角形全等的判定定理,熟练掌握三角形全等的判定方法是解题关键.9.(提出问题)如图1,在直角ABC 中,∠BAC =90°,点A 正好落在直线l 上,则∠1、∠2的关系为(探究问题)如图2,在直角ABC 中,∠BAC =90°,AB =AC ,点A 正好落在直线l 上,分别作BD ⊥l 于点D ,CE ⊥l 于点E ,试探究线段BD 、CE 、DE 之间的数量关系,并说明理由.(解决问题)如图3,在ABC 中,∠CAB 、∠CBA 均为锐角,点A 、B 正好落在直线l 上,分别以A 、B 为直角顶点,向ABC 外作等腰直角三角形ACE 和等腰直角三角形BCF ,分别过点E 、F 作直线l 的垂线,垂足为M 、N .①试探究线段EM 、AB 、FN 之间的数量关系,并说明理由;②若AC =3,BC =4,五边形EMNFC 面积的最大值为【答案】提出问题:1290∠+∠=︒;探究问题:BD CE DE +=,理由见解析;解决问题:①EM FN AB +=,理由见解析;②492. 【分析】 提出问题:根据平角的定义、角的和差即可得;探究问题:先根据垂直的定义可得90ADB CEA ∠=∠=︒,再根据直角三角形的两锐角互余、角的和差可得2ABD ∠=∠,然后根据三角形全等的判定定理与性质可得,BD AE AD CE ==,最后根据线段的和差即可得;解决问题:①如图(见解析),同探究问题的方法可得,EM AD FN BD ==,再根据线段的和差即可得;②如图(见解析),同探究问题的方法可得,ACD EAM BCD FBN ≅≅,再根据三角形全等的性质可得,ACD EAM BCD FBN S S S S ==,然后利用三角形的面积公式将五边形EMNFC 面积表示出来,由此即可得出答案.【详解】提出问题:12180,90BAC BAC ∠+∠+∠=︒∠=︒,2190∴∠+∠=︒,故答案为:1290∠+∠=︒;探究问题:BD CE DE +=,理由如下:,BD l CE l ⊥⊥,90ADB CEA ∴∠=∠=︒,190ABD ∴∠+∠=︒,由提出问题可知,1290∠+∠=︒,2ABD ∴∠=∠,在ABD △和CAE 中,2ADB CEA ABD AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩,()ABD CAE AAS ∴≅,,BD AE AD CE ∴==,DE AE AD BD CE ∴=+=+,即BD CE DE +=;解决问题:①EM FN AB +=,理由如下:同探究问题的方法可证:,EM AD FN BD ==,AB AD BD EM FN ∴=+=+,即EM FN AB +=;②如图,过点C 作CD l ⊥于点D ,同探究问题的方法可证:,ACD EAM BCD FBN ≅≅,,ACD EAM BCD FBN S S S S ∴==, ACE 和BCF △都是等腰直角三角形,且3,4AC BC ==,3,4AE AC BF BC ∴====, 191,8222ACE BCF S AC AE S BC BF ∴=⋅==⋅=, ∴五边形EMNFC 面积为EAM ACE ACD BCD BCF FBN S S S S S S +++++, 982ACD ACD BCD BCD S S S S =+++++, ()2522ACD BCD SS =++, 2522ABC S =+, 则当ABC 面积取得最大值时,五边形EMNFC 面积最大,设ABC的BC边上的高为h,则122ABCS BC h h=⋅=,在ABC中,CAB∠、CBA∠均为锐角,∴当90ACB∠=︒时,h取得最大值,最大值为3AC=,ABC∴面积的最大值为236ABCS=⨯=,则五边形EMNFC面积的最大值为2549 2622⨯+=,故答案为:492.【点睛】本题考查了垂直的定义、三角形全等的判定定理与性质、等腰直角三角形的定义等知识点,熟练掌握三角形全等的判定定理与性质是解题关键.10.如图,在△ABC中,AC=BC,直线l经过顶点C,过A,B两点分别作l的垂线AE,BF,E,F为垂足.AE=CF,求证:∠ACB=90°.【答案】见解析【分析】根据题意易得Rt△ACE≌Rt△CBF,则有∠EAC=∠BCF,然后根据等角的余角相等及领补角可求证.【详解】证明:如图,在Rt △ACE 和Rt △CBF 中,AC BC AE CF=⎧⎨=⎩, ∴Rt △ACE ≌Rt △CBF (HL ),∴∠EAC =∠BCF ,∵∠EAC+∠ACE =90°,∴∠ACE+∠BCF =90°,∴∠ACB =180°﹣90°=90°.【点睛】本题主要考查直角三角形全等的判定与性质,熟练掌握三角形全等的判定条件及性质是解题的关键.11.如图1,在△ABC 中,∠ACB =90°,AC =BC ,过C 在△ABC 外作直线MN ,AM ⊥MN 于点M ,BN ⊥MN 于点N .(1)求证:MN =AM +BN ;(2)如图2,若过点C 作直线MN 与线段AB 相交,AM ⊥MN 于点M ,BN ⊥MN 于点N (AM >BN ),(1)中的结论是否仍然成立?说明理由.【答案】(1)见解析;(2)不成立,理由见解析【分析】(1)根据垂直的定义得到∠AMC=∠CNB=90°,则∠MAC+∠ACM=90°,又∠ACB=90°,则∠ACM+∠NCB=90°,于是根据等量代换得到∠MAC=∠NCB ,根据“AAS ”可证明△ACM ≌△CBN ,根据全等的性质得到AM=CN ,CM=BN ,则MN=MC+CN=AM+BN .(2)根据已知条件能证得△ACM ≌△CBN ,利用全等的性质得到AM=CN ,CM=BN ,而MN=CN-CM=AM-BN .【详解】解:(1)∵AM ⊥MN 于点M ,BN ⊥MN 于点N ,∴∠AMC=∠CNB=90°,∴∠MAC+∠ACM=90°,∵∠ACB=90°,∴∠ACM+∠NCB=90°,∴∠MAC=∠NCB ,在△ACM 和△CBN 中,AMC CNB MAC NCB AC BC ∠=∠⎧⎪∠=∠⎨⎪=⎩\ ∴ACM ≌△CBN ,∴AM=CN ,CM=BN ,∴MN=MC+CN=AM+BN .(2)题(1)中的结论不成立,同题(1)证明可知:ACM ≌△CBN ,∴AM=CN ,CM=BN ,∴MN=CN-CM=AM-BN ,【点睛】本题主要考查的是全等三角形的性质与判断,正确的掌握全等三角形的性质与判断是解题的关键.12.在平面直角坐标系中,函数443y x =-+的图像分别交x 轴、y 轴于点A C 、,函数y ax b =+的图象分别交x 轴、y 轴于点,B C ,且4OC OB =,过点C 作射线//CR x 轴. (1)求直线BC 的解析式;(2)点P 自点C 沿射线CR 以每秒1个单位长度运动,同时点Q 自点A 沿线段AC 以每秒1个单位长度的速度向终点C 运动,其中一个点停止运动时,另一个点也停止运动,连接PQ .设POC ∆的面积为S ,点Q 的运动时间为t (秒),求S 与t 的函数关系式,并直接写出t 的取值范围;(3)在(2)的条件下,过点P 作//PF CB ,交x 轴于点F ,连接QF ,在P Q 、运动的过程中,是否存在t 值,使得45PFQ ︒∠=,若存在,求t 值:若不存在,请说明理由.【答案】(1)44y x =+;(2)()222055S t t t =-+<<;(3)存在,1511或257【分析】(1)利用待定系数法求出A ,C 两点坐标,再求出点B 坐标即可解决问题; (2)想办法用t 表示点Q 坐标,利用三角形面积公式计算即可;(3)分两种情形,通过辅助线构造等腰直角三角形,利用相似三角形解决问题.【详解】解:(1)函数443y x =-+的图象分别交x 轴、y 轴于点A ,C , (3,0)A ∴,(0,4)C ,3OA =,4OC =,4OC OB =,1OB =∴,(1,0)B ∴-,设直线BC 的解析式为y kx b =+,则有40b k b =⎧⎨-+=⎩, 解得44k b =⎧⎨=⎩, ∴直线BC 的解析式为44y x =+.(2)如图1中,由题意AQ PC t ==,易知3(35Q t -,4)5t ,2142(4)2(05)255S t t t t t ∴=-=-+<< (3)存在;情形①如图2中,取点(4,3)M ,连接CM ,BM ,作MG CR ⊥垂足为G 交OA 于K ,作QH OA ⊥垂足为H .4CG CO ==,90CGM COB ∠=∠=︒,1MG BO ==()CGM COB ASA ∴≅△△,GCM OCB ∴∠=∠,CB CM =,90BCM OCG ∴∠=∠=︒,BCM ∴∆的等腰直角三角形,1345∴∠=∠=︒,//PF BC ,2145∴∠=∠=︒,445∠=︒,24∴∠=∠,//FQ BN ∴,QFH MBK ∴∠=∠,90QHF MKB ∠=∠=︒,QHF MKB ∴△∽△, ∴QH FH MK BK =,∴433(1)5535t t t ---=, 1511t ∴=. 情形②如图3中,由2445∠=∠=︒,可知90MNF ∠=︒,由QHF BKM △∽△得到QH HF BK MK=, ∴43(4)5553t t t --=, 257t ∴=, 综上所述1511t或257. 【点睛】此题考查一次函数的应用,直角三角形的性质及全等三角形以及相似三角形的判定及性质,属于综合性较强的题目,对于此类动点型题目,首先要确定符合题意的条件下动点所在的位置,然后用时间t 表示出有关线段的长度,进而建立关于线段的关系式,学会添加常用辅助线,构造特殊三角形解决问题,难度较大.13.已知:如图,在平面直角坐标系中,点A (a ,0)、C (b ,c ),且a 、b 、c满足()2b 32c -++∣=0. (1)求点A 、C 的坐标;(2)在x 轴正半轴上有一点E ,使∠ECA =45°,求点E 的坐标;(3)如图2,若点F 、B 分别在x 轴正半轴和y 轴正半轴上,且OB=OF ,点P 在第一象限内,连接PF ,过P 作PM ⊥PF 交y 轴于点M ,在PM 上截取PN=PF ,连接PO 、BN ,过P 作∠OPG=45°交BN 于点G ,求证:点G 是BN 的中点.【答案】(1)(-3,0);(3,-2);(2)(2,0);(3)证明见详解【分析】(1)根据题意,由算术平方根,绝对值和平方数的非负性,求出a 、b 、c 的值,即可得出点A 、C 的坐标;(2)通过辅助线作图,构造一线三垂直模型,证明ALG CKA S≌S ,求出点G 的坐标,由等面积法求出AE 长度即可求出点E 坐标;(3)作EO ⊥OP 交PG 的延长线于E ,连接EB 、EN 、PB ,只要证明四边形ENPB 是平行四边形即可.【详解】(1()2b 32c -++∣=0, 所以a=-3,b=3,c=-2,点A 坐标为(-3,0),点C 坐标为(3,-2),故答案为:(-3,0);(3,-2);(2)过点A 作AC 的垂线,交CE 的延长线于点G ,过点A 作x 轴的垂线KL ,过点C 作KL 的垂线于点K ,过点G 作KL 的垂线于点L ,过点G 作x 轴的垂线于M ,过点C作x 轴的垂线于N ,∵∠ECA =45°,AG ⊥AC ,∴∠CAG=90°,AG=AC ,△CAG 为等腰直角三角形,由一线三垂直模型可知,∠GAL=∠ACK ,在△ALG 和△CKA 中90GAL ACKAG A AC LG CKA ∠=∠∠=∠==︒⎧⎪⎨⎪⎩∴ALG CKA S ≌S ,∴AL=CK=AN=3+3=6,LG=AK=CN=2,∴GM=6,OM=3-2=1,∴点G 坐标为(-1,3),在Rt △ANC 中,AN=6,CN=2,由勾股定理得,由等面积法,得11()22AC AG AE GM CN ⨯⨯=⨯⨯+,∴11822AE ⨯⨯⨯, ∴AE=5,∴OE=AE-OA=5-3=2,故点E 坐标为(2,0),故答案为:(2,0);(3)如图,作EO ⊥OP 交PG 的延长线于E ,连接EB 、EN 、PB ,∵∠EOP=90°,∠EPO=45°,∴∠OEP=∠EPO=45°,∴EO=PO ,∵∠EOP=∠BOF=90°,∴∠EOB=∠POF ,在△EOB 和△POF 中,BO OF EOB POF OE OP =⎧⎪∠=∠⎨⎪=⎩∴△EOB ≌△POF ,∴EB=PF=PN ,∠1=∠OFP ,∵∠2+∠PMO=180°,∵∠MOF=∠MPF=90°,∴∠OMP+∠OFP=180°,∴∠2=∠OFP=∠1,∴EB ∥PN ,∵EB=PN ,∴四边形ENPB 是平行四边形,∴BG=GN ,即点G 是BN 的中点.【点睛】本题考查了算术平方根,绝对值和平方数的非负性,一线三垂直模型,等面积法求线段长度,三角形全等的判定和性质,平行四边形的判定和性质应用,熟练掌握图形的判定和性质是解题的关键.14.在平面直角坐标系中,已知点(),0A a 、()0,C b 满足2(2)0+=a(1)直接写出:a =____________,b =________.(2)点B 为x 轴正半轴上一点,如图1,BE AC ⊥于点E ,交y 轴于点D ,连接OE ,若OE 平分AEB ∠,求直线BE 的解析式.(3)在(2)的条件下,点M 为直线BE 上一动点,连OM ,将线段OM 绕点M 逆时针旋转90︒,如图2,点O 的对应点为N ,当点M 运动时,判断点N 的运动路线是什么图形,并说明理由.【答案】(1)2-,5-;(2)2y x 25=-;(3)点N 的运动路线是直线32077=--y x ,理由见解析【分析】(1)根据题意得到关于a 、b 的方程,求a 、b 即可;(2)如图1,过点O 作OF OE ⊥,交BE 于F ,分别证明EOC FOB ∆∆≌,AOC DOB ∆∆≌,得到OB OC =,OA OD =,确定点B 、D 坐标,利用待定系数法即可求解; (3)如图2,过点M 作MG x ⊥轴,垂足为G ,过点N 作⊥NH GM 交GM 的延长线于H ,证明NOM ∆为等腰直角三角形,得到=OG MH ,=GM NH ,设2,25⎛⎫- ⎪⎝⎭M m m ,则3,25--⎛⎫ ⎪⎝⎭H m m ,得到732,255⎛⎫--- ⎪⎝⎭N m m ,即752-=m x ,325--=m y ,消去m ,即可得到点N 运动轨迹.【详解】解:(1)由题意得a+2=0,b+5=0,解得a=2-,b=5-,故答案为:2-,5-;(2)如图1,过点O 作OF OE ⊥,交BE 于F ,∵BE AC ⊥,OE 平分AEB ∠,∴EOF ∆为等腰直角三角形,∴OE=OF ,∠BOF=∠COE=45°,∵BE AC ⊥于点E ,∴∠1+∠BAC=90°,∵∠2+∠BAC=90°,∴∠1=∠2,∴EOC FOB ∆∆≌,∴OB OC =,∵∠1=∠2, ∠AOC=∠DOB=90°,∴AOC DOB ∆∆≌,∴OA OD =,∵()2,0A -,()0,5C -,∴()0,2D -,()5,0B ,设直线BD 解析式为y kx b =+,∴250b k b =-⎧⎨+=⎩, ∴ 225b k =-⎧⎪⎨=⎪⎩, ∴直线BD ,即直线BE 的解析式为2y x 25=-;(3)由题意得,NOM ∆为等腰直角三角形如图2,过点M 作MG x ⊥轴,垂足为G ,过点N 作⊥NH GM 交GM 的延长线于H , ∵NOM ∆为等腰直角三角形,∴≌∆∆GOM HMN ,∴=OG MH ,=GM NH ,由(2)得直线BD 的解析式2y x 25=-, 设2,25⎛⎫- ⎪⎝⎭M m m ,则3,25--⎛⎫ ⎪⎝⎭H m m , ∴732,255⎛⎫--- ⎪⎝⎭N m m , 令752-=m x ,325--=m y , ∴32077=--y x , 即点N 的运动路线是直线32077=--y x .【点睛】本题为一次函数综合题,考查了三角形全等判定,等腰直角三角形性质,待定系数法等,综合性强,根据题意构造全等,理解函数图象是点的运动轨迹是解题的关键.15.如图,将Rt△ABC的斜边BC绕点B顺时针旋转90°得边BD,过点D作AB的垂线,交AB延长线于点E,求证:△EDB≌△ABC.【答案】见解析.【分析】先由旋转的性质得到BC=BD,∠DBC=90°=∠CAB,再运用“AAS”证得△EDB≌△ABC 即可.【详解】证明:∵BC绕点B顺时针旋转90°得边BD,∴BC=BD,∠DBC=90°=∠CAB,∴∠ABC+∠ACB=90°,∠ABC+∠DBE=90°,∴∠ACB=∠DBE,又∵∠CAB=∠DEB=90°,∴△EDB≌△ABC(AAS).【点睛】本题考查了全等三角形的判定和旋转的性质,根据旋转的性质得到判定全等三角形的条件是解答本题的关键.16.如图,已知在△ABC中,AB=AC,∠BAC=90°,分别过B、C向过A的直线作垂线,垂足分别为E、F.(1)如图①过A的直线与斜边BC不相交时,求证:EF=BE+CF;(2)如图②过A的直线与斜边BC相交时,其他条件不变,若BE=10,CF=3,求:FE 长.【答案】(1)见解析;(2)7【分析】(1)此题根据已知条件容易证明△BEA≌△AFC,然后利用对应边相等就可以证明题目的结论;(2)根据(1)知道△BEA≌△AFC仍然成立,再根据对应边相等就可以求出EF了.【详解】解:(1)∵BE⊥EA,CF⊥AF,∴∠BAC=∠BEA=∠CFE=90°,∴∠EAB+∠CAF=90°,∠EBA+∠EAB=90°,∴∠CAF=∠EBA,在△ABE和△AFC中,∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,∴△BEA≌△AFC.∴EA=FC,BE=AF.∴EF=EB+CF.(2)解:∵BE⊥EA,CF⊥AF,∴∠BAC=∠BEA=∠CFE=90°,∴∠EAB+∠CAF=90°,∠ABE+∠EAB=90°,∴∠CAF=∠ABE,在△ABE和△AFC中,∠BEA=∠AFC=90°,∠EBA=∠CAF,AB=AC,∴△BEA≌△AFC.∴EA=FC=3,BE=AF=10.∴EF=AF﹣CF=10﹣3=7.【点睛】此题主要考查了全等三角形的性质与判定,利用它们解决问题,经常用全等来证线段和的问题.17.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN 于E,(1)当直线MN绕点C旋转到图(1)的位置时,请你探究线段DE、AD、BE之间的数量关系并加以证明;(2)当直线MN绕点C旋转到图(2)的位置时,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.(3)当直线MN绕点C旋转到图(3)的位置时,试问DE、AD、BE具有怎样的等量关系?请直接写出这个等量关系.【答案】(1)DE=AD+BE,理由见详解;(2)发生变化,AD=BE+DE,理由见详解;(3)BE=AD+DE.【分析】(1)由题意易得∠CDA=∠BEC=90°,∠DCA+∠ECB=90°,∠DCA+∠DAC=90°,则有∠DAC=∠ECB,进而可知△ADC≌△CEB,然后根据全等三角形的性质及线段等量关系可求证;(2)由题意易得∠CDA=∠BEC=90°,∠DCA+∠CAD=90°,∠DCA+∠BCE=90°,则有∠DAC=∠ECB,进而可知△ADC≌△CEB,然后根据全等三角形的性质及线段等量关系可求证;(3)由题意易得∠CDA=∠BEC=90°,∠DCA+∠ECB=90°,∠EBC+∠BCE=90°,则有∠ACD=∠CBE,进而可知△ADC≌△CEB,然后根据全等三角形的性质及线段等量关系可得解.【详解】解:(1)DE=AD+BE,理由如下:∠ACB=90°,AD⊥MN于D,BE⊥MN于E,∴∠CDA=∠BEC=90°,∠DCA+∠ECB=90°,∠DCA+∠DAC=90°,∴∠DAC=∠ECB,AC=BC,∴△ADC≌△CEB,∴AD=CE,CD=BE,DE=DC+CE∴DE=AD+BE;(2)发生变化,AD=BE+DE,理由如下:∠ACB=90°,AD⊥MN于D,BE⊥MN于E,∴∠CDA=∠BEC=90°,∠DCA+∠CAD=90°,∠DCA+∠BCE=90°,∴∠DAC=∠ECB,AC=BC,∴△ADC≌△CEB,∴AD=CE,CD=BE,CE=DC+DE∴AD=BE+DE;(3)BE=AD+DE,理由如下:同理(2)的方法可得△ADC≌△CEB,∴AD=CE,CE=AD,CD=EC+DE∴BE=AD+DE.【点睛】本题主要考查三角形全等的判定与性质,熟练掌握三角形全等的性质与判定是解题的关键.18.如图,在ABC 中∠ACB=90°,AC=BC ,直线MN 经过点C ,且AD ⊥MN 于D ,BE ⊥MN 于E .(1)求证:ADC CEB △≌△;(2)若AD=2,BE=3,求ABC 的面积.【答案】(1)见解析;(2)132【分析】 (1)根据垂直定义求出∠BEC =∠ACB =∠ADC ,根据等式性质求出∠ACD =∠CBE ,根据AAS 证出△ADC 和△CEB 全等即可;(2)由(1)可推出CD =BE ,AD =CE ,进而可得到AC=AB=△ABC 面积即可.【详解】解:(1)证明:∵∠ACB =90°,AD ⊥MN ,BE ⊥MN ,∴∠BEC =∠ACB =∠ADC =90°,∴∠ACE+∠BCE =90°,∠BCE+∠CBE =90°,∴∠ACD =∠CBE ,在△ADC 和△CEB 中ADC=BEC ACD=CBE AC=BC ⎧⎪⎨⎪⎩∠∠∠∠,∴△ADC ≌△CEB (AAS );(2)∵△ADC ≌△CEB∴BE =CD ,AD =CE ,AC=BC ,又AD=2,BE=3,∴∴△ABC 的面积为11322=, 故△ABC 的面积为132.【点睛】全等三角形的性质和判定,全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具.在判定三角形全等时,关键是选择恰当的判定条件.二、填空题19.一个等腰直角三角尺不小心掉到两墙之间(如图),已知90,ACB AC BC ∠=︒=,从三角尺的刻度可知20,AB cm AD =为三块砖的厚度,BE 为两块砖的厚度,小聪很快就知道了砌墙所用砖块的厚度(每块砖的厚度相等,两块砖间的缝隙忽略不计)为____________cm .【答案】13【分析】设砖块的厚度为xcm ,由题意可知:AD=3x ,BE=2x ,根据等腰直角三角形的性质和勾股定理求出AC ,利用AAS 即可证出△DAC ≌△ECB ,从而得出CD=BE=2xcm ,利用勾股定理列出方程即可求出x .【详解】解:设砖块的厚度为xcm ,由题意可知:AD=3xcm ,BE=2xcm∵90,ACB AC BC ∠=︒=,20AB cm =∴222AC BC AB +=解得AC BC ==由题意可知:∠ADC=∠CEB=90°∴∠DAC +∠ACD=90°,∠ECB +∠ACD=90°∴∠DAC=∠ECB∴△DAC ≌△ECB∴CD=BE=2xcm在Rt △ADC 中,222AD DC AC +=即()()(22232x x +=解得:x=13. 【点睛】此题考查的是等腰直角三角形的性质、勾股定理和全等三角形的判定及性质,掌握等腰直角三角形的性质、勾股定理和全等三角形的判定及性质是解题关键.20.如图,在平面直角坐标系中,A(0,5),B(2,0),点C是第一象限内的点,且△ABC 是以AB为直角边,满足AB=AC,则点C的坐标为________.【答案】(5,7)【分析】依题∠BAC=90°,AB=AC,画出C点位置,利用全等三角形的判定与性质,即可求得点C的坐标.【详解】解:如图:当∠BAC=90°,AB=AC时,过点C作CD⊥y轴于点D,在△OAB和△DCA中,AOB CDA OAB DCA AB AC ∠∠⎧⎪∠∠⎨⎪⎩===,∴△OAB ≌△DCA (AAS ),∴AD=OB=2,CD=OA=5,∴OD=OA+AD=7,∴点C 的坐标为(5,7);【点睛】本题考查了坐标与图形、全等三角形的判定与性质、等腰直角三角形的性质,注意掌握数形结合思想的应用.21.如图,Rt △ABC 中,∠BAC=90°,AB=AC ,分别过点B . C 作过点A 的直线的垂线BD 、CE ,垂足分别为D 、 E ,若BD=4,CE=2,则DE=___.【答案】6【分析】先证明∠DBA=∠CAE ,从而根据AAS 定理证明△BDA ≌△AEC ,根据全等三角形的性质可得AD=CE=2,AE=BD=4,进而得到答案.【详解】解:∵∠BAC=90°,∴∠BAD+∠CAE=90°,∵BD ⊥DE ,∴∠BDA=90°,∴∠BAD+∠DBA=90°,∴∠DBA=∠CAE ,∵CE ⊥DE ,∴∠AEC=90°,在△BDA 和△AEC 中,ABD CAE BDA AEC AB AC ∠=∠⎧⎪∠=∠⎨⎪=⎩,∴△BDA ≌△AEC (AAS ),∴AD=CE=2,AE=BD=4,∴DE=AD+AE=2+4=6;故答案为:6.【点睛】本题考查了全等三角形的判定与性质、直角三角形的性质,关键是掌握全等三角形的判定定理与性质定理.22.如图,直线a 经过正方形ABCD 的顶点A ,已知BE a ⊥于点E ,DF a ⊥于点F .若3BE =,8DF =,则线段EF 的长为______.【答案】11【分析】根据题意易得△AEB ≌△DFA ,则有BE=AF ,DF=AE ,进而问题可得解.【详解】解:∵四边形ABCD 是正方形,∴AD=AB ,∠DAB=90°,∵BE a ⊥,DF a ⊥,∴∠DFA=∠AEB=90°,∴∠FAD+∠ADF=90°,又∵∠FAD+∠BAE=90°,∴∠ADF=∠BAE ,∴△AEB ≌△DFA ,∵3BE =,8DF =,∴BE=AF=3,DF=AE=8,∴EF=AF+AE=3+8=11;故答案为11.【点睛】本题主要考查全等三角形的判定与性质及正方形的性质,熟练掌握全等三角形的判定与性质及正方形的性质是解题的关键.23.如图,AO⊥OM,OA=7,点B为射线OM上的一个动点,分别以OB,AB为直角边,B为直角顶点,在OM两侧作等腰Rt△OBF、等腰Rt△ABE,连接EF交OM于P 点,当点B在射线OM上移动时,则PB的长度____________.【答案】7 2【分析】根据题意过点E作EN⊥BM,垂足为点N,首先证明△ABO≌△BEN,得到BO=ME;进而证明△BPF≌△MPE并分析即可得出答案.【详解】解:如图,过点E作EN⊥BM,垂足为点N,∵∠AOB=∠ABE=∠BNE=90°,∴∠ABO+∠BAO=∠ABO+∠NBE=90°,∴∠BAO=∠NBE,∵△ABE、△BFO均为等腰直角三角形,。
平行线几何模型(铅笔头模型)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)
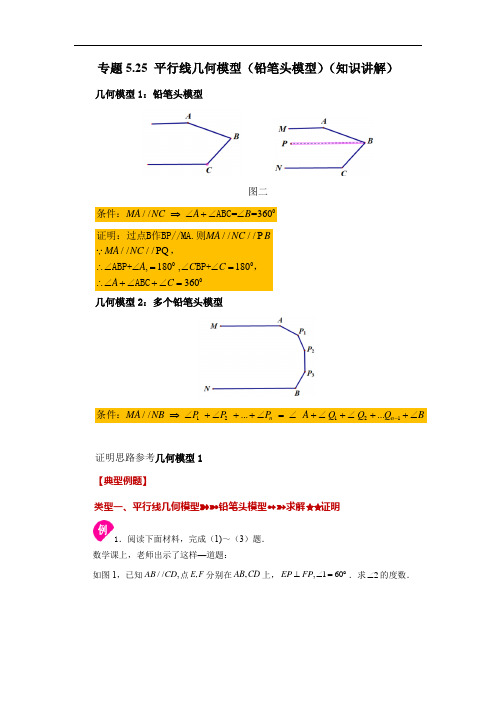
专题5.25 平行线几何模型(铅笔头模型)(知识讲解) 几何模型1:铅笔头模型图二0//==360MA NC A B ⇒∠+∠∠条件:ABC 000////P ////PQ ,180,180360MA NC BMA NC A C C A C ∴∠∠=∠∠=∴∠+∠+∠=证明:过点B 作BP//MA.则,ABP+BP+,ABC几何模型2:多个铅笔头模型12121//......n n MA NB P P P A Q Q Q B-⇒∠+∠++∠=∠+∠+∠++∠条件:证明思路参考几何模型1【典型例题】类型一、平行线几何模型➽➼铅笔头模型➻➸求解✬✬证明1.阅读下面材料,完成(1)~(3)题.数学课上,老师出示了这样—道题:如图1,已知//,AB CD 点,E F 分别在,AB CD 上,,160EP FP ⊥∠=︒.求2∠的度数.同学们经过思考后,小明、小伟、小华三位同学用不同的方法添加辅助线,交流了自己的想法:小明:“如图2,通过作平行线,发现13,24∠=∠∠=∠,由已知,EP FP ⊥可以求出2∠的度数.”小伟:“如图3这样作平行线,经过推理,得234,∠=∠=∠也能求出2∠的度数.”小华:∵如图4,也能求出2∠的度数.”(1) 请你根据小明同学所画的图形(图2),描述小明同学辅助线的做法,辅助线:______; (2) 请你根据以上同学所画的图形,直接写出2∠的度数为_________°;老师:“这三位同学解法的共同点,都是过一点作平行线来解决问题,这个方法可以推广.”请大家参考这三位同学的方法,使用与他们类似的方法,解决下面的问题:(3) 如图,//AB CD ,点,E F 分别在AB CD ,上,FP 平分,,EFD PEF PDF ∠∠=∠若,EPD a ∠=请探究CFE ∠与PEF ∠的数量关系((用含α的式子表示),并验证你的结论.【答案】(1)过点Р作//PQ AC ;(2)30;(3)2180CFE PEF a ∠-∠=-.【分析】(1)根据图中所画虚线的位置解答即可;(2)过点Р作//PQ AC ,根据平行线的性质可得∵1=∵3,∵2=∵4,由EP∵FP 可得∵3+∵4=90°,即可得出∵1+∵2=90°,进而可得答案;(3)设,CFE x PEF PDF y ∠=∠=∠=,过点P 作//PQ AB ,根据平行线的性质可得180,BEP EPQ CFE FEB x ∠+∠=︒∠=∠=,PDF DPQ ∠=∠,进而根据角的和差关系即可得答案.解:(1)由图中虚线可知PQ//AC ,∵小明同学辅助线的做法为过点Р作//PQ AC ,故答案为:过点Р作//PQ AC(2)如图2,过点Р作//PQ AC ,∵AB//CD ,∵PQ//AB//CD ,∵∵1=∵3,∵2=∵4,∵EP∵FP ,∵∵EPF=∵3+∵4=90°,∵∵1+∵2=90°,∵∵1=60°,∵∵2=30°,故答案为:30(3)如图,设,CFE x PEF PDF y ∠=∠=∠=,过点P 作//PQ AB ,180,BEP EPQ CFE FEB x ∴∠+∠=︒∠=∠=//,AB CD//,PQ CD ∴PDF DPQ ∴∠=∠DPQ EHF PDF y ∴∠=∠=∠=∵CFE FEB x FEP BEP ∠=∠==∠+∠()180x y a y ∴=+-+2180x y α∴-=-,即2180CFE PEF a ∠-∠=-.【点拨】本题考查平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;正确作出辅助线,熟练掌握平行线的性质是解题关键.举一反三:【变式】问题情境:如图1,AB ∵CD ,∵P AB =130°,∵PCD =120°,求∵APC 度数.思路点拨:小明的思路是:如图2,过P作PE∵AB,通过平行线性质,可分别求出∵APE、∵CPE 的度数,从而可求出∵APC的度数;小丽的思路是:如图3,连接AC,通过平行线性质以及三角形内角和的知识可求出∵APC 的度数;小芳的思路是:如图4,延长AP交DC的延长线于E,通过平行线性质以及三角形外角的相关知识可求出∵APC的度数.问题解决:请从小明、小丽、小芳的思路中任选一种思路进行推理计算,你求得的∵APC 的度数为°;问题迁移:(1)如图5,AD∵BC,点P在射线OM上运动,当点P在A、B两点之间运动时,∵ADP=∵α,∵BCP=∵β.∵CPD、∵α、∵β之间有何数量关系?请说明理由;(2)在(1)的条件下,如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出∵CPD、∵α、∵β间的数量关系.【答案】问题解决:110°;问题迁移:(1)∵CPD=∵α+∵β,理由见分析;(2)∵CPD =∵β﹣∵α,理由见分析【分析】小明的思路是:过P作PE∵AB,构造同旁内角,利用平行线性质,可得∵APC =110°.(1)过P作PE∵AD交CD于E,推出AD∵PE∵BC,根据平行线的性质得出∵α=∵DPE,∵β=∵CPE,即可得出答案;(2)画出图形(分两种情况:∵点P在BA的延长线上,∵点P在AB的延长线上),根据平行线的性质得出∵α=∵DPE,∵β=∵CPE,即可得出答案.解:小明的思路:如图2,过P作PE∵AB,∵AB∵CD,∵PE∵AB∵CD,∵∵APE=180°﹣∵A=50°,∵CPE=180°﹣∵C=60°,∵∵APC=50°+60°=110°,故答案为:110;(1)∵CPD=∵α+∵β,理由如下:如图5,过P作PE∵AD交CD于E,∵AD∵BC,∵AD∵PE∵BC,∵∵α=∵DPE,∵β=∵CPE,∵∵CPD=∵DPE+∵CPE=∵α+∵β;(2)当P在BA延长线时,∵CPD=∵β﹣∵α;理由:如图6,过P作PE∵AD交CD于E,∵AD∵BC,∵AD∵PE∵BC,∵∵α=∵DPE,∵β=∵CPE,∵∵CPD=∵CPE﹣∵DPE=∵β﹣∵α;当P在BO之间时,∵CPD=∵α﹣∵β.理由:如图7,过P作PE∵AD交CD于E,∵AD∵BC,∵AD∵PE∵BC,∵∵α=∵DPE,∵β=∵CPE,∵∵CPD=∵DPE﹣∵CPE=∵α﹣∵β.【点拨】本题考查了三角形的内角和定理,平行线的性质,主要考查学生的推理能力,解决问题的关键是作辅助线构造内错角以及同旁内角.类型二、平行线几何模型➽➼多铅笔头模型➻➸求解✬✬证明2.(1)如图1,AM∵CN,求证:∵∵MAB+∵ABC+∵BCN=360°;∵∵MAE+∵AEF+∵EFC+∵FCN=540°;(2)如图2,若平行线AM与CN间有n个点,根据(1)中的结论写出你的猜想并证明.【答案】(1)∵详见分析;∵详见分析;(2)猜想:若平行线间有n个点,则所有角的和为(n+1)•180°,证明详见分析【分析】(1)∵过点作BG∵AM,则AM∵CN∵BG,依据平行线的性质,即可得到∵ABG+∵BAM=180°,∵CBG+∵BCN=180°,即可得到结论;∵过E作EP∵AM,过F作FQ∵CN,依据平行线的性质,即可得到∵MAE+∵AEP=180°,∵FEP+∵EFQ=180°,∵CFQ+∵FCN=180°,即可得到结论;(2)过n个点作AM的平行线,则这些直线互相平行且与CN平行,即可得出所有角的和为(n+1)•180°.解:(1)∵证明:如图1,过点作BG∵AM,则AM∵CN∵BG∵∵ABG+∵BAM=180°,∵CBG+∵BCN=180°∵∵ABG+∵BAM+∵CBG+∵BCN=360°∵∵MAB+∵ABC+∵BCN=360°∵如图,过E作EP∵AM,过F作FQ∵CN,∵AM∵CN,∵EP∵FQ,∵∵MAE+∵AEP=180°,∵FEP+∵EFQ=180°,∵CFQ+∵FCN=180°∵∵MAE+∵AEF+∵EFC+∵FCN=180°×3=540°;(2)猜想:若平行线间有n个点,则所有角的和为(n+1)•180°.证明:如图2,过n个点作AM的平行线,则这些直线互相平行且与CN平行,∵结合(1)问得:所有角的和为(n+1)•180°.【点拨】本题主要考查了平行线的性质,解决问题的关键是作平行线,利用两直线平行,同旁内角互补得出结论.举一反三:【变式】如图,已知AB∵CD.(1)如图1所示,∵1+∵2=;(2)如图2所示,∵1+∵2+∵3=;并写出求解过程.(3)如图3所示,∵1+∵2+∵3+∵4=;(4)如图4所示,试探究∵1+∵2+∵3+∵4+∵+∵n=.【答案】(1)180°;(2)360°;(3)540°;(4)(n-1)×180°【分析】(1)由两直线平行,同旁内角互补,可得答案;(2)过点E作AB的平行线,转化成两个图1,同理可得答案;(3)过点E,点F分别作AB的平行线,转化成3个图1,可得答案;(4)由(2)(3)类比可得答案.解:(1)如图1,∵AB∵CD,∵∵1+∵2=180°(两直线平行,同旁内角互补).故答案为:180°;(2)如图2,过点E作AB的平行线EF,∵AB∵CD,∵AB∵EF,CD∵EF,∵∵1+∵AEF=180°,∵FEC+∵3=180°,∵∵1+∵2+∵3=360°;(3)如图3,过点E,点F分别作AB的平行线,类比(2)可知∵1+∵2+∵3+∵4=180°×3=540°,故答案为:540°;(4)如图4由(2)和(3)的解法可知∵1+∵2+∵3+∵4+…+∵n=(n-1)×180°,故答案为:(n-1)×180°.【点拨】此题考查了平行线的性质.注意掌握辅助线的作法是解此题的关键.。
北师大版数学七年级下册专题十四几何证明课件

证明:∵ ∠ = ∠,
∴ ∠ + ∠ = ∠ + ∠,即∠ = ∠.
在△ 和△ 中,
∠ = ∠,
ቐ∠ = ∠,
= ,
∴△ ≌△ ,∴ = .
4.如图,完成下列推理过程:
如图所示,点E在△ ABC外部,点D在BC边上,DE交AC于点
= ,
ቐ = ′ ,
= ′ ,
∴△ ≌△ ′ .
(2)若∠BAC = 100∘ ,求∠DAE的度数.
解:∵△ ≌△ ′,
∴ ∠ = ∠′,∴ ∠ = ∠′ = ∘ ,
∵ 以△ 的边所在直线为对称轴作△ 的轴对称图形△ ′,
∴ ∠ + ∠ = ∘ ,∵ ∠ = ∘ ,
∴ ∠ + ∠ 中,
∠ = ∠ = ∘ ,
ቐ∠ = ∠,
∴△ ≌△ .
= ,
(2)当AD = 3,BE = 1时,求DE的长.
解:∵△ ≌△ ,∴ = = , = = ,∴ = + =
+ = .
类型二 与轴对称有关的几何证明
8.如图,在△ ABC中,AB = AC,D,E是BC边上的点,连
接AD,AE,以△ ADE的边AE所在直线为对称轴作△ ADE
的轴对称图形△ AD′E,连接D′C,若BD = CD′.
∠ABC交AC于点F,AE ⊥ BF交BF的延长线于点E,AE,BC的
延长线交于点M.
(1)求证:AB = BM;
证明:由题意得 ⊥ ,∴ ∠ = ∠ = ∘ .
∵ 平分∠,∴ ∠ = ∠.
在△ 和△ 中,
∠ = ∠ = ∘ ,
∴ ∠ = ∠′ =
七年级上册几何证明题

七年级上册几何证明题引言在数学学科中,几何证明题是一种重要的题型。
通过解答几何证明题,不仅能够帮助学生提高对几何形状的理解,还能够培养学生的逻辑思维能力和推理能力。
本文将介绍七年级上册的一些典型的几何证明题,并提供相应的解答。
题目一:等腰三角形的性质证明题目描述:证明等腰三角形的两底角相等。
证明过程: 1. 假设三角形ABC是一个等腰三角形,其中AB=AC。
2. 根据等腰三角形的定义,我们知道AB=AC,即两边的长度相等。
3. 由于等腰三角形的两边相等,所以两个底角也一定相等。
4. 因此,我们可以得出结论:等腰三角形的两底角相等。
题目二:垂直线段的性质证明题目描述:证明垂直线段相互垂直。
证明过程: 1. 假设线段AB和线段CD是两条垂直线段。
2. 根据垂直线段的定义,我们知道线段AB和CD的斜率相乘等于-1。
3. 过点A和点C分别作AB所在直线和CD所在直线的垂线,设交点为E。
4. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角AED为直角。
5. 同理,过点B和点D分别作AB所在直线和CD所在直线的垂线,设交点为F。
6. 根据直线的性质,垂直相交的两条直线所成的角度为90度,即角BFD为直角。
7. 因此,我们可以得出结论:垂直线段相互垂直。
题目三:等边三角形的性质证明题目描述:证明等边三角形的三个内角都为60度。
证明过程: 1. 假设三角形ABC是一个等边三角形,其中AB=BC=AC。
2. 根据等边三角形的定义,我们知道AB=BC=AC,即三边的长度都相等。
3. 由于等边三角形的三边相等,所以三个角度也相等。
4. 假设角A的度数为x度,那么角B和角C的度数也分别为x度。
5. 根据角的性质,三个角的度数之和等于180度,所以x + x + x = 180。
6. 解以上方程,得到x = 60度。
7. 因此,我们可以得出结论:等边三角形的三个内角都为60度。
结论几何证明题是数学学科中的重要题型,通过解答这些题目,可以帮助学生加深对几何形状的理解。
七年级数学三角形典型例题

七年级数学三角形典型例题三角形是数学中一个重要的几何概念,也是初中数学中的典型例题之一。
学习三角形有助于培养学生的几何直观和空间想象能力,对于理解数学的几何概念和初步推导证明也起着重要的作用。
下面是七年级数学三角形常见的典型例题及其解析。
1. 已知三角形ABC的三边分别为AB = 3cm, AC = 4cm, BC =5cm,问该三角形是什么类型的三角形?解析:根据三角形的三边关系,我们可以用较长边的平方是否等于其他两边平方的和来判断三角形的类型。
即判断AB^2 = AC^2 + BC^2是否成立。
计算可得AB^2 = 3^2 = 9, AC^2 + BC^2 = 4^2 + 5^2 = 41,因此AB^2不等于AC^2 + BC^2。
所以该三角形不是直角三角形。
再用较长边的平方是否大于其他两边平方的和来判断三角形的类型。
即判断AB^2 > AC^2 + BC^2是否成立。
计算可得AB^2 = 3^2 = 9, AC^2 + BC^2 = 4^2 + 5^2 = 41,因此AB^2大于AC^2 + BC^2。
所以该三角形是锐角三角形。
因此,三角形ABC是锐角三角形。
2. 已知一个三角形的三个内角分别是30°,60°和90°,问这个三角形的三条边长是多少?等于180°,因此一个角为90°,另外两个角相加等于90°。
此题中,已知一个角为90°,另外两个角相加等于90°,因此这个三角形是直角三角形。
直角三角形中,较长边的平方等于其他两边平方的和。
设三边分别为a, b, c,则有a^2 = b^2 + c^2。
其中,已知一个角为90°,另外一个角为60°,所以三角形的两条边分别为c = a*sin60°和b = a*cos60°。
代入上式,可得a^2 = (a*sin60°)^2 + (a*cos60°)^2。
平行线几何模型(M模型)(知识讲解)-2022-2023学年七年级数学下册基础知识专项讲练(人教版)

专题5.22平行线几何模型(M模型)(知识讲解)几何模型1:M型模型(也称“猪蹄模型”)图一//=MA NC A B⇒∠∠+∠条件:ABC////PQ=,==MA NCA C CA C∴∠∠∠∠∴∠∠+∠证明:过点B作PQ//MA.,ABQ BQ,ABC几何模型2:鸡翅模型图三//-=MA NC A B⇒∠∠∠条件:C////PQ////PQ,,,MA NCMA NCA C CB CBQA C B∴∠∠∠∠∴∠=∠∠∴∠-∠=∠证明:过点B作PQ//MA.则,ABQ=BQ=,ABQ-几何模型3:折鸡翅模型图四//MA NC A B⇒∠=∠+∠条件:C ////PQ////PQ ,,,MA NC MA NC A C C ABC CBQ A ACB C∴∠∠∠∠∴∠=∠∠∴∠==∠+∠ 证明:过点B作PQ//MA.则,ABQ=BQ =,ABQ-几何模型4:多个M 型模型12121//......n n MA NB P P P A Q Q Q B-⇒∠+∠++∠=∠+∠+∠++∠条件:【典型例题】类型一、平行线几何模型➽➼猪蹄模型➻➸求解✬✬证明1.请阅读小明同学在学习平行线这章知识点时的一段笔记,然后解决问题.小明:老师说在解决有关平行线的问题时,如果无法直接得到角的关系,就需要借助辅助线来帮助解答,今天老师介绍了一个“美味”的模型“猪蹄模型”.即已知:如图1,AB CD ∥,E 为AB 、CD 之间一点,连接AE ,CE 得到AEC ∠.求证:AEC A C∠=∠+∠小明笔记上写出的证明过程如下:证明:过点E 作EF AB∥∵1A∠=∠∵AB CD ∥,EF AB∥∴EF CD∥∴2C∠=∠∴12AEC ∠=∠+∠∴AEC A C∠=∠+∠请你利用“猪蹄模型”得到的结论或解题方法,完成下面的两个问题.(1)如图,若AB CD ∥,60E ∠=o ,求B C F ∠+∠+∠;(2)如图,AB CD ∥,BE 平分ABG ∠,CF 平分DCG ∠,27G H ∠=∠+ ,求H ∠.【答案】(1)240 ;(2)51【分析】(1)作EM AB ∥,FN CD ∥,如图,根据平行线的性质得EM AB FN CD ∥∥∥,所以1B ∠=∠,23∠∠=,4180C ∠+∠= ,然后利用等量代换计算240B F C ∠+∠+∠= ;(2)分别过G 、H 作AB 的平行线MN 和RS ,根据平行线的性质和角平分线的性质可用ABG ∠和DCG ∠分别表示出H ∠和G ∠,从而可找到H ∠和G ∠的关系,结合条件可求得51H ∠= .解:(1)作EM AB ∥,FN CD ∥,如图,且AB CD ∥180∴180227BHC BHC -∠=∠+ ,∴51BHC ∠= .【点拨】本题考查了平行线的性质和判定的应用,能运用平行线的性质和判定进行推理是解此题的关键,注意:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,反之亦然.举一反三:【变式】阅读下面内容,并解答问题.已知:如图1,AB CD ,直线EF 分别交AB ,CD 于点E ,F .BEF ∠的平分线与DFE ∠的平分线交于点G .(1)求证:EG FG ⊥;(2)填空,并从下列①、②两题中任选一题说明理由.我选择题.①在图1的基础上,分别作BEG ∠的平分线与DFG ∠的平分线交于点M ,得到图2,则EMF ∠的度数为.②如图3,AB CD ,直线EF 分别交AB ,CD 于点E ,F .点O 在直线AB ,CD 之间,且在直线EF 右侧,BEO ∠的平分线与DFO ∠的平分线交于点P ,则EOF ∠与EPF ∠满足的数量关系为.【答案】(1)见解析;(2)①45︒;②结论:2EOF EPF ∠=∠【分析】(1)利用平行线的性质解决问题即可;(2)①利用基本结论EMF BEM MFD ∠=∠+∠求解即可;②利用基本结论EOF BEO DFO ∠=∠+∠,EPF BEP DFP ∠=∠+∠,求解即可.(1)证明:如图,过G 作GH AB ,AB CD ,AB GH CD ∴ ,BEG EGH DFG FGH ∠∠∠∠∴==,,180BEF DFE ∴∠+∠=EG 平分BEF ∠,FG 12GEB BEF ∴∠=∠,12GEB GFD ∴∠+∠=∠在EFG ∆中,GEF ∠+∠EGF GEB GFD ∴∠=∠+∠EG FG ∴⊥;)解:①如图2中,由题意,EM 平分BEG ∠,MF 1(2BEM MFD ∴∠+∠=∠EMF BEM MFD ∴∠=∠+∠故答案为:45︒;结论:2EOF EPF ∠=∠理由:如图3中,由题意,PE 平分BEO ∠,PF 2BEO BEP ∴∠=∠,DFO ∠类型二、平行线几何模型➽➼鸡翅模型➻➸求解✬✬证明2.已知直线12l l ∥,3l 和1l ,2l 分别交于C ,D 点,点A ,B 分别在线1l ,2l 上,且位于3l 的左侧,点P 在直线3l 上,且不和点C ,D 重合.(1)如图1,有一动点P 在线段CD 之间运动时,求证:12APB ∠=∠+∠;(2)如图2,当动点P 在C 点之上运动时,猜想APB ∠、1∠、2∠有何数量关系,并说明理由.【答案】(1)证明见解析;(2)21APB ∠=∠+∠,理由见解析.【分析】()1过点P 作1//PE l ,根据12l l //可知2//PE l ,故可得出1APE ∠=∠,2.BPE ∠=∠再由APB APE BPE ∠=∠+∠即可得出结论;()2过P 作//PE AC ,依据12l l //,可得//PE BD ,进而得到2BPE ∠=∠,1APE ∠=∠,再根据BPE APE APB ∠=∠+∠,即可得出21APB ∠=∠+∠.(1)证明:如图1,过点P 作1//PE l ,12//l l ,2//PE l ∴,1APE ∴∠=∠,2BPE ∠=∠.又APB APE BPE ∠=∠+∠ ,12APB ∴∠=∠+∠;(2)解:21APB ∠=∠+∠.理由如下:如图2,过P 作//PE AC ,12//l l ,//PE BD ∴,2BPE ∴∠=∠,1APE ∠=∠,BPE APE APB ∠=∠+∠ ,21APB ∴∠=∠+∠.【点拨】本题考查的是平行线的性质,根据题意作出辅助线,构造出平行线是解答此题的关键.举一反三:【变式】【原题】已知直线AB ∥CD ,点P 为平行线AB ,CD 之间的一点,如图1,若∠ABP =50°,∠CDP =60°,BE 平分∠ABP ,DE 平分∠CDP .(1)则∠P =______,∠E =______.(2)【探究】如图2,当点P 在直线AB 的上方时,若∠ABP =α,∠CDP =β,∠ABP 和∠CDP 的平分线交于点1E ,∠ABE 1与1CDE ∠的角平分线交于点2E ,∠ABE 2与∠CDE 2的角平分线交于点3E ,…以此类推,求∠E 2的度数,并猜想∠E n 的度数.(3)【变式】如图3,∠ABP 的角平分线的反向延长线和∠CDP 的补角的角平分线交于点E ,试直接写出∠P 与∠E 的数量关系.类型三、平行线几何模型➽➼多个M型模型➻➸求解✬✬证明3.探究:(1)如图①,已知AB CD,图中∠1,∠2,∠3之间有什么关系?(2)如图②,已知AB CD,图中∠1,∠2,∠3,∠4之间有什么关系?(3)如图③,已知AB CD,请直接写出图中∠1,∠2,∠3,∠4,∠5之间的关系;【答案】(1)∠1+∠3=∠2;(2)∠1+∠3=∠2+∠4;(3)∠1+∠3+∠5=∠2+∠4.【分析】(1)过点E作EM∥AB,根据平行线的性质及角的和差求解即可;(2)过点F作NF∥AB,结合(1)并根据平行线的性质及角的和差求解即可;(3)过点G作GM∥AB,结合(2)并根据平行线的性质及角的和差求解即可.(1)解:如图①,过点E作EM∥AB,∵AB∥CD,∴AB∥CD∥EM,∴∠1=∠NEM,∠3=∠MEF,∴∠1+∠3=∠NEM+∠MEF,即∠1+∠3=∠2;(2)如图②,过点F作NF∥AB,∵AB∥CD,∴AB ∥CD ∥FN ,∴∠4=∠NFH ,由(1)知,∠1+∠EFN =∠2,∴∠1+∠EFN +∠NFH =∠2+∠4,即∠1+∠3=∠2+∠4;(3)如图③,过点G 作GM ∥AB ,∵AB ∥CD ,∴AB ∥CD ∥GM ,∴∠5=∠MGN ,由(2)得,∠1+∠3=∠2+∠FGM ,∴∠1+∠3+∠5=∠2+∠FGM +∠MGN ,即∠1+∠3+∠5=∠2+∠4.【点拨】此题考查了平行线的性质,熟记两直线平行,内错角相等是解题的关键.举一反三:【变式】【发现】如图,已知AB ∥CD ,直线AB ,CD 被EF 所截.若EM ,FN 分别平分∠AEF 和∠DFE ,判断EM 与FN 之间的位置关系,并证明你的结论;【变式】如图,已知180AEF EFC ∠+∠=︒,∠M =∠N ,求证∠1=∠2;【拓展】如图,AB ∥CD ,∠1=∠2,求证∠M =∠N .∵AB∥CD,∴∠1=∠EPD.∵∠1=∠2,【点拨】本题考查平行线的性质和判定,熟练掌握平行线的性质和判定是解题的关键.类型四、平行线几何模型➽➼综合模型➻➸求解✬✬证明4.根据下列叙述填依据.(1)已知如图1,AB CD ∥,求∠B +∠BFD +∠D 的度数.解:过点F 作FE AB∥所以∠B +∠BFE =180°()因为AB CD ∥、FE AB ∥(已知)所以()所以∠D +∠DFE =180°()所以∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°(2)根据以上解答进行探索.如图(2)(3)AB EF 、∠D 与∠B 、∠F 有何数量关系(请选其中一个简要证明)备用图:(3)如图(4)AB EF ,∠C =90°,∠α与∠β、∠γ有何数量关系(直接写出结果,不需要说明理由)【答案】(1)两直线平行,同旁内角互补;FE CD ∥,平行于同一直线的两直线平行;两直线平行,同旁内角互补;(2)见解析;(3)90αβγ∠+∠-∠=︒【分析】(1)过点F 作FE AB ∥,得到∠B +∠BFE =180°,再根据AB CD 、FE AB ∥得到FE CD ∥,∠D +∠DFE =180°,最后利用角度的和差即可得出答案;(2)类比问题(1)的解题方法即可得解;(3)类比问题(1)的解题方法即可得解.(1)解:过点F 作FE AB ∥,如图,∴∠B +∠BFE =180°(两直线平行,同旁内角相等),∵AB CD ∥、FE AB ∥(已知)∴FE CD ∥(平行于同一直线的两直线平行),∴∠D +∠DFE =180°(两直线平行,同旁内角互补),∴∠B +∠BFE +∠D =∠B +∠BFE +∠EFD +∠D =360°;故答案为:两直线平行,同旁内角互补;FE CD ∥,平行于同一直线的两直线平行;两直线平行,同旁内角互补;(2)解:选图(2),∠D 与∠B 、∠F 的数量关系为:∠BDF +∠B =∠F ;理由如下:过点D 作DC//AB ,∴∠B =∠BDC ,∵AB EF ∥,DC AB ∥,∴DC EF ∥,∴∠CDF =∠F ,∴∠BDF +∠BDC =∠F ,即∠BDF +∠B =∠F ;选图(3),∠D 与∠B 、∠F 的数量关系:∠BDF +∠B =∠F过点D 作DC AB ∥,∴∠B =∠BDC ,∵AB EF ∥,DC AB ∥,∴DC EF ∥,∴∠CDF =∠F ,∴∠BDF +∠BDC =∠F ,即∠BDF +∠B =∠F∠BDF +∠B =∠F ;(3)解:90αβγ∠+∠-∠=︒如图(4)所示,过点C 作MC AB ∥,过D 作DN EF ∥,∴BCM α∠=∠,NDE g Ð=Ð,∵AB CM ∥,EF AB ∥,DN EF∥∴AB EF CM DN ∥∥∥,∴CDN MCD Ð=Ð,∵90MCD BCM Ð+Ð=°,CDN NDE b Ð=Ð+Ð,∴90αβγ∠+∠-∠=︒.【点拨】本题考查根据平行线的性质探究角的关系和平行线公理推论的运用,熟练掌握平行线的性质和平行线公理推论的运用是解题的关键.举一反三:【变式】已知:AB ∥EF ,在平面内任意选取一点C .利用平行线的性质,探究∠B 、∠F、∠C满足的数量关系.(1)将探究∠B、∠C、∠F之间的数量关系填写下表:(2)请选择其中一个图形进行说明理由.图(2)∠F-∠B=∠C图(3)∠B-∠F=∠C图(4)∠B+∠F+∠C=360°图(5)∠B-∠F=∠C图(6)∠F-∠B=∠C(2)解:图(1)∠C与∠B、∠F之间的数量关系是:∠B+∠F=∠C.理由:过点C作CG∥AB,∴∠BCG=∠B,∵AB∥EF,∴CG∥EF,∴∠GCF=∠F,∴∠BCG+∠GCF=∠B+∠F,∴∠B+∠F=∠BCF;图(2)∠C与∠B、∠F之间的数量关系是:∠F-∠B=∠C.理由:过点C作CG∥AB,∴∠BCG=∠B,∵AB∥EF,∴CG∥EF,∴∠GCF=∠F,∴∠GCF-∠BCG=∠F-∠B,∴∠F-∠B=∠BCF;图(3)∠C与∠B、∠F之间的数量关系是:∠B-∠F=∠C.理由:过点C作CG∥AB,∴∠BCG=∠B,∵AB∥EF,∴CG∥EF,∴∠GCF=∠F,∴∠BCG-∠GCF=∠B-∠F,∴∠B-∠F=∠BCF;图(4)∠C与∠B、∠F之间的数量关系是:∠B+∠F+∠C=360°.理由:过点C作CG∥AB,∴∠BCG+∠B=180°,∵AB∥EF,∴CG∥EF,∴∠GCF+∠F=180°,∴∠BCG+∠B+∠GCF+∠F=180°+180°,∴∠B+∠F+∠BCF=360°;图(5)∠C与∠B、∠F之间的数量关系是:∠B-∠F=∠C.理由:过点C作CG∥AB,∴∠BCG=∠B,∵AB∥EF,∴CG∥EF,∴∠GCF=∠F,∴∠BCG-∠GCF=∠B-∠F,∴∠B-∠F=∠BCF;图(6)∠C与∠B、∠F之间的数量关系是:∠F-∠B=∠C.理由:过点C作CG∥AB,∴∠BCG=∠B,∵AB∥EF,∴CG∥EF,∴∠GCF=∠F,∴∠GCF-∠BCG=∠F-∠B,∴∠F-∠B=∠BCF;【点拨】本题考查平行线的判定和性质,解题的关键是学会添加常用辅助线,构造平行线解决问题.。
华师大版七年级数学上册立体几何证明专题

华师大版七年级数学上册立体几何证明专题简介本文档介绍了华师大版七年级数学上册立体几何证明专题。
立体几何是数学中的一个重要分支,主要研究空间中的图形和对象。
本文档将涵盖常见的立体几何证明题目和解题方法,帮助读者提高解题能力。
目录1. 证明题目一: 零件的组合2. 证明题目二: 三棱柱的表面积3. 证明题目三: 平行四边形棱台的体积4. 证明题目四: 正方体的表面积和体积证明题目一: 零件的组合这个题目要求证明一个图形由几个零件组合而成。
我们需要分析每个零件的特征和位置,然后通过证明每个零件的特征是相等的,进而得出整个图形的特征是相等的。
具体的证明步骤和思路将在文中详细解释。
证明题目二: 三棱柱的表面积这个题目要求证明一个三棱柱的表面积的公式。
我们可以通过拆解三棱柱为几个简单的平面图形,然后计算每个平面图形的面积,最后将它们相加得出整个三棱柱的表面积。
在文中,将详细解释这个证明过程。
证明题目三: 平行四边形棱台的体积这个题目要求证明一个平行四边形棱台的体积的公式。
我们可以将平行四边形棱台拆解为两个三棱柱和一个平行四边形棱台,然后分别计算它们的体积并相加得出整个平行四边形棱台的体积公式。
具体的证明过程将在文中详细解释。
证明题目四: 正方体的表面积和体积这个题目要求证明一个正方体的表面积和体积的公式。
我们可以通过拆解正方体为六个面,然后计算每个面的面积和体积,最后将它们相加得出整个正方体的表面积和体积。
在文中,将详细解释这个证明过程。
总结立体几何证明题目需要通过分析和推理,来得出图形特征或公式的证明过程。
通过理解每个题目的要求,我们可以运用合适的解题方法,来解决立体几何证明题目。
本文档提供了一些常见题目的证明方法,希望读者能够在学习立体几何的过程中有所帮助。
初一几何证明题

初一几何证明题1.已知AB∥CD,∠1=∠2,证明:∠XXX∠XXX。
根据平行线内角相等的性质,可得∠1=∠2=∠XXX。
同时,因为AB∥CD,所以∠BEF+∠EFC=180°,即∠BEF=180°-∠XXX。
代入前面的等式,可得∠XXX∠XXX。
2.如图2,AB∥CD,∠3∶∠2=3∶1,求∠1的度数。
根据平行线内角相等的性质,可得∠1=180°-∠2.又因为∠3∶∠2=3∶1,所以∠3=3x,∠2=x。
代入前面的等式,可得∠1=180°-x。
因此,∠1+∠2+∠3=180°,即4x=180°,x=45°。
代入前面的等式,可得∠1=135°。
3.如图3,C在AB的延长线上,CE⊥AF于E,交FB于D,若∠F=40°,∠C=20°,求∠XXX的度数。
根据直角三角形的性质,可得∠CEA=90°。
又因为CE⊥AF,所以∠EAF=90°-∠F=50°。
根据三角形内角和为180°的性质,可得∠EFA=180°-∠F-∠EAF=90°。
因为AB∥CD,所以∠XXX∠EFA=90°。
4.如图4,EF∥AD,∠1=∠2,∠BAC=80°。
求证:∠AGD=100°。
因为EF∥AD,所以∠AGD=∠AGE。
又因为∠BAC=80°,所以∠XXX°-∠BAC/2=50°。
因为∠1=∠2,所以∠DGE=∠AGE=180°-∠1-∠GAC=50°。
因此,∠AGD=∠AGE=50°+∠DGE=100°。
5.如图5,B处在A处的南偏西57°的方向,C处在A处的南偏东15°方向,C处在B处的XXX°方向。
求∠C的度数。
根据题意,可画出如图6所示的图形。
初一下册数学角度几何解析题以及练习题(附答案)-七年级下册几何求角度数

七年级下册数学几何解析题以及练习题(附答案)宇文皓月9.(2011·扬州)如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A 、B 两岛的视角∠ACB =________.答案 105°解析 如图,∵(60°+∠CAB )+(45°+∠ABC )=180°,∴∠CAB +∠ABC =75°,在△ABC 中,得∠C =105°.12.如图所示,在△ABC 中,∠A =80°,∠B =30°,CD 平分∠ACB ,DE ∥AC .(1)求∠DEB 的度数;(2)求∠EDC 的度数.解 (1)在△ABC 中,∠A =80°,∠B =30°,∴∠ACB =180°-∠A -∠B =70°.∵DE ∥AC ,∴∠DEB =∠ACB =70°.(2)∵CD 平分∠ACB ,∴∠DCE =12∠ACB =35°. ∵∠DEB =∠DCE +∠EDC ,∴∠EDC =70°-35°=35°.13.已知,如图,∠1=∠2,CF ⊥AB 于F ,DE ⊥AB 于E ,求证:FG ∥BC .(请将证明弥补完整)证明 ∵CF ⊥AB ,DE ⊥AB (已知),∴ED∥FC( ).∴∠1=∠BCF( ).又∵∠1=∠2(已知),∴∠2=∠BCF(等量代换),∴FG∥BC( ).解在同一平面内,垂直于同一直线的两条直线互相平行;两直线平行,同位角相等;内错角相等,两直线平行.14.如图,已知三角形ABC,求证:∠A+∠B+∠C=180°.分析:通过画平行线,将∠A、∠B、∠C作等角代换,使各角之和恰为一平角,依辅助线分歧而得多种证法,如下:证法1:如图甲,延长BC到D,过C画CE∥BA.∵BA∥CE(作图所知),∴∠B=∠1,∠A=∠2(两直线平行,同位角、内错角相等).又∵∠BCD=∠BCA+∠2+∠1=180°(平角的定义),∴∠A+∠B+∠ACB=180°(等量代换).如图乙,过BC上任一点F,画FH∥AC,FG∥AB,这种添加辅助线的方法能证明∠A+∠B+∠C=180°吗?请你试一试.解∵FH∥AC,∴∠BHF=∠A,∠1=∠C.∵FG∥AB,∴∠BHF=∠2,∠3=∠B,∴∠2=∠A.∵∠BFC=180°,∴∠1+∠2+∠3=180°,即∠A+∠B+∠C=180°.15.(2010·玉溪)平面内的两条直线有相交和平行两种位置关系.(1)如图a,若AB∥CD,点P在AB、CD外部,则有∠B=∠BOD.又因∠BOD是△POD的外角,故∠BOD=∠BPD+∠D,得∠BPD=∠B-∠D.将点P移到AB、CD内部,如图b,以上结论是否成立?若成立,说明理由;若不成立,则∠BPD、∠B、∠D之间有何数量关系?请证明你的结论;(2)在图b中,将直线AB绕点B逆时针方向旋转一定角度交直线CD于点Q,如图c,则∠BPD、∠B、∠D、∠BQD之间有何数量关系?(不需证明)(3)根据(2)的结论求图d中∠A+∠B+∠C+∠D+∠E+∠F的度数.解(1)不成立,结论是∠BPD=∠B+∠D.延长BP交CD于点E,∵AB∥CD,∴∠B=∠BED.又∠BPD=∠BED+∠D,∴∠BPD=∠B+∠D.(2)结论:∠BPD=∠BQD+∠B+∠D.(3)设AC与BF交于点G.由(2)的结论得:∠AGB=∠A+∠B+∠E.又∵∠AGB =∠CGF ,∠CGF +∠C +∠D +∠F =360°,∴∠A +∠B +∠C +∠D +∠E +∠F =360°. 14.把一副经常使用的三角板如图所示拼在一起,那么图中∠ADE 是度. 2.如图,在△ABC 和△ABD 中,现给出如下三个论断:①AD =BC ;②∠C =∠D ;③∠1=∠2。
七年级数学尖子生培优竞赛专题辅导专题15 几何证明

专题15 几何证明专题解读】几何证明题的一般结构由已知条件和求证目标两部分组成.解答几何证明题的一般步骤如下:审题,寻找证明的思路,书写证明过程,最终实现求证目标.几何证明是初中数学学习的重要组成部分,也是学好初中数学的重要一环.要学好几何证明,不但需要我们具有扎实的基础、科学的方法、良好的数学学习习惯,还需要具有敢于尝试、不怕挫折的勇气,更需要有吃苦耐劳、持之以恒的精神.思维索引】例1.△ABC中,三个内角的平分线交于点O,过点O作∠ODC=∠AOC,交边BC于点D.B图1 图2(1)如图1,求∠BOD的度数;(2)如图2,作∠ABC外角∠ABE的平分线交CO的延长线于点F.①求证:BF∥OD;②若∠F=50°,求∠BAC的度数;③若∠F=∠ABC=40°,将△BOD绕点O顺时针旋转一定角度后得△B'OD'(0°<<360°),B'D'所在直线与FC平行,请直接写出所有符合条件的旋转角度的值.例2.如图1,直线MN 与直线AB 、CD 分别交于点E 、F ,∠1与∠2互补. (1)试判断直线AB 与直线CD 的位置关系,并说明理由;(2)如图2,∠BEF 与∠EFD 的角平分线交于点P ,EP 与CD 交于点G ,点H 是MN 上一点,且 GH EG ,求证:PF /∥GH ;(3)如图3,在(2)的条件下,连接PH ,K 是GH 上一点使∠PHK =∠HPK ,作PQ 平分∠EPK ,问∠HPQ 的大小是否发生变化?若不变,请求出其值;若变化,说明理由.CA图1 图2 图3例3.在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E 在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.(1)如图①,当点D在边BC上时,且n=36°,则∠BAD=_______,∠CDE=______;(2)如图②,当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由;(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.BD①②③素养提升1.如图,AB CD ,∠1=58°,FG 平分∠EFD ,则∠FGB 的度数等于( ) A .122°B .151°C .116°D .97°CA(第1题) (第2题) (第3题)2.如图,直线l ∥m ,将含有45°角的三角形板ABC 的直角顶点C 放在直线m 上.若∠1=25°,则∠2的度数为( ) A .20°B .35°C .44°D .67°3.如图,在正方形网格中,每个小方格都是边长为1的小正方形,点A 、B 是方格纸中的两个格点(网格线的交点称格点),在这个7×7的方格纸中,找出格点C ,使△ABC 的面积为3,则满足条件的格点C 的个数是( ) A .2个B .4个C .5个D .6个4.如图,将一副三角板和一张对边平行的纸条按下列方式摆放,两个三角板的一直角边重合,含30°角的直角三角板的斜边与纸条一边重合,含45°角的三角板的一个顶点在纸条的另一边上,则图中∠1的度数是( ) A .15°B .22.5°C .30°D .45°5.如图,AB ∥CD ,OE 平分∠BOC ,,OFOE OP CD ,∠ABO =,则下列结论:①∠BOE =1902;②OF 平分∠BOD ;③∠POE =∠BOF ;④∠POB =2∠DOF ,其中不正确的个数有( ) A .1个B .2个C .3个D .4个CDA(第4题) (第5题) (第6题)6.如图,长方形ABCD 中,AB =4cm ,BC =3cm ,点E 是CD 的中点,动点P 从A 点出发,以每秒1cm 的速度沿A →B →C →E 运动,最终到达点E .若点P 运动的时间为x 秒,那么当x =_______时,△APE 的面积等于5.7.各边长度都是整数、最大边长为8的三角形共有_______个.8.如图,点A 、C 、F 、B 在同一直线上,CD 平分∠ECB ,FG //CD .若∠ECA 为a ,则∠GFB 为 .GDEB C DPC NEMABP 8P 7P 6P 5P 4P 3P 2P 1(第8题) (第9题) (第10题)9.如图,∠ABC =∠ACB ,BD 、CD 、BE 分别平分△ABC 的内角∠ABC 、外角∠ACP 、外角∠MBC .以下结论:①AD //BC ;②DB ⊥BE :③∠BDC +∠ABC =90°;④∠A +2∠BEC =180°;⑤DB 平分∠ADC .其中正确的结论有: (填序号).10.如图,若平面内有点P 1、P 2、P 3、P 4、P 5、P 6、P 7、P 8,连接P 1P 3、P 2P 4、P 3P 5、P 4P 6、P 5P 7、P 6P 8、P 7P 1、P 8P 2,则∠P 1+∠P 2+∠P 3+∠P 4+∠P 5+∠P 6+∠P 7+∠P 8的度数是 .11.在△ABC 中,∠ACB =90°,BD 是△ABC 的角平分线,P 是射线AC 上任意一点(不与A 、D 、C 三点重合),过点P 作PQ ⊥AB ,垂足为Q ,交直线BD 于E . (1)如图1,当点P 在线段AC 上时,说明∠PDE =∠PED .(2)作∠CPO 的角平分线交直线AB 于点F ,则PF 与BD 有怎样的位置关系?画出图形并说明理由.图 1 图 2CBAE DQP CBA12.探究与发现:如图1,在△ABC 中,∠B =∠C =45°,点D 在BC 边上,点E 在AC 边上,且∠ADE =∠AED ,连接DE .(1)当∠BAD =60°时,求∠CDE 的度数;(2)当点D 在BC (点B 、C 除外)边上运动时,试探究∠BAD 与∠CDE 的数量关系;(3)深入探究:如图2,若∠B =∠C ,但∠C ≠45°,其它条件不变,试继续探究∠BAD 与∠CDE 的数量关系.图 1 图 2ABCDE EDCBA13.如图,AC⊥CB,垂足为C点,AC=CB=8cm,点Q是AC的中点,动点P由B点出发,沿射线BC 方向匀速移动.点P的运动速度为2cm/s.设动点P运动的时间为t s.为方便说明,我们分别记三角形ABC 面积为S,三角形PCQ的面积为S1,三角形P AQ的面积为S2,三角形ABP的面积为S3.(1)S3= cm2(用含t的代数式表示);(2)当点P运动几秒,S1=1S,说明理由;4(3)请你探索是否存在某一时刻,使得S1=S2=S3?若存在,求出t值;若不存在,说明理由.AQC B14.某课题研究小组就图形面积问题进行专题研究,他们发现如下结论:(1)有一条边对应相等的两个三角形面积之比等于这条边上的对应高之比;(2)有一个角对应相等的两个三角形面积之比等于夹这个角的两边乘积之比;……现请你继续对下面问题进行探究,探究过程可直接应用上述结论.(S表示面积)问题1:如图1,现有一块三角形纸板ABC,P1、P2三等分边AB,R1、R2三等分边AC.经探究知四边,请证明.形P1P2R2R1的面积恰为△ABC的面积的13问题2:若有另一块三角形纸板,可将其与问题1中的拼合成四边形ABCD,如图2,Q1、Q2三等分边DC.请探究四边形P1Q1Q2P2的面积与四边形ABCD的面积之间的关系.问题3:如图3,P1,P2,P3,P4五等分边AB,Q1,Q2,Q3,Q4五等分边DC.若S四边形ABCD=1,求四边形P2Q2Q3P3的面积.问题4:如图4,P1,P2,P3四等分边AB,Q1,Q2,Q3四等分边DC,P1Q1,P2Q2,P3Q3将四边形ABCD 分成四个部分,面积分别为S1,S₂,S3,S4.请直接写出含有S1,S₂,S3,S4的一个等式.专题15几何证明思维索引】例1.(1)∠BOD =90°; (2).①略 ②∠BAC =2∠F =100° ③x =30°,210° 例2.略例3.(1)64°,32° (2)∠BAD =2∠CDE (3)∠BAD =2∠CDE 素养提升】1.B ; 2.A ; 3.C ; 4.A ; 5.A ; 6.103或5;7.20;8.90°-2α:9.①②③④;10.720°; 11.(1)略; (2)当P 在线段AC 上时,此时PF ∥BD ,当P 在线段AC 的延长线上时,PF ⊥BD ; 12.(1)30°; (2)∠EDC =12∠BAD ; (3)∠EDC =12∠BAD ; 13.(1)8t ; (2)当点P 运动2秒或6秒时,S 1=14; (3)当43t =时,S 1=S 2=S 3; 14.(1) 122113ABC P P R R S S =△四边形; (2) 11223ABCD PQ Q P S S =四边形四边形; (3) 22331155P Q Q P ABCD S S ==四边形四边形; (4)S 2+S 3=S 1+S 4.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学几何证明
题(典型)
七年级数学几何证明题
1.如图,在ABC中,D在AB上,且ΔCAD和ΔCBE都是等边三角形,
求证:(1)DE=AB,(2)∠EDB=60°
2.如图,在ΔABC中,AD平分∠BAC,DE||AC,EF⊥AD交BC延长线于F。
求证:∠FAC=∠B
3.已知,如图,在△ ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线,若∠B=30
∠C=50°求:(1),求∠DAE 的度数。
(2) 试写出 ∠DAE 与 ∠C - ∠B 有何关系?(不必证明)
4、一个零件的形状如图,按规定∠A=90º ,∠ C=25º,∠B=25º,检验已量得∠BDC=150º,就判断这个零件不合格,运用三角形的有关知识说明零件不合格的理由。
C
D
B
A
C
D
A B
5、如图,已知DF∥AC,∠C=∠D,你能否判断CE∥BD?试说明你的理由
6、如图,△ABC中,D在BC的延长线上,过D作DE⊥AB于E,交AC于F. 已知∠A=30°,∠FCD=80°,求∠D。
7、如图,BE平分∠ABD,CF平分∠ACD,BE、CF交于G,
若∠BDC = 140°,∠BGC = 110°,则∠A ?
G
F E
D
C B
A
8、如图,AD⊥BC于D,EG⊥BC于G,∠E =∠1,求证AD平分∠BAC。
E
D C B
A
G
3
2
1
9、如图,直线DE交△ABC的边AB、AC于D、E,交BC延长线于F,若∠B=67°,∠ACB=74°,∠AED=48°,求∠BDF的度数.
10、如图,将一副三角板叠放在一起,使直角的顶点重合于O,
则∠AOC+∠DOB
E
D
C
B
A
11、如图,将两块直角三角尺的直角顶点C 叠放在一起. (1)若∠DCE=350,求∠ACB 的度数;
(2)若∠ACB=1400,求∠DCE 的度数;
(3)猜想:∠ACB 与∠DCE 有怎样的数量关系,并说明理由
E
O D C
B
A 12、已知:直线AB与直线CD相交于点O,∠BOC=45,
(1)如图1,若EO⊥AB,求∠DOE的度数;
(2)如图2,若EO平分∠AOC,求∠DOE的度数.
13、已知AOB
∠,P为OA上一点.
(1)过点P画一条直线PQ,使PQ∥OB;
(2)过点P画一条直线PM,使PM⊥OA交OB于点M;
(3)若︒
=
∠40
AOB,则=
∠PMO?
14、如图。
已知∠BOC = 2∠AOB,OD平分∠AOC,∠BOD = 14°,求∠AOB的度数.
15、如图,∠AOC和∠DOB都是直角,如果∠DOC =28°,那么∠AOB = ?O
D
C
B
A
A
C
B
D
16、已知:线段AB=5cm,延长AB到c,使AC=7cm,在AB的反向延长线上取点D,使BD=4BC,设线段CD的中点为E,问线段AE是线段CD的几分之一?
17、)复习“全等三角形”的知识时,老师布置了一道作业题:“如图①,已知,在△ABC中,AB=AC,P
是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP=∠BAC,连结BQ、CP,则
BQ=CP.”小亮是个爱动脑筋的同学,他通过对图①的分析,发现△ABQ≌△ACP,从而得到
BQ=CP.之后,他将点P移到△ABC外,原题中其他条件不变,发现“BQ=CP”仍然成立,请你就图
②给出证明.
18、如图所示:ΔABC的周长为24cm,AB=10cm,边AB的垂直平分线DE交BC边于点E,垂足为D,
求ΔAEC的周长.
第18题图
19、(6分)如图,AD是△ABC的角平分线,DE⊥AB,垂足为E,DF⊥AC,垂足为F,你能找出一对全
等的三角形吗?为什么它们是全等的?
第19题图
20、如图,AB=EB,BC=BF,
CBF
ABE∠
=
∠.EF和AC相等吗?为什么?
21、已知:如图,AD∥BE,∠1=∠2.求证:∠A=∠E.
(第21题图)22、已知:如图,AB//CD,∠ABE=∠DCF,请说明∠E=∠F的理由F
E
C
B
A
(第20题
2
1
3
F
D
C
B
H E
G
A
F
E
D
C
B
A
23、如图,在△ABC 中,D 是AB 上一点,DF 交AC 于点E ,DE=FE ,AE=CE ,
AB 与CF 有什么位置关系?说明你的理由.
24、下图是2002年8月在北京召开的第24届国际数学家大会会标中的图案,其中四边形ABCD 和四边形
EFGH 都是正方形。
小强看后马上猜出△ABF ≌△DAE ,并给出以下不完整的推理过程。
请你填空完成推理: (7分) 证明:∵四边形ABCD 和EFGH 都是正方形,
∴AB=DA, ∠DAB=90°, ∠GFE=∠HEF=90° ∴∠1+∠3=90°, ∠AFB=∠DEA =90°, ∴∠2+∠3=90° ( )
∴ ( ) 在△ABF 和△DAE 中
∴△ABF ≌△DAE ( ) 25、如图,交于点
是
的平分线,求
的度数.
26、如图, AD ∥BC , AD 平分∠EAC,你能确定∠B 与∠C 的数量关系吗?请说明理由。
1D 2
A
E
C
B
27.如图,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交AC 于E,∠A=35°,•∠D=42°,求∠ACD 的度数.
F
D
C
B
E
A
28、如图,在△ABC 中,∠ABC=500,∠ACB=800,BP 平分∠ABC ,CP 平分∠ACB ,则∠BPC 的大小.
P
C
B
A
29.如图,AB=EB ,BC=BF ,CBF ABE ∠=∠.EF 和AC 相等吗?为什么?
30、如图1,已知∠1 =∠2,∠B =∠C ,可推得AB ∥CD 。
理由如下:(10分)
∵∠1 =∠2(已知),且∠1 =∠4( ) ∴∠2 =∠4(等量代换)
∴CE ∥BF ( )
F
E
C
B
A
(第29题
∴∠ =∠3()又∵∠B =∠C(已知)
∴∠3 =∠B(等量代换)∴AB∥CD()
F
E
D C
B A
2
1
4
3。
