结构力学英文课件chapter-2
合集下载
结构力学第二章几何组成分析.李廉锟

geometrically stable system
结构
Under the action of any loads, the system still maintain its shape and remains its location if the deformations of the members are neglected.
F
E
2 rigid bodies, connected by 3 links, which are nonparallel and nonconcurrent cross the hinge, form an internally stable system with no redundant restraints. 。
Degrees of freedom of a system are the numbers of independent movements or coordinates which are required to locate the system fully.
for a point in plane n=2
C
structure formed by Attaching of binary systems 减二元体简化分析
W=3 ×10-(2×14+3)=-1<0 W=2 ×6-13=-1<0
计算自由度 = 体系真实 的自由度 ?
W=2 ×6-12=0 W=3 ×9-(2×12+3)=0
缺少联系 几何可变
W=2 ×6-11=1 W=3 ×8-(2×10+3)=1
summary
W>0, 缺少足够联系,体系几何可变 Restraints are not enough, unstable。 W=0, 具备成为几何不变体系所要求的最少 联系数目has the minimum necessary numbers of restraints for stable system。
《结构力学第2章》课件

《结构力学第2章》PPT 课件
结构力学是研究物体在外力作用下产生的应力和应变的学科。在建筑设计和 工程中,弹性力学有着广泛应用,本课件将带您深入了解弹性力学的基本理 论和应用。
弹性力学的基本概念
线弹性力学和平面弹性力学
介绍弹性力学研究的两个主要领域,涵盖了结 构力学的基础知识。
应力和应变的概念
引入应力和应变的概念,介绍了它们在弹性力 学中的重要性和计算方法。
应变-应力关系
介绍了弹性体中应变和应力之间的基本方 程,揭示了它们之间的关联。
平面弹性力学的基本理论
平面应力和平面应变 的基本方程
解释了平面弹性力学中应力和 应变的基本方程,为进一步的 研究提供基础。
平面问题的求解方法
介绍了平面问题的求解方法, 如解析法和数值计算方法,为 工程实践提供指导。
平面问题的应用
总结了弹性力学的核心概念和研究领域,强调 了它在物体力学研究中的重要性。
弹性力学在建筑设计和工程中有着广 泛应用
强调了弹性力学在建筑设计和工程实践中的重 要性,以及其对结构稳定性和变形控制的影响。
探讨了平面弹性力学在工程中 的应用,如桥梁设计和建筑物 承重分析。
建筑物中的弹性力学问题
弹性力学在建筑设计中的应用
探索了弹性力学在建筑物设计中的重要性,如结构 稳定性和变形控制。
建筑物的弹性问题和偏心受力
分析了建筑物中的弹性问题,以及由偏心受力引起 的应力分布和变形。
结论
弹性力学是研究物体在外力作用下ቤተ መጻሕፍቲ ባይዱ 生的应力和应变的学科
弹性行为的特征
深入探讨物体在受力作用下的弹性变形,解释 了弹性体的特点和规律。
本构关系的定义和表示
讲解了本构关系的概念,以及在弹性力学中如 何表示不同物体的本构关系。
结构力学是研究物体在外力作用下产生的应力和应变的学科。在建筑设计和 工程中,弹性力学有着广泛应用,本课件将带您深入了解弹性力学的基本理 论和应用。
弹性力学的基本概念
线弹性力学和平面弹性力学
介绍弹性力学研究的两个主要领域,涵盖了结 构力学的基础知识。
应力和应变的概念
引入应力和应变的概念,介绍了它们在弹性力 学中的重要性和计算方法。
应变-应力关系
介绍了弹性体中应变和应力之间的基本方 程,揭示了它们之间的关联。
平面弹性力学的基本理论
平面应力和平面应变 的基本方程
解释了平面弹性力学中应力和 应变的基本方程,为进一步的 研究提供基础。
平面问题的求解方法
介绍了平面问题的求解方法, 如解析法和数值计算方法,为 工程实践提供指导。
平面问题的应用
总结了弹性力学的核心概念和研究领域,强调 了它在物体力学研究中的重要性。
弹性力学在建筑设计和工程中有着广 泛应用
强调了弹性力学在建筑设计和工程实践中的重 要性,以及其对结构稳定性和变形控制的影响。
探讨了平面弹性力学在工程中 的应用,如桥梁设计和建筑物 承重分析。
建筑物中的弹性力学问题
弹性力学在建筑设计中的应用
探索了弹性力学在建筑物设计中的重要性,如结构 稳定性和变形控制。
建筑物的弹性问题和偏心受力
分析了建筑物中的弹性问题,以及由偏心受力引起 的应力分布和变形。
结论
弹性力学是研究物体在外力作用下ቤተ መጻሕፍቲ ባይዱ 生的应力和应变的学科
弹性行为的特征
深入探讨物体在受力作用下的弹性变形,解释 了弹性体的特点和规律。
本构关系的定义和表示
讲解了本构关系的概念,以及在弹性力学中如 何表示不同物体的本构关系。
结构力学英文课件 Chapter1

Introduction
③ Combination Joint
A
B
A:Rigid joint
C
D
B、D:Hinge joint C:Combination joint BF、CD Hinge joint,
E
F
G
BC、CF Rigid joint
3. Simplification of supports
长江三峡工程
Introduction
Introduction
上海南浦大桥
Introduction
Introduction
现代桥梁欣赏
Introduction
现代桥梁欣赏
Introduction
Introduction
中国民航飞机
Introduction
宇宙飞船
Introduction
Summary
Two words:
Simplification
Classification
Introduction
Fig.1 Main Teaching Building
Introduction
Fig.2
Introduction
Introduction
Introduction
Introduction
Introduction
Introduction
荷兰拦海大坝
Introduction
(1)、beam (2)、arch
(3)、truss (4)、rigid frame (5)、composite structure
梁
拱
桁架
刚架
组合结构
Introduction
结构力学(英) Chapter2 Equilibrium and Geometric Stability PPT精品课件

P1 m
A
m
a
XA
l
YA V
M
N
YA
V
M N
P2 P3 B
YB
YB
6
Statically Determinate Structures
P
A
C
B
a
RA Pb l
Pb / l
b l
RB
Pa l
P
Pa / l
Shear Diagram
The equations of statics alone are sufficient to compute the reactions and the distribution of internal forces.
M1 M2
+ Mx = M1,x M2,x = 0
z
+ My = M1,y M2,y = 0
+ Mz = M1,z M2,z = 0
x
3
Equilibrium of Planar Structure
4
External Forces
External Forces are the actions of other bodies to the structure under consideration.
n = number of structural components r = number of unknown reaction components If r = 3n, the structure is statically determinate If r > 3n, the structure is statically indeterminate
结构力学第二章

I
1 2
3
II
II
两刚片规则:两刚片之间用一个铰和一根链杆相联结,且铰 不在链杆的直线上;或者用三根既不平行也不交于一点的链 杆相联结,则组成几何不变体系,且无多余约束。
§2-2 无多余约束几何不变体系的组成规律
3)三个刚片之间的联结方式 B I II C III
三刚片规则:三个刚片之间用三个 不共线的铰(实或虚铰)两两相连,
动,体系是可变体系。 (2)当A 点沿公切线发生微小位移后,链 杆1和2不再共线,因此体系不再是可变 体系。
Ⅰ
§2-1 几何构造分析的几个概念
接近瞬变体系结构的受力分析
α
A
C P
α
B
NCA C
NCB P
取C结点:
Y 0
2 NCA Sin P
N CA
P 2 Sin
若α 很小,NCA就很大。
有多余约束的几何不变体系----超静定结构 几何可变体系----存在未能满足的平衡条件--机构
§2-3 几何构造分析方法
例2: 刚片I 2 地基作为刚片II 例3: 3 没有多余约束的几何不变体系 1 A 刚片I 没有多余约束的 几何不变体系 B C 刚片II 2 二元体 二元体 二元体
1
地基作为刚片III
§2-3 几何构造分析方法
(2)从体系内部出发进行组装
先运用各种规则把结构内部组装成一个几何不变体系, 然后运用规则把它与基础相连。 例1: 刚片I 2 A 刚片II 3 没有多余约束 的几何不变体系 2
体系进行几何构造分析的目的:
如何判别体系几何不变,几何可变; 怎样组成几何不变体系;
判断静定结构、超静定结构,
判定静定结构的基本部分、附属部分 ----静定结构解题的钥匙
结构力学英文课件chapter 2

n=0
n=1
(2 )Connecting restraints between rigid bodies we will pay more attention to connecting restraints between two rigid bodies. One rigid body has three degrees of freedom and two independent rigid bodies have six degrees of freedom in a planar coordinate system, when connecting them together, their degrees of freedom would be reduced. Now we will discuss the equivalent restraints of a few kinds
Purpose of analyzing geometric construction of structures is as following: (1) To estimate whether or not a system is geometrically stable, so as to determine whether the system can be used as a structure or not; (2) To discuss geometric construction rules of stable systems.
n=2
(2)The degrees of freedom of freedom of a rigid body The movement of a rigid body in planar coordinate system
n=1
(2 )Connecting restraints between rigid bodies we will pay more attention to connecting restraints between two rigid bodies. One rigid body has three degrees of freedom and two independent rigid bodies have six degrees of freedom in a planar coordinate system, when connecting them together, their degrees of freedom would be reduced. Now we will discuss the equivalent restraints of a few kinds
Purpose of analyzing geometric construction of structures is as following: (1) To estimate whether or not a system is geometrically stable, so as to determine whether the system can be used as a structure or not; (2) To discuss geometric construction rules of stable systems.
n=2
(2)The degrees of freedom of freedom of a rigid body The movement of a rigid body in planar coordinate system
第2章 结构动力学概述(中英文)

动荷载的定义 definition of dynamic loadings
荷载在大小、方向或作用点方面随时间变化,使 得质量运动加速度所引起的惯性力与荷载相比大 到不可忽略时,则把这种荷载称为动荷载。 A dynamic load is any load of which its magnitude, direction, and/or position varies with time. In general, if the inertial forces represent a significant portion of the total load equilibrated by the internal elastic forces of the structure, then this kind of load is defined as dynamic loading.
动荷载:
Dynamic loading:any load of which its magnitude, direction
and /or position varies with time
快慢标准: 是否会使结构产生显著的加速度. criteria: Whether a remarkable acceleration is exerted on the structure
静荷载 Static load 结构体系 Structural system 位移displacement 静力响应 Responses to static loads 内力internal force 应力stress
输入 input
输出 Output
大小 magnitude 方向 direction 作用点 position
结构力学PPT 第2章

被约束对象:结点A,刚片I 提供的约束:两根链杆1,2
1
所谓二元体,就是在保证两根链杆不共线的前提 下,将它们用一个单铰连接而成的装置。如图2.10(b) 中的BAC,就是一个二元体。 从二元体的性质可知:在一个体系上依次增加 (或去除)若干个二元体,不影响原体系的几何组成 性质。这是几何组成分析时经常使用到的二元体重要 特性。
Ⅰ 1
Ⅰ Ⅰ 1
Ⅰ A Ⅱ(参照刚片) (a) 实铰的相对位置固定
虚铰 O
O1
Ⅱ(参照刚片) (b) 虚铰的相对位置变化
实铰和虚铰示例
Ⅰ
Hale Waihona Puke ⅠA Ⅱ (a) 两刚片用铰结在一起的 两链杆相连
A Ⅱ (b) 两刚片用铰直接相连
实铰的常见情形
Ⅰ C A
Ⅰ C A [Ⅰ, Ⅱ] B B Ⅱ (b) 有限远虚铰情形2 D B
例题2 试分析图中铰结链杆体系的几何组成性质。
A B A B ② ③ Ⅰ ③ ②
① C (b) 暂不考虑支座 C (a) 原体系 D C Ⅰ
① D
D
(c) 将刚片Ⅰ等效为链杆 置于支座上再分析
解:可以暂不考虑支座,如图 (b)所示。可按照从①~ ③的顺序依次去除二元体,最后只剩链杆AB。经简化 后图 (c)所示体系为无多余约束的几何不变体系。原体 系是无多余约束的几何不变体系。
多余约束
必要约束
结论:只有必要约束才能对体系自由度有影响。
① A ②
B
③
① A ②
C
④
B
③
① A ②
B
③
(a)
(b)
(c)
§2.3 几何不变无多余约束的平面杆 件体系的组成规则
结构力学2_张金生教材配套课件(精品教程)

例5: 对图示体系作几何组成分析
方法1: 若基础与其它部分三杆相连,去掉基础只分析其它彭部怀分林-2
方法2: 利用规则将小刚片变成大刚片. 方法3: 将只有两个铰与其它部分相连的刚片看成链杆. 方法4: 去掉二元体.
例6: 对图示体系作几何组成分析
解: 该体系为无多余约束的几何不变体系. 方法2: 利用规则将小刚片变成大刚片.
§1. 几何组成分析
作业: 1-2 (d)试分析图示体系的几何组成 依次去掉二元体. 几何常变体系
§1. 几何组成分析
作业: 1-1 (b)试计算图示体系的计算自由度
解: W =8×3−11×2−3= −1 或: W =1×3+5×2−2×2−10= −1
由结果不能判定其是否能作为结构
§1. 几何组成分析
一. 三刚片规则 三刚片以不在一条直线上的三铰两两相联,构
成无多余约束的几何不变体系.
瞬变体系
N
=
P 2 Sin α
§1. 几何组成分析
§1-1 基本概念 §1-2 无多余约束的几何不变体系的组成规则 §1-3 几何组成分析举例
例1: 对图示体系作几何组成分析
解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束 的几何不变体系.
在一个体系上加减二元体不影响原体系的机动性质.
§1. 几何组成分析
§1-1 基本概念
一. 几何不变体系 几何可变体系 二. 刚片 几何形状不能变化的平面物体
三. 自由度 确定体系位置所需的独立坐标数
点
刚
的 自
几何不变体系的自由片 自度一定等于零
由 几何可变体系的自由由度一定大于零
度
度
§1. 几何组成分析
§1-2 无多余约束的几何不变体系的组成规则
方法1: 若基础与其它部分三杆相连,去掉基础只分析其它彭部怀分林-2
方法2: 利用规则将小刚片变成大刚片. 方法3: 将只有两个铰与其它部分相连的刚片看成链杆. 方法4: 去掉二元体.
例6: 对图示体系作几何组成分析
解: 该体系为无多余约束的几何不变体系. 方法2: 利用规则将小刚片变成大刚片.
§1. 几何组成分析
作业: 1-2 (d)试分析图示体系的几何组成 依次去掉二元体. 几何常变体系
§1. 几何组成分析
作业: 1-1 (b)试计算图示体系的计算自由度
解: W =8×3−11×2−3= −1 或: W =1×3+5×2−2×2−10= −1
由结果不能判定其是否能作为结构
§1. 几何组成分析
一. 三刚片规则 三刚片以不在一条直线上的三铰两两相联,构
成无多余约束的几何不变体系.
瞬变体系
N
=
P 2 Sin α
§1. 几何组成分析
§1-1 基本概念 §1-2 无多余约束的几何不变体系的组成规则 §1-3 几何组成分析举例
例1: 对图示体系作几何组成分析
解: 三刚片三铰相连,三铰不共线,所以该体系为无多余约束 的几何不变体系.
在一个体系上加减二元体不影响原体系的机动性质.
§1. 几何组成分析
§1-1 基本概念
一. 几何不变体系 几何可变体系 二. 刚片 几何形状不能变化的平面物体
三. 自由度 确定体系位置所需的独立坐标数
点
刚
的 自
几何不变体系的自由片 自度一定等于零
由 几何可变体系的自由由度一定大于零
度
度
§1. 几何组成分析
§1-2 无多余约束的几何不变体系的组成规则
结构力学英文课件Chapter 1 Introduction2

hree dimensional structure selected for analysis is represented by a line diagram. On this diagram ,each member of the structure is represented by a line coinciding with its centroidal axis; each connection between the members is represented by a kind of joint; the length of each member is represented by the distance between joints to which the member be attached; the position of the loads acting upon members is also transmitted to their centroidal axes. (3) The simplification of connections The connections between members of a structure are commonly simplified into joints. Two types of joins are commonly used to join members of structures:
1.3.2 simplifying point of analytical model
(1) The simplification of structural system Generally ,the actual structures are space, or three-dimensional, structures, whose members are connected as a space frame to undergo the loadings likely acting on it in various sense. Fortunately ,many actual three-dimensional structures can be subdivided, by discarding some subsidiary space restraints ,into plane structures for simplifying analysis. The book will mainly discuss the calculation problems of plane structures. (2) The simplification of members The main attention the book focuses on is the framed structures. A framed structure is comprised of members, whose crosssectional dimensions is much smaller than the length l.
1.3.2 simplifying point of analytical model
(1) The simplification of structural system Generally ,the actual structures are space, or three-dimensional, structures, whose members are connected as a space frame to undergo the loadings likely acting on it in various sense. Fortunately ,many actual three-dimensional structures can be subdivided, by discarding some subsidiary space restraints ,into plane structures for simplifying analysis. The book will mainly discuss the calculation problems of plane structures. (2) The simplification of members The main attention the book focuses on is the framed structures. A framed structure is comprised of members, whose crosssectional dimensions is much smaller than the length l.
结构力学理论英文课程课件 CVG3140【Tutorial】
Tutorial #1
CVG3140 – Theory of Structures 1 Example #3
Tutorial #1
CVG3140 – Theory of Structures 1 To find X (M=0 ) :
Tutorial #1
CVG3140 – Theory of Structures 1 Example #4:
CVG3140 – Theory of Structures 1
Tutorial #1
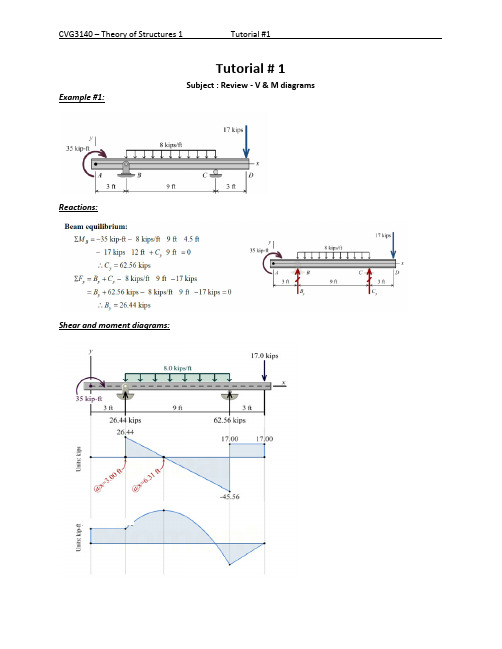
Tutorial # 1
Subject : Review - V & M diagrams Example #1:
Reactions:
Shear and moment diagrams:
CVG3140 – Theory of Structures 1 Example #2:
Area
(A )
i
(h )i
( A)i ∗ (h
)
Alternative: table
i
∫ f ( x) ∗ f
1 0
L
2
( x)dx
1
Example # 4 - Frame Use virtual work to calculate the vertical displacement at point “c” of the frame shown given that EI is given as 1X 105 Kn-m2 .
SI = (3m + r ) -(3j +ec)
m= # of members r = # reactions j= # of frame joints • support = joint • where two or more members meet = joint • free end = joint
结构力学(双语)绪论

Some examples of structures
结构力学的主要研究对象是杆件结构 The main objective of structural mechanics is framed structures 杆件结构
Framed stuctures
平面杆件结构 Plane structures: all the members and the applied loads lie in a single plane Otherwise the structures are spacial structure 空间 杆件结构
做题练习是学习结构力学的重要环节。不做一定 量的习题就很难对基本概念和方法有深入的理解和 掌握,也很难培养较好的计算能力。 Do exercises to solve some concrete problems is a key link in the study of the subject. If we don’t do a definite quantity of exercises it is difficult to understand the basic concepts and master the basic methods, and difficult to develop good ability to calculate.
II 计算能力Computing ability
(1)具有对各种结构确定计算步骤,进行计算的能力
determine the calculation procedure and calculate the structures。 (2)具有对计算结果进行定量校核或定性判断的能力the ability to verify the results quantitatively and judge the results qualitatively.
结构力学:自由度及几何分析PPT课件

个约束); r——支座链杆数(固定铰支座相当于2个链杆,
固定端支座或刚性连接相当于三根链杆)
3.铰接法
m=1,a=1,n=0 , r=4+3×2=10 则:
1自由度degree oWfWfre=e=do3m3m:m体--系运22动nn时-,-用来rr确定-为之3所×需的a独立坐标的数目。 ==33××11--1100 - 3×1 ①抛开基础,只分析上部。
A
a
A B
当杆通过铰 瞬变体系
引申、两刚片以不互相平行,也
不相交于一点的三根链杆相联,组成
B
无多余约束的几何不变体系。
如约束不满足限制条件,将出现下列几种形式的可变体系
瞬
瞬
常
变
变
变
体
体
体
系
系
系
2.3.3二元体规则
(将三刚片规则中的两个刚片换成链杆, 即为二元体规则)
在一个体系上增加或拿掉二元体,不 会改变原体系的几何构造性质。
2.3.1三刚片规则
三个刚片不在同一条直线上的三个铰两 两相连,体系几何不变。
同一条直线:不在同一条直线时,为瞬 变;
铰:可以是实铰,可以是虚铰。
A
图示为一无多余约束的几何不变体系
将杆AC,AB,BC均看成刚片,就成为三刚 片组成的无多余约束的几何不变体系
规则一、三刚片以不在一条直线上的三 C
增加或拿掉二元体,不会改变原体系的几何构造性质。
1 . 几 何 不 变 体 系 geometrically 1几何组成的目的、几何不变体系和几何可变体系
刚片法:W=3×3-2×2-5=0 结构力学:自由度及几何分析
unchangeable system :在任意荷载作 支承结构的地基
固定端支座或刚性连接相当于三根链杆)
3.铰接法
m=1,a=1,n=0 , r=4+3×2=10 则:
1自由度degree oWfWfre=e=do3m3m:m体--系运22动nn时-,-用来rr确定-为之3所×需的a独立坐标的数目。 ==33××11--1100 - 3×1 ①抛开基础,只分析上部。
A
a
A B
当杆通过铰 瞬变体系
引申、两刚片以不互相平行,也
不相交于一点的三根链杆相联,组成
B
无多余约束的几何不变体系。
如约束不满足限制条件,将出现下列几种形式的可变体系
瞬
瞬
常
变
变
变
体
体
体
系
系
系
2.3.3二元体规则
(将三刚片规则中的两个刚片换成链杆, 即为二元体规则)
在一个体系上增加或拿掉二元体,不 会改变原体系的几何构造性质。
2.3.1三刚片规则
三个刚片不在同一条直线上的三个铰两 两相连,体系几何不变。
同一条直线:不在同一条直线时,为瞬 变;
铰:可以是实铰,可以是虚铰。
A
图示为一无多余约束的几何不变体系
将杆AC,AB,BC均看成刚片,就成为三刚 片组成的无多余约束的几何不变体系
规则一、三刚片以不在一条直线上的三 C
增加或拿掉二元体,不会改变原体系的几何构造性质。
1 . 几 何 不 变 体 系 geometrically 1几何组成的目的、几何不变体系和几何可变体系
刚片法:W=3×3-2×2-5=0 结构力学:自由度及几何分析
unchangeable system :在任意荷载作 支承结构的地基
结构力学英文课件 Chapter 2

A
C
B
C’
Geometric Stability
This rule is also termed two components (二元体)。Two components rule is meant by two links without in the same straight form new joint. Adding or subtracting an unit of two components to (from) a system. Stability of the system do not change
We must analyze the geometric construction of the system.
Geometric Stability
Section3 Geometric construction analysis of planar systems
1、Rule 1 :
Rigid piece I is connected to hinge C by two links 1,2 , it forms a stable system provided that two links don’t lie on the same straight line .
2、EX.
EX.1
Stable system without redundant restraint
Geometric Stability
EX.2
EX.3
Stable system without redundant restraint
EX.4
Unstable system with 2redundant restraints AC \DB
结构力学英文 Chapter

(2) Canonical equations
1
11 1
12 2
13 3
1p
1
A
2
21 1
22 2
23 3
2p
2
B
Because M 3 0
11 1
12 2
1p
1
A
21
1
22
2
2p
2
B
Solution:
(3) Determine coefficients (Graph Multiplication)
After these, the structure is primary structure.
EX:
Find degree of indeterminacy, set up primary structure:
Section 3 Slope-Deflection equation
All members in structure are considered as a beam with a single span, the beam is fixed at two ends. Let’s discuss the internal force-bending moment at two ends under the actions of rotation and translation displacements and external loads.
When indeterminate structure is analyzed by using displacement method, every member is considered as a statically indeterminate beam with single span. So the primary structure is that every member is changed into an indeterminate beam with single span. A rigid arm is added at every rigid joint to prevent rotation of the joint (but can not prevent translation) at the same time, a link is added at joint where translation is possible. The link prevents translation of the joint.
结构力学STRUCTURALMECHANICSppt课件

3.拱
4.刚架
5.组合结构
平面结构和空间结构
RA
RB
y x
y
x z
-8-
§1-4
荷载的分类
1、根据荷载作用时间长短:恒载、活载。 2、按荷载作用的性质:静力荷载、动力荷载。
-9-
结构力学的任务:
(1)组成规律与合理形式,计算简图的合理选择; (2)内力与变形的计算方法.强度和刚度;
(3)稳定与动力反应。
结构力学的内容(从解决工程实际问题的角度提出) (1) 将实际结构抽象为计算简图; (2) 各种计算简图的计算方法; (3) 将计算结果运用于设计和施工。
结构力学的研究对象:平面的杆系结构。
1 绪论 2 结构的几何组成分析 3 静定结构内力计算 4 静定结构位移计算
8 9
影响线 矩阵位移法
10 结构的动力计算 11 结构的极限荷载 12 结构的稳定计算
5 力法
6 位移法 Байду номын сангаас 力矩分配法
结构力学的学习方法
研究性学习
先修课,公式,定理,概念,作业。 结合工程实际思考问题
§1-2 结构的计算简图
结构力学
-1-
第一章
绪
论
§1-1 结构力学的任务和学习方法
结构的定义: 建筑物中支承荷载而 起骨架作用的部分。 结构的几何分类: (1)杆件结构 (2)板壳结构 (3)实体结构
结构设计过程与步骤: (1)选择合理承重体系及构件几何尺寸;
(2)引入简化假定,取计算简图,进行结构分析; (3)依据结构分析结果,进行结构设计和构造处理。
换言之:铰结点可以传递力, 但不能传递弯矩。
4.支座的简化 (1) 铰支座 (2) 滚轴支座 (3) 固定支座
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Purpose of analyzing geometric construction of structures is as following: (1) To estimate whether or not a system is geometrically stable, so as to determine whether the system can be used as a structure or not; (2) To discuss geometric construction rules of stable systems.
n=0
n=1
(2 )Connecting restraints between rigid bodies we will pay more attention to connecting restraints between two rigid bodies. One rigid body has three degrees of freedom and two independent rigid bodies have six degrees of freedom in a planar coordinate system, when connecting them together, their degrees of freedom would be reduced. Now we will discuss the equivalent restraints of a few kinds
n=3
2.2.2 Restraints the devices or connections which can reduce the degrees of
freedom of a system are defined as restraints. The number of the degrees of freedom of a system reduced by the device or connection is named the number of its restraints. There are two kinds of restraints, support restraints and connecting restraints between rigid bodies. (1)Support restraints ①The roller support can restrict the translation of joint A in the direction perpendicular to its moving surface but cannot prevent its translation along its moving surface and rotation about joint A, i.e., one roller support reduces one degree of freedom and is equivalent to one restraint
Geometric construction analysis 2.1purpose of analyzing geometric construction of structures, of structure
stable and unstable structural systems in order to withstand and transmit load, the geometric shape of a structure system is variable under loads, the structural system cannot be used as a structure. it should be realized that all physical bodies deform when subjected to loads; the deformation in most engineering structures under service conditions are so small that their effect on the geometric construction analysis of the structures can be neglected.
n=2
②The hinged support can restrict the translation of joint A in verticar and horizontal directions but cannot prevent the rotation about joint A, i.e., one hinged support reduces two degrees of freedom and is equivalent to two restraints ③Restrict in vertical and horizontal directions and the rotation about A three restraints
2.2.1the degrees of freedom The degrees of freedom of a system are the numbers of independent movements which are required to locate the system fully.obviously, arigid body has three degrees of freedom in a planar coordinate system(six degrees of freedom in a three dimensional coordinate system),e.g., the position of member AB may be determined by three parameters Xa, Ya and (1)The degrees of freedom of a joint The movement of a point in a planar coordinate system can decomposed into two translations in any different directions i.e., a point possesses two independent moving styles or two independent coordinates are needed to locate its position in a planar coordinate system. So a joint has two degrees of freedom in a planar coordinate system .in fig the parameters Xa, Ya will locate joint A.
2.2 the concept of degrees of freedom and restraints In the analyzing geometric construction of structures, it is very feasible to consider one part of the members or joints of a system as an object which possesses degrees of freedom, whereas other part of the members or joints of the system as restraints which restricts the movement of the object. The relationship of these two parts are then analyzed and whether or not the system will be determined. Accordingly, the concept of degrees of freedom and restraints of a system is discussed first of all
(2)Geometrically unstable system Under the action of the loads, the system will change its shape and its location if the small deformations of the members are neglected as shown in fig,2.2 Corresponding to geometrically stable and unstable system, there are internally stable and unstable systems as well. A structure is considered to be internally stable, or rigid, if it maintains its shape and remains a rigid body when detached from the supports
n=2
(2)The degrees of freedom of freedom of a rigid body The movement of a rigid body in planar coordinate system
can beห้องสมุดไป่ตู้decomposed to two translations in any different directions and a rotation about some point in the system ,i.e.,a rigid body possesses three independent moving styles or three independent coordinates are needed to locate its position in a planar coordinate system. Therefore, a rigid body has three degrees of freedom in a planar coordinate system .the position of member AB may be determined by three parameters Xa, Ya and
