解算四元数
四元数

1 0 0 1 0 1 0 1 1 0 ,则集 H 内任意方阵可唯一表为 aIbE cJ dK ,即 , E 1 0 , J ;K c d a b 1 0 0 1 1 0 1 d c b a 0 1 1 0 1 1 0 2 2 2 H {aI bE cJ dK | a,b,c,dR} ,H 对矩阵减法封闭 ;且 E J K I , EJ K,JK E,KE J; JE K,KJ E,EK J ,矩阵乘法在 H 内封闭,故 H 对矩阵加,乘法构 1 来自
[d, b, c] [a, d, c] [a, b, d] 推论 [a, b, c] 0 d a b c a {b (c d)} (b d)(a c) (b c)(a d) [a, b, c] [a, b, c]
S() : 2a R
N( ) : a2 b2 c2 d2 R
证明: 0 0, oder, 0
0, und, 0 0 N( ) 0 0 ,即 0, und, 0 0 ,同理 0,und, 0 0 0 N( ) 0 证明:若 是方程 x 2 S( ) N( ) 0 的根,则 也是其根. 因为, 是方程 x 2 S( ) N( ) 0 的根 2 ( ) ( ) 0 2 ( ) ( ) 0 也是其根)
四矢外积: (a b) (c d) [a, b, d]c [a, b, c]d [c, d, a]b [c, d, b]a (V, V, V, V) V 三矢外积 三矢外积 (a b) (c d) ((a b) d)c ((a b) c)d [a, b, d]c [a, b, c]d; (a b) (c d) ((c d) a)b ((c d) b)a [c, d, a]b [c, d, b]a
四元数

二.四元数与姿态阵之间的关系
3.由于 || Q || q0 2 q12 q2 2 q3 2 =1,所以:
q0 2 q12 q2 2 q3 2 R Cb 2(q1q2 q0 q3 ) 2(q q q q ) 1 3 0 2
2(q1q2 q0 q3 ) q0 q1 q2 q3 2(q2 q3 q0 q1 )
构造四元数:
q0 cos
2
2 q2 m sin 2 q3 n sin 2
q1 l sin
Q q0 q1i0 q2 j0 q3 k0 cos cos
2
(li0 mj0 bk0 ) sin
2
2
u R sin
2
二.四元数与姿态阵之间的关系
记:
rx ' r 'R r ' y rz '
rx rR r y rz
l uR m n
二.四元数与姿态阵之间的关系
0 n m rx r (u r ) R n 0 l y 0 m l rz
q0 2 q12 q2 2 q3 2 CbR 2(q1q2 q0 q3 ) 2(q q q q ) 1 3 0 2 2(q1q2 q0 q3 ) q0 q1 q2 q3 2(q2 q3 q0 q1 )
2 2 2 2
2(q2 q3 q0 q1 ) 2 2 2 2 q0 q1 q2 q3 2(q1q3 q0 q2 )
二.四元数与姿态阵之间的关系
四元数

定义两个四元数:
其中表示矢量 ;而表示矢量。
跟复数、向量和矩阵一样,两个四元数之和需要将不同的元素加起来。 加法遵循实数和复数的所有交换律和结合律。
威廉·卢云·哈密顿
明确地说,四元数是复数的不可交换延伸。如把四元数的集合考虑成多维实数空间的话,四元数就代表着一 个四维空间,相对于复数为二维空间。
四元数是除环(除法环)的一个例子。除了没有乘法的交换律外,除法环与域是相类的。特别地,乘法的结 合律仍旧存在、非零元素仍有逆元素。
四元数形成一个在实数上的四维结合代数(事实上是除法代数),并包括复数,但不与复数组成结合代数。 四元数(以及实数和复数)都只是有限维的实数结合除法代数。
不只如此,哈密顿还创造了向量的内外积。他亦把四元数描绘成一个有序的四重实数:一个纯量和向量的组 合。若两个纯量部为零的四元数相乘,所得的纯量部便是原来的两个向量部的纯量积的负值,而向量部则为向量 积的值,但它们的重要性仍有待发掘。
哈密顿之后继续推广四元数,并出了几本书。最后一本《四元数的原理》(Elements of Quaternions)于 他死后不久出版,长达八百多页。
非奇异表达(和例如欧拉角之类的表示相比)
比矩阵更紧凑(更快速)
单位四元数的对可以表示四维空间中的一个转动。
所有单位四元数的集合组成一个三维球和在乘法下的一个群(一个李群)。是行列式为1的实正交3×3正交 矩阵的群的双面覆盖,因为每两个单位四元数通过上述关系对应于一个转动。群和同构,是行列式为1的复酉 2×2矩阵的群。令为形为的四元数的集合,其中或者都是整数或者都是分子为奇数分母为2的有理数。集合是一 个环,并且是一个格。该环中存在 24个四元数,而它们是施莱夫利符号为的正二十四胞体的顶点。
四元数计算法则

四元数计算法则
四元数是一种数学结构,用于描述三维空间的旋转和变换。
它由一个实部和三个虚部组成,可以表示为q = a + bi + cj + dk,其中i、j、k是虚数单位,满足i=j=k=ijk=-1。
四元数的加减法与复数相似,但是乘法则更加复杂。
四元数的乘法遵循以下法则:
1. 实部相乘,虚部相乘时,i=j=k=ijk=-1
2. i乘以j等于k,j乘以k等于i,k乘以i等于j
3. j乘以i等于-k,k乘以j等于-i,i乘以k等于-j
4. 任意两个虚数乘积可以表示为一个实数加上一个虚数
四元数的除法需要用到逆元,即q=q*/(q*q*),其中q*表示q的共轭。
四元数的共轭表示为q* = a - bi - cj - dk。
四元数的旋转可以通过四元数的乘法来实现。
以欧拉角为例,将欧拉角转换为四元数后,进行旋转就是将原始四元数与旋转四元数相乘。
同时,四元数也可以用于描述变换(如平移、缩放等),可以通过矩阵的方式表示。
总之,四元数是一种非常有用的数学工具,广泛应用于计算机图形学、虚拟现实、机器人控制等领域。
掌握四元数的计算法则,对于进行三维空间中的旋转和变换非常有帮助。
- 1 -。
四元数姿态解算原理

四元数姿态解算原理咱们先来说说姿态解算为啥这么重要。
你想啊,在好多地方都得知道一个物体的姿态,就像咱们玩遥控飞机的时候,如果不知道飞机在空中是啥姿势,是头朝上还是朝下,是横着飞还是斜着飞,那这飞机可就没法好好控制啦。
在机器人领域也是一样的,机器人得知道自己的胳膊、腿是啥姿势才能准确地干活呀。
那四元数是啥呢?简单来说,它就像是一种很特别的数学小工具。
四元数有四个部分,就像四个小伙伴一起合作来描述姿态。
这和咱们平常熟悉的用角度来描述姿态不太一样哦。
平常的角度描述有时候会遇到一些麻烦事儿,比如说会有万向节锁这种讨厌的问题。
就好比你想转动一个东西,结果发现有些方向转着转着就转不动了,就像被锁住了一样,多让人头疼呀。
但是四元数就很聪明啦,它能巧妙地避开这些问题。
想象一下四元数是一个小魔法盒。
这个小魔法盒里面的四个部分相互配合着来表示物体的旋转状态。
比如说有一部分像是负责说物体绕着x轴转了多少,另一部分负责绕y轴,还有的负责绕z轴,最后一部分就像是一个协调员,把前面三个部分协调得妥妥当当的。
在姿态解算的时候呢,就像是一场精彩的接力赛。
传感器会给我们一些数据,这些数据就像是接力赛的第一棒。
比如说加速度计能告诉我们物体受到的加速度,陀螺仪能告诉我们物体旋转的速度。
但是这些数据可不能直接就告诉我们物体的姿态呢,它们还需要经过四元数这个神奇的“加工厂”加工一下。
四元数会根据这些传感器的数据不断地更新自己。
就像它在说:“加速度计给了我这个信息,陀螺仪给了我那个信息,那我就调整一下我自己来表示新的姿态啦。
”这个调整的过程就像是它在做一种很精细的舞蹈动作,每个部分都在按照一定的规则动来动去。
而且四元数在计算姿态的时候特别稳定。
就像一个稳重的老大哥,不管外面的数据怎么波动,它都能比较准确地算出姿态来。
不像有些方法,数据稍微有点风吹草动就慌了神,算出的姿态就乱七八糟的。
再说说四元数在图形学里的应用吧。
你玩游戏的时候有没有想过那些超级酷炫的3D模型是怎么旋转的呀?很多时候就是靠四元数来搞定姿态的。
四元数及姿态解算

q1
q2
q3
q1 q2 q0 q3 q3 q0 q2 q1
q3 p0
q2 q1
p1
p2
M
'(q) P
q0 p3
(2-2)
(2-3) (2-4) (2-5) (2-6)
由此可知,四元数的乘法不满足交换律,除非四元数还原为纯数字。
第三讲 四元数及姿态解算
一、 四元数的起源
在古希腊的亚里斯多德时代就已经有了力的矢量分解了,即力可以分解为
F
ai
bj
(1-1)
但那个时代并不意味着 i j 。在此之前人们就已经有了对纯粹数字的认识和相应的运算
规则,但是纯数字和矢量是没有混在一起表示物理量的,1879 年高斯撰写了一篇未曾发表的 文章,其中提到了 a bi 的含义,可以看出他试图建立一个三分量的代数( a ,bi , a bi )。
t 0
dt 2
0
x y
z
x y 0 z z 0 y x
z
y
x
0
(4-2) (4-3) (4-4) (4-5)
在(4-5)的基础上,剔除所有的零元,则有
q0 (t) q1(t)
d dt
q1
(t
)
q2
(t
1r0
0r1
3r2
2r3
1 0
32rr00
3r1 2r1
0r2 1r2
四元数解算姿态完全解析及资料汇总
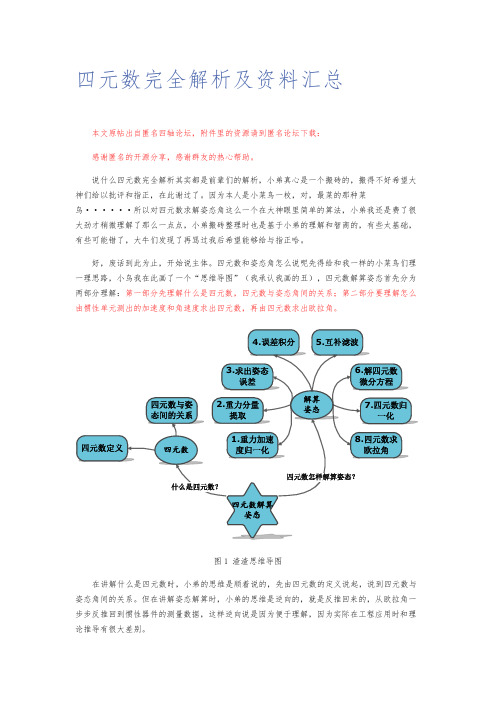
四元数完全解析及资料汇总本文原帖出自匿名四轴论坛,附件里的资源请到匿名论坛下载:感谢匿名的开源分享,感谢群友的热心帮助。
说什么四元数完全解析其实都是前辈们的解析,小弟真心是一个搬砖的,搬得不好希望大神们给以批评和指正,在此谢过了。
因为本人是小菜鸟一枚,对,最菜的那种菜鸟······所以对四元数求解姿态角这么一个在大神眼里简单的算法,小弟我还是费了很大劲才稍微理解了那么一点点,小弟搬砖整理时也是基于小弟的理解和智商的,有些太基础,有些可能错了,大牛们发现了再骂过我后希望能够给与指正哈。
好,废话到此为止,开始说主体。
四元数和姿态角怎么说呢先得给和我一样的小菜鸟们理一理思路,小鸟我在此画了一个“思维导图”(我承认我画的丑),四元数解算姿态首先分为两部分理解:第一部分先理解什么是四元数,四元数与姿态角间的关系;第二部分要理解怎么由惯性单元测出的加速度和角速度求出四元数,再由四元数求出欧拉角。
图1 渣渣思维导图在讲解什么是四元数时,小弟的思维是顺着说的,先由四元数的定义说起,说到四元数与姿态角间的关系。
但在讲解姿态解算时,小弟的思维是逆向的,就是反推回来的,从欧拉角一步步反推回到惯性器件的测量数据,这样逆向说是因为便于理解,因为实际在工程应用时和理论推导有很大差别。
实际应用时正确的求解顺序应该为图1中序号顺序,即1->2->3->…….但在笔者讲解姿态求解时思路是如图2的。
`图2 逆向讲解思路大家在看四元数时最好结合着代码一块看,小弟看的是匿名四轴的代码,感觉写的非常好也非常清晰,粘出来大家一块观摩。
红色部分是核心代码,总共分为八个步骤,和图1中的八个步骤是一一对应的。
讲解介绍时也是和代码对比起来讲解的。
代码可以去匿名官网上下载,都是开源的,不是小弟的,所以小弟不方便加在附件中。
好的,下面搬砖开始!。
嘿咻嘿咻·一.关于四元数的定义摘自秦永元的《惯性导航》,里面有非常好的讲解,大家可以直接看绪论和第九章就可以。
四元数概念

四元数概念四元数(Quaternions)是一种数学工具,它是由爱尔兰数学家 William Rowan Hamilton 于1843年发明的。
四元数被广泛应用于计算机图形和动画,机器人控制,摄影测量,化学和物理的研究中。
四元数具有复数的性质并且比复数更为丰富。
复数是由一个实部和一个虚部组成的,而四元数是由一个实部和三个虚部组成的。
四元数的定义如下:Quaternions = {a + bi + cj + dk | a, b, c, d∈R}i²=j²=k²=ijk=-1在四元数中,公式(1)具有一些有趣的特性,这使得四元数成为一种非常有用的工具。
其中一条是四元数具有完整的乘法结构,即使在虚部之间的乘法也是如此。
在计算机图形和动画应用中,四元数极为有用,因为它可以表示多种变换操作(如平移,旋转和缩放)。
q = cos(theta/2) + sin(theta/2)*(vi + vj + vk)这里,cos是余弦函数,sin是正弦函数,theta是旋转角度,v表示旋转轴的单位向量。
p + q = (a1 + a2) + (b1 + b2)i + (c1 + c2)j + (d1 + d2)kkp = ka + kb*i + kc*j + kd*k这些运算遵循基本的加、减和乘法法则,类似于向量的运算。
这些规则具有一些有趣的性质,四元数的乘法不是可交换的,即pq≠qp。
四元数是一种非常有用的数学工具,尤其是在计算机图形和动画,机器人控制,摄影测量,化学和物理的应用中。
它包含了复数所具有的性质,并增加了第三个和第四个虚部,使得它更加丰富和灵活。
四元数还具有证明某些矢量不变性的作用。
对于一个物体的旋转,它的角速度可以通过四元数的导数来表示,这个导数有一个重要的应用,即可以证明质心不受任何外部力矩的影响而保持恒定,这被称为质点定则证明。
四元数还与矩阵有密切的联系。
事实上,四元数乘法可以被转换为矩阵运算,它的实部和虚部也可以被表示为一个4x4的旋转矩阵。
四元数公式

四元数公式四元数的基本数学方程为 : q = cos (a/2) + i(x * sin(a/2)) + j(y * sin(a/2)) +k(z * sin(a/2)) 其中a表示旋转角度,(x,y,z)表示旋转轴下面是如何把具体的四元数与旋转轴和旋转角度对应起来。
1.指出旋转轴和旋转角度,如何转化为四元素。
假定旋转轴是:RAxis = Z轴,换算成三维空间单位向量就是RAxis = [0 0 1],旋转60度那么转化成四元数就是q.w=cos(60°/2) = 0.866q.x=RAix.xsin(60°/2) = 00.5=0q.y=RAix.ysin(60°/2) = 00.5=0q.z=RAix.zsin(60°/2) = 10.5=0.5例子验证:从三维空间中看,假定物体点A=[0 1 0],绕 RAxis = Z轴,旋转30度(假定顺时针为正,因为matlab就是顺时针为正,而下面的quat2dcm函数是matlab自带的)那么物体点A旋转后在世界坐标系下的坐标将是B=[0.866 0.5 0],如何用四元数计算出呢?思路是这样的:任何一个四元数对应着一个旋转3*3矩阵。
M=quat2dcm(q)*A’=[0.866;0.5;0],关于quat2dcm在软件matlab里面有。
从上面可以得到:RAix.x=RAix.y=0由cos(a/2) = 0.866,得到a = 60°或120°由RAix.z*sin(a/2) = 0.5,得到a = 60°或150°因此a = 60°(四元数的旋转角度一般是在0-360之间,之后就是多一圈的问题。
于是可得RAix.z = 1,因此其他q=[0.866,0,0,0.5]意味着旋转轴是RAxis =[0 0 1],旋转角度是60°,其他的类似可以计算。
四元数 四旋翼飞行器姿态解算

四元数四旋翼飞行器姿态解算四元数是用来描述空间旋转的数学工具,在飞行器姿态解算中具有重要的应用。
四旋翼飞行器是一种采用四个电动马达驱动的多旋翼飞行器,通过调节四个马达的转速实现飞行器的姿态控制。
在四旋翼飞行器的飞行过程中,需要实时获取飞行器的姿态信息,以便进行飞行控制。
四元数作为一种有效的姿态描述方法,被广泛应用于四旋翼飞行器的姿态解算中。
四元数是一种具有四个元素的数学结构,通常表示为q = w + xi + yj + zk,其中w、x、y、z分别表示四元数的实部和三个虚部。
四元数可以表示为一个旋转矩阵,通过四元数乘法运算可以实现空间旋转的复合。
在四旋翼飞行器的姿态解算中,通常使用四元数来描述飞行器的姿态状态。
四旋翼飞行器的姿态解算涉及到四元数的插值、积分和旋转等计算。
在飞行器的姿态控制过程中,需要将传感器获取的姿态信息进行融合处理,得到飞行器的姿态状态。
四元数插值可以实现飞行器姿态信息的平滑过渡,提高飞行的稳定性和平顺性。
四元数积分可以实现对飞行器姿态状态的更新,保持飞行器的正确姿态。
四元数旋转可以实现飞行器的姿态控制,使飞行器按照指定的姿态进行飞行。
在四旋翼飞行器的姿态解算中,需要考虑传感器误差、系统延迟和控制精度等因素。
传感器误差会影响到飞行器的姿态感知精度,需要通过滤波算法和校准方法来降低误差影响。
系统延迟会导致飞行器姿态状态的延迟更新,需要通过合理的控制策略来补偿延迟效应。
控制精度是指飞行器姿态控制的准确性,需要通过优化控制算法来提高飞行器的稳定性和精确性。
总的来说,四元数是一种有效的姿态描述方法,被广泛应用于四旋翼飞行器的姿态解算中。
通过四元数插值、积分和旋转等计算,可以实现对飞行器姿态状态的准确解算和控制。
在实际的飞行应用中,需要综合考虑传感器误差、系统延迟和控制精度等因素,全面提高飞行器的姿态解算精度和控制性能。
四旋翼飞行器的姿态解算是飞行控制领域的重要课题,将带来对未来飞行器飞行性能的提升和发展。
四元数法

[cos(b), sin(b)*sin(a), -sin(b)*cos(a);
sin(c)*sin(b), cos(c)*cos(a)-sin(c)*cos(b)*sin(a), cos(c)*sin(a)+sin(c)*cos(b)*cos(a);
cos(c)*sin(b), -sin(c)*cos(a)-cos(c)*cos(b)*sin(a), -sin(c)*sin(a)+cos(c)*cos(b)*cos(a)];
一阶算法:
(2-31)
二阶算法:
(2-32)
三阶算法:
(2-33)
四阶算法:
(2-34)
求解四元数微分方程除了以上的增量算法,还可以利用龙格—库塔法或阿达姆斯方法等数值积分算法求解微分方程。但迭代一定时间后,四元数会不满足 ,为了让其满足此式,必须进行归一化处理。
初始值的确定:
正负号的确定
可取
其中的 由初始的姿态矩阵求得
四元数是哈密顿于1843年建立的数学概念,但只有在近四十年中才在刚体运动学中得到实际应用。四元数是由1个实数单位1和3个虚数单位 , , 组成的包含4个实元的超复数。若将 , , 视为基矢量,则可以把四元数分为标量和矢量两部分组成。其形式为:
(2-22)
且 ,其中 为标量, 为矢量。
引入四元数后,则方向余弦矩阵可由四元数表示为
(2-23)
由(2-12),我们可得
(2-24)
利用毕卡逼近法求解可得: (2-25)
令:
(2-26)
(2-25)可简写ຫໍສະໝຸດ :(2-27)将 展开可得:
(2-28)
由于:
(2-29)
将式(2-29)代入式(2-28)整理可得:
基于四元数的姿态解算器或欧拉角解算器算法

基于四元数的姿态解算器或欧拉角解算器算法四元数姿态解算器和欧拉角姿态解算器都是用于表示三维空间中的旋转。
四元数是一种扩展了复数的数学概念,可以表示三维空间中的旋转,而欧拉角是一种用三个角度表示旋转的方法。
这两种方法都可以用于计算物体在三维空间中的姿态。
1. 四元数姿态解算器算法:
四元数由一个实部和一个虚部组成,可以表示为q = w + xi + yj + zk,其中w、x、y、z是实数,i、j、k是虚数单位。
四元数的运算包括加法、减法、乘法和共轭等。
四元数姿态解算器的算法步骤如下:
a) 初始化四元数q = [1, 0, 0, 0],表示初始时刻物体的姿态。
b) 读取陀螺仪的角速度数据,将其转换为四元数形式。
c) 使用四元数乘法更新物体的姿态。
d) 将更新后的四元数转换为欧拉角,以便进行其他计算或显示。
2. 欧拉角姿态解算器算法:
欧拉角是用三个角度表示旋转的方法,通常包括绕x轴的滚动角(roll)、绕y轴的俯仰角(pitch)和绕z轴的偏航角(yaw)。
欧拉角的运算包括加法、减法和乘法等。
欧拉角姿态解算器的算法步骤如下:
a) 初始化欧拉角θ = [0, 0, 0],表示初始时刻物体的姿态。
b) 读取陀螺仪的角速度数据,将其转换为欧拉角形式。
c) 使用欧拉角乘法更新物体的姿态。
d) 将更新后的欧拉角用于其他计算或显示。
需要注意的是,欧拉角在某些情况下可能会出现万向节死锁(gimbal lock)现象,这时需要使用四元数来表示旋转。
而在实际应用中,通常会将四元数和欧拉角结合起来使用,以便在不同场景下进行灵活切换。
四元数姿态解算和卡尔曼滤波

四元数姿态解算和卡尔曼滤波在四元数姿态解算和卡尔曼滤波领域,姿态解算是一个重要的问题。
姿态解算主要是通过传感器来获取物体在空间中的方位信息,其中四元数是一种广泛应用的姿态表示方法。
而卡尔曼滤波是一种常用的姿态解算算法。
四元数是一种用来表示旋转的数学工具,它由一个实部和三个虚部组成。
通过四元数,我们可以方便地描述物体在三维空间中的旋转和方位。
在姿态解算中,我们常常使用四元数来表示物体的姿态。
四元数具有很好的性质,比如可以方便地进行插值和运算,因此在姿态解算中得到了广泛的应用。
卡尔曼滤波是一种常见的姿态解算算法。
它主要通过融合多传感器的数据来进行姿态解算。
卡尔曼滤波利用传感器提供的测量值和先验知识,通过递推的方式对系统状态进行估计和修正,从而得到更准确的姿态信息。
在实际应用中,四元数姿态解算和卡尔曼滤波常常结合起来使用。
通过四元数来表示物体的姿态,然后利用卡尔曼滤波对姿态进行优化和修正。
这种组合可以有效地提高姿态解算的准确性和稳定性。
在具体的实现过程中,四元数姿态解算和卡尔曼滤波需要考虑多个因素,比如传感器类型、传感器误差、姿态模型等。
需要根据实际情况选择合适的算法和参数,以获得最佳的姿态解算效果。
总而言之,在姿态解算和卡尔曼滤波领域,四元数是一种重要的姿态表示方法,而卡尔曼滤波是一种常用的姿态解算算法。
它们的结合可以有效提高姿态解算的准确性和稳定性。
在实际应用中,我们需要根据具体情况选择合适的算法和参数,以获得最佳的姿态解算效果。
通过不断的研究和实践,我们相信四元数姿态解算和卡尔曼滤波在未来会有更广泛的应用。
四元数的理论和应用

四元数的理论和应用四元数,又称四元数实数,是由英国数学家汉密尔顿于1843年创造的一个新颖的数学体系。
与复数具有类似性质,四元数可以表示3D空间的旋转、陀螺的转动以及电磁场的量子性质,因此在工程、物理学等学科中具有广泛的应用。
一、四元数的定义四元数可以看作是较为一般性的复数,是由一个实部和三个虚部构成的算子,记作q=a+bi+cj+dk,其中i,j,k是虚数单位,具有如下的性质:i² = j² = k² = ijk = -1。
二、四元数的计算1. 四元数的加减法:对于两个四元数q1=a1+b1i+c1j+d1k和q2=a2+b2i+c2j+d2k,我们可以进行加减法运算:q1 + q2 = (a1+a2) + (b1+b2)i + (c1+c2)j + (d1+d2)kq1 - q2 = (a1-a2) + (b1-b2)i + (c1-c2)j + (d1-d2)k2. 四元数的乘法:四元数的乘法需要按照虚部单位的乘法规则进行运算,即:i² = j² = k² = ijk = -1ii = -1, ij = k, ik = -jji = -k, jj = -1, jk = iki = j, kj = -i, kk = -1因此,两个四元数的乘积为:q1q2 = (a1a2 - b1b2 - c1c2 - d1d2) + (a1b2 + b1a2 + c1d2 - d1c2)i + (a1c2 - b1d2 + c1a2 + d1b2)j + (a1d2 + b1c2 - c1b2 + d1a2)k3. 四元数的共轭:四元数的共轭是把虚部单位i,j,k交换位置,且取反,即:q* = a-bi-cj-dk4. 四元数的模长:四元数的模长表示为:|q| = sqrt(qq*) = sqrt(a²+b²+c²+d²)三、四元数在旋转表示上的应用四元数是一种非常方便的表示3D旋转的工具,示例见下图。
mpu6050四元数姿态解算结果

MPU6050是一款常用的三轴陀螺仪和三轴加速度计模块,它可以用于测量和解算飞行器的姿态角,是无人机和其他飞行器项目中常用的传感器之一。
在解算飞行器的姿态角时,使用四元数解算是一种常见且有效的方法。
本文将介绍MPU6050四元数姿态解算的结果,包括其原理、算法和实际应用。
一、MPU6050的工作原理1.1 三轴陀螺仪MPU6050的三轴陀螺仪可以测量飞行器围绕X、Y、Z轴的角速度,其工作原理是利用霍尔传感器测量角速度对应的旋转矢量。
通过积分得到飞行器当前的姿态角速度。
1.2 三轴加速度计MPU6050的三轴加速度计可以测量飞行器在X、Y、Z轴的加速度,其工作原理是利用加速度对应的位移变化,计算得到飞行器的加速度。
1.3 传感器融合MPU6050将三轴陀螺仪和三轴加速度计的数据进行融合,通过卡尔曼滤波等算法得到更为准确的姿态角度。
二、四元数解算姿态角2.1 四元数原理四元数是一种数学工具,用来描述旋转和姿态变换。
在飞行器姿态控制中,通常使用四元数来表示飞行器当前的姿态角。
四元数可以简洁地表示旋转,且在插值和积分运算中具有优势。
2.2 四元数解算算法MPU6050使用四元数解算算法,根据三轴陀螺仪的角速度数据来更新四元数,从而得到飞行器当前的姿态角。
四元数解算算法运用了加速度计和磁力计的数据,使得姿态角的计算更为准确和稳定。
2.3 解算结果MPU6050四元数解算的结果是飞行器当前的姿态角,包括俯仰角、横滚角和偏航角。
这些角度是飞行器在空间中的姿态,对于飞行器的稳定飞行和姿态控制具有重要意义。
三、MPU6050四元数姿态解算的实际应用3.1 无人机姿态控制在无人机项目中,MPU6050四元数姿态解算可以用于无人机的姿态控制。
通过实时更新无人机的姿态角,可以使无人机保持稳定飞行和响应操控信号。
3.2 姿态稳定相机MPU6050四元数姿态解算还可以应用在姿态稳定相机上。
通过获取相机的姿态角,可以使相机在运动中保持稳定,获得更加清晰和稳定的图像。
四元数姿态解算

四元数姿态解算1. 欧拉角法:欧拉角法(又称三参数法)是欧拉在1776 年提出来的,其原理是动坐标系相对参考坐标系之间的位置关系可以用一组欧拉角来描述。
解算欧拉角微分方程只需要解三个微分方程,与其它方法相比,需要求解的方程个数少一些但在用计算机进行数值积分时,要进行超越函数(三角函数)的运算,从而加大了计算的工作量。
用此方法求解得到的姿态矩阵永远是正交矩阵。
在进行加速度信息的坐标变换时变换后的信息中不存在非正交误差,得到的姿态矩阵不需要进行正交化处理。
当载体的纵摇角(俯仰角)为90 °时,将出现奇点,因此该方法不能进行全姿态解算,其使用存在一定的局限。
2. 方向余弦法:方向余弦法(称九参数法)用矢量的方向余弦来表示姿态矩阵的方法。
绕定点转动的两个坐标系之间的关系可以用方向余弦矩阵来表示。
方向余弦矩阵是随时间变化的,其变化规律的数学描述就是方向余弦矩阵的微分方程,方向余弦矩阵的即时值就可以通过求解该微分方程而得到。
该方法求解姿态矩阵避免了欧拉角法所遇到的奇点问题,可以全姿态工作。
但方向余弦矩阵具有九个元素,所以需要解九个微分方程,计算工作量较大,在工程上并不实用。
3. 三角函数法:三角函数法(又称六参数法)是将绕定点转动的两个坐标系之间的关系用三次转动等效地表示,将三次转动角度的正、余弦函数来表示姿态函数。
该方法虽然避免了欧拉角法的缺点,可以全姿态工作,但需要解六个微分方程,计算量也不小,工程上并不实用。
4. Rodrigues参数法:Rodrigues 数法是法国数学家Rodrigues 在1840 年提出的,该方法所描述的姿态是唯一的,并且具有简洁、直观的优点,其微分方程结构简单,无多余约束,计算效率优于当前广泛使用的四元数法。
由于Rodrigues 参数法存在旋转角有奇异值的缺陷,因此限制了其在工程上的应用。
Schaub 和Junkin 对该方法的缺陷,改进后仍然存在奇异值。
但是Rodriguess 参数法仍不失为解算姿态的有效途径。
P17四元数微分方程求解

姿态实时计算 概述
四元数的实时计算
b b b ω Eb = ω ib − ω iE 因假定“数学平台”跟踪地理坐标系,因 因假定“数学平台”跟踪地理坐标系,
此 四元数微分方程: 四元数微分方程:
ɺ q (t ) = (Ω b − Ω b )q (t ) ib iE
增量算法 四元数
2、四元数微分方程的计算: 、四元数微分方程的计算:
T X (t + T ) = X (t ) + [ K 1 + K 2 ] 2
数值积分 2阶 四元数 阶
(2)四元数微分方程 )
K 1 = Ω b (t )q(t )
Y = q(t ) + TK1
K 2 = Ω b (t + T )Y T q (t + T ) = q (t ) + ( K 1 + K 2 ) 2
四元数的实时计算因假定数学平台跟踪地理坐标系因其中i为单位四元数四阶龙格库塔积分四元数微分方程1一阶龙格库塔法rungekutta一个矩阵微分方程
四元数精确解1 姿态计算 四元数精确解
三、四元数微分方程式及其解 由第一章,四元数微分方程式: 由第一章,四元数微分方程式:
ɺ q = Ωb q
对
Ω b 的类似处理
ɺ X (t ) = f [ X (t ), ω (t )]
当初始条件已知,其一阶龙格 库塔的解为 库塔的解为: 当初始条件已知,其一阶龙格-库塔的解为
X (t + T ) = X (t ) + Tf [ X (t ), ω (t )]
数值积分 1阶 四元数 阶
(2)四元数微分方程 )
或
ɺ q = Ωb q ɺ − ω x / 2 − ω y / 2 − ω z / 2 λ λ 0 ɺ ω / 2 ω z / 2 − ω y / 2 P1 0 P1 = x ɺ P2 ω y / 2 − ω z / 2 ω x / 2 P2 0 ɺ ωz / 2 ωy / 2 −ωx / 2 0 P3 P3 q(t + T ) = q(t ) + TΩ b (t )q(t )
四元数用于飞机姿态解算

由上述矩阵L 可解算出三个姿态角
a rc ta n L L 1 1 2 1 a rc sinL 1 3 a rc ta n L L 3 2 3 3
奇异性问题:当
2
时,L110,L330
, 无法确定,姿态角解算出现奇异
姿态矩阵及姿态角的解算涉及超越函数计算,运算量较大
四元数理论及其应用
目 录 Contents
四元数的产生背景 四元数的定义和性质 四元数的应用举例 总结
四元数的产生背景
起源
发展
应用
Hamilton 于1843年 扩展复数到 更高维的层 次,指出矢 量之间的变 换
Maxwell将 四元数数量 部分和矢量 部分的分开 ,作了大量 矢量分析等
在飞行器 姿态解算 中的应用 ,来解决 大姿态角 的控制问 题
q0 q1i q2 j q3k q0 q1i q2 j q3k
q0 q1i q2 j q02 q12 q22
q3k q32
q* q2
2
q*q0q1iq2jq3k
q 2
q0 2q12q2 2q3 2
如果 q 1 ,则 q 1 q*
q
2
四元数的定义和性质
除法:分为左除和右除。对四元数 x , p 和 q
可同样求解,但 和 会出现突变,角度变化不平滑
若 2 ,cos0
0
0
1
Lsgnsin cos 0
sgncos sin 0
物理意义:第2次旋转使得第1次旋转和第3次旋转重合 无法具体确定 和 ,即有多组欧拉角与姿态四元数对应
四元数的应用举例(4) 大角度四元数与欧拉角的转换(姿态四元数 欧拉角) ①姿态小幅调整(如姿态稳定控制)
6轴传感器的解算方法

6轴传感器的解算方法
六轴传感器的解算方法主要有两种:欧拉角解算和四元数解算。
1. 欧拉角解算:
欧拉角解算方法将物体的旋转分解为绕三个坐标轴的连续旋转。
常见的欧拉角包括俯仰角(pitch)、横滚角(roll)和偏航角(yaw)。
六轴传感器通常通过三个加速度计和三个陀螺仪测
量这三个角度。
通过积分陀螺仪输出的角速度,再通过积分加速度计输出的角度,即可得到六轴传感器的姿态。
2. 四元数解算:
四元数解算方法使用四维复数表示三维物体的旋转。
四元数可以用来表示旋转轴和旋转角度,并且可以用于旋转的插值和积分。
四元数解算方法通常使用陀螺仪测量的角速度来更新四元数,然后将四元数转换为欧拉角或旋转矩阵来获取六轴传感器的姿态。
这两种解算方法在实时应用中各有优劣。
欧拉角解算方法简单易懂,但容易受到万向锁(gimbal lock)等问题的影响,而四
元数解算方法相对更复杂,但可以更好地处理旋转连续性和插值等问题。
具体使用哪种方法需要根据实际应用的需求和限制来决定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
// //三阶近似算法
// float delta2 = (gx*gx + gy*gy + gz*gz)*T*T;
// q0 = q0_last*(1-delta2/8) + (-q1_last*gx - q2_last*gy - q3_last*gz)*T*(0.5 - delta2/48);
// q0 = q0_last*(1 - delta2/8 + delta2*delta2/384) + (-q1_last*gx - q2_last*gy - q3_last*gz)*T*(0.5 - delta2/48);
// q1 = q1_last*(1 - delta2/8 + delta2*delta2/384) + ( q0_last*gx + q2_last*gz - q3_last*gy)*T*(0.5 - delta2/48);
*******************************************************************************/
void Get_Eulerian_Angle(struct _out_angle *angle)
{
angle->pitch = -atan2(2.0f*(q0*q1 + q2*q3),q0*q0 - q1*q1 - q2*q2 + q3*q3)*Radian_to_Angle;
// //二ቤተ መጻሕፍቲ ባይዱ近似算法
// float delta2 = (gx*gx + gy*gy + gz*gz)*T*T;
// q0 = q0_last*(1-delta2/8) + (-q1_last*gx - q2_last*gy - q3_last*gz)*halfT;
// q1 = q1_last*(1-delta2/8) + ( q0_last*gx + q2_last*gz - q3_last*gy)*halfT;
// 描述:
// 必须定义'halfT '为周期的一半,以及滤波器的参数Kp和Ki
// 四元数'q0', 'q1', 'q2', 'q3'定义为全局变量
// 需要在每一个采样周期调用'IMUupdate()'函数
// 陀螺仪数据单位是弧度/秒,加速度计的单位无关重要,因为会被规范化
// ==================================================================================
ex = ay*vz - az*vy;
ey = az*vx - ax*vz;
ez = ax*vy - ay*vx;
//误差累积,已与积分常数相乘
exInt = exInt + ex*Ki;
eyInt = eyInt + ey*Ki;
ezInt = ezInt + ez*Ki;
// q2 = q2_last*(1-delta2/8) + ( q0_last*gy - q1_last*gz + q3_last*gx)*halfT;
// q3 = q3_last*(1-delta2/8) + ( q0_last*gz + q1_last*gy - q2_last*gx)*halfT;
/******************************************************************************
函数原型: void Get_Eulerian_Angle(struct _out_angle *angle)
功 能: 四元数转欧拉角
az = az * norm;
//估计重力加速度方向在飞行器坐标系中的表示,为四元数表示的旋转矩阵的第三行
vx = 2*(q1*q3 - q0*q2);
vy = 2*(q0*q1 + q2*q3);
vz = q0*q0 - q1*q1 - q2*q2 + q3*q3;
//加速度计读取的方向与重力加速度方向的差值,用向量叉乘计算
float q1_last = q1;
float q2_last = q2;
float q3_last = q3;
//把加速度计的三维向量转成单位向量
norm = invSqrt(ax*ax + ay*ay + az*az);
ax = ax * norm;
ay = ay * norm;
// 变量定义
float q0 = 1, q1 = 0, q2 = 0, q3 = 0; // 四元数
float exInt = 0, eyInt = 0, ezInt = 0; // 误差积分累计值
// ==================================================================================
// 函数原型:void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
// 功 能:互补滤波进行姿态解算
// 输 入:陀螺仪数据及加速度计数据
// ==================================================================================
q1 = q1_last + ( q0_last*gx + q2_last*gz - q3_last*gy)*halfT;
q2 = q2_last + ( q0_last*gy - q1_last*gz + q3_last*gx)*halfT;
q3 = q3_last + ( q0_last*gz + q1_last*gy - q2_last*gx)*halfT;
// q1 = q1_last*(1-delta2/8) + ( q0_last*gx + q2_last*gz - q3_last*gy)*T*(0.5 - delta2/48);
// q2 = q2_last*(1-delta2/8) + ( q0_last*gy - q1_last*gz + q3_last*gx)*T*(0.5 - delta2/48);
#define Kp 90.0f // 比例常数
#define Ki 0.001f // 积分常数
#define halfT 0.0005f//半周期
#define T 0.001f // 周期为1ms
// ==================================================================================
angle->roll = asin (2.0f*(q0*q2 - q1*q3))*Radian_to_Angle;
Angle.pitch = angle->pitch;
Angle.roll = angle->roll;
Angle.yaw = out_angle.yaw;
}
// q3 = q3_last*(1-delta2/8) + ( q0_last*gz + q1_last*gy - q2_last*gx)*T*(0.5 - delta2/48);
// //四阶近似算法
// float delta2 = (gx*gx + gy*gy + gz*gz)*T*T;
out_angle.yaw = atan2(2 * q1 * q2 + 2 * q0 * q3, -2 * q2*q2 - 2 * q3* q3 + 1)* 57.3;
}
//Pitch是围绕X轴旋转,也叫作俯仰角
//roll是围绕Y轴旋转,也叫作翻滚角
//yaw是围绕Z轴旋转,也叫作偏航角
//用叉积误差来做PI修正陀螺零偏,即抵消陀螺读数中的偏移量
gx = gx + Kp*ex + exInt;
gy = gy + Kp*ey + eyInt;
gz = gz + Kp*ez + ezInt;
//一阶近似算法
q0 = q0_last + (-q1_last*gx - q2_last*gy - q3_last*gz)*halfT;
#include "IMU.h"
#include "math.h"
#include "Maths.h"
// ==================================================================================
//加Q: 4 4 8 2 2 2 46 5 讨论
void IMUupdate(float gx, float gy, float gz, float ax, float ay, float az)
{
float norm;
float vx, vy, vz;
float ex, ey, ez;
//四元数积分,求得当前的姿态
float q0_last = q0;
