张拉整体梭型结构及其MATLAB构型程序
全张拉结构,先进大跨结构概念与实例简介PPT

加拿大卡尔加里体育馆是北美冰球职业联赛卡尔加里 火焰队主场,于1983年竣工,曾举行过1988年冬季奥运 会的滑冰与冰球比赛项目。屋面结构 为鞍形索网结构。
(3)张拉膜结构
• 膜结构是以性能优良的织物为材料,利用柔性拉 索或刚性骨架将膜面绷紧,也可向膜内充气来支 承膜面,从而形成具有一定刚度并能覆盖较大空 间的结构体系。 • 膜结构可分为张拉膜结构和充气膜结构。 • 张拉膜结构是利用柔性钢索或刚性支承结构使膜 产生一定的预张力,从而形成具有一定刚度来承受 自重与外荷载的结构。 • 张拉膜结构包括悬挂膜结构,索膜结构,骨架支 撑膜结构。
(4)索杆结构
• 索杆结构是由铰接二力杆和索单元构成的结构体系,多用 于点支式玻璃幕墙结构支承体系。 • 其中张拉整体结构(全张力结构)是索杆结构的一个特例, 它由连续的拉索与不连续的压杆组成的自平衡结构体系。 • 索穹顶结构是在吸收了大量张拉整体结构体系研究成果的 基础上发展起来。迄今为止应用与实际工程张拉整体体系 的是周边支承于受压环梁上的索弯顶结构。 • 从结构的观点看,索穹顶结构体系是一种受力合理,结构 效率高的结构体系。它由连续的拉索和不连续的压杆组成, 完全体现了Fuller关于“压杆的孤岛存在于拉杆的海洋中 的思想”。
2.张拉结构适应性(以膜结构为例) (1)场所适应性
膜结构在空间和平面布局上的高度灵活性,使其往往与 特定的自然或城市环境极其自然地融为一体。
(2)空间适应性
膜结构能提供灵活可变的空间形状,满足使用者功能需 求。
(3)形态适应性
膜通过张拉具有多种艺术形态,具有极强的个性与表 现力,符合使用者的审美要求。
对第二条特点
单层轴对称无预应力悬索屋面
单层马鞍面车辐式张拉结构
单层轴对称无预应力悬索结构是一种可变体系,平衡形式随荷载 分布形式而变。为使单层悬索体系屋盖具有必要的稳定性,一般采用 重屋盖。而单层辐射状式张拉结构形式,悬索始终保持较大的张紧力, 提高其稳定性,使轻型屋盖的运用有了可能性。
张拉整体三棱柱几何作图法找形与找力

A b s tra c t The mechanics and the geometry are inextricably linked. A geometric drawing method can be used to find the form of a triangular prism of tensegrity structure with two parallel end faces, as well as to find the self-equilibrium forces in the triangular prism of tensegrity. The formulae for calculating the force density of self-equilibrium internal forces in triangular prism of tensegrity are derived. The geometric drawing method for form-finding and force-finding is simple in operating, intuitive and adjustable. The method can be implemented in the CAD software, and even can produce drawings on the paper. The formulae of the force density of self-equilibrium internal forces are simple and can be expressed visually. The form finding method is the geometric implementation of the force density method. K e y w ords triangular prism of tensegrity, form-finding,force-finding, force density method,geometric drawing method
四节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释

四节点四边形单元悬臂梁的matlab有限元编程-概述说明以及解释1.引言1.1 概述悬臂梁是一种常见的结构形式,在工程领域中被广泛应用。
四节点四边形单元是有限元分析中常用的元素类型,能够准确地模拟悬臂梁的受力情况。
Matlab是一种强大的数学工具,可以用来编程实现有限元分析。
本文旨在介绍如何利用Matlab进行四节点四边形单元悬臂梁的有限元编程,并对其进行分析和展望。
通过本文的研究,我们希望能够为工程实践提供一定的参考和指导,同时也为进一步的研究提供基础。
1.2 文章结构本文主要分为三个部分:引言、正文和结论。
引言部分将介绍文章的背景和目的,明确文章研究的问题和意义。
正文部分包括理论基础、Matlab有限元编程介绍和四节点四边形单元悬臂梁建模三个小节。
其中,理论基础将介绍与悬臂梁有关的理论知识,Matlab有限元编程介绍将详细介绍如何使用Matlab进行有限元分析,最后,四节点四边形单元悬臂梁建模将展示具体的悬臂梁建模过程。
结论部分将对实验结果进行分析与总结,探讨本研究的意义和潜在研究方向。
1.3 目的本文旨在利用Matlab编程实现四节点四边形单元悬臂梁的有限元分析,通过建立合适的数学模型,探索悬臂梁在受力状态下的力学特性。
具体目的包括:1. 建立悬臂梁的有限元数学模型,包括节点、单元和材料参数的设置;2. 实现悬臂梁在不同受力情况下的应力、应变、位移等力学性能的计算;3. 分析悬臂梁受力情况下的应力分布情况,探讨悬臂梁的破坏模式和极限承载能力;4. 验证Matlab编程方法的有效性和准确性,为工程实际中悬臂梁等复杂结构的有限元分析提供参考和借鉴。
通过本文的研究,旨在为工程实践提供可靠的数值计算工具和理论分析方法,为解决工程结构强度和稳定性问题提供一定的指导和参考价值。
2.正文2.1 理论基础在介绍四节点四边形单元悬臂梁的Matlab有限元编程之前,我们首先需要了解一些基本的理论知识。
悬臂梁是一种常见的结构形式,在工程领域中广泛应用于桥梁、建筑物等领域。
张拉整体结构外力与形变间关系分析及实验验证

衡 状态 的力学模型 , 对 非保 守力作用下张拉整体 结构 弹簧 的变形 量进行 了计算 ; 然后, 通过 三杆 六索张拉
整 体 结 构样 机 实 验 , 对 弹簧 变形 量进 行 了测 量 . 实验 与计 算结果 的对 比分析 , 验 证 了 张拉 整 体 结 构 力 学 模
型 的合 理 性 , 揭 示 了外 力 与 形 变 间 的 内在 数 学 关 系.
张拉 整 体 结 构 外 力 与形 变 问关 系 分析 及 实 验 验 证
李 团 结 , 车 明 奎
( 西安 电 子 科技 大 学 机 电工 程 学 院 , 陕 西 西安 7 1 0 0 7 1 )
摘 要 :针 对 张拉 整体 结 构 中杆 件 只 受轴 向压 力 , 绳 索和 弹簧 等 只 受 轴 向拉 力 的 情 况 , 采 用 拉 格 朗 日动 力 学 和样机 实验 , 对 外 力 作 用 下 张拉 整体 结 构 中弹 簧 变 形 量 进 行 了分 析 和 测 量. 首先, 推 导 了张 拉 整 体 结 构 平
s t r u c t u r e u n d e r t h e a c t i o n o f e x t e r n a l n o n c o n s e r v a t i v e f o r c e s i s a n a l y z e d .Th e n.b y me a n s o f t h e p r o t o t y p e
Ab s t r a c t : Th e t e n s e g r i t y s t r u c t u r e s s u f f e r t h e a x i a l p r e s s u r e i n s t r u t s a n d t h e a x i a l t e n s i o n i n c a b l e s a n d
matlab 在结构力学中的应用

Matlab在结构力学中的应用马晓光,于国清(白城师范学院机电系,白城师范学院土木系)摘要本文结合实例,介绍了Matlab在结构力学计算中的应用方法,展示了Matlab在结构有限元编程中的简捷性与高效性。
本文介绍的方法,在结构有限元计算中具有普遍的适用性。
关键词Matlab 有限元编程APPLICATION OF MATLAB IN STRUCTURAL MECHANICSMa Xiaoguang,Yu Guoqing( Baicheng Normal College, Baicheng Jilin 137000, China )Abstract This paper introduces a method of application of Matlab in structural FEM, taking a continuous beam as an example. The method indicates the neatness and high efficiency of Matlab in programming a structural FEM and can be applied to many kinds of structures.Keywords FEM; Matlab; programming;1引言Matlab既是强大的数学软件,又是一种简洁、高效的科技编程语言,这一点在结构力学有限元计算中得到了充分的体现。
Matlab最突出的特点就是处理矩阵的各种运算,而大量的矩阵运算正是结构有限元计算非常需要的。
此外,利用Matlab的绘图功能,还可直接绘出结构的内力图。
因此,Matlab 对于结构力学计算是十分有利的工具。
2MATLAB编程实例图1为三跨连续梁,设E=210Gpa, I=50×10-6m4。
计算梁的内力,并画出梁的弯矩图。
该结构可以用三弯矩方程求解,也可以用矩阵位移法求解。
matlab连续梁程序的编制与使用Word文档
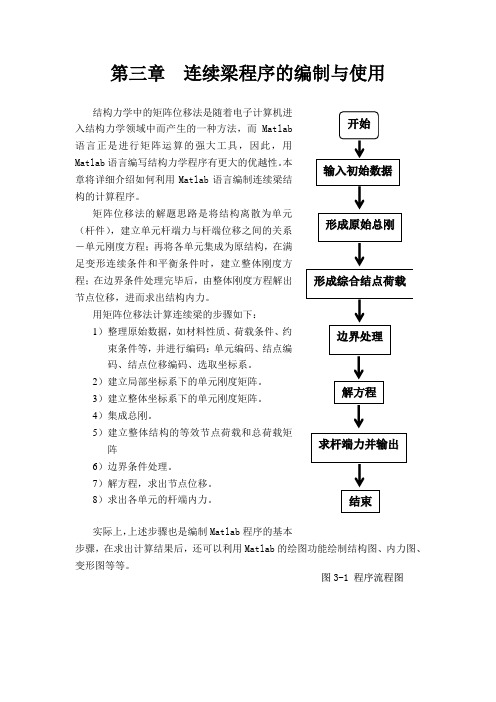
第三章连续梁程序的编制与使用入结构力学领域中而产生的一种方法,而Matlab语言正是进行矩阵运算的强大工具,因此,用Matlab语言编写结构力学程序有更大的优越性。
本章将详细介绍如何利用Matlab语言编制连续梁结构的计算程序。
矩阵位移法的解题思路是将结构离散为单元(杆件),建立单元杆端力与杆端位移之间的关系-单元刚度方程;再将各单元集成为原结构,在满足变形连续条件和平衡条件时,建立整体刚度方程;在边界条件处理完毕后,由整体刚度方程解出节点位移,进而求出结构内力。
用矩阵位移法计算连续梁的步骤如下:1)整理原始数据,如材料性质、荷载条件、约束条件等,并进行编码:单元编码、结点编码、结点位移编码、选取坐标系。
2)建立局部坐标系下的单元刚度矩阵。
3)建立整体坐标系下的单元刚度矩阵。
4)集成总刚。
5)建立整体结构的等效节点荷载和总荷载矩阵6)边界条件处理。
7)解方程,求出节点位移。
8)求出各单元的杆端内力。
实际上,上述步骤也是编制Matlab程序的基本步骤,在求出计算结果后,还可以利用Matlab的绘图功能绘制结构图、内力图、变形图等等。
图3-1程序流程图3.1 程序说明%******************************************************************* % 矩阵位移法解连续梁主程序%******************************************************************* ●功能:运用矩阵位移法解连续梁的基本原理编制的计算主程序。
●基本思想:结点(结点位移)编码默认为从左至右,从1开始顺序进行;杆端弯矩的方向默认为逆时针。
●荷载类型:可计算结点荷载,每单元作用的跨中集中力和均布荷载。
●说明:主程序的作用是通过赋值语句、读取和写入文件、函数调用等完成算法的全过程,即实现程序流程图的程序表达。
%-----------------------------------------------------------------------------------------------------1 程序准备format short e %设定输出类型clear all %清除所有已定义变量clc %清屏●说明:format short e -设定计算过程中显示在屏幕上的数字类型为短格式、科学计数法;clear all -清除所有已定义变量,目的是在本程序的运行过程中,不会发生变量名相同等可能使计算出错的情况;clc -清屏,使屏幕在本程序运行开始时%-----------------------------------------------------------------------------------------------------2 打开文件FP1=fopen('input.txt','rt'); %打开输入数据文件存放初始数据FP2=fopen('output.txt','wt'); %打开输出数据文件存放计算结果●说明:FP1=fopen('input.txt','rt'); -打开已存在的输入数据文件input.txt,且设置其为只读格式,使程序在执行过程中不能改变输入文件中的数值,并用文件句柄FP1来FP2=fopen('output.txt','wt'); -打开输出数据文件,该文件不存在时,通过此命令创建新文件,该文件存在时则将原有内容全部删除。
matlab混凝土张力本构模型

matlab混凝土张力本构模型混凝土是一种常见的建筑材料,其力学性能的研究对于建筑结构的设计和安全具有重要意义。
混凝土的张力本构模型是描述混凝土在拉伸过程中应力和应变关系的数学模型。
在matlab中,可以通过编写程序来实现混凝土张力本构模型的计算和分析。
混凝土的张力本构模型通常采用双曲线模型或抛物线模型。
其中,双曲线模型是最常用的模型之一。
该模型假设混凝土在拉伸过程中的应力和应变关系可以用以下公式表示:σ = fct(ε) = fct0 + (fct1 - fct0) * (1 - exp(-ε/ε0))其中,σ表示混凝土的应力,ε表示混凝土的应变,fct0和fct1分别表示混凝土的初始强度和极限强度,ε0表示混凝土的应变硬化系数。
在matlab中,可以通过编写函数来实现混凝土张力本构模型的计算。
以下是一个示例程序:function [sigma] = fct(epsilon)% 双曲线模型fct0 = 0.8; % 初始强度fct1 = 3.5; % 极限强度epsilon0 = 0.002; % 应变硬化系数sigma = fct0 + (fct1 - fct0) * (1 - exp(-epsilon/epsilon0));end通过调用该函数,可以计算混凝土在不同应变下的应力值。
例如,当应变为0.001时,应力为1.6;当应变为0.002时,应力为2.3;当应变为0.003时,应力为2.8。
混凝土的张力本构模型在建筑结构的设计和安全评估中具有重要作用。
通过使用matlab编写程序,可以方便地计算混凝土在不同应变下的应力值,为建筑结构的设计和安全提供有力支持。
张拉整体棱柱结构的拓扑构型(圆柱型结构到圆环型结构)

S3q s3q1 s3q2 s3qi s3qn 3n ,i [1, n]
张拉整体棱柱结构中全部第二类竖索可以表示为,
(26)
S3 S31 S32 S3q S3m2
3n(m 2)
, q [1, m 2]
(27)
对于第 q∈[1,m-2]层第二类竖索, 该层索的索矩阵可以表示为节点矩阵与常数矩阵相乘 的形式,即
S1k s1k1 s1k 2 s1kp s1k,2n 32n , p [1, 2n]
张拉整体棱柱结构中所有的鞍索可以表示为
(11)
S1 S11 S12 S1k S1m1 32n(m1) , k [1, m 1]
(12)
对于第 k∈[1,m-1]层鞍索, 该层鞍索的索矩阵可以表示为节点矩阵与常数矩阵相乘的形 式,即
第m单元
第i单元
鞍索
竖索
第2单元 鞍索
第1单元
(a)理论模型
第m单元
第m-1单元
第4单元
第3单元 第二类竖索 第2单元 s12n 第1单元 n111 b11 s31 n211 s11 s21 n112 n2 s2n+1 12 b12 s22 n113 s32 s12 n2 s1n+2 13 b13 s33 n21,n-1 s13 s2n-2 n11,n-1 b1,n-1s2n-1 n11n s1n-1 s3n-1 n2 s12n-1 1n b1n s2n s3n s1n 第二类竖索 鞍索
右旋棱柱的上水平索和左旋棱柱的下水平索全部去掉重新组合(如图 2 所示) ,同时,增加 同时连接两个棱柱结构节点的辅助索(如图 2 细虚线所示)以保持结构的平衡和稳定性。拓 扑完成后的结构由 2 个张拉整体棱柱单元组成, 每个张拉整体单元分别有 4 根压杆, 将该结 构命名为 2 层 4 杆张张拉整体棱柱结构。 在 2 层 4 杆张拉整体棱柱结构的基础上, 沿其轴向继续增加单元棱柱结构, 仍按如前所 述方法进行单元棱柱结构的连接,同时结构中相邻单元压杆的旋向相反,最终可获得多层 4 杆张拉整体棱柱结构。
4杆张拉整体机器人单步驱动方式分析

ऐഗටरຍ4杆张拉整体机器人单步驱动方式分析Analysis for driving the 4-bar tensegrity robot to roll 田云峰1,罗阿妮2,刘贺平2TIAN Yun-feng1, LUO A-ni2, LIU He-ping2(1.中国空空导弹研究院,洛阳 471000;2.哈尔滨工程大学 机电学院,哈尔滨 150001)摘 要:基于4杆张拉整体结构,一种4杆张拉整体机器人被提出。
此机器人是通过变形来实现整体翻滚和移动。
首先分析4杆张拉整体结构的结构特点,提出了将其转化为张拉整体机器人的方法,并对其运动方式进行了初步分析。
而后利用仿真分析,研究了其单步驱动方式。
最后,根据三种单步驱动方式的组合,探讨了机器人向预定目标运动的方法。
关键词:张拉整体结构;张拉整体机器人;变形;翻滚;驱动方案;对角索。
中图分类号:TP242 文献标识码:A文章编号:1009-0134(2019)07-0093-050 引言张拉整体结构的定义是由不连续的受压杆构件和连 续的受拉绳索构件组成的索杆张拉结构[1,2],其概念最早 由Fuller[3,4]和Snelson[5]在上世纪首先提出。
张拉整体结 构中,所有构件只承受轴向力,整体质量较轻。
受拉的 绳索构件彼此相连,组成一个索网结构,由受压杆构件 从内部支撑,形成预期的空间形状。
由于杆构件彼此间 不接触,整体结构具有一定的弹性,这样既能对外界冲 击有一定的缓冲作用,又能够对其内部有一定的保护作 用。
结构所承受的外力能够被分配到所有构件,避免了 载荷对局部的集中影响。
这是由于张拉整体结构的这些 特点,使得其一直受到各行业研究人员的关注。
近些年来,一些研究人员尝试着把张拉整体结构应 用于机器人领域。
在张拉整体机器人的研究中,六杆球 形机器人是绝对的研究热点。
“超级球”,即六杆球 形机器人,是NASA艾姆斯研究中心的智能机器人组和 动态张拉力机器人实验室的一个正在进行的项目,其目 的是要将此机器人用于太空探索任务[6~8]。
机械优化大作业-MATLAB复合型法

机床主轴机构优化设计机床主轴是机床中重要的零件之一,一般多为支撑空心阶梯轴。
为了便于使用材料力学进行结构分析,常常将阶梯轴简化成以当量直径表示的等截面轴。
如图0.1所示是一个已经简化处理的专用机床双主轴的力学模型。
从机床主轴制造成本较低和加工精度较高的要求出发,需要考虑主轴的自重和外身段挠度这样两个重要因素。
对于专用机床来说,并不追求过高的加工精度。
因此选取零件自身重量轻为设计目标,将主轴的刚度作为约束条件。
一、设计变量和目标函数当主轴的材料选定之后,与主轴重量设计方案有关设计变量主轴的外径D、孔径d、两支承跨度l、和外伸段长度a,如图0.1所示。
由于机床主轴的孔径主要取决于待加工棒料的直径,不能作为设计变量处理。
因此,设计变量为机床主轴重量最轻优化设计目标函数为二、约束条件1.刚度性条件机床的加工质量在很大程度上取决于主轴的刚度,主轴刚度是一个很重要的性能指标。
因此,要求主轴悬臂端挠度不超过给定的变形量y 0 。
根据材料力学可知,主轴悬臂端挠度为)()()(44231232d x E 3x x Fx 64EJ 3a l Fa y -+=+=π式中,)(44d -D 64J π=是空心主轴的惯性矩;E=2.1x105MPa 是主轴的弹性模量;F 是作用主轴外伸端的力。
整理得到主轴刚度的约束条件为0d x E 3x x Fx 64X g 442312301≥-+-=)()()(πy2.设计边界条件三个设计变量的边界约束条件为max min l l l ≤≤max min D D D ≤≤maxmin a a a ≤≤3.具体算例已知某机床主轴悬臂端受到的切削力F=15000N ,主轴内径d=30mm ,悬臂端许用挠度y 0=0.05mm 。
要求主轴两支承跨度mm lmm 650300≤≤,外径mm D mm 14060≤≤,悬臂长度mm a mm 15090≤≤。
建立优化的数学模型)30)((7854.0)(22231++=x x x X fTT a D l x x x X ],,[],,[321==0)30()(7009.91)(..44231231≥-+⨯-=x x x x X g t s01300/)(12≥-=x X g0650/1)(13≥-=x X g0160/)(24≥-=x X g0140/1)(25≥-=x X g0190/)(36≥-=x X g0150/1)(37≥-=x X g4.基于matlab 程序的复合形法实现优化(1)算法原理复合形法来源于无约束优化问题的单纯形法,通过构造复合形来求得最优解,新的复合形通过替换旧的复合形中的坏点(目标函数最大或次大的点)得到,替换方式仍是单纯性法中的反应、压缩、扩展这几个基本方法。
AutoLISP实现张拉整体索穹顶优化设计程序前处理模块

AutoLISP实现张拉整体索穹顶优化设计程序前处理模块霍俊芳;曹喜
【期刊名称】《内蒙古工业大学学报(自然科学版)》
【年(卷),期】2004(023)002
【摘要】本文通过对Aut0LISP的组码(DXF文件)进行深入细致的分析和研究,成功地提取出实体的信息,生成张拉整体索穹顶优化设计所需的数据文件,完成了程序系统的前处理模块.最后进行了算例分析.
【总页数】4页(P133-136)
【作者】霍俊芳;曹喜
【作者单位】内蒙古工业大学建筑工程学院,呼和浩特,010062;内蒙古工业大学建筑工程学院,呼和浩特,010062
【正文语种】中文
【中图分类】TU311.41
【相关文献】
1.张拉整体索穹顶结构找形分析 [J], 张娜;牛少儒
2.张拉整体索穹顶结构优化设计程序系统的后处理模块的设计 [J], 曹喜;郝员洪
3.张拉整体单元结构特性及其构成索穹顶的方法 [J], 傅丰
4.张拉整体索穹顶结构成型方法的试验研究 [J], 王帆;郭正兴;胡云霞
5.张拉整体索穹顶结构的预应力优化设计 [J], 李红果;张爱国
因版权原因,仅展示原文概要,查看原文内容请购买。
张拉整体结构非线性有限元找形的研究

4.2 温度荷载施加应变法
有时虽然张拉整体结构较简单,但是张拉整体结构形状不规则,用 4.1 方法找形往往不
-4-
收敛,这时用温度施加应变则能成功找形。此方法和 4.1 方法的区别是通过施加温度荷载 施加应变,而非直接施加应变。温度荷载逐步加载,则可实现应变逐步变化。每增加一个 荷载步找形一次,直至荷载达到预定荷载大小。
(3)
式中,{∆ε L }为线性应变增量,{∆ε NL }为非线性应变增量,[B] 为几何矩阵。由于大变形
问题中 [B] 是{∆de }的函数,因而 [B] 是非线性的,为方便表示,可以写成
[B] = [BL ]+ [BNL ]
(4)
式中,[BL ]为线性几何矩阵,[BNL ]为非线性几何矩阵。令δ {de }为单元节点虚位移向量,
实现此过程的最简单的方法就是增加辅助的杆单元,每次找形结束后减小辅助单元的 弹性模量然后再进行找形,重复这一操作,直到辅助单元的弹性模量足够小。辅助单元最 好根据工程经验添加,加入辅助单元后,结构形成一静定或超静定结构,只要控制得当一 般结构都能找形成功。
下面是一双层 SVD 张拉整体结构找形的例子:如(图 3)所示,与 1、2、3 节点位端 点的杆单元为辅助杆单元。
⎡ 1 0 0 −1 0 0⎤
⎢ ⎢
0
00
0
0 0⎥⎥
∫ K Le =
BLT EBL dv
=
Ac E x2
⎢0 ⎢⎢− 1
0 0
0 0
0 1
0 0⎥ 0 0⎥⎥
⎢ 0 0 0 0 0 0⎥
⎢
⎥
⎢⎣ 0 0 0 0 0 0⎥⎦
⎡ 1 0 0 −1 0 0 ⎤
⎢ ⎢
matlab优化工具箱使用方法PPT课件

第17页/共73页
只用于大型算法的参数: l Hessian – 用户定义的目标函数的Hessian矩阵。 l HessPattern – 用于有限差分的Hessian矩阵的 稀疏形式。若不方便求fun函数的稀疏Hessian矩阵 H,可以通过用梯度的有限差分获得的H的稀疏结 构(如非零值的位置等)来得到近似的Hessian矩 阵H。若连矩阵的稀疏结构都不知道,则可以将 HessPattern设为密集矩阵,在每一次迭代过程中, 都将进行密集矩阵的有限差分近似(这是缺省设 置)。这将非常麻烦,所以花一些力气得到 Hessian矩阵的稀疏结构还是值得的。
v (3 2x)2 x
现在要求在区间(0,)上确定一个x,使 最大化。因为优化工具箱中要求目标函数 最小化,所以需要对目标函数进行转换, 即要求 最小化。
9
第9页/共73页
首先编写M文件 opt21_3o.m: function f = myfun(x) f = -(3-2*x).^2 * x; 然后调用fminbnd函数(磁盘中M文件名 为opt21_3.m): x = fminbnd(@opt21_3o,0,1.5)
2
第2页/共73页
x = fminbnd(fun,x1,x2,options,P1,P2,...)提供另外 的参数P1,P2等,传输给目标函数fun。如果没有设 置options选项,则令options=[]。
[x,fval] = fminbnd(...)返回解x处目标函数的值。
[x,fval,exitflag] = fminbnd(...)返回exitflag值描 述fminbnd函数的退出条件。
18
第18页/共73页
l MaxPCGIter – PCG迭代的最大次数。 l PrecondBandWidth – PCG前处理的上带宽,缺 省时为零。对于有些问题,增加带宽可以减少迭代 次数。 l TolPCG – PCG迭代的终止容限。 l TypicalX – 典型x值。 只用于中型算法的参数: l DerivativeCheck – 对用户提供的导数和有限差 分求出的导数进行对比。 l DiffMaxChange – 变量有限差分梯度的最大变化。 l DiffMinChange - 变量有限差分梯度的最小变化。 l LineSearchType – 一维搜索算法的选择。
matlab计算平面杆系的支反力程序

matlab计算平面杆系的支反力程序平面杆系的支反力是结构力学中重要的概念之一,通过计算支反力,我们可以了解杆系在各个支点上所受的力的大小和作用方向。
本文将介绍如何利用Matlab进行平面杆系的支反力计算。
首先,我们需要明确平面杆系的几何形状和受力情况。
平面杆系是由多根杆件和多个支点组成的结构,每根杆件都有一定的长度和质量,同时还会受到外部力的作用,如重力等。
在计算支反力之前,我们需要先确定杆件的几何参数和材料特性。
在利用Matlab进行支反力计算之前,我们首先需要构建一个表示平面杆系的模型。
可以使用Matlab的矩阵和向量来表示杆件的节点、长度、质量、材料特性等信息。
通过建立约束方程和平衡方程,我们可以将杆系的受力情况转化为一个线性方程组。
对于平面杆系的支反力计算,常用的方法有静力学方法和力矩平衡法。
静力学方法是通过平衡方程来求解支反力,而力矩平衡法则是通过考虑力矩平衡关系来计算支反力。
在Matlab中,我们可以使用线性代数的方法来求解线性方程组。
利用Matlab的线性代数工具箱中的函数,我们可以方便地求解支反力。
这些函数包括求解线性方程组的函数、计算矩阵转置的函数等。
在进行计算之前,我们首先需要将平面杆系的几何形状和受力情况转化为数学模型。
通过建立几何方程和力平衡方程,我们可以得到一个包含未知量的线性方程组。
利用Matlab的线性代数工具箱,我们可以方便地求解这个线性方程组,得到平面杆系的支反力。
在编写Matlab程序时,我们需要考虑代码的可读性和可维护性。
良好的程序结构和注释是非常重要的,可以帮助我们更好地理解代码,并且便于以后的修改和维护。
总结起来,通过Matlab计算平面杆系的支反力是一项复杂的任务,但是通过良好的建模和利用Matlab强大的计算能力,我们可以准确地求解平面杆系的支反力,为结构设计和分析提供重要的依据。
通过编写可读性强且注释详细的Matlab程序,我们可以更好地理解和应用这个计算过程,为工程实践提供有指导性的意义。
有限元节点往棱边转化matlab程序

有限元节点往棱边转化matlab程序下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!并且,本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!有限元分析是工程领域中常用的一种数值计算方法,通过将结构划分为多个小单元(有限元),然后对每个小单元进行独立的力学分析,最终得到整个结构的应力、应变和变形情况。
Matlab在张拉膜结构力密度找形法中的应用

—250— Matlab 在张拉膜结构力密度找形法中的应用卢迎华,王 璠,刘人怀,杜 冰(暨南大学力学与土木工程系,广州 510632)摘 要:找形分析(Form-finding)是张拉膜结构分析中最基本也是最难解决的问题。
文章应用Matlab 软件,根据力密度找形原理编制了相应的计算程序,并进行了工程的实例分析,说明了Matlab 在张拉膜力密度法找形分析中是一个快速、方便、而且有效的工具,可以应用于大型复杂柔性结构体系的找形分析。
关键词:Matlab ;张拉膜;力密度;找形Application of Matlab in Force Density Form-finding Method ofTensile Membrane StructureLU Yinghua, WANG Fan, LIU Renhuai, DU Bing(Department of Mechanics and Civil Engineering, Jinan University, Guangzhou 510632)【Abstract 】Form-finding methods are the most basic and difficult problem in the analysis of tensile membrane construction. This paper presents compile of programs about force density form-finding method and Matlab, relative calculation programs, and analyzes some structure engineering examples, puts forward the significant conclusion.【Key words 】Matlab; Tensile membrane; Force density; Form-finding计 算 机 工 程Computer Engineering 第32卷 第7期Vol.32 № 7 2006年4月April 2006·工程应用技术与实现·文章编号:1000—3428(2006)07—0250—03文献标识码:A中图分类号:TP311Matlab 是美国Mathworks 公司推出的一种集矩阵计算、数值计算、信号处理、数据统计分析、图形显示等多功能于一体的科学计算软件。
三杆张拉整体的结构刚度分析

三杆张拉整体的结构刚度分析罗阿妮;伍承旭;刘贺平【摘要】Three-bar tensegrity structure is the basis of tensegrity system.In order to better study the mechanical performance of tensegrity system,the factors that influence the stiffness of a three-bar tensegrity structure were in-vestigated in this study.Matlab software was utilized to establish the mathematical and finite-element models of the three-bar tensegrity structure in accordance with the structural theory of tensegrity.Numerical simulation calcula-tions were performed to obtain the pretightening force; the elastic modulus of material; and the effects of the section size of the structure on axial, radial, and torsional deformation under axial force and torque.The analysis of simu-lation data revealed that tensegrity structural stiffness is mainly influenced by pretightening force, followed by the e-lastic modulus of the materials and the sectional size of structural parts.Results provide theoretical support for the improvement of the stiffness of the tensegrity structure.%三杆张拉整体结构是张拉整体结构体系的基础,为了更好的研究张拉整体结构体系的力学性能,本文对三杆张拉整体结构刚度影响因素进行了研究.根据张拉整体的构型理论,利用Matlab软件编程,建立了三杆张拉整体结构的数学模型以及有限元模型.通过数值仿真计算,分析了在轴向力和扭矩作用下,预紧力、材料弹性模量以及构件截面尺寸对结构轴向、径向、扭转变形的影响.由仿真计算数据结果得出:对张拉整体结构刚度的主要影响因素是预紧力,而材料弹性模量、构件截面尺寸等影响因素次之,该结论为改善张拉整体结构刚度提供了一定的理论支持.【期刊名称】《哈尔滨工程大学学报》【年(卷),期】2017(038)009【总页数】6页(P1450-1455)【关键词】张拉整体;弹性刚度;几何刚度;预紧力;弹性模量;截面尺寸;平衡矩阵【作者】罗阿妮;伍承旭;刘贺平【作者单位】哈尔滨工程大学机电学院,黑龙江哈尔滨 150001;哈尔滨工程大学机电学院,黑龙江哈尔滨 150001;哈尔滨工程大学机电学院,黑龙江哈尔滨150001【正文语种】中文【中图分类】TU399Abstract:Three- bar tensegrity structure is the basis of tensegrity system. In order to better study the mechanical performance of tensegrity system,the factors that influence the stiffness of a three- bar tensegrity structure were investigated in this study. Matlab software was utilized to establish the mathematical and finite- element models of the three- bar tensegrity structure in accordance with the structural theory of tensegrity. Numerical simulation calculations were performed to obtain the pretightening force; the elastic modulus of material; and the effects of the section size of the structure on axial, radial, and torsional deformation under axial force and torque. The analysis of simulation data revealed that tensegrity structural stiffness is mainly influenced by pretightening force,followed by the elastic modulus of the materials and the sectional size of structural parts. Results provide theoretical support for the improvementof the stiffness of the tensegrity structure.Keywords:tensegrity structures; elastic stiffness; geometric stiffness; pretightening force; modulus of elasticity; sectional dimension; equilibrium matrix自上世纪60年代美国建筑师Fuller提出张拉整体的概念至今,凭借其优越的结构特性,已经成为研究热点之一。
运用Matlab优化函数对指定构型控制律的设计

运用Matlab优化函数对指定构型控制律的设计裴登洪【摘要】Matlab软件为应用现代控制理论进行控制律设计提供了强大、方便的工具.本文介绍了一种基于频域模型跟踪的控制增稳控制律的设计方法,即首先依据功能需要建立控制律的构型,然后按照GJB要求建立标准的模型,最后利用Matlab软件优化工具箱函数对控制律参数进行优化设计.【期刊名称】《教练机》【年(卷),期】2012(000)002【总页数】7页(P9-15)【关键词】控制律;Matlab;构型;优化【作者】裴登洪【作者单位】洪都航空工业集团,江西南昌330024【正文语种】中文电传飞行控制系统是上世纪60年代末发展起来的、对飞机进行主动控制的现代飞行控制技术。
第三代战斗机设计时运用了大量的空气动力学最新理论研究成果,摆脱了以往飞机气动设计时单一的“附着流”设计原则,大胆采用边条翼、翼身融合体布局、前缘机动襟翼等先进的气动布局,并为提高飞机在亚、跨音速的机动性和敏捷性,普遍放宽了飞机的静稳定性,甚至使飞机是静不稳定的,如果使用传统的机械式操纵系统,则根本无法解决飞机的稳定性问题,而采用电传飞控系统,使用计算机即可实现对飞机的主动控制。
电传飞行控制技术在70年代末、80年代初开始应用于作战飞机,由于技术先进,在当时研制难度较大、周期较长,因此研制成本较高。
直到90年代,随着电子技术特别是计算机技术的发展,以及新技术和新材料的应用,电传飞行控制系统可靠性大大提高,研制成本也逐渐降低。
电传飞行控制系统目前已得到广泛的应用,并成为第三代战斗机的典型标志之一。
电传飞行控制系统实现了驾驶员操纵指令与飞机运动参数响应相对应的控制,即由原来机械系统的舵面偏度的控制转换为对飞机响应的控制。
电传飞控系统的控制律设计与飞控系统的性能及飞行品质密切相关,是保证系统功能和飞机飞行品质的最直接、最重要的关键环节。
国内现有的控制律设计一般采用经典控制理论,在控制律设计过程中,首先根据飞控系统的功能确定控制律的基本构型,然后在飞机线性化的基础上,根据飞机的飞行品质要求和系统稳定储备要求在飞行全包线确定控制律的反馈参数以及补偿滤波器的参数。
