东南大学《工程矩阵理论》试卷样卷及答案(修改)1
2022年东南大学工程管理专业《管理学》科目期末试卷A(有答案)

2022年东南大学工程管理专业《管理学》科目期末试卷A(有答案)一、选择题1、决定是否与另一个组织合并,如何重组以提高效率,或是否关闭一个亏损的工厂,这些都是典型的()。
A.确定型决策 B.非程序化决策C.例常型决策 D.重复性决策2、当一个管理者组织制订公司战略以寻求企业进一步发展时,他扮演的管理角色是明茨伯格所说的()。
A.领导者 B.发言人C.企业家D.混乱驾驭者3、依据情景领导理论,当下属有能力但无意愿干领导希望他们干的工作时,以下哪种领导风格最为合适?()A.告知 B.推销 C.参与 D.授权4、管理中与激励问题有关的公平理论是由()提出的。
A.马斯洛B.麦格雷戈C.赫茨伯格D.亚当斯5、企业选择产业中的一个或者一组细分市场,制定专门的战略向此市场提供产品或者服务,这是典型的()。
A.增长型战略 B.别具一格战略 C.专一化战略 D.公司层战略6、关于计划的实际效果,许多管理学家都进行过仔细研究,其基本结论是()。
A.制定正式计划的组织比不制定正式计划的组织绩效要好B.制定正式计划的组织不一定就有好的绩效C.制定正式计划会降低组织的灵活性D.好的计划可以消除变化7、在不确定情况下,除了有限信息的影响之外,另一个影响决策结果的因素是()。
A.风险性 B.环境的复杂性C.决策者心理定位 D.决策的时间压力8、一家公司董事会通过决议,计划在重庆建立汽车制造厂,建设周期为一年,需完成基础建设、设备安装、生产线调试等系列工作,()技术最适合来协调各项活动的资源分配。
A.甘特图B.负荷图C.PERT网络分析D.线性规划9、当态度之间以及态度与行为之间存在任何不协调或不一致时,我们称之为()。
A.态度紊乱 B.认知失调C.知觉混乱D.晕轮效应10、管理者在制定决策时,面临这样一种条件:在这种条件下,决策者能够估计出每一种备择方案的可能性或者结果。
我们称这种决策制定条件为()决策。
A.确定性 B.不确定性 C.风险性 D.概率性二、名词解释11、组织变革12、程序化决策13、SWOT分析14、利益相关者15、人际关系角色16、组织17、团队结构18、强制权三、简答题19、1.解释为何学习管理史如此重要。
工程矩阵理论试题A

杭州电子科技大学研究生考试卷(A卷)课程名称:工程矩阵理论学院自动化考试日期2014年 12月 20日专业控制科学与工程班级任课教师姓名考生姓名学号(完整)成绩一、单项选择题(每题4分,共20分)1. 设AÎC m´n,对A的奇异值分解,下列说法正确的是:(1)存在且唯一(2)存在但不唯一(3)可能不存在(4)可能存在但不唯一2. 设AÎC n´n,则A的幂序列E,A,A2/2!, A k/k!, (1)收敛于零(2)发散(3)收敛与否与具体)收敛与否与具体A A有关(4)收敛3. 设AÎC n´n满足A3=E,则下列说法正确的是:(1)A的最小多项式与特征多项式相同(2)A不可对角化(3)A的约当标准型中约当块的数目为n(4)不能确定A是否可对角化4. 设A为n阶方阵,则有:(1)R(A) Å N(A)= C n , (2)R(A) + N(A)= C n(3)R(A) Å N(A T)= C n, (4)R(A T) Å N(A T)= C n5. 设A为n阶Hermite矩阵,则:(1)A的n个特征值全大于零(2)存在可逆矩阵P使得P H AP=E(3)存在正线上三角矩阵R使得A=R H R(4)存在酉矩阵U使得U H AU=L,其中L为实对角矩阵二、填空题(每题4分,共20分)1. 设e1, e2, e3为3维线性空间V的一组基,s是V到自身的一个线性变换。
s在基e1, e2, e3下的第1 页共2 页第 2 页 共 2 页 矩阵为úúúûùêêêëé333231232221131211a a a a a a a a a ,则s 在基e 3, 2e 2, 3e 1下的矩阵为。
2. 设方阵A 满足A 2 = 3A, 则sin (3A ) = 。
矩阵理论试题答案最终版

阵
G
为
(2, 2) (2, t + 1) (2, t 2 − 1) 2 (t + 1, 2) (t + 1, t + 1) (t + 1, t − 1) (t 2 − 1, 2) (t 2 − 1, t + 1) (t 2 − 1, t 2 − 1)
1 ∫−1 4dt 1 = ∫ 2*(t + 1)dt −1 1 ∫ 2*(t 2 − 1)dt −1 −8 4 8 3 10 −4 = 4 3 3 −8 −4 16 3 15 3
2
x ' −1 0 x 1 = + y ' 0 2 y −1 求多项式 P(x)经此仿射变换所得到的曲线,变换后的曲线是什么曲线? 解:(1)由平面的四个点我们可得如下方程。
a0 + a1 *1 + a2 *12 = 0 2 −1 a0 + a1 *(−1) + a2 *(−1) = 2 1 a0 + a1 * 2 + a2 * 2 = a + a *(−3) + a *(−3) 2 = 2 2 0 1
∫ ∫ ∫
1 −1 1
1
−1
2*(t + 1)dt
−1
(t 2 + 2t + 1)dt
(t + 1) *(t 2 − 1)dt
1 2 ∫−1 (t + 1) *(t − 1)dt 1 2 2 t dt t ( 1) *( 1) − − ∫−1
∫
1
−1
2*(t 2 − 1)dt
南京工业大学18-19矩阵论试题

南京工业大学 矩阵论 试卷2018 ---2019 学年第 2 学期 使用班级 研18班级 学号 姓名一.填空(03').1. 设V 是实数域上主对角线上的元素之和等于0的2阶方阵组成的线性空间,则它的维数是 ,一组基是 ,任一矩阵a c Ab a ⎛⎫= ⎪-⎝⎭在此基下的坐标是 。
2. 在欧氏空间4R 中,内积按通常定义,则向量 )3,2,2,1(=α 的长度为 ,向量)3,2,2,1(=α与)1,5,1,3(=β之间的夹角>=<βα, 。
3. 在20101[]{,}R x a a x a a R =+∈中定义内积:⎰-=11)()(),(dx x g x f g f ,则2[]R x 在区间[1,1]-上关于该内积的一个标准正交基为 1β= ,2β= 。
4. 设⎪⎪⎪⎭⎫ ⎝⎛-=501210101A ,则矩阵1—范数1A = ,矩阵无穷范数∞A = 。
5. 设矩阵130039A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,则A 的加号广义逆矩阵A += 。
二)01('(1)证明:)0,1,3(),2,3,6(),5,3,1(321===ααα是3R 的一组基 ;(2)求向量)1,7,3(=α在基321,,ααα下的坐标。
三)01('.设向量组:),0,3,0,3(),1,1,0,2(),1,2,0,1(321=-==ααα)1,3,1,4(),1,0,1,1(21==ββ 令),(),,,(2123211ββαααL V L V ==,求21V V +和12V V I 的维数及一组基。
四)01('在3R 中对任意123(,,)a a a α=,定义:123122313(,,)(,,23)a a a a a a a a a σ=++-(1)证明:σ是3R 上的线性变换;(2)求σ在基)1,0,0(),0,1,0(),0,0,1(321===εεε下的矩阵。
五(15)'.设V 为3维的线性空间,321,,ααα为V 的一组基,σ是V 上的线性变换,且31)(αασ=,22)(αασ=,13)(αασ=,求:(1)σ在基321,,ααα下的矩阵; (2)σ的特征值和特征向量;(3)在V 中能否选择适当的一组基,使得σ在这组基下的矩阵是对角阵?如果能,写出这组基及对角阵。
工程矩阵理论试题A
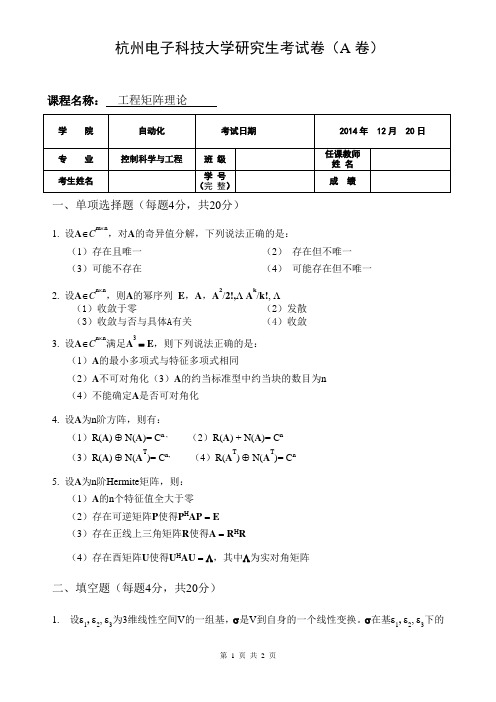
杭州电子科技大学研究生考试卷(A卷)课程名称:工程矩阵理论一、单项选择题(每题4分,共20分)1. 设A∈C m⨯n,对A的奇异值分解,下列说法正确的是:(1)存在且唯一(2)存在但不唯一(3)可能不存在(4)可能存在但不唯一2. 设A∈C n⨯n,则A的幂序列E,A,A2/2!, A k/k!,(1)收敛于零(2)发散(3)收敛与否与具体A有关(4)收敛3. 设A∈C n⨯n满足A3= E,则下列说法正确的是:(1)A的最小多项式与特征多项式相同(2)A不可对角化(3)A的约当标准型中约当块的数目为n(4)不能确定A是否可对角化4. 设A为n阶方阵,则有:(1)R(A) ⊕ N(A)= C n , (2)R(A) + N(A)= C n(3)R(A) ⊕ N(A T)= C n, (4)R(A T) ⊕ N(A T)= C n5. 设A为n阶Hermite矩阵,则:(1)A的n个特征值全大于零(2)存在可逆矩阵P使得P H AP=E(3)存在正线上三角矩阵R使得A=R H R(4)存在酉矩阵U使得U H AU=Λ,其中Λ为实对角矩阵二、填空题(每题4分,共20分)1. 设ε1, ε2, ε3为3维线性空间V的一组基,σ是V到自身的一个线性变换。
σ在基ε1, ε2, ε3下的矩阵为⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡333231232221131211a a a a a a a a a ,则σ在基ε3, 2ε2, 3ε1下的矩阵为。
2. 设方阵A 满足A 2= 3A, 则sin (3A ) = 。
3.矩阵A = diag 21312,,0203⎛⎫⎡⎤⎡⎤ ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭,则A 的最小多项式为 。
4. 设X = (x 1, x 2, , x n )T 为变向量,α = (a 1, a 2, , a n )T 为常向量,H = (h ij )n ⨯n 为常矩阵,则:,()=HX X XT D D。
5. 设A ∈C n ⨯n 为Hermite 矩阵,X ∈C n ,A 的n 个特征值为λ1,λ2, ,λn ,满足λ1 ≤ λ2 ≤ ≤ λn ,则: XX AXX H X H 0max ≠ =。
东南大学工程矩阵理论试题及答案

et = f(1) = g(1) = c0(t) + c1(t) + c2(t), (1+t)et = f ¢(1) = g¢(1) = c1(t) + 2c2(t), 由此可得 c0(t) = 0, c1(t) = (1-t)et, c2(t) = tet, 于是有 AeAt = (1-t)etA + tetA2.
0ö æ1 1÷ø çè1
2 2
ö ÷ø
=
æ çè
0 1
0 2
ö ÷ø
=
0E11
+
0E12
+
1E21
+
2E22,
æ1 1 0 0ö
由此可见
f
在
£2´2
的基
E11,
E12,
E21,
E22
下的矩阵
A
=
ç ç ç
2 0
2 0
0 1
0÷
1
÷ ÷
.
è0 0 2 2ø
张小向@seu
2
◆ 工程矩阵理论 ◆ 试题一 ◆ 答案仅供参考 ◆
2 a -1
0
3ö 4 ÷ , r(A-I) = 0 ÷ø
1, 2,
a = 8 / 3; a ¹ 8 / 3,
æ1 0 0 ö
æ1 1 0ö
当 a = 8/3 时, A 的 Jordan 标准形为 ç 0 1 0 ÷ ; 当 a ¹ 8/3 时, A 的 Jordan 标准形为 ç 0 1 0 ÷ .
则 QHQ = I, aHQ = (1, 0, ..., 0), QHa = (1, 0, ..., 0)H,
æ1+ k 0 L 0ö
东南大学《工程矩阵理论》试卷样卷及答案(修改)1

工程矩阵理论试卷样卷10b一、已知22C⨯的子空间1,x x V x y C yy ⎧⎫⎛⎫=∈⎨⎬⎪⎝⎭⎩⎭,2,x y V x y C x y ⎧⎫-⎛⎫=∈⎨⎬ ⎪-⎝⎭⎩⎭,分别求121212,,,V V V V V V +的一组基及它们的维数。
解:1V 的基为:11000011,⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭,2维。
2V 的基为:10011001,-⎛⎫⎛⎫⎪ ⎪-⎝⎭⎝⎭,2维。
设12V V η∈,比较12,V V ,则y x =-,x x x x η⎛⎫= ⎪--⎝⎭,所以基为1111η⎛⎫= ⎪--⎝⎭,1维。
12V V +为由12,V V 生成的空间,121100100100111001(,,,)V V L -⎛⎫⎛⎫⎛⎫⎛⎫+=⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭,其极大线性无关组为:110010001110,,⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭,即为12V V +的基,3维。
二、设22C⨯上的线性变换f 定义为:()tt f X t t ⎛⎫=⎪⎝⎭,22a b X C c d ⨯⎛⎫∀=∈ ⎪⎝⎭,其中,t 表示矩阵X 的迹()tr X a d =+。
1、求f 在V 的基11E ,12E ,21E ,22E 下的矩阵A ; 2、求f 的值域()R f 及核子空间()K f 的基及它们的维数; 3、问:()()R f K f +是否为直和?为什么?解:1、11221()()tr E tr E == 12120()()t r E t r E == 11221111()()f E f E ⎛⎫== ⎪⎝⎭ 12210000()()f E f E ⎛⎫== ⎪⎝⎭11122122111221221001100110011001()()f E E E E E E E E ⎛⎫ ⎪⎪= ⎪⎪⎝⎭,1001100110011001A ⎛⎫⎪⎪= ⎪⎪⎝⎭2、f 的值域()R f :X 的基为11E ,12E ,21E ,22E ,故11122122()((),(),(),())R f L f E f E f E f E =故()R f 的基即为11122122(),(),(),()f E f E f E f E 的极大线性无关组:1111⎛⎫⎪⎝⎭,()R f 为1维。
研究生课程-《矩阵分析》试题及答案

第一套试题答案一(10分)、证明:(1)设11k x +22k x +33k x =0, ①用σ作用式①两端,有111k x λ+222k x λ+333k x λ=0 ②1λ⨯①-②,有21223133()()0k x k x λλλλ-+-= ③再用σ作用式③两端,有2122231333()()0k x k x λλλλλλ-+-= ④ ③⨯2λ-④,有313233()()0k x λλλλ--=。
由于123,,λλλ互不相等,30x ≠,因此30k =,将其代入④,有20k =,利用①,有10k =。
故1x ,2x ,3x 是线性无关的。
(2)用反证法。
假设1x +2x +3x 是σ的属于特征值λ的特征向量,于是有123123()()x x x x x x σλ++=++即112223123()x x x x x x λλλλ++=++112223()()()0x x x λλλλλλ-+-+-=由于1x ,2x ,3x 线性无关,因此123λλλλ===,这与123,,λλλ互不相等矛盾。
所以,1x +2x +3x 不是σ的特征向量。
二(10分)、解:2312321232()()1;()(2);()(2)()1;()(2);()(2)1()(2)(2)A D D D d d d A λλλλλλλλλλλλλλλλλλλλ==-=-==-=-⎛⎫⎪- ⎪ ⎪-⎝⎭的行列式因子分别为,不变因子分别为,于是的Smith 标准形为.三(10分)、解:11121634E A λλλλ+⎛⎫ ⎪-= ⎪ ⎪---⎝⎭210001000(1)λλ⎛⎫ ⎪≅- ⎪ ⎪-⎝⎭A λλ2矩阵的初等因子为: -1, (-1),100:011001J ⎛⎫⎪= ⎪ ⎪⎝⎭故约当标准形为。
四(12分)、解:令()()()1120,E A λλλλ-=-++=得特征值123112λλλ==-=-,,,解齐次方程组()0,E A x -=()2;Tii α=1得基础解系解齐次方程组()0,E A x --=()101;Tα=-2得基础解系解齐次方程组()20,E A x --=()1;T ii α=-3得基础解系αααααα123123由于,,已两两正交,将,,单位化得()()()11121011623T T Tp i i p p i i --123=,=,= ()1,(2)1.3H U p p p U AU ⎛⎫⎪==- ⎪ ⎪⎝⎭123令分,则五(10分)、解:(){}11(1),01,()TAx o i N A span ξξ===解齐次方程组得基础解系,,;又(){}{}()232323010,,,,100,,00H H R A span o span A o i ξξξξξξ⎛⎫⎪===-= ⎪ ⎪-⎝⎭这里,; 显然(),0,iji j ξξ=≠当时;()().HN A R A ⊥故有()()()()()()()()()333(2)dim dim dim 3dim ,Q H H H H N A R A C N A R A N A R A C N A R A C ++=+==+=是的子空间且故。
矩阵论试卷(2012A)答案(1[1].5)
![矩阵论试卷(2012A)答案(1[1].5)](https://img.taocdn.com/s3/m/a30b5e8571fe910ef12df86e.png)
2
17 分
⇒ 由(1)的证明知,“=”成立时,有 A 酉相似于一对角阵,根据定理 4.5.2,A 为
正规阵 20 分
2× 2
三.(1) 对任意 X1 , X 2 ∈ W , k ∈ R, 都有 X1 + X 2 ∈ W , kX1 ∈ W , 所以, W 是 R ⎛ x11 线 性 子 空 间 , 设 X =⎜ ⎜x ⎝ 21 ⎛ x11 X =⎜ ⎜x ⎝ 21 0 ⎞ ⎟, x11 + x21 ⎟ ⎠
的
x12 ⎞ ⎟ ∈ W , 因 为 AX = XA, 所 以 , x22 ⎟ ⎠
⎛1 0⎞ ⎛0 0⎞ 5分 W 的一组基为 X1 = ⎜ ⎟ , X = ⎜ 2 ⎜0 1⎟ ⎜1 1 ⎟ ⎟, 维数是 2. ⎝ ⎠ ⎝ ⎠ ( 2 ) 对 任 意 X1 , X 2 ∈ W , k ∈ R, 都 有 T ( X 1 + X 2 ) = T ( X1 ) + T ( X 2 ) , 9分 T ( kX1 ) = kT ( X1 ) ,所以, T 为线性变换 ⎛1 0⎞ ⎛0 0⎞ (3)对于 W 的一组基为 X1 = ⎜ ⎜0 1⎟ ⎟, X 2 = ⎜ ⎜1 1 ⎟ ⎟, 有: ⎝ ⎠ ⎝ ⎠ ⎛ 0 0⎞ ⎛ − 1 0⎞ T ( X 1) = ⎜ ⎜ 0 0⎟ ⎟ = 0X1 + 0 X2 , T ( X 2 ) = ⎜ ⎜ 2 1⎟ ⎟ = −1 X1 + 2 X 2 , ⎝ ⎠ ⎝ ⎠ ⎛ 0 − 1⎞ ⎛ 0 −1⎞ T ( X 1 , X 2 ) = ( X 1 , X 2 )⎜ ⎜0 2 ⎟ ⎟ , T 在(1)中所取基下的矩阵是 A = ⎜ ⎜0 2 ⎟ ⎟ 14 分 ⎝ ⎠ ⎝ ⎠ ⎛1 0⎞ ⎛0 0⎞ (4)对于 W 的一组基为 X1 = ⎜ ⎜0 1⎟ ⎟, X 2 = ⎜ ⎜1 1 ⎟ ⎟, ⎝ ⎠ ⎝ ⎠ ⎛ − b 0⎞ ⎛ 0 0⎞ 若 T ( aX 1 + bX 2 ) = ⎜ ⎟ ⎜ 2b b ⎟ ⎟=⎜ ⎜ ⎟ ,则有: b = 0 , ⎝ ⎠ ⎝ 0 0⎠ 所以, Ker (T ) = {kI2 : k ∈ R )} ,维数为 1, 17 分 ⎛ −1 0⎞ R (T ) = {T ( X ) : X ∈ W } = span{T ( X 1 ), T ( X 2 )} = {k ⎜ ⎜ 2 1⎟ ⎟ : k ∈ R} , ⎝ ⎠
(建筑工程管理]东南大学工程矩阵理论试卷样卷及答案(修改]
![(建筑工程管理]东南大学工程矩阵理论试卷样卷及答案(修改]](https://img.taocdn.com/s3/m/06ed61b34b73f242326c5f2e.png)
(建筑工程管理)东南大学《工程矩阵理论》试卷样卷及答案(修改)工程矩阵理论试卷样卷10a壹、假如。
1、记。
证明:是的子空间。
2、若A是单位矩阵,求。
3、若,。
求这里V(A)的壹组基及其维数。
4、假如。
问:对上壹题中的和,是否为直和?说明理由。
解:1、证明子空间,即为证明该空间关于加法和数乘封闭。
即若有,,。
设,,,,是的子空间。
2、若A是单位矩阵,则,因为对单位阵I来说,恒成立,故,。
3、若,,设,有,即,,→有,故=故X的壹组基为,维数为2。
4、,即,其基为。
下面计算,若,则是直和。
=(、基的极大线性无关组),为极大线性无关组(能够不求,从上式即可见出),+不是直和。
二、假如,,于上定义变换如下:。
1、证明:是上的线性变换。
2、求于的基下的矩阵M。
3、试求M的jordan标准形,且写出的最小多项式。
4、问:能否找到的基,使得的矩阵为对角阵?为什么?解:1、有:,有←加法封闭,有←数乘封闭是上的线性变换。
2、3、M的若当标准形为,的最小多项式为4、,,基础解系为,,,,基础解系为这四个基础解系所对应的基均线性无关,故能找到找到的基,使得的矩阵为对角阵。
三、设的子空间,,求,使得。
解:思路:求V的基→由该基生成;的含义是指于V中找壹向量,使得的距离最短,即寻找于V中的正投影。
作图如右侧。
由,得V的基为,则,,或四、设,求及矩阵函数。
解:(2重根)时,,故A的jordan标准形为,A的最小多项式为。
令,(计算略)令,(太麻烦了,不算啦!)五、已知矩阵A的特征多项式及最小多项式均等于,且且矩阵。
1、分别给出A和B的jordan标准形;2、问:A和B是否相似?为什么?解:A的特征多项式及最小多项式均等于,故A的jordan标准形为:,A和B有相同的jordan标准形,故A、B相似。
六、已知矩阵,求A的广义逆矩阵。
解:对A进行分块:对进行满秩分解,对进行满秩分解,七、证明题:1、假如是欧几里德空间V中单位向量,V上的线性变换如下:对任意,(镜像变换)。
东南大学09-10-2工程矩阵理论学位考试(工程硕士)

共 5 页 第 页东南大学考试试卷课程名称 工程矩阵理论 考试学期 09-10-2得分适用专业工程硕士考试形式闭卷考试时间长度 120分钟)已知22⨯C的子空间1|,a a V x y C b b ⎧⎫⎛⎫=∈⎨⎬ ⎪⎝⎭⎩⎭, 2|,a b V x y C b a ⎧⎫⎛⎫=∈⎨⎬⎪--⎝⎭⎩⎭1V ,2V ,21V V ⋂,21V V +的一组基及它们的维数.(12%)在3R 的子空间{}(,,)|230W x y z x y z =-+=,(1,1,0)η=.求0W η∈,0min Wξηηηξ∈-=-.共 5 页 第 页四. (12%)已知矩阵101002101A ⎛⎫ ⎪= ⎪⎪⎝⎭.1. 求一个多项式()f λ,使得()Atf A Ae =;2. 求A 的广义逆矩阵+A .五. (12%)已知矩阵,A B 的F-范数和算子2-范数分别是2,F A a A b==,2,FBc B d==,分别求分块矩阵A O M OB ⎛⎫= ⎪⎝⎭的F-范数和算子2-算子. 六. (12%)设矩阵102001b c A a ⎛⎫⎪= ⎪⎪⎝⎭,1000312B y x ⎛⎫ ⎪= ⎪⎪⎝⎭三. (14%)记11122122121101,,001111A A A A -⎛⎫⎛⎫⎛⎫====⎪ ⎪ ⎪--⎝⎭⎝⎭⎝⎭.已知22⨯C 上的线性变换f 满足()ij ij f E A =(,1,2)i j =. 1. 求f 在基11122122,,,E E E E 下的矩阵;2. 分别求f 的值域()R f 和核子空间()K f 的基和维数; 3. 求f 的特征多项式和最小多项式.共 5 页 第 页.根据参数,,,,a b c x y 讨论,A B 可能的Jordan 标准形,并问:参数满足什么条件时,矩阵A 与B 是相似的? 七. (10%)n 维欧氏空间V 上的线性变换f 定义如下:()(,)f x ax b x ωω=-,V x ∈∀。
2012年前所有的东南大学工程矩阵考博试卷

1. 2.
A
B
3
14%
0 1
8 6 5
A100-2A50
A
3
2 0
10%
n
A
A2=7I-6A
A+7I
r
det
A+2I
14%
f
n
V
,
V
(f ( ), )=( ,f ( ))
1. 2.
V V
f f
Hermite
26% 1. 2. A2 3. 4.
n
A A
A
1 A3=A2
A A2=A BA A Hermite a B A BA=A*A
⎛ −1 −2 6 ⎞ ⎜ ⎟ 四 (15 分)已知 A = ⎜ −1 0 3 ⎟ 。 ⎜ −1 −1 4 ⎟ ⎝ ⎠
1.求 sin At ; 2.计算 d sin At 。 dt
⎛ 1 2 1⎞ ⎜ ⎟ 五 (10 分)求矩阵 A = ⎜ 0 0 1⎟ 的 QR 分解。 ⎜ 1 2 1⎟ ⎝ ⎠
六 (10 分) 设 T 是 n 维线性空间 V 上的线性变换, 证明: T (V ) ⊆ T −1 (0) 的充要条件是 T 2 = 0 。 七 (10 分) 设 ⋅ 是 C n×n 上的 F-范数。证明:若 A < 1 , E 为 n 阶单位 阵,则矩阵 E − A 可逆,且
1 1 ≤ ( E − A) −1 ≤ 。 1− A E−A
E21=
0 0 1 0
0 1 0 0
E22=
0 0 0 1
M 3. 4. 2 2
f
R
f f
K
K
f
C2 2= R
f
12%
a
矩阵分析试题A参考答案及评分标准样本

重庆邮电大学 级研究生(矩阵分析)考卷( A 卷)参考答案及评分细则一 、 已知 1(1,2,1,0)T α=, 2(1,1,1,1)T α=-, 1(2,1,0,1)T β=-, 2(1,1,3,7)T β=-求12{,}span αα与12{,}span ββ的和与交的基和维数。
( 10分) 解: 因为12{,}span αα+12{,}span ββ=1212{,,,}span ααββ (2分)由于秩1212{,,,}ααββ=3, 且121,,ααβ是向量组1212,,,ααββ的一个极大相信无关组, 因此和空间的维数是3, 基为121,,ααβ。
(2分) 设{}1212{,},span span ξααββ∈于是由交空间定义可知11221122k k l l ξααββ=+=+ 此即121211212111011030117k k l l -⎛⎫⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪-- ⎪ ⎪ ⎪ ⎪+--= ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭解之得1122122,4,3(k l k l l l l =-==-为任意数) (2分) 于是11222[5,2,3,4]T k k l ξαα=+=-, 1122l l ξββ=+(很显然)因此交空间的维数为1, 基为T [-5,2,3,4] (2分)二、 证明: Jordan 块 10()0100a J a a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦相似于矩阵 0000a a a εε⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦, 这里0ε≠为任意实数。
( 10分) 证明: 由于容易求出两个λ-矩阵的不变因子均为31,1,()a λ-, 从而这两个λ-矩阵相似,于是矩阵10()0100a J a a a ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦与0000a a a εε⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦相似.三、 求矩阵101120403A -⎛⎫ ⎪= ⎪ ⎪-⎝⎭的(1)Jordan 标准型; ( 2) 变换矩阵P ; ( 3) 计算100A 。
矩阵论考试题和答案(详细)

因此 B = Udiag (λ ,L , λ )U = Vdiag (λ ,L , λ )V H = E 。
H
1 3 1
1 3 n
1 3 1
1 3 n
-------------4
(2)因为 A ≥ 0 ,所以 A 的特征值均非负。设 A 的特征值为 λ1 ,L , λn ,且 λ1 ≥ L ≥ λn ≥ 0 , 则 A2 的特征值为 λ12 ,L , λn2 ,于是
AT Ax = AT b
的解, 所以不相容线性方程组 Ax = b 的最小二乘解唯一当且仅当 AT A 非奇异, 即 rank ( AT A) = n 。因为 rank ( AT A) = rank ( A) ,所以不相容线性方程组 Ax = b 的最 小二乘解唯一当且仅当 A 列满秩。 -----------4
记 P = U H V = ( pij ) ,则 diag (λ1 ,L , λn ) P = Pdiag (λ1 ,L , λn ) ,从而
λi pij = λ j pij (i, j = 1,L , n) ,
于是
1 1
λi3 pij = λ j3 pij (i, j = 1,L , n) ,
即
diag (λ13 ,L , λn3 ) P = Pdiag (λ13 ,L , λn3 ) ,
A + = C T ( CC
T
-----------------5
1 4 0 1 − 4
)−1 ( B T B )−1 B T
1 − 4 = 0 1 4
0 1 0
---------5
1 (2)因为 AA + b = 2 ≠ b ; 所以不相容的。 -----------3 2 1 4 -----------3 其极小最小二乘通解为 x = A + b = 2 1 − 4 (3)因为 x 是不相容线性方程组 Ax = b 的最小二乘解当且仅 x 是如下相容线性方程组
东南大学 数学建模试卷 09-10-2A

共6页第1页东南大学考试卷(A 卷)姓名 学号 班级课程名称 数学建模与实验 考试学期得分适用专业 各专业考试形式闭卷考试时间长度 120分钟一.填空题:(每题2分,共10分)1. 阻滞增长模型0.5(10.001)(0)100dx x x dtx ⎧=-⎪⎨⎪=⎩的解为。
2. 用Matlab 做常微分方程数学实验,常用的命令有。
3. 整数m 关于模12可逆的充要条件是:。
4. 根据Malthus 模型,如果自然增长率为2%,则人口数量增长为初值3倍所需时间为(假设初值为正)。
5. 请补充判断矩阵缺失的元素13192A ⎛⎫⎪=⎪ ⎪⎝⎭。
二.选择题:(每题2分,共10分)1. 在下列Leslie 矩阵中,不能保证模最大特征值唯一的是 ()A. 0230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭; B. 1.1 1.230.20000.40⎛⎫ ⎪ ⎪ ⎪⎝⎭; C. 0030.20000.40⎛⎫⎪⎪ ⎪⎝⎭; D.以上都不对 2. 判断矩阵能通过一致性检验的标准是()A. 0.1C R <B. 0.1C I <C.0.1C R >D.0.01C R <3. 模28倒数表中可能出现的数是 () A. 12 B.5 C.14 D.74. 线性最小二乘法得到的函数不可能为()A.线性函数B. 对数函数C. 样条函数D. 指数函数 5. 关于泛函极值问题,下面的描述正确的有()A.泛函()J x 在x *处取极值的充要条件是泛函变分()0J x δ*=;B.泛函()J x 在x *处取极值的充分条件是泛函变分()0J x δ*=; C. 泛函()J x 在x *处取极值的必要条件是泛函变分()0J x δ*=;D.A,B,C 均正确学号姓名三.判断题(每题2分,共10分)1. Hill密码体系中,任意一个可逆矩阵都可以作为加密矩阵。
()2. 拟合函数不要求通过样本数据点。
()3. Matlab软件内置命令程序可以直接求解一般的整数线性规划问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
工程矩阵理论试卷样卷10b
一、已知22
C
⨯的子空间
1,x x V x y C y
y ⎧⎫⎛⎫
=∈⎨⎬
⎪⎝⎭⎩⎭,2,x y V x y C x y ⎧⎫-⎛⎫=∈⎨⎬ ⎪-⎝⎭⎩⎭
,分别求121212,,,V V V V V V +I 的一组基及它们的维数。
解:1V 的基为:11000011,⎛⎫⎛⎫
⎪ ⎪⎝⎭⎝⎭
,2维。
2V 的基为:10011001,-⎛⎫⎛⎫
⎪ ⎪-⎝⎭⎝⎭
,2维。
设12V V η∈I ,比较12,V V ,则y x =-,x x x x η⎛⎫=
⎪--⎝⎭,所以基为1111η⎛⎫
= ⎪--⎝⎭
,1维。
12V V +为由12,V V 生成的空间,121100100100111001(,,,)V V L -⎛⎫⎛⎫⎛⎫⎛⎫
+=
⎪ ⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭⎝⎭
,其极大线性无关组为:110010001110,,⎛⎫⎛⎫⎛⎫
⎪ ⎪ ⎪-⎝⎭⎝⎭⎝⎭
,即为12V V +的基,3维。
二、设22
C
⨯上的线性变换f 定义为:
()t
t f X t t ⎛⎫=
⎪⎝⎭,22
a b X C c d ⨯⎛⎫∀=∈ ⎪⎝⎭
,其中,t 表示矩阵X 的迹()tr X a d =+。
1、求f 在V 的基11E ,12E ,21E ,22E 下的矩阵A ; 2、求f 的值域()R f 及核子空间()K f 的基及它们的维数; 3、问:()()R f K f +是否为直和?为什么? 解:1、11221()()tr E tr E == 12120()()tr E tr E ==
11221111()()f E f E ⎛⎫== ⎪⎝⎭ 1221
0000()()f E f E ⎛⎫
== ⎪⎝⎭
111221221112212210011
00110011
001()()f E E E E E E E E ⎛⎫ ⎪
⎪= ⎪
⎪⎝⎭,1
0011
00110011001A ⎛⎫
⎪
⎪
= ⎪
⎪
⎝⎭
2、f 的值域()R f :
X Q 的基为11E ,12E ,21E ,22E ,故11122122()((),(),(),())R f L f E f E f E f E = 故()R f 的基即为11122122(),(),(),()f E f E f E f E 的极大线性无关组:1111⎛⎫
⎪⎝⎭
,()R f 为1维。
核子空间()K f :AX O =,X 的基础解系:001100
010001,,-⎛⎫⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭
,()K f 为3维。
3、观察得:()R f 的基与()K f 线性无关,维数的和为4,故()()R f K f +是直和。
三、已知矩阵A 的特征多项式()A C λ及最小多项式()A m λ相等,均等于2
1()λλ-,矩阵110001000B ⎛⎫ ⎪= ⎪ ⎪⎝⎭。
分别求A 和B 的jordan 标准形;问:A 与B 是否相似?为什么?
解:由矩阵A 的特征多项式()A C λ及最小多项式()A m λ相等,均等于2
1()λλ-,得100001000A J ⎛⎫ ⎪= ⎪ ⎪⎝⎭
2
11001100()I B λλλλλλ--⎛⎫ ⎪-=-=- ⎪ ⎪⎝⎭,100001000B J ⎛⎫
⎪= ⎪ ⎪⎝⎭。
A 与B 相似,因为它们有相同的jordan
标准形。
四、已知矩阵34500001110101A ⨯⎛⎫ ⎪= ⎪ ⎪⎝⎭,求A 的广义逆矩阵A +
解:对A 进行满秩分解:500010000111010101010010A ⎛⎫⎛⎫
⎪ ⎪
=→ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
3()A r ∴=,A 应该分解为343334
500100001101010100010A B C ⨯⨯⨯⎛⎫⎛⎫ ⎪ ⎪=⋅=⋅ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭
∴
111143
1000100010005005005000101010101010110110110010001000100100100100()()()()H H H H
H
H
H
H
A C CC
B B B +----⨯=⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫
⎪ ⎪ ⎪ ⎪ ⎪ ⎪=⋅ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎛⎫ ⎪
⎪= ⎪ ⎪⎝⎭
五、已知矩阵A O M O B ⎛⎫
=
⎪⎝⎭
,
其中,矩阵A ,B 的F 范数及算子2范数分别是5F A =,4F
B =,23A =,
22B =,试求F
M
和2
M。
解:F
范数定义为F
⋅
=
F
M
==算子2
范数定义为2
⋅
=,23A =表示A 中特征值最大为3,22B =表示B 中特征值
最大为2,M 的特征值即为A 、B 全部特征值,故2
M 为A 、B 中特征值的最大值,2
3M
=。
六、设V 是一n 维欧氏空间,V ω∈是一单位向量,,a b 是一参数,V 上的线性变换f 定义为:
(),,f a b V ηηηωωη=-<>∀∈,问:当,a b 取何值时,f 是正交变换?
解:扩充ω为V 的一组标准正交基1,,,n ωωω⋅⋅⋅⋅⋅⋅,则:
(),()f a b a b a b ωωωωωωωω=-<>=-=- 1111(),f a b a ωωωωωω=-<>=
⋅⋅⋅⋅⋅⋅
(),n n n n f a b a ωωωωωω=-<>=
22200000
00(,,)(,,)(,,)n n n a b a f A a ωωωωωωωωω-⋅⋅⋅⎛⎫ ⎪⋅⋅⋅ ⎪⋅⋅⋅=⋅⋅⋅=⋅⋅⋅ ⎪⋅⋅⋅ ⎪
⎝⎭ 若f 是正交变换,则A 必须为正交矩阵,A 的行向量或列向量必须为标准正交基。
∴10,a b =±=
七、证明题:
1、假如A 是H 阵,证明:iA
e 是酉矩阵。
证明:要证iA
e 是酉矩阵,即证()
iA
iA H
e e I ⋅=
根据矩阵多项式的性质,H
H
iA iA
iA iA O e e
e e I --⋅=== (Q iA 与H iA -可交换) ∴iA
e
是酉矩阵
2、设⋅是相容矩阵范数,证明:对任意方阵A ,A 的谱半径()A A ρ≤。
证明:设A 的特征值λ,η为与λ对应的θ≠的特征向量,有A ηλη= 两边取范数,A ηλη=
Q ⋅是相容范数,∴A A ληληηη=⋅=≤⋅ Q ηθ≠,∴0η>,A λ≤,∴()A A ρ≤
(若考虑⋅仅为方阵上的相容矩阵范数,则只需将η扩充为()η
θθ⋅⋅⋅的方阵即可)。
