2018年“大梦杯”福建省初中数学竞赛试题+参考答案及评分标准
2018年大梦杯省初中数学竞赛试题

年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准 考试时间 年月日 ∶-∶ 满分分一、选择题(共小题,每小题分,共分)。
每道小题均给出了代号为,,,的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得分).若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( ) .3- .2- .1-. 【答案】【解答】依题意,21616(31)0m m =++=△。
因此,2310m m ++=。
∴231m m =--,231m m +=-。
∴3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( )11.1.1 【答案】【解答】依题意,点C 坐标为()2mm ,,点F 的坐标为()2m n n -+,。
由二次函数2y ax =的图像过C 、F 两点,得222()2m am m n a n ⎧=⎪⎪⎨⎪+=-⎪⎩,消去a ,得2220n mn m --=。
∴2()210n n m m -⨯-=,解得1nm=(舍负根)。
∴1nm=。
.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( )(第题图).25 .35 .37 .47【答案】【解答】如图,连AG ,并延长交BC 于点F 。
∵G 为ABC △的重心,且12BD BC =, ∴F 为BC 中点,且21AG GF =,DB BF FC ==。
过点F 作FM DE ∥,交AC 于点M 。
则13CM CF CE CD ==,21AE AG EM GF ==。
一道“大梦杯”赛题的七种解法

一道“大梦杯”赛题的七种解法赛题既是知识综合应用的集散地,也是一题多解的主战场,探究赛题的解法,有利于培养缜密的数学思维,创新的思维意识和创新精神.下面就向大家一例. 原题:如图1,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC =( ) A .25 B .35 C .37 D .47(2018年“大梦杯”福建省初中数学竞赛试题)解法1:如图1,连AG ,并延长交BC 于点F ,因为G 为ABC △的重心,且12BD BC =, 所以F 为BC 中点,且21AG GF =,DB BF FC ==. 过点F 作FM DE ∥,交AC 于点M ,则13CM CF CE CD ==,21AE AG EM GF ==.设CM k =,则3CE k =,2EM k =,4AE k =.所以7AC k =,所以4477AE k AC k ==.所以选D.点评:此法精髓在于添加平行线构造相似基本图形---“A ”字型图,其次,巧设参数也是解题的一种重要方法,值得借鉴.解法2:如图2,连接AG ,并延长交BC 于点F.因为G 为△ABC 重心,且BD=21BC , 所以F 为BC 的中点,且12=GF AG ,DB=BF=FC. 过点F 作FH ∥AC 交DE 点H,则12=FH AE ,32=CE FH ,设FH=k.则AE=2k,CE=23k,所以AC=27k,所以==k kAC AE 27274,所以选D.点评:此法精髓在于添加平行线构造相似基本图形---“8”字型图. 解法3:如图3,连接AG ,并延长交BC 于点F.因为G 为△ABC 重心,且BD=21BC , 所以F 为BC 的中点,且12=GF AG ,DB=BF=FC. 过点G 作GH ∥AC 交FC 点H,则13=GH AC ,31=CF FH ,79373===FC FC DHDC GH EC 设GH=7k.则AC=21k,CE=9k,AE=12k,所以==k k AC AE 211274,所以选D.点评:依据比例的特点,整体设参数是此法的优势.解法4:如图4,连接AG ,并延长交BC 于点F.因为G 为△ABC 重心,且BD=21BC , 所以F 为BC 的中点,且12=GF AG ,DB=BF=FC. 过点A 作AH ∥BC 交DE 的延长线于点H,则EC AE DC AH =,12==GF AG DF AH ,设DF=2k.则AH=4k,DC=3k,所以3434==k k EC AE ,所以434+=+AE EC AE , 所以AC AE =74,所以选D.点评:构造两个相似的“8”字型图是一个亮点,其次,熟练运用比例的合比性质是解题的另一个特色.解法5:如图5,连接AG ,并延长交BC 于点F.因为G 为△ABC 重心,且BD=21BC , 所以F 为BC 的中点,且12=GF AG ,DB=BF=FC. 过点G 作GH ∥DC 交AC 点H,则32=FC GH ,DC GH EC EH =,12=HC AH ,设GH=2k.则FC=3k,DC=9k,所以 92=EC EH ,设EH=2m ,则EC=9m,HC=7m,所以AH=14m ,AE=12m ,AC=21m ,所以==m m AC AE 211274,所以选D.点评:两次设参数是此法的一个重要特点.解法6:如图6,连接AG ,并延长交BC 于点F.因为G 为△ABC 重心,且BD=21BC , 所以F 为BC 的中点,且12=GF AG ,DB=BF=FC. 过点D 作DH ∥AC 交AF 的延长线于点H,则21==FD FC DH AC ,21==FD FC FH AF ,GH AG DH AE =,设FG=k.则AG=2k,AF=3k,FH=6k,所以AE=72DH ,AC=21DH ,所以AC AE =72DH :21DH =74,所以选D.点评:此法也是双“8”字型相似图形的基本应用,熟练掌握灵活构造基本图形,把陌生转化熟悉求解释学习数学的重要技能之一.解法7:如图7,连AG ,并延长交BC 于点F . 因为 G 为ABC △的重心,且12BD BC =, 所以 F 为BC 中点,且21AG GF =,DB BF FC ==. 所以 23FD DC =,21AG GF =.在AFC △中,利用梅涅劳斯定理,得1FD CE AGDC EA GF⋅⋅=.所以 22131CE EA ⋅⋅=,34CE EA =.所以 47AE AC =.所以选D.点评:熟记梅涅劳斯定理的条件和结论,并灵活运用定理是解题的关键.。
2017-2018学年福建省八年级(上)竞赛数学试卷及答案与解析

2017-2018学年福建省八年级(上)竞赛数学试卷;一、选择题(每小题5分,共40分)1.下列四组数据中,不能作为直角三角形的三边长的是()A.7,24,25 B.6,8,10 C.9,12,15 D.3,4,62.设M=(x﹣3)(x﹣7),N=(x﹣2)(x﹣8),则M与N的关系为()A.M<N B.M>N C.M=N D.不能确定3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…,解答下列问题:3+32+33+…+32015的末位数字是()A.1 B.3 C.7 D.94.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是()A.x+y+z=0 B.x+y﹣2z=0 C.y+z﹣2x=0 D.z+x﹣2y=05.已知△ABC中,AB=AC,高BD、CE交于点O,连接AO,则图中全等三角形的对数为()A.3 B.4 C.5 D.66.如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是()A.4 B.5 C.6 D.77.点P(3,﹣5)关于y轴对称的点的坐标为()A.(﹣3,﹣5)B.(5,3) C.(﹣3,5)D.(3,5)8.下列四个命题中,真命题有()①两条直线被第三条直线所截,内错角相等.②如果∠1和∠2是对顶角,那么∠1=∠2.③三角形的一个外角大于任何一个内角.④如果x2>0,那么x>0.A.1个 B.2个 C.3个 D.4个二、填空题(每小题5分,共40分);9.若2a3x b y+5与5a2﹣4y b2x是同类项,则xy=.10.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为.11.如果(a2+b2+2)(a2+b2﹣2)=45,则a2+b2的值为.12.已知(a+25)2=1000,则(a+15)(a+35)的值为.13.计算(1﹣)()﹣(1﹣﹣)()的结果是.14.如图,在△ABC中,I是三内角平分线的交点,∠BIC=130°,则∠A=.15.如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是.16.如图,AB=AC,则数轴上点C所表示的数为.三、解答题(每小题10分,共40分)17.已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.18.已知a=2015x+2014,b=2015x+2015,c=2015x+2016.求a2+b2+c2﹣ab﹣bc﹣ca的值.19.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.20.已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.2017-2018学年福建省八年级(上)竞赛数学试卷参考答案与试题解析一、选择题(每小题5分,共40分)1.下列四组数据中,不能作为直角三角形的三边长的是()A.7,24,25 B.6,8,10 C.9,12,15 D.3,4,6【考点】勾股数.【分析】根据勾股定理的逆定理:如果三角形有两边的平方和等于第三边的平方,那么这个三角形是直角三角形.如果没有这种关系,这个就不是直角三角形.【解答】解:A、72+242=252,符合勾股定理的逆定理,故能作为直角三角形的三边长;B、62+82=102,符合勾股定理的逆定理,故能作为直角三角形的三边长;C、92+122=152,符合勾股定理的逆定理,故能作为直角三角形的三边长;D、32+42≠62,不符合勾股定理的逆定理,故不能作为直角三角形的三边长.故选D.2.设M=(x﹣3)(x﹣7),N=(x﹣2)(x﹣8),则M与N的关系为()A.M<N B.M>N C.M=N D.不能确定【考点】多项式乘多项式.【分析】根据多项式乘多项式的运算法则进行计算,比较即可得到答案.【解答】解:M=(x﹣3)(x﹣7)=x2﹣10x+21,N=(x﹣2)(x﹣8)=x2﹣10x+16,M﹣N=(x2﹣10x+21)﹣(x2﹣10x+16)=5,则M>N.故选:B.3.观察下列等式:31=3,32=9,33=27,34=81,35=243,36=729,37=2187…,解答下列问题:3+32+33+…+32015的末位数字是()A.1 B.3 C.7 D.9【考点】尾数特征.【分析】根据31=3,32=9,33=27,34=81,35=243,36=729,37=2187…得出3+32+33+34…+32015的末位数字相当于:3+7+9+1+…+3+7+9,进而得出末尾数字.【解答】解:∵31=3,32=9,33=27,34=81,35=243,36=729,37=2187…∴末尾数,每4个一循环,∵2015÷4=503…3,∴3+32+33+34…+32015的末位数字相当于:3+7+9+1+…+3+7+9=(3+9+7+1)×503+19=10079的末尾数为9.故选:D.4.若实数x、y、z满足(x﹣z)2﹣4(x﹣y)(y﹣z)=0,则下列式子一定成立的是()A.x+y+z=0 B.x+y﹣2z=0 C.y+z﹣2x=0 D.z+x﹣2y=0【考点】完全平方公式.【分析】首先将原式变形,可得x2+z2+2xz﹣4xy+4xz+4y2﹣4yz=0,则可得(x+z﹣2y)2=0,则问题得解.【解答】解:∵(x﹣z)2﹣4(x﹣y)(y﹣z)=0,∴x2+z2﹣2xz﹣4xy+4xz+4y2﹣4yz=0,∴x2+z2+2xz﹣4xy+4y2﹣4yz=0,∴(x+z)2﹣4y(x+z)+4y2=0,∴(x+z﹣2y)2=0,∴z+x﹣2y=0.故选:D.5.已知△ABC中,AB=AC,高BD、CE交于点O,连接AO,则图中全等三角形的对数为()A.3 B.4 C.5 D.6【考点】等腰三角形的性质;全等三角形的判定.【分析】根据等腰三角形的性质以及全等三角形的判定和性质定理解答.【解答】解:∵高BD、CE交于点O,∴∠AEO=∠ADO=90°,图中的全等三角形有:①在△AEC与Rt△ADB中,,∴△AEC≌△ADB(AAS),∴∠ABO=∠ACO,∵AB=AC,∴∠ABC=∠ACB,∴∠CBO=∠BCO,∴OB=OC;②在△ABO与Rt△ACO中,,∴△ABO≌△ACO(SSS),∴∠BAO=∠CAO,③在△AEO与Rt△ADO中,,∴△AEO≌△ADO(AAS),④在△BOE与△COD中,,∴△BOE≌△COD(AAS);⑤在△BCE与△CBD中,∴△BCE≌△CBD(AAS).共有5对.故选C.6.如图,在△ABC中,∠C=90°,∠BAC=30°,AB=8,AD平分∠BAC,点PQ分别是AB、AD边上的动点,则PQ+BQ的最小值是()A.4 B.5 C.6 D.7【考点】轴对称﹣最短路线问题;含30度角的直角三角形.【分析】如图,作点P关于直线AD的对称点P′,连接QP′,由△AQP≌△AQP′,得PQ=QP′,欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,即当BP′⊥AC 时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.【解答】解:如图,作点P关于直线AD的对称点P′,连接QP′,在△AQP和△AQP′中,,∴△AQP≌△AQP′,∴PQ=QP′∴欲求PQ+BQ的最小值,只要求出BQ+QP′的最小值,∴当BP′⊥AC时,BQ+QP′的值最小,此时Q与D重合,P′与C重合,最小值为BC的长.在Rt△ABC中,∵∠C=90°,AB=8,∠BAC=30°,∴BC=AB=4,∴PQ+BQ的最小值是4,故选A.7.点P(3,﹣5)关于y轴对称的点的坐标为()A.(﹣3,﹣5)B.(5,3) C.(﹣3,5)D.(3,5)【考点】关于x轴、y轴对称的点的坐标.【分析】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可直接得到答案.【解答】解:点P(3,﹣5)关于y轴对称的点的坐标为(﹣3,﹣5),故选:A.8.下列四个命题中,真命题有()①两条直线被第三条直线所截,内错角相等.②如果∠1和∠2是对顶角,那么∠1=∠2.③三角形的一个外角大于任何一个内角.④如果x2>0,那么x>0.A.1个 B.2个 C.3个 D.4个【考点】命题与定理.【分析】根据平行线的性质对①进行判断;根据对顶角的性质对②进行判断;根据三角形外角性质对③进行判断;根据非负数的性质对④进行判断.【解答】解:两条平行直线被第三条直线所截,内错角相等,所以①错误;如果∠1和∠2是对顶角,那么∠1=∠2,所以②正确;三角形的一个外角大于任何一个不相邻的内角,所以③错误;如果x2>0,那么x≠0,所以④错误.故选A.二、填空题(每小题5分,共40分)9.若2a3x b y+5与5a2﹣4y b2x是同类项,则xy=﹣2.【考点】同类项.【分析】根据同类项的定义,含有相同的字母,相同字母的指数相同,即可列出关于x和y的方程组,求得x和y的值,进而求得代数式的值.【解答】解:根据题意得:,解得:,则xy=2×(﹣1)=﹣2.故答案为﹣2.10.如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,则∠1+∠2的度数为45°.【考点】平行线的性质.【分析】首先过点B作BD∥l,由直线l∥m,可得BD∥l∥m,由两直线平行,内错角相等,可得出∠2=∠3,∠1=∠4,故∠1+∠2=∠3+∠4,由此即可得出结论.【解答】解:过点B作BD∥l,∵直线l∥m,∴BD∥l∥m,∴∠4=∠1,∠2=∠3,∴∠1+∠2=∠3+∠4=∠ABC,∵∠ABC=45°,∴∠1+∠2=45°.故答案为:45°.11.如果(a2+b2+2)(a2+b2﹣2)=45,则a2+b2的值为7.【考点】换元法解一元二次方程.【分析】根据题意,可以设a2+b2=m,从而可以求得m的值,进而求得a2+b2的值,注意a2+b2的值不小于0.【解答】解:设a2+b2=m,则(m+2)(m﹣2)=45,∴m2﹣4=45,解得,m=7或m=﹣7,∴a2+b2=7或a2+b2=﹣7(舍去),故答案为:712.已知(a+25)2=1000,则(a+15)(a+35)的值为900.【考点】平方差公式.【分析】将(a+15)(a+35)变形为(a+25﹣10)(a+25+10),根据平方差公式得到原式=(a+25)2﹣100,再将(a+25)2=1000整体代入即可求解.【解答】解:(a+15)(a+35)=(a+25﹣10)(a+25+10)=(a+25)2﹣100,∵(a+25)2=1000,∴原式=1000﹣100=900.故答案为:900.13.计算(1﹣)()﹣(1﹣﹣)()的结果是.【考点】整式的混合运算.【分析】设a=1﹣﹣﹣﹣,b=+++,然后根据整式的乘法与加减混合运算进行计算即可得解.【解答】解:设a=1﹣﹣﹣﹣,b=+++,则原式=a(b+)﹣(a﹣)•b=ab+a﹣ab+b=(a+b),∵a+b=1﹣﹣﹣﹣++++=1,∴原式=.故答案为:.14.如图,在△ABC中,I是三内角平分线的交点,∠BIC=130°,则∠A=80°.【考点】三角形内角和定理.【分析】先根据角平分线的定义得到∠IBC=∠ABC,∠ICB=∠ACB,再根据三角形内角和定理得∠BIC+∠IBC+∠ICB=180°,则∠BIC=180°﹣(∠ABC+∠ACB),由于∠ABC+∠ACB=180°﹣∠A,所以∠BIC=90°+∠A,然后把∠BIC=130°代入计算可得到∠A的度数.【解答】解:∵BI、CI分别平分∠ABC、∠ACB,∴∠IBC=∠ABC,∠ICB=∠ACB,∵∠BIC+∠IBC+∠ICB=180°,∴∠BIC=180°﹣(∠IBC+∠ICB)=180°﹣(∠ABC+∠ACB),∵∠A+∠ABC+∠ACB=180°,∴∠ABC+∠ACB=180°﹣∠A,∴∠BIC=180°﹣=90°+∠A,∵∠BIC=130°,∴90°+∠A=130°∴∠A=80°.故答案为:80°.15.如图钢架中,焊上等长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是12°.【考点】等腰三角形的性质.【分析】设∠A=x,根据等边对等角的性质以及三角形的一个外角等于与它不相邻的两个内角的和求出∠AP7P8,∠AP8P7,再根据三角形的内角和定理列式进行计算即可得解.【解答】解:设∠A=x,∵AP1=P1P2=P2P3=…=P13P14=P14A,∴∠A=∠AP2P1=∠AP13P14=x,∴∠P2P1P3=∠P13P14P12=2x,∴∠P3P2P4=∠P12P13P11=3x,…,∠P7P6P8=∠P8P9P7=7x,∴∠AP7P8=7x,∠AP8P7=7x,在△AP7P8中,∠A+∠AP7P8+∠AP8P7=180°,即x+7x+7x=180°,解得x=12°,即∠A=12°.故答案为:12°.16.如图,AB=AC,则数轴上点C所表示的数为﹣1.【考点】勾股定理;实数与数轴.【分析】根据勾股定理列式求出AB的长,即为AC的长,再根据数轴上的点的表示解答.【解答】解:由勾股定理得,AB==,∴AC=,∵点A表示的数是﹣1,∴点C表示的数是﹣1.故答案为:﹣1.三、解答题(每小题10分,共40分)17.已知:3a=2,3b=6,3c=18,试确定a、b、c之间的数量关系.【考点】幂的乘方与积的乘方.【分析】根据同底数幂的乘法以及幂的乘方即可列出等式求出a、b、c之间的数量关系.【解答】解:∵2×18=62,∴3a×3c=(3b)2,∴3a+c=32b,∴a+c=2b18.已知a=2015x+2014,b=2015x+2015,c=2015x+2016.求a2+b2+c2﹣ab﹣bc﹣ca的值.【考点】因式分解的应用.【分析】原式变形后,利用完全平方公式配方后,将已知等式代入计算即可求出值.【解答】解:∵a=2015x+2014,b=2015x+2015,c=2015x+2016,∴a﹣b=﹣1,b﹣c=﹣1,a﹣c=﹣2,则原式=(2a2+2b2+2c2﹣2ab﹣2bc﹣2ac)= [(a﹣b)2+(b﹣c)2+(a﹣c)2]=×(1+1+4)=3.19.如图,△ABC是边长为6的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合),过P作PE⊥AB于E,连接PQ交AB于D.(1)当∠BQD=30°时,求AP的长;(2)当运动过程中线段ED的长是否发生变化?如果不变,求出线段ED的长;如果变化请说明理由.【考点】等边三角形的性质;全等三角形的判定与性质;含30度角的直角三角形.【分析】(1)由△ABC是边长为6的等边三角形,可知∠ACB=60°,再由∠BQD=30°可知∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,在Rt△QCP中,∠BQD=30°,PC=QC,即6﹣x=(6+x),求出x的值即可;(2)作QF⊥AB,交直线AB于点F,连接QE,PF,由点P、Q做匀速运动且速度相同,可知AP=BQ,再根据全等三角形的判定定理得出△APE≌△BQF,再由AE=BF,PE=QF且PE∥QF,可知四边形PEQF是平行四边形,进而可得出EB+AE=BE+BF=AB,DE=AB,由等边△ABC的边长为6可得出DE=3,故当点P、Q运动时,线段DE的长度不会改变.【解答】解:(1)∵△ABC是边长为6的等边三角形,∴∠ACB=60°,∵∠BQD=30°,∴∠QPC=90°,设AP=x,则PC=6﹣x,QB=x,∴QC=QB+BC=6+x,∵在Rt△QCP中,∠BQD=30°,∴PC=QC,即6﹣x=(6+x),解得x=2,∴AP=2;(2)当点P、Q同时运动且速度相同时,线段DE的长度不会改变.理由如下:作QF⊥AB,交直线AB于点F,连接QE,PF,又∵PE⊥AB于E,∴∠DFQ=∠AEP=90°,∵点P、Q速度相同,∴AP=BQ,∵△ABC是等边三角形,∴∠A=∠ABC=∠FBQ=60°,在△APE和△BQF中,∵∠AEP=∠BFQ=90°,∴∠APE=∠BQF,,∴△APE≌△BQF(AAS),∴AE=BF,PE=QF且PE∥QF,∴四边形PEQF是平行四边形,∴DE=EF,∵EB+AE=BE+BF=AB,∴DE=AB,又∵等边△ABC的边长为6,∴DE=3,∴点P、Q同时运动且速度相同时,线段DE的长度不会改变.20.已知△ABC中,∠A:∠B:∠C=3:4:2,AD、BE是角平分线.求证:AB+BD=AE+BE.【考点】全等三角形的判定与性质.【分析】延长AB到F,使BF=BD,连DF,首先证明△ADF≌△ADC,推出AF=AC,由BE是角平分线,推出∠CBE=∠ABC=40°推出∠EBD=∠C,推出BE=EC,推出BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.【解答】证明:延长AB到F,使BF=BD,连DF,∴∠F=∠BDF,∵∠A:∠B:∠C=3:4:2,∴∠ABC=80°,∠ACB=40°,∴∠F=40°,∠F=∠ACB,∵AD是平分线,∴∠BAD=∠CAD,在△ADF和△ADC中,,∴△ADF≌△ADC,∴AF=AC,∵BE是角平分线,∴∠CBE=∠ABC=40°∴∠EBD=∠C,∴BE=EC,∴BE+AE=EC+AE=AC=AF=AB+BF=AB+BD.∴AB+BD=AE+BE.2017年3月1日。
“大梦杯”福建省初中数学竞赛试题参考答案

2019年“大梦杯”福建省初中数学竞赛试题参考答案考试时间2019年3月17日9∶00-11∶00满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若一次函数2y x =+与反比例函数4y x=的图像交于11()A x y ,,22()B x y ,两点,则1212x x y y +的值为()A .8B .6C .6-D .8-【答案】D【解答】由24y x y x =+⎧⎪⎨=⎪⎩,得2240x x +-=……………①。
依题意,1x ,2x 是方程①的两根,于是122x x +=-,124x x =-。
∴121212121212441616484x x y y x x x x x x x x +=+⋅=+=-+=--。
2.如图,ABC △为圆O 的内接三角形,D 为BC 中点,E 为OA 中点,40ABC ∠=︒,80BCA ∠=︒,则OED ∠的大小为()A .15︒B .18︒C .20︒D .22︒【答案】C【解答】如图,连结OC 。
由40ABC ∠=︒,80BCA ∠=︒,得60BAC ∠=︒。
∵D 为BC 中点,∴OD BC ⊥,1602DOC BOC BAC ∠=∠=∠=︒。
∴30OCD ∠=︒,12OD OC =。
又E 为OA 中点,∴12OE OA OD ==。
结合40ABC ∠=︒,知24060140EOD AOC COD ∠=∠+∠=⨯︒+︒=︒,(第2题图)(第2题答题图)11(180)(180140)2022OED EOD ∠=︒-∠=︒-︒=︒。
3.已知二次函数2()2f x x ax b =++,若()(1)f a f b =+,其中1a b ≠+,则(1)(2)f f +的值为()A .8B .10C .12D .14【答案】A【解答】由已知条件及二次函数图像的对称性,知124a b a++=-。
2018年度初级中学数学联赛试题参考材料内容规范标准答案和评分规范标准整理汇编

2018 年初中数学联赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设 7 分和 0 分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试(A)一、选择题:(本题满分 42 分,每小题 7 分)1.设二次函数 y = x 2+ 2ax + a 2的图象的顶点为 A ,与 x 轴的交点为 B , C .当△ ABC 为等边三角2形时,其边长为 ()A. 62 2 .C. 2 3D. 3 2 .【答】C.由题设知 A (-a ,- a 2 ) .设 B (x ,0) , C (x ,0) ,二次函数的图象的对称轴与 x 轴的交点为 D ,则2 12= 4a2- 4 ⨯ a 2BC =| x - x2 |= (x + x )2 - 4x x 2 = 2a 2 .11212a 233又 AD = BC ,则| - |= ⋅ 2a 2 ,解得 a 2 = 6 或 a 2 = 0 (舍去).2 2 2所以,△ ABC 的边长 BC = 2a 2= 2 .32.如图,在矩形 ABCD ∠BAD的平分线交 BD于点 E AB =1 ∠CAE = 15︒,则 BE =)中,,,(32 -1.D.-1.A. .B..C. 2 32 3【答】D.E延长 AE 交 BC 于点 F ,过点 E 作 BC 的垂线,垂足为 H .由已知得 ∠BAF = ∠FAD = ∠AFB = ∠HEF = 45︒, BF = AB = 1,B∠EBH = ∠ACB = 30︒ .设 BE = x ,则 HF = HE = x , BH = 3x .2 2因为 BF = BH + HF ,所以1 = 3x + x ,解得 x = -1.所以 BE =-1 .332 23.设 p , q 均为大于 3 的素数,则使 p 2 + 5 pq + 4q 2为完全平方数的素数对 ( p , q ) 的个数为( )A.1.B.2.C.3.D.4.【答】B.2018 年初中数学联赛试题参考答案及评分标准第 1 页(共 10 页)设 p 2 + 5 pq + 4q 2 = m 2 ( m 为自然数),则 ( p + 2q )2 + pq = m 2,即(m - p - 2q )(m + p + 2q ) = pq .由于 p , q 为素数,且 m + p + 2q > p , m + p + 2q > q ,所以 m - p - 2q =1 , m + p + 2q = pq ,从而 pq - 2 p - 4q -1 = 0 ,即 ( p - 4)(q - 2) = 9 ,所以 ( p , q ) = (5,11) 或 (7, 5) .所以,满足条件的素数对 ( p , q ) 的个数为 2.4.若实数 a , b 满足 a - b = 2,(1 - a )2 (1 + b ) 255-= 4 ,则 a- b=()abA.46.B.64.C.82.D.128.【答】C.(1 - a )2(1 + b )2由条件-= 4 得 a - b - 2a 2 - 2b 2 - 4ab + a 3 - b 3= 0 ,ba即 (a - b ) - 2[(a - b )2 + 4ab ] + (a - b )[(a - b )2+ 3ab ] = 0 ,又 a - b = 2,所以 2 - 2[4 + 4ab ] + 2[4 + 3ab ] = 0 ,解得 ab = 1.所以 a 2 + b 2 = (a - b ) 2 + 2ab = 6 ,a 3 -b 3 = ( a - b )[( a - b ) 2 + 3ab ] =14 , a 5 - b 5 = (a 2 + b 2 )(a 3 - b 3 ) - a 2b 2(a - b ) = 82 .5.对任意的整数 x , y ,定义 x @ y = x + y - xy ,则使得 ( x @ y ) @ z + ( y @ z ) @ x +( z @ x ) @ y= 0 的整数组 (x , y , z ) 的个数为( )A.1.B.2.C.3.D.4.【答】D.(x @ y ) @ z = (x + y - xy ) @ z = (x + y - xy ) + z - (x + y - xy )z = x + y + z - xy - yz - zx + xyz ,由对称性,同样可得( y @ z ) @ x = x + y + z - xy - yz - zx + xyz , (z @ x ) @ y = x + y + z - xy - yz - zx + xyz .所以,由已知可得 x + y + z - xy - yz - zx + xyz = 0 ,即 (x -1)( y -1)(z -1) = -1.所以, x , y , z 为整数时,只能有以下几种情况:⎧ x -1 = 1,⎧ x -1 = 1,⎧x -1 = -1,⎧x -1 = -1,⎪⎪⎪= 1, ⎪= -1,⎨ y -1 = 1,或 ⎨y -1 = -1,或 ⎨ y -1或 ⎨y -1 ⎪ ⎪ ⎪= 1,⎪-1 = -1,⎩z -1 = -1, ⎩ z -1 = 1, ⎩ z -1 ⎩z所以, (x , y , z ) = (2,2,0) 或 (2,0,2) 或 (0,2,2) 或 (0,0,0) ,故共有 4 个符合要求的整数组.2018 年初中数学联赛试题参考答案及评分标准 第 2 页(共 10 页)6.设 M =1 + 1 + 1 + + 1 ,则 1 的整数部分是()2018 2019 2020 2050MA.60.B.61.C.62.D.63.【答】B.因为 M < 20181 ⨯ 33 ,所以 M 1 >201833 = 61 335.又 M = ( 20181 + 20191 + + 20301) + ( 20311+ 20321+ + 20501) > 20301 ⨯13 + 20501 ⨯ 20 = 832301345,所以 M 1 <832301345 = 6111851345 ,故 M 1的整数部分为 61.二、填空题:(本题满分 28 分,每小题 7 分)1.如图,在平行四边形 ABCD 中,BC = 2AB ,CE ⊥ AB 于 E ,F 为 AD 的中点,若 ∠AEF = 48︒, 则 ∠B = _______.【答】 84︒ . AF设 BC 的中点为 G ,连结 FG 交 CE 于 H ,由题设条件知 FGCD 为菱形.D由 AB // FG // DC 及 F 为 AD 的中点,知 H 为 CE 的中点.又 CE ⊥ AB ,所以 CE ⊥ FG ,所以 FH 垂直平分 CE ,故E H∠DFC = ∠GFC = ∠EFG = ∠AEF = 48︒ .BCG所以 ∠B = ∠FGC =180︒ - 2 ⨯ 48︒ = 84︒ .2.若实数 x , y 满足 x 3 + y 3+ 1 (x + y ) = 15 ,则 x + y 的最大值为.42【答】3.由 x 3 + y 3 + 1 (x + y ) =15可得 ( x + y )( x 2 - xy + y 2 ) + 1 ( x + y ) =15,即4242( x + y )( x 2 - xy + y 2 + 1 ) = 15.①4 2令 x + y = k ,注意到 x 2 - xy + y 2 +14 = ( x - 2y ) 2 + 43y 2 +14 > 0 ,故 x + y = k > 0 .又因为 x 2 - xy + y 2 + 14 = ( x + y ) 2 - 3xy + 14 ,故由①式可得 k 3 - 3xyk + 14 k = 152 ,所以k 3 + 1k - 15xy =4 2 .3kk 3 + 1 k - 15 于是, x , y 可看作关于 t 的一元二次方程 t 2- kt + 4 2= 0 的两根,所以3kk 3 + 1 k - 152 ∆ = ( - k ) 2 - 4 ⋅4 ≥ 0 ,3k化简得 k 3 + k - 30 ≤ 0 ,即 (k - 3)(k 2+ 3k +10) ≤ 0 ,所以 0 < k ≤ 3.故 x + y 的最大值为 3.2018 年初中数学联赛试题参考答案及评分标准 第 3 页(共 10 页)3.没有重复数字且不为 5 的倍数的五位数的个数为 .【答】21504.显然首位数字不能为 0,末位不能为 0 和 5.当首位数字不为 5 时,则首位只能选 0,5 之外的 8 个数.相应地个位数只能选除 0,5 及万位数之外的 7 个数,千位上只能选万位和个位之外的 8 个数,百位上只能选剩下的 7 个数,十位上只能选剩下的 6 个数.所以,此时满足条件的五位数的个数为 8⨯7 ⨯8⨯7 ⨯6 = 18816 个.当首位数字为 5 时,则个位有 8 个数可选,依次千位有 8 个数可选,百位有 7 个数可选, 十位有 6 个数可选.所以,此时满足条件的五位数的个数为 8⨯8⨯ 7 ⨯ 6 = 2688 个.所以,满足条件的五位数的个数为18816 + 2688 = 21504 (个).4.已知实数 a ,b , c 满足 a + b + c = 022 2a 5 +b 5 +c 5, a+ b + c =1 ,则=.abc【答】 5 .2由已知条件可得 ab + bc + ca = 1 [(a + b + c )2 - (a 2 + b 2 + c 2 )] = - 1 ,a 3 + b 3+ c 3 = 3abc ,所以2 2a 5 +b 5 +c 5 = (a 2 + b 2 + c 2 )(a 3 + b 3 + c 3 ) -[a 2 (b 3 + c 3 ) + b 2 (a 3 + c 3 ) + c 2 (a 3 + b 3 )]= 3abc - [ a 2b 2 ( a + b ) + a 2 c 2 ( a + c ) + b 2 c 2 (b + c )] = 3abc + (a 2b 2c + a 2c 2b + b 2c 2a )= 3abc + abc (ab + bc + ca ) = 3abc -12 abc =52 abc .a 5 +b 5 +c 5 = 5所以abc 2 .第一试(B)一、选择题:(本题满分 42 分,每小题 7 分)1.满足 (x 2 + x -1) x +2= 1的整数 x 的个数为()A.1.B.2.C.3.D.4.【答】C.当 x + 2 = 0 且 x 2+ x -1 ≠ 0 时, x = -2 .当 x 2 + x -1 = 1时, x = -2 或 x = 1.当 x 2+ x -1 = -1且 x + 2 为偶数时, x = 0 .所以,满足条件的整数 x 有 3 个. 2.已知x 1 , x 2 , x 3 ( x 1 < x 2 < x 3 ) 为关于 x 的方程 x 3 - 3 x 2 + ( a +2) x- a = 0 的三个实数根,则4x 1 - x 12 + x 22 + x 32 =( )A.5.B.6.C.7.D.8.2018 年初中数学联赛试题参考答案及评分标准第 4 页(共 10 页)【答】A.方程即 (x -1)(x 2- 2x + a ) = 0 ,它的一个实数根为 1,另外两个实数根之和为 2,其中必有一根小 于 1,另一根大于 1,于是 x 2 = 1, x 1 + x 3 = 2 ,故4 x - x 2 + x 2 + x 2 = ( x + x )( x - x ) + 4 x + 1 = 2( x - x ) + 4 x +1 = 2( x + x ) + 1 =5 .112331311311313.已知点 E , F 分别在正方形 ABCD 的边 CD , AD 上, CD = 4CE , ∠EFB = ∠FBC ,则 tan ∠ABF = ( )A. 1 .B. 3 .C. 2 .D. 3 .2 52 2【答】B.不妨设 CD = 4 ,则 CE = 1, DE = 3.设 DF = x ,则 AF = 4 - x , EF = x 2+ 9 .作 BH ⊥ EF 于点 H .因为 ∠EFB = ∠FBC = ∠AFB , ∠BAF = 90︒ = ∠BHF , BF 公共,所以△ BAF ≌△ BHF ,所以 BH = BA = 4 .由 S 四边形= S ∆ABF + S ∆BEF + S ∆DEF + S∆BCE得AFDABCD111142 = ⋅ 4 ⋅ (4 - x ) + ⋅ 4 ⋅ x 2+ 9 + ⋅3 ⋅ x + ⋅ 4 ⋅1,2 2 2 2H8解得 x = .5E12 AF 3C所以 AF = 4 - x = 5 , tan ∠ABF = AB =5 .B4.方程 3 += 39 + x x 的实数根的个数为( )A.0.B.1.C.2.D.3. 【答】B.令 y = 9 + x ,则 y ≥ 0 ,且 x = y 2 -9 ,原方程变为 3 + y = 3 y 2 - 9 ,解得 y =1或 y = 6 ,从而可得 x = -8 或 x = 27 .检验可知: x = -8 是增根,舍去; x = 27 是原方程的实数根. 所以,原方程只有 1 个实数根.5.设 a , b , c 为三个实数,它们中任何一个数加上其余两数之积的 2017 倍都等于 2018,则这样的三元数组 (a , b , c ) 的个数为( )A.4.B.5.C.6.D.7.【答】B.由已知得, a + 2017bc = 2018 , b + 2017ac = 2018 , c + 2017ab = 2018 ,两两作差,可得 (a - b )(1 - 2017c ) = 0 , (b - c )(1 - 2017a ) = 0 , (c - a )(1 - 2017b ) = 0 .2018 年初中数学联赛试题参考答案及评分标准 第 5 页(共 10 页)由 (a - b )(1 - 2017c ) = 0 ,可得 a = b 或 c = 20171.(1)当 a = b = c 时,有 2017a 2+ a - 2018 = 0 ,解得 a = 1 或 a = - 2018 .2017(2)当 a = b ≠ c 时,解得 a = b =1 , c = 2018 - 1 .2017 2017(3)当 a ≠ b 时,c = 1 ,此时有:a =1 , b = 2018 - 1 ,或 a = 2018 - 1 , b = 1 . 2017 20172017 2017 2017故这样的三元数组 (a , b , c ) 共有 5 个.6.已知实数 a , b 满足 a 3 - 3a 2 + 5a = 1, b 3 - 3b 2+ 5b = 5 ,则 a + b = ()A.2.B.3.C.4.D.5.【答】A.有已知条件可得 (a -1)3+ 2(a -1) = -2 , (b -1)3+ 2(b -1) = 2 ,两式相加得( a - 1) 3 + 2( a - 1) + (b - 1) 3 + 2(b - 1) = 0 ,因式分解得 ( a + b - 2)[( a - 1) 2 - ( a - 1)(b - 1) + (b - 1) 2 + 2] = 0 .因为(a -1)2 - (a -1)(b -1) + (b -1)2 + 2 = [(a -1) - 1 (b -1)]2 + 3 (b -1)2+ 2 > 0 ,2 4所以 a + b - 2 = 0 ,因此 a + b = 2 .二、填空题:(本题满分 28 分,每小题 7 分)1.已知 p , q , r 为素数,且 pqr 整除 pq + qr + rp -1,则 p + q + r = _______.【答】10 .设 k = pq + qr + rp -1 = 1 + 1 + 1 -1 ,由题意知 k 是正整数,又 p , q , r ≥2 ,所以 k <3 ,从 pqrp q r pqr 2而 k = 1 ,即有 pq + qr + rp -1 = pqr ,于是可知 p , q , r 互不相等.当 2 ≤ p < q < r 时, pqr = pq + qr + rp -1 < 3qr ,所以 q < 3 ,故 q = 2 .于是 2qr = qr + 2q + 2r-1,故 (q - 2)(r - 2) = 3,所以 q - 2 = 1, r - 2 = 3 ,即 q = 3, r = 5 ,所以, ( p , q , r ) = (2,3,5) .再由 p , q , r 的对称性知,所有可能的数组 ( p , q , r ) 共有 6 组,即 (2,3,5),(2,5,3) ,(3,2,5) ,(3,5,2) ,(5,2,3) , (5,3,2) .于是 p + q + r = 10 .2018 年初中数学联赛试题参考答案及评分标准 第 6 页(共 10 页)2.已知两个正整数的和比它们的积小 1000,若其中较大的数是完全平方数,则较小的数为 .【答】8.设这两个数为 m 2, n (m 2> n ) ,则 m 2+ n = m 2n -1000 ,即 ( m 2 - 1)( n - 1) =1001 .又1001 = 1001⨯1 = 143 ⨯ 7 = 91⨯11 = 77 ⨯13 ,所以 ( m 2 - 1, n -1) = (1001,1) 或 (143, 7) 或 (91,11)或 (77,13) ,验证可知只有 (m 2 -1, n -1) = (143,7) 满足条件,此时 m 2= 144, n = 8 .3 . 已知 D 是 △ ABC 内一点, E 是 AC 的中点, AB = 6 , BC =10 , ∠BAD = ∠BCD ,∠EDC = ∠ABD ,则 DE = .【答】4.F延长 CD 至 F ,使 DF = DC ,则 DE // AF 且 DE = 1 AF ,2 A 所以 ∠AFD = ∠EDC = ∠ABD ,故 A , F , B , D 四点共圆,于是DE∠BFD = ∠BAD = ∠BCD ,所以 BF = BC = 10 ,且 BD ⊥ FC ,故 ∠FAB = ∠FDB = 90︒ .BC1又 AB = 6 ,故 AF = = 8 ,所以 DE = AF = 4 .102 - 6224.已知二次函数 y = x 2 + 2(m + 2n +1)x + (m 2 + 4n 2+ 50) 的图象在 x 轴的上方,则满足条件的正整数对 (m , n ) 的个数为.【答】16.因为二次函数的图象在 x 轴的上方,所以 ∆ = [2(m + 2n +1)]2- 4(m 2+ 4n 2+ 50) < 0 ,整理得4mn + 2m + 4n < 49 ,即 (m +1)(2n +1) <512 .因为 m , n 为正整数,所以 (m +1)(2n +1) ≤ 25 .又 m +1 ≥ 2 ,所以 2n +1 <252 ,故 n ≤ 5 .当 n = 1时, m +1 ≤ 253 ,故 m ≤ 223 ,符合条件的正整数对 (m , n ) 有 8 个;当 n = 2 时, m +1 ≤ 5 ,故 m ≤ 4 ,符合条件的正整数对 (m , n ) 有 4 个; 当 n = 3 时, m +1 ≤ 257 ,故 m ≤187 ,符合条件的正整数对 (m , n ) 有 2 个;当 n = 4 时, m +1 ≤259 ,故 m ≤ 179 ,符合条件的正整数对 (m , n ) 有 1 个;当 n = 5 时, m +1 ≤ 1125 ,故 m ≤ 1411 ,符合条件的正整数对 (m , n ) 有 1 个.综合可知:符合条件的正整数对 (m , n ) 有 8+4+2+1+1=16 个.2018 年初中数学联赛试题参考答案及评分标准 第 7 页(共 10 页)第二试 (A )一、(本题满分 20 分)设 a , b , c , d 为四个不同的实数,若 a , b 为方程 x 2-10cx -11d = 0 的根,c , d为方程 x 2-10ax -11b = 0 的根,求 a + b + c + d 的值.解 由韦达定理得 a + b =10c , c + d =10a ,两式相加得 a + b + c + d = 10(a + c ) .……………………5 分因为 a 是方程 x 2-10cx -11d = 0 的根,所以 a 2-10ac -11d = 0 ,又 d = 10a - c ,所以a 2-110a +11c -10ac = 0 .① ……………………10 分 类似可得 c 2-110c +11a -10ac = 0 . ②……………………15 分①-②得 (a - c )(a + c -121) = 0 .因为 a ≠ c ,所以 a + c = 121,所以 a + b + c + d =10(a + c ) =1210 . ……………………20 分二、(本题满分 25 分)如图,在扇形 OAB 中, ∠AOB = 90︒,OA = 12 ,点 C 在 OA 上, AC = 4 ,点 D 为 OB 的中点,点 E 为弧 AB 上的动点, OE 与 CD 的交点为F . (1)当四边形 ODEC 的面积 S 最大时,求 EF ; (2)求 CE + 2DE 的最小值.解 (1)分别过 O , E 作 CD 的垂线,垂足为 M , N .由 OD = 6, OC = 8 ,得 CD = 10 .所以S = S ∆OCD + S ∆ECD = 12 CD ⋅ (OM + EN )≤ 12 CD ⋅OE = 12 ⨯10 ⨯12 = 60 ,当 OE ⊥ DC 时, S 取得最大值 60.ACEM FNODBG……………………5 分此时, EF = OE - OF = 12 - 6 ⨯8 = 36 .……………………10 分510(2)延长 OB 至点 G ,使 BG = OB = 12 ,连结 GC , GE .因为 OD = OE = 1 ,∠DOE = ∠EOG ,所以△ ODE ∽△ OEG ,所以 DE = 1 ,故 EG = 2DE .OEOG2EG 2……………………20 分所以 CE + 2DE = CE + EG ≥ CG = 242 + 82= 8 ,当 C , E , G 三点共线时等号成立.10 故 CE + 2DE 的最小值为 8.10 ……………………25 分2018 年初中数学联赛试题参考答案及评分标准 第 8 页(共 10 页)m 3 + n 3 - m 2 n 2三、(本题满分 25 分)求所有的正整数 m , n ,使得是非负整数.解 记 S = m 3 + n 3 - m 2 n 2 ,则(m + n )2S =(m + n )[(m + n )2 - 3mn ] - m 2 n 2= (m + n ) - 3mn - ( mn )2 . (m + n )2 m + nm + n因为 m , n 为正整数,故可令mn = q , p , q 为正整数,且 ( p , q ) = 1.m + n p于是 S = (m + n ) -3q - q 2 = (m + n ) - 3 pq + q2.pp 2 p 2因为 S 为非负整数,所以 p | q 2,又 ( p , q ) = 1,故 p = 1,即 (m + n ) | mn .①……………………10 分所以 n 2= n - mn 是整数,所以 (m + n ) | n 2 ,故 n 2 ≥ m + n ,即 n 2- m ≥ n .m + n m + n又由 S ≥ 0 ,知 m 3 + n 3 - m 2n 2 ≥ 0 .② 所以 n 3 ≥ m 2n 2 - m 3 = m 2(n 2- m ) ≥ m 2n ,所以 n ≥ m .由对称性,同理可得 m ≥ n ,故 m = n .……………………20 分把 m = n 代入①,得 2 | m ,则 m ≥ 2 .把 m = n 代入②,得 2m 3- m 4≥ 0 ,即 m ≤ 2 . 故 m = 2 .所以,满足条件的正整数 m , n 为 m = 2 , n = 2 .……………………25 分第二试 (B )一、(本题满分 20 分)若实数 a , b , c 满足 (a + b + c )(1 + 1 + 1 ) = 9 ,求 5a +b - 5c b + c - 5a c + a - 5b (a + b + c )( 1 + 1 + 1 ) 的值.a bc解 记 a + b + c = x , ab + bc + ca = y , abc = z ,则111111(a + b + c )(++) = x (++)a +b - 5c b + c - 5a c + a - 5b x - 6a x - 6b x - 6c= x [3x 2-12(a + b + c )x + 36(ab + bc + ca )] = x ( -9 x 2 + 36 y ),x - 6(a + b + c )x + 36(ab + bc + ca )x - 216abc -5 x 3 + 36 xy - 216z ……………………10 分2018 年初中数学联赛试题参考答案及评分标准 第 9 页(共 10 页).\结合已知条件可得x ( -9 x 2 + 36 y ) = 9 ,整理得 xy = 27 z .所以-5 x 3+ 36 xy - 216 z 52(a + b + c )( 1 + 1 + 1 ) = xy = 27 .……………………20 分a b zc 2二、(本题满分 25 分)如图,点 E 在四边形 ABCD 的边 AB 上,△ ABC 和△ CDE 都是等腰直角三角形, AB = AC , DE = DC .(1)证明: AD // BC ;(2)设 AC 与 DE 交于点 P ,如果 ∠ACE = 30︒,求 DP .P E解 (1)由题意知 ∠ACB = ∠DCE = 45︒,BC = AC ,EC =,ADP所以 ∠DCA = ∠ECB , AC = DC ,所以△ ADC ∽△ BEC ,故 ∠DAC =EBC EC∠EBC = 45︒ ,所以 ∠DAC = ∠ACB ,所以 AD // BC .……………………10 分BC(2)设 AE = x ,因为 ∠ACE = 30︒,可得 AC = 3x , CE = 2x , DE = DC = 2x . 因为 ∠EAP = ∠CDP = 90︒ ,∠EPA = ∠CPD ,所以△ APE ∽△ DPC ,故可得 S ∆APE =12 S ∆DPC .……………………15 分又 S ∆EPC + S ∆APE = S ∆ACE =23x 2 , S ∆EPC + S ∆DPC = S ∆CDE = x 2 ,于是可得S ∆DPC = (2 -= (-1)x 2.3)x 2 , S ∆EPC 3 ……………………20 分S∆DPC 2 --1所以DP ==3 = 3 .……………………25 分PE S∆EPC -123三、(本题满分 25 分)设 x 是一个四位数, x 的各位数字之和为 m , x +1的各位数字之和为 n ,并且 m 与 n 的最大公约数是一个大于 2 的素数.求 x .解 设 x = abcd ,由题设知 m 与 n 的最大公约数 (m , n ) 为大于 2 的素数.若 d ≠ 9 ,则 n = m +1 ,所以 ( m , n ) =1,矛盾,故 d = 9 .……………………5 分若 c ≠ 9 ,则 n = m +1 - 9 = m -8 ,故 ( m , n ) = ( m ,8) ,它不可能是大于 2 的素数,矛盾,故 c = 9 .……………………10 分若 b = 9 ,显然 a ≠ 9 ,所以 n = m +1- 9 - 9 - 9 = m - 26 ,故 ( m , n ) = ( m , 26) =13 ,但此时可得n ≥ 13 , m = n + 26 ≥ 39 > 36 ,矛盾.……………………15 分若 b ≠ 9 ,则 n = m +1- 9 - 9 = m -17 ,故 ( m , n ) = ( m ,17) =17 ,只可能 n = 17, m = 34 .于是可得 x = 8899 或 9799 .……………………20 分……………………25 分2018 年初中数学联赛试题参考答案及评分标准第 10 页(共 10 页)。
大梦杯福建省初中数学竞赛试题

“大梦杯”福建省初中数学竞赛试题参考答案满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.设2323a =++-,则1a a+的整数部分为( ) A .1 B .2 C .3 D .4 【答案】 B【解答】由22322323236a =+++⋅-+-=,知6a =。
于是166a a +=+,2111()62866a a +=++=+,214()9a a <+<。
因此,1a a+的整数部分为2。
(注:4234233131232362222a +-+-=++-=+=+=) 2.方程22()32x x x +=-的所有实数根之和为( ) A .1 B .3 C .5 D .7 【答案】 A 【解答】方程22()32x x x +=-化为2222(2)3(2)x x x x -+=-。
即3251060x x x -+-=,2(1)(46)0x x x --+=。
解得1x =。
经检验1x =是原方程的根。
∴ 原方程所有实数根之和为1。
3.如图,A 、B 、C 三点均在二次函数2y x =的图像上,M 为线段AC 的中点,BM y ∥轴,且2MB =。
设A 、C 两点的横坐标分别为1t 、2t (21t t >),则21t t -的值为( )A .3B .23C .22±D .22 【答案】 D【解答】依题意线段AC 的中点M 的坐标为221212()22t t t t ++,。
(第3题)由BM y ∥轴,且2BM =,知B 点坐标为221212(2)22t t t t ++-,。
由点B 在抛物线2y x =上,知22212122()22t t t t++-=。
整理,得22221211222282t t t t t t +-=++,即221()8t t -=。
2018九年级数学竞赛试卷(含答案)

九年级数学竞赛试卷考试时间:100分钟 总分:150分姓名: 班级: 得分:一、选择题(每题5分,共50分)1、如果|x-2 |+x-2=O ,那么x 的取值范围是( ).A .x>2B .x<2C .x≥2D .x≤22、已知n 是整数,现有两个代数式:(1)2n+3,(2)4n-l 其中,能表示“任意奇数”的( ).A .只有(1)B .只有(2)C .有(1)和(2)D .一个也没有3、在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是 ( )A.∠AB.∠BC.∠CD.∠B 或∠C4、如果有理数a 、b 、c 满足关系a<b<0<c ,那么代数式32cab ac bc -的值( ). A .必为正数 B .必为负数 C .可正可负 D .可能为O 5、已知一次函数y=mx+│m+1│的图像与y 轴交于点(0,3),且y 随x 的增大而减小,则m 的值为( ).A .2B .-4C .-2或-4D .2或-46、设y=ax 15+bx 13+cx 11-5(a 、b 、c 为常数),已知当x=7时,y=7,则x= -7时,y 的值等于( )A 、-7B 、-17C 、17D 、不确定7、已知b>a>0,a 2+b 2=4ab ,则ba b a -+等于( ). A .-21B . 3C .2D .-38、将一个正方形分割成n 个小正方形(n>1),则n 不可能取( ).A .4B .5C .8D .99、若x 取整数,则使分式1-2x 36x +的值为整数的x 值有( ). (A)3个 (B)4个 (C)6个 (D)8个10、已知1x ,2x ,3x 的平均数为5,1y ,2y ,3y 的平均数为7,则1123x y +,2223x y +,3323x y +的平均数为( )(A)31(B)313 (C)935 (D)17二、填空题(每题8分,共40分)11、已知a 是质数,b 是奇数,且a 2+b=2001,则a+b= . 12、已知 m >0 ,且对任意整数 k ,2018123k m+均为整数,则 m 的最大值为 . 13、已知某三角形的三条高线长 a ,b ,c 为互不相等的整数,则 a + b + c 的最小值 为 .14、如果用四则运算的加、减、除法定义一种新的运算,对于任意实数x 、y 有则=15、如图5所示,圆的周长为4个单位长度,在圆的4等分点处标上0,1,2,3.先让圆周上数字0所对应的数与数轴上的数-1所对应的点重合,再让数轴按逆时针方向绕在该圆上,那么数轴上的数-2007将与圆周上的数字_________重合.二、简答题(每题20分,共60分)16、现有两种理财方式供王老师选择.方案一:购买一款分红产品,前三年每年 年初交 10 万元,第 6 年年初返 6 万元,以后每年处返1.5 万元;方案二:购 买一款年利率 5%,满一年计息的储蓄产品,第一年初存款10 万元,接下来 两年每年年初追加本金 10 万元,并将之前的本息全部续存.请问哪个选择更划算?请说明理由.(参考数据:1.054 + 1.053 + 1.052 =3.47563125 )y x yx y x -+=*()()31*191211**-5 -4 -3 -2 -117、一筐苹果,若分给全班同学每人3个,则还剩下25 个;若全班同学一起吃,其中5个同学每人每天吃1个,其他同学每人每天吃2个,则恰好用若干天吃完.问筐里最多共有多少个苹果?18、求证:不存在3个有理数的平方和等于15.九年级答案:一、DAABB BDBBA二、11、1999 12、2/3 13、9 14、163/113 15、2 三、1617、18。
2018年“大梦杯”福建省初中数学竞赛试题+参考答案及评分标准
2018年“大梦杯〞省初中数学竞赛试题考试时间 2018年3月18日 9∶00-11∶00 总分值150分一、选择题〔共5小题,每题7分,共35分〕。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分〕1.假设关于x 的方程244310x mx m +--=有两个相等的实数根,那么32442m m m ++-的值为〔 〕A .3-B .2-C .1-D .12.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n 〔m n <〕。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
假设二次函数2y ax =的图像过C 、F 两点,那么nm=〔 〕A .31+B .21+C .231-D .221-3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,那么AEAC=〔 〕 A .25B .35C .37D .474.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=︒,假设ABC △外接圆的半径 为2,那么AH =〔 〕A .23B .22C .4D .31+5.满足方程22419151x xy y -+=的整数对()x y ,有〔 〕 A .0对 B .2对 C .4对D .6对HOBCA〔第4题图〕〔第2题图〕 EG〔第3题图〕二、填空题〔共5小题,每题7分,共35分〕6.a ,b ,c 为正整数,且a b c >>。
假设b c +,a c +,a b +是三个连续正整数的平方,那么222a b c ++的最小值为。
7.如图,ABCD 为矩形,E 为对角线AC 的中点,A 、B 在x 轴上。
假设函数4y x=〔0x >〕的图像过D 、E 两点,那么矩形ABCD 的面积为。
8.如图,ABC △是边长为8的正三角形,D 为AB 边上一点,1O ⊙为ACD △的切圆,2O ⊙为CDB △的边DB 上的旁切圆。
2018年福建省数学奥校初三上期期末测试题(含解答)

福建省数学奥林匹克学校2018~2019学年第一学期初三年段数学竞赛试题第二试考试日期:2018年12月28日下午2:00~4:00;考试时间:120分钟;满分:100分 考生注意:请将所有答案填写在答卷纸上,否则不计分 一、选择题:(每小题4分,共计40分): 1、已知点P 在第二象限,且到x 轴的距离是2,到y 轴的距离是3,则点P 的坐标是( ) A、(3,2) B、(-2,3) C、(-3,2) D、(3,-2)2、已知Rt △ABC 中∠C=900,AB=10 cm , AC=5 cm ,则以C 为圆心,4 cm为半径的圆与AB 的关系为( )A、相离 B、相切 C、相交 D、不能确定3、如图1,PA 、PB 分别切⊙O 于A 、B 两点,∠P=700,则∠C 等于( )A 、700B 、550C 、1100D 、14004、已知一次函数k kx y -=,y 随x 的减少而减少,则该函数的图象经过 ( )A 、第一、二、三象限B 、第一、二、四象限C 、第一、三、四象限D 、第二、三、四象限5、如图,PAB 是⊙O 的割线,PO 交⊙O 于C ,若PC=CO ,PA=4,AB=5,则⊙O 的半径为( )A 、6B 、23C 、32D 、96、如图:OA 、BA 分别表示甲、乙两名学生运动的图象,图中s 和t 分别表示运动路程和时间,根据图象判断快者的速度比慢者的速度每秒快( )A 、2.5米B 、2米C 、1.5米D 、1米 7、抛物线222+-=x x y 的顶点坐标是( )A、(2,0) B、(1,1) C、(-1,1) D、(1,2) 8、若A(a ,6)、B(2,a )、C(0,2)三点共线,则a 的值为( ) A 、4或-2 B 、4或-1 C 、-4或1 D 、-4或29、如图,⊙O 是Rt △ABC 的内切圆,∠C=900,AO 的延长线交BC 于D 点,AC=4,CD=1,则⊙O 的半径为( )A 、1.25B 、0.8C 、0.75D 、1.210、如图,⊙O 1和⊙O 2内切于P ,⊙O 2的弦AB 经过⊙O 1的圆心O 1交⊙O 1于C 、D ,若AC :CD :DB=3:4:2,则⊙O 1和⊙O 2的直径之比为( ) A 、2:7 B 、2:5 C 、1:4 D 、1:3 二、填空题:(每小题4分,共计40分)1、若直线y=-x +m 与直线y=2x +n 的交点关于x 轴对称的点的坐标是(1,2),则mn= ;2、如图,梯形ABCD 中,AD ∥BC ,DC ⊥BC ,AB=8,BC=5,若以AB 为直径的⊙O 与DC 相切于点E ,则CD= ;3、HJ 牌小汽车的油箱可装汽油30升,原来装有汽油10升,现在再加汽油x 升,如果每升汽油3元,油箱内的汽油总价y (元)与x (升)之间的函数式为: ; 4、如图,P 是反比例函数xky的图象上一点,过点P 分别向x 轴、y 轴作垂线,所得到的图中阴影部分的面积是6,则这个反比例函数解析式是 ;5、已知AB 是半圆O 的直径,P 是AB 延长线上一点,PC 切半圆于C 点, 若2⌒ BC =⌒ AC ,则∠P 的度数为 ;6、已知抛物线y=x 2+bx +c 的对称轴为x=2,当x 时,y 随x 的增大而减小。
大梦杯数学竞赛试题及答案

大梦杯数学竞赛试题及答案【试题一】题目:已知函数 \(f(x) = 3x^2 - 2x + 1\),求函数的极值。
【答案】首先,我们对函数 \(f(x)\) 求导得到 \(f'(x) = 6x - 2\)。
令导数等于零,解得 \(x = \frac{1}{3}\)。
将 \(x = \frac{1}{3}\) 代入原函数,得到 \(f(\frac{1}{3}) = \frac{8}{3}\)。
由于导数在 \(x < \frac{1}{3}\) 时为负,在 \(x > \frac{1}{3}\) 时为正,所以\(x = \frac{1}{3}\) 处函数取得极小值,极小值为\(\frac{8}{3}\)。
【试题二】题目:解方程 \(2x^2 - 5x + 3 = 0\)。
【答案】这是一个一元二次方程,我们可以使用求根公式来解它。
求根公式为\(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)。
在这个方程中,\(a = 2\),\(b = -5\),\(c = 3\)。
计算判别式 \(\Delta = b^2 - 4ac = (-5)^2 - 4 \cdot 2 \cdot 3 = 25 - 24 = 1\)。
因为判别式大于零,所以有两个实根。
代入求根公式得到 \(x = \frac{5 \pm1}{4}\),即 \(x_1 = 2\) 和 \(x_2 = \frac{3}{2}\)。
【试题三】题目:证明:对于任意正整数 \(n\),\(1^3 + 2^3 + 3^3 + \ldots + n^3 = \left(\frac{n(n + 1)}{2}\right)^2\)。
【答案】我们使用数学归纳法来证明这个等式。
首先验证 \(n = 1\) 时等式成立,左边是 \(1^3 = 1\),右边是 \(\left(\frac{1(1 +1)}{2}\right)^2 = 1\),等式成立。
福建省初中数学竞赛试卷

福建省初中数学竞赛试卷一、选择题(每题1分,共5分)1. 下列数中,是无理数的是()A. √9B. √16C. √2D. √12. 下列函数中,奇函数是()A. y = x²B. y = x³C. y = |x|D. y = x² + 13. 下列等式中,正确的是()A. a² + b² = (a + b)²B. (a + b)² = a² + 2ab + b²C. (a b)² = a² 2ab + b²D. a² b² = (a + b)(a b)4. 一个等差数列的前三项分别是1、3、5,那么第10项是()A. 19B. 21C. 23D. 255. 下列图形中,面积和周长都不变的是()A. 正方形B. 长方形C. 圆D. 三角形二、判断题(每题1分,共5分)1. 两个负数相乘,结果是正数。
()2. 平行线的性质是同位角相等。
()3. 任何两个奇数相加都是偶数。
()4. 一次函数的图像是一条直线。
()5. 相似三角形的面积比等于边长比的平方。
()三、填空题(每题1分,共5分)1. 若a:b=3:4,则(a+b):b=______。
2. 已知x² + x = 12,则x² + 2x + 1 = ______。
3. 一次函数y = 2x + 3的图像与y轴的交点坐标是______。
4. 若等腰三角形的底边长为10,腰长为8,则其面积为______。
5. 一个正方体的体积是64立方厘米,则其表面积是______平方厘米。
四、简答题(每题2分,共10分)1. 请解释有理数的概念。
2. 简述平行线的性质。
3. 什么是二次方程?请举例说明。
4. 如何求解一元一次不等式?5. 简述三角形相似的判定条件。
五、应用题(每题2分,共10分)1. 小明有3个苹果,小红的苹果数量是小明的2倍,他们一共有多少个苹果?2. 一辆汽车行驶100千米,速度为60千米/小时,求汽车行驶这段路程所需的时间。
2018年全国初中数学联合竞赛试题参考答案及评分标准【直接打印】精品

2018年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准.第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分.如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数.第一试一、选择题:(本题满分42分,每小题7分)1.已知21a ,32b,62c ,那么,,a b c 的大小关系是()A.ab cB.ac b C.bacD.b ca【答】C. 因为121a,132b,所以110ab,故ba .又(62)(21)6ca(21),而22(6)(21)3220,所以621,故ca .因此ba c .2.方程222334x xy y的整数解(,)x y 的组数为()A .3.B .4.C .5.D .6.【答】B. 方程即22()234xy y,显然x y 必须是偶数,所以可设2x y t ,则原方程变为22217ty,它的整数解为2,3,t y从而可求得原方程的整数解为(,)x y =(7,3),(1,3),(7,3),(1,3),共4组.3.已知正方形ABCD 的边长为1,E 为BC 边的延长线上一点,CE =1,连接AE ,与CD 交于点F ,连接BF 并延长与线段DE 交于点G ,则BG 的长为()A .63B .53C .263D .253【答】D.过点C 作CP//BG ,交DE 于点P.因为BC =CE =1,所以CP 是△BEG 的中位线,所以P 为EG 的中点.又因为AD =CE =1,AD//CE ,所以△ADF ≌△ECF ,所以CF =DF ,又CP//FG ,所以FG 是△DCP 的中位线,所以G 为DP 的中点.因此DG =GP =PE =13DE =23.连接BD ,易知∠BDC =∠EDC =45°,所以∠BDE =90°. 又BD =2,所以BG =22225BDDG293.4.已知实数,a b 满足221a b ,则44a ab b 的最小值为()PGFEBCADA .18. B .0. C .1. D .98.【答】B.442222222219()2122()48aabbab a bab a b ab ab .因为222||1ab a b ,所以1122ab ,从而311444ab,故2190()416ab,因此219902()488ab,即44908aabb.因此44a abb 的最小值为0,当22,22a b或22,22ab时取得.5.若方程22320x pxp 的两个不相等的实数根12,x x 满足232311224()xxxx ,则实数p的所有可能的值之和为()A .0.B .34. C .1.D .54.【答】 B.由一元二次方程的根与系数的关系可得122x x p ,1232x x p ,所以2222121212()2464x x x x x x p p,332212121212()[()3]2(496)xxx x x x x x p pp.又由232311224()x x x x 得223312124()x x x x ,所以2246442(496)p p p pp ,所以(43)(1)0p pp ,所以12330,,14p p p .代入检验可知:1230,4p p 均满足题意,31p 不满足题意. 因此,实数p 的所有可能的值之和为12330()44p p .6.由1,2,3,4这四个数字组成四位数abcd (数字可重复使用),要求满足a cb d .这样的四位数共有()A .36个.B .40个.C .44个.D .48个.【答】C.根据使用的不同数字的个数分类考虑:(1)只用1个数字,组成的四位数可以是1111,2222,3333,4444,共有4个.(2)使用2个不同的数字,使用的数字有6种可能(1、2,1、3,1、4,2、3,2、4,3、4).如果使用的数字是1、2,组成的四位数可以是1122,1221,2112,2211,共有4个;同样地,如果使用的数字是另外5种情况,组成的四位数也各有4个.因此,这样的四位数共有6×4=24个.(3)使用3个不同的数字,只能是1、2、2、3或2、3、3、4,组成的四位数可以是1232,2123,2321,3212,2343,3234,3432,4323,共有8个.(4)使用4个不同的数字1,2,3,4,组成的四位数可以是1243,1342,2134,2431,3124,3421,4213,4312,共有8个.因此,满足要求的四位数共有4+24+8+8=44个.二、填空题:(本题满分28分,每小题7分)1.已知互不相等的实数,,a b c 满足111abct b c a,则t_________.【答】1.由1a t b 得1bt a,代入1bt c得11t tac ,整理得2(1)()0ct ac ta c ①又由1c t a 可得1ac at ,代入①式得22()0ctatac ,即2()(1)0c a t,又c a ,所以210t,所以1t.验证可知:11,1a b caa时1t;11,1a bcaa时1t .因此,1t .2.使得521m是完全平方数的整数m 的个数为.【答】1.设2521mn (其中n 为正整数),则2521(1)(1)mnn n ,显然n 为奇数,设21n k (其中k 是正整数),则524(1)mk k ,即252(1)m k k .显然1k,此时k 和1k 互质,所以252,11,m k k 或25,12,m k k 或22,15,m k k 解得5,4k m .因此,满足要求的整数m 只有1个.3.在△ABC 中,已知AB =AC ,∠A =40°,P 为AB 上一点,∠ACP =20°,则BC AP=.【答】3.设D 为BC 的中点,在△ABC 外作∠CAE =20°,则∠BAE =60°. 作CE ⊥AE ,PF ⊥AE ,则易证△ACE ≌△ACD ,所以CE =CD =12BC.又PF =PA sin ∠BAE =PA sin 60°=32AP ,PF =CE ,所以32AP =12BC ,因此BC AP=3.4.已知实数,,a b c 满足1abc,4a b c ,22243131319a b c aa bb cc ,则222abc =.【答】332.因为22313(3)(1)(1)(1)aa aa abc a bc a a bcbc a b c ,所以FEDBCAP2131(1)(1)a aa b c .同理可得2131(1)(1)b b b a c ,2131(1)(1)c cc a b .结合22243131319ab c aa bb cc 可得1114(1)(1)(1)(1)(1)(1)9b c a c a b ,所以4(1)(1)(1)(1)(1)(1)9a b c a b c .结合1abc,4a b c,可得14ab bc ac. 因此,222233()2()2a bca bc ab bc ac .实际上,满足条件的,,a b c 可以分别为11,,422.第二试(A)一、(本题满分20分)已知直角三角形的边长均为整数,周长为30,求它的外接圆的面积.解设直角三角形的三边长分别为,,a b c (a b c ),则30a b c .显然,三角形的外接圆的直径即为斜边长c ,下面先求c 的值.由a b c 及30a b c 得303a b c c ,所以10c . 由a b c 及30a b c 得302a b c c ,所以15c . 又因为c 为整数,所以1114c .……………………5分根据勾股定理可得222abc ,把30ca b 代入,化简得30()4500ab a b ,所以22(30)(30)450235a b ,……………………10分因为,a b 均为整数且a b ,所以只可能是22305,3023,ab解得5,12.a b ……………………15分所以,直角三角形的斜边长13c ,三角形的外接圆的面积为1694.……………………20分二.(本题满分25分)如图,PA 为⊙O 的切线,PBC 为⊙O 的割线,AD ⊥OP 于点D .证明:2ADBD CD .DPOABC2018年全国初中数学联合竞赛试题参考答案及评分标准第1页(共4页)证明:连接OA ,OB ,OC.∵OA ⊥AP ,A D ⊥OP ,∴由射影定理可得2PAPD PO ,2ADPD OD . ……………………5分又由切割线定理可得2PAPB PC ,∴PB PC PD PO ,∴D 、B 、C 、O 四点共圆,……………………10分∴∠PDB =∠PCO =∠OBC =∠ODC ,∠PBD =∠COD ,∴△PBD ∽△COD ,……………………20分∴PD BD CD OD,∴2AD PD OD BD CD .……………………25分三.(本题满分25分)已知抛物线216yxbx c 的顶点为P ,与x 轴的正半轴交于A 1(,0)x 、B 2(,0)x (12x x )两点,与y 轴交于点C ,PA 是△ABC 的外接圆的切线.设M 3(0,)2,若AM//BC ,求抛物线的解析式.解易求得点P 23(3,)2b bc ,点C (0,)c .设△ABC 的外接圆的圆心为D ,则点P 和点D 都在线段AB 的垂直平分线上,设点D 的坐标为(3,)b m .显然,12,x x 是一元二次方程2106x bx c的两根,所以21396x b bc ,22396x bbc ,又AB 的中点E 的坐标为(3,0)b ,所以AE =296b c .……………………5分因为PA 为⊙D 的切线,所以PA ⊥AD ,又A E ⊥PD ,所以由射影定理可得2AEPE DE ,即2223(96)()||2bc b c m ,又易知0m,所以可得6m. ……………………10分又由DA =DC 得22DA DC ,即22222(96)(30)()bc mb mc ,把6m代入后可解得6c (另一解0c 舍去).……………………15分又因为AM//BC ,所以OA OM OBOC,即223||3962|6|396b b c bbc.……………………20分把6c 代入解得52b (另一解52b舍去). 因此,抛物线的解析式为215662y xx . ……………………25分2018年全国初中数学联合竞赛试题参考答案及评分标准第1页(共5页)精品文档强烈推荐2018年全国初中数学联合竞赛试题参考答案及评分标准第4页(共7页)精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有精品推荐强力推荐值得拥有。
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标...

)))))))))2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .1 【答案】 A【解答】依题意,21616(31)0m m =++=△。
因此,2310m m ++=。
∴ 231m m =--,231m m +=-。
∴ 3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A .31+ B .21+ C .231- D .221- 【答案】 B【解答】依题意,点C 坐标为()2mm ,,点F 的坐标为()2mn n -+,。
由二次函数2y ax =的图像过C 、F 两点,得222()2m am m n a n ⎧=⎪⎪⎨⎪+=-⎪⎩,消去a ,得2220n mn m --=。
∴ 2()210n n m m -⨯-=,解得21nm=+(舍负根)。
∴ 21nm=+。
(第2题图)3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( ) A .25 B .35 C .37 D .47【答案】 D【解答】如图,连AG ,并延长交BC 于点F 。
∵ G 为ABC △的重心,且12BD BC =, ∴ F 为BC 中点,且21AG GF =,DB BF FC ==。
福建数学竞赛试题及答案

福建数学竞赛试题及答案一、选择题(每题5分,共10分)1. 若函数\( f(x) = 3x^2 - 2x + 1 \),求\( f(-1) \)的值。
A. 6B. 2C. -2D. 42. 已知圆的半径为5,圆心在原点,求圆上一点到圆心的距离。
A. 3B. 4C. 5D. 6二、填空题(每题5分,共10分)3. 若\( a \)和\( b \)互为相反数,且\( a + b = 0 \),则\( a \)的值为______。
4. 一个直角三角形的两条直角边分别为3和4,求斜边的长度,其值为______。
三、解答题(每题15分,共30分)5. 已知等差数列的首项为2,公差为3,求第10项的值。
6. 一个长方体的长、宽、高分别为2米、3米和4米,求其体积。
四、证明题(每题15分,共15分)7. 证明:对于任意正整数\( n \),\( 1^3 + 2^3 + ... + n^3 = (1+ 2 + ... + n)^2 \)。
五、综合题(每题25分,共25分)8. 一个班级有50名学生,其中30名男生和20名女生。
如果从这50名学生中随机选择5名学生组成一个小组,求至少有2名女生的概率。
答案:一、选择题1. A. 6(将-1代入函数\( f(x) \)计算得到\( f(-1) = 3(-1)^2 -2(-1) + 1 = 6 \))2. C. 5(圆上任意一点到圆心的距离等于半径,即5)二、填空题3. 0(因为\( a \)和\( b \)互为相反数,所以它们的和为0)4. 5(根据勾股定理,斜边长度为\( \sqrt{3^2 + 4^2} = 5 \))三、解答题5. 第10项的值为47(首项为2,公差为3,根据等差数列通项公式\( a_n = a_1 + (n-1)d \),计算得到\( a_{10} = 2 + 9 \times 3= 29 \))6. 长方体的体积为24立方米(体积计算公式为\( V = 长 \times 宽\times 高 \),即\( 2 \times 3 \times 4 = 24 \))四、证明题7. 证明:根据等差数列求和公式,\( 1 + 2 + ... + n =\frac{n(n+1)}{2} \),将其平方得到\( \left(\frac{n(n+1)}{2}\right)^2 \)。
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准(解析版)

2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .1 【答案】 A【解答】依题意,21616(31)0m m =++=△。
因此,2310m m ++=。
∴ 231m m =--,231m m +=-。
∴ 3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A .31+ B .21+ C .231- D .221- 【答案】 B【解答】依题意,点C 坐标为()2mm ,,点F 的坐标为()2mn n -+,。
由二次函数2y ax =的图像过C 、F 两点,得222()2m am m n a n ⎧=⎪⎪⎨⎪+=-⎪⎩,消去a ,得2220n mn m --=。
∴ 2()210n n m m -⨯-=,解得21nm=+(舍负根)。
∴ 21nm=+。
(第2题图)3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( ) A .25 B .35 C .37 D .47【答案】 D【解答】如图,连AG ,并延长交BC 于点F 。
∵ G 为ABC △的重心,且12BD BC =, ∴ F 为BC 中点,且21AG GF =,DB BF FC ==。
2018年全国初中数学联赛试题参考答案和评分标准 精品

2018年全国初中数学联赛试题参考答案和评分标准精品2018年全国初中数学联合竞赛试题参考答案及评分标准说明:评阅试卷时,请依据本评分标准。
第一试,选择题和填空题只设7分和0分两档;第二试各题,请按照本评分标准规定的评分档次给分。
如果考生的解答方法和本解答不同,只要思路合理,步骤正确,在评卷时请参照本评分标准划分的档次,给予相应的分数。
第一试一、选择题:(本题满分42分,每小题7分)1.已知$a=1+\frac{1}{2+1}$,$b=3-2$,$c=6-2$,那么$a,b,c$的大小关系是()A。
$a<b<c$B。
$a<c<b$XXX<a<c$D。
$b<c<a$答】C.因为 $\frac{1}{2+1}=\frac{1}{3}$,所以$a=1+\frac{1}{3}=\frac{4}{3}$,$b=1$,$c=4$。
因为 $\frac{1}{3}<1$,所以$a<\frac{4}{3}+1=\frac{7}{3}<c$,所以 $b<a<c$。
2.方程$x^2+2xy+3y^2=34$的整数解$(x,y)$的组数为()A。
3B。
4C。
5D。
6答】B.方程即$(x+y)^2+2y^2=34$,显然$x+y$必须是偶数,所以可设$x+y=2t$,则原方程变为$2t^2+y^2=17$。
因为$2t^2\leq 16$,所以$t=\pm 2$,从而可求得原方程的整数解为$(x,y)=(-7,3),(1,3),(7,-3),(-1,-3)$,共4组。
3.已知正方形ABCD的边长为1,E为BC边的延长线上一点,$CE=1$,连接AE,与CD交于点F,连接BF并延长与线段DE交于点G,则BG的长为()A。
$\frac{65}{26}$B。
$\frac{3}{3}$C。
$\frac{2}{5}$D。
$\frac{9}{4}$答】D.过点C作$CP\parallel BG$,交DE于点P。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
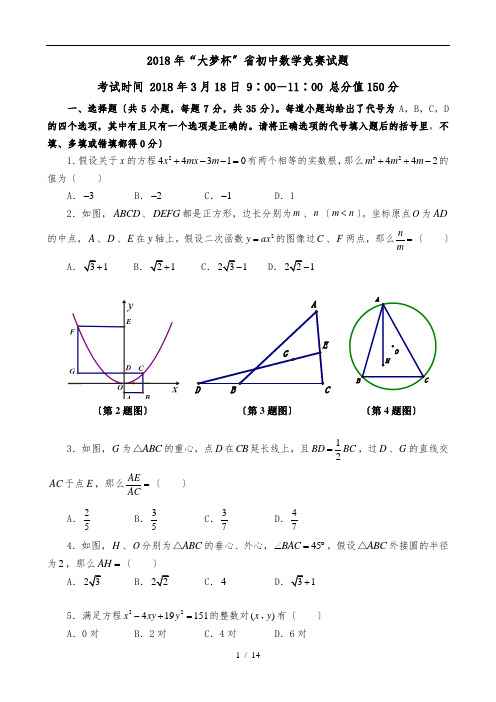
2018年“大梦杯”福建省初中数学竞赛试题 考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .12.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A .31+ B .21+ C .231- D .221-3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( ) A .25B .35C .37D .474.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=︒,若ABC △外接圆的半径 为2,则AH =( )A .23B .22C .4D .31+5.满足方程22419151x xy y -+=的整数对()x y ,有( ) A .0对 B .2对 C .4对 D .6对HOBCA(第4题图)(第2题图) EG(第3题图)6.已知a ,b ,c 为正整数,且a b c >>。
若b c +,a c +,a b +是三个连续正整数的平方,则222a b c ++的最小值为 。
7.如图,ABCD 为矩形,E 为对角线AC 的中点,A 、B 在x 轴上。
若函数4y x=(0x >)的图像过D 、E 两点,则矩形ABCD 的面积为 。
8.如图,ABC △是边长为8的正三角形,D 为AB 边上一点,1O ⊙为ACD △的内切圆,2O ⊙为CDB △的边DB 上的旁切圆。
若1O ⊙、2O ⊙的半径都是r ,则r = 。
9.若实数x 满足[][][]232018x x x ++=,则[]4x = 。
其中[]x 表示不超过x 的最大整数。
10.网络爬虫是一种互联网网页抓取工具。
其算法与数学的一个重要分支图论有着密切的联系。
图论可以追溯到大数学家欧拉提出的“哥尼斯堡七桥问题”。
图论中讨论的图是由一些节点和连接这些节点的线组成的。
请你回答下列问题:把一个矩形区域划分成n 个凸多边形区域(这些凸多边形区域除公共边外,没有公共部分)。
已知构成这n 个凸多边形的顶点中,恰有6个顶点在矩形内,12个顶点在矩形的边界上(含矩形的顶点);同时,任何三个顶点不共线(除矩形边界上的顶点共线外)。
若围成这n 个凸多边形的线段中,恰有18条线段在矩形区域内,则这n 个凸多边形中四边形个数的最大值为 。
ABO 1O 2CD(第7题图) (第8题图)11.已知二次函数224y x bx c =-+的图像交x 轴于1(0)A x ,、2(0)B x ,两点,且2112265x x x x +=。
若函数224y x bx c =-+在13b x b +≤≤+上的最小值为6-,求b ,c 的值。
12.如图,在圆内接四边形ABCD 中,AB AD =,M 是BC 边的中点,点N 在对角线BD 上,且满足BAN CAM ∠=∠。
求证:MN AC ∥。
(第12题图)13.已知关于x的方程299990--+=的两根都是素数,求k的值。
x kx k14.一个由36个单位小方格组成的66⨯的方格表中的n个小方格被染成了红色,使得任意两个红色小方格的中心之间的距离大于2,求n的最大值。
2018年“大梦杯”福建省初中数学竞赛试题参考答案及评分标准考试时间 2018年3月18日 9∶00-11∶00 满分150分一、选择题(共5小题,每小题7分,共35分)。
每道小题均给出了代号为A ,B ,C ,D 的四个选项,其中有且只有一个选项是正确的。
请将正确选项的代号填入题后的括号里,不填、多填或错填都得0分)1.若关于x 的方程244310x mx m +--=有两个相等的实数根,则32442m m m ++-的值为( )A .3-B .2-C .1-D .1 【答案】 A【解答】依题意,21616(31)0m m =++=△。
因此,2310m m ++=。
∴ 231m m =--,231m m +=-。
∴ 3222442(31)44232123m m m m m m m m m ++-=--++-=+-=--=-。
2.如图,ABCD 、DEFG 都是正方形,边长分别为m 、n (m n <)。
坐标原点O 为AD 的中点,A 、D 、E 在y 轴上。
若二次函数2y ax =的图像过C 、F 两点,则nm=( ) A .31+ B .21+ C .231- D .221- 【答案】 B【解答】依题意,点C 坐标为()2mm ,,点F 的坐标为()2mn n -+,。
由二次函数2y ax =的图像过C 、F 两点,得222()2m am m n a n ⎧=⎪⎪⎨⎪+=-⎪⎩,消去a ,得2220n mn m --=。
∴ 2()210n n m m -⨯-=,解得21nm=+(舍负根)。
∴ 21nm=+。
(第2题图)3.如图,G 为ABC △的重心,点D 在CB 延长线上,且12BD BC =,过D 、G 的直线交AC 于点E ,则AEAC=( ) A .25 B .35 C .37 D .47【答案】 D【解答】如图,连AG ,并延长交BC 于点F 。
∵ G 为ABC △的重心,且12BD BC =, ∴ F 为BC 中点,且21AG GF =,DB BF FC ==。
过点F 作FM DE ∥,交AC 于点M 。
则13CM CF CE CD ==,21AE AG EM GF ==。
设CM k =,则3CE k =,2EM k =,4AE k =。
∴ 7AC k =,4477AE k AC k ==。
另解:如图,连AG ,并延长交BC 于点F 。
∵ G 为ABC △的重心,且12BD BC =, ∴ F 为BC 中点,且21AG GF =,DB BF FC ==。
∴23FD DC =,21AG GF =。
在AFC △中,利用梅涅劳斯定理,得1FD CE AGDC EA GF⋅⋅=。
∴ 22131CE EA ⋅⋅=,34CE EA =。
∴ 47AE AC =。
(第3题图)(第3题答题图)(第3题答题图)4.如图,H 、O 分别为ABC △的垂心、外心,45BAC ∠=︒,若ABC △外接圆的半径为2,则AH =( )A. B. C .4 D1 【答案】 B【解答】如图,连结BO 并延长交O ⊙于点D ,连HC 、CD 、DA 。
∵ O 为ABC △的外心,∴ BD 为O ⊙直径,DC BC ⊥,DA AB ⊥。
又H 为ABC △的垂心, ∴ AH BC ⊥,CH AB ⊥。
∴ AH DC ∥,CH DA ∥。
∴ 四边形AHCD 为平行四边形,AH DC =。
∵ 45BAC ∠=︒,ABC △外接圆的半径为2, ∴ 45BDC BAC ∠=∠=︒,4BD =。
∴AH DC ==5.满足方程22419151x xy y -+=的整数对()x y ,有( ) A .0对 B .2对 C .4对 D .6对 【答案】 C【解答】方程22419151x xy y -+=化为22(2)15115x y y -=-。
依题意,215115A y =-为完全平方数。
由2151150A y =-≥,得215115y ≤。
结合y 为整数,得210y ≤。
故,20y =,1,4,9。
当20y =时,215115151A y =-=,不是完全平方数。
当21y =时,215115136A y =-=,不是完全平方数。
当24y =时,21511591A y =-=,不是完全平方数。
当29y =时,2215115164A y =-==。
∴ 方程化为229(2)16y x y ⎧=⎪⎨-=⎪⎩,即23(6)16y x =⎧⎨-=⎩,或23(6)16y x =-⎧⎨+=⎩ ∴ 364y x =⎧⎨-=⎩,或364y x =⎧⎨-=-⎩,或364y x =-⎧⎨+=⎩,或364y x =-⎧⎨+=-⎩。
∴ 103x y =⎧⎨=⎩,或23x y =⎧⎨=⎩,或23x y =-⎧⎨=-⎩,或103x y =-⎧⎨=-⎩。
∴ 满足方程的整数对有(103),、(23),、(23)--,、(103)--,,共4对。
(第4题图)二、填空题(共5小题,每小题7分,共35分)6.已知a ,b ,c 为正整数,且a b c >>。
若b c +,a c +,a b +是三个连续正整数的平方,则222a b c ++的最小值为 。
【答案】 1297【解答】依题意,设2(1)b c n +=-,则2a c n +=,2(1)a b n +=+,n 为正整数,且1n >。
∴ 22222()(1)(1)32a b c n n n n ++=-+++=+,可见n 为偶数,且2322n a b c +++=。
∴ 242n n a +=,222n b +=,242n nc -=。
可见,6n ≥,且当n 增大时,222a b c ++的值也随之增大。
又6n =时,30a =,19b =,6c =符合要求。
∴ 222a b c ++的最小值为222301961297++=。
7.如图,ABCD 为矩形,E 为对角线AC 的中点,A 、B 在x 轴上。
若函数4y x=(0x >)的图像过D 、E 两点,则矩形ABCD 的面积为 。
【答案】 8【解答】设()D D D x y ,,()E E E x y ,,则4D D E E x y x y ==。
作EF AB ⊥于F ,由E 为AC 中点,得F 为AB 中点,且1122EF BC AD ==。
∴ 2D E y y =。
结合2E E D D D E x y x y x y ==⋅,得2E D x x =。
∴ OA AF =,222D AB AF OA x ===。
∴ 矩形ABCD 的面积28D D S AB AD x y =⨯==。
(第7题图)(第7题答题图)。
