TREEPLAN使用详解
杉数求解器用法

杉数求解器用法杉数求解器是一种用于解决优化问题的工具,它可以求解线性规划、整数规划、混合整数规划等多种问题。
下面是使用杉数求解器的一般步骤:1. 安装杉数求解器:首先,您需要在您的计算机上安装杉数求解器。
您可以访问杉数科技的官网,下载并按照说明进行安装。
2. 准备问题:在开始使用杉数求解器之前,您需要准备要解决的问题。
这包括定义决策变量、目标函数和约束条件。
这些信息通常以数学模型的形式提供。
3. 导入问题:打开杉数求解器,选择“文件”菜单中的“打开”选项,然后选择您要导入的数学模型文件。
4. 设置参数:在杉数求解器中,您可以设置一些参数来控制问题的求解过程。
这些参数包括求解器的选择、时间限制、迭代次数等。
5. 运行求解:设置完参数后,您可以通过点击“求解”按钮来开始解决问题。
杉数求解器将尝试找到满足所有约束条件的决策变量的值,同时最大化或最小化目标函数。
6. 检查结果:求解完成后,杉数求解器将显示求解结果。
这包括最优解、最优值、迭代次数、时间等信息。
您还可以查看决策变量的取值、目标函数的值等详细信息。
7. 导出结果:如果您需要将结果分享给其他人或用于其他目的,您可以使用杉数求解器的导出功能将结果导出为所需的格式,如Excel、PDF等。
需要注意的是,使用杉数求解器需要一定的数学基础和编程经验。
如果您不熟悉这些概念,可能需要先学习一些基本的优化知识和编程技能。
同时,杉数求解器的使用也需要注意一些细节和技巧,如数学模型的建立、参数的设置、结果的解读等。
因此,建议在使用杉数求解器之前先仔细阅读相关文档和教程,或者寻求专业人士的帮助和指导。
treemap 用法

Treemap(树状图)是一种数据可视化方式,可以将一个数据集以矩形的方式展现出来,矩形的大小表示数据的大小,颜色表示数据的分类。
以下是Treemap的使用步骤:
准备数据:将需要展示的数据以一定的格式准备好,一般是一个层级结构,包含若干个节点和它们之间的关系,同时每个节点还有一个数值表示大小。
选择Treemap库:选择一种Treemap库进行使用,例如D3.js、ECharts等。
创建Treemap:通过调用Treemap库的相关函数,创建一个Treemap对象。
设置数据:将准备好的数据设置到Treemap对象中。
设置布局:设置Treemap的布局,包括节点大小、颜色、样式等。
绘制Treemap:使用Treemap库提供的函数将Treemap绘制在页面上。
交互与更新:对于需要支持交互和更新的Treemap,可以设置相关的事件监听器,以响应用户的交互操作并实现Treemap的动态更新。
需要注意的是,Treemap展示的是一种相对大小关系,而不是绝对大小关系,因此不适用于展示具体数值大小的数据。
江西财经大学——运筹学习题集06071015596
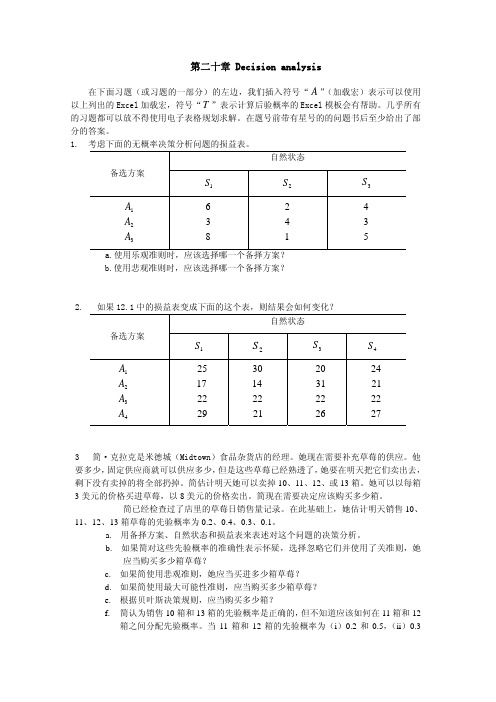
第二十章 Decision analysis在下面习题(或习题的一部分)的左边,我们插入符号“A ”(加载宏)表示可以使用以上列出的Excel 加载宏,符号“T ”表示计算后验概率的Excel 模板会有帮助。
几乎所有的习题都可以放不得使用电子表格规划求解。
在题号前带有星号的的问题书后至少给出了部分的答案。
1. 考虑下面的无概率决策分析问题的损益表。
自然状态备选方案1S 2S 3S321A A A 836 142 534 a.使用乐观准则时,应该选择哪一个备择方案? b.使用悲观准则时,应该选择哪一个备择方案?2. 如果12.1中的损益表变成下面的这个表,则结果会如何变化?自然状态备选方案1S2S3S 4S4321A A A A29221725 21221430 26223120 272221243 简·克拉克是米德城(Midtown)食品杂货店的经理。
她现在需要补充草莓的供应。
他要多少,固定供应商就可以供应多少,但是这些草莓已经熟透了,她要在明天把它们卖出去,剩下没有卖掉的将全部扔掉。
简估计明天她可以卖掉10、11、12、或13箱。
她可以以每箱3美元的价格买进草莓,以8美元的价格卖出。
简现在需要决定应该购买多少箱。
简已经检查过了店里的草莓日销售量记录。
在此基础上,她估计明天销售10、11、12、13箱草莓的先验概率为0.2、0.4、0.3、0.1。
a. 用备择方案、自然状态和损益表来表述对这个问题的决策分析。
b. 如果简对这些先验概率的准确性表示怀疑,选择忽略它们并使用了关准则,她应当购买多少箱草莓?c. 如果简使用悲观准则,她应当买进多少箱草莓?d. 如果简使用最大可能性准则,应当购买多少箱草莓?e. 根据贝叶斯决策规则,应当购买多少箱?f. 简认为销售10箱和13箱的先验概率是正确的,但不知道应该如何在11箱和12箱之间分配先验概率。
当11箱和12箱的先验概率为(i )0.2和0.5,(ii )0.3和0.4,(iii )0.5和0.2时重新使用贝叶斯决策规则进行决策。
Tree命令详解

最强最全的Tree命令详解/goody9807/archive/2007/09/11/1780717.aspx[Tree命令作用]以图形显示驱动器或路径的文件夹结构。
很多时候,这是一个非常有用的命令![Tree命令格式]可以在命令行窗口敲tree /?看帮助。
TREE [drive:][path] [/F] [/A]/F 显示每个文件夹中文件的名称。
/A 使用ASCII 字符,而不使用扩展字符。
使用/F参数时显示所有目录及目录下的所有文件,省略时,只显示目录,不显示目录下的文件;选用>PRN参数时,则把所列目录及目录中文件名打印输出tree c:\ | more出现由tree 命令产生的第一个输出命令提示符窗口,后面跟着-- More -- 提示。
输出暂停,直到用户按键盘上的任意键为止(Pause除外)。
空格:显示一整页按下:Ctrl+Break退出[Tree命令范例][例一]tree d: > d:\dTree.txt或者tree d:\ > d:\dTree.txt作用:把D盘下的所有目录结构以树状结构导出,以文本文件dTree.txt保存在文件夹d:\下。
[例二]tree d: /f > d:\dF.txt或者tree d:\ /f > d:\dF.txt作用:把D盘下的所有目录及文件结构以树状结构导出,以文本文件dF.txt保存在文件夹d:\下。
[例三]tree C:\WINDOWS\system32 /f > C:\s32f.txt作用:把C:\WINDOWS\system32 /f > C:\s32f.txt下的所有目录及文件结构以树状结构导出,以文本文件s32f.txt保存在文件夹c:\下。
[例四]tree E:\BitComet\Downloads /f > f:\download\tree\dl.txt作用:把E:\BitComet\Downloads下的所有目录及文件以树状结构导出,以文本文件dl.txt保存在文件夹f:\download\tree\下。
实例详解treeplan使用

实例详解Excel 2007 Tree plan(决策树)使用目录第一章安装 (3)1.1新建一个决策树 (4)1.2决策树示例 (7)第二章决策树详细步骤指导 (9)2.1D RIVE T EK 研究院的问题 (9)2.2节点和分支 (10)2.3最终收益 (11)2.4创建决策树 (12)2.5结果解释 (17)2.6格式化决策树 (18)2.7演示模型输入值 (19)第三章决策树解决方案 (21)3.1策略 (21)3.2收益分布 (21)3.3D RIVE T EK策略 (21)3.4策略选择 (25)3.5确定均等值 (25)3.6回滚方式 (27)3.7最优策略 (28)第四章敏感性分析 (31)4.1E XCEL中一个变量的敏感性分析 (31)4.2E XCEL双变量敏感性分析 (32)4.2.1策略区域 (33)4.2.2创建数据表 (33)4.2.3运用数据表功能得到结果 (34)4.2.4润色 (34)第一章安装Tree plan(以下称决策树)是在excel中画决策树的一个加载工具。
是由旧金山大学教授米歇尔R. 米德尔顿开发,并由杜克大学Fuqua商学院的詹姆斯E.史密斯教授改良使用。
决策树的所有功能都在一个名为TreePlan.xla的文件中,根据你的使用情况,共有以下3种安装方式。
第1种,偶然使用如果你只是偶然使用一次决策树,那么每次当你用的时候下载一次即可。
你也可以把TreePlan.xla文件放在一张软盘、电脑硬盘或网盘中。
第2种,选择性使用在这种场景下,你可以使用excel的加载项功能来安装决策树。
步骤如下:✓把TreePlan.xla保存在你电脑硬盘的某个地方✓如果你把TreePlan.xla文件保存在了excel或office子目录文件夹里,请直接到第三步。
否则,打开excel——单击office按钮——excel选项——加载项——转到——加载项对话框,单击浏览按钮,找到TreePlan.xla,单击确定。
系统发生分析软件PAUP和TreePuzzle使用方法介绍

基金项目国家自然科学基金资助项目(30370773)。
作者简介王勇(1965-),男,浙江衢州人,在读博士,副研究员,从事昆虫生物信息学研究。
*通讯作者,研究员,博士生导师,E!mail:kpchen@ujs.edu.cn收稿日期2007!09!03近年来,系统发生分析被广泛应用于研究不同生物DNA、蛋白质序列的进化关系[1-3],但由于系统发生分析是对过去已经发生的进化事件进行模拟,任何软件都不能保证所得出的结论就是真实的进化历史。
因此,在进行系统发生分析时,往往需要采用不同的分析方法同时进行。
而只有当多种分析方法获得的结果一致时,才可得出一个较为可靠的结论[4]。
PAUP和TreePuzzle是目前使用较多的系统发生分析软件,其中PAUP更是国内外不少科技期刊都指定使用的。
PAUP(phylogeneticanalysisusingparsimony,用最大简约法做系统发生分析)既能对DNA序列做邻近归并法(neighborjoining,NJ)、最大简约法(maximumparsimony,MP)和最大相似法(maximumlikelihood,ML)分析,又能对蛋白质序列做NJ和MP分析[5]。
TreePuzzle则是专门用于构建ML进化树的软件。
然而,PAUP软件使用方法比较复杂,特别是Windows版,不能进行菜单操作而需要自己输入命令。
TreePuzzle则是一个DOS版本的软件,使用上有较大的不便之处[6]。
初学者在没人指点的情况下,往往感觉一筹莫展。
为此,笔者通过研读软件的使用手册和有关资料[7]从序列信息模块、序列参数模块、运算命令模块3个方面介绍PAUP软件的使用方法,之后对TreePuzzle软件的使用和进化树的编辑与注释方法做一简要说明。
1序列信息模块要做PAUP分析,首先必须建立Nexus文件。
Nexus文件是PAUP软件的可执行文件,后缀名为.nex。
一般来说,Nexus文件包含以下3个模块:序列信息模块、参数设定模块、运算命令模块。
project-tree 用法

项目树(project-tree)是一种用于在命令行界面展示项目文件结构的工具。
它可以帮助用户快速了解项目的文件组织方式,方便查找和管理项目文件。
1. 介绍项目树项目树是一个非常实用的命令行工具,可以帮助用户以树形结构清晰展示项目的文件目录。
通过简单的命令,用户就可以清晰地查看项目中的文件结构,包括子文件夹、文件和其它相关信息。
这样一来,项目树不仅可以帮助我们更好地理解项目的结构,还可以提高我们对项目的管理效率。
2. 项目树的用法在使用项目树工具时,用户需要在命令行中输入特定的命令,并指定需要查看的项目路径。
如果我们需要查看一个名为"example_project"的项目文件结构,我们可以在命令行中输入以下命令:```bashproject-tree example_project```通过这个命令,我们就可以轻松地查看"example_project"项目的文件结构,清晰地了解项目中的文件组织方式。
3. 项目树的深度和广度在使用项目树工具时,我们可以通过指定不同的参数来控制所展示的文件结构深度和广度。
这个功能非常强大,因为可以根据实际需要来灵活展示项目的文件结构。
通过控制深度和广度,我们可以更精准地了解项目的细节和整体结构。
4. 项目树的个人观点在我看来,项目树是一个非常实用的工具。
它不仅可以帮助我们更好地理解项目的结构,还可以提高我们的工作效率。
特别是在处理大型项目时,项目树可以让我们快速定位和管理文件,让工作变得更加轻松。
项目树是一个非常值得推荐的工具。
它的简单易用和强大功能让我们在项目管理中受益良多。
我相信,只要你尝试了项目树,你会爱上它的便利和高效。
以上便是关于项目树的简要介绍和个人观点。
希望这篇文章可以帮助你更好地了解项目树工具,并在实际工作中得到更好的应用。
项目树(project-tree)的出现为项目文件结构的管理提供了极大的便利,不仅可以在命令行中轻松地查看项目的结构,还可以通过控制深度和广度来更加灵活地展示文件的细节和整体结构。
tree的用法总结大全4篇

tree的用法总结大全tree的用法总结大全精选4篇(一)1. 构建树(Tree):用于构建一个树形数据结构,可以使用Tree类或者其他相关数据结构来实现。
2. 遍历树:通过不同的遍历算法(前序遍历、中序遍历、后序遍历等)对树的节点进行访问和操作。
3. 查找树:根据特定的搜索规则在树中查找节点,如二叉搜索树的查找操作。
4. 插入节点:向树中插入新的节点,可以根据特定的插入规则将节点插入到合适的位置。
5. 删除节点:从树中删除指定的节点,可以根据特定的删除规则执行删除操作,并保持树的结构完整。
6. 查找树的高度:计算树的高度,即树的最大深度,可以使用递归或迭代方法实现。
7. 树的平衡:判断一个树是否平衡,即左右子树的高度差不超过1,可以使用递归方法实现。
8. 树的深度优先搜索(DFS):使用深度优先搜索算法对树进行遍历,可以使用递归或栈来实现。
9. 树的广度优先搜索(BFS):使用广度优先搜索算法对树进行遍历,使用队列来实现。
10. 判断树的相等:判断两棵树是否相等,即树的结构和节点值都相同。
11. 判断树的子树:判断一棵树是否是另一棵树的子树,即判断一个树的结构和节点值是否包含在另一个树中。
12. 树的序列化与反序列化:将树转化为字符串或其他形式的序列化数据,或者将序列化数据转化为树结构。
13. 二叉树的镜像:将一棵二叉树的左右节点互换,可以使用递归或迭代方法实现。
14. 树的修剪:删除树中所有不在给定范围内的节点,可以使用递归方法实现。
15. 树的路径求和:查找树中从根节点到叶子节点的路径,使得路径上节点值之和等于目标值。
16. 最近公共祖先:查找两个节点的最近公共祖先节点,可以使用递归方法实现。
17. 判断对称树:判断一棵树是否是对称的,即树的左子树和右子树是否对称。
18. 重建树:根据树的前序遍历和中序遍历结果重建树的结构,或者根据树的后序遍历和中序遍历结果重建树的结构。
19. 树的直径:计算树的直径,即树中任意两个节点之间的最大距离,可以使用深度优先搜索算法实现。
关于TreePlan加载宏的使用说明

关于TreePlan加载宏的使用说明:
请按如下步骤操作:
1.)首先打开一个Excel电子表格
2)然后用鼠标双击TreePlan,打开此软件,于是会在Excel电子表格中出现如下的对话框。
3)用鼠标点击“启用宏”,此时又回到Excel表格状态中。
4)在Excel表格中用鼠标点击“工具”栏,则会出现如下对话框:
5)用鼠标点击“Decision Tree”,则会在Excel表中出现一个工具菜单,如下图所示。
6)此时便可选择“New Tree”来创建一个决策树,结果会在Excel表格中出现
如下一棵默认的决策树。
如下图所示。
至此你已经画出了一棵最简单的决策树,至于如何使用这棵决策树,我会在课堂上详细讲授有关的内容。
tree-plan操作方法

TREE PLAN 软件操作方法
1、加载tree-plan插件
打开excel——工具——加载宏——浏览——找到treeplan插件所在的文件夹——双击treeplan.xla文件
2、启动treeplan软件
(1)CTR+T
(2)Excel——工具——Decision tree
3、比尔打工决策演示
(1)在Excel中任选一单元格,按下CTR+T,点“new tree”
(2)修改两个分支的名称,并把光标放在decision 2后面的方格内
(3)按下CTR+T,显示如下图所示的对话框
选中左侧的“change to event node”,并在右侧的“branches”栏目中,选择“two”
(两个分支),单击“ok”:
(4)修改两个分支(Event 3, Event 4)的名称,并把光标放在Event 3后面的方格内,按下CTR+T,显示如下图所示的对话框
(5)选中左侧的“change to decision node”,并在右侧的“branches”栏目中,选择“two”(两个分支),单击“ok”:
(6)如上面一至操作下去,最终形成:
(7)给每一个事件分支添加“概率值”,并在每一个分支的“左侧0点”处添加“货币值”(净现金流):
(8)灵敏度分析:excel——工具——加载宏——分析工具库——规划求解:
(9)打开“规划求解”,“目标单元格”选“13032”所在的F36,可变单元格选概率0.6所在的I17单元格,并把概率0.4所在的单元格改为“1- I17”,“值为”单选钮选中,并在后面的空格内输入“12000”
最终结果:。
伸展树(Splaytree)的基本操作与应用

伸展树(Splaytree)的基本操作与应⽤伸展树的基本操作与应⽤【伸展树的基本操作】 伸展树是⼆叉查找树的⼀种改进,与⼆叉查找树⼀样,伸展树也具有有序性。
即伸展树中的每⼀个节点 x 都满⾜:该节点左⼦树中的每⼀个元素都⼩于 x,⽽其右⼦树中的每⼀个元素都⼤于 x。
与普通⼆叉查找树不同的是,伸展树可以⾃我调整,这就要依靠伸展操作 Splay(x,S)。
伸展操作 Splay(x,S) 伸展操作 Splay(x,S)是在保持伸展树有序性的前提下,通过⼀系列旋转将伸展树 S 中的元素 x 调整⾄树的根部。
在调整的过程中,要分以下三种情况分别处理: 情况⼀:节点 x 的⽗节点 y 是根节点。
这时,如果 x 是 y 的左孩⼦,我们进⾏⼀次 Zig(右旋)操作;如果 x 是 y 的右孩⼦,则我们进⾏⼀次 Zag(左旋)操作。
经过旋转,x 成为⼆叉查找树 S 的根节点,调整结束。
如图 1 所⽰: 情况⼆:节点 x 的⽗节点 y 不是根节点,y 的⽗节点为 z,且 x 与 y 同时是各⾃⽗节点的左孩⼦或者同时是各⾃⽗节点的右孩⼦。
这时,我们进⾏⼀次Zig-Zig 操作或者 Zag-Zag 操作。
如图 2 所⽰: 情况三:节点 x 的⽗节点 y 不是根节点,y 的⽗节点为 z,x 与 y 中⼀个是其⽗节点的左孩⼦⽽另⼀个是其⽗节点的右孩⼦。
这时,我们进⾏⼀次 Zig-Zag 操作或者 Zag-Zig 操作。
如图 3 所⽰: 如图 4 所⽰,执⾏ Splay(1,S),我们将元素 1 调整到了伸展树 S 的根部。
再执⾏ Splay(2,S),如图 5 所⽰,我们从直观上可以看出在经过调整后,伸展树⽐原来“平衡”了许多。
⽽伸展操作的过程并不复杂,只需要根据情况进⾏旋转就可以了,⽽三种旋转都是由基本得左旋和右旋组成的,实现较为简单。
伸展树的基本操作 利⽤ Splay 操作,我们可以在伸展树 S 上进⾏如下运算: (1)Find(x,S):判断元素 x 是否在伸展树 S 表⽰的有序集中。
TREEPLAN使用详解

TREEPLAN使用详解一、安装TREEPLAN插件首先,用户需要在Excel中安装TREEPLAN插件。
安装步骤如下:1. 打开Excel,点击“文件”菜单,在下拉菜单中选择“选项”。
2. 在Excel选项对话框的左侧面板上,选择“添加功能区”选项。
3.在右侧的“主选项卡”部分,选择“分析工具”。
4.在下方的“已选项卡”部分,勾选“树状图和决策分析”选项,在“其他命令”选项下选择“工具”。
5. 点击“确定”按钮,TREEPLAN插件就会被安装到Excel中。
二、使用TREEPLAN插件安装完插件后,用户就可以开始使用TREEPLAN插件了。
下面我们将详细介绍如何使用TREEPLAN插件来构建和分析决策树。
1.构建决策树a. 在Excel中建立一个新的工作表。
首先,确定决策树的节点和叶节点。
通常,决策树的第一个节点是问题的根本原因或目标。
接下来,用户可以添加其他的节点和叶节点,用于描述决策树中的不同情况和结果。
b. 在Excel中选择“TREEPLAN”选项卡,然后点击“定义节点”按钮。
在弹出的对话框中,输入节点的名称和描述,点击“确定”按钮。
d.当决策树的结构绘制完毕后,用户可以使用“节点属性”和“叶节点属性”来定义各个节点和叶节点的属性。
点击对应节点或叶节点上的属性单元格,然后在工作表中输入属性值。
2.分析决策树b. 用户可以选择不同的分析方法,如最大期望(Maximization of Expected Value)、最小预期损失(Minimization of Expected Loss)和最小先行预算(Minimization of Expected Monetary Value)等。
3.预测和优化决策b.用户可以在决策树中选择一个特定的节点,然后在工作表中输入相应的输入值,即可根据决策树模型进行预测。
c.用户还可以使用“执行优化”按钮来优化决策。
用户可以定义优化的目标和约束条件,并使用不同的优化方法来寻找最佳决策。
树的简单路径

树的简单路径概述树是一种常见的数据结构,它由节点和边组成。
每个节点可以有零个或多个子节点,除了根节点外,每个节点都有一个父节点。
树的路径是指从树的根节点到叶节点的一条路径,其中每个节点都是相互连接的。
在树的路径中,简单路径是指路径上的节点都不重复。
也就是说,简单路径不允许经过同一个节点两次,因此它是唯一的。
在本文中,我们将讨论如何找出树的简单路径。
深度优先搜索(DFS)深度优先搜索是一种用于遍历或搜索树和图的算法。
它的基本思想是,从根节点开始,首先访问当前节点,然后按照某种顺序遍历它的子节点。
在处理树的简单路径问题时,我们可以使用深度优先搜索算法来找到所有可能的路径。
具体步骤如下: 1. 从根节点开始,将当前节点添加到路径中。
2. 如果当前节点是叶节点,则将路径添加到结果列表中。
3. 否则,递归地遍历当前节点的子节点。
4. 在递归返回之前,将当前节点从路径中删除。
代码实现下面是一个使用深度优先搜索算法找到树的简单路径的示例代码(以Python为例):def dfs(root, path, res):if not root:returnpath.append(root.val)if not root.left and not root.right:res.append(list(path)) # 将路径添加到结果列表中else:dfs(root.left, path, res)dfs(root.right, path, res)path.pop() # 将当前节点从路径中删除示例假设我们有以下树的结构:1/ \2 3/ \4 5我们可以使用上述代码来找到该树的所有简单路径。
首先,创建一个空的结果列表和一个空的路径列表。
然后,从根节点开始调用DFS函数,将根节点、路径列表和结果列表作为参数传递给它。
在DFS函数内部,我们首先将当前节点的值添加到路径列表中。
由于根节点不是叶节点,我们需要递归地调用DFS函数来遍历它的子节点。
pytrees简单实例

pytrees简单实例PyTrees是一个用于构建机器人行为树的Python库。
在机器人控制中,行为树是一种非常有用的工具,可以帮助机器人做出复杂的决策。
PyTrees提供了一种简单的方法来构建和管理这些行为树。
在本文中,我们将介绍PyTrees的一些基本概念和使用方法,并给出一些简单的示例来说明如何使用它。
PyTrees基本概念PyTrees是一个用于构建机器人行为树的Python库。
它提供了一些基本概念,包括行为树、行为、黑板和状态机。
行为树是由一系列行为和状态节点组成的树形结构。
每个节点都可以执行一个特定的行为或检查一个特定的状态。
行为节点可以是原子的,也可以是复合的。
原子行为节点执行一个特定的操作,例如移动机器人或执行抓取动作。
复合行为节点是由多个原子行为节点组成的节点,它们可以组合成更复杂的行为。
状态节点是用于检查机器人状态的节点。
例如,一个状态节点可以检查机器人是否已经到达目标位置,或者机器人是否已经抓取了一个物体。
黑板是一个共享数据的对象,用于在节点之间传递信息。
它可以存储机器人的状态、传感器数据等等。
状态机是一种行为树的扩展,它可以处理更复杂的任务。
状态机是由多个状态节点和转换节点组成的状态图。
状态节点检查机器人的状态,转换节点用于控制状态之间的转换。
使用PyTrees要使用PyTrees,我们需要安装它。
可以通过pip安装:```pip install py_trees```安装完成后,我们可以开始构建我们的行为树。
首先,我们需要定义一些行为和状态节点。
我们可以使用py_trees.decorators装饰器来定义它们。
例如,下面是一个简单的移动行为节点:```import py_trees@py_trees.decorators.behaviour(tree=py_trees.Tree(name='My Tree'))class Move(py_trees.behaviour.Behaviour):def __init__(self):super(Move, self).__init__(name='Move')def update(self):# Move robot to a new positionreturn py_mon.Status.SUCCESS```这个节点只是移动机器人到一个新的位置,并返回成功状态。
Smart Plant 3D 结构专业操作手册1.1

SmartPlant 3D结构专业入门手册(初版)主要目的:为结构专业建模人员提供入门帮助。
主要内容:一、初识SmartPlant 3D二、建立柱网三、建立模型四、绘制结构施工图如何使用:先阅读每节的简介,然后按照操作练习,完成上机操作,最后将会建立一框架的结构模型,生成一份图纸。
一、初识SmartPlant 3D1.SmartPlant 3D内容简介SmartPlant 3D(以下简称SP3D)是由intergraph公司开发的工厂设计软件。
软件设置不同的Task,将工厂设计中常用的专业进行分类,方便用户的使用。
软件中设置如下Task: Electrical, Common, Drawings and Reports, Equipment and Furnishings, Grids, Hangers and Supports, HVAC, Layout, Piping, Catalog, Space Management, Structural Analysis, Structure, Systems and Specifications.结构专业在使用时,经常用到的task有,Common, Drawings and Reports, Grids, Space Management, Structural Analysis, Structure。
其中Common 模块主要实现视图操作、定位、拷贝、粘贴等功能。
Common模块下的操作在其它模块下基本都可以实现。
Drawings and Reports模块能够实现出图和出报表,为满足不同公司的要求,图纸和报表一般需要定制。
本手册仅讲述如何在已经定制好的情况下,如何实现出图、报表工作。
Grids模块是柱网模块,用来定义结构柱网及标高。
Space Management是空间管理模块,定义Volume,实现出图。
Structural Analysis,结构分析模块,用来定义荷载类型,荷载组合等。
python的treepoem库用法

python的treepoem库用法Python的treepoem库用法treepoem库是一个用于生成树状图的Python库,可以用于可视化数据结构、流程图、组织结构等。
该库功能强大且简单易用,下面将介绍一些常用的用法。
1. 安装treepoem库首先需要在Python环境中安装treepoem库,可以通过pip命令进行安装:pip install treepoem2. 生成简单的树状图使用treepoem库可以很方便地生成简单的树状图,以下是一个示例代码:import treepoemtext = "A\n├─B\n│ ├─C\n│ └─D\n└─E"image = _barcode(barcode_type='qrcode', data=text)('') # 将生成的图像保存为文件上述代码中,首先定义了一个简单的树状图的文本,其中\n表示换行,├─表示一级节点,│表示竖直连接线,└─表示最后一个节点。
然后使用generate_barcode函数生成二维码图像,指定了barcode_type参数为qrcode表示生成的是二维码,data参数为上述定义的树状图文本。
最后使用save函数将生成的图像保存为文件。
3. 自定义树状图样式treepoem库还支持自定义树状图的样式,可以指定不同的节点形状、颜色等,以下是一个示例代码:import treepoemtext = "A\n├─B\n│ ├─C\n│ └─D\n└─E"image = _barcode(barcode_type='qrcode',data=text,options={'inncludetext': True, 'textcolor': 'red', ' bgcolor': 'yellow'})('')上述代码中,通过options参数可以指定自定义的样式选项,其中: - inncludetext参数用于控制是否在图像中包含文本,默认为False。
TREEPLAN使用详解

TREEPLAN使用详解第一章安装Tree plan(以下称决策树)就是在excel中画决策树的一个加载工具。
就是由旧金山大学教授米歇尔R、米德尔顿开发,并由杜克大学Fuqua 商学院的詹姆斯E、史密斯教授改良使用。
一、安装方式决策树的所有功能都在一个名为TreePlan、xla的文件中,根据您的使用情况,共有以下3种安装方式。
第1种,偶然使用如果您只就是偶然使用一次决策树,那么每次当您用的时候下载一次即可。
您也可以把TreePlan、xla文件放在一张软盘、电脑硬盘或网盘中。
直接双击“”加载第2种,选择性使用在这种场景下,您可以使用excel的加载项功能来安装决策树。
步骤如下:把TreePlan、xla保存在您电脑硬盘的某个地方。
如果您把TreePlan、xla文件保存在了excel 或office子目录文件夹里,请直接到第三步。
否则,打开excel——单击office按钮——excel选项——加载项——转到——加载项对话框,单击浏览按钮,找到TreePlan、xla,单击确定。
在加载项对话框中,可以瞧到已经有TreePlan、xla选项,选中决策树前面的方框,单击确定。
如果您为了释放内存不再用决策树了,那么在加载项对话框中,去掉决策树前面的方框中的对勾。
当您要使用的时候,选择加载项,并选中决策树即可。
如果您要从加载项中移除决策树,直接在您保存TreePlan、xla文件的地方把它删除即可。
下次当您打开excel并使用加载项时,会出现一个“未找到加载的TreePlan、xla文件,就是否从列表中删除?”的对话框,单价确定即可。
1)首先把加载宏放入如下安装文件件“D:\Program Files\MicrosoftOffice\Office15\Library‘’library 英[?la?br?r?] 美[la??br?r?] n、图书馆,藏书室;文库C:\Program Files\Microsoft Office\Office15\Library2)加载:文件-选项-加载项-加载项-treeplan-转到第3种,经常使用如果您希望只要打开excel就能够使用决策树,那么就把TreePlan、xla文件保存在Excel XL Start文件夹里。
antv treenode用法

antv TreeNode 用法AntV 是阿里巴巴出品的一款数据可视化解决方案,其核心产品 G2 以及基于 G2 的图表库 G6、图分析库 G6、图表编辑器 G6-Editor 以及数据建模引擎 G领域说明。
在 AntV 中,TreeNode 作为 G6 中的核心概念之一,被广泛应用于树状图的构建和展示。
在本篇文章中,我们将全面评估并深入探讨antv TreeNode 的用法,以便读者更好地理解和运用这一概念。
一、TreeNode 的基本概念1. 了解 TreeNodeTreeNode,即树节点,是树状图中的基本元素,它通常用来表示树状结构中的一个节点。
在 AntV 的 G6 库中,TreeNode 是树状图的核心模型,它具有丰富的属性和方法,用来描述和操作树节点的各种行为。
二、TreeNode 的属性和方法2.1 节点属性在 AntV 的 TreeNode 中,每个节点都具有一系列的属性,包括但不限于节点 ID、节点文本、节点样式、节点位置等。
这些属性可以帮助我们更好地定制和控制树节点的展示效果,使得树状图能够更好地呈现数据信息。
2.2 节点方法除了属性外,TreeNode 还具有丰富的方法用来操作节点,比如增加子节点、删除节点、修改节点信息等。
通过这些方法,我们可以动态地构建和更新树状图,使得其能够更好地适应不同的数据变化和交互需求。
三、使用 antv TreeNode 构建树状图3.1 数据准备在使用 antv TreeNode 构建树状图之前,我们首先需要准备好相应的数据,包括树节点的结构和属性信息。
这些数据可以来自于后端接口、本地存储或者前端计算等多种途径,我们需要将这些数据转化为 antv TreeNode 所需的格式。
3.2 节点渲染一旦数据准备就绪,我们就可以使用 antv TreeNode 的渲染方法将数据转化为可视化的树状图。
在渲染过程中,我们可以自定义节点的样式、交互行为等,使得树状图能够更好地展现数据并满足用户需求。
TREEPLAN使用详解

TREEPLAN使用详解嘿,小伙伴们!今天咱就来好好唠唠TREEPLAN这个超实用的工具咋个用哈。
TREEPLAN其实是一款专门用于决策树分析的软件,在很多领域都能派上大用场,像商业决策、风险评估啥的,都少不了它的身影。
一、安装和启动TREEPLAN咱得先把这玩意儿安装到自己的电脑上。
一般来说,你可以到它的官方网站或者一些正规的软件下载平台去下载安装包。
下载好了之后,按照提示一步一步安装就行啦,这过程就跟安装其他软件差不多,没啥特别复杂的。
安装完了,找到它的快捷方式或者在程序列表里找到它,双击就能启动咯。
二、界面认识启动之后,咱先来熟悉熟悉它的界面哈。
它的界面其实挺友好的,不会让人看着就头疼。
你会看到有菜单栏、工具栏这些常规的东西,菜单栏里有各种功能选项,像新建、打开、保存这些基本操作都能在这儿找到。
工具栏呢,就放了一些常用的工具按钮,比如绘制决策树的工具,用起来可方便啦。
还有一个很重要的区域就是绘图区,这就是咱绘制决策树的地方,就像在一张白纸上画画一样,你可以在这儿大展身手。
三、绘制决策树这可是TREEPLAN的核心功能啦。
绘制决策树的时候,咱先得确定好决策节点。
比如说,你要分析一个项目要不要投资,那这个“要不要投资”就是一个决策节点。
在绘图区点一下那个绘制节点的工具,然后在合适的位置点一下,一个决策节点就出来啦。
接着呢,从这个决策节点往外引出不同的分支,代表不同的决策选项,比如“投资”和“不投资”。
每个分支的末端还可以再添加新的节点,比如“投资”这个分支后面可以添加一些关于投资后可能出现的情况的节点,像“市场反应好”“市场反应一般”“市场反应差”等等。
四、数据输入和编辑绘制好决策树的结构之后,咱还得给它填上数据。
这数据可重要啦,它直接关系到最后的分析结果。
在每个节点上,你可以输入相关的概率、收益、成本这些数据。
比如说,“市场反应好”这个节点,你可以根据市场调研或者以往的经验,输入它发生的概率是多少,以及在这种情况下能获得的收益是多少。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一章安装Tree plan(以下称决策树)就是在excel中画决策树的一个加载工具。
就是由旧金山大学教授米歇尔R、米德尔顿开发,并由杜克大学Fuqua商学院的詹姆斯E、史密斯教授改良使用。
一、安装方式决策树的所有功能都在一个名为TreePlan、xla的文件中,根据您的使用情况,共有以下3种安装方式。
第1种,偶然使用如果您只就是偶然使用一次决策树,那么每次当您用的时候下载一次即可。
您也可以把TreePlan、xla文件放在一张软盘、电脑硬盘或网盘中。
直接双击“”加载第2种,选择性使用在这种场景下,您可以使用excel的加载项功能来安装决策树。
步骤如下:把TreePlan、xla保存在您电脑硬盘的某个地方。
如果您把TreePlan、xla文件保存在了excel 或office子目录文件夹里,请直接到第三步。
否则,打开excel——单击office按钮——excel选项——加载项——转到——加载项对话框,单击浏览按钮,找到TreePlan、xla,单击确定。
在加载项对话框中,可以瞧到已经有TreePlan、xla选项,选中决策树前面的方框,单击确定。
如果您为了释放内存不再用决策树了,那么在加载项对话框中,去掉决策树前面的方框中的对勾。
当您要使用的时候,选择加载项,并选中决策树即可。
如果您要从加载项中移除决策树,直接在您保存TreePlan、xla文件的地方把它删除即可。
下次当您打开excel并使用加载项时,会出现一个“未找到加载的TreePlan、xla文件,就是否从列表中删除?”的对话框,单价确定即可。
1)首先把加载宏放入如下安装文件件“D:\Program Files\MicrosoftOffice\Office15\Library‘’library 英 [ˈlaɪbrərɪ] 美 [laɪˌbrɛrɪ] n、图书馆,藏书室;文库C:\Program Files\Microsoft Office\Office15\Library2)加载:文件-选项-加载项-加载项-treeplan-转到第3种,经常使用如果您希望只要打开excel就能够使用决策树,那么就把TreePlan、xla文件保存在Excel XL Start文件夹里。
Excel XL Start文件夹路径:系统盘(通常为C盘)——Documents and Setting 文件夹——Application Data文件夹——Microsoft 文件夹——Excel 文件夹——XL Start 文件夹。
二、新建一个决策树您可以通过选择加载项-决策树或者按快捷键ctrl+t来新建一个决策树。
如果您的工作表没有马上出现一个决策树,就会出现一个有三个选项的对话框,如图,选择New Tree(新建树),就会出现一个决策树:决策树将以您选中的左上方的单元格为基准画一个默认的决策树,上图就就是选中B4单元格画的决策树。
(注意:决策树在的区域将会改写工作表中已经存在的值;尽可能从您保存数据的右面的区域开始画决策树;并且不要添加或删除决策树覆盖区域的行或列)。
三、添加分支或修改分支与节点对默认决策树添加分支或修改分支与节点来制作一个决策树。
1、如果要修改分支名称与概率,则单击包含分支名称与概率的单元格,直接修改即可。
2、如果要修改决策树的结构,比如添加或删除分支与节点,则选择那个节点或者包含节点的单元格进行修改,同时可以单击加载项中的决策树(decision tree)或快捷键ctrl+t,决策树会提供一个可以使用的命令的对话框。
添加前添加后1)添加分支:选择节点(一定选择节点所在的单元格,不能选择节点上面的图形)-选择Decision Tree 命令按钮-Add branch---okbranch英[brɑːn(t)ʃ] 美[bræntʃ]vt、分支;出现分歧vi、分支;出现分歧n、树枝,分枝;分部;支流删除分支与节点insert dicision:插入决策;add branch:添加分支;change to event:改变事件2)删除分支:选择要删除的分支节点单元格(一定选择节点所在的单元格,不能选择节点上面的图形)--选择Decision Tree 命令按钮—Remove previous branch移除树枝删除前删除后previous英['priːvɪəs] 美['privɪəs] adj、以前的;早先的;过早的adv、在先;在…以前3)添加事件节点:比如要为第一个事件添加一个新的事件节点,则选择紧挨着那个事件分支终点的空白单元格(G6),然后按ctrl+t。
决策树则出现如下对话框:change to event node:改变活动节点我们通过选择第二项Change to event node(改为事件节点)来把选择的终点变为事件节点,选择分支数目,这里默认为2个。
然后单击OK,决策树就会在终点的地方出现两个新的分支事件。
如图:4)节点类型决策树将根据您选择的不同出现不同的对话框。
当您选中一个事件节点,并按ctrl+t时,会出现如下对话框:当您选中一个决策节点时,会出现一个类似的对话框。
如果您想为此节点添加一个分支,则选择Add branch(添加分支)——单击OK即可。
添加前 添加后5)节点之前插入决策/事件节点如果您想在您选择的节点之前插入一个决策或事件节点,则单击Insert decision(插入决策节点)或Insert event(插入事件节点)——单击OK 即可。
6)选择的节点移除事件节点不能移除,要想移除,先转变为决策节点。
如果想把选择的节点移除:选择节点--选择Decision Tree 命令按钮—Shorten tree-ok删除后shorten tree:缩短树;shorten英['ʃɔːt(ə)n] 美['ʃɔrtn] vt、缩短;减少;变短vi、缩短;变短7)帮助如果想得到命令按钮的详细介绍,则单击Help按钮。
8)Copy subtree (复制子树)对于Copy subtree (复制子树)这个按钮在建立大的决策树就是很有帮助的。
如果有两个及以上的决策树就是相似的,则可以用复制粘贴子树而不就是分开添加各部分。
要复制一个子树,则单击您要复制的子树的根节点——单击Copy subtree按钮。
这表示要复制所选择的节点以及在这个节点后面所有的部分。
选择根节点—复制子树要粘贴子树,则选择要粘贴的节点——选择Paste subtree(粘贴子树)即可。
选择根节点—粘贴子树粘贴后paste英[peɪst] 美[pest] vt、张贴,裱糊;用浆糊粘n、面团,膏;糊状物,[胶粘] 浆糊9)用EXCEL的功能修改决策树格式因为决策树就是直接在Excel里做的,可以用EXCEL的功能修改决策树格式。
比如您可以对事件标签使用用粗体或斜体。
选择您需要修改格式的单元格,然后用excel格式按钮修改格式。
选中单元格-字体加粗决策、事件节点图形格式调整10)Select(选择)的对话框有一点可能很有帮助,就就是当您没有选中一个节点,按ctrl+t之后就会出现一个Select(选择)的对话框。
也可以在Node(节点)对话框中单击select按钮出现此对话框。
Cells n、[细胞] 细胞;单元格(cell的复数);牢房;小屋v、住在牢房中(cell的三单形式) cell英[sel] 美[sɛl] n、细胞;电池;蜂房的巢室;单人小室vi、住在牢房或小室中branch names:分支机构名称partial cash flows:部分现金流probabilities:概率;probability英[prɒbə'bɪlɪtɪ] 美['prɑbə'bɪləti] n、可能性;机率;rollback evs/ces:回滚evs /cesrollback eus:回滚eusterminal values:终端值connector英[kə'nektə(r)] 美[kə'nɛktɚ] n、连接器,连接头diagonal英[daɪ'æg(ə)n(ə)l] 美[daɪ'æɡənl] adj、斜的;对角线的; n、对角线;斜线通过这个对话框,您可以选择决策树中具有同一特性的元素。
比如,如果您选择Probabilities(概率)并单击OK,决策树就会选中所有包含概率的单元格,您就可以对所有的概率值进行格式化。
(由于excel的限制,在大型决策树中,Select对话框就是不可用的。
)11)部位明细Terminal value 终端值Rollback EVs/CEs( Expected Values:使用期望值)(Collective Evolution:集体进化)Expected英[ɪk'spektɪd]美[ɪk'spektɪd]adj、预期的;预料的collective英[kə'lektɪv]美[kə'lektɪv] adj、集体的;共同的n、集体evolution英[,iːvə'luːʃ(ə)n; 'ev-]美[ˌɛvəˈluʃən; (occas、) ˌ ivəˈluʃən]n、演变;进化论;进展Partial cash flows:部分现金流Probabilties:概率Branch names 分支名称回滚EUs(Exponential Utility :指数效用)exponential英[ˌekspə'nenʃl]美[ˌekspə'nenʃl]adj、指数的;幂的utility英[juːˈtɪlɪtɪ] n、实用;效用;公共设施;功用adj、实用的;通用的;有多种用途的四、决策树示例下图就是一个决策树的示例。
在这个事例中,这个公司需要作出如下决策:(1)就是否接受一个合同的提案;(2)采用哪种方式满足合同的要求。
决策树包含由分支连起来的决策节点、事件节点与终结点。
每个分支由包含公式、单元格引用、标签的单元格环绕。
您可以编辑各分支的标签、概率及现金流比如,如果公司决定采用合同的提案,则需支付50000美元,签订合同后可得250000美元。
如果采用自动方式,需支付50000美元,如果自动方式失败,需支付120000美元,采用机械方式则需花费120000美元。
决策树的值由嵌入到工作表中的公式直接计算得出。
终结点的值就是这个分支上所有现金流的与。
在事件节点旁边的返回值(上图中的90000)就是决策树计算的期望值,在决策节点旁边的返回值则就是两种选择的最大值。
在决策节点旁的值表明了哪种选择为最优决策。
比如,在1这个决策节点的值就是20000,这表明接收提案就是最优决策;在2这个决策节点的数值为90000,说明公司应该尝试自动方式,因为自动方式的收益90000大于采用机械方式的收益80000、可以通过选项按钮来选择决策树的计算方式。
