第四章空间统计分析初步
Arcgis第四章 空间分析

质心量算:它是描述地理目标空间分布的最有用的单一量算量
☆求取目标的重心位置,用于跟踪某些地理分布的变化,如人口重心的变化、 土地利用重心的迁移等 ☆对目标坐标值进行加权平均(ARCGIS中需要使用calculate geometry工具)
XG
• 形状量算
W X W
i i i i
i
YG
W Y W
☆ 缓冲区:空间对象在一定半径或一定条件下的邻域。 ☆ 缓冲区分析:指以点、线、面实体为基础,在其周 围建立一定宽度范围内的缓冲区多边形,用以分析 实体的邻近性或对周围的影响,从而实现空间数据 在水平方向得以扩展的空间分析方法
点的缓冲区
线的缓冲区
面的缓冲区
13
建立缓冲区的算法
• 缓冲区的种类 ☆点:圆形、三角形、矩形、环形。 ☆线:单侧、双侧对称、双侧不对称 ☆面:内侧、外侧 • 缓冲区的建立——中心线扩张法 主要包括:角平分线法 凸角圆弧法
定向网络(据ESRI)
连通性管理 网络属性(权重) 存在位置
非定向网络(据ESRI)
网络模式
Network Analyst扩展模块
几何网络分析工具 28
• 讨论
☆是否有所的空间网络都有分析的必
要性?
判断标准:网络中是否能够进行物质、
能量、信息的传输。
29
• 网络的基本组成
☆基本组成要素
链(Link):网络中的管线,资源传输的通道,构成网络的骨 架。如街道、河流、水管等。 结点(Node):链的端点或两(多)条链的交点。如道路叉 口、河流的交汇点等。 障碍(Barrier):禁止网络中资源流动的点 。如道路网中 施工的路段、供水网络中的水阀等。 拐角点(Turn):指网络中状态属性有阻力的结点 。如对拐 弯方向或时间有限制的路口。 中心(Center):网络中接受或分配资源的结点。如水库、 商业中心、电站等。 站点(Stop):在网络中资源增减的站点。如库房、汽车站 等。
空间统计分析方法与应用

空间统计分析方法与应用引言空间统计分析是一种将空间数据和统计学原理结合起来的分析方法,用于探索和理解地理现象在空间上的分布规律和相互作用关系。
随着GPS技术、遥感技术和地理信息系统的发展,空间数据的获取和处理能力得到了大幅提升,空间统计分析成为了地理学、城市规划、环境科学等领域的重要工具。
本文将介绍一些常用的空间统计分析方法和它们在实际应用中的作用。
空间统计分析方法空间自相关分析空间自相关分析是用来描述和测量空间数据的空间相关性的方法。
它通过计算各个地点的属性值与周围地点的属性值之间的相关性来判断空间数据的分布是否呈现出聚集、随机或分散的趋势。
其中,常用的指标包括Moran’s I和Geary’s C等。
空间自相关分析可以帮助我们了解地理现象的空间集聚性和空间异质性,并且能够为规划和决策提供依据。
空间插值分析空间插值分析是指根据已知的有限点数据,通过插值方法推测出未知位置的属性值。
常用的插值方法包括克里金插值、反距离加权插值和样条插值等。
空间插值分析可以帮助我们填补空间数据的缺失和提供空间数据的连续性表达,从而更好地理解地理现象的分布和变化。
空间聚类分析空间聚类分析是指通过将地理现象的空间数据划分为若干组或簇,来发现空间数据的集聚规律和地理特征。
常见的空间聚类方法有基于密度的聚类、基于网格的聚类和基于层次聚类的方法等。
空间聚类分析可以帮助我们发现空间数据中的热点区域和冷点区域,从而更好地理解地理现象的空间分布规律。
空间回归分析空间回归分析是一种结合了统计回归分析和空间自相关分析的方法。
它通过考虑空间相关性,分析影响地理现象的空间因素和非空间因素之间的关系。
空间回归分析可以帮助我们识别和量化空间变量对地理现象的影响程度,并且提供空间因素对地理现象预测和模拟的能力。
空间统计分析的应用城市规划空间统计分析在城市规划中有着广泛的应用。
通过空间自相关分析,我们可以了解城市不同区域的发展状况和经济社会差异。
空间统计分析方法

空间统计分析方法空间统计分析是一种统计学方法,旨在研究和分析地理空间上的模式和变化。
它结合了地理信息系统(GIS)和统计学的原理和技术,通过空间数据的收集、整理、分析和解释,揭示地理现象背后的模式和规律。
空间统计分析可以应用于环境科学、城市规划、农业、地质学等领域,帮助研究人员更好地理解和解决空间问题。
在空间统计分析中,主要涉及的方法包括空间自相关分析、空间插值、地理加权回归、空间点模式分析、空间聚类分析等。
首先,空间自相关分析用于研究地理空间数据中的相关性。
它主要包括全局自相关和局部自相关两种方法。
全局自相关分析通过计算全局指标,如Moran's I指数,来衡量地理空间的整体相关性。
局部自相关分析则用于检测地理空间中的局部聚集现象,如LISA (Local Indicators of Spatial Association)等方法可以识别出热点区域和冷点区域。
其次,空间插值是一种通过已知空间点数据来估计未知区域值的方法。
最常用的插值方法包括反距离权重法 (Inverse Distance Weighting)、克里金插值 (Kriging)、三角网插值法 (TIN interpolation)等。
空间插值在环境监测和资源管理中具有重要作用,可以有效地填补空间数据的空白。
地理加权回归 (Geographically Weighted Regression, GWR) 是一种用于空间数据建模的统计方法。
它考虑了空间数据的异质性和空间自相关性,通过在回归模型中引入空间权重矩阵,可以在不同地理位置上建立不同的回归关系。
GWR方法在城市研究和社会经济学中应用广泛,可以更精确地分析空间数据的影响因素。
空间点模式分析是一种用于研究点状空间数据分布的方法,旨在揭示点状数据背后的空间模式和聚集程度。
常用的点模式分析方法包括Ripley's K函数、Moran's I函数、Clark-Evans聚集指数等。
空间统计分析

空间统计分析目录一、内容综述 (2)1. 背景介绍 (3)2. 研究目的与意义 (4)二、空间统计分析概述 (5)1. 空间统计分析定义 (6)2. 空间统计分析的发展与应用领域 (7)三、数据收集与预处理 (9)1. 数据来源 (10)2. 数据收集方法 (10)3. 数据预处理流程 (12)四、空间数据的可视化分析 (13)1. 空间数据可视化技术 (14)2. 可视化工具与平台选择 (15)3. 可视化分析结果解读 (17)五、空间数据的探索性统计分析 (18)1. 空间数据的描述性统计 (19)2. 空间数据的探索性方法 (20)3. 探索性结果分析与解释 (21)六、空间数据的定量统计分析 (23)1. 空间自相关分析 (24)2. 空间回归分析 (25)3. 空间插值分析 (26)4. 其他空间统计模型与方法 (27)七、空间统计分析的应用案例 (28)1. 城市规划与管理领域应用案例 (29)2. 生态环境保护领域应用案例 (31)3. 经济学领域应用案例 (31)4. 社会学领域应用案例 (33)八、空间统计分析的挑战与展望 (34)1. 技术挑战与解决方案 (35)2. 数据质量与可靠性问题探讨 (37)3. 未来发展趋势预测与展望 (38)九、结论与建议 (39)1. 研究总结与主要发现 (40)2. 政策建议与实施建议 (41)3. 研究不足与展望未来的研究方向 (42)一、内容综述空间统计分析是统计学的一个分支,其研究主要集中在地理空间数据和相关领域的数据分析和解释上。
随着全球定位系统、遥感技术、地理信息系统等技术的不断发展,海量的空间数据不断生成,空间统计分析的重要性愈加凸显。
本文档旨在全面介绍空间统计分析的基本概念、方法、应用及其发展趋势。
我们要明确什么是空间统计分析,空间统计分析结合了统计学与地理学,研究如何利用统计学方法分析带有空间属性的数据,揭示其内在的空间分布规律、空间关联关系以及空间演变趋势。
空间统计分析范文

空间统计分析范文空间统计分析是地理信息科学中一种重要的数据分析方法,通过对空间数据的统计分析,可以揭示地理现象的空间分布规律、相互关系和演变趋势,为决策和规划提供科学依据。
本文将介绍空间统计分析的基本原理、常用方法和应用案例。
一、基本原理1.空间自相关性:地理现象在空间上的分布往往呈现出一定的相关性,即位于空间上相邻的地理单元的属性值相似性较高。
空间自相关性是空间统计分析的核心概念,通过计算空间自相关指标,可以测量地理现象的空间聚集程度和相关性程度。
2.空间插值方法:地理现象通常是以离散的点、线或面数据的形式存在,为了将其转化为连续的表面,需要使用空间插值方法。
常见的空间插值方法包括反距离加权插值、克里金插值和样条插值等,可以在空间上插值出地理现象的连续分布。
3.空间聚类分析:地理现象的分布往往呈现出一定的聚类性,即具有相似属性值的地理单元在空间上聚集成簇。
空间聚类分析可以帮助识别和描述地理现象的聚集区域,并进一步分析其成因和特征。
4.空间揭示:地理现象的空间分布往往是由一系列空间因素所决定的,空间统计分析可以通过空间回归、模式识别和空间关联等方法,揭示地理现象与空间因素之间的关系和影响。
二、常用方法1. 空间自相关分析:通过计算空间自相关指标,如Moran's I指数和Geary's C指数等,来测量地理现象的空间相关性和聚集程度。
2.空间插值分析:通过使用插值方法,如反距离加权插值、克里金插值和样条插值等,将离散的点、线或面数据插值为连续的表面,以便进行空间分析。
3. 空间聚类分析:通过使用聚类算法,如K-means聚类和DBSCAN聚类等,识别和描述地理现象的聚集区域,并分析其成因和特征。
4.空间回归分析:通过建立空间回归模型,揭示地理现象与空间因素之间的关系和影响,如空间滞后模型和空间错误模型等。
5. 空间模式识别:通过使用空间统计指标,如吉尼系数、Getis-Ord G*统计量和纳入法等,识别地理现象的空间分布模式和热点区域。
《空间统计分析》课件

空间回归分析
总结词
适用于具有空间依赖性和异质性的数据
VS
详细描述
空间回归分析适用于具有空间依赖性和异 质性的数据。这些数据通常在地理位置上 存在相关性,并且可能受到局部环境、社 会经济等因素的影响。例如,在疾病地理 学中,可以利用空间回归分析来研究疾病 发病率与地理位置之间的关系。
空间回归分析
总结词
R软件介绍
统计计算和图形呈现的编程语言
01
R是一种开源的统计计算和图形呈现的编程语言,广泛应用于数
据分析和数据挖掘领域。
强大的统计分析功能
02
R提供了大量的统计分析函数和包,可以进行各种统计分析,如
回归分析、聚类分析、主成分分析等。
灵活的可视化功能
03
R支持多种图形绘制系统,如基础图形、lattice和ggplot2等,
传感器数据
通过各种传感器采集的环境监 测数据,如气象站、水文站等
。
其他数据
包括商业数据、政府公开数据 等,涵盖了各种与空间位置相
关的信息。
空间数据的处理方法
数据清洗
去除重复、错误或不完 整的数据,确保数据质
量。
坐标转换
将数据从一种坐标系转 换到另一种坐标系,以
便进行空间分析。
数据聚合
将小区域数据合并为较 大区域,以便进行更高
森林火灾风险的空间分析
总结词
评估森林火灾风险的区域差异
详细描述
利用空间统计分析方法,评估不同区 域的森林火灾风险,识别高风险区域 ,为森林防火和资源管理提供科学依 据。
气候变化对农业产量的影响研究
总结词
分析气候变化对农业产量的影响程度
详细描述
通过空间统计分析,研究气候变化对农业产量的影响程度, 分析不同地区的气候变化对农业产量的贡献,为农业可持续 发展提供决策支持。
第四章空间统计分析

第四章空间统计分析空间统计分析是利用地理信息系统(GIS)和统计学方法,对空间数据进行分析和解释的一种方法。
它旨在揭示地理现象背后的空间关系和模式。
本文将从空间自相关、空间插值和空间聚类这三个方面对空间统计分析进行介绍。
首先,空间自相关是研究空间数据之间相关性的一种方法。
它用于检测地理现象在空间上的聚集程度和分布模式。
空间自相关分析的基本假设是空间数据之间存在其中一种空间关联性,即相邻区域的观测值具有相似的特征。
通过计算空间自相关指标,如Moran's I和Geary's C,可以确定数据之间的正相关、负相关或无相关性。
这些指标对于了解地理现象的空间分布模式以及其潜在的驱动因素非常有用。
其次,空间插值是将离散的观测数据转换为连续的空间表面的方法。
它的目标是填补空间上的观测缺失,并推断未来的观测值。
常用的空间插值方法有反距离加权插值(IDW)、克里金插值和泰森多边形插值。
这些方法根据不同的空间关系模型将观测值在空间上进行插值,并生成平滑的空间表面。
空间插值对于研究地理现象的分布特征和场景模拟具有重要的意义。
最后,空间聚类是将观测数据划分为具有相似特征的簇群的过程。
它用于识别地理现象的聚集模式和热点区域。
常用的空间聚类方法有DBSCAN、K-means和层次聚类等。
这些方法通过计算数据之间的距离和相似性,将观测值划分为相似的簇群,并确定其中的聚集区域。
空间聚类有助于发现地理现象的空间集聚现象,以及揭示其潜在的空间关联性。
空间统计分析在许多领域都有广泛的应用。
在城乡规划中,它可以帮助决策者了解不同区域的发展差异和人口分布情况,以便合理规划城市和农村的布局。
在环境科学中,空间统计分析可以用于研究污染源的扩散和影响范围,指导环境保护工作。
在社会经济研究中,空间统计分析可以用于探索不同地区的经济发展差异和产业分布模式。
在流行病学研究中,空间统计分析可以用于研究疾病的空间传播和热点区域的确定。
空间统计分析课件

平均数也分简单调和平均数和加权调和平均数,
其公式分别为
X t
n n1
i1 x i
n
Pi
X
tp
i1
n P i
i1 x i
几何平均数(geometric mean ):是n个数据连乘的 积开n次方根,计算公式为
n
X g n xi i 1
ห้องสมุดไป่ตู้•空间统计分析课件
(3)中位数(Median ) 一组数据按从小到大(或从大到小)的顺 序依次排列,处在中间位置的一个数(或 最中间两个数据的平均数,注意:和众数 不同,中位数不一定在这组数据中)。 中位数的定义可知,所研究的数据中有一 半小于中位数,一半大于中位数
•空间统计分析课件
9.2.2 代表数据离散程度的统计量
有时虽然两个数据集的平均数相等,但各数据分 布在平均数左右的疏密程度却不相同,也就是它 们的离散程度不一样,为了把一个数据集的离散 程度表现出来,就需要研究离散度。
离散程度越大,数据波动性越大,以小样本数据 代表数据总体的可靠性越低;离散程度越小,则 数据波动性小,以小样本数据代表数据总体的可 靠性越高。
标准差是方差的平方根,记为
1 n
n i1
(xi
x)2
•空间统计分析课件
(8)变差系数(coefficient of variation) 变差系数也称为离差系数或变异系数,是 标准差与均值的比值,以C v 表示
Cv x 10000
变差系数用来衡量数据相对变化的程度
•空间统计分析课件
9.2.3 代表数据分布形态的统计量
•空间统计分析课件
基本统计量
描述数据特征的统计量
集中趋势
平均数 中位数 众数 分位数
空间分析的原理与方法ppt课件

2
第一节 空间分析概述
二、空间分析的主要内容 由于GIS空间数据库中存储了包含空间特征的空间信息及与应
用相关的专题信息,因此GIS中的空间分析包含: 空间数据的空间特征分析 空间数据的非空间特征分析 空间特征和非空间特征的联合分析
(1)咨询式空间分析
主要根据已有数据实现空间数据的查询检索及集合分析。
(2)产生式空间分析
基于GIS中拓扑关系和空间操作运算、空间统计分析及将GIS作为 通用工具同其他专业模型结合,实现空间数据的模拟和分析。
8
第一节 空间分析概述
3、按空间数据特征看GIS空间分析分类 (1)空间数据的空间特性分析 空间位置分析:指通过空间坐标系中坐标值来确定空间物体的地理 位置。 空间分布分析:空间分布反映了同类空间物体的群体定位信息。 空间形态分析:空间形态反映了空间物体的几何特征,包括形态表 示和形态计算两个方面。 空间关系分析:空间关系反映了空间物体之间的各种关系。 (2)空间数据的非空间特性分析
和模拟空间现象的过程和规律。这类分析采用的方法主要是统计分析 方法,尤其是多元统计分析方法
从方法上,空间数据的非空间特征分析与一般的数据分析并无本质 的差别。在分析过程中,它并不考虑数据抽样点的空间位置,但由于 空间特征数据和非空间特征数据间不可分割的关系,对分析结果的解 释是基于地理空间的,也就是说,其结果常通过地图来反映空间现象 和规律。
3
第一节 空间分析概述
(1)空间数据的空间特征分析 从空间物体的位置、关系等方面去研究空间事物,最后对空
间事物做出定量的空间描述和分析,采用的主要方法为空间统 计学、图论、拓扑学、计算几何、图形学等。
第4章空间统计分析课件

2.1 简单的二进制邻接矩阵
123 456 789
车的行走方式
123 456 789 王、后的行走方式
16
17
18
19
20
2.2 基于距离的二进制空间权重矩阵
21
22
空间自相关按功能大致分为两类: 全域型空间自相关(Global Spatia Autocorrelation) 区域型空间自相关(Local Spatia Autocorrelation)
45
人均GDP局部Moran指数表
46
河南地级市人均GDP局部Moran指数
47
48
49
4.2 G统计量
全局G统计量的计算公式为: 对每一个区域单元的统计量为:
50
对统计量的检验与局部Moran指数相似,其检验值为
显著的正值表示在该区域单元周围,高观测值的区域 单元趋于空间集聚,而显著的负值表示低观测值的区 域单元趋于空间集聚。
25
3.1 Moran’s I
设研究区域中存在n个面积单元,第i个 单元上的观测值记为xi,观测变量在n个单 元中的均值记为 ,Moran’s I定义为:
26
-1≤ I ≤1 1表示极强的正空间自相关,-1表示极强的 负空间自相关。
27
对于Moran指数,可以用标准化统计量Z来检 验n个区域是否存在空间自相关关系,Z的计算公 式为:
第4章 空间统计分析
§4.1 空间自相关 Spatial autocorrelation
1
空间统计分析,即空间数据的统计分析,通过 空间位置建立数据间的统计关系。
空间统计学产生的原因: 大多数经典统计学分析要求样本相互独立, 而空间数据间并非完全独立,而是存在依赖性。
空间统计分析

空间统计分析空间统计分析是一种将统计学方法与地理信息系统(GIS)相结合的技术,用于研究地理空间数据的分布和关联性。
它主要通过空间统计指标、空间模式和空间回归等方法,探索地理现象的空间分布规律,揭示地理现象之间的相互作用关系。
本文将介绍空间统计分析的基本概念、常用方法和应用领域。
一、空间统计分析概述空间统计分析是一门研究地理现象和空间数据的统计学方法,它通过统计推断、空间模式、空间依赖和空间回归等技术,揭示地理空间现象分布的非随机性和空间自相关性。
空间统计分析主要包括以下几个方面的内容:1. 空间统计指标:用于描述地理空间数据的分布特征和空间相关性的指标,常用的指标包括平均距离、Moran's I指数、Geary's C指数等。
2. 空间模式:用于描述地理空间现象的分布模式和空间聚集程度,常用的模式包括均匀分布、随机分布、聚集分布等。
3. 空间回归:用于分析地理空间现象之间的因果关系和相互作用关系,常用的方法包括地理加权回归(GWR)、空间自回归(SAR)等。
二、空间统计分析方法空间统计分析方法多种多样,下面介绍几种常用的方法:1. 全局空间自相关分析:通过计算Moran's I指数或Geary's C指数等,判断地理空间现象是否存在空间自相关性。
这种方法适用于研究地理现象的整体空间分布规律。
2. 空间插值分析:通过插值方法(如反距离加权插值、克里金插值)将有限的点数据转化为连续的面数据,从而实现对未知位置的估计。
这种方法适用于研究地理现象的空间分布和变化趋势。
3. 空间聚类分析:通过聚类算法(如K均值聚类、DBSCAN聚类)将地理空间数据划分为不同的群集,以揭示地理现象的空间聚集特征和区域差异。
4. 空间交互分析:通过计算空间相关性指数(如Moran's I指数)和空间回归模型,揭示地理现象之间的空间关联性和相互作用关系。
三、空间统计分析应用领域空间统计分析在许多领域都有广泛的应用,以下列举几个典型的应用领域:1. 城市规划:空间统计分析可用于研究城市土地利用、人口分布和交通网络等,为城市规划和土地管理提供科学依据。
空间格局统计与空间分析空间格局统计

空间格局统计与空间分析空间格局统计空间格局统计是地理信息系统(GIS)中的一项重要技术,用于描述和计量人类活动和自然现象在空间上的分布和变化规律。
通过对空间格局的统计分析,可以更好地理解和解释现象背后的规律,并为决策提供科学依据。
本文将从空间格局的概念、统计方法和应用场景等角度对空间格局统计进行分析。
首先,空间格局是指地表或地表以下的自然、社会和经济现象在空间上的分布和组织方式。
它反映了人类活动和自然现象的特点、变化和相互关系。
空间格局统计是一种对这些空间格局进行描述、测量和分析的方法。
它可以利用地理信息系统的专业工具和方法,通过对空间数据的统计和空间模式的检测,来揭示地理现象的规律和内在机制。
在具体的统计方法上,空间格局统计主要包括聚类分析、离散分析、插值分析和核密度分析等。
聚类分析是一种用于检测空间聚集现象的方法,通过计算地理空间对象之间的相似性,将它们划分为不同的区域或群落。
离散分析则是一种用于衡量空间分布的离散程度的方法,通常采用标准差、方差或离散系数等指标来评估。
插值分析则是一种用于估计未被观测到的地理现象的值的方法,它可以通过已知的点值来推断其他位置的值。
核密度分析则是一种用于检测空间点密度分布的方法,可以揭示人口、交通、资源等地理现象的热点和冷点区域。
空间格局统计有广泛的应用场景,包括城市规划、环境保护、交通管理等。
在城市规划中,空间格局统计可以用于分析城市空间结构的演变和预测未来的发展趋势,为城市规划提供科学依据。
在环境保护中,空间格局统计可以用于评估生态系统的健康状况和环境质量,为环境保护决策提供支持。
在交通管理中,空间格局统计可以用于分析交通流量和拥堵情况,优化交通网络的布局和行车路线。
综上所述,空间格局统计是一种重要的地理信息系统技术,它通过对地理现象在空间上的分布和变化规律进行分析,可以揭示现象背后的规律和内在机制,并为决策提供支持。
随着地理信息系统技术的不断发展和应用,空间格局统计在各个领域中的应用前景将越来越广阔。
空间统计分析方法的原理与应用

空间统计分析方法的原理与应用空间统计分析是一种广泛应用于地理信息系统(GIS)领域的方法,可用于探究地理现象的空间分布规律、评估模式和预测趋势。
空间统计分析方法基于地理数据的空间变异性,通过数学和统计技术,分析和解释地理现象在空间上的特征和相互关系。
本文将介绍空间统计分析的原理及其在不同领域的应用。
一、空间统计分析的原理空间统计分析的核心原理是考察地理现象的空间相关性和模式。
其基本步骤包括数据准备、空间自相关分析、空间插值和空间聚类分析。
下面将分别介绍这些步骤的原理。
1. 数据准备首先,需要收集相关的地理数据,这些数据可以是点、线或面要素,如人口分布、土地利用、交通网络等。
数据准备包括数据清理、转换和整理,以保证数据的质量和适用性。
2. 空间自相关分析空间自相关分析旨在测量地理现象在空间上的相关性。
常用的指标包括莫兰指数和Geary's C。
莫兰指数可以衡量地理现象在空间上的聚集程度,而Geary's C可以测量地理现象在空间上的离散程度。
3. 空间插值空间插值是一种用于填补空间数据缺失值或生成连续表面的方法。
常用的插值方法包括反距离加权插值、克里金插值和样条插值。
这些方法可以基于已有的空间数据,推断未知位置上的值。
4. 空间聚类分析空间聚类分析用于寻找地理现象的空间集聚模式。
常用的空间聚类算法包括DBSCAN和K-means。
这些算法可以将空间数据划分为具有相似属性的区域。
二、空间统计分析的应用空间统计分析方法广泛应用于各个领域,包括城市规划、环境管理、自然资源管理等。
以下将介绍一些常见的应用案例。
1. 城市规划空间统计分析可以帮助城市规划者了解城市功能区的分布和连接性。
通过分析人口密度、交通网络和服务设施的空间分布,可以指导城市规划决策,优化城市布局和交通规划。
2. 环境管理空间统计分析在环境管理中的应用包括水资源管理、土壤污染评估和生态系统保护等。
通过分析水体和土壤的空间变异性,可以评估水资源的可持续利用和土壤污染的程度,并提供决策支持。
空间统计分析

当Moran’s I 接近期望值(-1/(n-1),随着样本数量的增大,该值趋于0)时,
表明不存在空间自相关,观测值在空间上随机排列,满足经典统计分析所要求的独 立、随机分布假设。
Байду номын сангаас
29
随机检验(Permutation test)
(the Second Law of Geography)。
13
基本分析方法/分析指标
空间权重矩阵
空间权重矩阵是对空间邻接关系的定义,是空间统计分析运算的基础 之一。
全局空间自相关 局部空间自相关
14
空间权重矩阵
空间权重矩阵(spatial weight matrix)
对空间邻居(spatial neighborhood)或邻接关系的描述,通常定义一个二 元对称空间权重矩阵W,来表达n个位置的空间区域的邻近关系。 目前对于空间权重指标的构建,主要基于两类特征:连通性(Continuity) 和距离(Distance)。此外,还可以通过面积、可达度等方式对空间权重指 标进行构建。
通常约定,一个空间单元与其自身不属于邻居关系,即矩阵中主对角线上元素值为0。
18
在实际应用中,一般根据以下两种规则定义邻居: 公共边界 如果第i和第j个空间单元具有公共边界,则认为它们是邻居,空间权重矩阵中 的元素为1;否则,不是邻居,元素为0。 距离 如果第i和第j个空间单元之间的距离位于给定的临界距离d之内,则认为它们 是邻居,空间权重矩阵中的元素为1;否则,不是邻居,元素为0。 Cliff-Ord广义空间权重矩阵
3 4 4
1 2
3 2 3
空间统计概述总结范文

空间统计是一种利用空间分析方法对地理现象进行定量描述和推断的统计学方法。
随着地理信息系统(GIS)和遥感技术的发展,空间统计在地理学、环境科学、城市规划等领域得到了广泛应用。
本文将从空间概率、概率密度、不确定性以及统计推断等方面对空间统计进行概述总结。
一、空间概率空间概率是指地理现象在空间分布上的概率,它遵循地理学第一定律。
在空间统计中,我们关注的是要素之间的空间相关性,即要素在空间分布上的相互依赖性。
例如,如果两个地区同时发生滑坡的概率高于其中一个地区与第三个地区同时发生滑坡的概率,那么这两个地区之间存在较强的空间相关性。
二、概率密度概率密度是指测量值的偏差在任意方向上都会出现一定的散布,而散布的概率理论上会形成正态分布的对称曲线。
在空间上,我们可以将这个分布想象成一个钟形,任何一个事件在任意区域发生的概率,就是这个钟表面在这个区域上的所占体积。
通过分析概率密度,我们可以了解地理现象在空间上的分布特征。
三、不确定性不确定性是空间统计中的一个重要概念,它来源于数据的不确定性。
了解数据中的不确定性,研究这些不确定性如何影响分析结果是空间统计研究的重要内容。
例如,地统计学采用随机过程来模拟插值的变异情况,从而降低不确定性对分析结果的影响。
四、统计推断统计推断是空间统计的核心内容,通过样本分析推理以求得到关于包括了样本在内的更大群体的结论。
与经典统计相比,空间统计在分析要素之间的相关性方面具有独特优势。
在空间分析中,我们通常在所有可获得的数据上进行操作,很少或几乎没有一个用于提取数据并进行推理的总体概念。
此外,我们认为每个样本观测值是相互依赖的,除非相距很远。
五、空间统计的主要内容1. 聚合:空间统计关注地理现象在空间上的整体性,通过对要素进行聚合分析,揭示地理现象在空间分布上的规律。
2. 整体性:空间统计强调地理现象在空间上的相互联系和影响,通过分析要素之间的空间相关性,揭示地理现象在空间上的整体特征。
第四章 空间统计分析

1 当区域i和j的距离小于d时 wij 其它 0
(二)全局空间自相关
衡量空间自相关的指标有Moran指数I、Geary系数C、 G统计量等,他们都有全局指标和局部指标两种。全 局空间关联指标用于探测某现象在整个研究区域的 空间分布模式,分析其是否有聚集特性存在。 Moran指数I是由 Moran于 1948年提出的 ,反映的是 空间邻接或空间邻近的区域单元属性值的相似程度。 Geary 系数与Moran指数存在负相关关系。 由于 Moran指数不能判断空间数据是高值聚集还是 低值聚集 , Getis和 Ord于 1992提出了全局 G系数。 G系数一般采用距离权 , 要求空间单元的属性值为正。
S0 Wij
i 1 j n n
S1 Wij Wji
i 1 j 1
n
n
2
2
4 n xi x n n 2 S3 Wi. W .i k i 1 2 i 1 n 2 xi x n Wi.为空间相临权重矩阵i 行 W.i为i 列 j 1
第1节 探索性空间统计分析
一、基本原理与方法 (一)空间权重矩阵 (二)全局空间自相关 (三)局部空间自相关 二、应用实例 三、软件实现
一、基本原理与方法
空间自相关(Spatial autocorrelation)是指同一个变量在 不同空间位置上的相关性。目的在于检验空间单元与其 相邻的空间单元的属性间是否具相似性。 如何定义“相邻”?——空间权重矩阵 空间自相关分析可分以下 3个过程: 首先建立空间权重矩阵,以明确研究对象在空间位置上的 相互关系; 其次进行全局空间自相关分析,判断整个区域是否存在空 间自相关现象或集聚现象; 最后进行局部空间自相关分析,找出空间自相关现象存在 的局部区域。
空间统计知识点归纳总结

空间统计知识点归纳总结一、空间统计概念空间统计是利用空间数据来揭示空间数据的分布规律和空间关联性,以得出空间模式和空间变化规律的统计学方法。
空间统计主要包括空间数据的统计描述、空间数据的空间关联性分析、空间数据的空间模式分析等内容。
二、空间数据的统计描述1. 空间数据类型:空间数据可分为点数据、线数据和面数据三类。
点数据是指地理空间上的一个具体位置;线数据是由多个点按照一定顺序连接而成的线条;面数据是由多个点按照一定顺序连接而成的封闭图形。
2. 空间数据的属性统计:对空间数据的属性进行统计描述,包括均值、方差、标准差等。
3. 空间数据的空间集聚性分析:利用聚集指数、泰斯特指数等指标来描述空间数据的聚集性。
三、空间数据的空间关联性分析1. 空间数据的自相关分析:用于描述空间数据与自身在空间上的相关性,如Moran's I、Geary's C指数等。
2. 空间数据的空间异质性分析:用于描述空间数据的异质性,比如LISA(Local Indicators of Spatial Association)等方法来描述空间数据的异质性。
四、空间数据的空间模式分析1. 空间数据的空间聚类分析:用于描述空间数据的聚类模式,如K均值聚类、DBSCAN聚类、层次聚类等方法。
2. 空间数据的空间分布模式分析:用于描述空间数据的分布模式,如核密度估计、距离分布函数等方法。
五、空间统计方法1. 空间插值方法:用于根据少量采样点推断整个区域的属性值,如克里金插值、反距离插值等。
2. 空间回归方法:用于描述变量之间在空间上的相关性,如空间误差模型、空间Durbin 模型等。
3. 空间模式识别方法:用于识别空间模式,如空间聚类算法、空间分布模式描述算法等。
六、空间统计应用1. 地理信息系统(GIS)中的空间统计:用于描述和分析地理空间数据的分布规律和空间关联性。
2. 城市规划中的空间统计:用于评估城市空间结构和发展规划,如用核密度估计来评估城市空间密集度。
空间统计分析实验报告
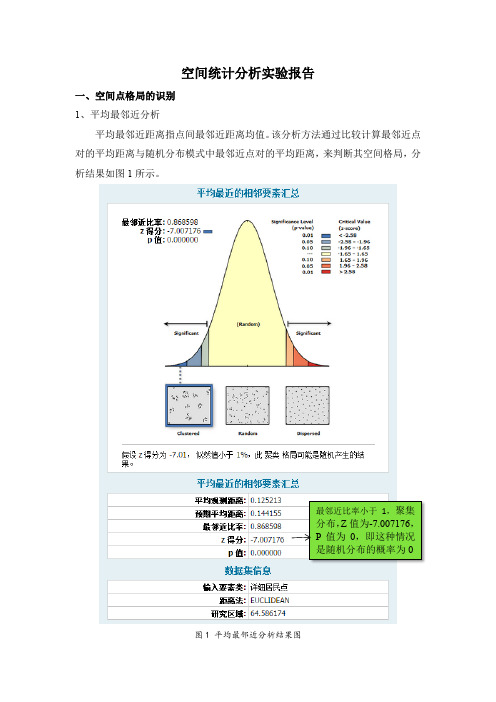
空间统计分析实验报告一、空间点格局的识别1、平均最邻近分析平均最邻近距离指点间最邻近距离均值。
该分析方法通过比较计算最邻近点对的平均距离与随机分布模式中最邻近点对的平均距离,来判断其空间格局,分析结果如图1所示。
图1 平均最邻近分析结果图最邻近比率小于1,聚集分布,Z值为-7.007176,P值为0,即这种情况是随机分布的概率为0计算结果共有5个参数,平均观测距离,预期平均距离,最邻近比率,Z 得分,P值。
P值就是概率值,它表示观测到的空间模式是由某随机过程创建而成的概率,P 值越小,也就是观测到的空间模式是随机空间模式的可能性越小,也就是我们越可以拒绝开始的零假设。
最邻近比率值表示要素是否有聚集分布的趋势,对于趋势如何,要根据Z值和P值来判断。
本实验中的最邻近比率小于1 ,聚集分布,Z值为-7.007176,P值为0,即这种情况是随机分布的概率为0,该结果说明云南省详细居民点的分布是聚集分布的,不存在随机分布。
2、多距离空间聚类分析基于Ripley's K 函数的多距离空间聚类分析工具是另外一种分析事件点数据的空间模式的方法。
该方法不同于此工具集中其他方法(空间自相关和热点分析)的特征是可汇总一定距离范围内的空间相关性(要素聚类或要素扩散)。
本实验中第一次将距离段数设为10,距离增量设为1,第二次将距离段数设为5,距离增量同样为1,得到如图2和图3所示的结果。
从图中可以看出,小于3千米的距离内,观测值大于预测值,居民点聚集,大于3千米,观测值小于预测值,居民点离散。
且聚集具有统计意义上的聚集,离散并未具有统计意义上的显著性。
图2 K函数聚类分析结果1小于3千米,居民点聚集,且聚集具有统计意义上的聚集,大于3千米,居民点离散,离散并未具有统计意义上的显著性图3 K函数聚类分析结果23、密度制图前面的最邻近分析和K函数聚类分析只能得到从数值上的出空间分布的状态,但并不能直观看到分布集聚或分散的位置、形状和大小。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
式中:Wij表示区域i与j的临近关系,它可以根
据邻接标准或距离标准来度量。
两种最常用的确定空间权重矩阵的规则:
(1)简单的二进制邻接矩阵
1 当区域i和j相邻接 wij 其它 0
(2)基于距离的二进制空间权重矩阵
1 当区域i和j的距离小于d时 wij 其它 0
(二)全局空间自相关
Moran指数和Geary系数是两个用来度
量空间自相关的全局指标。 Moran指数反映的是空间邻接或空间邻 近的区域单元属性值的相似程度, Geary 系数与Moran指数存在负相该变量的 全局Moran指数I,用如下公式计算:
I n wij xi x x j x
第一节 探索性空间统计分析
一、基本原理与方法 (一)空间权重矩阵 (二)全局空间自相关 (三)局部空间自相关 二、应用实例
一、基本原理与方法
(一)空间权重矩阵
通常定义一个二元对称空间权重矩阵W,来表
达n个位置的空间区域的邻近关系,其形式如下:
w11 w W 21 wn1 w12 w22 wn 2 w1n w2 n wnn
当Z值为零时,观测值呈独立随机分布。
(三)局部空间自相关
局部空间自相关分析方法包括三种
分析方法: 1.空间联系的局部指标(LISA) 2.G统计量 3.Moran散点图
1.空间联系的局部指标(LISA)
空 间 联 系 的 局 部 指 标 ( Local indicators of
spatial association ,缩写为LISA)满足下列两 个条件: ( 1 )每个区域单元的 LISA ,是描述该区域单 元周围显著的相似值区域单元之间空间集聚程 度的指标; ( 2 )所有区域单元 LISA 的总和与全局的空间 联系指标成比例。
LISA包括局部Moran指数(Local Moran) 和局部Geary指数(Local Geary),下面 重点介绍和讨论局部Moran指数。
局部Moran指数被定义为:
I i ( xi x ) wij ( x j x ) 2 S j
n( xi x ) wij ( x j x )
2
Geary
系数C计算公式如下:
C
n 1 wij xi x j 2
n n i 1 j 1 n
2 wij xi x
i 1 j 1 i 1
n
n
2
式中:C为Geary系数;其它变量同上式。
如果引入记号:
S 0 wij
i 1 j 1 n n
n n i 1 j 1 n
w x
i 1 j 1 ij i 1
n
n
i
x
w ( x
i 1 j i ij
n
n
i
x)(x j x)
n ij
2
S
2
w
i 1 j i
n
式中: I 为Moran指数
1 2 S ( xi x ) n i 1 n x xi n i 1
zi ( xi x )
z T [ z1 , z 2 ,, z n ]
z j (x j x)
则全局Moran指数I的计算公式也可以进一步 写成:
n I S0
w
i 1 j 1
n
n
ij
( xi x )(x j x )
i
(x
i 1
n
x)
2
n S0
w
2 ( x x ) i i j
可进一步写成
I i
nzi wij z j
j
z z
T
z i wij z j
j
式中:其中 zi 和 z j 是经过标准差标准化的观测值。
局部Moran指数检验的标准化统计量为:
Z (I i ) I i E(I i ) VAR( I i )
显著的正值表示在该区域单元周围,高观测值
的区域单元趋于空间集聚,而显著的负值表示低 观测值的区域单元趋于空间集聚
与Moran指数只能发现相似值(正关联)或非相似
性观测值(负关联)的空间集聚模式相比,具有能 够探测出区域单元属于高值集聚还是低值集聚的 空间分布模式。
3.Moran散点图
以(Wz,z)为坐标点的Moran散点图,常来 研究局部的空间不稳定性,它对空间滞后因 子Wz和z数据对进行了可视化的二维图示。 全局Moran指数,可以看作是Wz对于z的线性 回归系数,对界外值以及对 Moran 指数具有 强烈影响的区域单元,可通过标准回归来诊 断出。 由于数据对(Wz,z)经过了标准化,因此界 外值可易由 2 - sigma 规则可视化地识别出来。
2. G统计量
全局G统计量的计算公式为:
G wij xi x j / xi x j
i j i j
对每一个区域单元的统计量为:
Gi wij x j / x j
i j
对统计量的检验与局部Moran指数相似,其检验
值为:
Z (Gi )
Gi E (Gi ) VAR(Gi )
第四章 空间统计分析初步
本章主要内容:
探索性空间统计分析 地统计分析方法
空间统计分析
空间统计分析,即空间数据(Spatial
Data)的统计分析,是现代计量地理学 中一个快速发展的方向领域。 空间统计分析,其核心就是认识与地理 位置相关的数据间的空间依赖、空间关 联或空间自相关,通过空间位置建立数 据间的统计关系。
对于Moran指数,可以用标准化统计量Z来检
验n个区域是否存在空间自相关关系,Z的计算 公式为: I E(I )
Z VAR( I )
当Z值为正且显著时,表明存在正的空间自相
关,也就是说相似的观测值(高值或低值)趋于 空间集聚;
当Z值为负且显著时,表明存在负的空间自相
关,相似的观测值趋于分散分布;
i 1 j 1 n i 1
n
n
ij i
z zj
zi
2
n z T Wz S0 zT z
Moran指数I的取值一般在[-1,1]之间,小于0 表示负相关,等于0表示不相关,大于0表示 正相关; Geary系数C的取值一般在[0,2]之间,大于1 表示负相关,等于1表示不相关,而小于1表 示正相关。
