八年级期末试卷练习(Word版含答案)

合集下载

八年级下册数学期末试卷达标训练题(Word版含答案)

武汉科技大学城市学院试题纸（2013——2014学年第二学期）课程名称：画法几何与工程制图卷型：A卷专业：土木（4、5、6、7班）考试方式：开卷年级：13级学生学号: 学生姓名:一、填空题（每空1分，共18分）1、建筑施工图简称______ _，包括_____________、_____________、_____________、_____________和_____________。

2、房屋施工图的特点是、、。

3、建筑总平面图中标注的尺寸是以_______为单位，一般标注到小数点后_____位；其它建筑图样（平、立、剖面）中所标注的尺寸则以_______为单位；标高都以______ _为单位。

4、总平面图中新建房屋的层数标注在_____________，一般低层、多层用_____表示，高层用________表示。

5、由混凝土和钢筋两种材料构成的构件，称为__________构件。

为了保护钢筋、防止锈蚀、防火，及加强钢筋与混凝土的粘结力，在构件中受力钢筋的外面要留有。

二、选择题（每小题2分，共14分）1、下面说法正确的是（）。

A、剖面图中被剖切到的部分（断面），不画它的组成材料的图例。

B、剖面图和断面图是同一概念。

C、剖面图和断面图的剖视方向都是通过编号的注写位置来表示的。

D、剖切平面是一个假想的平面，实际并不存在。

2、下列拉丁字母中，不得用做定位轴线编号的是（）。

A、OB、RC、SD、T3、下图所示的符号是（）A、指北针B、风玫瑰图C、风向指示图D、风速指示图4、能反映建筑物各层的平面形状和大小、各层房间的分隔和联系的是（）。

A、建筑立面图B、建筑剖面图C、建筑平面图D、建筑详图5、当形体对称时，以对称线为界，一半画外型投影图，一半画剖面图，这种剖面图称为（）。

A、全剖面图B、半剖面图C、局部剖面图D、阶梯剖面图6、建筑总平面图中，表示原有建筑物要用（）A、细实线B、中实线C、粗实线D、中虚线7、详图符号的圆圈直径是（）A、6mmB、8mmC、10mmD、14mm三、根据立体图绘制形体的三面投影图（尺寸在图中量取，每小题10分，计20分）四、补绘形体的第三投影（每小题5分，计10分）五、绘制形体的1-1、2-2、3-3断面图（10分）六、补全平面图形ABCDE的两面投影（6分）七、补全组合体H面、V面上所缺的图线（10分）八、补绘下列直线或平面的第三面投影，并在横线上注明其相对投影面的位置（每小题3分，计12分）武汉科技大学城市学院参考答案纸（2013——2014学年第二学期）课程名称：画法几何与工程制图卷型：A卷专业：土木（4、5、6、7班）年级： 13级考试方式：开卷一、填空题（18分）1、建施建筑总平面图建筑平面图建筑立面图建筑剖面图建筑详图2、采用正投影法绘制采用较小比例采用各种图例和符号3、米两位毫米米4、图例线框右上角点数数字5、钢筋混凝土保护层二、选择题（每小题2分，共14分）1、下面说法正确的是（D ）。

人教版八年级下册英语期末试卷(Word版,含答案)

人教版八年级下册英语期末试卷考生注意：1．本试卷分为试题卷和答题卷，考生应在答题卡上作答，在试题卷、草稿纸上答题无效。

2．答题前，考生须先将自己的姓名、条形码号分别在试题卷和答题卷上填写清楚。

3．答题完成后，请将试题卷、答题卷、草稿纸放在桌上，由监考老师统一收回。

4．本试卷含听力和笔试两个部分，共四道大题，满分150分，时量100分钟。

Part 1 听力部分(30分)Ⅰ.听力技能。

（共二节，每小题1.5分，满分30分）第一节听下面5段对话，每段对话后有一个小题，从题后所给的A、B、C三个选项中选出相应图片或正确答案。

听下面一段对话，回答第1小题。

1．What will the girl do?A．B．C．听下面一段对话，回答第2小题。

2．Which place has the man been to three times?A．The space museum. B．The library. C．The water park.听下面一段对话，回答第3小题。

3．What is Peter reading?A．A story about Yu Gong. B．A story about Nv Wa. C．A story about Hou Yi.听下面一段对话，回答第4小题。

4．Who was cooking when the earthquake happened?A．Eric. B．Eric’s mother. C．Eric’s father.听下面一段对话，回答第5小题。

5．Where is Cathy going?A．B．C．第二节听下面5段对话或独白，每段对话或独白后有2—4个小题，从题后所给的A、B、C三个选项中选出正确答案。

听第六段对话，回答第6至7小题。

6．When did the boy’s father buy the bike?A．Four years ago. B．Five years ago. C．Six years ago. 7．Why does he want to sell it?A．Because he wants to buy a new one.B．Because he doesn’t like it.C．Because he wants to take exercise.听第七段对话，回答第8至10小题。

八年级上册期末试卷综合测试(Word版含答案)

八年级上册期末试卷综合测试（Word 版含答案）一、八年级数学全等三角形解答题压轴题（难）1．已知,如图A 在x 轴负半轴上，B （0，-4），点E （-6,4）在射线BA 上，(1) 求证：点A 为BE 的中点(2) 在y 轴正半轴上有一点F, 使 ∠FEA=45°，求点F 的坐标.(3) 如图，点M 、N 分别在x 轴正半轴、y 轴正半轴上，MN=NB=MA ，点I 为△MON 的内角平分线的交点，AI 、BI 分别交y 轴正半轴、x 轴正半轴于P 、Q 两点, IH⊥ON 于H, 记△POQ 的周长为C△POQ.求证：C△POQ=2 HI.【答案】（1）证明见解析；（2）22(0,)7F ；（3）证明见解析. 【解析】试题分析：（1）过E 点作EG ⊥x 轴于G ，根据B 、E 点的坐标，可证明△AEG ≌△ABO ，从而根据全等三角形的性质得证；（2）过A 作AD⊥AE 交EF 延长线于D ，过D 作DK ⊥x 轴于K ，然后根据全等三角形的判定得到△AEG ≌△DAK ，进而求出D 点的坐标，然后设F 坐标为（0，y ），根据S 梯形EGKD =S 梯形EGOF +S 梯形FOKD 可求出F 的坐标；（3）连接MI 、NI ，根据全等三角形的判定SAS 证得△MIN ≌△MIA ，从而得到∠MIN=∠MIA 和∠MIN=∠NIB ，由角平分线的性质，求得∠AIB=135°×3-360°=45°再连接OI ，作IS⊥OM 于S, 再次证明△HIP ≌△SIC 和△QIP ≌△QIC ，得到C △POQ 周长.试题解析：（1）过E 点作EG⊥x 轴于G ，∵B （0，-4），E （-6,4），∴OB=EG=4，在△AEG 和△ABO 中，∵90EGA BOAEAG BAOEG BO∠=∠=︒⎧⎪∠=∠⎨⎪=⎩∴△AEG≌△ABO（AAS），∴AE=AB∴A为BE中点（2）过A作AD⊥A E交EF延长线于D，过D作DK⊥x轴于K，∵∠FEA=45°，∴AE=AD，∴可证△AEG≌△DAK，∴D（1,3），设F（0，y），∵S梯形EGKD=S梯形EGOF+S梯形FOKD，∴()()() 111347463222y y +⨯=+⨯++∴227y=∴220,7F⎛⎫⎪⎝⎭（3）连接MI、NI∵I 为△MON 内角平分线交点，∴NI 平分∠MNO，MI 平分∠OMN，在△MIN 和△MIA 中，∵MN MA NMI AMI MI MI =⎧⎪∠=∠⎨⎪=⎩∴△MIN ≌△MIA （SAS ），∴∠MIN=∠MIA ，同理可得∠MIN=∠NIB，∵NI 平分∠MNO，MI 平分∠OMN，∠MON=90°，∴∠MIN=135°∴∠MIN=∠MIA =∠NIB=135°，∴∠AIB=135°×3-360°=45°，连接OI ，作IS⊥OM 于S, ∵IH⊥ON，OI 平分∠MON，∴IH=IS=OH=OS ，∠HIS=90°，∠HIP+∠QIS=45°，在SM 上截取SC=HP ，可证△HIP≌△SIC，∴IP=IC，∠HIP=∠SIC ，∴∠QIC=45°，可证△QIP≌△QIC，∴PQ=QC=QS+HP ，∴C △POQ =OP+PQ+OQ=OP+PH+OQ+OS=OH+OS=2HI.2．如图，在平面直角坐标系中，A 、B 坐标为()6,0、()0,6，P 为线段AB 上的一点．（1）如图1，若P 为AB 的中点，点M 、N 分别是OA 、OB 边上的动点，且保持AM ON =，则在点M 、N 运动的过程中，探究线段PM 、PN 之间的位置关系与数量关系，并说明理由．（2）如图2，若P 为线段AB 上异于A 、B 的任意一点，过B 点作BD OP ⊥，交OP 、OA 分别于F 、D 两点，E 为OA 上一点，且PEA BDO =∠∠，试判断线段OD 与AE 的数量关系，并说明理由．【答案】（1）PM=PN ，PM ⊥PN ，理由见解析；（2）OD=AE ，理由见解析【解析】【分析】（1）连接OP ．只要证明△PON ≌△PAM 即可解决问题；（2）作AG ⊥x 轴交OP 的延长线于G ．由△DBO ≌△GOA ，推出OD=AG ，∠BDO=∠G ，再证明△PAE ≌△PAG 即可解决问题；【详解】（1）结论：PM=PN ，PM ⊥PN ．理由如下：如图1中，连接OP ．∵A 、B 坐标为（6，0）、（0，6），∴OB=OA=6，∠AOB=90°，∵P 为AB 的中点， ∴OP=12AB=PB=PA ，OP ⊥AB ，∠PON=∠PAM=45°， ∴∠OPA=90°，在△PON 和△PAM 中， ON AM PON PAM OP AP =⎧⎪∠=∠⎨⎪=⎩，∴△PON ≌△PAM （SAS ），∴PN=PM ，∠OPN=∠APM ，∴∠NPM=∠OPA=90°，∴PM ⊥PN ，PM=PN ．（2）结论：OD=AE ．理由如下：如图2中，作AG ⊥x 轴交OP 的延长线于G ．∵BD ⊥OP ，∴∠OAG=∠BOD=∠OFD=90°，∴∠ODF+∠AOG=90°，∠ODF+∠OBD=90°，∴∠AOG=∠DBO ，∵OB=OA ，∴△DBO ≌△GOA ，∴OD=AG ，∠BDO=∠G ，∵∠BDO=∠PEA ，∴∠G=∠AEP ，在△PAE 和△PAG 中，AEP G PAE PAG AP AP ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△PAE ≌△PAG （AAS ），∴AE=AG ，∴OD=AE ．【点睛】考查了等腰直角三角形的性质、全等三角形的判定和性质、坐标与图形性质、直角三角形的性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．3．如图（1），在ABC 中，90A ∠=︒，AB AC =，点D 是斜边BC 的中点，点E ，F 分别在线段AB ，AC 上，且90EDF ∠=︒．（1）求证：DEF 为等腰直角三角形；（2）若ABC 的面积为7，求四边形AEDF 的面积；（3）如图（2），如果点E 运动到AB 的延长线上时，点F 在射线CA 上且保持90EDF ∠=︒，DEF 还是等腰直角三角形吗．请说明理由．【答案】（1）证明见解析；（2）3.5；（3）是，理由见解析．【解析】【分析】（1）由题意连接AD，并利用全等三角形的判定判定△BDE≌△ADF(ASA)，进而分析证得DEF为等腰直角三角形；（2）由题意分析可得S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF，以此进行分析计算求出四边形AEDF的面积即可；（3）根据题意连接AD，运用全等三角形的判定判定△BDE≌△ADF(ASA)，进而分析证得DEF为等腰直角三角形.【详解】解：（1）证明：如图①，连接AD.∵∠BAC=90˚,AB=AC,点D是斜边BC的中点，∴AD⊥BC，AD=BD，∴∠1=∠B=45°，∵∠EDF=90°，∠2+∠3=90°，又∵∠3+∠4=90°，∴∠2=∠4，在△BDE 和△ADF中，∠1=∠B，AD=BD,∠2=∠4，∴△BDE≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°，∴ΔDEF为等腰直角三角形.（2）由（1）可知DE=DF，∠C=∠6=45°，又∵∠2+∠3=90°，∠2+∠5=90°，∴∠3=∠5，∴△ADE≌△CDF，∴S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF，∴ S∆ABC=2 S四边形AEDF,∴S四边形AEDF=3.5 .（3）是.如图②，连接AD.∵∠BAC=90°，AB=AC，D是斜边BC的中点，∴AD⊥BC,AD=BD ，∴∠1=45°，∵∠DAF=180°-∠1=180°—45°=135°，∠DBE=180°-∠ABC=180°-45°=135°，∴∠DAF=∠DBE，∵∠EDF=90°，∴∠3+∠4=90°，又∵∠2+∠3=90°，∴∠2=∠4,在△BDE和△ADF中，∠DAF=∠DBE，AD=BD,∠2=∠4,∴△BDE≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°，∴△DEF为等腰直角三角形.【点睛】本题考查等腰直角三角形的性质以及全等三角形的判定与性质，根据题意作辅助线构造出全等三角形是解题的关键．4．已知点P是线段MN上一动点，分别以PM，PN为一边，在MN的同侧作△APM，△BPN，并连接BM，AN．（Ⅰ）如图1，当PM＝AP，PN＝BP且∠APM＝∠BPN＝90°时，试猜想BM，AN之间的数量关系与位置关系，并证明你的猜想；（Ⅱ）如图2，当△APM，△BPN都是等边三角形时，（Ⅰ）中BM，AN之间的数量关系是否仍然成立？若成立，请证明你的结论；若不成立，试说明理由．（Ⅲ）在（Ⅱ）的条件下，连接AB得到图3，当PN＝2PM时，求∠PAB度数．【答案】（1）BM＝AN，BM⊥AN．（2）结论成立.（3）90°．【解析】【分析】(1)根据已知条件可证△MBP≌△ANP，得出MB＝AN，∠PAN＝∠PMB，再延长MB交∠=︒,因此有BM⊥AN；AN于点C，得出MCN90(2)根据所给条件可证△MPB≌△APN，得出结论BM＝AN；(3)取PB的中点C，连接AC，AB，通过已知条件推出△APC为等边三角形，∠PAC＝∠PCA＝60°，再由CA＝CB，进一步得出∠PAB的度数.【详解】解：（Ⅰ）结论：BM＝AN，BM⊥AN．理由：如图1中，∵MP＝AP，∠APM＝∠BPN＝90°，PB＝PN，∴△MBP≌△ANP（SAS），∴MB＝AN．延长MB交AN于点C．∵△MBP≌△ANP，∴∠PAN＝∠PMB，∵∠PAN+∠PNA＝90°，∴∠PMB+∠PNA＝90°，∴∠MCN＝180°﹣∠PMB﹣∠PNA＝90°，∴BM⊥AN．（Ⅱ）结论成立理由：如图2中，∵△APM，△BPN，都是等边三角形∴∠APM＝∠BPN＝60°∴∠MPB＝∠APN＝120°，又∵PM＝PA，PB＝PN，∴△MPB≌△APN（SAS）∴MB＝AN．（Ⅲ）如图3中，取PB的中点C，连接AC，AB．∵△APM，△PBN都是等边三角形∴∠APM＝∠BPN＝60°，PB＝PN∵点C是PB的中点，且PN＝2PM，∴2PC＝2PA＝2PM＝PB＝PN，∵∠APC＝60°，∴△APC为等边三角形，∴∠PAC＝∠PCA＝60°，又∵CA＝CB，∴∠CAB＝∠ABC＝30°，∴∠PAB＝∠PAC+∠CAB＝90°．【点睛】本题是一道关于全等三角形的综合性题目，充分考查了学生对全等三角形的判定定理及其性质的应用的能力，此类题目常常需要数形结合，借助辅助线才得以解决，因此，作出合理正确的辅助线是解题的关键.5．如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时，求 t 的值；(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。

八年级下册数学期末试卷模拟练习卷(Word版含解析)

八年级下册数学期末试卷模拟练习卷（Word 版含解析）一、选择题1．要使二次根式2x +有意义，则x 的取值范围是（）A ．x ＞﹣2B ．x ≥﹣2C ．x ≠﹣2D ．x ≤﹣2 2．在△ABC 中，a ，b ，c 为△ABC 的三边，下列条件不能判定△ABC 为直角三角形的是（）A ．a ：b ：c ＝1：3：2B ．a ＝32，b ＝42，c ＝52C ．a 2＝（c ﹣b ）（c +b ）D ．a ＝5，b ＝12，c ＝13 3．下列说法，属于平行四边形判定方法的有（）．①两组对边分别平行的四边形是平行四边形；②平行四边形的对角线互相平分；③两组对边分别相等的四边形是平行四边形；④平行四边形的每组对边平行且相等；⑤两条对角线互相平分的四边形是平行四边形；⑥一组对边平行且相等的四边形是平行四边形．A ．6个B ．5个C ．4个D ．3个4．比赛中给一名选手打分时，经常会去掉一个最高分，去掉一个最低分，这样的评分方式一定不会改变选手成绩数据的（）A ．众数B ．平均数C ．中位数D ．方差5．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ．CE ⊥AD 于点E ，AB ＝23，AC ＝4，BD ＝8，则CE ＝（）A ．72B ．2217C ．4217D ．76．如图，在Rt ACB ∆中，90ACB ︒∠=，25A ︒∠=，D 是AB 上一点，将Rt ABC ∆沿CD 折叠，使B 点落在AC 边上的E 处，则ADE ∠等于（）A ．25︒B ．30︒C ．35︒D ．40︒7．如图，在正方形ABCD 中，AP ∥CQ ，AP ＝CQ ，∠BQC ＝90°，若正方形ABCD 的面积为64，且AP+BQ＝10，则PQ的长为（）A．7B．27C．14D．2148．小张、小王两个人从甲地出发，去8千米外的乙地，图中线段OA、PB分别反映了小张、小王步行所走的路程S（千米）与时间t（分钟）的函数关系，根据图像提供的信息，小王比小张早到乙地的时间是__________分钟．A．4 B．6 C．16 D．10二、填空题9．已知332=-+--，则x y=____________．y x x10．菱形的周长为12cm，它的一个内角为60︒，则菱形的面积为______()2cm．11．如图，每个方格都是边长为1的小正方形，则AB＋BC＝_____．12．如图，在矩形ABCD中，对角线AC，BD相交于点O．若AB＝5，AD＝12，则OC＝______．13．在平面直角坐标系中，一次函数y＝kx+b的图象与直线y＝2x平行，且经过点A（1，6），则一次函数y＝kx+b的解析式为 ____．14．如图，已知矩形ABCD中(AD＞AB)，EF经过对角线的交点O，且分别交AD，BC于E，F，请你添加一个条件：______，使四边形EBFD是菱形．15．已知直线333y x =+与x 轴，y 轴分别交于点A ，B ，点C 是射线AB 上的动点，点D 在第一象限，四边形OACD 是平行四边形．若点D 关于直线OC 的对称点D 恰好落在y 轴上，则点C 的坐标为______．16．如图，在矩形ABCD 中，AB ＝5，BC ＝3，点E 为射线BC 上一动点，将△ABE 沿AE 折叠，得到△AB ′E ．若B ′恰好落在射线CD 上，则BE 的长为_____．三、解答题17．计算题（1）327-＋212＋348；（2）（2123-）×3；（3）21233++（1﹣3）0；（4）（5＋1）（5﹣1）﹣27．18．如图，有一直立标杆，它的上部被风从B 处吹折，杆顶C 着地，离杆脚2m ，修好后又被风吹折，因新断处D 比前一次低0.5m ，故杆顶E 着地比前次远1m ，求原标杆的高度．19．如图，每个小正方形的边长都为1．（1）求线段CD 与BC 的长；（2）求四边形ABCD 的面积与周长；（3）求证：90BCD ∠=︒．20．如图，∠A =∠B =40°，P 为AB 中点，点M 为射线AC 上（不与点A 重合）的任意一点，连接MP ，并使MP 的延长线交射线BD 于点N ，设∠BPN =α．（1）求证：APM ≅BPN ；（2）当α等于多少度时，以A 、M 、B 、N 为顶点的四边形是菱形？21．21+2(21)(21)+-22(2)1-21-21 （132+ ；（21n n ++= ；（321+32+43+10099+． 22．暑期将至，某游泳馆面向学生推出暑期优惠活动，活动方案如下．方案一：购买一张学生暑期专享卡，每次游泳费用按六折优惠；方案二：不购买学生暑期专享卡，每次游泳费用按八折优惠．设某学生暑期游泳x （次），按照方案一所需费用为y 1（元），且y 1＝k 1x +b ；按照方案二所需费用为y 2（元），且y 2＝k 2x ．其函数图象如图所示．（1）求k 1和b 的值；（2）八年级学生小华计划暑期前往该游泳馆游泳8次，应选择哪种方案所需费用更少？请说明理由．23．如图，矩形ABCD 中，AB=4，AD=3，∠A 的角平分线交边CD 于点E ．点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动，Q 为AP 的中点，过点Q 作QH ⊥AB 于点H ，在射线AE 的下方作平行四边形PQHM （点M 在点H 的右侧），设P 点运动时间为秒．（1）直接写出的面积（用含的代数式表示）．（2）当点M 落在BC 边上时，求的值．（3）在运动过程中，整个图形中形成的三角形是否存在全等三角形？若存在，请写出所有全等三角形，并求出对应的的值；若不存在请说明理由（不能添加辅助线）． 24．如图在平面直角坐标系之中，点O 为坐标原点，直线334y x =-+分别交x 、y 轴于点B 、A ．（1）如图1，点C 是直线AB 上不同于点B 的点，且CA AB =．则点C 的坐标为____________（2）点C 是直线AB 外一点，满足45BAC ∠=︒，求出直线AC 的解析式．（3）如图2，点D 是线段OB 上一点，将AOD △沿直线AD 翻折，点O 落在线段AB 上的点E 处，点M 在射线DE 上，在x 轴的正半轴上是否存在点N ，使以M 、A 、N 、B 为顶点的四边形是平行四边形？若存在，请求出点N 的坐标；若不存在，请说明理由． 25．如图，在等腰Rt ABC 中，90ACB ∠=︒，AC BC =，点D 为BC 边中点，点E 在线段AD 上，BED CAD α∠=∠=，过点C 作CF BE ⊥于F ，CF 交AD 于点G ．（1）求GCD ∠的大小（用含α的式子表示）（2）①求证：BE BC =；②写出AE AD=______的值．【参考答案】一、选择题1．B解析：B【分析】根据二次根式有意义的条件进行求解即可．【详解】∵2x +∴20x +≥，∴2x ≥-．故选：B ．【点睛】本题考查了二次根式，解一元一次不等式，明确二次根式有意义的条件是解题的关键． 2．B解析：B【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个是直角三角形判定则可．如果有这种关系，这个就是直角三角形．【详解】解：A 、∵a ：b ：c =132，∴设三边为：x 3，2x ，∵x 2+3）2=（2x ）2，∴该三角形符合勾股定理的逆定理，故是直角三角形，故选项不符合题意；B 、∵（32）2+（42）2≠（52）2，∴该三角形不符合勾股定理的逆定理，故不是直角三角形，故选项符合题意；C、∵a2=（c-b）（c+b），∴a2+b2=c2，该三角形符合勾股定理的逆定理，故是直角三角形，故选项不符合题意；D、∵52+122=132，∴该三角形符合勾股定理的逆定理，故是直角三角形，故选项不符合题意；故选：B．【点睛】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．3．C解析：C【解析】【分析】根据平行四边形的判定方法分析即可；【详解】两组对边分别平行的四边形是平行四边形，故①正确；平行四边形的对角线互相平分，是平行四边形的性质，故②错误；两组对边分别相等的四边形是平行四边形，故③正确；平行四边形的每组对边平行且相等，是平行四边形的性质，故④错误；两条对角线互相平分的四边形是平行四边形，故⑤正确；一组对边平行且相等的四边形是平行四边形，故⑥正确；故正确的是①③⑤⑥；故答案选C．【点睛】本题主要考查了平行四边形的判定，准确分析判断是解题的关键．4．C解析：C【解析】【分析】去掉一个最高分和最低分后不会对数据的中间的数产生影响，即中位数．【详解】解：统计每位选手得分时，去掉一个最高分和一个最低分，这样做不会对数据的中间的数产生影响，即中位数．故选：C．【点睛】本题考查了统计量的选择，解题的关键在于理解这些统计量的意义．5．C解析：C先根据平行四边形的性质可得2,4CD AB OC OD ====，再根据勾股定理的逆定理可得AC CD ⊥，然后利用勾股定理可得AD 的长，最后利用三角形的面积公式即可得．【详解】解：四边形ABCD 是平行四边形，4,8AB AC BD ===，112,422CD AB OC AC OD BD ====∴==， 22241216OC CD OD ∴+=+==，COD ∴是直角三角形，AC CD ⊥，在Rt ACD △中，AD ==1122Rt ACD S AD CE AC CD =⋅=⋅， 11422∴⨯=⨯⨯解得CE = 故选：C ．【点睛】本题考查了平行四边形的性质、勾股定理、勾股定理的逆定理等知识点，熟练掌握勾股定理的逆定理是解题关键．6．D解析：D【解析】【分析】先根据三角形内角和定理求出∠B 的度数，再由图形翻折变换的性质得出∠CED 的度数，再由三角形外角的性质即可得出结论．【详解】解：在Rt △ACB 中，∠ACB =90°，∠A =25°，∴∠B =90°-25°=65°，∵△CDE 由△CDB 折叠而成，∴∠CED =∠B =65°，∵∠CED 是△AED 的外角，∴∠ADE =∠CED -∠A =65°-25°=40°．故选：D ．【点睛】本题考查了三角形内角和定理，翻折变换的性质，根据题意得出∠ADE =∠CED -∠A 是解题关键．7．D解析：D【分析】延长AP 交BQ 于点E ，证明△ABE ≌△BCQ 可得△PEQ 为等腰直角三角形，PE ＝QE ＝BQ ﹣AP ，由四边形面积为64可得BQ 2+AP 2＝64，再由勾股定理得PQ ＝()22BQ AP -．【详解】解：延长AP 交BQ 于点E ，∵四边形ABCD 为正方形，∴AB ＝BC ，∠DAB ＝∠ABC ＝90°，∵AP ∥CQ ，∠BQC ＝90°，∴∠AEB ＝∠AEQ ＝90°，∵∠QBC +∠ABE ＝∠ABE +∠BAE ＝90°，∴∠QBC ＝∠BAE ，在Rt △ABE 和Rt △BCQ 中，AEB BQC BAE CBQ AB BC ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴Rt △ABE ≌Rt △BCQ （AAS ），∴BE ＝CQ ，AE ＝BQ ，∵AP ＝CQ ，∴PE ＝AE ﹣AP ＝BQ ﹣AP ，QE ＝BQ ﹣BE ＝BQ ﹣CQ ＝BQ ﹣AP ，∵正方形ABCD 的面积为64，∴AB ＝BC 648，∵AP ＝CQ ，AP +BQ ＝10，∴CQ +BQ ＝10，∵∠BQC ＝90°在Rt △BQC 中，BQ 2+CQ 2＝BC 2＝64，即BQ 2+AP 2＝64，∵（AP +BQ ）2＝AP 2+BQ 2+2AP •BQ ＝64+2AP •BQ ＝100，∴AP •BQ ＝18，在Rt △PEQ 中，由勾股定理得，PQ=== 故选：D ．【点睛】本题主要考查了正方形的性质、全等三角形的判定与性质、等腰三角形的性质和勾股定理，准确计算是解题的关键．8．B解析：B【分析】由函数图象求出OA 、PB 解析式，再把8y =代入解析式就可以求出小张、小王所用时间．【详解】解：由图象可知：设OA 的解析式为：y kx =，OA 经过点(60,5)，560k ∴=，得112k =， OA ∴函数解析式为：112y x =①，把8y =代入①得：1812x =，解得：96x =， ∴小张到达乙地所用时间为96（分钟）；设PB 的解析式为：y mx n =+，∴100605m n m n +=⎧⎨+=⎩，解得：1101m n ⎧=⎪⎨⎪=-⎩， PB ∴的解析式为：1110y x =-②，把8y =代入②得：18110x =-，解得：90x =，则小王到达乙地的时间为小张出发后90（分钟），∴小王比小张早到96906-=（分钟），故选：B ．【点睛】本题考查的一次函数的应用，关键是由图象求函数解析式．二、填空题9．-8【解析】【分析】根据二次根式的被开方数大于等于0可求出x 的值，进而求得结果．【详解】解：根据二次根式有意义的条件，得x =3，∴y =-2，∴()328x y =-=-，故答案为：-8．【点睛】本题考查了二次根式有意义的条件，被开方数大于等于0．10．A 解析：932【解析】【分析】由菱形的性质和已知条件得出3AB BC CD DA cm ====,AC BD ⊥由含30°角的直角三角形的性质得1322BO AB cm ==，由勾股定理求出OA ,可得BD ，AC 的长度，由菱形的面积公式可求解．【详解】如图所示:、∵AB = BC = CD = DA ，130?2BAO BAD ∠=∠=，AC BD ⊥， 12OA AC BO DO ==， ∵菱形的周长为12cm , ∴3AB BC CD DA cm ====，∴1322BO AB cm ==， ∴2233AB OB m OA =-= ∴233AC OA cm ==,23BD BO cm ==∴菱形ABCD 的面积212AC BD ⨯=．【点睛】本题考查了菱形的性质、含30° 角的直角三角形的性质、勾股定理;熟练掌握菱形的性质，并能进行推理计算是解决问题的关键．11．A解析：【解析】【分析】根据勾股定理可以求出AB 和BC 的长，进而可求出AB+BC 的值．【详解】解：∵每个方格都是边长为1的小正方形， ∴AB =BC ∴AB ＋BC =故答案为【点睛】本题考查了勾股定理．熟练掌握勾股定理是解题的关键．12．B解析：5【分析】根据勾股定理得出BD ，进而利用矩形的性质得出OC 即可．【详解】解：∵四边形ABCD 是矩形，∴∠BAD ＝90°，AC ＝BD ，OC ＝OA ，在Rt △ABD 中，BD 13，∴OC ＝12AC ＝12BD ＝.113652⨯=．故答案为：6.5．【点睛】此题考查矩形的性质和勾股定理，解答此题的关键是由矩形的性质和根据勾股定理得出BD 解答． 13．A解析：y ＝2x +4【分析】根据函数y ＝kx +b 的图象与直线y ＝2x 平行，且经过点A （1，6），即可得出k 和b 的值，即得出了函数解析式．【详解】解：∵函数y ＝kx +b 的图象与直线y ＝2x 平行，∴k ＝2，又∵函数y ＝2x +b 的图象经过点A （1，6），∴6＝2+b ，∴b ＝4，∴一次函数的解析式为y ＝2x +4，故答案为y ＝2x +4．【点睛】本题考查了一次函数的性质，待定系数法求解析式，理解两条直线平行，解析式中的k 值相等是解题的关键．14．E解析：EF ⊥BD【分析】通过证明△OBF ≌△ODE ，可证四边形EBFD 是平行四边形，若四边形EBFD 是菱形，则对角线互相垂直，因而可添加条件：EF ⊥BD ．【详解】当EF ⊥BD 时，四边形EBFD 是菱形．理由：∵四边形ABCD 是矩形，∴AD ∥BC ，OB=OD ，∴∠FBO=∠EDO ，在△OBF 和△ODE 中EDO FBO BO DOEOD FOB ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△OBF ≌△ODE （ASA ），∴OE=OF ，∴四边形EBFD 是平行四边形，∵EF ⊥BD ，∴四边形EBFD 是菱形．故答案为：EF ⊥BD.【点睛】本题考查了矩形的性质，平行四边形的判定，菱形的判定，以及全等三角形的判定方法，熟练掌握性质及判定方法是解答本题的关键.15．或．【分析】先根据题意求得，，，分点在第二象限和第一象限两种情况讨论，根据点关于直线的对称点恰好落在轴上，根据含30度角的直角三角形的性质，在第一象限时候，证明是等边三角形，在第二象限时候证明是解析：333,22⎛⎫ ⎪ ⎪⎝⎭或33,22⎛⎫- ⎪ ⎪⎝⎭．【分析】先根据题意求得30BAO ∠=︒，60ABO ∠=︒，12OB AB =，分C 点在第二象限和第一象限两种情况讨论，根据点D 关于直线OC 的对称点D 恰好落在y 轴上，根据含30度角的直角三角形的性质，在第一象限时候，证明BCO 是等边三角形，在第二象限时候证明ODD '是等边三角形，利用等边三角形的性质，分别求得C 点的坐标．【详解】333y x =+与x 轴，y 轴分别交于点A ，B ，令0y =，3x =-，∴(3,0)A -，令0x =，3y =，(0,3)B ∴，3,3OA OB ∴==，90AOB ∠=︒，2223AB AO BO ∴=+=，30BAO ∴∠=︒，60ABO ∠=︒，12OB AB ∴=， ①如图，当C 点在第二象限时，设DD '交x 轴于点E ，交AO 于点F ，CD 交y 轴于点G ，四边形OACD 是平行四边形，//AC OD ∴，//CD AO ，AC OD OD '==，30CAO ∠=︒，30DOE CAO ∴∠=∠=︒，30ODG DOE ∴∠=∠=︒，//CD AO ，AO OB ⊥，90DGD '∴∠=︒，9060DOG DOE ∴∠=︒-∠=︒，OD OD '=，30ODD OD D ''∴∠=∠=︒，点D 关于直线OC 的对称点为D 点，CO DD '∴⊥，60COB FOD '∴∠=∠=︒，60ABO ∠=︒，BCO ∴△是等边三角形，BO CO BC ∴==， 12BO AB =， 12BC AB =∴， C ∴点为AB 的中点，(3,0)A -，(0,3)B ，33(,)22C ∴-， ②如图，当C 点在第二象限时，延长DC 交y 轴于点H ，则CH OD '⊥，点D 关于直线OC 的对称点为D 点,CD CD OD OD ''∴==，DOC D OC '∠=∠，60ABO BOD ∠=∠=︒，ODD '∴△是等边三角形，60DOD '∴∠=︒，30DOC D OC '∴∠=∠=︒，12CH OC ∴=， 30BAO ∠=︒，90AOB ∠=︒，3CO AO ∴==， ∴32CH =，OH ∴===3(2C ∴．综合①②可知C 的坐标为32⎛ ⎝⎭或32⎛- ⎝⎭．故答案为: 32⎛ ⎝⎭或32⎛- ⎝⎭．【点睛】本题考查了一次函数图像的性质，平行四边形的性质，等边三角形的性质，含30度角的直角三角形的性质，勾股定理，轴对称的性质，此题方法比较多，利用等边三角形的性质是解题的关键．16．或15【分析】如图1，根据折叠的性质得到AB′＝AB ＝5，B′E ＝BE ，根据勾股定理得到BE2＝（3﹣BE ）2+12，于是得到BE ＝，如图2，根据折叠的性质得到AB′＝AB ＝5，求得AB ＝BF ＝解析：53或15 【分析】如图1，根据折叠的性质得到AB ′＝AB ＝5，B ′E ＝BE ，根据勾股定理得到BE 2＝（3﹣BE ）2+12，于是得到BE ＝53，如图2，根据折叠的性质得到AB ′＝AB ＝5，求得AB ＝BF ＝5，根据勾股定理得到CF ＝4根据相似三角形的性质列方程得到CE ＝12，即可得到结论．【详解】解：如图1，∵将△ABE 沿AE 折叠，得到△AB ′E ，∴AB ′＝AB ＝5，B ′E ＝BE ，∴CE ＝3﹣BE ，∵AD ＝3，∴DB ′＝4，∴B ′C ＝1，∵B ′E 2＝CE 2+B ′C 2，∴BE 2＝（3﹣BE ）2+12，∴BE ＝53，如图2，∵将△ABE沿AE折叠，得到△AB′E，∴AB′＝AB＝5，∵CD∥AB，∴∠1＝∠3，∵∠1＝∠2，∴∠2＝∠3，∵AE垂直平分BB′，∴AB＝BF＝5，∴CF＝4，∵CF∥AB，∴△CEF∽△ABE，CF CEAB BE∴=即4=53CECE+12,15CE BE ∴==综上所述：BE的长为：53或15故答案为：53或15．【点睛】本题考查折叠的性质、垂直平分线的性质、勾股定理及A字型相似的综合运用，注意分类讨论，属于中考常考题型．三、解答题17．（1）；（2）；（3）；（4）【分析】（1）根据立方根以及二次根式的加减运算求解即可；（2）根据二次根式的四则运算求解即可；（3）根据二次根式的除法以及零指数幂的运算求解即可；（4）根据平解析：（1）33-+2）623）6；（4）433-【分析】（1）根据立方根以及二次根式的加减运算求解即可；（2）根据二次根式的四则运算求解即可；（3）根据二次根式的除法以及零指数幂的运算求解即可；（4）根据平方差公式以及二次根式的加减运算，求解即可．【详解】解：（1）313=-+=-+（2）6==；（30(122116=⨯++=；（4）1)514=---【点睛】此题考查了二次根式的四则运算，涉及了零指数幂、立方根以及平方差公式，解题的关键是熟练掌握二次根式的有关运算．18．5米【分析】由题中条件，可设原标杆AB 的高为x ，进而再依据勾股定理建立方程，进而求解即可．【详解】解：依题意得AC ＝2，AE ＝3，设原标杆的高为x ，∵∠A ＝90°，∴由题中条件可得AB解析：5米【分析】由题中条件，可设原标杆AB 的高为x ，进而再依据勾股定理建立方程，进而求解即可．【详解】解：依题意得AC ＝2，AE ＝3，设原标杆的高为x ，∵∠A ＝90°，∴由题中条件可得AB 2+AC 2＝BC 2，即AB 2+22＝（x ﹣AB ）2，整理，得x 2﹣2ABx ＝4，同理，得（AB ﹣0.5）2+32＝（x ﹣AB +0.5）2，整理，得x 2﹣2ABx +x ＝9，解得x ＝5．∴原来标杆的高度为5米．【点睛】本题主要考查了勾股定理的应用，解题的关键在于能够熟练掌握勾股定理.19．（1），；（2）四边形的面积，的周长；（3）见解析【解析】【分析】（1）利用勾股定理直接计算即可得到答案；（2）利用四边形的周长公式计算四边形的周长即可，再利用割补法求解四边形的面积即可；解析：（1）BC =CD =2）四边形ABCD 的面积12.5=，ABCD 的周长5=；（3）见解析【解析】【分析】（1）利用勾股定理直接计算即可得到答案；（2）利用四边形的周长公式计算四边形的周长即可，再利用割补法求解四边形的面积即可；（3）利用勾股定理的逆定理证明即可.【详解】解：（1）BC =CD（2）5AB =，AD∴四边形ABCD 的周长55=，四边形ABCD 的面积111542124311222=⨯-⨯⨯-⨯⨯-⨯⨯- 2014 1.51=----12.5=（3）连接BD ，5BD =，222225BC CD +=+=，22525BD ==，222BC CD BD ∴+=，90BCD ∴∠=︒．【点睛】本题考查的是勾股定理与勾股定理的逆定理的应用，掌握利用勾股定理求解边长，利用勾股定理的逆定理判断直角三角形是解题的关键.20．（1）见解析；（2）90°【分析】（1）利用判定定理进行证明即可；（2）根据（1）能得出对角线互相平分，得出是平行四边形，即当∠BPN=90°时，AB⊥MN，以A、M、B、N为顶点的四边形是菱解析：（1）见解析；（2）90°【分析】（1）利用ASA判定定理进行证明即可；（2）根据（1）能得出对角线互相平分，得出是平行四边形，即当∠BPN=90°时，AB⊥MN，以A、M、B、N为顶点的四边形是菱形．【详解】（1）证明：P为AB中点，∴PA=PB，在△APM和△BPN中，APM BPN PA PBA B∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△APM≅△BPN；(2)连接MB、NA，由(1)知△APM≅△BPN，∴PM=PN，PA=PB，∴四边形MBNA为平行四边形，∴当∠BPN=90°时，AB⊥MN，∴四边形AMBN为菱形．【点睛】本题考查了三角形全等的判定及性质、菱形的判定，解题的关键是掌握相关的判定定理．21．（1）；（2）（3）9【解析】【详解】试题分析：（1）仔细阅读，发现规律：分母有理化，然后仿照规律计算即可求解；（2）根据规律直接写出结果；（3）根据规律写出结果，找出部分互为相反数的特点解析：（123）9【解析】【详解】试题分析：（1）仔细阅读，发现规律：分母有理化，然后仿照规律计算即可求解；（2）根据规律直接写出结果；（3）根据规律写出结果，找出部分互为相反数的特点，然后计算即可.试题解析：（1）原式（2）原式（3）由（2）可知：原式=﹣=9.22．（1）y1=15x+30；（2）选择方案一所需费用更少，理由见解析【分析】（1）利用待定系数法求解即可；（2）求出y2与x之间的函数关系式，将x=8分别代入y1、y2关于x的函数解析式，比较即解析：（1）y1=15x+30；（2）选择方案一所需费用更少，理由见解析【分析】（1）利用待定系数法求解即可；（2）求出y 2与x 之间的函数关系式，将x =8分别代入y 1、y 2关于x 的函数解析式，比较即可．【详解】解：（1）根据题意，得：138430k b b +=⎧⎨=⎩，解得：11830k b =⎧⎨=⎩， ∴方案一所需费用y 1与x 之间的函数关系式为y 1=18x +30， ∴k 1=18，b =30；（2）∵打折前的每次游泳费用为18÷0.6=30（元）， ∴k 2=30×0.8=24； ∴y 2=24x ，当游泳8次时，选择方案一所需费用：y 1=18×8+30=174（元），选择方案二所需费用：y 2=24×8=192（元）， ∵174＜192，∴选择方案一所需费用更少．【点睛】本题考查了一次函数的应用，解题的关键是理解两种优惠活动方案，求出y 1、y 2关于x 的函数解析式．23．（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是解析：（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是等腰直角三角形，然后根据等腰直角三角形的性质可得AH 的长，最后根据等腰直角三角形的面积公式即可得；（2）先根据平行四边形的性质可得，从而可得，再根据三角形中位线定理可得是的中位线，从而可得，然后与（1）所求的建立等式求解即可得；（3）分①当点H 是AB 的中点时，；②当点Q 与点E 重合时，；③当时，三种情况，分别求解即可得．【详解】（1）由题意得：，点Q为AP的中点，，四边形ABCD是矩形，，是BAD的角平分线，，，是等腰直角三角形，，则的面积为；（2）如图1，四边形PQHM是平行四边形，，点M在BC边上，，点Q为AP的中点，是的中位线，，由（1）知，，则，解得；（3）由题意，有以下三种情况：①如图2，当点H是AB的中点时，则，四边形PQHM是平行四边形，，，在和中，，，由（2）可知，此时；②如图3，当点Q与点E重合时，在和中，，，，则，解得；③如图4，当时，四边形ABCD是矩形，四边形PQHM是平行四边形，，，在和中，，，，，在中，，是等腰直角三角形，，，在中，，是等腰直角三角形，，则由得：，解得；综上，如图2，当时，；如图3，当时，；如图4，当时，．【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点，较难的是题（3），依据题意，正确分三种情况讨论并画出图形是解题关键．24．（1）（-4，6）；（2）y=x+3或y=-7x+3；（3）（，0）或（，0）【解析】【分析】（1）由及点不同于点，可知点是线段的中点，由点、的坐标即可求出点的坐标；（2）根据题意得到点C的解析：（1）（-4，6）；（2）y=17x+3或y=-7x+3；（3）（14，0）或（314，0）【解析】【分析】（1）由CA AB=及点C不同于点B，可知点A是线段BC的中点，由点A、B的坐标即可求出点C的坐标；（2）根据题意得到点C的两个位置，作线段AB的垂直平分线交AC于点G，交AC′于点H，交AB于点Q，连接BG、BH，作GP⊥y轴于点P，GF⊥x轴于点F，证明△GBF≌△GAP，得到BF=AP，GF=GP，列方程求出AP，得到OP和OF，可得点G和H 坐标，再利用待定系数法求解；（3）分平行四边形AMBN以AB为对角线，平行四边形ABNM以AB为一边，两种情况，画出图形分别求解．【详解】解：（1）如图1，直线334y x=-+，当0x=时，3y=；当0y=时，由3304x-+=，得4x=，(0,3)A∴，(4,0)B；CA AB =，且点C 不同于点B ，∴点A 是线段BC 的中点，即点C 与点B 关于点A 对称， ∴点C 的横坐标为4-，当4x =-时，3(4)364y =-⨯-+=，(4,6)C ∴-，故答案为：(4,6)-．（2）如图2，射线AC 在直线AB 的上方，射线AC '在直线AB 的下方，45BAC BAC ∠=∠'=︒；作线段AB 的垂直平分线交AC 于点G ，交AC '于点H ，交AB 于点Q ，连接BG 、BH ，则3(2,)2Q ；作GP y ⊥轴于点P ，GF x ⊥轴于点F ，则AG BG =，AH BH =，BG AG =，BH AH =，45GBA BAC ∴∠=∠=︒，45HBA BAC ∠=∠'=︒，90BGA GAH AHB ∴∠=∠=∠=︒，∴四边形AHBG 是正方形；180AGB AOB ∠+∠=︒， 180GBF OAG ∴∠+∠=︒，180GAP OAG ∠+∠=︒， GBF GAP ∴∠=∠，90GFB GPA ∠=∠=︒，()GBF GAP AAS ∴∆≅∆，BF AP ∴=，GF GP =，90FOP OPG GFO ∠=∠=∠=︒，∴四边形OFGP 是正方形，OF OP ∴=， 4OB =，3OA =，43BF AP ∴-=+，43AP AP ∴-=+，解得12AP =， 17322OP OF ∴==+=， 7(2G ∴，7)2；点H 与点G 关于点3(2,)2Q 对称，1(2H ∴，1)2-；设直线AC 的解析式为y kx b =+，则77223k b b ⎧+=⎪⎨⎪=⎩，解得173k b ⎧=⎪⎨⎪=⎩， 137y x ∴=+；设直线AC '的解析式为y mx n =+，则11223m n n ⎧+=-⎪⎨⎪=⎩，解得73m n =-⎧⎨=⎩，73y x ∴=-+，综上所述，直线AC 的解析式为137y x =+或73y x =-+．（3）存在，如图3，平行四边形AMBN 以AB 为对角线，延长ED 交y 轴于点R ，设OD r =，由折叠得，90AED AOD ∠=∠=︒，ED OD =，ED r ∴=，ED AB ⊥；35AB =，3AE AO ==，532BE ∴=-=，13462AOB S ∆=⨯⨯=，且AOD ABD AOB S S S ∆∆∆+=，∴1135622r r ⨯+⨯=，解得32r =， 32ED OD ∴==， 3(2D ∴，0)；90DOR DEB ∠=∠=︒，ODR EDB ∠=∠，()ODR EDB ASA ∴∆≅∆，2RO BE ∴==，(0,2)R ∴-，设直线DE 的解析式为2y px =-，则3202p -=，解得43p =， 423y x ∴=-；点N 在x 轴上，且//AM BN ，//AM x ∴轴，∴点M 与点A 的纵坐标相等，都等于3，当3y =时，由4233x -=，得154x =， 15(4M ∴，3)，154BN AM ==， 151444ON ∴=-=， 1(4N ∴，0)；如图4，平行四边形ABNM 以AB 为一边，则//AM x 轴，且154AM BN ==．1531444ON =+=， 31(4N ∴，0)，综上所述，点N 的坐标为1(4，0)或31(4，0)．【点睛】此题重点考查一次函数的图象和性质、用待定系数法求一次函数的解析式、平行四边形的判定、全等三角形的判定与性质、关于某点成中心对称的点的坐标等知识与方法，解题的关键是正确地作出所需要的辅助线，第（2）题、第（3）题都要分类讨论，此题难度较大，属于考试压轴题．25．（1）见解析；（2）①见解析；② 【分析】（1）根据直角三角形中两锐角互余以及三角形外角的性质可得结果；（2）①延长AD 至Q ，使得，连接BQ ，可证，根据已知以及等腰三角形的性质可得结论； ②作，解析：（1）见解析；（2）①见解析；②25AE AD = 【分析】（1）根据直角三角形中两锐角互余以及三角形外角的性质可得结果；（2）①延长AD 至Q ，使得AD QD =，连接BQ ，可证()ACD QBD SAS ≌，根据已知以及等腰三角形的性质可得结论；②作,BP EQ CK AD ⊥⊥，连接CE ，证明CK EK =，设CD x =，则2BC AC x ==，根据勾股定理求得AE 、AD 的长度，求比值即可．【详解】解：（1）在Rt ABC 中，90ACB ∠=︒， ∴90CAD ADC ∠+∠=︒ ∵CAD α∠=， ∴90ADC α∠=︒-， ∵CF BE ⊥，∴90EFG ∠=︒∵BED α∠=，∴90EGC BED EFG α∠=∠+∠=︒+，∵EGC ADC GCD ∠=∠+∠，∴()()90902GCD EGC ADC ααα∠=∠-∠=︒+-︒-=；（2）①延长AD 至Q ，使得AD QD =，连接BQ ，∵点D 为BC 边中点，∴CD BD =,又∵ADC QDB ∠=∠，∴()ACD QBD SAS ≌，∴CAD Q ∠=∠，AC QB =∵BED CAD α∠=∠=，∴Q BED α∠=∠=，∴EB QB =，∴AC EB =，∵AC BC =，∴BE BC =；②作,BP EQ CK AD ⊥⊥，连接CE ，∴90CKA DPB ∠=∠=︒，由（2）知,AC QB CAD Q =∠=∠，∴()ACK QBP AAS ≌∴CK BP =，∵90,90CAD ADC DCA ADC ∠+∠=︒∠+∠=︒,又∵BED CAD α∠=∠=，2GCD α∠=，∴902CBE α∠=︒-，∵BC BE =，∴45BCE BEC α∠=∠=︒+，∴45ECK CEK ∠=∠=︒，∴CK EK =，设CD x =，则2BC AC x ==， ∴225AD AC CD x =+， ∵1122CK AD AC CD =， ∴52CKx x x =， ∴25CK x EK ==， ∴2222255()5DK CD CK x x =-=-， ∴52535DE DK EK x =+=， ∴35255AE AD DE x =-==， ∴252555AE AD x==，故答案为：25．【点睛】本题主要考查三角形综合问题，涉及到全等三角形判定与性质，等腰三角形的判定与性质，勾股定理等知识点，作出合理辅助线构造全等三角形以及应用勾股定理表示出各线段的长度是解题的关键．。

八年级期末试卷复习练习(Word版含答案)

八年级期末试卷复习练习(Word 版含答案)一、选择题1．若代数式20213x -有意义，x 应满足的条件是（） A ．2021x ≥ B ．2021x > C ．2021x ≠ D ．2021x ≤- 2．要做一个直角三角形的木架，以下面各组木棒为三边，刚好能做成的是（） A ．5，6，7B ．10，4，8C ．10，26，24D ．9，15，173．如图，在四边形ABCD 中，对角线AC 和BD 相交于点O ，下列条件不能判断四边形ABCD 是平行四边形的是（）A ．//AB DC ，ABC ADC ∠=∠ B ．AB DC =，AD BC = C ．OA OC =，OB OD =D ．//AD BC ，AB CD =4．某商场招聘员工一名，现有甲、乙、丙三人竞聘，通过计算机、语言和商品知识三项测试，他们各自成绩（百分制）如下表所示，若商场需要招聘负责将商品拆装上架的人员，对计算机、语言和商品知识分别赋权2，3，5，那么从成绩看，应该录取（）应试者计算机语言商品知识甲 60 70 80 乙 80 70 60 丙708060A ．甲B ．乙C ．丙D ．任意一人都可5．如图，在正方形ABCD 和正方形CEFG 中，点D 在CG 上，BC ＝1，CE ＝3，H 是AF 的中点，那么CH 的长是（）A ．25B 5C ．35D ．26．如图，在三角形纸片ABC 中，∠A ＝60°，∠B ＝70°，将纸片的一角折叠，使点C 落在△ABC 外，若∠2＝18°，则∠1的度数为（）A ．50°B ．118°C ．100°D ．90°7．△ABC 中，AB ＝6，BC ＝5，AC ＝7，点D 、E 、F 分别是三边的中点，则△DEF 的周长为（） A ．5B ．9C ．10D ．188．已知函数222y kx k =++（k 为常数，0k >）的图象经过点(),a b ，且实数a ，b ，k 满足等式：()2224212a k b b bk +++=+，则一次函数()2220y kx k k =++>与y 轴的交点坐标为（） A ．()0,2B ．()0,31-C ．()0,623-D ．()0,4二、填空题9．二次根式9x +在实数范围内有意义，则x 的取值范围是__．10．菱形的周长为20cm ，一条对角线长为8cm ，则菱形的面积为______cm 2． 11．在Rt ABC ∆中，90C ∠=︒，4AC =，3BC =，则AB =______.12．如图，在矩形ABCD 中，∠BOC ＝120°，AB ＝10，则BD 的长为_______．13．定义：对于一次函数y ＝kx +b ，我们把点（b ，k ）称为这个一次函数的伴随点．已知一次函数y ＝﹣2x +m 的伴随点在它的图象上，则m ＝_____．14．如图，请你添加一个适当的条件___，使平行四边形ABCD 成为菱形．15．正方形111A B C O ，2221A B C C ，3332A B C C ，…按如下图所示的方式放置．点1A ，2A ，3A ，…和点1C ，2C ，3C ，…分别在直线()0y kx b k =+>和x 轴上，已知正方形111A B C O 的边长为1，正方形2221A B C C 边长为2，则7A 的坐标是______．16．如图，DE 为△ABC 的中位线，点F 在DE 上，且∠AFB ＝90°，若AB ＝5，BC ＝8，则EF 的长为______．三、解答题17．计算：（1）1325045183++-；（2）163438222⎛⎫⨯-+÷ ⎪ ⎪⎝⎭． 18．如图，一架长2.5m 的梯子AB 斜靠在墙AC 上，∠C ＝90°，此时，梯子的底端B 离墙底C 的距离BC 为0.7m（1）求此时梯子的顶端A 距地面的高度AC ；（2）如果梯子的顶端A 下滑了0.9m ，那么梯子的底端B 在水平方向上向右滑动了多远？19．如图是由边长为1的小正方形构成6×6的网格，每个小正方形的顶点叫做格点．四边形ABCD 的顶点都是格点，点E 是边AD 与网格线的交点．仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：（1）直接写出四边形ABCD 的形状；（2）在BC 边上画点F ，连接EF ，使得四边形AEFB 的面积为5；（3）画出点E 绕着B 点逆时针旋转90°的对应点G ；（4）在CD 边（端点除外）上画点H ，连接EH ，使得EH ＝AE +CH ．20．如图，在ABC 中，3AB =，4BC =，5AC =，2BD =，EF 是ABC 的中位线．求证：四边形BDFE 是矩形．21．阅读下面的材料，解答后面提出的问题：黑白双雄，纵横江湖；双剑合壁，天下无敌，这是武侠小说中的常见描述，其意思是指两个人合在一起，取长补短，威力无比，在二次根式中也有这种相辅相成的“对子”，如：(2 33＝1，5252)＝3, 它们的积不含根号，我们说这两个二次根式互为有理化因式，其中一个是另一个的有理化因式．于是，二次根式除法可以这样解：31333⨯⨯32323+-()()23232323-+＝7＋3一个式子把分母中的根号化去或把根号中的分母化去，叫做分母有理化．解决问题：(1)47的有理化因式是，将32分母有理化得；(2)已知x 3232+-y3232-+,则11x y+＝；(3)已知实数x，y满足(x22017x-y22017y-－2017＝0，则x＝，y＝．22．某市出租车收费标准分白天和夜间分别计费，计费方案见下列表格及图象（其中a，b，c为常数）行驶路程收费标准白天夜间（22时至次日5时）不超过2km的部分起步价6元起步价a元超过2km不超出10km的部分每公里2元每公里b元超出10km的部分每公里3元每公里c元设行驶路程为km x 时，白天的运价为1y （元），夜间的运价为2y （元）．如图，折线ABCD 表示2y 与x 之间的函数关系式，线段EF 表示当02x ≤≤时，1y 与x 的函数关系式，根据图表信息，完成下列各题：（1）填空：a =______，b =______，c =______；（2）当210x <≤时，求1y 的函数表达式；（3）若幸福小区到阳光小区的路程为12km ，小明从幸福小区乘出租车去阳光小区，白天收费比夜间收费少多少元?23．如图，在▱ABCD 中，连接BD ，AB BD ⊥，且AB BD ＝，E 为线段BC 上一点，连接AE 交BD 于F ．（1）如图1，若22AB =，BE ＝1，求AE 的长度；（2）如图2，过D 作DH ⊥AE 于H ，过H 作HG ⊥AD 交AD 于G ，交BD 于M ，过M 作MN ∥AD 交AE 于N ，连接BN ，证明：2NH BN =；（3）如图3，点E 在线段BC 上运动时，过D 作DH ⊥AE 于H ，延长DH 至Q ，使得12QH AH =，M 为AD 的中点，连接QM ，若42AD =，当QM 取最大值时，请直接写出△ADH 的面积．24．如图1，在平面直角坐标系xOy 中，直线AB 交y 轴于点A (0，3)，交x 轴于点B (﹣4，0)．(1)求直线AB 的函数表达式；(2)如图2，在线段OB 上有一点C （点C 不与点O 、点B 重合），将AOC 沿AC 折叠，使点O 落在AB 上，记作点D ，在BD 上方，以BD 为斜边作等腰直角三角形BDF ，求点F 的坐标；(3)在(2)的条件下，如图3，在平面内是否存在一点E ，使得以点A ，B ，E 为顶点的三角形与ABC 全等（点E 不与点C 重合），若存在，请直接写出满足条件的所有点E 的坐标，若不存在，请说明理由．25．如图1，ABC ∆中，CD AB ⊥于D ，且::2:3:4BD AD CD =；（1）试说明ABC ∆是等腰三角形；（2）已知Δ40ABC S =cm 2，如图2，动点M 从点B 出发以每秒1cm 的速度沿线段BA 向点A 运动，同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动，当其中一点到达终点时整个运动都停止．设点M 运动的时间为t (秒)． ①若DMN ∆的边与BC 平行，求t 的值；②在点N 运动的过程中，ADN ∆能否成为等腰三角形?若能，求出t 的值；若不能，请说明理由．【参考答案】一、选择题 1．A 解析：A 【分析】根据二次根式根号下的数大于等于零即可求解．【详解】解：∵2021x - ∴20210x -≥，解得：2021x ≥，故选A ．【点睛】本题考查了二次根式以及一元一次不等式的解法，掌握二次根式根号下数的取值范围与一元一次不等式解法即可解题．2．C解析：C由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方即可．【详解】解：A 、因为222567+≠，故不能作为直角三角形三边长度，不符合题意；B 、因为2224810+≠，故不能作为直角三角形三边长度，不符合题意；C 、因为222102426+=，故能作为直角三角形三边长度，符合题意；D 、因为22291517+≠，故不能作为直角三角形三边长度，不符合题意．故选：C ．【点睛】本题考查勾股定理的逆定理的应用，解题的关键是判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．3．D解析：D 【解析】【分析】根据平行四边形的判定定理逐项判断即可．【详解】A 、由//AB DC ，得180ABC ACD ∠+∠=︒，又ABC ADC ∠=∠，得180ADC ACD ∠+∠=︒，得//AD BC ，可得到四边形ABCD 是平行四边形，故A 选项不符合题意B 、由AB DC =，AD BC =，可得到四边形ABCD 是平行四边形，故B 选项不符合题意； C 、由OA OC =，OB OD =，可得到四边形ABCD 是平行四边形，故C 选项不符合题意； D 、由//AD BC ，AB CD =，不可得到四边形ABCD 是平行四边形，故D 选项符合题意．故选：D ．【点睛】本题主要考查了平行四边形的判定，解题的关键是理解并掌握平行四边形的判定定理，并会灵活运用．4．A解析：A 【解析】【分析】分别按照2，3，5的赋权计算甲，乙，丙的平均数，再录取最高分即可. 【详解】解：根据题意，甲的最终成绩为60270380573235⨯+⨯+⨯=++（分)，乙的最终成绩为80270360567235⨯+⨯+⨯=++（分)，丙的最终成绩为70280360568235⨯+⨯+⨯=++（分)，所以应该录取甲，故选：A ．本题考查的是加权平均数的含义与计算，理解赋权2，3，5的含义是解题的关键.5．B解析：B 【分析】连接AC 、CF ，如图，根据正方形的性质得∠ACD =45°，∠FCG =45°，AC =2，CF =32，则∠ACF =90°，再利用勾股定理计算出AF =25，然后根据直角三角形斜边上的中线求CH 的长．【详解】连接AC 、CF ，如图，∵四边形ABCD 和四边形CEFG 都是正方形，∴∠ACD =45°，FCG =45°，AC =2BC =2，CF =2CE =32， ∴∠ACF =45°+45°=90°，在Rt △ACF 中，AF =()()22232=25+，∵H 是AF 的中点， ∴CH =12AF =5 ．故选B ．【点睛】本题考查了正方形的性质：正方形的四条边都相等，四个角都是直角；正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；正方形具有四边形、平行四边形、矩形、菱形的一切性质．两条对角线将正方形分成四个全等的等腰直角三角形．也考查了直角三角形斜边上的中线性质及勾股定理．6．B解析：B 【解析】【分析】在△ABC 中利用三角形内角和定理可求出∠C 的度数，由折叠的性质，可知：∠CDE ＝∠C ′DE ，∠CED ＝∠C ′ED ，结合∠2的度数可求出∠CED 的度数，在△CDE 中利用三角形内角和定理可求出∠CDE 的度数，再由∠1＝180°﹣∠CDE ﹣∠C ′DE 即可求出结论．【详解】解：在△ABC 中，∠A ＝60°，∠B ＝70°，∴∠C ＝180°﹣∠A ﹣∠B ＝50°．由折叠，可知：∠CDE ＝∠C′DE ，∠CED ＝∠C′ED ， ∴∠CED ＝18022︒+∠＝99°， ∴∠CDE ＝180°﹣∠CED ﹣∠C ＝31°，∴∠1＝180°﹣∠CDE ﹣∠C′DE ＝180°﹣2∠CDE ＝118°．故选：B ．【点睛】本题考查了三角形内角和定理以及折叠的性质，利用三角形内角和定理及折叠的性质求出∠CDE 的度数是解题的关键．7．B解析：B 【解析】【分析】根据三角形中位线定理求得,,DE DF EF ,进而求得三角形的周长．【详解】解：∵点D ，E 分别AB 、BC 的中点，AC ＝7， ∴DE ＝12AC ＝3.5，同理，DF ＝12BC ＝2.5，EF ＝12AB ＝3， ∴△DEF 的周长＝DE ＋EF ＋DF ＝9，故选：B ．【点睛】本题考查了三角形中位线定理，理解三角形中位线定理是解题的关键．8．C解析：C 【分析】将点(),a b 代入函数222y kx k =++中，得到关于a ，b ，k 的关系式，将k 看作常数，再联立满足的等式组成二元一次方程组，将a ，b 用含k 的式子表示出来，此时再回代入函数222y kx k =++中，求解出k 的值，最后在一次函数中令x=0，求解出y 的值，最终表示出交点坐标即可．【详解】解：将点(),a b 代入函数222y kx k =++中，得：2b 2a 2k k =++，又∵()2224212a k b b bk +++=+，化简可得：()()2222222242+42+4k 4bk+=02+2k-b 0a kb b bk a b b a b +++=+--+-= 此时联立方程组可得：()22222220b ka k a b k b ⎧=++⎪⎨++-+-=⎪⎩①② ，解得：2a kb k =-⎧⎨=⎩，∴点(),a b 的坐标可表示为（-k ，2k ），将（-k ，2k ）代入222y kx k =++得：222k 22k k =-++，解得1k=- ∵k 为常数且0k >，∴1k=-此时一次函数(((2222=2+2=+6y kx k x x =++--+--令x=0，解得：6y=- ∴交点坐标为0,6-．故选：C ．【点睛】本题考查了一次函数与二元一次方程组，联立二元一次方程组并正确求解是解题的关键．二、填空题9．x ≥﹣9 【解析】【分析】由二次根式的非负性可得x +9≥0，即可求解．【详解】解：∵∴x +9≥0， ∴x ≥﹣9，故答案为x ≥﹣9．【点睛】)0a ≥的式子叫二次根式，熟练掌握二次根式成立的条件是解答本题的关键．10．24【解析】【分析】画出符合题意的图形，利用菱形的对角线互相垂直平分，求解另一条对角线的长，再利用菱形的面积等于两条对角线的长之积的一半即可得到答案．【详解】解：如图，菱形ABCD 的周长为20cm ，一条对角线AC 的长为8cm ，5,4,,,AD AB BC CD cm OA OC cm OB OD AC BD ∴=======⊥2222543OD AD AO ∴--，26,BD OD cm ∴==2116824.22ABCD S AC BD cm ∴==⨯⨯=菱形故答案为：24.【点睛】本题考查的是菱形的性质，菱形的面积，掌握菱形的性质及菱形的面积的计算是解题的关键．11．5【解析】【分析】根据勾股定理222AB AC BC =+即可求得AB 的长度．【详解】在直角ABC 中，90C ∠=︒，∴根据勾股定理222AB AC BC =+，∴2222435AB AC BC +=+，故答案为：5．【点睛】本题考查了勾股定理在直角三角形中的运用，本题中正确的运用勾股定理是解题的关键． 12．B解析：20【分析】先根据矩形的性质和∠BOC =120∘，证明△AOB 是等边三角形，即可得到OB =AB =10，BD =2OB =20.【详解】解：∵四边形ABCD是矩形，∴OA=12AC，OB=12BD，AC=BD，∴OA=OB，∵∠BOC=120∘，∴∠AOB=60∘，∴△AOB是等边三角形，∴OB=AB=10，∴BD=2OB=20；故答案为：20.【点睛】本题主要考查了矩形的性质，等边三角形的性质与判定，解题的关键在于能够熟练掌握相关知识进行求解.13．2【分析】根据题意可以求得一次函数y＝﹣2x+m的伴随点，然后根据一次函数y＝﹣2x+m的伴随点在它的图象上，从而可以求得m的值．【详解】解：由题意可得，y＝﹣2x+m的伴随点是（m，﹣2），∵一次函数y＝﹣2x+m的伴随点在它的图象上，∴﹣2＝﹣2m+m，解得，m＝2，故答案为：2．【点睛】本题考查一次函数图象上点的坐标特征，解答本题的关键是明确题意，利用一次函数的性质解答．14．AC BD⊥【分析】根据对角线互相垂直的平行四边形是菱形解题．【详解】解：由对角线互相垂直的平行四边形是菱形得，应添加条件：AC BD⊥故答案为：AC BD⊥．【点睛】本题考查菱形的判定，是重要考点，掌握相关知识是解题关键．15．（63，64）【分析】由题意易得，然后把点的坐标代入直线求解，进而可得点，，…..；由此可得规律为，最后问题可求解．【详解】解：∵四边形，是正方形，且正方形的边长为，正方形边长为，∴，∴解析：（63，64）【分析】由题意易得()()()()21110,1,1,1,1,0,1,2A A B C ，然后把点12,A A 的坐标代入直线()0y kx b k =+>求解，进而可得点()33,4A ，()47,8A ，…..；由此可得规律为()1121,2n n n A ---，最后问题可求解．【详解】解：∵四边形111A B C O ，2221A B C C 是正方形，且正方形111A B C O 的边长为1，正方形2221A B C C 边长为2，∴211111*********,2C O A B A O C C C B C A A B C B ========，∴()()()()21110,1,1,1,1,0,1,2A A B C ，12123O C C O C C =+=，∵点123,,A A A ….在直线()0y kx b k =+>上，∴把点12,A A 的坐标代入得：21k b b +=⎧⎨=⎩，解得：11k b =⎧⎨=⎩， ∴直线1y x =+，当x =3时，则有314y =+=，∴()33,4A ，同理可得()47,8A ，∵11213141210,211,213,217-----=-=-=-=，…..；∴()1121,2n n n A ---， ∴()763,64A ；故答案为()63,64．【点睛】本题主要考查正方形的性质及一次函数的应用，熟练掌握正方形的性质及一次函数的图象与性质是解题的关键．16．5【详解】试题解析：∵∠AFB=90°，D 为AB 的中点，∴DF=AB=2.5，∵DE 为△ABC 的中位线，∴DE=BC=4，∴EF=DE-DF=1.5，故答案为1.5．【点睛】直角三解析：5【详解】试题解析：∵∠AFB=90°，D为AB的中点，∴DF=12AB=2.5，∵DE为△ABC的中位线，∴DE=12BC=4，∴EF=DE-DF=1.5，故答案为1.5．【点睛】直角三角形斜边上的中线性质：在直角三角形中，斜边上的中线等于斜边的一半和三角形的中位线性质：三角形的中位线平行于第三边，并且等于第三边的一半．三、解答题17．（1）；（2）【分析】（1）先化简每个二次根式，再合并同类二次根式即可；（2）先计算并化简括号内的，合并结果，再算除法．【详解】解：（1）===；（2）====【点睛】解析：（1）2）7 2【分析】（1）先化简每个二次根式，再合并同类二次根式即可；（2）先计算并化简括号内的，合并结果，再算除法．【详解】解：（1=13⨯==；（2）÷=43⎛+⨯÷ ⎝=(÷= =72 【点睛】本题主要考查了二次根式的混合运算，在二次根式的混合运算中，如能结合题目特点，灵活运用二次根式的性质，选择恰当的解题途径，往往能事半功倍．18．（1）2.4米；（2）1.3m【分析】（1）直接利用勾股定理求出AC 的长，进而得出答案；（2）直接利用勾股定理得出B′C ，进而得出答案．【详解】解：（1）∵∠C ＝90°，AB ＝2.5，BC解析：（1）2.4米；（2）1.3m【分析】（1）直接利用勾股定理求出AC 的长，进而得出答案；（2）直接利用勾股定理得出B ′C ，进而得出答案．【详解】解：（1）∵∠C ＝90°，AB ＝2.5，BC ＝0.7，∴AC2.4=（米），答：此时梯顶A 距地面的高度AC 是2.4米；（2）∵梯子的顶端A 下滑了0.9米至点A ′，∴A ′C ＝AC −A ′A ＝2.4−0.9＝1.5（m ），在Rt △A ′CB ′中，由勾股定理得：A ′C 2＋B ′C 2＝A ′B ′2，∴1.52＋B ′C 2＝2.52，∴B ′C ＝2（m ），∴BB ′＝CB ′−BC ＝2−0.7＝1.3（m ），答：梯子的底端B 在水平方向滑动了1.3m ．【点睛】此题主要考查了勾股定理的实际应用，熟练掌握勾股定理是解题关键．19．（1）正方形；（2）见解析；（3）见解析；（4）见解析【解析】【分析】（1）利用勾股定理和勾股定理的逆定理可证明四边形ABCD为正方形；（2）延长EO交BC于F，则根据正方形为中心对称图形得解析：（1）正方形；（2）见解析；（3）见解析；（4）见解析【解析】【分析】（1）利用勾股定理和勾股定理的逆定理可证明四边形ABCD为正方形；（2）延长EO交BC于F，则根据正方形为中心对称图形得到AE＝CF，则可根据梯形的面积公式计算出四边形AEFB的面积为5；（3）延长DC交过B点的铅垂线于G点，通过证明△BAE≌△BCG得到BG＝BE；（4）利用网格特点，作∠EBG的平分线交CD于H点，证明△BEH≌△BGH，则EH＝HG，则AE＝CG，则有EH＝AE+CH．【详解】解：（1）∵AB＝BC＝CD＝AD＝2213+＝10，∴四边形ABCD为菱形，∵BD＝2224+＝25，∴AD2+AB2＝BD2，∴∠BAD＝90°，所以四边形ABCD为正方形；（2）如图，点F为所作；（3）如图，点G为所作；（4）如图，H点为所作．【点睛】本题考查了作图—旋转变换，解题的关键是熟练掌握轴对称变换和旋转变换的定义，并据此得出变换后的对应点．20．见解析【分析】根据中位线的性质得出、，进而得出四边形是平行四边形，再根据勾股定理的逆定理得出是直角三角形，且，则四边形是矩形．【详解】证明：∵是的中位线，∴，．∵，∴．∴四边形是平行四解析：见解析【分析】根据中位线的性质得出//EF BC 、EF BD =，进而得出四边形BDFE 是平行四边形，再根据勾股定理的逆定理得出ABC 是直角三角形，且90B ∠=︒，则四边形BDFE 是矩形．【详解】证明：∵EF 是ABC 的中位线，∴//EF BC ，122EF BC ==． ∵2BD =，∴EF BD =．∴四边形BDFE 是平行四边形．∵3AB =，4BC =，5AC =，∴222AB BC AC +=．∴ABC 是直角三角形，且90B ∠=︒．∴四边形BDFE 是矩形．【点睛】本题考查了三角形的中位线、勾股定理的逆定理，平行四边形的判定、矩形的判定等知识点，熟悉并运用以上性质定理是解题的关键．21．（1）,;（2）10 ;（3），.【解析】【详解】(1) ∵,∴ 的有理化因式为 ;∵,∴ 分母有理化得: .(2). ∵ ,∴(3) ∵(x ＋)(y ＋)－2017＝0∴,∴解析：（1）43;（2）10 ;（3）【解析】【详解】(1) ∵(41679+=-=,∴ 44∵63===∴分母有理化得: 3 .(2). ∵x =5y ==-∴1110y x x y xy ++==(3) ∵(x y －2017＝0∴2017=,∴2017= ∴y x∴x y -整理得：2017xy -∴2220x xy y -+= ,x=y将x=y 代入可得：x =y =故答案为点睛：此题考查了分母有理化，正确选择两个二次根式，使它们的积符合平方差公式是解本题的关键.22．（1）7，2.4，3.6；（2）y=2x+2；（3）5.4元【分析】（1）a 即为AB 与y 轴的交点的纵坐标，可结合图象，单价=总价÷路程，b 、c 便可以求出；（2）利用表格中的数据求解即可；（3解析：（1）7，2.4，3.6；（2）y =2x +2；（3）5.4元【分析】（1）a 即为AB 与y 轴的交点的纵坐标，可结合图象，单价=总价÷路程，b 、c 便可以求出；（2）利用表格中的数据求解即可；（3）利用待定系数法求解求出当x ＞10时，y 2与x 之间的函数关系式，再把x =12分别代入y 1和y 2的函数表达式即可解答．【详解】解：解：（1）由图可知，a =7，b =（26.2-7）÷（10-2）=2.4，c =（29.8-26.2）÷（11-10）=3.6（元）；故答案为7，2.4，3.6；（2）当2＜x ≤10时，求y 1的函数表达式为y 1=6+2（x -2）=2x +2；（3）设当x ＞10时，y 2与x 之间的函数关系式为y 2=kx +b ，根据题意得，1129.81026.2k b k b +=⎧⎨+=⎩，解得： 3.69.8k b =⎧⎨=-⎩， ∴y 2与x 之间的函数关系式为y 2=3.6x -9.8（x ＞10）；当x ＞10时，y 1与x 之间的函数关系式为6+2×（10-2）+3（x -10）=3x -8（x ＞10）．当x =12时，y 2=3.6×12-9.8=33.4（元），y 1=3×12-8=28（元），33.4-28=5.4（元），答：白天收费比夜间收费少5.4元．【点睛】本题主要考查一次函数的应用问题，熟练掌握一次函数的性质是解答本题的关键． 23．（1）见解析；（2）见解析；（3）．【分析】（1）分别过点作，垂足分别为，勾股定理解即可；（2）连接，过点作于点，设，经过角度的变换得出，再证明，得出，，结合已知条件，继而证，得出，，进而得到解析：（1）见解析；（2）见解析；（3 【分析】（1）分别过点,B E 作,BS AD ER AD ⊥⊥，垂足分别为,S R ，勾股定理解Rt ARE △即可；（2）连接BH ，过点N 作NT AD ⊥于点T ，设BAN α∠=，经过角度的变换得出BAN HDB ∠=∠，再证明ATN △≌HGD △，得出，AN HD =，结合已知条件，继而证BAN ≌BDH △，得出ABN DBH ∠=∠，NB HB =，进而得到NBH △是等腰直角三角形，从而得证；（3）分别作,AD AQ 的中垂线，交于点O ，根据作图，先判断MQ 最大的时候的位置，进而由12QH AH =，AD =,AH HD ，从而求得△ADH 的面积．【详解】（1）如图，分别过点,B E 作,BS AD ER AD ⊥⊥，垂足分别为,S RAB BD ⊥，AB BD ＝，22AB =ABD ∴是等腰直角三角形，ASB △是等腰直角三角形 224AD AB BD ∴=+=∴122AS SD AD ===,2BS AS == 四边形ABCD 是平行四边形//AD BC ∴,BS AD ER AD ⊥⊥，1BE ＝∴四边形SBER 是矩形∴SR BE =1=，2RE SB ==3AR AS SR ∴=+=在Rt ARE △中22223213AE AR RE =+=+= （2）连接BH ，过点N 作NT AD ⊥于点T ，设BAN α∠=BAD 是等腰直角三角形45BAD BDA ∴∠=∠=︒45HAD BAD BAN α∴∠=∠-∠=︒- DH AE ⊥，9045ADH HAD α∴∠=︒-∠=︒+4545HDB ADH ADB αα∴∠=∠-∠=︒+-︒= BAN HDB ∴∠=∠NT AD ⊥9090(45)45ANT HAD αα∴∠=︒-∠=︒-︒-=︒+，90ATN ∠=︒ANT ADH HDG ∴∠=∠=∠HG AD ⊥90HGD ∴∠=︒ATN HGD ∴∠=∠又45BDA ∠=︒9045DMG MDG ∴∠=︒-∠=︒GD GM ∴=//MN AD ，HG AD ⊥，NT AD ⊥∴四边形TNMG 是矩形GM TN ∴=TN GD ∴=在ATN △和HGD △中ANT HDG TN GDATN HGD ∠=∠⎧⎪=⎨⎪∠=∠⎩∴ATN △≌HGD △（ASA ）AN HD ∴=在BAN 和BDH △中AB BD BAN HDB AN HD =⎧⎪∠=∠⎨⎪=⎩∴BAN ≌BDH △（SAS ）ABN DBH ∴∠=∠，NB HB =ABN NBD DBH NBD ∠+∠=∠+∠即ABD NBH ∠=∠AB BD ⊥90ABD ∴∠=︒90NBH ∴∠=︒NBH ∴△是等腰直角三角形∴NH =即NH =（3）分别作,AD AQ 的中垂线，交于点O ，由题意，当点E 在线段BC 上运动时，AQD ∠不变，AD 的长度不变，则,,A D Q 三点共圆，则点Q 在以O 为圆心OQ 为半径的圆上运动，DH AE ⊥，12QH AH =tan 2AH AQD QH∴∠== 在OMQ 中MQ MO OQ ≤+∴当,,M O Q 三点共线时，MQ 取得最大值，此时情形如图：,AB BD BM AD =⊥∴AM MD =,,M O Q 三点共线，∴点Q 在AB 的垂直平分线上QA QD ∴=DH AE ⊥,tan 2AH AQDQH∠== 设QH x =，则AH 2x =5AQ x ∴=QD =DH x ∴=-AD =222AH DH AD ∴+=即222(2))x x +-= 得：2x =△ADH 的面积12AH DH =⋅12)2x x =⨯⋅-21)x =1)=∴当QM 取最大值时，△ADH 【点睛】本题考查了平行四边形的性质，矩形的性质与判定，等腰三角形的性质，垂直平分线的性质，圆的性质，勾股定理，三角形三边关系，三角形全等的证明与性质，动点问题等，本题是一道综合性比较强的题，熟练平面几何的性质定理是解题的关键．24．（1）；（2）；（3）或或【解析】【分析】(1)直接利用待定系数法，即可得出结论；(2)先求出AD ＝3，AB ＝5，进而求出点D 的坐标，再构造出△BMF ≌△FND ，得出BM ＝FN ，FM ＝DN ，解析：（1）334y x =+；（2）197(,)55F -；（3）5(,3)2E -或3312(,)105-或73(,)105- 【解析】【分析】(1)直接利用待定系数法，即可得出结论；(2)先求出AD ＝3，AB ＝5，进而求出点D 的坐标，再构造出△BMF ≌△FND ，得出BM ＝FN ，FM ＝DN ，设F （m ，n ），进而建立方程组求解，即可得出结论；(3)分两种情况，①当ABC ABE '≌时，利用中点坐标公式求解，即可得出结论；②当ABC BAE ≌时，当点E 在AB 上方时，根据AE ∥BC ，AE BC =即可得出结论；③当点E 在AB 下方时，过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴，过点E '作E P BP '⊥，证明QAE PBE '''△≌△，即可得出结论．【详解】(1)设直线AB 的函数表达式为y kx b =+，直线AB 交y 轴于点A (0，3)，交x 轴于点B (﹣4，0)，403k b b -+=⎧∴⎨=⎩343k b ⎧=⎪∴⎨⎪=⎩ ∴直线AB 的函数表达式为334y x =+； (2)如图，过点D 分别引,x y 轴的垂线，交,x y 轴于,G H 两点，∵点A （0，3），点B （-4，0），∴OA =3，OB =4，∴AB 2234+=5，由折叠知，AD =OA =3，532DB ∴=-=设(,)D a b -(0,0)a b >>,DG b DH a ∴==,4,3BG a AH b =-=-222222,AD DH AH DB BG DG=+=+∴()()2222223342a b a b ⎧+-=⎪⎨-+=⎪⎩ 解得：436a b -=D 在334y x =+上，334b a ∴=-+ 4363412a b a b -=⎧∴⎨+=⎩ 解得12565a b ⎧=⎪⎪⎨⎪=⎪⎩，126(,)55D ∴-，过点F 作FM ⊥x 轴于M ，延长HD 交FM 于N ，∴∠BMF =∠FND =90°，∴∠BFM +∠FBM =90°，∵△BFD 是等腰直角三角形，∴BF =DF ，∠BFD =90°，∴∠BFM +∠DFN =90°，∴∠FBM =∠DFN ，∴△BMF ≌△FND （AAS ），∴BM =FN ，FM =DN ，设F （m ，n ），则125645n m n m ⎧=--⎪⎪⎨⎪-=+⎪⎩ 19575m n ⎧=-⎪⎪∴⎨⎪=⎪⎩ 197(,)55F ∴-；（3）设OC =a ，则BC =4-a ，由折叠知，∠BDC =∠ADC =∠AOC =90°，CD =OC =a ，在Rt △BDC 中，222BC CD BD =+，∴()2244a a -=+， ∴a =32， 335(,0),,222C OC BC ∴-==， ∵点A ，B ，E 为顶点的三角形与△ABC 全等，①当△ABC ≌△ABE '时，∴BE '=BC ，∠ABC =∠ABE '，连接CE '交AB 于D ，则CD =E 'D ，CD ⊥AB ，由(1)知， 126(,)55D -设E '（b ，c ）， ∴131216(),(0)22525b c -=-+= ∴3312,105b c =-=， ∴3312(,)105E '-； ②当△ABC ≌BAE 时，当点E 在AB 上方时，∴AC =BE ，BC =AE ，EAB CBA =∠∠，∴AE ∥BC ， ∴5(,3)2E -； ③当点E 在AB 下方时，AC =BE ''，BC =AE ''，ABC ABE '△≌△，∴BC BE '=，当ABC BAE ''△≌△时，ABE BAE '''∴△≌△，AE BE '''∴=,BAE ABE '''∠=∠，过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴，过点E '作E P BP '⊥，//PB AQ ∴,90P AQE ''∠=∠=︒，PBA QAB ∴∠=∠，PBA ABE QAB BAE '''∴∠-∠=∠-，即PBE QAE '''∠=∠，90P AQE ''∠=∠=︒，QAE PBE '''∴△≌△，,PE QE AQ PE ''''∴==，点3312(,)105E '-,(4,0)B -， ∴AQ PB ==125，PE QE '''==33741010-+=， 123355OQ ∴=-=， ∴73(,)105E ''-， ∴满足条件的点E 的坐标为5(,3)2E -或3312(,)105-或73(,)105-．【点睛】本题考查了待定系数法，折叠的性质，等腰直角三角形的性质，全等三角形的判定和性质，平移的性质，勾股定理，中点坐标公式，构造出全等三角形，分类讨论是解题的关键．25．（1）证明见解析；（2）①t 值为5或6；②点N 运动的时间为6s ，，或时，为等腰三角形.【分析】（1）设BD ＝2x ，AD ＝3x ，CD ＝4x ，则AB ＝5x ，由勾股定理求出AC ，即可得出结论；（2解析：（1）证明见解析；（2）①t值为5或6；②点N运动的时间为6s，365s，或5s时，ΔADN为等腰三角形.【分析】（1）设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，由勾股定理求出AC，即可得出结论；（2）①由△ABC的面积求出BD、AD、CD、AC；再分当MN∥BC时，AM＝AN和当DN∥BC时，AD＝AN两种情况得出方程，解方程即可；②分三种情况：AD=AN；DA=DN；和ND=NA，三种情况讨论即可【详解】解：（1）设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，在Rt△ACD中，AC＝22AD CD＝5x，∴AB＝AC，∴△ABC是等腰三角形；（2）①S△ABC＝12×5x×4x＝40cm2，而x＞0，∴x＝2cm，则BD＝4cm，AD＝6cm，CD＝8cm，AC＝10cm．当MN∥BC时，AM＝AN，即10−t＝t，此时t＝5，当DN∥BC时，AD＝AN，此时t＝6，综上所述，若△DMN的边与BC平行时，t值为5或6；②ΔADN能成为等腰三角形，分三种情况：（ⅰ）若AD=AN=6，如图：则t=61=6s；（ⅱ）若DA=DN，如图：过点D 作DH AC ⊥于点H ，则AH =NH ，由1122ACD S AD CD AC DH =⋅=⋅，得11681022DH ⨯⨯=⨯⨯，解得245DH =，在Rt ADH 中，222224186()55AH AD DH =-=-=， 3625AN AH ∴==， 3615AN t s ∴==；（ⅲ）若ND =NA ，如图：过点N 作NQ AB ⊥于点Q ，则AQ =DQ =3，142NQ CD ==， 2222345AN AQ NQ ∴=++=，51AN t s ∴==；综上，点N 运动的时间为6s ，365s ，或5s 时，ΔADN 为等腰三角形. 【点睛】此题主要考查了等腰三角形的性质，平行线的性质，三角形的面积公式，勾股定理，解本题的关键是熟练掌握方程的思想方法和分类讨论思想．。

八年级数学下册期末试卷试卷(word版含答案)

八年级数学下册期末试卷试卷（word版含答案）一、选择题1．下列式子中，一定属于二次根式的是（）A．6-B．2x-C．39D．32．若以下列各组数值作为三角形的三边长，则不能围成直角三角形的是（）A．4、6、8 B．3、4、5C．5、12、13 D．1、3、103．如图，在四边形ABCD中，AB∥CD，要使四边形ABCD是平行四边形，下列可添加的条件不正确的是（）A．AD=BC B．AB=CD C．AD∥BC D．∠A=∠C4．一组数据2，x，4，3，3的平均数为3，则中位数为（）A．2 B．2.5 C．4 D．35．下列是勾股数的有( )① 3、4、5；② 5、12 、13；③ 9、40 、41；④ 13、14、15；⑤71017、、；⑥11 、60 、61A．6组B．5组C．4组D．3组6．如图，菱形纸片ABCD，∠A=60°，P为AB中点，折叠菱形纸片ABCD，使点C落在DP 所在的直线上，得到经过点D的折痕DE，则∠DEC等于（）A．60°B．65°C．75°D．80°⊥，垂足为B，且7．如图，数轴上点A对应的数是0，点B对应的数是1，BC ABBC=，以A为圆心，AC为半径画弧，交数轴于点D，则点D表示的数为（）2A．2.2 B．2C．3D．58．如图，把Rt△ABC放在平面直角坐标系内，其中∠CAB＝90°，BC＝13，点A、B的坐标分别为（1，0），（6，0），将△ABC沿x轴向右平移，当点C落在直线y＝2x﹣4上时，线段BC扫过的面积为（）A．84 B．80 C．91 D．78二、填空题9．若二次根式21x 在实数范围内有意义，则x的取值范围是____．10．已知菱形ABCD的两条对角线分别长6和8，则它的面积是_____．11．如图，已知一根长8m的竹竿在离地3m处断裂，竹竿顶部抵着地面，此时，顶部距底部有____m．12．如图，在Rt△ABC中，∠ACB＝90°，D、E、F分别为AB、AC、BC的中点，若CD＝5，则EF＝___．13．已知一次函数y ＝kx ﹣b ，当自变量x 的取值范围是1≤x ≤3时，对应的因变量y 的取值范围是5≤y ≤10，那么k ﹣b 的值为_______．14．如图，在四边形ABCD 中，AB CD ≠，E ，F ，G ，H 分别是AB ，BD ，CD ，AC 的中点，要使四边形EFGH 是菱形，四边形ABCD 还应满足的一个条件是______．15．如图，直线142y x =-+与坐标轴分别交于点A ，B ，点P 是线段AB 上一动点，过点P作PM ⊥x 轴于点M ，作PN ⊥y 轴于点N ，连接MN ，则线段MN 的最小值为_________．16．如图，ABC 的周长为26cm ，中位线3cm EF =，中位线6cm DF =，则中位线DE 的长为______cm ．三、解答题17．计算：（1）（525 （21822+3；（3）（π﹣2021）01112|32|()2-++-+．18．由于大风，山坡上的一颗甲树从A 点处被拦腰折断，其顶点恰好落在一棵树乙的底部C 处，如图所示，已知AB ＝4米，BC ＝13米，两棵树的水平距离是12米，求甲树原来的高度．19．图（a ）、图（b ）是三张形状大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1请在图a ）、图（b ）中，分别画出符合要求的图形，所画图形各顶点必须与方格纸中的小正方形顶点重合具体要求如下：（1）画一个面积为10的等腰直角三角形；（2）画一个面积为12的平行四边形20．如图，在平行四边形ABCD 中，点E 是边AB 的中点，连接CE 并延长CE 交DA 的延长线于点F ，连接AC ，BF ．（1）求证：四边形AFBC 是平行四边形（2）当AEC ∠的度数为______度时，四边形AFBC 是菱形；（3）若52D ∠=︒，则当AEC ∠的度数为______度时，四边形AFBC 是矩形． 21．学习了二次根式的乘除后，老师给同学们出了这样一道题：已知a 3，求221a a -+的值．刘峰想了想，很快就算出来了，下面是他的解题过程：解：∵()()()2221211111aa a aa a a a a a a--+-=== ---，又∵a＝13，∴13a=，∴原式＝3．你认为刘峰的解法对吗？如果对，请你给他一句鼓励的话；如果不对，请找出错误的原因，并改正．22．黄埔区某游泳馆推出以下两种收费方式．方式一：顾客不购买会员卡，每次游泳付费40元．方式二：顾客先购买会员卡，每张会员卡800元，仅限本人一年内使用，凭卡游泳，每次游泳再付费20元．设你在一年内来此游泳馆游泳的次数为x次，选择方式一的总费用为y1（元），选择方式二的总费用为y2（元）．（1）请分别写出y1，y2与x之间的函数表达式；（2）如果你在一年内来此游泳馆游泳的次数超过60次，为省钱，你选择哪种方式？23．社团活动课上，数学兴趣小组的同学探索了这样的一个问题：如图1，，点为边上一定点，点B为边上一动点，以AB为一边在∠MON的内部作正方形ABCD，过点C作，垂足为点F（在点O、之间），交BD与点E，试探究的周长与的长度之间的等量关系该兴趣小组进行了如下探索：（动手操作，归纳发现）（1）通过测量图1、2、3中线段、、EF和的长，他们猜想的周长是长的_____倍．请你完善这个猜想（推理探索，尝试证明）为了探索这个猜想是否成立，他们作了如下思考，请你完成后续探索过程：（2）如图，过点C作，垂足为点G则又四边形ABCD正方形，，则在与中，（类比探究，拓展延伸）（3）如图，当点F在线段的延长线上时，直接写出线段、EF、与长度之间的等量关系为．24．如图①，直线AB与x轴负半轴、y轴正半轴分别交于两点，的长度分别为a和b，且满足.（1）AOB是________三角形.（2）如图②，正比例函数的图象与直线AB交于点Q，过两点分别作于M，于N，若，，求MN的长.（3）如图③，E为AB上一动点，以AE为斜边作等腰直角，P为BE的中点，连，试问：线段是否存在某种确定的数量关系和位置关系？写出你的结论并说明理由.25．如图，在长方形ABCD 中，4AB =，6BC =．延长BC 到点E ，使3CE =，连接DE ．动点P 从点B 出发，沿着BE 以每秒1个单位的速度向终点E 运动，点P 运动的时间为t 秒．（1）DE 的长为；（2）连接AP ，求当t 为何值时，≅ABP DCE ；（3）连接DP ，求当t 为何值时，PDE △是直角三角形；（4）直接写出当t 为何值时，PDE △是等腰三角形．【参考答案】一、选择题 1．D 解析：D 【分析】根据二次根式的定义，被开方数大于等于0进行判断即可得到结果．【详解】解：A 、被开方数不是非负数，没有意义，所以A 不合题意； B 、x ≥2时二次根式有意义，x ＜2时没意义，所以B 不合题意； C 39C 不合题意； D 3D 符合题意；故选：D ．【点睛】本题考查了二次根式的定义，解题的关键是掌握二次根式的定义．2．A解析：A【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形．【详解】解：A、42+62≠82，不符合勾股定理的逆定理，故本选项符合题意；B、32+42=52，符合勾股定理的逆定理，故本选项不符合题意；C、52+122=132，符合勾股定理的逆定理，故本选项不符合题意；D、12+32=2，符合勾股定理的逆定理，故本选项符合题意．故选：A．【点睛】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．3．A解析：A【解析】【分析】根据平行四边形的判定方法，逐项判断即可．【详解】解：A、当AB∥CD，AD=BC时，四边形ABCD可能为等腰梯形，所以不能证明四边形ABCD为平行四边形；B、AB∥CD，AB=DC，一组对边分别平行且相等，可证明四边形ABCD为平行四边形；C、AB∥CD，AD∥BC，两组对边分别平行，可证明四边形ABCD为平行四边形；D、∵AB∥CD，∴∠A+∠D=180°，∵∠A=∠C，∴∠C+∠D=180°，∴AD∥BC，∴四边形ABCD为平行四边形；故选：A．【点睛】本题主要考查平行四边形的判定方法，熟练掌握平行四边形的判定方法是解题的关键．4．D解析：D【解析】【分析】先根据平均数的定义求出x的值，再根据中位数的定义进行解答即可．【详解】解：∵数据2，x，4，3，3的平均数是3，∴（2+x+4+3+3）÷5=3，∴x=3，把这组数据从小到大排列为：2，3，3，3，4，则这组数据的中位数为3；故选D．【点睛】本题主要考查了平均数和中位数，掌握平均数的计算公式和中位数的定义是解题的关键．5．C解析：C【分析】根据勾股定理的逆定理分别进行计算，然后判断即可.【详解】解：①2223+4=5，故3、4、5是勾股数；②2225+12=13，故5、12 、13是勾股数；③2229+40=41，故9、40 、41是勾股数；④222，故13、14、15不是勾股数；13+1415⑤222(7)+(10)=(17)，但71017、、不是整数，故71017、、不是勾股数；⑥22211+60=61，故11 、60 、61是勾股数是勾股数的共4组故选：C【点睛】本题考查了了勾股数，关键是找出数据之间的关系，掌握勾股定理逆定理．6．C解析：C【解析】【分析】连接BD，由菱形的性质及∠A=60°，得到三角形ABD为等边三角形，P为AB的中点，利用三线合一得到DP为角平分线，得到∠ADP=30°，∠ADC=120°，∠C=60°，进而求出∠PDC=90°，由折叠的性质得到∠CDE=∠PDE=45°，利用三角形的内角和定理即可求出所求角的度数．【详解】连接BD，∵四边形ABCD为菱形，∠A=60°，∴△ABD为等边三角形，∠ADC=120°，∠C=60°，∵P为AB的中点，∴DP为∠ADB的平分线，即∠ADP=∠BDP=30°，∴∠PDC=90°，∴由折叠的性质得到∠CDE=∠PDE=45°，在△DEC中，∠DEC=180°-（∠CDE+∠C）=75°．故选C．【点睛】此题考查了翻折变换（折叠问题），菱形的性质，等边三角形的性质，以及内角和定理，熟练掌握折叠的性质是解本题的关键．7．D解析：D【解析】【分析】首先根据勾股定理求出AC的长，再根据同圆的半径相等可知AD＝AC，再根据条件：点A对应的数是原点，可求出D点坐标．【详解】⊥，解：∵BC AB∠＝90︒，∴ABC∴AC=∵以A为圆心，AC为半径画弧，交数轴于点D，∴AD AC==∴点D故选D．【点睛】此题考查实数与数轴，勾股定理，解题关键是利用勾股定理求出AC．8．A解析：A【分析】首先根据题意作出图形，则可得线段BC扫过的面积应为平行四边形BCC′B′的面积，其高是AC的长，底是点C平移的路程．则可由勾股定理求得AC的长，由点与一次函数的关系，求得A′的坐标，即可求得CC′的值，继而求得答案．【详解】解：如下图：∵点A 、B 的坐标分别为（1，0）、（6，0），∴AB ＝5．∵∠CAB ＝90°，BC ＝13，∴AC 22135-12．∴A′C′＝12．∵点C′在直线y ＝2x ﹣4上，∴2x ﹣4＝12，解得：x ＝8．即OA′＝8．∴CC′＝AA′＝OA′﹣OA ＝8﹣1＝7，∴''BCC B S ＝7×12＝84，即线段BC 扫过的面积为84．故选：A ．【点睛】此题考查了一次函数的性质、平移的性质、勾股定理以及平行四边形的性质．能根据性质得出''BCC B 的底'CC 和高'AC 是解决此题的关键.二、填空题9．12x ≥【解析】【分析】根据二次根式有意义的条件可直接进行求解．【详解】 21x -210x -≥，解得：12x ≥；故答案为12x ≥．【点睛】本题主要考查二次根式有意义的条件，熟练掌握二次根式有意义的条件是解题的关键． 10．24【解析】【详解】试题分析：本题直接根据菱形面积等于两条对角线的长度的乘积的一半进行计算．S=6×8÷2=24．考点：菱形的性质．11．A解析：4【解析】【详解】解：解如图所示：在Rt ∆ABC 中，BC=3，AC=5，由勾股定理可得：AB 2+BC 2=AC 2设旗杆顶部距离底部AB=x 米，则有32+x 2=52，解得x=4故答案为：4．【点睛】本题考查勾股定理．12．C解析：5【分析】已知CD 是Rt △ABC 斜边AB 的中线，那么AB =2CD ，EF 是△ABC 的中位线，则EF 应等于AB 的一半．【详解】△ABC 是直角三角形，CD 是斜边的中线，1,222510,CD AB AB CD ∴=∴==⨯= 又EF 是△ABC 的中位线，∴EF =12×10 =5，故答案为：5．【点睛】此题主要考查了三角形中位线定理以及直角三角形斜边上的中线等知识，用到的知识点为：（1）直角三角形斜边的中线等于斜边的一半；（2）三角形的中位线等于对应边的一半，熟练掌握这些定理是解题关键．13．5或10【分析】本题分情况讨论①k ＞0时，x =1时对应y =5；②k ＞0时，x =1时对应y =10．【详解】解：①k ＞0时，由题意得：x =1时，y =5，∴k -b =5；②k ＜0时，由题意得：x =1时，y =10，∴k -b =10；综上，k -b 的值为5或10．故答案为：5或10．【点睛】本题考查了待定系数法求函数解析式，注意本题需分两种情况，不要漏解．14．AD BC =【分析】根据三角形的中位线平行于第三边并且等于第三边的一半可得//EF AD 且12EF AD =，同理可得//GH AD 且12GH AD =，//EH BC 且12EH BC =，然后证明四边形EFGH 是平行四边形，再根据邻边相等的平行四边形是菱形解答．【详解】解：还应满足AD BC =．理由如下：E ，F 分别是AB ，BD 的中点，//EF AD ∴且12EF AD =，同理可得：//GH AD 且12GH AD =，//EH BC 且12EH BC =， //EF GH ∴且EF GH =，∴四边形EFGH 是平行四边形，AD BC =， ∴1122AD BC =，即EF EH =，EFGH ∴是菱形．故答案是：AD BC =．【点睛】本题考查了中点四边形，其中涉及到了菱形的判定，平行四边形的判定，三角形的中位线定理，根据三角形的中位线平行于第三边并且等于第三边的一半得到四边形EFGH 的对边平行且相等从而判定出平行四边形是解题的关键，也是本题的突破口．15．【分析】如图，连接，依题意，四边形是矩形，则，当时，最小，底面积法求得即可．【详解】如图，连接，PM ⊥x 轴，PN ⊥y 轴，四边形是矩形，，当时，最小，直线与坐标轴分别交于点A ，B ，解析：855【分析】如图，连接OP ，依题意，四边形OMPN 是矩形，则OP MN =，当OP AB ⊥时，OP 最小，底面积法求得OP 即可．【详解】如图，连接OP ，PM ⊥x 轴，PN ⊥y 轴，90AOB ∠=︒∴四边形OMPN 是矩形，∴OP MN =，∴当OP AB ⊥时，OP 最小，直线142y x =-+与坐标轴分别交于点A ，B ，令0,4x y ==，)4(0,A ∴令0,8y x ==，(0,8)B ∴4,8OA OB ∴==，22224845AB OA OB ∴=++=当OP AB ⊥时，1122ABC S OA OB OP AB =⨯=⨯△，85545OA OB OP AB ⨯∴===∴MN OP ==85．85．【点睛】本题考查了矩形的性质，勾股定理，垂线段最短，找到MN OP =是解题的关键．16．4【分析】根据三角形中位线定理分别求出BC、AB，根据三角形的周长公式求出AC，根据三角形中位线定理计算即可．【详解】解：∵中位线EF=3cm，中位线DF=6cm，∴BC=6cm，AB=解析：4【分析】根据三角形中位线定理分别求出BC、AB，根据三角形的周长公式求出AC，根据三角形中位线定理计算即可．【详解】解：∵中位线EF=3cm，中位线DF=6cm，∴BC=6cm，AB=12cm，∵△ABC的周长26cm，∴AC=8cm，∴中位线DE的长为4cm，故答案为：4．【点睛】本题主要考查的是三角形中位线定理的应用，掌握三角形的中位线平行于第三边，且等于第三边的一半是解题的关键．三、解答题17．（1）﹣1；（2）1；（3）5+【分析】（1）利用平方差公式计算即可；（2）先化简二次根式，再计算分子上的加法，继而计算除法，最后计算减法即可；（3）先计算零指数幂、负整数指数幂、化简二次根解析：（1）﹣1；（2）1；（3）【分析】（1）利用平方差公式计算即可；（2）先化简二次根式，再计算分子上的加法，继而计算除法，最后计算减法即可；（3）先计算零指数幂、负整数指数幂、化简二次根式，去绝对值符号，再计算加减即可．【详解】解：（1）原式＝222＝4﹣5＝﹣1；（2）原式＝3222+﹣3 ＝422﹣3 ＝4﹣3＝1；（3）原式＝1+23+2﹣3+2＝5+3．【点睛】本题考查实数的混合运算．主要考查二次根式的混合运算，零指数幂和负整数指数幂，平方差公式，化简绝对值等．掌握相关法则，能分别化简是解题关键．18．19米【分析】如图所示，过点C 作CD ⊥AB 交AB 延长线于D ，则根据题意可以得到CD=12米，根据勾股定理即可求出BD 的长，再利用勾股定理求出AC 的长即可得到AC+AB 的长.【详解】解：如图所解析：19米【分析】如图所示，过点C 作CD ⊥AB 交AB 延长线于D ，则根据题意可以得到CD =12米，根据勾股定理即可求出BD 的长，再利用勾股定理求出AC 的长即可得到AC +AB 的长.【详解】解：如图所示，过点C 作CD ⊥AB 交AB 延长线于D由题意得：CD =12，AB ＝4米，BC ＝13米在Rt △BCD 中222213125BD BC CD =-=-=米∴9AD AB BD =+=米在Rt △ACD 中222212915AC CD AD =+=+=米∴19AC AB +=米∴甲树原来的高度是19米.【点睛】本题主要考查了勾股定理的应用，解题的关键在于能够熟练掌握勾股定理.19．（1）见解析；（2）见解析【解析】【分析】（1）根据等腰直角三角形的性质求出边长分别为、、，再网格中找到相应的格点，作图即可；（2）根据平行四边形的面积为12，确定底边长为4、高为3，在网格解析：（1）见解析；（2）见解析【解析】【分析】（1）根据等腰直角三角形的性质求出边长分别为25、25、210，再网格中找到相应的格点，作图即可；（2）根据平行四边形的面积为12，确定底边长为4、高为3，在网格中找到相应的格点，作图即可．【详解】解：（1）根据等腰直角三角形的面积为为10，设两个直角边为x ，则21102x = 解得25x =，由勾股定理得，斜边长为22(25)(25)210+=222524=+，在网格中找到到相应的格点使得两条直角边为25，连线即可，其中25是以2，4为直角边的直角三角形的斜边，如图（a ）（2）根据平行四边形的面积为12，可以作底边长为4、高为3的平行四边形，在图中选取相应的格点，使得平行四边形的边长为为4、高为3，如图（b ）【点睛】此题考查了等腰直角三角形的性质，勾股定理，平行四边形的性质，熟练掌握相关基本性质是解题的关键．20．（1）见解析；（2）90；（3）104【分析】（1）根据题意，可以先证明和全等，然后即可得到，然后对角线互相平分的四边形是平行四边形可以证明结论成立；（2）根据菱形的性质，可以得到的度数；（解析：（1）见解析；（2）90；（3）104【分析】（1）根据题意，可以先证明AEF ∆和BEC ∆全等，然后即可得到EC EF =，然后对角线互相平分的四边形是平行四边形可以证明结论成立；（2）根据菱形的性质，可以得到AEC ∠的度数；（3）根据矩形的性质，可以得到AEC ∠的度数．【详解】（1）证明：四边形ABCD 是平行四边形，//DA CB ∴，EAF EBC ∴∠=∠，点E 是边AB 的中点，AE BE ∴=，在AEF ∆和BEC ∆中，EAF ECB AE BE AEF BEC ∠=∠⎧⎪=⎨⎪∠=∠⎩， ()AEF BEC ASA ∴∆≅∆，EF EC ∴=，又AE BE =，∴四边形AFBC 是平行四边形；（2）当AEC ∠的度数为90︒时，四边形AFBC 是菱形，理由：四边形AFBC 是菱形，AB CF ∴⊥，90AEC ∴∠=︒，故答案为：90；（3）当AEC ∠的度数为104度时，四边形AFBC 是矩形，理由：四边形AFBC 是矩形，AB CF ∴=，EC EB ∴=，ECB EBC ∴∠=∠，四边形ABCD 是平行四边形，52D ∠=︒，52D EBC ∴∠=∠=︒，52ECB ∴∠=︒，5252104AEC ECB EBC ∴∠=∠+∠=︒+︒=︒，故答案为：104．【点睛】本题考查了平行四边形的判定与性质、全等三角形的判定与性质、矩形的性质、菱形的性质，解题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．21．答案见解析.【解析】【分析】直接利用二次根式的性质化简进而得出答案．【详解】刘峰的解法错误，原因是：错误地运用了＝这个公式，正确解法是：∵a＝＝＜1，∴a﹣1＜0，∴＝＝＝＝解析：答案见解析.【解析】【分析】直接利用二次根式的性质化简进而得出答案．【详解】刘峰的解法错误，(0)(0)a aa a⎧⎨-<⎩这个公式，正确解法是：∵a1，∴a﹣1＜0，∴＝|1|(1)aa a--＝1(1)aa a--＝﹣1a，∴【点睛】此题主要考查了二次根式的性质与化简，正确化简二次根式是解题关键．22．（1）y1=40x，y2=20x+800；（2）在一年内来此游泳馆游泳的次数超过60次，为省钱，应选择方式二【分析】（1）根据题意可以写出y1，y2与x之间的函数表达式；（2）将x=15代入（解析：（1）y1=40x，y2=20x+800；（2）在一年内来此游泳馆游泳的次数超过60次，为省钱，应选择方式二【分析】（1）根据题意可以写出y1，y2与x之间的函数表达式；（2）将x=15代入（1）中函数关系式，求出相应的函数值，然后比较大小即可解答本题．【详解】解：（1）当游泳次数为x时，方式一费用为：y1=40x，方式二的费用为：y2=20x+800；（2）若一年内来此游泳馆游泳的次数为60次，方式一的费用为：y1=40×60=2400（元），方式二的费用为：y2=20×60+800=2000（元），∵2400＞2000，∴在一年内来此游泳馆游泳的次数超过60次，为省钱，应选择方式二．【点睛】本题考查一次函数的应用，解答本题的关键是明确题意，求出y1，y2与x之间的函数表达式，利用一次函数的性质解答．23．（1）2；（2）证明见解析过程；（3）AE+EF-AF=2OA．【分析】（1）通过测量可得；（2）过点C作CG⊥ON，垂足为点G，由AAS可证△ABO≌△BCG，可得BG=AO，BO=CG，由解析：（1）2；（2）证明见解析过程；（3）AE+EF-AF=2OA．【分析】（1）通过测量可得；（2）过点C作CG⊥ON，垂足为点G，由AAS可证△ABO≌△BCG，可得BG=AO，BO=CG，由SAS可证△ABE≌△CBE，可得AE=CE，由线段的和差关系可得结论；（3）过点C作CG⊥ON，垂足为点G，由AAS可证△ABO≌△BCG，可得BG=AO，BO=CG，由SAS可证△ABE≌△CBE，可得AE=CE，可得结论．【详解】解：（1）△AEF的周长是OA长的2倍，故答案为：2；（2）如图4，过点C作CG⊥ON，垂足为点G，则∠CGB=90°，∴∠GCB+∠CBG=90°，又∵四边形ABCD是正方形，∴AB=BC，∠ABC=90°，∠DBC=∠DBA=45°，则∠CBG+∠ABO=90°，∴∠GCB=∠ABO，在△BCG与△ABO中，，∴△BCG≌△ABO（AAS），∴BG=AO，CG=BO，∵∠AOB=90°=∠CGB=∠CFO，∴四边形CGOF是矩形，∴CF=GO，CG=OF=OB，在△ABE和△CBE中，，∴△ABE≌△CBE（SAS），∴AE=CE，∴△AEF的周长=AE+EF+AF=CE+EF+AF=CF+AF=GO+AF=BG+BO+AF=2AO；（3）如图5，过点C作CG⊥ON于点G，则∠CGB=90°，∴∠GCB+∠CBG=90°，又∵四边形ABCD是正方形，∴AB=BC，∠ABC=90°，∠DBC=∠DBA=45°，则∠CBG+∠ABO=90°，∴∠GCB=∠ABO，在△BCG与△ABO中，∴△BCG≌△ABO（AAS），∴BG=AO，BO=CG，∵∠AOB=90°=∠CGB=∠CFO，∴四边形CGOF是矩形，∴CF=GO，CG=OF=OB，在△ABE和△CBE中，，∴△ABE≌△CBE（SAS），∴AE=CE，∴AE+EF-AF=EF+CE-AF=NB+BO-（OF-AO）=OA+OB-（OB-OA）=2OA．【点睛】本题是四边形综合题，考查了全等三角形的判定和性质，正方形的性质，矩形的判定和性质，添加恰当的辅助线构造全等三角形是本题的关键．24．（1）等腰直角；（2）6；（3）PO=PD且PO⊥PD.理由见解析.【解析】【分析】（1）已知a2-2ab+b2=0，化简可得a=b，然后可得△AOB为等腰直角三角形；（2）证明△MAO≌△解析：（1）等腰直角；（2）6；（3）PO=PD且PO⊥PD.理由见解析.【解析】【分析】（1）已知a2-2ab+b2=0，化简可得a=b，然后可得△AOB为等腰直角三角形；（2）证明△MAO≌△NOB，得出AM=ON，然后求出MN的值；（3）根据已知E为中点，联想到延长DP到点C，使DP=PC，再连接OD、OC、BC，先证明△DEP≌△CBP得到边角的等量关系，再证明△OAD≌△OBC，最后可得出△DOC为等腰直角三角形，从而得出结论．【详解】解：（1）∵a2-2ab+b2=0，∴（a-b）2=0，∴a=b，∵∠AOB=90°，∴△AOB为等腰直角三角形.故答案为：等腰直角；（2）∵∠MOA+∠MAO=90°，∠MOA+∠MOB=90°，∴∠MAO=∠MOB，∵AM⊥OQ，BN⊥OQ，∴∠AMO=∠BNO=90°，在△MAO和△BON中，，∴△MAO≌△NOB（AAS），∴AM=ON，∴MN=ON-OM=AM-OM=6；（3）PO=PD且PO⊥PD.理由如下：如图，延长DP到点C，使DP=PC，连接OD、OC、BC，在△DEP和△CBP，，∴△DEP≌△CBP（SAS），∴CB=DE=DA，∠DEP=∠CBP=135°，则∠CBO=∠CBP-∠ABO=135°-45°=90°，又∵∠BAO=45°，∠DAE=45°，∴∠DAO=90°，在△OAD 和△OBC ，，∴△OAD ≌△OBC(SAS)，∴OD=OC ，∠AOD=∠COB ，∴∠COD=∠AOB=90°，∴△DOC 为等腰直角三角形，∴PO=PD ，且PO ⊥PD ．【点睛】本题重点考查的是全等三角形的判定与性质，等腰三角形的判定与性质以及一次函数的相关知识，根据已知条件构造出全等三角形是解题的关键，难度较大．25．（1）5；（2）秒时，ΔABP ≅ΔDCE ；（3）当秒或秒时，ΔPDE 是直角三角形；（4）当秒或秒或秒时，ΔPDE 为等腰三角形．【分析】（1）根据长方形的性质及勾股定理直接求解即可；（2）根据全解析：（1）5；（2）3t =秒时，；（3）当23t =秒或6t =秒时，是直角三角形；（4）当3t =秒或4t =秒或296t =秒时，为等腰三角形．【分析】（1）根据长方形的性质及勾股定理直接求解即可；（2）根据全等三角形的性质可得：3BP CE ==，即可求出时间t ；（3）分两种情况讨论：①当90PDE ∠=︒时，在两个直角三角形中运用两次勾股定理，然后建立等量关系求解即可；②当90DPE ∠=︒时，此时点P 与点C 重合，得出BP BC =，即可计算t 的值；（4）分三种情况讨论：①当PD DE =时，②当PE DE =时，③当PD PE =时，分别结合图形，利用各边之间的关系及勾股定理求解即可得．【详解】解：（1）∵四边形ABCD 为长方形，∴4AB CD ==，CD BC ⊥，在中， 221695DE DC CE =+=+=，故答案为：5；（2）如图所示：当点P 到如图所示位置时，，∵4AB CD ==，3CE =， ∴，仅有如图所示一种情况，此时，3BP CE ==， ∴31BP t ==， ∴3t =秒时，；（3）①当90PDE ∠=︒时，如图所示：在中， 222PD PE DE =-，在中， 222PD PC DC =+，∴2222PE DE PC DC -=+，9PE t =-，6PC t =-，∴()()22229564t t --=-+，解得：23t =； ②当90DPE ∠=︒时，此时点P 与点C 重合，∴BP BC =，∴6t =；综上可得：当23t =秒或6t =秒时，是直角三角形；（4）若为等腰三角形，分三种情况讨论：①当PD DE =时，如图所示：∵PD DE =，DC BE ⊥，∴3PC CE ==，∴3BP BC PC =-=， ∴31BP t ==； ②当5PE DE ==时，如图所示：954BP BE PE =-=-=，∴41BP t ==； ③当PD PE =时，如图所示：3PE PC CE PC =+=+，∴3PD PE PC ==+，在中，222PD CD PC =+，即()22234PC PC +=+，解得：76PC =，296BP BC PC =-=， ∴2916BP t ==；综上可得：当3t =秒或4t =秒或296t =秒时，为等腰三角形．【点睛】题目主要考查勾股定理解三角形，等腰三角形的性质，全等三角形的性质等，理解题意，分类讨论作出相应图形是解题关键．。

人教版八年级下册地理期末复习综合测试卷1(Word版,含答案)

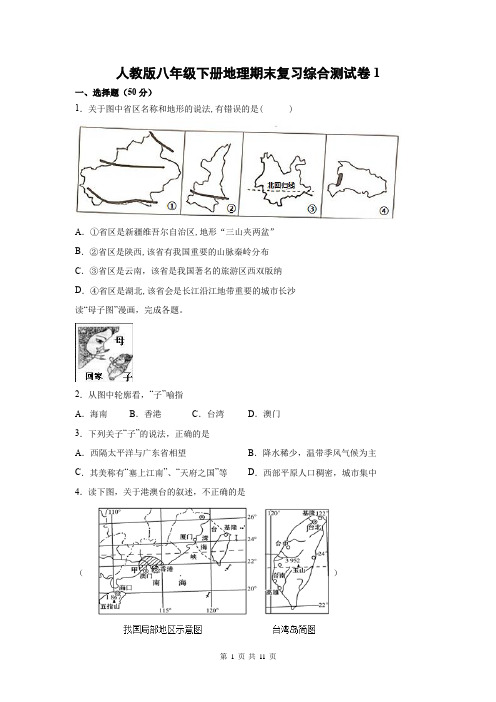
人教版八年级下册地理期末复习综合测试卷1一、选择题（50分）1．关于图中省区名称和地形的说法,有错误的是( )A．①省区是新疆维吾尔自治区,地形“三山夹两盆”B．②省区是陕西,该省有我国重要的山脉秦岭分布C．③省区是云南，该省是我国著名的旅游区西双版纳D．④省区是湖北,该省会是长江沿江地带重要的城市长沙读“母子图”漫画，完成各题。

2．从图中轮廓看，“子”喻指A．海南B．香港C．台湾D．澳门3．下列关子“子”的说法，正确的是A．西隔太平洋与广东省相望B．降水稀少，温带季风气候为主C．其美称有“塞上江南”、“天府之国”等D．西部平原人口稠密，城市集中4．读下图，关于港澳台的叙述，不正确的是（）A．香港、澳门和台湾都濒临南海B．港澳和台湾形成了“前店后厂”的经营模式C．香港有“东方之珠”的美誉，澳门的支柱产业是博彩旅游业D．台湾岛的地势特征是中部高四周低我国疆域辽阔，不同地区的地理环境差异很大，各地人民的生产与生活习俗也有较大的差别。

读我国四大地理区域图，完成下列各题。

5．关于图中四大地理区域的叙述，正确的是( )A．我国种植业主要分布在甲地区和乙地区B．甲地区每年都举办那达慕大会C．制约丙地区农业生产的主要因素是水源D．丁地区煤铁资源丰富，有我国最大的综合性工业基地6．秦岭—淮河一线作为乙、丁两地区分界线，南北两侧的水热条件、农作物分布和耕作制度明显不同。

某学校地理课外小组利用歌谣总结该线南北两侧地理事物特点，下面歌谣说法不正确的是( )A．秦淮线以南，耕地多水田；年熟一或二，水稻为重点。

B．秦岭淮河线，南北农特点；以北为旱地，多用水灌溉。

C．湿润半湿润，八百等降线；亚热暖温带，一月零度线。

D．南河流量大，水位变化显；沙少汛期长，冬季无冰现。

7．北方地区地形A．以盆地和高原为主B．以平原和高原为主C．以山地丘陵为主D．以山地和高原为主读“西北地区简图”,完成下面小题。

8．西北地区植被景观自东向西变化的主要影响因素是( )A．地形因素B．纬度因素C．海陆因素D．人类活动9．西北地区生态环境脆弱,以下开发与保护措施不当的是 ( )A．合理发展畜牧业B．大力发展种植业C．适度发展旅游业D．防治土地荒漠化西成高铁（西安—成都）是我国首次建成的山区高标准现代化铁路。

期末达标测试卷(B卷) 2022-2023学年统编版语文八年级下册(word版含答案)

2022-2023学年人教部编版八年级下学期语文期末达标测试卷（B卷）试卷满分120分，考试时间120分钟一、积累与运用（31分）1.下列加粗字的注音不完全正确的一项是（）（2分）A.轻盈（yíng）矗立（chù）翡翠（fěi）B.眺望（tiào）犹豫（yù）苍劲（jìn）C.闸门（zhá）砚池（yàn）擦拭（shì）D.硕大（shuò）喧哗（xuān）驿道（yì）2.下列句中加粗词语使用不正确的一项是（）（2分）A.红军曾在我们村安营扎寨。

B.人们正在散步时，突然天降大雨，真是大煞风景。

C.儿童时代的事至今仍历历在目，使我回味无穷。

D.这些人对个人利益斤斤计较，而对广大群众的疾苦却漫不经心。

3.下列句子中标点符号使用不正确的一项是（）（2分）A.李白的“浮云游子意，落日故人情”（《送友人》）、“朝如青丝暮成雪”（《将进酒》）都是脍炙人口的名句。

B.不知不觉，三年的高中生活转瞬即逝。

李萍上了大学，张华当TIA，我进了部队：我们都有美好的前途。

C.材料是文章的血肉，结构是文章的骨骼。

骨骼完整匀称，人才能身姿挺拔；结构井然有序，文章才就立得起来。

D.据王璨的《英雄记抄》说，诸葛亮与徐庶、石广元、孟公威等人一道游学读书，“三人务于精熟，而亮独观其大略。

”4.下列关于文学常识表述，有误的一项是（）（2分）A.顾拜旦是法国教育家、社会活动家，现代奥林匹克运动的创始人，他终生倡导奥林匹克精神，被誉为“现代奥林匹克之父”。

B.《在长江源头各拉丹冬》是美国著名作家马克·吐温创作的一篇游记，这篇文章以散文笔法，叙述奇人奇事、惊险的旅途、怪异的车夫，富有传奇色彩。

C.《礼记》又名《小戴礼记》，相传是西汉经学家戴圣编纂的，是中国古代重要的典章制度选集，是一部儒家思想的资料汇编。

D.《卖炭翁》的作者是唐代诗人白居易，通过卖炭翁的遭遇，深刻地揭露了“宫市”的腐败本质，表达了作者对下层劳动人民的深切同情。

八年级数学上册期末试卷综合测试(Word版含答案)

八年级数学上册期末试卷综合测试（Word 版含答案）一、八年级数学全等三角形解答题压轴题（难）1．取一副三角板按图()1拼接，固定三角板60,()30ADC D ACD ∠=∠=，将三角板45()ABC BAC BCA ∠=∠=绕点A 依顺时针方向旋转一个大小为a 的角00)45(a ≤≤得到ABM ，图()2所示．试问：()1当a 为多少时，能使得图()2中//AB CD ？说出理由，()2连接BD ，假设AM 与CD 交于,E BM 与CD 交于F ，当00)45(a ≤≤时，探索DBM CAM BDC ∠+∠+∠值的大小变化情况，并给出你的证明．【答案】（1）15°；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105，证明见解析．【解析】【分析】（1）由//AB CD 得到30BAC C ∠=∠=，即可求出a ；（2）DBM CAM BDC ∠+∠+∠的大小不变，是105︒,由FEM CAM C ∠=∠+∠，30C ∠=︒， EFM BDC DBM ∠=∠+∠， 45M ∠=︒，即可利用三角形内角和求出答案.【详解】()1当a 为15时，//AB CD ，理由：由图()2，若//AB CD ，则30BAC C ∠=∠=， 453015a CAM BAM BAC ∴=∠=∠-∠=-︒=︒，所以，当a 为15时，//AB CD ．注意：学生可能会出现两种解法：第一种：把//AB CD 当做条件求出a 为15，第二种：把a 为15当做条件证出//AB CD ，这两种解法都是正确的．()2DBM CAM BDC ∠+∠+∠的大小不变，是105︒证明： ,30FEM CAM C C ∠=∠+∠∠=︒,30FEM CAM ∴∠=∠+︒,EFM BDC DBM ∠=∠+∠, DBM CAM BDC EFM CAM ∴∠+∠+∠=∠+∠,180,45EFM FEM M M ∠+∠+∠=∠=︒,3045180BDC DBM CAM ∴∠+∠+∠+︒+︒=︒,1803045105DBM CAM BDC ∴∠+∠+∠=︒--=︒,所以，DBM CAM BDC ∠+∠+∠的大小不变，是105.【点睛】此题考查旋转的性质，平行线的性质，三角形的外角定理，三角形的内角和，（2）中将角度和表示为三角形的外角是解题的关键.2．(1)如图1：在四边形ABCD 中，AB =AD ，∠BAD =120°，∠B =∠ADC =90°．E ，F 分别是BC ，CD 上的点．且∠EAF =60°．探究图中线段EF ，BE ，FD 之间的数量关系．小明同学探究的方法是：延长FD 到点G ．使DG =BE ．连结AG ，先证明△ABE ≌△ADG ，再证明△AEF ≌△AGF ，可得出结论，他的结论是（直接写结论，不需证明）；(2)如图2，若在四边形ABCD 中，AB =AD ，∠B +∠D =180°，E 、F 分别是BC ，CD 上的点，且∠EAF 是∠BAD 的二分之一，上述结论是否仍然成立，并说明理由．(3)如图3，四边形ABCD 是边长为5的正方形，∠EBF =45°，直接写出三角形DEF 的周长．【答案】（1）EF=BE+DF．（2）成立，理由见解析；（3）10.【解析】【分析】（1）如图1，延长FD到G，使得DG=DC,先证△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，进一步根据题意得∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.(2)如图2，延长FD到点G．使DG=BE．连结AG，证得△ABE≌△ADG，得到AE=AG，∠BAE=∠DAG，再结合题意得到∠EAF=∠GAF，再证明△AEF≌△AGF，得到EF=FG，最后运用线段的和差证明即可.（3）如图3，延长DC到点G，截取CG=AE，连接BG，先证△AEB≌△CGB，得到BE=BG，∠ABE=∠CBG，结合已知条件得∴∠CBF+∠CBG=45°，再证明△EBF≌△GBF，得到EF=FG，最后求三角形的周长即可.【详解】解答：（1）解：如图1，延长FD到G，使得DG=DC在△ABE和△ADG中，∵DC DGB ADG AB AD=⎧⎪∠=∠⎨⎪=⎩∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵EAF GAFAF AF⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；故答案为：EF=BE+DF．（2）解：结论EF=BE+DF仍然成立；理由：如图2，延长FD到点G．使DG=BE．连结AG在△ABE和△ADG中，∵DG BEB ADGAB AD=⎧⎪∠=∠⎨⎪=⎩，∴△ABE≌△ADG（SAS），∴AE=AG，∠BAE=∠DAG，∵∠EAF=12∠BAD，∴∠GAF=∠DAG+∠DAF=∠BAE+∠DAF=∠BAD-∠EAF=∠EAF，∴∠EAF=∠GAF，在△AEF和△GAF中，∵AE AGEAF GAFAF AF=⎧⎪∠=∠⎨⎪=⎩，∴△AEF≌△AGF（SAS），∴EF=FG，∵FG=DG+DF=BE+DF，∴EF=BE+DF；（3）解：如图3，延长DC到点G，截取CG=AE，连接BG，在△AEB与△CGB中，∵A BOG AF BF ⎪∠=∠⎨⎪=⎩，∴△AEB ≌△CGB （SAS ），∴BE =BG ，∠ABE =∠CBG ．∵∠EBF =45°，∠ABC =90°，∴∠ABE +∠CBF =45°，∴∠CBF +∠CBG =45°．在△EBF 与△GBF 中，∵BE BG EBF GBF BF BF =⎧⎪∠=∠⎨⎪=⎩，∴△EBF ≌△GBF （SAS ），∴EF =GF ，∴△DEF 的周长=EF +ED +CF =AE +CF +DE +DF =AD +CD =10．【点睛】本题主要考查了三角形全等的判定和性质，灵活运用全等三角形的性质和判定是解答本题的关键.但本题分为三问，难度不断增加，对提升思维能力大有好处.3．如图，△ABC 中，D 是BC 的中点，过D 点的直线GF 交AC 于F ，交AC 的平行线BG 于G 点，DE ⊥DF ，交AB 于点E ，连结EG、EF ．（1）求证：BG ＝CF ；（2）请你判断BE +CF 与EF 的大小关系，并说明理由．【答案】（1）详见解析；（2）BE +CF ＞EF ，证明详见解析【分析】（1）先利用ASA判定△BGD≅CFD，从而得出BG=CF；（2）利用全等的性质可得GD=FD，再有DE⊥GF，从而得到EG=EF，两边之和大于第三边从而得出BE+CF＞EF．【详解】解：（1）∵BG∥AC，∴∠DBG＝∠DCF．∵D为BC的中点，∴BD＝CD又∵∠BDG＝∠CDF，在△BGD与△CFD中，∵DBG DCFBD CDBDG CDF∠=∠⎧⎪=⎨⎪∠=∠⎩∴△BGD≌△CFD（ASA）．∴BG＝CF．（2）BE+CF＞EF．∵△BGD≌△CFD，∴GD＝FD，BG＝CF．又∵DE⊥FG，∴EG＝EF（垂直平分线到线段端点的距离相等）．∴在△EBG中，BE+BG＞EG，即BE+CF＞EF．【点睛】本题考查了三角形全等的判定和性质，要注意判定三角形全等的一般方法有：SSS、SAS、AAS、ASA、HL．4．如图1，在ABC∆中，ACB∠是直角，60B∠=︒，AD、CE分别是BAC∠、BCA∠的平分线，AD、CE相交于点F．（1）求出AFC∠的度数；（2）判断FE与FD之间的数量关系并说明理由．（提示：在AC上截取CG CD=，连（3）如图2，在△ABC∆中，如果ACB∠不是直角，而（1）中的其它条件不变，试判断线段AE、CD与AC之间的数量关系并说明理由．【答案】（1）∠AFC＝120°；（2）FE与FD之间的数量关系为：DF＝EF．理由见解析；（3）AC＝AE+CD．理由见解析．【解析】【分析】（1）根据三角形的内角和性质只要求出∠FAC，∠ACF即可解决问题;（2）根据在图2的 AC上截取CG=CD，证得△CFG≌△CFD (SAS),得出DF= GF；再根据ASA 证明△AFG≌△AFE，得EF=FG，故得出EF=FD；（3）根据(2) 的证明方法，在图3的AC上截取AG=AE，证得△EAF≌△GAF (SAS)得出∠EFA=∠GFA；再根据ASA证明△FDC≌△FGC，得CD=CG即可解决问题．【详解】（1）解：∵∠ACB＝90°，∠B＝60°，∴∠BAC＝90°﹣60°＝30°，∵AD、CE分别是∠BAC、∠BCA的平分线，∴∠FAC＝15°，∠FCA＝45°，∴∠AFC＝180°﹣（∠FAC+∠ACF）＝120°（2）解：FE与FD之间的数量关系为：DF＝EF．理由：如图2，在AC上截取CG＝CD，∵CE是∠BCA的平分线，∴∠DCF＝∠GCF，在△CFG和△CFD中，CG CDDCF GCFCF CF=⎧⎪∠=∠⎨⎪=⎩，∴△CFG≌△CFD（SAS），∴DF＝GF．∠CFD＝∠CFG由（1）∠AFC＝120°得，∴∠CFD＝∠CFG＝∠AFE＝60°，∴∠AFG＝60°，又∵∠AFE＝∠CFD＝60°，∴∠AFE＝∠AFG，在△AFG和△AFE中，AFE AFGAF AFEAF GAF∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△AFG≌△AFE（ASA），∴EF＝GF，∴DF＝EF；（3）结论：AC＝AE+CD．理由：如图3，在AC上截取AG＝AE，同（2）可得，△EAF≌△GAF（SAS），∴∠EFA＝∠GFA，AG＝AE∵∠BAC+∠BCA=180°-∠B=180°-60°=120°∴∠AFC＝180°﹣(∠FAC+∠FCA)＝180°-12(∠BAC+∠BCA)=180°-12×120°=120°，∴∠EFA＝∠GFA＝180°﹣120°＝60°＝∠DFC，∴∠CFG＝∠CFD＝60°，同（2）可得，△FDC≌△FGC（ASA），∴CD＝CG，∴AC＝AG+CG＝AE+CD．【点睛】本题考查了全等三角形的判定和性质的运用，全等三角形的判定和性质是证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造全等三角形．5．如图，Rt△ABC≌Rt△CED（∠ACB＝∠CDE＝90°），点D在BC上，AB与CE相交于点F(1) 如图1，直接写出AB与CE的位置关系(2) 如图2，连接AD交CE于点G，在BC的延长线上截取CH＝DB，射线HG交AB于K，求证：HK＝BK【答案】（1）AB ⊥CE ；（2）见解析.【解析】【分析】（1）由全等可得∠ECD=∠A ，再由∠B+∠A=90°，可得∠B+ECD=90°，则AB ⊥CE. （2）延长HK 于DE 交于H ，易得△ACD 为等腰直角三角形，∠ADC=45°，易得DH=DE ，然后证明△DGH ≌△DGE ，所以∠H=∠E ，则∠H=∠B ，可得HK=BK.【详解】解：（1）∵Rt △ABC ≌Rt △CED ，∴∠ECD=∠A ，∠B=∠E ，BC=DE ，AC=CD∵∠B+∠A=90°∴∠B+ECD=90°∴∠BFC=90°，∴AB ⊥CE（2）在Rt △ACD 中，AC=CD ，∴∠ADC=45°，又∵∠CDE=90°，∴∠HDG=∠CDG=45°∵CH ＝DB ，∴CH+CD=DB+CD ，即HD=BC ，∴DH=DE ，在△DGH 和△DGE 中，DH=DE HDG=EDG=45DG=DG ⎧⎪∠∠⎨⎪⎩∴△DGH ≌△DGE （SAS ）∴∠H=∠E又∵∠B=∠E∴∠H=∠B ，∴HK=BK【点睛】本题考查全等三角形的判定与性质，利用全等找出角相等，再利用等角对等边判定线段相等是本题的关键.6．如图（1），在ABC 中，90A ∠=︒，AB AC =，点D 是斜边BC 的中点，点E ，F 分别在线段AB ，AC 上，且90EDF ∠=︒．（1）求证：DEF为等腰直角三角形；（2）若ABC的面积为7，求四边形AEDF的面积；（3）如图（2），如果点E运动到AB的延长线上时，点F在射线CA上且保持∠=︒，DEF还是等腰直角三角形吗．请说明理由．90EDF【答案】（1）证明见解析；（2）3.5；（3）是，理由见解析．【解析】【分析】（1）由题意连接AD，并利用全等三角形的判定判定△BDE≌△ADF(ASA)，进而分析证得DEF为等腰直角三角形；（2）由题意分析可得S四边形AEDF=S∆ADF+S∆ADE=S∆BDE+S∆CDF，以此进行分析计算求出四边形AEDF的面积即可；（3）根据题意连接AD，运用全等三角形的判定判定△BDE≌△ADF(ASA)，进而分析证得DEF为等腰直角三角形.【详解】解：（1）证明：如图①，连接AD.∵∠BAC=90˚,AB=AC,点D是斜边BC的中点，∴AD⊥BC，AD=BD，∴∠1=∠B=45°，∵∠EDF=90°，∠2+∠3=90°，又∵∠3+∠4=90°，∴∠2=∠4，在△BDE 和△ADF中，∠1=∠B，AD=BD,∠2=∠4，∴△BDE≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°，∴ΔDEF为等腰直角三角形.（2）由（1）可知DE=DF，∠C=∠6=45°，又∵∠2+∠3=90°，∠2+∠5=90°，∴∠3=∠5，∴△ADE ≌△CDF ，∴S 四边形AEDF =S ∆ADF +S ∆ADE =S ∆BDE +S ∆CDF ，∴ S ∆ABC =2 S 四边形AEDF ,∴S 四边形AEDF =3.5 .（3）是.如图②，连接AD.∵∠BAC=90°，AB=AC ，D 是斜边BC 的中点，∴AD ⊥BC,AD=BD ，∴∠1=45°，∵∠DAF=180°-∠1=180°—45°=135°，∠DBE=180°-∠ABC=180°-45°=135°，∴∠DAF=∠DBE ，∵∠EDF=90°，∴∠3+∠4=90°，又∵∠2+∠3=90°，∴∠2=∠4,在△BDE 和△ADF 中，∠DAF=∠DBE ，AD=BD,∠2=∠4,∴△BDE ≌△ADF(ASA),∴DE=DF,又∵∠EDF=90°， ∴△DEF 为等腰直角三角形.【点睛】本题考查等腰直角三角形的性质以及全等三角形的判定与性质，根据题意作辅助线构造出全等三角形是解题的关键．7．如图，在ABC ∆中，903, 7C AC BC ∠=︒==，，点D 是BC 边上的动点，连接AD ，以AD 为斜边在AD 的下方作等腰直角三角形ADE ．（1）填空：ABC ∆的面积等于；（2）连接CE ，求证：CE 是ACB ∠的平分线；（3）点O 在BC 边上，且1CO =，当D 从点O 出发运动至点B 停止时，求点E 相应的运动路程．【答案】（1）212；（2）证明见解析；（3）32【解析】【分析】（1）根据直角三角形的面积计算公式直接计算可得；（2）如图所示作出辅助线，证明△AEM ≌△DEN （AAS ），得到ME=NE ，即可利用角平分线的判定证明；（3）由（2）可知点E 在∠ACB 的平分线上，当点D 向点B 运动时，点E 的路径为一条直线，再根据全等三角形的性质得出CN=1()2AC CD +，根据CD 的长度计算出CE 的长度即可．【详解】解：（1）903, 7C AC BC ∠=︒==， ∴112137222ABC S AC BC =⨯=⨯⨯=，故答案为：212 （2）连接CE ，过点E 作EM ⊥AC 于点M ，作EN ⊥BC 于点N ，∴∠EMA=∠END=90°，又∵∠ACB=90°，∴∠MEN=90°，∴∠MED+∠DEN=90°，∵△ADE 是等腰直角三角形∴∠AED=90°，AE=DE∴∠AEM+∠MED=90°，∴∠AEM=∠DEN∴在△AEM 与△DEN 中，∠EMA=∠END=90°，∠AEM=∠DEN ，AE=DE∴△AEM ≌△DEN （AAS ）∴ME=NE∴点E 在∠ACB 的平分线上，即CE 是ACB ∠的平分线（3）由（2）可知，点E在∠ACB的平分线上，∴当点D向点B运动时，点E的路径为一条直线，∵△AEM≌△DEN∴AM=DN，即AC-CM=CN-CD在Rt△CME与Rt△CNE中，CE=CE，ME=NE，∴Rt△CME≌Rt△CNE（HL）∴CM=CN∴CN=1() 2AC CD+，又∵∠MCE=∠NCE=45°，∠CME=90°，∴CE=22() CN AC CD=+，当AC=3，CD=CO=1时，CE=2(31)22 2+=当AC=3，CD=CB=7时，CE=2(37)52 2+=∴点E的运动路程为：522232-=，【点睛】本题考查了全等三角形的综合证明题，涉及角平分线的判定，几何中动点问题，全等三角形的性质与判定，解题的关键是综合运用上述知识点．8．如图，在边长为 4 的等边△ABC 中，点 D 从点A 开始在射线 AB 上运动，速度为 1 个单位/秒，点F 同时从 C 出发，以相同的速度沿射线 BC 方向运动，过点D 作 DE⊥AC，连结DF 交射线 AC 于点 G(1)当 DF⊥AB 时，求 t 的值；(2)当点 D 在线段 AB 上运动时，是否始终有 DG=GF?若成立，请说明理由。

八年级下册数学期末试卷复习练习(Word版含答案)

八年级下册数学期末试卷复习练习(Word 版含答案) 一、选择题 1．若式子4x -在实数范围内有意义，则x 的取值范围是（） A ．4x >B ．4x <C ．4x ≥D ．4x ≤ 2．若以下列各组数值作为三角形的三边长，则不能围成直角三角形的是（） A ．4、6、8B ．3、4、5C ．5、12、13D ．1、3、10 3．已知四边形ABCD ，以下有四个条件．能判四边形ABCD 是平行四边形的有（）A ．//AB CD ，AD BC =B ．AB AD =，BC CD = C ．A B ∠=∠，C D ∠=∠ D ．//AB CD ，//AD BC 4．甲、乙、丙、丁四人进行射击测试，记录每人10次射击成绩，得到各人的射击成绩平均数和方差如表中所示，则成绩最稳定的是（）统计量甲乙丙丁平均数9.2 9.2 9.2 9.2 方差 0.60 0.620.50 0.44 A ．甲 B ．乙 C ．丙 D ．丁5．如图1，点F 从菱形ABCD 的顶点A 出发，沿A →D →B 以1cm/s 的速度匀速运动到点B ，图2是点F 运动时，△FBC 的面积y （cm 2）随时间x （s ）变化的关系图象，则a 的值为（）A ．2B ．322C ．32D ．256．如图，在ABC 中，∠B+∠C ＝α，按图进行翻折，使////,//B D C G BC B E FG '''，则∠C 'FE 的度数是（）A ．2αB ．90°﹣2αC ．α﹣90°D ．2α﹣180°7．如图，在四边形ABCD 中，E 、F 分别是AB 、AD 的中点，若6EF =，13BC =，△的面积为（）CD=，则BCD5A．60 B．48 C．30 D．158．已知：如图1，点G是BC的中点，点H在AF上，动点P以每秒2cm的速度沿图1的边线运动，运动路径为：G→C→D→E→F→H，相应的△ABP的面积y（cm2）关于运动时间t（s）的函数图象如图2，若AB=6cm，则下列四个结论中正确的个数有（）①图1中的BC长是8cm，②图2中的M点表示第4秒时y的值为24cm2，③图1中的CD长是4cm，④图2中的N点表示第12秒时y的值为18cm2．A．1个B．2个C．3个D．4个二、填空题9．在函数y＝3x+中，自变量x的取值范围是_______．10．已知一个菱形有一个内角为120︒，周长为16cm，那么该菱形的面积等于________ ．11．长方形的一条对角线的长为10cm，一边长为6cm，它的面积是________cm2. 12．如图，在矩形ABCD中，点E在AD上，且EC平分BED∠，若1AB=，45∠=︒，则DE的长为__________．EBC13．一次函数y=kx+3的图象过点A（1，4），则这个一次函数的解析式_____．14．如图，矩形ABCD中，对角线AC和BD交于点O，过O的直线分别交AD和BC于点E、F，已知AD=4 cm，图中阴影部分的面积总和为6 cm 2，则矩形的对角线AC长为___cm.15．在平面直角坐标系中，Q 是直线122y x =-+上的一个动点，将Q 绕点(1,0)P 顺时针旋转90︒，得到点Q '连接OQ '，则OQ '的最小值为__________．16．如图，AD 是ABC 的中线，45,ADC ∠=︒把ADC 沿AD 折叠，使点C 落在点'C 处，'BC 与BC 的长度比是_______________________．三、解答题17．计算：（1）218﹣6×31272+-；（2）（5﹣2）2﹣（13﹣2）（13+2）；（3）（1+3）•（2﹣3）；（4）332232---． 18．笔直的河流一侧有一旅游地C ，河边有两个漂流点A ，B ．其中AB ＝AC ，由于某种原因，由C 到A 的路现在已经不通，为方便游客决定在河边新建一个漂流点H （A ，H ，B 在同一直线上），并新修一条路CH ，测得BC ＝5千米，CH ＝4千米，BH ＝3千米．（1）判断△BCH 的形状，并说明理由；（2）求原路线AC 的长．19．下图各正方形网格中，每个小正方形的边长都是1，每个小正方形的顶点都称为格点．（1）在图①中，画出一条以格点为端点，长度为8的线段AB ．（2）在图②中，以格点为顶点，画出三边长分别为3，22，5的三角形． 20．如图所示，在矩形ABCD 中，AB =4cm ，BC =8cm ，AC 的垂直平分线EF 分别交BC ，AD 于点E ，F ，垂足为O ，连接AE ，CF ．（1）求证：四边形AFCE 为菱形；（2）求AF 的长．21．阅读，并回答下列问题：公元322r a r a a+≈+2的近似值. （12211+1321212≈+=⨯2看23124⎛⎫⎛⎫+- ⎪ ⎪⎝⎭⎝⎭2≈___________≈______________；依次算法，所得2的近似值会越来越精确.（22取近似值577408时，求近似公式中的a 和r 的值. 22．某超市以每千克40元的价格购进一种干果，计划以每千克60元的价格销售，为了让顾客得到实惠，现决定降价销售，已知这种干果销售量y （千克）与每千克降价x （元）（0＜x ＜20）之间满足一次函数关系，其图象如图所示．（1）求y 与x 之间的函数关系式；（2）当每千克干果降价3元时，超市获利多少元？23．如图，矩形ABCD中，AB=4，AD=3，∠A的角平分线交边CD于点E．点P从点A出发沿射线AE以每秒2个单位长度的速度运动，Q为AP的中点，过点Q作QH⊥AB于点H，在射线AE的下方作平行四边形PQHM（点M在点H的右侧），设P点运动时间为秒．（1）直接写出的面积（用含的代数式表示）．（2）当点M落在BC边上时，求的值．（3）在运动过程中，整个图形中形成的三角形是否存在全等三角形？若存在，请写出所有全等三角形，并求出对应的的值；若不存在请说明理由（不能添加辅助线）．24．请你根据学习函数的经验，完成对函数y＝|x|﹣1的图象与性质的探究．下表给出了y 与x的几组对应值．x…﹣3﹣2﹣10123…y…m10﹣1012…【探究】（1）m＝；（2）在给出的平面直角坐标系中，描出表中各对对应值为坐标的点，并根据描出的点，画出该函数的图象；（3）根据函数图象，当y随x的增大而增大时，x的取值范围是；【拓展】（4）函数y1＝﹣|x|＋1的图象与函数y＝|x|﹣1的图象交于两点，当y1≥y时，x的取值范围是；（5）函数y2＝﹣|x|＋b（b＞0）的图象与函数y＝|x|﹣1的图象围成的四边形的形状是，该四边形的面积为18时，则b的值是．25．如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D．（Ⅰ）若设AP＝x，则PC＝，QC＝；（用含x的代数式表示）（Ⅱ）当∠BQD＝30°时，求AP的长；（Ⅲ）在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由．【参考答案】一、选择题1．C解析：C【分析】根据二次根式有意义的条件列出不等式，解不等式得到答案．【详解】x-≥，由题意得，40解得，4x≥，故选：C．【点睛】本题考查的是二次根式有意义的条件，掌握二次根式的被开方数是非负数是解题的关键．2．A解析：A【分析】根据勾股定理的逆定理：如果三角形有两边的平方和等于第三边的平方，那么这个三角形是直角三角形．如果没有这种关系，这个就不是直角三角形．【详解】解：A 、42+62≠82，不符合勾股定理的逆定理，故本选项符合题意；B 、32+42=52，符合勾股定理的逆定理，故本选项不符合题意；C 、52+122=132，符合勾股定理的逆定理，故本选项不符合题意；D 、12+32=2，符合勾股定理的逆定理，故本选项符合题意．故选：A ．【点睛】本题考查了勾股定理的逆定理，在应用勾股定理的逆定理时，应先认真分析所给边的大小关系，确定最大边后，再验证两条较小边的平方和与最大边的平方之间的关系，进而作出判断．3．D解析：D【解析】【分析】根据平行四边形的判定方法进行分析即可．【详解】解：．A 、//AB CD ，AD BC =，不能判断四边形为平行四边形，故不符合题意； B 、AB AD =，BC CD =，不能判断四边形为平行四边形，故不符合题意；C 、A B ∠=∠，CD ∠=∠，不能判断四边形为平行四边形，故不符合题意；D 、//AB CD ，//AD BC ，可以根据两组对边分别平行的四边形是平行四边形进行判定，故符合题意；故选：D ．【点睛】本题考查了平行四边形的判定方法，解题的关键是：熟练掌握平行四边形的判定方法． 4．D解析：D【解析】【分析】根据方差的性质：方差越小，表示数据波动越小，也就是越稳定，据此进行判断即可．【详解】解：∵甲、乙、丙、丁的方差分别为0.60，0.62，0.50，0.44，又∵0.44＜0.50＜0.60＜0.62，∴丁的方差最小即丁的成绩最稳定，故选D ．【点睛】此题主要考查方差的应用，解题的关键是熟知方差的性质．5．B解析：B【分析】通过分析图象，点F 从点A 到D 用as ，此时，△FBC 的面积为a ，依此可求菱形的高DE ，再由图象可知，BD =6，应用两次勾股定理分别求BE 和a ．【详解】解：过点D 作DE ⊥BC 于点E ，由图象可知，点F 由点A 到点D 用时为as ，△FBC 的面积为acm 2．∴AD =a ，∴12BC •DE =12AD •DE =12a •DE =a ，∴DE =2，当点F 从D 到B 6，∴BD 6，Rt △DBE 中，BE 22BD DE -2∵ABCD 是菱形，∴EC =a 2，DC =a ，Rt △DEC 中，a 2=22+（a 22，解得a =322，故选：B ．【点睛】本题综合考查了菱形性质和一次函数图象性质，解答过程中要注意函数图象变化与动点位置之间的关系．6．D解析：D【解析】【分析】设∠ADB′＝γ，∠AGC′＝β，∠CEB′＝y ，∠C′FE ＝x ，利用平行线的性质，三角形内角和定理构建方程组即可解决问题．【详解】解：设∠ADB′＝γ，∠AGC′＝β，∠CEB′＝y ，∠C′FE ＝x ，∵////''B D C G BC ，∴B γ=∠，C β=∠，∴γ+β＝∠B+∠C ＝α，∵EB′∥FG ，∴∠CFG ＝∠CEB′＝y ，∴x+2y ＝180°①，根据平行线的性质和翻折的性质可得：B γ=∠，//'BD B E ，∴y B =∠，∵γ+y ＝2∠B ，同理可得出：β+x ＝2∠C ，∴γ+y+β+x ＝2α，∴x+y ＝α②，②×2﹣①可得x ＝2α﹣180°，∴∠C′FE ＝2α﹣180°．故选：D ．【点睛】本题考查三角形内角和定理，平行线的性质，翻折变换等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．7．C解析：C【解析】【分析】连接BD ，根据三角形中位线定理求出BD ，根据勾股定理的逆定理得到∠BDC =90°，然后求得面积即可．【详解】解：连接BD ，∵E 、F 分别是A B 、AD 中点，∴BD =2EF =12，∵CD 2+BD 2=25+144=169，BC 2=169，∴CD 2+BD 2=BC 2，∴∠BDC =90°，∴S △DBC =12BD •CD =12×12×5=30，故选：C ．【点睛】本题考查的是三角形中位线定理、勾股定理的逆定理，掌握三角形的中位线平行于第三边，并且等于第三边的一半是解题的关键．8．D解析：D【分析】①根据题意得：动点P在GC上运动的时间是2秒，又由动点的速度，可得GC和BC的长；②由（1）可得BC的长，又由AB=6cm，可以计算出△ABP的面积，计算可得y的值；③动点P在DC上运动的时间是2秒，又由动点的速度，可得CD的长；④根据图2中的N点表示第12秒时，表示点P到达H点，即可得出△ABP的面积；【详解】解：①根据函数图象可以知：从0到2，y随x的增大而增大，经过了2秒，P运动了4cm，因而CG=4cm，BC=8cm；②第4秒时P到达D点.P在CD段时，底边AB不变，高不变，因而面积不变，面积y=12×6×8=24cm2；③第4秒时P到达D点.由图象可知CD=2⨯2=4cm④图2中的N点表示第12秒时，表示点P到达H点.AF=BC+DE=8+2⨯3=14,所以AH=AF-FH=14-2⨯4=6.△ABP的面积=12⨯6⨯6=18cm2．则四个结论正确；故选D【点睛】此题考查了动点问题的函数图象，要能根据函数图象的性质和图象上的数据分析得出函数的类型和所需要的条件，结合实际意义得到正确的结论．二、填空题9．x≥﹣3【解析】【分析】根据二次根式的被开方数要为非负数，即x+3≥0，解此不等式即可．【详解】解：根据题意得：x+3≥0，解得：x≥﹣3．故答案为：x≥﹣3．【点睛】本题考查了函数自变量的确定，熟练掌握二次根式有意义的条件是解题的关键．10．E解析：2【解析】【分析】作AE BC⊥于E，由三角函数求出菱形的高AE，再运菱形面积公式=底×高计算即可；【详解】作AE BC ⊥于E ，如图所示，∵四边形ABCD 是菱形，周长为16cm ，120BCD ∠=︒，∴4AB BC cm ==，60B ∠=︒， ∴()3sin 4sin 60423AE AB B cm ==⨯︒=⨯=， ∴菱形的面积()242383BC AE cm ==⨯=．故答案为283cm ．【点睛】本题主要考查了菱形的性质，结合三角函数的计算是解题的关键．11．48【解析】【分析】先根据勾股定理求出长方形的另一条边，然后根据面积公式计算即可.【详解】解：∵长方形的一条对角线的长为10cm ，一边长为6cm ，由勾股定理可知：长方形的另一条边221068-=cm∴长方形的面积为：6×8=48 cm 2.故答案为：48.【点睛】此题考查的是勾股定理和长方形的面积，掌握用勾股定理解直角三角形是解决此题的关键. 12．D 21【分析】由矩形的性质和角平分线的定义得出∠DEC =∠ECB =∠BEC ，推出BE =BC ，求得 AE =AB =1，然后依据勾股定理可求得BC 的长；【详解】解：∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠DEC =∠BCE ，∵EC 平分∠DEB ，∴∠DEC =∠BEC ，∴∠BEC=∠ECB，∴BE=BC，∵四边形ABCD是矩形，=∴∠A=90°，AD BC∵∠ABE=45°，∴∠ABE=∠AEB=45°，∴AB=AE=1，由勾股定理得：BE==，∴BC=AD=BE，∴=-,DE AD AE11．【点睛】本题考查了矩形的性质，等腰三角形的性质与判定，勾股定理的应用；熟练掌握矩形的性质，证出BE=BC是解题的关键．13．A解析：y=x+3【解析】因为一次函数y=kx+3的图象过点A（1，4），所以k+3=4，解得，k=1，所以，该一次函数的解析式是：y=x+3，故答案是：y=x+3【点睛】运用了待定系数法求一次函数解析式，一次函数图象上点的坐标特征．直线上任意一点的坐标都满足函数关系式y=kx+b（k≠0）．14．A解析：5【解析】∵阴影部分的面积总和为6 cm 2，∴矩形面积为12 cm 2；∴AB×AD=12，∴AB=12÷4=3cm.∴5AC cm15．【分析】利用等腰直角三角形构造全等三角形，求出旋转后的坐标，进而可得点所在直线的函数关系式，然后根据勾股定理求解即可解决问题．【详解】解：作轴于点，轴于，，，，在和△中，，△，解析：5【分析】利用等腰直角三角形构造全等三角形，求出旋转后Q '的坐标，进而可得点Q '所在直线的函数关系式，然后根据勾股定理求解即可解决问题．【详解】解：作QM x ⊥轴于点M ，Q N x '⊥轴于N ，90PMQ PNQ QPQ ∠=∠'=∠'=︒，90QPM NPQ PQ N NPQ ∴∠+∠'=∠'+∠'=︒，QPM PQ N ∴∠=∠'，在PQM 和△Q PN '中，90PMQ PNQ QPM PQ NPQ PQ ∠=∠'=︒⎧⎪∠=∠'⎨⎪='⎩， PQM ∴△≌△()Q PN AAS '，PN QM ∴=，Q N PM '=，设1(,2)2Q m m -+，|1|Q N PM m ∴'==-，1|2|2QM m =-+， 1|3|2ON m ∴=-， 1(32Q m ∴'-，1)m -，设点(Q x '，)y '，则1321x m y m⎧=-⎪⎨⎪=-⎩'，整理，得：25y x '=-，则点(Q x '，)y '在直线25y x '=-上，设直线25y x '=-与x 轴，y 轴的交点分别为E 、F ，如图，当OQ EF '⊥时，OQ '取得最小值，令0y '=，则250x -=，解得52x =， ∴25OE =，令0x =，则5y '=-，∴5OF =，在Rt OEF 中，222255()5522EF OE OF ++，当OQ EF '⊥时，则1122OEF S EF OQ OE OF =⋅'=⋅△， ∴5525552OE OF OQ EF ⨯⋅'== OQ ∴'5 5【点睛】本题考查的是一次函数图象上点的坐标特征，一次函数的性质，三角形全等，坐标与图形的变换－旋转，勾股定理，表示出点Q '的坐标以及点Q '所在直线的函数关系式是解题的关键．16．【分析】设BD=CD=x ，由题意可知∠ADC=45°，且将ADC 沿AD 折叠，故，则可运用勾股定理，将用x 进行表示，即可得出的值．【详解】解：∵点D 是BC 的中点，设BD=CD=x ，则BC=2x 22【分析】设BD=CD=x ，由题意可知∠ADC=45°，且将ADC 沿AD 折叠，故ADC'=45∠︒，则Rt C'DB △可运用勾股定理，将BC'用x 进行表示，即可得出BC':BC 的值．【详解】解：∵点D是BC的中点，设BD=CD=x，则BC=2x，∠︒，C'D=x，又∵∠ADC=45°，将ADC沿AD折叠，故ADC'=45∴C'DC=C'DB=90∠∠︒，C'DB△是直角三角形，根据勾股定理可得：，∴:，2．【点睛】本题主要考察了折叠问题与勾股定理，解题的关键在于通过折叠的性质，得出直角三角形，并运用勾股定理．三、解答题17．（1）3﹣3；（2）﹣4；（3）﹣1+；（4）﹣【分析】（1）直接利用二次根式的性质以及立方根的性质，进而合并同类二次根式得出答案；（2）直接利用乘法公式化简，再合并得出答案；（3）直接利用解析：（1）3；（2）﹣3）﹣4【分析】（1）直接利用二次根式的性质以及立方根的性质，进而合并同类二次根式得出答案；（2）直接利用乘法公式化简，再合并得出答案；（3）直接利用二次根式的混合运算法则计算得出答案；（4）直接利用二次根式的性质化简，进而得出答案．【详解】解：（1）633=3；（22）22）（3）（•（23（4)11-11【点睛】本题主要考查了二次根式的混合运算以及立方根的性质，正确化简二次根式是解题关键．18．（1）直角三角形，理由见解析；（2）原来的路线AC的长为千米．【分析】（1）根据勾股定理的逆定理解答即可；（2）根据勾股定理解答即可．【详解】解：（1）△HBC是直角三角形，理由是：在△解析：（1）直角三角形，理由见解析；（2）原来的路线AC的长为256千米．【分析】（1）根据勾股定理的逆定理解答即可；（2）根据勾股定理解答即可．【详解】解：（1）△HBC是直角三角形，理由是：在△CHB中，∵CH2+BH2=42+32=25，BC2=25，∴CH2+BH2=BC2，∴△HBC是直角三角形且∠CHB=90°；（2）设AC=AB=x千米，则AH=AB-BH=（x-3）千米，在Rt△ACH中，由已知得AC=x，AH=x-3，CH=4，由勾股定理得：AC2=AH2+CH2，∴x2=（x-3）2+42，解这个方程，得x=256，答：原来的路线AC的长为256千米．【点睛】本题考查勾股定理的应用，解决本题的关键是掌握勾股定理的逆定理和定理．19．（1）见解析；（2）见解析【解析】【分析】（1）根据实际上直角边长为2和2的直角三角形的斜边长，即可解答；（2）实际上是直角边长为2和2的直角三角形的斜边长，实际上是直角边长为2和1的直解析：（1）见解析；（2）见解析【解析】【分析】（1）根据8实际上直角边长为2和2的直角三角形的斜边长，即可解答；（2）22实际上是直角边长为2和2的直角三角形的斜边长，5实际上是直角边长为2和1的直角三角形的斜边长，即可解答．【详解】（18实际上直角边长为2和2的直角三角形的斜边长，如图①线段AB即为所求线段；（2）本题中22实际上是直角边长为2和25长为2和1的直角三角形的斜边长，据此可找出如图②中的三角形即为所求．【点睛】本题主要考查了勾股定理，解题的关键是确定直角三角形的直角边长后根据边长画出所求的线段和三角形．20．（1）见解析；（2）AF=5【分析】（1）根据EF是AC的垂直平分线可以得到AF=CF，AE=CE，再只需证明△AFO≌△CEO即可得到答案；（2）根据四边形AECF是菱形可以得到AE=EC解析：（1）见解析；（2）AF=5【分析】（1）根据EF是AC的垂直平分线可以得到AF=CF，AE=CE，再只需证明△AFO≌△CEO即可得到答案；（2）根据四边形AECF是菱形可以得到AE=EC=x，则BE=8-x，然后利用勾股定理求解即可.【详解】解：（1）∵EF是AC的垂直平分线，∴AF =CF ，AE =CE ，AO =CO∵四边形ABCD 是矩形，∴AF ∥EC∴∠FAO =∠ECO ，∠AFO =∠CEO ，在△AFO 和△CEO 中，AFO CEO AO COFAO ECO ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AFO ≌△CEO （AAS ），∴AF =EC ，∴AF =FC =AE =EC ，∴四边形AECF 是菱形；（2）由（1）得AE =CE =AF ，设AE =CE =AF =x ，则BE =8-x ，∵四边形ABCD 是矩形，∴∠B =90°，在直角三角形ABE 中222AB BE AE +=，∴()22248x x +-=，解得x =5，∴AF =5，21．（1）；（2）或；或【解析】【分析】根据近似公式计算出近似值的过程和方法计算的近似值和确定a 和r 的值.【详解】（1）根据近似公式可知：≈故答案为；（2）∵∴∴∴整理，解析：（1）1343222-+⨯；1712（2）1712a =或2417；1144r =-或2289 【解析】【分析】的近似值和确定a 和r 的值.【详解】（1≈1343222-+⨯≈1712故答案为1343222-+⨯；1712（2）∵2r a a≈≈+ ∴225772408a r r a a ⎧+=⎪⎨+=⎪⎩∴5772()408r a a =⨯- ∴25772()2408a a a +⨯-= 整理，22045774080a a -+= 解得：1712a =或2417a = ∴1144r =-或2289r = 故答案为1712a =或2417 ；1144r =-或2289 【点睛】本题考查二次根式的估算，审清题意，根据题目所给的近似公式计算是解题关键. 22．（1）y=10x+100（0＜x ＜20）；（2）当每千克干果降价3元时，超市获利2210元【分析】（1）由待定系数法即可得到函数的解析式；（2）根据（1）的解析式将x=3代入求出销售量，再根据解析：（1）y =10x +100（0＜x ＜20）；（2）当每千克干果降价3元时，超市获利2210元【分析】（1）由待定系数法即可得到函数的解析式；（2）根据（1）的解析式将x=3代入求出销售量，再根据每千克利润×销售量=总利润列式求解即可．【详解】解：（1）设y与x之间的函数关系式为：y=kx+b，把（2，120）和（4，140）代入得，2120 4140k bk b+=⎧⎨+=⎩，解得：10100kb=⎧⎨=⎩，∴y与x之间的函数关系式为：y=10x+100（0＜x＜20）；（2）根据题意得，销售量y=10×3+100=130，（60-3-40）×130=2210（元），答：当每千克干果降价3元时，超市获利2210元．【点睛】本题考查的是一次函数的应用，解题的关键是利用待定系数法求出y与x之间的函数关系式，此类题目主要考查学生分析、解决实际问题能力，又能较好的考查学生“用数学”的意识．23．（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是解析：（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是等腰直角三角形，然后根据等腰直角三角形的性质可得AH的长，最后根据等腰直角三角形的面积公式即可得；（2）先根据平行四边形的性质可得，从而可得，再根据三角形中位线定理可得是的中位线，从而可得，然后与（1）所求的建立等式求解即可得；（3）分①当点H是AB的中点时，；②当点Q与点E重合时，；③当时，三种情况，分别求解即可得．【详解】（1）由题意得：，点Q为AP的中点，，四边形ABCD是矩形，，是BAD的角平分线，，，是等腰直角三角形，，则的面积为；（2）如图1，四边形PQHM是平行四边形，，点M在BC边上，，点Q为AP的中点，是的中位线，，由（1）知，，则，解得；（3）由题意，有以下三种情况：①如图2，当点H是AB的中点时，则，四边形PQHM是平行四边形，，，在和中，，，由（2）可知，此时；②如图3，当点Q与点E重合时，在和中，，，，则，解得；③如图4，当时，四边形ABCD是矩形，四边形PQHM是平行四边形，，，在和中，，，，，在中，，是等腰直角三角形，，，在中，，是等腰直角三角形，，则由得：，解得；综上，如图2，当时，；如图3，当时，；如图4，当时，．【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点，较难的是题（3），依据题意，正确分三种情况讨论并画出图形是解题关键．24．（1）2；（2）见解析；（3）x≥0；（4）﹣1≤x≤1；（5）正方形；5【解析】【分析】（1）把x＝﹣3代入y＝|x|﹣1，即可求出m；（2）描点连线画出该函数的图象即可求解；（3）根据解析：（1）2；（2）见解析；（3）x≥0；（4）﹣1≤x≤1；（5）正方形；5【解析】【分析】（1）把x＝﹣3代入y＝|x|﹣1，即可求出m；（2）描点连线画出该函数的图象即可求解；（3）根据图象即可解答；（4）画出函数y1＝﹣|x|＋1的图象，根据图象即可得当y1≥y时，x的取值范围；（5）取b＝3，在同一平面直角坐标系中画出y2＝﹣|x|＋3的图象，结合y1＝﹣|x|＋1的图象可得围成的四边形的形状是正方形，根据正方形的面积公式即可求解．【详解】解：（1）①把x＝﹣3代入y＝|x|﹣1，得m＝3﹣1＝2，故答案为：2；（2）该函数的图象如图，（3）根据函数图象，当y随x的增大而增大时，x的取值范围是x≥0，故答案为：x≥0；（4）画出函数y1＝﹣|x|＋1的图象如图，由图象得：当y1≥y时，x的取值范围为﹣1≤x≤1，故答案为：﹣1≤x≤1；（5）取b＝3，在同一平面直角坐标系中画出y2＝﹣|x|＋3的图象，如图：由图象得：y1＝﹣|x|＋1的图象与函数y＝|x|﹣1的图象围成的四边形的形状是正方形，y2＝﹣|x|＋3的图象与函数y＝|x|﹣1的图象围成的四边形的形状是正方形，∴函数y2＝﹣|x|＋b（b＞0）的图象与函数y＝|x|﹣1的图象围成的四边形的形状是正方形，∵y＝|x|﹣1，y2＝﹣|x|＋b（b＞0），∴y与y2的图象围成的正方形的对角线长为b＋1，∵该四边形的面积为18，∴1（b＋1）2＝18，2解得：b＝5（负值舍去），故答案为：正方形，5．【点睛】本题是一次函数综合题，考查了一次函数的图象与性质，一次函数图象上点的坐标特征，利用了数形结合思想．正确画出函数的图象是解题的关键．25．（Ⅰ）6﹣x，6+x；（Ⅱ）2；（Ⅲ）线段DE的长度不会改变.DE=3【分析】(1)根据等边三角形的性质可知AB＝BC＝AC＝6，然后根据题意解答即可;（2）在（1）的基础上，再利用直角三角形解析：（Ⅰ）6﹣x，6+x；（Ⅱ）2；（Ⅲ）线段DE的长度不会改变.DE=3【分析】(1)根据等边三角形的性质可知AB＝BC＝AC＝6，然后根据题意解答即可;（2）在（1）的基础上，再利用直角三角形30°所对的边等于斜边的一半进行解答即可. (3) 作QF⊥AB，交直线AB的延长线于点F，连接QE，PF;根据题意和等边三角形的性质证明△APE≌△BQF（AAS），进一步说明四边形PEQF是平行四边形，最后说明DE＝AB，即可说明DE的长度不变.【详解】解：（Ⅰ）∵△ABC是边长为6的等边三角形，∴AB＝BC＝AC＝6，设AP＝x，则PC＝6﹣x，QB＝x，∴QC＝QB+BC＝6+x，故答案为6﹣x，6+x；（Ⅱ）∵在Rt △QCP 中，∠BQD ＝30°，∴PC ＝12QC ，即6﹣x ＝12（6+x ），解得x ＝2，∴AP ＝2；（Ⅲ）当点P 、Q 运动时，线段DE 的长度不会改变．理由如下：作QF ⊥AB ，交直线AB 的延长线于点F ，连接QE ，PF ，又∵PE ⊥AB 于E ，∴∠DFQ ＝∠AEP ＝90°，∵点P 、Q 速度相同，∴AP ＝BQ ，∵△ABC 是等边三角形，∴∠A ＝∠ABC ＝∠FBQ ＝60°，在△APE 和△BQF 中，∵∠AEP ＝∠BFQ ＝90°，∴∠APE ＝∠BQF ，∴在△APE 和△BQF 中，AEP BFQ A FBQ AP BQ ∠=∠⎧⎪∠=∠⎨⎪=⎩， ∴△APE ≌△BQF （AAS ），∴AE ＝BF ，PE ＝QF 且PE ∥QF ，∴四边形PEQF 是平行四边形，∴DE ＝12EF ，∵EB +AE ＝BE +BF ＝AB ，∴DE ＝12AB ，又∵等边△ABC 的边长为6，∴DE ＝3，∴当点P 、Q 运动时，线段DE 的长度不会改变．【点睛】本题考查全等三角形的判定和性质、等边三角形的性质、平行四边形的判定和性质，其中灵活运用等边三角形的性质和全等三角形的判定是解答本题的关键.。

人教版数学八年级下册数学期末试卷试卷(word版含答案)

人教版数学八年级下册数学期末试卷试卷（word 版含答案）一、选择题1．下列式子中不一定是二次根式的是（）A ．3B ．4C ．aD ．2a 2．下列语句不能判定ABC 是直角三角形的是（） A ．2220a b c +-=B ．::3:4:5A BC ∠∠∠= C ．::3:4:5a b c =D ．A B C ∠+∠=∠ 3．如图，在四边形ABCD 中，对角线AC 、BD 相交于点O ，下列条件不能判定四边形ABCD为平行四边形的是（）A ．AB ∥CD ，AD ∥BCB ．AD ∥BC ，AB ＝CD C ．OA ＝OC ，OB ＝ODD ．AB ＝CD ，AD ＝BC 4．一组数据：1，2，3，2，1，0．这组数据的中位数是（） A ．1B ．2C ．3D ．1.5 5．某三角形三条中位线的长分别为3、4、5，则此三角形的面积为（）A ．6B ．12C ．24D ．48 6．如图，菱形ABCD 中，120D ∠=︒，则1∠=（）A ．60°B ．30°C ．25°D ．15° 7．如图，点E 在正方形ABCD 的边CD 上，若△ABE 的面积为8，CE ＝3，则线段BE 的长为（）A ．5B ．1C ．4D ．68．在平面直角坐标系中，定义：已知图形W 和直线l ，如果图形W 上存在一点Q ，使得点Q 到直线l 的距离小于或等于k ，则称图形W 与直线l “k 关联”．已知线段AB ，其中点(1,1)A ，(3,1)B ．若线段AB 与直线y x b =-+2”，则b 的取值范围是( ) A ．-2B ．0≤b≤4 C ．0≤b≤6 D 2二、填空题9．若二次根式12x -有意义，则x 的取值范围是________．10．如图，在菱形ABCD 中对角线AC 、BD 相交于点O ，若AB =3，BD =4，则菱形ABCD 的面积为_____．11．如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形，设直角三角形较长直角边长为a ，较短直角边长为b ．若ab ＝4，大正方形的面积为16，则小正方形的边长为______．12．在矩形ABCD 中，AB ＝4，BC ＝3，过点A 作∠DAC 的角平分线交BC 的延长线于点H ，取AH 的中点P ，连接BP ，则S △ABP ＝___．13．一次函数2y x b =+的图象经过点()1,3-，则b =___________．14．如图，矩形ABCD 的对角线AC ，BD 相交于点O ，分别过点C ，D 作BD ，AC 的平行线，相交于点E ．若AD=6，则点E 到AB 的距离是________．15．如图，在平面直角坐标系中，直线y ＝﹣x +2与x 轴交于点A ，与y 轴交于点B ，点P 是线段AB 的三等分点（AP ＞BP ），点C 是x 轴上的一个动点，连接BC ，以BC 为直角边，点B 为直角顶点作等腰直角△BCD ，连接DP ．则DP 长度的最小值是___．16．如图，在Rt△ACB中，∠ACB＝90°，BC＝6，AC＝9.折叠△ACB，使点A与BC的中点D重合，折痕交AB于E，交AC于点F，则CF＝___．三、解答题17．计算（1）（7+3）（7-3）（2）1 18322-+18．有一架5米长的梯子搭在墙上，刚好与墙头对齐，此时梯脚与墙的距离是3米（1）求墙的高度？（2）若梯子的顶端下滑1米，底端将水平动多少米？19．图（a）、图（b）是三张形状大小完全相同的方格纸，方格纸中的每个小正方形的边长均为1请在图a）、图（b）中，分别画出符合要求的图形，所画图形各顶点必须与方格纸中的小正方形顶点重合具体要求如下：（1）画一个面积为10的等腰直角三角形；（2）画一个面积为12的平行四边形20．如图，在矩形ABCD 中，点E 在边BC 上，点F 在BC 的延长线上，且BE ＝CF ．求证：（1）△ABE ≌DCF ；（2）四边形AEFD 是平行四边形；探究：连结DE ，若DE 平分∠AEC ，直接写出此时四边形AEFD 的形状．21．观察下列各式: 51282213322042,,,,? (22225182133201)------------ ()1化简以上各式，并计算出结果;()2以上式子与其结果存在一定的规律．请按规律写出第5个式子及结果．()3猜想第n 个式子及结果(用含n (1n ≥的整数)的式子写出)，并对猜想进行证明． 22．为了鼓励小强做家务，小强每月的费用都是根据上月他的家务劳动时间所得奖励加上基本生活费从父母那里获取的．若设小强每月的家务劳动时间为x 小时，该月可得（即下月他可获得）的总费用为y 元，则y （元）和x （小时）之间的函数图象如图所示．（1）根据图象，请你写出小强每月的基本生活费；父母是如何奖励小强家务劳动的？（2）若小强2月份希望有300元费用，则小强1月份需做家务多少时间？23．如图，M 为正方形ABCD 的对角线BD 上一点.过M 作BD 的垂线交AD 于E ，连BE ，取BE 中点O ．（1）如图1，连，试证明；（2）如图2，连接，并延长交对角线BD 于点N ，试探究线段之间的数量关系并证明；（3）如图3,延长对角线BD 至Q 延长至P ,连若,且，则．（直接写出结果）24．如图，已知点()4,0A 、()0,2B ，线段OA OC =且点C 在y 轴负半轴上，连接AC ．（1）如图1，求直线AB 的解析式；（2）如图1，点P 是直线CA 上一点，若3ABC ABP SS =，求满足条件的点P 坐标；（3）如图2，点M 为直线5:2l x =上一点，将点M 水平向右平移6个单位至点N ，连接BM 、MN 、NC ，求BM MN NC ++的最小值及此时点N 的坐标．25．已知，如图，在三角形ABC ∆中，20AB AC cm ==，BD AC ⊥于D ，且16BD cm =．点M 从点A 出发，沿AC 方向匀速运动，速度为4/cm s ；同时点P 由B 点出发，沿BA 方向匀速运动，速度为1/cm s ，过点P 的动直线//PQ AC ，交BC 于点Q ，连结PM ，设运动时间为()t s ()05t <<，解答下列问题：（1）线段AD =_________cm ；（2）求证：PB PQ =；（3）当t 为何值时，以P Q D M 、、、为顶点的四边形为平行四边形？26．如图1，ABC ∆中，CD AB ⊥于D ，且::2:3:4BD AD CD =；（1）试说明ABC ∆是等腰三角形；（2）已知Δ40ABC S =cm 2，如图2，动点M 从点B 出发以每秒1cm 的速度沿线段BA 向点A 运动，同时动点N 从点A 出发以相同速度沿线段AC 向点C 运动，当其中一点到达终点时整个运动都停止．设点M 运动的时间为t (秒)．①若DMN ∆的边与BC 平行，求t 的值；②在点N 运动的过程中，ADN ∆能否成为等腰三角形?若能，求出t 的值；若不能，请说明理由．【参考答案】一、选择题1．C解析：C【分析】根据二次根式的性质即可判断．【详解】342a a a 可能为负数，故不一定是二次根式故选C ．【点睛】此题主要考查二次根式的识别，解题的关键是熟知二次根式的定义．2．B解析：B【分析】由勾股定理的逆定理，只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可．【详解】解：A 、由2220a b c +-=，可得222+=a b c ，故是直角三角形，不符合题意； B 、∵::3:4:5A B C ∠∠∠=，∴∠C ＝180°×575345=︒++，故不是直角三角形，符合题意；C 、32＋42＝52，能构成直角三角形，不符合题意；D 、∵∠A ＋∠B ＝∠C ，∴∠C ＝90°，故是直角三角形，不符合题意；故选：B ．【点睛】本题考查勾股定理的逆定理的应用．判断三角形是否为直角三角形，已知三角形三边的长，只要利用勾股定理的逆定理加以判断即可．3．B解析：B【解析】【分析】根据平行四边形的判定方法即可判断．【详解】A 、根据两组对边分别平行的四边形是平行四边形，可以判定；B 、无法判定，四边形可能是等腰梯形，也可能是平行四边形；C 、根据对角线互相平分的四边形是平行四边形，可以判定；D 、根据两组对边分别相等的四边形是平行四边形，可以判定；故选：B ．【点睛】本题考查平行四边形的判定，解题的关键是掌握平行四边形的判定定理．4．D解析：D【解析】【分析】根据中位数的定义求解即可．【详解】解：将这组数据重新排列为0、1、1、2、2、3，∴这组数据的中位数为51+221. ，故选：D ．【点睛】本题主要考查中位数，将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的个数是奇数，则处于中间位置的数就是这组数据的中位数．如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数．5．C解析：C【分析】先根据三角形的中位线定理：三角形的中位线平行于第三边，且等于第三边的一半，即求出原三角形的边长分别为6、8、10，再根据勾股定理的逆定理判断原三角形的形状，即可根据三角形面积公式求得面积．【详解】解：∵三角形三条中位线的长为3、4、5，∴原三角形三条边长为3264285210⨯=⨯=⨯=，，，2226810+=，∴此三角形为直角三角形，168242S ∴=⨯⨯=，故选C ．【点睛】本题考查的是三角形的中位线定理、勾股定理的逆定理，属于基础应用题，熟知性质定理是解题的关键．6．B解析：B【解析】【分析】由菱形的性质可得AB =BC ，∠B =∠D =120°，由菱形的性质可求解．【详解】解：∵四边形ABCD 是菱形，∴AB =BC ，∠B =∠D =120°，∴∠1=30°，故选：B【点睛】本题考查了菱形的性质，等腰三角形的性质，掌握菱形的性质是本题的关键． 7．A解析：A【解析】【分析】根据正方形的性质，可求出正方形的面积，从而确定边长，然后在Rt △BCE 中利用勾股定理求解即可．【详解】解：∵四边形ABCD 为正方形， ∴12ABE S AB AD =，ABCD S AB AD =正方形， ∴22816ABE ABCD S S ==⨯=正方形，∴正方形的边长4BC =，在Rt △BCE 中，BC =4，CE =3， ∴5BE ，故选：A ．【点睛】本题考查正方形的性质，理解正方形的性质以及熟练运用勾股定理是解题关键． 8．C解析：C【分析】如图（见解析），先画出图形，再根据定义求出两个临界位置时b 的值，由此即可得．【详解】如图，过点B 作直线y x b =-+的垂线，垂足为点D ，连接OA ，延长AB 交直线y x b =-+于点C由题意，有以下两个临界位置：①点A 到直线y x b =-+(1,1)AOA ∴==145∠=︒当直线y x b =-+经过原点O 时，0b =，245∠=︒2190∴∠+∠=︒OA ∴即为点A 到直线y x =-的距离，此时0b =②点B 到直线y x b =-+BD //AB x 轴45BCD ∴∠=︒，且点C 的纵坐标与点A 的纵坐标相同，即为1Rt BCD ∴是等腰直角三角形2BC ∴==∴点C 的横坐标为325+=(5,1)C ∴将点(5,1)C 代入直线y x b =-+得：51b -+=解得6b =则b 的取值范围是06b ≤≤故选：C ．【点睛】本题考查了等腰直角三角形的判定与性质、一次函数的几何应用等知识点，理解新定义，求出两个临界位置时b的值是解题关键．二、填空题9．2x<【解析】【分析】根据二次根式被开放数为非负数，分式的分母不为零求解即可．【详解】解：∵2x-∴2-x＞0，解得：x<2．故答案为：x<2．【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式被开放数为非负数是解题的关键．10．A解析：45【解析】【分析】根据勾股定理求出对角线AC的长，然后利用菱形面积公式计算即可．【详解】解：四边形ABCD是菱形，4BD=，2OB∴=，3AB=，2222325OA AB OB∴--=，225AC OA∴==，则S菱形ABCD1125445 22AC BD==⨯=故答案为：45【点睛】本题主要考查了菱形的性质，勾股定理，菱形的面积公式等知识点，利用勾股定理求出AC 是关键．11【解析】【分析】由题意可知：中间小正方形的边长为a-b ，根据勾股定理以及题目给出的已知数据即可求出小正方形的边长．【详解】解：由题意可知：中间小正方形的边长为a-b ，∵每一个直角三角形的面积为:12ab=12×4=2, ∴412⨯ab+2()a b - =16， ∴2()a b -=16-8=8，∴，故答案为．【点睛】本题考查勾股定理的应用，解题的关键是熟练运用勾股定理以及完全平方公式,本题属于基础题型．12．A解析：8【分析】由勾股定理可得AC ＝5，根据角平分线的性质可证∠H ＝∠CAH ＝∠DAH ，即AC ＝CH ＝5，则可求S △ABH 的值，由P 是中点，可得S △ABP 的值．【详解】解：∵四边形ABCD 是矩形，∴AD //BC ，∠ABC ＝90°，∵AB ＝4，BC ＝3，∴AC5，∵AH 平分∠DAC ，∴∠DAH ＝∠CAH ，∵AD //BC ，∴∠DAH ＝∠H ，∴∠H ＝∠CAH ，∴AC ＝CH ＝5，∵BH ＝BC +CH ，∴BH ＝8，∵S △ABH ＝12AB ×BH ＝12×4×8＝16，∵P 是AH 的中点∴S △ABP ＝12S △ABH ＝8；故答案为：8．【点睛】此题主要考查矩形的性质与判定综合，解题的关键是矩形的性质及勾股定理的应用． 13．5-【分析】利用一次函数图象上点的坐标特征，把点()1,3-的坐标代入函数表达式即可求出b 的值．【详解】解：∵一次函数2y x b =+的图象经过点()1,3-，∴2+b=-3，解得b=-5．故答案为：-5．【点睛】本题考查了一次函数图象上点的坐标特征，牢记直线上任意一点的坐标都满足函数关系式y=kx+b （k≠0）是解题的关键．14．E解析：9【详解】试题解析：连接EO ，延长EO 交AB 于H .∵DE ∥OC ,CE ∥OD ，∴四边形ODEC 是平行四边形，∵四边形ABCD 是矩形，∴OD =OC ，∴四边形ODEC 是菱形，∴OE ⊥CD ，∵AB ∥CD ，AD ⊥CD ，∴EH ⊥AB ,AD ∥OE ,∵OA ∥DE ，∴四边形ADEO 是平行四边形，∴AD =OE =6，∵OH ∥AD ，OB =OD ，∴BH =AH ，132OH AD ∴==，∴EH =OH +OE =3+6=9，故答案为:9.点睛:平行四边形的判定:两组对边分别平行的四边形是平行四边形.15．【分析】过点B 作BM ⊥轴于点B ，使BM=OB ，利用SAS 证得△BOC △BMD ，再证明M 、D 、A 三点共线，推出四边形AMBO 是正方形，当且仅当PD ⊥AM 时，线段DP 的长度取得最小值，利用勾股定理即解析：43【分析】过点B 作BM ⊥y 轴于点B ，使BM =OB ，利用SAS 证得△BOC ≅△BMD ，再证明M 、D 、A 三点共线，推出四边形AMBO 是正方形，当且仅当PD ⊥AM 时，线段DP 的长度取得最小值，利用勾股定理即可求解．【详解】解：过点B 作BM ⊥y 轴于点B ，使BM =OB ，连接DM ，AD ，∵直线y ＝﹣x +2与x 轴交于点A ，与y 轴交于点B ，∴令0y =，则2x =；令0x =，则2y =；∴点A 的坐标为(2，0)，点B 的坐标为(0，2)，∴OA =OB =BM =2，∵BM ⊥y 轴，∴∠OBM =90°，∴点M 的坐标为(2，2)，∵△BCD 是等腰直角三角形，∴BC =BD ，∠CBD =90°，∴∠CBD =∠OBM =90°，∴∠CBD -∠OBD =∠OBM -∠OBD ，∴∠CBO =∠DBM ，在△BOC 和△BMD ，BC BD CBO DBM OB MB =⎧⎪∠=∠⎨⎪=⎩，∴△BOC ≅△BMD (SAS )，∴∠BOC =∠BMD =90°，∴BM ⊥DM ，∴DM ∥OB ，∵M 、D 、A 三点的横坐标相同，都为2，∴M 、D 、A 三点共线，∴四边形AMBO 是正方形，∴∠BAM =45°，∵AB=点P 是线段AB 的三等分点（AP ＞BP ），∴AP =23AB 当且当PD ⊥AM 时，线段DP 的长度取得最小值，此时，△PAD 为等腰直角三角形，∴PD =43， ∴线段DP 长度最小值为43，故答案为：43．【点睛】本题考查了一次函数的的图象与坐标轴的交点问题，正方形的判定和性质，等腰直角三角形的判定和性质，全等三角形的判定和性质等知识点，证得四边形AMBO 是正方形，以及当PD ⊥AM 时，线段DP 的长度取得最小值是解题的关键．16．4【分析】由题可知CD=3，由折叠的性质可知AF=FD ，设,则，在Rt 中利用勾股定理列方程，即可求得答案．【详解】∵D 为BC 中点，BC=6,∴,由折叠可知AF=DF ，设，∵AC=9,解析：4【分析】由题可知CD =3，由折叠的性质可知AF =FD ，设AF DF x ==,则9FC x =-，在Rt DCF 中利用勾股定理列方程，即可求得答案．∵D 为BC 中点，BC =6, ∴132BD CD BC ===,由折叠可知AF =DF ，设AF DF x ==，∵AC =9,∴9CF x =-，又∵90ACB ∠=︒∴在Rt ACB △中，222DF CF CD =+, 即：2223(9)x x =+-解得：5x =，则CF =954-=故填：4．【点睛】本题考查轴对称的性质，勾股定理，解题关键是熟练掌握轴对称的性质和勾股定理．三、解答题17．（1）4；（2）【分析】（1）根据二次根式运算法则结合平方差公式进行计算即可；（2）先将题目中的二次根式化解为最简二次根式，然后根据二次根式的加减运算法则计算即可．【详解】解：（1）原式；解析：（1）4；（2）2【分析】（1）根据二次根式运算法则结合平方差公式进行计算即可；（2）先将题目中的二次根式化解为最简二次根式，然后根据二次根式的加减运算法则计算即可．【详解】解：（1）原式73=-4=；（2）原式===本题考查了二次根式的混合运算，平方差公式，熟练掌握二次根式的混合运算法则是解本题的关键．18．（1）4米；（2）1米【分析】（1）利用勾股定理可以得出梯子的顶端距离地面的高度．（2）由（1）可以得出梯子的初始高度，下滑4米后，可得出梯子的顶端距离地面的高度，再次使用勾股定理，已知梯子的解析：（1）4米；（2）1米【分析】（1）利用勾股定理可以得出梯子的顶端距离地面的高度．（2）由（1）可以得出梯子的初始高度，下滑4米后，可得出梯子的顶端距离地面的高度，再次使用勾股定理，已知梯子的底端距离墙的距离为7米，可以得出，梯子底端水平方向上滑行的距离．【详解】解：（1）根据勾股定理：墙的高度4AC==（米)；（2）梯子下滑了1米，即梯子距离地面的高度1413'=-=-=（米)．AC AC根据勾股定理：4B C'=（米)则431'='-=-=（米)，即底端将水平动1米．BB CB CB答：（1）墙的高度是4米；（2）若梯子的顶端下滑1米，底端将水平动1米．【点睛】本题考查了勾股定理的应用，要求熟练掌握利用勾股定理求直角三角形边长．19．（1）见解析；（2）见解析【解析】【分析】（1）根据等腰直角三角形的性质求出边长分别为、、，再网格中找到相应的格点，作图即可；（2）根据平行四边形的面积为12，确定底边长为4、高为3，在网格解析：（1）见解析；（2）见解析【解析】【分析】（1）根据等腰直角三角形的性质求出边长分别为的格点，作图即可；（2）根据平行四边形的面积为12，确定底边长为4、高为3，在网格中找到相应的格点，作图即可．解：（1）根据等腰直角三角形的面积为为10，设两个直角边为x ，则21102x = 解得25x =，由勾股定理得，斜边长为22(25)(25)210+=222524=+，在网格中找到到相应的格点使得两条直角边为25，连线即可，其中25是以2，4为直角边的直角三角形的斜边，如图（a ）（2）根据平行四边形的面积为12，可以作底边长为4、高为3的平行四边形，在图中选取相应的格点，使得平行四边形的边长为为4、高为3，如图（b ）【点睛】此题考查了等腰直角三角形的性质，勾股定理，平行四边形的性质，熟练掌握相关基本性质是解题的关键．20．（1）见解析；（2）证明见解析；探究：菱形【分析】（1）根据矩形性质直接根据边角边证明△ABE ≌DCF 即可；（2）证明AE ∥DF ，AE ＝DF ，可得结论；探究：证明FD ＝FE ，可得结论．【详解析：（1）见解析；（2）证明见解析；探究：菱形【分析】（1）根据矩形性质直接根据边角边证明△ABE ≌DCF 即可；（2）证明AE ∥DF ，AE ＝DF ，可得结论；探究：证明FD ＝FE ，可得结论．【详解】.证明：（1）∵四边形ABCD 为矩形，∴AB ＝DC ，∠B ＝∠DCF ，∵BE ＝CF ，∴△ABE ≌DCF ；（2）∵△ABE ≌DCF ，∴∠AEB ＝∠F ，AE ＝DF ，∴AE ∥DF ，∴AE ＝DF ，∴四边形AEFD 是平行四边形．（3）此时四边形AEFD 是菱形．理由：如图1中，连接DE ．∵DE 平分∠AEC ，∴∠AED ＝∠DEF ，∵AD ∥EF ，∴∠ADE ＝∠DEF ，∴∠ADE ＝∠AED ，∴AD ＝AE ，∵四边形AEFD 是平行四边形，∴四边形AEFD 是菱形．【点睛】本题属于四边形综合题，考查了矩形的性质，平行四边形的判定和性质，菱形的判定等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．21．；；第个式子为及结果为，证明见解析【解析】【分析】（1）分别把每个式子的第二项进行分母有理化，观察结果；（2）根据（1）的结果写出第5个式子及结果；（3）根据（1）的规律可得，然后分母有理解析：()11,2,3,4----；(29525295-=--；()3第n 个式子为及结果为2244n n n n n+-=-+-，证明见解析【解析】【分析】（1）分别把每个式子的第二项进行分母有理化，观察结果；（2）根据（1）的结果写出第5个式子及结果；（3）根据（12244n n n n+-+- 【详解】解：(1211==-22=2==-=3==-····4==-(25=-()3第n个式子为及结果为n=-证明：左边=2nn===--=右边n=-成立【点睛】本题主要考查分母有理化的知识点，解答本题的关键是找出上述各式的变化规律，此题难度一般．22．（1）小强每月的基本生活费为元，当劳动时间不大于20小时，每小时劳动奖励为元，一个月内劳动时间超过小时，每小时劳动奖励为元；（2）小时【分析】（1）根据函数图象与轴的交点即可求得基本生活费，根据解析：（1）小强每月的基本生活费为150元，当劳动时间不大于20小时，每小时劳动奖励为2.5元，一个月内劳动时间超过20小时，每小时劳动奖励为4元；（2）45小时【分析】（1）根据函数图象与y 轴的交点即可求得基本生活费，根据函数图像是分段的，即可描述出父母是如何奖励小强做家务劳动的；（2）根据劳动时间超过30小时的部分的解析式即可求得1月份需做家务的时间【详解】解：（1）根据函数图象可知，当0x =时，150y =，∴小强每月的基本生活费为150元设劳动时间在20小时内的解析式为：1y ax b ()020x <≤将点()()0,150,20,200代入，得15020200b a b =⎧⎨+=⎩ 解得 2.5150a b =⎧⎨=⎩∴1 2.5150y x =+当20x >时，设2y mx n =+，将点()()20,200,30,240，代入得，2020030240m n m n +=⎧⎨+=⎩ 解得4120m n =⎧⎨=⎩则24120y x =+()20x >∴当020x <≤时，每小时劳动奖励为2.5元，一个月内劳动时间超过20小时，则每小时劳动奖励为4元（2）令2300y =，则3004120x =+解得45x =答：小强2月份希望有300元费用，则小强1月份需做家务45小时．【点睛】本题考查了一次函数的应用，理解题意，求得分段函数的解析式是解题的关键． 23．（1）见解析；（2），理由见解析；（3）【分析】（1）由直角三角形的性质得AO=MO=BE=BO=EO ，得∠ABO=∠BAO ，∠OBM=∠OMB ，证出∠AOM=∠AOE+∠MOE=2∠ABO+2解析：（1）见解析；（2），理由见解析；（3）【分析】（1）由直角三角形的性质得AO=MO=12BE=BO=EO ，得∠ABO=∠BAO ，∠OBM=∠OMB ，证出∠AOM=∠AOE+∠MOE=2∠ABO+2∠MBO=2∠ABD=90°即可；（2）在AD上方作AF⊥AN，使AF=AN，连接DF、MF，证△ABN≌△ADF（SAS），得BN=DF，∠DAF=∠ABN=45°，则∠FDM=90°，证△NAM≌△FAM（SAS），得MN=MF，在Rt△FDM中，由勾股定理得FM2=DM2+FD2，进而得出结论；（3）作P关于直线CQ的对称点E，连接PE、BE、CE、QE，则△PCQ≌△ECQ，∠ECQ=∠PCQ=135°，EQ=PQ=9，得∠PCE=90°，则∠BCE=∠DCP，△PCE是等腰直角三角形，得CE=CP=PE，证△BCE≌△DCP（SAS），得∠CBE=∠CDB=∠CBD=45°，则∠EBQ=∠PBE=90°，由勾股定理求出BE=，PE=6，即可得出PC的长．【详解】解：（1）证明：四边形ABCD是正方形，，，，，是BE的中点，，，，；（2），理由如下：在AD上方作，使，连接DF、，如图2所示：则，四边形ABCD是正方形，∴=，，AB AD，，，在和中，，，，，，，，在和中，，，，在中，，即；（3）作P关于直线的对称点E，连接、BE、CE、，如图3所示：则，，，，，是等腰直角三角形，，在和中，，，，，，，，，，，；故答案为：32【点睛】本题是四边形综合题目，考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、直角三角形的判定、勾股定理、轴对称的性质等知识；本题综合性强，熟练掌握正方形的性质和勾股定理，证明三角形全等是解题的关键．24．（1）；（2）点P 的坐标为（，）或（，）；（3）的最小值为；点N 的坐标为（，）．【解析】【分析】（1）直接利用待定系数法，即可求出直线的解析式；（2）根据题意，先求出点C 的坐标，然后求出直线解析：（1）122y x =-+；（2）点P 的坐标为（163，43）或（83，43-）；（3）BM MN NC ++的最小值为6157N 的坐标为（172，711）．【解析】【分析】（1）直接利用待定系数法，即可求出直线的解析式；（2）根据题意，先求出点C 的坐标，然后求出直线AC 的解析式，由3ABC ABP S S =，得到3AC AP =，再分别求出AC 和AP 的长度，即可求出点P 的坐标；（3）根据题意，6MN =为定值，在图中找出一点B '，使得B N BM '=，即点B '、N 、C 三点共线时，使得BM MN NC ++有最小值，此时求出B C B N NC BM NC ''=+=+，即可得到答案．【详解】解：（1）设直线AB 为y kx b =+，把点()4,0A 、()0,2B ，代入，则402k b b +=⎧⎨=⎩，解得：122k b ⎧=-⎪⎨⎪=⎩，∴122y x =-+；（2）∵线段4OA OC ==，且点C 在y 轴负半轴上，∴点C 的坐标为（0，-4），∵点A 为（4，0），∴直线AC 的解析式为：4y x =-；∵点B 到直线AC 的距离就是△ABC 和△ABP 的高，∴△ABC 和△ABP 的高相同，∵3ABC ABP SS =， ∴11322AC h AP h ••=⨯••， ∴3AC AP =， ∵AC ==∴13AP =⨯ ∵点P 在直线AC 上，则设点P 为（x ，x -4），∴4AP x ==-=， ∴443x -=， ∴163x =或83x =， ∴点P 的坐标为（163，43）或（83，43-）；（3）根据题意，∵点B 与点M 的水平距离为52， ∴在点N 的右边水平距离为52处作直线11x =，如图：令点B '为（11，2），此时有B N BM '=，∵6MN =，∴66BM MN NC BM NC B N NC '++=++=++，∴当点B '、N 、C 三点共线时，使得BM MN NC ++有最小值，最小值为：66BM MN NC B N NC B C ''++=++=+；∵点B '（11，2），点C 为（0，-4），∴直线B C '的解析式为：6411y x =-， 2211(24)157B C '++∴BM MN NC ++有最小值为：66157B C '+=+∵点N 的横坐标为：517622+=， ∴点N 的纵坐标为：6177411211y =⨯-=， ∴点N 的坐标为：（172，711）．【点睛】本题考查了一次函数的性质，利用勾股定理求两点之间的距离，最短路径问题，坐标与图形，解题的关键是熟练掌握一次函数的图形和性质，正确找出使得线段之和最小时的临界点，注意运用数形结合的思想进行解题．25．（1）12；（2）证明见详解；（3）或t=4s ．【分析】（1）由勾股定理求出AD即可；（2）由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB，再由等腰三角形的判定定理即可得出结论；（3解析：（1）12；（2）证明见详解；（3）125t s=或t=4s．【分析】（1）由勾股定理求出AD即可；（2）由等腰三角形的性质和平行线的性质得出∠PBQ=∠PQB，再由等腰三角形的判定定理即可得出结论；（3）分两种情况：①当点M在点D的上方时，根据题意得：PQ=BP=t，AM=4t，AD=12，得出MD=AD-AM=12-4t，由PQ∥MD，当PQ=MD时，四边形PQDM是平行四边形，得出方程，解方程即可；②当点M在点D的下方时，根据题意得：PQ=BP=t，AM=4t，AD=12，得出MD=AM-AD=4t-12，由PQ∥MD，当PQ=MD时，四边形PQDM是平行四边形，得出方程，解方程即可．【详解】（1）解：∵BD⊥AC，∴∠ADB=90°，∴2222201612AD AB BD=-=-=（cm），（2）如图所示：∵AB=AC，∴∠ABC=∠C，即∠PBQ=∠C，∵PQ∥AC，∴∠PQB=∠C，∴∠PBQ=∠PQB，∴PB=PQ；（3）分两种情况：①当点M在点D的上方时，如图2所示：根据题意得：PQ=BP=t，AM=4t，AD=12，∴MD=AD-AM=12-4t，∵PQ∥AC，∴PQ∥MD，∴当PQ=MD时，四边形PQDM是平行四边形，即：当t=12-4t，时，四边形PQDM是平行四边形，解得：125t=（s）；②当点M在点D的下方时，如图3所示：根据题意得：PQ=BP=t，AM=4t，AD=12，∴MD=AM-AD=4t-12，∵PQ∥AC，∴PQ∥MD，∴当PQ=MD时，四边形PQDM是平行四边形，即：当t=4t-12时，四边形PQDM是平行四边形，解得：t=4（s）；综上所述，当125t s=或t=4s时，以P、Q、D、M为顶点的四边形为平行四边形．【点睛】本题是四边形综合题目，考查了平行四边形的判定、等腰三角形的判定与性质、勾股定理以及分类讨论等知识；本题综合性强，熟练掌握平行四边形的判定方法，进行分类讨论是解决问题（3）的关键．26．（1）证明见解析；（2）①t值为5或6；②点N运动的时间为6s，，或时，为等腰三角形.【分析】（1）设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，由勾股定理求出AC，即可得出结论；（2解析：（1）证明见解析；（2）①t值为5或6；②点N运动的时间为6s，365s，或5s时，ΔADN为等腰三角形.【分析】（1）设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，由勾股定理求出AC，即可得出结论；（2）①由△ABC的面积求出BD、AD、CD、AC；再分当MN∥BC时，AM＝AN和当DN∥BC时，AD＝AN两种情况得出方程，解方程即可；②分三种情况：AD=AN；DA=DN；和ND=NA，三种情况讨论即可【详解】解：（1）设BD＝2x，AD＝3x，CD＝4x，则AB＝5x，在Rt△ACD中，AC＝22AD CD＝5x，∴AB＝AC，∴△ABC是等腰三角形；（2）①S△ABC＝12×5x×4x＝40cm2，而x＞0，∴x＝2cm，则BD＝4cm，AD＝6cm，CD＝8cm，AC＝10cm．当MN∥BC时，AM＝AN，即10−t＝t，此时t＝5，当DN∥BC时，AD＝AN，此时t＝6，综上所述，若△DMN的边与BC平行时，t值为5或6；②ΔADN能成为等腰三角形，分三种情况：（ⅰ）若AD=AN=6，如图：则t=61=6s；（ⅱ）若DA=DN，如图：过点D 作DH AC ⊥于点H ，则AH =NH ，由1122ACD S AD CD AC DH =⋅=⋅，得11681022DH ⨯⨯=⨯⨯，解得245DH =，在Rt ADH 中，222224186()55AH AD DH =-=-=， 3625AN AH ∴==， 3615AN t s ∴==；（ⅲ）若ND =NA ，如图：过点N 作NQ AB ⊥于点Q ，则AQ =DQ =3，142NQ CD ==， 2222345AN AQ NQ ∴=++=，51AN t s ∴==；综上，点N 运动的时间为6s ，365s ，或5s 时，ΔADN 为等腰三角形. 【点睛】此题主要考查了等腰三角形的性质，平行线的性质，三角形的面积公式，勾股定理，解本题的关键是熟练掌握方程的思想方法和分类讨论思想．。

八年级下册数学期末试卷练习(Word版含答案)

八年级下册数学期末试卷练习（Word 版含答案）一、选择题1．要使二次根式3x -有意义，x 的值可以是（） A ．﹣1B ．0C ．2D ．42．已知下列三角形的各边长：①3、4、5，②3、4、6，③5、12、13，④5、11、12其中直角三角形有（） A ．4个B ．3个C ．2个D ．1个3．四边形ABCD 的对角线AC 和BD 相交于点O ，下列判断正确的是（） A ．若AO ＝OC ，则ABCD 是平行四边形 B ．若AC ＝BD ，则ABCD 是平行四边形C ．若AO ＝BO ，CO ＝DO ，则ABCD 是平行四边形 D ．若AO ＝OC ，BO ＝OD ，则ABCD 是平行四边形4．如图是甲、乙两人6次投篮测试（每次投篮10个）成绩的统计图，甲、乙两人测试成绩方差分别记作2S 甲、2S 乙，则下列结论正确的是（）A ．22 S S <甲乙B ．22S S >甲乙 C ．22S S =甲乙 D ．无法确定5．如图，点E 是边长为8的正方形ABCD 的对角线BD 上的动点，以AE 为边向左侧作正方形AEFG ，点P 为AD 的中点，连接PG ，在点E 运动过程中，线段PG 的最小值是（）A．2 B．2C．22D．426．如图，在菱形ABCD中，∠BAD＝80°，AB的垂直平分线交对角线AC于点F，垂足为E，连接DF，则∠CFD等于（）A．50°B．60°C．70°D．80°7．如图，在直角三角形ABC中，∠C=90°，AB=10，AC=8，点E，F分别为AC和AB的中点，则EF=()A．3 B．4 C．5 D．68．如图1，在矩形ABCD中，E是CD上一点，动点P从点A出发沿折线AE→EC→CB运动到点B时停止，动点Q从点A沿AB运动到点B时停止，它们的速度均为每秒1cm．如果点P、Q同时从点A处开始运动，设运动时间为x（s），△APQ的面积为ycm2，已知y与x的函数图象如图2所示，以下结论：①AB＝5cm；②cos∠AED＝35；③当0≤x≤5时，y＝225x；④当x＝6时，△APQ是等腰三角形；⑤当7≤x≤11时，y＝55522x+．其中正确的有（）A．2个B．3个C．4个D．5个二、填空题9．2021x-x的取值范围是____________．10．已知菱形ABCD的边长为4,∠A=60°，则菱形ABCD的面积为_________．11．如图，在△ ABC 中，∠C＝90°，∠ABC 的平分线 BD 交 AC 于点 D．若 BD＝10cm，BC＝8cm，则点 D 到直线 AB 的距离= ________．12．如图，在矩形ABCD 中，AB =8，AD =6，将矩形沿EF 翻折，使点C 与点A 重合，点B 落在B ′处，折痕与DC ，AB 分别交于点E ，F ，则DE 的长为______．13．已知一次函数的图象经过(2,0)，(0,4)-两点，则该一次函数解析式是______． 14．如图，O 是矩形ABCD 的对角线AC 、BD 的交点，OM ⊥AD ，垂足为M ，若AB=8，则OM 长为_______．15．如图，已知直线1:1l y x =+与x 轴交于点,A 与直线21:22l y x =+交于点B ，点C 为x 轴上的一点，若ABC ∆为直角三角形，则点C 的坐标为__________．16．如图，矩形ABCD 中，AB ＝6，BC ＝8，E 为AD 中点，F 为AB 上一点，将△AEF 沿EF 折叠后，点A 恰好落到CF 上的点G 处，则折痕EF 的长是_____．三、解答题17．（1）148312242÷+⨯- （2）(32126)2352--⨯+18．台风是一种自然灾害，它以台风中心为圆心在周围上千米的范围内形成极端气候，有极强的破坏力，有一台风中心沿东西方向AB 由点A 行驶向点B ，已知点C 为一海港，且点C 与直线AB 上两点A 、B 的距离分别为300km 和400km ，又AB ＝500km ，以台风中心为圆心周围250km 以内为受影响区域．（1）海港C 会受台风影响吗？为什么？（2）若台风的速度为20km/h ，台风影响该海港持续的时间有多长？19．如图，每个小正方形的边长都是1．A 、B 、C 、D 均在网格的格点上．（1）求边BC 、BD 的长度．（2）∠BCD 是直角吗？请证明你的判断．（3）找到格点E ，画出四边形ABED ，使其面积与四边形ABCD 面积相等（一个即可，且E 与C 不重合）．20．如图，在平行四边形ABCD 中，点P 是AB 边上一点（不与A ，B 重合），过点P 作PQ ⊥CP ，交AD 边于点Q ，且∠QPA ＝∠PCB ，QP ＝QD ．（1）求证：四边形ABCD 是矩形；（2）求证：CD ＝CP ．21．743+743+7212+437+=，4312⨯=，即：22(4)(3)7+=，4312=2227437212(4)243(3)((43)23++=+⨯+=+=问题：（1）填空：423+=__________，526-=____________﹔（2）进一步研究发现：形如2m n ±的化简，只要我们找到两个正数a ，b （a b >），使a b m +=，ab n =，即22()()a b m +=，a b n ⨯=﹐那么便有：2m n ±=__________．（3）化简：415-（请写出化简过程）22．由于持续高温和连日无雨，某水库的蓄水量y （万立方米）与干旱时间t （天）之间的关系满足一次函数y kt b =+，（k ，b 为常数，且k ≠0），其图象如图所示．（1）由图象知k = ，其实际意义是；（2）若水库的蓄水量小于360万立方米时，将发生严重干旱警报，那么多少天后将发生严重干旱警报？（3）在（2）的条件下，照这样干旱下去，预计再持续多少天，水库将干涸？ 23．如图，四边形ABCD ，，动点P 从点B 出发，沿BC 方向以每秒的速度运动到C 点返回，动点Q 从点A 出发，在线段AD 上以每秒的速度向点D 运动，点P ，Q 分别从点B ，A 同时出发，当点Q 运动到点D 时，点P 停止运动，设运动时间为t （秒）．（1）当时，是否存在点P ，便四边形PQDC 是平行四边形，若存在，求出t 值；若不存在，请说明理由；（2）当t 为何值时，以C ，D ，Q ，P 为顶点的四边形面积等于；（3）当时，是否存在点P ，使是等腰三角形？若存在，请求出所有满足要求的t 的值；若不存在，请说明理由．24．直线1l ：3y x =-交x 轴于A ，交y 轴于B ．（1）求AB 的长；（2）如图1，直线1l 关于y 轴对称的直线2l 交x 轴于点C ，直线3l ：12y x b =+经过点C ，点D 、T 分别在直线2l 、3l 上．若以A 、B 、D 、T 为顶点的四边形是平行四边形，求点D 的坐标；（3）如图2，平行y 轴的直线2x =交x 轴于点E ，将直线1l 向上平移5个单位长度后交x轴于M ，交y 轴于N ，交直线2x =于点P ．点()2,F t t 在四边形ONPE 内部，直线PF 交OE于G ，直线OF 交PE 于H ，求()GE ME HE +的值．25．探究：如图①，△ABC 是等边三角形，在边AB 、BC 的延长线上截取BM =CN ，连结MC 、AN ，延长MC 交AN 于点P ．（1）求证：△ACN ≌△CBM ；（2）∠CPN = °；（给出求解过程）（3）应用：将图①的△ABC 分别改为正方形ABCD 和正五边形ABCDE ，如图②、③，在边AB 、BC 的延长线上截取BM =CN ，连结MC 、DN ，延长MC 交DN 于点P ，则图②中∠CPN = °；（直接写出答案）（4）图③中∠CPN = °；（直接写出答案）（5）拓展：若将图①的△ABC 改为正n 边形，其它条件不变，则∠CPN = °（用含n 的代数式表示，直接写出答案）．【参考答案】一、选择题 1．D 解析：D 【分析】二次根式的被开方数大于等于零，由此计算解答．【详解】解：∵30x -≥，x≥，∴3观察只有D选项符合，故选：D．【点睛】此题考查二次根式有意义的条件：被开方数大于等于零．2．C解析：C【分析】判断是否可以构成直角三角形，只需验证两小边的平方和是否等于最长边的平方，即可得出答案．【详解】解：①222+=，能构成直角三角形；345②222+≠，不能构成直角三角形；346③222+=，能构成直角三角形；51213④222+≠，不能构成直角三角形；51112∴其中直角三角形有2个；故选：C．【点睛】本题主要考查了勾股定理的逆定理：如果三角形的三边长a，b，c满足222a b c，那么+=这个三角形就是直角三角形．3．D解析：D【解析】【分析】根据平行四边形的判定条件进行逐一判断即可.【详解】解：∵AO＝OC，BO＝OD，∴四边形的对角线互相平分∴D能判定ABCD是平行四边形．若AO＝BO，CO＝DO，证明AC=BD，并不能证明四边形ABCD是平行四边形，故C错误，若AO＝OC，条件不足，无法明四边形ABCD是平行四边形，故A错误，若AC＝BD，条件不足，无法明四边形ABCD是平行四边形，故B错误，故选D．【点睛】本题主要考查了平行四边形的判定，解题的关键在于能够熟练掌握平行四边形的判定条件. 4．A解析：A【解析】【分析】根据甲、乙的进球的统计图可知，甲的成绩波动幅度比乙的波动幅度小，由此即可得到答案．【详解】解：有题意可知，甲的成绩波动幅度比乙的波动幅度小，∴22S S甲乙，故选A．【点睛】本题主要考查了方差的定义，解题的关键在于能够熟练掌握，波动越小，方差越小．5．C解析：C【分析】连接DG，可证△AGD≌△AEB，得到G点轨迹，利用点到直线的最短距离进行求解．【详解】解：连接DG，如图，，∵四边形ABCD、四边形AEFG均为正方形，∴∠DAB＝∠GAE＝90°，AB＝AD，AG＝AE，∵∠GAD+∠DAE＝∠DAE+∠BAE，∴∠GAD＝∠BAE，∵AB＝AD，AG＝AE，∴△AEB≌△AGD（S A S），∴∠PDG＝∠ABE＝45°，∴G点轨迹为线段DH，当PG⊥DH时，PG最短，在Rt△PDG中，∠PDG＝45°，P为AD中点，DP＝4，设PG＝x，则DG＝x，由勾股定理得，x2+x2＝42，解得x＝2．故选：C．【点睛】本题主要考查正方形的性质，全等三角形的判定和性质，掌握连接DG，得到G点轨迹，是解题的关键．6．D解析：D 【解析】【分析】连接BF ，根据菱形的性质得出△ADF ≌△ABF ，从而得到∠ABF =∠ADF ，然后结合垂直平分线的性质推出∠ABF =∠BAC ，即可得出结论．【详解】解：如图，连接BF ，∵四边形ABCD 是菱形，∠BAD =80°， ∴AD =AB ，∠DAC =∠BAC=12∠BAD =40°，在△ADF 和△ABF 中， AD AB DAF BAF AF AF =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△ABF （SAS ）， ∴∠ABF =∠ADF ，∵AB 的垂直平分线交对角线AC 于点F ，E 为垂足， ∴AF =BF ，∴∠ABF =∠BAC =40°， ∴∠DAF =∠ADF =40°， ∴∠CFD =∠ADF +∠DAF =80°．故选：D ．【点睛】本题考查菱形的性质，全等三角形的判定与性质以及三角形的外角定理等，理解图形的基本性质是解题关键．7．A解析：A 【解析】【详解】∵直角三角形ABC 中，∠C ＝90°，AB ＝10，AC ＝8， ∴221086BC =-=．∵点E 、F 分别为AC 、AB 的中点，∴EF 是△ABC 的中位线， ∴116322EF BC ==⨯=．故选A ．8．B解析：B 【分析】根据图中相关信息即可判断出正确答案. 【详解】解：图2知：当57x ≤≤ 时y 恒为10，∴当5x ＝时，点Q 运动恰好到点B 停止，且当57x ≤≤ 时点P 必在EC 上， 5AB cm ∴＝，故①正确； ∵当57x ≤≤ 时点P 必在EC 上，且当7x ＞时，y 逐渐减小， ∴当7x ＝时，点Q 在点B 处，点P 在点C 处，此时10y ＝，47BC cm AE EC cm ∴+＝，＝，设EC acm ＝，则7AE a cm ＝（﹣）， 5DE a cm ＝（﹣），在Rt ADE ∆ 中，由勾股定理得：222457a a +（﹣）＝（﹣），解得：2a ＝，235EC cm DE cm AE cm ∴＝，＝，＝， 35DE cos AED AE ∴∠＝=，故②正确；当05x ≤≤ 时，由5AE cm ＝知点P 在AE 上，过点P 作PH AB ⊥，如图：35DE cos EAB cos AED AE ∠∠＝＝=， 45sin EAB ∴∠＝，AP AQ xcm ＝＝，45PH xcm ∴＝，212•25y AQ PH y ∴＝＝＝x ，故③正确；当6x ＝时，5AQ AB cm ＝＝，172PQ cm AP cm ＝，＝， APQ ∴∆ 不是等腰三角形，故④不正确；当711x ≤≤时，点P 在BC 上，点Q 和点B 重合，115555(74)2222y AQ PQ x x ==⨯⨯+-=-+ 故⑤ 不正确；故选B ．【点睛】本题主要考查了动点问题的函数图像，理解题意，读懂图像信息，灵活运用所学知识是解题关键，属于中考选择题中的压轴题.二、填空题 9．x ≥2021【解析】【分析】直接利用二次根式的定义分析得出答案．【详解】解：∵2021x -有意义，∴20210x -≥，解得：2021x ≥．故答案为：2021x ≥．【点睛】本题主要考查了二次根式有意义的条件，正确掌握定义是解题关键．10．A解析：83【解析】【分析】作出图形，利用30°直角三角形的性质求出高，利用菱形的面积公式可求解．【详解】如图所示，菱形ABCD 中，AB=AD=4，∠A=60°，过点D 作DE ⊥AB 于点E ，则3sin 6043DE AD =︒== ∴菱形ABCD 的面积为AB ∙DE=4×2383故答案为：83【点睛】本题考查了菱形的性质，熟练运用30°直角三角形的性质以及菱形的面积公式是本题的关键．11．D解析：6cm【解析】【分析】过点D作DE⊥AB于E，利用勾股定理列式求出CD，再根据角平分线上的点到角的两边距离相等可得DE=CD即可求解．【详解】如图，过点D作DE⊥AB于E，∵∠C=90°，BD=10cm，BC=8cm，∴226BD BC-cm，∵∠C=90°，BD是∠ABC的平分线，∴DE=CD=6cm，即点D到直线AB的距离是6cm．故答案为：6cm．【点睛】本题考查了勾股定理、角平分线的性质、点到直线的距离等知识，在解题时要能灵活应用各个知识点是本题的关键．12．D解析：7 4【分析】设DE=x，则CE=8-x，根据折叠的性质知：CE=8-x．在直角△AED中，利用勾股定理列出关于x的方程并解答即可．【详解】解：如图，在矩形ABCD中，AB=DC=8，AD=6．设DE=x，则CE=8-x，根据折叠的性质知：AE=CE=8-x．在直角△AED中，由勾股定理得：AD2+DE2=AE2，即62+x2=（8-x）2．解得x=74．即DE的长为74．故答案是：74．【点睛】本题主要考查了翻折变换（折叠问题），矩形的性质，解题时，借用了方程思想，求得了相关线段的长度．13．y=2x-4【分析】由一次函数的图象经过（2，0），（0，-4）两点，可设一次函数解析式为y=kx+b（k≠0）．然后将点的坐标代入解析式，故得2k+b=0，b=-4．进而推导出函数解析式为y=2x-4．【详解】解：设该一次函数的解析式为：y=kx+b（k≠0）．由题意得：2004k bk b+=⎧⎨⋅+=-⎩，解得：24kb=⎧⎨=-⎩，∴该一次函数的解析式为y=2x-4．故答案为：y=2x-4．【点睛】本题主要考查用待定系数法求一次函数解析式，熟练掌握用待定系数法求一次函数解析式是解决本题的关键．14．A解析：4【解析】【分析】根据三角形的中位线即可求解.【详解】∵O 是矩形ABCD 的对角线AC 、BD 的交点，∴O 是AC 中点，又OM ⊥AD ，AD ⊥CD ∴12∥OM CD ,又AB=CD=8 故OM=4故填：4【点睛】此题主要考查矩形的性质，解题的关键是熟知三角形中位线的性质.15．(2，0)或（5，0）【分析】先求出A ，再求出，解得，则点B （2，3），分类讨论直角顶点，当点C 为直角顶点时，当点B 为直角顶点时，根据△ABC 为等腰直角三角形即可求出点C 坐标．【详解】与轴交解析：(2，0)或（5，0）【分析】先求出A ，再求出1122y x y x =+⎧⎪⎨=+⎪⎩，解得=23x y ⎧⎨=⎩，则点B （2，3），分类讨论直角顶点，当点C 为直角顶点时，当点B 为直角顶点时，根据△ABC 为等腰直角三角形即可求出点C 坐标．【详解】1:1l y x =+与x 轴交于点A ，∴y=0，x=-1，∴A(-1，0)，直线1:1l y x =+与直线21:22l y x =+交于点B ， 1122y x y x =+⎧⎪⎨=+⎪⎩，解得=23x y ⎧⎨=⎩， ∴B （2，3），当点C 为直角顶点时，∴BC ⊥AC ，∴BC ∥y 轴，B 、C 横坐标相同，C （2，0），当点B为直角顶点时，∴BC⊥AB，1:1l y x=+，k=1，∴∠BAC=45°，∴△ABC为等腰直角三角形，∴AB=()222+1+3=32，AC=2AB=6，AO=1，CO=AC-AO=5，C（5，0），C点坐标为（2，0）或（5，0）．故答案为：（2，0）或（5，0）．【点睛】本题考查等腰直角三角形的性质，掌握直角三角形的顶点分两种情况讨论解决问题是关键．16．【分析】连接EC，利用矩形的性质以及折叠的性质，即可得到△CDE与△CGE全等，设AF=x，则可得CF=x+6，BF=6-x，在Rt△BCF中利用勾股定理即可得到x的值，在Rt△AEF中利用勾股4133【分析】连接EC，利用矩形的性质以及折叠的性质，即可得到△CDE与△CGE全等，设AF=x，则可得CF=x+6，BF=6-x，在Rt△BCF中利用勾股定理即可得到x的值，在Rt△AEF中利用勾股定理即可求出EF的长度．【详解】解：如图所示，连接CE，∵E 为AD 中点，∴AE ＝DE ＝4，由折叠可得，AE ＝GE ，∠EGF ＝∠A ＝90°，∴DE ＝GE ，又∵∠D ＝90°，∴∠EGC ＝∠D ＝90°，又∵CE ＝CE ，∴Rt △CDE ≌Rt △CGE （HL ），∴CD ＝CG ＝6，设AF ＝x ，则GF ＝x ，BF ＝6﹣x ，CF ＝6＝x ，∵∠B ＝90°，∴Rt △BCF 中，BF 2+BC 2＝CF 2，即（6﹣x ）2+82＝（x+6）2，解得x ＝83， ∴AF ＝83， ∵∠A ＝90°，∴Rt △AEF 中，EF 22AE AF +2284()3+4133 4133【点睛】本题主要考查了矩形的性质以及折叠问题，解题时我们常常设要求的线段长为x ，然后根据折叠和轴对称的性质用含x 的代数式表示其他线段的长度，选择适当的直角三角形，运用勾股定理列出方程求出答案．三、解答题17．（1）；（2）【分析】（1）先计算二次根式的除法和乘法，再进行二次根式的加减运算；（2）先化简最简二次根式，然后进行二次根式的乘法，最后合并同类二次根式即可．【详解】（1）原式；解析：（1）4；（2）18-【分析】（1）先计算二次根式的除法和乘法，再进行二次根式的加减运算；（2）先化简最简二次根式，然后进行二次根式的乘法，最后合并同类二次根式即可．【详解】（1）原式=4=4=（2）原式=⨯624=--18=-【点睛】本题考查了二次根式的混合运算，掌握二次根式的运算法则并能正确进行运算是关键． 18．（1）会，理由见解；（2）7h【分析】（1）利用勾股定理的逆定理得出△ABC 是直角三角形，进而利用三角形面积得出CD 的长，从而判断出海港C 是否受台风影响；（2）利用勾股定理得出ED 以及EF 的长解析：（1）会，理由见解；（2）7h【分析】（1）利用勾股定理的逆定理得出△ABC 是直角三角形，进而利用三角形面积得出CD 的长，从而判断出海港C 是否受台风影响；（2）利用勾股定理得出ED 以及EF 的长，进而得出台风影响该海港持续的时间．【详解】解：（1）如图所示，过点C 作CD ⊥AB 于D 点，∵AC =300km ，BC =400km ，AB =500km ，∴222AC BC AB +=，∴△ABC 为直角三角形， ∴1122··AC BC AB CD =， ∴300400500CD ⨯=，∴240km CD =，∵以台风中心为圆心周围250km 以内为受影响区域，∴海港C 会受到台风影响；（2）由（1）得CD =240km ，如图所示，当EC =FC =250km 时，即台风经过EF 段时，正好影响到海港C ，此时△ECF为等腰三角形，∵2270km=-=，ED EC CD∴EF=140km，∵台风的速度为20km/h，∴140÷20=7h，∴台风影响该海港持续的时间有7h．【点睛】本题考查的是勾股定理在实际生活中的运用，解答此类题目的关键是构造出直角三角形，再利用勾股定理解答．19．（1），；（2）不是直角，证明见解析；（3）见解析【解析】【分析】（1）利用勾股定理求解即可．（2）利用勾股定理的逆定理判断即可．（3）利用等高模型解决问题即可．【详解】解：（1）BC解析：（12922）不是直角，证明见解析；（3）见解析【解析】【分析】（1）利用勾股定理求解即可．（2）利用勾股定理的逆定理判断即可．（3）利用等高模型解决问题即可．【详解】解：（1）BC2225+29，BD22+4244（2）结论：不是直角．理由：∵CD5BC29，BD=42∴BC2+CD2≠BD2，∴∠BCD≠90°．（3）如图，四边形ABED即为所求．【点睛】本题考查作图-应用与设计作图，勾股定理，勾股定理的逆定理，四边形的面积等知识，解题的关键是掌握勾股定理以及勾股定理的逆定理解决问题，属于中考常考题型．20．（1）见解析；（2）见解析【分析】（1）根据垂直求出∠QPC=90°，求出∠QPA+∠BPC=90°，求出∠BPC+∠PCB=90°，根据三角形内角和定理求出∠B=90°，再根据矩形的判定得出即解析：（1）见解析；（2）见解析【分析】（1）根据垂直求出∠QPC=90°，求出∠QPA+∠BPC=90°，求出∠BPC+∠PCB=90°，根据三角形内角和定理求出∠B=90°，再根据矩形的判定得出即可；（2）连接CQ，根据全等三角形的判定定理HL推出Rt△CDQ≌Rt△CPQ，根据全等三角形的性质推出即可．【详解】解：证明：（1）∵PQ⊥CP，∴∠QPC=90°，∴∠QPA+∠BPC=180°-90°=90°，∵∠QPA=∠PCB，∴∠BPC+∠PCB=90°，∴∠B=180°-（∠BPC+∠PCB）=90°，∵四边形ABCD是平行四边形，∴四边形ABCD是矩形；（2）连接CQ，∵四边形ABCD是矩形，∴∠D=90°，∵∠CPQ=90°，∴在Rt△CDQ和Rt△CPQ中，CQ CQ DQ PQ=⎧⎨=⎩， ∴Rt △CDQ ≌Rt △CPQ （HL ），∴CD =CP ．【点睛】本题考查了三角形内角和定理，垂直的定义，矩形的判定和性质，全等三角形的性质和判定，能求出∠B =90°和Rt △CDQ ≌Rt △CPQ 是解此题的关键．21．（1），；（2）；（3）【解析】【分析】（1）根据题目所给的方法将根号下的数凑成完全平方的形式进行计算；（2）根据题目给的a ，b 与m 、n 的关系式，用一样的方法列式算出结果；（3）将写成，4解析：（112)a b >；（3【解析】【分析】（1）根据题目所给的方法将根号下的数凑成完全平方的形式进行计算；（2）根据题目给的a ，b 与m 、n 的关系式，用一样的方法列式算出结果；（34写成3522+，就可以凑成完全平方的形式进行计算．【详解】解：（11；（2)a b ===>；（3．【点睛】本题考查二次根式的计算和化简，解题的关键是掌握二次根式的运算法则．22．（1）；水库蓄水量每天减少30万立方米；（2）38；（3）12【分析】（1）根据图像运用待定系数法求得函数解析式即可得k 的值，解释k 的具体意义即可；（2）根据（1）中函数解析式，令万立方米时，解析：（1）30-；水库蓄水量每天减少30万立方米；（2）38；（3）12【分析】（1）根据图像运用待定系数法求得函数解析式即可得k 的值，解释k 的具体意义即可；（2）根据（1）中函数解析式，令360y =万立方米时，求出对应的干旱天数t 即可；（3）根据（1）中函数解析式，令0y =万立方米时，求出对应的干旱天数t ，减去（2）中的干旱天数即为所求．【详解】解：（1）一次函数y kt b =+，（k ，b 为常数，且k ≠0），根据图像可得：900=2030040k b k b+⎧⎨=+⎩，解得：301500k b =-⎧⎨=⎩，所以一次函数解析式为：301500y t =-+，k 的值代表每干旱一天水库蓄水量将减少30万立方米,故答案为：-30；水库蓄水量每天减少30万立方米；（2）由（1）知一次函数解析式为：301500y t =-+，令360y =，即360301500t =-+，解得：38t =，故38天后将发生严重干旱警报；（3）由（1）知一次函数解析式为：301500y t =-+，令0y =，即0301500t =-+，解得：50t =，503812-=(天)，故预计再持续12天，水库将干涸．【点睛】此题考查了函数的图像问题，一次函数的实际应用，根据图像求出一次函数的解析式是解题的关键．23．（1）存在，t=3；（2）秒；（3）存在，t=3秒或t=秒【分析】（1）根据运动得出CP=15-3t ，DQ=12-2t ，进而用平行四边形的对边相等建立方程求解即可；（2）要使以C 、D 、Q 、P 为解析：（1）存在，t =3；（2）秒；（3）存在，t =3秒或t =秒【分析】（1）根据运动得出CP =15-3t ，DQ =12-2t ，进而用平行四边形的对边相等建立方程求解即可；（2）要使以C 、D 、Q 、P 为顶点的梯形面积等于30cm 2，可以分为两种情况，点P 、Q 分别沿A D 、BC 运动或点P 返回时，再利用梯形面积公式，即=30，因为Q 、P点的速度已知，A D、A B、BC的长度已知，用t可分别表示DQ、BC的长，解方程即可求得时间t；（3）使△PQD是等腰三角形，可分三种情况，即PQ=P D、PQ=Q D、QD=PD；可利用等腰三角形及直角梯形的性质，分别用t表达等腰三角形的两腰长，再利用两腰相等即可求得时间t．【详解】解：（1）∵四边形PQDC是平行四边形∴DQ=CP当0＜t＜5时，点P从B运动到C，∵DQ=AD-AQ=12-2t，CP=15-3t，∴12-2t=15-3t解得t=3，∴t=3时，四边形PQDC是平行四边形；（2）如图2，①当点P是从点B向点C运动，由（1）知，CP=15-3t，DQ=12-2t，∵以C、D、Q、P为顶点的四边形面积等于30cm2，∴S四边形CDQP＝＝30，即12(15−3t+12−2t)×10＝30，解得：t=，②当点P是从点C返回点B时，由运动知，DQ=12-2t，CP=3t-15，∵以C、D、Q、P为顶点的四边形面积等于30cm2，∴S四边形CDQP＝12(DQ+CP)•AB=12(12−2t+3t−15)×10＝30，解得：t=9（舍去），∴当t为秒时，以C、D、Q、P为顶点的四边形面积等于30cm2；（3）当PQ=PD时，如图3，作PH⊥AD于H，则HQ=HD，∵QH =HD =12DQ =12（12-2t ）=6-t ，由AH =BP ，∴6-t +2t =3t解得：t =3秒；当PQ =DQ 时，QH =AH -AQ =BP -AQ =3t -2t =t ，DQ =12-2t ，∵DQ 2=PQ 2=t 2+102，∴（12-2t ）2=102+t 2，整理得：3t 2-48t +44=0，解得：t =秒， ∵0＜t ＜5，∴t =秒，当DQ =PD 时，DH =AD -AH =AD -BP =12-3t ，∵DQ 2=PD 2=PH 2+HD 2=102+（12-3t ）2∴（12-2t ）2=102+（12-3t ）2即5t 2-24t +100=0，∵△＜0，∴方程无实根，综上可知，当t =3秒或t =秒时，△PQD 是等腰三角形．【点睛】本题是四边形综合题，主要考查了平行四边形的判定与性质、梯形的面积、等腰三角形的性质，解题的关键是分类思想与方珵思想的综合运用．24．（1）；（2）点D 的坐标为或或；（3）．【解析】【分析】（1）根据直线的解析式求出其与x 轴的交点A 和与y 轴的交点B 的坐标，进而求出OA 与OB 的长度，再使用勾股定理即可求出AB 的长度；（2）根解析：（1）32AB =2）点D 的坐标为(2,1)--或(4,1)-或(2,5)-；（3）()8GE ME HE +=．【解析】【分析】（1）根据直线1l 的解析式求出其与x 轴的交点A 和与y 轴的交点B 的坐标，进而求出OA 与OB 的长度，再使用勾股定理即可求出AB 的长度；（2）根据直线1l 和直线2l 关于y 轴对称求出直线2l 的解析式，再求出直线3l 的解析式，根据点D 在直线2l 上，可设点(,3)D m m --，然后分类讨论点D 是在线段BC 上，还是在线段BC 的延长线上，或者在线段CB 的延长线上，在每一种情况下结合平行四边形的性质和平移的性质，可用含有m 的式子表示点T 的坐标，再根据点T 在直线3l 上求出m 的值，即可求出点D 的坐标；（3）根据平移的性质求出直线MN 的解析式，再结合直线x =2求出点(2,0)E ，点(2,4)P 和点(2,0)M -，进而求出ME 的长度，然后再结合点()2,F t t 求出直线:(2)2PF y t x t =+-和直线:OF y tx =，进而求出点2,02t G t ⎛⎫ ⎪+⎝⎭和(2,2)H t ，即可得到GE 与HE 的长度，最后再代入计算()GE ME HE +即可．【详解】解：（1）∵直线1:3l y x =-交x 轴于A ，交y 轴于B ，∴0A y =，0B x =．∴03A x =-，03B y =-．∴3A x =，3B y =-．∴(3,0)A ，(0,3)B -．∴3OA =，3OB =．∵AO BO ⊥， ∴AB =（2）∵直线1l 关于y 轴对称的直线2l 交x 轴于点C ，直线1l 交x 轴与点(3,0)A ， ∴点A 与点C 关于y 轴对称．∴(3,0)C -．∵点(0,3)B -在y 轴上，∴直线2l 经过点B ．∴设直线23:l y kx =-．∵直线2l 经过点(3,0)C -，∴033k =--．解得：1k =-．∴直线23:l y x =--．∵直线31:2l y x b =+经过点(3,0)C -， ∴10(3)2b =⨯-+．解得：32b =． ∴直线31322:y x l =+． ∵点D 在直线23:l y x =--上，∴设点(,3)D m m --．①如下图所示，当点D 在线段BC 上时．∵四边形ABDT 是平行四边形，∴//,AT BD AT BD =．∴BD 经过平移之后到达AT ．∴(3,)T m m +-．∵点T 在直线31322:y x l =+上， ∴13(3)22m m -=++，解得2m =-． ∴1(2,1)D --；②如下图所示，当点D 在线段BC 的延长线上时．∵四边形ABTD 是平行四边形，∴//,AD BT AD BT =．∴AD 经过平移之后到达BT ．∴(3,6)T m m ---．∵点T 在直线31322:y x l =+上， ∴136(3)22m m --=-+，解得4m =-． ∴2(4,1)D -；③如下图所示，当点D 在线段CB 的延长线上时．∵四边形ADBT 是平行四边形，∴//,AT DB AT DB =．∴BD 经过平移之后到达TA ．∴(3,)T m m -．∵点T 在直线31322:y x l =+上， ∴13(3)22m m =-+，解得2m =． ∴3(2,5)D -．综上所述，点D 的坐标为(2,1)--或(4,1)-或(2,5)-．（3）直线1l 向上平移5个单位长度得到的直线MN 解析式为352y x x =-+=+． ∵直线x =2与x 轴交于点E ，与直线MN 交于点P ，直线MN 交x 轴于点M ，∴(2,0)E ，2P x =，0M y =．∴22P y =+，02M x =+．∴4P y =，2M x =-．∴(2,4)P ，(2,0)M -．∴2(2)4E M ME x x =-=--=，设直线PF 的解析式为y px q =+，∵直线PF 经过点(2,4)P 与()2,F t t ， ∴242,,p q t tp q =+⎧⎨=+⎩解得2,2p t q t =+⎧⎨=-⎩． ∴直线PF 的解析式为(2)2y t x t =+-．∵直线PF 与x 轴交于点G ，∴0G y =．∴0(2)2G t x t =+-．解得：22G t x t =+． ∴2,02t G t ⎛⎫ ⎪+⎝⎭． ∴24222E G t GE x x t t =-=-=++．设直线OF 的解析式为y =cx ，∵直线OF 经过点()2,F t t ， ∴2t ct =．解得：c t =．∴直线OF 的解析式为y tx =．∵直线OF 与直线2x =交于点H ．∴2H x =．∴22H H y tx t t ==⨯=．∴(2,2)H t ．∴202H E HE y y t t =-=-=． ∴4()(42)82GE ME HE t t +=+=+．【点睛】本题考查了一次函数的综合应用，涉及坐标与长度的关系，勾股定理，轴对称和平移的性质，平行四边形的性质和判定定理，代数式求值，应用一次函数的性质正确求出点的坐标是解题关键． 25．（1）见解析；（2）120；（3）90；（4）72；（5）.【分析】（1）利用等边三角形的性质得到BC=AC ，∠ACB=∠ABC ，从而得到△ACN ≌△CBM.（2）利用全等三角形的性质得到∠C解析：（1）见解析；（2）120；（3）90；（4）72；（5）360n. 【分析】（1）利用等边三角形的性质得到BC=AC ，∠ACB=∠ABC ，从而得到△ACN ≌△CBM.（2）利用全等三角形的性质得到∠CAN=∠BCM ，再利用三角形的外角等于与它不相邻的两个内角的和，即可求解.（3）利用正方形（或正五边形）的性质得到BC=DC ，∠ABC=∠BCD ，从而判断出△DCN ≌△CBM ，再利用全等三角形的性质得到∠CDN=∠BCM ，再利用内角和定理即可得到答案.（4）由（3）的方法即可得到答案.（5）利用正三边形，正四边形，正五边形，分别求出∠CPN 的度数与边数的关系式，即可得到答案.【详解】（1）∵△ABC 是等边三角形，∴BC=AC ，∠ACB=∠BAC=∠ABC=60︒，∴∠ACN=∠CBM=120︒，在△CAN 和△CBM 中，CN BM ACN CBM AC BC =⎧⎪∠=∠⎨⎪=⎩， ∴△ACN ≌△CBM.（2）∵△ACN ≌△CBM.∴∠CAN=∠BCM ，∵∠ABC=∠BMC+∠BCM ，∠BAN=∠BAC+∠CAN ，∴∠CPN=∠BMC+∠BAN=∠BMC+∠BAC+∠CAN=∠BMC+∠BAC+∠BCM=∠ABC+∠BAC=60︒+60︒,=120︒，故答案为：120.（3）将等边三角形换成正方形，∵四边形ABCD 是正方形，∴BC=DC ，∠ABC=∠BCD=90︒，∴∠MBC=∠DCN=90︒，在△DCN 和△CBM 中，DC BC DCN MBC CN BM =⎧⎪∠=∠⎨⎪=⎩， ∴△DCN ≌△CBM ，∴∠CDN=∠BCM ，∵∠BCM=∠PCN ，∴∠CDN=∠PCN ，在Rt △DCN 中，∠CDN+∠CND=90︒，∴∠PCN+∠CND=90︒，∴∠CPN=90︒，故答案为：90.（4）将等边三角形换成正五边形，∴∠ABC=∠DCB=108︒，∴∠MBC=∠DCN=72︒，在△DCN 和△CBM 中，DC BC DCN MBC CN BM =⎧⎪∠=∠⎨⎪=⎩， ∴△DCN ≌△CBM ，∴∠BMC=∠CND ，∠BCM=∠CDN ，∵∠BCM=∠PCN ，∴∠CND=∠PCN ，在△CDN 中，∠CDN+∠CND=∠BCD=108︒，∴∠CPN=180︒-(∠CND+∠PCN)=180︒-(∠CND+∠CDN)=180︒-108︒，=72︒，故答案为：72.（5）正三边形时，∠CPN=120︒=3603，正四边形时，∠CPN=90︒=3604，正五边形时，∠CPN=72︒=3605，正n 边形时，∠CPN=360n ，故答案为：360n . 【点睛】此题考查正多边形的性质，三角形全等的判定及性质，图形在发生变化但是解题的思路是不变的，依据此特点进行解题是解此题的关键.。

北京市东城区2023-2024学年八年级上学期期末考试语文试卷(word版,含答案)

北京市东城区2023-2024学年八年级上学期期末考试语文2024.1学校______班级_____姓名_____教育ID 号____一、基础・运用（共13分）杭州第19届亚运会圆满闭幕，亚运会中有关非遗文化的精彩瞬间至今仍令人回味。

在综合实践课程中，你所在的小组完成了相关展板的文字介绍。

现在你根据小组成员的意见修改。

1.在展览文字介绍的封面，用正楷字书写“亚运让非遗熠熠生辉”九个字作为标题。

（1分）前言将“你”“我”汇成“我们”亚运会通过体育竞技的方式，将亚洲各国和地区紧密联系到了一起，让翘．首以盼的“亚洲命运共同体”更加真切可感。

也正是通过这项盛事，亚洲多姿多彩的文化得以章显。

从风雅颂歌到梅兰竹菊，满满的东方文化元素向八方宾朋展现一场体育盛会如何牵手“中国式浪漫”，一个现代之城如何在守正创新中再现马可・波罗笔下记载的“世界最富丽名贵之城”。

杭州及其协办城市努力向世界展示了一个欣欣向荣的中国，让世界与之联结。

2.有同学认为画横线的词语中有错别字，对加点字的读音也有疑问。

下列判断错误．．的一项是（2分） A.“翘”应读为“qi áo ”B “章显”应写为“彰显” C.“载”应读为“z ǎi ”D.“联结”应写为“联节”第一部分亚运刮起“非遗风”走进亚运村，非物质文化遗产展览陈列区前的宾客总是摩肩接踵．．．．。

一条长达60米的“中华龙”风筝精．妙绝伦．．．，象征着华夏文明的源远流长、博大精深。

典雅的瓷器、精美的扇子、精致的丝绸设计者自出心裁．．．．，呈现出中华文化的深沉与繁华。

很多宾客对其中一把巨大的西湖绸伞印象尤为深刻。

它顶天立地．．．．，设计奇巧，制作精细，既实用，又有艺术欣赏价值，将伞与丝绸有机结合起来。

乘着这阵“非遗风”，各方来宾感悟着中华文化的独特魅力。

3.你检查文段中使用的成语后发现，下列成语使用不恰当．．．的一项是（2分） A.摩肩接踵 B.精妙绝伦 D. 自出心裁 D.顶天立地第二部分跟着亚运去“采风”就在2022年，“中国庙统制茶技艺及其相关习俗”项目正式入选联合国教科文组织新一批人类非物质文化遗产代表作名录，径山茶宴正是其中一项。

八年级下册数学期末试卷复习练习(Word版含答案)

八年级下册数学期末试卷复习练习(Word 版含答案) 一、选择题 1．式子1x -在实数范围内有意义，则x 的取值范围是（）A ．x ＜1B ．x ≥0C ．x ＞1D ．x ≥1 2．下列条件中，不能判断ABC （a 、b 、c 为三边，A ∠、B 、C ∠为三内角）为直角三角形的是（）A ．2221,2,3a b c ===B ．::3:4:5a b c =C ．A B C ∠+∠=∠D ．::3:4:5A B C ∠∠∠= 3．给出下列命题，其中错误命题的个数是（）①四条边相等的四边形是正方形；②四边形具有不稳定性；③有两个锐角对应相等的两个直角三角形全等；④一组对边平行的四边形是平行四边形．A ．1B ．2C ．3D ．44．期间，红星中学门卫对周末提前返校的5名学生进行体温检测，记录如下：36.1℃，36.5℃，36.9℃，36.5℃，36.6℃，则这5名学生体温的众数是（）A ．36.1℃B ．36.6℃C ．36.5℃D ．36.9℃ 5．如图，平行四边形ABCD 的对角线AC 与BD 相交于点O ．CE ⊥AD 于点E ，AB ＝23，AC ＝4，BD ＝8，则CE ＝（）A ．72B ．2217C ．4217D ．76．如图，在平行四边形纸片ABCD 中，对角线AC 与BD 相交于点E ，∠AEB ＝45°，BD ＝4，将纸片沿对角线AC 对折，使得点B 落在点B ′的位置，连接DB '，则DB '的长为（）A ．22B ．23C ．42D ．15 7．△ABC 中，AB ＝6，BC ＝5，AC ＝7，点D 、E 、F 分别是三边的中点，则△DEF 的周长为（）A ．5B ．9C ．10D ．188．一个容器内有进水管和出水管，开始4min 内只进水不出水，在随后的8min 内既进水又出水，第12min 后只出水不进水.进水管每分钟的进水量和出水量每分钟的出水量始终不变，容器内水量y （单位：L ）与时间x （单位：min ）之间的关系如图所示．根据图象有下列说法：①进水管每分钟的进水量为5L ；②412x ≤≤时，5154y x =+；③当12x =时，30y =；④当15y =时，3x =，或17x =．其中正确说法的个数是（） A ．1个 B ．2个 C ．3个 D ．4个二、填空题9．若二次根式1x -在实数范围内有意义，则x 的取值范围是______________． 10．如图，菱形ABCD 的边长为5cm ，正方形AECF 的面积为18cm 2，则菱形的面积为 ___cm 2．11．如图，矩形ABCD 的对角线AC 与BD 相交于点O ，∠AOD ＝60°，AD ＝4，则AB ＝___．12．如图，已知矩形ABCD 的对角线AC 的长为10cm ，顺次连结各边中点E 、F 、G 、H 得四边形EFGH ，则四边形EFGH 的周长为______cm ．13．定义：对于一次函数y kx b =+，我们把点(),b k 称为这个一次函数的伴随点.已知一次函数4y x m =+-的伴随点在它的图象上，则=m __________．14．在矩形ABCD 中，∠B 的平分线BE 与AD 交于点E ，∠BED 的平分线EF 与DC 交于点F ，若AB =9，DF =2FC ，则BC =___________.（结果保留根号）15．在平面直角坐标系中，矩形OABC 的顶点O 为坐标原点，顶点A ，C 分别在x 轴和y 轴上，OA ＝4，OC ＝3，D 为AB 边的中点，E 是OA 边上的一个动点，当△CDE 的周长最小时，则点E 的坐标为_____．16．如图所示，将矩形ABCD 沿直线AE 折叠（点E 在边CD 上），折叠后顶点D 恰好落在边BC 上的点F 处，若AD ＝5，AB ＝4，则EC 的长是_____．三、解答题17．计算：（1）1632（2）2055+；（3）2214524-；（4）11 12333-⎛⎫+-- ⎪⎝⎭．18．湖的两岸有A，B两棵景观树，数学兴趣小组设计实验测量两棵景观树之间的距离，他们在与AB垂直的BC方向上取点C，测得30BC=米，50AC=米．求：（1）两棵景观树之间的距离；（2）点B到直线AC的距离．19．如图，在4×3正方形网格中，每个小正方形的边长都是1，正方形顶点叫格点，连接两个网格格点的线段叫网格线段，点A固定在格点上．（1）若a是图中能用网格线段表示的最小无理数，b是图中能用网格线段表示的最大无理数，则a＝，b＝；（2）请你画出顶点在格点上且边长为5的所有菱形ABCD，你画出的菱形面积为；20．已知：如图，在ABC中，AD是BAC∠的平分线，//,//DE AC DF AB．求证：四边形AEDF是菱形．21．阅读理解题：定义：如果一个数的平方等于﹣1，记为i2＝﹣1，这个数i叫做虚数单位，把形如a+bi （a，b为实数）的数叫做复数，其中a叫这个复数的实部，b叫做这个复数的虚部，它的加、减、乘、除运算与代数式的运算类似．例如：计算：（2﹣i）+（5+3i）＝（2+5）+（﹣1+3）i＝7+2i；（1+i）×（2﹣i）＝1×2﹣i+2×i﹣i2＝2+（﹣1+2）i+1＝3+i；根据以上信息，完成下列问题：（1）填空：i3＝，i4＝，i+i2+i3+…+i2021＝；（2）计算：（1+i）×（3﹣4i）﹣（﹣2+3i）（﹣2﹣3i）；（3）已知a+bi＝2543i-（a，b为实数），求2222(24)x a x b++-+的最小值．22．某景区今年对门票价格进行动态管理．节假日期间，10人以下（包括10人）不打折，10人以上超过10人的部分打折；非节假日期间全部打折．设游客为x人，非节假日门票费用y1（元）及节假日门票费用y2（元）与游客x（人）之间的函数关系如图所示．（1）求不打折的门票价格；（2）求y1、y2与x之间的函数关系式；（3）导游小王5月2日（五一假日）带A旅游团，5月8日（非节假日）带B旅游团到该景区旅游，两团共计50人，两次共付门票费用3040元，求A、B两个旅游团各多少人？（温馨提示：节假日的折扣与非节假日的折扣不同）23．如图①，C为线段BD上的一点，BC≠CD，分别以BC，BD为边在BD的上方作等边△ABC和等边△CDE，连接AE，F，G，H分别是BC，AE，CD的中点，连接FG，GH，FH．（1）△FGH的形状是；（2）将图①中的△CDE绕点C顺时针旋转，其他条件不变，（1）的结论是否成立？结合图②说明理由；（3）若BC＝，CD＝4，将△CDE绕点C旋转一周，当A，E，D三点共线时，直接写出△FGH的周长．24．已知：直线364y x=+与x轴、y轴分别相交于点A和点B，点C在线段AO上．将BCO∆沿BC折叠后，点O恰好落在AB边上点D处．（1）直接写出点A、点B的坐标：（2）求AC的长；（3）点P为平面内一动点，且满足以A、B、C、P为顶点的四边形为平行四边形，请直接回答：①符合要求的P点有几个？②写出一个符合要求的P点坐标．25．某数学活动小组在一次活动中，对一个数学问题作如下研究：（1）如图1，△ABC中分别以AB，AC为边向外作等腰△ABE和等腰△ACD使AE＝AB，AD ＝AC，∠BAE＝∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．（2）如图2，△ABC中分别以AB，AC为边向外作等腰Rt△ABE和等腰Rt△ACD，∠EAB＝∠CAD＝90°，连接BD，CE，若AB＝4，BC＝2，∠ABC＝45゜，求BD的长．（3）如图3，四边形ABCD中，连接AC，CD＝BC，∠BCD＝60°，∠BAD＝30°，AB＝15，AC＝25，求AD的长．【参考答案】一、选择题1．D解析：D【分析】根据二次根式中的被开方数必须是非负数列出不等式，解不等式即可得出结果．【详解】10x ∴-≥．解得1≥x ．故选D ．【点睛】本题考查了二次根式有意义的条件，熟练掌握二次根式有意义的条件是解题的关键． 2．D解析：D【分析】综合勾股定理以及直角三角形的性质逐项分析即可．【详解】A 、∵2221,2,3a b c ===，∴222+=a b c ，ABC 是以C ∠为直角的直角三角形，不符合题意；B 、∵::3:4:5a b c =，∴222+=a b c ，ABC 是以C ∠为直角的直角三角形，不符合题意；C 、∵A B C ∠+∠=∠，180A B C ∠+∠+∠=︒，∴90C ∠=︒，ABC 是以C ∠为直角的直角三角形，不符合题意；D 、∵::3:4:5A B C ∠∠∠=，180A B C ∠+∠+∠=︒，∴45A ∠=︒，60B ∠=︒，75C ∠=︒，ABC 不是直角三角形，符合题意；故选：D ．【点睛】本题考查直角三角形的性质，熟练掌握勾股定理以及直角三角形的基本性质是解题关键． 3．C解析：C【解析】【分析】利用正方形的判定、直角三角形全等的判定、平行四边形的判定定理对每个选项依次判定解答．【详解】①四条边相等的四边形是菱形，故①错误；②四边形具有不稳定性，故②正确；③两直角三角形隐含一个条件是两直角相等，两个锐角对应相等，因此构成了AAA ，不能判定全等，故③错误；④一组对边平行且相等的四边形是平行四边形，故④错误；综上，错误的命题有①③④共3个．故选：C ．【点睛】本题考查了命题与定理的知识，解题的关键是了解正方形的判定、平行四边形的判定及直角三角形全等的判定．4．C解析：C【解析】【分析】根据众数的定义：一组数据中出现次数最多的数据，进行求解即可．【详解】解：∵36.5℃出现了两次，出现的次数最多，∴这组数据的众数为36.5℃，故选C ．【点睛】本题主要考查了众数的定义，解题的关键在于能够熟知众数的定义．5．C解析：C【分析】先根据平行四边形的性质可得2,4CD AB OC OD ====，再根据勾股定理的逆定理可得AC CD ⊥，然后利用勾股定理可得AD 的长，最后利用三角形的面积公式即可得．【详解】解：四边形ABCD 是平行四边形，4,8AB AC BD ===，112,422CD AB OC AC OD BD ====∴==， 22241216OC CD OD ∴+=+==，COD ∴是直角三角形，AC CD ⊥，在Rt ACD △中，AD ==1122Rt ACD S AD CE AC CD =⋅=⋅， 11422∴⨯=⨯⨯解得CE = 故选：C ．【点睛】本题考查了平行四边形的性质、勾股定理、勾股定理的逆定理等知识点，熟练掌握勾股定理的逆定理是解题关键．6．A解析：A【解析】【分析】先利用平行四边形的性质得到122BE DE BD ===，再由折叠的性质得到45BEA B EA '==∠∠，2B E BE '==，由此可得到90B ED '=∠，再利用勾股定理求解即可．【详解】解：∵四边形ABCD 是平行四边形， ∴122BE DE BD ===，由折叠的性质可知：45BEA B EA '==∠∠，2B E BE '==，∴90B EB BEA B EA ''∠=∠+∠=， ∴18090B ED B EB ''==∠-∠，∴在直角三角形B ED '中2222B D B E ED ''=+=，故选A ．【点睛】本题主要考查了平行四边形的性质，折叠的性质，勾股定理，解题的关键在于能够熟练掌握相关知识进行求解．7．B解析：B【解析】【分析】根据三角形中位线定理求得,,DE DF EF ,进而求得三角形的周长．【详解】解：∵点D ，E 分别AB 、BC 的中点，AC ＝7，∴DE ＝12AC ＝3.5，同理，DF ＝12BC ＝2.5，EF ＝12AB ＝3，∴△DEF 的周长＝DE ＋EF ＋DF ＝9，故选：B ．【点睛】本题考查了三角形中位线定理，理解三角形中位线定理是解题的关键．8．C解析：C【分析】根据图象可知进水的速度为5（L/min），再根据第10分钟时容器内水量为27.5L可得出水的速度，从而求出第12min时容器内水量，利用待定系数法求出4≤x≤12时，y与x之间的函数关系式，再对各个选项逐一判断即可．【详解】解：由图象可知，进水的速度为：20÷4＝5（L/min），故①说法正确；出水的速度为：5−（27.5−20）÷（10−4）＝3.75（L/min），第12min时容器内水量为：20＋（12−4）×（5−3.75）＝30（L），故③说法正确；15÷3＝3（min），12＋（30−15）÷3.75＝16（min），故当y＝15时，x＝3或x＝16，故说法④错误；设4≤x≤12时，y与x之间的函数关系式为y＝kx＋b，根据题意，得420 1027.5k bk b+=⎧⎨+=⎩，解得5415kb⎧=⎪⎨⎪=⎩，所以4≤x≤12时，y＝54x＋15，故说法②正确．所以正确说法的个数是3个．故选：C．【点睛】此题考查了一次函数的应用，解题时首先正确理解题意，利用数形结合的方法即可解决问题．二、填空题9．1≥x【解析】【分析】直接利用二次根式有意义的条件分析得出答案．【详解】解：∵二次根式1x -在实数范围内有意义，∴1x -≥0，解得：1≥x ．故答案为1≥x ．【点睛】此题主要考查了二次根式有意义的条件，正确把握二次根式的定义是解题关键． 10．A解析：24【解析】【分析】由正方形的性质可求AC 的长，由勾股定理可求BO 的值，可求BD 的值，即可求菱形ABCD 的面积．【详解】解：如图，连接AC ，BD 交于O ，∵正方形AECF 的面积为18cm 2，∴正方形AECF 的边长为32，∴AC 2=6（cm ），∴AO =3（cm ），∵四边形ABCD 是菱形，∴AC ⊥BD ，BO =DO ，∴BO 22AB AO -（cm ），∴BD =2BO =8（cm ），∴菱形ABCD 的面积=12AC ×BD =24（cm 2），故答案为：24．【点睛】本题考查正方形的性质，菱形的性质，勾股定理，熟练运用正方形的性质是本题的关键． 11．B解析：43【解析】【分析】由矩形对角线的性质得到AO DO =，结合题意证明ADO △是等边三角形，解得BD 的长，在Rt ABD △中，理由勾股定理解题即可．【详解】解：矩形ABCD 中，AC=BD 且AO=OC ,BO=DOAO DO ∴=ADO ∴△是等腰三角形∠AOD ＝60°ADO ∴△是等边三角形AD DO AO ∴==AD ＝44DO ∴=28BD DO ∴==Rt ABD △中 22228443AB BD AD =-=-=故答案为：43．【点睛】本题考查矩形的性质、等边三角形的判定与性质、勾股定理等知识，是重要考点，掌握相关知识是解题关键． 12．B解析：20【分析】首先根据矩形的性质得出10cm BD AC ==，然后利用三角形中位线的性质求解即可．【详解】连接BD ，∵四边形ABCD 是矩形，∴10cm BD AC ==．∵E 、F 、G 、H 分别是矩形四条边的中点，∴115cm,5cm 22EH FG BD EF GH AC ======， ∴四边形EFGH 的周长为5420cm ⨯=，故答案为：20．【点睛】本题主要考查矩形的性质和三角形中位线的性质，掌握矩形的性质是关键．13．43【分析】先写出4y x m =+-的伴随点，再根据伴随点在它的图象上代入一次函数解析式，计算即可求得m ．【详解】解：4y x m =+-的伴随点为(),4m -，因为4y x m =+-伴随点在它的图象上，则有44m m -=+- 解得43m =．故答案为:43．【点睛】本题考查一次函数图象上点的坐标特征．一次函数图象上任意一点的坐标都满足函数关系式y=kx+b ．14．E 解析：3【分析】先延长EF 和BC ，交于点G ，再根据条件可以判断三角形ABE 为等腰直角三角形，并求得其斜边BE 的长，然后根据条件判断三角形BEG 为等腰三角形，最后根据△EFD ∽△GFC 得出CG 与DE 的倍数关系，并根据BG=BC+CG 进行计算即可．【详解】延长EF 和BC ，交于点G ．∵矩形ABCD 中，∠B 的角平分线BE 与AD 交于点E ，∴∠ABE=∠AEB=45°，∴AB=AE=9，∴直角三角形ABE 中，又∵∠BED 的角平分线EF 与DC 交于点F ，∴∠BEG=∠DEF ．∵AD ∥BC ，∴∠G=∠DEF ，∴∠BEG=∠G ，∴．由∠G=∠DEF ，∠EFD=∠GFC ，可得△EFD ∽△GFC ， ∴122CG CF CF DE DF CF ===. 设CG=x ，DE=2x ，则AD=9+2x=BC ．∵BG=BC+CG ，∴，解得，∴BC=9+2（32-3）=62+3．故答案为62+3．考点：矩形的性质；等腰三角形的判定；相似三角形的判定与性质．15．（，0）【分析】作点D关于x轴对称点F，根据题意求出D点的坐标，从而得到F点的坐标，同时连接CF，则CF与x轴的交点即为所求E点，此时满足△CDE的周长最小，利用CF的解析式求解即可．【详解】解析：（83，0）【分析】作点D关于x轴对称点F，根据题意求出D点的坐标，从而得到F点的坐标，同时连接CF，则CF与x轴的交点即为所求E点，此时满足△CDE的周长最小，利用CF的解析式求解即可．【详解】解：作点D关于x轴对称点F，如图，∵四边形OABC是矩形，∴OC＝BD＝3，点C的坐标为()0,3，∵D为AB边的中点，∴AD＝32，∵OA＝4，∴D 点的坐标为34,2⎛⎫ ⎪⎝⎭，则F 点的坐标为34,2⎛⎫- ⎪⎝⎭，根据轴对称的性质可得：EF ＝ED ，∴C △CDE ＝CD +CE +DE ＝CD +CE +EF ，其中CD 为定值，当CE +EF 值最小时，△CDE 周长最小，此时点C ，E ，F 三点共线，设直线CF 的解析式为：()0y kx b k =+≠，将()0,3和34,2⎛⎫- ⎪⎝⎭代入解析式得： 3342b k b =⎧⎪⎨+=-⎪⎩，解得：983k b ⎧=-⎪⎨⎪=⎩， ∴直线CF 的解析式为：938y x =-+，令0y =，得：9308x -+=，解得：83x =， ∴点E 坐标（83，0），故答案为：803⎛⎫ ⎪⎝⎭，．【点睛】本题考查一次函数与轴对称的综合运用，理解最短路径的求解方法，熟悉待定系数法求一次函数解析式是解题关键．16．5【分析】由折叠可得，．再由矩形性质结合勾股定理即可求出BF 的长，从而求出CF 的长．设，则，在中，利用勾股定理列出关于x 的等式，解出x 即可．【详解】解：由折叠可知，，∵四边形ABCD 是矩形解析：5【分析】由折叠可得5AD AF ==，DE EF =．再由矩形性质结合勾股定理即可求出BF 的长，从而求出CF 的长．设EC x =，则4DE EF x ==-，在Rt CEF 中，利用勾股定理列出关于x 的等式，解出x 即可．【详解】解：由折叠可知5AD AF ==，DE EF =，∵四边形ABCD 是矩形，∴在Rt ABF 中，3BF ==，∴532CF BC BF =-=-=．设EC x =，则4DE EF x ==-，∴在Rt CEF 中，222+=CF CE EF ，即2222(4)x x +=-，解得： 1.5x =．故EC 的长为1.5．故答案为1.5．【点睛】本题考查折叠的性质，矩形的性质和勾股定理．利用数形结合的思想是解答本题的关键．三、解答题17．（1）2；（2）3；（3）143；（4）【分析】(1)将二次根式化简合并进行计算即可；(2)将二次根式有理化进行计算即可；(3)根据平方差公式化简计算即可；(4)先将二次根式、绝对值、负指解析：（1）2；（2）3；（3）143；（4【分析】(1)将二次根式化简合并进行计算即可；(2)将二次根式有理化进行计算即可；(3)根据平方差公式化简计算即可；(4)先将二次根式、绝对值、负指数幂化简，再合并同类项即可．【详解】（1）2==，（21535==，（31311143=⨯=，（4113333-⎛⎫-= ⎪⎝⎭【点睛】本题考查的是二次根式的混合运算，将各个式子化为最减是解答此题的关键． 18．（1）A ，B 两点间的距离是40米；（2）点B 到直线AC 的距离是24米．【分析】（1）根据勾股定理解答即可；（2）根据三角形面积公式解答即可．【详解】（1）因为是直角三角形，所以由勾股定解析：（1）A ，B 两点间的距离是40米；（2）点B 到直线AC 的距离是24米．【分析】（1）根据勾股定理解答即可；（2）根据三角形面积公式解答即可．【详解】（1）因为ABC 是直角三角形，所以由勾股定理，得222AC BC AB =+．因为50AC =米，30BC =，所以22250301600AB =-=．因为0AB >，所以40AB =米．即A ，B 两点间的距离是40米．（2）过点B 作BD AC ⊥于点D ．因为1122ABC S AB BC AC BD =⋅=⋅△，所以AB BC AC BD ⋅=⋅．所以30402450AB BC BD AC ⋅⨯===（米），即点B 到直线AC 的距离是24米．【点睛】本题考查了勾股定理的应用，属于基础题，关键是掌握勾股定理在直角三角形中的表达式．19．（1）；（2）见解析，菱形面积为4或5.【解析】【分析】（1）根据题意，画出图形，即可求解；（2）先画出边长为的所有菱形ABCD ，，然后求出面积即可．【详解】解：如图，（1）∵a 是图解析：（12）见解析，菱形面积为4或5.【解析】【分析】（1）根据题意，画出图形，即可求解；（2ABCD ，，然后求出面积即可．【详解】解：如图，（1）∵a是图中能用网格线段表示的最小无理数，∴22112a=+=，∵b是图中能用网格线段表示的最大无理数，224225b=+=；（2）∵22215+=，即可画出图形，如图，菱形ABC1D1和菱形ABC2D2即为所求；菱形ABC1D1的面积为12442⨯⨯=；菱形ABC2D2223110+=，故菱形ABC2D2的面积为1101052；5ABCD的面积为4或5．【点睛】本题主要考查了应用设计与作图以及勾股定理等知识，熟练掌握菱形的性质是解题关键．20．见解析．【分析】根据四边形是平行四边形，再证明有一组邻边相等即可．【详解】解：∵，∴四边形是平行四边形，∵平分，∴，∵，∴，∴，∴，∴平行四边形是菱形．【点睛】本题考查了解析：见解析．【分析】根据//,//DE AC DF AB 四边形AEDF 是平行四边形，再证明有一组邻边相等即可．【详解】解：∵//,//DE AC DF AB ，∴四边形AEDF 是平行四边形，∵AD 平分BAC ∠，∴12∠=∠，∵//DE AC ，∴23∠∠=，∴13∠=∠，∴AE DE =，∴平行四边形AEDF 是菱形．【点睛】本题考查了平行线的性质，菱形的判定，等腰三角形的判定，解题关键是熟练运用相关性质，准确进行推理证明．21．（1）﹣i ，1，；（2）﹣i ﹣6；（3）的最小值为25．【解析】【分析】（1）根据题目所给条件可得i3=i2•i ，i4=i2•i2计算即可得出答案；（2）根据多项式乘法法则进行计算，及题目所解析：（1）﹣i ，1，20221i i i--；（2）﹣i ﹣6；（325．【解析】【分析】（1）根据题目所给条件可得i 3=i 2•i ，i 4=i 2•i 2计算即可得出答案；（2）根据多项式乘法法则进行计算，及题目所给已知条件即可得出答案；（3）根据题目已知条件，a +bi ＝4+3i ，求出a 、b ，即可得出答案．【详解】（1）i 3＝i 2•i ＝﹣1×i ＝﹣i ，i 4＝i 2•i 2＝﹣1×（﹣1）＝1，设S ＝i +i 2+i 3+…+i 2021，iS ＝i 2+i 3+…+i 2021+i 2022，∴（1﹣i ）S ＝i ﹣i 2022，∴S ＝20221i i i--，故答案为﹣i ，1，20221i i i--；（2）（1+i ）×（3﹣4i ）﹣（﹣2+3i ）（﹣2﹣3i ）＝3﹣4i +3i ﹣4i 2﹣（4﹣9i 2）＝3﹣i +4﹣4﹣9＝﹣i ﹣6；（3）a +bi ＝2543i -＝25(43)(43)(43)i i i +-+＝10075169i ++＝4+3i ， ∴a ＝4，b ＝3，x ，0）到点A （0，4），B （24，3）的最小距离，∵点A （0，4）关于x 轴对称的点为A '（0，﹣4），连接A 'B 即为最短距离，∴A 'B 25，25．【点睛】此题考查了实数的运算，以及规律型：数字的变化类，弄清题中的新定义是解本题的关键．22．（1）80元/人；（2）y1＝48x ，y2＝；（3）A 旅游团30人，B 旅游团20人【分析】（1）由函数图象，节假日期间，10人的购票款数为800元，购票款数除以人数，可得不打折的门票价格；（2解析：（1）80元/人；（2）y 1＝48x ，y 2＝80(010)64160(10)x x x x ≤≤⎧⎨+>⎩；（3）A 旅游团30人，B 旅游团20人【分析】（1）由函数图象，节假日期间，10人的购票款数为800元，购票款数除以人数，可得不打折的门票价格；（2）利用待定系数法求正比例函数解析式求出1y ，分010x 与10x >，利用待定系数法求2y 与x 的函数关系式即可；（3）设A 团有x 人，表示出B 团的人数为(50)x -，然后分010x 与10x >两种情况，根据（2）的函数关系式列出方程求解即可．【详解】解：（1）8001080÷=（元/人），答：不打折的门票价格是80元/人；（2）设110y k =，解得：48k =，148y x ∴=，当010x 时，设280y x =，当10x >时，设2y mx b =+，则10800201440m b m b +=⎧⎨+=⎩，解得：64m =，160b =，264160y x ∴=+，280(010)64160(10)x x y x x ⎧∴=⎨+>⎩；（3）设A 旅游团x 人，则B 旅游团(50)x -人，若010x ，则8048(50)3040x x +-=，解得：20x ，与10x 不相符，若10x >，则6416048(50)3040x x ++-=，解得：30x =，与10x >相符，503020-=（人)，答：A 旅游团30人，B 旅游团20人．【点睛】本题考查了一次函数的应用，利用了待定系数法求一次函数解析式，准确识图获取必要的信息是解题的关键，（3）要注意分情况讨论．23．（1）等边三角形；（2）成立，理由见解析；（3）或．【分析】（1）根据题意先判断出四边形ABCE 和四边形ACDE 都是梯形．得出FG 为梯形ABCE 的中位线，GH 为梯形ACDE 的中位线．从而得出，．解析：（1）等边三角形；（2）成立，理由见解析；（3）或．【分析】（1）根据题意先判断出四边形ABCE 和四边形ACDE 都是梯形．得出FG 为梯形ABCE 的中位线，GH 为梯形ACDE 的中位线．从而得出，．即证明为等边三角形．（2）先判断出PF ，PG 是△ABC 和△CDE 的中位线，再判断出∠FPG ＝∠FCH ，进而证明△FPG ≌△FCH ，得出结论FG ＝FH ，∠PFG ＝∠CFH ，最后证明出∠GFH=，即证明△FGH 为等边三角形．（3）①当点E 在AE 上时，先求出CM ，进而求出AM ，即可求出AD ，再判断出，进而求出BE=AD=2，，即可判断出，再求出BN 、EN ，进而求出BD ，最后即可求出FH ，即可得出结果；②当点D 在AE 的延长线上时同①的方法即可得出结果．【详解】（1）∵ABC 和都为等边三角形，且边长不相等．∴，．∴四边形ABCE和四边形ACDE都是梯形．又∵F、G、H分别是BC、AE、CD中点，∴FG为梯形ABCE的中位线，GH为梯形ACDE的中位线．∴，．∴，．∴为等边三角形．故答案为：等边三角形．（2）取AC的中点P，连接PF，PG，∵△ABC和△CDE都是等边三角形，∴AB＝BC，CE＝CD，∠BAC＝∠ACB＝∠ECD＝∠B＝60°．又F，G，H分别是BC，AE，CD的中点，∴FP＝12AB，FC＝12BC，CH＝12CD，PG＝12CE，PG∥CE，PF∥AB．∴FP＝FC，PG＝CH，∠GPC＋∠PCE＝180°，∠FPC＝∠BAC＝60°，∠PFC＝∠B＝60°．∴∠FPG＝∠FPC＋∠GPC＝60°＋∠GPC，∠GPC＝180°－∠PCE．∴∠FCH＝360°－∠ACB－∠ECD－∠PCE＝360°－60°－60°－（180°－∠GPC）＝60°＋∠GPC．∴∠FPG＝∠FCH．∴△FPG≌△FCH（SAS）．∴FG＝FH，∠PFG＝∠CFH．∴∠GFH＝∠GFC＋∠CFH＝∠GFC＋∠PFG＝∠PFC＝60°．∴△FGH为等边三角形．所以成立．（3）①当点D在AE上时，如图，∵ABC是等边三角形，∴，．∵是等边三角形，∴，，过点C作于M，∴，在中，根据勾股定理得，,在中，根据勾股定理得，, ∴,∵,∴，∴，连接BE，在和中，，∴（SAS），∴BE=AD=2, ，∵，∴，∴，过点B作于N，∴，在中，，∴，∴,DN=DE-EN=3，连接BD，根据勾股定理得：，∵点H是CD中点，点F是BC中点，∴FH是的中位线，∴，由（2）可知，△FGH为等边三角形．∴△FGH的周长．②当点D在AE的延长线上时，如图，同理可求，所以△FGH的周长．即满足条件的△FGH的周长位或．【点睛】本题考查等边三角形的判定和性质，全等三角形的判定和性质，勾股定理，含30角的直角三角形的性质，三角形的中位线定理．属于几何变换综合题，综合性强，较难．24．（1）A（-8，0）、B（0，6）；（2）5；（3）①3个；②（-5，6）或（-11，-6）或（5，6）．【解析】【分析】（1）利用待定系数法解决问题即可．（2）由翻折不变性可知，OC=CD解析：（1）A（-8，0）、B（0，6）；（2）5；（3）①3个；②（-5，6）或（-11，-6）或（5，6）．【解析】【分析】（1）利用待定系数法解决问题即可．（2）由翻折不变性可知，OC=CD，OB=BD=6，∠ODB=∠BOC=90°，推出AD=AB-BD=4，设CD=OC=x，在Rt△ADC中，根据AD2+CD2=AC2，构建方程即可解决问题．（3）①根据平行四边形的定义画出图形即可判断．②利用平行四边形的性质求解即可解决问题．【详解】解：（1）对于直线364y x=+，令x=0，得到y=6，∴B（0，6），令y=0，得到x=8-，∴A（8-，0）；（2）∵A（8-，0），B（0，6），∴OA=8，OB=6，∵∠AOB=90°，∴228610AB+=，由翻折不变性可知，OC=CD，OB=BD=6，∠ODB=∠BOC=90°，∴AD=AB-BD=4，设CD=OC=x，在Rt △ADC 中，∵∠ADC=90°，∴AD 2+CD 2=AC 2，∴42+x 2=（8-x ）2，解得：x=3，∴OC=3，AC=OA -OC=8-3=5．（3）①符合条件的点P 有3个，如图所示：②∵A （-8，0），C （-3，0），B （0，6），当AB 为对角线时，1//BP AC ，由平行四边形的性质，得15BP AC ==，∴P 1（-5，6）；当AB 为边时，//AB CP ，点P 在第三象限时，有点B 向下平移6个单位，向左平移3个单位得到点C ，∴点A 向下平移6个单位，向左平移3个单位得到点P 2，∴P 2（-11，-6）；点P 在第二象限时，有35BP AC ==，∴P 3（5，6）；∴点P 的坐标为：（-5，6）或（-11，-6）或（5，6）．【点睛】本题属于一次函数综合题，考查了待定系数法，解直角三角形，平行四边形的判定和性质等知识，解题的关键是熟练掌握基本知识，学会用分类讨论的思想思考问题，属于中考常考题型．25．（1）CE=BD ，见解析；（2）6；（3）20【分析】（1）证△EAC ≌△BAD 即可；（2）证△EAC ≌△BAD ，得BD=CE ，易得∠EBC=90゜，从而在Rt △EBC 中运用勾股定理即可求得结解析：（1）CE =BD ，见解析；（2）6；（3）20（1）证△EAC ≌△BAD 即可；（2）证△EAC ≌△BAD ，得BD =CE ，易得∠EBC =90゜，从而在Rt △EBC 中运用勾股定理即可求得结果；（3）连接BD ，把△ACD 绕点D 顺时针旋转60゜得到△EBD ，连接AE ，则可得BE =AC ，△ADE 是等边三角形，从而易得AB ⊥AE ，在Rt △BAE 中由勾股定理可求得AE ，也即AD 的长．【详解】（1）∵∠EAB =∠CAD∴∠BAC +∠EAB =∠BAC +∠CAD即∠EAC =∠BAD在△EAC 和△BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴△EAC ≌△BAD (SAS )∴CE =BD（2）∵∠EAB =∠CAD =90゜∴∠BAC +∠EAB =∠BAC +∠CAD即∠EAC =∠BAD∵△EAB 、△CAD 都是等腰直角三角形，且∠EAB =∠CAD =90゜∴AE =AB =4，∠EBA =45゜，AC =AD∴由勾股定理得：BE ==在△EAC 和△BAD 中AE AB EAC BAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴△EAC ≌△BAD (SAS )∴CE =BD∵∠EBC =∠EBA +∠ABC =45゜+45゜=90゜∴在Rt △EBC中，由勾股定理得：6CE∴BD =6（3）如图，连接BD∵CD =BC ，∠BCD =60゜∴△BCD 是等边三角形把△ACD 绕点D 顺时针旋转60゜得到△EBD ，点E 与点A 对应，连接AE则BE =AC =25，△ADE 是等边三角形∴∠DAE =60゜，AD =AE∴∠BAE =∠BAD +∠DAE =30゜+60゜=90゜在Rt△BAE中，由勾股定理得：2222=-=-=251520AE BE AB∴AD=20【点睛】本题是三角形的综合题，考查了三角形全等的判定与性质，等腰三角形的性质，等边三角形的判定与性质，勾股定理，旋转变换，第三问作旋转变换是关键，也是难点．本质上来说，前两问也可看成把△EAC绕A点逆时针旋转的角度一定角度而得到△BAD．。

北京市密云区2022~2023学年第一学期初二数学期末试卷(word版含答案)

北京市密云区2022-2023学年第一学期期末考试八年级数学试卷 2023．1考生须知1．本试卷共6页，共三道大题，28道小题，满分100分．考试时间120分钟． 2．在试卷和答题卡上准确填写学校、班级、姓名和考号．3．试题答案一律填涂或书写在答题卡上，在试卷上作答无效，作图必须使用．．．．．．2B ．．铅笔．．. 4．考试结束，请将本试卷和答题纸一并交回．一、选择题（本题共16分，每小题2分）下面各题均有四个选项，其中只有一个．．选项是符合题意的. 1.若分式14x -有意义，则实数x 的取值范围是（）A ．x ≠-4B ．x =-4C ．x ≠4D ．x =42．《国语·楚语》记载：“夫美者，上下、内外、大小、远近皆无害焉，故曰美”．这一记载充分表明传统美的本质特征在于对称和谐．中国建筑布局一般都是采用均衡对称的方式建造，更具脱俗的美感和生命力．下列建筑物的简图中，不是．．轴对称图形的是（）A ．B ．C ．D ．3. 在下列各式的计算中，正确的是（）A ．B ．x 2+x 2=x 4C ．x 8÷x 2=x 6D ．4. 我国的泉州湾跨海大桥是世界首座跨海高铁大桥，其创新采用的“石墨烯重防腐涂装体系”，将实现30年超长防腐寿命的突破．石墨烯作为本世纪发现的最具颠覆性的新材料之一，其理论厚度仅有0.00000000034m ，请将0.00000000034用科学记数法表示为（）A ．0.34×109B ．0.34×10-9C ．3.4×1010D ．3.4×10-105. 在平面直角坐标系xOy 中，点M (1，-6)关于y 轴的对称点N 的坐标是（） A ．(-1，-6) B ．(-1，6) C ． (1，6) D ． (-6，1)325()x x =22(3)6x x =6．正五边形的外角和为（）A ．720°B ．540°C ．360°D ．180°7. 下列各式中，从左到右的变形是因式分解的是（）A . B.C. D.8. 如图，在Rt △ABC 中，∠C=90°，以△ABC 的一边为腰画等腰三角形，使得它的第三个顶点在△ABC 的其他边上，则可以画出的不同的等腰三角形的个数最多是（）A ．3个B ．4个C ．6个D ．7个二、填空题（本题共16分，每小题2分）9．若分式的值为0，则x 的值为 .10. 计算：(12a 3-6a 2+3a )÷3a = .11.已知：如图，AB 平分∠CAD ．请添加一个条件，使得△ABC ≌△ABD .（要求：不添加辅助线，只需填一个答案即可）12. 若等腰三角形的两边长分别为9和4，则第三边的长是 .13．如图1，在边长为a 的正方形中挖去一个边长为b 的小正方形（a>b ），把余下的部分拼成一个矩形（如图2），根据两个图形中阴影部分的面积相等，写出一个正确的等式为 .图1 图21x x-x x x x +=+2)1(22)1(12+=++x x x 3)(32-+=-+y x x xy x 5)3(4622-+=++x x x14. 若，，则．15. 如图，Rt △ABC 中，∠BAC =90°，AB=AC ．在BC 上截取BD ＝BA ，作∠ABC 的平分线与AD 相交于点P ，连接PC ．若△ABC 的面积为8cm 2，则△BPC 的面积为 cm 2．16. 在平面直角坐标系xOy 中，A （1，3），B （3，-1），点P 在 y 轴上，当P A+PB 取得最小值时，点P 的坐标为．三、解答题（共68分，其中17题6分，18~23题每题5分，24~26题每题6分，27、28题每题7分） 17．因式分解（1）（2）2+-y xy x 882218. 计算：19.计算：20. 解分式方程：22211121x x x x x -÷+--+101()(3)25π---+-351310++=+-x x x 2=x a 5=y a =+yx a 32m mn -21. 密云水库是首都的“生命之水”，作为北京重要的水源地，保持水质成为重中之重．如图所示，点A 和点B 分别表示两个水质监测站，点C 表示某一时刻监测人员乘坐的监测船的位置．其中，B 点在A 点的西南方向，船只C 在A 点南偏东25°方向和B 点北偏东75°方向的交汇处，求此时从船只C 看A 、B 两个水质监测站的视角∠ACB 的度数．22. 数学课上，李老师布置如下任务：如图，已知△ABC ，点D 是AB 边上的一个定点，在AC 边上确定一点E ，使DE//BC ．下面是小莉设计的尺规作图过程．作法：① 以点D 为圆心，BD 长为半径作弧交BC 边于点F ，连接DF ． ② 作∠ADF 的角平分线，交AC 边于点E ；则点E 即为所求．根据小莉设计的尺规作图过程，（1）使用直尺和圆规，补全图形；（保留作图痕迹）（2）完成下面的证明，并在括号内填写推理的依据．证明：∵DB ＝DF ，∴∠B ＝．（） ∵DE 是∠ADF 的角平分线， ∴∠ADF ＝2∠ADE ．∵∠ADF ＝∠B ＋∠DFB ，（）即∠ADF ＝2∠B ， ∴∠ADE=∠B ．∴ DE//BC ．23. 已知，求代数式的值．22360a a +-=3(21)(21)(21)a a a a +-+-24. 已知：在Rt △ABC 中，∠ACB =90°，∠A =30°，AB 边的垂直平分线分别交AC 于点D ，交AB 于点E ．（1）求证：DE=DC ；（2）连接EC ，若AB =6，求△EBC 的周长.25．交通是经济的脉络和文明的纽带．截至2020年底，我国高速铁路运营里程五年间翻了近一番，稳居世界第一，居民出行更加便捷．据悉，甲乙两城市相距800千米，乘坐高铁列车比乘坐普通列车的运行时间缩短了4小时，已知高铁列车的平均速度是普通列车平均速度的2.5倍，求高铁列车的平均速度．26. 阅读材料，解决问题爱因斯坦是20世纪著名的物理学家，他创立的相对论影响了人类对世界的看法．有趣的是，这位科学巨匠闲暇之余喜欢琢磨一些数学趣题．一次，爱因斯坦在计算一道两位数乘法运算时，联想到了“头同尾合十”的速算方法．所谓“头同尾合十”是指：两个因数的十位数字相同，个位数字相加刚好为10；其对应的速算方法是：第一步:用两个因数的个位数字相乘,把得到的乘积作为结果的后两位,如果乘积是一位数,就把这个数作为结果的个位,十位用0表示；第二步:用相同的十位数字乘以比它大1的数，把得到的乘积放在第一步结果的前面．像这样组成的数就是两位数相乘的结果．例如：速算74×76，先算4×6=24，再算7×（7+1）=56，则74×76=5624；速算59×51，先算9×1=09，再算5×（5+1）=30，则59×51=3009；（1）利用上述速算方法，计算47×43的积为；（2）用和分别表示两个两位数，其中a 表示十位数字，b 和c 表示它们的个位数字，且b+c =10．① 依据题意，两位数 =10a+b ，则两位数 = ； ② 为说明该速算方法的正确性，请你证明 =100a (a +1)+bc 成立．ab ab ac ac ab ac27.如图，在△ABC中，∠BAC=60°，∠C=40°，∠BAC与∠ABC的角平分线AD、BE 分别交BC、AC边于点D和点E．（1）求证：△BEC是等腰三角形；（2）用等式表示线段AB、AC、BD之间的数量关系，并证明．28.对于平面直角坐标系xOy中的点M和图形G，给出如下定义：点N为图形G上任意一点，当点P是线段MN的中点时，称点P是点M和图形G的“中立点”．（1）已知点A（4，0），若点P是点A和原点的中立点，则点P的坐标为；（2）已知点B（-2，3），C（1，3），D（-2，0）．①连接BC，求点D和线段BC的中立点E的横坐标x E的取值范围；②点F为第一、三象限角平分线上的一点，在△BCD的边上存在点F和△BCD 的中立点，直接写出点F的横坐标x F的取值范围．北京市密云区2022-2023学年第一学期期末考试八年级数学试卷参考答案及评分标准 2023.01一、选择题（本题共16分，每小题2分）二、填空题（本题共16分，每小题2分）9．1； 10．4a 2-2a +1；11．AC=AD ；（答案不唯一） 12．9； 13. a 2-b 2=(a+b )(a -b ) 或 (a+b )(a -b )=a 2-b 2； 14．10； 15．4； 16．（0，2）．三、解答题（本题共68分．其中17题6分，18~23题每题5分，24~26题每题6分，27、28题每题7分）说明：与参考答案不同，但解答正确相应给分．17. （1）原式＝m （m 2-n 2） ……………………1分＝m （m+n ）（m -n ） ……………………3分（2）原式＝2（x 2-4xy +4y 2） ……………………4分＝2（x -2y ）2 …………………6分18. 原式=5+1-2 ………………………3分=4 ………………………5分19．原式=2211(1)(1)(1)xx x x x -÷++-- ……………………2分221(1)1(1)(1)x x x x x -=-⋅++-211(1)x x x x -=-++ ……………………3分21(1)(1)x x x x x x -=-++ ………………………4分1(1)x x x +=+1=……………………5分x20．解：10-x=x+3+5………………………2分-x-x=3+5-10-2x= -2x=1 …………………4分检验：当x=1时，x+3≠0∴原分式方程的解为x=1 …………………5分21．解：由题意可知，∠BAD=45°，∠DAC=25°∴∠BAC=70°……………………………2分∵BE∥AD∴∠ABE=∠BAD=45°………………………3分∵∠EBC=75°∴∠ABC=75°-45°=30°………………………4分在△ABC中，∠ACB=180°-70°-30°=80°…………………5分22．（1）……………2分（2）证明：∵DB＝DF，∴∠B＝∠DFB ．（等边对等角）……………………4分∵DE是∠ADF的角平分线，∴∠ADF＝2∠ADE．∵∠ADF＝∠B＋∠DFB，（三角形外角性质）………………5分即∠ADF＝2∠B，∴∠ADE=∠B．∴DE//BC．23．原式=6a2+3a-（4a2-1）………………………1分=6a 2+3a -4a 2+1 ……………………………2分=2a 2+3a +1 ……………………3分 ∵2a 2+3a -6=0∴2a 2+3a =6 ………………………4分 ∴原式=6+1=7． …………………………………5分 24．（1）证明：∵在Rt △ABC 中，∠ACB =90°，∠A =30°∴∠ABC= 60° ………………………1分 ∵DE 是AB 边的垂直平分线∴AD=DB∴∠A=∠ABD=30° …………………………2分 ∴∠CBD= 60°-30°=30°∴BD 平分∠ABC∵DE ⊥AB ，AC ⊥BC∴DE=DC ……………3分（2）解：∵在Rt △ABC 中，∠ACB =90°，∠A =30° ，AB =6 ∴132BC AB == ………………………………4分 ∵DE 是AB 边的垂直平分线∴132BE AB == ∴BC=BE ∵∠ABC= 60°∴△EBC 是等边三角形 ……………………5分 ∴△EBC 的周长为9． ……………………6分25．解：设普通列车的平均速度为x km/h ，则高铁列车的平均速度为2.5x km/h ……1分80080042.5x x=- ……………………3分解得：x =120 ……………………4分经检验：x =120是原分式方程的解，且符合实际意义 ………………5分 ∴2.5x=2.5×120=300km/h ……………………6分答：高铁列车的平均速度为300km/h ．26．（1）2021 ……………1分（2）①10a +c ； ……………………2分② 证明：=（10a +b ）（10a +c ） …………………3分 =100a 2+10ac +10ab +bc …………………4分 =100a 2+10a （b +c ）+bc …………………5分 ∵b+c =10∴原式=100a 2+100a +bc=100a (a +1)+bc …………………6分即： =100a (a +1)+bc 成立，该速算方法正确． 27 .（1）证明：在△ABC 中，∠BAC=60°，∠C=40° ∴∠ABC =80° ………………………1分 ∵BE 平分∠ABC ∴∠EBC = 40°∴∠EBC =∠C …………………2分 ∴EB=EC∴△BEC 是等腰三角形． …………………3分（2）AB+BD=AC ………………4分证明：延长AB 至F ，使BF=BD ，连接DF ∴∠F=∠BDF∵∠ABC =∠F+∠BDF=80° ∴2∠F=80°∠F=40° ∵∠C=40°∴∠F=∠C ………………5分 ∵AD 平分∠BAC ∴∠BAD=∠CAD ∵AD=AD∴△AFD ≅△ACD …………………6分 ∴AF=AC ∴AB+BF=AC即：AB+BD=AC ………………7分28．（1）P （2，0） ………………1分（2）① 连接BD ，取BD 中点E 1 ∵B （-2，3），D （-2，0）∴E 1点的横坐标x E =-2 ………………2分连接CD ，取CD 中点E 2过点C 作CF ⊥x 轴交x 轴于点F ，则F （1，0） ∴CF=3，DF=3∴△DCF 是等腰直角三角形 ∵E 2是CD 中点，连接E 2F ∴E 2F ⊥CD ，∠E 2FD=45°ab ac⨯∴△DE2F也是等腰直角三角形过点E2作E2H⊥x轴交x轴于点H，∴点H是DF的中点，DH=32∴OH=31222-=∴E2点的横坐标x E=12-…………………4分∴-2≤x E≤12-……………………5分② -3≤x F≤4 …………………7分八年级数学试卷第11页（共6页）。

人教版八年级下册数学期末试卷复习练习(Word版含答案)

人教版八年级下册数学期末试卷复习练习(Word 版含答案)一、选择题1．若二次根式2x -有意义，则x 的取值范围是（）．A ．2x >B ．2x ≥C ．2x <D ．2x ≤ 2．下列条件中，不能得出ABC 是直角三角形的是（）A ．13a =，5c =，12b =B ．222a c b -=C ．::3:3:4a b c =D ．::2:5:3A B C ∠∠∠=3．如图，四边形ABCD 的对角线交于点O ，下列不能判定四边形ABCD 为平行四边形的是（）A ．AB ＝CD ，AD ＝BCB ．∠ABC ＝∠ADC ，AB ∥CD C ．OA ＝OC ，OB ＝ODD ．AB ∥CD ，AD ＝BC 4．八（3）班七个兴趣小组人数分别为4、4、5、x 、6、6、7，已知这组数据的平均数是5，则这组数据的中位数是（）A ．6B ．5C ．4D ．3 5．△ABC 中，AB=15，AC=13，高AD=12，则△ABC 的周长为（） A ．42 B ．32 C ．42或32 D ．37或33 6．如图，在Rt △ABC 中，C ∠=90°，沿着过点B 的一条直线BE 折叠△ABC ，使点C 恰好落在AB 的中点D 处，则A ∠的度数为（）A ．30°B ．45°C ．60°D ．75°7．如图，以Rt △ABC （AC ⊥BC ）的三边为边，分别向外作正方形，它们的面积分别为S 1﹑S 2﹑S 3，若S 1＋S 2＋S 3＝12，则S 1的值是（）A ．4B ．5C ．6D ．78．如图，若正比例函数y ＝kx 图象与四条直线x ＝1，x ＝2，y ＝1，y ＝2相交围成的正方形有公共点，则k 的取值范围是( )A ．k ≤2B ．k ≥12C ．0＜k ＜12D ．12≤k ≤2 二、填空题9．使式子351x x -+有意义的x 的取值范围是______． 10．正方形ABCD 的对角线长为2，面积为______．11．直角三角形的直角边长分别为8，15，斜边长为x ，则2x =__________．12．如图，把矩形ABCD 沿EF 折叠，若140∠=︒，则∠=AEF ______°．13．若函数y=kx+4的图象平行于直线y=3x ，则此函数的表达式是_____．14．如图，在矩形ABCD 中，AB =4，BC =8，对角线AC 、BD 相交于点O ，过点O 作OE 垂直AC 交AD 于点E ，则DE 的长是_____________．15．如图，平面直角坐标系中，直线112y x =+与x 轴、y 轴分别交于A 、B 两点，以AB 为边在第二象限内作正方形ABCD ，在y 轴上有一个动点M ，当MDC △的周长最小的时候，点M 的坐标是______．16．已知如图，点()()()2,0,4,0,3,7A B D --，设F 为线段BD 上一点（不含端点），连接AF ，一动点M 从点A 出发，沿线段AF 以每秒1个单位的速度运动到F ，再沿线段FD 以每秒2个单位的速度运动到D 后停止，当点F 的坐标是____时，点M 在整个运动过程中用时最少。

八年级下册数学期末试卷综合测试卷(word含答案)(1)

八年级下册数学期末试卷综合测试卷（word含答案）(1) 一、选择题1．函数y＝35xx--的自变量x的取值范围是（）A．x≠5B．x＞3且x≠5C．x≥3D．x≥3且x≠5 2．由下列线段组成的三角形不是直角三角形的是（）A．7，24，25 B．4，5，41C．3，5，4 D．4，5，6 3．下列关于平行四边形的命题中，错误的是（）A．两组对角分别相等的四边形是平行四边形B．一组对边相等，另一组对边平行的四边形是平行四边形C．一组对边平行，一组对角相等的四边形是平行四边形D．一组对边平行且相等的四边形是平行四边形4．下表记录了甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的平均数与方差：甲乙丙丁平均数()cm183183183183方差 5.7 3.5 6.78.6要从中选择一名发挥稳定的运动员去参加比赛，应该选择（）A．甲B．乙C．丙D．丁5．如图，已知矩形ABCD的对角线AC的长为10cm，连结矩形各边中点E、F、G、H得四边形EFGH，则四边形EFGH的周长为（）cm．A．20 B．202C．203D．256．如图，已知E为邻边相等的平行四边形ABCD的边BC上一点，且∠DAE=∠B=80º，那么∠CDE的度数为（）A．20º B．25º C．30º D．35º7．如图，在△ABC中，BC＝2∠C＝45°，若D是AC的三等分点（AD＞CD），且AB ＝BD ，则AB 的长为（）A ．2B ．5C ．3D ．528．一条公路旁依次有A 、B 、C 三个村庄，甲、乙两人骑自行车分别从A 村、B 村同时出发前往C 村，甲、乙之间的距离()km s 与骑行时间()t h 之间的函数关系如图所示，下列结论：①A 、B 两村相距8km ；②甲出发2h 后到达C 村；③甲每小时比乙我骑行8km ；④相遇后，乙又骑行了15min 或45min 时两人相距2km .其中正确结论的个数是（）A ．1B ．2C ．3D ．4二、填空题9．若13x x --在实数范围内有意义，则x 的取值范围是____________． 10．如图，菱形ABCD 的对角线AC ，BD 相交于点O ，已知4OA =，菱形ABCD 的面积为24，则BD 的长为______．11．如图，两个较大正方形的面积分别为225、289，则字母A 所代表的正方形的边长为_____12．如图，在矩形ABCD 中，点E 在AD 上，且EC 平分BED ∠，若1AB =，45EBC ∠=︒，则DE 的长为__________．13．已知一次函数y x b =-+的图象过点()8,2，那么此一次函数的解析式为__________． 14．若顺次连接四边形ABCD 四边中点所得的四边形是菱形，则原四边形的对角线AC 、BD 所满足的条件是________．15．在平面直角坐标系中，矩形OABC 的顶点O 为坐标原点，顶点A ，C 分别在x 轴和y 轴上，OA ＝4，OC ＝3，D 为AB 边的中点，E 是OA 边上的一个动点，当△CDE 的周长最小时，则点E 的坐标为_____．16．如图，∠ABD ＝∠BDC ＝90°，AB ＝12，BC ＝8，CD ＝10A 与点D 重合，折痕为HG ，则线段BH 的长为___．三、解答题17．计算：（1）218×12﹣24；（2）48÷3﹣12×12＋24． 18．如图，在甲村到乙村的公路一旁有一块山地正在开发．现A 处需要爆破，已知点A 与公路上的停靠站B ，C 的距离分别为400 m 和300 m ，且AC ⊥AB ．为了安全起见，如果爆破点A 周围半径260 m 的区域内不能有车辆和行人，问在进行爆破时，公路BC 段是否需要暂时封闭？为什么?19．如图，4×10长方形网格中，每个小正方形的顶点称为格点，每个小正方形的边长均为1，点A ，B ，E ，F 都在格点上，按下列要求作图，使得所画图形的顶点均在格点上．（1）在图中画出以AB 为边的正方形ABCD ；（2）在图中画出以EF 为边的等腰三角形EFG ，且△EFG 的周长为1010+；（3）在（1）（2）的条件下，连接CG ，则线段CG 的长为．20．如图，在ABCD 中，两条对角线AC 和BD 相交于点O ，并且6BD =，8AC =，5BC =．（1）AC 与BD 有什么位置关系？为什么？（2）四边形ABCD 是菱形吗？为什么？21．阅读材料：规定初中考试不能使用计算器后，小明是这样解决问题的：已知a 23+,求2281a a -+的值.他是这样分析与解的：∵a 23+2323(23)(23)-=+-， ∴23a -= ∴2(2)3,a -= 2443a a -+=∴241a a -=-, ∴2281a a -+=2（24)1a a -+=2(1)11⨯-+=-.请你根据小明的分析过程，解决如下问题：（1）若a 21-,直接写出2481a a -+的值是 . （21315375121119+++++ 22．为丰富同学们的课余活动，某校成立了篮球课外兴趣小组，计划购买一批篮球，需购买A 、B 两种不同型号的篮球共300个．已知购买3个A 型篮球和2个B 型篮球共需340元，购买2个A 型篮球和1个B 型篮球共需要210元．（1）求购买一个A 型篮球、一个B 型篮球各需多少元？（2）若该校计划投入资金W 元用于购买这两种篮球，设购进的A 型篮球为t 个，求W 关于t 的函数关系式；（3）学校在体育用品专卖店购买A 、B 两种型号篮球共300个，经协商，专卖店给出如下优惠：A 种球每个降价8元，B 种球打9折，计算下来，学校共付费16740元，学校购买A 、B 两种篮球各多少个？23．如图，矩形ABCD 中，AB=4，AD=3，∠A 的角平分线交边CD 于点E ．点P 从点A 出发沿射线AE 以每秒2个单位长度的速度运动，Q 为AP 的中点，过点Q 作QH ⊥AB 于点H ，在射线AE 的下方作平行四边形PQHM （点M 在点H 的右侧），设P 点运动时间为秒．（1）直接写出的面积（用含的代数式表示）．（2）当点M 落在BC 边上时，求的值．（3）在运动过程中，整个图形中形成的三角形是否存在全等三角形？若存在，请写出所有全等三角形，并求出对应的的值；若不存在请说明理由（不能添加辅助线）． 24．如图，在平面直角坐标系中，直线28y x =+与x 轴交于点A,与y 轴交于点B,过点B 的直线x 轴于点C ，且AB=BC ．（1）求直线BC 的表达式（2）点P 为线段AB 上一点，点Q 为线段BC 延长线上一点，且AP=CQ,PQ 交x 轴于点P ，设点Q 的横坐标为m ，求PBQ ∆的面积（用含m 的代数式表示）（3）在（2）的条件下，点M 在y 轴的负半轴上，且MP=MQ ，若45BQM ︒∠=求点P 的坐标．25．如图，Rt △CEF 中，∠C ＝90°，∠CEF ，∠CFE 外角平分线交于点A ，过点A 分别作直线CE ，CF 的垂线，B ，D 为垂足．（1）∠EAF ＝ °（直接写出结果不写解答过程）；（2）①求证：四边形ABCD 是正方形．②若BE ＝EC ＝3，求DF 的长．（3）如图（2），在△PQR 中，∠QPR ＝45°，高PH ＝5，QH ＝2，则HR 的长度是（直接写出结果不写解答过程）．【参考答案】一、选择题1．D解析：D【分析】根据二次根式和分式有意义的条件列出不等式，求解不等式即可．【详解】根据题意得：x﹣3≥0且x﹣5≠0，解得x≥3且x≠5．∴自变量x的取值范围是x≥3且x≠5．故选：D．【点睛】本题考查了二次根式和分式由意义的条件，理解二次根式和分式由意义的条件是解题的关键．2．D解析：D【分析】根据勾股定理的逆定理对各选项进行逐一判断即可．【详解】解：A、∵72+242=625=252，∴能够成直角三角形，故本选项不符合题意；B、∵42+52412，∴能够成直角三角形，故本选项不符合题意；C、∵32+42=52，∴能够成直角三角形，故本选项不符合题意；D、∵42+52≠62，∴不能够成直角三角形，故本选项符合题意．故选：D．【点睛】本题考查的是勾股定理的逆定理，即如果三角形的三边长a，b，c满足a2+b2=c2，那么这个三角形就是直角三角形．3．B解析：B【解析】【分析】根据平行四边形的判定方法，一一判断即可．【详解】解：A. 两组对角分别相等的四边形是平行四边形,正确；根据平行四边形的判定方法，可得结论；B. 一组对边相等，另一组对边平行的四边形是平行四边形，错误；如：等腰梯形；C. 一组对边平行，一组对角相等的四边形是平行四边形正确，由题意可以证明两组对边分别平行，四边形是平行四边形；D. 一组对边平行且相等的四边形是平行四边形，正确，根据平行四边形的判定方法，可得结论．故选：B【点睛】本题考查平行四边形的判定，解题的关键是熟练掌握平行四边形的判定方法，属于中考基础题．4．B解析：B【解析】【分析】首先比较出甲、乙、丙、丁四名跳高运动员最近几次选拔赛成绩的方差的大小关系，然后根据方差越大，波动性越大，判断出应该选择谁参加比赛即可．【详解】解：因为3.5＜5.7＜6.7＜8.6，所以乙最近几次选拔赛成绩的方差最小，所以要从中选择一名发挥稳定的运动员去参加比赛，应该选择乙．故选：B．【点睛】此题主要考查了方差的含义和应用，要熟练掌握，解答此题的关键是要明确：方差反映了一组数据的波动大小，方差越大，波动性越大，反之也成立．5．A解析：A【分析】连接BD，根据三角形中位线定理易得四边形EFGH的各边长等于矩形对角线的一半，而矩形对角线相等，从而算出周长即可．【详解】连接BD，∵H、G是AD与CD的中点，∴HG是△ACD的中位线，∴HG=1AC=5cm，同理EF=5cm，2∵四边形ABCD是矩形，∴根据矩形的对角线相等，即BD=AC=10cm，∵H、E是AD与AB的中点，∴EH是△ABD的中位线，∴EH=1BD=5cm，同理FG=5cm，2∴四边形EFGH的周长为20cm．故选A．【点睛】熟练掌握矩形对角线相等和三角形中位线等于第三边的一半的性质是解决本题的关键. 6．C解析：C【解析】【分析】依题意得出AE=AB=AD，∠ADE=50°，又因为∠B=80°故可推出∠ADC=80°，∠CDE=∠ADC-∠ADE，从而求解．【详解】∵AD∥BC，∴∠AEB=∠DAE=∠B=80°，∴AE=AB=AD，在三角形AED中，AE=AD，∠DAE=80°，∴∠ADE=50°，又∵∠B=80°，∴∠ADC=80°，∴∠CDE=∠ADC-∠ADE=30°．故选：C．【点睛】考查菱形的边的性质，同时综合利用三角形的内角和及等腰三角形的性质，解题关键是利用等腰三角形的性质求得∠ADE的度数．7．B解析：B【解析】【分析】作BE ⊥AC 于E ，根据等腰三角形三线合一性质可得AE =DE ，根据∠C ＝45°，得出∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°，可得BE =CE ，利用勾股定理求出CE =BE =2，根据D 是AC 的三等分点得出AE =DE =121233AC AC ⨯==CD ，求出CD =1，利用勾股定理2222215AB BE AE =+=+=即可．【详解】解：作BE ⊥AC 于E ，∵AB ＝BD ，∴AE =DE ，∵∠C ＝45°，∴∠EBC =180°-∠C -∠BEC =180°-45°-90°=45°，∴BE =CE ，在Rt △BEC 中，∴()22222+222BE CE CE BC ===，∴CE =BE =2，∵D 是AC 的三等分点， ∴CD =13AC ，AD =AC -CD =1233AC AC AC -=， ∴AE =DE =121233AC AC ⨯==CD ， ∴CE =CD +DE =2CD =2，∴CD =1，∴AE =1，在Rt △ABE 中，根据勾股定理2222215AB BE AE =+=+=．故选B ．【点睛】本题考查等腰三角形的性质，等腰直角三角形判定与性质，勾股定理，三等分线段，掌握等腰三角形的性质，等腰直角三角形判定与性质，勾股定理，三等分线段是解题关键． 8．C解析：C【分析】由图像与纵轴的交点可得出A 、B 两地的距离；当s=0时，即为甲、乙相遇的时候，同理根据图像的拐点判断其他即可.【详解】解：由图像可知A 村、B 村相离8km ，故①正确；甲出发2h 后到达C 村，故②正确；当0≤t≤1时，易得一次函数的解析式为s=-8t+8，故甲的速度比乙的速度快8km/h ，故③正确；当1≤t≤1.5时，函数图象经过点（1，0）（1.5，4）设一次函数的解析式为s=kt+b则有：104 1.5k b k b =+⎧⎨=+⎩解得21k b =⎧⎨=⎩ ∴s=2t+1当s=2时，得2=2t+1，解得t=0.5＜1，不符合题意，④错误.故答案为C.【点睛】本题考查了一次函数的应用和函数与方程的思想，解题的关键在于读懂图象，根据图像的信息进行解答.二、填空题9．1≥x 且3x ≠【解析】【分析】根据分母不等于0，且被开方数是非负数列式求解即可．【详解】由题意得10x -≥且30x -≠解得1≥x 且3x ≠故答案为：1≥x 且3x ≠【点睛】本题考查了代数式有意义时字母的取值范围，代数式有意义时字母的取值范围一般从几个方面考虑：①当代数式是整式时，字母可取全体实数；②当代数式是分式时，考虑分式的分母不能为0；③当代数式是二次根式时，被开方数为非负数．10．A解析：6【解析】【分析】根据菱形的性质得到AC =8，根据菱形的面积等于两条对角线乘积的一半，即可求解．【详解】解：∵四边形ABCD 为菱形；∴AC =2OA =8，12ABCD S AC BD =⋅菱形, ∴12482BD =⨯⨯, ∴BD =6，故答案为：6【点睛】本题考查了菱形的性质，解题的关键是熟记菱形面积的两种表示法：（1）底乘高，（2）对角线乘积的一半，本题运用的是第二种．11．E解析：8【解析】【分析】根据正方形的面积等于边长的平方，由正方形PQED 的面积和正方形PRQF 的面积分别表示出PR 的平方及PQ 的平方，又三角形PQR 为直角三角形，根据勾股定理求出QR 的平方，即可求小正方形的边长．【详解】如图，∵正方形PQED 的面积等于225，∴即PQ 2=225,∵正方形PRGF 的面积为289，∴PR 2=289，又△PQR 为直角三角形，根据勾股定理得：PR 2=PQ 2+QR 2，∴QR 2=PR 2−PQ 2=289−225=64，∴QR=8，即字母A 所代表的正方形的边长为8.【点睛】本题考查勾股定理，根据勾股定理求出小正方形的面积是关键.12．D21【分析】由矩形的性质和角平分线的定义得出∠DEC =∠ECB =∠BEC ，推出BE =BC ，求得 AE =AB =1，然后依据勾股定理可求得BC 的长；【详解】解：∵四边形ABCD 是矩形，∴AD ∥BC ，∴∠DEC =∠BCE ，∵EC 平分∠DEB ，∴∠DEC =∠BEC ，∴∠BEC =∠ECB ，∴BE =BC ，∵四边形ABCD 是矩形，∴∠A =90°，AD BC =∵∠ABE =45°，∴∠ABE =∠AEB =45°，∴AB =AE =1，由勾股定理得：BE ==，∴BC =AD =BE， ∴1DE AD AE =-,1．【点睛】本题考查了矩形的性质，等腰三角形的性质与判定，勾股定理的应用；熟练掌握矩形的性质，证出BE =BC 是解题的关键．13．10y x =-+【分析】用待定系数法即可得到答案.【详解】解：把()8,2代入y x b =-+得82b -+=，解得10b =，所以一次函数解析式为10y x =-+．故答案为10y x =-+【点睛】本题考查求一次函数解析式，解题的关键是熟练掌握待定系数法.14．A解析：AC BD =【分析】如下图，根据三角形中位线的定理，可得AG=EF=12AC ，GF=AE=12BD ，再根据菱形四条边相等的性质，可得出AC 与BD 的关系．【详解】如下图，点E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点∵点E、F是AB、BC的中点∴EF=12AC同理可得：AG=EF=12AC，GF=AE=12BD∵要使得四边形HEFG是菱形，则HE=EF=FG=GH ∴只需AC=BD即可故答案为：AC=BD【点睛】本题考查菱形的性质和三角形中位线的性质，解题关键是得出AG=EF=12 AC，GF=AE=12 BD．15．（，0）【分析】作点D关于x轴对称点F，根据题意求出D点的坐标，从而得到F点的坐标，同时连接CF，则CF与x轴的交点即为所求E点，此时满足△CDE的周长最小，利用CF的解析式求解即可．【详解】解析：（83，0）【分析】作点D关于x轴对称点F，根据题意求出D点的坐标，从而得到F点的坐标，同时连接CF，则CF与x轴的交点即为所求E点，此时满足△CDE的周长最小，利用CF的解析式求解即可．【详解】解：作点D关于x轴对称点F，如图，∵四边形OABC 是矩形，∴OC ＝BD ＝3，点C 的坐标为()0,3，∵D 为AB 边的中点，∴AD ＝32， ∵OA ＝4，∴D 点的坐标为34,2⎛⎫ ⎪⎝⎭，则F 点的坐标为34,2⎛⎫- ⎪⎝⎭，根据轴对称的性质可得：EF ＝ED ，∴C △CDE ＝CD +CE +DE ＝CD +CE +EF ，其中CD 为定值，当CE +EF 值最小时，△CDE 周长最小，此时点C ，E ，F 三点共线，设直线CF 的解析式为：()0y kx b k =+≠，将()0,3和34,2⎛⎫- ⎪⎝⎭代入解析式得： 3342b k b =⎧⎪⎨+=-⎪⎩，解得：983k b ⎧=-⎪⎨⎪=⎩， ∴直线CF 的解析式为：938y x =-+，令0y =，得：9308x -+=，解得：83x =， ∴点E 坐标（83，0），故答案为：803⎛⎫ ⎪⎝⎭，．【点睛】本题考查一次函数与轴对称的综合运用，理解最短路径的求解方法，熟悉待定系数法求一次函数解析式是解题关键．16．5【分析】在Rt△BDC中由勾股定理可求出BD，根据翻折变换可得AH＝HD，在Rt△BDH 中由勾股定理可得答案．【详解】解：在Rt△BDC中，∵BC＝8，CD＝2，∴BD＝，由题意，得解析：5【分析】在Rt△BDC中由勾股定理可求出BD，根据翻折变换可得AH＝HD，在Rt△BDH中由勾股定理可得答案．【详解】解：在Rt△BDC中，∵BC＝8，CD＝∴BD=由题意，得AH＝HD，设BH＝x，则AH＝12﹣x＝HD，在Rt△BDH中，由勾股定理得，HB2+BD2＝HD2，即x2)2＝(12﹣x)2，解得x＝5，即HB＝5，故答案为：5．【点睛】本题考查了翻折变换，勾股定理．掌握翻折变换的性质及勾股定理是解题的关键．三、解答题17．（1）；（2）【分析】（1）先利用二次根式的性质化简，然后根据二次根式的混合计算法则求解即可；（2）先利用二次根式的性质化简，然后根据二次根式的混合计算法则求解即可．【详解】解：（1）解析：（1）2）4【分析】（1）先利用二次根式的性质化简，然后根据二次根式的混合计算法则求解即可；（2）先利用二次根式的性质化简，然后根据二次根式的混合计算法则求解即可．【详解】解：（1）===（22=4=4=【点睛】本题主要考查了利用二次根式的化简和二次根式的混合运算，熟练掌握相关计算法则是解题的关键．18．需要封闭，理由见解析【分析】过作于先求解再利用等面积法求解再与260比较，可得答案.【详解】解：过作于所以进行爆破时，公路BC 段需要暂时封闭.【点睛】解析：需要封闭，理由见解析【分析】过A 作AK BC ⊥于,K 先求解,BC 再利用等面积法求解,AK 再与260比较，可得答案.【详解】解：过A 作AK BC ⊥于,K,400,300,AB AC AB AC22500,BC AB AC11,AB AC BC AK22AK300400500,240,AK240260,所以进行爆破时，公路BC段需要暂时封闭.【点睛】本题考查的是勾股定理的应用，利用等面积法求解直角三角形斜边上的高，掌握“等面积法求解直角三角形斜边上的高”是解题的关键.19．（1）见解析；（2）见解析；（3）【解析】【分析】（1）根据正方形的判定画出以AB为边的正方形ABCD即可；（2）画出以EF为边的等腰三角形EFG，且△EFG的周长为等腰三角形即可；（3）解析：（1）见解析；（2）见解析；（35【解析】【分析】（1）根据正方形的判定画出以AB为边的正方形ABCD即可；（2）画出以EF为边的等腰三角形EFG，且△EFG的周长为1010（3）由勾股定理求出CG即可．【详解】解：（1）如图，所作正方形ABCD即为以AB为边的正方形ABCD；（2）如图，所作△EFG即为以EF为边的等腰三角形EFG，且△EFG的周长为1010+（3）如图，CG22+512【点睛】本题考查作图-应用与设计，勾股定理，解题的关键是理解题意，根据GE=GF=5画出等腰三角形．20．（1）AC⊥BD，证明见解析；（2）四边形ABCD是菱形，见解析【分析】（1）首先根据平行四边形的性质得出OC， OB的长，再利用勾股定理逆定理求出∠BOC=90，可得AC与BD的位置关系；（解析：（1）AC⊥BD，证明见解析；（2）四边形ABCD是菱形，见解析【分析】（1）首先根据平行四边形的性质得出OC，OB的长，再利用勾股定理逆定理求出∠BOC=90︒，可得AC与BD的位置关系；（2）菱形的判定方法：对角线互相垂直平分的四边形是菱形，可得答案．【详解】解：（1）AC⊥BD；理由如下：在ABCD中，132==OB BD，142OC AC==∵22291625+=+==OB OC BC∴∠BOC＝90︒∴AC⊥BD．（2）四边形ABCD是菱形∵四边形ABCD是平行四边形（已知），AC⊥BD（已证）∴四边形ABCD是菱形．【点睛】此题主要考查了菱形的判定，平行四边形的性质，以及勾股定理的逆定理的运用，解题的关键是根据条件证出BO2+CO2=CB2．21．（1）5；（2）5.【解析】【详解】试题分析: 根据平方差公式，可分母有理化，根据整体代入，可得答案．试题解析：（1）∵a=，∴4a2-8a+1=4×()2-8×（）+1=5；（2）解析：（1）5；（2）5.【解析】【详解】试题分析: 根据平方差公式，可分母有理化，根据整体代入，可得答案．试题解析：（1）∵， ∴4a 2-8a+1)2-8×）+1=5；（2）原式=12×=12×） =12×10=5.点睛：本题主要考查了分母有理化，利用分母有理化化简是解答此题的关键． 22．（1）一个A 型篮球为80元，一个B 型篮球为50元；（2）函数解析式为：；（3）A 型篮球120个，则B 型篮球为180个．【分析】（1）设一个A 型篮球为x 元，一个B 型篮球为y 元，根据题意列出方程组求解析：（1）一个A 型篮球为80元，一个B 型篮球为50元；（2）函数解析式为：()30150000300W t t =+≤≤；（3）A 型篮球120个，则B 型篮球为180个．【分析】（1）设一个A 型篮球为x 元，一个B 型篮球为y 元，根据题意列出方程组求解即可得；（2）A 型篮球t 个，则B 型篮球为()300t -个，根据单价、数量、总价的关系即可得；（3）根据A 型篮球与B 型篮球的优惠政策求出单价，然后代入（2）解析式中求解即可得．【详解】解：（1）设一个A 型篮球为x 元，一个B 型篮球为y 元，根据题意可得：323402210x y x y +=⎧⎨+=⎩，解得：8050x y =⎧⎨=⎩，∴一个A 型篮球为80元，一个B 型篮球为50元；（2）A 型篮球t 个，则B 型篮球为()300t -个，根据题意可得：()()805030030150000300W t t t t =+-=+≤≤，∴函数解析式为：()30150000300W t t =+≤≤；（3）根据题意可得：A 型篮球单价为()808-元，B 型篮球单价为500.9⨯元，则()()16740808500.9300t t =-+⨯⨯-，解得：120t =，300180t -=，∴A 型篮球120个，则B 型篮球为180个．【点睛】题目主要考查二元一次方程组及一次函数的应用，理解题意，列出相应方程是解题关键．23．（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是解析：（1）；（2）；（3）存在，如图2（见解析），当时，；如图3（见解析），当时，；如图4（见解析），当时，．【分析】（1）先根据线段中点的定义可得，再根据矩形的性质、角平分线的定义可得，从而可得是等腰直角三角形，然后根据等腰直角三角形的性质可得AH 的长，最后根据等腰直角三角形的面积公式即可得；（2）先根据平行四边形的性质可得，从而可得，再根据三角形中位线定理可得是的中位线，从而可得，然后与（1）所求的建立等式求解即可得；（3）分①当点H 是AB 的中点时，；②当点Q 与点E 重合时，；③当时，三种情况，分别求解即可得．【详解】（1）由题意得：，点Q 为AP 的中点，，四边形ABCD 是矩形，，是BAD的角平分线，，，是等腰直角三角形，，则的面积为；（2）如图1，四边形PQHM是平行四边形，，点M在BC边上，，点Q为AP的中点，是的中位线，，由（1）知，，则，解得；（3）由题意，有以下三种情况：①如图2，当点H是AB的中点时，则，四边形PQHM是平行四边形，，，在和中，，由（2）可知，此时；②如图3，当点Q与点E重合时，在和中，，，，则，解得；③如图4，当时，四边形ABCD是矩形，四边形PQHM是平行四边形，，，在和中，，，，在中，，是等腰直角三角形，，，在中，，是等腰直角三角形，，则由得：，解得；综上，如图2，当时，；如图3，当时，；如图4，当时，．【点睛】本题考查了矩形的性质、三角形中位线定理、三角形全等的判定定理与性质、等腰直角三角形的判定与性质等知识点，较难的是题（3），依据题意，正确分三种情况讨论并画出图形是解题关键．24．（1）y=-2x+8；（2）S=16m-2m2；（3）（-2，4）【解析】【分析】（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求BC 的解析式；（2）过点P作PG解析：（1）y=-2x+8；（2）S=16m-2m2；（3）（-2，4）【解析】【分析】（1）先求出点A，点B坐标，由等腰三角形的性质可求点C坐标，由待定系数法可求BC 的解析式；（2）过点P作PG⊥AC，PE∥BC交AC于E，过点Q作HQ⊥AC，由“AAS”可证△AGP≌△CHQ，可得AG=HC=m-4，PG=HQ=2m-8，由“AAS”可证△PEF≌△QCF，可得S△PEF=S△QCF，即可求解；（3）如图2，连接AM，CM，过点P作PE⊥AC，由“SSS”可证△APM≌△CQM，△ABM≌△CBM，可得∠PAM=∠MCQ，∠BQM=∠APM=45°，∠BAM=∠BCM，由“AAS”可证△APE≌△MAO，可得AE=OM，PE=AO=4，可求m的值，可得点P的坐标．【详解】解：（1）∵直线y=2x+8与x轴交于点A，与y轴交于点B，∴点B（0，8），点A（-4，0）∴AO=4，BO=8，∵AB=BC，BO⊥AC，∴AO=CO=4，∴点C（4，0），设直线BC解析式为：y=kx+b，由题意可得：804bk b=⎧⎨=+⎩，解得：28kb=-⎧⎨=⎩，∴直线BC解析式为：y=-2x+8；（2）如图1，过点P作PG⊥AC，PE∥BC交AC于E，过点Q作HQ⊥AC，设△PBQ的面积为S，∵AB=CB，∴∠BAC=∠BCA，∵点Q横坐标为m，∴点Q（m，-2m+8）∴HQ=2m-8，CH=m-4，∵AP=CQ，∠BAC=∠BCA=∠QCH，∠AGP=∠QHC=90°，∴△AGP≌△CHQ（AAS），∴AG=HC=m-4，PG=HQ=2m-8，∵PE∥BC，∴∠PEA=∠ACB，∠EPF=∠CQF，∴∠PEA=∠PAE，∴AP=PE，且AP=CQ，∴PE=CQ，且∠EPF=∠CQF，∠PFE=∠CFQ，∴△PEF≌△QCF（AAS）∴S△PEF=S△QCF，∴△PBQ的面积=四边形BCFP的面积+△CFQ的面积=四边形BCFP的面积+△PEF的面积=四边形PECB的面积，∴S=S△ABC-S△PAE=12×8×8-12×（2m-8）×（2m-8）=16m-2m2；（3）如图2，连接AM，CM，过点P作PE⊥AC，∵AB=BC，BO⊥AC，∴BO是AC的垂直平分线，∴AM=CM，且AP=CQ，PM=MQ，∴△APM≌△CQM（SSS）∴∠PAM=∠MCQ，∠BQM=∠APM=45°，∵AM=CM，AB=BC，BM=BM，∴△ABM≌△CBM（SSS）∴∠BAM=∠BCM，∴∠BCM=∠MCQ，且∠BCM+∠MCQ=180°，∴∠BCM=∠MCQ=∠PAM=90°，且∠APM=45°，∴∠APM=∠AMP=45°，∴AP=AM，∵∠PAO+∠MAO=90°，∠MAO+∠AMO=90°，∴∠PAO=∠AMO，且∠PEA=∠AOM=90°，AM=AP，∴△APE≌△MAO（AAS）∴AE=OM，PE=AO=4，∴2m-8=4，∴m=6，∴P（-2，4）．【点睛】本题是一次函数综合题，考查了待定系数法求解析式，全等三角形的判定和性质，等腰三角形的性质，添加恰当辅助线构造全等三角形是本题的关键．25．（1）45；（2）①见解析；②DF的长为2；（3）【分析】（1）根据平角的定义得到∠DFE+∠BEF＝360°﹣90°＝270°，根据角平分线的定义得到∠AFE＝DFE，∠AEF＝BEF，求得∠解析：（1）45；（2）①见解析；②DF的长为2；（3）15 7【分析】（1）根据平角的定义得到∠DFE+∠BEF＝360°﹣90°＝270°，根据角平分线的定义得到∠AFE＝12∠DFE，∠AEF＝12∠BEF，求得∠AEF+∠AFE＝12（∠DFE+∠BEF），根据三角形的内角和定理即可得到结论；（2）①作AG⊥EF于G，如图1所示：则∠AGE＝∠AGF＝90°，先证明四边形ABCD是矩形，再由角平分线的性质得出AB＝AD，即可得出四边形ABCD是正方形；②设DF＝x，根据已知条件得到BC＝6，由①得四边形ABCD是正方形，求得BC＝CD＝6，根据全等三角形的性质得到BE＝EG＝3，同理，GF＝DF＝x，根据勾股定理列方程即可得到结论；（3）把△PQH沿PQ翻折得△PQD，把△PRH沿PR翻折得△PRM，延长DQ、MR交于点G，由（1）（2）得：四边形PMGD是正方形，MR+DQ＝QR，MR＝HR，DQ＝HQ＝2，得出MG＝DG＝MP＝PH＝6，GQ＝4，设MR＝HR＝a，则GR＝6﹣a，QR＝a+2，在Rt△GQR 中，由勾股定理得出方程，解方程即可．【详解】解：（1）∵∠C＝90°，∴∠CFE+∠CEF＝90°，∴∠DFE+∠BEF＝360°﹣90°＝270°，∵AF平分∠DFE，AE平分∠BEF，∴∠AFE＝12∠DFE，∠AEF＝12∠BEF，∴∠AEF +∠AFE ＝12（∠DFE +∠BEF ）＝12⨯270°＝135°，∴∠EAF ＝180°﹣∠AEF ﹣∠AFE ＝45°，故答案为：45；（2）①作AG ⊥EF 于G ，如图1所示：则∠AGE ＝∠AGF ＝90°， ∵AB ⊥CE ，AD ⊥CF ， ∴∠B ＝∠D ＝90°＝∠C ， ∴四边形ABCD 是矩形，∵∠CEF ，∠CFE 外角平分线交于点A ， ∴AB ＝AG ，AD ＝AG ， ∴AB ＝AD ，∴四边形ABCD 是正方形； ②设DF ＝x ， ∵BE ＝EC ＝3， ∴BC ＝6，由①得四边形ABCD 是正方形， ∴BC ＝CD ＝6，在Rt △ABE 与Rt △AGE 中，AB AGAE AE=⎧⎨=⎩ ， ∴Rt △ABE ≌Rt △AGE （HL ）， ∴BE ＝EG ＝3，同理，GF ＝DF ＝x ，在Rt △CEF 中，EC 2+FC 2＝EF 2，即32+（6﹣x ）2＝（x +3）2，解得：x ＝2， ∴DF 的长为2；（3）解：如图2所示：把△PQH沿PQ翻折得△PQD，把△PRH沿PR翻折得△PRM，延长DQ、MR交于点G，由（1）（2）得：四边形PMGD是正方形，MR+DQ＝QR，MR＝HR，DQ＝HQ＝2，∴MG＝DG＝MP＝PH＝5，∴GQ＝3，设MR＝HR＝a，则GR＝5﹣a，QR＝a+2，在Rt△GQR中，由勾股定理得：（5﹣a）2+32＝（2+a）2，解得：a＝157，即HR＝157；故答案为：157．【点睛】本题考查了正方形的判定与性质、全等三角形的判定与性质、角平分线的性质、勾股定理、矩形的判定、翻折变换的性质等知识；本题综合性强，有一定难度．。

人教版八年级期末试卷测试卷(word版,含解析)

人教版八年级期末试卷测试卷（word 版，含解析）一、选择题 1．若代数式252x x --有意义，则x 的取值范围是（） A ．2x ≠ B ．25x ≤ C ．25x ≤且2x ≠ D ．25x ≥且2x ≠ 2．下列条件中，能判断△ABC 是直角三角形的是（）A ．a ：b ：c ＝3：4：4B ．a ＝1，b ＝2，c ＝3C ．∠A ：∠B ：∠C ＝3：4：5D ．a 2：b 2：c 2＝3：4：53．小玲的爸爸在钉制平行四边形框架时，采用了一种方法：如图所示，将两根木条AC 、BD 的中点重叠并用钉子固定，则四边形ABCD 就是平行四边形，这种方法的依据是（）A ．对角线互相平分的四边形是平行四边形B ．一组对边平行且相等的四边形是平行四边形C ．两组对边分别相等的四边形是平行四边形D ．两组对角分别相等的四边形是平行四边形 4．水稻科研人员为了比较甲乙两种水稻秧苗谁出苗更整齐，每种秧苗各随机抽取60株，分别量出每株高度，发现两组秧苗的平均高度和中位数均相同，甲、乙的方差分别是3.6，6.3，则下列说法正确的是（）A ．甲秧苗出苗更整齐B ．乙秧苗出苗更整齐C ．甲、乙出苗一样整齐D ．无法确定甲、乙出苗谁更整齐 5．甲、乙两艘轮船同时从港口出发，甲以16海里/时的速度向北偏东75︒的方向航行，它们出发1.5小时后，两船相距30海里，若乙以12海里/时的速度航行，则它的航行方向为（）A ．北偏西15︒B ．南偏西75°C ．南偏东15︒或北偏西15︒D ．南偏西15︒或北偏东15︒ 6．如图，在ABC 中，∠B+∠C ＝α，按图进行翻折，使////,//B D C G BC BE FG '''，则∠C 'FE 的度数是（）A ．2αB ．90°﹣2αC ．α﹣90°D ．2α﹣180°7．如图，在ABCD 中，对角线AC ，BD 相交于点O ，点E 是BC 的中点，若8OE =，则AB 的长为（）A ．16B ．18C ．20D ．228．如图，菱形ABCD 的边长为4cm ，60ABC ∠=︒，且M 为BC 的中点，P 是对角线BD 上的一动点，则PM PC +的最小值为（）A ．4cmB ．3cmC ．25cmD ．23cm二、填空题9．代数式2021x -中，字母x 的取值范围是____________．10．如图，在菱形ABCD 中，对角线BD ＝4，AC ＝3BD ，则菱形ABCD 的面积为 _____．11．如图，一个密封的圆柱形油罐底面圆的周长是10m ，高为13m ，一只壁虎在距底面1m 的A 处，C 处有食物，壁虎沿油罐的外侧面爬行到C 处捕食，它爬行的最短路线长为_____m ．12．如图，在Rt ABC △中，90ACB ∠=︒，CD AB ⊥于点D ，3ACD BCD ∠=∠，点E 是斜边AB 的中点，若2CD =，则CE 的长为_____．13．若一次函数2y x b =+(b 为常数)的图象经过点(b ，9)，则b =____．14．如图，在矩形ABCD 中，AB=3，AD=4，点P 在AD 上，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE+PF 等于_____．15．如图，已知直线1:1l y x =+与x 轴交于点,A 与直线21:22l y x =+交于点B ，点C 为x 轴上的一点，若ABC ∆为直角三角形，则点C 的坐标为__________．16．在一次自行车越野赛中，出发m h 后，小明骑行了25km ，小刚骑行了18km ，此后两人分别以a km/h ，b km/h 匀速骑行，他们骑行的时间t （单位：h ）与骑行的路程s （单位：km ）之间的函数关系如图所示，观察图象，下列说法：①出发m h 内小明的速度比小刚快；② a =26；③小刚追上小明时离起点43km ；④此次越野赛的全程为90km ，正确的有______________（把正确结论的序号填在横线上）.三、解答题17．计算：（1()20382(3)π---；（2）21(22)24322-．18．明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》：“平地秋千未起，踏板一尺离地，送行二步恰竿齐，五尺板高离地…”翻译成现代文为：如图，秋千OA 静止的时候，踏板离地高一尺（1AC =尺），将它往前推进两步（10EB =尺），此时踏板升高离地五尺（5BD =尺），求秋千绳索（OA 或OB ）的长度．19．图①、图②均是44⨯的正方形网格，小正方形的边长为1，每个小正方形的顶点称为格点，点A 、B 均在格点上，只用无刻度的直尺，在给定的网格中按要求画图，所画图形的顶点均在格点上，所画图形不全等，不要求写画法．（1）在图①中以线段AB 为边画一个正方形ABCD ．（2）在图②中以线段AB 为边画一个菱形ABEF ．20．如图，在平行四边形ABCD 中，M ，N 是对角线BD 上的点，且BM DN =，DE 平分ADB ∠交AB 于点E ，BF 平分DBC ∠交CD 于点F ．（1）求证：四边形EMFN 是平行四边形；（2）当四边形EMFN 是菱形时，求证：四边形BEDF 是菱形．21．阅读下面的解答过程，然后作答： 2a b + m 和n ，使m2+n2=a 且b ，则a+2b 可变为m2+n2+2mn ，即变成（m+n ）2，从而使得2a b +化简．例如：∵5+26=3+2+26=（3）2+（2）2+26=（3+2）2∴526+=()232+=3+2请你仿照上例将下列各式化简（1）423+，（2）7210-．22．某电影院普通票价20元/张，暑假为了促销，新推出两种优惠卡：①金卡售价600元/张，每次凭卡不再收费．②银卡售价150元/张，每次凭卡另收10元．暑假普通票正常出售，两种优惠卡仅限暑假使用，不限次数．设看电影x 次时，所需总费用为y 元．（1）分别写出选择银卡、普通票消费时，y 与x 之间的函数关系式；（2）在同一坐标系中，若三种消费方式对应的函数图象如图所示，请求出点A ，B ，C 的坐标；（3）请根据函数图象，提出1条合算的消费建议．23．如图1，四边形ACBD 中，AC =AD ，BC =BD ．我们把这种两组邻边分别相等的四边形叫做“筝形”，如图2，在“筝形”ACBD 中，对角线AB =CD ，过点B 作BE ⊥AC 于E 点，F 为线段BE 上一点，连接FA 、FD ，FA =FB ．（1）求证：△ABF ≌△CDA ；（2）如图3，FA 、FD 分别交CD 、AB 于点M 、N ，若AM =MF ，求证：BN =CM +MN ．24．如图1，在平面直角坐标系xOy 中，直线AB 交y 轴于点A (0，3)，交x 轴于点B (﹣4，0)．(1)求直线AB 的函数表达式；(2)如图2，在线段OB 上有一点C （点C 不与点O 、点B 重合），将AOC 沿AC 折叠，使点O 落在AB 上，记作点D ，在BD 上方，以BD 为斜边作等腰直角三角形BDF ，求点F 的坐标；(3)在(2)的条件下，如图3，在平面内是否存在一点E ，使得以点A ，B ，E 为顶点的三角形与ABC 全等（点E 不与点C 重合），若存在，请直接写出满足条件的所有点E 的坐标，若不存在，请说明理由．25．（解决问题）如图1，在ABC ∆中，10AB AC ==，CG AB ⊥于点G ．点P 是BC 边上任意一点，过点P 作PE AB ⊥，PF AC ⊥，垂足分别为点E ，点F ．（1）若3PE =，5PF =，则ABP ∆的面积是______，CG =______．（2）猜想线段PE ，PF ，CG 的数量关系，并说明理由．（3）（变式探究）如图2，在ABC ∆中，若10AB AC BC ===，点P 是ABC ∆内任意一点，且PE BC ⊥，PF AC ⊥，PG AB ⊥，垂足分别为点E ，点F ，点G ，求PE PF PG ++的值．（4）（拓展延伸）如图3，将长方形ABCD 沿EF 折叠，使点D 落在点B 上，点C 落在点C '处，点P 为折痕EF 上的任意一点，过点P 作PG BE ⊥，PH BC ⊥，垂足分别为点G ，点H ．若8AD =，3CF =，直接写出PG PH +的值．26．在平面直角坐标系xOy 中，对于点P 给出如下定义：点P 到图形1G 上各点的最短距离为1d ，点P 到图形2G 上各点的最短距离为2d ，若12d d =，就称点P 是图形1G 和图形2G 的一个“等距点”．已知点()6,0A ，()0,6B ．（1）在点()6,0D -，()3,0E ，()0,3F 中，______是点A 和点O 的“等距点”；（2）在点()2,1G --，()2,2H ，()3,6I 中，______是线段OA 和OB 的“等距点”；（3）点(),0C m 为x 轴上一点，点P 既是点A 和点C 的“等距点”，又是线段OA 和OB 的“等距点”．①当8m =时，是否存在满足条件的点P ，如果存在请求出满足条件的点P 的坐标，如果不存在请说明理由；②若点P 在OAB 内，请直接写出满足条件的m 的取值范围．【参考答案】一、选择题1．B解析：B【分析】根据二次根式被开方数大于等于零及分式有意义的条件：分母不等于零解答．【详解】解：由题意得：250,20x x -≥-≠，得25x ≤，故选：B ．【点睛】此题考查二次根式被开方数大于等于零及分式有意义的条件，熟记两个条件是解题的关键．2．B解析：B【分析】根据勾股定理的逆定理，以及三角形的内角等于180︒逐项判断即可．【详解】A ，设3a x =，4b x ，4=c x ，此时()()()222344x x x +≠，故ABC 不能构成直角三角形，故不符合题意；B ，2221+=，故ABC 能构成直角三角形，故符合题意C ，::3:4:5A B C ∠∠∠=且180A B C ∠+∠+∠=︒，设3A x ∠=，4B x ∠=，5C x ∠=，则有12180x =︒，所以15x =︒，则75C ∠=︒，故ABC 不能构成直角三角形，故不符合题意；D ，设23a x =，24b x =，25c x =，则345x x x +≠，即222a b c +≠，故ABC 不能构成直角三角形，故不符合题意；故选：B【点睛】本题考查了勾股定理的逆定理，和三角形的内角和等知识，能熟记勾股定理的逆定理内容和三角形内角和等于180︒是解题关键．3．A解析：A【解析】【分析】根据平行四边形的判定定理解答即可.【详解】由已知可得AO=CO ，BO=DO ，∴四边形ABCD 是平行四边形，依据是：对角线互相平分的四边形是平行四边形，故选：A.【点睛】此题考查平行四边形的判定定理，熟练掌握平行四边形的五种判定定理并运用解决问题是解题的关键.4．A解析：A【解析】【分析】根据方差的意义可作出判断．方差是用来衡量一组数据波动大小的量，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．【详解】解：∵甲、乙的方差的分别为3.6、6.3，∴甲的方差小于乙的方差，∴甲秧苗出苗更整齐．故选：A ．【点睛】本题考查方差的意义．方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定．5．C解析：C【分析】先求出出发1.5小时后，甲乙两船航行的路程，进而可根据勾股定理的逆定理得出乙船的航行方向与甲船的航行方向垂直，进一步即可得出答案．【详解】解：出发1.5小时后，甲船航行的路程是16×1.5=24海里，乙船航行的路程是12×1.5=18海里；∵222241857632490030+=+==，∴乙船的航行方向与甲船的航行方向垂直，∵甲船的航行方向是北偏东75°，∴乙船的航行方向是南偏东15°或北偏西15°．故选：C ．【点睛】本题考查了勾股定理的逆定理和方位角，属于常考题型，正确理解题意、熟练掌握勾股定理的逆定理是解题的关键．6．D解析：D【解析】【分析】设∠ADB′＝γ，∠AGC′＝β，∠CEB′＝y ，∠C′FE ＝x ，利用平行线的性质，三角形内角和定理构建方程组即可解决问题．【详解】解：设∠ADB′＝γ，∠AGC′＝β，∠CEB′＝y ，∠C′FE ＝x ，∵////''B D C G BC ，∴B γ=∠，C β=∠，∴γ+β＝∠B+∠C ＝α，∵EB′∥FG ，∴∠CFG ＝∠CEB′＝y ，∴x+2y ＝180°①，根据平行线的性质和翻折的性质可得：B γ=∠，//'BD B E ，∴y B =∠，∵γ+y ＝2∠B ，同理可得出：β+x ＝2∠C ，∴γ+y+β+x ＝2α，∴x+y ＝α②，②×2﹣①可得x ＝2α﹣180°，∴∠C′FE ＝2α﹣180°．故选：D．【点睛】本题考查三角形内角和定理，平行线的性质，翻折变换等知识，解题的关键是学会利用参数解决问题，属于中考常考题型．7．A解析：A【解析】【分析】根据平行四边形的性质可得OB=OD，根据点E是BC的中点可得OE为△BCD的中位线，进而可得BC长．【详解】解：∵四边形ABCD是平行四边形，∴OB=OD，AB=CD，∵E是BC的中点，∴OE是△BCD的中位线，∴CD=2EO，∵EO=8，∴CD=2EO=16，∴AB=CD=16，故选：A．【点睛】此题主要考查了平行四边形的性质，以及三角形中位线的性质，掌握平行四边形的性质，三角形中位线的性质是解题关键．8．D解析：D【分析】根据菱形的性质，得知A、C关于BD对称，根据轴对称的性质，将PM+PC转化为AP+PM，再根据两点之间线段最短得知AM为PM+PC的最小值．【详解】∵四边形ABCD为菱形，∴A、C关于BD对称，∴连AM交BD于P，则PM+PC=PM+AP=AM，根据两点之间线段最短，AM 的长即为PM+PC 的最小值．连接AC ，∵四边形ABCD 是菱形，∴AB=BC ，又∵∠ABC=60°，∴△ABC 为等边三角形，又∵BM=CM ，∴AM ⊥BC ，∴AM=2222=42=23AB BM --，故选D.【点睛】本题考查了轴对称---最短路径问题，解答过程要利用菱形的性质及等腰三角形的性质，转化为两点之间线段最短的问题来解．二、填空题 9．x ≥2021【解析】【分析】直接利用二次根式的定义分析得出答案．【详解】解：∵2021x -∴20210x -≥，解得：2021x ≥．故答案为：2021x ≥．【点睛】本题主要考查了二次根式有意义的条件，正确掌握定义是解题关键．10．A解析：24【解析】【分析】先求出AC ，由菱形的面积公式可求解．【详解】解：∵BD ＝4，AC ＝3BD ，∴AC ＝12，∴菱形ABCD 的面积＝2AC BD ⨯＝4122⨯＝24，故答案为：24．【点睛】本题考查了菱形的性质，利用菱形的性质求解面积是解题的关键．对角线互相垂直的四边形的面积等于对角线积的一半．11．A解析：13【解析】【分析】根据题意画出圆柱的侧面展开图的平面图形，进而利用勾股定理得出答案．【详解】解：如图所示：由题意可得：AD =5m ，CD =12m ，则AC =2212513+=(m)，故答案为：13．【点睛】本题主要考查了平面展开图的最短路径问题，正确画出平面图形是解题的关键． 12．2【分析】根据角之间的关系求得45DEC ∠=︒，从而求得CE 的长．【详解】解：∵3ACD BCD ∠=∠，90ACB ∠=︒∴22.5BCD ∠=︒又∵CD AB ⊥∴9022.5BCD B BAC ∠=︒-∠=∠=︒，90CDE ∠=︒又∵点E 是斜边AB 的中点∴CE AE =∴22.5ECA BAC ∠=∠=︒∴45BEC ∠=︒∴CDE △为等腰直角三角形∴222CE CD DE +故答案为2．【点睛】此题主要考查了直角三角形的有关性质，熟练掌握勾股定理、斜边中线等于斜边一半等性质是解题的关键．13．3【分析】把点(b ，9)代入函数解析式，即可求解．【详解】∵一次函数2y x b =+(b 为常数)的图象经过点(b ，9)，∴92b b =+，解得：b=3，故答案是：3．【点睛】本题主要考查一次函数图象上的点的坐标特征，掌握待定系数法，是解题的关键． 14．A 解析：125【详解】解：设AC 与BD 相交于点O ，连接OP ，过D 作DM ⊥AC 于M ，∵四边形ABCD 是矩形， ∴，AC=BD ，∠ADC=90°．∴OA=OD ． ∵AB=3，AD=4，∴由勾股定理得：22345+ ． ∵1134522ACD S DM ∆=⨯⨯=⨯⋅ ，∴DM=125． ∵AOD APO DPO S S S ∆∆∆=+， ∴111222AO DM AO PE DO PF ⋅⋅=⋅+⋅ ． ∴PE+PF=DM=125．故选B ． 15．(2，0)或（5，0）【分析】先求出A ，再求出，解得，则点B （2，3），分类讨论直角顶点，当点C 为直角顶点时，当点B 为直角顶点时，根据△ABC 为等腰直角三角形即可求出点C 坐标．【详解】与轴交解析：(2，0)或（5，0）【分析】先求出A ，再求出1122y x y x =+⎧⎪⎨=+⎪⎩，解得=23x y ⎧⎨=⎩，则点B （2，3），分类讨论直角顶点，当点C 为直角顶点时，当点B 为直角顶点时，根据△ABC 为等腰直角三角形即可求出点C 坐标．【详解】1:1l y x =+与x 轴交于点A ，∴y=0，x=-1，∴A(-1，0)，直线1:1l y x =+与直线21:22l y x =+交于点B ， 1122y x y x =+⎧⎪⎨=+⎪⎩，解得=23x y ⎧⎨=⎩， ∴B （2，3），当点C 为直角顶点时，∴BC ⊥AC ，∴BC ∥y 轴，B 、C 横坐标相同，C （2，0），当点B 为直角顶点时，∴BC ⊥AB ，1:1l y x =+，k=1，∴∠BAC=45°，∴△ABC 为等腰直角三角形，∴=6，AO=1，CO=AC-AO=5，C （5，0），C 点坐标为（2，0）或（5，0）．故答案为：（2，0）或（5，0）．【点睛】本题考查等腰直角三角形的性质，掌握直角三角形的顶点分两种情况讨论解决问题是关键．16．①②④【解析】试题解析：由图象可知，出发mh内小明的速度比小刚快，故①正确；由图象可得，，解得，，故②正确；小刚追上小明走过的路程是：36×（0.5+0.7）=36×1.2=43.2k解析：①②④【解析】试题解析：由图象可知，出发mh内小明的速度比小刚快，故①正确；由图象可得，()()()() 250.70.7 {25 2.5218a m m m bm m a m bbm++-+++-+＝＝＝，解得，26 {360.5abm＝＝＝，故②正确；小刚追上小明走过的路程是：36×（0.5+0.7）=36×1.2=43.2km＞43km，故③错误；此次越野赛的全程是：36×（0.5+2）=36×2.5=90km，故④正确；故答案为①②④．三、解答题17．（1）﹣1；（2）【分析】（1）化简立方根，算术平方根，零指数幂，然后再计算；（2）先算乘方，然后算乘法，化简绝对值，最后算加减．【详解】解：（1），，；（2），，．【点睛解析：（1）﹣1；（2）10+【分析】（1）化简立方根，算术平方根，零指数幂，然后再计算；（2）先算乘方，然后算乘法，化简绝对值，最后算加减．【详解】π-，解：（1()03=-+-，221=-；1-（2）(22=+82=+82=10【点睛】题目主要考查实数的混合运算，包括立方根、算数平方根、乘方、绝对值、二次根式的运算等，熟练掌握运算法则是解题关键．18．秋千绳索的长度为尺．【分析】设OA=OB=x尺，表示出OE的长，在中，利用勾股定理列出关于x的方程求解即可．【详解】解：设尺，由题可知：尺，尺，∴（尺），尺，在中，尺，尺，尺，由勾股解析：秋千绳索的长度为14.5尺．【分析】设OA =OB =x 尺，表示出OE 的长，在Rt OEB 中，利用勾股定理列出关于x 的方程求解即可．【详解】解：设OA OB x ==尺，由题可知：5EC BD ==尺，1AC =尺，∴514EA EC AC =-=-=（尺），()4OE OA AE x =-=-尺，在Rt OEB 中，()4OE x =-尺，OB x =尺，10EB =尺，由勾股定理得：()222410x x =-+，解得：14.5x =，则秋千绳索的长度为14.5尺．【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理，学会利用方程解决问题是解题的关键． 19．（1）见解析；（2）见解析【解析】【分析】（1）根据正方形的判定进行画图即可；（2）根据菱形的判定进行画图即可．【详解】解：（1）如图所示：，，∴，∴∠ABC=90°，∴四边形AB解析：（1）见解析；（2）见解析【解析】【分析】（1）根据正方形的判定进行画图即可；（2）根据菱形的判定进行画图即可．【详解】解：（1）如图所示：AC AB CD AD BC === ∴222AB BC AC +=，∴∠ABC =90°，∴四边形ABCD 是正方形；（2）如图所示22====+=，AB EF AF BE125∴四边形ABEF是菱形．【点睛】本题主要考查了菱形的判定，正方形的判定，勾股定理和勾股定理的逆定理，解题的关键在于能够熟练掌握相关知识进行求解．20．（1）见解析；（2）见解析【分析】（1）连接EF交MN于O，证△ADE≌△CBF（ASA），得DE=BF，再证DE∥BF，则四边形BEDF是平行四边形，得OE=OF，OB=OD，然后证OM=ON 解析：（1）见解析；（2）见解析【分析】（1）连接EF交MN于O，证△ADE≌△CBF（ASA），得DE=BF，再证DE∥BF，则四边形BEDF是平行四边形，得OE=OF，OB=OD，然后证OM=ON，即可得出结论；（2）由菱形的性质得EF⊥MN，由（1）得四边形BEDF是平行四边形，即可得出结论．【详解】证明：（1）连接EF交MN于O，∵四边形ABCD是平行四边形，∴∠A=∠C，AD=BC，AD∥BC，∴∠ADB=∠DBC，∵DE平分∠ADB，BF平分∠DBC，∴∠ADE=∠EDB=∠CBF=∠FBD，在△ADE和△CBF中，A C AD BCADE CBF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△ADE ≌△CBF （ASA ），∴DE =BF ，∵∠EDB =∠FBD ，∴DE ∥BF ，∴四边形BEDF 是平行四边形，∴OE =OF ，OB =OD ，∵BM =DN ，∴OB -BM =OD -DN ，即OM =ON ，∴四边形EMFN 是平行四边形；（2）∵四边形EMFN 是菱形，∴EF ⊥MN ，由（1）得：四边形BEDF 是平行四边形，∴平行四边形BEDF 是菱形．【点睛】本题考查了菱形的判定与性质、平行四边形的判定与性质、全等三角形的判定与性质、平行线的平对于性质等知识；熟练掌握菱形的判定与性质，证明△ADE ≌△CBF 是解题的关键，属于中考常考题型．21．（1）1+；（2）.【解析】【分析】参照范例中的方法进行解答即可.【详解】解：（1）∵，∴；（2）∵，∴.解析：（1）2-【解析】【分析】参照范例中的方法进行解答即可.【详解】解：（1）∵222++=，41(1∴1=（2）∵2227-=-=，∴22．（1）y＝10x+150，y＝20x；（2）A（0，150），B（15，300），C（45，600）；（3）当0＜x＜15时，选择普通消费更划算；当x＝15时，银卡，普通票总费用相同，均比金卡划算；解析：（1）y＝10x+150，y＝20x；（2）A（0，150），B（15，300），C（45，600）；（3）当0＜x＜15时，选择普通消费更划算；当x＝15时，银卡，普通票总费用相同，均比金卡划算；当15＜x＜45时，银卡消费更划算；当x＝45时，金卡，银卡的总费用相同，均比普通票划算；当x＞45时，金卡消费更划算．【分析】（1）弄清题意，结合图象易知普通票为正比例函数图象，银卡为一次函数图象，依题意写出即可；（2）银卡函数关系式y＝10x+150，令x＝0时即可求出A点坐标，令银卡函数与普通卡函数关系式相等即可找到B点坐标，令银卡函数关系式y＝600，即可找到C点坐标；（3）结合图象分当0＜x＜15时，x＝15时，15＜x＜45时，x＝45时，x＞45时五段，依次分析出最合算的消费建议即可．【详解】解：（1）由题意得，选择银卡时，y与x之间的函数关系式为：y＝10x+150；选择普通票时，y与x之间的函数关系式为：y＝20x；（2）由题意可得：当y＝10x+150，x＝0时，y＝150，故A（0，150），当10x+150＝20x，解得：x＝15，则y＝300，故B（15，300），当y＝10x+150＝600时，解得：x＝45，故C（45，600）；（3）如图所示，由A、B、C三点坐标可得：当0＜x＜15时，选择普通消费更划算；当x＝15时，银卡，普通票总费用相同，均比金卡划算；当15＜x＜45时，银卡消费更划算；当x＝45时，金卡，银卡的总费用相同，均比普通票划算；当x＞45时，金卡消费更划算．【点睛】本题考查一次函数应用，重点掌握一次函数的基本性质熟练应用，能结合实际灵活运用是解题的关键．23．（1）证明见解析；（2）证明见解析【分析】（1）根据已知条件可得△ABC≌△ABD，再根据∠AOC+∠AOD=180°，进而可证得AB⊥CD，进而得到∠ACO=∠ABE，进而证得△ABF≌△CD解析：（1）证明见解析；（2）证明见解析【分析】（1）根据已知条件可得△ABC≌△ABD，再根据∠AOC+∠AOD=180°，进而可证得AB⊥CD，进而得到∠ACO=∠ABE，进而证得△ABF≌△CDA；（2）取AB中点H，根据已知条件可知MO为△AFH的中位线，进而可证得△AFH≌△DAO，进一步得到△AFD为等腰直角三角形，然后过点F作FI⊥AF交AB于点I，取CD上点G使MG=MN，连接AG，先证△AFI≌△DAM，而后△FMN≌△FIN，得到∠FIN =∠FMN，进而可证△AMG≌△FMN，得到∠AGM=∠FNM，进而证得△ACG≌△FBN，得到BN=CG，再根据CG=CM+MG，得到BN=CM+MG，又MG=MN，继而得到BN=CM+MN．【详解】证明：（1）∵AC=AD，BC=BD，AB=AB，∴△ABC≌△ABD，∴∠CAO=∠DAO，又∵∠ACO=∠ADO，∴∠AOC=∠AOD，又∵∠AOC+∠AOD=180°，∴∠AOC=∠AOD=90°，∴AB⊥CD，在Rt△AOC中，∠ACO+∠CAO=90°，在Rt△AEB中，∠ABE+∠CAO=90°，∴∠ACO=∠ABE，又∵AC=AD，FA=FB，∴∠ACO=∠ADO=∠ABF=∠FAB，∵，∴△ABF≌△CDA；（2）如图，取AB中点H，∵△ABF是等腰三角形，∴FH⊥AB，∵AM=MF且MO⊥AB，∴MO为△AFH的中位线，∴AO=OH=，又∵AH===DO，由△ABF≌△CDA，可知：AF=BF=AC=AD，∴△AFH≌△DAO，∴∠AFH=∠DAO，∵∠FAH+∠AFH=90°，∴∠FAH+∠DAO=90°，∴∠FAD=90°，∴△AFD为等腰直角三角形，过点F作FI⊥AF交AB于点I，取CD上点G使MG=MN，连接AG，由△AFH≌△DAO可得∠FAI=∠ADM，又∵AD=AF，∴△AFI≌△DAM，∴FI=AM，又∵AM=MF，∴FI=MF，由FI⊥AF可知∠AFI=90°，∠AFN=45°，∴∠NFI=∠AFI-∠AFN=90°-45°=45°，∴∠MFN=∠NFI ，又∵FI=FM ，∴△FMN ≌△FIN ，∴∠FIN =∠FMN ，又∵∠AMD=∠FIA ，∴∠AMD=∠FMN ，又∵AM=FM ，MG=MN ，∴△AMG ≌△FMN ，∴∠AGM=∠FNM ，又∵∠FNM=∠FNB ，∴∠AGM=∠FNB ，又∵∠ACG=∠FBN ，AC=FB,∴△ACG ≌△FBN ，∴BN=CG ，又∵CG=CM++MG ，∴BN=CM+MG ，又∵MG=MN ，∴BN=CM+MN ．【点睛】本题考查全等三角形的判定与性质、等腰三角形的性质、中位线等知识，解题的关键是综合运用相关知识解题．24．（1）；（2）；（3）或或【解析】【分析】(1)直接利用待定系数法，即可得出结论；(2)先求出AD ＝3，AB ＝5，进而求出点D 的坐标，再构造出△BMF ≌△FND ，得出BM ＝FN ，FM ＝DN ，解析：（1）334y x =+；（2）197(,)55F -；（3）5(,3)2E -或3312(,)105-或73(,)105- 【解析】【分析】(1)直接利用待定系数法，即可得出结论；(2)先求出AD ＝3，AB ＝5，进而求出点D 的坐标，再构造出△BMF ≌△FND ，得出BM ＝FN ，FM ＝DN ，设F （m ，n ），进而建立方程组求解，即可得出结论；(3)分两种情况，①当ABC ABE '≌时，利用中点坐标公式求解，即可得出结论；②当ABC BAE ≌时，当点E 在AB 上方时，根据AE ∥BC ，AE BC =即可得出结论；③当点E 在AB 下方时，过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴，过点E '作E P BP '⊥，证明QAE PBE '''△≌△，即可得出结论．【详解】(1)设直线AB 的函数表达式为y kx b =+，直线AB 交y 轴于点A (0，3)，交x 轴于点B (﹣4，0)，403k b b -+=⎧∴⎨=⎩ 343k b ⎧=⎪∴⎨⎪=⎩ ∴直线AB 的函数表达式为334y x =+； (2)如图，过点D 分别引,x y 轴的垂线，交,x y 轴于,G H 两点，∵点A （0，3），点B （-4，0），∴OA =3，OB =4，∴AB 2234+=5，由折叠知，AD =OA =3，532DB ∴=-=设(,)D a b -(0,0)a b >>,DG b DH a ∴==,4,3BG a AH b =-=-222222,AD DH AH DB BGDG =+=+∴()()2222223342a b a b ⎧+-=⎪⎨-+=⎪⎩解得：436a b -=D 在334y x =+上，334b a ∴=-+ 4363412a b a b -=⎧∴⎨+=⎩解得12565a b ⎧=⎪⎪⎨⎪=⎪⎩， 126(,)55D ∴-，过点F 作FM ⊥x 轴于M ，延长HD 交FM 于N ，∴∠BMF =∠FND =90°，∴∠BFM +∠FBM =90°，∵△BFD 是等腰直角三角形，∴BF =DF ，∠BFD =90°，∴∠BFM +∠DFN =90°，∴∠FBM =∠DFN ，∴△BMF ≌△FND （AAS ），∴BM =FN ，FM =DN ，设F （m ，n ），则125645n m n m ⎧=--⎪⎪⎨⎪-=+⎪⎩ 19575m n ⎧=-⎪⎪∴⎨⎪=⎪⎩ 197(,)55F ∴-；（3）设OC =a ，则BC =4-a ，由折叠知，∠BDC =∠ADC =∠AOC =90°，CD =OC =a ，在Rt △BDC 中，222BC CD BD =+，∴()2244a a -=+， ∴a =32， 335(,0),,222C OC BC ∴-==， ∵点A ，B ，E 为顶点的三角形与△ABC 全等，①当△ABC ≌△ABE '时，∴BE '=BC ，∠ABC =∠ABE '，连接CE '交AB 于D ，则CD =E 'D ，CD ⊥AB ，由(1)知， 126(,)55D -设E '（b ，c ）， ∴131216(),(0)22525b c -=-+= ∴3312,105b c =-=， ∴3312(,)105E '-； ②当△ABC ≌BAE 时，当点E 在AB 上方时，∴AC =BE ，BC =AE ，EAB CBA =∠∠，∴AE ∥BC ， ∴5(,3)2E -； ③当点E 在AB 下方时，AC =BE ''，BC =AE ''，ABC ABE '△≌△，∴BC BE '=，当ABC BAE ''△≌△时，ABE BAE '''∴△≌△，AE BE '''∴=,BAE ABE '''∠=∠，过点E ''作E Q y ''⊥轴于Q ,过点B 作BP x ⊥轴，过点E '作E P BP '⊥，//PB AQ ∴,90P AQE ''∠=∠=︒，PBA QAB ∴∠=∠，PBA ABE QAB BAE '''∴∠-∠=∠-，即PBE QAE '''∠=∠，90P AQE ''∠=∠=︒，QAE PBE '''∴△≌△，,PE QE AQ PE ''''∴==，点3312(,)105E '-,(4,0)B -， ∴AQ PB ==125，PE QE '''==33741010-+=， 123355OQ ∴=-=， ∴73(,)105E ''-， ∴满足条件的点E 的坐标为5(,3)2E -或3312(,)105-或73(,)105-．【点睛】本题考查了待定系数法，折叠的性质，等腰直角三角形的性质，全等三角形的判定和性质，平移的性质，勾股定理，中点坐标公式，构造出全等三角形，分类讨论是解题的关键．25．（1）15，8；（2），见解析；（3）；（4）4【分析】解决问题（1）只需运用面积法：，即可解决问题；（2）解法同（1）；（3）连接、、，作于，由等边三角形的性质得出，由勾股定理得出，得出的解析：（1）15，8；（2）PE PF CG +=，见解析；（3）534）4【分析】解决问题（1）只需运用面积法：ABC ABP ACP S S S ∆∆∆=+，即可解决问题；（2）解法同（1）；（3）连接PA 、PB 、PC ，作AM BC ⊥于M ，由等边三角形的性质得出152BM BC ==，由勾股定理得出2253AM AB BM =-=，得出ABC ∆的面积12532BC AM =⨯=，由ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积1111()2532222BC PE AC PF AB PG AB PE PF PG =⨯+⨯+⨯=++=，即可得出答案；（4）过点E 作EQ BC ⊥，垂足为Q ，易证BE BF =，过点E 作EQ BF ⊥，垂足为Q ，由解决问题（1）可得PG PH EQ +=，易证EQ DC =，BF DF =，只需求出BF 即可．【详解】解：（1）∵PE AB ⊥，10AB =，3PE =，∴ABP ∆的面积111031522AB PE =⨯=⨯⨯=， ∵PE AB ⊥，PF AC ⊥，CG AB ⊥，且ABC ABP ACP S S S ∆∆∆=+，∴AB CG AB PE AC PF ⋅=⋅+⋅，∵AB AC =，∴358CG PE PF =+=+=.故答案为：15，8.（2）∵PE AB ⊥，PF AC ⊥，CG AB ⊥，且ABC ABP ACP S S S ∆∆∆=+，∴AB CG AB PE AC PF ⋅=⋅+⋅，∵AB AC =，∴CG PE PF =+.（3）连接PA 、PB 、PC ，作AM BC ⊥于M ，如图2所示：∵10AB AC BC ===，∴ABC ∆是等边三角形，∵AM BC ⊥，∴152BM BC ==， ∴222210553AM AB BM =--=∴ABC ∆的面积11105325322BC AM =⨯=⨯⨯=， ∵PE BC ⊥，PF AC ⊥，PG AB ⊥，∴ABC ∆的面积BCP =∆的面积ACP +∆的面积APB +∆的面积111222BC PE AC PF AB PG =⨯+⨯+⨯1()2AB PE PF PG =++ 253=，∴22535310PE PF PG ⨯++==. （4）过点E 作EQ BC ⊥，垂足为Q ，如图3所示：∵四边形ABCD 是矩形，∴AD BC =，90C ADC ∠=∠=︒，∵8AD =，3CF =，∴5BF BC CF AD CF =-=-=，由折叠可得：5DF BF ==，BEF DEF ∠=∠，∵90C ∠=︒，∴2222534DC DF FC =--，∵EQ BC ⊥，90C ADC ∠=∠=︒，∴90EQC C ADC ∠=︒=∠=∠，∴四边形EQCD 是矩形，∴4EQ DC ==，∵//AD BC ，∴DEF EFB ∠=∠，∵BEF DEF ∠=∠，∴BEF EFB ∠=∠，∴BE BF =，由解决问题（1）可得：PG PH EQ +=，∴4PG PH +=，即PG PH +的值为4.【点睛】本题是四边形综合题目，考查了矩形的性质与判定、等腰三角形的性质与判定、平行线的性质与判定、等边三角形的性质、勾股定理等知识，考查了用面积法证明几何问题，考查了运用已有的经验解决问题的能力，体现了自主探究与合作交流的新理念，是充分体现新课程理念难得的好题．26．（1）点E ；（2）点H ；（3）①存在，点P 的坐标为（7，7）；②【分析】（1）根据“等距点”的定义，即可求解；（2）根据“等距点”的定义，即可求解；（3）①根据点P 是线段OA 和OB 的“等距点解析：（1）点E ；（2）点H ；（3）①存在，点P 的坐标为（7，7）；②60m -<<【分析】（1）根据“等距点”的定义，即可求解；（2）根据“等距点”的定义，即可求解；（3）①根据点P 是线段OA 和OB 的“等距点”，可设点P （x ，x ）且x ＞0，再由点P 是点A 和点C 的“等距点”，可得22AP CP = ，从而得到()()222286x x x x -+=-+ ，即可求解； ②根据点P 是线段OA 和OB 的“等距点”，点P 在∠AOB 的角平分线上，可设点P （a ，a ）且a ＞0，根据OA =OB ，可得OP 平分线段AB ，再由点P 在OAB 内，可得0<<3a ，根据点P 是点A 和点C 的“等距点”，可得22AP CP = ，从而得到()()22226a m a a a -+=-+，整理得到()()()2666m a m m -=+-，即可求解．【详解】解：（1）根据题意得：()6612AD =--= ，633AE =-= ，AF == ，6OD = ，3OE = ，3OF = ，∴AE OE = ，∴点()3,0E 是点A 和点O 的“等距点”；（2）根据题意得：线段OA 在x 轴上，线段OB 在y 轴上，∴点()2,1G --到线段OA 的距离为1，到线段OB 的距离为2，点()2,2H 到线段OA 的距离为2，到线段OB 的距离为2，点()3,6I 到线段OA 的距离为6，到线段OB 的距离为3，∴点()2,2H 到线段OA 的距离和到线段OB 的距离相等，∴点()2,2H 是线段OA 和OB 的“等距点”；（3）①存在，点P 的坐标为（7，7），理由如下：∵点P 是线段OA 和OB 的“等距点”，且线段OA 在x 轴上，线段OB 在y 轴上， ∴可设点P （x ，x ）且x ＞0，∵点P 是点A 和点C 的“等距点”，∴22AP CP = ，∵点C （8，0），()6,0A ，∴()()222286x x x x -+=-+ ，解得：7x = ，∴点P 的坐标为（7，7）；②如图，∵点P 是线段OA 和OB 的“等距点”，且线段OA 在x 轴上，线段OB 在y 轴上， ∴点P 在∠AOB 的角平分线上，可设点P （a ，a ）且a ＞0，∵()6,0A ，()0,6B ．∴OA =OB =6，∴OP 平分线段AB ，∵点P 在OAB 内，∴当点P 位于AB 上时，此时点P 为AB 的中点，∴此时点P 的坐标为6060,22++⎛⎫ ⎪⎝⎭，即()3,3 ， ∴0<<3a ，∵点P 是点A 和点C 的“等距点”，∴22AP CP = ，∵点(),0C m ，()6,0A ，∴()()22226a m a a a -+=-+，整理得：()()()2666m a m m -=+- ，当6m = 时，点C （6，0），此时点C 、A 重合，则a =6（不合题意，舍去），当6m ≠时，62m a +=， ∴6032m +<<，解得：60m -<< ，即若点P 在OAB 内，满足条件的m 的取值范围为60m -<<．【点睛】本题主要考查了平面直角坐标系内两点间的距离，点到坐标轴的距离，等腰三角形的性质，角平分线的判定等知识，理解新定义，利用数形结合思想解答是解题的关键．。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

八年级期末试卷练习（Word版含答案）一、初二物理机械运动实验易错压轴题（难）1．爱科学的佳佳在“测量平均速度”时，想研究测量从斜面上滑下的物体在不同阶段时的平均速度，设计了如图所示的实验装置；让小车从带有刻度（分度值为1cm）的斜面顶端由静止滑下，图中的圆圈是小车到达A、B、C三个位置时电子表的显示时间（圆圈里面的数字分别表示“小时：分：秒”），则：（1）根据图中所给信息可以判断，小车从斜面顶端运动到底端的过程中______ （选填“是”或“不是”）做匀速直线运动（2）图中AC段的路程是______ cm；在实验前必须熟练使用秒表，在测量小车到达C点的时间时，如果小车到达C点还没有停止计时，则测得AC段的平均速度________（选填“偏大”“偏小”或“不变”）。

【来源】陕西省西安市西北工业大学附属中学2017-2018学年八年级（上）期末物理试题【答案】不是 9.00 偏小【解析】【详解】(1)[1]前段路程为4cm用时2s，后段路程为5cm用时1s，所以小车从斜面顶端运动到底端的过程中不是做匀速直线运动；(2)[2]图中AC段的路程为10.00cm-1.00cm=9.00cm；[3] 如果小车到达C点还没有停止计时，则测得的时间偏大，由svt可知，当测得的时间t偏大时会导致平均速度v偏小的。

2．如图所示，在测量小车运动的平均速度实验中，让小车从斜面的A点由静止开始下滑并开始计时，分别测出小车到达B点和C点的时间，即可算出小车在各段的平均速度。

（1）根据实验的原理___________，需要测量的物理量是小车运动的路程和所用的时间。

对小车运动的各段长度进行测量并分段做了标记，因_________的测量误差较大，需多次测量。

（2）图中AB 段的距离AB =s ________cm ，测得时间AB =1.6s t ，则AB 段的平均速度AB =v ________cm/s 。

（3）如果小车过了B 点才停止计时，则测得的平均速度AB v 会偏________。

（4）实验中应多次测量，每次测量时必须让小车从__________由静止开始下滑。

（5）发AB v ________AC v 。

填（“>”、“<”或“=”）（6）物体的运动常常可以用图像来描述，图中能反映图甲小车运动情况的是______。

（选填“A ”或“B ”）【来源】安徽省芜湖市繁昌县第三中学2019--2020学年八年级（上）期中考试物理试题【答案】s v t=时间 40.0 25.0 小同一位置 > B 【解析】【详解】(1)[1]测小车平均速度实验原理是 s v t=。

[2]小车下滑运动时，时间测量误差较大，所以需多次测量。

(2)[3]读图得AB 80.0cm 40.0cm 40.0cm s =-=。

[4]由平均速度公式得：AB AB 40.0cm 25.0cm/s 1.6ss v t ===。

(3)[5]小车过了B 点才停止计时，时间测量值偏大，所以平均速度会偏小。

(4)[6]多次测量为了保证运动距离相同，所以每次测量时必须让小车同一位置由静止开始下滑。

(5)[7]在斜面上下滑的小车做加速运动，所以BC AB t t <，即BC AB BC 2t t t <+。

又因为AC AB BC 2s v t t =+ AB ABAB 22s s v t t == 所以AB AC v v <。

(6)[8]小车在斜面上做加速运动，所以能反映小车运动情况的是B 图像。

3．某同学在探究速度的变化实验中，要测自己骑自行车下坡时（不蹬脚踏板及不抓刹车手把），自行车速度的变化情况：(1) 测量原理是____________；(2) 根据实验要求你认为应该选择的器材有___________和__________；(3) 该同学找了一段90m 长的下坡路，并测得一些数据，请你帮他将表格中的数据补充完整；t 2＝__________s ，v ＝____________m/s 。

（4）分析表格中的数据，你得到的结论是___________。

【来源】云南省昆明实验中学2019-2020学年八年级（上）期中考试物理试题【答案】v =s t ；刻度尺；秒表； 6； 6；自行车下坡时速度越来越大。

【解析】【详解】(1)[1] 测量原理是v =s t； (2)[2][3]根据测量原理可知要测量长度和时间，故应该选择的器材有刻度尺和秒表；(3)[4]后半程速度为22245m 6s 7.5m/s s t v[5]全程平均速度为90m6m/s15m/ssvt(4)[6]比较1v、2v可知自行车下坡时速度越来越大。

4．如图所示，让小车从斜面的A点由静止开始下滑，分别测出小车到达B点和C点的时间，即可测出不同阶段的平均速度；（1）该实验原理是______；（2）为了方便计时，应使斜面的坡度较______（选填“大”或“小”）；（3）小车通过AB段时测得时间AB 1.6st=，则AB段的平均速度ABv=______cm/s；（4）在测量小车到达B点的时间时，如果小车过了B点才停止计时，测得AB段的平均速度ABv会偏______（选填“大”或“小”）。

【来源】山东省东营市垦利区2019-2020学年八年级（上）期末考试物理试题【答案】svt=小 25.0 偏小【解析】【详解】(1)[1]测平均速度的原理为svt=；(2)[2]为了方便计时，应使小车运动的速度慢一些，所以应使斜面的坡度较小；(3)[3]小车通过AB段时测得时间AB 1.6st=，则AB段的平均速度：ABABAB40cm25.0cm/s1.6ssvt===；(4)[4]如果让小车过了B点才停止计时，会导致时间的测量结果偏大，由公式svt=知，平均速度会偏小。

5．小明在测小车的平均速度的实验中，设计了如图所示的实验装置：小车从带刻度的斜面顶端由静止下滑，图中的圆圈是小车到达A、B、C三处时电子表的显示（数字分别表示“小时:分:秒”）（1）该实验测小车平均速度的实验原理是_______________；（2）实验中使用的斜面的坡度较________（选填“大”或“小”），其目的是________（选填“缩短”或“增长”）测量时间，以减小测量时间的误差；（3）实验前必须学会熟练使用电子表，一定要注意在释放小车的同时开始计时，到碰到挡板的同时停止计时，如果让小车过了A 点才开始计时，会使所测AC 段的平均速度AC v 偏_____（填“大”或“小”）；（4）小车通过全过程平均速度1v =_______m/s ；若2s 的路程正好是全部路程的一半，则小车通过上半段路程的平均速度2=v ________m/s ；（5）下列图中，能够反映小车运动过程的图象的是_________．① ② ③ ④【来源】陕西省榆林市一中分校2019-2020学年八年级11月月考物理试题【答案】v=s t 小增长大 0.24 0.2 ③ 【解析】【分析】【详解】(1)测小车平均速度的实验原理是：v =s t； (2)斜面坡度越大，小车沿斜面向下加速运动越快，运动时间会越短，计时会越困难，所以为使计时方便，斜面坡度应较小；(3)如果让小车过了A 点后才开始计时,计时晚一些,所计时间偏小,由公式v =s t知所计算出的速度偏大；(4)由图知,小车从顶端到底端时间t AC =5s,总路程：s AC =120cm=1.2m ，故全程平均速度：v 1=AC AC s t =1.2m 5s=0.24m/s ；上半段的路程s AB =0.6m,小车运动时间t AB =3s ，小车通过上半段路程的平均速度：v 2=AB AB s t =0.6m 3s=0.2m/s ； (5) 由图知,BC 段时间t BC =2s,s BC =0.6m ，所以：v BC =BC BC s t =0.6m 2s=0.3m/s ， v BC >v 2，所以小车在下滑过程中速度越来越快，图像中①表示小车静止不动，②表示小车做匀速直线运动，③表示小车的速度逐渐增大，④表示小车做匀速直线运动，故③正确．二、初二物理光现象实验易错压轴题（难）6．小明用图甲的装置探究“平面镜成像的特点”，操作如下：①在竖立的玻璃板前点燃蜡烛A ，可以看到蜡烛A 在玻璃板中的像，取一支外形相同但不点燃的蜡烛B 在玻璃板后面来回移动，直到看上去它跟蜡烛A 的像完全重合；②移去蜡烛B ，在其原来位置上放置一块光屏，观察光屏上是否有蜡烛的像；③将玻璃板倾斜，再次观察“蜡烛A 的像”，如图乙所示。

请你解答下列问题：(1)实验不用平面镜而用玻璃板的目的是便于______；(2)操作①中通过玻璃板能够看到蜡烛A 的像是由于发生了光的______；蜡烛B 与蜡烛A 的像完全重合，说明像与物的大小______；(3)操作②的探究目的是______；(4)操作③中蜡烛A 此时的像是图乙中的______（选填“A 1”、“A 2”或“A 3”)。

【答案】确定像的位置反射相等探究像的虚实 A 2【解析】【分析】【详解】(1)[1]镜子和玻璃板都是平面镜，而且镜子的反射效果好，成像清晰，但镜子不透光，不能看到背面的物体；玻璃板成像比较暗，但透光，可以看到镜子后的物体。

本实验的关键是确定像的位置，为解决这一关键点，选择玻璃板而不选镜子。

(2)[2]操作①中通过玻璃板能够看到蜡烛的像是由于发生了光的反射。

[3]蜡烛B 与蜡烛A 的像完全重合，说明像与物的大小相等。

(3)[4]操作②的探究目的是探究像的虚实，虚像不会出现在光屏上。

(4)[5]如果玻璃板没有放正，蜡烛的像与蜡烛不在同一水平面上，像与物关于平面镜对称，操作③中蜡烛A 此时的像是图乙中的2A 。

7．如图所示，小明同学为了探究平面镜成像特点，准备如下器材：各种粗细相同长度不同的烛若干5mm 厚和2mm 厚的两块玻璃板、白纸、火柴等。

请回答下列问题：(1)用玻璃板代替平面镜的好处是______，应选择______mm 厚的玻璃板做实验。

(2)如图甲所示，小明把蜡烛A 点燃放在玻璃板前面，再把其他各支蜡烛依次放在玻璃板后面适当位置，当蜡烛B 故在后面时，从玻璃板前面看蜡烛B 好像也被点燃了一样。

此时，后面的蜡烛B 与蜡烛A 的大小关系是：______。

(3)实验中若移开蜡烛B ，用白纸做光屏放在像的位置，不透过玻璃板，直接观察白纸，看不到蜡烛A 的像，说明平面镜成的是______（选填“虚”或“实”）像。

(4)实验中玻璃板应竖直放置在水平桌面上，若向左倾斜玻璃板，如图乙所示，蜡烛A 的像将______移动（选填“向上”“向下”或“不”）。

(5)如图丙所示，两个平面镜L 1和L 2平行竖直放置，两镜相距s ，物体A 在两镜之间，A 在L 1中的一个像是A 1，A 2在L 2中的一个像是A 2，已知A 1、A 2相距1s ，当物体A 在两镜之同移动时，A 在两镜里成的像A 1、A 2的距离1s 的变化情况是______（选填“变大”“不变”或“变小”）。

八年级期末试卷练习(Word版 含答案)

八年级下册数学期末试卷达标训练题(Word版含答案)

人教版八年级下册英语期末试卷(Word版,含答案)

八年级上册期末试卷综合测试(Word版 含答案)

八年级下册数学期末试卷模拟练习卷(Word版含解析)

八年级期末试卷复习练习(Word版含答案)

八年级数学下册期末试卷试卷(word版含答案)

人教版八年级下册地理期末复习综合测试卷1(Word版,含答案)

期末达标测试卷(B卷) 2022-2023学年统编版语文八年级下册(word版含答案)

八年级数学上册期末试卷综合测试(Word版 含答案)

八年级下册数学期末试卷复习练习(Word版含答案)

人教版数学八年级下册数学期末试卷试卷(word版含答案)

八年级下册数学期末试卷练习(Word版含答案)

北京市东城区2023-2024学年八年级上学期期末考试语文试卷(word版,含答案)

八年级下册数学期末试卷复习练习(Word版含答案)

北京市密云区2022~2023学年第一学期初二数学期末试卷(word版含答案)

人教版八年级下册数学期末试卷复习练习(Word版含答案)

八年级下册数学期末试卷综合测试卷(word含答案)(1)

人教版八年级期末试卷测试卷(word版,含解析)

八年级期末试卷练习(Word版含答案)

八年级上册期末试卷综合测试(Word版含答案)

八年级数学上册期末试卷综合测试(Word版含答案)