相关系数的计算
相关系数r计算

相关系数r计算
相关系数r是用于衡量两个变量之间线性相关程度的指标。
计算相关系数r需要使用两个变量的一组数据,以下是计算r的公式:
r = nΣXY - ΣXΣY / [(nΣX^2 - (ΣX)^2)(nΣY^2 - (ΣY)^2)]^(1/2)
其中,n为数据组数,Σ为求和符号,X和Y分别表示两个变量的数据。
计算r的步骤如下:
1. 计算X和Y的平均数,分别表示为X和Y。
2. 计算每组数据的(X - X)和(Y - Y)的乘积,分别表示为XY。
3. 分别求出ΣX、ΣY、ΣXY、ΣX^2和ΣY^2。
4. 带入公式计算r的值,得到一个介于-1和1之间的数值,越接近1或-1表示两个变量线性相关程度越高,越接近0表示两个变量线性相关程度越低。
需要注意的是,相关系数r只能反映两个变量之间的线性关系,不能反映其他类型的关系。
同时,如果两个变量之间没有线性关系,计算出来的r也会接近0,但不能说明两个变量没有其他类型的关系。
- 1 -。
数据分析中的相关系数计算方法

数据分析中的相关系数计算方法数据分析是一种重要的工具,可以帮助我们理解数据之间的关系。
而相关系数是衡量两个变量之间相关性强弱的指标之一。
在数据分析中,计算相关系数是一个常见的任务。
本文将介绍一些常用的相关系数计算方法。
一、皮尔逊相关系数(Pearson correlation coefficient)皮尔逊相关系数是最常见的相关系数计算方法之一。
它衡量的是两个变量之间的线性相关性。
皮尔逊相关系数的取值范围是-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关。
计算皮尔逊相关系数的公式如下:r = cov(X, Y) / (σX * σY)其中,cov(X, Y)表示X和Y的协方差,σX和σY分别表示X和Y的标准差。
二、斯皮尔曼相关系数(Spearman correlation coefficient)斯皮尔曼相关系数是一种非参数的相关系数计算方法,它衡量的是两个变量之间的单调关系,不仅仅局限于线性关系。
斯皮尔曼相关系数的取值范围也是-1到1,具有和皮尔逊相关系数相似的解释。
计算斯皮尔曼相关系数的公式如下:ρ = 1 - (6 * Σd^2) / (n * (n^2 - 1))其中,d表示X和Y的等级差,n表示样本数量。
三、切比雪夫相关系数(Chebyshev correlation coefficient)切比雪夫相关系数是一种衡量两个变量之间的最大差异的相关系数计算方法。
它不仅考虑了线性关系,还考虑了非线性关系。
切比雪夫相关系数的取值范围是0到1,其中0表示无相关,1表示完全相关。
计算切比雪夫相关系数的公式如下:r = max(|Xi - Yi|) / max(|Xi - Xj|)其中,Xi和Yi表示X和Y的观测值,Xj表示X的观测值。
四、肯德尔相关系数(Kendall correlation coefficient)肯德尔相关系数是一种衡量两个变量之间的等级关系的相关系数计算方法。
三种常用的不同变量之间相关系数的计算方法
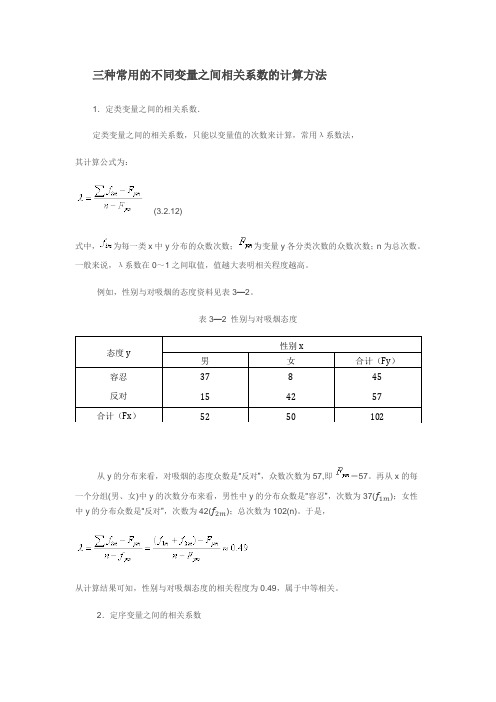
三种常用的不同变量之间相关系数的计算方法1.定类变量之间的相关系数.定类变量之间的相关系数,只能以变量值的次数来计算,常用λ系数法,其计算公式为:(3.2.12)式中,为每一类x中y分布的众数次数;为变量y各分类次数的众数次数;n为总次数。
一般来说,λ系数在0~1之间取值,值越大表明相关程度越高。
例如,性别与对吸烟的态度资料见表3—2。
表3—2 性别与对吸烟态度态度y性别x男女合计(Fy)容忍反对37158424557合计(Fx)52 50 102从y的分布来看,对吸烟的态度众数是“反对”,众数次数为57,即=57。
再从x的每一个分组(男、女)中y的次数分布来看,男性中y的分布众数是“容忍”,次数为37(f1m);女性中y的分布众数是“反对”,次数为42(f2m);总次数为102(n)。
于是,从计算结果可知,性别与对吸烟态度的相关程度为0.49,属于中等相关。
2.定序变量之间的相关系数定序变量之间的相关测量常用Gamma系数法和Spearman系数法。
Gamma系数法计算公式为:(3.2.13)式中,G为系数;Ns为同序对数目;Nd为异序对数目。
所谓序对是指表明高低位次的两两配对,如果一对个案在变量x,y的分类表现位次一致,则为同序对;如果位次相反,则为异序对。
G系数取值在—1--十1之间。
G=1,表示完全正相关;G=-1,表示完全负相关;G=0,表示完全不相关;-1<G<0,表示负相关;0<G<1,表示正相关。
Spearman系数法计算公式为:(3.2.14)式中,P为系数;D为所测定的两个数列中每对项目之间的登记差,这个差的正值之和等于负值之和;N为项数。
系数p主要代表两个定序变量的等级相关程度,其取值范围和相关程度含义与G系数相同。
3.定距变量之间的相关系数定距变量之间的相关测量常用Pearson系数法。
对于未分组资料,Pearson系数法计算公式为:对于已分组资料,Pearson系数法计算公式为r系数取值范围和相关程度的含义与G系数相同。
相关系数计算公式解释

相关系数计算公式解释在统计学中,相关系数(Correlation Coefficient)是一种定量测量变量之间关系的重要工具。
它揭示了两个变量之间的相互影响程度,即当一个变量增加或减少时,另一个变量相应增加或减少的程度。
相关系数可以用来预测变量之间的关系,以及变量的变化趋势。
相关系数可以用来衡量两个变量之间的关系。
它可以测量变量之间的关系强度、方向以及程度。
它的取值范围是从-1到1,当取值在-1到0之间时,表示变量之间的相关性是负的,当取值在0到1之间时,表示变量之间的相关性是正的。
计算相关系数有几种方法,其中最常用的方法是Pearson积矩相关系数。
它是从数据的观测值中计算的,根据以下公式进行计算:Pearson积矩相关系数公式:r=∑(x-x-)(y-y-)/√[∑(x-x-)2∑(y-y-)2]其中,x和y分别表示两个变量;x-y-分别表示两个变量的均值;∑表示所有观测值的和;√表示根号。
在计算Pearson积矩相关系数时,首先要对所有变量计算出均值,然后计算每个变量与其均值差异的平方和,最后将它们相除,得出Pearson积矩相关系数。
由于Pearson积矩相关系数只能用于分析线性的变量关系,因此在处理非线性关系时,要使用Spearman或Kendall等非线性相关系数。
Spearman等级相关系数(Spearman Rank CorrelationCoefficient)与Pearson积矩相关系数类似,但是只针对等级变量。
它用来评估两个等级变量之间的关系,而不考虑其具体数值。
它的计算公式为:Spearman等级相关系数公式:r=∑d2/n(n2-1)/6其中,d表示两个变量间的排序差(Rank Differnece);n表示样本总数。
Kendallτ检验主要用于判断两组有序数据之间的相关性。
它的计算公式为:Kendallτ检验公式:τ=2C/n(n-1)其中,C表示两组数据之间的共赢(Concordant)对数;n表示样本总数。
相关系数和β的计算公式

相关系数和β的计算公式
相关系数r的计算公式是ρXY=Cov(X,Y)/√[D(X)]√[D(Y)]。
公式描述:公式中Cov(X,Y)为X,Y的协方差,D(X)、D(Y)分别为X、Y的方差。
公式。
若Y=a+bX,则有:
令E(X) =μ,D(X) =σ。
则E(Y) = bμ+a,D(Y) = bσ。
E(XY) = E(aX + bX) = aμ+b(σ+μ)。
Cov(X,Y) = E(XY)−E(X)E(Y) = bσ。
缺点
需要指出的是,相关系数有一个明显的缺点,即它接近于1的程度与数据组数n 相关,这容易给人一种假象。
因为,当n较小时,相关系数的波动较大,对有些样本相关系数的绝对值易接近于1。
当n较大时,相关系数的绝对值容易偏小。
特别是当n=2时,相关系数的绝对值总为1。
因此在样本容量n较小时,我们仅凭相关系数较大就判定变量x与y 之间有密切的线性关系是不妥当的。
相关系数和协方差的计算公式

相关系数和协方差的计算公式相关系数和协方差是统计学中常用的两个概念,用于衡量变量之间的关系以及变量的变动程度。
相关系数衡量了两个变量之间的线性关系的强度和方向,而协方差则衡量了两个变量的总体变动趋势。
下面我将简单介绍一下这两个概念的计算公式和意义。
相关系数是用来衡量两个变量之间的相关程度的。
它的取值范围在-1到1之间,绝对值越接近1表示两个变量之间的相关性越强,绝对值越接近0则表示两个变量之间的相关性越弱。
具体计算公式如下:相关系数 = 协方差 / (标准差1 * 标准差2)其中,协方差表示两个变量之间的总体变动趋势,可以用以下公式计算:协方差= Σ((X - X平均)*(Y - Y平均)) / N其中,X和Y分别表示两个变量的取值,X平均和Y平均表示两个变量的平均值,N表示样本容量。
协方差的取值可以为正、负或零。
正值表示两个变量之间的变动趋势一致,负值表示两个变量之间的变动趋势相反,零值表示两个变量之间没有线性关系。
协方差的大小无法直观地表示两个变量之间的关系强度,因此需要用相关系数来进行标准化。
相关系数的取值范围在-1到1之间,可以直观地表示两个变量之间的相关程度。
相关系数和协方差在统计学中有着广泛的应用。
它们可以帮助我们了解两个变量之间的关系,找出变量之间的相互影响,从而更好地进行数据分析和预测。
在实际应用中,我们可以通过计算相关系数和协方差来评估股票之间的相关性、商品价格之间的关联程度等。
同时,相关系数和协方差也是回归分析、因子分析等统计方法的基础。
相关系数和协方差是统计学中重要的概念,用于衡量变量之间的关系和变动趋势。
它们的计算公式简单明了,应用广泛,对于数据分析和预测具有重要的意义。
了解和掌握相关系数和协方差的计算方法,有助于我们更好地理解和分析数据,做出准确的决策。
相关系数公式及变形

相关系数公式及变形
相关系数是统计学中一个非常重要的概念,它可以用来衡量两个变量之间的线
性关系。
相关系数公式定义如下:
相关系数:ρxy = cov(x,y)/σxσy
式中,cov表示x,y变量的协方差,σx和σy分别表示x和y的标准差。
可
以看出,相关系数的值范围在-1和1之间,其中,当相关系数为1时表示两个变
量之间存在显著的正相关,相关系数为-1时表示两个变量之间存在显著的负相关,相关系数为0时表示两个变量之间不存在显著的线性关系。
相关系数(ρxy)的值的大小会受到因素的影响,因此计算出的相关系数的值
会有所变化。
为了能更好地计算出相关系数的值,引入了另一个公式,称为变形的相关系数公式:
ρxyx'y=cov(x,y)/(σx√σy')
式中,x'表示标准化的x,y'表示标准化的y,σx'表示标准化后x的标准差,σy'表示标准化后y的标准差。
因此,可以看出,计算相关系数时,采用变形后的相关系数公式可以更加准确
和可靠地计算出相关系数的值,从而更好地评估两个变量之间的线性关系。
总之,相关系数是统计学中一项重要的概念,通过使用变形后的相关系数公式,可以更准确可靠地估算两个变量之间的相关性。
概率论相关系数公式

概率论相关系数公式
概率中相关系数的计算公式:r=Cm(t0-t)。
相关系数是最早由统计学家卡尔·皮尔逊设计的统计指标,是研究变量之间线性相关程度的量,一般用字母r表示。
由于研究对象的不同,相关系数有多种定义方式,较为常用的是皮尔逊相关系数。
概率,亦称“或然率”,它是反映随机事件出现的可能性(likelihood)大小。
随机事件是指在相同条件下,可能出现也可能不出现的事件。
例如,从一批有正品和次品的商品中,随意抽取一件,“抽得的是正品”就是一个随机事件。
设对某一随机现象进行了n次试验与观察,其中A事件出现了m次,即其出现的频率为m/n。
经过大量反复试验,常有m/n越来越接近于某个确定的常数(此论断证明详见伯努利大数定律)。
该常数即为事件A出现的概率,常用P(A)表示。
相关系数计算方法

相关系数计算方法
相关系数是一种用于衡量两个变量之间线性关系强度的统计量,其取值范围在-1到1之间。
当相关系数为正时,两个变量呈正相关,即随着一个变量的增加,另一个变量也会增加;当相关系数为负时,两个变量呈负相关,即随着一个变量的增加,另一个变量会减少;当相关系数为0时,两个变量之间没有线性关系。
相关系数的计算方法有多种,以下介绍几种常见的方法。
1.皮尔逊相关系数法:皮尔逊相关系数是最常用的相关系数计算方法之一,它反映的是两个变量之间的线性关系程度。
计算公式为:r = cov(X,Y) / (σX * σY),其中,cov(X,Y)表示X和Y的协方差,σX和σY表示X和Y的标准差。
2.斯皮尔曼等级相关系数法:斯皮尔曼等级相关系数是一种非参数统计方法,它适用于数据不满足正态分布的情况。
计算公式为:ρ= 1 - [6Σd^2 / (n*(n^2-1))],其中,d表示两个变量在等级上的差异,n表示样本个数。
3.切比雪夫相关系数法:切比雪夫相关系数是一种测量两个变量之间相关性的方法,它不受数据分布的影响。
计算公式为:r = Σ(Xi - Xmean) * (Yi - Ymean) / (n * sX * sY),其中,Xi和Yi分别表示第i个样本的数值,Xmean和Ymean分别表示X和Y的平均值,sX和sY分别表示X和Y的标准差。
以上三种方法是常见的相关系数计算方法,每种方法都有其适用范围和限制条件,需要根据具体情况选择合适的方法进行计算。
在实
际应用中,相关系数常用于分析两个变量之间的关系,例如研究气温与降雨量之间的关系、销售额与广告投入之间的关系等。
相关系数r的计算公式 方差

相关系数r的计算公式方差相关系数r是用来衡量两个变量之间的线性相关程度的统计量,其取值范围在-1和1之间。
相关系数趋近于1表示两个变量之间存在强正相关关系,趋近于-1表示存在强负相关关系,而趋近于0则表示两个变量之间关系较弱或无相关关系。
相关系数r的计算公式如下:r = cov(X, Y) / (σX * σY)其中,cov表示X和Y的协方差,σX表示X的标准差,σY表示Y的标准差。
具体计算步骤如下:1. 计算X和Y的平均值,分别表示为X与Y的平均值,记作μX和μY。
2. 计算X与Y的离差平方和,记作∑(X-μX)^2和∑(Y-μY)^2。
3. 计算X与Y的离差乘积和,记作∑(X-μX)(Y-μY)。
4. 计算X和Y的标准差,表示为σX和σY。
5. 计算相关系数r,其中cov(X, Y)表示X和Y的协方差。
方差是统计学中常用的一种衡量数据分散程度的指标。
它表示各个数据与其平均值之间的差异程度,越大则数据分散程度越大,反之越小。
方差的计算公式如下:Var(X) = ∑(X-μ)² / N其中,Var(X)表示X的方差,∑(X-μ)²表示X与其平均值的离差平方和,N表示样本大小。
方差的计算步骤如下:1. 计算X的平均值,表示为μ。
2. 计算X与其平均值的离差平方和,表示为∑(X-μ)²。
3. 计算X的方差,表示为Var(X)。
方差可以帮助我们判断数据的分散程度,进而对不同数据集之间的差异进行比较和分析。
在统计分析和建模中,方差是一个重要的指标,常用于描述数据的离散分布程度,并可以作为其他统计量的基础。
参考内容:1. 《数理统计学教程(第四版)》(吴喜之、韩有志、王稼琦著)2. 《统计学(第八版)》(罗伯特·尼尔·奇兹、哈维·戴维勒维著)3. 《经济统计学(第九版)》(曹宗晟、袁春生著)。
回归方程的相关系数公式

回归方程的相关系数公式
摘要:
一、回归方程的相关系数公式简介
二、相关系数的计算方法
三、相关系数的应用场景
四、相关系数与回归系数的关系
正文:
一、回归方程的相关系数公式简介
在回归分析中,相关系数是一个非常重要的概念,用于衡量两个变量之间的线性关系的强度和方向。
相关系数的公式为:r = ∑((x_i-平均x)*(y_i-平均y)) / (√∑(x_i-平均x)^2 * ∑(y_i-平均y)^2)。
其中,x_i和y_i分别表示样本中的每个数据点的x值和y值,平均x和平均y分别表示x值和y值的平均值。
二、相关系数的计算方法
相关系数的计算方法主要有两种:一种是基于样本数据的方法,另一种是基于总体数据的方法。
基于样本数据的方法又分为两种:一种是简单平均法,另一种是加权平均法。
基于总体数据的方法也有两种:一种是基于总体均值和总体协方差的方法,另一种是基于总体方差和总体协方差的方法。
三、相关系数的应用场景
相关系数在回归分析中有很多应用场景,比如:判断两个变量之间是否存在线性关系;判断两个变量之间的线性关系的强度和方向;预测一个变量的值,给定另一个变量的值;评估一个回归模型的拟合优度等。
四、相关系数与回归系数的关系
相关系数和回归系数是两个不同的概念,但它们之间有一定的关系。
相关系数表示的是两个变量之间的线性关系的强度和方向,而回归系数表示的是当一个变量增加一个单位时,另一个变量的预期变化量。
相关系数p值计算公式

相关系数p值计算公式相关系数的p值是衡量两个变量之间关系强度的统计显著性值。
一般情况下,当p值小于0.05时,我们认为两个变量之间的关系是显著的。
相关系数的p值计算公式如下:1. 简单相关系数(Pearson相关系数)的p值计算公式:p = 2 * (1 - T.cdf(abs(r), n-2))其中,T是t分布,r是相关系数,n是样本的大小。
2. 斯皮尔曼相关系数(Spearman相关系数)的p值计算公式:p = 2 * (1 - T.cdf(abs(rs), n-2))其中,rs是斯皮尔曼相关系数,n是样本的大小。
在以上公式中,T.cdf(是累积分布函数,用于计算t分布中大于等于一些值的概率。
下面,我们将对这两个公式进行详细解释。
1. 简单相关系数(Pearson相关系数)的p值计算公式:假设我们有两个变量:X和Y,它们的简单相关系数为r。
我们想要计算这个相关系数的p值。
首先,我们需要计算t值。
t值的计算公式如下:t = r * sqrt((n-2) / (1 - r^2))其中,r是相关系数,n是样本的大小。
接下来,我们使用t值来计算p值。
p值的计算公式如下:p = 2 * (1 - T.cdf(abs(r), n-2))其中,T是t分布,T.cdf(是累积分布函数,用于计算t分布中大于等于一些值的概率。
2. 斯皮尔曼相关系数(Spearman相关系数)的p值计算公式:斯皮尔曼相关系数是一种通过将原始数据转换为秩次来计算的相关系数。
假设两个变量X和Y的斯皮尔曼相关系数为rs。
我们想要计算这个相关系数的p值。
首先,我们需要计算t值。
t值的计算公式如下:t = rs * sqrt((n-2) / (1 - rs^2))其中,rs是斯皮尔曼相关系数,n是样本的大小。
接下来,我们使用t值来计算p值。
p值的计算公式如下:p = 2 * (1 - T.cdf(abs(rs), n-2))其中,T是t分布,T.cdf(是累积分布函数,用于计算t分布中大于等于一些值的概率。
三种常用的不同变量之间相关系数的计算方法

三种常用的不同变量之间相关系数的计算方法在统计学中,相关系数用于衡量两个变量之间的线性关系强弱。
常用的三种不同变量之间相关系数的计算方法包括:皮尔逊相关系数、斯皮尔曼等级相关系数和切比雪夫距离。
下面将分别介绍这三种方法的计算过程和特点。
一、皮尔逊相关系数(Pearson Correlation Coefficient)皮尔逊相关系数是衡量两个连续型变量之间线性相关程度的常用方法。
它的取值范围为-1到1,其中-1表示完全负相关,1表示完全正相关,0表示无相关关系。
计算皮尔逊相关系数的步骤如下:1.计算每个变量的均值。
2.计算每个变量与其均值的差值。
3.将每个变量与其均值的差值相乘,并对相乘结果求和。
4.将每个变量与其均值的差值的平方相乘,并对相乘结果求和。
5.将步骤3的结果除以步骤4的结果的平方根,得到相关系数。
优点:1.适用于连续型变量的线性关系分析。
2.可以直接衡量两个变量之间的线性相关程度。
3.系数取值范围明确,易于解释。
缺点:1.只能衡量线性关系,对于非线性关系效果不好。
2.对异常值敏感,可能会影响结果的准确性。
3.不能判断因果关系,只是衡量相关性。
二、斯皮尔曼等级相关系数(Spearman's Rank Correlation Coefficient)斯皮尔曼等级相关系数是衡量两个变量之间的相关程度,不要求变量是连续型的,适用于等级变量或有序变量。
它将变量的原始数值替换为它们的排名,并衡量排名之间的关系。
计算斯皮尔曼等级相关系数的步骤如下:1.对每个变量的数值进行排序,得到它们的排名。
2.计算每个变量的排名差,即(对应的第一个变量的排名-对应的第二个变量的排名)。
3.计算排名差的平方,并对平方和求和。
4.根据样本大小和公式计算相关系数。
优点:1.不需要变量满足正态分布的假设。
2.可以应用于等级变量或有序变量。
3.对于非线性关系也能较好地适应。
缺点:1.只能测量变量之间的单调关系,无法捕捉到非单调的关系。
协方差和相关系数的计算公式

协方差和相关系数的计算公式协方差和相关系数是统计学中常用的两个概念,用于描述变量之间的关系程度。
在概率论和统计学中,协方差表示两个变量的总体协同变动的方向和程度。
相关系数则度量两个变量之间线性相关的强度和方向。
接下来我们会分别介绍协方差和相关系数的计算公式及其详细解释。
1. 协方差(Covariance):协方差是用来衡量两个随机变量关系的一种统计量。
它表示两个随机变量在同一时间(或同一试验中)波动的程度。
总体协方差的计算公式如下:Cov(X, Y) = Σ[ (Xᵢ - μₓ) * (Yᵢ - μᵧ) ] / N其中-X和Y分别是随机变量X和Y的取值;-μₓ和μᵧ分别是随机变量X和Y的总体均值;-N是样本个数;-Σ表示对所有样本求和。
样本协方差的计算公式如下:Cov(X, Y) = Σ[ (Xᵢ - X̄) * (Yᵢ - Ȳ) ] / (n - 1)其中-X̄和Ȳ分别是X和Y的样本均值;-n是样本个数;-Σ表示对所有样本求和。
解释:协方差的计算公式可以通过观察上面的公式看出,它是两个变量之间差值的乘积的平均值。
如果协方差为正,表示两个变量呈正相关,当一个变量上升时,另一个变量也上升;如果协方差为负,表示两个变量呈负相关,当一个变量上升时,另一个变量下降;如果协方差为零,则表示两个变量之间不存在线性关系。
2. 相关系数(Correlation coefficient):相关系数是用于度量两个变量之间线性相关程度的一种统计量。
它的值介于-1和1之间。
总体相关系数的计算公式如下:ρ(X, Y) = Cov(X, Y) / (σₓ * σᵧ)其中- Cov(X, Y)是协方差;-σₓ是X的总体标准差;-σᵧ是Y的总体标准差。
样本相关系数的计算公式如下:r(X, Y) = Cov(X, Y) / (sₓ * sᵧ)其中- Cov(X, Y)是协方差;-sₓ是X的样本标准差;-sᵧ是Y的样本标准差。
解释:相关系数是通过协方差来度量两个变量之间的线性关系程度,其值介于-1和1之间。
统计学原理中 相关系数名词解释

一、相关系数的概念相关系数用来衡量两个变量之间的线性相关程度,是统计学中常用的一种指标。
相关系数的取值范围在-1到1之间,值越接近-1或1,说明两个变量之间的线性相关程度越强,值越接近0,说明两个变量之间的线性相关程度越弱或没有线性相关关系。
二、相关系数的计算方法相关系数的计算方法有多种,其中最常用的是皮尔逊相关系数。
皮尔逊相关系数的计算步骤如下:1. 计算两个变量的均值。
2. 计算两个变量与均值的差值,并将差值相乘。
3. 将上一步的结果相加,并除以两个变量的标准差的乘积。
除了皮尔逊相关系数外,还有斯皮尔曼相关系数、肯德尔相关系数等其他计算方法。
不同的计算方法适用于不同类型的变量和数据分布。
三、相关系数的应用领域相关系数在各个领域都有着广泛的应用,特别是在自然科学、社会科学和工程技术领域。
以下是一些相关系数在实际中的应用案例:1. 医学研究中,可以使用相关系数来衡量药物与疾病之间的相关性,以及疾病发展的趋势。
2. 金融领域中,相关系数可以帮助分析不同资产之间的相关程度,从而进行风险管理和资产配置。
3. 市场营销中,相关系数可以用来分析产品销售量与广告投入之间的相关性,为市场策略提供依据。
四、相关系数的局限性尽管相关系数在许多情况下都是一种有效的分析工具,但它也有一些局限性。
以下是一些相关系数的局限性:1. 相关系数只能反映两个变量之间的线性相关程度,而不能反映非线性关系或者其他类型的关系。
2. 相关系数不能用于说明因果关系,即使两个变量之间存在很强的相关性,也不能说明其中一个变量是另一个变量的原因。
在使用相关系数进行分析时,需要结合具体的问题和实际情况进行综合考虑,不能过分依赖相关系数的结果进行决策。
五、结语相关系数作为统计学中重要的工具之一,对于研究变量之间的关系具有重要意义。
在实际应用中,需要根据具体情况选择合适的相关系数计算方法,并结合其他分析方法进行综合分析,以获得更为全面和准确的结论。
统计学中的相关系数与协方差的计算方法

统计学中的相关系数与协方差的计算方法在统计学中,相关系数和协方差是常用的两个指标,用于衡量两个变量之间的关系和变化。
它们的计算方法可以帮助我们理解和分析数据之间的关联性和变化趋势。
本文将详细介绍相关系数和协方差的计算方法。
一、相关系数的计算方法相关系数是用来度量两个变量之间相关程度的指标,它的取值范围在-1到1之间。
相关系数越接近1,表示两个变量正相关性越强;越接近-1,表示两个变量负相关性越强;接近0则表示两个变量之间没有线性相关关系。
相关系数的计算方法有多种,最常用的是皮尔逊相关系数。
其计算公式如下:r = Cov(X, Y) / (σX * σY)其中,r表示相关系数,Cov(X, Y)表示X和Y的协方差,σX和σY 表示X和Y的标准差。
协方差的计算方法如下:Cov(X, Y) = Σ((Xi - μX) * (Yi - μY)) / n其中,Xi和Yi分别表示第i个样本点的X和Y的取值,μX和μY 分别表示X和Y的均值,n表示样本个数。
标准差的计算方法如下:σX = √(Σ((Xi - μX)^2) / n)标准差同样可以通过上述公式求得。
通过计算相关系数,可以了解到两个变量之间的线性关系的强度和方向,进而进行数据分析和预测。
二、协方差的计算方法协方差用于衡量两个变量的总体变化趋势是否一致。
协方差的取值范围为负无穷到正无穷。
当协方差为正值时,表示两个变量变化趋势一致;当协方差为负值时,表示两个变量变化趋势相反;当协方差为0时,表示两个变量之间没有线性关系。
协方差的计算方法与相关系数类似,计算公式如下:Cov(X, Y) = Σ((Xi - μX) * (Yi - μY)) / N其中,Σ表示求和,Xi和Yi分别表示第i个样本的X和Y的取值,μX和μY分别表示X和Y的均值,N表示总体样本个数。
通过计算协方差,可以判断两个变量是否具有相关性,进而进行数据分析和预测。
三、相关系数和协方差的应用相关系数和协方差是统计学中常用的指标,广泛应用于数据分析和金融市场等领域。
相关系数法

相关系数法相关系数是统计学中一种常用的方法,用于衡量两个变量之间的相关程度。
它可以帮助我们了解两个变量之间的线性关系,并通过给出一个数值来描述这种关系的强度和方向。
在实际应用中,相关系数常被用于研究市场中不同资产之间的相关性、评估医学研究中的变量关联、分析经济学数据中的相关关系等。
下面是一些关于相关系数的参考内容。
1. 相关系数的定义与计算方法:相关系数是衡量两个变量间关系强度和方向的统计量。
最常见的相关系数是皮尔逊相关系数(Pearson correlation coefficient),它可以用来衡量两个变量的线性关系。
计算公式为:r = (ΣXiYi - n X Ȳ) / [√((ΣXi^2 - n X^2) * (ΣYi^2 - n Ȳ^2)) ]其中,r表示相关系数,Xi和Yi分别为变量X和Y的观测值,X和Ȳ分别为变量X和Y的均值,n为观测数量。
2. 相关系数的取值范围和解释:相关系数r的取值范围在-1到1之间。
当r=1时,表示两个变量完全正相关,即一个变量增加,另一个变量也随之增加;当r=-1时,表示两个变量完全负相关,即一个变量增加,另一个变量减少;当r=0时,表示两个变量无相关性,即两个变量之间没有线性关系。
此外,相关系数的绝对值越接近1,表示线性关系越强。
3. 相关系数的推断统计学:对于给定的样本数据,通过计算样本相关系数r,我们可以进行相关性推断统计学,进而判断总体相关系数是否显著不为零。
这通常涉及到假设检验和置信区间的计算。
假设检验的零假设为“总体相关系数等于零”,备择假设为“总体相关系数不等于零”。
通过计算相关系数的标准误差和t 统计量,可以计算得出相关系数的显著性水平和p值,从而决定是否拒绝零假设。
同样,通过计算相关系数的置信区间,可以得到一定置信水平下总体相关系数的取值范围,进一步提供了我们对总体相关系数的估计。
4. 相关系数的局限性:相关系数只能衡量两个变量之间的线性关系,对于非线性关系的描述能力较弱。
相关系数表达式

相关系数表达式相关系数是用于衡量两个变量之间线性关系密切程度的统计量,通常用r 表示。
其表达式如下:r = [(nΣxy) - (ΣxΣy)] / sqrt([(nΣx^2) - (Σx)^2][(nΣy^2) - (Σy)^2])其中,n 为数据对数,Σxy、Σx、Σy、Σx^2 和Σy^2 分别为数据对中x、y 值的乘积、x 值的和、y 值的和、x 值的平方和和y 值的平方和。
相关系数的取值范围为-1 ~ 1,当r>0 时表示正相关,r<0 时表示负相关,r=0 时表示无相关。
相关系数越接近1 或-1,则意味着两个变量之间的关系越强。
但需要注意的是,相关系数只能反映两个变量之间的线性关系,如果变量之间存在非线性关系,则相关系数并不能准确地描述它们之间的关系。
相关系数的计算可以通过以下步骤进行:1. 计算每对数据的乘积(xy)。
假设有n 对数据(x1, y1), (x2, y2), ... (xn, yn),则第i 对数据的乘积为xi * yi。
2. 计算所有x 值的和(Σx)和所有y 值的和(Σy)。
即将所有的x 值相加得到Σx,将所有的y 值相加得到Σy。
3. 计算所有x 值的平方和(Σx^2)和所有y 值的平方和(Σy^2)。
即将所有的x 值平方后相加得到Σx^2,将所有的y 值平方后相加得到Σy^2。
4. 计算n 乘以Σxy 的和与Σx 乘以Σy 的差值。
即n * Σxy - Σx * Σy。
5. 计算(nΣx^2) - (Σx)^2 和(nΣy^2) - (Σy)^2 的乘积的平方根。
即sqrt([(nΣx^2) - (Σx)^2][(nΣy^2) - (Σy)^2])。
6. 将第四步得到的结果除以第五步得到的结果,得到相关系数r 的值。
这个相关系数表达式的计算步骤确保了该值能够衡量两个变量之间的线性关系密切程度。
通过计算相关系数,我们可以了解两个变量之间的关系是正相关、负相关还是无关。
注会财管中相关系数公式

注会财管中相关系数公式在注会财管中,相关系数是一个重要的概念,它用于衡量两个变量之间的线性关系。
本文将详细介绍相关系数公式以及相关系数在财务中的应用。
一、相关系数公式相关系数的定义是:两个变量之间的线性关系的强度和方向。
在数学上,相关系数是一个介于-1 和1 之间的数值,它表示了两个变量之间的正相关、负相关或无关。
相关系数公式为:r = √(Σ(x_i-平均x)*(y_i-平均y)^2 / (n-1)) / √(Σ(x_i-平均x)^2 / (n-1)) * √(Σ(y_i-平均y)^2 / (n-1))其中,r 为相关系数,x_i 和y_i 分别为两个变量的每一个观测值,平均x 和平均y 分别为x_i 和y_i 的平均值,n 为观测值的数量。
相关系数与协方差有密切的关系。
协方差是两个变量之间的线性关系的度量,它反映了两个变量的变化趋势是否一致。
协方差为0 时,两个变量之间不存在线性关系;协方差为正时,两个变量之间存在正线性关系;协方差为负时,两个变量之间存在负线性关系。
相关系数的性质包括:1)相关系数的取值范围是-1 到1;2)当相关系数为1 时,表示两个变量完全正相关;当相关系数为-1 时,表示两个变量完全负相关;当相关系数为0 时,表示两个变量之间不存在线性关系;3)相关系数与协方差的关系为:相关系数=协方差/标准差的乘积。
二、相关系数在财务中的应用相关系数在财务领域有广泛的应用,主要包括投资组合风险管理、资产定价模型和财务分析。
在投资组合风险管理中,相关系数用于衡量不同资产之间的相关性,从而帮助投资者了解投资组合的风险分散情况。
相关系数的绝对值越接近1,表示两个资产之间的相关性越强;相关系数的绝对值越接近0,表示两个资产之间的相关性越弱。
在资产定价模型中,相关系数用于计算投资组合的预期收益和风险。
在资本资产定价模型(CAPM)中,相关系数用于计算投资组合的预期收益和市场风险溢价。
在套利定价模型(APT)中,相关系数用于确定投资组合的预期收益与一组影响因素之间的关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七侠五义
1
相关系数的计算
计算
我现在计算1x 和2x 的相关系数。
也就是第三产业占总值比和人均GDP 的相关系数。
∑∑∑===----=
n
k n
k k
k
n
k k k
x x
x x
x x x x
r 1
1
2
222
111
221112)
()
()
)((
其中1x ,2x 是指数据1x ,2x 的平均值。
现在分别计算分子的)(11x x k -,)(22x x k -,
∑=--n
k k k
x x x x
1
2211))((的值。
分别计算分母的
∑=-n
k k
x x
1
2
11)(,∑=-n
k k x x 1
2
22)(,
∑∑==--n
k n
k k
k
x x
x x
1
1
222
11)()
(的值。
这种计算用EXCEL ,很方便!
七侠五义
2
七侠五义
3
利用表格中的数据,算得结果
∑∑∑===----=
n
k n
k k
k
n
k k k
x x
x x
x x x x
r 1
1
2
222
111
221112)()
()
)((=
680.9240
.933337286539161261942.92
⨯=0.791980253
计算结果得到,第三产业占总值比(1x )和人均GDP(2x )的相关系数为0.791980253。
补充:
相关系数的大小:11≤≤-ij r 。
以上面1x 和2x 为例,在统计学中, ①如果12r =1,即1x 和2x 是正相关的。
则存在a >0,使得b ax x +=21。
反过来是
一样的,存在c >0,使得d cx x +=12。
(是常数d b ,)
②如果12r =1-,即1x 和2x 是负相关的。
则存在a >0,使得b ax x +-=21。
反过来
是一样的,存在c >0,使得d cx x +-=12。
(是常数d b ,)。
