2019年高职单招考试试题数学
完整)2019年浙江高职考数学试卷

完整)2019年浙江高职考数学试卷2019年浙江省单独考试招生文化考试数学试题卷本试题卷共三大题,共4页,满分150分,考试时间120分钟。
考生事项:1.答题前,请务必将自己的姓名和准考证号用黑色字迹的签字笔或钢笔分别填写在试题卷和答题纸规定的位置上。
2.答题时,请按照答题纸上的“注意事项”要求,在答题纸相应的位置上规范作答。
在本题卷上的作答一律无效。
一、单项选择题(本大题共20小题,1-10小题每小题2分,11-20小题每小题3分,共50分)在每小题列出的四个备选答案中,只有一个是符合题目要求的。
错涂、多涂或未涂均不得分)1.已知集合A={-1},B={-3,-1,1,3},则A∩B的值为A。
{-1,1}B。
{-1}C。
{1}D。
Ø2.不等式x^2-4x≤0的解集为A。
[0,4]B。
(0,4)C。
[-4,0)∪(0,4]D。
(-∞,0]∪[4,+∞)3.函数f(x)=ln(x-2)+1/(x-3)的定义域为A。
(2,+∞)B。
(0,4)C。
(-∞,2]∪[3,+∞)D。
(2,3)∪(3,+∞)4.已知平行四边形ABCD,则向量AB+BC= A。
BDB。
DBC。
ACDD。
DC5.下列函数以π为周期的是A。
y=sin(x-π)B。
y=2cosxC。
y=sin2xD。
y=sin(x)6.本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法的总数是A。
400B。
380C。
190D。
407.已知直线的倾斜角为60°,则此直线的斜率为A。
-√3B。
-√3/3C。
√3/3D。
√38.若sinα>0且tanα<0,则角α终边所在象限是A。
第一象限B。
第二象限C。
第三象限D。
第四象限9.椭圆标准方程为(x^2/4)+(y^2/9)=1,一个焦点为(-3,0),则t的值为A。
-1B。
0C。
1D。
310.已知两直线l1、l2分别平行于平面β,则两直线l1、l2的位置关系为A。
四川省2019年高职对口招生数学试题

XX省2019年高职对口招生数学试题一、选择题(共60分)1.设集合A={-2,2},B={-1,2} ,则AUB ()A. 2B. 2, 1C. 2,2D.2,1,22.函数fx1的定义域()1x2A. 1,1B.1,C. ,1D.1,3.已知角的终边经过点1,1,则cos ()A.2B.2C.1 12 2 2D.24.已知平面向量a 5,4 ,b 3,2,c 7,6 ,则a+b-c=()A.0,0B.1,0C.0,1D.1,15.绝对值不等式x 3 4 的解集为()A. ,1B.7,C. 1,7D. ,1U7,6.函数fx sin2x3在区间,上的图像大致为()7.与直线3x 2y70 垂直的直线的斜率是()A. 2B.2C.3 33 3 2D.椭圆x 2y228.1的焦点坐标是()4 3A.1,0,1,0B. 3,0,3,0C. 2,0,2,0D.7,0,7,09.已知球的半径为6cm,则它的体积为()A.36cm3B.144cm3C.288cm3D.864cm3(11)4lg5 lg20()10.计算:16A.1B.2C.3D.411.“x 0”是”x1”的()条件。
A.充分不必要B. 必要不充分C.充要条件D.既不充分也不必要12.某科技公司从银行贷款500万元,贷款期限为6年,年利率为5.7600,利息按“复利计息法”(把当年的本金与利息的和作为次年的本金来计算利息的方法)计算.如果6年后一次性还款,那么这家科技公司应偿还银行的钱是()A.500 0.9424 5万元B.500 0.9424 6万元C.500 1.0576 5万元D.500 1.0576 6万元13.已知a ln 1,b23,clog1,则a,b,c的大小关系为()2 213A.bcaB.b acC.cb aD.cab14.已知甲、乙两个城市相距120千米,小王开汽车以100千米/时匀速从甲城市驶往乙城市,到达乙城市后停留1小时,再以80千米/时匀速返回甲城市.汽车从甲城市出发时,时间x(小时)记为0.在这辆汽车从甲城市出发至返回到甲城市的这段时间内,该汽车离甲城市的距离y(千米)表示成时间x(小时)的函数为()A. y 100x,0 x1.2,B.y100x,0 x1.2, 80x, x1.2. 12080x,x 1.2. 100x, 0 x1.2,100x, 0 x 1.2,C.y 120, 1.2x2.2 D.y 120, 1.2 x 2.2 120 80x 2.2 x 3.7 29680x 2.2 x 3.715.函数f a a 12 a 2 2 a3 2 a10 2的单调增区间为()A.5,B.5.5,C.6,D.6.5,二、填空题(共20分)16. 已知平面向量a=2, 1 ,b= 3, 2,则a?b.17. 双曲线x2y21的离心率为.318. 16.二项式x 2的展开式中常数项为(用数字作答)x19.为落实精准扶贫工作,某单位计划从7名优秀干部中任选3名到贫困村驻村工作,不同的选派方案有种.20.计算:tan200tan4003tan200tan400.(用数字作答)三、解答题。
川省2019年高职对口招生数学试题

四川省2019年高职对口招生数学试题(总9页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除四川省2019年高职对口招生数学试题一、选择题(共60分)1. 设集合A={-2,2},B={-1,2},则A B =( ){}{}{}{}.2.2,1.2,2.2,1,2A B C D -----2.函数()21f x x =-的定义域( ) ()()()().1,1.1,.,1.1,A B C D --+∞-∞+∞3. 已知角α的终边经过点()1,1-,则cos α=( )2211....2222A B C D --4. 已知平面向量()()()5,43,2,7,6===a ,b c ,则a +b -c =( )()()()().0,0.1,0.0,1.1,1A B C D5. 绝对值不等式34x -<的解集为( )()()()()().,1.7,.1,7.,17,A B C D -∞-+∞--∞-+∞ 6. 函数()sin 23f x x π⎛⎫=+ ⎪⎝⎭在区间[],ππ-上的图像大致为( )7. 与直线3270x y --=垂直的直线的斜率是( )A.32-B.32C.23-D.238. 椭圆22143x y +=的焦点坐标是 ( )()()())()()()).1,0,1,0.3,0,3,0.2,0,2,0.7,0,7,0A B C D ----9. 已知球的半径为6cm ,则它的体积为( )3333.36.144.288.864A cm B cm C cm D cm ππππ10. 计算:=++-20lg 5lg 16141)(( )A.1B.2C.3D.4 11. “0>x ”是”1>x ”的( )条件。
A.充分不必要B.必要不充分C.充要条件D.既不充分也不必要 12. 某科技公司从银行贷款500万元,贷款期限为6年,年利率为005.76,利息按“复利计息法”(把当年的本金与利息的和作为次年的本金来计算利息的方法)计算. 如果6年后一次性还款,那么这家科技公司应偿还银行的钱是( )5656.5000.9424.5000.9424.500 1.0576.500 1.0576A B C D ⨯⨯⨯⨯万元万元万元万元13. 已知21ln=a ,32-=b ,31log 21=c ,则,,a b c 的大小关系为( ) ....A b c aB b a cC c b aD c a b >>>>>>>>14.已知甲、乙两个城市相距120千米,小王开汽车以100千米/时匀速从甲城市驶往乙城市,到达乙城市后停留1小时,再以80千米/时匀速返回甲城市.汽车从甲城市出发时,时间x (小时)记为0.在这辆汽车从甲城市出发至返回到甲城市的这段时间内,该汽车离甲城市的距离y (千米)表示成时间x (小时)的函数为( )100,0 1.2,.80, 1.2.x x A y x x ≤≤⎧=⎨>⎩ 100,0 1.2,.12080, 1.2.x x B y x x ≤≤⎧=⎨->⎩ 100,0 1.2,.120, 1.2 2.212080 2.2 3.7x x C y x x x ≤≤⎧⎪=<≤⎨⎪-<≤⎩100,0 1.2,.120,1.22.229680 2.23.7x x D y x x x ≤≤⎧⎪=<≤⎨⎪-<≤⎩ 15.函数()()()()()222212310f a a a a a =-+-+-+⋅⋅⋅+-的单调增区间为( )[)[)[)[).5,.5.5,.6,.6.5,A B C D +∞+∞+∞+∞二、填空题(共20分)16. 已知平面向量()()2,13,2---a =,b =,则a •b .17. 双曲线2213y x -=的离心率为 .18. 二项式621x x ⎛⎫+ ⎪⎝⎭的展开式中常数项为 .(用数字作答) 19. 为落实精准扶贫工作,某单位计划从7名优秀干部中任选3名到贫困村驻村工作,不同的选派方案有 种. 20. 计算:=++000040tan 20tan 340tan 20tan .(用数字作答)三、解答题。
2019年单独招生考试-九江职业技术学院-《数学》样卷

九江职业技术学院2019年单独招生考试《数学》样卷(满分120分)一、选择题:本大题共5小题,每小题4分,共20分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合{P 0,1}=、}2,1{Q --=,则Q P 中最小的数是( )A. 0B. 1C. 1-D. 2-2.求值:cos 3π=( );A .0B .12C .1D .2 3.下列四个命题正确的是( );A.三点确定一个平面B.不在同一条直线上的三点确定一个平面C.两条直线确定一个平面D.两条平行直线不能确定一个平面4.平面内同时经过点(0,0)与点(1,1)的直线方程为( );A .x y =B .x y -=C .x y 2=D .x y 2-=5.已知向量)1,1(=a ,)1,1(-=b ,则向量a b -等于( );A .)1,2(-B .(2,0)C .(0,2)D . (0,2)-二、填空题:本大题共4小题,每小题7分,共28分。
6.函数y =的定义域为 ;7.设三个数1,,9a 成等差数列,则a= ;8.九江市某中学高三(1)班共有52人,在去年高考中有13人考上了本科院校,另有26人考上了专科与高职院校,则该班去年的高考升学率为 ;9.圆心在原点,面积为4π的圆的方程为____________;三、判断题:本大题共5小题,每小题4分,共20分,正确的打∨错误的打⨯.10.奇函数的图像必关于原点对称. )(11.若b a =,则必有b a =. )(12.平面内两条直线相交,则其对顶角相等. )(13.三角形的三个内角和为180. )(14.sin45sin 60> . )(四、解答题:本大题共3个小题,共52分。
15.(17分) 已知1sin 2θ=,并且20πθ<<,求:(1)θcos 的值;(2)θsin2的值.16.(20分) 已知焦点为(,0)2p 的抛物线22y px =经过点(1,2). (1)求p 的值;(2)求该抛物线的焦点坐标;(3)求该抛物线的准线方程.17.(15分) 传说,有一个古罗马人临终时,给怀孕的妻子写了一份遗嘱:生下来的如果是儿子,就把遗产的三分之二给儿子,母亲拿三分之一;生下来的如果是女儿,就把遗产的三分之一给女儿,母亲拿三分之二.结果这位妻子生了一男一女,问应该怎样分配他的遗产,才能最接近遗嘱的要求?。
2019年浙江省高等职业技术教育招生考试数学试卷及答案

2019年浙江省高等职业技术教育招生考试
数学试卷
注意事项
1、所有试题均需在答题纸上作答,未在规定区域内答题,每错一个区域扣卷面总分1分,在试卷和草稿纸上作答无效。
2、答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸和试卷上。
3、选择题每小题选出答案后,用2B铅笔把答题纸上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
非选择题目用黑色字迹的签字笔或钢笔将答案写在答题纸上。
4、在答题纸上作图,可先用2B铅笔,确定后必须用黑色字迹的签字或钢笔模黑。
2019年浙江省高等职业技术教育招生考试
数学参考答案。
2019年浙江省单独考试招生文化考试数学试卷

2019 年浙江省单独考试招生文化考试数学试卷2019 年浙江省单独考试招生文化考试数学试题卷姓名:准考证号:本试题卷共三大题,共 4 页。
满分 150 分,考试时间 120 分钟。
一、单项选择题(本大题共 20 小题,1-10 小题每小题 2 分,11-20 小题每小题 3 分,共 50 分)(在每小题列出的四个备选答案中,只有一个是符合题目要求的.错涂、多涂或未涂均不得分)1.已知集合 A -1,0,1, B -3,-1,1,3 ,则 A B ()A. -1,1B.-1C.1D. 2.不等式 x2 4x 0 的解集为()A.0, 4B. 0, 43.函数 f x ln x 2 1 的定义域为(x3A. 2, B.2, C. 4,0 0, 4)D. ,0 4, C. , 2 3, D.2,3 3,4.已知平行四边形 ABCD,则向量 AB BC ()A. BDB. DB5.下列函数以 为周期的是()C. ACD. CAA.ysin x 8 B. y 2cos xC. y sin xD. y sin 2x6.本学期学校共开设了 20 门不同的选修课,学生从中任选 2 门,则不同的选法的总数是( )7.已知直线的倾斜角为 60 ,则此直线的斜率为()A. 3 3B. 3C. 38.若 sin 0且 tan 0,则角 终边所在象限是()A.第一象限B.第二象限C.第三象限1数学试题 第1页(共 6 页)D. 3 3D.第四象限2019 年浙江省单独考试招生文化考试数学试卷9.椭圆标准方程为 x2 y2 1 ,一个焦点为 3,0 ,则 t 的值为()2t 4 4 tA. 110.已知两直线 l1 、 l2 分别平行于平面 ,则两直线 l1 、 l2 的位置关系为(A.平行B.相交C.异面) D.以上情况都有可能11.圆的一般方程为 x2 y2 8x 2 y 13 0 ,则其圆心和半径分别为()A. 4, 1, 4B. 4, 1, 2C. 4,1, 4D. 4,1, 212.已知 100 张奖券共有 2 张一等奖、5 张二等奖、10 张三等奖,现从中任取一张,中奖概率是()A. 1 10000B. 1 5013. a 、 b 、 c 为实数,则下列各选项中正确的是(C. 3 100)D. 17 100A. a b 0 a c b cB. a b 0 a bC. a b 0 2a 2bD. a b c 0 ab ac14. sin1050 的值为()A. 2 2B. 3C. 1D. 122215.双曲线 x2 y2 1的实轴长为 10,焦距为 26,则双曲线的渐近线方程为()a2 b2A. y 13 x 5B. y 12 x 5C. y 5 x 12D. y 5 x 1316.方程 y x2 4x 4 所对应曲线的图形是()y 2 1 -1 O12 A.3 4xy 2 1 -1 O12 B.3 4x2数学试题 第2页(共 6 页)2019 年浙江省单独考试招生文化考试数学试卷yy2211-1 O123 4x-1 O123 4xC.D.17.若角 的终边经过点 4, 3 ,则 cos 2 的值为()A. 7 25B. 16 25C. 7 25D. 16 2518.动点 M 在 y 轴上,当它与两定点 E 4,10 、F 2,1 在同一条直线上时,点 M 的坐标是()A. 0,6B. 0,5C. 0, 4D. 0,319.“ 2019k2 1 1”是“ k 1”的()A.充分不必要条件B.必要不充分条件 C.充分且必要条件 D.既不充分也不必要条件20.某旅游景点有个人票和团队票两种售票方式,其中个人票每人 80 元,团队票(30 人以上含 30 人)打七折,按照购票费用最少原则,建立实际游览人数 x 与购票费用 y (元)的函数关系,以下正确的是()80x, 0 x 24, x N, A. y 1344, 24 x 30, x N ,56x, x 30, x N80x, 0 x 21, x N, B. y 1680, 21 x 30, x N,56x, x 30, x N80x, 0 x 24, x N, C. y 1920, 24 x 30, x N ,56x, x 30, x N80x, 0 x 21, x N, D. y 2400, 21 x 30, x N ,56x, x 30, x N二、填空题(本大题共 7 小题,每小题 4 分,共 28 分)y21.等比数列 1 ,1, 4 ,16 , 的第 5 项是.422.化简: cos tan .23. 2x y6 展开式的第 5 项为.O24.圆柱的轴截面是边长为 3 的正方形,则圆柱的体积等于.25.如图所示,函数 y f x 的图象关于直线 x 8 对称,则 f 6816 x第 25 题图f 13 (填“>”、3数学试题 第3页(共 6 页)“<”或“=”).26.正数 x 、 y 满足 lg x lg y 2,则 x y 的最小值等于2019 年浙江省单独考试招生文化考试数学试卷.27.已知椭圆中心在原点且对称轴为坐标轴,它与双曲线 x2 y2 1有且仅有两个公共点,它们的离 3心率之积为 1,则椭圆标准方程为.三、解答题(本大题共 8 小题,共 72 分)(解答应写出文字说明及演算步骤)28.(本题满分7分)计算: sin1 lg1000 0.25 2532 3!52 .229.(本题满分 8 分)在 ABC 中, B C 30 , a 2 3 . (1)求 c ;(4 分) (2) N 为 AC 中点时,求 ABN 的面积.(4 分)30.(本题满分 9 分)已知圆 C 的圆心为 1,1 ,半径为 2 .(1)写出圆 C 的标准方程;(3 分) (2)试判断直线 x y 1 0 与圆 C 的位置关系;若相交,求出两点之间的距离.(6 分)31.(本题满分 9 分)已知 、 为第二象限角,且满足 sin 2 2 , sin 3 求:35(1) cos ;(5 分)(2)函数 f x cos cos x cos sin x 的最大值.(4 分)32.(本题满分 9 分)已知抛物线的顶点在原点,焦点坐标为 F 3,0 .(1)求抛物线的标准方程;(3 分)(2)若抛物线上点 M 到焦点的距离为 4,求点 M 的坐标.(6 分)4数学试题 第4页(共 6 页)2019 年浙江省单独考试招生文化考试数学试卷33.(本题满分 10 分)如图,正三棱锥 P ABC 的侧棱长为 2 3 ,底面边长为 4 . (1)求正三棱锥 P ABC 的全面积;(4 分) (2)线段 PA 、 AB 、 AC 的中点分别为 D 、 E 、 F ,求二面角 D EF A的余弦值.(6 分)PDCF AEB 第 33 题图34.(本题满分 10 分)体育场北区观众席共有 10500 个座位.观众席座位编排方式如图所示,由内而 外依次记为第 1 排、第 2 排、…….从第 2 排起,每一排比它前一排多 10 个座位,且最后一排有 600 个座位. (1)北区观众席共有多少排(7 分)(2)现对本区前 5 排的座位进行升级改造,改造后各排座位数组成数列bn .bn 满足:① b1 等于 原第 1 排座位数的一半;② bn bn1 n2 n 2,3, 4,5 .求第 5 排的座位数.(3 分)北区观众席—— —最后一排第2排 第1排—— —比赛场地第 34 题图5数学试题 第5页(共 6 页)2019 年浙江省单独考试招生文化考试数学试卷35.(本题满分 10 分)电影《流浪星球》上映期间,一场电影的票价定为 50 元时,电影院满座,满座时可容纳 600 人.若票价每提高 5x x N 元,售出票数就减少 30x 张.(1)若票价为 60 元,求实际售出的电影票数;(2 分)(2)写出一场电影的票房收入 R (元)与 x 的函数关系式;(3 分)(3)已知放映一场电影所需的总成本我 60020 x 元,若不考虑其他因素,票价定为多少时,电影院能获得最大利润( 5 分)6数学试题 第6页(共 6 页)2019 年浙江省单独考试招生文化考试数学试卷7数学试题 第7页(共 6 页)。
新疆维吾尔自治区2019年三校生高职考试数学

新疆维吾尔自治区2019年三校生高职考试数学一、选择题1.集合A ={1,2}的子集个数有A.4个B.3个C.2个D.1个2.下列函数是指数函数的是A.y =x 3B.y =2x+1C.y =√xD.y =(12)x3.cos 1200=A.12B.−12C.√32D.−√32 4.下列说法正确的是A.若两个平面有一个公共点,则这两个平面相交于该点B.两个平面ABC 与DBC 交于线段BCC.若一条直线上有一点在一个平面内,则这条直线在这个平面内D.两条相交直线确定一个平面5.若cos α<0且tan α<0,则角α的终边所在的象限是A.第一象限B.第二象限C.第三象限D.第四象限6.x ∈R 是x ∈Q 的A.必要不充分条件B.充分不必要条件C.充要条件D.既不充分也不必要条件7.函数y =√x +1+lg (x −1)的定义域是A.[−1,+∞)B.(1,+∞)C.(−1,+∞)D.[1,+∞)8.不等式x 2−2<0的解集为A.{x|x<√2}B.{x|x<−√2}C.{x|−√2<x<√2}D.{x|x<−√2或x>√2}9.对于函数f(x)=x,以下说法正确的是A.奇函数且在R上单调递增B. 偶函数且在R上单调递减C. 偶函数且在R上单调递增D. 奇函数且在R上单调递减10.在等差数列{a n}中,a1=1,a3=5,则a10=A.37B.18C.36D.1911.已知圆的方程是(x+1)2+(y−2)2=2,则其圆心坐标和半径分别为A.圆心(−1,2),半径2B. 圆心(−1,2),半径√2C. 圆心(1,−2),半径2D. 圆心(1,−2),半径√212.抛掷一枚质地均匀的硬币两次,出现“两次正面”的概率是A.23B.13C.14D.1213.已知等比数列{a n}的通项公式为a n=(−1)n2n,则公比q=A.−2B.2C.12D.−1214.下列命题正确的是A.锥体的体积等于底面积与高之积B.球的体积比等于半径的平方比C.长方体的体积等于长宽高之积D.直径是1的球的表面积S=4π15.在等比数列{a n}中,首项a1=2,公比q=−1,则其前10项的和等于A.−20B.0C.2D.−216.已知直线l:2x +3y +1=0,则此直线的斜率是A.23B.32C.−23D.−3217.下列说法正确的是A.不在同一平面内的两条直线叫异面直线B.若一个平面内的两条直线平行于另一个平面,则这两个平面平行C.若一条直线与一个平面内的两条直线垂直,则这条直线垂直于这个平面D.若一条直线垂直于一个平面,则这条直线垂直于该平面内的所有直线18.已知向量a ⃗=(1,m ),向量b ⃗⃗=(m,2),若a ⃗‖b⃗⃗,则实数m 的值为 A.−√2B.√2C.−√2或√2D.2或−219.已知sin α=√32且α∈(π2,3π2),则角α等于A.2π3B.π6C.π3D.5π620.已知函数f (x )为偶函数,且f (2)=1,若g (x )=xf (x ),则g (−2)=A.1B.−1C.−2D.2二、填空题21.若点p (3,4)是角α终边上的一点,则cos α=22.已知a ⃗=(1,2),向量b ⃗⃗=(−2,−1),则a ⃗+2b⃗⃗= 23.已知a,b 满足0<a <1且2<b <3,则a +b 的取值范围是24.三角形的内角和等于1800是_______事件(填不可能、必然或随机)25.有不同颜色的四件上衣与不同颜色的三条长裤,如果一条长裤与一件上衣配成一套,则不同的配法有______种26.已知f(x)={1(x>0)−1(x<0),则f(−5)=27.比大小:0.7−0.2_________0.7−0.528.点A(2,4)与点B(−4,2)中点的坐标是29.已知直线l1:x+2y−3=0,直线l2:ax+y+5=0,若l1⊥l2,则a=30.函数f(x)=2sin x,当x∈[00,1800]时,函数f(x)的最大值是三、解答题31.计算:lg2+lg25−lg3+(π−1)032.已知全集U={−1,0,2,3,4,6},集合A={−1,2,3,4},集合B={x|x2−5x−6=0},求:(1)A∪B(2)C U A33.已知sinα=35,且α是第二象限的角,求:(1)cosα(2)tanα34.已知向量a⃗=(−7,6),向量b⃗⃗=(3,−4),求:(1)a⃗⋅b⃗⃗(2)|b⃗⃗|35.在等差数列{a n}中,S n是其前n项和,已知a4=11,a6=19,求:(1)a n(2)S n36.已知圆方程x2+y2=16,直线方程4x−3y=m,若直线与圆相切,求:(1)m的值(2)直线与两坐标轴所围成图形的面积37.书架上有语文书4本,数学书8本,英语书3本,物理书5本,从中任取1本,求:(1)取到语文书的概率(2)取到数学书或物理书的概率38.已知一个正方体的棱长为2cm,以正方体的对角线长为直径做一个球,求这个球的体积和表面积。
2019江苏高职单招院校单独招生联合测试真题卷(数学)

2019江苏高职单招院校单独招生联合测试真题卷数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷包含选择题(第1题~第10题,共10题40分)、填空题(第11题~第15题,共5题20分)和解答题(第16题~第20题,共5题40分),满分100分。
考生答题全部答在答题卡上,答在本试卷上无效。
本次考试时间为75分钟。
考试结束后,请将本试卷和答题卡一并放在桌面,等待监考员收回。
2.答题前,请您务必将自己的姓名、准考证号用书写黑色字迹的0.5毫米签字笔填写在本试卷及答题卡上。
3.请认真核对监考员在答题卡右上角所粘贴条形码上的姓名、准考证号是否与本人的相符合。
4.答选择题必须用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,请用橡皮擦干净后,再选涂其他答案。
答非选择题必须用书写黑色字迹的0.5毫米签字笔写在答题卡上的指定位置,在其他位置答题一律无效。
参考公式:椎体的体积公式1=3V Sh ,其中S 是椎体的底面积,h 是椎体的高.一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.已知集合{}1,3A =,{}3log ,3B m =,若{}1,2,3A B =U ,则实数m = ( )A .2B .3C .6D .92.盒中装有大小、形状都相同的6个小球,分别标以号码1,2,3,4,5,6,从中随机取出一个小球,其号码为奇数的概率是 ( )A .12 B .13 C .14 D .163.已知函数()cos()(0)6f x x πωω=->的最小正周期为π,则ω的值为 ( )A .1B .2C .πD .2π4.如图,在ABC ∆中,AB a =u u u r r ,AC b =u u u r r .若点D 满足2BD DC =u u u r u u u r , 则AD =u u u r( )(第4题)A .2133a b +r rB .2133a b -r rC .1233a b +r rD .1233a b -r r5.如图是一个算法流程图,若输出x 的值为3,则输出s 的值为 ( )(第5题)A .2B .4C .8D .166.若变量x y ,满足22x y x x y ≤⎧⎪≤⎨⎪+≥⎩,则2z y x =-的最大值为 ( )A .-1B .0C .1D .2 7.在平面直角坐标系中,已知第一象限的点(),a b 在直线210x y +-=上,则12a b+的最小值为( ) A .11 B .9 C .8 D . 6 8.已知1(1)212f x x -=-,且()6f m =,则实数m 的值为 ( )A .12-B .14-C .1-D .34- 9.已知等差数列{}n a 的前n 项和为n S ,若151,15,a S ==则10S = ( ) A .55B .45C .35D .2510.已知圆C 与圆22(1)1x y ++=关于直线0x y +=对称,则圆C 的标准方程为 ( )A .22(11x y +-=) B .221x y += C .22(11x y -+=) D .22(11x y ++=)二、填空题(本大题共5小题,每小题4分,共20分) 11.若复数z 满足1i 42i z +=-() (i 为虚数单位),则z = .12.设平面向量(2),(1,2)a y b ==v v ,,若//a b v v ,则2a b +=vv .13.如图,已知三棱锥P ABC -中, PA ⊥底面,3ABC PA =,底面ABC 是边长为2的正三角形,三棱锥P ABC -的体积为 .(第13题)的频率为 . 分组 [10,20) [20,30) [30,40) [40,50) [50,60) [60,70]频数54321215.已知函数[]()211,1,3f x x a x x =-++∈图象上任意两点连线都与x 轴不平行,则实数a 的取值范围是 .三、解答题(本大题共5小题,共40分.解答时应写出文字说明、证明过程或演算步骤)16.(本题满分6分) 已知5cos α=,(0,)2πα∈. (1)求sin α和sin()4πα+的值; (2) 求tan2α的值.17.(本题满分6分)如图,在三棱锥S ABC -中,点D ,E ,F 分别为棱AC , SA , SC 的中点. (1)求证://EF 平面ABC ;(2)若SA SC =,BA BC =,求证:AC ⊥SB .(第17题)18.(本题满分8分)已知椭圆C 的中心在原点,焦点在x 轴上,短轴长为2,且点3在椭圆C 上. (1)求椭圆C 的方程;(2)若点P 在第二象限,2160F PF ∠=︒,求三角形12PF F 的面积. 19.(本题满分10分)已知正项数列{}n a 的前n 项和为n S ,且n S 是1与n a 的等差中项. (1)求数列{}n a 的通项公式;(2)求数列12n n a a +⎧⎫⎨⎬⎩⎭的前n 项和n T . 20.(本题满分10分)已知函数x a x x x f ln 2)(2+-= )(R a ∈.(1)当1=a 时,求函数)(x f 在))1(,1(f 处的切线方程; (2)当0>a 时,求函数)(x f 的单调区间.2019江苏高职单招院校单独招生联合测试真题卷数学答案一、1.D 解析:由题意知,3log 2,9m m =∴=.故选D .2.A 解析:从6个球中随机取出一个小球共有6种方法,其中号码为偶数的为1,3,5,共三种,由古典概型的概率公式可得,其号码为偶数的概率是3162P ==.故选A . 3.B 解析:由2||T πω=得,22πωπ==.故选B. 4.C 解析:∵2BD DC =u u u r u u u r ,∴2()AD AB AC AD -=-u u u r u u u r u u u r u u u r ,∴322AD AB AC a b =+=+u u u r u u u r u u u r r r ,∴1233AD a b =+u u u r r r.故选C .5.C 解析:1,13,2,234,338,4s k s k s k s k ==≤→==≤→==≤→==,不满足43k =≤,输出s =8.故选C .6.A 解析:作出可行域如图所示,由2z y x =-,得2yx z =+,由图可知,当直线2y x z =+过可行域内的点(11)C ,时,直线在y 轴上的截距最大,即121z =-=-.故选A .7.B 解析:∵第一象限的点()a b ,在直线210x y +-=上,∴210a b +-=,即21a b +=,且00a b >,>,∴()12122222()25529b a b aa b a b a b a b a b+=++=++≥+⋅=.故选B . 8.D 解析:由题意可得,7173216112244x x m x -=⇒==-=-=-,.故选D .9.A 解析:设等差数列{}n a 的公差为d ,则51545+152S a d ⨯==,1010,1d d ∴==,则101109101045552S a d ⨯=+=+=.故选A. 10.C 解析:由题意,圆22(1)1x y ++=的圆心为(0,1)-,半径为1r =,圆心(0,1)-关于直线0x y +=的对称点为(1,0),则圆C 的圆心为(1,0),半径为1,圆C 的标准方程为22(11x y -+=).故选C.二、11解析:由题意得,42i (42i)(1i)13i 1i (1i)(1i)z ---===-++-,故z =12.解析:由题意得2210y ⨯-⨯=,解得4y =,则()24,8a b +=v v ,故2a b +==v v13解析:因为该三棱锥是一个底面是等边三角形的直棱锥,所以该三棱锥的体积为1112233322ABC V S PA ∆=⋅=⨯⨯⨯⨯=14.0.3 解析:在区间[30,60)的频数为3+2+1=6,所以频率为630.32010P ===. 15.已知函数()[]2()211,1,3f x x a x x =-++∈图象上任意两点连线都与x 轴不平行,则实数a 的取值范围是 .15.1522∞∞U (-,][,+) 解析:由题意知函数()f x 在[]1,3上是单调函数,所以对称轴2112a +≤或2132a +≥,解得12a ≤或52a ≥,即实数a 的取值范围是1522∞∞U (-,][,+). 三、16.解析:(1)cos 5α=Q ,(0,)2πα∈,sin 5α∴==.(2分)sin()sin cos cos sin (44425510πππαααα+=+=+=.(4分)(2)由(1)得,sin tan 2cos ααα==,则22tan 44tan21tan 143ααα===---.(6分) 17.证明:(1)∵EF 是SAC ∆的中位线, ∴EF ∥AC .又∵EF ⊄平面ABC ,AC ⊂平面ABC , ∴EF ∥平面ABC .(3分)(2)∵SA SC =, AD DC =,∴SD ⊥AC . ∵BA BC =, AD DC =,∴BD ⊥AC .又∵SD ⊂平面SBD ,BD ⊂平面SBD ,SD DB D =I , ∴AC ⊥平面SBD ,(5分) 又∵SB ⊂平面SBD , ∴AC ⊥SB .(6分)18.解析:(1) 因为C 的焦点在x 轴上且短轴为2,故可设椭圆C 的方程为1222=+y ax (1>a ),因为点在椭圆C 上,所以14312=+a, (2分) 解得42=a , 所以,椭圆C 的方程为1422=+y x .(4分) (2) 设12,PF x PF y ==,由椭圆的定义得,4x y +=,由余弦定理得,2222cos 60412x y xy c +-︒==,即2212x y xy +-=,则2[()2]12x y xy xy +--=,解得,43xy =,(6分)从而得12114sin 6022323PF F S xy ∆=︒=⨯⨯=1sin 602S xy =︒=33.(8分) 19.解析:(1)由等差中项可得1n a =+,即24(1)n n S a =+,当1n =时,11a =;当2n ≥时,2114(1)n n S a --=+,又24(1)n n S a =+,由1n n n a S S -=-得,2211444(1)(1)n n n n n a S S a a --=-=+-+,(2分)化简得,221142121n n n n n a a a a a --=++---,221121210n n n n a a a a ---+---=,221121)(21)0n n n n a a a a ---+-++=(,即2211)(1)0n n a a ---+=(,则11()(2)0n n n n a a a a --+--=,又10,2n n n a a a ->∴-=Q ,(4分)故{}n a 是以1为首项,2为公差的等差数列,即21na n =-.当1n =时,11a =满足上式.综上,数列{}n a 的通项公式是21n a n =-.(6分) (2)12211(21)(21)2121n n a a n n n n -==--+-+Q,(8分) 111111(1)()()1335212121n T n n n ∴=-+-++-=--++L .(10分) 20.解析:(1)当1=a 时,,122)('xx x f +-=则,1)1(',1)1(=-=f f所以切线方程为11-=+x y .即2-=x y .(3分))0(2222)('22>+-=+-=x xax x x a x x f )(,令0)('=x f ,0 222=+-a x x , ①当,084≤-=∆a 即21≥a 时,,0)('≥x f ,函数)(x f 在),(∞+0上单调递增;(5分) ②当,084>-=∆a 且0>a ,即210≤<a 时,由,0 222=+-a x x ,得22112,1ax -±=, 由,0)('>x f ,得22110a x --<<或2211ax -+>;(7分) 由,0)('<x f ,得x a<--22112211a -+<.(9分) 综上,当21≥a 时,)(x f 的单调递增区间是),(∞+0; 当210<<a 时,)(x f 的单调递增区间是)2211,0(a --,),2211(+∞-+a ; 单调递减区间是)2211,2211(aa -+--.(10分)2019江苏高职单招院校单独招生联合测试真题卷数学注意事项考生在答题前请认真阅读本注意事项及各题答题要求1.本试卷包含选择题(第1题~第10题,共10题40分)、填空题(第11题~第15题,共5题20分)和解答题(第16题~第20题,共5题40分),满分100分。
2019年吉林省高职高专院校单独招生统一考试数学试卷

绝密★启用前2019年吉林省高职高专院校单独招生统一考试数 学 试 题一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求,把答案涂在答题卡相应的位置上。
1.已知全集U={-1,1,3,5,7},集合A ={-1,1,3},B ={5},则C U A ∪B 是( )A .{1,3}B . {5,7}C .{3,5,7}D .{-1,1}2.“x =1”是“x 2=1”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D . 既不充分也不必要条件3.直线√3x −y +1=0的斜率是( ) A. 1 B. -1 C.3 D. -34.已知d c b a >>, ,那么下列不等式成立的是( )A .bc ac >B .bd ac >C .d b c a ->-D .d b c a +>+5.如果直线 a ‖平面α,直线b ⊂α,则直线 a 与b 的位置关系是( )A .平行B .异面C .平行或异面D .相交6.观察下列数的特点,1,1,2,3,5,8,x ,21,34,55,……中,其中x 为( )A .12B .13C .14D .157.已知圆的方程()()51222=++-y x ,它的圆心所在的象限是( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限8. 设向量a=(x ,2),b=(-2,4),且a ⊥b ,则x=( )A .4B .1C .-1D .-49.一个盒子中有20张奖券,其中一等奖2张,二等奖4张,三等奖8张,小明从盒子中任取一张奖券,小名中奖的概率是( )A .12B .35C .710D .4510. 双曲线1162522=-y x ,则它的渐近线方程为( )A . 4x ±5y =0B .3x ±5y =0C . 5x ±3y =0D .5x ±4y =011.已知a =0.32,b =log 20.3,c =20.3,则a,b,c 之间的大小关系是( )A. a <c <bB. a <b <cC. b <c <aD. b <a <c12.如图所示的4个图象中,与所给3件事吻合最好的顺序(其中s 表示离开家的距离,t 表示离开家的时间)为 ( )① 我离开家不久,发现自己把作业本忘在家里了,于是立刻返回家里取了作业本再上学; ② 我骑着车一路以常速行驶,只是在途中遇到一次交通堵塞,耽搁了一些时间; ③ 我出发后,心情轻松,缓缓行进,后来为了赶时间开始加速。
【2019】年全国普通高等学校运动训练、民族传统体育专业单招考试数学试卷含答案

2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试 数学试卷一、选择题:本大题共10小题,每小题6分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合M =x │x >―1,N ={x |x 2>1},则M ∩N =( )A.{x |x >―1}B. x │x >―1 或 {x |x >1}C. {x |x >1}D. {x |―1<x <1}2.已知向量a =(1,2),b =(1,-3),则|3a +b |=( )3.点(1,-1)到直线x ―2y ―8=0的距离是( )4.已知( )5.若2x +5>14,则的取值范围是( )A.(-7,+∞)B.(7,+∞)C.(-3,+∞)D.(3,+∞)6.已知圆锥的母线长为4,底面周长为2π,该圆锥的表面积是( )A. 4πB. 5πC. 8πD. 9π7.从1,2,3,4,5这5个数中,任取2个不同的数,其和为偶数的概率是( )A .34 B. 35 C . 12 D. 258.记等差数列{a n }的前n 项和为S n ,若a 5+a 6+a 7=15,则S 11=( )A.110B.80C.55D.309.若方程x 2+y 2+4ax ―2y +5a =0表示的曲线是圆,则a 的取值范围是( )A.(14,1)B. (―1,―14)C.( ―∞,14 )∪(1,+∞)D. ( ―∞,―1 )∪(―14,+∞)10.函数f (x )=sin x cos x +cos 2x 的最大值是 ( )二、填空题:本题共6小题,每小题6分,共36分.的系数是_________.(用数字作答)12.双曲线x 24―y 2=1的离心率是_________.13.已知{a n }是各项均为正数的等比数列,且a 3,3a 2,a 4,成等差数列,则的公比为 .14.在ΔABC 中,AC =2,BC =3,AB =4,则cos ∠ACB =_________.15.已知二次函数f (x )=ax 2―3a 2x ―1,若f (x )在(1,+∞)单调递增,则a 的取值范围是_________.16.已知正四棱柱ABCD ―A 1B 1C 1D 1的底面边长为2,点P 是底面A 1B 1C 1D 1的中心,且点P 到直线AB 的距离是3,则ΔPAC 的面积为_________.三、解答题:本题共3小题,每小题18分,共54分.解答应写出文字说明、证明过程或演算步骤.【淘宝店学子之家精品店出品haiwang103】17.(18分)A ,B ,C 成等差数列.(1)求B ;(2.18.(18分)已知椭圆c :x 2a 2+y 2b 2=1(a >b >0) 4.(1)求C 的方程(2)过点(-3,0)且斜率k 的直线l 与椭圆C 交于A ,B 两点,O 为坐标原点,当AO ⊥BO 时,求k 的值。
2019年陕西省普通高校职业教育单独招生考试数学答案

数学试题答案及评分参考 第1页(共4页)绝密★考试启用前2019年陕西省普通高校职业教育单独招生考试数学试题答案及评分参考二、填空题(每小题5分,共20分)13. 22-14. 1(,)4-∞- 15. 1816. 70 三、解答题(共70分)17.(本小题满分10分)解: (1) 令212019n a n =-=,得 1010n =+∈N ,(2分) 所以 2019是数列的第1010项.(4分)(2) 11a =. 当2n ≥时,1(21)[2(1)1]2n n a a n n --=----=可见 {}n a 是首项11a =,公差 2d =的等差数列.(7分)21()[1(21)]22n n n a a n n S n ++-===.(10分)18. (本小题满分12分)解:(1)由()0f α=,得 4cos 3sin 0αα-= ○1 又22sin cos 1αα+= ○2 (2分)由 ○1,○2及 α为第三象限的角,得 4sin 5α=- ,(4分)由 ○1得sin 4tan cos 3ααα==.(6分)(2)当3πα=时,()23sin f x x =-,数学试题答案及评分参考 第2页(共4页)因为sin [1,1]x ∈-,所以 当1sin -=x 即322x k ππ=+时, ()f x 取最大值5, x 的取值集合为⎭⎬⎫⎩⎨⎧∈+=z k k x x ,232|ππ , (10分) 当1sin =x ,即22x k ππ=+时,()f x 取最小值1-, x 的取值集合为⎭⎬⎫⎩⎨⎧∈+=z k k x x ,22|ππ.(12分)19. (本小题满分12分)解一:(1) (cos ,sin ), (sin ,cos )a b θθθθ==-,(cos sin ,sin cos )c a b λθλθθλθ=+=-+, (cos sin ,sin cos )d a b λθλθθλθ=-=+-,(2分)(cos sin )(cos sin )(sin cos )(sin cos )c d θλθθλθθλθθλθ⋅=-⋅+++⋅-21λ=- ,(4分) 若c d ⊥,则0c d ⋅=及 0λ>,得 1λ=.(6分)(2)由(1) (cos sin ,sin cos )c θλθθλθ=-+,(cos sin ,sin cos )d θλθθλθ=+-,222(cos sin )(sin cos )c θλθθλθ=-++21λ=+ ,222(cos sin )(sin cos )d θλθθλθ=++-21λ=+,(10分) 易见 22cd =. 从而 c d =.(12分) 解二: 1a a b b ⋅=⋅=,0a b b a ⋅=⋅=.(3分)数学试题答案及评分参考 第3页(共4页)(1) 若c d ⊥,则0c d ⋅= 以及22()()1c d a b a b a a b b λλλλ⋅=+⋅-=⋅-⋅=-,得21λ=. 又由 0λ>,得 1λ=.(6分)(2) 222()()21c c c a b a b a a a b b b λλλλλ=⋅=+⋅+=⋅+⋅+⋅=+ , (8分)222()()21d d d a b a b a a a b b b λλλλλ=⋅=-⋅-=⋅-⋅+⋅=+ , (10分)由此知,22cd =,从而 c d =.(12分)20. (本小题满分12分) (1) 证明:如图,四棱柱1111D C B A ABCD -为正四棱柱,⊥∴DC 平面C C BB 11 , (3分)又 ⊂DC 平面MDC ,故平面⊥MDC 平面C C BB 11. (6分) (2)解: 正四棱柱1111D C B A ABCD -中,311==AB D A ,M 到平面D D AA 11的距离等于3=BA ,(9分)1111133M AA D AA D V S AB -∆=⋅=.(12分)21. (本小题满分12分)解:(1)设该企业生产电子元件产量为Q ,聘用劳动力人数为x ,购买设备台数为y ,由题意知20Q xy =,15256000x y +=.(3分)所以 1(12003)5y x =-,数学试题答案及评分参考 第4页(共4页)故21()20(12003)4(12003)4800125Q x x x x x x x =⨯-=-=-.即该企业生产电子元件产量与聘用劳动力人数的函数表达式为:2()480012Q x x x =-.(6分)(2)由(1)知,2()12(400)Q x x x =--212(200)480000x =--+.(10分)故当200x =,1(1200600)1205y =-=时,max 480000Q =, 即该企业应聘用200个劳动力,购买120台设备,产量达到最大值,最大值为480000. (12分)22. (本小题满分12分)解:(1)由于 频率=频数/样本容量,故 样本容量=频数/频率=1200.05=, 所以 200.153a =⨯=,从而 2015932b =----=, 进而 0.120bc ==. (4分)(2)由频率分布表及(1)知,产品的质量指标在95以上的频率为70%,由此可推断产品的质量指标在95以上的概率大约在70%左右,所以认为该产品不符合“质量指标值不低于95的产品至少占全部产品的%80”的规定. (8分) (3)样本平均数为1(180590910031102120)10020x =⨯+⨯+⨯+⨯+⨯=, (10分)样本方差为2222221(1(80100)5(90100)9(100100)3(110100)2(120100))20100,s =⨯-+⨯-+⨯-+⨯-+⨯-=样本标准差为10s =,估计该产品总体的质量指标的平均数约为100,标准差约为10. (12分)。
2019单招数学试卷 (1)
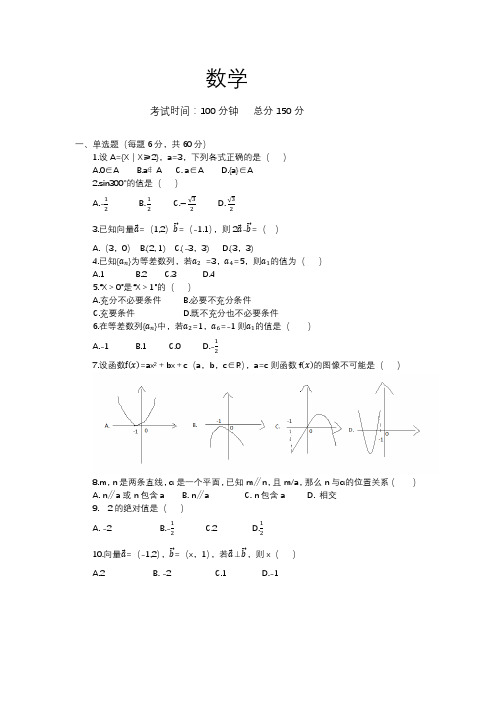
数学考试时间:100分钟总分150分一、单选题(每题6分,共60分)1.设A={X|X≥2},a=3,下列各式正确的是()A.0∈AB.a∉AC. a∈AD.{a}∈A2.sin300°的值是()A.-12B.12C.−√32D.√323.已知向量a⃗=(1,2)b⃗⃗=(-1.1),则2a⃗-b⃗⃗=()A.(3,0)B.(2, 1)C.(-3,3)D.(3,3)4.已知{a n}为等差数列,若a2=3,a4=5,则a1的值为()A.1B.2C.3D.45.“X>0”是“X>1”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.在等差数列{a n}中,若a2=1,a6=-1则a1的值是()A.-1B.1C.0D.-127.设函数f(x)=ax²+bx+c(a,b,c∈R),a=c则函数f(x)的图像不可能是()8.m,n是两条直线,α是一个平面,已知m∥n,且m/a,那么n与α的位置关系()A. n∥a或n包含aB. n∥aC. n包含aD. 相交9. 2的绝对值是()A. -2B.-12C.2 D.1210.向量a⃗=(-1,2),b⃗⃗=(x,1),若a⃗⊥b⃗⃗,则x()A.2B. -2C.1D.-1二、填空题(每题10分,共30分)11.根据程序图输出的的S值为()12.已知复数Z=3+4i(i为虚数单位),则|Z|=()13.sin60°=()三、解答题(每题20分,共60分)14.已知函数f(x)=x²-4x,x∈【1,5】,则f(x)的最大值和最小值是多少。
15.已知全集U={1,2,3,4,5},其子集A={1,3},B={2,5}求:(1)∁uA;(2)A∪B;( 3 ) A∩B;( 4 ) (∁uA)∪(∁uB);16.画三视图。
2019年浙江省单独考试招生文化考试数学(含答案)

=-2.
29.(8分)
解:(1)由已知得∠A=120°,
由正弦定理得 = ,即 ,
C=2.
(2)由已知得S△ABN= S△ABC,
S△ABC= acsin30°=1×2 ×2× = ,
S△ABN= .
30.(9分)
解:(1)由已知得圆C的标准方程为(x+1)2+(y-1)2=2
11.圆的一般方程为 ,则其圆心和半径分别为
A. B.
C. D.
12.已知100张奖券共有2张一等奖、5张二等奖、10张三等奖,现从中任取一张,中奖概率是
A. B.
C. D.
13. 、 、 为实数,则下列各选项中正确的是
A. B.
C. D.
14. 的值为
A. B.
C. D.
15.双曲线 的实轴长为10,焦距为26,则双曲线的渐近线方程为
(1)求正三棱锥 的全面积;(4分)
(2)线段 、 、 的中点分别为 、 、 ,求二面角 的余弦值.(6分)
34.(本题满分10分)体育场北区观众席共有10500个座位.观众席座位编排方式如图所示,由内而外依次记为第1排、第2排、…….从第2排起,每一排比它前一排多10个座位,且最后一排有600个座位.
31.(本题满分9分)已知 、 为第二象限角,且满足 , 求:
(1) ;(5分)
(2)函数 的最大值.(4分)
32.(本题满分9分)已知抛物线的顶点在原点,焦点坐标为 .
(1)求抛物线的标准方程;(3分)
(2)若抛物线上点 到焦点的距离为4,求点 的坐标.(6分)
33.(本题满分10分)如图,正三棱锥 的侧棱长为 ,底面边长为 .
2019年浙江省高职考单招单考数学试卷(附答案)

2019浙江省高职单独考试数学试卷(满分150分,考试时间120分钟)一、单项选择题(本大题共20小题,1―10小题每小题2分,11―20每小题3分,共50分.)1. 已知集合A ={-1,0,1},集合B ={-3,-1,1,3},则A ∩B =( ) A. {-1,1} B. {-1} C. {1}D. ∅2. 不等式x 2-4x ≤0的解集为( )A. [0,4]B. (0,4)C. [-4,0)∪(0,4]D. (-∞,0]∪[4,+∞)3. 函数f (x )=ln (x −2)+1x −3的定义域为( ) A. (2,+∞) B. [2,+∞) C. (-∞,2]∪[3,+∞)D. (2,3)∪(3,+∞)4. 已知平行四边形ABCD ,则向量⃗AB +⃗B C =¿( ) A. ⃗BDB. ⃗DBC. ⃗ACD. ⃗C A5. 下列函数以π为周期的是( ) A .y =sin (x −π8)B. y =2cos xC. y =sin xD. y =sin2x6. 本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法的总数是( ) A. 400B. 380C. 190D. 407. 已知直线的倾斜角为60°,则此直线的斜率为( ) A.−√33B. −√3C. √3D. √338. 若sin α>0且tan α<0,则角α终边所在象限是( ) A. 第一象限 B. 第二象限 C. 第三象限D.第四象限9. 椭圆标准方程为x 22t +4+y 24−t=1,一个焦点为(-3,0),则t 的值为( ) A. -1 B. 0 C. 1 D. 310.已知两直线l 1、l 2分别平行于平面β,则两直线l 1、l 2的位置关系为( ) A. 平行 B. 相交 C. 异面 D. 以上情况都有可能11.圆的一般方程为x 2+y 2-8x +2y +13=0,则其圆心和半径分别为( ) A. (4,-1),4 B. (4,-1),2 C. (-4,1),4 D. (-4,1),212.已知100张奖券中共有2张一等奖、5张二等奖、10张三等奖,现从中任取一张,中奖概率为( ) A.110000B.150C.3100D.1710013. a 、b 、c 为实数,则下列各选项中正确的是( ) A. a -b <0⇔a -c <b -c B. a -b >0⇔a >-b C . a -b >0⇔-2a >-2b D . a >b >c >0⇔a b >a c 14.sin1050°的值为( ) A. √22B. √32C.−12D.1215. 双曲线x2a2−y2b2=1的实轴长为10,焦距为26,则双曲线的渐渐近线方程为( )A. y=±135x B. y=±125x C. y=±512x D. y=±513x16.方程y=√x2−4x+4所对应曲线的图形是( )17.若角α的终边经过点(4,-3),则cos2α的值为( )A. 725B.−1625C.−725D.162518.动点M在y轴上,当它与两定点E(4,10)、F(-2,1)在同一条直线上时,点M的坐标是( )A. (0,6)B. (0,5)C. (0,4)D. (0,3)19.“2019k2−1=1”是“k=1”的( )A. 充分不必要条件B. 必要不充分条件C. 充分且必要条件D. 既不充分也不必要条件20.某旅游景点有个人票和团队票两种售票方式,其中个人票每人80元,团队票(30人以上含30人)打七折. 按照购票费用最少原则,建立实际游览人数x与购票费用y(元)的函数关系,以下正确的是()A. y={80x,0≤x<24,x∈N1344,24≤x≤30,x∈N56x,x>30,x∈N B. y={80x,0≤x<21,x∈N1680,21≤x≤30,x∈N56x,x>30,x∈NC. y={80x,0≤x<24,x∈N1920,24≤x≤30,x∈N56x,x>30,x∈N D. y={80x,0≤x<21,x∈N2400,21≤x≤30,x∈N56x,x>30,x∈N二、填空题(本大题共7小题,共28分)21.等比数列14,1,4,16,…的第5项是_____.22.化简:cos(π+θ)tan(π-θ)=_____.23.(2x-y)6展开式的第5项为_____.24.圆柱的轴截面是边长为3的正方形,则圆柱的体积等于_____.25.如图所示,函数y=f(x)的图象关于直线x=8对称,则f(6)_____f(13)(填,“>”、“<”或“=”).26.正数x、y满足lg x+lg y=2,则x+y的最小值等于_____.27.已知椭圆中心在原点且对称轴为坐标轴,它与双曲线x2−y 23=1有且仅有两个公共点,它们的离心率之积为1,则椭圆标准方程为_______________.三、解答题(本大题共8小题,共72分)(解答应写出文字说明及演算步骤)28.(本题满分7分)计算:sin π2−l g1000+0.25−12÷5√32−3!+√(−5)2.29.(本题满分8分)在△ABC中,∠B=∠C=30°,a=2√3.(1)求c;(4分)(2)N为AC中点时,求△ABN的面积.(4分)30.(本题满分9分)已知圆C的圆心为(-1,1),半径为√2.(1)写出圆C的标准方程;(3分)(2)试判断直线x+y-1=0与圆C的位置关系;若相交,求出两交点间的距离.(6分)31.(本题满分9分)已知α、β为第二象限角,且满足sinα=2√23,sinβ=35,求:(1)cos(α-β);(2)函数f (x)=cosαcos x+cosβsin x的最大值.(4分)32.(本题满分9分)已知抛物线的顶点在原点,焦点坐标为F(3,0).(1)求抛物线的标准方程(3分)(2)若抛物线上点M到焦点的距离为4,求点M的坐标.(6分)33.(本题满分10分)如图,正三棱锥P-ABC的侧棱长为2√3,底面边长为4.(1)求正三棱锥P-ABC的全面积;(4分)(2)线段P A、AB、AC的中点分别为D、E、F,求二面角D-EF-A的余弦值.(6分)34.(本题满分10分)体育场北区观众席共有10500个座位. 观众席座位编排方式如图所示,由内而外依次记为第1排、第2排、……. 从第2排起,每一排比它前一排多10个座位,且最后一排有600个座位.(1)北区观众席共有多少排?(7分)(2)现对本区前5排的座位进行升级改造,改造后各排座位数组成数列{b n}. {b n}满足:①b1等于原第1排座位数的一半;②b n=b n-1+n2(n=2,3,4,5). 求第5排的座位数.(3分)35.(本题满分10分)电影《流浪地球》上映期间,一场电影的票价定为50元时,电影院满座,满座时可容纳600人. 若票价每提高5x(x∈N)元,售出票数就减少30x张.(1)若票价为60元,求实际售出的电影票数;(2分)(2)写出一场电影的票房收入R(元)与x的函数关系式;(3分)(3)已知放映一场电影所需的总成本为600(20-x)元,若不考虑其他因素,票价定为多少时,电影院能获得最大利润?(5分)答案一、单项选择题1. A2. A3. D4. C5. D6. C7. C8. B9. D 10. D 11. B 12. D 13. A 14. C 15.B16. A 17. A 18. C 19. B 20. B二、填空题21. 64 22. 23. 24. 25. > 26. 20 27. 或三、解答题28. -229.(1)2;(2)30.(1);(2)直线与圆相交,31.(1);(2)32.(1);(2)33.(1);(2)34.(1)21排;(2)254个35.(1)540张;(2);(3)票价定为85元时,电影院能获得最大利润。
