编译原理教程课后习题答案——第三章
清华版编译原理课后答案——第三章参考答案

第三章1、L(G[S])={ abc }2、L(G[N])={ n位整数或空字符串| n>0 }3、G[E]:E—>E+D | E-D | DD—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 94、L(G[Z])={ a n b n | n>0 }5、(1) 考虑不包括“0”的情况G[S]:S—>0S | ABC | 2 | 4| 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8考虑包括“0”的情况:G[S]:S—>AB | CB—>AB | CA—>0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>0 | 2 | 4 | 6 | 8(2)方法1:G[S]:S—> ABC | 2 | 4 | 6 | 8A—>1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9B—>AB | 0B | εC—>0 | 2 | 4 | 6 | 8方法2:G[S]:S—>AB | CB—> AB | 0B | C | 0A—> 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9C—>2 | 4 | 6 | 86、设<表达式>为E,<项>为T,<因子>为F,注:推导过程不能省略,以下均为最左推导(1) E => T => F => i(4) E => E+T => T+T => T*F+T => F*F+T => i*F+T => i*i+T => i*i+F => i*i+i(6) E => E+T => T+T => F+T => i+T => i+T*F => i+F*F => i+i*F => i+i*I7、<表达式><表达式>*<表达式><表达式>+<表达式>i i i<表达式><表达式>+<表达式>i <表达式>*<表达式>i i8、是有二义性的,因为句子abc 有两棵语法树(或称有两个最左推导或有两个最右推导)最左推导1:S => Ac => abc最左推导2:S => aB => abc9、(1)(2) 该文法描述了变量a 和运算符+、*组成的逆波兰表达式10、(1) 该文法描述了各种成对圆括号的语法结构(2) 是有二义性的,因为该文法的句子()()存在两种不同的最左推导:最左推导1:S => S(S)S => (S)S => ()S => ()S(S)S => ()(S)S => ()()S => ()()最左推导2:S => S(S)S => S(S)S(S)S => (S)S(S)S => ()S(S)S => ()(S)S => ()()S => ()()11、(1) 因为从文法的开始符E 出发可推导出E+T*F ,推导过程如下:E => E+T => E+T*F ,所以E+T*F 是句型。
编译原理练习答案蒋宗礼第三章

在整个分裂过程中,所有新结点均用不同的名字,保留 X 和 Y 为全图的唯一初态结点 和终态结点。至此,我们得到了一个非确定有限自动机M,
第二部分
例题与习题
重点与难点
重点:词法分析器的输入、输出,用于识别符号的状态转移图的构造,根据状态转移图实现 词法分析器。 难点:词法的正规文法表示、正规表达式表示、状态转移图表示,它们之间的转换。
l, d 初态 ① l
②
其它
终态
③
例 4 叙述下面的正规式描述的语言,并画出接受该语言的最简 DFA 的状态转换图。 * * (1|01) 0 【解】描述的语言是,所有不含子串 001 的 0 和 1 的串。
例 5 给定如下正规式 0(0|1)*1 (1) 写出相应的正规文法。 (2) 画出相应的状态转移图。 【解】 (1) 引入非终结符 S, A, S → 0(0|1)*1 →0A + + A →(0|1)*1→(ε | (0|1) )1→1| (0|1) 1→1| (0|1) (0|1)*1→1| 0A|1A 得到正规文法 G[S]: S 0A A 0A|1A|1 (2) (1)中给出的是一个右线性文法。 。 按照由右线性正规文法构造状态转换图的方法,构造相应的状态转移图如图 1
则(U|V) 、 (U·V)和(U)*也都是正规式,它们所表示的正规集分别为 L(U) ∪L(V)、 L (U) L (V)(连接积)和(L (U))*(闭包) 。 仅通过有限次使用上述三步骤定义的表达式才是∑上的正规式, 仅由这些正规式所表示 的字集才是∑上的正规集。 令 U、V 和 W 均为正规式,则下述关系成立: (1)U|V=V|U(交换律) (2)U|(V|W)=(U|V)W 或 U(VW)=(UV)W (结合律) (3)U(V|W)=UV|UW 或 (V|W)U=VU|WU(分配律) (4)ε U=Uε =U 若两个正规式所表示的正规集相同,则认为二者等价。 例如:b(ab)*=(ba)*b, (a|b)*=(a*b*)*。 注意: a*b*、(a|b)* 、(ab)* 、a*|b*相互都不等价,它们表示的含义如图所示
编译原理第三章答案

“编译技术”第三章作业3-1构造下列正规式相应的DFA:(1)1(0|1)*101(2)a((a|b)*|ab*a)*b解:由转换系统构造确定有穷自动机对状态重命名:DFA的状态转换图:(2)构造该正规式的装换系统:由转换系统构造确定有穷自动机对状态重命名:DFA的状态转换图:3-2 对下面的FA,将它确定化并最小化。
a解:由转换系统构造确定有穷自动机对状态重命名:DFA的状态转换图:最小化:初始划分={T0,T1,T2}{T0,T1,T2}a={T, Φ, Φ},所以划分为({ T},{Φ, Φ})即{T}3-3 给出下述文法所对应的正规式:S →0A|1BA→1S|1B→0S|0解:S→0A→01S→0A→01S→010A→0101S→0101OA→0101O1S…S→1B→10S→1B→10S→101B→1010S→10101B→101010S…所以可得正规式=(01|10)(01|10)*3-4 构造下述文法G[S]的自动机:S→A0S→A0|S1|0该自动机是确定的吗?若不确定,则对它确定化。
该自动机可识别的语言是什么?解:文法转换为自动机:因为是左线性文法,要增加一个开始状态X,并将开始符号S看成终态。
因为A经0可达到不同的状态,所以,该自动机为NFA。
确定化:对状态重命名:该自动机表达的语言用正规式表示为:00(0|10)*3-5试用有限自动机理论证明下列正规表达式是等价的。
(1)(a|ba)*b(2)(a*ba)*a*b解:(1)(2)因为最小化后,两者的状态图是一样的,都为:所以正规式(a|ba)*b和正规式(a*ba)*a*b是等价的。
编译原理课后习题答案+清华大学出版社第二版

用以引用非局部(包围它的过程)变量时,寻找该变量的地址。 DL: 动态链,指向调用该过程前正在运行过程的数据段基地址,用以过程执行结束释放
数据空间时,恢复调用该过程前运行栈的状态。 RA: 返回地址,记录调用该过程时目标程序的断点,即调用过程指令的下一条指令的地
编译程序大致有哪几种开发技术?
答案:
(1)自编译:用某一高级语言书写其本身的编译程序。 (2)交叉编译:A 机器上的编译程序能产生 B 机器上的目标代码。 (3)自展:首先确定一个非常简单的核心语言 L0,用机器语言或汇编语言书写出它的编
译程序 T0,再把语言 L0 扩充到 L1,此时 L0⊂ L1 ,并用 L0 编写 L1 的编译程序 T1,再把语 言 L1 扩充为 L2,有 L1 ⊂ L2 ,并用 L1 编写 L2 的编译程序 T2,……,如此逐步扩展下 去, 好似滚雪球一样,直到我们所要求的编译程序。 (4)移植:将 A 机器上的某高级语言的编译程序搬到 B 机器上运行。
(main).
答案: 程序执行到赋值语句 b∶=10 时运行栈的布局示意图为:
1
《编译原理》课后习题答案第二章
第 3题 写出题 2 中当程序编译到 r 的过程体时的名字表 table 的内 容。
name
kind
level/val
adr
size
答案:
题 2 中当程序编译到 r 的过程体时的名字表 table 的内容为:
盛威网()专业的计算机学习网站
2
《编译原理》课后习题答案第一章
合实现方案,即先把源程序翻译成较容易解释执行的某种中间代码程序,然后集中解释执行 中间代码程序,最后得到运行结果。
编译原理第三章练习题答案

编译原理第三章练习题答案编译原理第三章练习题答案编译原理是计算机科学中的重要课程之一,它研究的是将高级语言程序转化为机器语言的过程。
在编译原理的学习过程中,练习题是提高理解和应用能力的重要途径。
本文将为大家提供编译原理第三章的练习题答案,希望能够对大家的学习有所帮助。
1. 什么是词法分析?请简要描述词法分析的过程。
词法分析是编译过程中的第一个阶段,它的主要任务是将源程序中的字符序列划分为有意义的词素(token)序列。
词法分析的过程包括以下几个步骤:1)扫描:从源程序中读取字符序列,并将其转化为内部表示形式。
2)识别:根据预先定义的词法规则,将字符序列划分为不同的词素。
3)分类:将识别出的词素进行分类,如关键字、标识符、常量等。
4)输出:将分类后的词素输出给语法分析器进行进一步处理。
2. 什么是正则表达式?请给出一个简单的正则表达式示例。
正则表达式是一种用于描述字符串模式的工具,它由一系列字符和操作符组成。
正则表达式可以用于词法分析中的词法规则定义。
以下是一个简单的正则表达式示例:[a-z]+该正则表达式表示匹配一个或多个小写字母。
3. 请简要描述DFA和NFA的区别。
DFA(Deterministic Finite Automaton)和NFA(Nondeterministic Finite Automaton)是有限状态自动机的两种形式。
它们在词法分析中常用于构建词法分析器。
DFA是一种确定性有限状态自动机,它的状态转换是确定的,每个输入符号只能对应一个状态转换。
相比之下,NFA是一种非确定性有限状态自动机,它的状态转换是非确定的,每个输入符号可以对应多个状态转换。
4. 请简要描述词法分析器的实现过程。
词法分析器的实现过程包括以下几个步骤:1)定义词法规则:根据编程语言的语法规范,定义词法规则,如关键字、标识符、常量等。
2)构建正则表达式:根据词法规则,使用正则表达式描述不同类型的词素。
3)构建有限状态自动机:根据正则表达式,构建DFA或NFA来识别词素。
编译原理(龙书)答案第三章

3.3.2, 3.3.6, 3.3.7, 3.3.8, 3.3.9,3.6.3, 3.6.4, 3.6.53.7.1, 3.7.2, 3.7.33.8.1, 3.8.23.9.3《编译原理》(龙书)第三章答案3.3.2 描述下列正则表达式代表的语言。
a) a(a|b)*ab) ((ε|a)b*)*c) (a|b)*a(a|b)(a|b)d) a*ba*ba*ba*e) (aa|bb)*((ab|ba)(aa|bb)*(ab|ba)(aa|bb)*)*答案(a)由a开头并结尾的由a和b构成的字符串(b)由a和b构成的字符串(c)倒数第三位为a的由a和b构成的字符串(d)仅含3个b的由a和b构成的字符串(e)含有偶数个a和偶数个b的由a和b构成的字符串注意:请准确描述语言的性质而不是列举满足正则表达式的串3.3.6 写出满足下列定义的字符a) The first ten letters in either upper or lower caseb) The lowercase consonantsc) The “digits” in a hexadecimal numberd) The characters that can appear at the end of a legitimate English sentence答案(a)a-jA-J(b)a-j(c)0-9a-f(d).?!3.3.7 写出匹配字符串“\ 的正则表达式答案:\”\\3.6.3 对于图3.29表示的NFA,列出aabb的所有路径。
这个NFA能否接受aabb? 答案:aabb的所有路径01223 00111 012000 00000 01222 00011 00123存在路径1223和0123所以能接受aabb3.6.4 对于图3.30表示的NFA,列出aabb的所有路径。
这个NFA能否接受aabb? 答案:01012301012120301230301212030303232030303212303030321212由于存在03210这样的环,所以这里有无数种路径存在路径终止于3,所以能接受aabb3.6.5 给出以下NFA的Transition Table(a) 图3.29(b) 图3.30(c) 图3.26答案:3.7.1 把下列NFA转化为DFA(a)图3.26(b)图3.29(c)图3.30答案:(a)(b)注意:以上答案并不唯一,等价即可3.7.2 用算法3.22模拟NFA(输入为aabb)(a)图3.29(b)图3.30答案:F={3} 所以返回yesF={3},所以返回yes3.7.3 用算法3.23和3.20把下列正则表达式转换为DFAa) (alb)*b) (a*lb* )*c) ((ela)b*)*d) (alb)*abb(alb)*答案:a) NFAb) NFAc) NFAd) NFA注意:这道题要求大家按照算法构造NFA和DFA,有些同学的NFA没有完全按照算法构造。
编译原理第三版课后习题答案

编译原理第三版课后习题答案编译原理是计算机科学中的一门重要课程,它研究的是如何将高级程序语言转换为机器语言的过程。
而《编译原理》第三版是目前被广泛采用的教材之一。
在学习过程中,课后习题是巩固知识、提高能力的重要环节。
本文将为读者提供《编译原理》第三版课后习题的答案,希望能够帮助读者更好地理解和掌握这门课程。
第一章:引论习题1.1:编译器和解释器有什么区别?答案:编译器将整个源程序转换为目标代码,然后一次性执行目标代码;而解释器则逐行解释源程序,并即时执行。
习题1.2:编译器的主要任务是什么?答案:编译器的主要任务是将高级程序语言转换为目标代码,包括词法分析、语法分析、语义分析、中间代码生成、代码优化和目标代码生成等过程。
第二章:词法分析习题2.1:什么是词法分析?答案:词法分析是将源程序中的字符序列划分为有意义的词素(token)序列的过程。
习题2.2:请给出识别下列词素的正则表达式:(1)整数:[0-9]+(2)浮点数:[0-9]+\.[0-9]+(3)标识符:[a-zA-Z_][a-zA-Z_0-9]*第三章:语法分析习题3.1:什么是语法分析?答案:语法分析是将词法分析得到的词素序列转换为语法树的过程。
习题3.2:请给出下列文法的FIRST集和FOLLOW集:S -> aAbA -> cA | ε答案:FIRST(S) = {a}FIRST(A) = {c, ε}FOLLOW(S) = {$}FOLLOW(A) = {b}第四章:语义分析习题4.1:什么是语义分析?答案:语义分析是对源程序进行静态和动态语义检查的过程。
习题4.2:请给出下列文法的语义动作:S -> if E then S1 else S2答案:1. 计算E的值2. 如果E的值为真,则执行S1;否则执行S2。
第五章:中间代码生成习题5.1:什么是中间代码?答案:中间代码是一种介于源代码和目标代码之间的表示形式,它将源代码转换为一种更容易进行优化和转换的形式。
编译原理教程课后习题答案——第三章

第三章语法分析3.1 完成下列选择题:(1) 文法G:S→xSx|y所识别的语言是。
a. xyxb. (xyx)*c. xnyxn(n≥0)d. x*yx*(2) 如果文法G是无二义的,则它的任何句子α。
a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导,但它们对应的语法树相同(3) 采用自上而下分析,必须。
a. 消除左递 a. 必有ac归b. 消除右递归c. 消除回溯d. 提取公共左因子(4) 设a、b、c是文法的终结符,且满足优先关系ab和bc,则。
b. 必有cac. 必有bad. a~c都不一定成立(5) 在规范归约中,用来刻画可归约串。
a. 直接短语b. 句柄c. 最左素短语d. 素短语(6) 若a为终结符,则A→α·aβ为项目。
a. 归约b. 移进c. 接受d. 待约(7) 若项目集Ik含有A→α·,则在状态k时,仅当面临的输入符号a∈FOLLOW(A)时,才采取“A→α·”动作的一定是。
a. LALR文法b. LR(0)文法c. LR(1)文法d. SLR(1)文法(8) 同心集合并有可能产生新的冲突。
a. 归约b. “移进”/“移进”c.“移进”/“归约”d. “归约”/“归约”【解答】(1) c (2) a (3) c (4) d (5) b (6) b (7) d (8) d3.2 令文法G[N]为G[N]: N→D|NDD→0|1|2|3|4|5|6|7|8|9(1) G[N]的语言L(G[N])是什么?(2) 给出句子0127、34和568的最左推导和最右推导。
【解答】(1) G[N]的语言L(G[N])是非负整数。
(2) 最左推导:NNDNDDNDDDDDDD0DDD01DD012D0127NNDDD3D34NNDNDDDDD5DD56D568最右推导:NNDN7ND7N27ND27N127D1270127NNDN4D434NNDN8ND8N68D685683.3 已知文法G[S]为S→aSb|Sb|b,试证明文法G[S]为二义文法。
编译原理(清华大学-第2版)课后习题答案

编译原理(清华⼤学-第2版)课后习题答案第三章N=>D=> {0,1,2,3,4,5,6,7,8,9}N=>ND=>NDDL={a |a(0|1|3..|9)n且 n>=1}(0|1|3..|9)n且 n>=1{ab,}a nb n n>=1第6题.(1) <表达式> => <项> => <因⼦> => i(2) <表达式> => <项> => <因⼦> => (<表达式>) => (<项>)=> (<因⼦>)=>(i)(3) <表达式> => <项> => <项>*<因⼦> => <因⼦>*<因⼦> =i*i(4) <表达式> => <表达式> + <项> => <项>+<项> => <项>*<因⼦>+<项>=> <因⼦>*<因⼦>+<项> => <因⼦>*<因⼦>+<因⼦> = i*i+i (5) <表达式> => <表达式>+<项>=><项>+<项> => <因⼦>+<项>=i+<项> => i+<因⼦> => i+(<表达式>) => i+(<表达式>+<项>)=> i+(<因⼦>+<因⼦>)=> i+(i+i)(6) <表达式> => <表达式>+<项> => <项>+<项> => <因⼦>+<项> => i+<项> => i+<项>*<因⼦> => i+<因⼦>*<因⼦> = i+i*i第7题第9题语法树ss s* s s+aa a推导: S=>SS*=>SS+S*=>aa+a*11. 推导:E=>E+T=>E+T*F语法树:E+T*短语: T*F E+T*F直接短语: T*F句柄: T*F12.短语:直接短语:句柄:13.(1)最左推导:S => ABS => aBS =>aSBBS => aBBS=> abBS => abbS => abbAa => abbaa 最右推导:S => ABS => ABAa => ABaa => ASBBaa => ASBbaa => ASbbaa => Abbaa => a1b1b2a2a3 (2) ⽂法:S → ABSS → AaS →εA → aB → b(3) 短语:a1 , b1 , b2, a2 , , bb , aa , abbaa,直接短语: a1 , b1 , b2, a2 , ,句柄:a114 (1)S → ABA → aAb | εB → aBb | ε(2)S → 1S0S → AA → 0A1 |ε第四章1. 1. 构造下列正规式相应的DFA (1)1(0|1)*101NFA(2) 1(1010*|1(010)*1)*0NFA(3)NFA(4)NFA2.解:构造DFA 矩阵表⽰b其中0 表⽰初态,*表⽰终态⽤0,1,2,3,4,5分别代替{X} {Z} {X,Z} {Y} {X,Y} {X,Y,Z} 得DFA状态图为:3.解:构造DFA矩阵表⽰构造DFA的矩阵表⽰其中表⽰初态,*表⽰终态替换后的矩阵4.(1)解构造状态转换矩阵:{2,3} {0,1}{2,3}a={0,3}{2},{3},{0,1}{0,1}a={1,1} {0,1}b={2,2}(2)解:⾸先把M的状态分为两组:终态组{0},和⾮终态组{1,2,3,4,5} 此时G=( {0},{1,2,3,4,5} ) {1,2,3,4,5}a={1,3,0,5} {1,2,3,4,5}b={4,3,2,5}由于{4}a={0} {1,2,3,5}a={1,3,5}因此应将{1,2,3,4,5}划分为{4},{1,2,3,5}G=({0}{4}{1,2,3,5}){1,2,3,5}a={1,3,5}{1,2,3,5}b={4,3,2}因为{1,5}b={4} {23}b={2,3}所以应将{1,2,3,5}划分为{1,5}{2,3}G=({0}{1,5}{2,3}{4}){1,5}a={1,5} {1,5}b={4} 所以{1,5} 不⽤再划分{2,3}a={1,3} {2,3}b={3,2}因为 {2}a={1} {3}a={3} 所以{2,3}应划分为{2}{3}所以化简后为G=( {0},{2},{3},{4},{1,5})7.去除多余产⽣式后,构造NFA如下G={(0,1,3,4,6),(2,5)} {0,1,3,4,6}a={1,3}{0,1,3,4,6}b={2,3,4,5,6}所以将{0,1,3,4,6}划分为 {0,4,6}{1,3} G={(0,4,6),(1,3),(2,5)}{0,4,6}b={3,6,4} 所以划分为{0},{4,6} G={(0),(4,6),(1,3),(2,5)}不能再划分,分别⽤ 0,4,1,2代表各状态,构造DFA 状态转换图如下;b8.代⼊得S = 0(1S|1)| 1(0S|0) = 01(S|ε) | 10(S|ε) = (01|10)(S|ε)= (01|10)S | (01|10)= (01|10)*(01|10)构造NFA由NFA可得正规式为(01|10)*(01|10)=(01|10)+9.状态转换函数不是全函数,增加死状态8,G={(1,2,3,4,5,8),(6,7)}(1,2,3,4,5,8)a=(3,4,8) (3,4)应分出(1,2,3,4,5,8)b=(2,6,7,8)(1,2,3,4,5,8)c=(3,8)(1,2,3,4,5,8)d=(3,8)所以应将(1,2,3,4,5,8)分为(1,2,5,8), (3,4)G={(1,2,5,8),(3,4),(6,7)}(1,2,5,8)a=(3,4,8) 8应分出(1,2,5,8)b=(2,8)(1,2,5,8)c=(8)(1,2,5,8)d=(8)G={(1,2,5),(8),(3,4),(6,7)}(1,2,5)a=(3,4,8) 5应分出G={(1,2), (3,4),5, (6,7) ,(8) }去掉死状态8,最终结果为 (1,2) (3,4) 5,(6,7) 以1,3,5,6代替,最简DFA为b正规式:b*a(da|c)*bb*第五章1.S->a | ^ |( T )(a,(a,a))S => ( T ) => ( T , S ) => ( S , S ) => ( a , S) => ( a, ( T )) =>(a , ( T , S ) ) => (a , ( S , S )) => (a , ( a , a ) ) S=>(T) => (T,S) => (S,S) => ( ( T ) , S ) => ( ( T , S ) , S ) => ( ( T , S , S ) , S ) => ( ( S , S , S ) , S )=> ( ( ( T ) , S , S ) , S ) => ( ( ( T , S ) , S , S ) , S ) =>( ( ( S , S ) , S , S ) , S ) => ( ( ( a , S ) , S , S ) , S ) => ( ( ( a , a ) , S , S ) , S ) => ( ( ( a , a ) , ^ , S ) , S ) => ( ( ( a , a ) , ^ , ( T ) ) , S )=> ( ( ( a , a ) , ^ , ( S ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , S ) => ( ( ( a , a ) , ^ , ( a ) ) , a )S->a | ^ |( T )T -> T , ST -> S消除直接左递归:S->a | ^ |( T )T -> S T’T’ -> , S T’ | ξSELECT ( S->a) = {a}SELECT ( S->^) = {^}SELECT ( S->( T ) ) = { ( }SELECT ( T -> S T’) = { a , ^ , ( }SELECT ( T’ -> , S T’ ) = { , }SELECT ( T’ ->ξ) = FOLLOW ( T’ ) = FOLLOW ( T ) = { )}构造预测分析表分析符号串( a , a )#分析栈剩余输⼊串所⽤产⽣式#S ( a , a) # S -> ( T )# ) T ( ( a , a) # ( 匹配# ) T a , a ) # T -> S T’# ) T’ S a , a ) # S -> a# ) T’ a a , a ) # a 匹配# ) T’,a) # T’ -> , S T’# ) T’ S , , a ) # , 匹配# ) T’ S a ) # S->a# ) T’ a a ) # a匹配# ) T’) # T’ ->ξ# ) ) # )匹配# # 接受2.E->TE’E’->+E E’->ξT->FT’T’->T T’->ξF->PF’F’->*F’F’->ξP->(E) P->a P->b P->∧SELECT(E->TE’)=FIRST(TE’)=FIRST(T)= {(,a,b,^)SELECT(E’->+E)={+}SELECT(E’->ε)=FOLLOW(E’)= {#,)}SELECT(T->FT’)=FIRST(F)= {(,a,b,^}SELECT(T’ —>T)=FIRST(T)= {(,a,b,^)SELECT(T’->ε)=FOLLOW(T’)= {+,#,)}SELECT(F ->P F’)=FIRST(F)= {(,a,b,^}SELECT(F’->*F’)={*}SELECT(F’->ε)=FOLLOW(F’)= {(,a,b,^,+,#,)}3. S->MH S->a H->Lso H->ξK->dML K->ξL->eHf M->K M->bLM FIRST ( S ) =FIRST(MH)= FIRST ( M ) ∪FIRST ( H ) ∪{ξ}∪{a}= {a, d , b , e ,ξ} FIRST( H ) = FIRST ( L ) ∪{ξ}= { e , ξ}FIRST( K ) = { d , ξ}FIRST( M ) = FIRST ( K ) ∪{ b } = { d , b ,ξ}FOLLOW ( S ) = { # , o }FOLLOW ( H ) = FOLLOW ( S ) ∪{ f } = { f , # , o }FOLLOW ( K ) = FOLLOW ( M ) = { e , # , o }FOLLOW ( L ) ={ FIRST ( S ) –{ξ} } ∪{o} ∪FOLLOW ( K )∪{ FIRST ( M ) –{ξ} } ∪FOLLOW ( M )= {a, d , b , e , # , o }FOLLOW ( M ) ={ FIRST ( H ) –{ξ} } ∪FOLLOW ( S )∪{ FIRST ( L ) –{ξ} } = { e , # , o }SELECT ( S-> M H) = ( FIRST ( M H) –{ξ} ) ∪FOLLOW ( S )= ( FIRST( M ) ∪FIRST ( H ) –{ξ} ) ∪FOLLOW ( S )= { d , b , e , # , o }SELECT ( S-> a ) = { a }SELECT ( H->L S o ) = FIRST(L S o) = { e }SELECT ( H ->ξ) = FOLLOW ( H ) = { f , # , o }SELECT ( K->ξ) = FOLLOW ( K ) = { e , # , o }SELECT ( L-> e H f ) = { e }SELECT ( M->K ) = ( FIRST( K ) –{ξ} ) ∪FOLLOW ( M ) = {d,e , # , o }SELECT ( M -> b L M )= { b }4 . ⽂法含有左公因式,变为S->C $ { b, a }C-> b A { b }C-> a B { a }A -> b A A { b }A-> a A’ { a }A’-> ξ{ $ , a, b }A’-> C { a , b }B->a B B { a }B -> b B’ { b }B’->ξ{ $ , a , b }B’-> C { a, b }5. <程序> --- S <语句表>――A <语句>――B <⽆条件语句>――C <条件语句>――D <如果语句>――E <如果⼦句> --FS->begin A end S->begin A end { begin }A-> B A-> B A’ { a , if }A-> A ; B A’-> ; B A’ { ; }A’->ξ{ end }B-> C B-> C { a } B-> D B-> D { if }C-> a C-> a { a }D-> E D-> E D’ { if }D-> E else B D’-> else B { else }D’->ξ{; , end } E-> FC E-> FC { if }F-> if b then F-> if b then { if }⾮终结符是否为空S-否A-否A’-是B-否C-否D-否D’-是E-否F-否FIRST(S) = { begin }FIRST(A) = FIRST(B) ∪FIRST(A’) ∪{ξ} = {a , if , ; , ξ} FIRST(A’) ={ ; , ξ}FIRST(B) = FIRST(C) ∪FIRST(D) ={ a , if }FIRST(C) = {a}FIRST(D) = FIRST(E)= { if }FIRSR(D’) = {else , ξ}FIRST(E) = FIRST(F) = { if }FIRST(F) = { if }FOLLOW(S) = {# }FOLLOW(A) = {end}FOLLOW(A’) = { end }FOLLOW(B) = {; , end }FOLLOW (C) = {; , end , else }FOLLOW(D) = {; , end }FOLLOW( D’ ) = { ; , end }FOLLOW(E) = { else , ; end }FOLLOW(F) = { a }S A A’ B C D D’ E F if then else begin end a b ;6. 1.(1) S -> A | B(2) A -> aA|a(3)B -> bB |b提取(2),(3)左公因⼦(1) S -> A | B(2) A -> aA’(3) A’-> A|ξ(4) B -> bB’(5) B’-> B |ξ2.(1) S->AB(2) A->Ba|ξ(3) B->Db|D(4) D-> d|ξ提取(3)左公因⼦(1) S->AB(2) A->Ba|ξ(3) B->DB’(4) B’->b|ξ(5) D-> d|ξ3.(1) S->aAaB | bAbB(2) A-> S| db(3) B->bB|a4(1)S->i|(E)(2)E->E+S|E-S|S提取(2)左公因⼦(1)S->i|(E)(2)E->SE’(3)E’->+SE’|-SE’ |ξ5(1)S->SaA | bB(2)A->aB|c(3)B->Bb|d消除(1)(3)直接左递归(1)S->bBS’(2)S’->aAS’|ξ(3)A->aB | c(4) B -> dB’(5)B’->bB’|ξ6.(1) M->MaH | H(2) H->b(M) | (M) |b消除(1)直接左递归,提取(2)左公因⼦(1)M-> HM’(2)M’-> aHM’ |ξ(3)H->bH’ | ( M )(4)H’->(M) |ξ7. (1)1)A->baB4)B->a将1)、2)式代⼊3)式1)A->baB2)A->ξ3)B->baBbb4)B->bb5)B->a提取3)、4)式左公因⼦1)A->baB2)A->ξ3)B->bB’4)B’->aBbb | b5)B->a(3)1)S->Aa2)S->b3)A->SB4)B->ab将3)式代⼊1)式1)S->SBa2)S->b3)A->SB4)B->ab消除1)式直接左递归1)S->bS’2)S’->BaS’ |ξ3)S->b4)A->SB5)B->ab删除多余产⽣式4)1)S->bS’(5)1)S->Ab2)S->Ba3)A->aA4)A->a5)B->a提取3)4)左公因⼦1)S->Ab4)A’-> A |ξ5)B->a将3)代⼊1)5)代⼊21)S->aA’b2)S->aa3)A->aA’4)A’-> A |ξ5)B->a提取1)2)左公因⼦1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξ5)B->a删除多余产⽣式5)1)S-> aS’2)S’->A’b | a3)A->aA’4)A’-> A |ξA A’S’S将3)代⼊4)1)S-> aS’2)S’->A’b | a3)A->aA ’4)A’-> aA’ |ξ3)S’->a4)S’->b5)A->aA ’6)A’-> aA’ |ξ对2)3)提取左公因⼦1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b5)A->aA ’6)A’-> aA’ |ξ删除多余产⽣式5)1)S->aS’2)S’->aS’’3)S’’->A’b|ξ4)S’->b第六章1S → a | ∧ | ( T )T → T , S | S解:(1) 增加辅助产⽣式 S’→#S#求 FIRSTVT集FIRSTVT(S’)= {#}FIRSTVT(S)= {a ∧ ( }= { a ∧ ( } FIRSTVT (T) = {,} ∪ FIRSTVT( S ) = { , a ∧ ( }求 LASTVT集LASTVT(S’)= { # }LASTVT(S)= { a ∧ )}LASTVT (T) = { , a ∧ )}(2)因为任意两终结符之间⾄多只有⼀种优先关系成⽴,所以是算符优先⽂法(3)a ∧( ) , #F 1 1 1 1 1 1g 1 1 1 1 1 1f 2 2 1 3 2 1g 2 2 2 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1f 3 3 1 3 3 1g 4 4 4 1 2 1(4)栈优先关系当前符号剩余输⼊串移进或规约#<·( a,a)# 移进#( <· a ,a)# 移进#(T <·, a)# 移进#(T,<· a )# 移进#(T,a ·> ) # 规约#(T,T ·> ) # 规约#(T =·) # 移进#(T) ·> #规约#T =·#接受4.扩展后的⽂法S’→#S# S→S;G S→G G→G(T) G→H H→a H→(S)T→T+S T→S(1)FIRSTVT(S)={;}∪FIRSTVT(G) = {; , a , ( }FIRSTVT(G)={ ( }∪FIRSTVT(H) = {a , ( }FIRSTCT(H)={a , ( }FIRSTVT(T) = {+} ∪FIRSTVT(S) = {+ , ; , a , ( }LASTVT(S) = {;} ∪LASTVT(G) = { ; , a , )}LASTVT(G) = { )} ∪LASTVT(H) = { a , )}LASTVT(H) = {a, )}LASTVT(T) = {+ } ∪LASTVT(S) = {+ , ; , a , ) }构造算符优先关系表因为任意两终结符之间⾄多只有⼀种优先关系成⽴,所以是算符优先⽂法(2)句型a(T+S);H;(S)的短语有:a(T+S);H;(S) a(T+S);H a(T+S) a T+S (S) H直接短语有: a T+S H (S)句柄: a素短语:a T+S (S)最左素短语:a(3)(4)不能⽤最右推导推导出上⾯的两个句⼦。
蒋立源编译原理第三版第三章习题与答案(修改后)
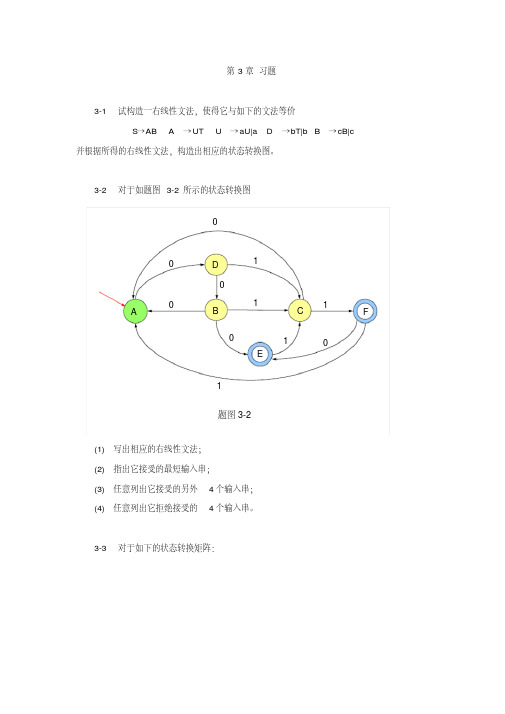
3-1 试构造一右线性文法,使得它与如下的文法等价 S→AB A → UT U → aU|a D →bT|b B → cB|c
并根据所得的右线性文法,构造出相应的状态转换图。
3-2 对于如题图 3-2 所示的状态转换图 0
0 0 A
D
1
0 1
B
C1
F
0
1
0
E
1 题图 3-2
(1) 写出相应的右线性文法; (2) 指出它接受的最短输入串; (3) 任意列出它接受的另外 4 个输入串; (4) 任意列出它拒绝接受的 4 个输入串。
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(3) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(3) 之 (a) 所示, 给各状态重新命名,即令:
[S]=1, [A]=2, [S,B]=3 且由于 3 的组成中含有 M的终态 B,故 3 为 DFAM′的终态。于是,所构造之 DFAM′的 状态转换矩阵和状态转换图如答案图 3-4-(3) 之(b) 及(c) 所示。
π0:{1,2}, {3}
( ⅱ) 为得到下一分划,考察子集 {1,2} 。因为
{2} b ={3}
但
{1}
b=
故 1 和 2 可区分,于是便得到下一分划
π1: {1}, {2}, {3}
此时子集已全部分裂,故最小化的过程宣告结束, M′即为状态数最小的 DFA。
(4) 将 NFA M确定化后得 DFA M′,其状态转换矩阵如答案图 3-4-(4) 之 (a) 所示, 给各状态重新命名,即令:
编译原理 第3章习题解答
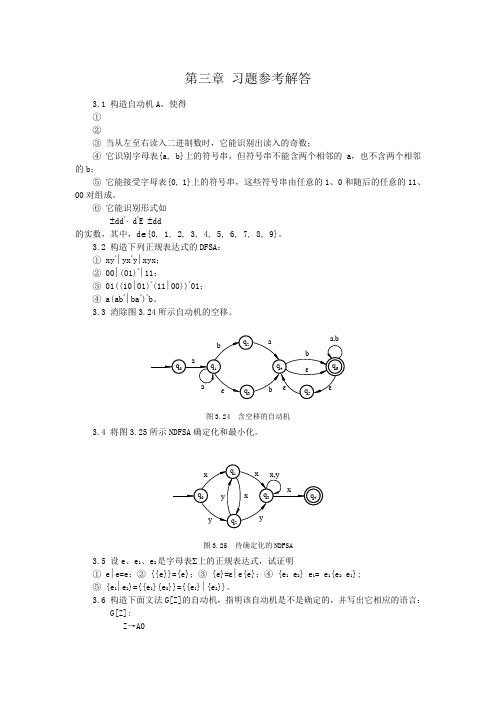
第三章习题参考解答3.1 构造自动机A,使得①②③当从左至右读入二进制数时,它能识别出读入的奇数;④它识别字母表{a, b}上的符号串,但符号串不能含两个相邻的a,也不含两个相邻的b;⑤它能接受字母表{0, 1}上的符号串,这些符号串由任意的1、0和随后的任意的11、00对组成。
⑥它能识别形式如±dd*⋅ d*E ±dd的实数,其中,d∈{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}。
3.2 构造下列正规表达式的DFSA:① xy*∣yx*y∣xyx;② 00∣(01)*∣11;③ 01((10∣01)*(11∣00))*01;④ a(ab*∣ba*)*b。
3.3 消除图3.24所示自动机的空移。
图3.24 含空移的自动机3.4 将图3.25所示NDFSA确定化和最小化。
图3.25 待确定化的NDFSA3.5 设e、e1、e2是字母表∑上的正规表达式,试证明① e∣e=e;② {{e}}={e};③ {e}=ε∣e{e};④ {e1 e2} e1= e1{e2 e1};⑤ {e1∣e2}={{e1}{e2}}={{e1}∣{e2}}。
3.6 构造下面文法G[Z]的自动机,指明该自动机是不是确定的,并写出它相应的语言: G[Z]:Z→A0A→A0∣Z1∣03.7 设NDFSA M=({x, y},{a, b},f, x, {y}), 其中,f(x, a)={x, y}, f(x, b)={y}, f(y, a)=∅, f(y, b)={x, y}。
试对此NDFSA 确定化。
3.8 设文法G[〈单词〉]:〈单词〉→〈标识符〉∣〈无符号整数〉 〈标识符〉→〈字母〉∣〈标识符〉〈字母〉∣〈标识符〉〈数字〉 〈无符号整数〉→〈数字〉∣〈无符号整数〉〈数字〉 〈字母〉→a ∣b 〈数字〉→1∣2试写出相应的有限自动机和状态图。
3.9 图3.29所示的是一个NDFSA A ,试构造一个正规文法G ,使得L(G)= L(A)。
编译原理课后习题答案+清华大学出版社第二版

注意:如果问编译程序有哪些主要构成成分,只要回答六部分就可以。如果搞不清楚, 就回答八部分。
第 2题
若 PL/0 编译程序运行时的存储分配策略采用栈式动态分配,并用动态链和静态链的方
式分别解决递归调用和非局部变量的引用问题,试写出下列程序执行到赋值语句 b∶=10
时运行栈的布局示意图。 var x,y; procedure p; var a; procedure q; var b;
begin (q)
答案:
PL/0 编译程序所产生的目标代码中有 3 条非常重要的特殊指令,这 3 条指令在 code 中的位置和功能以及所完成的操作说明如下:
INT 0 A 在过程目标程序的入口处,开辟 A 个单元的数据段。A 为局部变量的个数+3。 OPR 0 0
3
《编译原理》课后习题答案第二章
在过程目标程序的出口处,释放数据段(退栈),恢复调用该过程前正在运行的过程的数 据段基址寄存器 B 和栈顶寄存器 T 的值,并将返回地址送到指令地址寄存器 P 中,以使调 用前的程序从断点开始继续执行。
3
《编译原理》课后习题答案第一章
第6题
计算机执行用高级语言编写的程序有哪些途径?它们之间的主要区别是什么?
答案:计算机执行用高级语言编写的程序主要途径有两种,即解释与编译。 像 Basic 之类的语言,属于解释型的高级语言。它们的特点是计算机并不事先对高级语
言进行全盘翻译,将其变为机器代码,而是每读入一条高级语句,就用解释器将其翻译为一 条机器代码,予以执行,然后再读入下一条高级语句,翻译为机器代码,再执行,如此反 复。
编译原理(第三版)第3章课后练习及参考答案中石大版

第3章练习P47作业布置:P47 4 ,9,11,14(1)4、已知文法G[Z]:(1)Z::=aZb (2)Z::=ab写出L(G[Z])的全部元素解:L(G[Z])={a n b n,n>=1}9、考虑下面的上下文无关文法:S→SS* | SS+ | a(1)表明通过此文法如何生成串aa+a*,并为该串构造语法树(2)该文法生成的语言是什么?解:(1)推导过程见语法树。
语法树如下(2)该文法生成的语言为用递归逆波兰式表示的运算式。
逆波兰式是将运算对象写在前面,把运算符写在后面。
11、G[E]:E→T|E+T|E-TT→F|T*F|T/FF → (E)|i证明E+T*F 是它的一个句型,指出这个句型的所有短语、直接短语和句柄。
解:可为E+T*F 构造一棵语法树(见下图),所以它是句型。
从语法树中容易看出,E+T*F 的短语有:T*F 是句型E+T*F 的相对于T 的短语,也是相对于规则T →T*F 的直接短语。
E+T*F 是句型E+T*F 的相对于E 的短语。
句型E+T*F 的句柄(最左直接短语)是T*F 。
14、给出生成下述语言的上下文无关文法:(1){a n b n a m b m |n,m>=0}(2){1n 0m 1m 0n |n,m>=0}(3){WaW r |W 属于{0|a}*,W r 表示W 的逆}解:(1)所求文法为G[S]=({S,A},{a,b},P,S),其中P 为:S →AA A →aAb|ε (2)所求文法为G[S]=({S,A},{0,1},P,S),其中P 为: S →1S0|AA →0A1|ε(3)W 属于{0|a}*是指W 可以的取值为{ε,0,a,00,a0,aa0,00aa,a0a0,…}E E + T T * F如果W=aa0a00,则W r=00a0aa。
所求文法为G[S]=({S,P,Q},{0,a},P,S),其中P为:S 0S0|aSa|a。
编译原理第3章习题解答
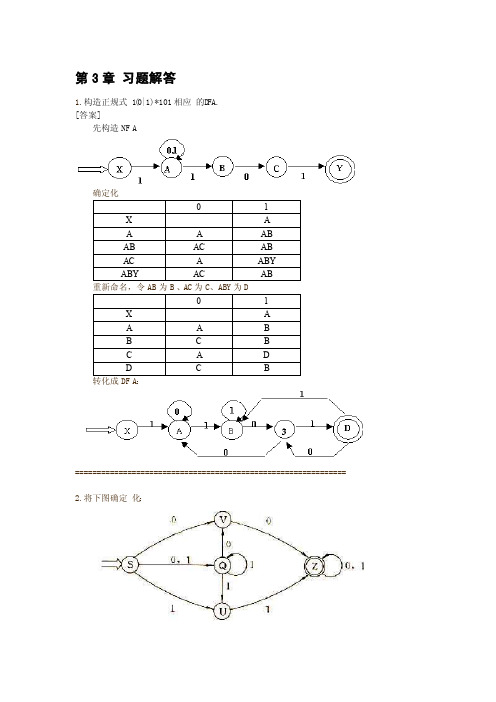
第3章习题解答1.构造正规式1(0|1)*101相应的D FA.[答案]先构造NFA确定化============================================================== 2.将下图确定化:[答案]E、Z为F。
转化为DFA:================================================================ 3.把下图最小化:[答案](1)初始分划得Π0:终态组{0},非终态组{1,2,3,4,5}对非终态组进行审查:{1,2,3,4,5}a {0,1,3,5}而{0,1,3,5}既不属于{0},也不属于{1,2,3,4,5} ∵{4} a {0},所以得新分划 (2)Π1:{0},{4},{1,2,3,5} 对{1,2,3,5}进行审查: ∵{1,5} b {4}{2,3} b {1,2,3,5},故得新分划 (3)Π2:{0},{4},{1, 5},{2,3} {1, 5} a {1, 5}{2,3} a {1,3},故状态2和状态3不等价,得新分划 (3)Π3:{0},{2},{3},{4},{1, 5} 这是最后分划了 (4)最小DFA :======================================= 4.构造一个D F A ,它接收Σ={0,1}上所有满足如下条件的字符串:每个1都有0直接跟在右边。
并给出该语言的正规式和正规文法。
[答案]按题意相应的正规表达式是0*(100*)*0* 构造相应的D F A ,首先构造N F A 为用子集法确定化可最小化,终态组为G 1={C, D},非终态组为G 2={S, A, B} 对于G2分析:f(S,0)=A, f(A,0)=A, 后继状态均属于G2 而f(B,0)=C, 后继状态属于G 1 将G2分割成G 21={S ,A}, G22={B}经检查DFA最小状态集有三个,可用S、B、D表示。
编译原理第3章习题及答案(文法和语言)

17.教材3.14题
18.教材3.16题
习题 第3章 文法和语言 参考答案
1.写一文法,使其语言是偶整数集合。
解:允许以0打头
G:N→+A|-A|A
A→DA|E
D→0|1|2|3|4|5|6|7|8|9
E→0|2|4|6|8
2.写一文法,使其语言是偶整数集合,但不允许由0打头。
Q→b
A→aAQBR|a
R→c
11.已知C语言的下标变量形如:
a[E][E]…[E]
按第10题要求的文法G2的形式写出下标变量文法。
解:G:S→aA
A→[EB
B→]A
B→]
12.设有文法G1:S → aBcA
S → aBdB
A → bA
A → aB
B → BdBຫໍສະໝຸດ → a将其改写成文法G2,使得对每个非终结符均无两个不同规则能导出相同的终结开头符。
解:二义性文法G:S→aS|Sa|a
∵句子aa存在两棵语法树:
∴G是二义性文法。
17.教材3.14题
解:(1) G1:S→CD (2) G2:S→1S0|A (3) G3:S→0S0|aSa|a
C→aCb|A→0A1|
D→aDb|
18.教材3.16题
解:(1) G1:A→aA|(2) G2:A→aA|aB (3) G3:A→aA|bB|cC|
A → a
将其改写成以下形式的文法G2,每条规则形如:
V → pX1X2…Xn
或V → q
其中V和Xi为非终结符,p和q为终结符。
11.已知C语言的下标变量形如:
a[E][E]…[E]
按第10题要求的文法G2的形式写出下标变量文法。
编译原理第3章课后习题答案

consonant -> [b-df-hj-np-tv-z] ctnvowels->(consonant*)(((a+)(consonant*))+)(((e+)(consonant*))+)
(((i+)(consonant*))+)(((o+)(consonant*))+)(((u+)(consonant*))+)
Dtran[I,b] =ε-closure(move(I,b))= ε-closure({5, 16})=G DFA D 的转换表 Dtran NFA 状态 {0,1,2,4,7} {1,2,3,4,6,7,8} {1,2,4,5,6,7} {1,2,4,5,6,7,9} {1,2,4,5,6,7,10,11,12,13,15} {1,2,3,4,6,7,8,12,13,14,15,17,18} {1,2,4,5,6,7, 12,13,15,16,17,18} {1,2,4,5,6,7, 9,12,13,15,16,17,18} {1,2,4,5,6,7, 10,11,12,13,15,16,17,18} 可得 DFA 的如下状态转换图: DFA 状态 A B C D E F G H I a B B B B F F F F F b C D C E G H G I G
编译原理第 2 版参考习题答案 (3 章) 第 3 章 词法分析 3.2.2 试描述下列正则表达式定义的语言 (1) a( a|b )*a 答: { aa, aaa, aba, aaaa, aaba, abaa, abba, ... },(按穷举法) 或以 a 开头和结尾,长度大于等于 2 的 a,b 串 (2) ( (ε|a)b*) )* 答: 由 a 和 b 组成的任意符号串 (自然语言描述)
编译原理第三章习题讲解

词法分析器的实现
实现词法分析器可以采用工具如Lex或Flex,这些工具可以根据词法规则自动生成相 应的词法分析器代码。
也可以手动编写词法分析器的代码,但需要熟练掌握正则表达式和有限自动机等相 关知识。
在实现过程中,需要注意处理输入缓冲区的管理、记号的输出和错误处理等问题。
02
习题二:语法分析
语法分析概述
03
中间代码生成的方法
包括解析、语义分析和控制流分析等步骤,最终将源代码转换为中间代
码。
代码优化技术
代码优化概述
通过各种技术手段对中间代码进行优化,以提高目标 代码的执行效率。
常见的代码优化技术
包括常量折叠、死代码消除、循环展开、内联函数等。
代码优化策略
根据程序特性和系统环境选择合适的优化策略,以达 到最佳的优化效果。
3
词法分析器通常采用正则表达式或有限自动机来 实现。
词法分析算法
01
词法分析算法通常采用“自顶向下”的分词方法,即从源代码 的开头开始,逐步识别出各个记号。
02
常用的分词算法有正向最大匹配法、逆向最大匹配法和双向最
大匹配法等。
在词法分析过程中,需要特别注意处理源代码中的注释、字符
03
串文字和符号文字等特殊情况。
03
实现过程中还需要注意处理各 种语法错误和异常情况,以确 保语法分析的正确性和可靠性 。
03
习题三:语义分析
语义分析概述
语义分析是编译过程的核心环 节之一,主要负责对源程序的 语法结构进行分析,并检查其
语义是否合法。
语义分析的目的是在语法分 析的基础上,进一步确定源 程序中各个语句的含义,以
及它们之间的关系。
编译器设计实践概述
编译原理课后习题答案ch3

答案: 可为句子 a+a*a 构造两个不同的最右推导: 〈运算符〉 〈表达式〉 最右推导 1 〈表达式〉 〈表达式〉 〈表达式〉 〈运算符〉a 〈表达式〉* a 〈表达式〉 〈运算符〉 〈表达式〉* a 〈表达式〉 〈运算符〉a * a 〈表达式〉+ a * a a+a*a 〈运算符〉 〈表达式〉 最右推导 2 〈表达式〉 〈表达式〉 〈表达式〉 〈运算符〉 〈表达式〉 〈运算符〉 〈表达式〉 〈表达式〉 〈运算符〉 〈表达式〉 〈运算符〉 a 〈表达式〉 〈运算符〉 〈表达式〉 * a 〈表达式〉 〈运算符〉a * a 〈表达式〉+ a * a a+a*a
<表达式>
<表达式>
+
<项>
<项> <项> <因子> <因子> i i i * <因子>
盛威网()专业的计算机学习网站
3
《编译原理》课后习题答案第三章
第7题 证明下述文法 G[〈表达式〉]是二义的。 〈表达式〉∷=a|(〈表达式〉)|〈表达式〉 〈运算符〉 〈表达式〉 〈运算符〉∷=+|-|*|/
a
B
A c a b
c
b
第9题 考虑下面上下文无关文法: S→SS*|SS+|a (1)表明通过此文法如何生成串 aa+a*,并为该串构造语法树。 (2)G[S]的语言是什么? S 答案: S (1)此文法生成串 aa+a*的最右推导如下 S=>SS*=>SS*=>Sa*=>SS+a*=>Sa+a*=>aa+a* (2)该文法生成的语言是:*和+的后缀表达式,即逆波兰式。 S + a S
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章语法分析3.1 完成下列选择题:(1) 文法G:S→xSx|y所识别的语言是。
a. xyxb. (xyx)*c. xnyxn(n≥0)d. x*yx*(2) 如果文法G是无二义的,则它的任何句子α。
a. 最左推导和最右推导对应的语法树必定相同b. 最左推导和最右推导对应的语法树可能不同c. 最左推导和最右推导必定相同d. 可能存在两个不同的最左推导,但它们对应的语法树相同(3) 采用自上而下分析,必须。
a. 消除左递 a. 必有ac归b. 消除右递归c. 消除回溯d. 提取公共左因子(4) 设a、b、c是文法的终结符,且满足优先关系ab和bc,则。
b. 必有cac. 必有bad. a~c都不一定成立(5) 在规范归约中,用来刻画可归约串。
a. 直接短语b. 句柄c. 最左素短语d. 素短语(6) 若a为终结符,则A→α·aβ为项目。
a. 归约b. 移进c. 接受d. 待约(7) 若项目集Ik含有A→α·,则在状态k时,仅当面临的输入符号a∈FOLLOW(A)时,才采取“A→α·”动作的一定是。
a. LALR文法b. LR(0)文法c. LR(1)文法d. SLR(1)文法(8) 同心集合并有可能产生新的冲突。
a. 归约b. “移进”/“移进”c.“移进”/“归约”d. “归约”/“归约”【解答】(1) c (2) a (3) c (4) d (5) b (6) b (7) d (8) d3.2 令文法G[N]为G[N]: N→D|NDD→0|1|2|3|4|5|6|7|8|9(1) G[N]的语言L(G[N])是什么?(2) 给出句子0127、34和568的最左推导和最右推导。
【解答】(1) G[N]的语言L(G[N])是非负整数。
(2) 最左推导:NNDNDDNDDDDDDD0DDD01DD012D0127NNDDD3D34NNDNDDDDD5DD56D568最右推导:NNDN7ND7N27ND27N127D1270127NNDN4D434NNDN8ND8N68D685683.3 已知文法G[S]为S→aSb|Sb|b,试证明文法G[S]为二义文法。
【解答】 由文法G[S]:S →aSb|Sb|b ,对句子aabbbb 可对应如图3-1所示的两棵语法树。
图3-1 句子aabbbb 对应的两棵不同语法树因此,文法G[S]为二义文法(对句子abbb 也可画出两棵不同语法树)。
3.4 已知文法G[S]为S →SaS|ε,试证明文法G[S]为二义文法。
【解答】 由文法G[S]:S →SaS|ε,句子aa 的语法树如图3-2所示。
图3-2 句子aa 对应的两棵不同的语法树由图3-2可知,文法G[S]为二义文法。
3.5 按指定类型,给出语言的文法。
(1) L={aibj|j >i ≥0}的上下文无关文法;(2) 字母表Σ={a,b}上的同时只有奇数个a 和奇数个b 的所有串的集合的正规文法;(3) 由相同个数a 和b 组成句子的无二义文法。
【解答】 (1) 由L={aibj|j >i ≥0}知,所求该语言对应的上下文无关文法首先应有S →aSb 型产生式,以保证b 的个数不少于a 的个数;其次,还需有S →Sb 或S →b 型的产生式,用以保证b 的个数多于a 的个数。
因此,所求上下文无关文法G[S]为G[S]:S →aSb|Sb|b(2) 为了构造字母表Σ={a,b}上同时只有奇数个a 和奇数个b 的所有串集合的正规式,我们画出如图3-3所示的DFA ,即由开始符S 出发,经过奇数个a 到达状态A ,或经过奇数个b 到达状态B ;而由状态A 出发,经过奇数个b 到达状态C(终态);同样,由状态B 出发经过奇数个a 到达终态C 。
由图3-3可直接得到正规文法G[S]:S →aA|bB A →aS|bC|bB →bS|aC|aC →bA|aB|ε图3-3 习题3.5的S a S b a S b S b b a S b S b Sa S bb S S S a S S a εεεS S S a SS a εεε(a)(b )(3) 我们用一个非终结符A 代表一个a(即有A →a),用一个非终结符B 代表一个b(即有B →b);为了保证a 和b 的个数相同,则在出现一个a 时应相应地出现一个B ,出现一个b 时则相应出现一个A 。
假定已推导出bA ,如果下一步要推导出连续两个b 时,则应有bAbbAA 。
也即为了保证b 和A 的个数一致,应有A →bAA ;同理有B →aBB 。
此外,为了保证递归地推出所要求的ab 串,应有S →aBS 和S →bAS 。
由此得到无二义文法G[S]为G[S]:S →aBS|bAS|εA →bAA|aB →aBB|b3.6 有文法G[S]: S →aAcB|BdA →AaB|cB →bScA|b(1) 试求句型aAaBcbbdcc 和aAcbBdcc 的句柄;(2) 写出句子acabcbbdcc 的最左推导过程。
【解答】 (1) 分别画出对应句型aAaBcbbdcc 和aAcbBdcc 的语法树如图3-4的(a)、(b)所示。
图3-4 习题3.6的语法树(a) aAaBcbbdcc; (b) aAcbBdcc对树(a),直接短语有3个:AaB 、b 和c ,而AaB 为最左直接短语(即为句柄)。
对树(b),直接短语有两个:Bd 和c ,而Bd 为最左直接短语。
能否不画出语法树,而直接由定义(即在句型中)寻找满足某个产生式的候选式这样一个最左子串(即句柄)呢?例如,对句型aAaBcbbdcc ,我们可以由左至右扫描找到第一个子串AaB ,它恰好是满足A →AaB 右部的子串;与树(a)对照,AaB 的确是该句型的句柄。
是否这一方法始终正确呢?我们继续检查句型aAcbBdcc ,由左至右找到第一个子串c ,这是满足A →C 右部的子串,但由树(b)可知,c 不是该句型的句柄。
由此可知,画出对应句型的语法树然后寻找最左直接短语是确定句柄的好方法。
(2) 句子acabcbbdcc 的最左推导如下:SaAcBaAaBcBacaBcBacabcBacabcbScAacabcbBdcAacabcbbdcAacabcbbdcc3.7 对于文法G[S]: S →(L)|aS|aL →L,S|S(1) 画出句型(S,(a))的语法树;(2) 写出上述句型的所有短语、直接短语、句柄、素短语和最左素短语。
【解答】 (1) 句型(S, (a))的语法树如图3-5所示。
图3-5 句型(S,(a))的语法树 A a B b S c AB A c a S B d b b S c A B A c a S B d c (a )(b )c (L )S L ,S S (L )Sa(2) 由图3-5可知:短语:S 、a 、(a)、S,(a)、(S,(a));直接短语:a 、S ;句柄:S ;素短语:素短语可由图3-5中相邻终结符之间的优先关系求得,即:#⋖ (⋖,⋖ (⋖a ⋗)⋗)⋗#因此,素短语为a 。
3.8 下述文法描述了C 语言整数变量的声明语句:G[D]: D →TLT →int|long|shortL →id|L,id(1) 改造上述文法,使其接受相同的输入序列,但文法是右递归的;(2) 分别用上述文法G[D]和改造后的文法G[D ′]为输入序列int a,b,c 构造分析树。
【解答】 (1) 消除左递归后,文法G[D ′]如下:D →TL T →int|long|short L →idL图3-6 两种文法为int a,b,c 构造的分析树(a) 文法G(D); (b) 文法G ′(D)3.9 考虑文法G[S]: S →(T) | a+S | aT →T,S | S消除文法的左递归及提取公共左因子,然后对每个非终结符写出不带回溯的递归子程序。
【解答】 消除文法G[S]的左递归:S →(T) | a+S | aT →ST ′T ′→,ST ′| ε提取公共左因子:S →(T) | aS ′S ′→+S | εT →ST ′T ′→,ST ′| ε改造后的文法已经是LL(1)文法,不带回溯的递归子程序如下:void match (token t){if ( lookahead==t)lookahead=nexttoken;else error ( );}void S ( ){ L ,c L D T int L ,b a ,b L DT int a L′L′,c L′(a )(b )if ( lookahead==′a′)match (′a′);else if ( lookahead==′(′){match (′(′);T ( );void S′( ){if ( lookahead==′+′){match (′+′);S ( );}}void T ( ){S ( );T′( );}void T′( ){if ( lookahead==′, ′){match (′, ′);S ( );T′( );}}3.10 已知文法G[A]: A→aABl|aB→Bb|d(1) 试给出与G[A]等价的LL(1)文法G[A′];(2) 构造G[A′]的LL(1)分析表;(3) 给出输入串aadl#的分析过程。
【解答】(1) 文法G[A]存在左递归和回溯,故其不是LL(1)文法。
要将G[A]改造为LL(1)文法,首先要消除文法的左递归,即将形如P→Pα| β的产生式改造为P→βP′P→αP′| ε来消除左递归。
由此,将产生式B→Bb|d改造为B→dB′B′→bB′| ε其次,应通过提取公共左因子的方法来消除G[A]中的回溯,即将产生式A→aABl|a 改造为A→aA′A′→ABl | ε最后得到改造后的文法为G[A′]:A→aA′A′→ABl | εB→dB′B′→bB′| ε求得:FIRST(A)={a} FIRST(A′)={a, ε}FIRST(B)={d} FIRST(B′)={b, ε}对文法开始符号A,有FOLLOW(A)={#}。
由A′→ABl得FIRST(B)\{ ε}⊂FOLLOW(A),即FOLLOW(A)={#,d};由A′→ABl得FIRST(′l′) ⊂FOLLOW(B),即FOLLOW(B)={l};由A→aA′得FOLLOW(A) ⊂FOLLOW(A′),即FOLLOW(A′)={#,d};由B→dB′得FOLLOW(B) ⊂FOLLOW(B′),即FOLLOW(B′)={l}。
对A′→ABl来说,FIRST(A)∩FOLLOW(A′)={a}∩{#,d}=Φ,所以文法G′[A]为所求等价的LL(1)文法。
(2) 构造预测分析表的方法如下:①对文法G[A′]的每个产生式A→α执行②、③步。
