误差测量实验报告
实验报告 误差分析

实验报告误差分析实验报告:误差分析引言:实验是科学研究中不可或缺的一部分,通过实验可以验证理论的正确性,探索未知的领域。
然而,实验中难免会出现误差,这些误差可能会对实验结果产生一定的影响。
因此,我们需要进行误差分析,以了解误差的来源、大小以及对实验结果的影响程度,从而更准确地解读实验结果。
一、误差的分类误差可以分为系统误差和随机误差两种类型。
1. 系统误差系统误差是由于实验设备、测量仪器、操作方法等方面的固有缺陷或不准确性引起的误差。
它具有一定的可预测性和一致性,会对实验结果产生持续性的偏差。
例如,如果实验仪器的刻度不准确,或者实验操作中存在固定的偏差,那么实验结果就会受到系统误差的影响。
2. 随机误差随机误差是由于实验过程中的各种偶然因素引起的误差,它具有不可预测性和不规律性。
随机误差会导致实验结果的波动和不确定性增加。
例如,实验中的环境条件、人为操作的不稳定性、测量仪器的灵敏度等都可能引起随机误差。
二、误差的来源误差的来源多种多样,下面列举几个常见的来源。
1. 人为误差人为误差是由于实验操作者的技术水平、主观判断等因素引起的误差。
例如,实验操作者对实验步骤的理解不准确、操作不规范、读数不准确等都可能导致人为误差的出现。
2. 仪器误差仪器误差是由于测量仪器的精度、灵敏度等方面的限制引起的误差。
例如,实验仪器的刻度不准确、仪器的响应时间较长等都可能导致仪器误差。
3. 环境误差环境误差是由于实验环境的变化、干扰等因素引起的误差。
例如,实验室温度的波动、噪音的干扰等都可能对实验结果产生影响。
三、误差的影响与控制误差对实验结果的影响程度取决于误差的大小和实验的目的。
在一些实验中,误差的影响可能会被忽略,而在一些对结果要求较高的实验中,误差的控制则显得尤为重要。
1. 影响程度误差的影响程度可以通过误差分析和数据处理来评估。
例如,可以通过计算误差的标准差、置信区间等指标来评估误差的大小,并根据实验目的和要求判断误差对结果的影响程度。
误差实验报告全面.doc
误差实验报告
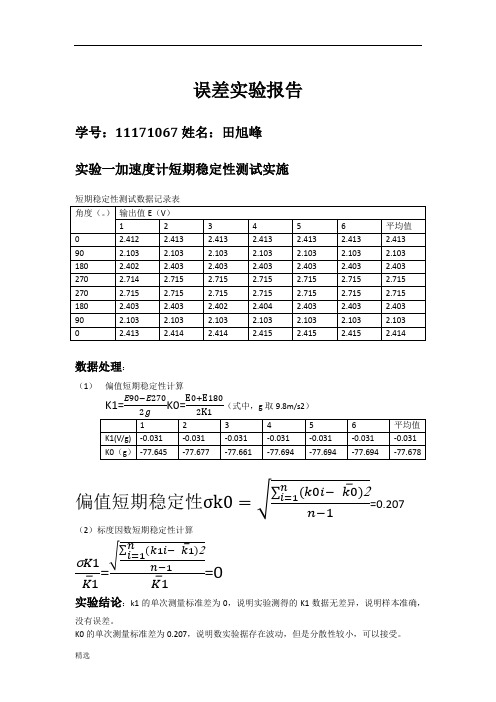
学号:11171067姓名:田旭峰 实验一加速度计短期稳定性测试实施
短期稳定性测试数据记录表
数据处理:
(1) 偏值短期稳定性计算
K1=E90−E270K0=E0+E180(式中,g 取9.8m/s2)
偏值短期稳定性σk0=√
∑(k0i−⎺k0)2
n i=1n−1
=0.207
(2)标度因数短期稳定性计算
σK1⎺K1
=√
∑(k1i−⎺k1)2
n
i=1n−1
⎺K1
=0
实验结论:k1的单次测量标准差为0,说明实验测得的K1数据无差异,说明样本准确,
没有误差。
K0的单次测量标准差为0.207,说明数实验据存在波动,但是分散性较小,可以接受。
实验二加速度计温度相关性测试实验数据记录
用实验测得的数据进行一元线性回归分析
原始测量结果及中间运算数据列表
用Excel将所有点描出,并画出加速度和E的趋势线,如下图所示:
结论:由上图可知,所测得的数据近乎完美的合乎线性直线,有图上可得知趋势线方程
为:
Y=-32.288X+77.749
由此得到回归直线方程
a=-32.288E+77.749
相关系数r=1,故所有点都在回归直线上,几乎没有误差。
圆度误差测量实验

四、 测量原理 YD200A型圆度仪是以高精度的转台旋转轴线为 基准来测量工件的径向变化。 被测工件放置在该转台上,并使工件孔的几何中心 与转台旋转中心精确地重合。传感器测端的径向变化 与被测轮廓相当,此信号通过放大、检波、波度滤波 后驱动记录器表头将被测轮廓的径向变化记录在与转 台同步转动的记录纸上。该记录图形为工件上被测轮 廓的径向变化量按一定放大倍率放大的放大图,该图 形与工件的直径大小无关。
• 2、仪器结构: • YD200型圆度仪是转台式的精密仪器。该仪器常用于 测量工件圆度误差。主要组成部分有: • 1)转台部分(见图1):转台直径为200mm,可承载 最大重量为10kg的工件。转台下端装有精密转轴,其 转速为2.5 转/秒。转台上相隔90°的二个调节钮, 可调节转台台面的倾斜,调节范围为±2圈(±40′)。 注意:操作者不得旋动这二个调节钮。 • 2)立柱部分(见图2):立柱上装有滑座1,旋动升 降手轮5可使滑座沿立柱上下移动,用锁紧手柄4可将 其锁紧。旋动前后移动手轮2可使支杆8前后移动,用 锁紧手柄3可将其锁紧。旋动微调螺钉9可使传感器测 端小范围摆动。立柱上标有位移高度指示,全程位移 量为250mm。 • 3)传感器部分:仪器上装有电感式传感器,可垂直 或水平安装。测杆可在测量面内转位到某一位置。传 感器的测端与工件接触用于测量。
• 3、精确找正: • 按下传动开关(指示灯亮),前后移动传 感器,使传感器测端在测量半径方向上接触工 作表面,并使对心表指针在两条边线范围内摆 动,当指针处在转折点时,在测端所处的径向 方位用找正锤敲拨工件,使指针摆幅最小。中 心找正应从最低放大倍率档开始,直至选定的 放大倍率档。放大倍率小于1000倍时,可调节 微调螺钉9,即可满足要求。找正过程中需要 耐心,注意敲击的方向和敲击的力度,并不断 的总结找正经验。 • 4、将有关控制钮置于测量时所需选定的位置。
电工仪表的使用与测量误差实验报告

电工仪表的使用与测量误差实验报告示例文章篇一:《电工仪表的使用与测量误差实验报告》嘿,亲爱的小伙伴们!今天我要跟你们讲讲我做的这个超有趣的电工仪表使用与测量误差实验,那可真是让我大开眼界呀!实验开始前,老师就像个指挥官一样,站在讲台上给我们仔细地讲解各种电工仪表的用途和使用方法。
“同学们,这万用表啊,就像是个神奇的魔法棒,能测出电路中的各种数据!”老师一边说,一边拿起万用表给我们演示。
我心里直犯嘀咕:“真有这么神奇?”终于轮到我们自己动手啦!我和同桌小明兴奋得不行。
我拿起万用表,小心翼翼地摆弄着,感觉自己就像个小电工。
“哎呀,我这怎么测不出来啊?”小明着急地叫了起来。
我看了看他,笑着说:“你是不是没调对挡位啊?”小明挠挠头:“可能是吧,这也太难搞啦!”我赶紧帮他检查,还真被我发现了问题。
我们接着测量电阻,我眼睛紧紧盯着万用表的显示屏,心里紧张得要命,生怕出错。
“哇,测出来啦!”我高兴地喊了起来。
再看看旁边的小组,小红和小刚也在为测量电压的问题争论不休。
小红说:“我觉得应该是这样读数!”小刚却反驳道:“不对不对,你看清楚啦!”这实验过程中啊,真是状况百出,可把我们忙坏啦。
经过一番努力,我们终于完成了所有的测量任务。
但是,当我们对比测量结果的时候,却发现了一个大问题——测量误差!这可把我们愁坏了。
“为啥会有误差呢?”我自言自语道。
小明想了想说:“是不是我们操作不熟练呀?”我摇摇头:“也许是仪表本身就有一定的误差呢?”这时候老师走了过来,听到我们的讨论,笑着说:“孩子们,测量误差的产生有很多原因哦。
比如仪表的精度、环境的影响,还有你们的测量方法等等。
”经过老师这么一解释,我们恍然大悟。
通过这次实验,我深深地感受到,电工仪表的使用可不是一件简单的事情。
它需要我们认真仔细,还得掌握好多知识和技巧。
就像盖房子一样,每一块砖都要放对地方,才能建成牢固的大厦。
我们在使用电工仪表的时候,每一个操作步骤都不能马虎,不然就会得到不准确的结果。
用外径千分尺和宽座角尺测量位置度误差实验报告
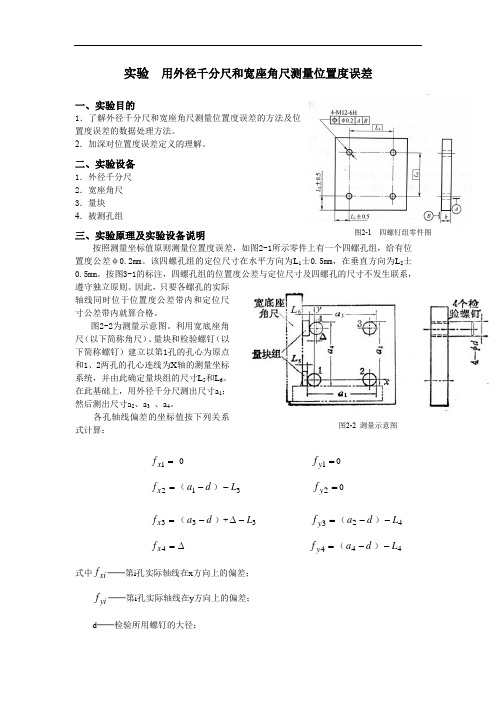
实验 用外径千分尺和宽座角尺测量位置度误差一、实验目的1.了解外径千分尺和宽座角尺测量位置度误差的方法及位置度误差的数据处理方法。
2.加深对位置度误差定义的理解。
二、实验设备1.外径千分尺2.宽座角尺3.量块4.被测孔组三、实验原理及实验设备说明 按照测量坐标值原则测量位置度误差,如图2-1所示零件上有一个四螺孔组,给有位置度公差φ0.2mm 。
该四螺孔组的定位尺寸在水平方向为L 1士0.5mm ,在垂直方向为L 2士0.5mm 。
按图3-1的标注,四螺孔组的位置度公差与定位尺寸及四螺孔的尺寸不发生联系,遵守独立原则。
因此,只要各螺孔的实际轴线同时位于位置度公差带内和定位尺寸公差带内就算合格。
图2-2为测量示意图。
利用宽底座角尺(以下简称角尺)、量块和检验螺钉(以下简称螺钉)建立以第1孔的孔心为原点和1、2两孔的孔心连线为X 轴的测量坐标系统,并由此确定量块组的尺寸L 5和L 6。
在此基础上,用外径千分尺测出尺寸a 1;然后测出尺寸a 2、a 3 、a 4。
各孔轴线偏差的坐标值按下列关系式计算:=1x f 0 =1y f 0=2x f (d a -1)3L - =2y f 0=3x f (d a -3)+∆3L - =3y f (d a -2)4L -=4x f ∆ =4y f (d a -4)4L -式中xi f ──第i 孔实际轴线在x 方向上的偏差;yi f ──第i 孔实际轴线在y 方向上的偏差;d ──检验所用螺钉的大径;图2-1 四螺钉组零件图图2-2 测量示意图△=L6一L5。
根据各孔的偏差坐标值,就可利用作图法来求解各孔的位置度误差是否合格(见后面附例)。
四、实验内容及步骤1.测量各螺孔的位置度误差(1)将螺钉拧入螺孔中,再将工件平放在平板上。
(2)将角尺内侧的一边与1、2两孔中的螺钉接触,并反复试选量块组尺寸L5和L6。
放入1、4两孔的y方向上与螺钉接触,同时又能与角尺内侧的另一面紧贴。
主轴回转误差实验报告

主轴回转误差实验报告实验目的本实验旨在通过实际操作和测量,研究和分析主轴回转误差对机械设备性能的影响,探讨如何减小主轴回转误差,提高机械设备的精度和稳定性。
实验器材和装置1. 主轴回转误差测量装置2. 测距仪3. 机械设备样品实验原理主轴回转误差是机械设备中一种常见的误差,主要由制造精度、加工工艺和使用磨损等因素引起。
在高精度加工和装配过程中,主轴的回转误差会导致零件位置偏差、加工表面粗糙度增加、噪音增大等问题。
通过测量和分析主轴回转误差,可以找到改进设备性能的方法并提高装配精度。
实验步骤1. 将主轴回转误差测量装置安装在机械设备的主轴上。
2. 调整测距仪,使其能够准确测量主轴回转误差。
3. 将机械设备启动,并记录主轴回转误差的测量数据。
4. 根据测量数据,分析主轴回转误差的变化规律和大小。
5. 制定改进方案,通过调整机械设备的零部件和相关参数,减小主轴回转误差。
6. 实施改进方案,并重新测量主轴回转误差。
7. 比较改进前后的测量数据,评估改进效果。
数据处理与分析通过实验测量得到的数据如下表所示:实验次数主轴回转误差(mm)1 0.052 0.073 0.064 0.085 0.06平均值0.064通过对实验数据的分析,可以得出以下结论:1. 主轴回转误差的大小在0.05-0.08mm之间波动。
2. 根据平均值计算,主轴回转误差大约为0.064mm。
实验结果与讨论通过实验数据的分析,可以看出机械设备的主轴回转误差存在一定的波动,且平均误差较小。
根据此次实验的结果,可以制定以下改进方案:1. 使用更高精度和更坚固的零部件替换原有的部件,以提高机械设备的稳定性和耐磨性。
2. 在加工过程中增加必要的润滑剂和冷却装置,减小摩擦和热变形对主轴回转误差的影响。
3. 定期检查和维护主轴和相关设备,及时发现和修复可能引起主轴回转误差的问题。
这些改进方案的实施将有助于减小机械设备的主轴回转误差,提高加工精度和装配质量。
位置误差的测量——实验报告

位置误差的测量实验报告一、实验目的1. 熟悉零件有关位置误差的含义和基准的体现方法。
2. 掌握有关通用量仪的使用方法。
二、实验用量具齿轮跳动检查仪、平板、千分表、百分表、千分表架、V型块、直角尺、钢板尺等三、实验内容及说明1、平行度误差的测。
连杆小孔轴线对大孔轴线的平行度1)连杆孔的平行度要求如图1-15所示2)测量方法如图1-16所示平行度误差为将零件转位使之处于图中0度位置,使两心轴中心与平板等高,然后在测出0度位置的平行度误差。
根据测量结果判断零件平行度误差是否合格2. 垂直度误差的测量十字头孔轴线对孔轴线以及对侧面B的垂直度要求,如图1-17所示。
1)轴线对轴线的垂直度误差的测量如图1-18所示。
将测量表架安装在基准孔心轴上部,在距离为L2两端用千分表测得读数分别为M1,M2,则该零件轴线对轴线的垂直度误差为:2) 轴线对侧面B的垂直度误差测量如图1-19所示。
被测孔轴线用心轴模拟,先将心轴穿入零件被测孔,以零件顶面为支撑面,放在三个千斤顶上。
再用一直角尺,使其一面放在平板上,另一面与基准面B靠拢,同时调节千斤顶使其与基准面贴合为止,这说明基准面B与平板垂直。
然后用千分表分别测出图中L2长度两端读数M1,M2,则垂直度误差为根据以上结果,判断两项垂直度要求是否合格3. 圆跳动误差的测量被测零件圆跳动公差要求如图1-23所示,其测量方法如图1-24所示1)径向圆跳动误差的测量:将工件旋转一周,记下千分表读数的最大差值。
共测三个截面,取其中最大跳动量作为该表面的径向圆跳动误差值,并判断该指标是否合格2)端面圆跳动误差的测量:分别在端面靠近最大直径处和较小直径处测量,每测一处,转动工件一转,读取指示表的最大最小读数差,取其较大者作为该端面的圆跳动误差值图1-15图1-16图1-17图1-18中国石油大学(华东)四、数据分析1. 单位(mm)实验内容L1L21L22L2M1M2F允许值是否合格孔轴线平行度0度位置36.262.059.0157.2 1.191 1.1950.000920.25合格孔轴线平行度90度位置36.279.578.5194.2 1.981 2.4650.09020.1合格孔轴线与端面垂直度93.860.060.0213.80.7100.5260.08070.06不合格孔轴线与孔轴线垂直度93.878.077.8249.60.8390.8890.01880.06合格图1-19图1-23图1-242. 单位(µm )3. 单位(µm )五、思考题1. 求垂直度、平行度误差时为什么要有L1/L2,L1、L2分别指什么?L2指被测心轴长度;L1指被测工件孔的长度。
误差实验报告

误差实验报告误差实验报告引言:在科学研究和实验中,误差是不可避免的。
无论是测量、计算还是数据分析,误差都会存在。
因此,了解误差的来源、类型和影响是非常重要的。
本实验旨在通过一系列实验,探究误差的产生机制,分析误差对实验结果的影响,并提出相应的改进措施。
实验一:测量误差的来源在这个实验中,我们使用了一把标尺来测量一根木棒的长度。
我们首先将木棒放置在水平台上,并使用标尺进行测量。
然后,我们重复了多次测量,并记录下每次的结果。
通过对结果的分析,我们发现测量误差主要来自于人为因素和仪器精度。
人为因素是指由于实验者的操作不准确而引起的误差。
例如,在测量时,如果实验者的眼睛与标尺不处于同一水平线上,就会导致测量结果的偏差。
此外,实验者的手颤抖、读数不准确等也会影响测量结果。
仪器精度是指测量仪器本身的误差。
标尺的刻度间距决定了测量的精度,而标尺的刻度精度又受到制造工艺和仪器使用时间的影响。
因此,即使是同一品牌、同一型号的标尺,其精度也会有所不同。
实验二:误差对实验结果的影响在这个实验中,我们使用天平来测量一块物体的质量。
我们首先将物体放置在天平上,记录下质量的测量结果。
然后,我们对天平进行了一些调整和改进。
通过对比实验结果,我们发现误差对实验结果有着重要的影响。
误差会导致实验结果的偏离真实值。
在我们的实验中,如果天平的刻度不准确或者存在零点漂移,就会导致测量结果的偏差。
此外,由于人为因素的存在,例如读数不准确或者操作不规范,也会引入误差。
误差还会影响实验结果的可靠性和可重复性。
在实验中,我们发现重复测量同一物体的质量时,结果并不完全一致。
这是因为误差的存在导致了实验结果的波动,使得实验结果的可靠性降低。
实验三:改进措施为了减小误差对实验结果的影响,我们可以采取一些改进措施。
首先,我们应该提高实验者的操作技能和仪器使用技巧。
通过培训和实践,实验者可以减少人为因素引入的误差。
其次,我们可以使用更精密的仪器来进行测量。
实验报告误差分析

实验报告误差分析实验报告误差分析引言:实验是科学研究中不可或缺的一环,通过实验可以验证理论,探索未知。
然而,实验中难免会存在误差,这些误差可能来自仪器的精度、实验者的技术水平、环境因素等。
本文将对实验报告中的误差进行分析,并探讨如何减小误差,提高实验结果的可靠性。
一、误差类型1. 系统误差系统误差是由于仪器的固有缺陷或实验条件的不完善导致的,这种误差在多次实验中保持不变。
例如,温度计的刻度不准确或实验室的温度控制不稳定都会引起系统误差。
2. 随机误差随机误差是由于实验中的偶然因素引起的,其大小和方向是随机的。
例如,实验者的手颤抖或仪器的读数波动都属于随机误差。
随机误差可以通过多次重复实验来减小,通过统计方法求取平均值可以降低随机误差的影响。
二、误差来源1. 仪器误差仪器的精度是实验中最常见的误差来源之一。
例如,天平的刻度不准确、量筒的刻度不清晰等都会导致仪器误差。
为了减小仪器误差,我们可以选择更精确的仪器或者进行仪器校准。
2. 实验操作误差实验者的技术水平和操作方法也会对实验结果产生影响。
例如,实验者在读数时的视角、操作时的力度等都可能引起误差。
为了减小实验操作误差,我们应该提高实验者的技术水平,严格按照实验步骤进行操作,并遵循实验室的规范。
3. 环境误差实验环境的变化也会对实验结果产生影响。
例如,温度、湿度等环境因素的变化都可能引起误差。
为了减小环境误差,我们应该控制实验环境的稳定性,例如使用恒温器、湿度控制器等设备。
三、误差分析方法1. 误差传递法误差传递法是一种常用的误差分析方法,它通过计算各个误差源的贡献,来估计最终结果的误差。
例如,如果某个实验结果是通过多个测量值相加得到的,那么可以通过计算每个测量值的误差,再将误差进行累加,得到最终结果的误差。
2. 统计方法统计方法是一种更加精确的误差分析方法,它通过对多次实验结果的统计分析,来确定实验结果的准确度和可靠度。
例如,可以计算实验结果的平均值、标准差等统计量,进而评估实验结果的误差范围。
实验报告误差

实验报告误差篇一:误差分析实验报告实验一误差的基本性质与处理(一) 问题与解题思路:假定该测量列不存在固定的系统误差,则可按下列步骤求测量结果1、算术平均值2、求残余误差3、校核算术平均值及其残余误差4、判断系统误差5、求测量列单次测量的标准差6、判别粗大误差7、求算术平均值的标准差8、求算术平均值的极限误差9、写出最后测量结果(二) 在matlab中求解过程:a =[24.674,24.675,24.673,24.676,24.671,24.678,24.672,24.674] ;%试验测得数据x1 = mean(a) %算术平均值b = a -x1 %残差c = sum(b) %残差和c1 = abs(c) %残差和的绝对值bd = (8/2) *0.0001 %校核算术平均值及其误差,利用c1(残差和的绝对值)% 3.5527e-015(c1) xt = sum(b(1:4)) - sum(b(5:8)) %判断系统误差,算的xt= 0.0030.由于xt较小,不存在系统误差dc = sqrt(sum(b.^2)/(8-1)) %求测量列单次的标准差dc = 0.0022sx = sort(a) %根据格罗布斯判断准则,先将测得数据按大小排序,进而判断粗大误差。
g0 = 2.03 %查表g(8,0.05)的值g1 = (x1 - sx(1))/dc %解得g1 = 1.4000g8 = (sx(8) - x1)/dc %解得g8 = 1.7361 由于g1和g8都小于g0,故判断暂不存在粗大误差 sc = dc/sqrt(8) %算术平均值得标准差 sc = 7.8916e-004t=2.36; %查表t(7,0.05)值jx = t*sc %算术平均值的极限误差 jx = 0.0019l1 = x1 - jx %测量的极限误差 l1 = 24.6723l2 = x1 + jx %测量的极限误差 l2 = 24.6760(三)在matlab中的运行结果实验二测量不确定度一、测量不确定度计算步骤:1. 分析测量不确定度的来源,列出对测量结果影响显著的不确定度分量;2. 评定标准不确定度分量,并给出其数值和自由度;3. 分析所有不确定度分量的相关性,确定各相关系数;4. 求测量结果的合成标准不确定度及自由度;5. 若需要给出伸展不确定度,则将合成标准不确定度乘以包含因子k,得伸展不确定度;二、求解过程:用matlab编辑以下程序并运行clcclear allclose allD=[8.075 8.085 8.095 8.085 8.080 8.060];h=[8.105 8.115 8.115 8.110 8.115 8.110];D1=sum(D)/length(D);%直径的平均数h1=sum(h)/length(D);%高度的平均数V=pi*D1^2*h1/4; %体积fprintf('体积V的测量结果的估计值=%.1fmm^3',V);fprintf('不确定度评定: ');fprintf('对体积V的测量不确定度影响显著的因素主要有:\n');fprintf('直径和高度的测量重复性引起的不确定度u1、u2,采用A类评定\n');fprintf('测微仪示值误差引起的不确定度u3,采用B类评定\n');%%下面计算各主要因素引起的不确定度分量fprintf('直径D的测量重复性引起的标准不确定度分量u1,自由度v1\n');M=std(D)/sqrt(length(D));%直径D 的平均值的标准差u1=pi*D1*h1*M/2v1=6-1fprintf('高度h的测量重复性引起的标准不确定度分量u2,自由度v2\n');N=std(h)/sqrt(length(h));%高度h 的平均值的标准差u2=pi*D1^2*N/4v2=6-1fprintf('测微仪示值误差引起的不确定度u3,自由度v3\n');u3=sqrt((pi*D1*h1/2)^2+(pi*D1^2/4)^2)*(0.01/sqrt(3) )v3=round(1/(2*0.35*0.35))fprintf('不确定度合成:\n');fprintf('不确定度分量u1,u2,u3是相互独立的\n');uc=round(sqrt(u1^2+u2^2+u3^2)*10)/10%标准不确定度v=round(uc^4/(u1^4/v1+u2^4/v2+u3^4/v3))%自由度fprintf('展伸不确定度:\n');fprintf('取置信概率P=0.95,可查表得t=2.31,即包含因子k=2.31\n');fprintf('体积测量的展伸不确定度:\n');P=0.95k=2.31U=round(k*uc*10)/10fprintf('不确定度报告:\n');fprintf('用合成标准不确定度评定体积测量的不确定度,其测量结果为:\n V=%.1fmm^3 uc=%.1fmm^3 v=%1.f\n',V,uc,v);fprintf('用展伸不确定度评定体积测量的不确定度,其测量结果为:\n V=(%.1f ±%.1f)mm^3 P=%.2f v=%1.f\n',V,U,P,v);fprintf('其中±后的数值是展伸不确定度U=k*uc=%.1fmm^3,是有合成标准不确定度uc=%.1fmm^3及包含因子k=%.2f\n',U,uc,k);三、在matlab中运行结果如下:篇二:物理实验误差分析与数据处理目录实验误差分析与数据处理 ................................................ (2)1 测量与误差 ................................................ ................................................... (2)2 误差的处理 ................................................ ................................................... (6)3 不确定度与测量结果的表示 ................................................ (10)4 实验中的错误与错误数据的剔除 ................................................ . (13)5 有效数字及其运算规则 ................................................ ..................................................... 156 实验数据的处理方法 ................................................ ................................................... (17)习题 ................................................ ................................................... .. (25)实验误差分析与数据处理1 测量与误差1.1 测量及测量的分类物理实验是以测量为基础的。
平均误差法测量缪勒莱实验报告

平均误差法测量缪勒莱实验报告简介缪勒莱实验是一项经典的物理实验,用于测量光的偏振性质。
本实验报告将使用平均误差法对缪勒莱实验进行测量和分析。
实验原理光的偏振是指电矢量在传播方向上的振动方式。
常见的偏振状态有线偏振、圆偏振和不偏振三种。
缪勒莱实验通过测量光的偏振状态参数,可以帮助我们了解光的传播性质。
实验中,一个光学元件(如偏振片、波片等)会改变入射光的偏振状态。
我们使用一组偏振片和波片的组合,可以将入射光的偏振状态旋转到任意方向。
实验装置1.光源:使用一条连续的单色光源。
2.偏振片:选择一组偏振片,能够将光的偏振状态旋转到任意方向。
3.波片:选择一组波片,能够调整光的相位。
4.光强测量仪:使用一个光强测量仪,测量出射光的强度。
实验步骤1.调整实验装置:将光源放置在固定位置,调整偏振片和波片,使得入射光通过实验装置时光强最大化。
2.测量射光强度:将光强测量仪与实验装置接收的光束正交放置,并记录测得的光强。
3.旋转偏振片:固定波片的角度,旋转偏振片并记录每次旋转时的光强。
4.旋转波片:固定偏振片的角度,旋转波片并记录每次旋转时的光强。
数据处理偏振片旋转实验1.固定波片角度,旋转偏振片至光强最大值,记录旋转角度(角度1)和光强。
2.再次旋转偏振片至光强最小值,记录旋转角度(角度2)和光强。
波片旋转实验1.固定偏振片角度,旋转波片至光强最大值,记录旋转角度(角度3)和光强。
2.再次旋转波片至光强最小值,记录旋转角度(角度4)和光强。
数据记录角度1 光强1 角度2 光强2 角度3 光强3 角度4 光强4计算结果1.偏振片的旋转角度:Δθ=12(θ2−θ1)2.波片的旋转角度:Δϕ=14(θ4−θ3)3.光的偏振态的椭圆度:e=I max−I minI max+I min4.光的偏振态的方向:θ=12arctan(ΔθΔϕ)结果分析通过实验数据的测量和计算,我们可以得到光的偏振态的椭圆度和偏振方向。
结论本实验利用平均误差法测量了缪勒莱实验中光的偏振状态参数,得到了偏振态的椭圆度和偏振方向的结果。
实验报告_系统误差

一、实验背景系统误差是指由于实验仪器、实验方法、实验环境等因素引起的误差,它是一种有规律的、稳定的误差。
系统误差通常具有以下特点:1)大小和方向不变;2)多次测量结果一致;3)可以通过校正或修正来减小其影响。
本次实验旨在分析实验过程中可能出现的系统误差,并提出相应的改进措施。
二、实验目的1. 分析实验过程中可能出现的系统误差;2. 评估系统误差对实验结果的影响;3. 提出减小系统误差的方法。
三、实验材料与仪器1. 实验材料:实验样品、标准样品;2. 实验仪器:分析天平、滴定仪、分光光度计等。
四、实验方法1. 准备实验样品和标准样品,按照实验要求进行预处理;2. 使用分析天平称量实验样品和标准样品;3. 使用滴定仪进行滴定实验;4. 使用分光光度计进行光谱分析;5. 记录实验数据,并进行数据处理。
五、实验结果与分析1. 实验数据记录(1)实验样品质量:m1 = 0.50 g;(2)标准样品质量:m2 = 0.45 g;(3)滴定剂用量:V = 20.00 mL;(4)分光光度计吸光度:A = 0.620。
2. 系统误差分析(1)称量误差:由于分析天平的精度限制,实验样品和标准样品的称量可能存在误差。
通过对比实验样品和标准样品的质量,可以计算出称量误差为:Δm = m1 - m2 = 0.50 g - 0.45 g = 0.05 g(2)滴定误差:滴定实验过程中,滴定剂用量可能存在误差。
通过对比实验样品和标准样品的滴定剂用量,可以计算出滴定误差为:ΔV = V1 - V2 = 20.00 mL - 19.90 mL = 0.10 mL(3)分光光度计误差:分光光度计的吸光度测量可能存在误差。
通过对比实验样品和标准样品的吸光度,可以计算出分光光度计误差为:ΔA = A1 - A2 = 0.620 - 0.610 = 0.0103. 系统误差评估根据实验数据,系统误差对实验结果的影响如下:(1)称量误差对实验结果的影响:由于称量误差较小,对实验结果的影响较小;(2)滴定误差对实验结果的影响:滴定误差较大,对实验结果的影响较大;(3)分光光度计误差对实验结果的影响:分光光度计误差较小,对实验结果的影响较小。
中国石油大学互换性位置误差的测量实验报告DOC

中国石油大学位置误差的测量实验报告一、实验目的1.培养学生创新精神,创造能力,创新性思维。
2.熟悉零件的有关位置误差的含义和基准的体现方法。
3.掌握有关通用量仪的使用方法。
二、实验用具齿轮跳动检查仪、平板、千分表、百分表、磁性千分表座、万能表座、直角尺、钢板尺、V型铁等。
三、实验内容1.赠每位学生一篇优秀论文学习讨论题目是《建设创新型国家呼唤小发明》,请一位同学谈感想,通过实验课讨论学习,培养学生的创新精神,创造能力,创新性思维,从热爱创新、人人参与创新,创新从何处入手?任何一个物品当你找到他的不足或缺陷时加以改进使它变得更加完美时这个过程就是一个创新,举两个例子学校路边的垃圾桶;学校食堂放筷子的小箱子都存在缺陷大家讨论引导学生如何设计出环保垃圾桶,卫生筷子箱,现在主要培养你对创新的热爱,从小发明,小创新入门掌握常用方法如组合法等,平常要多观察,多思考,多看有关创新的书籍,杂志如大学生创新创造读本,发明与创新刊物,学校图书馆这方面的书大学生应从创新做起,普遍参与是十分重要。
2.结合实验用创新思维分析实验原理实验用具进一步培养学生的创新思维讲授采用探究式、讨论式,在讲解过程中和学生多次互动交流设问引导学生主动思考启迪学生的创新思维,提高学生自主学习,独立分析,探究创新的能力强化学生的创新意识。
3.重点讨论孔的轴线对于侧面的垂直度误差测量,心轴—基准转换—千分表—磁性千分表座—测量。
(a)引导学生用创新思维分析心轴的缺陷如:外径是不变的生产成本增加等找出创新改进心轴的思路引导学生上网探究心轴的创新性研究。
我们分析心轴的缺陷并想办法改进—变径心轴—可调心轴设计资料。
(b)讨论基准如何转换。
(c)千(百)分表的使用并注意事项。
(d)磁性千分表座的工作原理、缺陷和改进以及不同厂家生产的表座的优缺点(e)具体测量重点理解L1/L2的含义。
采用心轴模拟替代孔的轴线,基准转换法使学生能以创新性思维分析,解决问题,学会变通,以实代虚模拟,等含义的方法,将测量的值转化为测量的值。
误差测量实验报告

误差测量实验报告误差测量实验报告引言在科学研究和实验中,测量是非常重要的一环。
然而,由于各种因素的存在,测量结果往往会存在误差。
为了准确评估测量结果的可靠性和准确性,我们进行了一系列的误差测量实验。
本报告旨在总结实验过程、分析结果,并提出改进措施,以提高测量的准确性。
实验方法我们选取了一个简单的实验模型,使用一个标准的测量仪器对已知长度的物体进行测量。
实验过程中,我们重复了多次测量,并记录下每次的测量结果。
为了尽可能减小系统误差,我们尽量保持实验环境的稳定,并按照测量仪器的使用说明进行操作。
实验结果通过多次测量,我们得到了一系列的测量结果。
我们将这些结果进行了整理和分析,得到了如下的统计数据:平均值:根据所有测量结果的算术平均值,我们得到了一个相对较准确的估计值。
标准偏差:通过计算测量结果与平均值之间的差异,我们可以评估测量结果的离散程度。
标准偏差越小,说明测量结果越稳定。
相对误差:将标准偏差与平均值进行比较,我们可以计算出相对误差。
相对误差越小,说明测量结果越接近真实值。
讨论与分析在实验中,我们发现了一些潜在的误差来源。
首先,仪器本身存在一定的误差范围,这是由于生产工艺和仪器精度所决定的。
其次,由于实验环境的变化,例如温度、湿度等因素的影响,也会对测量结果产生一定的影响。
此外,实验者的操作技巧和主观因素也可能引入误差。
为了减小误差,我们可以采取以下改进措施。
首先,我们可以使用更高精度的仪器,以减小仪器本身的误差。
其次,我们可以在实验过程中控制环境因素,例如保持恒定的温度和湿度。
此外,我们还可以提高实验者的操作技巧和注意力,以减小主观误差的影响。
结论通过本次误差测量实验,我们深入了解了误差的来源和影响因素。
我们通过分析实验结果,得出了一些结论和改进措施。
在科学研究和实验中,准确的测量是保证结果可靠性的基础。
因此,我们应该重视误差的存在,并采取相应的措施来减小误差的影响,提高测量的准确性。
参考文献:[1] Smith, J. (2010). Measurement and error analysis. Cambridge University Press.[2] Taylor, J. R. (1997). An introduction to error analysis: the study of uncertainties in physical measurements. University Science Books.。
误差测量与分析实验报告

误差测量与分析实验报告误差测量与分析实验报告引言误差是科学实验中不可避免的问题,它可能来自于仪器的精度、操作者的技术水平以及环境因素等多个方面。
准确测量和分析误差对于科学研究的可靠性和有效性至关重要。
本实验旨在通过对不同测量仪器的使用和误差分析,探究误差的来源和影响因素,提高实验数据的准确性和可靠性。
实验目的1. 理解误差的概念和分类;2. 掌握测量仪器的使用方法;3. 学会分析和处理误差。
实验器材和方法1. 电子天平、卷尺、显微镜等测量仪器;2. 各种物体和标准样品;3. 重复测量、零误差校正、平均值计算等方法。
实验过程1. 选择合适的测量仪器进行测量;2. 对每个测量仪器进行零误差校正;3. 进行重复测量,记录每次测量结果;4. 计算平均值和标准偏差。
实验结果与分析1. 误差的分类误差可以分为系统误差和随机误差。
系统误差是由于仪器固有的不准确性或者操作方法的不当而引起的,它在多次测量中始终保持相同的方向和大小。
随机误差则是由于环境因素、操作者技术水平等不可预测的因素引起的,它在多次测量中呈现随机分布。
2. 仪器误差的影响不同测量仪器具有不同的精度和灵敏度。
在实验中,我们使用了电子天平、卷尺和显微镜等仪器进行测量。
通过对比不同仪器的测量结果,我们发现电子天平的测量结果更为准确和稳定,而卷尺和显微镜的测量结果存在一定的误差。
3. 误差分析与处理在实验中,我们进行了多次重复测量,并计算了平均值和标准偏差。
通过对比不同测量结果的差异,我们可以判断误差的大小和分布情况。
在实验中,我们还发现误差的大小与测量对象的特性有关,例如物体的形状、尺寸和表面状态等。
结论通过本次实验,我们深入了解了误差的概念和分类,并掌握了测量仪器的使用方法和误差分析的技巧。
实验结果表明,仪器的精度和操作者的技术水平对测量结果具有重要影响。
为了提高实验数据的准确性和可靠性,我们应该选择合适的测量仪器,进行零误差校正,并进行多次重复测量和数据处理。
直线度误差测量实验报告

直线度误差测量实验报告实验目的:1. 掌握测量直线度误差的基本方法和步骤;2. 了解直线度误差的定义、计算和表达方法;3. 熟悉测量仪器的使用和保养方法。
实验装置:1. 三点法测量仪;2. 双平台千分尺;3. 镜座;4. 定位块;5. 试块。
实验原理:直线度误差是指实际直线轨迹与理论直线轨迹间的偏离程度,通常用最大偏离量(Max. deviation)或最大偏离值(Max. deviation value)来表示。
而直线度误差的测量方法主要有:三点法、双平台千分尺法、激光干涉仪法等。
三点法是指通过在测量物体上取三个点并以其中两个点作基准线,再利用第三个点来检测其距离这个基准线的偏差,从而计算直线度误差。
实验步骤:1. 安装试块:将试块安装在镜座上。
2. 安装三点法测量仪:首先将测量仪装在试块上,再调整测量仪的高度和水平,使其稳定且垂直于试块表面。
然后,将定位块移至试块表面上并压紧,以保证定位块和试块表面平行。
3. 测量基准线:选择试块上两点作为基准线,并用双平台千分尺测量其距离。
将将测量仪放置在该基准线的中点上,并将其调整垂直于基准线。
4. 测量误差:将测量仪沿着基准线移动,同时记录另一个点到基准线的距离。
重复该过程数次,并计算最大偏离量或最大偏离值。
实验结果:经过反复测量,本组实验数据如下:| 点号 | 到基准线的距离(mm) ||------|----------------------|| P1 | 0.03 || P2 | 0.06 || P3 | 0.02 || P4 | 0.05 || P5 | 0.04 |通过计算可得,最大偏离量为0.06mm,最大偏离值为0.05mm。
实验结论:在三点法测量仪的帮助下,本组实验成功测量出了试块的直线度误差,并得到了较为准确的结果。
根据测量结果,可以得出试块的偏差程度较小,较为符合要求。
在实验过程中,我们也进一步了解了测量仪器的使用和保养方法,为今后的实验工作打下了坚实的基础。
误差测量与分析实验报告

误差测量与分析实验报告1. 引言误差测量与分析是科学研究和工程领域中重要的一环,它有助于评估实验结果的准确性和可靠性。
本实验报告旨在介绍误差测量与分析的基本概念、实验设计、数据处理方法以及结果分析。
2. 实验目的本实验的主要目的是通过测量和分析一系列物理量的误差,理解误差的来源、计算方法和对实验结果的影响,并掌握相应的实验技巧和数据处理方法。
3. 实验器材和方法3.1 实验器材在本实验中使用的器材包括:•测量工具:尺子、千分尺、量角器等•实验设备:天平、温度计、计时器等•电子设备:万用表、数据采集仪等3.2 实验方法本实验分为以下几个步骤:3.2.1 准备工作在进行实验之前,需要对实验器材进行校准和准备。
确保测量工具的准确度和实验设备的正常工作。
3.2.2 实验测量按照实验设计要求,进行一系列物理量的测量。
在测量过程中,尽量减小人为误差的产生,保证数据的准确性。
3.2.3 数据处理将所得到的测量数据整理并进行误差分析。
计算测量数据的平均值、标准偏差等统计量,并绘制相应的图表。
3.2.4 结果分析根据实验数据和误差分析的结果,对实验结果进行讨论和分析。
评估实验的准确性和可靠性,并提出改进措施。
4. 数据处理和结果分析4.1 数据整理将实验测量得到的数据整理成表格或者图表的形式,便于后续的数据处理和结果分析。
4.2 误差分析根据测量数据的统计特征,计算平均值、标准偏差和相对误差等指标,以评估测量结果的准确性和可靠性。
4.3 结果讨论根据误差分析的结果,讨论实验结果的合理性和可靠性。
分析误差的来源,探讨可能的改进方法和实验技巧。
5. 结论通过误差测量与分析实验,我们深入了解了误差的概念、计算方法和对实验结果的影响。
实验结果表明,合理的误差分析可以提高实验结果的准确性和可靠性,并为进一步的研究提供参考。
6. 参考文献[1] 张三,李四. 测量与误差分析实验指导. 出版社,年份.[2] 王五,赵六. 实验数据处理与统计分析. 出版社,年份.注意:本文档为示例文档,实际情况下应根据实验内容和要求进行相应的调整和补充。
实验误差分析实验报告心得

实验误差分析实验报告心得实验误差分析实验报告心得在进行科学实验过程中,误差是不可避免的。
无论是人为操作的不精确,还是仪器设备的限制,都可能导致实验结果与理论值存在差异。
因此,对实验误差进行分析和评估,是保证实验结果准确性和可靠性的重要环节。
1. 引言实验误差分析是实验报告中不可或缺的一部分。
通过对实验误差的分析,可以帮助我们深入了解实验过程中可能存在的问题,并提供改进实验方法和结果解释的依据。
2. 实验误差类型实验误差可以分为系统误差和随机误差两种类型。
系统误差是由于实验设计或仪器设备本身的固有问题而引起的,具有一定的规律性。
而随机误差则是由于实验过程中的偶然因素所导致的,具有不确定性。
3. 实验误差来源实验误差的来源多种多样。
首先,人为操作不准确是常见的误差来源之一。
例如,在称量实验物质时,由于称量手法不规范或读数不准确,就会导致实验结果的误差。
其次,仪器设备的精度也会对实验结果产生影响。
如果使用的仪器精度较低或者校准不准确,就会引入额外的误差。
此外,环境条件的变化也可能对实验结果产生干扰。
例如,温度、湿度等因素的变化都可能对实验结果产生一定的影响。
4. 实验误差评估方法为了评估实验误差的大小和影响程度,我们可以采用一系列的统计学方法。
首先,可以计算实验数据的平均值和标准差,以了解数据的集中趋势和离散程度。
其次,可以绘制误差棒图或误差曲线图,直观地展示实验数据的误差范围。
此外,还可以进行假设检验,以判断实验结果是否与理论值存在显著差异。
5. 实验误差分析案例以化学实验为例,假设我们要测定某种溶液的浓度。
在实验过程中,我们使用了分光光度计测量吸光度,并根据标准曲线计算出溶液的浓度。
然而,在实验中发现,多次重复测量得到的吸光度值存在较大的差异。
通过对实验误差的分析,我们发现可能的误差来源包括:试剂的配制误差、分光光度计的仪器误差以及操作人员读数不准确等。
为了减小误差,我们可以采取以下改进措施:精确称量试剂、校准分光光度计、提高操作人员的技术水平等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
误差测量与处理课程实验
报告
学生:学号:
学院:
专业年级:
指导教师:
年月
实验一 误差的基本性质与处理
一、实验目的
了解误差的基本性质以及处理方法。
二、实验原理
(1)正态分布
设被测量的真值为0L ,一系列测量值为i L ,则测量列中的随机误差i δ为
i δ=i L -0L (2-1)
式中i=1,2,…..n.
正态分布的分布密度 ()()2
2
2f δ
σδ
-=
(2-2)
正态分布的分布函数 ()()2
2
2F e
d δ
δ
σδδ
--∞
=
(2-3)
式中σ-标准差(或均方根误差); 它的数学期望为
()0
E f d δδδ+∞
-∞
==⎰
(2-4)
它的方差为
()22f d σδδδ
+∞
-∞
=⎰
(2-5)
(2)算术平均值
对某一量进行一系列等精度测量,由于存在随机误差,其测得值皆不相同,应以全部测得值的算术平均值作为最后的测量结果。
1、算术平均值的意义
在系列测量中,被测量所得的值的代数和除以n 而得的值成为算术平均值。
设 1l ,2l ,…,n l 为n 次测量所得的值,则算术平均值 121...n
i
n i l l l l x n n
=++=
=∑ 算术平均值与真值最为接近,由概率论大数定律可知,若测量次数无限增加,则算术平均值x 必然趋近于真值0L 。
i v = i l -x
i l ——第i 个测量值,i =1,2,...,;n i v ——i l 的残余误差(简称残差)
2、算术平均值的计算校核
算术平均值及其残余误差的计算是否正确,可用求得的残余误差代数和性质来校核。
残余误差代数和为:
1
1
n n
i
i
i i v l nx ===-∑∑
当x 为未经凑整的准确数时,则有
1
n
i
i v
==∑0
1)残余误差代数和应符合:
当
1n i
i l =∑=nx ,求得的x 为非凑整的准确数时,1n
i
i v =∑为零;
当
1n
i
i l =∑>nx ,求得的x 为凑整的非准确数时,1n
i
i v =∑为正;其大小为求x 时的余数。
当
1
n
i
i l =∑<nx ,求得的x 为凑整的非准确数时,1
n
i
i v =∑为负;其大小为求x 时的亏数。
2)残余误差代数和绝对值应符合:
当n 为偶数时,
1n
i i v =∑≤
2
n
A; 当n 为奇数时,
1
n
i
i v =∑≤0.52n A ⎛⎫- ⎪⎝⎭
式中A为实际求得的算术平均值x末位数的一个单位。
(3)测量的标准差
测量的标准偏差称为标准差,也可以称之为均方根误差。
1、测量列中单次测量的标准差
σ==
式中n—测量次数(应充分大)
i
δ—测得值与被测量值的真值之差
σ=
2、测量列算术平均值的标准差
x
σ=
3、标准差的其他计算法
别捷尔斯法:
n
i
v
σ=
∑
三、实验容:
1.对某一轴径等精度测量9次,得到下表数据,求测量结果。
按下列步骤求测量结果。
1、算术平均值
2、求残余误差
3、校核算术平均值及其残余误差
4、判断系统误差
5、求测量列单次测量的标准差
6、判别粗大误差
7、求算术平均值的标准差
8、求算术平均值的极限误差
9、写出最后测量结果
四、实验总结
运行编制的程序,分析运行结果,并写出实验报告。
%计算算数平均值
L=[24.774,24.778,24.771,24.780,24.772,24.777,24.773,24.775,24.774]; format short
averageL=mean(L);
disp(['数据的平均值averageL=',num2str(averageL)]);
%计算残余误差
vi=L-averageL;
n=length(vi);
disp('各残余误差如下所示:');
%校核算术平均值和其残余误差
for k=1:n
disp(num2str(vi(k)));
end
sumvi=sum(vi(k));
if sum(L)==n*averageL
disp('平均值计算正确');
elseif sum(L)>n*averageL&sumvi>0&sumvi==sum(L)-n*averageL
disp('平均值计算正确');
elseif sum(L)<n*averageL&sumvi<0&sumvi==sum(L)-n*averageL
disp('平均值计算正确');
else disp('平均值计算错误');
end
%判断系统误差
if mod(n,2)~=0
h=(n+1)/2;
else
h=n/2;
end
vi1=vi([1:h]);vi2=vi([(h+1):end]);
sumvi1=sum(vi1);sumvi2=sum(vi2);
delta=sumvi1-sumvi2;
if delta<=1e-2
disp('此次测量无系统误差');
else
disp('此次测量有系统误差');
end
%求单次测量的标准差
xgm1=std(L);disp(['单次测量的标准差:',num2str(xgm1)]);
xgm11=1.253*sum(abs(vi))/sqrt(n*(n-1));
u=xgm11/xgm1-1;
if abs(u)<2/sqrt(n-1)
disp('再次确定测量列无系统误差');
else
disp('再次确定测量列有系统误差');
end
%判别粗大误差
for m=1:n
c=0;
if abs(vi(m))>=3*xgm1
disp(['第',num2str(m),'个数',num2str(L(m)),'含有粗大误差']); L(m)=[];
c=c+1;
else
end
end
if c==0
disp('无粗大误差');
end
%求算术平均值的标准差
xgm2=xgm1/sqrt(n);disp(['算术平均值的标准差:',num2str(xgm2)]);
%求算术平均值的极限误差
t=2.31;
Blimx=t*xgm2;
%写出最后测量结果
disp(['最后测量结果是:',num2str(averageL),'±',num2str(Blimx)]);
运行后的结果如下所示:
数据的平均值averageL=24.7749
各残余误差如下所示:
-0.00088889
0.0031111
-0.0038889
0.0051111
-0.0028889
0.0021111
-0.0018889
0.00011111
-0.00088889
平均值计算正确
此次测量无系统误差
单次测量的标准差:0.0029345
再次确定测量列无系统误差
无粗大误差
算术平均值的标准差:0.00097816
最后测量结果是:24.7749±0.0022595。
