汽车振动分析报告期末复习题(车辆工程专业用)
振动习题——精选推荐

振动习题例1:提升机系统重物重量N W 51047.1?=钢丝绳的弹簧刚度 cm N k /1078.54=重物以v=15m/s 的速度匀速下降时求:绳的上端突然被卡住时,(1)重物的振动频率,(2)钢丝绳中的最⼤张⼒。
解:振动频率s rad Wgk/6.190==ω重物匀速下降时处于静平衡位置,若将坐标原点取在绳被卡住瞬时重物所在位置则 t=0 时,有: 00=x v x =0&振动解:)()6.19sin(28.1)sin()(00cm t t vt x ==ωω )sin()cos()(0000t x t x t x ωωω&+=振动解: )( )6.19sin(28.1)sin()(00cm t t vt x ==ωω绳中的最⼤张⼒等于静张⼒与因振动引起的动张⼒之和:)(1021.21074.01047.1555max N kA W kA T T s ?=?+?=+=+=由于km v vkkA ==0ω为了减少振动引起的动张⼒,应当降低升降系统的刚度例2:重物落下,与简⽀梁做完全⾮弹性碰撞梁长 L ,抗弯刚度 EJ求:梁的⾃由振动频率和最⼤挠度解:取平衡位置以梁承受重物时的静平衡位置为坐标原点建⽴坐标系静变形λ由材料⼒学:EJ mgl 483=λ⾃由振动频率为:λωg =0348ml EJ=撞击时刻为零时刻,则 t=0 时,有:λ-=0xgh x 20=&则⾃由振动振幅为:20020???? ??+=ωx x A &λλh 22+=梁的最⼤扰度:λλ+=A max)sin()cos()(0000t x t x t x ωωω&+=例:圆盘转动圆盘转动惯量 Iθk 为轴的扭转刚度,定义为使得圆盘产⽣单位转⾓所需的⼒矩在圆盘的静平衡位置上任意选⼀根半径作为⾓位移的起点位置由⽜顿第⼆定律:=+θθθk I && 扭振固有频率020=+θωθ&& I k /0θω= 由上例可看出,除了选择了坐标不同之外,⾓振动与直线振动的数学描述是完全相同的。
汽车检测期末复习资料及答案

汽车检测期末复习资料及答案第一篇:汽车检测期末复习资料及答案汽车检测复习资料及答案一、选择题1.下列选项,(A)是汽油发动机启动困难的现象之一。
(A)有着火征兆(B)无着火征兆(C)不能启动(D)顺利启动2.电控燃油喷射发动机燃油压力检测时,将油压表接在供油管和(C)之间。
(A)燃油泵(B)燃油滤清器(C)分配油管(D)喷油器15.主减速器(B)损坏,可引起汽车在转弯时产生异响,而在直线行驶时没有异响。
(A)圆锥齿轮(B)行星齿轮(C)圆柱齿轮(D)轴承16.桑塔纳2000GLS型轿车JV型发动机怠速转速在800±1500r/min时,点火提前角应为(A)。
(A)11o~13o(B)11o~12o(C)10o~11o(D)9o~10o17.温度传感器是(D)传感器。
(A)生物(B)化学(C)生物和化学(D)物理22.变速器倒挡轴与中间轴轴承孔轴线的平行度误差应小于(C)mm。
(A)0.06(B)0~0.06(C)0.10(D)0.06~0.1024.柴油发动机运转不稳,这种故障往往伴随着排气管排出(C)。
(A)白烟而产生敲击声(B)白烟而不产生敲击声(C)黑烟而产生敲击声(D)黑烟不产生敲击声28.汽车后桥壳弯曲校正的方法一般采用(B)校正。
(A)敲击(B)热压(C)冷压(D)火焰29.两只电阻串联时,阻值为10Ω。
并联时阻值为1.6Ω。
则两只电阻阻值分别为(A)。
(A)2Ω和8Ω(B)3Ω和7Ω(C)4Ω和6Ω(D)5Ω和5Ω34.用汽车万用表测量空调出风口湿度时,温度传感器应放在(D)。
(A)驾驶室内(B)驾驶室外(C)高压管路内(D)风道内35.霍尔元件产生的霍尔电压为(A)级。
(A)mv(B)v(C)kv(D)μv36.将220V的交流试灯接在点火线圈一次绕组两端的接线柱上,灯亮,则表示(C)故障。
(A)有断路(B)有搭铁(C)无断路(D)有断路或搭铁39.用剖切平面完全地剖开机件后,所得到的剖视图叫做(A)。
《汽车振动与噪声控制》考试资料

构还必须保持必要间隙。如采用液压挺杆,可从根本上消除气门间隙,从而消除传动中的撞击,并可有效地 控制气门落座速度。从而使得配气机构的噪声显著降低。 ◆发动机燃烧噪声控制措施? (课件版) (1)隔热活塞 采用隔热活塞可提高缸壁温度,缩短滞燃期,降低直喷式柴油机的燃烧噪声。 (2)延迟喷油定时 一般而言,喷油时间早则燃烧噪声大,而喷油时间适当延迟,可减小燃烧噪声。但 喷油过迟,燃烧进入气缸时的空气温度和压力反而变低,从而使着火延迟期延长,燃烧噪声增大。 (3)改进燃烧室结构形状 在其他条件相同的情况下,直喷式燃烧室中的球形和斜置圆桶形燃烧室的燃烧 噪声最低, 分隔式燃烧室的燃烧噪声一般也较低, ω 形直喷式燃烧室和浅盆形直喷式燃烧室的燃烧噪声最大。 (4)调节喷油泵 喷油率对燃烧噪声的影响很大。 试验表明, 喷油率提高一倍, 燃烧噪声就会增加 6dB, 可用减少喷油泵供油率的方法来减少燃烧噪声,但也要注意高速性能的恶化和增加怠速噪声的问题。 (5)废气再循环和进气节流 提高废气再循环率可减少燃烧率,使发动机获得平稳的运转,而进气节流 可使气缸内的压力降低和着火时间延迟,两者结合能有效降低燃烧噪声。 (6)采用增压技术 柴油机增压后可使进入气缸的空气充量密度增加,使压缩终了时气缸内的温度和压 力增高,降低燃烧噪声。 (7)提高压缩比 提高压缩比可以提高压缩终了的温度和压力,缩短着火延迟期,降低燃烧噪声。 (8)改善燃油品质 十六烷值高的燃料着火延迟较短,燃烧过程柔和,燃烧噪声降低。 (9)电子控制 根据转速、负荷、进气温度、燃油温度等精确控制喷油定时,降低燃烧噪声。 (课本版) (1)合理设置延迟喷油定时。通常喷油时间早,产生燃烧噪声大,但过迟喷油时间影响动力特性; (2)合理设计燃烧室形状,改进燃烧室结构形状和参数,不但直接影响柴油机的性能,而且影响着火延迟 期、压力升高率,从而影响燃烧噪声; (3)适当提高压缩比和延迟喷油提前角,使用高十六烷值的燃料,以缩短着火延迟期; (4)采用进气增压,依靠进气压力和温度的增高缩短着火延迟期; (5)调节喷油系喷油率对燃烧噪声的影响非常大,喷油率提高,燃烧噪声就会相应增加,可用减少喷油泵 供油率的方法来减少燃烧噪声,但应注意高速性能的恶化和怠速噪声增加问题。 ◆制动噪声的控制措施? 1.制动器设计时,增加制动鼓的刚性,并减小制动蹄的刚性 增加制动鼓的刚性,可以提高制动鼓的固有频率,减小制动噪声,但不需无限提高鼓的固有频率,当制 动噪声接近环境背景噪声时,鼓的刚性就足够了;降低制动蹄的刚性,使其固有频率降低,并改善摩擦片与 制动鼓的接触及压力分布,可以降低制动噪声。 2.增加制动鼓与制动蹄对振动的衰减 对制动鼓和制动蹄的结构件采用阻尼处理,可以衰减振动能量,降低噪声辐射;在制动鼓和制动蹄的接 触部分,配置减振材料,可以衰减振动。 3.合理匹配制动鼓和制动蹄的刚性 装配后的鼓和蹄的固有频率不是单独设计时的固有频率,而比单独设计时有所增加,并且鼓的固有频率 增加比蹄的固有频率略高。因此,在设计时,可以使鼓的固有频率比蹄的高,制动噪声能够降低。 4.改善摩擦衬片特性和衰减振动的能力 一般情况下,减小摩擦系数、降低制动蹄的刚度、减小摩擦衬片的包角等措施可降低噪声,但是,减小 摩擦系数会降低制动效果,此时必须采取措施,以保证制动容量。 5.盘式制动器优化结构设计 增大制动盘对振动的衰减、限制摩擦衬片振动及控制振动的传播,是盘式制动器优化结构的主要措施。 合理设计零部件结构,限制衬片振动,选用阻尼大的材料等。
车辆工程期末考试试题答案

车辆工程期末考试试题答案一、选择题1. 汽车发动机的四个冲程分别是:进气、压缩、做功和排气。
以下哪个选项不是这四个冲程之一?A. 进气B. 压缩C. 做功D. 制动答案:D2. 以下哪个因素不是影响汽车燃油效率的主要因素?A. 发动机效率B. 车辆重量C. 轮胎气压D. 驾驶者情绪答案:D3. 车辆悬挂系统的主要功能是什么?A. 提供动力B. 支撑车身C. 减震D. 转向答案:C二、简答题1. 请简述车辆制动系统的工作原理。
答案:车辆制动系统通常包括液压制动系统和气压制动系统。
液压制动系统通过踩踏制动踏板,使液压油通过制动主缸推动制动器,从而产生制动力。
气压制动系统则通过压缩空气推动制动器,实现制动。
2. 描述一下车辆传动系统的组成及其功能。
答案:车辆传动系统主要由离合器、变速器、传动轴和差速器组成。
离合器用于控制发动机与变速器之间的连接与断开;变速器用于改变传动比,适应不同的行驶条件;传动轴将动力从变速器传递到差速器;差速器则允许车轮以不同速度旋转,以适应转弯。
三、计算题1. 已知某汽车发动机的排量为2000cc,压缩比为10:1,求其理论最大输出功率(假设燃烧效率为30%)。
答案:首先计算发动机的燃烧室体积,2000cc / 10 = 200cc。
每个冲程中,燃烧室体积的燃料和空气混合物可以产生200cc * 10 = 2000cc的膨胀力。
假设每个冲程产生的压力为P,那么每个冲程的功率为P * 2000cc * 30%。
由于一个工作循环包括四个冲程,所以实际输出功率为P * 2000cc * 30% / 4。
但是,由于没有具体的P值,我们无法直接计算出功率。
四、论述题1. 论述车辆安全性的重要性及其在现代汽车设计中的应用。
答案:车辆安全性是保障驾驶者和乘客生命安全的重要因素。
现代汽车设计中,安全性的应用包括但不限于:防撞结构、安全气囊、防抱死制动系统(ABS)、电子稳定控制(ESC)等。
这些系统和结构能够在碰撞发生时减少伤害,提高车辆的稳定性和操控性,从而降低事故的发生率。
汽车测试技术期末复习题

汽车测试技术期末复习题汽车测试技术是一门涉及汽车性能评估、故障诊断和维护的重要学科。
以下是一些期末复习题,帮助学生巩固知识点:1. 汽车动力性能测试:- 描述汽车动力性能测试的主要内容。
- 解释如何通过加速测试评估汽车的动力性能。
2. 汽车燃油经济性测试:- 阐述燃油经济性测试的目的和方法。
- 讨论影响燃油经济性的主要因素。
3. 汽车制动性能测试:- 描述制动性能测试的步骤和重要性。
- 解释制动距离和制动稳定性的概念。
4. 汽车排放测试:- 列举汽车排放的主要污染物。
- 说明排放测试的流程和标准。
5. 汽车振动和噪声测试:- 描述振动和噪声测试的仪器和方法。
- 分析振动和噪声对驾驶舒适性的影响。
6. 汽车耐久性测试:- 阐述耐久性测试的目的和测试条件。
- 讨论如何通过耐久性测试评估汽车的可靠性。
7. 汽车故障诊断技术:- 列举常见的汽车故障诊断工具和方法。
- 描述故障诊断的基本流程。
8. 汽车维护与保养:- 描述定期维护的重要性和基本步骤。
- 讨论不同部件的保养周期和方法。
9. 汽车测试技术的新发展:- 探讨当前汽车测试技术的新趋势和创新。
- 分析这些新技术如何提高测试的准确性和效率。
10. 案例分析:- 提供一个汽车性能测试的案例,要求学生分析测试结果,并提出可能的改进措施。
复习题的目的是帮助学生系统地回顾和巩固本学期所学的知识,为期末考试做好准备。
希望这些题目能够激发学生的思考,加深对汽车测试技术的理解。
汽车振动分析

汽车振动分析编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(汽车振动分析)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为汽车振动分析的全部内容。
研究生试卷2013 年—2014年度第 2 学期评分:______________________课程名称:振动理论专业:车辆工程年级: 2013级任课教师:李伟研究生姓名:王荣学号: 2130940008注意事项1.答题必须写清题号;2.字迹要清楚,保持卷面清洁;3.试题随试卷交回;4.考试课按百分制评分,考查课可按五级分制评分;5.阅完卷后,授课教师一周内将成绩在网上登记并打印签名后,送研究生部备案;6.试题、试卷请授课教师保留三年被查。
《汽车振动分析》总结王荣(重庆交通大学机电与汽车工程学院重庆 400074)摘要:本课程由浅入深、循序渐进,从单自由度系统的简单问题逐渐加深到多自由度的分析,甚至是无限自由度系统,并从简单激励的振系逐渐推广到随机激振振系。
作为汽车理论及汽车设计等课程的基础,其对于分析汽车的行驶平顺性、乘坐舒适性、发动机的减振和隔离等具有良好的参考价值。
关键词:单自由度;多自由度;简单激振;随机激振The Conclusion of “Automotive VibrationAnalysis”Abstract: The course progressively, step by step, gradually discusses from the simple question of a single degree of freedom system to the analysis of a multi—degree of freedom system, even to the analysis of the infinite degree of freedom system. In addition, the course extends from simple energized vibration system to random energized vibration system. As the basis of Vehicle Theory and Vehicle Design, this course has direct reference value for the analysis of vehicle ride, comfort of passenger, engine vibration damping and isolation.Keywords:Single-Degree—of-Freedom; Multi—Degree—of—Freedom; Simple Energized Vibration System ;Random Energized Vibration System0 引言随着科学技术的日新月异和人民生活水平的日益提高,人们对汽车的动态性能,例如:汽车行驶的舒适性,操纵的稳定性,车内噪声水平及音质等等——提出了愈来愈高的要求。
汽车工程期末考试试题

汽车工程期末考试试题### 汽车工程期末考试试题#### 一、选择题(每题2分,共20分)1. 汽车发动机的四个冲程中,哪个冲程是对外做功的?A. 进气冲程B. 压缩冲程C. 做功冲程D. 排气冲程2. 以下哪个不是汽车传动系统的主要组成部分?A. 变速器B. 差速器C. 转向系统D. 驱动轴3. 汽车制动系统的主要作用是什么?A. 提高车速B. 保持车速C. 减速或停车D. 转向4. 现代汽车中,哪个系统负责控制发动机的燃油供应?A. 点火系统B. 排放控制系统C. 燃油喷射系统D. 冷却系统5. 以下哪个因素不会影响汽车的燃油经济性?A. 发动机效率B. 车辆重量C. 轮胎气压D. 驾驶习惯...(此处省略剩余选择题)#### 二、简答题(每题10分,共30分)1. 简述汽车发动机的工作原理,并说明其对环境可能产生的影响。
2. 解释什么是ABS(防抱死制动系统),并说明其在汽车安全中的作用。
3. 描述汽车悬挂系统的基本功能,并简要说明不同类型的悬挂系统。
#### 三、计算题(每题15分,共30分)1. 假设一辆汽车在水平路面上以恒定速度行驶,其发动机输出功率为75千瓦,轮胎与路面的摩擦系数为0.7。
请计算该汽车的牵引力。
2. 某汽车在紧急制动时,其制动距离为40米,初速度为20米/秒。
如果制动过程中的减速度是恒定的,请计算该汽车的减速度。
#### 四、论述题(20分)1. 论述新能源汽车与传统燃油汽车在环境影响、能源效率和经济性方面的比较。
#### 五、案例分析题(20分)1. 假设你是一名汽车工程师,你的团队正在设计一款新型电动汽车。
请分析在设计过程中需要考虑的关键因素,并提出你的设计方案。
注意:- 请在答题纸上清晰、准确地书写答案。
- 确保你的答案逻辑清晰,论点明确。
- 计算题需要写出详细的计算过程和最终答案。
祝你考试顺利!。
汽车振动学复习题

汽车振动学复习题一、填空题1、不同情况进行分类,振动系统大致可分成(线性振动)和非线性振动;确定振动和(不确定振动);(自由振动)和强迫振动;周期振动和(非周期振动);(连续系统)和离散系统。
2、在离散系统中,弹性元件储存(势能),惯性元件储存(动能),(阻尼)元件耗散能量。
3、周期运动的最简单形式是(简谐振动),它是时间的单一(正弦)或(余弦)函数。
4、叠加原理是分析(线性系统)的振动性质的基础。
5、叠加原理在( 线性振动系统 )中成立,在一定的条件下,可以用线性关系近似( 非线性关系 )。
6、系统的固有频率是系统(本身)的频率,它只与系统的(刚度)和(质量)有关,与系统受到的激励无关。
7、周期运动可以用( 简谐函数 )的( 级数 )形式表示。
8、根据系统、激励与响应的关系,常见的振动问题,可以分为( 振动设计 )、( 系统识别 )和( 环境预测 )三类基本课题。
二、简答题1、简述振动系统的实际阻尼、临界阻尼、阻尼比的联系与区别。
答:实际阻尼是指振动系统的真实阻尼值,用于度量系统自身消耗振动能量的能力;临界阻尼是概念阻尼,是指一个特定的阻尼值,大于或等于该阻尼值,系统的运动不是振动,而是一个指数衰运动;阻尼比等于实际阻尼与临界阻尼之比。
2、在分析振动系统时,为什么要进行线性化处理?线性化的方法有哪些?答:P23、多自由度系统振动的振型指的是什么?机械系统某一给定振动模态的振型,指在某一固有频率下,由中性面或中性轴上的点偏离其平衡位置的最大位移值所描述的图形。
4、简述线性多自由度系统动力响应分析方法。
多自由度系统在外部激励作用下的响应分析称为动力响应分析;常用的动力响应分析方法有振型叠加法和变换方法(傅里叶变换或拉普拉斯变换);当系统的质量矩阵、阻尼矩阵、刚度矩阵可以同时对角化的时候,可以把系统的运动微分方程解藕,得到一组彼此独立的单自由度运动微分方程,求出这些单自由度运动微分方程的解后,采用振型叠加,即可得到系统的动力响应;傅里叶变换或拉普拉斯变换就是对各向量做傅里叶变换和拉普拉斯变换,得到的系统的频响函数矩阵或传递函数矩阵,然后进行傅里叶逆变换或拉普拉斯逆变换得到系统的响应。
汽车振动分析作业习题与参考答案(更新)
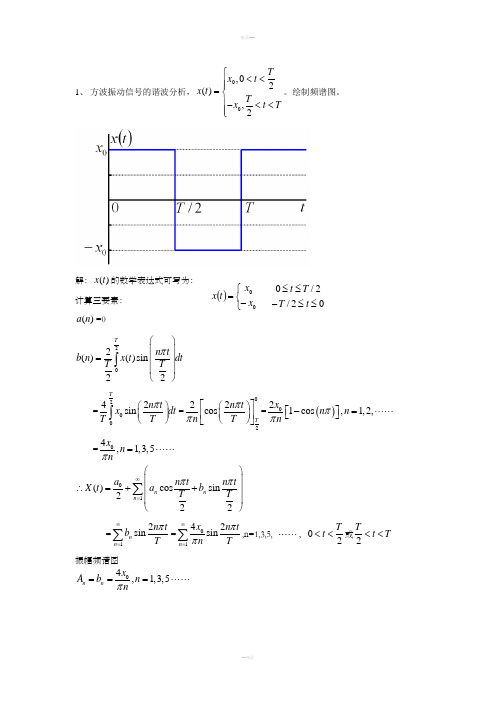
1、 方波振动信号的谐波分析,00,02(),2T x t x t T x t T⎧<<⎪⎪=⎨⎪-<<⎪⎩。
绘制频谱图。
解:()x t 的数学表达式可写为: 计算三要素:()a n =0202()()sin 22Tn t b n x t dt T T π⎛⎫ ⎪= ⎪⎪⎝⎭⎰=20042sin Tn t x dt T T π⎛⎫ ⎪⎝⎭⎰=0222cos T n t n T ππ⎡⎤⎛⎫ ⎪⎢⎥⎝⎭⎣⎦=()021cos ,1,2,x n n n ππ-=⋅⋅⋅⋅⋅⋅⎡⎤⎣⎦ =4,1,3,5x n nπ=⋅⋅⋅⋅⋅⋅ 01()cos sin 222n n n a n t n t X t a b T T ππ∞=⎛⎫ ⎪∴=++ ⎪ ⎪⎝⎭∑=12sin n n n t b T π∞=∑=0142sin n x n t nT ππ∞=∑,n=1,3,5, ⋅⋅⋅⋅⋅⋅,02T t <<或2Tt T <<振幅频谱图4,1,3,5n n x A b n nπ===⋅⋅⋅⋅⋅⋅ ()⎩⎨⎧≤≤-≤≤-=02/2/00t T T t x x t x相位频谱图1tan 0,1,3,5nn n a n b φ-⎛⎫===⋅⋅⋅⋅⋅⋅⎪⎝⎭2、 求周期性矩形脉冲波的复数形式的傅立叶级数,绘频谱图。
解: 数学表达式:计算三要素:傅立叶级数复数形式:频谱图0000,0sin ,0,n x t n TA x n t n n n T ππ⎧=⎪⎪=⎨⎪≠-∞<<∞⎪⎩()⎪⎪⎪⎩⎪⎪⎪⎨⎧≤≤≤≤--≤≤-=220222200000T t t t t t x t t T t x 偶函数 T x t a 0002=2sin 2010tn n x a n ωπ⋅=0=n b 2sin 22010tn n x a ib a X n n nn ωπ⋅==-=()2sin 1101012/2/02/2/102/2/02/2/010********t n n x tin e e T x t in e T x dt e x T dt e t x T X t in t in t t t in t in t t tin T T n ωπωωωωωωω⋅=--⋅=-⋅=⋅⋅=⋅⋅=-------⎰⎰T t x t n n x X n 00010002sinlim =⋅=→ωπ()∑∑∞-∞=∞-∞===n tin n t in n e n t n x e X t x 112sin 010ωωωπ2.1解:(1)能量法222341222111()()222e a a k x k x k x a a += 2232122244e a a k k k a a ∴=+(2)能量法222 (1214)111222e a m x m x m x a ⎛⎫+= ⎪⎝⎭212124e a m m m a ∴=+(3)固有频率222132224211e e k a k a k p m a m a m +==+2.3解:平衡位置系统受力如图 则122,2F G F G == 弹簧1k 变形112G x k =,弹簧变形222Gx k =,且m 静位移1222x x x =+ 12124422e G G Gx x x k k k ∴==+=+ ()1212,4e e k k k m m k k ∴==+∴固有圆频率()121212e e k k k p m k k m==+2.5解对数衰减率:111110ln ln 0.06920 2.5j A j A δ+=== 相对阻尼系数:22110.01122110.069ζππδ===⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭衰减系数:9.80.0110.3140.012n k g n ms ζωζζ===== 阻尼系数:220.3149 5.652(/)c nm N s m ==⨯⨯= 临界阻尼: 5.652513.8(/)0.011c cc N s m ζ=== 2.7解受力分析如图-xs ’)单自由度振动系统振动微分方程()2022s sn n n smx c x x kx mx cx kx cx x x x x ζωωζω+-+=∴++=∴++=设iwtcs x e =,则()c cs x H x ω=22222()212n n n i iH i iζωωζλωωωζωωλζλ∴==-+-+()H ω=,相位差角:122tan ()12ζλπϕλ-=--()()()()()i iwt i wt s x t H x t H e ae ϕϕωω--===()0sin )s x a t x t t ωωϕ=∴=-Xa =其中,n ωλω==ζ= 2.8 解:1、 系统的振动微分方程为:0=⎪⎭⎫ ⎝⎛-+++•••s x x k kx x c x m即:s kx kx x c x m =++2激励函数为:()T t t Tdk kx s ≤≤=0 傅立叶级数三要素:kd tdt T dk T a T ==⎰002()0cos 20=⋅=⎰dt nwt t T dk T a T n()πn kd dt nwt t T d k T b T n -=⋅=⎰sin 20所以,激励函数的前四项为:()()()∑=⋅+⋅+=41sin cos 2n n n s t n b t n a a kx ωω)4sin 413sin 312sin 21(sin 2wt wt wt wt d k d k+++-=π 系统稳态响应的前三项为:])6()91(3)3sin()4()41(2)2sin()2()1()sin([24)2()1(2)sin(4222322222221312222ζλλψζλλψζλλψπλζλψ+--++--++---=+--+=∑=wt wt wt dd n n k nwt b d x n n n 其中3,2,1,12arctan22=-=n n n n λλζψ2.9 解:运用杜哈美积分法())]03.0sin()02.0(sin(50)03.0cos()02.0cos(5.0[)03.0sin()03.0(sin )(1)03.0sin(03.0)];01.0sin(50)01.0cos(5.0[)01.0sin()01.0(sin )50(1)01.0sin(01.0);01.00(50)(;)(sin )(1sin )(sin )(1sin )/(cos 20001.0020001.00000000000.0p p p p p mpF p p d p f mp p p x s t p p p mp F p pd p F F mpp px s t t t F F t f d t p f mppt p d t p f mp pt p x pt x t t t ---+=-+==+-+=--+==≤≤-=-+=-+⎪⎭⎫ ⎝⎛+=⎰⎰⎰⎰υτττυυτττυτττυτττχ时,当时,当4.1解直接法()11121221111221222213222212320()0()0()0m x k k x k x m x k x k x x m x k x x k x m x k x k k x ++-=⎧+--=⎧⎪⇒⎨⎨+-+=-++=⎪⎩⎩122111223222000k k k m x x k k k m x x +-⎡⎤⎡⎤⎡⎤⎡⎤∴+=⎢⎥⎢⎥⎢⎥⎢⎥-+⎣⎦⎣⎦⎣⎦⎣⎦其中,122223k k k K k k k +-⎡⎤=⎢⎥-+⎣⎦拉格朗日法系统为无阻尼自由振动系统,拉格朗日方程形式为:0ii id TT Udt q q q δδδδδδ⎛⎫-+= ⎪⎝⎭ 广义坐标为:12,x x2211221122T m x m x =+ 0,1,2iTi x δδ== 111111,T d T m x m x x dt x δδδδ⎛⎫== ⎪⎝⎭222222,T d T m x m x x dt x δδδδ⎛⎫== ⎪⎝⎭()2221122132111222U k x k x x k x =+-+ 112212213212(),()U U k x k x x k x x k x x x δδδδ=--=-+ ∴()11121221111221222213222212320()0()0()0m x k k x k x m x k x k x x m x k x x k x m x k x k k x ++-=⎧+--=⎧⎪⇒⎨⎨+-+=-++=⎪⎩⎩影响系数法令121,0x x ==11112112k k x k x k k =+=+ 2112212k k k x k ==-=-令120,1x x ==22223223k k x k x k k =+=+122223k k k K k k k +-⎡⎤∴=⎢⎥-+⎣⎦4.2解:直接法∴111213311113112332212123222111222333232331333122233()()0()0()()0()0()()0()0J k r k r J k r k r k r k r J k r k r J k r k r k r k r J k r k r J k r k r k r k r θθθθθθθθθθθθθθθθθθθθθθθθθθθ⎧⎧----=++--=⎪⎪+---=⇒-++-=⎨⎨⎪⎪+-+-=--++=⎩⎩ ∴12300100000100001J M J J J ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦131311223223211121112k r k rk r k r K k rk r k r k r kr k rk rk r k r +----⎡⎤⎡⎤⎢⎥⎢⎥=-+-=--⎢⎥⎢⎥⎢⎥⎢⎥--+--⎣⎦⎣⎦4.3解a,1234mmMmm⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,1222233334444k k kk k k kKk k k kk k+-⎡⎤⎢⎥-+-⎢⎥=⎢⎥-+-⎢⎥-⎢⎥⎣⎦b,1234mmMmm⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,222233334444k kk k k kKk k k kk k-⎡⎤⎢⎥-+-⎢⎥=⎢⎥-+-⎢⎥-⎢⎥⎣⎦c,1234mmMmm⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦,12222333344443k k kk k k kKk k k kk k k+-⎡⎤⎢⎥-+-⎢⎥=⎢⎥-+-⎢⎥-+⎢⎥⎣⎦4.4解:质心位于距左端34l处0324l m xdx mllx lm⎛⎫+⎪==⎪⎪⎝⎭⎰令1,0xθ==11211223442 k kx kx kl kl k k kx kx l=+===-=-令0x=,1θ=22233544448l l k k k l l kl θθ=+= ∴刚度矩阵为,222528kl kK kl kl ⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦令1,0x θ==1122m mx m ∴==21120m m ==令0,1x θ==222524m I ml θ==,3222445()424ll m l I x dx m ml l -=+=⎰∴质量矩阵为,2205024mM ml ⎡⎤⎢⎥=⎢⎥⎣⎦22202205502428kl mk x x klml kl θθ⎡⎤-⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥∴+=⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥-⎣⎦⎢⎥⎣⎦特征矩阵为,22222222552824n n nkl k m H K M kl kl ml ωωω⎡⎤--⎢⎥=-=⎢⎥⎢⎥--⎢⎥⎣⎦将20n H K M ω=-=整理为,22422221440335n n m ll km k l ωω-+=求得特征值为,2120.735k k m m ω⎛=≈ ⎝,222 3.265k k mm ω⎛=+≈ ⎝ 2n H K M ω=-的伴随阵,2222558242222n n kl kl ml adjH kl k m ωω⎡⎤-⎢⎥=⎢⎥⎢⎥-⎢⎥⎣⎦将22120.735, 3.265k km mωω==代入 得对应特征向量,1211,1.0599.06A A l l ⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦则主振型矩阵为,111.0599.06A l l ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦模态质量矩阵为21111201.0599.06 1.0599.065024TT P mM A MA ml l l l l ⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==--⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦2.2340019.1mm ⎡⎤=⎢⎥⎣⎦模态刚度矩阵为21111221.0599.06 1.0599.06528TT P kl k K A KA kl kl l l l l ⎡⎤-⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥--⎢⎥⎢⎥⎢⎥-⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎣⎦1.6420062.362kk ⎡⎤=⎢⎥⎣⎦归一化因子为,i α==∴归一化因子方阵,0.669000.229R ⎤=⎥⎦ ∴正则振型矩阵为,110.6690.2290.66901.0599.060.708 2.07500.229N A AR ll l l ⎡⎤⎡⎤⎡⎤⎢⎥⎥===--⎢⎥⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦⎦正则模态质量矩阵为,20.6690.2290.6690.229200.9990.0000.7082.0750.708 2.07550.000 1.002024TTN N N mM A MA ml ll l l ⎡⎤⎡⎤⎡⎤⎡⎤⎥⎥⎢===--⎢⎥⎢⎥⎢⎥⎢⎣⎦⎢⎥⎢⎥⎣⎦⎦正则模态刚度矩阵为,20.6690.2290.6690.22920.7340.00020.7082.0750.708 2.07550.0003.16528T TN N N kl kk K A KA kl m kl l l l l ⎡⎤-⎡⎤⎡⎤⎢⎥⎡⎤⎥⎥===⎢--⎢⎥⎢⎥⎢⎥⎣⎦⎢-⎢⎥⎢⎥⎦⎦⎢⎣⎦第一阶主振型示意图,1N 为节点1第二阶主振型示意图,2N 为节点1.265习题4.6解:(1)直接法,受力如图f f k mz)r r l ϕ2m ρϕ2()()0()()0r r f f r r r f f f mz k z l k z l m k z l l k z l l ϕϕρϕϕϕ+++-=⎧⎪⎨++--=⎪⎩222()()0()()0f r r r f f r r f f r r f f mz k k z k l k l m k l k l z k l k l ϕρϕϕ+++-=⎧⎪⇒⎨+-++=⎪⎩ 运动微分方程为222000f r r r f f r rf f r r f f k k k l k l mz z k l k lk l k l m ρϕϕ+-⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥-+⎣⎦⎣⎦⎣⎦⎣⎦ 特征矩阵为222222f r r r f fr r f f r r f f k k m k l k l H K M k l k l k l k l m ωωωρ⎡⎤+--=-=⎢⎥-+-⎢⎥⎣⎦由20H K M ω=-=得()()2422222()0f r r r f f f r f r m k k m kl k l m k k l l ρωρω⎡⎤-+++++=⎣⎦21ω=22ω=H 的伴随矩阵22222r r f ff f r r f f r r f r k l k l m k l k l adjH k l k l k k m ωρω⎡⎤+--=⎢⎥-+-⎢⎥⎣⎦将固有频率21ω、22ω代入adjH ,得主振型:22(1)(2)1211,f r f r f f r r f f r r k k m k k m A A k l k l k l k l ωω⎡⎤⎡⎤⎢⎥⎢⎥+-+-==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦(2)f f r r k l k l = 则运动微分方程变为22200000f r r r f f k k mz z k l k l m ρϕϕ+⎡⎤⎡⎤⎡⎤⎡⎤+=⎢⎥⎢⎥⎢⎥⎢⎥+⎣⎦⎣⎦⎣⎦⎣⎦ z自由度的固有频率为ω=ϕ自由度的固有频率为ω=两运动互不相关 (3)2f r l l ρ=()()21,22fr f f r r f f r rf rll k l k l k l k l ml l ω++±-=若f f r r k l k l >()()2212,f r rf r ffrl l k l l k ml ml ωω++==,(1)(2)111,1f r A A l l ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦⎣⎦若f f r r k l k l <()()2212,f r ff r rrfl l k l l k ml ml ωω++==,(1)(2)111,1f r A A l l ⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥⎣⎦⎣⎦4.9柔度矩阵 F=1111122123k ⎡⎤⎢⎥⎢⎥⎢⎥⎣⎦刚度矩阵 K=1210121011F k --⎡⎤⎢⎥⎢⎥=--⎢⎥⎢⎥-⎣⎦质量矩阵 000000J M J J ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦所以222362422322025600nn nn n n nk J kH K M k k J kJ J k Jk k kk J ωωωωωωω--=-=---=-+-+=--解得:2(1)2(2)2(3)0.2, 1.5, 3.2nn n k k k J J Jωωω===(1)(2)(3)N1111.80.5 1.22.240.750.441111.80.5 1.22.240.750.440.330.740.62A0.60.370.740.740.560.27P0.5TCpA A AA⎡⎤⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥===-⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥∴=-⎢⎥⎢⎥-⎣⎦∴⎡⎤⎢⎥⎢⎥=-⎢⎥⎢⎥-⎣⎦=对应主振型正则振型矩阵TN NPNiNi2Pi PiN0.67P A P0.11.5T sin t0.249.26000 1.81000 2.634.07k00K K00.75k0008.97kPXK M0.6XTP p PTp PJA MA JJA Aωω⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥∴==-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦=-∴=质量模态矩阵 M刚度模态矩阵简谐力作用下2222N N2274.07k9.26J0.110.75k1.81J0.248.97k 2.63J0.0094.07k9.26J0.539X=A X0.75k1.81J0.4938.97k 2.63Jωωωωωω⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥-⎢⎥⎢⎥-⎣⎦∴-⎡⎤⎢⎥-⎢⎥⎢⎥=⎢⎥-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦物理坐标下位移响应4.102222(1)2(2)(1)(2)P TP P Pi Pi i i 0202202113,,A ,A 1111A 11Q 0P P A P Q 2Q X P (1cos t)/n nnnn m k k M K m kk k mk H K M kk mk k m m ωωωωωωω-⎡⎤⎡⎤==⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦--∴=-==--⎡⎤⎡⎤∴====⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎡⎤∴=⎢⎥⎢⎥-⎣⎦⎡⎤⎡⎤=∴==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦=-对应主振型由杜哈梅积分得2P 2P P 0m X 2k Q(1cos t)312mQ X A X (13k 1ω⎡⎤⎢⎥∴=⎢⎥-⎢⎥⎣⎦⎡⎤∴==-⎢⎥⎢⎥⎣⎦5.1 解:系统质量刚度矩阵分别为22,2m kk m k k k M K m kk k m kk -⎡⎤⎡⎤⎢⎥⎢⎥--⎢⎥⎢⎥==⎢⎥⎢⎥--⎢⎥⎢⎥-⎣⎦⎣⎦第一瑞丽商:假设21111112111112111,0.2;2211111222;1233123411,0.1234;22111112221,0.112331234TTTT A KA k A p A MA m A MA k p A MFMA m k p trD m⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥===⎢⎥⎢⎥⎣⎦⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎣⎦1则第二瑞丽商:1系统柔度矩阵 F=k 假设 A 则邓克莱法:m D=FM=则k这三种方法中,第二瑞丽商精度最高,邓克莱法计算结果偏小。
汽车振动分析解析习题三

汽车振动分析解析习题三引言汽车振动是指汽车行驶过程中由于道路不平整、发动机工作不平稳等因素引起的车辆部件的振动现象。
对汽车的振动进行分析解析,不仅可以帮助我们了解振动现象的成因和特性,还可以为汽车设计和优化提供参考。
本文将介绍汽车振动分析解析的习题三,包括问题描述、求解过程和最终结果。
问题描述一辆汽车行驶在一条水平道路上,假设汽车的质量为m,发动机输出功率为P,行驶速度为v。
已知汽车的弹簧刚度为k,阻尼常数为c。
现在要求分析汽车的振动情况。
求解过程步骤一:建立力学模型由于汽车行驶过程中存在许多力的作用,为了简化问题,我们可以将汽车视为一个单自由度弹簧振子模型。
汽车的质量可以视为振子的质量,弹簧刚度和阻尼常数可以视为振子的弹簧刚度和阻尼常数。
步骤二:列出振动方程根据单自由度振子的运动方程,可以得到汽车振动的微分方程为:m * x'' + c * x' + k * x = F(t)其中,m为振子的质量,x为振子的位移,c为振子的阻尼常数,k为振子的弹簧刚度,F(t)为外力的作用。
在本问题中,外力即为汽车产生的振动力。
步骤三:求解振动方程根据振动方程,我们可以求解该微分方程并得到振动的解析解。
由于本问题涉及到汽车行驶的情况,我们需要考虑发动机的工作状态和道路的不平整程度。
步骤四:分析振动情况通过解析解,我们可以对汽车的振动情况进行分析。
可以研究振动的频率、振幅、相位等特性,并与实际情况进行比较。
通过分析振动情况,可以了解振动的成因,进一步优化汽车的设计和改善行驶舒适性。
最终结果通过以上求解过程和振动分析,我们可以得知汽车振动的特性,并进行进一步的优化和改进。
同时,我们也能更好地了解汽车行驶过程中振动的成因,为汽车的设计和行驶舒适性提供参考。
总结本文介绍了汽车振动分析解析的习题三,包括问题描述、求解过程和最终结果。
通过分析汽车的振动情况,我们可以更好地了解振动的成因和特性,并为汽车的设计和优化提供参考。
汽车振动学习题解答

sin( d dt) dv en (t )d
en (t ) v
n
则
I2
n (cost ent cosdt) ( d )(sint ent sin dt)
2 2 n
(
d
)2
x(t) F0
2md
t 0
en (t )
cos(
d
dt)d
t 0
en (t )
cos(
d
dt)d
0.2389
2
nTd
n
Td
3.9242rad / s
又知 所以
n2
k m
2 n
c m
F0 2N
X
m
k
n2
c 2m
3rad / s
F0
31.8195 kg
n 59.66 Ns / m
0.7645
n 7.41mm
k (1 2 )2 (2)2
2 arctan 1 2
41.32o
2t
2
sin
4t
xp
R
2
cos t
R l
2
cos 2t
1 12
R l
3
2
cos 2t
cos 4t
因此 f2 (t) m2 xp
m2 R
2
cos
t
R l
cos
2t
1 12
R l
3
cos
2t
cos
4t
从而 f (t) f1(t) f2 (t)
(m1
m2
)R
2
cos t
m2 R
2
R l
cos
2t
汽车振动学考试及答案

汽车振动学考试及答案一、单项选择题(每题2分,共20分)1. 汽车振动的来源主要包括()。
A. 发动机B. 传动系统C. 悬挂系统D. 所有以上选项答案:D2. 汽车振动分析中,以下哪个参数不是基本参数()。
A. 自然频率B. 阻尼比C. 模态质量D. 功率答案:D3. 汽车振动控制中,以下哪个方法不是常用的振动控制方法()。
A. 阻尼减振B. 隔振C. 吸振D. 增压答案:D4. 汽车振动分析中,以下哪个不是振动模态分析的步骤()。
A. 数据采集B. 数据处理C. 模态参数识别D. 振动测试答案:D5. 汽车振动分析中,以下哪个参数不是振动响应分析的基本参数()。
A. 振动加速度B. 振动速度C. 振动位移D. 振动频率答案:D6. 汽车振动分析中,以下哪个不是振动测试的基本要求()。
A. 测试信号的线性B. 测试信号的稳定性C. 测试信号的随机性D. 测试信号的重复性答案:C7. 汽车振动分析中,以下哪个不是振动控制的目标()。
A. 降低振动幅度B. 减少振动频率C. 提高乘坐舒适性D. 延长汽车使用寿命答案:B8. 汽车振动分析中,以下哪个不是振动模态分析的基本参数()。
A. 模态频率B. 模态阻尼比C. 模态质量D. 模态形状答案:B9. 汽车振动分析中,以下哪个不是振动测试的基本设备()。
A. 振动传感器B. 信号放大器C. 数据采集器D. 振动控制器答案:D10. 汽车振动分析中,以下哪个不是振动控制的基本方法()。
A. 阻尼减振B. 隔振C. 吸振D. 振动放大答案:D二、多项选择题(每题3分,共15分)11. 汽车振动的来源主要包括()。
A. 发动机B. 传动系统C. 悬挂系统D. 轮胎答案:ABCD12. 汽车振动分析中,以下哪些参数是基本参数()。
A. 自然频率B. 阻尼比C. 模态质量D. 模态形状答案:ABCD13. 汽车振动控制中,以下哪些方法是常用的振动控制方法()。
运输设备振动分析与减震设计考核试卷

A.阻尼损耗
B.摩擦损耗
C.热损耗
D.所有以上概念
19.以下哪个不是运输设备振动的常见危害?()
A.降低乘坐舒适度
B.增加噪音污染
C.减少燃料消耗
D.降低设备寿命
20.在减震设计中,以下哪个方法可以提高系统的阻尼比?()
A.增加质量
17. AC
18. ABCD
19. ABCD
20. ABCD
三、填空题
1.频率幅值相位
2.噪音振动
3.时域频域模态
4.振动能量
5.结构
6.阻尼自然频率
7.橡胶空气弹簧金属弹簧
8.质量刚度
9.降低增加阻尼
10.结构阻尼材料技术
四、判断题
1. ×
2. ×
3. √
4. ×
5. √
6. ×
7. ×
8. ×
9. √
2.减震设计的目的是为了减小运输设备在运行过程中的______和______。
3.振动分析的主要方法有______分析、______分析和______分析。
4.减震器的主要功能是消耗振动能量,减少______的传递。
5.在振动测试中,加速度传感器通常用来测量______的振动。
6.振动的幅值与______和______有关。
A.结构裂纹
B.噪音增大
C.行驶稳定性下降
D.所有以上现象
6.以下哪些材料可以作为减震元件使用?()
A.橡胶
B.空气弹簧
C.金属弹簧
D.磁性材料
7.在进行振动测试时,以下哪些参数需要记录?()
A.振动的频率
B.振动的幅值
铁路车辆振动分析与减振技术考核试卷

4.振动分析帮助识别轨道维护需求,悬挂设计优化提升舒适度,减振技术应用降低维修成本,提高运行安全性和乘客满意度。
A.优化轨道设计
B.使用减振性能更好的悬挂系统
C.提高列车运行速度
D.定期进行轨道维护
15.在铁路车辆振动分析中,以下哪些模型被广泛应用?()
A.多体动力学模型
B.有限元模型
C.统计模型
D.经验模型
16.以下哪些是被动减振器的主要特点?()
A.结构简单
B.成本较低
C.需要外部能源输入
D.减振效果固定
(结束)
二、多选题(本题共20小题,每小题1.5分,共30分,在每小题给出的四个选项中,至少有一项是符合题目要求的)
1.铁路车辆振动会对以下哪些方面产生影响?()
A.乘客的舒适度
B.轨道的维护成本
C.车辆的结构完整性
D.列车的运行速度
2.以下哪些是铁路车辆减振技术的目标?()
A.降低车辆与轨道的相互作用力
B.有限元模型
C.神经网络模型
D.集成电路模型
19.以下哪种减振器根据其工作原理属于被动减振器?()
A.主动磁流变液减振器
B.自适应空气弹簧悬挂
C.传统液压减振器
D.电子控制悬挂
20.在高速列车中,以下哪个因素对振动控制的影响最小?()
A.车辆与轨道的匹配
B.车辆的设计速度
C.列车运行的气候条件
D.乘客的分布
B.车辆悬挂系统设计不当
C.车辆超载
D.气候变化
2.减振技术主要目的是为了改善下列哪一项?()
汽车振动分析第二章+-+强迫振动其他激励-副本

(k m 2 ic )Bei(t ) a(k ic )eit
Bei
a k
k ic m 2 ic
稳态响应的幅值:
B Bei
a
k
k ic m 2 ic
k ic
a
k m 2 ic
a
k 2 (c)2 (k m 2 )2 (c)2
a
1 (2)2 (1 2 )2 (2)2
汽车振动分析
授课对象:本科生 学科专业:车辆工程 授 课:黄雪涛
电话:15634886176
第一章单自由度系统的振动
1 单自由度振动系统 2 单自由度无阻尼自由振动 3 单自由度有阻尼自由振动
4 强迫振动
教学内容
一、偏心质量引起的强迫振动 二、支座引起的强迫振动 三、工程中的受迫振动问题
引言
常用机械中包含着大量的作旋转运动的零部件,例如各种 传动轴、主轴、电动机和汽轮机的转子等,统称为回转体。
支承的运动规律: xs a sin t
mx c(x xs ) k(x xs ) 0 整理: mx cx kx kxs cxs
mx cx kx kasint ca cost
弹簧传递过来的激振力 kxs 阻尼器传递过来的激振力 cxs
采用复数解法: 支承运动 xs aeit
解:(1)共振时的振幅
Bmax
me
2 M
0.1m
e 0.1m
(2)若要使系统共振时振幅为0.01 m
Bm a x
1
2
me M M
0.01m
M 9 M
二、支座引起的强迫振动
❖ 简谐振动不一定都是由激励力引起,振系支座的周期 性运动同样可使振系发生强迫振动,如机器振动引起 的仪表振动,汽车驶过不平路面产生的振动等
车辆工程考试及答案

车辆工程考试及答案一、单项选择题(每题2分,共20分)1. 汽车的动力源是()。
A. 电池B. 发动机C. 电动机D. 燃料电池答案:B2. 车辆工程中,车辆的总质量是指()。
A. 空车质量B. 车辆自重C. 车辆自重加上载重D. 车辆自重加上乘客和货物的重量答案:D3. 车辆的制动距离与下列哪个因素无关?()A. 车速B. 制动器类型C. 路面状况D. 车辆颜色答案:D4. 车辆的燃油经济性通常用()来衡量。
A. 马力B. 扭矩C. 百公里油耗D. 加速度答案:C5. 车辆的转向系统包括()。
A. 转向盘和转向器B. 转向盘和转向灯C. 转向盘和雨刷器D. 转向盘和制动器答案:A6. 车辆的悬挂系统主要作用是()。
A. 增加车辆的载重能力B. 减少车辆的摩擦力C. 吸收路面不平造成的冲击D. 提高车辆的加速度答案:C7. 车辆的排放标准中,欧VI标准指的是()。
A. 欧洲第六阶段排放标准B. 欧洲第五阶段排放标准C. 北美第六阶段排放标准D. 亚洲第六阶段排放标准答案:A8. 车辆的ABS系统的主要作用是()。
A. 提高车辆的加速度B. 减少车辆的油耗C. 减少车辆的制动距离D. 防止车辆在紧急制动时发生侧滑答案:D9. 车辆的ESP系统是指()。
A. 电子稳定程序B. 电子制动力分配系统C. 电子助力转向系统答案:A10. 车辆的CVT是指()。
A. 连续可变变速器B. 离合器变速器C. 双离合变速器D. 自动变速器答案:A二、多项选择题(每题3分,共15分)11. 以下哪些是车辆工程中常见的动力传递系统?()A. 手动变速器B. 自动变速器C. 无级变速器答案:ABCD12. 车辆的安全性包括哪些方面?()A. 主动安全B. 被动安全C. 环境安全D. 经济安全答案:ABC13. 车辆的底盘系统包括哪些部分?()A. 发动机B. 变速器C. 悬挂系统D. 转向系统答案:BCD14. 车辆的环保性能主要体现在哪些方面?()A. 排放标准B. 噪音控制C. 能源消耗D. 材料回收答案:ABCD15. 车辆的舒适性包括哪些方面?()A. 座椅舒适度B. 噪音控制C. 空调效果D. 驾驶稳定性答案:ABCD三、判断题(每题2分,共20分)16. 车辆的马力越大,其加速性能越好。
汽车振动试题

3.1 图示不计质量的刚杆,长度为2l ,在其中点和左端附以质量12,m m ,两端的弹簧刚度为12,k k 。
求此系统的运动方程。
(注:分别使用直接法和拉格朗日法,运动方程写成矩阵形式)
3.2推导图示系统的运动方程。
(注:分别使用直接法和拉格朗日法,运动方程写成矩阵形式)
3.3 推导图示系统的运动方程。
绳与圆盘间无相对滑动。
(注:分别使用直接法和拉格朗日法,运动方程写成矩阵形式)
3.4 图示质量为M 、半径为r 的两个相同的圆柱体之间用弹簧k 1联系,右侧的圆柱体用弹簧k 2与固定端连接。
设圆柱体自由地在水平表面上滚动。
(注:用拉格朗日方程推导系统的运动方程)
3.5用拉格朗日方程推导系统的运动方程。
圆柱体的质量为m 、半径为r ,它沿
半径为R 的半圆槽无滑动地滚动。
(θ较小时,21
cos 1,1cos 2
θθθ≈−≈)。
总结(习题)汽车理论期末考试.

第四章习题 3.已知轴距 L,质心至前轴距离 a 、质心至后轴 距离 b,质心高度 hg,制动器制动力分配系数 ,根 据汽车同步附着系数的定义,推导出同步附着系数 0用上述参数表示的计算式?
•青岛大学车辆工程系
29
汽车理论
第五章习题 1. 某小客车质量 m 为 2000kg ,轴距 L 为 3.2m , 前后轮为单胎,每一前轮侧偏刚度为-665N/(°), 每一后轮侧偏刚度为-655N/(°),水平静止时前轴 负荷率为53%。试求: (1) 求稳态转向特性属于何种类型。 (2) 求特征车速或临界车速。 (3) 当前轮转角 =12°时, u=6.5m/s 等速转向行 驶时的横摆角速度。
•青岛大学车辆工程系
7
汽车理论
2. 某轿车车重 21.24kN ,发动机的最大扭矩为 325Nm,主减速器的传动比为4.0,传动系效率为 0.85 ,车轮半径为 0.33m,若滚动阻力系数为 0.02 , 四档传动比为1,计算允许最大坡度角为35度时, 所采用的四档变速器的各档传动比。
•青岛大学车辆工程系
ab max E f g
=6.5m/s2
•青岛大学车辆工程系
19
汽车理论
4.5解(4)
单回路: 双回路:a) 1失效时:
G
F1 F 2 P
G F P
F P
1
2
G
F 2 1 F G 21 G 0.7G 1 1 P P 2 2
•青岛大学车辆工程系
21
汽车理论
4.5解(4)
单回路: 双回路:c)
G
F1 F 2 P
G F P
F P
1
2
G
汽车振动分析报告期末复习题(车辆工程专业用)

1. 圆筒质量m 。
质量惯性矩o J ,在平面上在弹簧k 的限制下作纯滚动,如下图所示,求其固有频率。
2. 下图示的弹簧质量系统,两个弹簧的连接处有一激振力t P t P ωsin )(0=的作用,求质量m 稳态响应的幅值。
3. 建立如下图所示系统的运动微分方程并求稳态响应。
4. 如下图所示等截面悬臂梁,梁长度为L ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
在梁的a 位置作用有集中载荷)(t F 。
已知梁的初始条件为零。
求解梁的响应。
(假定已知第i 阶固有频率为i ω,相应的模态函数为)(x i φ,∞=~1i ))(t2x x m 11x k(t P 22x k t Aωsin 1=x m )x -5. 两个均匀刚性杆如图所示,具有相同长度但不同质量,使用影响系数法求系统运动方程。
6. 如下图所示量自由度系统。
(1)求系统固有频率和模态矩阵,并画出各阶主振型图形;(2)当系统存在初始条件⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡0210)0()0(x x x 和⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡00)0()0(21xx时,试采用模态叠加法求解系统响应。
7. 如下图所示等截面梁,长度为l ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
集中质量m ,卷簧刚度1k ,直线弹簧刚度2k 。
写出系统的动能和势能表达式,系统质量阵和刚度阵表达式。
8 物块M 质量为m 1。
滑轮A 与滚子B 的半径相等,可看作质量均为m 2、半径均为r 的匀质圆盘。
斜面和弹簧的轴线均与水平面夹角为β,弹簧的刚度系数为k 。
又m 1 g >m 2 g sin β , 滚子B 作纯滚动。
试用能量法求:(1)系统的微分方程;(2)系统的振动周期。
9 在右图示系统中,质量为m 1、半径为R 的匀质圆盘,可沿水平面作纯滚动。
质量不计的水平直杆AB 用铰链A 、B 分别与圆盘A 、匀质直杆BC 连接。
杆BC 长为L ,质量为m 2,在B 连接一刚度系数为k 的水平弹簧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 圆筒质量m 。
质量惯性矩o J ,在平面上在弹簧k 的限制下作纯滚动,如下图所示,求其固有频率。
2. 下图示的弹簧质量系统,两个弹簧的连接处有一激振力t P t P ωsin )(0=的作用,求质量m 稳态响应的幅值。
3. 建立如下图所示系统的运动微分方程并求稳态响应。
4. 如下图所示等截面悬臂梁,梁长度为L ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
在梁的a 位置作用有集中载荷)(t F 。
已知梁的初始条件为零。
求解梁的响应。
(假定已知第i 阶固有频率为i ω,相应的模态函数为)(x i φ,∞=~1i ))(t2x x m 11x k(t P 22x k t Aωsin 1=x m )x -5. 两个均匀刚性杆如图所示,具有相同长度但不同质量,使用影响系数法求系统运动方程。
6. 如下图所示量自由度系统。
(1)求系统固有频率和模态矩阵,并画出各阶主振型图形;(2)当系统存在初始条件⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡0210)0()0(x x x 和⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡00)0()0(21xx时,试采用模态叠加法求解系统响应。
7. 如下图所示等截面梁,长度为l ,弹性模量为E ,横截面对中性轴的惯性矩为I ,梁材料密度为ρ。
集中质量m ,卷簧刚度1k ,直线弹簧刚度2k 。
写出系统的动能和势能表达式,系统质量阵和刚度阵表达式。
8 物块M 质量为m 1。
滑轮A 与滚子B 的半径相等,可看作质量均为m 2、半径均为r 的匀质圆盘。
斜面和弹簧的轴线均与水平面夹角为β,弹簧的刚度系数为k 。
又m 1 g >m 2 g sin β , 滚子B 作纯滚动。
试用能量法求:(1)系统的微分方程;(2)系统的振动周期。
9 在右图示系统中,质量为m 1、半径为R 的匀质圆盘,可沿水平面作纯滚动。
质量不计的水平直杆AB 用铰链A 、B 分别与圆盘A 、匀质直杆BC 连接。
杆BC 长为L ,质量为m 2,在B 连接一刚度系数为k 的水平弹簧。
在图示的系统平衡位置时,弹簧具有原长。
试用能量法求:(1)系统的微振动的运动微分方程;(2)系统的微振动周期。
yxl0cx 2k b x 1k ax m10 在右图示振动系统中,已知:物块的质量为m ,两弹簧的刚度系数分别为k 1、k 2 ,有关尺寸L 、b 已知,不计杆重。
试求:(1) 建立物块自由振动微分方程;(2)求初始条件0000==xx 、下系统的振动运动方程。
11在右图示振动系统中,已知:二物体的质量分别为1m 和2m ,弹簧的刚度系数分别为1k 、2k 、3k 、4k 、5k ,物块的运动阻力不计。
试求:(1)采用影响系数法写出系统的动力学方程;(2)假设m m m ==21,k k k ==21,k k k k 31543===,求出振动系统的固有频率和相应的振型;(3)假定系统存在初始条件⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡42)0()0(21x x ,⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡26)0()0(21x x,采用模态叠加法求系统响应。
12 在右图示振动系统中,已知:匀质杆AB ,质量m = 3 kg ,长为L = 2m ,弹簧的刚度系数k 1 = 2 N/m ,k 2 = 1 N/m 。
设杆AB 铅垂时为系统的平衡位置,杆的线位移,角位移均极微小。
在质心C 点作用有一水平力F = sin ωt 。
以质心水平位移x 和转角θ为广义坐标。
试求: (1) 系统的动力学方程和固有频率; (2)问ω的值等于多少时,才能使系统的强迫振动为转动而无平动?并求该强迫振动方程。
13 在图示振动系统中,已知:重物C 的质量m 1,匀质杆AB 的质量m 2,长为L ,匀质轮O 的质量m 3,弹簧的刚度系数k 。
当AB 杆处于水平时为系统的静平衡位置。
试采用能量法求系统微振时的固有频率。
图114 质量为m 1的匀质圆盘置于粗糙水平面上,轮缘上绕有不可伸长的细绳并通过定滑轮A 连在质量为m 2的物块B 上;轮心C 与刚度系数为k 的水平弹簧相连;不计滑轮A ,绳及弹簧的质量,系统自弹簧原长位置静止释放。
试采用能量法求系统的固有频率。
15 在右图示振动系统中,重物质量为m ,外壳质量为2m ,每个弹簧的刚度系数均为k 。
设外壳只能沿铅垂方向运动。
采用影响系数方法:(1)以x 1和x 2为广义坐标,建立系统的微分方程;(2)求系统的固有频率。
16 在右图示振动系统中,物体A 、B 的质量均为m ,弹簧的刚度系数均为k ,刚杆AD 的质量忽略不计,杆水平时为系统的平衡位置。
采用影响系数方法,试求:(1)以x 1和x 2为广义坐标,求系统作微振动的微分方程;(2)系统的固有频率方程。
17 在右图示振动系统中,已知:物体的质量m 1、m 2及弹簧的刚度系数为k 1、k 2、k 3、k 4。
(1)采用影响系数方法建立系统的振动微分方程;(2)若k 1= k 3=k 4= k 0,又k 2=2 k 0,求系统固有频率;(3)取k 0 =1,m 1=8/9,m 2 =1,系统初始位移条件为x 1(0)=9和x 2(0)=0,初始速度都为零,采用模态叠加法求系统响应。
18 一匀质杆质量为m ,长度为L ,两端用弹簧支承,弹簧的刚度系数为k 1和k 2。
杆质心C 上沿x方向作用有简谐外部激励t ωsin 。
右图所示水平位置为静平衡位置。
(1)以x 和θ为广义坐标,采用影响系数方法建立系统的振动微分方程;(2)取参数值为m=12,L =1,k 1 =1,k 2 =3,求出系统固有频率;(2)系统参数仍取前值,试问当外部激励的频率ω为多少时,能够使得杆件只有θ方向的角振动,而无x 方向的振动?19质量为m 的质点由长度为l 、质量为m 1的均质细杆约束在铅锤平面作微幅摆动,如下图所示。
求系统的固有频率。
x x 1 x 22x 1x θx C t ωsin20 质量为m 、半径为R 的均质柱体在水平面上作无滑动的微幅滚动,在CA=a 的A 点系有两根弹性刚度系数为k 的水平弹簧,如下图所示。
求系统的固有频率。
21 转动惯量为J 的圆盘由三段抗扭刚度分别为1k ,2k 和3k 的轴约束,如下图所示。
求系统的固有频率。
22 在下图所示的系统中,已知()b a m i k i , ,3,2,1 和=,横杆质量不计。
求固有频率。
mg ba a F +=2x x 223 质量1m 在倾角为α的光滑斜面上从高h 处滑下无反弹碰撞质量2m ,如下图所示。
确定系统由此产生的自由振动。
24 质量为m 、长为l 的均质杆和弹簧k 及阻尼器c 构成振动系统,如下图所示。
以杆偏角θ为广义坐标,建立系统的动力学方程,给出存在自由振动的条件。
若在弹簧原长处立即释手,问杆的最大振幅是多少?发生在何时?最大角速度是多少?发生在何时?是否在过静平衡位置时?25 一弹簧质量系统沿光滑斜面作自由振动,如图T 2-1所示。
已知,︒=30α,m = 1 kg ,k = 49 N/cm ,开始运动时弹簧无伸长,速度为零,求系统的运动规律。
26 下图所示系统中,已知m ,c ,1k ,2k,0F 和ω。
求系统动力学方程和稳态响应。
x k 2x2 (11xk - )11x xc -1l c27 如下图所示,重物1W 悬挂在刚度为k 的弹簧上并处于静平衡位置,另一重物2W 从高度为h 处自由下落到1W 上而无弹跳。
求2W 下降的最大距离和两物体碰撞后的运动规律。
28在下图所示系统中,已知m ,1k ,2k ,0F 和ω,初始时物块静止且两弹簧均为原长。
求物块运动规律。
29 求下图中系统的固有频率,悬臂梁端点的刚度分别是1k 及3k ,悬臂梁的质量忽略不计。
30由一对带偏心质量的等速反向旋转齿轮构成的振动机械安装在弹簧和阻尼器构成的支承上,如下图所示。
当齿轮转动角速度为ω时,偏心质量惯性力在垂直方向大小为x k)1x x k - 2xm (2k2W 2W 1t me ωωsin 2。
已知偏心重W = 125.5 N ,偏心距e = 15.0 cm ,支承弹簧总刚度系数k = 967.7N /cm ,测得垂直方向共振振幅cm X m 07.1=,远离共振时垂直振幅趋近常值cm X 32.00=。
求支承阻尼器的阻尼比及在m in 300r =ω运行时机器的垂直振幅。
31 如下图所示,一质量m 连接在一刚性杆上,杆的质量忽略不计,求下列情况系统作垂直振动的固有频率: (1)振动过程中杆被约束保持水平位置; (2)杆可以在铅锤平面微幅转动; (3)比较上述两种情况中哪种的固有频率较高,并说明理由。
32 求下图所示系统的固有频率,刚性杆的质量忽略不计。
33 下图所示是一个倒置的摆。
摆球质量为m ,刚杆质量可忽略,每个弹簧的刚度为2k 。
(1)求倒摆作微幅振动时的固有频率;(2)摆球质量m 为0.9 kg 时,测得频率()n f 为1.5 Hz ,m 为1.8 kg 时,测得频率为0.75mgx 1x Amg l l F 2112+=x x 2Hz ,问摆球质量为多少千克时恰使系统处于不稳定平衡状态?34 如下图所示,质量为m 2的均质圆盘在水平面上可作无滑动的滚动,鼓轮绕轴的转动惯量为I ,忽略绳子的弹性、质量及各轴承间的摩擦力,求此系统的固有频率。
35 如下图所示,刚性曲臂绕支点的转动惯量为I 0,求系统的固有频率。
36 一长度为l 、质量为m 的均匀刚性杆铰接于O 点并以弹簧和粘性阻尼器支承,如下图所示。
写出运动微分方程,并求临界阻尼系数和无阻尼固有频率的表达式。
θ零平衡位置37 下图所示的系统中,刚杆质量不计,写出运动微分方程,并求临界阻尼系数及阻尼固有频率。
38 两质量均为m 的质点系于具有力F 的弦上,如下图所示。
忽略振动过程中弦力的变化写出柔度矩阵,建立频率方程。
求系统的固有频率和模态,并计算主质量、主刚度,确定主坐标。
39 下图所示的均匀刚性杆质量为m 1,求系统的频率方程。
40 多自由度振动系统质量矩阵M 和刚度矩阵K 均为正定。
对于模态i x 和j x 证明:()01=-j T i Mx MK x ,()01=-j T i Kx KM x41 长为l 、密度为ρ、抗扭刚度为GI p 的的等直圆轴一端有转动惯量为J 的圆盘,另一端连l接抗扭刚度为k 的弹簧,如下图所示。
求系统扭振的频率方程。
42长为l 、单位长度质量为ρl 的弦左端固定,右端连接在一质量弹簧系统的物块上,如图E6.5所示。
物块质量为m ,弹簧刚度系数为k ,静平衡位置在y = 0处。
弦线微幅振动,弦力F 保持不变,求弦横向振动的频率方程。
另外,平常的作业也应作为复习题进行练习。
值得一提的是最后一章《连续系统振动方程》中关于各种结构振动方程的推导都需要复习,以实现理解、掌握。
