轴对称及轴对称图形(复习)
轴对称图形全章复习

《轴对称图形》全章复习【知识网络】【要点梳理】要点一、轴对称1.轴对称图形和轴对称(1)轴对称图形如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,这个图形就叫做轴对称图形,这条直线就是它的对称轴.轴对称图形的性质:轴对称图形的对称轴,是任何一对对应点所连线段的垂直平分线.(2)轴对称定义:把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称,这条直线叫做对称轴.成轴对称的两个图形的性质:①关于某条直线对称的两个图形形状相同,大小相等,是全等形;②如果两个图形关于某条直线对称,则对称轴是任何一对对应点所连线段的垂直平分线;③两个图形关于某条直线对称,如果它们的对应线段或延长线相交,那么它们的交点在对称轴上.(3)轴对称图形与轴对称的区别和联系区别:轴对称是指两个图形的位置关系,轴对称图形是指具有特殊形状的一个图形;轴对称涉及两个图形,而轴对称图形是对一个图形来说的.联系:如果把一个轴对称图形沿对称轴分成两个图形,那么这两个图形关于这条轴对称;如果把成轴对称的两个图形看成一个整体,那么它就是一个轴对称图形.2.线段的垂直平分线垂直并且平分一条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.3.作轴对称图形(1)几何图形都可以看作由点组成,我们只要分别作出这些点关于对称轴的对应点,再连接这些点,就可以得到原图形的轴对称图形;(2)对于一些由直线、线段或射线组成的图形,只要作出图形中的一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.4.用坐标表示轴对称点(x,y)关于x轴对称的点的坐标为(x,-y);点(x,y)关于y轴对称的点的坐标为(-x,y);点(x,y)关于原点对称的点的坐标为(-x,-y).要点二、线段、角的轴对称性1.线段的轴对称性(1)线段是轴对称图形,线段的垂直平分线是它的对称轴.(2)线段垂直平分线的性质定理:线段垂直平分线上的点到线段两端的距离相等;(3)线段垂直平分线的性质定理的逆定理:到线段两个端距离相等的点在线段的垂直平分线2.角的轴对称性(1)角是轴对称图形,角的平分线所在的直线是它的对称轴.(2)角平分线上的点到角两边的距离相等.(3)角的内部到角两边距离相等的点在角的平分线上.要点三、等腰三角形1.等腰三角形(1)定义:有两边相等的三角形,叫做等腰三角形.(2)等腰三角形性质①等腰三角形的两个底角相等,即“等边对等角”;②等腰三角形顶角的平分线、底边上的中线与底边上的高线互相重合(简称“三线合一”).特别地,等腰直角三角形的每个底角都等于45°.(3)等腰三角形的判定如果一个三角形有两个角相等,那么这两个角所对的边也相等(即“等角对等边”).2.等边三角形(1)定义:三条边都相等的三角形,叫做等边三角形.(2)等边三角形性质:等边三角形的三个角相等,并且每个角都等于60°.(3)等边三角形的判定:①三条边都相等的三角形是等边三角形;②三个角都相等的三角形是等边三角形;③有一个角为60°的等腰三角形是等边三角形.3.直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半.。
八年级数学复习考点1 轴对称及轴对称图形的意义
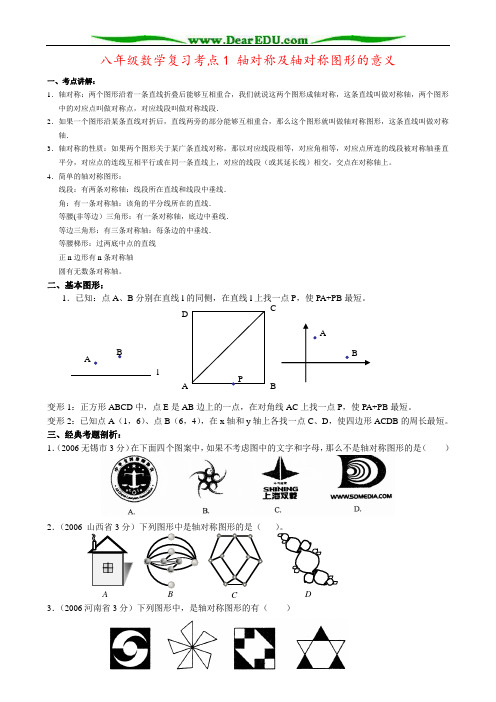
ABCDP八年级数学复习考点1 轴对称及轴对称图形的意义一、考点讲解:1.轴对称:两个图形沿着一条直线折叠后能够互相重合,我们就说这两个图形成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做对称点,对应线段叫做对称线段.2.如果一个图形沿某条直线对折后,直线两旁的部分能够互相重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴.3.轴对称的性质:如果两个图形关于某广条直线对称,那以对应线段相等,对应角相等,对应点所连的线段被对称轴垂直平分,对应点的连线互相平行或在同一条直线上,对应的线段(或其延长线)相交,交点在对称轴上。
4.简单的轴对称图形:线段:有两条对称轴:线段所在直线和线段中垂线. 角:有一条对称轴:该角的平分线所在的直线. 等腰(非等边)三角形:有一条对称轴,底边中垂线. 等边三角形:有三条对称轴:每条边的中垂线. 等腰梯形:过两底中点的直线 正n 边形有n 条对称轴 圆有无数条对称轴。
二、基本图形:1.已知:点A 、B 分别在直线l 的同侧,在直线l 上找一点P ,使PA+PB 最短。
变形1:正方形ABCD 中,点E 是AB 边上的一点,在对角线AC 上找一点P ,使PA+PB 最短。
变形2:已知点A (1,6)、点B (6,4),在x 轴和y 轴上各找一点C 、D ,使四边形ACDB 的周长最短。
三、经典考题剖析:1.(2006无锡市3分)在下面四个图案中,如果不考虑图中的文字和字母,那么不是轴对称图形的是( )2.(2006 山西省3分)下列图形中是轴对称图形的是( )。
3.(2006河南省3分)下列图形中,是轴对称图形的有( )ABABlB A CDA.4个B.3个C.2个D.1个4.(2006鸡西市3分)在下列四个图案中,既是轴对称图形,又是中心对称图形的是( )(A) (B) (C) (D)5.(2006苏州市3分)如图,如果直线m 是多边形ABCDE 的对称轴,其中∠A=1300, ∠B=1100.那么∠BCD 的度数等于 ( ) A. 400B.500C .60D.7006.(2006梅州市3分)小明在镜中看到身后墙上的时钟,实际时间最接近8时的是下图中的( )7.(2006 湛江市6分)如图5,请你画出方格纸中的图形关于点O 的中心对称图形,并写出整个图形的对称轴的条数.四、针对性训练:1.(2006宜昌市3分)从汽车的后视镜中看见某车车牌的后5位号码是 ,该车的后5位号码实际是 。
人教版初二数学13章轴对称图形复习知识点

如图,AD与BC相交于点O,OA=OC,∠A=∠C,BE=DE.求证:OE垂直平分BD.
5.如图,AC=AD,BC=BD,则有( )
A
A.AB垂直平分CD
B.CD垂直平分AB
底边上的高互相重合。
(3)判别方法:①有两条边相等(概念)
②等角对等边
2.等边三角形 (1)三边都相等的三角形叫做等边三角形,它是轴对称图形,有三条对称轴。
(2)性质:等边三角形的三个角都是60° (3)判定: ①三个角都相等的三角形是等边三角形 ②有一个角是60°的等腰三角形是等边三角形 ③有三个边都相等的三角形是等边三角形
∴ AE+EF+AF =BE+EF+CF=10cm
C∠EAF= ∠BAC-∠BAE-∠CAF =120°- ∠B- ∠C=60°
例6 如图,△ABC中,AB=AC,∠A=50°,AB的垂直平分线交AC于D,求∠ FBC的度数。
A
解:∵ AB=AC, ∠A=50°
∴ ∠ABC= ∠C=65°
又∵ AC是线段AB的垂直平分线
;
(x,-y)
(-x,y)
1.已知点P1(a,3)和点P2(4,b)关于y轴对称,则(a+b)2007= -1
2.点A(2,5)与点B(2,-3)关于直线 y=1
对称.
知识点6
•等腰三角形的性质:等边对等角 三线合一
• 等腰三角形的判定: ①有两条边相等(概念) ②等角对等边
知识点7
初中阶段五种基本的尺规作图 (1)作一条线段等于已知线段; (2)作一个角等于已知角; (3)作已知角的平分线; (4)作线段的垂直平分线; (5)过直线外一点作已知直线的垂线。
中考数学专题复习练习:轴对称与轴对称图形

典型例题一例01.下列图形中,不是轴对称图形的是( )(A )有两个角相等的三角形(B )有一个内角是的直角三角形︒45(C )有一个内角是,另一个内角为的三角形︒30︒120(D )有一个角是的直角三角形︒30分析:在(A )中,有两个角相等的三角形一定是等腰三角形,而等腰三角形一定是轴对称图形,它的对称轴为底边上的高(或底边上的中线或顶角的平分线). 而(B )和(C )中的两个三角形同样也是等腰三角形,所以也是轴对称图形. 那么(D )中三角形的三个内角各不相等,不是等腰三角形,所以(D )不是轴对称图形.解答:选(D )说明:在三角形中,只有等腰三角形才是轴对称图形,而不是等腰三角形的三角形就一定不是轴对称图形.典型例题二例02.已知:直线MN ,同侧两点A 、B (如图)求作:点P ,使P 在MN 上,并且最小.BP AP +作法 1.作点A 关于直线MN 的对称点.A '2.连结交MN 于PA A '点P 就是所求作的点.说明 这类问题经常遇到,可以和生活中的问题结合衍生出许多应用问题,但本质都是这道题.典型例题三例03.在图(a )中,分别作出点P 关于OA 、OB 的对称点,,连结交OA 1P 2P 21P P 于M ,交OB 于N ,若,则的周长为多少?cm P P 521=PMN ∆作法:略.解答:如图(b )所示,∵,P 关于OA 对称,1P ∴PMM P =1同理可得.PN N P =2∴的周长PMN ∆MN PN PM ++=N P MN M P 21++=cmP P 521==∴的周长为. PMN ∆cm 5 说明 准确作图是关键.典型例题四例04.已知:(如图)四边形ABCD 和过点D 的直线MN ,求作:四边形,使四边形与四边形ABCD 关于MN 对称.D C B A ''''D C B A ''''作法 1.作,垂足为E ;延长BE 到,使,得到点B 的对称MN BE ⊥B 'BE E B ='点.2.同法作点A 和点C 的对称点.C A ''3.因为D 在对称轴MN 上,所以点D 的对称点重合.D '4.连结、、.B A ''C B ''D C ''四边形即为所求.D C B A '''' 说明 关键是掌握概念和基本作图.典型例题五例05.有一条小河(如图所示),两岸有A 、B 两地,要设计道路并在河上垂直于河岸架一座桥,用来连接A 、B 间路线怎样走,桥应架在何处,才能使A 到B 的距离最短.分析:桥梁无论架在何处均垂直于河岸,因此桥梁的长度是定值,决定路程长度的关键是选取建桥点的位置,相对应地在河岸A 地同测取一点,使B 与河岸距离等于与河B 'B '岸到桥头的距离之和,于是,这个总是转化为“直线同侧有两点A 、,欲在直线上求一B '点,使这一点与A 、距离之和最短.B '已知:如图,河岸AB 两地求作:线段CD ,使CD 与、均互相垂直,并且最小.1l 2l BD CD AC ++作法:(1)作,与、分别交点、E ,并且1l B B ⊥'1l 2l E 'BEE B =''(2)在上取一点使(或者找到点关于的对称点)E E 'B ''E B E B ''='''B '1l B ''(3)连结,与交于C 点,作,与交于D 点,CD 即为所求作的线段.B A ''l 2l CD ⊥2l 典型例题六例06.如图所示,P 是平分线AD 上一点,P 与A 不重合,.BAC ∠AB AC >求证:ABAC PB PC -<-分析:用对称法. 可利用轴对称图形的知识找出点B 关于直线AD 的对称点,因AD B '为的平分线,故在AC 上,连结,从而构造与两个轴对称图BAC ∠B 'P B 'P B A '∆ABP ∆形,再利用三角形两边之差小于第三边来证明.证明:作点B 关于直线AD 的对称点,连结.B 'P B '∵AD 是的平分线,BAC ∠∴点在AC 上(是以角平分线AD 所在直线为对称轴的轴对称图形),B 'BAC ∠又∵AP 在对称轴AD 上,∴,P B BP B A AB '='=,在中,C B P '∆∵,C B B P PC '<'-,AB AC B A AC C B -='-=' ,P B BP '=∴.AB AC BP PC -<-说明:和就是利用角平分线AD 构造出的轴对称图形,这种方法对于证BAC ∆P B A '∆明有关线段的不等关系非常方便、有效.典型例题七例07.如图,E 、F 是的边AB 、AC 上的点,在BC 上求一点M ,使的ABC ∆EMF ∆周长最小.分析 因为E 、F 是定点,所以EF 是定值. 要使△EMF 的周长最小,只要MF ME +最小.解答 (1)作点F 关于直线BC 的对称点.F '(2)连结交BC 于M ,点M 就是所求.F E '说明 这类问题在日常生活中经常可以遇到.典型例题八例08.如图,过C 作的平分线AD 的垂线,垂足为D ,作交AC 于BAC ∠AB DE //E .求证:.CE AE =分析 由已知条件容易得到,从而. 要证明,只须证明32∠=∠DE AE =CE AE =,联想到AD 是角平分线又是垂线,若延长CD 交AB 的延长线于P ,则C 、P 关CE DE =于直线AD 对称,于是问题可以解决.解答 延长CD 交AB 的延长线于P .在和中,ADP ∆ADC ∆⎪⎩⎪⎨⎧∠=∠=∠=∠ADP ADC ADAD 21∴(角边角)ADC ADP ∆≅∆故.ACD P ∠=∠又∵,AP DE //∴,P ∠=∠4则.,4CE DE ACD =∠=∠∵,AB DE //∴,31∠=∠又∵,21∠=∠∴,32∠=∠∵(等边对等角),AE DE =∴.CE AE =说明 全等三角形是证明角或线段相等的一种方法,但不是惟一方法,不要一证线段相等就找全等三角形. 等腰三角形的判定定理及其推论,中垂线的性质,都是证线段相等的重要途径.典型例题九例09.如图,AD 是中的平分线,且.ABC ∆BAC ∠AC AB >求证:.DC BC>分析 由于AD 是的平分线,所以可以以AD 为轴构造轴对称图形,即把BAC ∠ADC ∆沿AD 翻折,这样,就可以在中解决问题.︒180DC DE =BED ∆证明 在AB 上截取AE ,使,连结DE .AC AE =∵AD 是的平分线,BAC ∠∴,21∠=∠在和中,AED ∆ACD ∆⎪⎩⎪⎨⎧=∠=∠=)()(21)(公共边已证作图AD AD AC AE ∴(边角边),ACD AED ∆≅∆∴,DC DE =∴(全等三角形对应边对应角相等),43∠=∠∵,(内角和定理的推论),3∠>∠BED B ∠>∠4∴(大角对大边),ED BD B BED >∠>∠,∴.DC BD >说明 本题中的的就是利用角平分线构造出来的轴对称图形. 本题还有AED ∆ACD ∆其他构造轴对称图形的方法,比如把沿AD 翻折,也可证明结论.ADB ∆︒180选择题1.选择题(1)在下列命题中:①两个全等三角形是轴对称图形②两个关于直线对称的图形是全等形l ③等边三角形是轴对称图形④线段有三条对称轴正确命题的个数是()(A )1 (B )2 (C )3 (D )4(2)下列图形是一定轴对称图形的是()(A )任意三角形 (B )有一个角等于的三角形︒60(C )等腰三角形 (D )直角三角形(3)P 为内一点,且,则P 点是()ABC ∆PC PB PA ==(A )三条中线的交点 (B )三条高的交点(C )三个角的平分线的交点 (D )三边垂直平分线的交点(4)已知:D 为的边BC 的中点,且,下面各结论不正确的是()ABC ∆BC AD ⊥(A ) (B )ACD ABC ∆≅∆CB ∠=∠(C )AD 是的平分线 (D )是等边三角形BAC ∠ABC ∆(5)正五角星的对称轴有()(A )1条 (B )2条 (C )5条 (D )10条(6)等边三角形的对称轴共有()(A )1条 (B )3条 (C )6条 (D )无数条(7)下列四个图形①等腰三角形 ②等边三角形 ③等腰直角三角形 ④直角三角形中,一定是轴对称图形的有()(A )1个 (B )2个 (C )3个 (D )4个(8)下列图形中,不一定是轴对称图形的是()(A )线段 (B )角 (C )三角形 (D )等腰直角三角形参考答案:1.选择题(1)B (2)C (3)D (4)D (5)C (6)B (7)C (8)C 填空题1.填空题(1)等边三角形的对称轴有______条.(2)如果沿着一条直线折叠,两个点能互相重合,那么这两个点叫做_______.(3)把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么这两个图形_______.(4)如果一个图形沿着某一条直线折叠,直线两旁的部分能够互相重合,那么这个图形叫做_______.参考答案1.填空题(1)3 (2)对称点 (3)轴对称 (4)轴对称图形解答题1.如图,已知线段AB 及直线MN ,求作线段AB 关于MN 的对称图形.2.如图,已知及直线EF ,求作关于EF 的对称图形.ABC ∆ABC ∆3.如图,已知折线ABC 及直线PQ ,求作折线ABC 关于直线PQ 的对称图形.4.如图,已知,分别以OM ,ON 为对称轴作三角形与它对称.ABC ∆5.在中,,,垂足为H ,点B 关于AH 的对称点是. ABC ∆C B ∠=∠2BC AH ⊥B '求证:.AB C B ='6.如图,已知:在直线MN 的同侧有两点A 和B .求作:MN 上一点,使.BCN ACM ∠=∠7.如图,EFGH 是一个矩形的台球台面,有黑白两球分别位于A ,B 两点位置上,试问:怎样撞击黑球A ,求能使A 先碰撞台边EF 反弹后两击中白球B ?参考答案1.略 2.略 3.略 4.略5.证明:连结,则易证,B A 'B A AB '=B B A B '∠=∠∵,∴,即.B CAC B B A '∠+∠='∠B ∠=C ∠=2B CA C '∠=∠AB C B AB =''=6.作法:作点A 关于MN 的对称点,连结,与MN 的交点为C ,则点C 就是所A 'A B '要求作的点. 证明:略.7.作点A 关于EF 的对称点,连结与EF 的交点为C ,则沿AC 方向撞击黑球A 'B A '就可以满足要求.。
第一章轴对称图形-复习课课件1

辨析与思考:
(1)如果一个图形沿着某条直线对折,两侧的图形能够完
全重合,这个图形就是轴对称图形
()
(2)全等图形不一定是轴对称图形。 ( )
(3)线段的对称轴是它的垂直平分线
Байду номын сангаас
()
(4)等边三角形有3条对称轴。
()
(5)一个角的角平分线就是这个角的对称轴 ( )
(2)小丽用如图①的直角三角形铁皮,烙一块与铁皮形状、 大小相同的饼。如果烙好一面后就把饼翻身,那么这块 并不能正好落在“锅”中。如图②,小丽将饼切了一刀, 然后将两小块都翻身,结果饼就能正好落在“锅”中了, 这是为什么?
(3)如果用来烙饼的既不是等腰三角形也不是直角三角形 (如图③),那么烙好一面后,怎样将烙饼翻身,才能使 烙饼仍能正好落在锅中?
20世纪著名数学家赫尔 曼·外 尔所说的,“对称是一 种思想,人们毕生追求,并创造 次序、美丽和完善……”
知识点复习:
轴对称 一个图形沿着某一条直线折叠,
如果它能够与另一个图形______,那么就
说这两个图形成轴对称.这条直线就是
______.两个图形中的对应点叫做
.
轴对称图形 一个图形沿着某条直线对折,
CF⊥BD于F,交DE于G,DF= 1 BC,试
说明∠FCB= 1∠B
2
2
D
F
A
G
B
E
C
本节课小结:
本节课我们复习了哪些知识点? 你对本节课所复习的知识又有了哪些新的
认识?
设计轴对称图案
图案的对称不但要求图形对称外,有 时颜色也“对称”。
轴对称及轴对称图形(复习课)

8 B
⒊如图,在梯形ABCD中,AD∥BC, 如图,在梯形ABCD中 AD∥BC, ABCD DC的中点 EF⊥AB于点 的中点, 于点F E是DC的中点,EF⊥AB于点F. 求证:S梯形ABCD=AB×EF. 求证: =AB×EF.
A F E D
B
C
G
平移底,梯形转化成:三角形. 平移底,梯形转化成:三角形.
5.在梯形ABCD中,AB∥DC,AD= 在梯形ABCD中 AB∥DC,AD= ABCD BC,AB=1,DC=5,AC⊥BD,BE⊥CD, BC,AB=1,DC=5,AC⊥BD,BE⊥CD, 则梯形的面积= 则梯形的面积= .
A B
D
E
C
F
6.如图,梯形ABCD中,AD∥BC,E、F 如图,梯形ABCD中 AD∥BC, ABCD 分别是AD BC的中点,∠B+∠C=90° AD、 的中点,∠B+∠C=90 分别是AD、BC的中点,∠B+∠C=90°, 请说明EF= (BC-AD). 请说明EF= 1 BC-AD).
D C B
E
5、如图,△ABC中,AB的垂直平分线 如图, ABC中 分别交AB BC于点 AB、 于点D AC的垂直 分别交AB、BC于点D、E,AC的垂直 平分线分别交AC BC于点 AC、 于点F 平分线分别交AC、BC于点F、G,若 BC=20, AEG的周长为多少 的周长为多少? BC=20,则△AEG的周长为多少?
A
F
N E
B M
C
10、已知△ABC是等腰三角形,过 10、已知 ABC是等腰三角形,过
△ABC的一个顶点的一条直线,把 ABC的一个顶点的一条直线,把 △ABC分成两个小三角形,如果这 ABC分成两个小三角形,如果这 两个小三角形也是等腰三角形,问 △ABC顶角的度数是多少? ABC顶角的度数是多少?
章节复习(三)轴对称
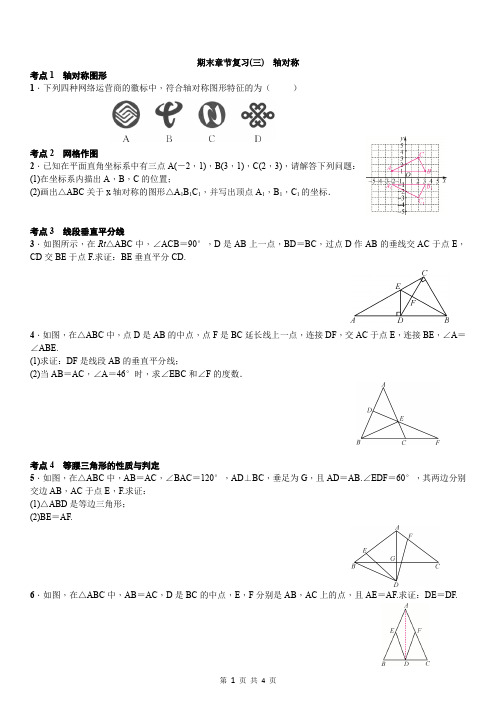
期末章节复习(三)轴对称考点1轴对称图形1.下列四种网络运营商的徽标中,符合轴对称图形特征的为()考点2网格作图2.已知在平面直角坐标系中有三点A(-2,1),B(3,1),C(2,3),请解答下列问题:(1)在坐标系内描出A,B,C的位置;(2)画出△ABC关于x轴对称的图形△A1B1C1,并写出顶点A1,B1,C1的坐标.考点3线段垂直平分线3.如图所示,在Rt△ABC中,∠ACB=90°,D是AB上一点,BD=BC,过点D作AB的垂线交AC于点E,CD交BE于点F.求证:BE垂直平分CD.4.如图,在△ABC中,点D是AB的中点,点F是BC延长线上一点,连接DF,交AC于点E,连接BE,∠A=∠ABE.(1)求证:DF是线段AB的垂直平分线;(2)当AB=AC,∠A=46°时,求∠EBC和∠F的度数.考点4等腰三角形的性质与判定5.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.求证:(1)△ABD是等边三角形;(2)BE=AF.6.如图,在△ABC中,AB=AC,D是BC的中点,E,F分别是AB,AC上的点,且AE=AF.求证:DE=DF.7.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥BC,垂足为G,且AD=AB.∠EDF=60°,其两边分别交边AB,AC于点E,F.求证:(1)△ABD是等边三角形;(2)BE=AF.考点5等边三角形的性质与判定8.如图,已知△ABC是等边三角形,E,D,G分别在AB,BC,AC边上,且AE=BD=CG.连接AD,BG,CE,相交于点F,M,N.(1)求证:AD=CE;(2)求∠DFC的度数;(3)试判断△FMN的形状,并说明理由.考点630°角的直角三角形的性质9.如图,如图,一艘轮船以每小时20海里的速度沿正北方航行,在A处测得灯塔C在北偏西30°方向上,轮船航行2小时后到达B处,在B处测得灯塔C在北偏西60°方向上,当轮船到达灯塔C的正东方向D处时,则轮船航程AD的距离是()A.20海里B.40海里C.60海里D.80海里第9题图第10题图第1题图第3题图考点7最短路径问题10.如图,在等边△ABC中,BD平分∠ABC交AC于点D,点E,F分别是线段BD,BC上的动点,则CE+EF 的最小值等于()A.BD B.CD C.CE D.AC一、选择题(每小题3分,共30分)1.誉为全国第三大露天碑林的“浯溪碑林”,摩崖上铭刻着500多方古今名家碑文,其中悬针篆文具有较高的历史意义和研究价值,下面四个悬针篆文明显不是轴对称图形的是()2.点(3,-2)关于x轴对称的点的坐标是()A.(3,2) B.(-3,-2) C.(-3,2) D.(3,-2)3.如图,△ABC与△A′B′C′关于直线MN对称,P为MN上任一点,下列结论中错误的是()A.△AA′P是等腰三角形B.MN垂直平分AA′,CC′C.△ABC与△A′B′C′面积相等D.直线AB,A′B′的交点不一定在MN上4.等腰三角形的一边长为6,另一边长为13,则它的周长为()A.25 B.25或32 C.32 D.195.如图,将△ABC沿直线DE折叠后,使得点B与点A重合,已知AC=5 cm,△ADC的周长为17 cm,则BC的长为()A.7 cm B.10 cm C.12 cm D.22 cm第5题图第6题图第7题图第8题图第9题图第10题图6.如图,AD,CE分别是△ABC的中线和角平分线.若AB=AC,∠CAD=20°,则∠ACE的度数是()A.20°B.35°C.40°D.70°7.如图,在等边△ABC中,D是AC边上的中点,延长BC到点E,使CE=CD,则∠E的度数为()A.15°B.20°C.30°D.40°8.如图,点P是∠AOB外的一点,点M,N是∠AOB两边上的点,点P关于OA的对称点Q恰好落在MN上,点P关于OB的对称点R落在MN的延长线上.若PM=2.5 cm,PN=3 cm,MN=4 cm,则线段QR的长为()A.4.5 cm B.5.5 cm C.6.5 cm D.7 cm9.如图,A,B两点在正方形网格的格点上,每个方格都是边长为1的正方形,点C也在格点上,且△ABC为等腰三角形,满足条件的点C有()A.6个B.7个C.8个D.9个10.如图,在△ABC中,AB=20 cm,AC=12 cm,点P从点B出发以3 cm/s的速度向点A运动,点Q从点A同时出发以2 cm/s的速度向点C运动,其中一个动点到达端点时,另一个动点也随之停止运动,当△APQ是以∠A为顶角的等腰三角形时,运动的时间是()A.2.5 s B.3 s C.3.5 s D.4 s二、填空题(每小题4分,共20分)11.如图,△ABC与△A1B1C1关于某条直线成轴对称,则∠A1=_______.第11题图第12题图第13题图第14题图第15题图12.如图,AB=AC,BD=BC,若∠A=40°,则∠ABD的度数是______.13.如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连接OP,以O为圆心,OP长为半径画弧交BC于点D,连接PD.如果PO=PD,那么AP的长是______.14.如图,在△ABC中,AB=4,BC=6,∠B=60°,将△ABC沿着射线BC的方向平移2个单位长度后,得到△A′B′C′,连接A′C,则△A′B′C的周长为_______.15.如图,点P是∠AOB内部的一点,∠AOB=30°,OP=8 cm,M,N是OA,OB上的两个动点,则△MPN周长的最小值为______cm.三、解答题(共50分)16.(7分)某科技公司研制开发了一种监控违章车辆的电子仪器.如图,有三条两两相交的公路,你认为这个监控仪器安装在什么位置可离三个路口的交叉点的距离相等,以便及时进行监控?17.(8分)如图,在△ABC中,AD平分∠BAC,BD⊥AD,垂足为D,过点D作DE∥AC,交AB于点E.求证:△BDE是等腰三角形.18.(10分)如图,△ABC为等边三角形,∠1=∠2=∠3.(1)求∠BEC的度数;(2)△DEF是等边三角形吗?为什么?19.(12分)如图,已知在等腰Rt△OAB中,∠AOB=90°,在等腰Rt△EOF中,∠EOF=90°,连接AE,BF.求证:(1)AE=BF;(2)AE⊥BF.20.(13分)如图,已知等腰△ABC中,AB=AC,点D,E分别在边AB,AC上,且AD=AE,连接BE,CD交于点F.(1)判断∠ABE与∠ACD的数量关系,并说明理由;(2)求证:过点A,F的直线垂直平分线段BC.。
第五章 轴对称图形基本概念复习

轴对称图形基本概念复习一、轴对称图形与轴对称1.轴对称是指两个图形的位置关系,轴对称图形是指一个具有特殊特征的图形;2.轴对称是针对两个图形而言,轴对称图形是针对一个图形说的。
概念针对性练习: 1.(09年株洲市中考)下列四个图形中,不是..轴对称图形的是( )A .B .C .D .2.关于轴对称以下说法正确的个数是( )①对称点到对称轴的距离相等②对称点的连线与对称轴互相垂直③对应线段的交点或对应线段延长线的交点一定在对称轴上④轴对称图形就是轴对称⑤轴反射不改变图形的形状和大小。
A .5 B .4 C .3 D .2 二、线段的垂直平分线1.如果点A 与B 关于直线EF 对称,则直线EF 是线段AB 的_____________2.如果直线CD 是线段AB 的垂直平分线,那么点A 与点B 关于___________3.已知AC=BC ,AD=BD ,那么直线CD 是线段AB 的________________ 4.已知EF 是线段AB 的垂直平分线,那么________=____________5.如图,点D 在△ABC 的边BC 上,且BC=BD+AD ,则点D 在________的垂直平分线上。
6.如图,在△ABC 中,AB=AC ,DE 是AB 的垂直平分线,△BCE 的周长为14,BC=6,则AB=__________7.到△ABC 三个顶点距离相等的点是△ABC 的_____________ 三、角平分线的性质1.如图,OP 是∠AOB 的平分线,PE ⊥OA 于E ,PF ⊥OB 于F ,请写出其中相等的线段:_________________________ 2. 到三角形三边距离相等的点是 ( )A . 三边的垂直平分线的交点B . 三个内角的平分线的交点C . 三条高的交点D . 三条中线的交点3.如图,在△ABC 中,∠C=900,AD 平分∠CAB ,BC=8,BD=5,那么D 点 到直线AB 的距离是__________ 4.如图,OP 平分∠AOB ,PC ⊥OA ,PD ⊥OB ,垂足分别是C 、D ,下列结论错误的是( )A .PC=PDB .OC=ODC .∠CPO=∠DPOD .OC=PC四、与三角形有关的线段 1.如图1,图中所有三角形的个数为 ,在△ABE 中,AE 所对的角是 ,∠ABC 所对的边是 ,AD 在△ADE 中,是 的对边,在△ADC 中,是 的对边;2.如图2,已知∠1=0.5∠BAC ,∠2 =∠3,则∠BAC 的平分线为 ,∠ABC 的平分线A B DCBCEDA AO B EF P AC DAOB C D P为 ;3.如图3,D 、E 是边AC 的三等分点,图中有 个三角形,BD 是三角形 中 边上的中线,BE 是三角形 中 边上的中线;4.若等腰△的两边长分别为7和8,则其周长为 ;5. 如图,图中共有三角形( )A 、4个B 、5个C 、6个D 、8个 6.下列长度的三条线段中,能组成三角形的是 ( )A 、 3,5 ,8B 、8,8,18C 、0.1,0.1,0.1D 、3,40,8 7.如果线段a ,b ,c 能组成三角形,那么,它们的长度比可能是( ) A 、1∶2∶4 B 、1∶3∶4 C 、3∶4∶7 D 、2∶3∶48.如果三角形的两边分别为7和2,且它的周长为偶数,那么第三边的长为____ 五、三角形的内角1.在△ABC 中,∠A = 60°∠B = 30°,则∠C = ;2.在△ABC 中,∠C = 60°∠A -∠B = 20°,则∠B = ;3.三角形的三个内角之比为1∶3∶5,那么这个三角形的最大内角为 ;4.在△ABC 中,∠A =∠B = 4∠C ,则∠C = ;5.如图1,∠1+∠2+∠3+∠ 4 = ;6.如图2,CD 平分∠ACB ,AE ∥DC 交BC 的延长线于E ,若∠ACE = 80°,则∠CAE = ;7.如图3,∠A=32°∠B=45°∠C=388. 如图4,D 是AB 上的一点,E 是AC ∠ABE = 28°,则∠CEF 的度数是 9.如图5,∠1+∠2+∠3+∠ 4的值为 六、三角形的外角1.三角形的外角指的是 所形成的角2. 三角形的外角的性质: ⑴ 三角形的一个外角等于 ,⑵ 三角形3.⑴ ∠α⑶ ∠α123A A B C C CD DEEE 123A BC D121233430°1344520α°°⑸ ∠α= ⑹ ∠α= ;4.如图1,AB ∥CD ,∠A= 38°∠C= 80°,则∠M 为_____________5.如图2,D 是△ABC 中边上一点,E 是BD 上一点,则对∠1、∠2、∠A 之间关系描述正确的是( )A 、∠A <∠1 >∠2 B 、∠2 >∠1 >∠A C 、∠1 >∠2 >∠A D 、无法确定七、常见的几个重要作图1.作出△ABC 关于直线EF 的对称图形。
2020中考数学专题复习:图形和变换(轴对称、轴对称图形)(共29张PPT)

3- 2
例题6.
A O
Q
F
B E
综合提优
①求证:DQ=AE;②推断:GF:AE的值;
D
G
C
综合提优
A
D BC:AB=k(k为常数).探究GF与AE之间的数量
关系,并说明理由;
MO
F
B
E
G P
C
A
5X
O2 10 F 3 10 x
4X 5X
拓展应用:在(2)的条件下,连接CP,当k= 2 D 时,若tan∠CGP= 3 ,GF=2 10 ,求CP的长.3
2. 下列图形中,为轴对称图形的是( D )
基础训练
3.(2017黑龙江哈尔滨)下列图形中,既是轴对称图形
又是中心对称图形的是 ( D )
基础训练
4.如图所示,在Rt△ABC中,
∠C= 90°,以顶点A为圆心,适当
长为半径画弧,分别交AC,AB
于点M、N,再分别以点M,N为
圆心,大于0.5MN的长为半径画
例题讲解
∵以△ADE、△AD′E,关于直线AE 成轴对称图形∴AD=AD′, ∵在△ABD和△ACD′中
∴△ABD≌△ACD′(sss)
(2)解:∵△ABD≌△ACD′,∴∠BAD=∠CAD′, ∴∠BAC=∠DAD′=120°, ∵以△ADE的边AE所在直线为对称轴作△ADE的轴对称图形 △AD′E, ∴∠DAE=∠D′AE= ∠DAD′=60°,即∠DAE=60°
E是边CD上一点,连接AE.折叠该纸片,使点A落在AE
上的G点,并使折痕经过点B,得到折痕BF,点F在AD上.
若DE=5,则GE的长为
.
例题讲解
12
由折叠及轴对称的性质可知, △ABF≌△GBF,BF垂直平分AG,
第13章《轴对称》复习课

等腰三角形的判定及性质:
等边三角形的判定及性质:
达标测试
1.(-2,1)点关于x轴对称的点坐标为(_-__2_,__-_1_.)
2.等腰三角形的顶角为50度,则一腰上的高线
与底边的夹角是_2_5__度;
3.仔细观察下列图案,并按规律在横线上画出
合适的图形.
短?
B 小区
A小区
煤气主管
)
道)
例5、已知:如图,CD是RtΔABC斜边上的高, ∠A的平分线AE交CD于点F。 求证:CE要得到CE=CF, 只要有∠CEF=∠CFE;
例6:如图,AD是△ABC的中线,∠ADC=60°, 把△ADC沿直线AD折过来, C落在C′的位置, (1)在图中找出点C′,连结BC′; (2)如果BC=4,求BC′的长。
讲练平台
A
例1:如图,如果△ACD的周长为17cm, D
△ABC的周长为25cm,根据这些条件,
你可以求出哪条线段的长?
BE C
思路点拨:
(1)△ACD的周长=AD +CD+AC=17; (2)△ABC的周长=AB+AC+BC=25; (3)由DE是BC的垂直平分线得:BD=CD;
所以AD+CD=AD+BD=AB。 (4)由(2)-(1)得BC=8cm.
解(:1)画CO垂直AD,并延 长到C′,使得OC′=OC,
C′
点C′即为所求。
O
(2)连结C′D,由对称性得 CD=CD′,∠CD′A=∠CDA=60°; 所以∠BDC′=60°, 所以,△C′BD是等边三角形, 所以,BC′=BD=2.
小结点评:
1、翻折变换后得到的图
C′
形与原图形关于折痕对称;对
第十三章 轴对称【复习课件】

(人教版)
知识框架
知识清单详解
知识点一:轴对称图形和轴对称
1.轴对称图形:一个图形沿着某一条直线对折,直 线两旁的部分能够完全重合,有这样形状的图形叫 轴对称图形。 2.轴对称:有两个图形,如果沿着某条直线对折这 两个图形能够完全重合,那么这两个图形的位置关 系叫做轴对称。 3.对称轴:对折的直线为轴对称图形或轴对称的对 称轴。 4.轴对称图形和轴对称图形的性质:
ACBC. .行 义 换C. .∠ ∠.13线 得 后1700EA900° °的 到 有DCc0°CDm°∠性 角==或,∠∠,A质 相17OBB204BDD和 等CCc0°. .=DDm°∠角 ,, ,2400平 进E又 即° °DO分 行D∠,E线 等∥E即CD的 量DB.证=C∠定 代,在△E所9EDcOC以mD,或为,1等2c腰m之三间角形。 分 三 ∠ 解 ∴ 又 ∴ ∴ 故分 所 解 底 ( 1故D分 和 要 证 解 角 当 边 故解 理 ∵ ∴ ∴ ∴A析 角 E∠ ∠ 选: ∵0.解 又 ∴ ∴ 又 ∴ 答 所 DDD角析 以 : 选20进 关析 能 : 形 腰 选5: 由 DO∠△E⊥C: 形 AE:∵A) °7cEE=A∠ 以: ∵ △ ∵ :=DDD: 要 ( :,0m: 否 当 的 长 :行 系∥ =△ :EA3C∠根 的在BEC=A若 ,°,DOOc=E,∵ EADAC==A为因 分1D讨 ,题 组 腰 三 是B∵EODEDAmEECCA8∠E据 性△ ,) 44,而B=O为∥△由 的 ,EC=D,D0为 两700论 此目 成 长 边5∠DO+=2是CA题 质AA°° °若07没c为等DE∠cB长 即CEDBD-∠种4°0给 三 是 关m, 时E平等CmCCD意 可∠ 是CC角40;°有时D等腰=BD是 可平 , ,中 -B情°,0还 周出 角 系2∴分O2C是腰可 得∠ ∠AA为°或明c,腰三+分求DD5CD,况角7等 形 ,要 长m∠∠3Ec, 等三=判EAB∠底0角1确时 因三角=∠得=m4DA. D进没°0应 是腰 . 应5EA3即 腰角断EC为A0角为0腰, 为cDO角形cA。=D的 °行有;°三 排用1OBmmC三∠形出9EB,顶、2因5=形B, ;0=,角C讨明,三角 除c+∠角, E,∠A中 °则角m底为5C平D论确4角形 ;> .B形∴ ∴DA⊥-点另,0分2∴O=E分8.是°有形+2D∠∠,CDB,0外则别2,∠E=C°线顶的两<E=AC,8A两另是符ADDCE0,=B角条三5ODCE==根° 1个处多,合D=D, ,A0还边边=∠E据, °C角两少不三∠,,是长关B等所.为个,符角DC又底系为OD腰以角所合形B, A角验2E是以三三c=,m2cm,
第二章 轴对称图形总复习

1 l AB 第二章 轴对称图形总复习一、必备知识点1.轴对称定义:如果把一个图形沿着 后,能够 重合,那么这两个图形关于这条直线成轴对称,这条直线叫做 ,两个图形中的对应点叫做 。
2.轴对称图形定义:如果把一个图形沿着 ,直线两旁的部分能够 ,那么这个图形叫做轴对称图形,这条直线叫做 。
3.轴对称的性质: ⑴成轴对称的两个图形 。
⑵如果两个图形成轴对称,那么对称轴是 。
4.线段的垂直平分线定义:垂直并且平分一条线段的直线,叫做这条线段的垂直平分线。
(也称线段的中垂线)5.线段的轴对称性:①线段是轴对称图形,对称轴有两条,一条是 ,另一条是 。
②性质:线段的垂直平分线上的点到 相等。
③判定:到 的点,在这条线段的 上。
结论:线段的垂直平分线是到线段两端距离相等的点的集合6.角的轴对称性:①角是 图形,对称轴是 。
②性质:角平分线上的点到 相等。
③判定:在角的内部,到 的点,在 上。
7.等腰三角形定义:有 的三角形叫等腰三角形,其中相等的边叫做腰,另一条边叫做底。
等腰三角形是 ,对称轴是 。
性质:等腰三角形 相等, 相等(简称 );等腰三角形的 互相重合。
(三线合一)8.判定:如果一个三角形 ,那么 (简称 );9.等边三角形是特殊的 ,具备 的一切性质。
除此之外,等边三角形有 , , 。
10.等边三角形的判定: 是等边三角形; 的三角形是等边三角形; 是等边三角形。
11.直角三角形的性质:① 直角三角形两锐角② 直角三角形斜边上的中线是斜边的 。
B AC E DO P l A B M2 二、学力检测一、选择题1.下列命题中:①两个全等三角形合在一起是一个轴对称图形;②等腰三角形的对称轴是底边上的中线;③等边三角形一边上的高就是这边的垂直平分线;④一条线段可以看着是以它的垂直平分线为对称轴的轴对称图形. 正确的说法有( )个 A .1个 B .2个 C .3个 D .4个2.下列图形中:①平行四边形;②有一个角是30°的直角三角形;③长方形;④等腰三角形. 其中是轴对称图形有( )个A .1个B .2个C .3个D .4个3.已知∠AOB =30°,点P 在∠AOB 的内部,P 1与P 关于OA 对称,P 2与P 关于OB 对称,则△P 1OP 2是 ( ) A .含30°角的直角三角形; B .顶角是30的等腰三角形;C .等边三角形D .等腰直角三角形. 4.如图:等边三角形ABC 中,BD =CE ,AD 与BE 相交于点P ,则 ∠APE 的度数是 ( ) A .45° B .55°C .60°D .75°5. 下列关于等腰三角形的性质叙述错误的是( ) A .等腰三角形两底角相等B .等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合C .等腰三角形是中心对称图形D .等腰三角形是轴对称图形6.已知点P 在线段AB 的垂直平分线上,点Q 在线段AB 的中垂线外,则 ( ) A .PA+PB >QA+QB B .PA+PB <QA+QB D .PA+PB =QA+QB D .不能确定7.已知△ABC 与△A 1B 1C 1关于直线MN 对称,且BC 与B 1C 1交与直线MN 上一点O , 则 ( ) A .点O 是BC 的中点 B .点O 是B 1C 1的中点 C .线段OA 与OA 1关于直线MN 对称 D .以上都不对8.如图:已知∠AOP=∠BOP=15°,PC ∥OA ,PD ⊥OA ,若PC=4,则PD= ( ) A .4 B .3C .2D .1 9.∠AOB 的平分线上一点P 到OA 的距离 为5,Q 是OB 上任一点,则 ( ) A .PQ >5 B .PQ≥5C .PQ <5D .PQ≤510.等腰三角形的周长为15cm ,其中一边长为3cm .则该等腰三角形的底长为 ( ) A .3cm 或5cm B .3cm 或7cm C .3cm D .5cmB AD PO C P AEC B D3 二.填空题11.线段轴是对称图形,它有_______条对称轴. 12.等腰△ABC 中,若∠A=30°,则∠B=________.13.在Rt △ABC 中,∠C=90°,AD 平分∠BAC 交BC 于D ,若CD=4,则点D 到AB 的距离是__________. 14.等腰△ABC 中,AB=AC=10,∠A=30°,则腰AB 上的高等于___________. 15.如图,在△ABC 中,∠ABC=∠ACB=72°,BD 、CE 分别是∠ABC 和∠A CB 的平分线,它们的交点为F ,则图中等腰三角形有___________个.16.(2012•梧州)如图,在△ABC 中,AB=AD=DC ,∠BAD=32°,则∠BAC= °___________.17.若D 为△ABC 的边BC 上一点,且AD=BD ,AB=AC=CD , 则∠BAC=____________.18.△ABC 中,AB 、AC 的垂直平分线分别交BC 于点E 、F ,若∠BAC=115°,则∠EAF=___________. 三.解答题19.如图:已知∠AOB 和C 、D 两点,求作一点P ,使PC=PD ,且P 到∠AOB 两边的距离相等.A C··DOB4 20.如图:AD 为△ABC 的高,∠B=2∠C ,用轴对称图形说明:CD=AB+BD .21.有一本书折了其中一页的一角,如图:测得AD=30cm,BE=20cm ,∠BEG=60°,求折痕EF的长.22.如图:△ABC 中,AB=AC=5,AB 的垂直平分线DE 交AB 、AC 于E 、D ,① 若△BCD 的周长为8,求BC 的长;② 若BC=4,求△BCD 的周长.ACDBBCDEA5 23.等边△ABC 中,点P 在△ABC 内,点Q 在△ABC 外,且∠ABP=∠ACQ ,BP=CQ ,问 △APQ是什么形状的三角形?试说明你的结论.24. 如图1,已知矩形ABED ,点C 是边DE 的中点,且AB=2AD . (1)判断△ABC 的形状,并说明理由;(2)保持图1中△ABC 固定不变,绕点C 旋转DE 所在的直线MN 到图2中(当垂线段AD 、BE 在直线MN 的同侧),试探究线段AD 、BE 、DE 长度之间有什么关系?并给予证明;(3)保持图2中△ABC 固定不变,继续绕点C 旋转DE 所在的直线MN 到图3中的位置(当垂线段AD 、BE 在直线MN 的异侧).试探究线段AD 、BE 、DE 长度之间有什么关系?并给予证明.A CBPQ。
第一章轴对称图形(复习课)079PPT课件

直线对称; ④连结DF,EF. (2)通过观察和测量,猜想△DEF是什么三角形.
等腰三角形、梯形的 轴对称性
回顾与复习
等腰三角形的性质: A
= (
P
且PC=PD
O
∴点P在∠AOB的平分线上.
DB
简单应用
1. 指出下列图案是否是轴对称图形, 如果是请指出有几条对称轴
(5)
(6)
简单应用
2. 下列说法正确的是( B )
⑴ 全等的两个图形一定对称.
⑵ 成轴对称的两个图形一定全等. √
⑶ 若两个图形关于某直线对称,则它们 的对应点一定位于对称轴的两侧.
线段的垂直平分线 上的点到线段两端 的距离相等.
A
·P
a
B
练:《补充》/17(1)
动脑筋
12 如图,要在河边
修建一个水泵站, 向张庄、李庄送水. 修
在河边什么地方,可使使用的水管B最短?
A
∟
· ·P
a
把问题转化成第10题的形式画图。
练:《补充》/17(2) 课本38页/9
练一练
《课本》37-38页 复习巩固/1.2.3.4.5,9
4
形,首先应确定 对称轴,然后找
·D2
C·
出对称点。且点D 必须在格点上
·A ·B
综上所述:
·D 3
·D1
方格纸中符合要求的点D有4个。
8.分别画出(1)(2)(3)中,已知△ABC 关于直线l 的对称△A′B′C′
l
A
∟
轴对称图形 基础知识复习讲义

【知识点 11】 实数概念: 】 实数概念:
有理数
正有理数
实数的分类: 实数的分类:
实数 正无理数 负无理数
〖基础回顾〗 基础回顾〗 1.与数轴上的点一一对应的数是 . 。 的点到原点的距离是_________ _________。 2. 数轴上表示 − 6 的点到原点的距离是_________。 点M在数轴上与原点相距 5 个单位,则点 表示的实数为 在数轴上与原点相距 个单位,则点M表示的实数为 3. −7.2 5
·北师大版
4、在△ABC中, AB=15,AD=12,BD=9,AC=13,求 、 中 , , 求 的周长和面积。 △ABC的周长和面积。 的周长和面积
·北师大版
【知识点 4】 勾股定理与方程的综合运用 】 〖基础回顾〗 基础回顾〗 1.AC=6cm,BC=8cm,现将直角边AC沿直线 折叠,使它落 , ,现将直角边 沿直线AD折叠, 沿直线 折叠 在斜边AB上 且与AE重合 你能求出CD的长吗 重合, 的长吗? 在斜边 上,且与 重合,你能求出 的长吗?
. M N
【知识点 7】等腰三角性是
等腰三角形的性质: 等腰三角形的性质 等腰三角形的判定: 等腰三角形的判定
图形,它的对称轴是 图形 它的对称轴是
〖基础回顾〗 基础回顾〗
1.等腰三角形ABC中,AB=AC,AD是角平分线,则“①AD⊥BC,②BD=DC, .等腰三角形 是角平分线, 中 , 是角平分线 ⊥ , , ③∠B=∠C,④∠BAD=∠CAD”中,结论正确的个数是( ) ∠ , ∠ 中 结论正确的个数是( A、4 B、3 C、2 D、1 、 、 、 、 2.如果等腰三角形的一个底角为 °,那么其余两个角为 .如果等腰三角形的一个底角为50° 那么其余两个角为______和___ __ 和 如果等腰三角形的一个角为80° 那么它的一个底角为__________ 如果等腰三角形的一个角为 °,那么它的一个底角为 已知等腰三角形的一个角是110° 已知等腰三角形的一个角是 °,则其余两角为 3.一个等腰三角形的两边分别为8cm和6cm,则它的周长为 .一个等腰三角形的两边分别为8 4.已知:如图1.5-20,点D、E在△ABC的边 上,AD=AE,BD=EC. 1.5的边BC上 .已知:如图1.5 20, 、 在 的边 = = 求证: = 求证:AB=AC
轴对称全章复习
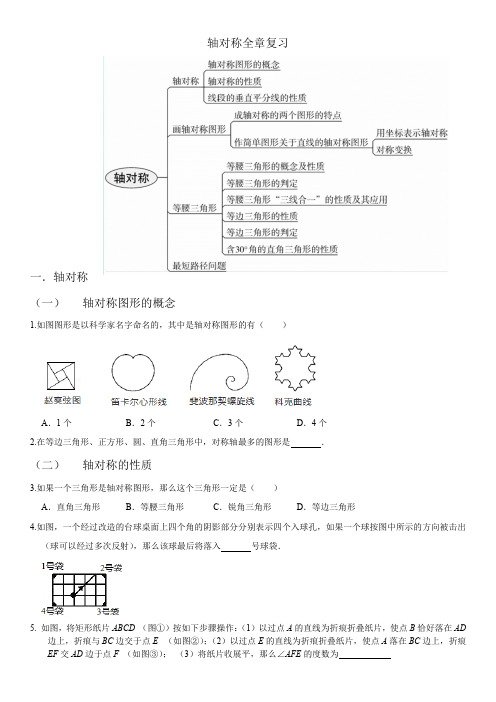
轴对称全章复习一.轴对称(一)轴对称图形的概念1.如图图形是以科学家名字命名的,其中是轴对称图形的有()A.1个B.2个C.3个D.4个2.在等边三角形、正方形、圆、直角三角形中,对称轴最多的图形是.(二)轴对称的性质3.如果一个三角形是轴对称图形,那么这个三角形一定是()A.直角三角形B.等腰三角形C.锐角三角形D.等边三角形4.如图,一个经过改造的台球桌面上四个角的阴影部分分别表示四个入球孔,如果一个球按图中所示的方向被击出(球可以经过多次反射),那么该球最后将落入号球袋.5.如图,将矩形纸片ABCD(图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E(如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F(如图③);(3)将纸片收展平,那么∠AFE的度数为6.如图,分别以△ABC的边AB,AC所在直线为对称轴作△ABC的对称图形△ABD和△ACE,∠BAC=150°,线段BD与CE相交于点O,连接BE、ED、DC、OA.有如下结论:①∠EAD=90°;②∠BOE=60°;③OA平分∠BOC;④EA=ED;⑤BP=EQ.其中正确的结论个数是()A.4个B.3个C.2个D.1个二.轴对称图形(一)作简单图形关于直线的轴对称图形7.如图4×5的方格纸中,在除阴影之外的方格中任意选择一个涂黑,与图中阴影部分构成轴对称图形的涂法有种.8.已知如下图,求作△ABC关于对称轴l的轴对称图形△A′B′C′.9.如图所示,由每一个边长均为1的小正方形构成的8×8正方形网格中,点A,B,C,M,N均在格点上(小正方形的顶点为格点),利用网格画图.(1)画出△ABC关于直线MN对称的△A′B′C′;(2)在线段MN上找一点P,使得∠APM=∠CPN.(保留必要的画图痕迹,并标出点P位置)(二)找对称轴10.如图,网格中的△ABC与△DEF为轴对称图形.(1)利用网格线作出△ABC与△DEF的对称轴l;(2)如果每一个小正方形的边长为1,请直接写出△ABC的面积=.11.ΔABC与ΔA'B'C'关于直线l对称,求作直线l(三)坐标表示轴对称12.点P(a+2,2a﹣5)关于y轴的对称点在第二象限,则a的取值范围是()A.a<﹣2B.﹣2<a<C.﹣<a<2D.a>13点P(﹣3,2)关于直线x=1对称的点的坐标为.三.轴对称图形(一)线段垂直平分线的性质和判定14.如图,∠ACD=90°,∠D=15°,B点在AD的垂直平分线上,若AC=4,则BD=15.如图,在△ABC中,∠ACB=90°,△ABD是△ABC的轴对称图形,点E在AD上,点F在AC的延长线上.若点B恰好在EF的垂直平分线上,并且AE=5,AF=13,则DE=.16.如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.(1)求∠APO+∠DCO的度数;(2)求证:点P在OC的垂直平分线上.17.如图,已知△ABC是等腰直角三角形,∠BAC=90°,BE是∠ABC的平分线,DE⊥BC,垂足为D.(1)请你写出图中所有的等腰三角形;(2)请你判断AD与BE垂直吗?并说明理由.(3)如果BC=10,求AB+AE的长.(二)等腰三角形(1)等腰三角形的性质和判定18.①等腰三角形一个角为70°,则其他两个角分别是_____.②等腰三角形一腰上的高与另一腰的夹角是20°,则等腰三角形的底角等于__ _.③等腰三角形的一边长为5cm,周长是20,则它另两边为④如图,在△ABC中,∠ACB=90°,∠BAC=40°,在直线AC上找点P,使△ABP是等腰三角形,求∠APB的度数.⑤在平面直角坐标系xOy中,已知点P(3,4),点Q在x轴上,△PQO是等腰三角形,在图中标出满足条件的点Q位置19.已知:如图,D、E分别为AB、AC上的点,AC=BC=BD,AD=AE,DE=CE,求∠B的度数.20.如图,在△ABC中,AB=AC,∠BAD=30°,∠CAD=50°,AE=AD,(1)求∠EDC的度数.(2)若把条件“∠CAD=50°”去掉,你是否还能求出∠EDC的度数?若能,请写出求解过程;若不能,请说明理由.21.(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数;(2)如果把第(1)题中“AB=AC”的条件去掉,其余条件不变,那么∠DAE的度数会改变吗?说明理由;(3)如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC 有怎样的大小关系?22.如图,△ABC为等边三角形,BD平分∠ABC交AC于点D,DE∥BC交AB于点E.(1)求证:△ADE是等边三角形.(2)求证:AE=AB.23.两个全等的含30°,60°角的三角板ADE和三角板ABC如图所示放置,E,A,C三点在一条直线上,连接BD,取BD的中点M,连接ME,MC.试判断△EMC的形状,并说明理由.24.在平面直角坐标系中,等腰三角形ABC的顶点A的坐标为(3,3)(1)若底边BC在x轴上,①点B的坐标为(﹣1,0),则满足条件的C点的坐标为;②设点B、点C的坐标分别为(m,0)、(n,0),则m、n应满足的条件为;(2)若底边BC的两端分别在x轴,y轴上,①点B的坐标为(﹣1,0),则满足条件的C点的坐标为;②设点B、点C的坐标分别为(m,0)、(0,n),则m、n应满足怎样的条件?请说明理由.(2)等边三角形的性质和判定25.如图,在平面直角坐标系中,点A的坐标为(1,0),以线段OA为边在第四象限内作等边三角形AOB,点C为x轴正半轴上一动点(OC>1),连接BC,以线段BC为边在第四象限内作等边△CBD,连接DA并延长,交y轴于点E.①△OBC与△ABD全等吗?判断并证明你的结论;②当点C运动到什么位置时,以A,E,C为顶点的三角形是等腰三角形?26.等边△ABC边长为6,P为BC上一点,含30°、60°的直角三角板60°角的顶点落在点P上,使三角板绕P点旋转.(1)如图1,当P为BC的三等分点,且PE⊥AB时,判断△EPF的形状;(2)在(1)问的条件下,FE、PB的延长线交于点G,如图2,求△EGB的面积;27.在Rt△ABC中,∠ACB=90°,∠A=30°,BD是△ABC的角平分线,DE⊥AB于点E.(1)如图1,连接EC,求证:△EBC是等边三角形;(2)点M是线段CD上的一点(不与点C,D重合),以BM为一边,在BM的下方作∠BMG=60°,MG交DE延长线于点G.请你在图2中画出完整图形,并直接写出MD,DG与AD之间的数量关系;(3)如图3,点N是线段AD上的一点,以BN为一边,在BN的下方作∠BNG=60°,NG交DE延长线于点G.试探究ND,DG与AD数量之间的关系,并说明理由.(3)含300角的直角三角形的性质28.如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s.(1)连接AQ、CP交于点M,则在P、Q运动的过程中,∠CMQ变化吗?若变化,则说明理由,若不变,则求出它的度数;(2)请求出何时△PBQ是直角三角形?29.如图,Rt△ACB中,∠ACB=90°,∠A=30°,∠ABC的角平分线BE交AC于点E.点D为AB上一点,且AD=AC,CD,BE交于点M.(1)求∠DMB的度数;(2)若CH⊥BE于点H,证明:AB=4MH.30.如图所示,已知△ABC中,AB=AC,∠DBC=∠D=60°,AE平分∠BAC,若BD=9cm,DE=2cm,求BC的长.四.最短路径问题31.如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).(1)请画出△ABC向左平移5个单位长度后得到的△A1B1C1;(2)请画出△ABC关于x轴对称的△A2B2C2;(3)请求出△ABC的面积;(4)请在y轴上找一点P,使得P A+PC最小.32.已知:如图,四边形ABCD中,∠A=∠B=90°,∠C=60°,CD=2AD,AB=4.(1)在AB边上求作点P,使PC+PD最小;(2)求出(1)中PC+PD的最小值.。
八年级数学上册前两章复习指南

第1章轴对称与轴对称图形复习总体要求:复习首先要熟悉课本,认真的看几遍课本后,一定要做到,合上课本,能知道本章共几节,每节都有哪些定理和定义。
1.1 我们身边的轴对称图形复习要求:1.知道轴对称图形和两个图形关于某条直线成轴对称的定义;2.知道上述两定义的联系和区别;3.能判断一个图形是否是轴对称图形本节关键:1.常见图形中的轴对称图形有:线段、角、等腰三角形、等腰梯形、长方形、菱形、正多边形和圆,其中线段有两条对称轴,分别是它的垂直平分线(也称中垂线)和它本身所在的直线;角有一条对称轴,是它的角平分线所在的直线;等腰梯形有一条对称轴,正n边形有n条对称轴;圆有无数条对称轴。
2.注意课本7页第4题的图(1)中的两幅图案并不关于直线l成轴对称。
3. 轴对称图形和两个图形关于某条直线成轴对称的区别:轴对称图形是指一个具有特殊形状的图形;两个图形关于某条直线成轴对称是指两个图形的特殊的形状和位置关系。
联系:(1)定义中都有一条直线,都要沿这条直线折叠重合;(2)如果把轴对称图形沿对称轴分成两部分,那么这两个图形关于这条直线成轴对称;如果把两个关于某直线成轴对称的图形看作一个整体,那么它就是一个轴对称图形。
1.2 线段的垂直平分线一.复习要求:1.知道什么是线段的垂直平分线;2.能熟练运用线段的垂直平分线的性质定理:线段垂直平分线上的点,到这条线段两个端点的距离相等.二.本节关键:(一). 线段垂直平分线的性质定理的应用格式:PD ABPA PB =∴垂直平分(二). 线段垂直平分线的性质定理的作用:1.在计算题或证明题中用来证明两条线段相等.例1如图1,等腰△ABC 中,AB =AC ,AB +BC =13,AB 边的垂直平分线MN 交AC 于点D ,求△BCD 的周长.分析:第一步:我们首先来看本题的已知条件: AB =AC ,AB +BC =13, MN 垂直平分AB ,由其中的“MN 垂直平分AB ”,我们还可以立刻得到DA =DB ;第二步:然后来看一下本题的未知,即要求解的东西: △BCD 的周长,即BC +CD +BD第三步:找已知和未知的联系:本题未知和已知的联系比较直接, △BCD 的周长=BC +CD +BD = BC +CD +AD = BC +AC= BC + AB =13.解:MN 垂直平分MN ∴DA =DB ∴于是△BCD 的周长=BC +CD +AD = BC +AC= BC + AB =13. 反思:本题的解决所用到的知识点主要是线段垂直平分线的性质定理,所用到的思想方法主要是转化思想和整体思想,例如将BD 转化为AD ,然后将CD +AD 转化为AC ,再将AC 转化为 图1B N M DC AAB,进一步将BC+AC转化为BC + AB,最终求得结果.收获: (1)通过本题,我们知道,对线段垂直平分线的性质定理要熟悉其内容和应用格式;(2)再一个,看到已知条件应立刻想到可以推得的结论,这样利于我们找到已知和未知之间的联系,至少可以让已知和未知离的更近一些;(3)本题所体现的转化思想我们也应该认真体会领悟,很多题目就是在这样不断转化当中得到答案的;(4)本题的解答中还运用了整体思想,求解△BCD的周长,我们并没有一条边一条边的去求解,而是将整个三角形的周长当做一个整体一起求,这也应该当做一个经验储存起来,以后碰到类似的问题也可以采用相同的方法.相应练习:①.如图,已知ABC∆的周长为8cm,∆中,AB=AC,D是AB的中点,且DE⊥AB,已知BCE且AC=BC+2cm,求AB,BC的长.②.如图,已知ABC∆的∆中,AB=AC,DE垂直平分AB交AB于D,交AC于E,若ABC周长为28,BC=8,求BCE∆的周长.①分析:第一步:已知条件:AB=AC,DE垂直平分AB, BCE∆的周长=BE+CE+BC=8 cm, AC=BC+2cm,由“DE垂直平分AB”可立刻推得AE=BE.第二步:未知结论: AB,BC的长第三步:找已知和未知联系:由AB=AC可知,要求AB,只需求出AC即可;故本题可转化为求AC,BC;因为AC=BC+2cm,所以我们需要找出AC和BC之间另外的关系,这样我们就可以得到关于AC,BC的二元一次方程组,进而求出AC,BC.看来我们需要再看一下本题的另外两个条件, BCE∆的周长=BE+CE+BC=8 cm,在这个等式中有BC,我们可以看一下BE和CE是否和AC有关系,不难发现,BE+CE= AE+CE=AC,即AC+BC=8 cm.解答:B A ,8DE AB AD BDAE BE BE CE BC AE CE BC AC BC ⊥==++=++=+=∴∴联立AC =BC +2可得:825cm,3cmAC BC AC BC AC BC +=⎧⎨=+⎩==解得: 反思: 本题的解决所用到的知识点主要是线段垂直平分线的性质定理,所用到的思想方法主要是转化思想和方程思想(所谓方程思想,就是通过设未知数,寻找已知和未知之间的等量关系,构造方程或方程组,然后求解方程完成未知向已知的转化的一种思想方法),当然构造方程的目的其实还是方便进行转化.收获:我们看到,很多时候解决和几何图形有关的问题时,需要借助于方程思想,本题本身就有一个方程AC =BC +2,但只这一个不够,这使我们想到去构造另一个方程以和它组成方程组.以后在解决类似的问题时,我们也可以考虑用方程思想;当然,本题也反复应用了转化思想.② BCE ∆的周长=18(自己分析解答)先分析,再解答,完了之后进行反思,并争取有所收获.2.用来作图①(1)如图,用尺规分别作出线段AB 与BC 的垂直平分线;(2)在(1)中,如果线段AB 与BC 的垂直平分线 交于点P ,那么P A 与PC 相等吗?为什么?②如图,要在任庄A ,李村B ,菜屯C 三个村庄之间修一座变电站O ,使它到三个村庄的距离相等,你能在图中找出点O 的位置吗?解答:只需连接AC ,AB ,然后作它们的中垂线12,l l ,两条中垂线的交点既是点O 的位置.(三)易混淆知识点1.三角形三边垂直平分线的交点( )A.必在三角形的内部 B 必在三角形的外部 C 必在三角形的一边上 D 以上都有可能 解答:此题最容易选A 选项,实际上应该选D.反思:对于涉及几何图形的题目,当题目不给出图形时,我们就应该自己画出所有可能的图形,然后针对每种图形进行分析解答,像本题,没有明确指出(画出)三角形到底是什么样的三角形,我们至少应该画出锐角三角形、直角三角形、钝角三角形各一个,并分别画出它们三边的垂直平分线,然后看看到底交点在哪里.这实际上是在运用分类讨论的思想(分类讨论,就是当问题所给的对象不能进行统一研究时,就需要对研究对象按某个标准进行分类,然后对每一类分别研究得出每一类的结论,最后综合各类结果得到整个问题的解答.)解决问题.收获:当以后再碰到没有几何图形的几何题目时,我们也应该考虑分类讨论.2.在ABC ∆内部有一点P ,到ABC ∆三个顶点的距离相等,即,PA PB PC ==则点P 一定是( )A.三角形三边中线的交点B.三角形三遍高的交点C.三角形三边垂直平分线的交D.三角形三个角的平分线的交点 解答:这个题很容易选成D,实际上选C.反思:在学习角平分线性质定理之前,这个题倒不容易做错,学了之后就容易做错,三角形三边垂直平分线的交点是到三角形各顶点的距离相等,而三角形各内角平分线的交点是到三角形各边的距离相等.其实,这个题也容易做对,你只需要将两幅图形画在一起,认真的进行对比,找出它们在形式上的不同(其实差别还是很多的),然后再搞清它们实质上的区别即可(一个是利用了线段的垂直平分线性质定理,一个是利用了角平分线的性质定理).收获:对数学上的一些相似的定理,要放在一起对比学习一下,这样有利于分清它们各自的条件和结论,可以有效避免这个定理的条件推出那个定理的结论,俗话说的“不怕不识货,就怕货比货”,我们在数学上不妨拿来用一下.3.平面上到三点A 、B 、C 距离相等的点( )A.只有一个B.有两个C.三个或三个以上D.有一个或者一个都没有 解答:这个题容易选A,实际上应选D.反思:这里还是分类讨论的问题,这里没说三个点是否在同一条直线上,我们就应该分三个点在同一条直线上和不在同一条直线上两种情况解答.收获:永远记住,没有几何图形的几何问题,一般需要分类讨论.实际上1题和3题还告诉我们一个道理,那就是考虑问题要全面一些.(四)线段的垂直平分线的性质定理深入研究思考题:如图,PD AB 垂直平分,请找出图中所有相等的量,并一一给以证明.解答:,,,,,ADP BDP ADP BDPPA PB AD BD A B ADP BDP APD BPD S S C C ∆∆∆=∆==∠=∠∠=∠∠=∠= (1) ,90PD ABAD BD ADP BDP ∴=∠=∠=︒垂直平分 (2)PD AB PA PB =∴垂直平分大家都看到了,,,AD BD ADP BDP PA PB =∠=∠=很容易证明,而且,ADP BDP ADP BDP S S C C ∆∆∆=∆=也容易证明,但,A B ∠=∠APD BPD ∠=∠该如何证明呢?(3)分析:要证明,A B ∠=∠只需证明PA PB =即可.证明: PD ABPA PB A B=∠=∠∴∴垂直平分(4)分析:要证明APD BPD ∠=∠,我们可以先证明,A B ∠=∠,ADP BDP ∠=∠然后利用内角和证明.证明: 180,180180,18090PD ABPD ABPA PB A BA ADP APDB BDP BPD APD A ADP BPD B BDPAPD BPDADP BDP ⊥∴=∴∠=∠∠+∠+∠=︒∠+∠+∠=︒∠=︒-∠-∠∠=︒-∠-∠∠=∠∴∴∴∠=∠=︒垂直平分 这里,大家想一想,还有没有其他的方法来证明APD BPD ∠=∠?这里我再提供一种思路:证明: ,PD ABPA PBPA PB PD AB APD BPD==⊥∠=∠∴∴垂直平分大家可以想一想,这是运用了什么定理?收获:通过对垂直平分线性质定理的的深入研究,我们不难发现,数学中的定理是彼此有着千丝万缕的联系的,这不正像这个我们生活着的大千世界吗?这也是学习数学的乐趣之一,当你能够通过认真思考,总结将所学的知识融会贯通之时,你就更能游刃有余的解决那些所谓的难题,谁能说这里面没有无穷的乐趣呢? APD BPD ∠=∠的证明还告诉我们,解决同一个问题,可以有不同的方法,希望同学们致力于一题多解,这样可以开阔你们的思路,帮助你们更好的熟悉定理,锻炼数学思维,当你只有一种武器对付敌人时,你是受限制的,当你有两种或更多的武器对付敌人时,你已经进入了自由的毫无拘束的世界!1.2 角的平分线一.复习要求:1.知道角平分线性质定理的内容;2.能熟练运用角平分线的性质定理:角平分线上的点,到这个角的两边的距离相等.二.本节关键:(一). 角平分线的性质定理的应用格式:,OP AOBPA OA PB OB PA PB∠⊥⊥=∴平分注意: (1)在角平分线性质定理的应用格式中,“,PA OA PB OB ⊥⊥”是必不可少的,因为“,PA OA PB OB ⊥⊥”可以表明,PA PB 是垂线段,而点P 到直线,OA OB 的距离正好是指P 到直线,OA OB 的垂线段的长度;(2)另一方面,只是OP AOB ∠平分并不足以说明PA PB =,如下图:OP AOB ∠平分,但PA PB ≠(3)当然,只有,PA OA PB OB ⊥⊥也不足以证明PA PB =,如下图:,PA OA PB OB ⊥⊥,但PA PB ≠(4)上一节课学的线段的垂直平分线的性质定理也有同样的问题:正确的应用格式如下:PD ABPA PB =∴垂直平分①只是PD AB ⊥不足以证明PA PB =,如下图:PD AB ⊥,但PA PB ≠②只是PD 平分AB 也不足以证明PA PB =,如下图:PD 平分AB ,但PA PB ≠(二). 角平分线的性质定理的作用:1.在计算题或证明题中用来证明两条线段相等.例1如图,△ABC 中,BD 平分,90,6,15ABC A AD BC ∠∠=︒==,求△BCD 的面积.分析:我们首先来看本题的已知条件: BD 平分,90,6,15ABC A AD BC ∠∠=︒==,由BD 平分ABC ∠,我们立刻可以想到点D 到ABC ∠两边的距离相等,这样就可以得到BC 边上的高等于AD ,即等于6,又BC 已知,这样就可以求出△BCD 的面积了. 解:如下图,作DE BC ⊥于点E,6111564522BDC BD ABCDA BA DE BCDE DA S BC DE ∆∠⊥⊥===⋅⋅=⨯⨯=∴∴平分 反思:本题的解决所用到的知识点主要是角平分线的性质定理,所用到的思想方法主要是转化思想.收获: (1)通过本题,我们知道,角平分线的性质定理要熟悉其内容和应用格式;(2)本题的辅助线需要用虚线作出来,而且在证明的第一步就需要将作了什么辅助线说出来.相应练习:①.如图,在△ABC 中,AD 平分,5,3,BAC AB AC ∠==则_____.ABD ACD S S ∆∆=分析:三角形的面积等于底乘以高的一半,故要求面积比,需先确定底边和高,因为,AB AC 已知,不妨将它们确定为底边,这样就需要将它们上面的高作出来,如下图,,DE DF 即分别为,AB AC 上的高,从而有:11555221133322ABDACD AB DE DE S DE S DF AC DF DF ∆∆⋅⋅⨯⨯====⋅⋅⨯⨯.解答:作,DE AB E DF AC F ⊥⊥于点于点,11555221133322ABD ACD AD BACDE AB DF ACDE DF AB DE DE S DE S DF AC DF DF ∆∆∠⊥⊥=⋅⋅⨯⨯====⋅⋅⨯⨯∴∴平分 反思:本题用到的知识点主要是角平分线性质定理和三角形面积公式,以后碰到类似的问题,我们也应该想到去作高,然后结合角平分线性质定理和三角形面积公式来解决.另外“作,DE AB E DF AC F ⊥⊥于点于点”还是要列在解答过程中.追问: ____BD CD= 请同学们思考上述问题,我只是把图画在下面,请同学们根据图的提示自己解答.②.如图,已知BD 平分,,36,18,12,ABC ABC DE AB S AB BC ∆∠⊥===则___.DE =分析:先看已知,由BD 平分ABC ∠,我们不难想到这个题很可能要过点D 向BC 作垂线以得到一条垂线段(如下图,不妨设为DF ),并且本题很可能会用到DE DF =;由36ABC S ∆=可知整个三角形的面积为36,结合DE DF =,我们不妨将ABC S ∆分解为()()111111181236222222ABD CBD S S AB DE BC DF AB DE BC DE DE AB BC DE ∆∆+=⋅⋅+⋅⋅=⋅⋅+⋅⋅=+=+=从而求得125DE =解答:作DF BC F ⊥于点()(),111122221118123622125ABC ABD CBD BD ABCDE AB DF BCDE DFS S S AB DE BC DF AB DE BC DE DE AB BC DE DE ∆∆∆∠⊥⊥==+=⋅⋅+⋅⋅=⋅⋅+⋅⋅=+=+==∴∴∴平分 反思:解答本题用到的知识点主要是角平分线性质定理和三角形面积公式,所用到的思想方法主要是转化思想和方程思想,如将DF 转化为DE ,将ABC S ∆转化为ABD CBD S S ∆∆+等都是转化,DE 的求出则是借助于建立了方程.收获:自己想想通过解这个题,你都是得到了那些经验,好好总结一下,每做完一个题,都反思一下本题用到了哪些知识点,用到了什么思想方法,以及你是怎么想到用这些知识点的,你又怎么想到了用这样的思想方法,久而久之,你自然就会成为解题高手,而不是那个腋下只有一个玉米的狗熊.③.如图,在△ABC 中,AD 平分,//,//,BAC PE AB PF AC ∠请问点D 到,PE PF 的距离相等吗?解答:如下图,作,DM PE M DN PF N ⊥⊥于点与点AD 平分BAC ∠12//13//243434,PE ABPF ACDM PE DN PF DMDN ∠=∠∠=∠∠=∠∠=∠∠=∠⊥⊥=∴∴∴∴∴注意:在本题的证明中,必须作出,DM DN ,因为没有它们,根本谈不上点D 到,PE PF 的距离;另外34∠=∠的证明也必须严格按照上面的过程证明,绝对不可以像下面这样证明:,//,//AD BAC PE AB PF ACPD EPF ∠∠∴平分平分首先没有这样的定理,其次,虽然道理上讲是对的,但跨度太大,省略了太大步骤,就好比一个人是没办法从一楼直接上三楼一样.④.如图,四边形ABCD 中,90,//,,A AD BC DP ADC CP BCD ∠=︒∠∠平分平分,请问点P 是边AB 的中点吗?为什么?解答:如下图,作PE DC E ⊥于点,//1801801809090,DP ADCPA DA PE DCPA PEAD BCB A B A CP BCDPB DB PE CDPB PEPA PB∠⊥⊥=∠+∠=︒∠=︒-∠=︒-︒=︒∠⊥⊥==∴∴∴∴∴平分平分注意:在本题的证明中,90∠=︒的证明,只能用“两直线平行,同旁内角互补”来证B明,不可错用“两直线平行,内错角相等”或“两直线平行,同位角相等”来证明,因为,A B∠∠根本不是内错角,也不是同位角.2.用来作图①.如图,某校学生开运动会,要选一起点C,两名运动员先从C点出发分别到E,F 两处取物品,然后负重回到C,再分别将物品送到OA,OB的路上,你能找到一个公平的点C吗?两运动员又应沿怎样的路线走?与的交点解答:只需连接EF,并作它的垂直平分线m,然后作AOB∠的平分线,n m n即为C.②如图,直线n,,表示相互交叉的公路,现要建一个货物中转站,要求它到三条k,m公路的距离相等,则可供选择的地址有()处.A.一处B.两处C.三处D.四处解答:如下图,有四处点,,,A B C D处都可以做为中转站.③如图所示, 在△ABC 中,20,30,40,AB BC CA O ===为其三条角平分线的交点,则________.AOB AOCS S ∆∆=分析:如下图,由点O 为其三条角平分线的交点可知,其道三角形各边的距离相等,从而其面积比可以转化为边长比.即:112122AOB AOC AB OD S AB S AC AC OF ∆∆⋅⋅===⋅⋅(三)易混淆知识点1.三角形三个内角平分线的交点( )A.必在三角形的内部 B 必在三角形的外部 C 必在三角形的一边上 D 以上都有可能解答:此题选A 选项,不要误选D.反思:这个题目容易同“三角形三边垂直平分线交点”相混淆,注意辨别.2.在ABC ∆内部有一点P ,到ABC ∆三个边的距离相等,即,PA PB PC ==则点P 一定是( )A.三角形三边中线的交点B.三角形三遍高的交点C.三角形三边垂直平分线的交D.三角形三个角的平分线的交点 解答:这个题选D,不要误选为C.(四)角平分线性质定理的深入研究思考题:如图,,,PO AOB PA OA PB OB ∠⊥⊥平分,请找出图中所有相等的量,并一一给以证明.解答:,90,,,AOP BOP OAP OBP PA PB OPA OPB OA OB ∠=∠∠=∠=︒=∠=∠=(1),90,AOP BOP OAP OBP PA PB ∠=∠∠=∠=︒=都非常容易证明;(2)OPA OPB ∠=∠的证明可以用三角形的内角和定理:180,180180,180,90AOP OAP OPA BOP OBP OPB OPA AOP OAP OPB BOP OBPAOP BOP OAP OBP OPA OPB∠+∠+∠=︒∠+∠+∠=︒∠=︒-∠-∠∠=︒-∠-∠∠=∠∠=∠=︒∠=∠∴∴(3)如何证明OA OB =呢?可以运用角平分线的性质定理:如下三幅图,我们对原题逐步进行改造(按图1,图2,图3)之后就可以证明了:12,OA PA OB PB OA OB∠=∠⊥⊥=∴追问: 如图,原题的条件为,,PO AOB PA OA PB OB ∠⊥⊥平分,现在再连接AB ,则:(1)PAB PBA ∠=∠吗?为什么?(2)OAB OBA ∠=∠吗?为什么?(3)OP 垂直平分AB 吗?为什么?(1)(2)问自己证明,(3)问的证明如下:(),,OP AOBPA OA PB OBPA PBPA PB OP AB AC BC OP AB∠⊥⊥==⊥=∴∴∴平分等腰三角形底边上的中线与底边上的高互相重合垂直平分追问之对应练习:①.如图,OP 平分AOB ∠,PA OA ⊥,PB OB ⊥,垂足分别为A ,B ,下列结论中不一定成立的是( )A .PA PB = B .PO 平分APB ∠C .OA OB =D .AB 垂直平分OP解答:选D,好好想想为什么.②.如图,在△ABC 中,90,,,,A AB AC BD ABC DE C ∠=︒=∠⊥平分证明△DEC 的周长等于BC 的长.解答:略,靠自己的力量解决.链接中考:1.如图,在四边形ABCD 中,AB BC =,BF 是ABC ∠的平分线,AF DC ∥,连接,AC CF .求证:CA 是DCF ∠的平分线.分析:由AB BC =,BF 是ABC ∠的平分线可得BF 所在的直线垂直平分AC ,从而有FA FC =,从而有FAC FCA ∠=∠,又由AF DC ∥可得FAC ACD ∠=∠,从而有ACD FCA ∠=∠,即CA 是DCF ∠的平分线.2.如图,在△ABC 中,∠A =α.∠ABC 与∠ACD 的平分线交于点A 1,得∠A 1;∠A 1BC 与∠A 1CD 的平分线相交于点A 2,得∠A 2; ……;∠A 2008BC 与∠A 2008CD 的平分线相交于点A 2009,得∠A 2009 .则∠A 2009= .解答: 20092α希望同学们能认真系统的复习角平分线性质定理,我相信你们肯定能很好的掌握好角平分线性质定理.BA C DA 1A 2A D FB C1.4 等腰三角形一.复习要求:1.知道等腰三角形的对称轴;2.能熟练运用“等边对等角”解决问题;3.能熟练运用“三线合一”解决问题;4.充分意识到等腰三角形的“求角的度数”和“求边长周长”都容易出现两种情况(这实际上是在运用分类讨论思想解决问题),同时必须得意识到“求边长周长”时的两种情况中有时会有一种情况构不成三角形;5.意识到“面积法”是解决三角形问题的一种非常重要的方法;6.充分意识到等腰三角形有锐角等腰三角形、等腰直角三角形和钝角等腰三角形三种,不要一自己画图时,就只画一个锐角等腰三角形.7.会用等边三角形的每个内角都等于60︒解决问题.8.会利用几种基本作图作等腰三角形.二.本节关键:(一). 知道等腰三角形是轴对称图形:等腰三角形是轴对称图形,它的对称轴是底边的垂直平分线.它的对称轴还可以描述为(1)顶角平分线所在的直线;(2)底边上的高所在的直线;(3)底边上的中线所在的直线.但以下的一些说法是错误的:(1)顶角的平分线(×) 因为顶角的平分线是一条射线,而对称轴必须是直线(2)高所在的直线(×) 因为这里的高有可能不是底边上的高(二).知道“等边对等角”、“三线合一”和“等边三角形的每个内角都等于60︒”的应用格式:1.等边对等角的应用格式:AB AC B C=∠=∠∴ 2.三线合一的应用格式:(建议学习这个定理的应用格式之前,先看一下“动态演示三线合一”)(1)如果碰到这样的题目:如图, △ABC 中,,,AB AC AD BAC =∠平分那么AD BC ⊥吗?BD CD =吗?我们的解答就是:,,AB AC AD BAC AD BC BD CD=∠⊥=∴平分 注意1:当然,有时候,我们只需要得到AD BC ⊥这个结论,这时我们的解答就变成了:,AB AC AD BACAD BC =∠⊥∴平分也有时候,我们只需要得到BD CD =(或者说“AD 是BC 边上的中线”、“点D 是BC 边的中点”),这时我们的解答就变成了:,AB AC AD BACBD CD =∠=∴平分注意2:“,AD BC BD CD ⊥=”是我们通过“,AB AC AD BAC =∠平分”推出的结论,这个结论实际上表明了AD 垂直于BC 且平分了BC ,或者换句话说AD 是垂直平分BC 的.当有的题目要求我们证明某条线垂直平分另一条线时,我们就经常采用证明“某条线”是等腰三角形的顶角的平分线,而“另一条线”则恰好是等腰三角形的底边的方法.(2)如果碰到这样的题目:如图, △ABC 中,,,AB AC BD CD ==那么AD BC ⊥吗?,AD BAC ∠平分吗?我们的解答就是:,,AB AC BD CDAD BC AD BAC ==⊥∠∴平分(3)如果碰到这样的题目:如图, △ABC 中,,,AB AC AD BC =⊥那么BD CD =吗?AD BAC ∠平分吗?我们的解答就是:,,AB AC AD BCBD CD AD BAC=⊥=∠∴平分注意: [1]在(1)(2)(3)三种情况中,条件“,AB AC AD BAC =∠平分”、“ ,AB AC BD CD ==”或“,AB AC AD BC =⊥”中都有“AB AC =”,这是必不可少的,因为一般的三角形是不具备“三线合一”的,只有等腰三角形具备“三线合一”,所以在条件中必须通过“AB AC =”表明等腰三角形的身份;[2]当然了,在条件“,AB AC AD BAC =∠平分”中,“AD BAC ∠平分”也是必不可少的; 在条件“ ,AB AC BD CD ==”中,“BD CD =”同样必不可少;在条件“,AB AC AD BC =⊥”中,“AD BC ⊥”同样必不可少.[3] “AB AC =”除了表明三角形是等腰三角形之外,还恰到好处的表明了,AB AC 就是等腰三角形的腰,互相重合的就应该是A ∠的平分线、BC 边上的高和BC 边上的高.因为等腰三角形底角的平分线和腰上的高、腰上的中线并不重合,如下图:所以在用“三线合一”证明问题时,必须在条件中以“AB AC =”这样的方式表明谁是腰,而不只是笼统的说“三角形是一个等腰三角形”,如下面的证明就是错误的证明,至少是不准确的证明:AB AC =,BD CD AD BC AD BACABC =⊥∠∴∴平分三角形是等腰三角形3.“等边三角形的每个内角都等于60︒”的应用格式:60AB BC CA A B C ==∠=∠=∠=︒∴ 注意:有时我们可能只需要A ∠60=︒,这时我们可以这样写:60AB BC CA A ==∠=︒∴ (三). 等边对等角的应用:例题1 如图, △ABC 中,,,AB AC BC BD AD ===求△ABC 中各个角的度数.分析:根据题目中的已知条件“,AB AC BC BD AD ===”,我们可以得到很多对相等的角,从而可以比较的容易得到图形中各角之间的关系,我们不妨设其中的一个角为x ,将与其有关系的角用含x 的代数式表示出来,最后看是否能利用三角形的内角和定理得到关于x 的一个方程,从而将x 求出来,进而求出△ABC 中各个角的度数.解答:AB ACABC CBD BC BDC CBD ADABD A=∠=∠=∠=∠=∠=∠∴∴∴ 设A x ∠=,则ABD A x ∠=∠=,BDC ∠是△ABD 的外角 2BDC A ABD x x x ∠=∠+∠=+=∴22180221803636,272C BDC xABC C xA C ABC x x x x A ABC C x ∠=∠=∠=∠=∠+∠+∠=︒++=︒=︒∠=︒∠=∠==︒∴∴∴∴∴ 反思:本题的解决所用到的知识点主要是“等边对等角”、“三角形的内角和定理”、和“等边对等角”,所用到的思想方法主要是转化思想和方程思想,如将等边转化为等角,将A ABD ∠+∠转化为BDC ∠,再将BDC ∠转化为C ∠,再将C ∠转化为ABC ∠,方程思想就不必说了.收获:在求角的题目中,“三角形的内角和定理”、“三角形的一个外角等于和它不相邻的两个内角的和”、“等边对等角”是经常会用到的定理,另外像“两直线平行,同位角相等内错角相等以及同旁内角互补”、“同角的补角相等,同角的余角相等”、“垂直会推出直角”、“邻补角”、“n 边形的内角和为()2180n -⋅︒,外角和为360︒”等定理或定义也经常用到,要熟悉这些定理或定义的内容,这样求角时才能做到游刃有余.当然了,求角的度数绕不开转化,甚至是不停的转化,有时可能还需要作平行线或连接两点的线段等辅助线.方程思想有时也是必不可少的.希望同学们在解题的同时多反思,不断积累经验.相应练习:1.①如图, △ABC 中,,,,___.AB AC BC BD AD DE EB A ====∠=则解答:45︒,自己解决.②如图,在△ABC 中,,,75,___.AB AC BD ABC BDC A =∠∠=︒∠=平分则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
集合定义:角平分线是到角两端距离 相等的点的集合。
7、等腰三角形的对称性:
等腰三角形是轴对称图形有,1条,顶角 平分线所在直线是它的对称轴.
性质:等腰三角形的两个底角相等; 等腰三角形的顶角平分线、底边上的 中线、底边上高互相重合。(简称 “三线合一”).
判定:等角对等边。
8、等边三角形的对称性:
等边三角形是轴对称图形,有3条对称轴 性质:三条边相等,三个角都是60° 判定:3个角相等的三角形是等边三角形 有一个角等于60°的等腰三角形是等边三
角形; 有两个角等于60°的三角形是等腰三角形。
直角三角形斜边上的中线等于斜边的一半
梯形中常见辅助线
1.如图,在梯形ABCD中,AD∥BC, ∠B=70°,∠C=40°, 求证:CD=BC-AD.
A
D
E
B
F
CA
D
平移一腰,梯形转化成B:平行四边和三 C 角形延.长两腰,将梯形转化成三角形.
2.如图,在梯形ABCD中,AD∥BC,
AB=DC=AD=5,BC=11,求梯形
ABCD的面积.
线段的性质:线段垂直平分线上的点 到线段两端的距离相等;
线段的判定:到线段两端距离相等的 点在线段的垂直平分线上。
集合定义:线段的垂直平分线是到线 段两端距离相等的点的集合。
6、角的对称性:
角是轴对称图形,角平分线所在直线 是它的对称轴;
角平分线性质:角平分线上的点到角 两端的距离相等;
A
D
BE
FC
作梯形的高,梯形转化成:长方形和 直角三角形.
⒊如图,在梯形ABCD中,AD∥BC, E是DC的中点,EF⊥AB于点F.
求证:S梯形ABCD=AB×EF.
AD F
E
B
CG
平移底,梯形转化成:三角形.
⒋如图,等腰梯形ABCD中,AD∥BC,
AC⊥BD, AD+BC=10,DE⊥BC于E,
(2)∠AOE=120° (3)CM=CN
(4)△CMN为正△
B
OD M
N
A
C
E
7.已知:在ΔABC中,D是BC上一 点,DE⊥AC于E,DF⊥AB于F,且DE=DF.
线段AD与EF有何关系?并说明理由.
C E
D
A
B
F
8.如图AC=BC,且AC⊥BC,D为AC 上的一点,BD=2AE,AE⊥BE,
9、等腰梯形的对称性
定义:一组对边平行,一组对边不平行, 两腰相等的四边形为等腰梯形。
对称性:等腰梯形是轴对称图形,有1条对 称轴,过两底中点的直线是它的对称轴;
性质:等腰梯形同一底上的两个角相等;
等腰梯形的对角线相等。
判定:在同一底上的两个角相等的梯形 是等腰梯形。
三、重要的数学思想:
第一章:轴对称及轴对称图形 (复习课)
一、知识结构
轴对称及轴对称图形
——————————————————————
线 角等 等 等
段
腰边 腰
三三 梯
角角 形
形形
二、知识点回顾:
1、轴对称:如果把一个图形沿着某 一条直线折叠后,能够与另一个图形 重合,那么这两个图形关于这条直线 成轴对称。
2、轴对称图形:把一个图形沿一条 直线折叠,如果直线两旁的部分能互 相重合,那么这个图形叫轴对称图形。
2
A ED
C
BG
F
H
小明的妈妈买了一部29英寸(74厘米) 的电视机。小明量了电视机的屏幕后, 发现屏幕只有58厘米长和46厘米宽, 他觉得一定是售货员搞错了。你能解 释这是为什么吗?
3、轴对称图形和轴对称的区别与联系?
轴对称
轴对称图形
图形
两个图形之间
区
的对称关系
别 对称点位置 在两个图形上
一个图形自身 的对称特征
在同一个图形上
对称轴条数
一条
至少一条
联系
1.都沿某直线翻折后能够互相重合; 2.它们可以互相转化;如果把轴对称的 两个图形看作一个整体,那么它就是 一个轴对称图形;如果把轴对称图形 沿对称轴分成两个部分,那么两个部 分就是关于这条对称轴成轴对称。
A
D
C
E
B
5、如图,△ABC中,AB的垂直平分线 分别交AB、BC于点D、E,AC的垂直 平分线分别交AC、BC于点F、G,若 BC=20,则△AEG的周长为多少?
A
D
F
B
C
EG
6.如图,△ABC和△CDE都是等边三 角形,且点A,C,E在一条直线上. 证:△MNC为等边三角形.
(1)说明AD=BE
求证:BE平分∠ABC.
A
ED
FC
B
9.如图在△ABC中,CF⊥AB,BE⊥AC, M,N分别是BC与EF的中点, 试说明: MN⊥EF.
A
F
N
E
B
C
M
10、已知△ABC是等腰三角形,过 △ABC的一个顶点的一条直线,把 △ABC分成两个小三角形,如果这 两个小三角形也是等腰三角形,问 △ABC顶角的度数是多少?
2、在等腰△ABC中,若周长为的如垂图直,平在分△线AB分C别中交,A边B、A
D
BC于点D、E,且AE平分
∠BAC=80°若∠B=30 ° , 则∠C=_______.
CE
B
4、如图,在△ABC中, ∠ACB=900,AB 的中垂线交BC于E,垂足为 D,∠CAE:∠EAB=3:1,则∠B=___ .
分类思想:主要用于等腰三角形; 方程思想:主要用于计算边和角; 化归思想:主要用于把梯形问题转化
为三角形来处理。 建模思想:主要用于建立等腰三角形
模型
四、几种常见辅助线作法:
等腰三角形:作顶角的平分线。 直角三角形:作斜边上的中线。
五、巩固习题:
1、在等腰△ABC中,若∠A=80°, 则∠B=_______.
4、轴对称的性质:
◆成轴对称的两个图形全等
◆如果两个图形成轴对称,那么对称 轴是对称点连线的垂直平分线。
◆对称点的连线互相平行
◆对称线段所在直线互相平行或相交 于对称轴上的一点
◆成轴对称的两个图形的任何对应部 分也成轴对称
5、线段的对称性:
线段是轴对称图形,有2条对称轴,一 条是线段的垂直平分线所在直线,一 条是线段本身所在直线;
求DE的长.
A
D
B
E CF
平移对角线,将梯形转化成:
平行四边形、三角形.
5.在梯形ABCD中,AB∥DC,AD=
BC,AB=1,DC=5,AC⊥BD,BE⊥CD,
则梯形的面积=
.
A
B
D
E
C
F
6.如图,梯形ABCD中,AD∥BC,E、F 分别是AD、BC的中点,∠B+∠C=90°, 请说明EF= 1(BC-AD).
