小学六年级-阴影部分面积及 答案完整
小学六年级阴影部分面积专题复习经典例题(含答案)

小学六年级阴影部分面积专题复习经典例题(含答案)欢迎下载研究必备资料, 本文主要涉及组合图形的面积计算。
以下是各题的解答和点评:1.求如图阴影部分的面积。
(单位: 厘米)分析: 阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积。
利用梯形和半圆的面积公式代入数据即可解答。
解答: $(4+6)\times4\div2\div2-3.14\times2^2=10-6.28=3.72$(平方厘米)。
答案: 阴影部分的面积是3.72平方厘米。
点评:组合图形的面积一般都是转化到已知的规则图形中利用公式计算, 这里考查了梯形和圆的面积公式的灵活应用。
2.如图, 求阴影部分的面积。
(单位: 厘米)分析:根据图形可以看出, 阴影部分的面积等于正方形的面积减去4个扇形的面积。
正方形的面积等于(10×10)100平方厘米, 4个扇形的面积等于半径为(10÷2)5厘米的圆的面积。
解答: 扇形的半径是: $10\div2=5$(厘米);$10\times10-3.14\times5\times5=100-78.5=21.5$(平方厘米)。
答案: 阴影部分的面积为21.5平方厘米。
点评:组合图形的面积计算需要注意各部分之间的关系, 特别是涉及到圆形时需要注意半径的计算。
3.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
4.求出如图阴影部分的面积: 单位: 厘米。
解答:该题缺少图形, 无法回答。
5.求如图阴影部分的面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
6.求如图阴影部分面积。
(单位: 厘米)解答:该题缺少图形, 无法回答。
7.计算如图中阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
8.求阴影部分的面积。
单位: 厘米。
解答:该题缺少图形, 无法回答。
9.如图是三个半圆, 求阴影部分的周长和面积。
(单位: 厘米)分析: 阴影部分可以看成是两个半圆和一个矩形组成的, 可以分别计算各部分的周长和面积再相加。
(完整)小学六年级求阴影部分面积试题和答案100
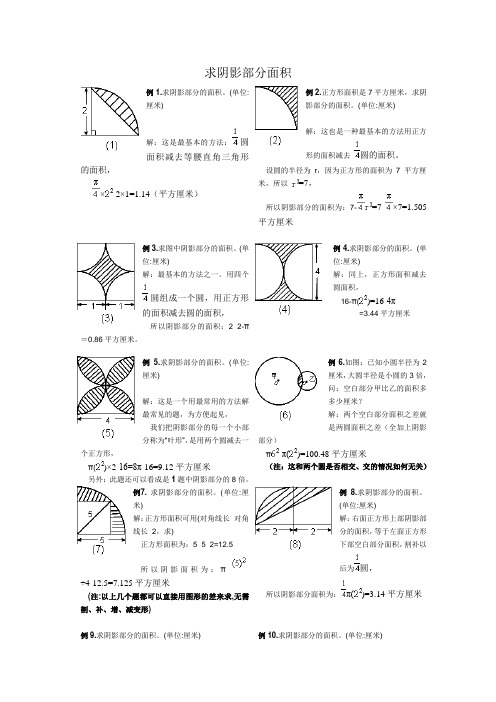
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例 5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7. 求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学六年级圆阴影部分面积含答案
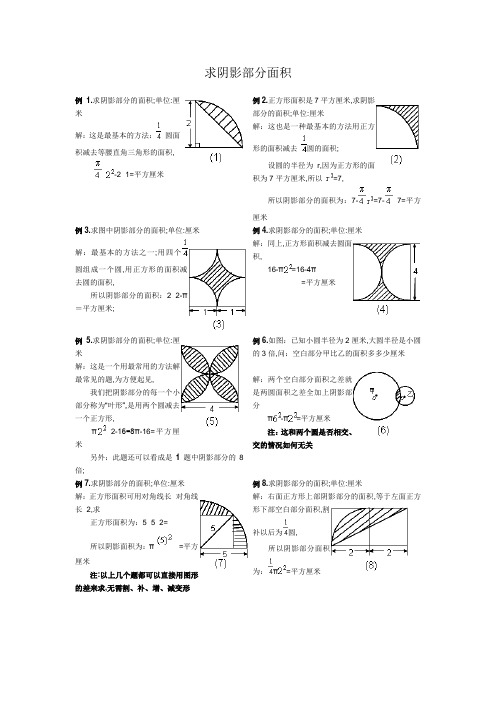
求阴影部分面积例 1.求阴影部分的面积;单位:厘米解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=平方厘米例2.正方形面积是7平方厘米,求阴影部分的面积;单位:厘米解:这也是一种最基本的方法用正方形的面积减去圆的面积;设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=平方厘米例3.求图中阴影部分的面积;单位:厘米解:最基本的方法之一;用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=平方厘米; 例4.求阴影部分的面积;单位:厘米解:同上,正方形面积减去圆面积,16-π=16-4π=平方厘米例 5.求阴影部分的面积;单位:厘米解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π×2-16=8π-16=平方厘米另外:此题还可以看成是1题中阴影部分的8倍;例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米解:两个空白部分面积之差就是两圆面积之差全加上阴影部分π-π=平方厘米注:这和两个圆是否相交、交的情况如何无关例7.求阴影部分的面积;单位:厘米解:正方形面积可用对角线长×对角线长÷2,求正方形面积为:5×5÷2=所以阴影面积为:π÷=平方厘米注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形例8.求阴影部分的面积;单位:厘米解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π=平方厘米例9.求阴影部分的面积;单位:厘米解:把右面的正方形平移至左边的正方形部分,则阴影部分合成一个长方形,所以阴影部分面积为:2×3=6平方厘米例10.求阴影部分的面积;单位:厘米解:同上,平移左右两部分至中间部分,则合成一个长方形,所以阴影部分面积为2×1=2平方厘米注: 8、9、10三题是简单割、补或平移例11.求阴影部分的面积;单位:厘米解:这种图形称为环形,可以用两个同心圆的面积差或差的一部分来求;π-π×=×=平方厘米例12.求阴影部分的面积;单位:厘米解:三个部分拼成一个半圆面积.π÷2=平方厘米例13.求阴影部分的面积;单位:厘米解: 连对角线后将"叶形"剪开移到右上面的空白部分,凑成正方形的一半.所以阴影部分面积为:8×8÷2=32平方厘米例14.求阴影部分的面积;单位:厘米解:梯形面积减去圆面积,4+10×4-π=28-4π=平方厘米 .例15.已知直角三角形面积是12平方厘米,求阴影部分的面积;分析: 此题比上面的题有一定难度,这是"叶形"的一个半.解: 设三角形的直角边长为r,则=12,=6圆面积为:π÷2=3π;圆内三角形的面积为12÷2=6,阴影部分面积为:3π-6×=平方厘米例16.求阴影部分的面积;单位:厘米解:π+π-π=π116-36=40π=平方厘米例17.图中圆的半径为5厘米,求阴影部分的面积;单位:厘米解:上面的阴影部分以AB为轴翻转后,整个阴影部分成为梯形减去直角三角形,或两个小直角三角形AED、BCD面积和;所以阴影部分面积为:5×5÷2+5×10÷2=平方厘米例18.如图,在边长为6厘米的等边三角形中挖去三个同样的扇形,求阴影部分的周长;解:阴影部分的周长为三个扇形弧,拼在一起为一个半圆弧,所以圆弧周长为:2××3÷2=厘米例19.正方形边长为2厘米,求阴影部分的面积;解:右半部分上面部分逆时针,下面部分顺时针旋转到左半部分,组成一个矩形;所以面积为:1×2=2平方厘米例20.如图,正方形ABCD的面积是36平方厘米,求阴影部分的面积;解:设小圆半径为r,4=36,r=3,大圆半径为R,=2=18,将阴影部分通过转动移在一起构成半个圆环,所以面积为:π-÷2=π=平方厘米例21.图中四个圆的半径都是1厘米,求阴影部分的面积;解:把中间部分分成四等分,分别放在上面圆的四个角上,补成一个正方形,边长为2厘米,所以面积为:2×2=4平方厘米例22.如图,正方形边长为8厘米,求阴影部分的面积;解法一: 将左边上面一块移至右边上面,补上空白,则左边为一三角形,右边一个半圆.阴影部分为一个三角形和一个半圆面积之和. π÷2+4×4=8π+16=平方厘米解法二: 补上两个空白为一个完整的圆.所以阴影部分面积为一个圆减去一个叶形,叶形面积为:π÷2-4×4=8π-16 所以阴影部分的面积为:π-8π+16=平方厘米例23.图中的4个圆的圆心是正方形的4个顶点,,它们的公共点是该正方形的中心,如果每个圆的半径都是1厘米,那么阴影部分的面积是多少解:面积为4个圆减去8个叶形,叶形面积为:π-1×1=π-1所以阴影部分的面积为:4π-8π-1=8平方厘米例24.如图,有8个半径为1厘米的小圆,用他们的圆周的一部分连成一个花瓣图形,图中的黑点是这些圆的圆心;如果圆周π率取,那么花瓣图形的的面积是多少平方厘米分析:连接角上四个小圆的圆心构成一个正方形,各个小圆被切去个圆,这四个部分正好合成3个整圆,而正方形中的空白部分合成两个小圆.解:阴影部分为大正方形面积与一个小圆面积之和.为:4×4+π=平方厘米例25.如图,四个扇形的半径相等,求阴影部分的面积;单位:厘米分析:四个空白部分可以拼成一个以2为半径的圆.所以阴影部分的面积为梯形面积减去圆的面积,4×4+7÷2-π=22-4π=平方厘米例26.如图,等腰直角三角形ABC和四分之一圆DEB,AB=5厘米,BE=2厘米,求图中阴影部分的面积; 解: 将三角形CEB以B为圆心,逆时针转动90度,到三角形ABD位置,阴影部分成为三角形ACB 面积减去个小圆面积,为: 5×5÷2-π÷4=平方厘米例27.如图,正方形ABCD的对角线AC=2厘米,扇形ACB是以AC为直径的半圆,扇形DAC是以D为圆心,AD为半径的圆的一部分,求阴影部分的面积;解: 因为2==4,所以=2以AC为直径的圆面积减去三角形ABC面积加上弓形AC面积,π-2×2÷4+π÷4-2=π-1+π-1=π-2=平方厘米例28.求阴影部分的面积;单位:厘米解法一:设AC中点为B,阴影面积为三角形ABD面积加弓形BD的面积,三角形ABD的面积为:5×5÷2=弓形面积为:π÷2-5×5÷2=所以阴影面积为:+=平方厘米解法二:右上面空白部分为小正方形面积减去小圆面积,其值为:5×5-π=25-π阴影面积为三角形ADC减去空白部分面积,为:10×5÷2-25-π=π=平方厘米例29.图中直角三角形ABC的直角三角形的直角边AB=4厘米,BC=6厘米,扇形BCD所在圆是以B为圆心,半径为BC的圆,∠CBD=,问:阴影部分甲比乙面积小多少解: 甲、乙两个部分同补上空白部分的三角形后合成一个扇形BCD,一个成为三角形ABC,此两部分差即为:π×-×4×6=5π-12=平方厘米例30.如图,三角形ABC是直角三角形,阴影部分甲比阴影部分乙面积大28平方厘米,AB=40厘米;求BC 的长度;解:两部分同补上空白部分后为直角三角形ABC,一个为半圆,设BC长为X,则40X÷2-π÷2=28所以40X-400π=56则X=厘米例31.如图是一个正方形和半圆所组成的图形,其中P为半圆周的中点,Q为正方形一边上的中点,求阴影部分的面积;解:连PD、PC转换为两个三角形和两个弓形,两三角形面积为:△APD面积+△QPC面积= 5×10+5×5=两弓形PC、PD 面积为:π-5×5所以阴影部分的面积为:+π-25=平方厘米例32.如图,大正方形的边长为6厘米,小正方形的边长为4厘米;求阴影部分的面积;解:三角形DCE的面积为:×4×10=20平方厘米梯形ABCD的面积为:4+6×4=20平方厘米从而知道它们面积相等,则三角形ADF面积等于三角形EBF面积,阴影部分可补成圆ABE的面积,其面积为:π÷4=9π=平方厘米例33.求阴影部分的面积;单位:厘米解:用大圆的面积减去长方形面积再加上一个以2为半径的例34.求阴影部分的面积;单位:厘米解:两个弓形面积为:π-3×4÷2=π-6阴影部分为两个半圆面积减去两个弓形面积,结果为π+π-π-6=π4+-+6=6平方厘米圆ABE面积,为π+π-6=×13π-6=平方厘米例35.如图,三角形OAB是等腰三角形,OBC是扇形,OB=5厘米,求阴影部分的面积;解:将两个同样的图形拼在一起成为圆减等腰直角三角形π÷4-×5×5÷2=π-÷2=平方厘米。
小学六年级-阴影部分面积及答案完整
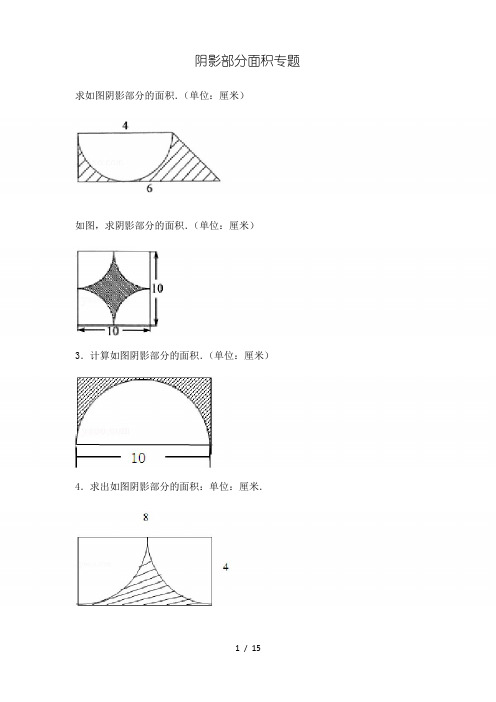
阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5.求如图阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.7.计算如图中阴影部分的面积.单位:厘米.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
(完整版)小学六年级求阴影部分面积试题和答案100
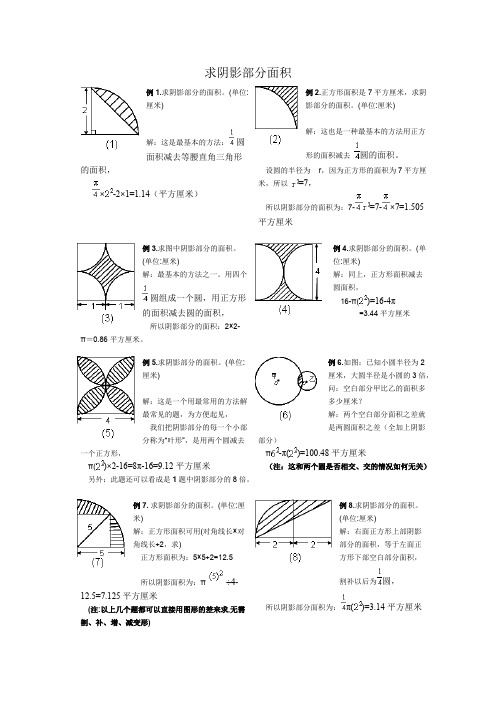
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法: 圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去 圆的面积。
设圆的半径为 r ,因为正方形的面积为7平方厘米,所以 =7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形, π()×2-16=8π-16=9.12平方厘米 另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分) π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5 所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
超全六年级阴影部分的面积(详细答案)
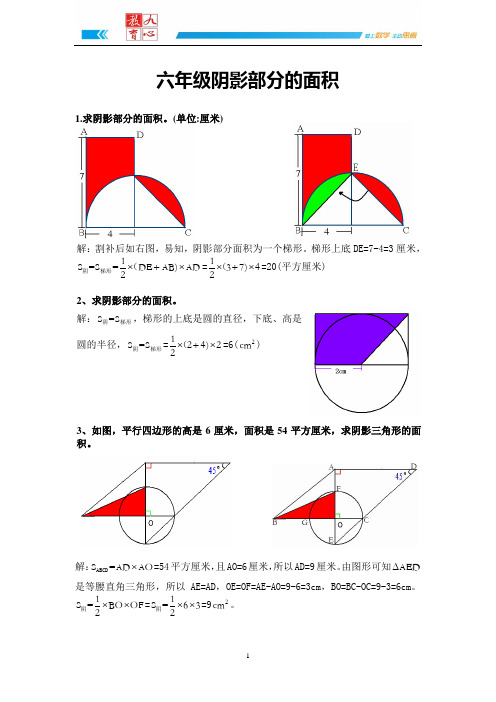
六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
小学六年级-阴影部分面积-专题复习-典型例题(含答案)

阴影部分面积专题例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案
tat i me an dAl l t h i ng si nt he i rb ei n ga re go od fo rs o 求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法: 圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为 r ,因为正方形的面积为7平方厘米,所以 =7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个 圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积, 16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形, π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(完整版)小学六年级求阴影部分面积试题和答案

例2.正方形面积是7平方厘米,求阴影部分的面 积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减 去圆面积减去等腰直角三角形的面积,面积。
设圆的半径为r ,因为正方形的面积为7平方厘米,所以求阴影部分面积例1.求阴影部分的面积。
(单位:厘米) 解:这是最基本的方法例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)圆组成一个圆,用正方形的面积减去圆的面积, 所以阴影部分的面积:2X 2-n= 0.86平方厘米。
)=16-4 n=3.44平方厘米505平方厘米例3.求图中阴影部分的面积。
(单位:厘米) 解:最基本的方法之一。
用四个X7=1.例4.求阴影部分的面积。
(单位:厘米) 解:同上,正方形面积减去圆面积,16- n (例6.如图:已知小圆半径为 2厘米,大圆 半径是小圆的3倍,问:空白部分甲比乙 的面积多多少厘米?解:两个空白部分面积之差就是两圆面积 之差(全加上阴影部分)例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的 题,为方便起见,我们把阴影部分的每一个小部分称为 叶形”是用两个圆减去一个正方形,◎n()X n2-16=8 n16=9.12 平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
)=100. 48平方厘米Z冗冗(注:这和两个圆是否相交、交的情况如何无关)例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积, 等于左面正方形下部空白部分面积, 割 补 以 后 为例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长X 对角线长煜, 求) 正方形面积为:5X5^2=12.5 所 以 阴 影 面 积 为:-n)—2所以阴影部分面积为: 例11.求阴影部分的面积。
(单位:厘米) 解:这种图形称为环形,可以用两个同心圆 的面积差或差的一部分来求。
超全六年级阴影部分的面积(详细答案)

六年级阴影部分的面积1.求阴影部分的面积。
(单位:厘米)解:割补后如右图,易知,阴影部分面积为一个梯形。
梯形上底DE=7-4=3厘米,1S =S =DE AB)AD 2⨯+⨯阴梯形(=137)42⨯+⨯(=20(平方厘米)2、求阴影部分的面积。
解:S =S 阴梯形,梯形的上底是圆的直径,下底、高是圆的半径,S =S 阴梯形=124)22⨯+⨯(=6(2cm )3、如图,平行四边形的高是6厘米,面积是54平方厘米,求阴影三角形的面积。
解:S =AD AO ⨯ABCD =54平方厘米,且AO=6厘米,所以AD=9厘米。
由图形可知AED∆是等腰直角三角形,所以AE=AD ,OE=OF=AE-AO=9-6=3cm ,BO=BC-OC=9-3=6cm 。
1S =BO OF 2⨯⨯阴=1S =632⨯⨯阴=92cm 。
4、如图是一个平行四边形,面积是50平方厘米,求阴影积分的面积。
解:方法一:过C 点作CF AD ⊥交AD 于点F ,可知AECF 是长方形,面积=5×6=302cm ,ABE CFD S =S ∆∆=(50-30)÷2=102cm 。
方法二:BC=S ABCD ÷AE=50÷5=10cm ,BE=BC-EC=10-6=4cm ,ABE S ∆=BE ×AE ÷2 =4×5÷2=102cm5、下图是一个半圆形,已知AB=10厘米,阴影部分的面积为24.25平方厘米,求图形中三角形的高。
解:S =S -S ∆阴半圆=21AB 22π⎛⎫⨯⨯ ⎪⎝⎭-24.25=21103.1422⎛⎫⨯⨯ ⎪⎝⎭-24.25=152cm , 三角形的高=2S ∆÷AB=2×15÷10=3cm 。
6、如图,一个长方形长是10cm ,宽是4cm ,以A 点和C 点为圆心各画一个扇形,求画中阴影部分的面积是多少平方厘米?解:BECD 1S =S -S 4阴大圆=ABCD 11S -S S 44⎛⎫- ⎪⎝⎭大圆小圆=ABCD 11S +S -S 44大圆小圆=()2213.1410-4-1044⨯⨯⨯ =25.942cm 。
小学六年级圆_阴影部分面积含答案
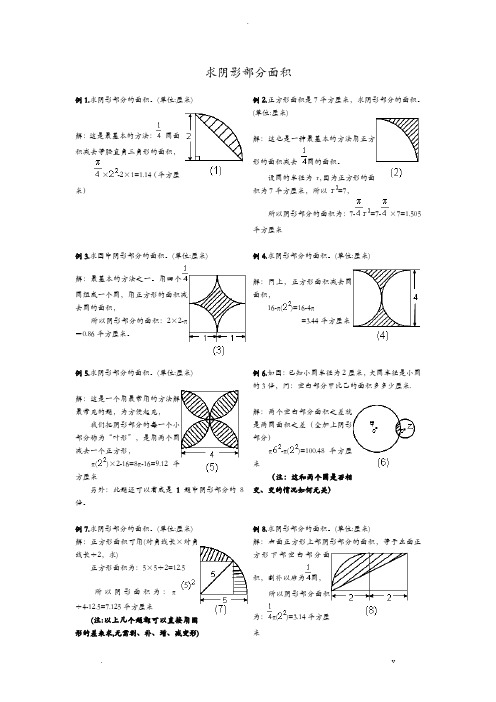
求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米.解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米) 解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形) 例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学六年级-阴影部分面积及答案完整

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
超全六年级阴影部分的面积(详细答案)
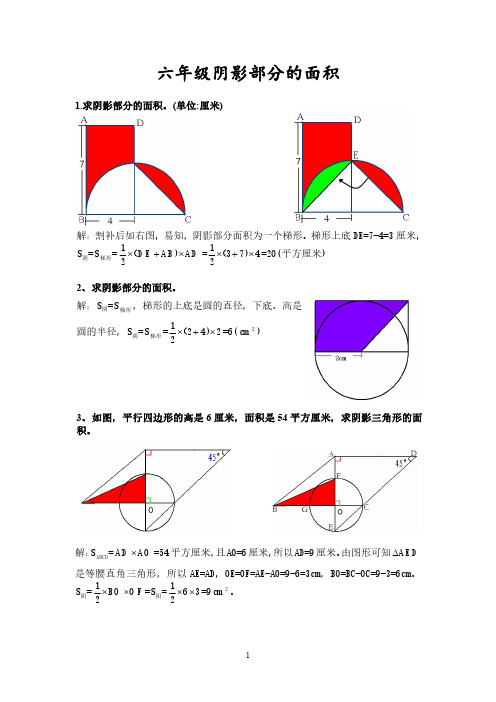
26、求下图阴影部分的面积。(单位:厘米)
解: S阴
S 梯形ABCE
SE C G
SA BG
=(CE+AB)·BC÷2+CE·CG÷2-AB·(BC+CG) ÷2=(2+4)×4÷2+2×2÷2-4×(4+2)÷2
=12+2-12=2 cm 2 。
解:连接
AC,可知 SABC=
1 2 SABCD
,A
BC
与
A
BE
等高,BE=
1 2
BC,所以 SABE=
1 2 SA BC
=
1 4 SA BCD
=
1 20 =5 cm 4
2
。
4
14、如图,已知半圆的面积是 31.4 平方厘米,求长方形的面积。 解:S半圆 =31.4,圆的半径 r2 = 2S半圆 =2×31.4 ÷3.14=20,。长方形的宽为 r,长为 2r,所以 长方形的面积=r×2r=2 r2 =2×20=40 cm 2 。
SA BC D SA BE SD E C
= 1AB BE 1D E D C
2
2
= 1 92 1 32 =36 cm 2 。
2
2
6
22、求下图阴影部分的面积。
解:如图,阴影的上半部分是一个半圆,下半部分是长方形与 2 个四分之一圆的 差,这 3 个圆的半径都相等=8÷2=4 厘米。
S阴
S半圆+
S正
1 -
4
S圆
=4- 1 r2 =4-3.14=0.86 cm 2 4
1 35、如下图,长方形中阴影部分的面积等于长方形面积的 ,如果 BC=12 厘米,
小学六年级-阴影部分面积及答案完整

阴影部分面积专题求如图阴影部分的面积.(单位:厘米)如图,求阴影部分的面积.(单位:厘米)3.计算如图阴影部分的面积.(单位:厘米)4.求出如图阴影部分的面积:单位:厘米.5.求如图阴影部分的面积.(单位:厘米)6.求如图阴影部分面积.(单位:厘米)7.计算如图中阴影部分的面积.单位:厘米.8.求阴影部分的面积.单位:厘米.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)10.求阴影部分的面积.(单位:厘米)11.求下图阴影部分的面积.(单位:厘米)12.求阴影部分图形的面积.(单位:厘米)13.计算阴影部分面积(单位:厘米).14.求阴影部分的面积.(单位:厘米)15.求下图阴影部分的面积:(单位:厘米)16.求阴影部分面积(单位:厘米).17.求阴影部分的面积.(单位:厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1.求如图阴影部分的面积.(单位:厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积.分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积,利用梯形和半圆的面积公式代入数据即可解答.解答解:(4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算,这里考查了梯形和圆的面积公式的灵活应用.2.如图,求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面积,即:3.14×5×5=78.5(平方厘米).解答解:扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积,即半径为5厘米的圆的面积.3.计算如图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析分析图后可知,10厘米不仅是半圆的直径,还是长方形的长,根据半径等于直径的一半,可以算出半圆的半径,也是长方形的宽,最后算出长方形和半圆的面积,用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解:10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力,组合图形可以是两个图形拼凑在一起,也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形,再根据条件去进一步解答.4.求出如图阴影部分的面积:单位:厘米.考点组合图形的面积.专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积,代入数据即可求解.解答解:8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.考点圆、圆环的面积.分析由图可知,正方形的边长也就是半圆的直径,阴影部分由4个直径为4厘米的半圆组成,也就是两个圆的面积,因此要求阴影部分的面积,首先要算1个圆的面积,然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解:S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的,再根据已知条件去计算.6.求如图阴影部分面积.(单位:厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积.分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积,再将题目中的数据代入相应的公式进行计算.解答解:图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形,需要把握好正方形、三角形、梯形及平行四边形的面积公式,再将题目中的数据代入相应的公式进行计算.考点组合图形的面积.分析由图意可知:阴影部分的面积=圆的面积,又因圆的半径为斜边上的高,利用同一个三角形的面积相等即可求出斜边上的高,也就等于知道了圆的半径,利用圆的面积公式即可求解.解答解:圆的半径:15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,=×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用,同时考查了学生观察图形的能力.8.求阴影部分的面积.单位:厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积.分析(1)圆环的面积等于大圆的面积减小圆的面积,大圆与小圆的直径已知,代入圆的面积公式,从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解:(1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式,解答此题的关键是找准圆的半径.9.如图是三个半圆,求阴影部分的周长和面积.(单位:厘米)考点组合图形的面积;圆、圆环的面积.专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等,所以图中阴影部分的周长,就是直径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积,利用半圆的面积公式即可求解.解答解:周长:3.14×(10+3),=3.14×13,=40.82(厘米);面积:×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,=×3.14×(42.25﹣25﹣2.25),=×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法,根据半圆的弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的弧长,是解决本题的关键.10.求阴影部分的面积.(单位:厘米)考点圆、圆环的面积.分析先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积,进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解:r=3,R=3+3=6,n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况,应主要灵活运用.11.求下图阴影部分的面积.(单位:厘米)考点组合图形的面积.分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米,再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,相减即可求解.解答解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积,本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12.求阴影部分图形的面积.(单位:厘米)考点组合图形的面积.分析求阴影部分的面积可用梯形面积减去圆面积的,列式计算即可.解答解:(4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积,即可列式解答.13.计算阴影部分面积(单位:厘米).考点组合图形的面积.专题平面图形的认识与计算.分析如图所示,阴影部分的面积=平行四边形的面积﹣三角形①的面积,平行四边形的底和高分别为10厘米和15厘米,三角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行四边形和三角形的面积公式即可求解.解答解:10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出,可以用平行四边形和三角形的面积差求出.14.求阴影部分的面积.(单位:厘米)考点梯形的面积.分析如图所示,将扇形①平移到扇形②的位置,求阴影部分的面积就变成了求梯形的面积,梯形的上底和下底已知,高就等于梯形的上底,代入梯形的面积公式即可求解.解答解:(6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法,关键是利用平移的办法变成求梯形的面积.15.求下图阴影部分的面积:(单位:厘米)考点组合图形的面积.分析根据三角形的面积公式:S=ah,找到图中阴影部分的底和高,代入计算即可求解.解答解:2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积,本题组合图形是一个三角形,关键是得到三角形的底和高.16.求阴影部分面积(单位:厘米).考点组合图形的面积.分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积,梯形的上底和高都等于圆的半径,上底和下底已知,从而可以求出阴影部分的面积.解答解:(4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径,且阴影部分的面积=梯形的面积﹣圆的面积.17.(2012•长泰县)求阴影部分的面积.(单位:厘米)考点组合图形的面积.分析由图可知,阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积=(a+b)h,半圆的面积=πr2,将数值代入从而求得阴影部分的面积.解答解:×(6+8)×(6÷2)﹣×3.14×(6÷2)2=×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积,解题关键是看懂图示,把图示分解成梯形,半圆和阴影部分,再分别求出梯形和半圆的面积.。
(完整)小学六年级-阴影部分面积-专题-复习-经典例题(含答案)-推荐文档

小升初阴影部分面积专题1. 求如图阴影部分的面积. (单位: 厘米)2. 如图, 求阴影部分的面积. (单位: 厘米)3. 计算如图阴影部分的面积. (单位: 厘米)4. 求出如图阴影部分的面积: 单位: 厘米.5. 求如图阴影部分的面积. (单位: 厘米)6. 求如图阴影部分面积. (单位: 厘米)7. 计算如图中阴影部分的面积. 单位: 厘米.8. 求阴影部分的面积. 单位: 厘米.9. 如图是三个半圆, 求阴影部分的周长和面积. (单位: 厘米)10. 求阴影部分的面积. (单位: 厘米)11. 求下图阴影部分的面积. (单位: 厘米)12. 求阴影部分图形的面积. (单位: 厘米)13. 计算阴影部分面积(单位: 厘米).14. 求阴影部分的面积. (单位: 厘米)15. 求下图阴影部分的面积: (单位: 厘米)16. 求阴影部分面积(单位: 厘米).17. (2012•长泰县)求阴影部分的面积. (单位: 厘米)☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆参考答案与试题解析1. 求如图阴影部分的面积. (单位: 厘米)考点组合图形的面积;梯形的面积;圆、圆环的面积. 1526356分析阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的面积, 利用梯形和半圆的面积公式代入数据即可解答.解答解: (4+6)×4÷2÷2﹣3.14×÷2,=10﹣3.14×4÷2,=10﹣6.28,=3.72(平方厘米);答:阴影部分的面积是3.72平方厘米.答: 阴影部分的面积是3.72平方厘米.答:阴影部分的面积是3.72平方厘米.点评组合图形的面积一般都是转化到已知的规则图形中利用公式计算, 这里考查了梯形和圆的面积公式的灵活应用.2. 如图, 求阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析根据图形可以看出:阴影部分的面积等于正方形的面积减去4个扇形的面积.正方形的面积等于(10×10)100平方厘米, 4个扇形的面积等于半径为(10÷2)5厘米的圆的面积, 即:3.14×5×5=78.5(平方厘米).解答解: 扇形的半径是:10÷2,=5(厘米);10×10﹣3.14×5×5,100﹣78.5,=21.5(平方厘米);答:阴影部分的面积为21.5平方厘米.答: 阴影部分的面积为21.5平方厘米.答:阴影部分的面积为21.5平方厘米.点评解答此题的关键是求4个扇形的面积, 即半径为5厘米的圆的面积.3. 计算如图阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析分析图后可知, 10厘米不仅是半圆的直径, 还是长方形的长, 根据半径等于直径的一半, 可以算出半圆的半径, 也是长方形的宽, 最后算出长方形和半圆的面积, 用长方形的面积减去半圆的面积也就是阴影部分的面积.解答解: 10÷2=5(厘米),长方形的面积=长×宽=10×5=50(平方厘米),半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米),阴影部分的面积=长方形的面积﹣半圆的面积,=50﹣39.25,=10.75(平方厘米);答:阴影部分的面积是10.75.答: 阴影部分的面积是10.75.答:阴影部分的面积是10.75.点评这道题重点考查学生求组合图形面积的能力, 组合图形可以是两个图形拼凑在一起, 也可以是从一个大图形中减去一个小图形得到;像这样的题首先要看属于哪一种类型的组合图形, 再根据条件去进一步解答.4. 求出如图阴影部分的面积: 单位: 厘米.考点组合图形的面积. 1526356专题平面图形的认识与计算.分析由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为半径的半圆的面积, 代入数据即可求解.解答解: 8×4﹣3.14×42÷2,=32﹣25.12,=6.88(平方厘米);答:阴影部分的面积是6.88平方厘米.答: 阴影部分的面积是6.88平方厘米.答:阴影部分的面积是6.88平方厘米.点评解答此题的关键是:弄清楚阴影部分的面积可以由哪些图形的面积和或差求出.5. 求如图阴影部分的面积. (单位: 厘米)考点圆、圆环的面积. 1526356分析由图可知, 正方形的边长也就是半圆的直径, 阴影部分由4个直径为4厘米的半圆组成, 也就是两个圆的面积, 因此要求阴影部分的面积, 首先要算1个圆的面积, 然后根据“阴影部分的面积=2×圆的面积”算出答案.解答解: S=πr2=3.14×(4÷2)2=12.56(平方厘米);阴影部分的面积=2个圆的面积,=2×12.56,=25.12(平方厘米);答:阴影部分的面积是25.12平方厘米.答: 阴影部分的面积是25.12平方厘米.答:阴影部分的面积是25.12平方厘米.点评解答这道题的关键是重点分析阴影部分是由什么图形组成的, 再根据已知条件去计算.6. 求如图阴影部分面积. (单位: 厘米)考点长方形、正方形的面积;平行四边形的面积;三角形的周长和面积. 1526356分析图一中阴影部分的面积=大正方形面积的一半﹣与阴影部分相邻的小三角形的面积;图二中阴影部分的面积=梯形的面积﹣平四边形的面积, 再将题目中的数据代入相应的公式进行计算.解答解: 图一中阴影部分的面积=6×6÷2﹣4×6÷2=6(平方厘米);图二中阴影部分的面积=(8+15)×(48÷8)÷2﹣48=21(平方厘米);答:图一中阴影部分的面积是6平方厘米, 图二中阴影部分的面积是21平方厘米.答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.答: 图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.答:图一中阴影部分的面积是6平方厘米,图二中阴影部分的面积是21平方厘米.点评此题目是组合图形, 需要把握好正方形、三角形、梯形及平行四边形的面积公式, 再将题目中的数据代入相应的公式进行计算.7. 计算如图中阴影部分的面积. 单位: 厘米.考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积= 圆的面积, 又因圆的半径为斜边上的高, 利用同一个三角形的面积相等即可求出斜边上的高, 也就等于知道了圆的半径, 利用圆的面积公式即可求解.解答解: 圆的半径: 15×20÷2×2÷25,=300÷25,=12(厘米);阴影部分的面积:×3.14×122,= ×3.14×144,=0.785×144,=113.04(平方厘米);答:阴影部分的面积是113.04平方厘米.答: 阴影部分的面积是113.04平方厘米.答:阴影部分的面积是113.04平方厘米.点评此题考查了圆的面积公式及其应用, 同时考查了学生观察图形的能力.8. 求阴影部分的面积. 单位: 厘米.考点组合图形的面积;三角形的周长和面积;圆、圆环的面积. 1526356分析(1)圆环的面积等于大圆的面积减小圆的面积, 大圆与小圆的直径已知, 代入圆的面积公式, 从而可以求出阴影部分的面积;(2)阴影部分的面积=圆的面积﹣三角形的面积, 由图可知, 此三角形是等腰直角三角形, 则斜边上的高就等于圆的半径, 依据圆的面积及三角形的面积公式即可求得三角形和圆的面积, 从而求得阴影部分的面积.(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.(2)阴影部分的面积=圆的面积﹣三角形的面积,由图可知,此三角形是等腰直角三角形,则斜边上的高就等于圆的半径,依据圆的面积及三角形的面积公式即可求得三角形和圆的面积,从而求得阴影部分的面积.解答解: (1)阴影部分面积:3.14×﹣3.14×,=28.26﹣3.14,=25.12(平方厘米);(2)阴影部分的面积:3.14×32﹣×(3+3)×3,=28.26﹣9,=19.26(平方厘米);答:圆环的面积是25.12平方厘米, 阴影部分面积是19.26平方厘米.答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.答: 圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.答:圆环的面积是25.12平方厘米,阴影部分面积是19.26平方厘米.点评此题主要考查圆和三角形的面积公式, 解答此题的关键是找准圆的半径.9. 如图是三个半圆, 求阴影部分的周长和面积. (单位: 厘米)考点组合图形的面积;圆、圆环的面积. 1526356专题平面图形的认识与计算.分析观察图形可知:图中的大半圆内的两个小半圆的弧长之和与大半圆的弧长相等, 所以图中阴影部分的周长, 就是直径为10+3=13厘米的圆的周长, 由此利用圆的周长公式即可进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的面积, 利用半圆的面积公式即可求解.解答解: 周长: 3.14×(10+3),=3.14×13,=40.82(厘米);面积: ×3.14×[(10+3)÷2]2﹣×3.14×(10÷2)2﹣×3.14×(3÷2)2,= ×3.14×(42.25﹣25﹣2.25),= ×3.14×15,=23.55(平方厘米);答:阴影部分的周长是40.82厘米, 面积是23.55平方厘米.答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.答: 阴影部分的周长是40.82厘米,面积是23.55平方厘米.答:阴影部分的周长是40.82厘米,面积是23.55平方厘米.点评此题主要考查半圆的周长及面积的计算方法, 根据半圆的弧长=πr, 得出图中两个小半圆的弧长之和等于大半圆的弧长, 是解决本题的关键.10. 求阴影部分的面积. (单位: 厘米)考点圆、圆环的面积. 1526356分析先用“3+3=6”求出大扇形的半径, 然后根据“扇形的面积”分别计算出大扇形的面积和小扇形的面积, 进而根据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答即可.解答解: r=3, R=3+3=6, n=120,,=,=37.68﹣9.42,=28.26(平方厘米);答:阴影部分的面积是28.26平方厘米.答: 阴影部分的面积是28.26平方厘米.答:阴影部分的面积是28.26平方厘米.点评此题主要考查的是扇形面积计算公式的掌握情况, 应主要灵活运用.11. 求下图阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米, 再求出空白三角形的面积10×(10÷2)÷2=25平方厘米, 相减即可求解.解答解: 3.14×(10÷2)2÷2﹣10×(10÷2)÷2=39.25﹣25=14.25(平方厘米).答:阴影部分的面积为14.25平方厘米.答: 阴影部分的面积为14.25平方厘米.答:阴影部分的面积为14.25平方厘米.点评考查了组合图形的面积, 本题阴影部分的面积=半圆的面积﹣空白三角形的面积.12. 求阴影部分图形的面积. (单位: 厘米)考点组合图形的面积. 1526356分析求阴影部分的面积可用梯形面积减去圆面积的, 列式计算即可.解答解: (4+10)×4÷2﹣3.14×42÷4,=28﹣12.56,=15.44(平方厘米);答:阴影部分的面积是15.44平方厘米.答: 阴影部分的面积是15.44平方厘米.答:阴影部分的面积是15.44平方厘米.点评解答此题的方法是用阴影部分所在的图形(梯形)面积减去空白图形(扇形)的面积, 即可列式解答.13. 计算阴影部分面积(单位: 厘米).考点组合图形的面积. 1526356专题平面图形的认识与计算.分析如图所示, 阴影部分的面积=平行四边形的面积﹣三角形①的面积, 平行四边形的底和高分别为10厘米和15厘米, 三角形①的底和高分别为10厘米和(15﹣7)厘米, 利用平行四边形和三角形的面积公式即可求解.解答解: 10×15﹣10×(15﹣7)÷2,=150﹣40,=110(平方厘米);答:阴影部分的面积是110平方厘米.答: 阴影部分的面积是110平方厘米.答:阴影部分的面积是110平方厘米.点评解答此题的关键是明白:阴影部分的面积不能直接求出, 可以用平行四边形和三角形的面积差求出.14. 求阴影部分的面积. (单位: 厘米)考点梯形的面积. 1526356分析如图所示, 将扇形①平移到扇形②的位置, 求阴影部分的面积就变成了求梯形的面积, 梯形的上底和下底已知, 高就等于梯形的上底, 代入梯形的面积公式即可求解.解答解: (6+10)×6÷2,=16×6÷2,=96÷2,=48(平方厘米);答:阴影部分的面积是48平方厘米.答: 阴影部分的面积是48平方厘米.答:阴影部分的面积是48平方厘米.点评此题主要考查梯形的面积的计算方法, 关键是利用平移的办法变成求梯形的面积.15. 求下图阴影部分的面积: (单位: 厘米)考点组合图形的面积. 1526356分析根据三角形的面积公式:S=ah, 找到图中阴影部分的底和高, 代入计算即可求解.解答解: 2×3÷2=6÷2=3(平方厘米).答:阴影部分的面积是3平方厘米.答: 阴影部分的面积是3平方厘米.答:阴影部分的面积是3平方厘米.点评考查了组合图形的面积, 本题组合图形是一个三角形, 关键是得到三角形的底和高.16. 求阴影部分面积(单位: 厘米).考点组合图形的面积. 1526356分析由图意可知:阴影部分的面积=梯形的面积﹣圆的面积, 梯形的上底和高都等于圆的半径, 上底和下底已知, 从而可以求出阴影部分的面积.解答解: (4+9)×4÷2﹣3.14×42×,=13×4÷2﹣3.14×4,=26﹣12.56,=13.44(平方厘米);答:阴影部分的面积是13.44平方厘米.答: 阴影部分的面积是13.44平方厘米.答:阴影部分的面积是13.44平方厘米.点评解答此题的关键是明白:梯形的下底和高都等于圆的半径, 且阴影部分的面积=梯形的面积﹣圆的面积.17. (2012•长泰县)求阴影部分的面积. (单位: 厘米)考点组合图形的面积. 1526356分析由图可知, 阴影部分的面积=梯形的面积﹣半圆的面积.梯形的面积= (a+b)h, 半圆的面积= πr2, 将数值代入从而求得阴影部分的面积.解答解: ×(6+8)×(6÷2)﹣×3.14×(6÷2)2= ×14×3﹣×3.14×9,=21﹣14.13,=6.87(平方厘米);答:阴影部分的面积为6.87平方厘米.答: 阴影部分的面积为6.87平方厘米.答:阴影部分的面积为6.87平方厘米.点评考查了组合图形的面积, 解题关键是看懂图示, 把图示分解成梯形, 半圆和阴影部分, 再分别求出梯形和半圆的面积.。
小学六年级求阴影部分面积试题和标准答案附面积公式

求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,×-2×1=1.14(平方厘米)例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以=7,所以阴影部分的面积为:7-=7-×7=1.505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π÷4-12.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)例8.求阴影部分的面积。
(单位:厘米)解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
小学六年级求阴影部分面积试题和标准答案

小学六年级求阴影部分面积试题和答案————————————————————————————————作者:————————————————————————————————日期:2求阴影部分面积例1.求阴影部分的面积。
(单位:厘米)解:这是最基本的方法:圆面积减去等腰直角三角形的面积,例2.正方形面积是7平方厘米,求阴影部分的面积。
(单位:厘米)解:这也是一种最基本的方法用正方形的面积减去圆的面积。
设圆的半径为r,因为正方形的面积为7平方厘米,所以×-2×1 =1.14(平方厘米)=7,所以阴影部分的面积为:7-=7-×7=1. 505平方厘米例3.求图中阴影部分的面积。
(单位:厘米)解:最基本的方法之一。
用四个圆组成一个圆,用正方形的面积减去圆的面积,所以阴影部分的面积:2×2-π=0.86平方厘米。
例4.求阴影部分的面积。
(单位:厘米)解:同上,正方形面积减去圆面积,16-π()=16-4π=3.44平方厘米例5.求阴影部分的面积。
(单位:厘米)解:这是一个用最常用的方法解最常见的题,为方便起见,我们把阴影部分的每一个小部分称为“叶形”,是用两个圆减去一个正方形,例6.如图:已知小圆半径为2厘米,大圆半径是小圆的3倍,问:空白部分甲比乙的面积多多少厘米?解:两个空白部分面积之差就是两圆面积之差(全加上阴影部分)π()×2-16=8π-16=9.12平方厘米另外:此题还可以看成是1题中阴影部分的8倍。
π-π()=100.48平方厘米(注:这和两个圆是否相交、交的情况如何无关)例7.求阴影部分的面积。
(单位:厘米)解:正方形面积可用(对角线长×对角线长÷2,求)正方形面积为:5×5÷2=12.5所以阴影面积为:π例8.求阴影部分的面积。
(单位:厘米) 解:右面正方形上部阴影部分的面积,等于左面正方形下部空白部分面积,割补以后为÷4-1 2.5=7.125平方厘米(注:以上几个题都可以直接用图形的差来求,无需割、补、增、减变形)圆,所以阴影部分面积为:π()=3.14平方厘米例9.求阴影部分的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个小图形得到;像这样的题首先要看属于哪一种类型的 组合图形,再根据条件去进一步解答. 4.求出如图阴影部分的面积:单位:厘米.
考 组合图形的面积.1526356 点 专 平面图形的认识与计算. 题 分 由题意可知:阴影部分的面积=长方形的面积﹣以4厘米为 析 半径的半圆的面积,代入数据即可求解. 解 解:8×4﹣3.14×42÷2, 答 =32﹣25.12,
阴影部分面积专题
求如图阴影部分的面积.(单位:厘米) 如图,求阴影部分的面积.(单位:厘米) 3.计算如图阴影部分的面积.(单位:厘米) 4.求出如图阴影部分的面积:单位:厘米.
5.求如图阴影部分的面积.(单位:厘米)
6.求如图阴影部分面积.(单位:厘米)
7.计算如图中阴影部分的面积.单位:厘米.
考 组合图形的面积.1526356 点 分 分析图后可知,10厘米不仅是半圆的直径,还是长方形的 析 长,根据半径等于直径的一半,可以算出半圆的半径,也
是长方形的宽,最后算出长方形和半圆的面积,用长方形 的面积减去半圆的面积也就是阴影部分的面积. 解 解:10÷2=5(厘米), 答 长方形的面积=长×宽=10×5=50(平方厘米), 半圆的面积=πr2÷2=3.14×52÷2=39.25(平方厘米), 阴影部分的面积=长方形的面积﹣半圆的面积, =50﹣39.25, =10.75(平方厘米); 答:阴影部分的面积是10.75. 点 这道题重点考查学生求组合图形面积的能力,组合图形可 评 以是两个图形拼凑在一起,也可以是从一个大图形中减去
11.求下图阴影部分的面积.(单位:厘米)
考 组合图形的面积.1526356 点 分 先求出半圆的面积3.14×(10÷2)2÷2=39.25平方厘米, 析 再求出空白三角形的面积10×(10÷2)÷2=25平方厘米,
相减即可求解. 解 解:3.14×(10÷2)2÷2﹣10×(10÷2)÷2 答 =39.25﹣25
=15.44(平方厘米); 答:阴影部分的面积是15.44平方厘米. 点 解答此题的方法是用阴影部分所在的图形(梯形)面积减 评 去空白图形(扇形)的面积,即可列式解答.
13.计算阴影部分面积(单位:厘米).
考 组合图形的面积.1526356 点 专 平面图形的认识与计算. 题 分 如图所示,阴影部分的面积=平行四边形的面积﹣三角形① 析 的面积,平行四边形的底和高分别为10厘米和15厘米,三
考 组合图形的面积.1526356 点 分 由图意可知:阴影部分的面积=梯形的面积﹣ 析
圆的面积,梯形的上底和高都等于圆的半径,上底和下底 已知,从而可以求出阴影部分的面积. 解 解:(4+9)×4÷2﹣3.14×42× 答
, =13×4÷2﹣3.14×4, =26﹣12.56, =13.44(平方厘米); 答:阴影部分的面积是13.44平方厘米. 点 解答此题的关键是明白:梯形的下底和高都等于圆的半 评 径,且阴影部分的面积=梯形的面积﹣
14.求阴影部分的面积.(单位:厘米)
考 梯形的面积.1526356 点 分 如图所示,将扇形①平移到扇形②的位置,求阴影部分的 析 面积就变成了求梯形的面积,梯形的上底和下底已知,高
就等于梯形的上底,代入梯形的面积公式即可求解.
解 解:(6+10)×6÷2, 答 =16×6÷2,
=96÷2, =48(平方厘米); 答:阴影部分的面积是48平方厘米. 点 此题主要考查梯形的面积的计算方法,关键是利用平移的 评 办法变成求梯形的面积.
÷2, =10﹣3.14×4÷2, =10﹣6.28, =3.72(平方厘米); 答:阴影部分的面积是3.72平方厘米. 点 组合图形的面积一般都是转化到已知的规则图形中利用公 评 式计算,这里考查了梯形和圆的面积公式的灵活应用. 2.如图,求阴影部分的面积.(单位:厘米)
考 组合图形的面积.1526356 点 分 根据图形可以看出:阴影部分的面积等于正方形的面积减
析 去4个扇形的面积.正方形的面积等于(10×10)100平方 厘米,4个扇形的面积等于半径为(10÷2)5厘米的圆的面 积,即:3.14×5×5=78.5(平方厘米).
解 解:扇形的半径是: 答 10÷2,
=5(厘米); 10×10﹣3.14×5×5, 100﹣78.5, =21.5(平方厘米); 答:阴影部分的面积为21.5平方厘米. 点 解答此题的关键是求4个扇形的面积,即半径为5厘米的圆 评 的面积. 3.计算如图阴影部分的面积.(单位:厘米)
求阴影部分的面积,首先要算1个圆的面积,然后根据“阴 影部分的面积=2×圆的面积”算出答案. 解 解:S=πr2 答 =3.14×(4÷2)2 =12.56(平方厘米); 阴影部分的面积=2个圆的面积, =2×12.56, =25.12(平方厘米); 答:阴影部分的面积是25.12平方厘米. 点 解答这道题的关键是重点分析阴影部分是由什么图形组成 评 的,再根据已知条件去计算. 6.求如图阴影部分面积.(单位:厘米)
角形①的底和高分别为10厘米和(15﹣7)厘米,利用平行 四边形和三角形的面积公式即可求解.
解 解:10×15﹣10×(15﹣7)÷2, 答 =150﹣40,
=110(平方厘米); 答:阴影部分的面积是110平方厘米. 点 解答此题的关键是明白:阴影部分的面积不能直接求出, 评 可以用平行四边形和三角形的面积差求出.
×3.14×[(10+3)÷2]2﹣
×3.14×(10÷2)2﹣
×3.14×(3÷2)2, =
×3.14×(42.25﹣25﹣2.25), =
×3.14×15, =23.55(平方厘米); 答:阴影部分的周长是40.82厘米,面积是23.55平方厘 米. 点 此题主要考查半圆的周长及面积的计算方法,根据半圆的 评 弧长=πr,得出图中两个小半圆的弧长之和等于大半圆的 弧长,是解决本题的关键. 10.求阴影部分的面积.(单位:厘米)
☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆☆
参考答案与试题解析
1.求如图阴影部分的面积.(单位:厘米)
考 组合图形的面积;梯形的面积;圆、圆环的面积.1526356 点 分 阴影部分的面积等于梯形的面积减去直径为4厘米的半圆的 析 面积,利用梯形和半圆的面积公式代入数据即可解答. 解 解:(4+6)×4÷2÷2﹣3.14× 答
分的面积; (2)阴影部分的面积=圆的面积﹣三角形的面积,由图可 知,此三角形是等腰直角三角形,则斜边上的高就等于圆 的半径,依据圆的面积及三角形的面积公式即可求得三角 形和圆的面积,从而求得阴影部分的面积. 解 解:(1)阴影部分面积: 答 3.14×
﹣3.14×
, =28.26﹣3.14, =25.12(平方厘米); (2)阴影部分的面积: 3.14×32﹣
×3.14×122, =
×3.14×144, =0.785×144, =113.04(平方厘米); 答:阴影部分的面积是113.04平方厘米. 点 此题考查了圆的面积公式及其应用,同时考查了学生观察 评 图形的能力.
8.求阴影部分的面积.单位:厘米.
考 组合图形的面积;三角形的周长和面积;圆、圆环的面 点 积.1526356 分 (1)圆环的面积等于大圆的面积减小圆的面积,大圆与小 析 圆的直径已知,代入圆的面积公式,从而可以求出阴影部
=6.88(平方厘米); 答:阴影部分的面积是6.88平方厘米. 点 解答此题的关键是:弄清楚阴影部分的面积可以由哪些图 评 形的面积和或差求出. 5.求如图阴影部分的面积.(单位:厘米)
考 圆、圆环的面积.1526356 点
分 由图可知,正方形的边长也就是半圆的直径,阴影部分由4 析 个直径为4厘米的半圆组成,也就是两个圆的面积,因此要
15.求下图阴影部分的面积:(单位:厘米)
考 组合图形的面积.1526356 点 分 根据三角形的面积公式:S=ah,找到图中阴影部分的底和 析 高,代入计算即可求解. 解 解:2×3÷2 答 =6÷2
=3(平方厘米). 答:阴影部分的面积是3平方厘米. 点 考查了组合图形的面积,本题组合图形是一个三角形,关 评 键是得到三角形的底和高. 16.求阴影部分面积(单位:厘米).
评 平行四边形的面积公式,再将题目中的数据代入相应的公 式进行计算.
7.计算如图中阴影部分的面积.单位:厘米.
考 组合图形的面积.1526356 点 分 由图意可知:阴影部分的面积= 析
圆的面积,又因圆的半径为斜边上的高,利用同一个三角 形的面积相等即可求出斜边上的高,也就等于知道了圆的 半径,利用圆的面积公式即可求解. 解 解:圆的半径:15×20÷2×2÷25, 答 =300÷25, =12(厘米); 阴影部分的面积:
考 圆、圆环的面积.1526356 点 分 先用“3+3=6”求出大扇形的半径,然后根据“扇形的面积 析
”分别计算出大扇形的面积和小扇形的面积,进而根 据“大扇形的面积﹣小扇形的面积=阴影部分的面积”解答 即可. 解 解:r=3,R=3+3=6,n=120, 答 , =
,
=37.68﹣9.42, =28.26(平方厘米); 答:阴影部分的面积是28.26平方厘米. 点 此题主要考查的是扇形面积计算公式的掌握情况,应主要 评 灵活运用.
径为10+3=13厘米的圆的周长,由此利用圆的周长公式即可 进行计算;阴影部分的面积=大半圆的面积﹣以10÷2=5厘 米为半径的半圆的面积﹣以3÷2=1.5厘米为半径的半圆的 面积,利用半圆的面积公式即可求解. 解 解:周长:3.14×(10+3), 答 =3.14×13, =40.82(厘米); 面积:
=14.25(平方厘米). 答:阴影部分的面积为14.25平方厘米. 点 考查了组合图形的面积,本题阴影部分的面积=半圆的面积 评 ﹣空白三角形的面积. 12.求阴影部分图形的面积.(单位:厘米)
考 组合图形的面积.1526356
