大学物理第7章静电场练习题
大学物理静电场练习题带标准答案

大学物理静电场练习题带答案————————————————————————————————作者:————————————————————————————————日期:大物练习题(一)1、如图,在电荷体密度为ρ的均匀带电球体中,存在一个球形空腔,若将带电体球心O 指向球形空腔球心O '的矢量用a 表示。
试证明球形空腔中任一点电场强度为 . A 、03ρεa B 、0ρεa C 、02ρεa D 、3ρεa2、如图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R .试求环中心O 点处的场强A 、02πR λε-B 、0πRλε- C 、00ln 22π4λλεε+ D 、00ln 2π2λλεε+3、 如图所示,一导体球半径为1R ,外罩一半径为2R 的同心薄导体球壳, 外球壳所带总电荷为Q ,而内球的电势为0V ,求导体球和球壳之间的电势差 (填写A 、B 、C 或D ,从下面的选项中选取)。
A 、1020214R Q V R R πε⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭ B 、102024R Q V R R πε⎛⎫- ⎪⎝⎭C 、0024Q V R πε- D 、1020214R Q V R R πε⎛⎫⎛⎫+-⎪ ⎪⎝⎭⎝⎭4.如图所示,电荷面密度为1σ的带电无限大板A 旁边有一带电导体B ,今测得导体表面靠近P 点处的电荷面密度为2σ。
求:(1)P 点处的场强 ;(2)导体表面靠近P 点处的电荷元S ∆2σ所受的电场力 。
A 、20σεB 、202σεC 、2202S σε∆D 、220S σε∆5.如图,在一带电量为Q 的导体球外,同心地包有一各向同性均匀电介质球壳,其相对电容率为r ε,壳外是真空,则在壳外P 点处(OP r =)的场强和电位移的大小分别为[ ]Q Opr)(A )2200,44r Q QE D rr εεε==ππ; (B )22,44r Q QE D r r ε==ππ; (C )220,44Q QE D r r ε==ππ; (D )2200,44Q QE D r r εε==ππ。
大学物理静电场习题

q (B)
4? ? 0
(D) q 6? 0
a
a
O a/2
q
[D ]
7.8.静电场中某点电势的数值等于
(A)试验电荷q0置于该点时具有的电势能. (B)单位试验电荷置于该点时具有的电势能.
[C ]
(C)单位正电荷置于该点时具有的电势能.
(D)把单位正电荷从该点移到电势零点外力所作的功
标准化作业(11)
第 7、8 章
真空中的静电场 导体与电介质
1、关于电场强度定义式
? E?
? F / q0
下列说法中哪个是正确的?
?
(A) 场强E 的大小与试探电荷q0的?大小成反比.
(B) (C)
对试场探中电某荷点受,力试F? 探的电方荷向受就力是场F 强与qE?0的的比方值向不.因q0而变.
(D)
若场中某点不放试探电荷q0,则
?
F =0
,从而E? =0.[ B ]
A
静电场中某点的电场强度,其大小和方向与 __________________________ 相同.
答:单位正试验电荷置于该点时所受到的电场力
【D】
2.一电场强度为
? E
的均匀电场,E?
的方向与沿
x 轴正向,如图所示.
则通过图中一半径为R的半球面的电场强度通量为
? r
?
?q r2 4? ε0r2
dr?
q 4? ε0r2
?r2 ? R?
【D】
【C】
8.6. 两个半径相同的金属球,一为空心,一为实心,
把两者各自孤立时的电容值加以比较,则
(A) 空心球电容值大.
(B) 实心球电容值大.
(C) 两球电容值相等.
大学物理第7章真空中的静电场答案

Q 与坐标原点0的距离为ydE方向沿轴正向。
4二;0x (x _ L )(2)如图7— 2图b ,设通过棒的端点与棒垂直上任一点• dx2 4二;°r第七章 真空中的静电场7- 1在边长为a 的正方形的四角,依次放置点电荷 q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为 一^甘4)= 4二;。
(2 a ) 5q 2,方向由q 指向-4q 。
2二;°a 7 — 2如图,均匀带电细棒,长为 L ,电荷线密度为 入。
(1) 求棒的延长线上任一点 P 的场强;(2)求通过棒的端点与棒垂直上 任一点Q 的场强。
解:(1)如图7 — 2图a ,在细棒上任取电荷元 dq ,建立如图坐标, P 与坐标原点0的距离为x ,贝U dq = ■ d ■,设棒的延长线上任一点 dE4二;0(x _ )2 4二;0(x _ )2 则整根细棒在 P 点产生的电场强度的大小为 dq 0 n_(」L 一丄x - L x习题7—2图adE y■ dx 2 4二;0rdE x 亠si n ,4 二;°r因x 二ytg pdxcos2 -习题7—2图b代入上式,则E x 二-dE xPL QE「dE「石石。
込还R S Z= 4jy y2L27— 3 一细棒弯成半径为R的半圆形,均匀分布有电荷q,求半圆中心0处的场强。
解:如图,在半环上任取dl=Rdr的线元,其上所带的电荷为dq=,Rd=对称分析E y=o。
dE x■ Rd v24二0RE = dE x sin -4二0R 02 0Rq2 二2;0R2,如图,方向沿x轴正向。
7 —4如图线电荷密度为入1的无限长均匀带电直线与另一长度为I、线电荷密度为 & 的均匀带电直线在同一平面内,二者互相垂直,求它们间的相互作用力。
习题解答---大学物理第7章习题--2

专业班级_____ ________学号________第七章静电场中的导体和电介质一、选择题:1,在带电体A旁有一不带电的导体壳B,C为导体壳空腔的一点,如下图所示。
则由静电屏蔽可知:[ B ](A)带电体A在C点产生的电场强度为零;(B)带电体A与导体壳B的外表面的感应电荷在C点所产生的合电场强度为零;(C)带电体A与导体壳B的表面的感应电荷在C点所产生的合电场强度为零;(D)导体壳B的、外表面的感应电荷在C点产生的合电场强度为零。
解答单一就带电体A来说,它在C点产生的电场强度是不为零的。
对于不带电的导体壳B,由于它在带电体A这次,所以有感应电荷且只分布在外表面上(因其部没有带电体)此感应电荷也是要在C点产生电场强度的。
由导体的静电屏蔽现象,导体壳空腔C点的合电场强度为零,故选(B)。
2,在一孤立导体球壳,如果在偏离球心处放一点电荷+q,则在球壳、外表面上将出现感应电荷,其分布情况为 [ B ](A)球壳表面分布均匀,外表面也均匀;(B)球壳表面分布不均匀,外表面均匀;(C)球壳表面分布均匀,外表面不均匀;(D)球壳的、外表面分布都不均匀。
解答 由于静电感应,球壳表面感应-q ,而外表面感应+q ,由于静电屏蔽,球壳部的点电荷+q 和表面的感应电荷不影响球壳外的电场,外表面的是球面,因此外表面的感应电荷均匀分布,如图11-7所示。
故选(B )。
3. 当一个带电导体达到静电平衡时:[ D ](A) 表面上电荷密度较大处电势较高 (B) 表面曲率较大处电势较高。
(C)导体部的电势比导体表面的电势高。
(D)导体任一点与其表面上任一点的电势差等于零。
4. 如图示为一均匀带电球体,总电量为+Q ,其外部同心地罩一、外半径分别为r 1、r 2的金属球壳、设无穷远处为电势零点,则在球壳半径为r 的P 点处的场强和电势为: [ D ](A )E=r Q U r Q 0204,4πεπε=(B )E=0,104r Q U πε= (C )E=0,rQ U 04πε=(D )E=0,204r Q U πε=5. 关于高斯定理,下列说法中哪一个是正确的? [ C ](A )高斯面不包围自由电荷,则面上各点电位移矢量D为零。
大学物理简明教程(第2版)(赵近芳)习题答案,习题7 静电场
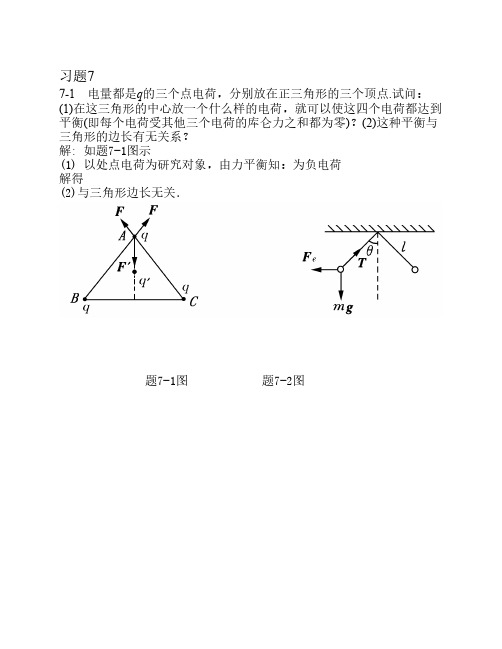
7-1 电量都是q的三个点电荷,分别放在正三角形的三个顶点.试问: (1)在这三角形的中心放一个什么样的电荷,就可以使这四个电荷都达到 平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与 三角形的边长有无关系? 解: 如题7-1图示 (1) 以处点电荷为研究对象,由力平衡知:为负电荷 解得 (2)与三角形边长无关.
解: 电容上电量 电容与并联 其上电荷 ∴
题7-15图
题7-12图 (2)外壳接地时,外表面电荷入地,外表面不带电,内表面电荷仍为. 所以球壳电势由内球与内表面产生:
7-13 在半径为R1的金属球之外包有一层外半径为R2的均匀电介质球壳, 介质相对介电常数为r,金属球带电Q。试求: (1)电介质内、外的电场强度; (2)电介质层内、外的电势; (3)金属球的电势。 解: 利用有介质时的高斯定理 (1)介质内场强
; 介质外场强 (2)介质外电势 介质内电势 (3)金属球的电势
7-14 计算球形电容器的电容和能量。已知球形电容器的内外半径分别为 R1和R2,带电量分别为Q和-Q。为简单起见,设球内外介质介电常数均 为0。 解:,
R1 R2 r o 和, 体积元 能量 电容器的电容
7-15 如题7-15图所示,,,,上电压为50 V.求:.
题7-1图
题7-2图
题7-2图 7-2 两小球的质量都是m,都用长为l的细绳挂在同一点,它们带有相 同电量,静止时两线夹角为2θ,如题7--2图所示.设小球的半径和线的质 量都可以忽略不计,求每个小球所带的电量. 解: 如题7-2图示
解得
7-3 在真空中有A,B两平行板,相对距离为d,板面积为S,其带电量 分别为+q和-q.则这两板之间有相互作用力f,有人说,又有人说,因 为f=qE,,所以试问这两种说法对吗?为什么?f到底应等于多少? 解: 题中的两种说法均不对.第一种说法中把两带电板视为点电荷是不 对的,第二种说法把合场强看成是一个带电板在另一带电板处的场强也
7.真空中的静电场 大学物理习题答案

l
xd x
2
k l a ( ln ) 4 0 a la
方向沿 x 轴正向。
7-4 一半径为 R 的绝缘半圆形细棒,其上半段均匀带电量+q,下半段均匀带电量-q,如图 7-4 所示,求半 圆中心处电场强度。 解:建立如图所示的坐标系,由对称性可知,+q 和-q 在 O 点电场强度沿 x 轴的分量之和为零。取长为 dl 的线元,其上所带电量为
大学物理练习册—真空中的静电场
库仑定律 7-1 把总电荷电量为 Q 的同一种电荷分成两部分, 一部分均匀分布在地球上, 另一部分均匀分布在月球上, 24 使它们之间的库仑力正好抵消万有引力, 已知地球的质量 M=5.98l0 kg, 月球的质量 m=7.34l022kg。 (1)求 Q 的最小值; (2)如果电荷分配与质量成正比,求 Q 的值。 解: (1)设 Q 分成 q1、q2 两部分,根据题意有 k
x
d 时 2
1 E d S 2 E1S 2 xS , E1 x 1 S 0 0
28
大学物理练习册—真空中的静电场
x
d 时 2
1 d d E d S S 2 2 E 2 S 0 2 2 S , E 2 0
r R sin , x R cos
x
d E
sin cos d 2 0
因为球面上所有环带在 O 处产生的电场强度方向相同, E 2 0
2 0
sin cos d i i 4 0
7-6 一无限大均匀带电薄平板,面电荷密度为 ,平板中部有一半径为 R 的圆孔, 如图 7-6 所示。求圆孔 中心轴线上的场强分布。 (提示:利用无穷大板和圆盘的电场及场强叠加原理) 解:利用补偿法,将圆孔看作由等量的正、负电荷重叠而成,即等效为一个 完整的带电无穷大平板和一个电荷面密度相反的圆盘叠加而成。 R 无穷大平板的电场为
大学物理第7章真空中的静电场答案解析

第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7-1图0 dqξd ξ习题7-2 图a204r dxdE πελ=θπελcos 420rdxdE y =, θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===, 代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y+--πελ,方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy ==2204Ly y L+πελ7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7-2 图byx习题7-3图2022R q επ=,如图,方向沿x 轴正向。
大学静电场试题及答案

大学静电场试题及答案一、选择题1. 静电场中的电场线是从正电荷出发,终止于负电荷。
A. 正确B. 错误答案:A2. 电场强度的方向是正电荷所受电场力的方向。
A. 正确B. 错误答案:A3. 电场中某点的电势与该点的电场强度大小无关。
A. 正确B. 错误答案:A4. 电容器的电容与两极板间的距离成反比。
A. 正确B. 错误答案:B5. 电场中某点的电势与该点的电场强度方向无关。
A. 正确B. 错误答案:A二、填空题1. 电场强度的定义式为_______,其中E表示电场强度,F表示电场力,q表示试探电荷。
答案:E = F/q2. 电势差的定义式为_______,其中U表示电势差,W表示电场力做的功,q表示试探电荷。
答案:U = W/q3. 电容器的电容公式为_______,其中C表示电容,Q表示电荷量,V表示电势差。
答案:C = Q/V4. 电场力做功的公式为_______,其中W表示功,q表示电荷量,U表示电势差。
答案:W = qU5. 电场中某点的电势与该点的电场强度大小_______关系。
答案:无关三、简答题1. 简述电场强度和电势的概念及其物理意义。
答案:电场强度是描述电场强弱和方向的物理量,其大小等于单位正电荷在该点所受的电场力,方向与正电荷所受电场力的方向相同。
电势是描述电场能的性质的物理量,它表示单位正电荷在电场中从某点移到参考点(通常取无穷远处)所做的功。
2. 电容器的电容与哪些因素有关?请简述其关系。
答案:电容器的电容与电容器的几何尺寸、两极板间的距离以及介质的介电常数有关。
电容与两极板的面积成正比,与两极板间的距离成反比,与介质的介电常数成正比。
四、计算题1. 一个平行板电容器,其极板面积为0.05平方米,两极板间的距离为0.01米,介质为空气(介电常数ε₀=8.85×10^-12 F/m)。
求该电容器的电容。
答案:C = ε₀ * A / d = 8.85×10^-12 * 0.05 / 0.01 =4.425×10^-11 F2. 已知电场中某点的电势为100V,试探电荷为-2C,求该点的电场强度。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7章 习题精选(一)选择题7-1、下列几种说法中哪一个是正确的(A )电场中某点场强的方向,就是点电荷在该点所受电场力的方向. (B )在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同.(C )场强可由q F E /计算,其中q 为试验电荷,q 可正、可负,F 为试验电荷所受电场力.(D )以上说法都不正确.[ ]7-2、图中实线为某电场的电场线,虚线表示等势面,由图可看出: (A )C B A E E E ,C B A V V V .(B )C B A E E E ,C B A V V V . (C )C B A E E E ,C B A V V V .(D )C B A E E E ,C B A V V V .[ ]7-3、关于电场强度定义式0/q F E,下列说法中哪个是正确的(A )场强E的大小与试验电荷0q 的大小成反比.(B )对场中某点,试验电荷受力F与0q 的比值不因0q 而变. (C )试验电荷受力F 的方向就是场强E的方向.(D )若场中某点不放试验电荷0q ,则0 F ,从而0 E.[ ]7-4、有一边长为a 的正方形平面,在其中垂线上距中心O 点垂直距离为a /2处,有一电量为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A )03 q . (B )04 q (C )03 q . (D )06 q[ ]7-5、已知一高斯面所包围的体积内电荷代数和0 q ,则可肯定:(A )高斯面上各点场强均为零. (B )穿过高斯面上每一面元的电场强度通量均为零. (C )穿过整个高斯面的电场强度通量为零. (D )以上说法都不对.[ ]q7-6、点电荷Q 被曲面S 所包围,从无穷远处引入另一点电荷q 至曲面外一点,如图,则引入前后: (A )曲面S 的电场强度通量不变,曲面上各点场强不变. (B )曲面S 的电场强度通量变化,曲面上各点场强不变. (C )曲面S 的电场强度通量变化,曲面上各点场强变化. (D )曲面S 的电场强度通量不变,曲面上各点场强变化.[ ]7-7、高斯定理0/d q S E S(A )适用于任何静电场. (B )只适用于真空中的静电场. (C )只适用于具有球对称性、轴对称性和平面对称性的静电场.(D )只适用于虽然不具有(C )中所述的对称性、但可以找到合适的高斯面的静电场.[ ]7-8、关于高斯定理的理解有下面几种说法,其中正确的是:(A )如果高斯面上E处处为零,则该面内必无电荷.(B )如果高斯面内无电荷,则高斯面上E处处为零.(C )如果高斯面上E处处不为零,则高斯面内必有电荷.(D )如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零.[ ]7-9、静电场中某点电势的数值等于(A )试验电荷q 0置于该点时具有的电势能. (B )单位试验电荷置于该点时具有的电势能. (C )单位正电荷置于该点时具有的电势能.(D )把单位正电荷从该点移到电势零点外力所做的功.[ ]7-10、图中所示为轴对称性静电场的E ~r 曲线,请指出该电场是由下列哪一种带电体产生的(E 表示电场强度的大小,r 表示离对称轴的距离).(A )“无限长”均匀带电圆柱面. (B )“无限长”均匀带电圆柱体. (C )“无限长”均匀带电直线. (D )“有限长”均匀带电直线.[ ]7-11、如图所示,边长为l 的正方形,在其四个顶点上各放有等量的点电荷.若正方形中心O 处的场强值和电势值都等于零,则:(A )顶点a 、b 、c 、d 处都是正电荷.(B )顶点a 、b 处是正电荷,c 、d 处是负电荷. (C )顶点a 、c 处是正电荷,b 、d 处是负电荷. (D )顶点a 、b 、c 、d 处都是负电荷.[ ]7-12、图中所示为一球对称性静电场的电势分布曲线,r 表示离对称中心的距离.请指出该电场是由下列哪一种带电体产生的. (A )半径为R 的均匀带负电球面.(B )半径为R 的均匀带负电球体. (C )正点电荷. (D )负点电荷.[ ]7-13、已知某电场的电场线分布情况如图所示.现观察到一负电荷从M 点移到N 点.有人根据这个图作出下列几点结论,其中哪个是正确的(A )电场强度N M E E . (B )电势N M V V . (C )电势能pN pM E E . (D )电场力的功0 W .[ ]7-14、有三个直径相同的金属小球.小球1和小球2带等量异号电荷,两者的距离远大于小球直径,相互作用力为F .小球3不带电并装有绝缘手柄.用小球3先和小球1碰一下,接着又和小球2碰一下,然后移去.则此时小球1和2之间的相互作用力为:(A )0. (B )F /4. (C )F /8. (D )F /2.[ ]7-15、一“无限大”均匀带电平面A ,其附近放一与它平行的有一定厚度的“无限大”平面导体板B ,如图所示.已知A 上的电荷面密度为 ,则在导体板B 的两个表面1和2上的感应电荷面密度为:(A ) 1, 2. (B ) 211 , 212 .(C ) 211 , 212 . (D ) 1,02 .[ ]baA+7-16、A 、B 为两导体大平板,面积均为S ,平行放置,如图所示.A 板带电荷1Q ,B 板带电荷2Q ,如果使B 板接地,则AB 间电场强度的大小E 为(A )S Q 012 . (B )S Q Q 0212 . (C )S Q01 . (D )SQ Q 0212 .[ ]7-17、两个同心薄金属球壳,半径分别为1R 和2R (12R R ),若分别带上电荷1q 和2q ,则两者的电势分别为1V 和2V (选无穷远处为电势零点).现用导线将两球壳相连接,则它们的电势为(A )1V . (B )2V . (C )21V V . (D ))(2121V V .[ ]7-18、如图所示,一带负电荷的金属球,外面同心地罩一不带电的金属球壳,则在球壳中一点P 处的场强大小与电势(设无穷远处为电势零点)分别为:(A )00 V E ,. (B )00 V E ,. (C )00 V E ,. (D )00 V E ,.[ ]7-19、在一不带电荷的导体球壳的球心处放一点电荷,并测量球壳内外的场强分布.如果将此点电荷从球心移到球壳内其它位置,重新测量球壳内外的场强分布,则将发现:(A )球壳内、外场强分布均无变化. (B )球壳内场强分布改变,球壳外不变. (C )球壳外场强分布改变,球壳内不变. (D )球壳内、外场强分布均改变.[ ]7-20、电场强度0/q F E这一定义的适用范围是:(A )点电荷产生的电场. (B )静电场. (C )匀强电场. (D )任何电场.[ ]7-21、在边长为b 的正方形中心放置一点电荷Q ,则正方形顶角处的场强为: (A )20π4b Q . (B )20π2b Q . (C )20π3b Q . (D )20πb Q. [ ]7-22、一“无限大”均匀带电平面A 的右侧放一与它平行的“无限大”均匀带电平面B .已知A 面电荷面密度为 ,B 面电荷面密度为 2,如果设向右为正方向,则两平面之间和平面B 右侧的电场强度分别为:+Q 2A B(A )002 ,. (B )00 ,. (C )00232 ,. (D )002 , . [ ]7-23、一带有电量Q 的肥皂泡(可视为球面)在静电力的作用下半径逐渐变大,设在变大的过程中其球心位置不变,其形状保持为球面,电荷沿球面均匀分布,则在肥皂泡逐渐变大的过程中:(A )始终在泡内的点的场强变小. (B )始终在泡外的点的场强不变. (C )被泡面掠过的点的场强变大. (D )以上说法都不对.[ ]7-24、两个同心均匀带电球面,半径分别为a R 和b R (a R <b R ),所带电荷分别为a Q 和b Q .设某点与球心相距r ,当b R r 时,该点的电场强度的大小为:(A )2b b 2a 0π41R Q r Q . (B ) 2b a 0π41r Q Q . (C ) 2b a 0π41r Q Q . (D )2a 0π41r Q . [ ]7-25、关于高斯定理的理解有下面几种说法,其中正确的是: (A )如果高斯面内有净电荷,则通过高斯面的电通量必不为零.(B )如果高斯面内无电荷,则高斯面上E处处为零.(C )如果高斯面上E处处不为零,则该面内必有电荷. (D )高斯定理仅适用于具有高度对称性的电场.[ ]7-26、一点电荷放在球形高斯面的中心处,下列哪一种情况,通过该高斯面的电通量会发生变化. (A )将另一点电荷放在高斯面外. (B )将另一点电荷放在高斯面内. (C )将球心处的点电荷移开,但仍在高斯面内. (D )将高斯面缩小.[ ]7-27、在已知静电场分布的条件下,任意两点1P 和2P 之间的电势差决定于: (A )1P 和2P 两点的位置. (B )1P 和2P 两点处的电场强度的大小和方向. (C )试验电荷所带电荷的正负. (D )试验电荷所带的电量.[ ]7-28、带电导体达到静电平衡时,其正确结论是:(A )导体表面上曲率半径小处电荷密度较小.(B )表面曲率半径较小处电势较高.(C )导体内部任一点电势都为零. (D )导体内任一点与其表面上任一点的电势差等于零.[ ]7-29、一个平行板电容器,充电后与电源断开,当用绝缘手柄将电容器两极板间距离拉大,则两极板间的电势差U ,电场强度的大小E ,将发生如下变化.(A )U 减小,E 减小. (B )U 增大,E 增大.(C )U 增大,E 不变. (D )U 减小,E 不变.[ ](二)填空题7-1、根据定义,静电场中某点的电场强度等于置于该点的___________________所受到的电场力.7-2、电场线稀疏的地方电场强度________;密集的地方电场强度________.(填“较大”或“较小”)7-3、均匀带电细圆环圆心处的场强为______________.7-4、一电偶极子,带电量为C 1025 q ,间距cm 5.0 L ,则系统电矩为_____________Cm .7-5、在静电场中作一任意闭合曲面,通过该曲面的电场强度通量的值取决于________________.7-6、两个平行的“无限大”均匀带电平面,其电荷面密度分别为 和 ,则两平面之间的电场强度大小为___________________,方向为_____________________.7-7、一个均匀带电球面半径为R ,带电量为Q .在距球心r 处(r <R )某点的电势为________________.7-8、在电荷为q 的点电荷的静电场中,将一电荷为0q 的试验电荷从a 点(距离q 为a r )沿任意路径移动到b 点(距离q 为b r ),外力克服静电场力所做的功 W ____________________.7-9、电荷为C 1059 的试验电荷放在电场中某点时,受到N 10209 的向下的力,则该点的电场强度大小为____________,方向____________.+ +2 AB C7-10、两个平行的“无限大”均匀带电平面,其电荷面密度分别为 和 2 ,如图所示,则A 、B 、C 三个区域的电场强度分别为:E A =______________,E B =________________,E C =_____________(设方向向右为正).7-11、一半径为R 的带有一缺口的细圆环,缺口长度为d (d <<R )环上均匀带有正电,电荷为q ,如图所示.则圆心O 处的场强大小 E ______________,场强方向为____________.7-12、半径为R 的半球面置于场强为E的均匀电场中,其对称轴与场强方向一致,如图所示.则通过该半球面的电场强度通量为___________.7-13、一均匀带正电的导线,电荷线密度为 ,其单位长度上总共发出的电场线条数(即电场强度通量)是____________.7-14、如图,点电荷q 和-q 被包围在高斯面S 内,则通过该高斯面的电场强度通量 SS E d =_________,式中E为__________________处的场强.7-15、在点电荷+q 和-q 的静电场中,作出如图所示的三个闭合面S 1、S 2、S 3,则通过这些闭合面的电场强度通量分别是:1Φ=___________,2Φ=___________,3Φ=________________.7-16、描述静电场的两个基本物理量是__________________;它们的定义公式是_______________和_________________.7-17、图示BCD 是以O 点为圆心,以R 为半径的半圆弧,在A 点有一电荷为+q 的点电荷,O 点有一电荷为-q 的点电荷.线段R BA .现将一单位正电荷从B 点沿半圆弧轨道BCD 移到D 点,则电场力所做的功为_____________.7-18、半径为R 的均匀带电圆环,电荷线密度为 .设无穷远处为电势零点,则圆环中心O 点的电势V =_____________________.7-19、静电场的场强环路定理的数学表示式为:____________.该式的物理意义____________________1 2 3该定理表明,静电场是____________场.7-20、电荷为Q 的点电荷固定在空间某点上,将另一电荷为q 的点电荷放在与Q 相距r 处.若设两点电荷相距无限远时电势能为零,则此时系统的电势能E p =___________________.7-21、一空气平行板电容器,两极板间距为d ,充电后板间电压为U .然后将电源断开,在两板间平行地插入一厚度为d /3的金属板,则板间电压变成U =________________.7-22、如图所示,两同心导体球壳,内球壳带电荷+q ,外球壳带电荷-2q .静电平衡时,外球壳的电荷分布为:内表面_____________;外表面_______________.7-23、如图所示,把一块原来不带电的金属板B ,移近一块已带有正电荷Q 的金属板A ,平行放置.设两板面积都是S ,板间距离是d ,忽略边缘效应.当B 板不接地时,两板间电势差U AB =_____________;B 板接地时两板间电势差 ABU _____________.7-24、一个不带电的金属球壳的内、外半径分别为R 1和R 2,今在中心处放置一电荷为q 的点电荷,则球壳的电势U =_____________.7-25、一平行板电容器充电后切断电源,若使两电极板距离增加.则电容将____________,两极板间电势差将__________.(填“增大”、“减小”或“不变”)(三)计算题7-1、电荷为q 1=×10-6C 和q 2=×10-6C 的两个点电荷相距20cm ,求离它们都是20cm 处的电场强度.(真空介电常量-2-12120m N C 108.85 )S7-2、如图所示,一长为10cm 的均匀带正电细杆,其电荷为×10-8C ,试求在杆的延长线上距杆的端点5cm 处的P 点的电场强度.(2-290C m N 10941)7-3、绝缘细线弯成的半圆环,半径为R ,其上均匀地带有正电荷Q ,试求圆心O 点的电场强度.7-4、“无限长”均匀带电的半圆柱面,半径为R ,设半圆柱面沿轴线OO'单位长度上的电荷为 ,试求轴线上一点的电场强度.7-5、真空中两条平行的“无限长”均匀带电直线相距为a ,其电荷线密度分别为 和 .试求:在两直线构成的平面上,两线间任一点的电场强度(选Ox 轴如图所示,两线的中点为原点).7-6、真空中一立方体形的高斯面,边长a =,位于图中所示位置.已知空间的场强分布为:bx E x ,0z y E E .常量b =1000N/(C m ).试求通过该高斯面的电通量.7-7、如图所示,两个点电荷+q 和-3q ,相距为d ,试求:(1)在它们的连线上电场强度0 E的点与电荷为+q 的点电荷相距多远(2)若选无穷远处电势为零,两点电荷之间电势0 V 的点与电荷为+q 的点电荷相距多远7-8、一“无限大”平面中部有一半径为R 的圆孔,设平面上均匀带电,电荷面密度为 .如图所示,试求通过小孔中心O 并与平面垂直的直线上各点的场强和电势(选O 点的电势为零).7-9、一个带等量异号电荷的均匀带电同心球面,半径分别为m 03.01 R 和m 10.02 R .已知两者的电势差为450V ,求内球面上所带的电荷.7-10、厚度为d 的“无限大”均匀带电导体板两表面单位面积上电荷之和为 .试求图示离左板面距离为a 的一点与离右板面距离为b 的一点之间的电势差.12。
