东南大学《材料科学基础ii》三元相图习题1.doc
材料科学基础 第07章+三元相图

第二节
• • • • •
三元匀晶相图
相图分析 水平截面图 合金的平衡冷却凝固过程 垂直截面图 三元相图的基本形状
第二节
三元匀晶相图
1.相图分析
形成条件:三组元在液态和固态都能无限互溶。 空间形貌:三棱柱体的相图,三 个侧面为两两组成的三个二元匀 晶相图,内部有两个曲面将相图 分为三个区间。 点:在三组元的上方有三个点 a、 b、c分别为三组元的熔点。 曲面:上面的曲面称为液相面, 下面的曲面称为固相面。 相区:液相区 ―― 液相面之上; 固相区 ―― 固相面以下;两相区 ―― 液相面和固相面之间包围的 区间L+α 。
第二节
三元匀晶相图
3.合金的平衡冷却凝固过程
整个结晶在一温度范围内完成, 由于有结晶潜热的放出,在冷却曲 线上凝固时下降平缓,曲线在凝固 开始和结束处有明显的转折。 如果不过分考究转变过程的内 涵,三元匀晶反应的过程与二匀晶 反应基本相同。都是进行选分结晶, 在平衡缓慢冷却过程中,都可得到 成分均匀的固溶体。 如果在非平衡冷却过程,同样 会出现晶内偏析,若晶体以树枝晶 方式长大,便得到枝晶偏析组织。 在结晶过程中,也存在成分过冷的 影响。
如图所示,其中一个坐标轴 表示B组元的质量分数,另 一个坐标轴表示C组元的质 量分数,则余下部分就是A 组元的分数。在直角坐标中, 根据两组元的含量变化范围, 可以采用不同比例的刻度。
第一节
三元相图成分表示方法
三元相图的基本形状
以浓度平面为基础,垂直于浓 度平面的高度坐标为温度,以此构 成的空间图形,空间中任一点代表 了系统一固定状态,在图中表示每 一状态的相平衡情况,相区之间分 界也有二元相图的曲线发展为曲面。 如果浓度平面为浓度三角形,则其 三元相图为三棱柱体,它的三个侧 面为三组元两两组成的二元相图。 要认识三元相图,必须熟悉二元相 图的所有规律。
材料科学基础三元相图共67页

43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
Байду номын сангаас
材料科学基础三元相图
21、静念园林好,人间良可辞。 22、步步寻往迹,有处特依依。 23、望云惭高鸟,临木愧游鱼。 24、结庐在人境,而无车马喧;问君 何能尔 ?心远 地自偏 。 25、人生归有道,衣食固其端。
41、学问是异常珍贵的东西,从任何源泉吸 收都不可耻。——阿卜·日·法拉兹
材料科学基础相图分析题

相图分析(26分)1、判读如下A-B-C三元相图(1)指出如下三元体系中化合物D和F的性质。
(2分)(2)划分副三角形并判定各界线上的温降方向(4分)(3)判定各界线的性质。
(3分)(4)判定无变量点性质,并写出液相组成在无变点处的反应式。
(4分)(5)分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例及固相中各物质的比例。
(7分)(6)指出N点组成的A、B、C混合物在平衡加热时最先在哪一点的温度出现液相?(2分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(4分)2、判读如下三元相图(共26分)(1)指出如下三元体系中化合物D1、D2和D3的性质。
(3分)(2)划分副三角形。
(2分)(3)判定各界线上的温降方向及界线的性质(转熔线上用双箭头表示)。
(4分)(4)判定无变量点性质,并写出冷却时无变点处的平衡反应式。
(5分)(5)分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例,固相中各固相的比例。
(6分)(6)说明组成为N点A-B-C混合物在平衡加热时最先在哪一点的温度出现液相?(1分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(3分)3、判读如下三元相图(24分)(1)指出如下三元体系中化合物D的性质。
(2分)(2)划分副三角形及判定各界线上的温降方向。
(4分)(3) 判定各界线的性质。
(2分)(4) 判定无变量点性质,并写出液相组成在无变点处的反应式。
(3分)(5) 分析M点熔体的析晶过程,并计算液相组成刚到析晶结束点的固液相的比例,固相中各固相的比例。
(6分)(6) 说明组成为N点A-B-C混合物在平衡加热时最先在哪一点的温度出现液相?(2分)(7) 画出A-B二元系统示意相图,并标出各区域的平衡相组成。
(5分)4、下图是A-B-C三元系统相图,根据相图回答下列问题:(24分)(1)指出如下三元体系中化合物S的性质。
(2分)(2)划分副三角形及判定各界线上的温降方向。
材料科学基础三元合金相图

的
3.如何控制使性能最佳
凝 固
凝固前的液体/晶胚
类别
基本规律
形核 热力学条件(临界半径/形核功)
影响因素及控制
长大 本质原子跨过界面;方式?界
面/扩散控制?
.
3
匀晶相图 二 元 共晶相图 相 图 包晶相图
平衡凝固
非平衡 凝固
晶内偏析、枝 晶偏析、成分 过冷、伪共晶、 离异共晶、包 晶偏析
相图与性能:力学性能、加工性能、 铸造性能、热处理可能性
LA+C
三 相 平 衡 共 晶 线
——
LA+B
E1
E2 L B + C
E
TA
A3 A2 A1
E3
A
.
E1
TC
E C3 C2 C1
C
TB B3 B2 E2 B1
B
71
点
四 相 平 衡 共 晶
——
TA
A3 A2 A1
E3
A
E1
TC
E C3 C2 C1
C
.
TB B3 B2 E2 B1
B
72
2.等温截面
假设:合金O在
B
一定温度下处于
α,β两相平衡,成
分点分别为α及b,
B%
O, α,β中A组元含
量分别为Cf, Ce, Cg,B组元含量 分别为Af’, Ae’, Ag’, e’ 合金O重量分数
f’
g’
O
为1。
A
ef
C% g ← A% C
.
22
CeWα+Cg (1-Wα)=(Wα+Wβ)Cf Ae’Wα+Ag’ (1-Wα)= (Wα+Wβ)Af’
材料科学基础三元相图

一.三元相图的成分表示法:等腰三角形
材料科学基础三元相图
一.三元相图的成分表示法:直角坐标系
材料科学基础三元相图
3.浓度三角形中特殊线: 3.1 平行浓度三角形任一边的直线
3.2 从浓度三角形的一个顶点到对边的任意直线
材料科学基础三元相图
二、杠杆定律及重心法则
单相平衡勿须计算,四相平衡无从计算 1.两相平衡:杠杆定律
2.合金的凝固过程和组织
各点合金的组织
如表4-3(表中nmp区需修正) 如合金I:L→A 剩余液相交np于n1:L+A→M 至n2点,A消失,L→M 液相沿e1E:L→M+B 液相成分在E点:L→M+B+C
材料科学基础三元相图
材料科学基础三元相图
3.等温截面
材料科学基础三元相图
4。变温截面
材料科学基础三元相图
2.三元相图分析 法 总 结 --- 三 相 平 衡 -- 三 相
反应的判定--:
投影图判断三 相反应
液相单变量线穿 过两旁固相成分点连 线的为二元共晶型, 而单变线穿过两旁 固相成分点连线延 长线为二元包晶反 应,且靠近单变线 的为生成相
材料科学基础三元相图
3.三元相图分析法总结---四相平衡
x合金结晶:
L→A,L+A→M,L→M,L→M+C,L→M+B+C
y合金结晶: L→A,L+A→M,L+A→M+C,L→M+C,L→M+B+C 5.固相有固溶度时的包共晶 包共晶:Lα+P→Md1+γc1 包晶反应 LE→Md2+βb+γc2 d1d2,c2c1为M+γ二元共晶结 束面投影
东南大学材料科学基础习题

x Dt
Cs=1%,C0=0.1%,Cx=0.45%,x=0.05带入后 可以得到
erf
0.05 2 Dt
0.6111
查表求得 t=5.2h
同样可以求得(2)
(3)课堂上已讲过 x Dt
4.870℃渗碳与927℃渗碳相比,优点是热处理产品 晶粒细小,淬火变形小,
问:
1. 870℃渗碳需要多少时间才能获得与927℃渗碳10小 时相同的渗层厚度?(已知D0、Q,忽略不同温度下 碳在奥氏体铁中的溶解度差别);
θ+η
θ+η’
2.根据有关数据画二元相图
画出坐标(C%---T) 汇出三相平衡反应,并给出反应类型 连接相应点
3.分析含碳量0.2%和1.5%的铁碳合金按亚稳系统从
液态平衡冷却到室温的转变过程。用冷却曲线说 明各阶段的组织,并画出各合金在730℃和720℃ 显微组织的示意图。
0.2%C
扩散习题
1. 一个封闭钢管,外径为1.16cm,内径为0.86cm,长度为 10cm。管内为渗碳气氛,管外为脱碳气氛。在1000℃保温 100h 后(达到平稳态扩散),共有3.60g 碳逸出钢管。钢管 的碳浓度分布如下所示:
r/cm 0.553 0.540 0.527 0.516
w(C)/% 0.28 0.46 0.65 0.82
3. 列式说明Fe-Fe3C-Fe3P三元系中的合金在下列温度范 围内发生哪些无液相参与的三相平衡转变:
1)1005~745℃;2)950~745℃;3)745~725℃
4. 请说明发生相图所示的包共晶转变后,哪个成分范围 内的合金仍有液相?并说明这些合金继续冷却时还会 发生哪些转变。
1.三元系液相面的投影图 2.由液相直接结晶出的单一 固体 液相线划分的区域 3.课上讲过,注意题目的本 意应该是两四相平衡反应之 间的三相平衡转变 4. L—+Fe3P
三元合金相图习题

三元合金相图习题三元合金相图一、填空1. 三元相图等温截面的三相区都是___________________形。
2. 图1是A-B-C三元系成分三角形的一部分,其中X 合金的成分是_____________________。
图13. 图2是三元系某变温截面的一部分,其中水平线代表________________反应,反应式为______________________ 。
图24.图3是某三元系变温截面的一部分,合金凝固时,L+M+C将发生_________________反应。
图图35. 三元相图的成分用__________________________表示。
6. 四相平衡共晶反应的表达式__________________________。
7. .图6是A-B-C三元共晶相图的投影图,在常温下:合金I的组织是______________________________________合金II的组织是_______________________________________合金III的组织是______________________________________图48.三元相图有如下几类投影图(1)_____________________________(2)________________________________(3)__________________________(4 )________________________________。
9. 三元系中两个不同成分合金,合成一个新合金时,则这三个合金成分点____________________________。
10. 四相平衡包共晶反应式为__________________________。
11. 三元相图垂直截面可用于分析__________________________________。
12. 三元系三条单变量线相交于__________,就代表一个__________________,并可根据单变量线箭头_____________判断__________________。
三元相图1

§2 三元系平衡相的定量法则
1、直线法则:设合金o在某一 、直线法则:设合金 在某一 温度处于两相平衡, 温度处于两相平衡,这两 个相的成分点分别为a 个相的成分点分别为a和b, aob一定在一条直线上 一定在一条直线上, 则aob一定在一条直线上, 点位于a、b点之间. a、b点之间 o点位于a、b点之间. 2、杠杆定律 、 o点处于两相平衡 a点为 点处于两相平衡, 点为 点处于两相平衡 α相成分点 b点为 相成分点 相成分点, 点为 相成分点, 点为β相成分点 相成分点 则两相的质量之比为
通过分析不同温度的等温截面图, 通过分析不同温度的等温截面图,可以分析合金 状态随温度的变化情况: 状态随温度的变化情况: 合金X:
温度为液相和固相共存,且液相的相对量多,固 在t1温度 相的相对量少。 温度仍为液相和固相共存,但液相的相对量减少, 在t2 温度 固相的相对量增多。 温度为单相的固相。 在t3 温度
f =3-3+1=1,温度一定, f =0,三个平衡相的成分确定,可以 计算其相对量。 设某一温度下,合金 合金N处 设某一温度下 合金 处 于三相平衡(αβγ),各相的成 于三相平衡 各相的成 分点分别为D、 、 , 分点分别为 、E、F,则合 金N的成分点必位于三角形 的成分点必位于三角形 DEF的重心(质量重心)上, 的重心( 的重心 质量重心) 合金的重量与三相的重量存 在如下关系 —— 重心法则
3等温截面水平截面等温截面水平截面水平截面确定在某一温度下的相组成和相平衡关系用与成分三角形平行的平面与立体图在某温度相截将其截用与成分三角形平行的平面与立体图在某温度相截线投影到成分三角形平面上所得到的图形
第五章 三元合金
三元系:由三个组元组成的合金系。 三元系:由三个组元组成的合金系。 由于在二元合金中加入第三组元, 由于在二元合金中加入第三组元,组元间的相 互作用往往不是加和性的, 互作用往往不是加和性的,这第三组元的加入 会改变合金组元间的溶解度,甚至会出现新相。 会改变合金组元间的溶解度,甚至会出现新相。
材料科学基础-三元相图

液/固相线(共轭线):
连接线: o \ n、m。
两平衡相的相对数量比为: 杠杆定律
连接线:
由试验数据标出。
连接线能相交吗?
➢T温度下,同一成分的合金有固定 的平衡相;
➢连接线不可能相交; ➢一般不平行于三角形的边。
4.变温截面(垂直截面动画)
(1)平行于成分三角形一边的变温截面
(2)过成分三角形一顶点的变温截面
•6.5 相图热力学
第6章 相图
•6.4 三元相图 (Ternary diagram) •6.4.1 等边三角形的成分表示法 •6.4.2 三元相图中的基本法则 •6.4.3 三元匀晶相图 •6.4.4 固态互不溶解的三元共晶相图 •6.4.5 三元相图的几何规律及分析 •6.4.6 典型的三元相图
顺时针或逆时针都可以。
三角形内的点: 代表三元系的成分。
A%?
14
• 由O顺次作平行于三个边的线段oa、ob、oc。
a c
b
用oa, ob, oc分别表示组元A、B、C的质量分数。
Oa+Ob+Oc = AB = 100%
15
数值的标注要方向一致,
顺时针或逆时针都可以。
顺时针
逆时针
6.4.2 三元相图中的基本法则
三元匀晶相图 空间模型:
三元匀晶相图
固态互不溶解的三元共晶相图的空间模型
• /21cn/%E6%9D%90%E
6%96%99%E7%A7%91%E5%AD%A6%E5%9F%BA%E7%A1%
/doc/chap8/82.htm
5
固态有限溶解的三元共晶相图的空间模型
•6.5 相图热力学
6.4.1 等边三角形的成分表示法
第8章-三元相图-笔记及课后习题详解(已整理-袁圆-2014.8.7)

第8章-三元相图-笔记及课后习题详解(已整理-袁圆-2014.8.7)第8章三元相图8.1 复习笔记一、三元相图的基础三元相图的基本特点:完整的三元相图是三维的立体模型;三元系中的最大平衡相数为四。
三元相图中的四相平衡区是恒温水平面;三元系中三相平衡时存在一个自由度,所以三相平衡转变是变温过程,反应在相图上,三相平衡区必将占有一定空间。
1.三元相图成分表示方法(1)等边成分三角形图8-1 用等边成分三角形表示三元合金的成分三角形内的任一点S都代表三元系的某一成分点。
(2)等边成分三角形中的特殊线①等含量规则:平行于三角形任一边的直线上所有合金中有一组元含量相同,此组元为所对顶角上的元素。
②等比例规则:通过三角形定点的任何一直线上的所有合金,其直线两边的组元含量之比为定值。
③背向规则:从任一组元合金中不断取出某一组元,那么合金浓度三角形位置将沿背离此元素的方向发展,这样满足此元素含量不断减少,而其他元素含量的比例不变。
④直线定律:在一确定的温度下,当某三元合金处于两相平衡时,合金的成分点和两平衡相的成分点必定位于成分三角形中的同一条直线上。
(3)成分的其他表示方法:①等腰成分三角形:两组元多,一组元少。
②直角成分坐标:一组元多,两组元少。
③局部图形表示法:一定成分范围内的合金。
(1)杠杆定律(2)重心定律二、固态互不溶解的三元共晶相图1.相图的空间模型图8-5 组元在固态完全不互溶的三元共晶相图A、B、C三组元的初始结晶面:ae1Ee3a、be1Ee2b、ce2Ee3c共晶转变线:e1E:L→A+Be2E:L→B+Ce3E:L→C+AE点为三元共晶点:LE→A+B+C2.截面图(1)垂直截面图:①垂直截面图中的水平线不一定是恒温转变线,但三相区之间的水平线是恒温转变线;②At截面是一个特殊截面,结晶出的是纯组元A相,由直线法则可知a’q’是连接线。
故该温度下可求A和L的相对量。
图8-6 垂直截面图(a)浓度三角形(b)rs截面(c)At截面(2)水平截面图①两相区和单相区之间的分界线是曲线;②两相区和三相区之间的分界线是直线,实际山是两个相区分界的联结线;③三相区是三角形。
东南大学《材料科学基础ii》三元相图习题1.doc
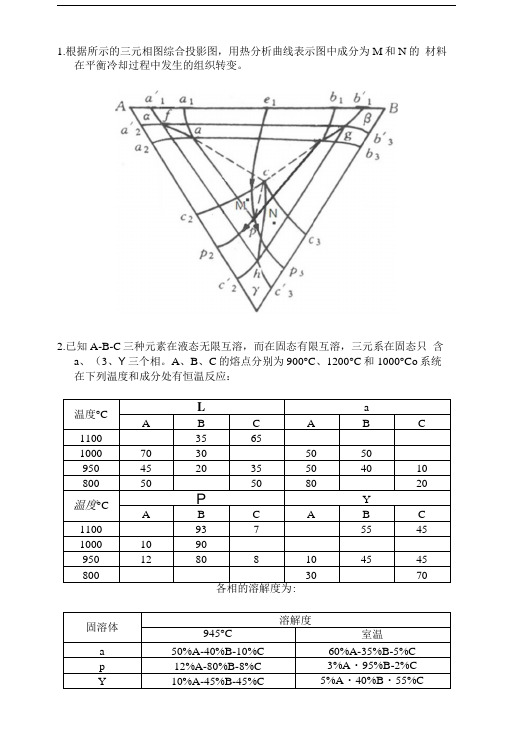
1.根据所示的三元相图综合投影图,用热分析曲线表示图中成分为M和N的材料在平衡冷却过程中发生的组织转变。
2.已知A-B-C三种元素在液态无限互溶,而在固态有限互溶,三元系在固态只含a、(3、Y三个相。
A、B、C的熔点分别为900°C、1200°C和1000°Co系统在下列温度和成分处有恒温反应:温度°CL aA B C A B C1100 35 651000 70 30 50 50950 45 20 35 50 40 10 800 50 50 80 20温度°CP YA B C A B C1100 93 7 55 45 1000 10 90950 12 80 8 10 45 45 800 30 70各相的溶解度为:固溶体溶解度945°C 室温a 50%A-40%B-10%C 60%A-35%B-5%C p 12%A-80%B-8%C 3%A・95%B-2%C Y 10%A-45%B-45%C 5%A・40%B・55%C组成三元相图的三个二元系的相在室温下溶解度为请根据上述条件解决以下问题:(1)画出系统的综合投影图;(2)说明每个恒温反应的类型;(3)画出成分为30%A.55%B.15%C的合金凝固过程的热分析曲线,并计算该合金在945°C时各相的相对百分数;(4)画出成分为20%A-35%B-45%C合金凝固过程的热分析曲线。
组成三元相图的三个二元系的相在室温下溶解度为请根据上述条件解决以下问题:(1)画出系统的综合投影图;(2)说明每个恒温反应的类型;(3)画出成分为30%A.55%B.15%C的合金凝固过程的热分析曲线,并计算该合金在945°C时各相的相对百分数;(4)画出成分为20%A-35%B-45%C合金凝固过程的热分析曲线。
东南材料科学基础 第5章-II 三元相图提纲

A B C O b b' c C ’a a ’ 第5章-II 三元相图5.10 基本概念三元系: 三个组元组成的合金系独立变量:温度T 组元浓度 X A 、X B (X C =1-X A -X B )三元相图的几何形状 :完整的三元相图: 空间三维模型,实用三元相图: 平面图(截面面图和投影图)5.10.1三元相图的成分表示方法1. 等边三角形表示法 (图1) ● 成分三角形 ● 三角形中的点如何表示成分 X A =Ca , X B =Ab , X C =Bc, 可证: X A +X B +X C =100% ●网格三角形 (图2)图1图2用途:相当于坐标纸。
已知三角形中某一点的位置,可用网格三角形测出该点对应的材料的成分 ● 成分三角形中的特殊的点和线 (图3) ➢ 顶点: 纯组元➢ 平行于三角形某边的直线: 此材料中和边相对的组元含量相等 ➢ 过三角形顶点的直线:对应的材料中两组元浓度比相等ABCaa ’CPb图3 图4 2. 直角三角形表示法 (图4)P 点的成分:X B =Ab, X C =Ac, X A =1-X B -X C 3、 3. 其它表示法如:等腰成分三角形 局部图形5.10.2 自由能-成分曲面和公切面法则1.三元相图中的相律f=C-P+1 ∵ C=3 ∴ f=0 时, P=4最多只能是四相平衡;P=1时, f=3, 有三个自由度 因此自由能与成分的关系要用空间曲面表示。
(图5) 2.公切面法则 ● 两相平衡图5公切面可在自由能-成分曲面上滚动, 得到一对共轭曲线,这对曲线上的点是一一对应的,对应点之间的连线称之为连接线。
(图6)● 三相平衡 公切面是唯一的 (图7) ● 四相平衡 有公切面,四点共面5.10.3 杠杆定理和重心法则1.杠杆定理aboaabob==%%βα%100⨯=PMOMWα%100⨯=QRORWβ%100⨯=STOTWγA BCabo .图6 图7(1)共线法则当三元系处于两相平衡时,此两相的成分点和材料的成分点位于成分三角形的同一直线上。
材料科学基础二元相图01.答案

24
25
26
27
28
29
30
7.3 二元相图分析
7.3.1 匀晶相图和固溶体凝固
匀晶转变
Lα
液相线
L (单相区) L+α
由液相结晶出单相固溶体的过程
TB
匀晶相图及特点
表示匀晶转变的相图 在固态、液态无限互溶
TA
两相区 固相线
α (单相区)
匀晶反应的条件
具有相同的晶体结构 原子半径接 近 (相差不超过15%) 相同的原子价 相似的电负性
38
问答题: 从结晶条件和过程分析,纯金属和单相固溶体合金结晶时的 异同点?
①
相同点:基本过程:形核-长大;
热力学条件:⊿T>0; 能量条件:能量起伏; 结构条件:结构起伏。
② 不同点:合金在一个温度范围内结晶
合金结晶是选分结晶:需成分起伏。
39
例题:图1为一匀晶相图,试根据相图确定:
(1)计算wB = 40 %的合金开始凝固出来的固相成分为多少? (2)若开始凝固出来的固体成分为wB = 60 %,合金的成分为多少? (3)成分为wB = 70%的合金最后凝固时的液体成分为多少? (4)若合金成分为wB = 60 %,凝固到某温度时液相成分wB = 40 %,固相 成分为wB = 85%,此时液相和固相的相对量各为多少?
A
B
只发生 匀晶转变的二元合金: Cu-Ni, Au-Ag, Au-Pt等; 二元陶瓷:NiO-CoO, CoO-MgO, NiO-MgO等
特殊匀晶相图:
L
L
α
A B A
α
如:Cu-Au
如:Pb-Tl
B
★ ∵
极点处结晶在恒温下进行,自由度为0,而不是1。 xL = xα 增加了一个约束条件
材料学基础第5章三元相图

材料科学基础
第五章
5.6三元相图小结
材料科学基础
第五章
一、单相状态 f=3-1+1=3,而一个温度变量和两个成分变量之间没有任何
相互制约的关系,因此,不论是等温截面还是变温截面,单相区可能具 有多种多样的形状。 二、两相平衡 立体图:共轭曲面。 成分变化:蝶形规则。 等温图:共轭曲线(可用杠杆定律) 变温截面:判定转变温度范围和相转变过程,不能用杠杆定律。 三、三相平衡 立体图:三棱柱,棱边是三个平衡相单变量线。
二、投影图
材料科学基础
第五章
投影图的作用:合金结晶过程分析、相组成物相对量计算、组织组成 物相对量计算。
图8.17 三元共晶相图的投影区
表8.2 各典型区域合金的凝固组织过程及室温组织
材料科学基础
第五章
区
凝固过程
室温组织
Ⅰ
L→α
α
Ⅱ
L→α ,α→βⅡ
α+βⅡ
Ⅲ
L→α ,α→βⅡ,α β
α+βⅡ+γⅡ
(1)当给定合金在一定温度下处于两相平衡状态时,若其中一相的成分 给定,则根据直线法则,另一相的成分点必位于两已知成分点连线的 延长线上。 (2)如果两个平衡相的成分点已知,则合金的成分点必然位于两平衡相 成分点的连线上,根据两平衡相的成分,可用杠杆定律求出合金的成 分。
5.2.2重心定律
x,y,z分别为α,β,γ成分点,则
材料科学基础
第五章
投影图有两种。一种是把空间相图中所有相区间的交线部投影到浓度 三角形中,借助对立体图空间构造的了解,可以用投影图来分析合 金的冷却和加热过程。另一种是把一系列水平截面中的相界线投影 到浓度三角形中。每一条线上注明相应的温度,这样的投影图叫等 温线投影图。等温线可反映空间相图中各种相界面的变化趋势,等 温线越密,表示这个相面越陡。
材基2习题

习 题第一章 相 平 衡1. 简述SiO 2的多晶转变现象,为什么在硅酸盐产品中SiO 2经常以介稳状态存在?2. 图1-1示意表示出生成一个不一致熔融化合物A m B n 和形成固溶体S B(A)的二元系统,试完成此相图的草图。
3. 对于图1-2所示的相图,试进行:(1)标出初晶区;(2)画出温度下降方向;(3)确定相界线性质;(4)确定无变量点性质;(5)分析1,2,3点的结晶过程。
4. 对于图1-3所示的相图,试进行:(1)标出初晶区;(2)画出温度下降方向;(3)确定相界线性质;(4)确定无变量点性质;(5)分析1,2,3点的结晶过程。
5. 某种陶瓷制品以长石K 2O ⋅Al 2O 3⋅6SiO 2和高岭土Al 2O 3⋅2SiO 2⋅2H 2O 配料,在12000C 烧成。
观察烧成制品的显微结构,发现由莫来石晶体和玻璃相组成,问:(1)配料中,长石和高岭土各为多少?(2)制品结构中,莫来石和玻璃相各为多少?m n A A m B n B图1-1 图1-2A AB B 图1-36. 氧化物AO 和SiO 2以一定配比混合成均匀的粉状配合物,加热至熔融状态,7. 右图为含有一个三元化合物D (A m B n C q )的三元系统相图,试判断:(1)图中各界线的温度走向和性质;(2)该三元化合物是一致熔融还是不一致熔融化合物?(3)确定各无变量点的性质;(4)分析图中1、2、3点的析晶过程。
8. 为什么在硅砖生产中Al 2O 3是很有害的杂质,而加入少量CaO 能促进鳞石英的形成而又不明显降低其耐火度。
第二章 固 相 反 应2. 试比较杨得方程、卡特方程和金斯特林格方程的优缺点及适用条件。
3.为观察尖晶石的形成,用过量的MgO 粉包围1μ的Al 2O 3球形颗粒。
在固定温度实验中的第一个小时有20%的Al 2O 3反应成尖晶石。
试根据(1)无球形几何校正;(2)用杨得方程作球形校正,计算完全反应的时间。
材料科学基础试卷(二)与答案

材料科学基础试卷(二)与参考答案一、名词解释(每小题1分,共10分)1.晶胞2.间隙固溶体3.临界晶核4.枝晶偏析5.离异共晶6.反应扩散7.临界分切应力8.回复9.调幅分解10.二次硬化二、判断正误(每小题1分,共10分)正确的在括号内画“√”, 错误的画“×"1.金属中典型的空间点阵有体心立方、面心立方和密排六方三种.()2.作用在位错线上的力F的方向永远垂直于位错线并指向滑移面上的未滑移区。
( )3.只有置换固溶体的两个组元之间才能无限互溶,间隙固溶体则不能. ( )4.金属结晶时,原子从液相无序排列到固相有序排列,使体系熵值减小,因此是一个自发过程。
( )5.固溶体凝固形核的必要条件同样是ΔG B<0、结构起伏和能量起伏。
()6.三元相图垂直截面的两相区内不适用杠杆定律。
()7.物质的扩散方向总是与浓度梯度的方向相反. ( )8.塑性变形时,滑移面总是晶体的密排面,滑移方向也总是密排方向。
()9.和液固转变一样,固态相变也有驱动力并要克服阻力,因此两种转变的难易程度相似。
()10.除Co以外,几乎所有溶入奥氏体中的合金元素都能使C曲线左移,从而增加钢的淬透性. ( )三、作图题(每小题5分,共15分)1. 在简单立方晶胞中标出具有下列密勒指数的晶面和晶向:a )立方晶系(421),(231),[112];b)六方晶系(1112),[3112]。
2. 设面心立方晶体中的(111)为滑移面,位错滑移后的滑移矢量为2a[110]。
(1)在晶胞中画出柏氏矢量b 的方向并计算出其大小。
(2)在晶胞中画出引起该滑移的刃型位错和螺型位错的位错线方向,并写出此二位错线的晶向指数. 3. 如下图所示,将一锲形铜片置于间距恒定的两轧辊间轧制。
试画出轧制后铜片经再结晶后晶粒大小沿片长方向变化的示意图。
四、相图分析(共20分)(1) 就Fe-Fe 3C 相图,回答下列问题:1。
默画出Fe —Fe 3C 相图,用相组成物填写相图;2. 分析含碳量为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.根据所示的三元相图综合投影图,用热分析曲线表示图中成分为M和N的材料
在平衡冷却过程中发生的组织转变。
2.已知A-B-C三种元素在液态无限互溶,而在固态有限互溶,三元系在固态只含
a、(3、Y三个相。
A、B、C的熔点分别为900°C、1200°C和1000°Co系统
在下列温度和成分处有恒温反应:
温度°C
L a
A B C A B C
1100 35 65
1000 70 30 50 50
950 45 20 35 50 40 10 800 50 50 80 20
温度°C
P Y
A B C A B C
1100 93 7 55 45 1000 10 90
950 12 80 8 10 45 45 800 30 70
各相的溶解度为:
固溶体
溶解度
945°C 室温
a 50%A-40%B-10%C 60%A-35%B-5%C p 12%A-80%B-8%C 3%A・95%B-2%C Y 10%A-45%B-45%C 5%A・40%B・55%C
组成三元相图的三个二元系的相在室温下溶解度为
请根据上述条件解决以下问题:
(1)画出系统的综合投影图;
(2)说明每个恒温反应的类型;
(3)画出成分为30%A.55%B.15%C的合金凝固过程的热分析曲线,并计算该合金在945°C时各相的相对百分数;
(4)画出成分为20%A-35%B-45%C合金凝固过程的热分析曲线。
组成三元相图的三个二元系的相在室温下溶解度为
请根据上述条件解决以下问题:
(1)画出系统的综合投影图;
(2)说明每个恒温反应的类型;
(3)画出成分为30%A.55%B.15%C的合金凝固过程的热分析曲线,并计算该合金在945°C时各相的相对百分数;
(4)画出成分为20%A-35%B-45%C合金凝固过程的热分析曲线。
