数值分析实验报告--Runge现象的产生和克服
数值分析(计算方法)课程设计实验报告(附程序)

n=4 时,max[L(X)-h(X)]=0.4020;
n=8 时,max[L(X)-h(X)]=0.1708;
n=10 时,max[L(X)-h(X)]=0.1092。
图象分析: 从图象可以看出随着插值节点数的增加出现异常的摆动,中间能较好的接近 原函数,但两边却出现很大的误差。
(3).对定义在(-5,5)上的函数
程序代码 2:
x=[-1:0.2:1]; y=1./(1+25.*x.^2); x0=[-1:0.01:1]; y0=lagrange(x,y,x0); y1=1./(1+25.*x0.^2);
plot(x0,y0,'--r'); hold on; plot(x0,y1,'-b'); x2=abs(y0-y1); max(x2) ; 程序代码3: n=3; for i=1:n x(i)=cos(((2.*i-1).*pi)./(2.*(n+1))); y(i)=1./(1+25.*x(i).*x(i)); end x0=-1:0.01:1; y0=lagrange(x,y,x0); y1=1./(1+25.*x0.^2); plot(x0,y0,'--r') hold on plot(x0,y1,'-b')
以 x1,x2,„,xn+1 为插值节点构造上述各函数的 Lagrange 插值多项式, 比较其 结果。
设计过程: 已知函数 f(x)在 n+1 个点 x0,x1,…,xn 处的函数值为 y0,y1,…,yn 。 求一 n 次多 项式函数 Pn(x),使其满足: Pn(xi)=yi,i=0,1,…,n. 解决此问题的拉格朗日插值多项式公式如下
数值分析实验报告

实验2.1 多项式插值的振荡现象实验目的:在一个固定的区间上用插值逼近一个函数,显然Lagrange 插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时,Ln(x)是否也更加靠近被逼近的函数。
Runge 给出的一个例子是极著名并富有启发性的。
实验容:设区间[-1,1]上函数 f(x)=1/(1+25x 2)。
考虑区间[-1,1]的一个等距划分,分点为 x i = -1 + 2i/n ,i=0,1,2,…,n ,则拉格朗日插值多项式为201()()125nn i i i L x l x x ==+∑. 其中,l i (x),i=0,1,2,…,n 是n 次Lagrange 插值基函数。
实验步骤与结果分析:实验源程序function Chap2Interpolation% 数值实验二:“实验2.1:多项式插值的震荡现象”% 输入:函数式选择,插值结点数% 输出:拟合函数及原函数的图形promps = {'请选择实验函数,若选f(x),请输入f,若选h(x),请输入h,若选g(x),请输入g:'};titles = 'charpt_2';result = inputdlg(promps,'charpt 2',1,{'f'});Nb_f = char(result);if(Nb_f ~= 'f' & Nb_f ~= 'h' & Nb_f ~= 'g')errordlg('实验函数选择错误!');return;endresult = inputdlg({'请输入插值结点数N:'},'charpt_2',1,{'10'});Nd = str2num(char(result));if(Nd <1)errordlg('结点输入错误!');return;endswitch Nb_fcase 'f'f=inline('1./(1+25*x.^2)'); a = -1;b = 1;case 'h'f=inline('x./(1+x.^4)'); a = -5; b = 5;case 'g'f=inline('atan(x)'); a = -5; b= 5;endx0 = linspace(a, b, Nd+1); y0 = feval(f, x0);x = a:0.1:b; y = Lagrange(x0, y0, x);fplot(f, [a b], 'co');hold on;plot(x, y, 'b--');xlabel('x'); ylabel('y = f(x) o and y = Ln(x)--');%--------------------------------------------------------------------function y=Lagrange(x0, y0, x);n= length(x0); m=length(x);for i=1:mz=x(i);s=0.0;for k=1:np=1.0;for j=1:nif(j ~= k)p = p*(z - x0(j))/(x0(k) - x0(j));endends = s + p*y0(k);endy(i) = s;end实验结果分析(1)增大分点n=2,3,…时,拉格朗日插值函数曲线如图所示。
Runge现象的研究

[ ] =a a0 , a1,, an T ∈ Rn+1
1
=V
1
x0 x1
x0n x1n
∈
R ( n +1)×( n +1)
1
xn
xnn
[ ] =y y0 , y1,, yn T ∈ Rn+1
DOI: 10.12677/aam.2019.88175
Received: August 6th, 2019; accepted: August 21st, 2019; published: August 28th, 2019
Abstract
Firstly, this paper explains the Runge phenomenon generated by high-order polynomial interpolation, and proves that the interpolation polynomial divergence is obtained by calculating the systematic error. Secondly, taking the Runge function, inverse trigonometric function and fractional function as examples, the interpolation polynomial of the function is obtained by using the equally spaced Newton interpolation, and then the interpolation residual function expression is obtained, and then the midpoint of adjacent two nodes is calculated. The error at the location determines that the above three functions have generated the Runge phenomenon. Thirdly, the three algorithms of Chebyshev node, piecewise linear interpolation and cubic spline interpolation are introduced and verified, which can avoid the Runge phenomenon. Finally, the approximation performance index is proposed, and based on the optimal polynomial construction coefficient and order double determination method, the algorithm has excellent function approximation effect while avoiding the Runge phenomenon.
数值分析实验报告

天津工业大学数值分析实验报告电子与信息工程学院例题一用Gauss 消去法来解方程组x 1+x 2+x 3=612x 1−3x 2+3x 3=15−18x 1+3x 2−x 3=−15模型:高斯(Gauss )消去法高斯消去法的基本思想是:先逐次消去变量,将方程组化成同解的上三角形方程组,此过程成为消元过程。
然后按方程相反顺序求解上三角方程组,得到原方程组的解,此过程称为回代过程。
这种方法称为Gauss 消去法。
将方程组改成如下形式a 11 1x 1+a 12 1x 2+······+a 1n 1xn =b 11a 21 1 x 1+a 22 1 x 2+······+a 2n 1 xn =b 2 1 : ∶ ∶ ∶ : ∶ ∶ ∶ a n 1 1x 1+a n 2 1 x 2+······+a nn 1xn =b n1 (2-1) 消元过程:第一步:设a 11 1≠0,记l i 1=a i 1/a 11 1(i =2,3,······,n ),方程中第i 个方程减去第一个方程乘以l i 1,完成第一次消元。
将上述方程式可以改写为a 111x 1+a 12 1x 2+······+a 1n 1xn =b 1 1a 22 2 x 2+······+a 2n 2 xn =b 2 2 ∶ ∶ ∶ ∶ ∶ ∶ a n 22 x 2+······+a nn 2 xn =b n 2(2-2) 其中a ij (2)=a ij (1)−l i 1a 1j (1),b i (2)=b i(1)−l i 1b 1 1(i ,j =2,3·········,n )。
数值分析实验报告--实验2--插值法

1 / 21数值分析实验二:插值法1 多项式插值的震荡现象1.1 问题描述考虑一个固定的区间上用插值逼近一个函数。
显然拉格朗日插值中使用的节点越多,插值多项式的次数就越高。
我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。
龙格(Runge )给出一个例子是极著名并富有启发性的。
设区间[-1,1]上函数21()125f x x=+ (1)考虑区间[-1,1]的一个等距划分,分点为n i nix i ,,2,1,0,21 =+-= 则拉格朗日插值多项式为201()()125nn ii iL x l x x ==+∑(2)其中的(),0,1,2,,i l x i n =是n 次拉格朗日插值基函数。
实验要求:(1) 选择不断增大的分点数目n=2, 3 …. ,画出原函数f(x)及插值多项式函数()n L x 在[-1,1]上的图像,比较并分析实验结果。
(2) 选择其他的函数,例如定义在区间[-5,5]上的函数x x g xxx h arctan )(,1)(4=+=重复上述的实验看其结果如何。
(3) 区间[a,b]上切比雪夫点的定义为 (21)cos ,1,2,,1222(1)k b a b ak x k n n π⎛⎫+--=+=+ ⎪+⎝⎭(3)以121,,n x x x +为插值节点构造上述各函数的拉格朗日插值多项式,比较其结果,试分析2 / 21原因。
1.2 算法设计使用Matlab 函数进行实验, 在理解了插值法的基础上,根据拉格朗日插值多项式编写Matlab 脚本,其中把拉格朗日插值部分单独编写为f_lagrange.m 函数,方便调用。
1.3 实验结果1.3.1 f(x)在[-1,1]上的拉格朗日插值函数依次取n=2、3、4、5、6、7、10、15、20,画出原函数和拉格朗日插值函数的图像,如图1所示。
Matlab 脚本文件为Experiment2_1_1fx.m 。
可以看出,当n 较小时,拉格朗日多项式插值的函数图像随着次数n 的增加而更加接近于f(x),即插值效果越来越好。
数值分析Runge现象计算实验

数值分析实验报告(02)一、实验目的通过上机绘制Runge 函数图像,理解高次插值的病态性质。
二、实验内容在区间[-1,1]上分别取n=10,n=20用两组等距节点对龙格(Runge)函数21()125f x x =+作多项式插值,对每个n 值分别画出()f x 和插值函数的图形。
三、编程思路(相关背景知识、算法步骤、流程图、伪代码)四、程序代码(Matlab 或C 语言的程序代码)function yt=Untitled8(x,y,xt)%UNTITLED5 ´Ë´¦ÏÔʾÓйش˺¯ÊýµÄÕªÒª% ´Ë´¦ÏÔʾÏêϸ˵Ã÷n=length(x);ny=length(y);if n~=nyerror('²åÖµ½ÚµãxÓ뺯ÊýÖµy²»Ò»ÖÂ');endm=length(xt);yt=zeros(1,m);for k=1:nlk=ones(1,m);for j=1:nif j~=klk=lk.*(xt-x(j))/(x(k)-x(j));endend ;yt=yt+y(k)*lk;endn=input('n=');x=linspace(-1,1,n);y=1./(1+25.*x.^2);xf=linspace(-1,1,100);yf=1./(1+25.*xf.^2)xl=xf;yl=Untitled8(x,y,xf);plot(xf,yf,'-b',xl,yl,'-r')五、数值结果及分析(数值运行结果及对结果的分析)当n=10时当n=20六、实验体会(计算中出现的问题,解决方法,实验体会)出现符号错误,代码函数变量不明重新输入,查询错误,找到并改正编码需要认真仔细,一定要头脑清晰,避免出现一些低级错误。
数值分析实验报告--Runge现象的产生和克服

数值分析实验报告(四)题目:Runge现象的产生和克服学院:机电工程学院(二专业)专业:机械设计制造及其自动化班级:1008108班姓名:***学号:**********号Runge现象的产生和克服摘要:对于多项式插值运算,随着插值阶数的逐渐增多,如果带入离散点过于密集,使得定义域中的“边缘区域”,没有有效的点,将导致插值函数的边缘区域大幅度的偏离函数的真值,该现象称之为“Runge现象”。
0 前言(目的与意义):了解Runge现象,体会插值运算的不准确性,以及其差值带来的误差甚至是错误。
1 数学背景:插值运算的误差公式:|w n (x)||R n (x)|<M n+1(n+1)!M n+1=max{f(n+1)(x i)}于是,如果函数的n+1阶导数一旦很大,则会出现函数的误差很大的情况。
2 程序及代码:(1)lagrange多项式插值函数syms f x p dp lx L;f=1/(1+25*x^2);N=input('请输入插值节点数N=');xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);syms x;p=p*(x-xx(i));enddp=diff(p);for j=1:(N+1)x=xx(j);k=eval(dp);syms x;lx=p/((x-xx(j))*k);L=L+lx*ff(j);endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);S(i)=eval(L);fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onezplot(L,[-1,1])hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off(2)分段线性插值函数syms f x p lx;f=1/(1+25*x^2);N=input('请输入插值节点数N=');xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);endsyms xfor i=1:Nfor j=1:(N+1)if j==ilx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1)); else if j==i+1lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i)); elselx(i,j)=0;endendendendp=lx*ff';aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(p(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(p(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off(3):三转角插值法函数syms f x df s s1 s2 s3 s4;f=1/(1+25*x^2);df=diff(f);N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);dff(i)=eval(df);endsyms xfor i=1:Ns1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^2*(h+2*(xx(i+1)-x))*ff(i+1)/h^3; s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2;s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2;s(i)=s1+s2+s3+s4;endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off(4).三弯矩插值法函数:syms f x ddf s;f=1/(1+25*x^2);ddf=diff(diff(f));N=input('请输入插值节点数N=');h=2/N;xx=-1:2/N:1;p=1; L=0;ff=zeros(1,length(xx));for i=1:(N+1)x=xx(i);ff(i)=eval(f);ddff(i)=eval(ddf);endsyms xfor i=1:NA=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6;B=ff(i)-h^2*ddff(i)/6;s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3*ddff(i+1)/(6*h)+A*(x-xx(i))+B; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];for i=1:length(aa)x=aa(i);for j=1:N+1if x<xx(j)breakendendS(i)=eval(s(j-1));fff(i)=eval(f);ende=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2;ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e)ezplot(f,[-1,1])hold onxxx=(-1:0.01:1);for i=1:length(xxx)x=xxx(i);for j=1:N+1if x<xx(j)breakendendSS(i)=eval(s(j-1));endplot(xxx,SS,'r')hold onplot(xx,ff,'*')hold onplot(aa,S,'o')hold off3 总结与评价:函数的Runge现象可以通过三转角插值和三弯矩插值来解决,而且对于三转角和三弯矩插值来说,带入的数据越多,其插值效果越好4 实验结果:图1:观察Runge现象图2:分段线性插值图3:三转角插值:图4:三弯矩插值:。
高等数值分析插值程序题Runge现象

⾼等数值分析插值程序题Runge现象插值程序题1.对Runge函数RR(xx)=1/(1+25xx2)在区间[-1,1]做下列插值逼近,并和RR(xx)的图像进⾏⽐较,并对结果进⾏分析。
(1)等距节点xx ii=?1+ii?,?=0.1,0≤?≤20,20次netown插值多项式图像;(2)节点xx ii=cos?2ii+142ππ?,(i=0,1,2,…,20),20次Lagrange插值多项式的图像;(3)等距节点xx ii=?1+ii?,?=0.1,0≤?≤20,20次分段线性插值函数图像;(4)等距节点xx ii=? 1+ii?,?=0.1,0≤?≤20,20次三次样条插值函数的图像。
解:(1)20次等距节点netown插值多项式和R(xx)的图像⽐较图如下所⽰(求值点之间的间隔为0.0001,以下相同):从图像可以看出,在插值区间中部netown插值多项式与原Runge函数符合得较好;但在插值区间的两端两者的差别很⼤(netown在区间[-1,-0.9]的最⼩值为-59.7819),此时的插值余项不满⾜要求,因此⽤等距20次netown插值多项式来对Runge 函数在区间[-1,1]做插值逼近并不合适,会出现明显的Runge现象。
(2)20次⾮等距节点Lagrange插值多项式(切⽐雪夫多项式零点插值)和R(xx)的图像⽐较图如上所⽰。
此时插值的节点并不等距,插值节点两边密,中间疏,虽然此时Lagrange插值多项式也是20次,但相⽐等距netown插值,⾮等距Lagrange插值曲线与原函数吻合得很好,没有出现明显的Runge现象,两端⽐较密的插值节点较好地抑制了Runge现象。
为了⽐较节点选取对⾼次插值结果的影响,⽤20次等距Lagrange插值也原函数在区间[-1,1]进⾏了插值,其与原函数图像⽐较如下:其图像与(1)中netown插值⼏乎⼀样,因此对⾼次插值多项式,插值时适当的选取插值节点,能有效的抑制Runge现象。
数值分析实验报告 课后答案_【khdaw_lxywyl】

包含工大硕士生数值分析课上机试验所有试题及答案 实验一:非线性方程求解 程序1:二分法: syms f x;f=input('请输入f(x)=');A=input('请输入根的估计范围[a,b]='); e=input('请输入根的误差限e='); while (A(2)-A(1))>e c=(A(1)+A(2))/2; x=A(1); f1=eval(f); x=c;f2=eval(f); if (f1*f2)>0 A(1)=c; elseA(2)=c; end endc=(A(1)+A(2))/2;fprintf('c=%.6f\na=%.6f\nb=%.6f\n',c,A)用二分法计算方程:1.请输入f(x)=sin(x)-x^2/2请输入根的估计范围[a,b]=[1,2] 请输入根的误差限e=0.5e-005 c=1.404413 a=1.404411 b=1.4044152.请输入f(x)=x^3-x-1请输入根的估计范围[a,b]=[1,1.5] 请输入根的误差限e=0.5e-005 c=1.324717 a=1.324715 b=1.324718程序2:newton 法: syms f x;f=input('请输入f(x)=');w ww .k hd aw .c o m课后答案网df=diff(f);x0=input('请输入迭代初值x0='); e1=input('请输入奇异判断e1='); e2=input('请输入根的误差限e2='); N=input('请输入迭代次数限N='); k=1;while (k<N) x=x0; if abs(eval(f))<e1fprintf('奇异!\nx=%.6f\n 迭代次数为:%d\n',x0,k) break elsex1=x0-eval(f)/eval(df); if abs(x1-x0)<e2fprintf('x=%.6f\n 迭代次数为:%d\n',x1,k) break elsex0=x1; k=k+1; end end end if k>=Nfprintf('失败\n') end用newton 法计算方程: 1.请输入f(x)=x*exp(x)-1请输入迭代初值x0=0.5请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.567143 迭代次数为:42.请输入f(x)=x^3-x-1请输入迭代初值x0=1请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10w ww .k hd aw .c o m课后答案网x=1.324718 迭代次数为:53.1:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.45 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:43.2:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.65 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:93.3:请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 x=0.500000 迭代次数为:4程序3:改进的newton 法: syms f x;f=input('请输入f(x)='); df=diff(f);x0=input('请输入迭代初值x0='); e1=input('请输入奇异判断e1='); e2=input('请输入根的误差限e2='); N=input('请输入迭代次数限N='); k=1;while (k<N) x=x0; if abs(eval(f))<e1fprintf('奇异!\nx=%.6f\n 迭代次数为:%d\n',x0,k) break elsew ww .k hd aw .c o m课后答案网x1=x0-2*eval(f)/eval(df); if abs(x1-x0)<e2fprintf('x=%.6f\n 迭代次数为:%d\n',x1,k) break elsex0=x1; k=k+1; end end end if k>=Nfprintf('失败\n') end用改进的newton 法计算方程: 1.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=10 失败2.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=20 失败3.请输入f(x)=(x-1)^2*(2*x-1)请输入迭代初值x0=0.55 请输入奇异判断e1=0.1e-010 请输入根的误差限e2=0.5e-005 请输入迭代次数限N=100 失败实验二:Gauss 列主元消去法 程序1:Gauss 列主元消去法A=input('请输入线性方程组的增广矩阵A='); n=length(A)-1; x=zeros(n,1);w ww .k hd aw .c o m课后答案网aa=zeros(n,1); for j=1:n for i=1:(n+1)AA(j,i)=abs(A(j,i)); end endfor k=1:(n-1) for i=k:naa(i-(k-1))=AA(i,k); end for i=k:nif AA(i,k)==max(aa) break end end if AA(i,k)==0 breakfprintf('方程组系数矩阵奇异\n'); else for j=k:(n+1) jh=A(i,j); A(i,j)=A(k,j); A(k,j)=jh; end endfenzi=A(k,k); for j=k:(n+1)A(k,j)=A(k,j)/fenzi; end for p=(k+1):n jj=A(p,k); for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j); end end endif k==(n-1)x(n)=A(n,(n+1))/A(n,n); for i=(n-1):(-1):1w ww .k hd aw .c o m课后答案网he=0; for j=(i+1):nhe=he+A(i,j)*x(j); endx(i)=A(i,(n+1))-he; end end x用Gauss 列主元消去法解方程组:1.请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5.643,3]x =-0.4653 -0.0700 0.38002.请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.9464 0.6071 -0.14293.请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0.20000.7000程序2:不选主元的高斯消去法A=input('请输入线性方程组的增广矩阵A='); n=length(A)-1; x=zeros(n,1); for k=1:(n-1) if A(k,k)==0 breakfprintf('方程组不能用普通的高斯消去法解\n'); elsefenzi=A(k,k); for j=k:(n+1)A(k,j)=A(k,j)/fenzi; endw ww .k hd aw .c o m课后答案网for p=(k+1):n jj=A(p,k); for j=k:(n+1)A(p,j)=A(p,j)-jj*A(k,j); end endx(n)=A(n,(n+1))/A(n,n); for i=(n-1):(-1):1 he=0;for j=(i+1):nhe=he+A(i,j)*x(j); endx(i)=A(i,(n+1))-he; end end end x用不选主元的Gauss 消去法解方程组:1.请输入线性方程组的增广矩阵A=[4,-2,4,10;-2,17,10,3;-4,10,9,-7];x =2.9464 0.6071 -0.14292.请输入线性方程组的增广矩阵A=[1e-008,2,3,1;-1,3.172,4.623,2;-2,1.072,5.643,3];x =-0.4653 -0.07000.38003.请输入线性方程组的增广矩阵A=[0.3e-020,1,0.7;1,1,0.9]x =0 0.7000实验三:Runge 现象的产生和克服 程序1:lagrange 多项式插值 syms f x p dp lx L; f=1/(1+25*x^2);N=input('请输入插值节点数N=');w ww .k hd aw .c o m课后答案网xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); syms x;p=p*(x-xx(i)); enddp=diff(p); for j=1:(N+1) x=xx(j); k=eval(dp); syms x;lx=p/((x-xx(j))*k); L=L+lx*ff(j); endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i);S(i)=eval(L); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onezplot(L,[-1,1]) hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序2:分段线性插值 syms f x p lx; f=1/(1+25*x^2);N=input('请输入插值节点数N='); xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); end syms xw ww .k hd aw .c o m课后答案网for i=1:N for j=1:(N+1) if j==ilx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1)); else if j==i+1lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i)); elselx(i,j)=0; end end end end p=lx*ff';aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(p(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i); for j=1:N+1 if x<xx(j) break end endSS(i)=eval(p(j-1)); endplot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序3:三转角插值法w ww .k hd aw .c o m课后答案网syms f x df s s1 s2 s3 s4; f=1/(1+25*x^2); df=diff(f);N=input('请输入插值节点数N='); h=2/N;xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f); dff(i)=eval(df); end syms x for i=1:Ns1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^3*(h+2*(xx(i+1)-x))*ff(i+1)/h^3; s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2; s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2; s(i)=s1+s2+s3+s4; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(s(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i); for j=1:N+1 if x<xx(j) break end endSS(i)=eval(s(j-1)); endw ww .k hd aw .c o m课后答案网plot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off程序4:三弯矩插值法: syms f x ddf s; f=1/(1+25*x^2); ddf=diff(diff(f));N=input('请输入插值节点数N='); h=2/N;xx=-1:2/N:1; p=1; L=0;ff=zeros(1,length(xx)); for i=1:(N+1) x=xx(i); ff(i)=eval(f);ddff(i)=eval(ddf); end syms x for i=1:NA=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6; B=ff(i)-h^2*ddff(i)/6;s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3*ddff(i+1)/(6*h)+A*(x-xx(i))+B; endaa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa) x=aa(i); for j=1:N+1 if x<xx(j) break end endS(i)=eval(s(j-1)); fff(i)=eval(f); end e=0;for i=1:length(aa)e=e+(S(i)-fff(i))^2; ende=sqrt(e/(20*21));fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1]) hold onxxx=(-1:0.01:1); for i=1:length(xxx) x=xxx(i);w ww .k hd aw .c o m课后答案网for j=1:N+1 if x<xx(j) break end endSS(i)=eval(s(j-1)); endplot(xxx,SS,'r') hold onplot(xx,ff,'*') hold on plot(aa,S,'o') hold off图1:观察Runge 现象图2:分段线性插值w ww .k hd aw .c o m课后答案网图3:三转角插值:w ww .k hd aw .c o m课后答案网图4:三弯矩插值:w ww .k hd aw .c o m课后答案网实验四:多项式最小二乘法程序1:要求给出插值次数的多项式最小二乘法 syms x f;xx=input('请输入插值节点 as [x1,x2...]\n'); ff=input('请输入插值节点处对应的函数值 as [f1,f2...]\n'); m=input('请输入要求的插值次数m='); n=length(xx); for i=1:(m+1) syms fai x; fai=x^(i-1); for j=1:n x=xx(j);H(i,j)=eval(fai); end endA=ff*(H)'*inv(H*(H)'); syms x; f=0; for i=1:(m+1)w ww .k hd aw .c o m课后答案网f=f+A(i)*x^(i-1); endplot(xx,ff,'*') hold onezplot(f,[xx(1),xx(n)])用此程序作出课本上的两道题: 1. 请输入插值节点 as [x1,x2...] [0 0.9 1.9 3 3.9 5.0]请输入插值节点处对应的函数值 as [f1,f2...] [0 10 30 50 80 110]请输入要求的插值次数m=2 图:2.请输入插值节点 as [x1,x2...] [0 0.9 1.9 33.9 5.0]请输入插值节点处对应的函数值 as [f1,f2...] [19.0 32.3 49.0 73.3 97.8] 请输入要求的插值次数m=2 图:w ww .k hd aw .c o m课后答案网程序2:自适应多项式最小二乘法 syms x f nihef nihe;xx=input('请输入插值节点 as [x1,x2...]\n'); ff=input('请输入插值节点处对应的函数值 as [f1,f2...]\n'); n=length(xx); for m=1:(n-1) for i=1:(m+1) syms fai x; fai=x^(i-1); for j=1:nx=xx(j);H(i,j)=eval(fai); end endA=ff*(H)'*inv(H*(H)'); syms x f; f=0; for i=1:(m+1)f=f+A(i)*x^(i-1);w ww .k hd aw .c o m课后答案网endnihef(m)=f; for i=1:n x=xx(i);niheff(i)=eval(f); ee(i)=ff(i)-niheff(i); end e(m)=0; for i=1:(n-1)e(m)=(ee(i))^2+e(m); ende(m)=sqrt(e(m)/(n*(n-1))); eee(m)=1/e(m); endfor k=1:n if eee(k)==max(eee); break end end syms x;nihe=nihef(k); emcino=e(k); plot(xx,ff,'*') hold onezplot(nihe,[xx(1),xx(n)])fprintf('插值误差为e=%.6f',emcino) 用此程序作实验中要求的题目: 3.请输入插值节点 as [x1,x2...] [3 4 5 6 7 8 9]请输入插值节点处对应的函数值 as [f1,f2...] [2.01 2.98 3.50 5.02 5.47 6.02 7.05] 插值误差为e=0.000010 图:w ww .k hd aw .c o m课后答案网实验五:龙贝格积分法 程序:龙贝格积分: syms f x;f=input('请输入积分函数f='); A=input('请输入积分区间[a,b]='); e=input('请输入误差限e='); x=A(1); fa=eval(f); x=A(2); fb=eval(f);T(1)=(A(2)-A(1))*(fa+fb)/2; m=1;x=(A(1)+A(2));t=T(1)/2+(A(2)-A(1))*eval(f)/2; while abs(t-T(1))>e t=T(1); new=0; for i=1:(2^m)x=A(1)+(2*i-1)*(A(2)-A(1))/(2^(m+1));w ww .k hd aw .c o m课后答案网new=new+eval(f); endT(m+1)=T(m)/2+(A(2)-A(1))*new/(2^(m+1)); for i=m:(-1):1 L(m,i)=T(i); end for p=m:(-1):1T(p)=((4^(m+1-p))*T(p+1)-T(p))/(4^(m+1-p)-1); endm=m+1; endfprintf('数值积分结果为T(1)=%.8f\n',T(1)); fprintf('经过了%d 次迭代\n',m);用龙贝格积分法计算积分的近似值: 1.1请输入积分函数f=x^3请输入积分区间[a,b]=[6,100] 请输入误差限e=1000数值积分结果为T(1)=25000289.75465907 经过了15次迭代1.2请输入积分函数f=x^3请输入积分区间[a,b]=[6,100] 请输入误差限e=500数值积分结果为T(1)=24999982.87732918 经过了16次迭代2.1请输入积分函数f=sin(x)/x请输入积分区间[a,b]=[0.1e-010,1] 请输入误差限e=0.1e-004数值积分结果为T(1)=0.94607740 经过了12次迭代2.2请输入积分函数f=sin(x)/x请输入积分区间[a,b]=[0.1e-010,1] 请输入误差限e=0.1e-005数值积分结果为T(1)=0.94608236 经过了15次迭代w ww .k hd aw .c o m课后答案网3.1请输入积分函数f=sin(x^2) 请输入积分区间[a,b]=[0 1] 请输入误差限e=0.0001数值积分结果为T(1)=0.31031986 经过了11次迭代3.2请输入积分函数f=sin(x^2) 请输入积分区间[a,b]=[0,1] 请输入误差限e=0.1e-005数值积分结果为T(1)=0.31026911 经过了17次迭代实验六:常微分方程初值问题的数值解法程序1:R-K 和 修正Adams 预测-校正法的组合 syms f x y;f=input('请输入f(x,y)=');jx=input('请输入计算区间[a,b]='); yy(1)=input('请输入初值y0='); h=0.1;xx=jx(1):0.1:jx(2); for n=1:3x=xx(n); y=yy(n); k1=eval(f); x=xx(n)+h/2; y=yy(n)+k1*h/2; k2=eval(f);y=yy(n)+k2*h/2; k3=eval(f); x=xx(n+1); y=yy(n)+h*k3; k4=eval(f);yy(n+1)=yy(n)+(k1+2*k2+2*k3+k4)*h/6; endc(4)=yy(4); p(4)=yy(4); for i=1:4x=xx(i); y=yy(i); ff(i)=eval(f); endfor n=4:(length(xx)-1)p(n+1)=yy(n)+(55*ff(n)-59*ff(n-1)+37*ff(n-2)-9*ff(n-3))*h/24; m(n+1)=p(n+1)+251*(yy(n)-p(n))/270; x=xx(n+1); y=m(n+1);w ww .k hd aw .c o m课后答案网fff(n+1)=eval(f);c(n+1)=yy(n)+(9*fff(n+1)+19*ff(n)-5*ff(n-1)+ff(n-2))*h/24; yy(n+1)=c(n+1)-19*(c(n+1)-p(n+1))/270; y=yy(n+1); ff(n+1)=eval(f); endplot(xx,yy,'*') hold on程序2:Runge-Kutta 法 syms f x y;f=input('请输入f(x,y)=');jx=input('请输入计算区间[a,b]='); yy(1)=input('请输入初值y0='); h=0.1;xx=jx(1):0.1:jx(2); for n=1:(length(xx)-1) x=xx(n); y=yy(n); k1=eval(f); x=xx(n)+h/2; y=yy(n)+k1*h/2; k2=eval(f);y=yy(n)+k2*h/2; k3=eval(f); x=xx(n+1); y=yy(n)+h*k3; k4=eval(f);yy(n+1)=yy(n)+(k1+2*k2+2*k3+k4)*h/6; endplot(xx,yy,'o')程序3:第一题的求解析解的程序 syms sv x jx=[-1,0];sv=dsolve('Dy=(x^2-y^2)','y(-1)=0','x'); xxx=jx(1):0.01:jx(2); for n=1:length(xxx) x=xxx(n);yyy(n)=eval(sv); endplot(xxx,yyy)w ww .k hd aw .c o m课后答案网程序4:第二题的求解析解的程序 syms sv x jx=[0,1.5];sv=dsolve('Dy=(y-2*x/y)','y(0)=1','x'); xxx=jx(1):0.01:jx(2); for n=1:length(xxx) x=xxx(n);yyy(n)=eval(sv); endplot(xxx,yyy)图1:第一题的计算图形结果图2:第二题的计算图形结果:w ww .k hd aw .c o m课后答案网w ww .k hd aw .c o m课后答案网。
非线性方程求解数值分析上机实验报告

实验报告一题目:非线性方程求解摘要:非线性方程的解析解通常很难给出,因此线性方程的数值解法就尤为重要。
本实验采用两种常见的求解方法二分法和Newton法及改进的Newton法。
前言:(目的和意义)掌握二分法与Newton法的基本原理和应用。
数学原理:对于一个非线性方程的数值解法很多。
在此介绍两种最常见的方法:二分法和Newton 法。
对于二分法,其数学实质就是说对于给定的待求解的方程f(x),其在[a,b]上连续,f(a)f(b)<0,且f(x)在[a,b]内仅有一个实根x*,取区间中点c,若,则c恰为其根,否则根据f(a)f(c)<0是否成立判断根在区间[a,c]和[c,b]中的哪一个,从而得出新区间,仍称为[a,b]。
重复运行计算,直至满足精度为止。
这就是二分法的计算思想。
Newton法通常预先要给出一个猜测初值x0,然后根据其迭代公式产生逼近解x*的迭代数列{x k},这就是Newton法的思想。
当x0接近x*时收敛很快,但是当x0选择不好时,可能会发散,因此初值的选取很重要。
另外,若将该迭代公式改进为其中r为要求的方程的根的重数,这就是改进的Newton法,当求解已知重数的方程的根时,在同种条件下其收敛速度要比Newton法快的多。
程序设计:本实验采用Matlab的M文件编写。
其中待求解的方程写成function的方式,如下function y=f(x);y=-x*x-sin(x);写成如上形式即可,下面给出主程序。
二分法源程序:clear%%%给定求解区间b=1.5;a=0;%%%误差R=1;k=0;%迭代次数初值while (R>5e-6) ;c=(a+b)/2;if f12(a)*f12(c)>0;a=c;elseb=c;endR=b-a;%求出误差k=k+1;endx=c%给出解Newton法及改进的Newton法源程序:clear%%%% 输入函数f=input('请输入需要求解函数>>','s')%%%求解f(x)的导数df=diff(f);%%%改进常数或重根数miu=2;%%%初始值x0x0=input('input initial value x0>>');k=0;%迭代次数max=100;%最大迭代次数R=eval(subs(f,'x0','x'));%求解f(x0),以确定初值x0时否就是解while (abs(R)>1e-8)x1=x0-miu*eval(subs(f,'x0','x'))/eval(subs(df,'x0','x'));R=x1-x0;x0=x1;k=k+1;if (eval(subs(f,'x0','x'))<1e-10);breakendif k>max;%如果迭代次数大于给定值,认为迭代不收敛,重新输入初值ss=input('maybe result is error,choose a new x0,y/n?>>','s');if strcmp(ss,'y')x0=input('input initial value x0>>');k=0;elsebreakendendendk;%给出迭代次数x=x0;%给出解结果分析和讨论:1.用二分法计算方程在[1,2]内的根。
数值分析实验报告2——Runge现象
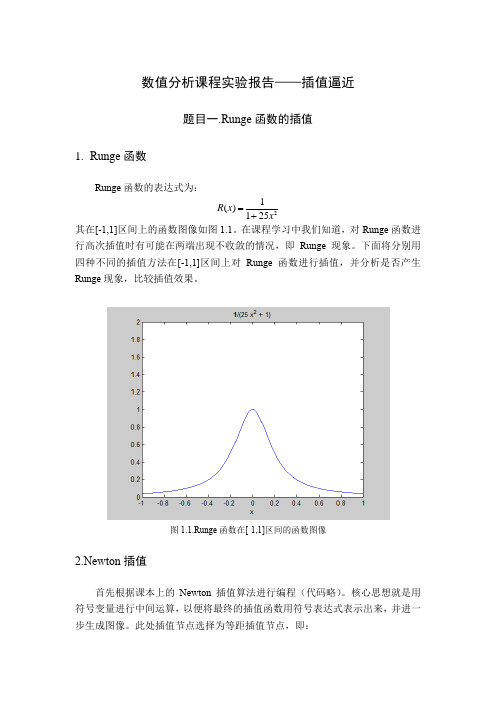
数值分析课程实验报告——插值逼近题目一.Runge 函数的插值1. Runge 函数Runge 函数的表达式为:21()125R x x =+ 其在[-1,1]区间上的函数图像如图1.1。
在课程学习中我们知道,对Runge 函数进行高次插值时有可能在两端出现不收敛的情况,即Runge 现象。
下面将分别用四种不同的插值方法在[-1,1]区间上对Runge 函数进行插值,并分析是否产生Runge 现象,比较插值效果。
图1.1.Runge 函数在[-1,1]区间的函数图像2.Newton 插值首先根据课本上的Newton 插值算法进行编程(代码略)。
核心思想就是用符号变量进行中间运算,以便将最终的插值函数用符号表达式表示出来,并进一步生成图像。
此处插值节点选择为等距插值节点,即:0.1(0,1,2,,)i x ih i =-+= (20)其中h=0.1。
插值曲线与原曲线的对比如图1.2(蓝色为原曲线,红色为插值曲线)。
从图中看出,在区间中部,二者吻合较好;但在区间两端二者则产生了明显偏差,甚至可以达到一个非常大的数值(e20量级)。
因此,在等距节点的20次Newton 插值下,产生了明显的Runge 现象。
图1.2.Newton 插值曲线与原曲线对比3. Lagrange 插值此处同样是根据Lagrange 插值的具体算法进行编程。
但插值节点不再是等距分布,而是如下形式:21cos()(0,1,2,,)42i i x i π+==…20 插值曲线与原曲线的对比如图1.3(蓝色为原曲线,红色为插值曲线)。
从图中看出,插值曲线与原曲线吻合的很好,没有产生明显的Runge 现象。
对比产生了明显Runge 现象的20次Newton 插值,Lagrange 插值的最高次数虽然也是20,但由于此处的插值节点不是等距分布的(事实上,此处采用的插值节点正是Chebyshev 多项式的零点),而是中间疏两边密,因此两侧较密的节点很好地抑制了Runge 现象。
数值分析实验报告Hermite插值法、Runge现象,比较Language插值、分段线性插值、分段三次Hermie插值

山东师范大学数学科学学院实验报告x 0.1 0.5 1 1.5 2 2.5 3y 0.95 0.84 0.86 1.06 1.5 0.72 1.9y' 1 1.5 2 2.5 3 3.5 4求质点在时刻1.8时的速度,并画出插值多项式的图像。
1)运用Hermite插值法画出图像,如图4-1,并求质点在时刻1.8时的速度。
>>clear>>clc>>X=[0.1 0.5 1 1.5 2 2.5 3;0.95 0.84 0.86 1.06 1.5 0.72 1.9;1 1.5 2 2.5 3 3.5 4];>> x=0.1:0.01:3;>> H=Hermite1(X,x);>> plot(x,H)>> hold on>> plot(X(1,:),X(2,:),'r*')>> H1_8=Hermite(X,1.8);>> plot(1.8,H1_8,'go')>> legend('插值图像','原始点','目标点');图4-1二、验证高次插值的Runge现象问题分析和算法设计(一)Language插值代码function [Ln] =Lagrange(X,x)%请输入2*n+1矩阵X,X中第一行每个元素都是插值节点,X中第二行每个元素都是插值节点对应的函数值;%第二章P24例一拉格朗日插值n=size(X,2);d=0;for m=1:1:nif x==X(1,m);d=m;breakendend运行结果和总结 运行结果 例:给定函数55,11)(2≤≤-+=x xx f ; (1) 验证表2-10的误差结果(高次插值的Runge 现象);(2) 以0.1为步长分别进行Language 插值、分段线性插值、分段三次Hermite插值,画出三种插值函数以及f(x)的图像,比较三种插值结果。
实验2:range现象的观察

令狐烈 一, 实验目的
1. 观察和感受 Runge 现象,明白盲目的采用高阶的插值多项式是不妥当的。 2. 从实验示例中感受 Faber 定理和插值法收敛定理。 3. 感受分段插值在长距离上插值的优越性。
二, 实验原理
对于区间[a,b]上的 f(x), 我们希望其多项式插值随着插值次数的增加, P(x)能够更加快速 的收敛于 f(x)。对于有些函数,这个期望可以实现。但是有些函数却是例外。 1901 年 Runge 给出这样的一个例子: 1 1 + 25������ 2 定义在[-5,5]上。如果 P(x)是由这个函数利用[-5,5]区间上的等距节点构造的插值多项 式, 那么序列||f-P||∞是无界的。 对于不大的 n, 我们就可以看到多项式 P (x) 的剧烈震荡。 这就是所谓的 Runge 现象。 对于 Range 现象,以下两个定理可以帮助我么进行理解: Faber 定理:对于任意给定的节点组: F x = ������ ≤ ������������ ������ < ������1 ������ < ⋯ … < ������������ ������ ≤ ������ (������ ≥ ������) 中可以在[a,b]上找到一个连续函数 f,使得 f 在这一组节点上的插值多项式不能一致收 敛于 f。 插值法收敛定理:若 f 是[a,b]上的连续函数,则总可以找到一组插值节点 ������ ≤ ������������ ������ < ������1 ������ < ⋯ … < ������������ ������ ≤ ������ (������ ≥ ������) 使得 f 在这组插值节点上的差值多项式 P 一致收敛与 f,即 ������������������ ������ − ������ ∞ = ������ Range 现象让人们明白, 盲目的采用高阶的插值多项式是不妥当的。 为此应当采用分段插值。
数值实验——观看Lagrange插值的Runge现象

数值实验 观看Lagrange 插值的Runge 现象一、 实验目的关于等距Lagrange 插值,当插值节点数太多时,差值多项式并非能收敛到被插函数()f x ,而是在区间两头会产生猛烈振荡的Runge 现象。
本实验的目的确实是验证这种Runge 现象。
二、 实验步骤实验中取插值函数为225()f x a x=+,其中a 是常数。
插值节点去区间[-5,5]的等距节点,关于n 阶插值多项式,步长10h n=,节点为1(1),1,2,...(1)k x x h k k n =+-=+,所取得的差值多项式为1111()()n n in k k i k ii kx x L x f x x x ++==≠-=-∑。
关于n 阶插值多项式,改变插值的阶数,能够取得不同的差值多项式,从而能够观看随阶数转变而产生的Runge 现象。
三、 程序与结果1、 程序、Runge 现象主程序:、Lagrange插值多项式计算程序:、生成多条差值曲线程序:2、计算结果图 1a =时225()1f x x =+的插值结果,其中红色虚线表示的是225()1f x x=+,中间两条没有显现Runge 现象的曲线的阶数自下至上为2和3,其余几条曲线自上而下别离对应于4、8、10阶插值曲线图 2a =时225()2f x x =+的插值结果,其中红色虚线表示的是225()2f x x=+,中间两条没有显现Runge 现象的曲线的阶数自下至上为2和3,其余几条曲线自上而下别离对应于4、8、10阶插值曲线图 3a =时225()3f x x =+的插值结果,其中红色虚线表示的是225()3f x x=+,中间两条没有显现Runge 现象的曲线的阶数自下至上为2和3,其余几条曲线自上而下别离对应于4、8、10阶插值曲线图 8a =时225()8f x x =+的插值结果,其中红色虚线表示的是225()8f x x=+图 15a =时225()15f x x =+的插值结果,其中红色虚线表示的是225()15f x x =+图 100a =时225()100f x x =+的插值结果,其中红色虚线表示被插函数四、 结果分析一、从图、图能够明显看到,1n =和2n =时,Runge 现象很明显,在边界上振荡很猛烈。
数学实验“欧拉数值算法,Runge-Kutta数值算法”实验报告(内含matlab程序)
西京学院数学软件实验任务书实验二十四实验报告一、实验名称:欧拉数值算法(显式,隐式,欧拉预估-校正法),Runge-Kutta 数值算法。
二、实验目的:进一步熟悉欧拉数值算法(显式,隐式,欧拉预估-校正法),Runge-Kutta 数值算法。
三、实验要求:运用Matlab/C/C++/Java/Maple/Mathematica 等其中一种语言完成程序设计。
四、实验原理:1.欧拉数值算法(显式):微分方程里最简单的方程形式莫过于一阶常微分方程的初值问题,即:0(,)()dy f x y a x b dx y a y ⎧=≤≤⎪⎨⎪=⎩其中a ,b 为常数。
因为其简单但又是求解其他方程的基础,所以发展了许多典型的解法。
所有算法中的f 就是代表上式中(,)f x y ,而y f 表示(,)f x y y ∂∂,x f 表示(,)f x y x∂∂。
简单欧拉法是一种单步递推算法。
简单欧拉法的公式如下所示:1(,)n n n n y y hf x y +=+简单欧拉法的算法过程介绍如下:给出自变量x 的定义域[,]a b ,初始值0y 及步长h 。
对0,1,()/k b a h =-,计算1(,)k k k k y y hf x y +=+2.欧拉数值算法(隐式):隐式欧拉法也叫退欧拉法,隐式欧拉法的公式如下所示:111(,)n n n n y y hf x y +++=+隐式欧拉法是一阶精度的方法,比它精度高的公式是:111[(,)(,)]2n n n n n n h y y f x y f x y +++=++ 隐式欧拉的算法过程介绍如下。
给出自变量x 的定义域[,]a b ,初始值0y 及步长h 。
对0,1,()/k b a h =-,用牛顿法或其他方法求解方111(,)k k k k y y hf x y +++=+得出1k y +。
3.欧拉预估-校正法:改进欧拉法是一种二阶显式求解法,其计算公式如下所示:1[,(,)]22n n n n n n h h y y hf x y f x y +=+++11(,)[(,)(,)]2n n n n n n n n t y hf x y h y y f x y f x t ++=+⎧⎪⎨=++⎪⎩ 4.Runge-Kutta 数值算法:二阶龙格-库塔法有多种形式,除了改进的欧拉法外,还有中点法。
数值分析实验报告

x0[i] = 0.01*i;//采用循环对数组变量x[100]赋值
}
rk_getback(x0, y0, 0.01, -50);//调用R-K函数计算得到每一个x(n)对应的y(n)值
CSeries embro = (CSeries)m_chart.Series(0);//使用画图控件Teechart进行画图
}
for (i = 0; i <= 200; i++)//利用插值多项式计算201个数值用于绘图
{
a1[i] = u + i*0.01;
b1[i] = 1 / (1 + 25 * a1[i] * a1[i]);
y[i] = Lagrange(a1[i], n, a2, b2);
}
m_chart.AddSeries(0);//用teechart绘制插值多项式函数图像
m3 = m.transpose()*y;//计算Y矩阵
m4 = m2*m3;//计算系数矩阵
CSeries serdemo = (CSeries)m_mchart.Series(0);//创建CSeries对象
MatrixXd m5(1, 4),m6(1,1);//创建1*4和1*1的矩阵
int i;
考虑在一个固定的区间上用插值逼近一个函数。显然Lagrange插值中使用的节点越多,插值多项式的次数就越高。我们自然关心插值多项式的次数增加时, 是否也更加靠近被逼近的函数。Runge给出的一个例子是极著名并富有启发性的。设区间[-1,1]上函数
考虑区间[-1,1]的一个等距划分,分点为
则拉格朗日插值多项式为
int i, n =19;
double j = 2.0 / (n ), u = -1.0, v = 1.0;
龙格现象实验报告

教
师
评
语
欢迎您的下载,
资料仅供参考!
致力为企业和个人提供合同协议,策划案计划书,学习资料等等
打造全网一站式需求
x=[-5:0.1:5];
y=lagrange(x0,y0,x);
y1=5./(1+x.^2);
plot(x,y,'--r')
hold on
plot(x,y1,'-b')
hold off
2)取n=10
x0=[-5:1:5];
y0=5./(0.25*0.25+x0.^2);
x=[-5:0.1:5];
y=lagrange(x0,y0,x);
function y=lagrange(x0,y0,x)
n=length(x0);m=length(x);
for i=1:m
z=x(i);
L=0.0;
for j=1:n
T=1.0;
for k=1:n
if k~=j
T=T*(z-x0(k))/(x0(j)-x0(k));
end
end
L=T*y0(j)+L;
x0=[-5:1:5];
y0=5./(1+x0.^2);
x=[-5:0.1:5];
y=lagrange(x0,y0,xБайду номын сангаас;
y1=5./(1+x.^2);
plot(x,y,'--r')
hold on
plot(x,y1,'-b')
hold off
2、a=0.25时,
1)取n=4
微分方程数值解法实验报告-Runge-Kutta格式、三阶Admas

《微分方程数值解法》课程实验报告1 实验内容要求:用经典三级三阶R-K 格式求解微分方程初值问题,并给出误差分析。
2算法描述先用C 的方法写出一个算法动态库,里面封装龙格库塔算法函数采用迭代原理,用递归实现,生成并模块化导出dll,lib 文件,两个文件中均包含了该函数偏移地址,在在源文件中隐式链接该库里的龙格库塔函数,从而得出结果.3 实验数据与实验结果 ⎩⎨⎧=-+-==1|1'0x y x y y1.0)1,0(=∈h x4 程序代码清单:Win32动态库Algorithm.dll 代码: #include <stdio.h> #include <math.h>#define e 2.718281828459045double x[11]={0.0,0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,1.0}; double y[12]={1.0,0}; int x1=0,x2=1; int count=1;void RungeKutta(double h){ double K1,K2,K3; double ExactSolution; double Error; if(count==12){ return; } K1=-y[count-1]+x[count-1]+1; K2=-(y[count-1]+h*K1/3)+(x[count-1]+h*K1/3)+1; K3=-(y[count-1]+2*h*K2/3)+(x[count-1]+2*h/3)+1; y[count]=y[count-1]+h*(K1+3*K3)/4; ExactSolution=x[count-1]+pow(e,-x[count-1]); Error=y[count-1]-ExactSolution; printf("%lf %lf %lf %lf\n",x[count-1],ExactSolution,y[count-1],Error);count++; RungeKutta(h); }模块化导出文件Algorithm.def代码:LIBRARY AlgorithmEXPORTSRungeKutta @1入口函数实现功能代码:#include <stdio.h>#pragma comment(lib,"../lib/Algorithm.lib")int main(){double h;printf("用三级三阶龙贝格库塔方法解微分方程y'=x-y+1,x属于区间(0,1)\n");printf("请输入系数h的值:\n");scanf("%lf",&h);printf("-----------------------------------------------------\nx 精确解 R-k解yn 误差:\n");RungeKutta(h);return 0;}5:运行结果:1 实验内容要求:用三阶Admas 预报修正格式求解差分方程初边值问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数值分析实验报告(四)题目:Runge现象的产生和克服
学院:机电工程学院(二专业)
专业:机械设计制造及其自动化
班级:1008108班
姓名:***
学号:**********号
Runge现象的产生和克服
摘要:对于多项式插值运算,随着插值阶数的逐渐增多,如果带入离散点过于密集,使得定义域中的“边缘区域”,没有有效的点,将导致插值函数的边缘区域大幅度的偏离函数的真值,该现象称之为“Runge现象”。
0 前言(目的与意义):了解Runge现象,体会插值运算的不准确性,以及其差值带来的误差甚至是错误。
1 数学背景:插值运算的误差公式:
|w n (x)|
|R n (x)|<M n+1
(n+1)!
M n+1=max{f(n+1)(x i)}
于是,如果函数的n+1阶导数一旦很大,则会出现函数的误差很大的情况。
2 程序及代码:
(1)lagrange多项式插值函数
syms f x p dp lx L;
f=1/(1+25*x^2);
N=input('请输入插值节点数N=');
xx=-1:2/N:1;
p=1; L=0;
ff=zeros(1,length(xx));
for i=1:(N+1)
x=xx(i);
ff(i)=eval(f);
syms x;
p=p*(x-xx(i));
end
dp=diff(p);
for j=1:(N+1)
x=xx(j);
k=eval(dp);
syms x;
lx=p/((x-xx(j))*k);
L=L+lx*ff(j);
end
aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];
for i=1:length(aa)
x=aa(i);
S(i)=eval(L);
fff(i)=eval(f);
end
e=0;
for i=1:length(aa)
e=e+(S(i)-fff(i))^2;
end
e=sqrt(e/(20*21));
fprintf('插值偏差为e=%.6f\n',e)
ezplot(f,[-1,1])
hold on
ezplot(L,[-1,1])
hold on
plot(xx,ff,'*')
hold on
plot(aa,S,'o')
hold off
(2)分段线性插值函数
syms f x p lx;
f=1/(1+25*x^2);
N=input('请输入插值节点数N=');
xx=-1:2/N:1;
p=1; L=0;
ff=zeros(1,length(xx));
for i=1:(N+1)
x=xx(i);
ff(i)=eval(f);
end
syms x
for i=1:N
for j=1:(N+1)
if j==i
lx(i,j)=(x-xx(i+1))/(xx(i)-xx(i+1)); else if j==i+1
lx(i,j)=(x-xx(i))/(xx(i+1)-xx(i)); else
lx(i,j)=0;
end
end
end
end
p=lx*ff';
aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];
for i=1:length(aa)
x=aa(i);
for j=1:N+1
if x<xx(j)
break
end
end
S(i)=eval(p(j-1));
fff(i)=eval(f);
end
e=0;
for i=1:length(aa)
e=e+(S(i)-fff(i))^2;
end
e=sqrt(e/(20*21));
fprintf('插值偏差为e=%.6f\n',e)
ezplot(f,[-1,1])
hold on
xxx=(-1:0.01:1);
for i=1:length(xxx)
x=xxx(i);
for j=1:N+1
if x<xx(j)
break
end
end
SS(i)=eval(p(j-1));
end
plot(xxx,SS,'r')
hold on
plot(xx,ff,'*')
hold on
plot(aa,S,'o')
hold off
(3):三转角插值法函数
syms f x df s s1 s2 s3 s4;
f=1/(1+25*x^2);
df=diff(f);
N=input('请输入插值节点数N=');
h=2/N;
xx=-1:2/N:1;
p=1; L=0;
ff=zeros(1,length(xx));
for i=1:(N+1)
x=xx(i);
ff(i)=eval(f);
dff(i)=eval(df);
end
syms x
for i=1:N
s1=(x-xx(i+1))^2*(h+2*(x-xx(i)))*ff(i)/h^3; s2=(x-xx(i))^2*(h+2*(xx(i+1)-x))*ff(i+1)/h^3; s3=(x-xx(i+1))^2*(x-xx(i))*dff(i)/h^2;
s4=(x-xx(i))^2*(x-xx(i+1))*dff(i+1)/h^2;
s(i)=s1+s2+s3+s4;
end
aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96]; for i=1:length(aa)
x=aa(i);
for j=1:N+1
if x<xx(j)
break
end
end
S(i)=eval(s(j-1));
fff(i)=eval(f);
end
e=0;
for i=1:length(aa)
e=e+(S(i)-fff(i))^2;
end
e=sqrt(e/(20*21));
fprintf('插值偏差为e=%.6f\n',e) ezplot(f,[-1,1])
hold on
xxx=(-1:0.01:1);
for i=1:length(xxx)
x=xxx(i);
for j=1:N+1
if x<xx(j)
break
end
end
SS(i)=eval(s(j-1));
end
plot(xxx,SS,'r')
hold on
plot(xx,ff,'*')
hold on
plot(aa,S,'o')
hold off
(4).三弯矩插值法函数:
syms f x ddf s;
f=1/(1+25*x^2);
ddf=diff(diff(f));
N=input('请输入插值节点数N=');
h=2/N;
xx=-1:2/N:1;
p=1; L=0;
ff=zeros(1,length(xx));
for i=1:(N+1)
x=xx(i);
ff(i)=eval(f);
ddff(i)=eval(ddf);
end
syms x
for i=1:N
A=(ff(i+1)-ff(i))/h-h*(ddff(i+1)-ddff(i))/6;
B=ff(i)-h^2*ddff(i)/6;
s(i)=(xx(i+1)-x)^3*ddff(i)/(6*h)+(x-xx(i))^3*ddff(i+1)/(6*h)+A*(x-xx(i))+B; end
aa=[-0.96:0.1:-0.06,0,0.06:0.1:0.96];
for i=1:length(aa)
x=aa(i);
for j=1:N+1
if x<xx(j)
break
end
end
S(i)=eval(s(j-1));
fff(i)=eval(f);
end
e=0;
for i=1:length(aa)
e=e+(S(i)-fff(i))^2;
end
e=sqrt(e/(20*21));
fprintf('插值偏差为e=%.6f\n',e)
ezplot(f,[-1,1])
hold on
xxx=(-1:0.01:1);
for i=1:length(xxx)
x=xxx(i);
for j=1:N+1
if x<xx(j)
break
end
end
SS(i)=eval(s(j-1));
end
plot(xxx,SS,'r')
hold on
plot(xx,ff,'*')
hold on
plot(aa,S,'o')
hold off
3 总结与评价:
函数的Runge现象可以通过三转角插值和三弯矩插值来解决,而且对于三转角和三弯矩插值来说,带入的数据越多,其插值效果越好
4 实验结果:
图1:观察Runge现象
图2:分段线性插值
图3:三转角插值:
图4:三弯矩插值:。
