材料热力学第三章-统计热力学基础2016
第3章热力学第二、三定律第8节相变和化学反应的吉布斯自由能变第9节热力学基本关系式解析

第九节 热力学基本关系式
几个函数的定义式 函数间关系的图示式 热力学基本方程 U, H, A, G的一阶偏导数 Maxwell 关系式 Maxwell 关系式的应用
几个函数的定义式
定义式适用于任何热力学平衡态体系,只是在特 定的条件下才有明确的物理意义。
H U pV
H Qp 恒压,不做非体积功
ΔG2=0, ΔG3=Vm(l)(P2-P1) =0.018×(101325-3168)
= 1.77J/mol
ΔG=ΔG1+ΔG2+ΔG3 = - 8583 J/mol < 0 所以该过程是不可逆过程。
此例还说明对于凝聚相,当温度不变,压力变化引起 的吉布斯自由能的改变量很小,可以忽略不计。
非平衡相变(可逆相变): 需设计一可逆过程计算
(
N x
)
y
2 z xy
所以
M N ( y )x ( x )y
Maxwell 关系式
热力学函数是状态函数,数学上具有全微分性质,
将上述关系式用到四个基本方程中, 就得到Maxwell关系式:
( M y
)x
N ( x )y
(1) dU TdS pdV
(
T V
)S
(
p S
)V
(2) dH TdS Vdp
(dG)T , p > Wf
不可逆
" "表示可逆,平衡
(dG)T , p,Wf 0 0 " "表示不可逆,自发
理想气体等温可逆过程 G =WR
(dA)T ,R Wmax 可逆
(dA)T W
(dA)T ,V ,Wf 0 0
不可逆
" "表示可逆,平衡 " "表示不可逆,自发
统计热力学基础3

2 mkT
h2
3/ 2
V
ln
N
5
2
Nk
ln
qt N
5 2
这就是Sackur-Tetrode公式,用来计算理想气 体的平动熵
对于1 mol 理想气体,Sackur-Tetrode 公式为
St,m
R
ln
2
mkT Lh3
Gt At pV
p
(
A V
)T
,N
代入相应的 U t , At 表示式即得。
转动和振动配分函数的贡献
(1) Helmholtz自由能 Ar和Av
Ar NkT ln qr Av NkT ln qv
kT
ge,0
exp
e,0
kT
2 mkT 3/2
h3
V
对于双原子分子
q总
gn,0
exp
n,0
kT
ge,0
exp
e,0
kT
2
mkT h3
3/ 2
V
8 2IkT
h2
exp
1 2
h
kT
1
exp
h
kT
08-4 配分函数的计算

e,0
kT
)[1
e,1 e,0
kT
电子能级间隔也很大, (e,1 e,0 ) 400 kJ mol-1 , 除F, Cl 少数元素外,方括号中第二项也可略去。虽然温度很高时,电 子也可能被激发,但往往电子尚未激发,分子就分解了。所以 通常电子总是处于基态,则:
1 (v ) v / T 2
qv
e
1 (v ) v / T 2
ev / 2T (1 ev / T )1
e vv / T (1 ev / T )
n0 基态分子分数 f 0 1 ev / T N
300 K 时
激发态 fex 1 f0 ev / T
物理化学II
7
统计热力学基础
配分函数的计算
2 h2 nx qt, x exp( 2) 8mkT a nx 1
exp( n )
nx 1 2 x
h (设 ) 2 8mkTa
2
因为 是一个很小的数值,所以求和号用积分号代替, 得:
2 qt,x exp( nx )dnx 0
配分函数的计算
配分函数的分离
t r q [ g t exp( )] [ g r exp( )] k BT k BT v e [ g v exp( )] [ g e exp( )] k BT k BT n [ g n exp( )] k BT
qt qr qv qe qn qt q内
平动, 转动,振动,电子,核运动
简并度 g i = gt •gr • gv • ge • gn
i / kBT
则
热力学与统计物理答案第三章.(DOC)

第三章 单元系的相变3.1 证明下列平衡判据(假设S >0);(a )在,S V 不变的情形下,稳定平衡态的U 最小.(b )在,S p 不变的情形下,稳定平衡态的H 最小.(c )在,H p 不变的情形下,稳定平衡态的S 最小.(d )在,F V 不变的情形下,稳定平衡态的T 最小.(e )在,G p 不变的情形下,稳定平衡态的T 最小.(f )在,U S 不变的情形下,稳定平衡态的V 最小.(g )在,F T 不变的情形下,稳定平衡态的V 最小.解:为了判定在给定的外加约束条件下系统的某状态是否为稳定的平衡状态,设想系统围绕该状态发生各种可能的自发虚变动. 由于不存在自发的可逆变动,根据热力学第二定律的数学表述(式(1.16.4)),在虚变动中必有đ,U T S W δδ<+ (1) 式中U δ和S δ是虚变动前后系统内能和熵的改变,đW 是虚变动中外界所做的功,T 是虚变动中与系统交换热量的热源温度. 由于虚变动只涉及无穷小的变化,T 也等于系统的温度. 下面根据式(1)就各种外加约束条件导出相应的平衡判据.(a ) 在,S V 不变的情形下,有0,đ0.S W δ==根据式(1),在虚变动中必有0.U δ< (2) 如果系统达到了U 为极小的状态,它的内能不可能再减少,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,S V 不变的情形下,稳定平衡态的U 最小.(b )在,S p 不变的情形下,有0,đ,S W pdV δ==-根据式(1),在虚变动中必有0,U p V δδ+<或0.H δ< (3)如果系统达到了H 为极小的状态,它的焓不可能再减少,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,S p 不变的情形下,稳定平衡态的H 最小.(c )根据焓的定义H U pV =+和式(1)知在虚变动中必有đ.H T S V p p V W δδδδ<+++在H 和p 不变的的情形下,有0,0,đ,H p W p V δδδ===-在虚变动中必有0.T S δ> (4)如果系统达到了S 为极大的状态,它的熵不可能再增加,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,H p 不变的情形下,稳定平衡态的S 最大.(d )由自由能的定义F U TS =-和式(1)知在虚变动中必有đ.F S T W δδ<-+在F 和V 不变的情形下,有0,đ0,F W δ==故在虚变动中必有0.S T δ< (5)由于0S >,如果系统达到了T 为极小的状态,它的温度不可能再降低,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,F V 不变的情形下,稳定平衡态的T 最小.(e )根据吉布斯函数的定义G U TS pV =-+和式(1)知在虚变动中必有đ.G S T p V V p W δδδδ<-++-在,G p 不变的情形下,有0,0,đ,G p W p V δδδ===-故在虚变动中必有0.S T δ< (6)由于0S >,如果系统达到了T 为极小的状态,它的温度不可能再降低,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,G p 不变的情形下,稳定的平衡态的T 最小.(f )在,U S 不变的情形下,根据式(1)知在虚变动中心有đ0.W >上式表明,在,U S 不变的情形下系统发生任何的宏观变化时,外界必做功,即系统的体积必缩小. 如果系统已经达到了V 为最小的状态,体积不可能再缩小,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,U S 不变的情形下,稳定平衡态的V 最小.(g )根据自由能的定义F U TS =-和式(1)知在虚变动中必有δδđ.F S T W <-+在,F T 不变的情形下,有δ0,δ0,F T ==必有đ0W > (8)上式表明,在,F T 不变的情形下,系统发生任何宏观的变化时,外界必做功,即系统的体积必缩小. 如果系统已经达到了V 为最小的状态,体积不可能再缩小,系统就不可能自发发生任何宏观的变化而处在稳定的平衡状态,因此,在,F T 不变的情形下,稳定平衡态的V 最小.3.2 试由式(3.1.12)导出式(3.1.13)解:式(3.1.12)为()()22222222δδ2δδδ0.S S S S U U V V U U V V ⎡⎤⎛⎫⎛⎫∂∂∂=++<⎢⎥ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎣⎦ (1)将2δS 改写为2δδδδδδδ.S S S S S U V U U V V U U V U U V V V ⎡∂∂∂∂⎤⎡∂∂∂∂⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥∂∂∂∂∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ (2)但由热力学基本方程TdS dU pdV =+可得 1,,V U S S p U T V T∂∂⎛⎫⎛⎫== ⎪ ⎪∂∂⎝⎭⎝⎭ (3) 代入式(2),可将式(1)表达为211δδδδδδδS p p S U V U U V V U T V T U T V T ⎡∂∂⎤⎡∂∂⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ 1δδδδ0.p U V T T ⎡⎤⎛⎫⎛⎫=+< ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦ (4) 以,T V 为自变量,有δδδV TU U U T V T V ∂∂⎛⎫⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭ δδ,V V p C T T p V T ⎡⎤∂⎛⎫=+- ⎪⎢⎥∂⎝⎭⎣⎦(5) 111δδδV TT V T T T V T ∂∂⎛⎫⎛⎫⎛⎫=+ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭ 21δ,T T =- (6) δδδV Tp p p T V T T T V T ∂∂⎛⎫⎛⎫⎛⎫=+ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭ 211δδ.V T p p T p T V T T T V ⎡⎤∂∂⎛⎫⎛⎫=-+ ⎪ ⎪⎢⎥∂∂⎝⎭⎝⎭⎣⎦(7) 将式(5)—(7)代入式(4),即得 ()()22221δδδ0,V TC p S T V T T V ∂⎛⎫=-+< ⎪∂⎝⎭ (8)这就是式(3.1.13).3.3 试由0V C >及0Tp V ∂⎛⎫< ⎪∂⎝⎭证明0p C >及0.S p V ∂⎛⎫< ⎪∂⎝⎭ 解:式(2.2.12)给出 2.p V TVT C C ακ-= (1) 稳定性条件(3.1.14)给出 0,0,V Tp C V ∂⎛⎫>< ⎪∂⎝⎭(2) 其中第二个不等式也可表为 10,T TV V p κ⎛⎫∂=-> ⎪∂⎝⎭(3) 故式(1)右方不可能取负值. 由此可知0,p V C C ≥>(4) 第二步用了式(2)的第一式.根据式(2.2.14),有 .S SV T pTVpC C Vp κκ⎛⎫∂ ⎪∂⎝⎭==⎛⎫∂ ⎪∂⎝⎭(5) 因为Vp C C 恒正,且1VpC C ≤,故 0,S TV V p p ⎛⎫⎛⎫∂∂≤< ⎪ ⎪∂∂⎝⎭⎝⎭(6)第二步用了式(2)的第二式.3.4 求证:(a ),,;V n T V S T n μ∂∂⎛⎫⎛⎫=- ⎪⎪∂∂⎝⎭⎝⎭ (b ),,.T pt n V p n μ⎛⎫∂∂⎛⎫=⎪⎪∂∂⎝⎭⎝⎭解:(a )由自由能的全微分(式(3.2.9))dF SdT pdV dn μ=--+ (1) 及偏导数求导次序的可交换性,易得 ,,.V n T VS T n μ∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ (2) 这是开系的一个麦氏关系.(b ) 类似地,由吉布斯函数的全微分(式(3.2.2))dG SdT Vdp dn μ=-++ (3)可得,,.T p T n V p n μ⎛⎫∂∂⎛⎫= ⎪ ⎪∂∂⎝⎭⎝⎭ (4) 这也是开系的一个麦氏关系.3.5 求证:,,.T V V nU T n T μμ∂∂⎛⎫⎛⎫-=- ⎪ ⎪∂∂⎝⎭⎝⎭ 解:自由能F U TS =-是以,,T V n 为自变量的特性函数,求F 对n 的偏导数(,T V 不变),有 ,,,.T V T V T VF U S T n n n ∂∂∂⎛⎫⎛⎫⎛⎫=- ⎪ ⎪ ⎪∂∂∂⎝⎭⎝⎭⎝⎭ (1) 但由自由能的全微分dF SdT pdV dn μ=--+可得 ,,,,,T VT V V n F n S n T μμ∂⎛⎫= ⎪∂⎝⎭∂∂⎛⎫⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ (2)代入式(1),即有,,.T V V nU T n T μμ∂∂⎛⎫⎛⎫-=- ⎪ ⎪∂∂⎝⎭⎝⎭ (3)3.6 两相共存时,两相系统的定压热容量p pS C T T ∂⎛⎫= ⎪∂⎝⎭,体胀系数1p V V T α∂⎛⎫= ⎪∂⎝⎭和等温压缩系数1T TV V p κ⎛⎫∂=- ⎪∂⎝⎭均趋于无穷,试加以说明. 解:我们知道,两相平衡共存时,两相的温度、压强和化学势必须相等.如果在平衡压强下,令两相系统准静态地从外界吸取热量,物质将从比熵较低的相准静态地转移到比熵较高的相,过程中温度保持为平衡温度不变. 两相系统吸取热量而温度不变表明它的(定压)热容量p C 趋于无穷. 在上述过程中两相系统的体积也将发生变化而温度保持不变,说明两相系统的体胀系 数1pV V T α∂⎛⎫= ⎪∂⎝⎭也趋于无穷. 如果在平衡温度下,以略高(相差无穷小)于平衡压强的压强准静态地施加于两相系统,物质将准静态地从比容较高的相转移到比容较低的相,使两相系统的体积发生改变. 无穷小的压强导致有限的体 积变化说明,两相系统的等温压缩系数1T TV V p κ⎛⎫∂=- ⎪∂⎝⎭也趋于无穷.3.7 试证明在相变中物质摩尔内能的变化为1.m p dT U L T dp ⎛⎫∆=- ⎪⎝⎭ 如果一相是气相,可看作理想气体,另一相是凝聚相,试将公式化简. 解:发生相变物质由一相转变到另一相时,其摩尔内能m U 、摩尔焓m H 和摩尔体积m V 的改变满足.m m m U H p V ∆=∆-∆ (1) 平衡相变是在确定的温度和压强下发生的,相变中摩尔焓的变化等于物质在相变过程中吸收的热量,即相变潜热L :.m H L ∆=克拉珀龙方程(式(3.4.6))给出,m dp L dT T V =∆ (3) 即 .m L dT V T dp∆= (4) 将式(2)和式(4)代入(1),即有 1.m p dT U L T dp ⎛⎫∆=- ⎪⎝⎭(5) 如果一相是气体,可以看作理想气体,另一相是凝聚相,其摩尔体积远小于气相的摩尔体积,则克拉珀龙方程简化为2.dp Lp dT RT = (6) 式(5)简化为1.m RT U L L ⎛⎫∆=- ⎪⎝⎭ (7)3.8 在三相点附近,固态氨的蒸气压(单位为Pa )方程为3754ln 27.92.p T=- 液态氨的蒸气压力方程为 3063ln 24.38.p T =-试求氨三相点的温度和压强,氨的汽化热、升华热及在三相点的熔解热.解:固态氨的蒸气压方程是固相与气相的两相平衡曲线,液态氨的蒸气压方程是液相与气想的两相平衡曲线. 三相点的温度t T 可由两条相平衡曲线的交点确定:3754306327.9224.38,t tT T -=- (1) 由此解出195.2.t T K = 将t T 代入所给蒸气压方程,可得5934Pa.t p =将所给蒸气压方程与式(3.4.8)In L p A RT =-+ (2) 比较,可以求得443.12010J,2.54710J.L L =⨯=⨯升汽氨在三相点的熔解热L 溶等于40.57310J.L L L =-=⨯溶升汽3.9 以C βα表示在维持β相与α相两相平衡的条件下1mol β相物质升高1K 所吸收的热量,称为β相的两相平衡摩尔热容量,试证明:.m p m m p V L C C V V T βββαβα⎛⎫∂=- ⎪-∂⎝⎭ 如果β相是蒸气,可看作理想气体,α相是凝聚相,上式可简化为,p L C C Tββα=- 并说明为什么饱和蒸气的热容量有可能是负的.解:根据式(1.14.4),在维持β相与α相两相平衡的条件下,使1mol β相物质温度升高1K 所吸收的热量C βα为 .m m m p TdS S S dp C T T T dT T p dT ββββα⎛⎫⎛⎫⎛⎫∂∂==+ ⎪ ⎪ ⎪∂∂⎝⎭⎝⎭⎝⎭ (1) 式(2.2.8)和(2.2.4)给出 ,.m p p m m T p S T C T S V p T ββββ⎛⎫∂= ⎪∂⎝⎭⎛⎫⎛⎫∂∂=- ⎪ ⎪∂∂⎝⎭⎝⎭ (2)代入式(1)可得 .m p p V dp C C T T dT βββα⎛⎫∂=- ⎪∂⎝⎭ (3) 将克拉珀龙方程代入,可将式(3)表为.m p m m p V L C C V V T βββαβα⎛⎫∂=- ⎪-∂⎝⎭ (4) 如果β相是气相,可看作理想气体,α相是凝聚相,m m V V αβ,在式(4)中略去m V α,且令m pV RT β=,式(4)可简化为 .p L C C Tββα=-(5) C βα是饱和蒸气的热容量. 由式(5)可知,当p L C T β<时,C βα是负的.3.10 试证明,相变潜热随温度的变化率为.m m p p m mp p V V dL L L C C dT T T T V V βαβαβα⎡⎤⎛⎫⎛⎫∂∂=-+--⎢⎥ ⎪ ⎪∂∂-⎢⎥⎝⎭⎝⎭⎣⎦ 如果β相是气相,α相是凝聚相,试证明上式可简化为.p p dL C C dTβα=- 解: 物质在平衡相变中由α相转变为β相时,相变潜热L 等于两相摩尔焓之差:.m m L H H βα=- (1)相变潜热随温度的变化率为 .m m m m p T p T H H H H dL dp dp dT T p dT T p dTββαα⎛⎫⎛⎫⎛⎫⎛⎫∂∂∂∂=+-- ⎪ ⎪ ⎪ ⎪∂∂∂∂⎝⎭⎝⎭⎝⎭⎝⎭ (2) 式(2.2.8)和(2.2.10)给出 ,,p pp T H C T H V V T p T ∂⎛⎫= ⎪∂⎝⎭⎛⎫∂∂⎛⎫=- ⎪ ⎪∂∂⎝⎭⎝⎭ (3)所以().m m p p m m p p V V dL dp dp C C V V T dT dT T T dTβαβαβα⎡⎤⎛⎫⎛⎫∂∂=-+---⎢⎥ ⎪ ⎪∂∂⎢⎥⎝⎭⎝⎭⎣⎦ 将式中的dp dT用克拉珀龙方程(3.4.6)代入,可得 ,m m p p m m p p V V dL L L C C dT T T T V V βαβαβα⎡⎤⎛⎫⎛⎫∂∂=-+--⎢⎥ ⎪ ⎪∂∂-⎢⎥⎝⎭⎝⎭⎣⎦ (4)这是相变潜热随温度变化的公式.如果β相是气相,α相是凝聚相,略去m V α和m pV T α⎛⎫∂ ⎪∂⎝⎭,并利用m pV RT β=,可将式(4)简化为.p p dL C C dTβα=- (5)3.11 根据式(3.4.7),利用上题的结果计及潜热L 是温度的函数,但假设温度的变化范围不大,定压热容量可以看作常量,试证明蒸气压方程可以表为ln ln .Bp A C T T=-+ 解: 式(3.4.7)给出了蒸气与凝聚相两平衡曲线斜率的近似表达式21.dp Lp dT RT = (1) 一般来说,式中的相变潜热L 是温度的函数. 习题3.10式(5)给出.p p dL C C dTβα=- (2) 在定压热容量看作常量的近似下,将式(2)积分可得()0,p p L L C C T βα=+- (3)代入式(1),得021,p pC C L dL p dT RT RTβα-=+ (4) 积分,即有ln ln ,Bp A C T T=-+ (5) 其中0,,p pC L B C A R C βα==是积分常数.3.12 蒸气与液相达到平衡. 以mdV dT表示在维持两相平衡的条件下,蒸气体积随温度的变化率. 试证明蒸气的两相平衡膨胀系数为111.m m dV LV dT T RT⎛⎫=-⎪⎝⎭解:蒸气的两相平衡膨胀系数为11.m m m p m m T dV V V dp V dT V T p dT ⎡⎤⎛⎫∂∂⎛⎫=+⎢⎥⎪ ⎪∂∂⎝⎭⎢⎥⎝⎭⎣⎦(1) 将蒸气看作理想气体,m pV RT =,则有11,11.m p m m m T V V T T V V p p∂⎛⎫= ⎪∂⎝⎭⎛⎫∂=- ⎪∂⎝⎭ (2)在克拉珀龙方程中略去液相的摩尔体积,因而有2.m dp L LpdT TV RT== (3) 将式(2)和式(3)代入式(1),即有111.m m dV L V dT T RT⎛⎫=-⎪⎝⎭(4)3.13 将范氏气体在不同温度下的等温线的极大点N 与极小点J 联起来,可以得到一条曲线NCJ ,如图所示. 试证明这条曲线的方程为()32,m m pV a V b =-并说明这条曲线划分出来的三个区域Ⅰ、Ⅱ、Ⅲ的含义.解:范氏方程为2.m mRT ap V b V =-- (1) 求偏导数得()232.m m Tm p RT aV V V b ⎛⎫∂=-+ ⎪∂-⎝⎭ (3) 等温线的极大点N 与极小点J 满足0,m Tp V ⎛⎫∂= ⎪∂⎝⎭ 即()232,mm RTa V Vb =- 或()()32.m m mRT aV b V b V =-- (3) 将式(3)与式(1)联立,即有()322,m m ma ap V b V V =-- 或()32m m m pV a V b aV =--()2.m a V b =- (4)式(4)就是曲线NCJ 的方程.图中区域Ⅰ中的状态相应于过热液体;区域Ⅲ中的状态相应于过饱和蒸气;区域Ⅱ中的状态是不能实现的,因为这些状态的0m Tp V ⎛⎫∂> ⎪∂⎝⎭,不满足平衡稳定性的要求.3.14 证明半径为r 的肥皂泡的内压强与外压强之差为4rσ. 解:以p β表示肥皂泡外气体的压强,p γ表示泡内气体的压强,p α表示肥皂液的压强,根据曲面分界的力学平衡条件(式(3.6.6)),有2,p p r αβσ=+(1)2,p p rγασ=+ (2)式中σ是肥皂液的表面张力系数,r 是肥皂泡的半径. 肥皂液很薄,可以认为泡内外表面的半径都是r . 从两式中消去p α,即有4.p p rγβσ-=(3)3.15 证明在曲面分界面的情形下,相变潜热仍可表为().m m mm L T S S H H βαβα=-=- 解:以指标α和β表示两相. 在曲面分界的情形下,热平衡条件仍为两相的温度相等,即.T T T αβ== (1)当物质在平衡温度下从α相转变到β相时,根据式(1.14.4),相变潜热为().m m L T S S βα=- (2)相平衡条件是两相的化学势相等,即()(),,.T p T p ααββμμ= (3)根据化学势的定义 ,m m m U TS pV μ=-+式(3)可表为,m m m m m m U TS p V U TS p V ααααββββ-+=-+因此()()m m m m m mL T S S U p V U p V βαβββααα=-=+-+.m m H H βα=- (4)3.16 证明爱伦费斯特公式:()(2)(1)(2)(1)(2)(1)(2)(1),.p p dp dT C C dp dT TV αακκαα-=--=- 解:根据爱氏对相变的分类,二级相变在相变点的化学势和化学势的一级偏导数连续,但化学势的二级偏导数存在突变. 因此,二级相变没有相变潜热和体积突变,在相变点两相的比熵和比体积相等. 在邻近的两个相变点(),T p 和(),T dT p dp ++,两相的比熵和比体积的变化也相等,即(1)(2)v v ,d d = (1)(1)(2).ds ds = (2)但v v v v .p Td υdT dp T p dT dp ακ⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭=- 由于在相变点(1)(2)v v =,所以式(1)给出(1)(1)(2)(2),dT dp dT dp ακακ-=-即(2)(1)(2)(1).dp dT αακκ-=- (3) 同理,有v .p T p pp s s ds dT dp T p C υdT dpT T C dT dp Tα⎛⎫∂∂⎛⎫=+ ⎪ ⎪∂∂⎝⎭⎝⎭∂⎛⎫=- ⎪∂⎝⎭=- 所以式(2)给出(1)(2)(1)(1)(2)(2)v v ,ppC C dT dp dT dp TTαα-=-即()(2)(1)(2)(1),v p p C C dp dT T αα-=- (4)式中(2)(1)v v v ==. 式(3)和式(4)给出二级相变点压强随温度变化的斜率,称为爱伦费斯特方程.3.17 试根据朗道自由能式(3.9.1)导出单轴铁磁体的熵函数在无序相和有序相的表达式,并证明熵函数在临界点是连续的。
统计热力学基础

(3)统计热力学基本假设 统计热力学基本假设是:当→∞的极限情况下,在实际系统 中任何力学量的长时间平均值〈Gt〉等于系综平均值〈G〉,只要 统计系综和实际系统的热力学状态及环境完全相同。 统计热力学的另一条基本假设:孤立系统(即N,V,E一定)的 全部可能达到的量子态是等概率的。
用于N,V,T一定的封闭系统时,该假设还可表述为:在定温 热浴中的系统,能量相同的各量子态有相同的概率。
P ( D) WD
Ω
WD WD
D
每一个微态的概率 P
1
Ω
统计热力学中把WD叫分布D的热力学概率。显然热力学概率 WD不同于数学概率P(A),WD≥1(正整数),而0≤P(A)≤1。
③WD的计算 定域子系统:
gin N! n WD gi N! n ! ni ! i i i
第四章 统计热力学基础
1.统计热力学基本概念 (1)统计热力学系统的分类 ①独立子系和相依子系(非独立子系) 统计热力学将组成系统的分子、原子及离子等统称为粒子或 简称子。 按照粒子间有无不可忽略的相互作用,系统可分为独立子系 (或近独立子系)——子间无相互作用;相依子系(非独立子 系)——子间有不可忽略的相互作用。 ②定域子系和离域子系 按照粒子的运动是否遍及系统的全体积,系统可分为定域子 系——子的运动是定域化的(不遍及系统的全体积);离域子系 (非定域子系)——子的运动是非定域化的(遍及系统的全体 积)。
能量守恒: U N P ,i i 粒子数守恒: N ni
ni是布居在能级上的粒子数;Pε,i是粒子分布在各能级εi上的概率;
(4)分布的微态数WD与系统的总微态数 任何一种分布,只指出在每个能级(或状态)上有多少个粒子, 实现这一分布尚有不同的方式,每一种可区别的方式代表分布 (或系统)的一个可区别的微观状态,简称微态。WD表示分布D 的微态数,用表示系统总的微态数。 (5)分布的概率 计算分布的概率用古典概型的计算公式。 ① 古典概型又叫等概率模型,既是概率的定义,又是计算概率 的基本公式,其特征是: (i)只有有限个基本事件;
《统计热力学》课件

欢迎来到《统计热力学》PPT课件!本课程将探索统计热力学的定义、原理、 应用领域,以及数学基础和研究方法。让我们开始这个精彩的学习之旅!
概述
介绍统计热力学的基本概念和作用。了解热力学与统计力学的关系以及统计热力学在物理、化学和生物等领域 的重要性。
定义
探索统计热力学的准确定义,包括如何描述微观粒子的状态、能量分布和统计规律。理解宏观热力学参数与微 观粒子行为之间的关系。
生物化学
探索统计热力学在生物大分子结构和功能研究中的重要性。
能源研究
研究统计热力学在能源转化、储存和优化中的应用及挑战。
数学基础
了解统计热力学所需的数学基础,包括概率论、统计学和微积分。探索数学 模型和统计方法在统计热力学中的应用。
研究方法
了解统计热力学的研究方法,包括计算模拟、实验技术和数据分析。探索如 何收集、处理和解释实验和模拟数据。
未来发展
展望统计热力学的未来发展方向,包括新的应用领域、研究技术和理论突破。让我们一起探索统计热力学的无 限可能!基本原理 Nhomakorabea1
统计力学
了解统计力学的基本原理,包括概率分布、平衡态和非平衡态,以及微正则、正 则和巨正则系综。
2
热力学基本定律
探索统计热力学与热力学基本定律的关系,包括熵增原理和热力学基本方程。
3
统计热力学的统一性
理解统计热力学与热力学之间的统一性,揭示宏观现象的微观基础。
应用领域
材料科学
了解统计热力学在材料制备、相变和材料性能预测中的应用。
热力学第二定律的统计解释
3 – 9 热力学第二定律的统计意义
第三章热力学基础
N1
2
4
N
Ω
(左)
2
22
24
2N
0
N个分子,Ωi
2 N。
若N=100, 则:
Ωi 2100 1030
而左右各半的平衡态及其附近宏观态的热力学概率则
占总微观状态数的绝大比例。 Ω(N左)
一般热力学系统 N的数量级约
N 很大
为1023,上述比例实际上是百分
概率小的状态
概率大的状态
讨论 N 个粒子在空间的分布问题
可分辨的粒子集中在 左空间的概率
N 1, 2
N 2, 4
3 – 9 热力学第二定律的统计意义
第三章热力学基础
b Aa
B
cd
ab
bc
c
a dcd
a bd
a bd
c
1 1264
A
bBa
cd
bd c
a
ab
c d
分子的分布
容器 A
的部
分B
设 S f(),求 f 的函数形式。
由 S 的可加性来分析:
1 S1, 1
1+2
S,
2 S2, 2 1、2彼此独立
∴ 应有: f( ) ln
3 – 9 热力学第二定律的统计意义
第三章热力学基础
S k ln
─ 玻耳兹曼熵公式
1877年玻耳兹曼提出了S ln 。
1900年普朗克引进了比例系数 k 。
ab cd
0
0a
b
c
d
bc ac ab a a d d d bc b
abbc cd d
第三章 热力学基础

(1)对等温过程,氢气 由1到2’态时环境对系统 所做的功为:
M V2' A' RT ln u V1 5 8.31 293 ln 0.1 2.80 104 J
26
M A CV (T2 T1 ) u 5 5 8.31 (736 293) 2 4 4.60 10 J
i C Pm R R CVm R C Pm CVm R 2
18
由 QV (E )V 及 QP (E ) P A P
当 ( E )V ( E )P , 有 QP QV 所以 C Pm CVm .
P
T2 T1
i 0 1 R C Pm 2 1 2 i CVm i R 2 单原子分子气体: i 3
(3) c→a ,等容升温过程
( )
o
V1
V2
V
A ca
M 0 , Qca Eca CVm T1 T2 7.79 103 J u
( )
Eabca Eab Ebc Eca Ebc Eca 0 Eca Ebc 7.79 10 J
比较 (1)(2)结果得 CVm
i R 2
二、等压过程
V V1 V2 1.过程方程 C或 T T1 T2
P 1
0
2.特点
2
V2 V
17
dP 0 , A PdV P (V2 V1 )
V1 3.应用 M i dE RdT u 2
V2
V1
M i E R(T2 T1 ) u 2
dV=0,dA=PdV=0,或 A=0 。 3. 应用
1
0
材料学中的热力学基础

材料学中的热力学基础材料学是物理学、化学、工程学的交叉学科,研究材料的结构、性质和制备过程。
其中,热力学是材料学中不可或缺的基础,涵盖了材料在温度变化下的能量转移和物质转化规律。
在此,我们将深入探讨材料学中热力学的基础知识和其重要性。
一、材料学中的热力学基础1. 热力学基础概述热力学是一门研究热现象的学科,其基础概念是热和功。
材料学中的热力学主要涉及材料在不同温度、压力下的热力学性质和热力学均衡,其中包括物质的相变、热力学稳定性和热力学状态方程等。
2. 熵熵是热力学中非常重要的一个概念,它是物质状态的度量。
材料学中,熵通常用于描述材料内部的有序和无序程度。
在材料学中,熵的增加通常与物质结构的紊乱程度、温度升高、压力降低等因素有关。
3. 自由能自由能是材料学中的另一个重要概念,它是描述材料在不同热力学条件下的稳定状态的参数。
自由能包括内能、焓和熵三个部分,其变化可表示为dF=dU-TdS+PdV。
材料状态的稳定通常表现为其自由能的最小值。
4. 相变相变是材料学热力学中的重要现象,指物质由一种组态转化为另一种组态的过程。
相变与物质的热力学性质密切相关,在不同温度和压力条件下,物质的相变规律也不同。
在材料学中,相变是材料性质改变、结构演化的基础。
二、热力学在材料学中的重要性热力学在材料学中具有不可替代的重要性,它是研究材料结构和性质的基础和支撑。
在材料学中,应用热力学原理可以解释材料中多种物理和化学现象、预测材料的性能等。
1. 材料制备过程材料的制备过程中,需要控制材料的组成、结构、性质等,这涉及到热力学。
通过对材料的热力学性质进行分析,可以确定合适的合成温度、反应条件等,从而控制材料的制备过程,获得理想的材料结构和性质。
2. 材料性质优化材料的性能改善和优化需要了解其热力学行为。
例如,根据材料的自由能变化,可以确定材料在不同条件下的稳定状态,从而预测材料的变形和断裂性质等。
热力学分析还可帮助调整材料的热稳定性、耐磨性、导电性、机械性能等,大大拓展了材料应用领域。
材料热力学 第三章 单组元材料热力学

Cp
H T
p
Cv
U T
v
H CpdT H (0K) U CvdT U(0K)
H(0K)和U(0K)是绝对零度的焓和内能, 目前其绝对值尚无法得知。
dS Q CdT
TT
S p
T 0
Cp T
dT
S(0K)
Sv
T 0
Cv T
dT
S (0K )
S(0K)为绝对零度下的熵,根据热力学第三定律(Third Law),认为单组元在绝对零度下的熵为0。
第三章 单组元材料热力学
3.2 晶体中的热空位
理想晶体中不存在空位,但实际金属晶体中存在空位。 随着温度升高,晶体中的空位浓度增加,大多数常用金 属(Cu、Al、Pb、W、Ag…)在接近熔点时,其空位 平衡浓度约为10-4,即晶格内每10000个结点中有一 个空位。
把高温时金属中存在的平衡空位通过淬火固定下来,形 成过饱和空位,这种过饱和空位状态对金属中的许多物 理过程(例如扩散、时效、回复、位错攀移等)产生重 要影响。
G
T
C pdT
0
T
T
0
Cp T
dT
H (0K)
F
T 0
Cv dT
T
T
0
Cv T
dT
U (0K)
能量均分定理在解释热容问题所遇到的巨大困 难迫使人们至新审查能量均分定理。能量均分 定理是由经典统计力学导出的,在经典物理包 括经典统计力学中有一个根本的假设就是能量 是连续改变的,能量均分定理在解释热容以及 热辐射问题上所遇到的不可克服的困难使得普 朗克提出量子论假设。
例题:
由实验求得Cp值: C p a bT cT 2 状态改变时:
材料热力学课件-第三章-2
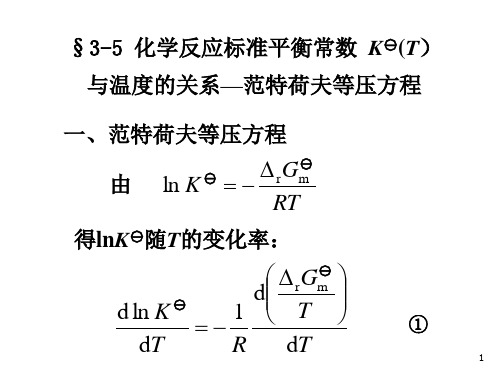
以△Hm =18.86kJmol-1代入
lnK
(T
)
r
H
m
B
RT
得 B = 0.045+(18860/2.303×8.3145×873)
= 1.17 lgK = - 18860 Jmol-1/(2.303RT) + 1.17
= -985/(T/K) + 1.17
13
(3)根据上式求1373 K 时的 lgK(1373 K)= - 983/1373 + 1.17
+1/2∑bBT 2 +1/3∑cBT 3
其中 △H0 =△rHm (298K)-298K×∑aB – 1/2×(298K)2 ∑bB -1/3(298K)3∑cB
22
△rHm(T)=△H0+∑aBT
+1/2∑bBT 2 +1/3∑cBT 3
代入dlnK(T) =[△rHm/RT2 ]dT,得
ln
△rGm –T 的近似直线关系是在BCp,m
很小或0时。因为
△rSm (T) = △rSm (298K) +
C T
B dT
298K
B p,m
B
T
19
dlnK dT
T
r
H
m
(T
RT 2
)
ln
K (T2 ) K (T1)
r
H
m
R
1 T2
1 T1
lnK
(T
)
r
H
m
B
RT
20
2、△rHm随温度变化
说明计算中做了哪些假设。
G 已知
f
m
Ag
统计热力学基础
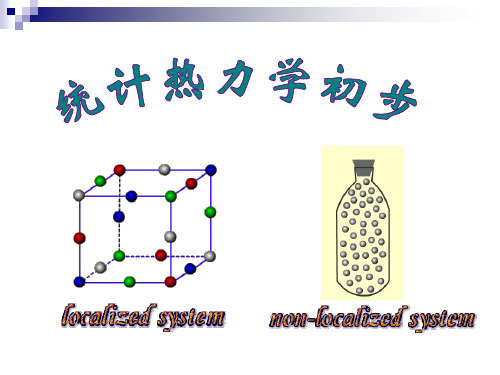
例2. 定域子系统中只有3个一维谐振子,它们分别在 A,B,C三个定点上振动,总能量为 9 hv,分析系统 2 可能有的能级分布及状态分布。 能级 能级分布 Ⅰ Ⅱ Ⅲ n0 n1 n2 n3
状态分布 0
3 0 0 WⅠ= 6 WⅡ = 3 WⅢ = 1 Ω = WⅠ+WⅡ+WⅢ=10
0=
1=
例如,某能级分布的微态数为WD,总微态数为Ω, 则该能级分布的数学概率 P 为:
WD 1 PD = Ω × WD = Ω
系统状态确定时,Ω为定值,微态数最大的分布 WD 最大,热力学概率也最大,称为最概然分布。
4、最概然分布与平衡分布 最概然分布虽然代表了系统微态数最多的一种 能级分布方式,但是它的数学概率是随着粒子数的 增多而减小的。 以粒子的空间分布为例来进行分析 例如,某一气体系统,粒子数为N,当系统达平 衡时,粒子在整个空间上的分布应是均匀的。 如果把整个空间分为大 小相等的两部分,则两部 分中所包含的粒子数应相 等,均为 N 。
2、等概率定理
对于U, V 和 N 确定的某一宏观系统,任何一 个可能出现的微观状态,都有相同的数学概率。 这个假设称为等概率定理。 例如,某宏观系统的总微态数为Ω ,则每一 种微观状态出现的数学概率 P 都相等,即:
1 P=Ω
3、最概然分布(最可几分布) 对于U, V 和 N 确定的宏观系统,微观上可能会 有多种能级分布方式,不同的能级分布所包含的状 态分布数不同,根据等概率定理,各微态出现的概 率相等,则各能级分布出现的概率不同。
§9.1
粒子各运动形式的能级及能级的简并度
根据前面的讨论及上述计算结果可以看出,各 种运动的能级间隔遵循如下关系:
Δn>Δe>Δv>Δr>Δt
第三章_单元系的相变_热力学统计物理

U p0 V
T0
代入平衡条件得到:
1 1 p p S U ( ) V ( 0 ) 0 T T0 T T0
9
上页得到: S U ( ) V (
1 T
1 T0
p T
p0 )0 T0
由于虚变动δU、δV 可任意变化,故上式要求:
UB U A W T
外界所作的功是
SB S A
W p(VB VA )
SB S A
U B U A p (VB V A ) T
G GB GA 0
在等温等压过程中,系统的吉布斯函数永不增 加。也就是说,在等温等压条件下,系统中发 生的不可逆过程总是朝着吉布斯函数减少的方 向进行的。
T T0
p p0
结果表明:达到平衡时整个系统的温度和压强是均匀的!
2、稳定平衡
近似有 而
~ S 2 S0 2 S 0 2~ S 2S 0
2
可以证明:
2 S0 2 S
2S 2S 2S 2S (U ) 2 2 UV 2 (V ) 2 0 U 2 UV V
4
二、热平衡的判据(热动平衡条件)
1、基本平衡判据
根据熵增加原理,孤立系统中发生的趋于平衡的过程 必朝着熵增加的方向进行。
熵判据:孤立系统平衡态是熵最大的态。 相对于平衡态的虚变动后的态的熵变小。 孤立系统处在稳定平衡状态的必要充分条件:
1 1 S S 2! S 3! S
U n H n F n
pdV dn
T ,V
18
定义:巨热力势
03-统计热力学基础

三、统计热力学基础(313题)一、选择题 ( 共38题 )1. 1 分 (1301)玻耳兹曼熵定理一般不适用于: ( )(A) 独立子体系 (B) 理想气体 (C) 量子气体 (D) 单个粒子2. 1 分 (1302)非理想气体是: ( )(A) 独立的全同粒子体系 (B) 相依的粒子体系(C) 独立的可别粒子体系 (D) 定域的可别粒子体系3. 2 分 (1304)下列各体系中属于独立粒子体系的是: ( )(A) 绝对零度的晶体 (B) 理想液体混合物(C) 纯气体 (D) 理想气体的混合物4. 1 分 (1362)玻耳兹曼分布 _______ 。
(A) 是最概然分布,但不是平衡分布(B) 是平衡分布,但不是最概然分布(C) 即是最概然分布,又是平衡分布(D) 不是最概然分布,也不是平衡分布5. 1 分 (1363)对于近独立非定位体系,在经典极限下能级分布 D 所拥有的微观状态数t 为:( )(A) ∏=i i i n !!i N N N t g (B) ∏=i i i n !!iN g N t n (C) ∏=ii n !!iN N N t g (D) ∏=i i n !!i N g N t n 6. 1 分 (1364)对于服从玻耳兹曼分布定律的体系,其分布规律为: ( )(A) 能量最低的单个量子状态上的粒子数最多(B) 第一激发能级上的粒子数最多(C) 视体系的具体条件而定(D) 以上三答案都不对7. 2 分 (1369)近独立定域粒子体系和经典极限下的非定域粒子体系的 ( )(A) 最概然分布公式不同(B) 最概然分布公式相同(C) 某一能量分布类型的微观状态数相同(D) 以粒子配分函数表示的热力学函数的统计表达示相同8. 2 分 (1370)如果我们把同一种分子分布在二个不同能级ε与ε'上的n 与n ' 个分子看成是“不同种”的分子 A 与 A',则这“两种分子”将可按 A' A 进行转化而达到平衡。
《热力学与统计物理》第三章 单元系的相变

三.化学势分析
Vm
O K
范氏方程的平衡曲线
B T, p A T, p
J
J
K O
G
B G+L
D
N
L
A
M
R
p
D NR BA M
p
d SmdT Vmdp
p
dT 0 O pO Vmdp
NDJ段:Gm 最大, 不稳定 OKBAMR段:Gm 最小, 稳定
BN段: 亚稳 过饱和蒸气
JA段:
过热液体
两相平衡曲线:两相平衡共存,温 度和压强只有一个独立。
三相点:三相平衡共存,温度和压 强完全确定。
临界点:汽化线终点,温度高于此 点,无液相。由于临界点的存在, 从两相中任意一相的某一个状态出 发,可以经绕过临界点的任意路径 连续进行气—液的过渡而无需经过 相分离(或两相共存)的状态。
固 三相点 •
RT ln pr p
将上式代入*,以及p 2 ,得 :
r
2 v ln pr
r 107 m, pr r 108 m, pr r 109 m, pr
RTr
p
可见,液滴的平衡蒸汽压与液滴的半径有关
p 1.011; p 1.115; p 2.966;
三.中肯半径与过饱和蒸气
S U pV ,
T
S0
U0
p0V0
T0
2.稳定性条件
2S0 2S
系统的平衡条件
2S 2S 0
TdS
dU
pdV
S U
V
1 T
,
S V
U
p T
以 T,V 为自变量,有:
1 T
T
1 T
V
T
热力学与统计物理第三章

2020/4/4
17
由开系的基本热力学方程知: dU TdS pdV dn
S
U
p V
T
n
S
U
p V
T
n
由熵的广延性质: S S S
δS
1 T
1 T
δU
p T
p T
δV
T
T
δn
利用熵判据,平衡时总熵应有极大值,所以: δS 0
2020/4/4
18
T T 热平衡条件
独立变化。
• 相平衡曲线 在单元两相系中,由相平衡
条件所得到的T—p之间的关系p = p( T ),在T—p图上所描述的曲线
称为相平衡曲线。
AC—汽化线,分开气相区和液相区; AB—熔解线,分开液相区和固相区; 0A—升华线,分开气相区和固相区。
2020/4/4
24
单元两相平衡共存时,必须满足下面三个平衡条件:
第三章 单元系的相变
单元系:化学上纯的物质系统。 相:被一定边界包围,性质均匀的部分。
2020/4/4
1
§3.1 热动平衡判据
一、熵判据
• 虚变动
为了对系统的平衡态作出判断,必须考虑系统在平衡态 附近的一切可能的变动,这里面就有趋向平衡态的变动和 离开平衡态的变动。在热力学范围内,不考虑涨落现象, 系统一旦达到平衡态以后,其性质就不再发生变化了。因 此,在平衡态附近的一切可能的变动就是理论上虚拟的, 并不代表系统真实的物理过程,引进它的目的完全是为了 从数学上方便地导出系统的平衡条件。这类似于理论力学 中的“虚位移”概念。并以δ表示之。
它对各种平衡态系统包括化学平衡系统均成立。
2020/4/4
22
热力学基础 第三章 相平衡.

φ-1个等式 φ-1个等式
μ1α=μ1β=μ1γ……μ1φ
μ2α=μ2β=μ2γ……μ2φ
……
μSα=μSβ=μSγ……μSφ
∵μB
=μBo + RT lnXB
∴μ1αo+ RTαlnX1α=μ1βo + RTβlnX1β 。。。。。
共S(φ-1)个X的关系式
(4) X1α+X1β+X1γ+…+X1φ=1
MN段:液态水,f=2
N 点:汽,水两相平衡,f=1
l
NO段:水蒸气,f=2
P
M
N O
s
A
O
g
T
三、若干单元相图示例
很多材料是以多种晶型存在的,而且晶型
之间在适宜条件下可以进行相互转变,该现 象称为同质多晶现象。在单组分体系中,同质 多晶也称同素异形体(或称变体)。
一种晶型转变成另一种形式的变体称为同 质多晶转变也可称为多晶(多形)转变。从热 力学角度看,一组同质多晶的变体中那一种 晶型是稳定的,应由它们的自由焓决定,自 由焓低的晶型是稳定的。材料具有多晶转变 的例子很多。金刚石与石墨是一个典型的例 子。
(1)除X外,只考虑T和P, f = K-φ+2,如考虑 磁场,电场,重力场,则f = K-φ+ n ,n为X外的 强度因素个数。如指定了P或T,则f=K-φ+1。
(2)如果某个相中某些组分没有,这仍不影响 相律。如总变数(3)中几个组成没有,则在关 系式(3)中,就相应少几个等式,相互抵消, 不影响相律。
•
=3 三相共存.
左下是气相, f=2 右上是固相, f=2
水的相图
p D
l
中间是液相, f=2 2.210 7 Pa
统计热力学基础
量子力学中把能级可能有的微观状态数称为
该能级的简并度,用符号gi 表示。简并度亦称为
退化度或统计权重。
简并度(degeneration)
例如,气体分子平动能的公式为:
N!
Hale Waihona Puke g Ni iN! i
i Ni !
非定位体系的最概然分布
同样采用最概然分布的概念,用Stiring公式
和Lagrange乘因子法求条件极值,得到微态数为
极大值时的分布方式
N
*(非定位)为:
i
N(i* 非定位) N
g ei / kT i g ei / kT i
i
由此可见,定位体系与非定位体系,最概然
的分布公式是相同的。
Boltzmann公式的其它形式
(1)将i能级和j能级上粒子数进行比较,用最 概然分布公式相比,消去相同项,得:
Ni*
N
* j
g ei / kT i
g e j / kT j
Boltzmann公式的其它形式
(2)在经典力学中不考虑简并度,则上式成为
Ni*
N
* j
i / kT
ee j / kT
(U,V , N)
N!
g Ni i
i
i Ni !
求和的限制条件仍为:
Ni N
Nii U
i
i
有简并度时定位体系的微态数
再采用最概然分布概念, i max ,用
Stiring公式和Lagrange乘因子法求条件极值,得
到微态数为极大值时的分布方式 Ni* 为:
材料热力学2.统计热力学基础.吴申庆

8.配分函数Z
配分函数是一个统计物理学中经常应用到 的概念,统计物理学通过对大量微观粒子统 计行为的计算,将微观物理状态与宏观物理 量相互联系起来,而配分函数就是联系微观 物理状态和宏观物理量的桥梁。
配分函数实际是体系所有粒子在各个能级 依最可几分布排布时候对体系状态的一个描 述。由配分函数可以方便地求出体系的内能、 广义力、熵、自由能等等热力学参量。
宏观热力学的简单概括: 研究对象——大量分子的集合体,不考虑分子 的结构,不涉及分子内部的运动和相互作用 研究基础——经验总结出的三大定律, 研究方法——运用逻辑推理,形成热力学理论 作 用——利用热力学数据,讨论平衡系统 各宏观性质之间的 关系,从而预测过程进行 的方向和限度。 优 点——高度的可靠性和普遍意义。 由于在研究过程中并不考虑个别分子的特殊结 构,所以对于凡是能明确描述或定义出的热力 学体系都能使用它的结论。
宏观热力学局限性——对事物没有微观的想象; 不研究过程的机理及速率;得不到具体系统的 具体规律,如:不能推导出理想气体的状态方 程。必须结合对系统的某些观察数据,才能得 到具体的结果;不能说明变化具有方向性的本 质。 统计热力学: 弥补了热力学方法的不足。 是以大量微观粒子组成的宏观体系为研究 对象,从物质的微观结构和微观运动形态出发, 利用统计平均的方法(如:概率、最可几分布 等)来获得系统的宏观性质。
材料热力学
Thermodynamics of Materials
材料科学与工程学院 吴申庆 2012.3
第二章:统计热力学基础
Basic Concepts of Statistical Thermodynamics
统计热力学:关于热现象的平衡态微观理论及 其变化规律的科学。 研究集合体处于平衡态时的热现象及其变化 规律.是统计物理的研究方向之一. 对象:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中k玻尔兹曼常数
k = R/N0 = 1.38X10-23J/k
25
3.3 配置熵(组态熵、混合熵)
二元置换固溶体AB为例混合前后之差,固溶体原子 总数N,其中A原子为n,B原子为N-n。
26
3.4 配置熵(组态熵、混合熵)
二元置换固溶体AB为例混合前后之差,固溶体 原子总数N,其中A原子为n,B原子为N-n。
出发点: 1)物质由大量的分子、离子、电子、光子等各 种微观粒子构成。 2)热现象是大量粒子运动的整体表现,与热现 象 有关的各种宏观性质可通过对相应微观性质的研究经
由统计平均得出。
4
3.1 基本概念
独立子系统 (Assembly of independent particales): 各粒子间除 可以产生弹性碰撞外,没有任何相互作用,如理 想气体。 相倚子系统(Assembly of interacting particales ):各粒子间存在 相互作用,如真实气体、液体等。 离域子系统(等同粒子体系) (Non-localized system): 各粒子可 在整个空间运动,无法分辨如气体、液体。
定域子系统(可辨粒子体系) (Localized system): 各粒子只能在
固定位置附近的小范围内运动,可以分辨,如固 体。
5
3.1 基本概念
体系相空间 相空间:描述微观体系中每一粒子的坐标空间 例如:确定分子的位置位置空间(X、Y、Z),速度 空间(Vx、Vy、Vz),6维相空间。
相点:每个粒子在相空间均用一个点表示,即相点。
N i ni e i gi e
代入到 E
i
ni gi e e
i
e N i gi e
i
i
i i ni E i i ni 0 得
i gi i e E i ni i N i i gi e
ω=
N! N! N1! N 2 !...N i ! N i !
i
3.2.2 热力学几率计算
可辨粒子体系(定域子系统, 晶体):
n1 , n2, , ni i 当各能级简并度是 g1 , g 2 , , g,各能级分布数是
W D N !
i
ni gi
ni !
等同粒子体系(离域子系统,理气):
22
3.2.3 最可几分布与Stirling公式
W总= W(U,V,N)= Σ WD 当dLnW = 0 成极大时,满足粒子数守恒、能量守恒。
W D N !
i
ni gi
取对数得
ni !
lnW D = lnN ! i ni lngi i lnni !
斯特林近似式
lnN ! NlnN N
S=f(W)
24
3.3 熵函数与微观状态数关系
宏观体系熵和热力学几率之间关系:S = f (W)
由于熵S与内能一样,是体系的容量性质,具有加和性,即 如果一个体系是由1和2两个小体系组成,则体系的熵为两个小 体系熵之和。 S = S1 + S2 W = W1 W2 结论: S = K ln W (Boltzmann关系式)
一套各能级的分布数n0 , n1, ..., ni , ... 组成
系统的一种能级分布方式,简称能级分布。
能级 能级简并度 粒子分布数
0 , 1 , 2 ,, i ,
g0 , g1 , g2 ,, gi ,
n0 , n1 , n2 ,, ni ,
3.2.1微观粒子的能量分布
3.2.2 热力学几率计算
在统计热力学中,用某一定态下的一切可能的微观态的数目表 示这一宏观态出现的几率,这个微观态的数目成为热力学几率。 显然热力学几率永远大于1. 设体系中有N个分子,在相空间中用N个代表点表示,把N个代表 点分配到m个相格中,若某一宏观态在第一相格 1 中的分子数 目为N1,在第二相格 2 中的分子数目为N2,在第i个相格 i 中的 分子数目Ni……,由排列组合规则得知热力学几率为
研究对象 : 大量微观粒子构成的宏观系统研究方法。从
微观结构和微观运动形态出发,利用统计方法来获得物
质的各种宏观性质。 研究作用: 统计热力学是宏观特性与微观性质的桥梁, 它弥补了热力学的不足。 利用统计热力数,其结果甚至比热力学第三定律所得的熵值更
准确。
3
3.1 基本概念
3.2.1微观粒子的能量分布
由各量子状态的状态分布数组成的一套状态
分布数表示一种状态分布方式,简称状态分布。
量子态: 量子态的能量: 粒子分布数:
0 ,1 ,2 ,...,i ,...
ε0 ,ε1 ,ε2 ,...,εi ,...
n0 ,n1 ,n2 ,...,ni ,...
3.2.1微观粒子的能量分布
g ini WD ni ! i
21
3.2.3 最可几分布与Stirling公式
由热力学第二定律可知,对孤立体系宏观上任何一 个过程总是自发地向着自由能最低、熵值最大的方 向发展,直到达到平衡状态;在微观上体现着过程 向着热力学几率最大的方向发展。因此,宏观的平 衡总是对应着微观的热力学几率最大的状态。数学 上几率最大的分布状态又称最可几分布。
一个系统可能有各种不同的能级分布方式,任 何能级分布方式都必须同时满足下面两个关系式:
n N n U
i i i i i
在以上两条件限制下,N、U、V 确定的平衡系 统可以由哪些种能级分布方式是完全确定的。
3.2.1微观粒子的能量分布
2. 状态分布
一个 N、U 和 V 确定的平衡系统,分 布在某量子状态 j 的粒子数叫作状态分 布数,用 nj 表示。 一个能级可能有多个量子状态
S - S0 S配置=k ln W k ln
. . .
X A= n/N, XA +XB = 1
N! n!( N n )!
S= Nk x ln x (1 x) ln(1 x)>0
27
3.4 配置熵(组态熵、混合熵)
X = 0.5 时,ΔS max = 1.38eu; X 0,d(ΔS) -∞; X 1,d(ΔS) +∞ 物质提纯不容易。
11
3.2.1 微观粒子的能量分布
例: 某平动能级的 (nx2 ny2 nz2 ) 45 试求该能级的简并度。
解:nx, ny, nz 是平动量子数,nx, ny, nz =1, 2, 3……,所以当 时, (nx2 ny2 nz2 ) 45 只能是2,4,5 三个数。所以能级的统计权重 (简并度)为: g = 3! = 6
lnWD NlnN N i ni lng i i (ni lnni ni ) gi NlnN N i ni 1 ln ni
23
3.3 熵函数与微观状态数关系
熵函数的统计表达:
体系热力学宏观性质都是体系内部大量粒子运动的综合表现。 温度时体系内部大量粒子平均动能的表现,而压力是大量粒子 碰撞器壁(压力)的综合表现。Boltzmann从统计观点出发,根 据一切不可逆过程中孤立体系的热力学几率都趋向最大值,同 时体系的熵也趋向最大值,即热力学几率与熵之间必有一定的 联系,提出体系某个宏观状态的热力学几率可以用状态函数熵 来表示,即熵是微观状态几率的宏观反映。以数学关系式表示:
3.2.1微观粒子的能量分布
粒子的能级 0 , 1 , i , 及相应的简并度 g0 , g1 ,, gi ,
完全确定的
一个含N个粒子的系统在每个能级上分布 了一定数目的粒子,分布在能级 i上的粒 子数 ni 称为能级 i 的能级分布数,简称分 布数。
3.2.1微观粒子的能量分布
i i i i i i i
gi NlnN N i ni 1 ln n
29
3.4 Maxwell-Boltzman能量分配定律
设:独立粒子体系 1)粒子数不变: N ①
2)内能不变: ② 3)最可几分布:
i ni
N i ni 0
E i i ni
j 相格 Nj = 0
对应的WD = 1
1
2
3
4
4
6
4
1
9
3.2.1微观粒子的能量分布
1. 能级分布
一个平衡系统: 粒子总数为N
热力学能为U
体积为V 每个粒子的运动状态是确定的
3.2.1 微观粒子的能量分布
简并度:体系的运动状态称为量子态,属于同一能级的 不同量子态数称为该能级的简并度。 能量是量子化的,但每一个能级上可能有若干个不同的 量子状态存在,反映在光谱上就是代表某一能级的谱线 常常是由好几条非常接近的精细谱线所构成。 量子力学中把能级可能有的微观状态数称为该能级 的简并度,用符号gi表示。 简并度亦称为统计权重。 简并度增加,将使粒子在同一能级上的微态数增加。 gi =1 无简并度
第3章 统计热力学基础
运用微观研究手段寻找大量粒子集合的统计规
律性,并根据所推导的统计规律去阐述宏观体系
的热力学定律及某些热力学无法解释的实验规律。
1
3.1 基本概念
大量微观粒子构成的宏观系统
宏观现象 →宏观性质
微观结构和运动 →宏观性质
宏观现象是微观运动的结果 宏观现象与微观现象有差别
2
3.1 基本概念
相格:将相空间划分为很小的dxdydz dVxdVydVz体积 单元即为相格。
6
3.1 基本概念
微观描述:a、e、d处于相格1中,
b、c处于相格2中, f处于相格3中. 宏观描述:N1=3; N2=2,
N3=1
结论:宏观性质取决于相格中的点数。
7
3.1 基本概念
