系统辨识matlab最小二乘法
一、 实验题目：最小二乘法在系统辨识中的应用
二、 实验目的
1.掌握系统辨识的理论、方法及应用
2.熟练Matlab 下最小二乘法编程
3.掌握M 序列产生方法
三、 实验设备
1、
硬件设备：计算机配置，P4、32位CPU 、512M 内存 2、 软件设备： windows xp 操作系统 、matlab6.5软件包
四、 实验原理
最小二乘理论是有高斯（K.F.Gauss ）在1795年提出：“未知量的最大可能值是这样一个数值，它使各次实际观测值和计算值之间的差值的平方乘以度量其精度的数值以后的和最小。
”。
单输入单输出离散时间动态系统差分方程为：
)()()()k (1i 1i k e i k u i k Z Z bn
i na i b a +-=-+∑∑==其中Z （k ）为输出变量，u(k)为输入变量，e(k)为偏差。
上式可以表示为)()()(-)k (1i 1i k e i k u i k Z Z bn
i na i b a +--=∑∑==各参数用矩阵表示 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--------------=)()1()()1()2()1()2()1()1()
0()1()0(a a b a b a n l u l u n l z l z n u u n z z n u u n z z H （1） T l z z z Z )](),2(),1([，⋯= （2）
其中l 为所需要采集的点数。
[]T
n e E )(........).........0(e = （3） []T bn anb a ........1.........1=θ （4）
Z=H*θ+E ，E=Z-H*θ，根据最小二乘理论E 必须最小对上式进行求导，推出 Z H H H T T 1)(-=θ
根据表达式Z H H H T T 1)(-=θ带入（1）（2）（4）即可求出a1....an b1.......bn 。
五、实验代码以及实验结果
m=20; %置M序列总长度
y1=1;y2=1;y3=1;y4=0;
for i=1:m
x1=xor(y3,y4);%异或运算
x2=y1;
x3=y2;
x4=y3;
if y4==0;
u(i)=1;
else
u(i)=-1;
end
y1=x1;y2=x2;y3=x3;y4=x4;
end
z=zeros(21,1);%定义输出观测值的长度21行*1列的0矩阵
ZL=zeros(19,1);%定义输出观测值的长度19行*1列的0矩阵
for k=3:21
z(k)=-1.5*z(k-1)-z(k-2)+u(k-1)+3*u(k-2) ;%用理想输出值作为观测值
ZL(k-2)=z(k);
end
%subplot(3,1,1) %画三行一列图形窗口中的第一个图形
%stem(u) %画出输入信号u的图形
%subplot(3,1,2) %画三行一列图形窗口中的第二个图形
%i=1:1:16; %横坐标范围是1到16，步长为1
%plot(i,z) %图形的横坐标是采样时刻i, 纵坐标是输出观测值z, 图形格式为连续曲线
%subplot(3,1,3) %画三行一列图形窗口中的第三个图形
%stem(z),grid %画出输出观测值z的图形，并显示坐标网格
for m=2:20
HL=[-z(m) -z(m-1) u(m) u(m-1)];
for n=1:4;
H((m-1),n)=HL(n);
end
end
c1=H'*H;
c2=inv(c1);
c3=H'*ZL;
c=c2*c3
a1=c(1), a2=c(2), b1=c(3), b2=c(4)
实验结果：
c =
1.5000
1.0000
1.0000
3.0000
a1 =
1.5000
a2 =
1.0000
b1 =
1
b2 =
3.0000
六、实验结果分析
通过实验结果可知所得的实验结果与待辨识的系统传递函数的系数很接近了。
即代码实现了待辨识系统的辨识。
但是在改变系统传递函数的系数时，系数超过一定范围系统将辨识不出来，然而改变M序列的脉冲个数后范围将变化，由此可知待辨识系统的参数选择和M序列脉冲个数有关。
七、实验心得
通过本次实验掌握了M序列的产生机理，以及如何用MATLAB产生M序列。
通过查帮助文档知道了如何使用循环指令以及如何产生一个随机矩阵，和全零矩阵。
写代码是由于对矩阵的知识有些模糊，通过查阅资料强化了矩阵方面的一些知识。
系统辨识最小二乘Matlab仿真
系统辨识和最小二乘参数估计Matlab仿真一、系统辨识在控制系统的分析中，首先要建立系统的数学模型，控制系统的数学模型是定量描述系统或过程内部物理量（或变量）之间关系的数学表达式。
一般来说，建立控制系统数学模型有两种基本方法：（1）机理建模（白箱模型）：即根据系统内在运行机制、物料和能量守恒等物理学、化学规律建立系统的数学模型，一般步骤如下：Step1：根据系统工作原理及其在控制系统中的作用，确定输入和输出；Step2：根据物料和能量守恒等关系列写基本方程式；Step3：消去中间量；Step4：获得系统模型；（2）实验法建模（黑箱模型）：即对于机理尚不清楚或机理过于复杂的系统，可以人为的对其施加某种测试信号，并记录其输出响应，或者记录正常运行时的输入输出数据，然后利用这些输入输出数据确定系统模型结构和参数。
多年来，系统辨识已经发展为一门独立学科分支，通过系统辨识建立一个对象的数学模型，通常包括两方面的工作：一是模型结构的确定（模型的类型、阶次），二是模型参数估计。
根据时间是否连续，参数模型又可以分为连续时间系统模型和离散时间系统参数模型，这两类模型均可采用输入输出模型和状态空间模型描述，离散系统采用差分方程描述，以单输入单输出（SISO）离散系统参数模型为例。
1.确定性模型SISO系统确定性模型可表示为：u(k)和y(k)分别为输入和输出，d为纯延时。
2.随机性模型如果受到随机扰动，则式子可写为：为系统随机扰动，其结构如图：系统辨识的一般步骤如图：从图中可以看出，利用辨识的方法建立系统数学模型，从实验设计到模型获得，需要这些步骤。
二、最小二乘参数估计1.批处理最小二乘考虑以下CAR模型：为白噪声，结构参数na、nb和d已知，参数估计的任务就是根据可测量的输入输出，确定如下参数：仿真实例：式中，为方差为1的白噪声，选用幅值为1的逆M序列作为输入，LS算法进行参数估计，仿真结果如图：仿真程序(Matlab):%批处理最小二乘参数估计（LS）clear all;a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次L=500; %数据长度uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)yk=zeros(na,1); %输出初值x1=1; x2=1; x3=1; x4=0; S=1; %移位寄存器初值、方波初值xi=randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值for k=1:Lphi(k,:)=[-yk;uk(d:d+nb)]'; %此处phi(k,:)为行向量，便于组成phi矩阵y(k)=phi(k,:)*theta+xi(k); %采集输出数据IM=xor(S,x4); %产生逆M序列if IM==0u(k)=-1;elseu(k)=1;endS=not(S); M=xor(x3,x4); %产生M序列%更新数据x4=x3; x3=x2; x2=x1; x1=M;for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endthetae=inv(phi'*phi)*phi'*y' %计算参数估计值thetae2.递推最小二乘在批处理最小二乘法时，由于每次处理的数据量较大，而且常常要求对象参数能够在线实时估计，解决的方法就是将其化成递推算法，其基本思想为：算法介绍：仿真实例:式中，为方差为0.1的白噪声，取初值，选择方差为1的白噪声作为输入信号u(k)，采用RLS算法进行参数估计，仿真结果如图：仿真程序（Matlab）：%递推最小二乘参数估计（RLS）clear all; close all;a=[1 -1.5 0.7]'; b=[1 0.5]'; d=3; %对象参数na=length(a)-1; nb=length(b)-1; %na、nb为A、B阶次L=400; %仿真长度uk=zeros(d+nb,1); %输入初值：uk(i)表示u(k-i)yk=zeros(na,1); %输出初值u=randn(L,1); %输入采用白噪声序列xi=sqrt(0.1)*randn(L,1); %白噪声序列theta=[a(2:na+1);b]; %对象参数真值thetae_1=zeros(na+nb+1,1); %thetae初值P=10^6*eye(na+nb+1);for k=1:Lphi=[-yk;uk(d:d+nb)]; %此处phi为列向量y(k)=phi'*theta+xi(k); %采集输出数据%递推最小二乘法K=P*phi/(1+phi'*P*phi);thetae(:,k)=thetae_1+K*(y(k)-phi'*thetae_1);P=(eye(na+nb+1)-K*phi')*P;%更新数据thetae_1=thetae(:,k);for i=d+nb:-1:2uk(i)=uk(i-1);enduk(1)=u(k);for i=na:-1:2yk(i)=yk(i-1);endyk(1)=y(k);endplot([1:L],thetae); %line([1,L],[theta,theta]); xlabel('k'); ylabel('参数估计a、b');legend('a_1','a_2','b_0','b_1'); axis([0 L -2 2]);。
利用Matlab进行系统辨识的技术方法
利用Matlab进行系统辨识的技术方法在Matlab中进行系统辨识的技术方法主要有参数估计法和非参数估计法两种。
1.参数估计法：参数估计法是通过拟合已知输入和输出数据的数学模型来估计系统的参数。
常用的参数估计方法包括最小二乘法（OLS）、最小二乘法（LSE）、最小二乘法（MLE）和极大似然估计法（MLE）等。
a) 最小二乘法（OLS）：OLS方法通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。
在Matlab中，可以使用lsqcurvefit函数来实现最小二乘法的系统辨识。
b) 最小二乘法（LSE）：LSE方法是通过最小化实际输出与模型预测输出之间的误差平方和来估计系统参数。
在Matlab中，可以使用lsqnonlin函数来实现最小二乘法的系统辨识。
c) 最小二乘法（MLE）：MLE方法是通过最大化似然函数来估计系统参数。
在Matlab中，可以使用mle函数来实现最大似然估计法的系统辨识。
2.非参数估计法：非参数估计法不需要事先指定系统的数学模型，而是直接根据输入和输出数据的统计特性进行系统辨识。
常用的非参数估计方法包括频域方法、时域方法和时频域方法等。
a) 频域方法：频域方法通过对输入和输出数据进行频谱分析来估计系统的频率响应。
常用的频域方法包括傅里叶变换、功率谱密度估计和频率响应函数估计等。
在Matlab中，可以使用fft函数和pwelch函数来实现频域方法的系统辨识。
b) 时域方法：时域方法通过对输入和输出数据进行时间序列分析来估计系统的时域特性。
常用的时域方法包括自相关函数估计和互相关函数估计等。
在Matlab中，可以使用xcorr函数来实现时域方法的系统辨识。
c) 时频域方法：时频域方法结合了频域方法和时域方法的优势，可以同时估计系统的频率响应和时域特性。
常用的时频域方法包括短时傅里叶变换和小波变换等。
在Matlab中，可以使用spectrogram函数和cwt函数来实现时频域方法的系统辨识。
系统辨识最小二乘法—课设报告
课 程 设 计 报 告学 院： 专业名称： 学生姓名： 指导教师： 时 间：课程设计任务书一、设计内容SISO 系统的差分方程为：)()2()1()2()1()(2121k k u b k u b k z a k z a k z υ+-+-=-+-+参数取真值为：[]0.35 0.39 0.715 1.642=T θ，利用MATLAB 的M 语言辨识系统中的未知参数1a 、2a 、1b 、2b 。
二、主要技术要求用参数的真值及差分方程求出)(k z 作为测量值，)(k υ是均值为0，方差为0.1、0.5和0.01的不相关随机序列。
选取一种最小二乘算法利用MATLAB 的M 语言辨识参数。
三、进度要求2周（6月28日-7月11日）完成设计任务，撰写设计报告3000字以上，应包含设计过程、 计算结果、 图表等内容。
具体进度安排：◆ 6月28日，选好题目，查阅系统辨识相关最小二乘法原理的资料。
◆ 6月29日，掌握最小二乘原理，用MATLAB 编程实现最小二乘一次完成算法。
◆ 6月30日，掌握以最小二乘算法为基础的广义最小二乘递推算法。
◆ 7月1日，用MATLAB 编程实现广义最小二乘递推算法。
◆ 7月2日，针对题目要求进行参数辨识，并记录观察相关数据。
◆ 7月3日-7月5日，对参数辨识结果进行分析，找出存在的问题，提出改进方案，验证改进优化结果。
◆ 7月6日-7月7日，撰写课程设计报告。
◆ 7月8日，对课程设计报告进行校对。
◆ 7月9日，打印出报告上交。
学 生王景 指导教师 邢小军1. 设计内容设SISO 系统的差分方程为：)()2()1()2()1()(2121k k u b k u b k z a k z a k z υ+-+-=-+-+ 式（1-1） 参数取真值为：[]0.35 0.39 0.715 1.642=Tθ，利用MATLAB 的M 语言辨识系统中的未知参数1a 、2a 、1b 、2b 。
用matlab实现最小二乘递推算法辨识系统参数
用matlab实现最小二乘递推算法辨识系统参数自动化系统仿真实验室指导教师：学生姓名班级计082-2 班学号撰写时间：全文结束》》-3-1 成绩评定：一．设计目的1、学会用Matlab实现最小二乘法辨识系统参数。
2、进一步熟悉Matlab的界面及基本操作；3、了解并掌握Matlab中一些函数的作用与使用；二．设计要求最小二乘递推算法辨识系统参数，利用matlab编程实现，设初始参数为零。
z(k)-1、5*z(k-1)+0、7*z(k-2)=1*u(k-1)+0、5*u(k-2)+v(k); 选择如下形式的辨识模型：z(k)+a1*z(k-1)+a2*z(k-2)=b1*u(k-1)+b2*u(k-2)+v(k);三．实验程序m=3;N=100;uk=rand(1,N);for i=1:Nuk(i)=uk(i)*(-1)^(i-1);endyk=zeros(1,N); for k=3:N yk(k)=1、5*yk(k-1)-0、7*yk(k-2)+uk(k-1)+0、5*uk(k-2);end%j=100;kn=0;%y=yk(m:j);%psi=[yk(m-1:j-1);yk(m-2:j-2);uk(m-1:j-1);uk(m-2:j-2)];%pn=inv(psi*psi);%theta=(inv(psi*psi)*psi*y);theta=[0 ;0;0;0];pn=10^6*eye(4);for t=3:Nps=([yk(t-1);yk(t-2);uk(t-1);uk(t-2)]);pn=pn-pn*ps*ps*pn*(inv(1+ps*pn*ps));theta=theta+pn*ps*(yk(t)-ps*theta);thet=theta;a1=thet(1);a2=thet(2);b1=thet(3);b2= thet(4);a1t(t)=a1;a2t(t)=a2;b1t(t)=b1;b2t(t)=b2;endt=1:N;plot(t,a 1t(t),t,a2t(t),t,b1t(t),t,b2t(t));text(20,1、47,a1);text(20,-0、67,a2);text(20,0、97,b1);text(20,0、47,b2);四．设计实验结果及分析实验结果图：仿真结果表明，大约递推到第步时，参数辨识的结果基本到稳态状态，即a1=1、5999，b1=1，c1=0、5，d1=-0、7。
Matlab最小二乘系统辨识
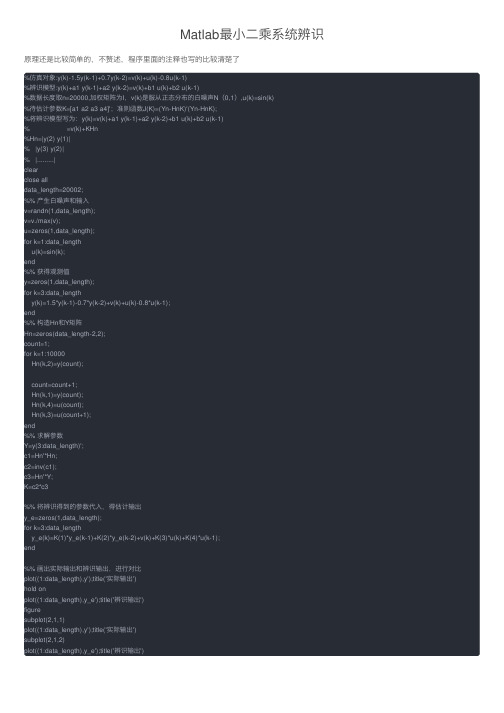
Matlab最⼩⼆乘系统辨识原理还是⽐较简单的，不赘述，程序⾥⾯的注释也写的⽐较清楚了%仿真对象:y(k)-1.5y(k-1)+0.7y(k-2)=v(k)+u(k)-0.8u(k-1)%辨识模型:y(k)+a1 y(k-1)+a2 y(k-2)=v(k)+b1 u(k)+b2 u(k-1)%数据长度取n=20000,加权矩阵为I，v(k)是服从正态分布的⽩噪声N（0,1）,u(k)=sin(k)%待估计参数K=[a1 a2 a3 a4]'；准则函数J(K)=(Yn-HnK)'(Yn-HnK);%将辨识模型写为：y(k)=v(k)+a1 y(k-1)+a2 y(k-2)+b1 u(k)+b2 u(k-1)% =v(k)+KHn%Hn=|y(2) y(1)|% |y(3) y(2)|% |.........|clearclose alldata_length=20002;%% 产⽣⽩噪声和输⼊v=randn(1,data_length);v=v./max(v);u=zeros(1,data_length);for k=1:data_lengthu(k)=sin(k);end%% 获得观测值y=zeros(1,data_length);for k=3:data_lengthy(k)=1.5*y(k-1)-0.7*y(k-2)+v(k)+u(k)-0.8*u(k-1);end%% 构造Hn和Y矩阵Hn=zeros(data_length-2,2);count=1;for k=1:10000Hn(k,2)=y(count);count=count+1;Hn(k,1)=y(count);Hn(k,4)=u(count);Hn(k,3)=u(count+1);end%% 求解参数Y=y(3:data_length)';c1=Hn'*Hn;c2=inv(c1);c3=Hn'*Y;K=c2*c3%% 将辨识得到的参数代⼊，得估计输出y_e=zeros(1,data_length);for k=3:data_lengthy_e(k)=K(1)*y_e(k-1)+K(2)*y_e(k-2)+v(k)+K(3)*u(k)+K(4)*u(k-1);end%% 画出实际输出和辨识输出，进⾏对⽐plot((1:data_length),y');title('实际输出')hold onplot((1:data_length),y_e');title('辨识输出')figuresubplot(2,1,1)plot((1:data_length),y');title('实际输出')subplot(2,1,2)plot((1:data_length),y_e');title('辨识输出')。
机械系统辨识及仿真最小二乘法
作业四宋家亮15030024一、实验题目用MatLAB辨识系统，系统输出分别叠加两种不同类型的噪声，针对每一种情况使用最小二乘整批算法、递推算法和广义最小二乘法实现辨识。
图1 图2二、实验思路及目的对图1、图2分别通过构造的系统给定输入（白噪声和M序列）并叠加噪声（白噪声和有色噪声），测得输出数据并显示，对未知系统定阶并用整批、递推、广义最小二乘算法进行辨识，显示辨识结果；比较三种算法对不同噪声模型的辨识精度（λ取相同的值），显示辨识结果的脉冲响应图像并于理想系统响应对比，对结果给予合理的解释；改变 值(0.01,0.02,0.03等)，比较辨识结果的精度，说明信噪比对各种算法辨识精度的影响。
三、实验过程1、设计界面利用guide编辑器针对所要实现的功能添加控件进行界面初步的设计，设计结果如图1.1所示图1.12、设置控件属性对界面的控件设置属性，形成实验所需要的最终界面，如图2.1所示：图2.1其中系统噪声和输入信号设置成可选择的属性，其value值作为后面函数中的控制条件，这个刚开始走了弯路，直接用string属性做控制条件，结果发现根本实现不了，请教大神后选择value值作为控制条件，因为value值默认为1，当通过下拉选项选择下一个信号时其value值会自动加1。
如图2.2所示。
图2.23、设计guide回调函数（1）噪声参数输入的回调函数本实验设计成噪声参数可输入的程序，所以为达到这一目的，添加了参数输入控件，通过如图3.1所示打开回调函数，添加如下程序，可以将输入的容转变成数字用于后续函数的运算。
global zaoshengxishuzaoshengxishu=get(handles.zaoshengxishu,'String'); zaoshengxishu=str2num(zaoshengxishu);%将输入的字符串λ变成数值图3.1（2）开始辨识按钮的回调函数（主体程序）如图3.2打开开始辨识按钮回调函数，添加主程序（见附录），这样通过点击该按钮可实现本实验的所有功能。
Matlab中的系统辨识和参数标识技巧
Matlab中的系统辨识和参数标识技巧引言：在工程和科学领域中，系统辨识是一项重要的任务。
通过对系统进行辨识和参数标定，我们可以建立数学模型来描述系统的行为。
在Matlab中，有许多工具和技巧可以用来进行系统辨识和参数标定。
本文将介绍一些常用的工具和技巧，以帮助读者更好地理解和应用这些方法。
一、准备工作在进行系统辨识和参数标定之前，我们首先需要准备一些基本的工作。
首先，我们需要收集系统的输入和输出数据。
输入数据通常是对系统施加的激励信号，例如阶跃信号或随机信号。
输出数据是系统对输入信号的响应。
收集足够量的数据对于准确辨识系统非常重要。
其次，我们需要确保数据的质量。
在收集数据时，我们需要注意采样频率和信噪比。
采样频率要足够高，以捕捉系统的快速动态响应；信噪比要足够高，以避免噪声对数据的影响。
如果数据质量不高，将会使得系统辨识和参数标定的结果不准确。
二、线性系统辨识线性系统辨识是系统辨识领域中的一项基本任务。
在Matlab中，可以使用System Identification Toolbox来进行线性系统辨识。
首先，我们可以使用中自相关函数（cross-correlation）来计算输入和输出数据之间的相关性。
这可以通过Matlab中的xcorr函数实现。
相关性分析可以帮助我们了解系统的输入和输出之间的关系，为后续的系统辨识提供参考。
接下来，我们可以使用频域分析方法来对系统进行辨识。
其中一个常用的方法是基于频率响应函数的辨识方法，例如最小二乘法（Least Squares）等。
这些方法可以通过Matlab中的tfest函数来实现。
另外，我们还可以使用时域辨识方法，例如最小均方误差法（Least Mean Squares）等。
时域辨识方法通常通过求解线性方程组来确定系统的参数。
在Matlab中，我们可以使用lsim和inv函数来实现这些方法。
三、非线性系统辨识与线性系统不同，非线性系统的辨识更加复杂。
系统辨识最小二乘参数估计matlab
最小二乘参数估计摘要：最小二乘的一次性完成辨识算法（也称批处理算法），他的特点是直接利用已经获得的所有（一批）观测数据进行运算处理。
这种算法在使用时，占用内存大，离线辨识，观测被辨识对象获得的新数据往往是逐次补充到观测数据集合中去的。
在应用一次完成算法时，如果要求在每次新增观测数据后，接着就估计出系统模型的参数，则需要每次新增数据后要重新求解矩阵方程()Z l T l l Tl ΦΦΦ-∧=1θ。
最小二乘辩识方法在系统辩识领域中先应用上已相当普及，方法上相当完善，可以有效的用于系统的状态估计，参数估计以及自适应控制及其他方面。
关键词：最小二乘（Least-squares ），系统辨识（System Identification ） 目录：1.目的 (1)2.设备 (1)3引言 (1)3.1 课题背景 (1)4数学模型的结构辨识 (2)5 程序 (3)5.1 M 序列子函数 ................................................................................... 错误!未定义书签。
5.2主程序................................................................................................. 错误!未定义书签。
6实验结果： ................................................................................................................................... 3 7参考文献： ................................................................................................... 错误!未定义书签。
如何在MATLAB中进行系统辨识
如何在MATLAB中进行系统辨识引言：在系统辨识中，我们通常会使用数据来推导出系统的数学模型，进而对系统进行建模和预测。
MATLAB作为一种强大的数值计算和分析工具，提供了丰富的系统辨识工具包，能够帮助我们实现这一目标。
本文将介绍如何使用MATLAB进行系统辨识，包括数据预处理、模型选择、参数估计等内容。
一、数据预处理系统辨识的第一步是数据预处理，即对采集到的数据进行处理和清洗，以提高后续建模和分析的准确性。
常见的数据预处理技术包括去除异常值、平滑数据、采样率调整等。
在MATLAB中，我们可以使用一系列内置的函数和工具箱来完成这些任务。
例如，使用"findoutliers"函数可以检测并去除异常值，使用"smoothdata"函数可以平滑数据，使用"resample"函数可以进行采样率调整等。
二、模型选择在系统辨识中，我们需要选择适合的数学模型来描述系统的行为。
常用的系统模型包括线性模型、非线性模型、时变模型等。
在MATLAB中，我们可以使用"sysident"工具箱中的函数来进行模型选择。
其中最常用的方法是ARX模型和ARMAX模型。
ARX模型适用于仅包含输入和输出的线性系统辨识，而ARMAX 模型适用于包含自回归项和移动平均项的线性系统辨识。
根据实际情况和需求，选择适合的模型进行建模。
三、参数估计参数估计是系统辨识中的关键步骤，其目的是通过观测数据来估计系统模型中的参数。
在MATLAB中，我们可以使用"arx"和"armax"函数进行参数估计。
这些函数将原始观测数据作为输入，并根据选择的模型类型进行系统参数的估计。
具体的参数估计方法包括最小二乘法、极大似然法、递推最小二乘法等。
根据系统模型和实际需求，选择合适的参数估计方法进行系统参数的估计。
四、模型验证模型验证是系统辨识中的重要环节，其目的是验证建立的系统模型是否能够准确地描述观测数据。
基于MATLAB的最小二乘法参数辨识与仿真_石贤良
展开后可得 z ( k ) = - a1 z ( k - 1 ) - a2 z ( k - 2 ) - . . . - ana z ( k - na ) + b 1u ( k - 1 ) + b2 u ( k - 2 ) + . . . + bnb z ( k - nb ) 模型 ( 1) 可化成最小二乘格式: S z ( k ) = h ( k ) H+ n ( k ) ( 2) S 记 H= [ a 1, a2, . . . a na b 1, b1, . . . , bnb ] 为待估计 的参数。 h( k ) = [ - z ( k - 1 ), . . . , - z ( k - na ), u ( k - 1 ), . . . , u( k - nb ) ] , 对于 k= 1 , 2 , . . . . L ( L 为数 据长度 ) , 方程 ( 2) 构成一个线性方程组, 写成 zL ( k ) = H L ( k ) H+ nL ( k ) z ( 1) ZL = h ( 1)
# 46#
微
处
理
机
2005 年
快速准确地估计出系统参数, 而且在对模型结构或 外部噪声干扰发生较大变化的情况下 , 也能获得较 好的辨识结果。在参数辨识仿真过程中 , 可根据实 验要求, 使用 M 语言编程不同的算法, 方便简捷。
表 1 最小二乘递推算法的辨识结果 ( N iose pow er= 0. 1) 参数 真值 估计值 图 3 被封装的最小二乘递推算法函数 a1 1. 5 1. 5004 a2 1 1. 003 a3 b1 b2 0 . 5 - 1. 5 - 0. 5 0. 5002 - 1. 498 - 0. 5001